Transmit Energy Efficiency of Two Cognitive Radar Platforms for Target Identification
Abstract
:1. Introduction
2. Procedure and Metric to Compare MAP-CRr and SHT-CRr
3. Brief Review of the Two Types of CRr
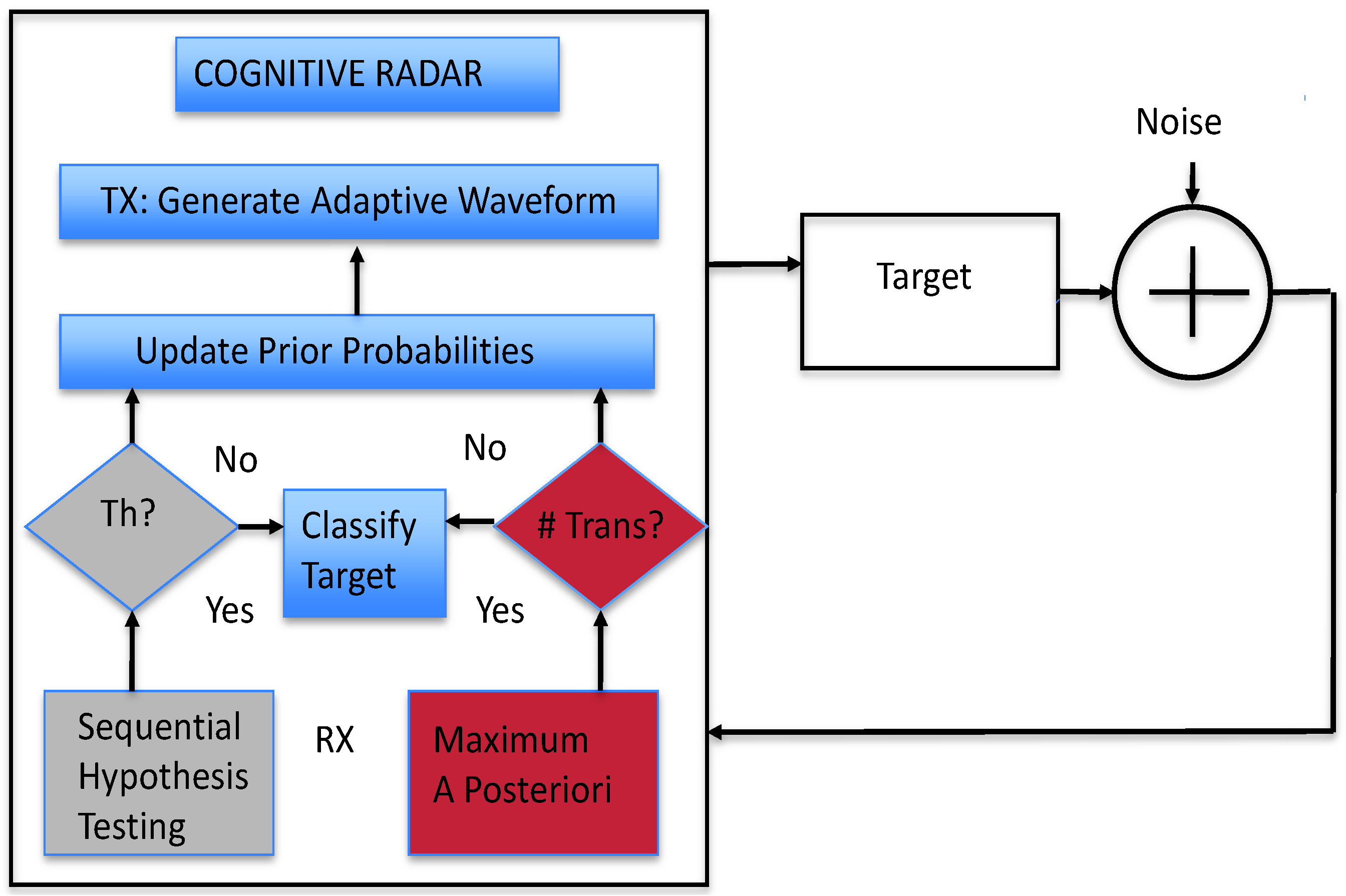
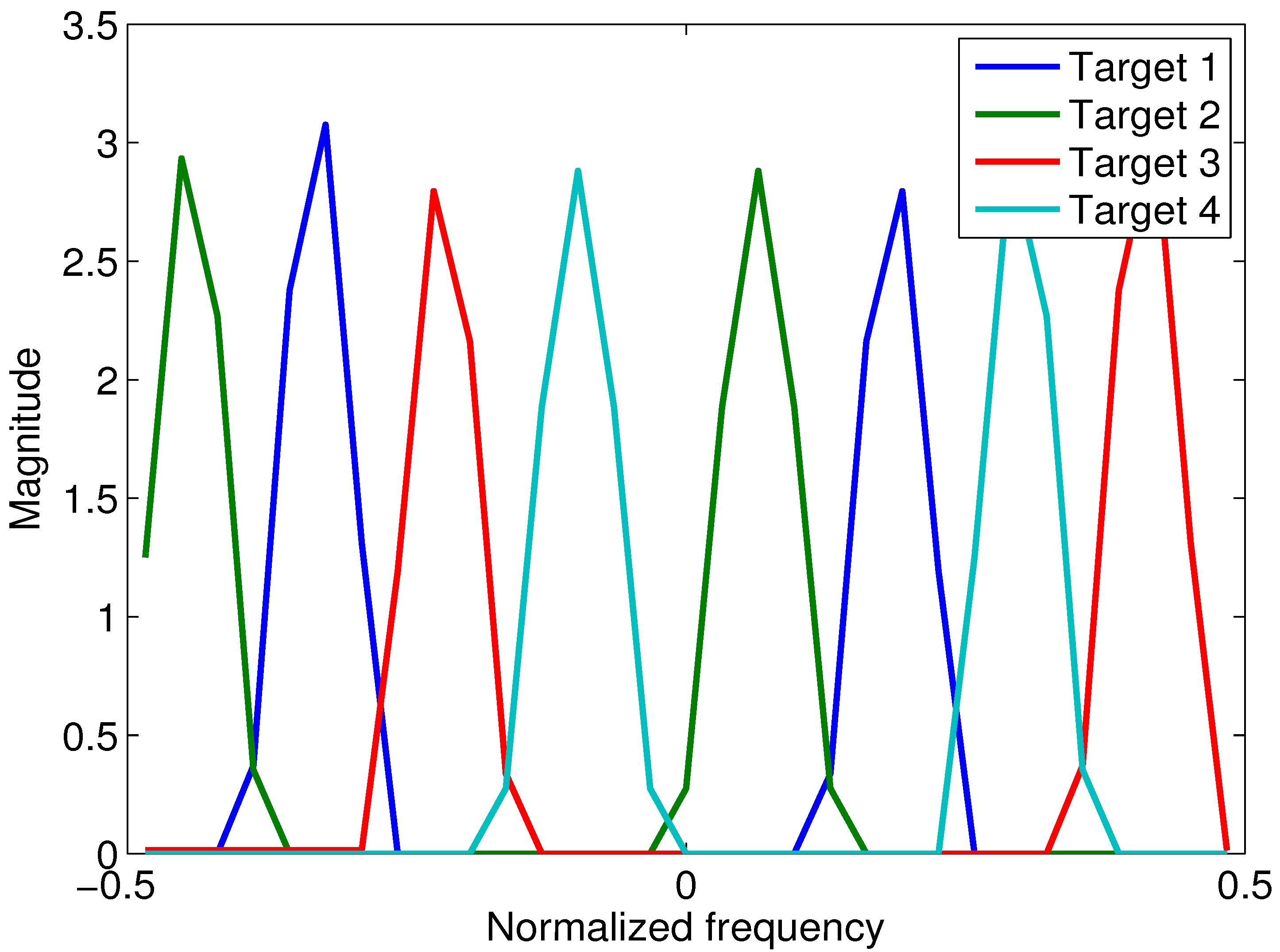
3.1. Matched Waveform to a Target Response
3.2. Multiple Hypothesis Testing
3.3. Transmit Adaptive Waveform
3.4. Probability Updating
3.5. MAP-CRr and SHT-CRr
4. and ANI

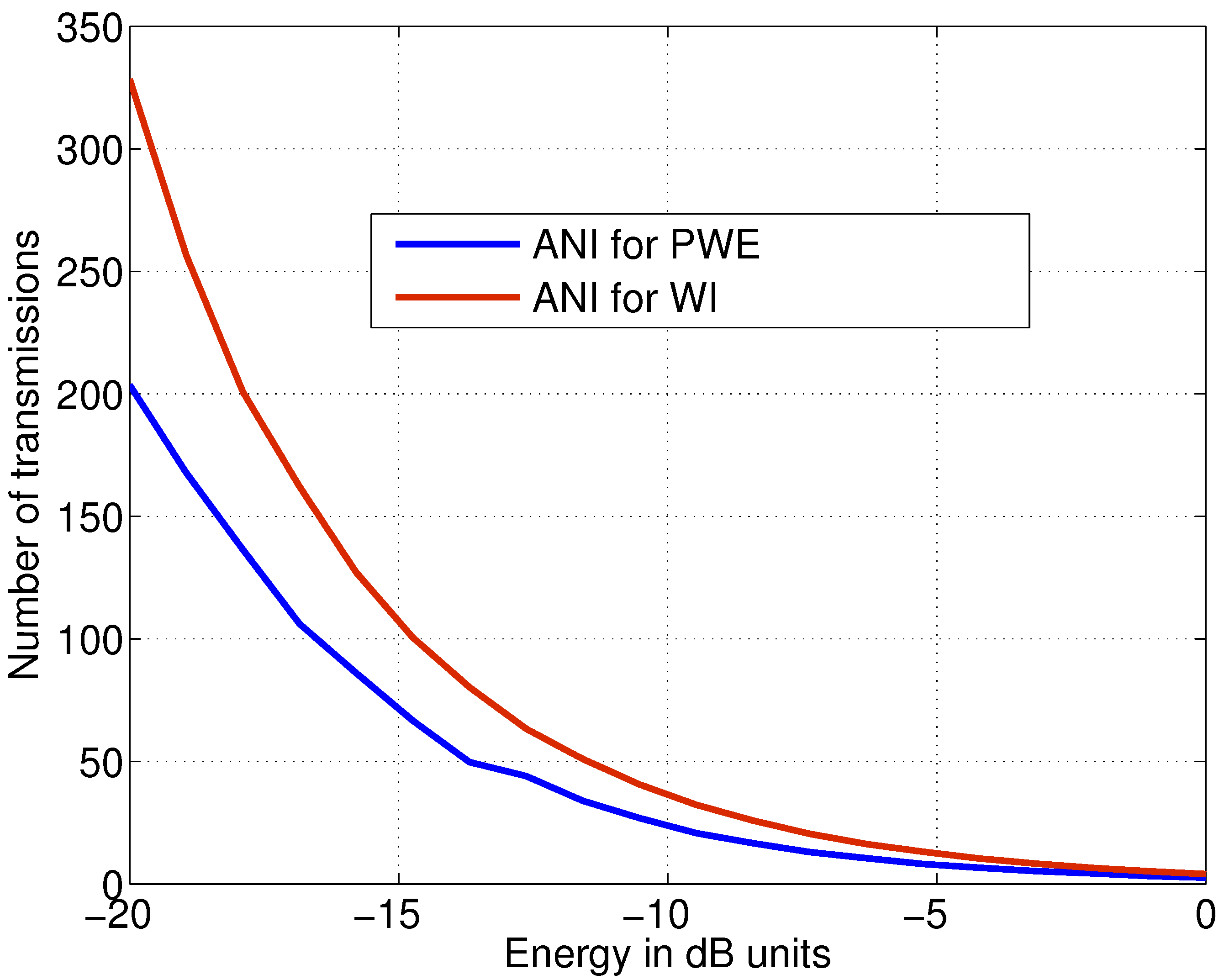
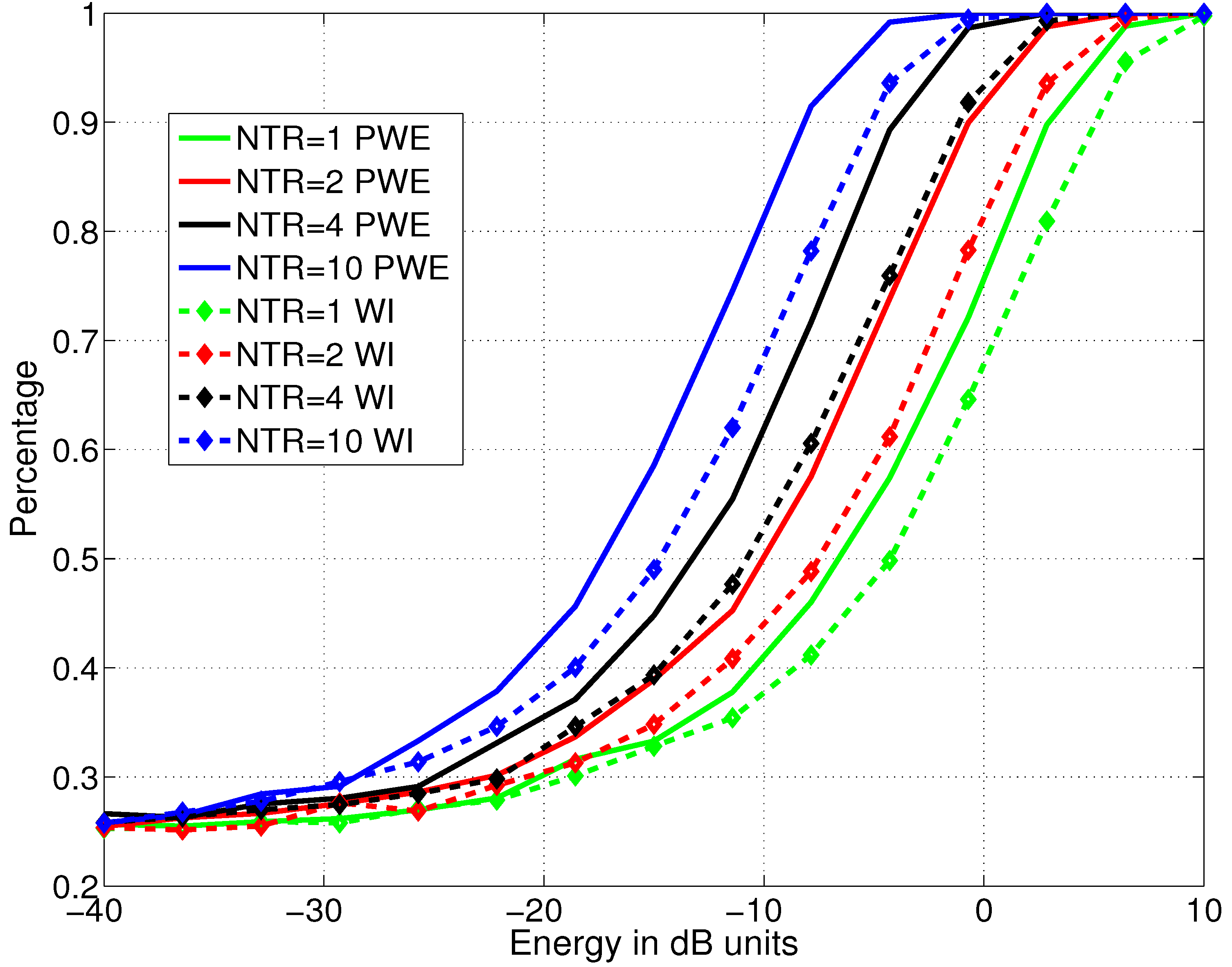
5. Comparing Total Transmit Energy
5.1. Comparison with the PWE Waveform
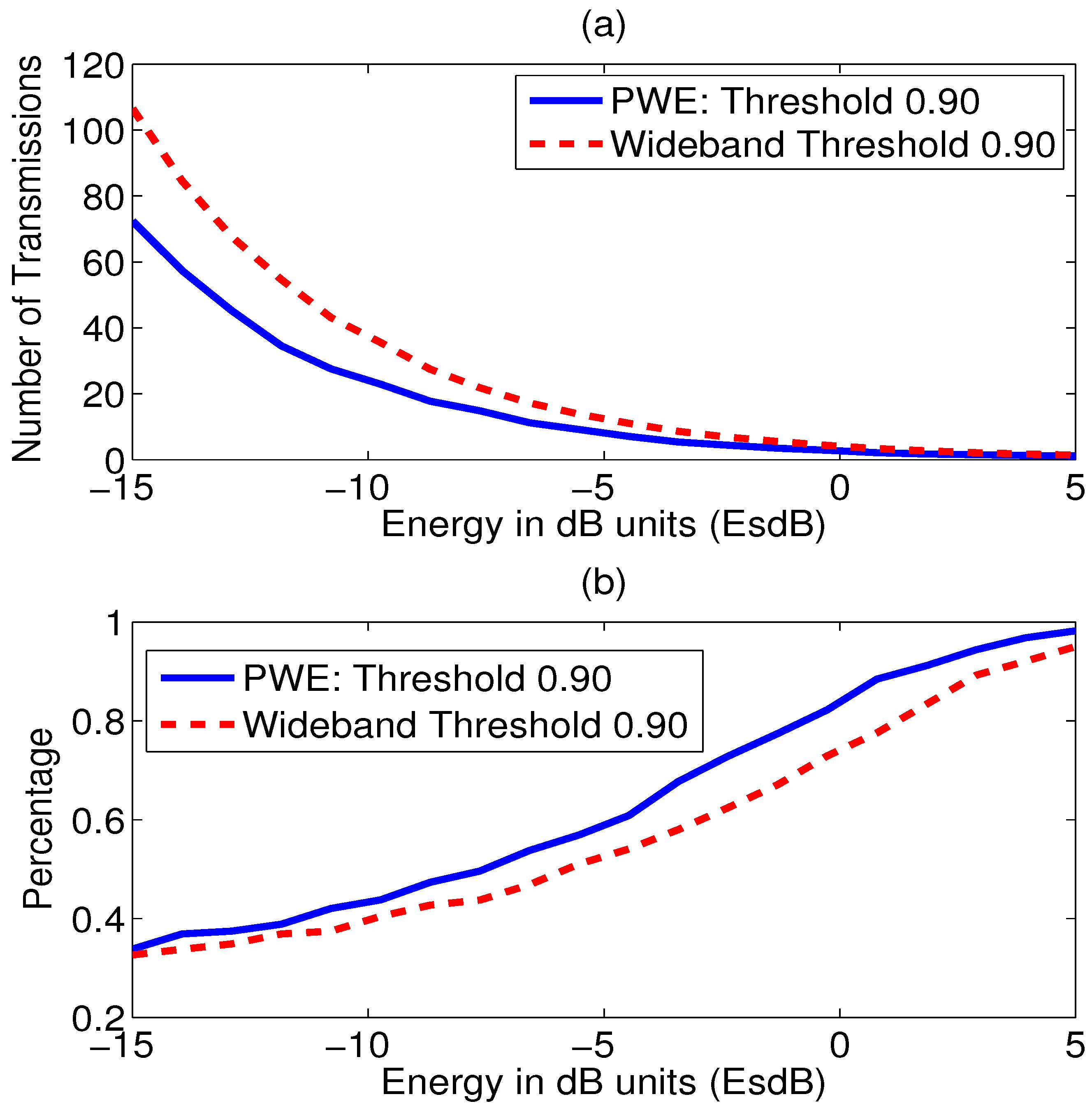
5.2. Comparison with the Wideband Waveform
6. Conclusions
Author Contributions
Conflicts of Interest
References
- US Department of the Air Force. Air Navigation; Department of the Air Force: Washington, DC, USA, 2001. [Google Scholar]
- Bowditch, N. The American Practical Navigator; National Imagery and Mapping Agency: Bethesda, MD, USA, 2002. [Google Scholar]
- Crippen, D. The air traffic control radar beacon system. IRE Trans. Aeronaut. Navig. Electron. 1957, ANE-4, 6–15. [Google Scholar] [CrossRef]
- Federal Aviation Administration. Air Traffic 101. Available online: http://www.faa.gov (accessed on 24 March 2015).
- Stimson, G. Introduction to Airborne Radar; SciTech Publishing: Mendham, NJ, USA, 1998. [Google Scholar]
- Kovaly, J.J. Synthetic Aperture Radar; Artech House: Norwood, MA, USA, 1978. [Google Scholar]
- Currie, A. Synthetic aperture radar. IET Electron. Commun. Eng. J. 1957, 3, 159–170. [Google Scholar] [CrossRef]
- Essen, H.; Makaruschka, R. Remote sensing of land and water with an airborne 94 GHz synthetic aperture radar. In Proceedings of the 25th European Microwave Conference, Bologna, Italy, 4 September 1995; pp. 567–570.
- Ulaby, F. Microwave Radar and Radiometric Remote Sensing; University of Michigan Press: Ann Arbor, MI, USA, 2013. [Google Scholar]
- Fuhrmann, D. Active-testing surveillance systems, or, playing twenty questions with a radar. In Proceedings of the 11th Annual Adaptive Sensor and Array Processing (ASAP) Workshop, Lexington, MA, USA, 11–13 March 2003.
- Haykin, S. Cognitive radar: A way of the future. IEEE Signal Process. Mag. 2006, 23, 30–40. [Google Scholar] [CrossRef]
- Guerci, J.R. Cognitive Radar: The Knowledge-Aided Fully Adaptive Approach; Artech House: Norwood, MA, USA, 2010. [Google Scholar]
- Aubry, A.; DeMaio, A.; Farina, A.; Wicks, M. Knowledge-aided (potentially cognitive) transmit signal and receive filter design in signal-dependent clutter. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 93–117. [Google Scholar] [CrossRef]
- Goodman, N.; Venkata, P.; Neifeld, M. Adaptive waveform design and sequential hypothesis testing for target recognition with active sensors. IEEE J. Sel. Top. Sig. Proc. Mag. 2007, 1, 105–113. [Google Scholar] [CrossRef]
- Hyeong-Bae, J.; Goodman, N. Adaptive waveforms for target class discrimination. In Proceedings of the 2007 Waveform Diversity and Design Conference, Pisa, Italy, 4–8 June 2007; pp. 395–399.
- Romero, R.; Goodman, N. Waveform design in signal-dependent interference and application to target recognition with multiple transmissions. IET Radar Sonar Navig. 2009, 3, 328–340. [Google Scholar] [CrossRef]
- Romero, R.; Bae, J.; Goodman, N. Theory and application of SNR and mutual information matched illumination waveforms. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 912–926. [Google Scholar] [CrossRef]
- Romero, R.; Goodman, N. Improved waveform design for target recognition with multiple transmissions. In Proceedings of the IEEE International Waveform Diversity and Design Conference, Orlando, FL, USA, 8–13 February 2009.
- Bell, M. Information theory and radar waveform design. IEEE Trans. Inform. Theory 1993, 39, 1578–1597. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romero, R.; Mourtzakis, E. Transmit Energy Efficiency of Two Cognitive Radar Platforms for Target Identification. Aerospace 2015, 2, 376-391. https://doi.org/10.3390/aerospace2030376
Romero R, Mourtzakis E. Transmit Energy Efficiency of Two Cognitive Radar Platforms for Target Identification. Aerospace. 2015; 2(3):376-391. https://doi.org/10.3390/aerospace2030376
Chicago/Turabian StyleRomero, Ric, and Emmanouil Mourtzakis. 2015. "Transmit Energy Efficiency of Two Cognitive Radar Platforms for Target Identification" Aerospace 2, no. 3: 376-391. https://doi.org/10.3390/aerospace2030376
APA StyleRomero, R., & Mourtzakis, E. (2015). Transmit Energy Efficiency of Two Cognitive Radar Platforms for Target Identification. Aerospace, 2(3), 376-391. https://doi.org/10.3390/aerospace2030376





