Multi-Aircraft Coordinated Target Assignment Based on Chaotic Mutation Adaptive Salp Swarm Algorithm
Abstract
1. Introduction
- When a traditional target assignment algorithm is used to establish the optimized objective function, the operational situational advantage of a single aircraft is numerically superposed with the target threat, and the maximum superimposed advantage of the formation is used as the objective function of the target assignment optimization algorithm. This model does not fully consider the coordination relationship between aircraft in the formation and treats these aircraft as independent individuals; therefore, there are certain limitations when solving the problem of multi-aircraft coordination.
- When a heuristic intelligent evolutionary algorithm is used to optimize the multi-aircraft coordinated target assignment problem, often only improvement in one aspect of the algorithm’s performance is considered, which makes it difficult to select the algorithm’s search and development capabilities for optimization. Therefore, improving and balancing the search and development capabilities of an algorithm is a key challenge in improving its performance.
- Multi-aircraft coordinated target assignment is essentially a constrained optimization problem; therefore, there are a large number of constraints. To obtain a target assignment scheme that satisfies these constraints, it is necessary to effectively solve the problem of multiple constraints.
2. Target Threat Assessment Model
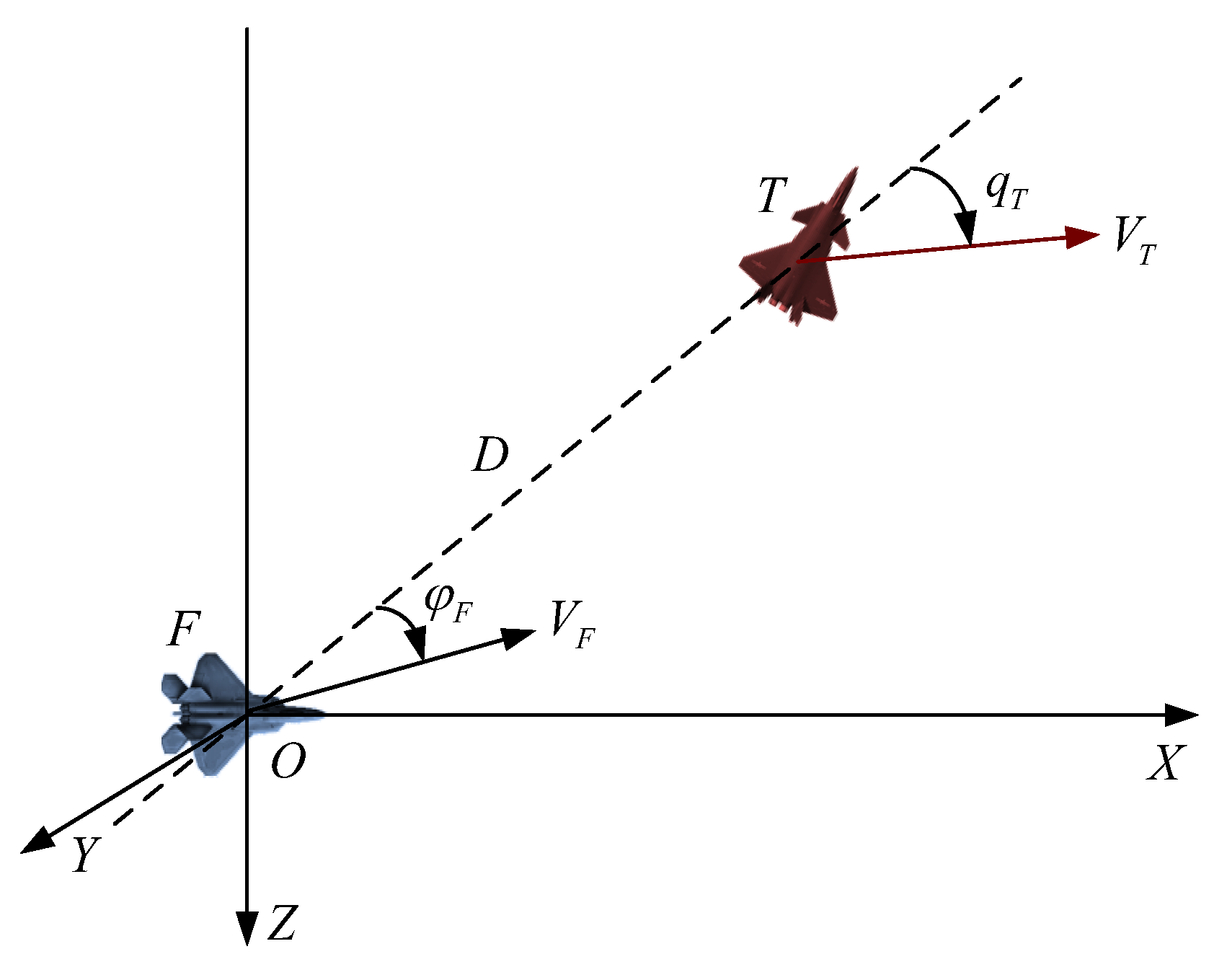
2.1. Single-Target Threat Assessment
2.2. Multi-Aircraft Coordinated Comprehensive Situational Advantage Assessment Model
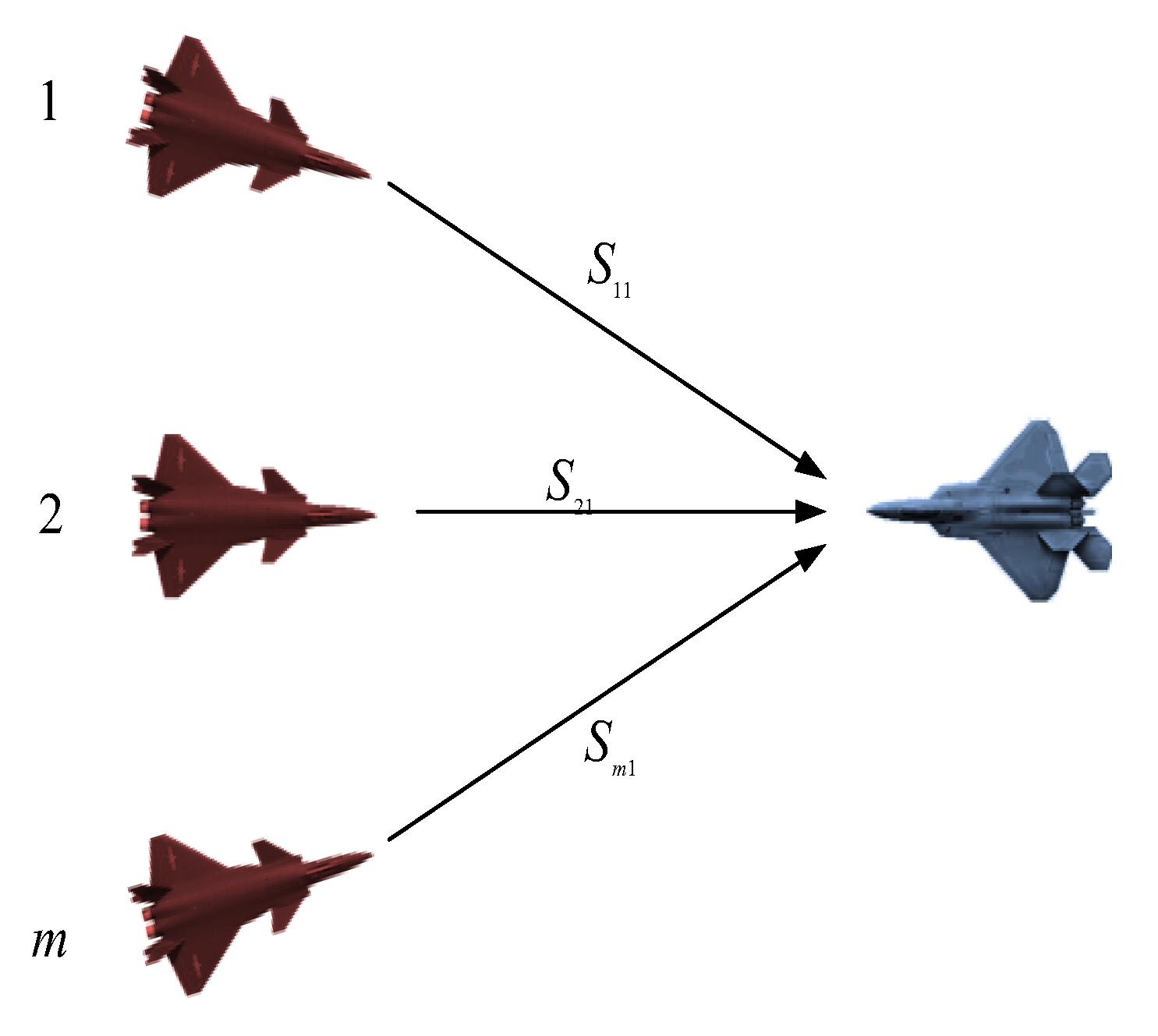
2.2.1. The Situation of Many to One
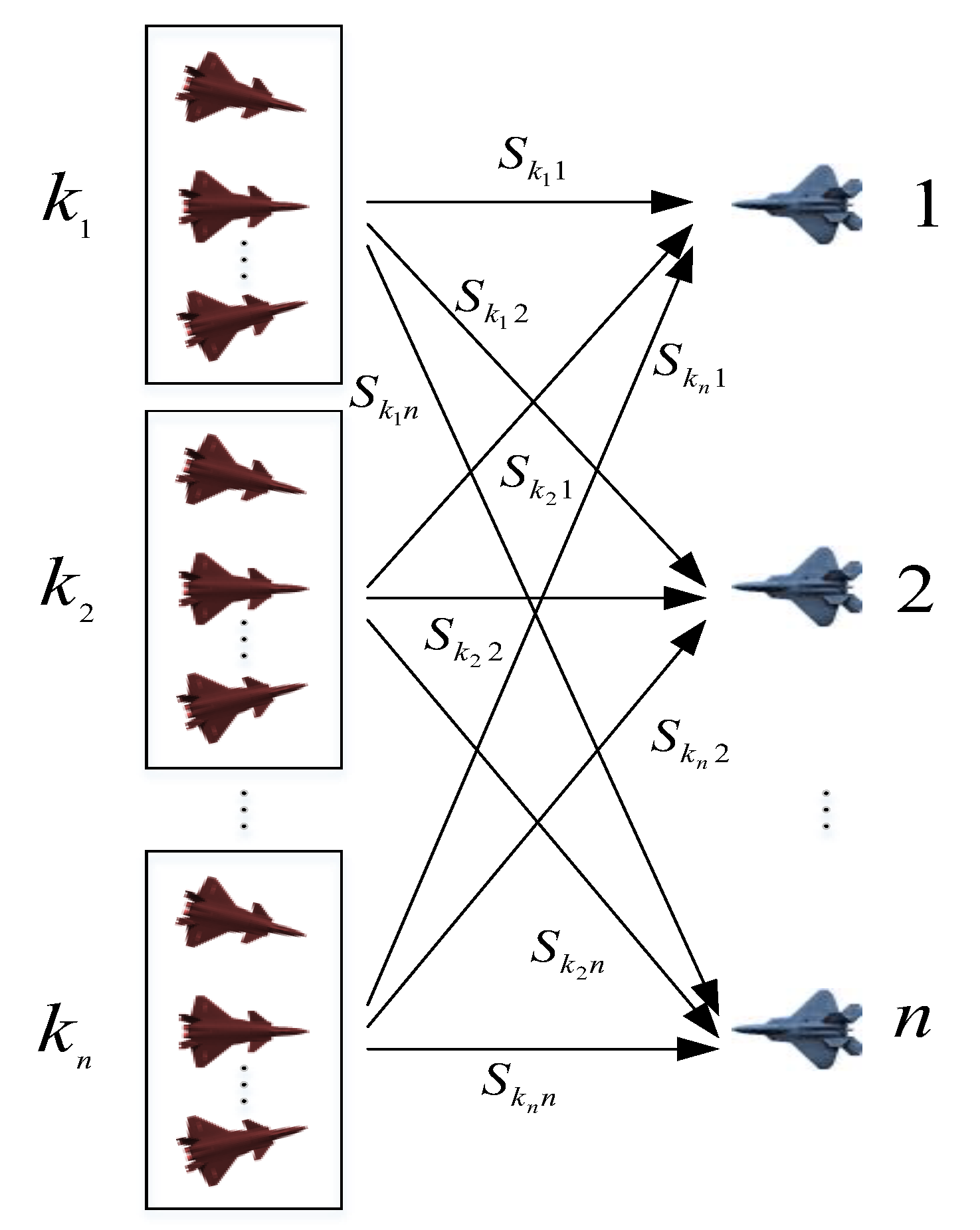
2.2.2. The Situation of Many to Many
2.3. Multi-Aircraft Coordinated Target Assignment Model
2.3.1. Target Assignment Model
2.3.2. Unified Modeling for Multi-Aircraft Coordinated Target Assignment Mode
2.3.3. Constraint Processing
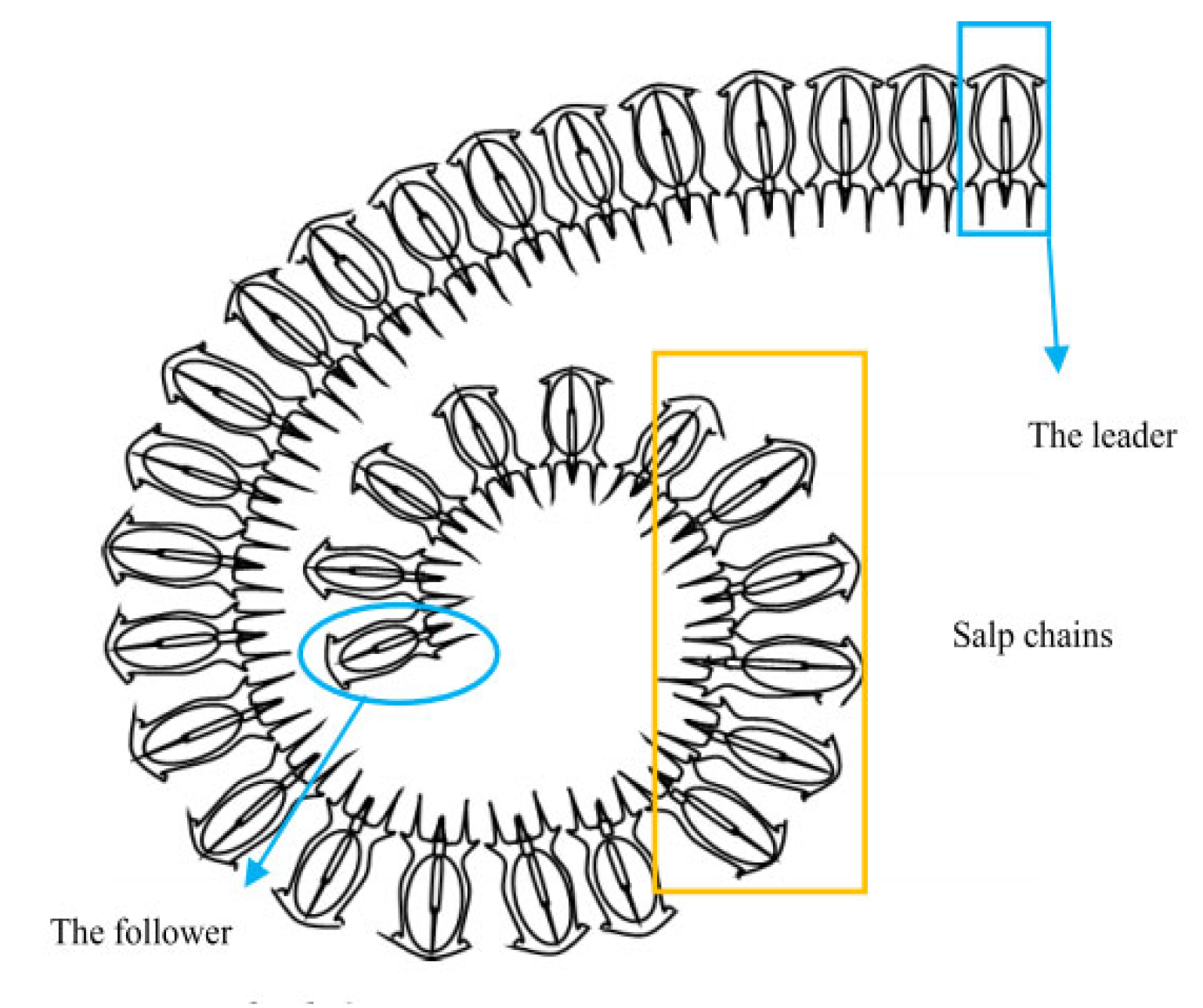
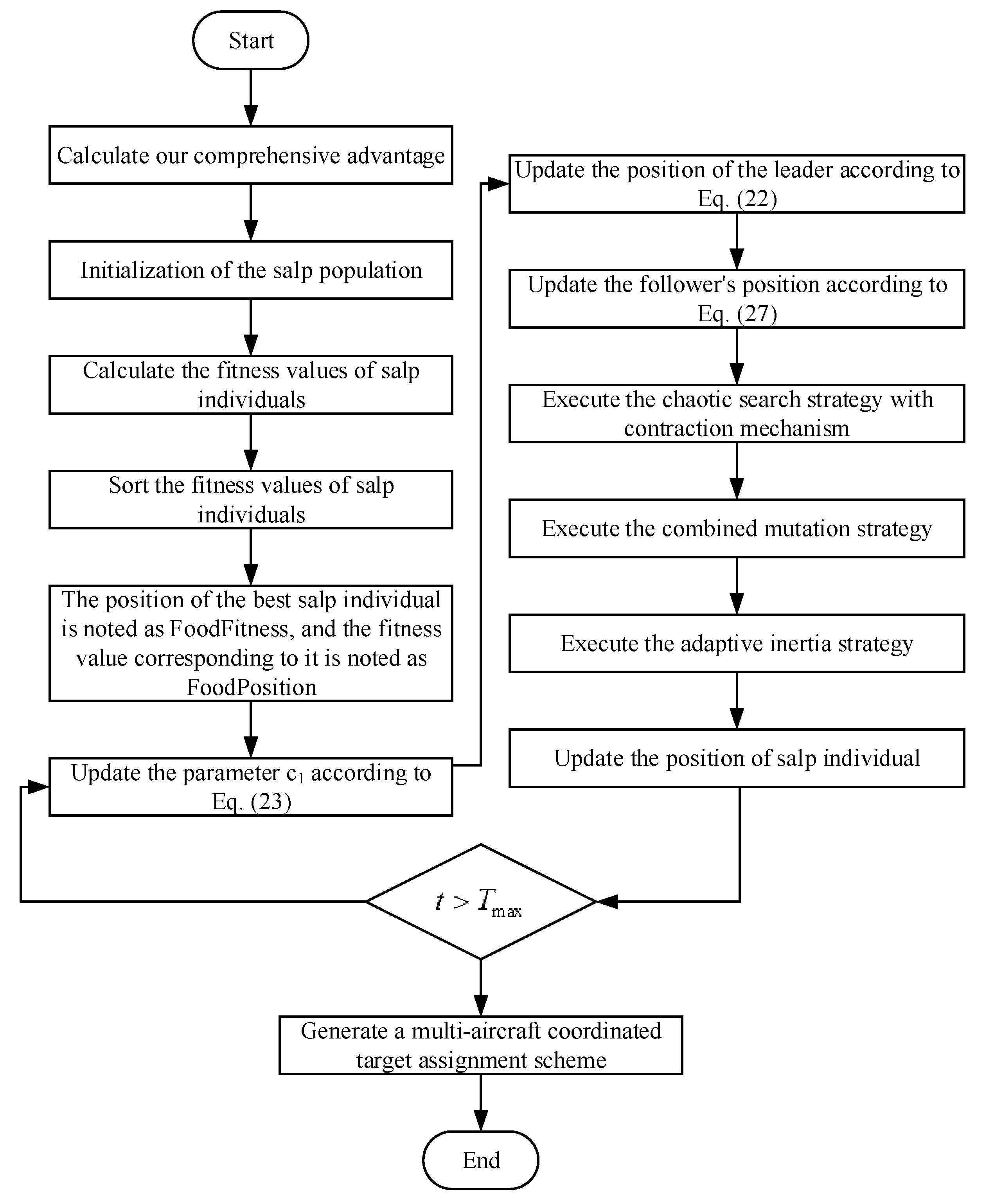
3. Salp Swarm Algorithm
| Algorithm 1: Salp swarm algorithm |
| 1. Initialize the randomly generated population of the salp swarm . 2. Calculate the fitness values of each salp. 3. 4. while stopping criteria not reached 5. Update by (23) 6. for each salp 7. if 8. Update the position of the leader salp by (22) 9. else 10. Update the position of the follower salp by (22) 11. end if 12. end for 13. Calculate the fitness values of every salp. 14. Update if there is a better solution. 15. end while 16. return the best solution and its fitness value. |
4. Adaptive Salp Swarm Algorithm Based on Chaotic Mutation (CMASSA)
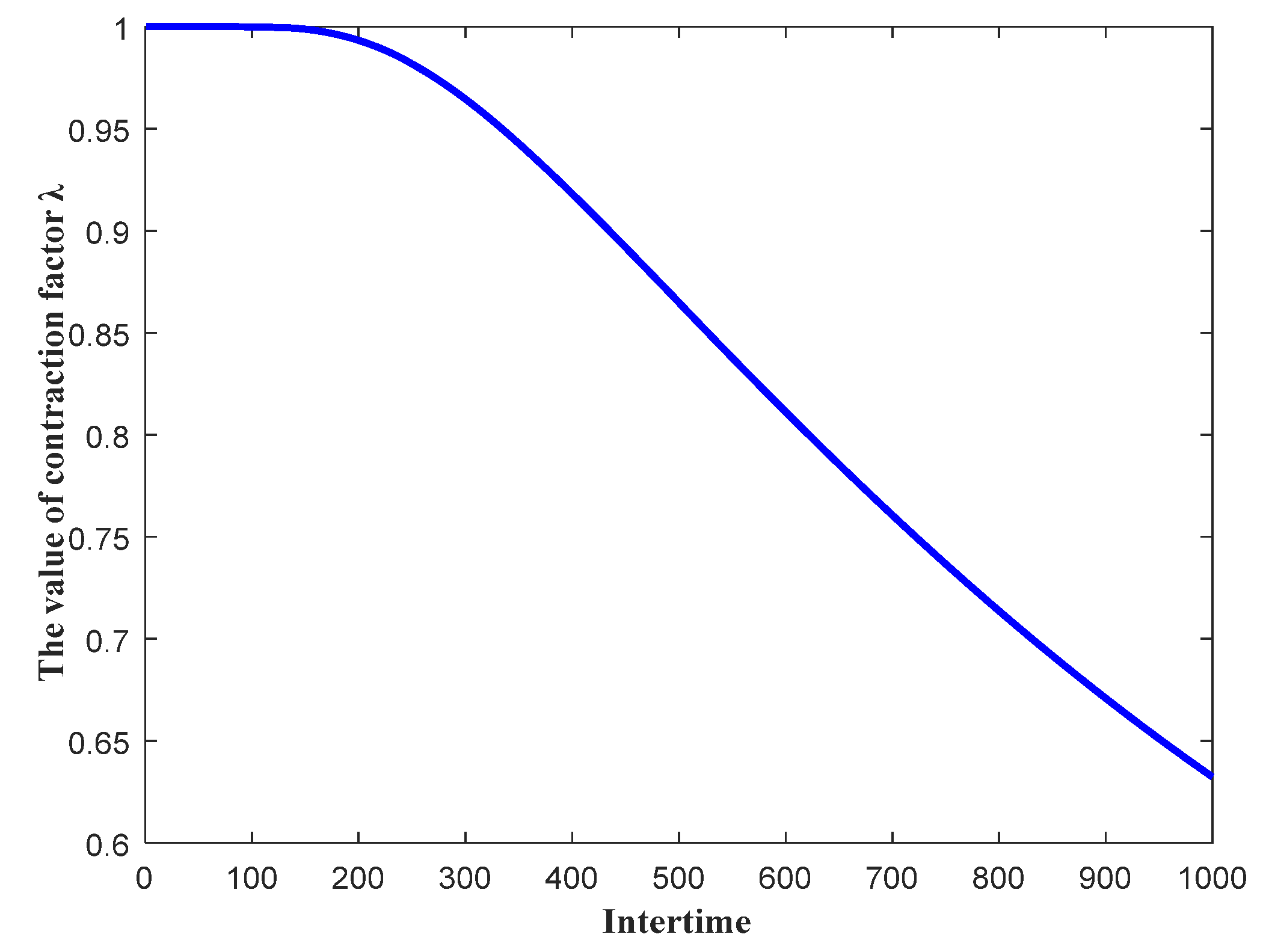
4.1. Chaotic Search Strategy with Contraction Mechanism
4.2. Combined Mutation Strategy
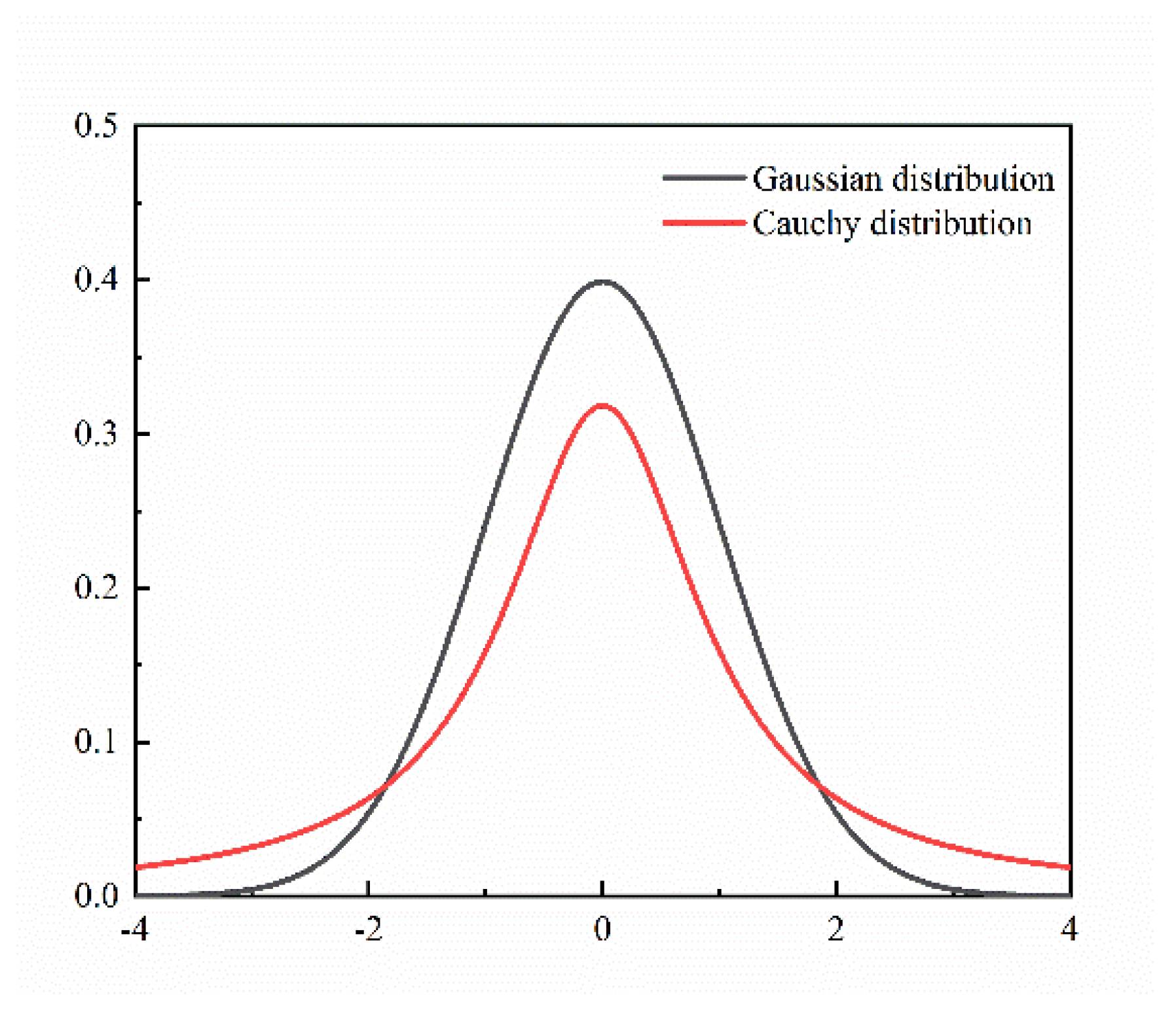
4.2.1. Gaussian Mutation
4.2.2. Cauchy Mutation
4.2.3. Combined Mutation
| Algorithm 2: Combined mutation |
| for (each individual ) Step 1 is described as follows: /*Execute the cycle times*/ for /*After the current salp individual , execute combined mutation of the positions of all salp individuals*/ /*Execute Gaussian mutation of the salp individuals by using Equation (33) to obtain */ /*Calculate the function fitness corresponding to the salp */ /*Execute Cauchy mutation of the salp individuals by using Equation (37) to obtain */ /*Calculate the function fitness corresponding to the salp */ /*After the current salp individual , record the positions of all salp individuals */ /*Calculate the function fitness corresponding to the salp */ end end Step 2 is described as follows: /*Combine the aforesaid three different individuals and fitness degrees described and record them as and , respectively*/ /*Sort the function fitness degrees in ascending order*/ /*Store in */ /*Based on the function fitness degrees sorted in ascending order, reorder */ for end /*From , select the optimal individual and find the corresponding fitness value*/ /*Use to update the position of the salp individuals after the current individual */ for end end |
4.3. Adaptive Inertia Weight Strategy
4.4. CMASSA Steps
| Algorithm 3: CMASSA pseudocode |
| Initialize the positions of all individuals in the salp population. Calculate the initial function fitness of each salp individual. The fitness values of all individuals in the salp population are sorted, the position of the best individual is recorded as , and the function fitness value corresponding to it is recorded as While for if then Update the position of the leader according to Equation (22) else Update the position of the follower according to Equation (27) end Use Equation (30) to execute the chaotic search strategy with the contraction mechanism to generate candidate individual position ; calculate the fitness of the candidate position , and record it as if then Update the optimal position and its fitness value end Execute the combined mutation step in Algorithm 2 end Output the optimal position and its fitness value |
4.5. Complexity of the CMASSA
5. Multi-Aircraft Coordinated Target Assignment Model Based on CMASSA
6. Simulation Analysis
6.1. Validate the Effectiveness of the Target Assignment Model Based on the Modified Salp Swarm Algorithm
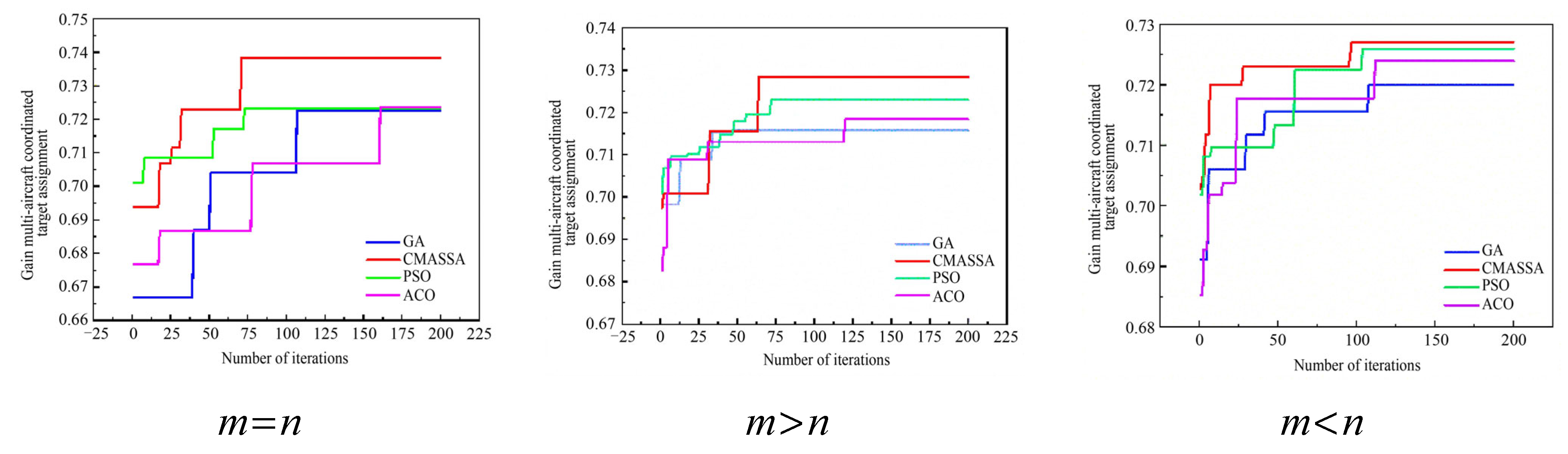
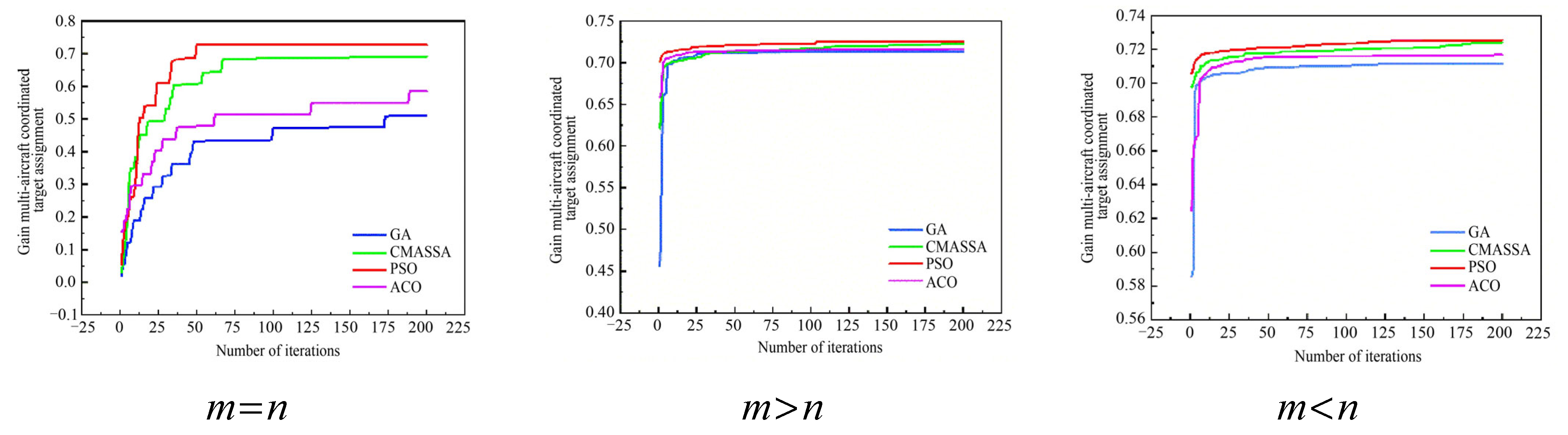
6.1.1. Static Target Assignment in Different Modes
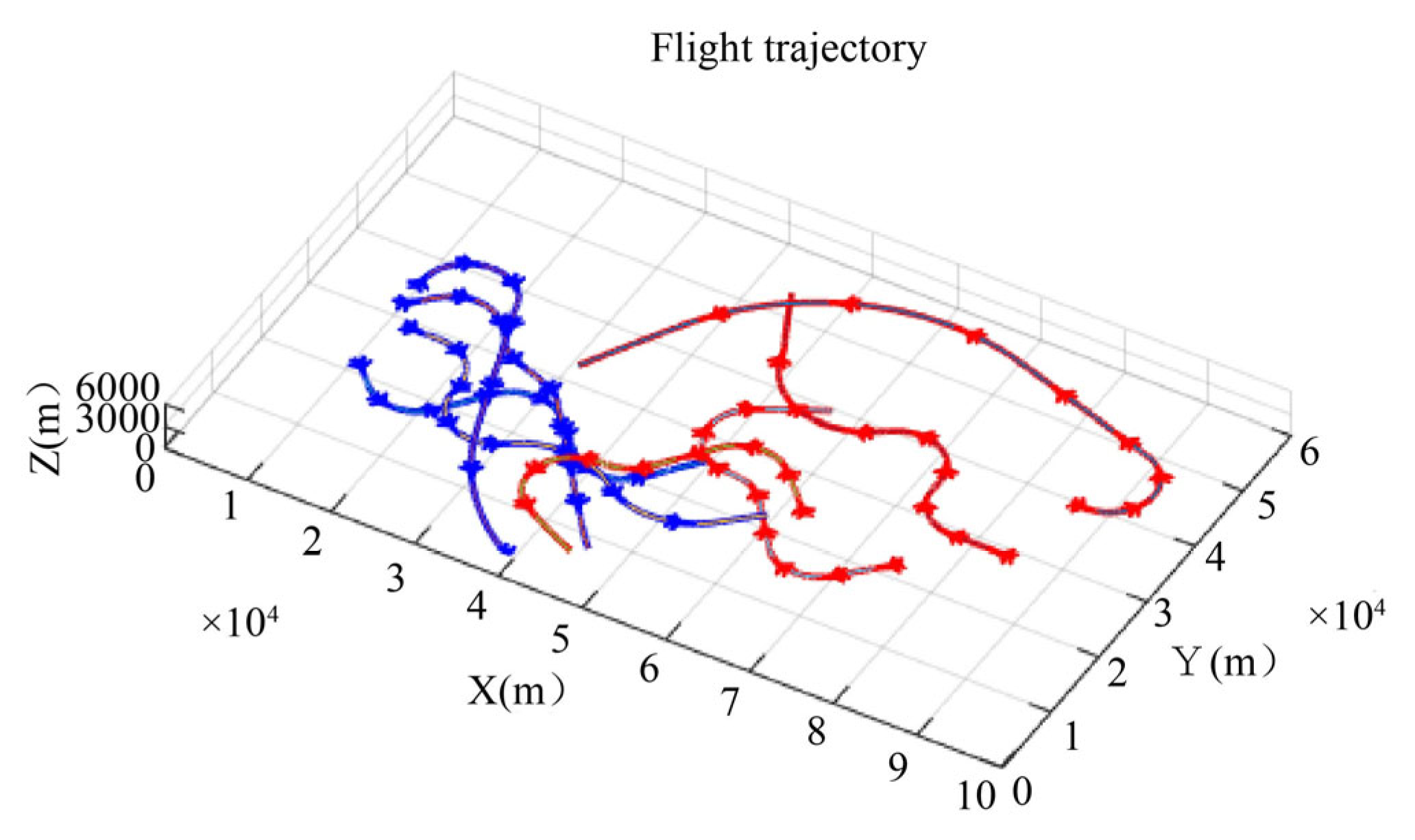
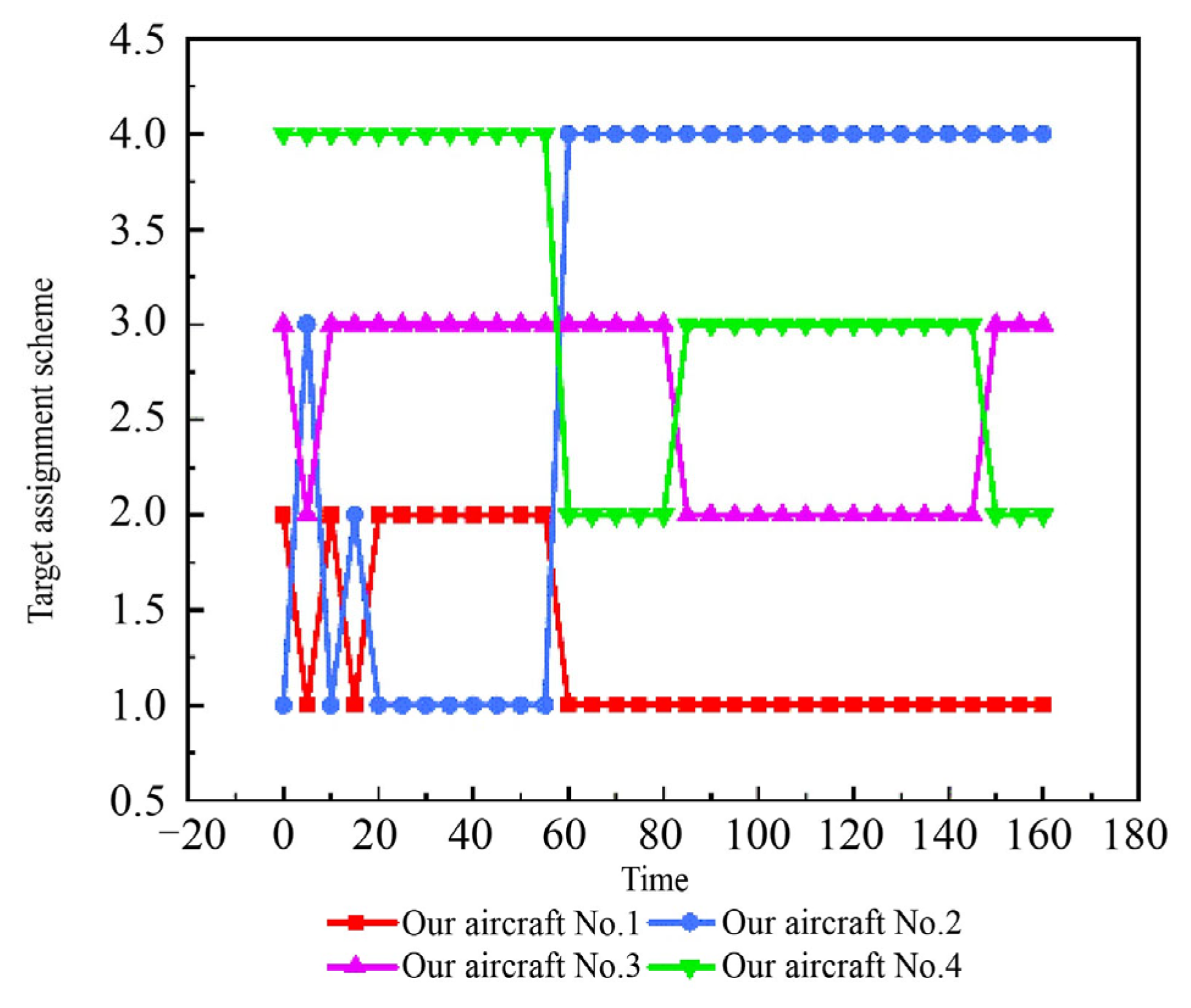
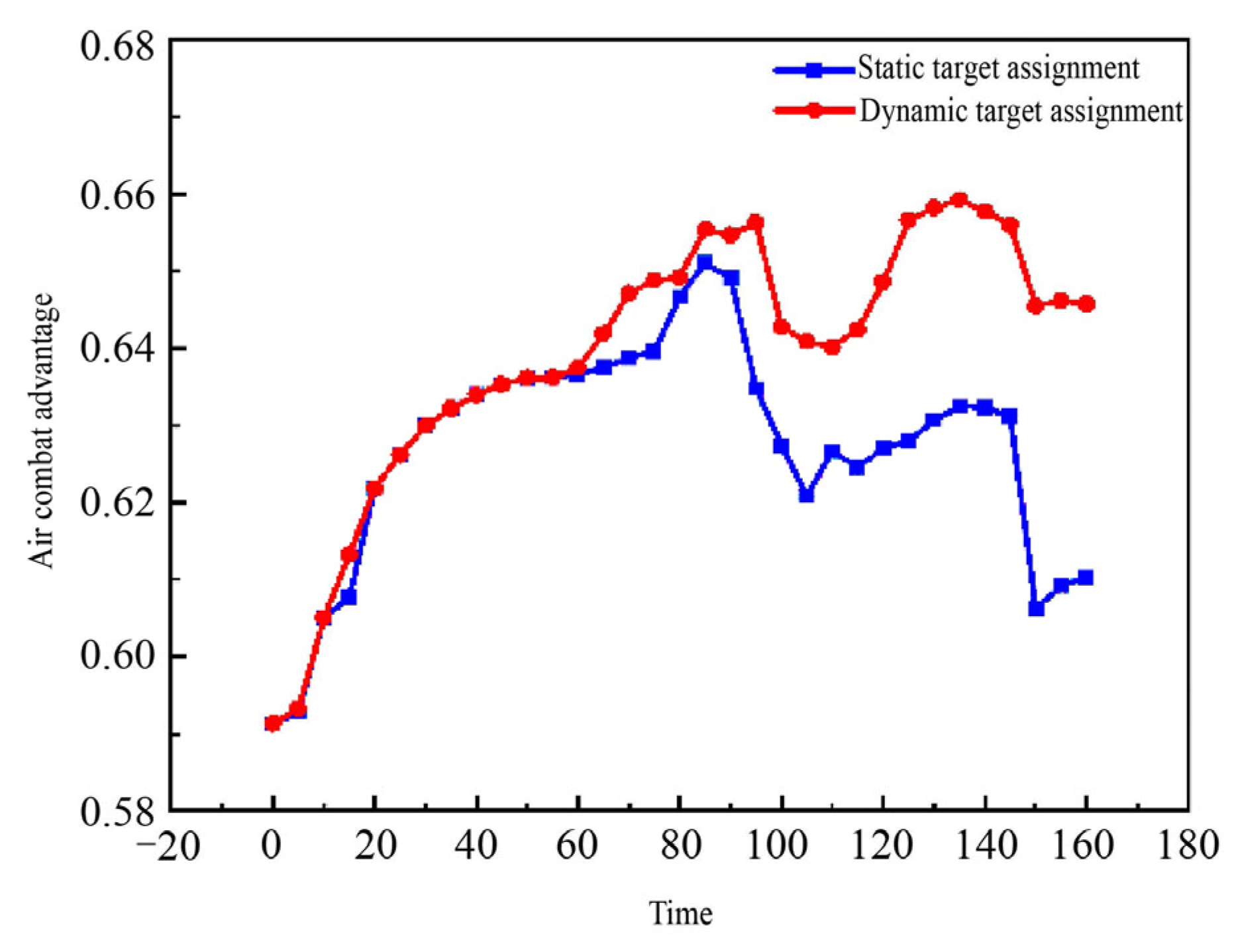
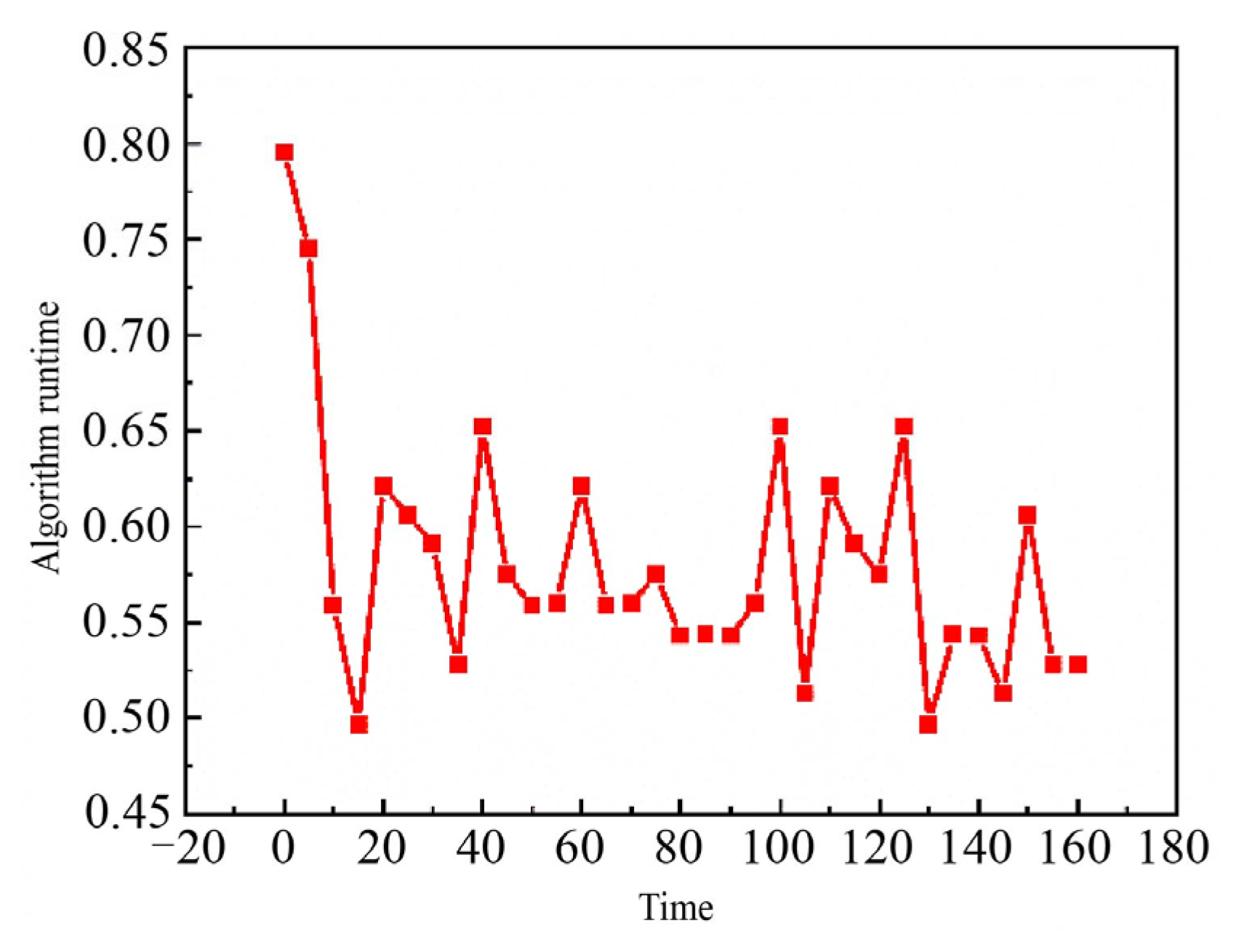
6.1.2. Dynamic Target Assignment in Different Modes
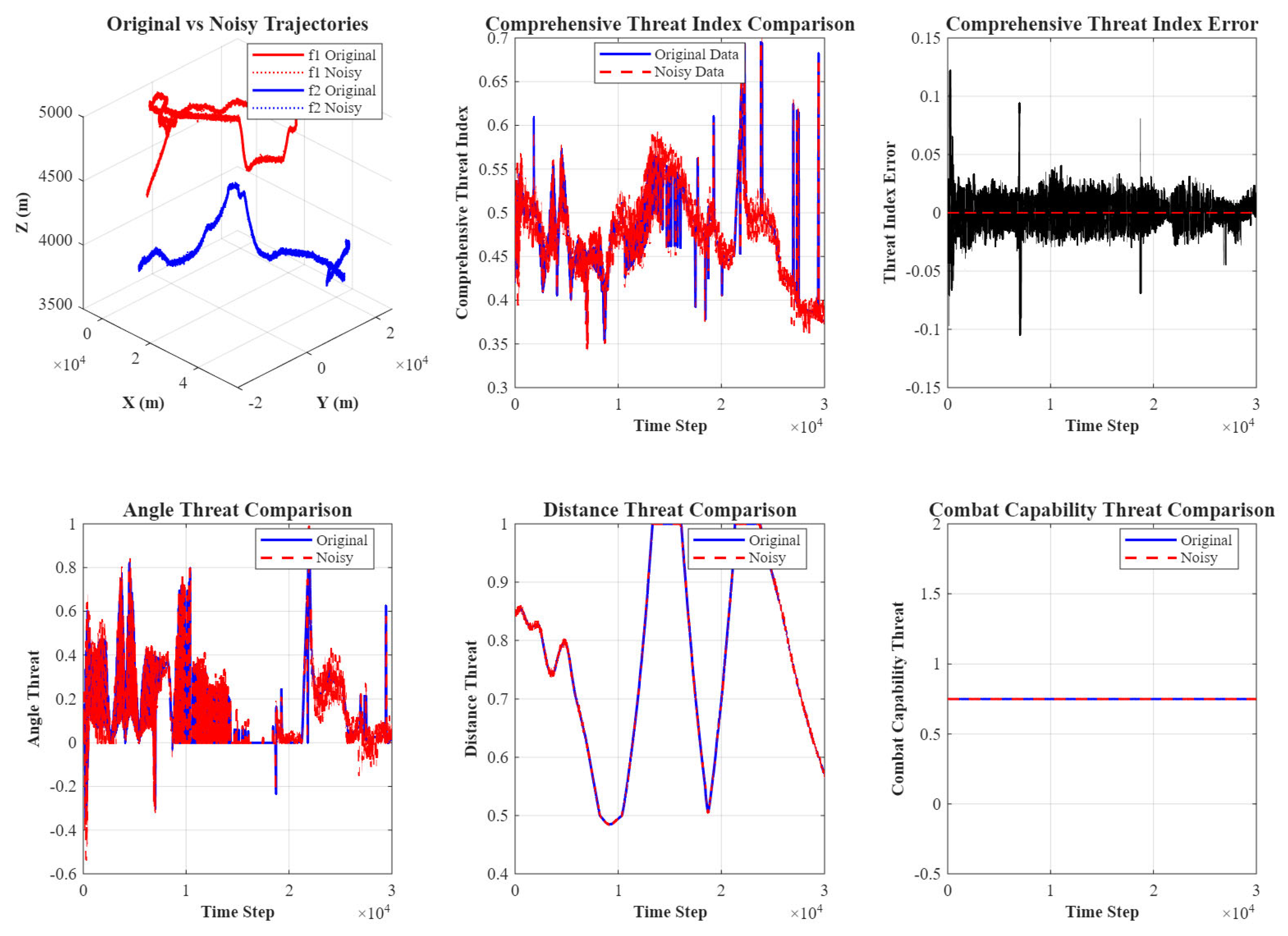
6.2. Verifying the Effectiveness of Threat Evaluation When Sensor Measurement Errors Are Present
6.3. Verifying the Effectiveness of the Algorithm
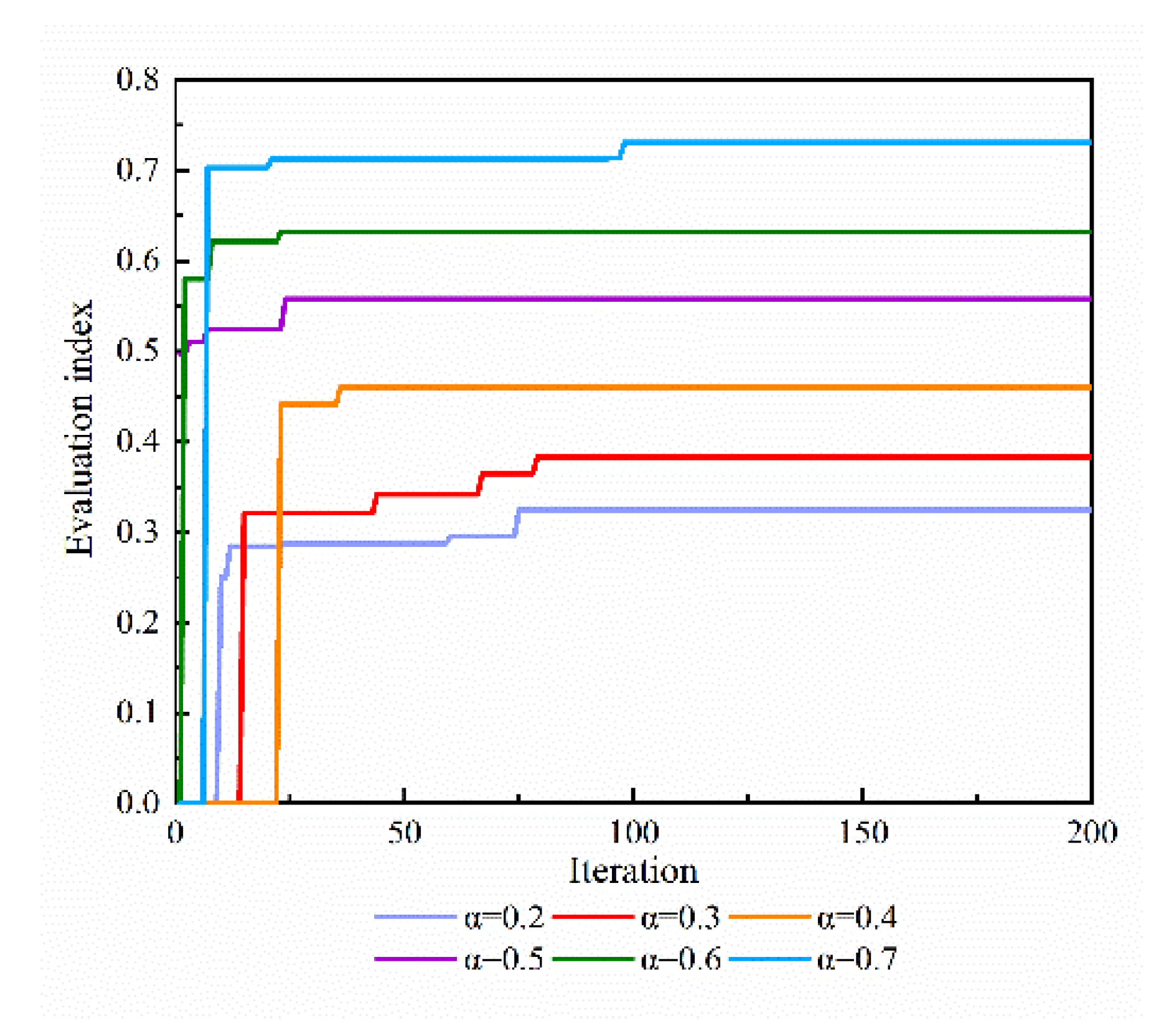
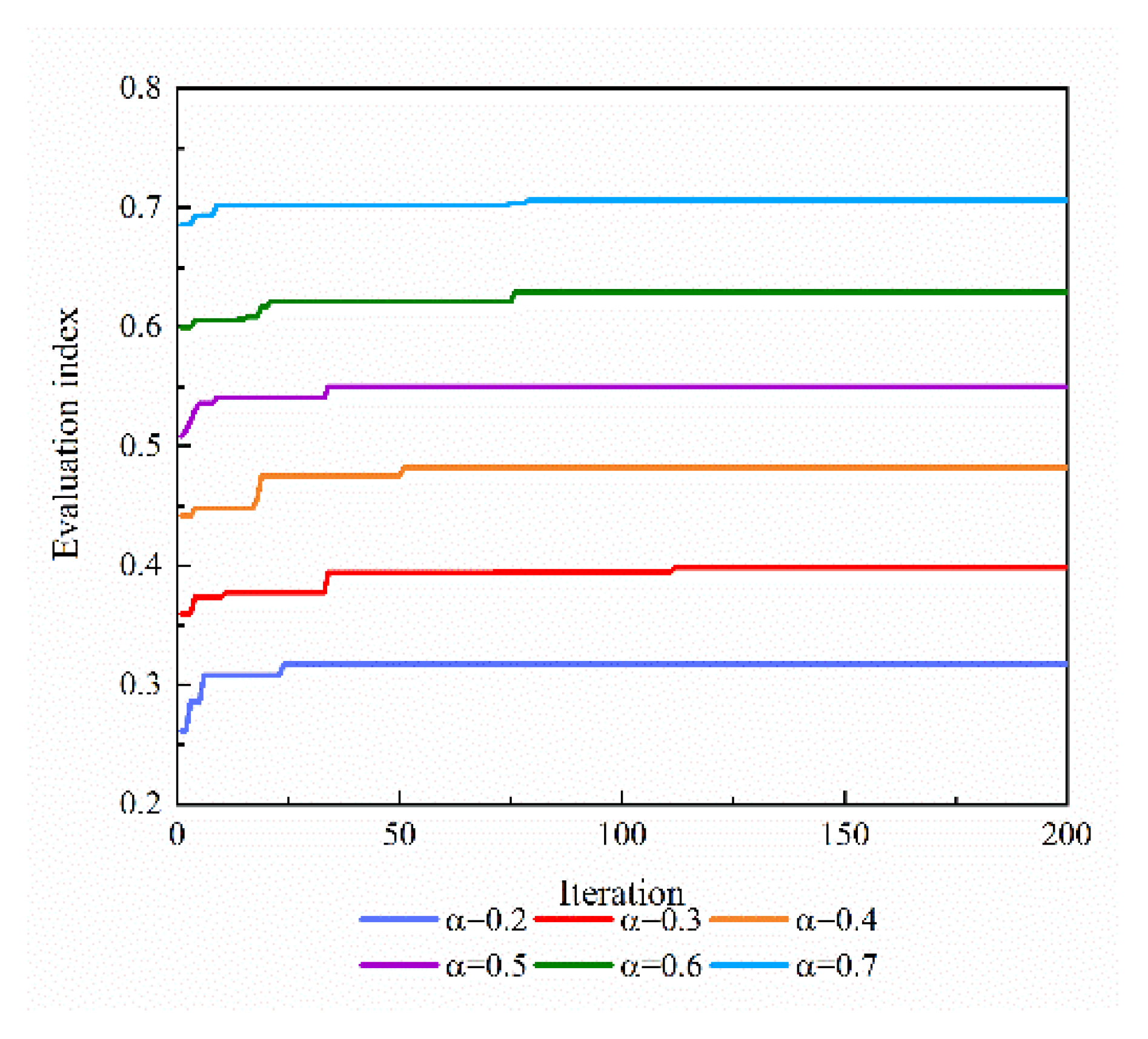
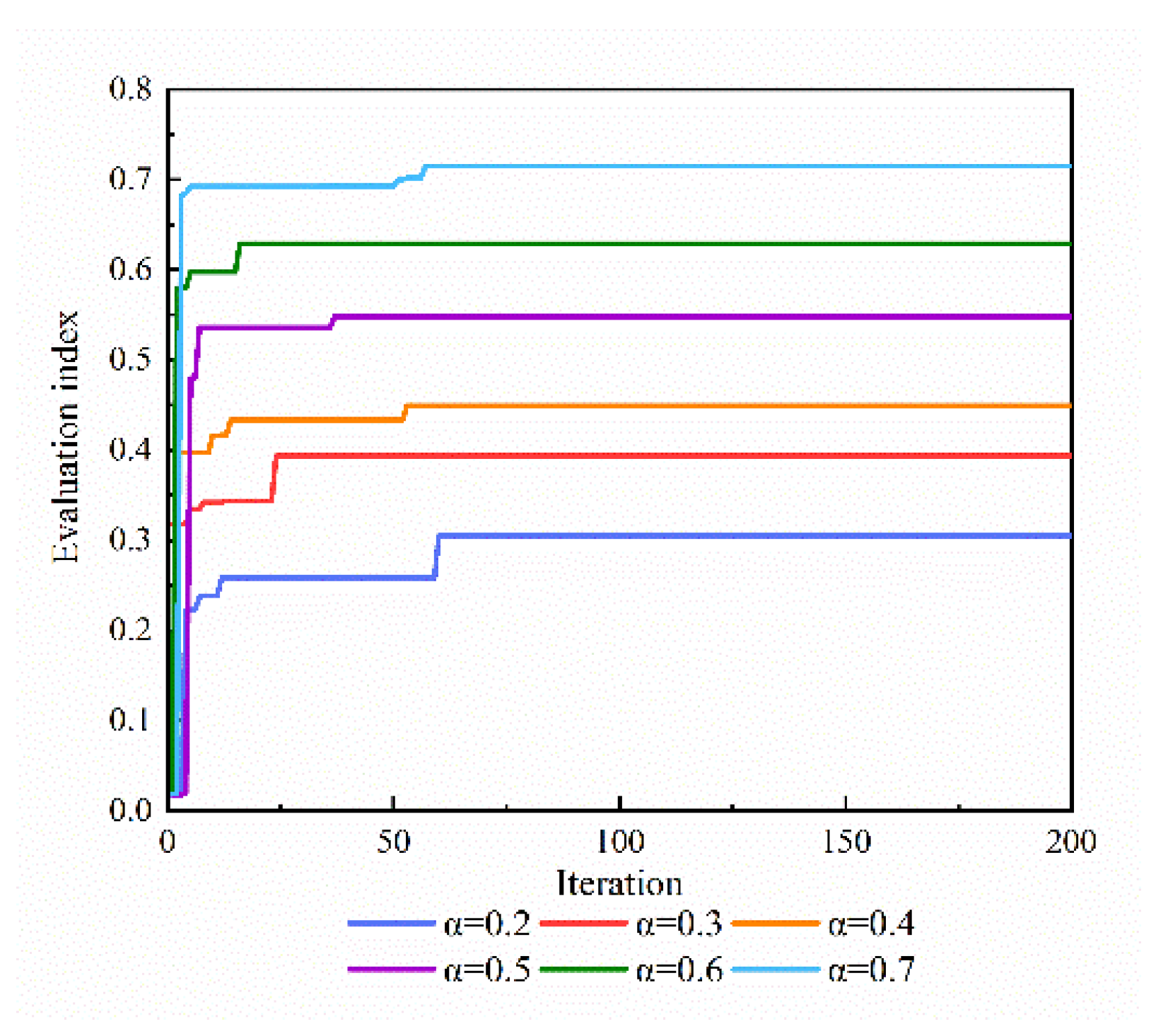
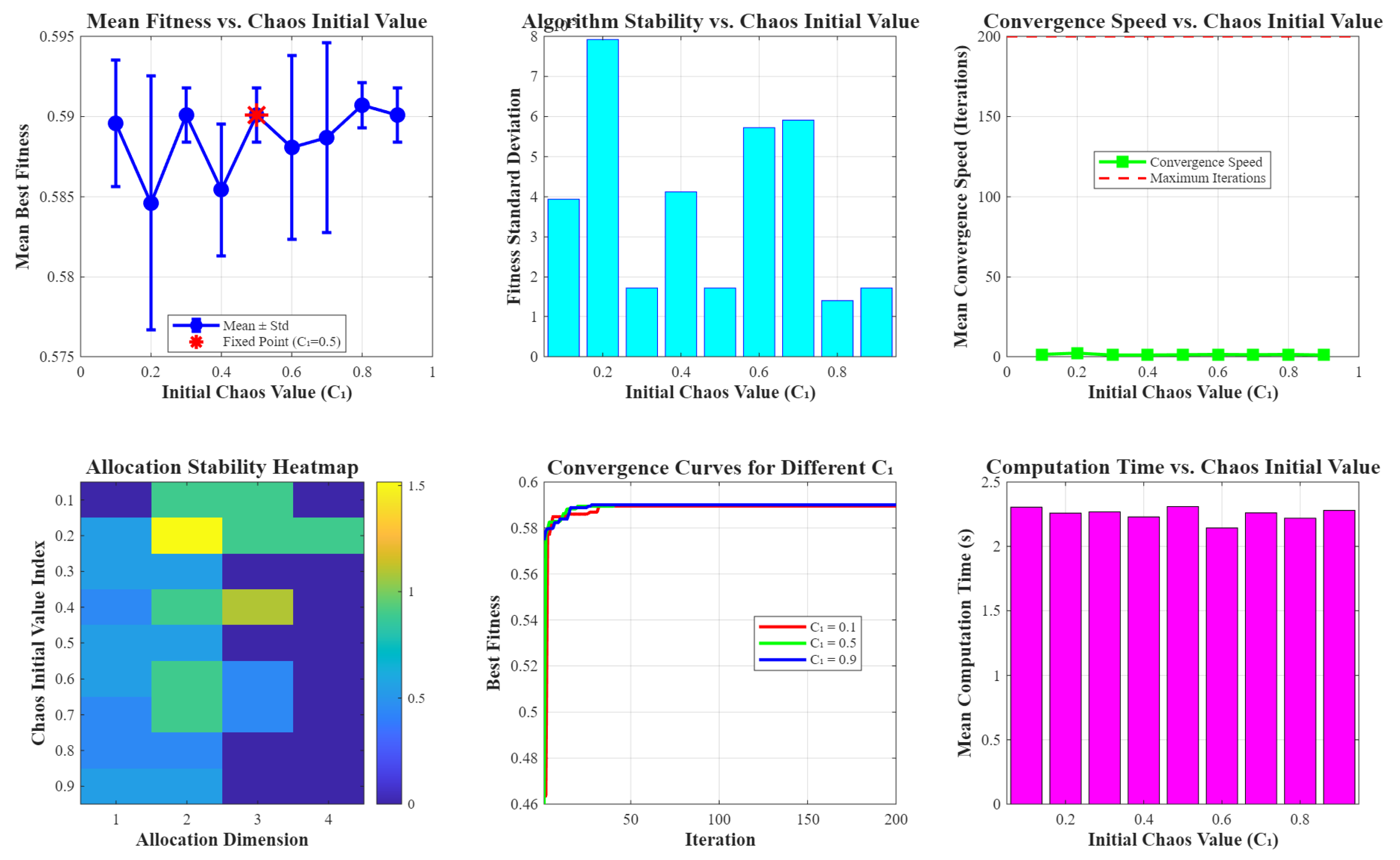
6.3.1. Sensitivity Analysis of Chaos Mapping Initialization
6.3.2. Algorithm Effectiveness Under Complex Conditions
6.4. CMASSA Algorithm Performance
7. Conclusions
7.1. Key Research Findings and Innovations
7.2. Research Limitations and Future Prospects
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SSA | Salp swarm algorithm |
| CMASSA | Adaptive salp swarm algorithm based on chaotic mutation |
| BSO | Beetle swarm optimization |
| PSO | Particle swarm optimization |
| GOA | Grasshopper optimization algorithm |
| GA | Genetic algorithm |
| ACO | Ant colony optimization |
| Number of our aircraft | |
| Number of enemy aircraft | |
| The relative distance between the enemy aircraft and our aircraft | |
| Relative altitude | |
| Speed of our aircraft | |
| Speed of enemy aircraft | |
| Azimuth of our aircraft | |
| Azimuth of enemy aircraft | |
| Target entry angle | |
| The maximum detection distance of the airborne radar | |
| Maximum missile attack zone | |
| Minimum missile attack zone | |
| Maximum the inescapable distance | |
| Minimum the inescapable distance | |
| The operational capability of our aircraft | |
| The operational capability of enemy aircraft | |
| The situational advantage of our aircraft over enemy aircraft | |
| The threat value of enemy aircraft to our aircraft | |
| The situational advantage of our aircraft over enemy aircraft | |
| The comprehensive situation of multi-aircraft coordination | |
| The coordinated threat to the target received by our formation | |
| The importance degree coefficient of operational situation | |
| The penalty term corresponding to the constraint | |
| The penalty term contraction coefficient | |
| Decision variable | |
| Optimization variable | |
| The follower salp’s dimension position component | |
| The dimension component of the location of food | |
| Population size | |
| The maximum value of the dimension search space | |
| The minimum value of the dimension search space | |
| The current number of iterations of the algorithm | |
| Maximum number of iterations | |
| Time difference | |
| Initial velocity | |
| Chaotic adjustment coefficient | |
| Chaotic variable | |
| The optimal alternate position | |
| The contraction control parameter | |
| The adaptive inertia weight | |
| The size of the salp population | |
| The number of evolutionary generations of the algorithm | |
| The number of simulation experiments | |
| The fitness value of the food (global optimal fitness) corresponding to the fitness function value (i.e., our comprehensive advantage value) in the paper | |
| The fitness value corresponding to , used for comparison with the current optimum |
References
- Li, W.; Fang, F.; Wang, Z.; Zhu, Y.; Peng, D. Intelligent maneuvering decision-making in two-UCAV cooperative air combat based on improved MADDPG with hybrid hyper network. Acta Aeronaut. Astronaut. Sin. 2024, 45, 529460. [Google Scholar]
- Ma, S.; Zhang, H.; Yang, G. Target threat level assessment based on cloud model under fuzzy and uncertain conditions in air combat simulation. Aerosp. Sci. Technol. 2017, 67, 49–53. [Google Scholar] [CrossRef]
- Moon, S.; Oh, E.; Shim, D.H. An integral framework of task assignment and path planning for multiple unmanned aerial vehicles in dynamic environments. J. Intell. Robot. Syst. 2013, 70, 303–313. [Google Scholar] [CrossRef]
- Zhang, J.; Guo, H.; Chen, T. Improvement in Hungarian Algorithm for Assignment Problem. Acta Armamentarii 2021, 42, 1339–1344. [Google Scholar]
- Luitpold, B. Coordinated Target Assignment and UAV Path Planning with Timing Constraints. J. Intell. Robot. Syst. 2019, 3, 857–869. [Google Scholar]
- Yi, X.; Zhu, A. An improved neuro-dynamics-based approach to online path planning for multi-robots in unknown dynamic environments. In Proceedings of the IEEE International Conference on Robotics and Biomimetics, Shenzhen, China, 12–14 December 2013; pp. 1–6. [Google Scholar]
- ElGibreen, H.; Youcef-Toumi, K. Dynamic task allocation in an uncertain environment with heterogeneous multi-agents. Auton. Robot. 2019, 43, 1639–1664. [Google Scholar] [CrossRef]
- Hunt, S.; Meng, Q.; Hinde, C. A Consensus-Based Grouping Algorithm for Multi-agent Cooperative Task Allocation with Complex Requirements. Cogn. Comput. 2014, 6, 338–350. [Google Scholar] [CrossRef]
- Qing, L.; Liu, Y.; Zeng, D. Target allocation method based on multi-objective particle swarm optimization algorithm. In Proceedings of the International Conference on Algorithm, Imaging Processing, and Machine Vision (AIPMV 2023), Qingdao, China, 9 January 2023; pp. 72–81. [Google Scholar]
- Li, J.; Yang, X.; Yang, Y.; Liu, X. Cooperative mapping task assignment of heterogeneous multi-UAV using an improved genetic algorithm. Knowl.-Based Syst. 2024, 296, 111830. [Google Scholar] [CrossRef]
- Alencar, R.C.; Santana, C.J.; Bastos-Filho, C.J. Optimizing Routes for Medicine Distribution Using Team Ant Colony System. Adv. Intell. Syst. Comput. 2020, 923, 40–49. [Google Scholar]
- Whitbrook, A.; Meng, Q.; Chung, P.W. Addressing robustness in time-critical, distributed, task allocation algorithms. Appl. Intell. 2019, 49, 1–15. [Google Scholar] [CrossRef]
- Xue, Y.; Jiang, B.; Huang, Y. Optimization strategy for multi-AGV multi-task assignment scheduling based on improved particle swarm genetic algorithm. In Proceedings of the 5th International Conference on Artificial Intelligence and Advanced Manufacturing, Brussels, Belgium, 20–21 October 2023; pp. 131–138. [Google Scholar]
- Chen, C.; Quan, W.; Shao, Z. Aerial Target Threat Assessment Based on Gated Recurrent Unit and Self-Attention Mechanism. J. Syst. Eng. Electron. 2024, 35, 361–373. [Google Scholar] [CrossRef]
- Sheng, L.; Li, L.; Wu, H.; Wang, P. Target Threat Assessment in Air Combat with BP Neural Network for UAV. J. Phys. Conf. Ser. 2023, 2506, 012010. [Google Scholar] [CrossRef]
- Kojadinovic, I.; Marichal, J.L. Entropy of bi-capacities. Eur. J. Oper. Res. 2007, 178, 164–184. [Google Scholar] [CrossRef]
- Ugajin, T. Mutual information of excited states and relative entropy of two disjoint subsystems in CFT. J. High Energy Phys. 2017, 2017, 184. [Google Scholar] [CrossRef]
- Panwar, K.; Deep, K. Discrete Salp Swarm Algorithm for Euclidean Travelling Salesman Problem. Appl. Intell. 2023, 53, 11420–11438. [Google Scholar] [CrossRef]
- Prajisha, C.; Vasudevan, A.R. An efficient intrusion detection system for MQTT-IoT using enhanced chaotic salp swarm algorithm and LightGBM. Int. J. Inf. Secur. 2022, 21, 1263–1282. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, A.; Bi, W.; Xu, S. Dynamic Gaussian mutation beetle swarm optimization method for large-scale weapon target assignment problems. Appl. Soft Comput. 2024, 162, 111798. [Google Scholar] [CrossRef]
- Hadikhani, P.; Lai, D.T.C.; Ong, W.H. A Novel Skeleton-Based Human Activity Discovery Using Particle Swarm Optimization with Gaussian Mutation. IEEE Trans. Hum.-Mach. Syst. 2023, 53, 538–548. [Google Scholar] [CrossRef]
- Wu, L.; Wu, J.; Wang, T. The improved grasshopper optimization algorithm with Cauchy mutation strategy and random weight operator for solving optimization problems. Evol. Intell. 2024, 17, 1751–1781. [Google Scholar] [CrossRef]
- Nithyanandam, C.; Mohankumar, G. Research on aircraft landing schedule using opposition-based genetic algorithm with Cauchy mutation. Int. J. Bus. Intell. Data Min. 2020, 16, 89–106. [Google Scholar] [CrossRef]
- Zong, Q.; QIN, X.; ZHANG, B.; Tian, B.; Dandan, W. Cooperative Task Allocation of Large-Scale UCAV Based on DPSO-GT-SA Algorithm. J. Tianjin Univ. (Sci. Technol.) 2018, 10, 7–11. [Google Scholar]
- Zhao, Y.; Chen, Y.; Zhen, Z.; Jiang, J. Multi-weapon multi-target assignment based on hybrid genetic algorithm in uncertain environment. Int. J. Adv. Robot. Syst. 2020, 17, 1–16. [Google Scholar] [CrossRef]
- Zhou, X.; Yang, K. Cooperative multi-task assignment modeling of UAV based on particle swarm optimization. Intell. Decis. Technol. 2024, 18, 919–934. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, S.; Chen, J.; Jiang, T.; Ye, F. Multi-UAV Cooperative Mission Assignment Algorithm Based on ACO method. In Proceedings of the 2020 International Conference on Computing, Networking and Communications (ICNC), Big Island, HI, USA, 17–20 February 2020; pp. 304–308. [Google Scholar]

| Operation | Time Complexity |
|---|---|
| Initialization | |
| Calculate initialized individual fitness | |
| Select the optimal individual | |
| Update the position of individual | |
| Calculate the fitness of updated individual | |
| Execute the chaotic search with contraction mechanism | |
| Execute combined mutation | |
| Identify the best individual from combined mutation | |
| Update the position of salp individuals after execution of the optimization strategy and calculate the fitness | |
| Execute adaptive inertia weight |
| Mode | Data | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| [10,25,4.2] | [14,15,4.1] | [13,18,4.3] | [11,21,4.5] | [8,25,4.7] | [12,15,4.4] | [12,16,4.3] | [16,26,4.1] | ||
| [21,21,3.2] | [26,20,2.6] | [24,21,2.8] | [25.27,2.8] | [10,20,2.7] | [11,21,3.1] | [22,26,3.3] | [33,20,3.5] | ||
| 10 | 5 | 3 | 45 | 0 | 15 | 19 | 68 | ||
| 26 | 12 | 36 | 8 | 16 | 19 | 67 | 53 | ||
| 400 | 360 | 380 | 289 | 290 | 310 | 358 | 316 | ||
| 389 | 370 | 396 | 316 | 282 | 352 | 338 | 305 | ||
| [26,21,3.6] | [21,25,3.2] | [23,28,3.3] | [21,24,3.5] | [21,19,3.8] | [22,25,3.3] | [26,22,4.1] | [23,26,3.4] | ||
| [12,15,4.2] | [16,18,4.6] | [14,21,3.9] | [18.26,4.1] | [19,28,3.2] | [16,22,3.7] | ||||
| 12 | 21 | 45 | 26 | 30 | 27 | 58 | 32 | ||
| 9 | 84 | 68 | 32 | 42 | 17 | ||||
| 256 | 343 | 309 | 262 | 287 | 311 | 258 | 296 | ||
| 301 | 386 | 298 | 287 | 268 | 362 | ||||
| [78,20,3.6] | [83,23,4.1] | [91,20,4.8] | [82,22,5.1] | [85,25,4.1] | [45,50,3.8] | ||||
| [28,25,4.2] | [26,22,3.8] | [24,21,4.5] | [25,22,3.4] | [19,26,4.3] | [21,23,3.2] | [26,29,2.3] | [23,29,3.1] | ||
| 29 | 33 | 48 | 51 | 68 | 43 | ||||
| 11 | 5 | 23 | 86 | 25 | 63 | 26 | 32 | ||
| 278 | 321 | 356 | 275 | 296 | 345 | ||||
| 362 | 301 | 342 | 320 | 287 | 381 | 349 | 296 |
| Our Aircraft | Target | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | 0.3217 | 0.4312 | 0.4379 | 0.1982 | 0.2454 | 0.4455 | 0.3407 | 0.4324 |
| 2 | 0.4423 | 0.4340 | 0.5311 | 0.4429 | 0.3525 | 0.5108 | 0.4101 | 0.4724 |
| 3 | 0.3533 | 0.4140 | 0.4375 | 0.3945 | 0.3280 | 0.5529 | 0.3331 | 0.4595 |
| 4 | 0.4594 | 0.5442 | 0.5378 | 0.3872 | 0.3672 | 0.4813 | 0.4459 | 0.4285 |
| 5 | 0.4499 | 0.4810 | 0.5540 | 0.4909 | 0.3750 | 0.5515 | 0.3975 | 0.4960 |
| 6 | 0.4355 | 0.3658 | 0.4350 | 0.4477 | 0.3567 | 0.5970 | 0.3388 | 0.5028 |
| 7 | 0.3569 | 0.4410 | 0.4810 | 0.2405 | 0.2687 | 0.3927 | 0.3978 | 0.3481 |
| 8 | 0.3839 | 0.5265 | 0.5260 | 0.3008 | 0.2873 | 0.3958 | 0.4321 | 0.3599 |
| Our Aircraft | Target | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | 0.4274 | 0.6679 | 0.5855 | 0.4517 | 0.5369 | 0.3879 | 0.5521 | 0.6438 |
| 2 | 0.4979 | 0.6328 | 0.4567 | 0.3753 | 0.4429 | 0.2126 | 0.4196 | 0.5266 |
| 3 | 0.4815 | 0.6706 | 0.5274 | 0.5959 | 0.5540 | 0.4022 | 0.5728 | 0.6547 |
| 4 | 0.6447 | 0.6589 | 0.5826 | 0.6291 | 0.7001 | 0.4696 | 0.4343 | 0.6688 |
| 5 | 0.3431 | 0.6215 | 0.4846 | 0.3595 | 0.4337 | 0.3400 | 0.4985 | 0.5828 |
| 6 | 0.5979 | 0.5195 | 0.4428 | 0.5883 | 0.6676 | 0.5230 | 0.4920 | 0.5207 |
| 7 | 0.5984 | 0.7033 | 0.6330 | 0.5503 | 0.5750 | 0.4754 | 0.5889 | 0.7131 |
| 8 | 0.5798 | 0.6510 | 0.5975 | 0.4571 | 0.4713 | 0.3763 | 0.5261 | 0.6358 |
| Target | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 3 | 8 | 6 | 1 | 5 | 7 | 2 | 4 | |
| 5 | 8 | 4 | 2 | 7 | 1 | 6 | 3 | |
| 5 | 8 | 2 | 3 | 6 | 7 | 4 | 1 | |
| 7 | 3 | 5 | 4 | 1 | 2 | 6 | 8 | |
| 7 | 6 | 1 | 2 | 4 | 5 | 3 | 8 | |
| 6 | 2 | 5 | 1 | 7 | 3 | 4 | 8 |
| Our Aircraft | Target | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 0.3697 | 0.5879 | 0.1238 | 0.1789 | 0.2945 | 0.2395 |
| 2 | 0.1654 | 0.3196 | 0.3598 | 0.4256 | 0.4889 | 0.2451 |
| 3 | 0.4428 | 0.2006 | 0.2892 | 0.1549 | 0.1993 | 0.1993 |
| 4 | 0.2356 | 0.3249 | 0.3593 | 0.5269 | 0.2085 | 0.2654 |
| 5 | 0.1598 | 0.4740 | 0.2259 | 0.3892 | 0.1628 | 0.2847 |
| 6 | 0.1265 | 0.2358 | 0.2965 | 0.3492 | 0.2782 | 0.4892 |
| 7 | 0.3182 | 0.3459 | 0.2559 | 0.1274 | 0.3654 | 0.1952 |
| 8 | 0.1564 | 0.2682 | 0.4152 | 0.3027 | 0.2182 | 0.2027 |
| Our Aircraft | Target | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 0.3265 | 0.4529 | 0.2458 | 0.1028 | 0.3316 | 0.2307 |
| 2 | 0.3689 | 0.5678 | 0.7521 | 0.4213 | 0.1895 | 0.2082 |
| 3 | 0.5361 | 0.2011 | 0.2356 | 0.1659 | 0.1879 | 0.3156 |
| 4 | 0.3187 | 0.2951 | 0.3275 | 0.1208 | 0.2685 | 0.2134 |
| 5 | 0.3490 | 0.2103 | 0.3516 | 0.6328 | 0.3598 | 0.2128 |
| 6 | 0.1553 | 0.2379 | 0.3341 | 0.1893 | 0.1466 | 0.2841 |
| 7 | 0.2172 | 0.4596 | 0.4520 | 0.2896 | 0.2029 | 0.2648 |
| 8 | 0.1905 | 0.3245 | 0.1124 | 0.4587 | 0.1526 | 0.2296 |
| Target | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 5 | 3, 6 | 1 | 7, 8 | 4 | 2 | |
| 6 | 2 | 1, 5 | 7, 8 | 4 | 3 | |
| 5 | 6 | 1, 2 | 7 | 4, 8 | 3 | |
| 2 | 3, 8 | 1, 6 | 7 | 5 | 4 | |
| 8 | 7 | 2, 6 | 3 | 4, 5 | 1 | |
| 5 | 6 | 2, 4 | 8 | 1 | 3, 7 |
| Our Aircraft | Target | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | 0.3567 | 0.4280 | 0.4285 | 0.4387 | 0.3323 | 0.4515 | 0.3463 | 0.3676 |
| 2 | 0.3943 | 0.3738 | 0.5111 | 0.5254 | 0.3626 | 0.4195 | 0.3221 | 0.3509 |
| 3 | 0.3692 | 0.4090 | 0.4901 | 0.4728 | 0.3605 | 0.6279 | 0.3655 | 0.4315 |
| 4 | 0.3564 | 0.4157 | 0.4161 | 0.3731 | 0.3427 | 0.3974 | 0.3047 | 0.2581 |
| 5 | 0.3544 | 0.5682 | 0.5828 | 0.4720 | 0.4630 | 0.6361 | 0.3933 | 0.4358 |
| 6 | 0.4982 | 0.4445 | 0.5046 | 0.4975 | 0.4464 | 0.5436 | 0.5058 | 0.4582 |
| Our Aircraft | Target | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | 0.4043 | 0.5994 | 0.4803 | 0.5529 | 0.4980 | 0.5138 | 0.5523 | 0.3949 |
| 2 | 0.4376 | 0.6214 | 0.6012 | 0.5641 | 0.4714 | 0.4162 | 0.5030 | 0.4129 |
| 3 | 0.5004 | 0.6360 | 0.6757 | 0.6506 | 0.6294 | 0.5576 | 0.5066 | 0.5554 |
| 4 | 0.5085 | 0.6752 | 0.6018 | 0.5470 | 0.6141 | 0.6230 | 0.6315 | 0.4629 |
| 5 | 0.2994 | 0.5596 | 0.4145 | 0.4293 | 0.2979 | 0.4396 | 0.4030 | 0.2801 |
| 6 | 0.5156 | 0.5868 | 0.5393 | 0.5572 | 0.5544 | 0.4147 | 0.5303 | 0.4532 |
| Target | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 3 | 1 | 2 | 6 | 5 | 1 | 2 | 4 | |
| 3 | 1 | 4 | 5 | 5 | 2 | 1 | 6 | |
| 5 | 1 | 4 | 3 | 5 | 2 | 6 | 2 | |
| 4 | 3 | 5 | 1 | 5 | 2 | 3 | 6 | |
| 3 | 2 | 6 | 1 | 4 | 5 | 4 | 6 | |
| 6 | 3 | 2 | 2 | 5 | 1 | 4 | 5 |
| Mode | Experiment 1 | Experiment 2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 16 | 16 | 50 | 200 | 20 | 24 | 24 | 50 | 200 | 10 | |
| 20 | 16 | 50 | 200 | 20 | 30 | 24 | 50 | 200 | 10 | |
| 16 | 20 | 50 | 200 | 20 | 24 | 30 | 50 | 200 | 10 | |
| Experiment | Mode | Average Time | Average Gain | Optimal Gain | Constraint Violation | Optimal Solution Variance |
|---|---|---|---|---|---|---|
| Experiment 1 | 4.5248 | 0.7295 | 0.7468 | 4.59% | 6.6327 × 10−5 | |
| 5.8367 | 0.7137 | 0.7268 | 4.17% | 3.2325 × 10−5 | ||
| 8.2039 | 0.7251 | 0.7365 | 2.14% | 4.1578 × 10−5 | ||
| Experiment 2 | 7.3081 | 0.9263 | 0.9453 | 6.23% | 8.2435 × 10−5 | |
| 10.2196 | 0.8734 | 0.9042 | 7.16% | 4.1365 × 10−4 | ||
| 13.8026 | 0.8109 | 0.8364 | 5.26% | 1.2684 × 10−4 |
| Mode | Methods | Number of Aircraft | Population Number | Iteration Times | Experiment Times | Average Time | Average Gain | Optimum Gain | Optimal Solution Variance |
|---|---|---|---|---|---|---|---|---|---|
| GA | 50 | 200 | 20 | 5.6027 | 0.5088 | 0.7347 | 0.1079 | ||
| CMASSA | 50 | 200 | 20 | 2.5824 | 0.7125 | 0.7309 | 0.0078 | ||
| PSO | 50 | 200 | 20 | 5.7294 | 0.5258 | 0.7038 | 0.0903 | ||
| ACO | 50 | 200 | 20 | 1.8527 | 0.7285 | 0.7406 | 3.3664 × 10−5 | ||
| GA | 50 | 200 | 20 | 9.6301 | 0.7157 | 0.7267 | 2.5787 × 10−5 | ||
| CMASSA | 50 | 200 | 20 | 8.0516 | 0.7209 | 0.7224 | 1.6451 × 10−5 | ||
| PSO | 50 | 200 | 20 | 7.7590 | 0.7169 | 0.7228 | 4.3039 × 10−5 | ||
| ACO | 50 | 200 | 20 | 5.2712 | 0.7229 | 0.7311 | 1.1720 × 10−5 | ||
| GA | 50 | 200 | 20 | 10.4380 | 0.7167 | 0.7247 | 7.9346 × 10−5 | ||
| CMASSA | 50 | 200 | 20 | 8.2359 | 0.7208 | 0.7231 | 1.9133 × 10−5 | ||
| PSO | 50 | 200 | 20 | 11.7663 | 0.7177 | 0.7183 | 3.5426 × 10−5 | ||
| ACO | 50 | 200 | 20 | 5.1259 | 0.7244 | 0.7304 | 1.5330 × 10−5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Lyu, Y.; Xi, Z.; Li, Y.; Wen, B.; Mu, Z. Multi-Aircraft Coordinated Target Assignment Based on Chaotic Mutation Adaptive Salp Swarm Algorithm. Aerospace 2026, 13, 43. https://doi.org/10.3390/aerospace13010043
Lyu Y, Xi Z, Li Y, Wen B, Mu Z. Multi-Aircraft Coordinated Target Assignment Based on Chaotic Mutation Adaptive Salp Swarm Algorithm. Aerospace. 2026; 13(1):43. https://doi.org/10.3390/aerospace13010043
Chicago/Turabian StyleLyu, Yue, Zhifei Xi, You Li, Bincheng Wen, and Zhonglin Mu. 2026. "Multi-Aircraft Coordinated Target Assignment Based on Chaotic Mutation Adaptive Salp Swarm Algorithm" Aerospace 13, no. 1: 43. https://doi.org/10.3390/aerospace13010043
APA StyleLyu, Y., Xi, Z., Li, Y., Wen, B., & Mu, Z. (2026). Multi-Aircraft Coordinated Target Assignment Based on Chaotic Mutation Adaptive Salp Swarm Algorithm. Aerospace, 13(1), 43. https://doi.org/10.3390/aerospace13010043





