Improving Control Performance of Tilt-Rotor VTOL UAV with Model-Based Reward and Multi-Agent Reinforcement Learning

Abstract

Tilt-rotor Vertical Takeoff and Landing Unmanned Aerial Vehicles (TR-VTOL UAVs) combine fixed-wing and rotary-wing configurations, offering optimized flight planning but presenting challenges due to their complex dynamics and uncertainties. This study investigates a multi-agent reinforcement learning (RL) control system utilizing Soft Actor-Critic (SAC) modules, which are designed to independently control each input with a tailored reward mechanism. By implementing a novel reward structure based on a dynamic reference response region, the multi-agent design improves learning efficiency by minimizing data redundancy. Compared to other control methods such as Actor-Critic Neural Networks (AC NN), Proximal Policy Optimization (PPO), Nonsingular Terminal Sliding Mode Control (NTSMC), and PID controllers, the proposed system shows at least a 30% improvement in transient performance metrics—including RMSE, rise time, settling time, and maximum overshoot—under both no wind and constant 20 m/s wind conditions, representing an extreme scenario to evaluate controller robustness. This approach has also reduced training time by 80% compared to single-agent systems, lowering energy consumption and environmental impact.

1. Introduction

Unmanned aerial vehicles (UAVs) have rapidly become integral across various industries, including surveillance, logistics, agriculture, and defense. This widespread adoption has driven the development of diverse UAV types, including fixed-wing, rotary-wing, vertical take-off and landing (VTOL), and tilt-rotor VTOL (TR-VTOL) platforms. TR-VTOL UAVs offer superior maneuverability but suffer from limited range and higher energy consumption [1]. Fixed-wing UAVs, on the other hand, are more energy-efficient and capable of longer range but require runways for take-off and landing, which limits their operational flexibility [2]. These constraints are particularly problematic in remote or military applications where infrastructure is sparse and continuous operation is essential [3].

TR-VTOL UAVs have emerged to address these trade-offs, combining the vertical flight capabilities of rotary-wing UAVs with the cruise efficiency of fixed-wing aircraft. Unlike conventional VTOLs that deactivate certain motors during mode transitions, TR-VTOLs utilize rotatable propulsion units that remain active in all phases, reducing structural load and vibration [4]. However, this hybrid configuration introduces additional control challenges. The transition between vertical and horizontal flight involves complex interactions among motor tilt dynamics, aerodynamic forces, and environmental disturbances, which complicate the control of both translational and rotational motion [5].

In response to these complexities, researchers have proposed various control strategies. Sheng et al. developed a compartmental aerodynamic model to characterize the dynamics of TR-VTOL UAVs and conducted a stability analysis in a simulation environment [6]. He et al. applied nonlinear sliding mode control to address external disturbances and parameter variations [7]. Similarly, Masuda et al. introduced an H-infinity-based control framework to enhance robustness against model uncertainties during the transition between flight modes [8]. In another study, Xie et al. proposed a robust attitude control method for a three-motor tilt-rotor UAV that achieves fixed-time convergence despite system uncertainties. Their control structure utilizes only input-output data within an actor-critic learning framework, enabling stable performance without full access to the system dynamics [9].

While model-based robust controllers offer improved performance in uncertain environments, their effectiveness relies heavily on accurate system models and tuning. In contrast, reinforcement learning (RL) has recently gained attention as a data-driven approach capable of learning optimal control policies through interaction with the environment. RL-based controllers can adapt to varying conditions and model uncertainties without requiring precise modeling. Several RL applications in UAV control have demonstrated promising results, including disturbance rejection, autonomous landing, and stabilization under complex conditions [10,11,12,13].

However, many of these approaches employ static reward functions, which may be insufficient for capturing the complexity of real-world dynamic environments. A static reward structure limits the agent’s ability to adapt its behavior when the operational context shifts. This limitation is particularly significant in TR-VTOL UAVs, where sudden aerodynamic changes, actuator nonlinearities, and time-varying disturbances are common [14,15].

To address this shortcoming, recent studies have explored the concept of dynamic reward functions, which allow the learning objective to evolve based on real-time performance feedback [16]. Nevertheless, most existing work on dynamic reward design is limited to basic UAV configurations and does not extend to tilt-rotor architectures [17]. Furthermore, the potential of multi-agent reinforcement learning (MARL) remains largely underutilized in this context. MARL enables the decomposition of complex control tasks into sub-agents, each responsible for a specific control axis such as roll, pitch, or yaw. This structure not only improves training convergence but also enhances control robustness by decoupling the policy learning process [18].

This study presents three main contributions. First, a multi-agent reinforcement learning structure was developed by assigning a separate learning agent to each control axis (roll, pitch, and yaw) of the TR-VTOL UAV, addressing its complex control requirements. This decomposition of control tasks enabled each agent to learn more quickly and efficiently, thereby reducing the overall training time and enhancing control performance. Second, a model-based dynamic reward function tailored to the vehicle’s dynamics was designed to guide the learning process by evaluating the system’s state at each training step. Compared to static reward structures, this approach improved both system stability and learning efficiency. Third, to simulate real-world challenges, random external disturbance forces were applied along the x, y, and z axes, allowing the system to demonstrate stable and reliable responses under dynamic environmental conditions. Collectively, these contributions show that the proposed method offers a robust control solution not only in terms of learning performance but also in terms of resilience to real-world uncertainties.

However, due to the complexity and risk of conducting real-world experiments on TR-VTOL UAVs, especially given the nonlinear dynamics and tilt transitions, this study was conducted in a simulation environment. Training reinforcement learning (RL) agents requires thousands of trial-and-error episodes, which is impractical and potentially unsafe in real-world settings. After validating the control framework in simulation, future work will focus on transferring the trained models to physical platforms through sim-to-real adaptation.

2. Modelling of VTOL

Although RL has found wide application in solving complex tasks for UAVs, training and adapting a policy for varying initial conditions and situations remain challenging. Policies learned in fixed environments using RL often prove fragile and prone to failure under changing environmental parameters. To address this, randomization techniques have been employed to develop the control policies for the TR-VTOL UAV [19]. The scenarios were designed taking into account random initial conditions, external disturbances, different axis angles, and variable height and speed inputs [20]. Throughout this process, both RL policies and the nominal reward function were continuously updated. The training process was completed after approximately 2500 episodes in the single-agent structure and approximately 120 episodes in the multi-agent structure, and these values are consistent with the scales commonly used in RL-based control literature to ensure policy stability [21].

RL, by its nature, relies on trial-and-error-based exploration, and agents initially perform stochastic and unpredictable actions while learning from environmental feedback. For TR-VTOL UAVs, such actions can increase the risk of hardware damage due to actuator saturation, sudden aerodynamic loads, or instability caused by rollover or ground effects. Even if the motors are oriented vertically and theoretically generate sufficient thrust for takeoff, the UAV may remain stationary due to inappropriate control signals from the RL agent. Excessive pitch or roll commands, ground effect disturbances, or center-of-gravity imbalances can redirect or counteract the vertical lift. In such cases, the actuators operate under high load without achieving the expected altitude change, leading to unnecessary stress on the hardware. Therefore, training was initiated in an environment where exploration is safe and repeatable, and disruptive effects can be controlled and incorporated into the simulation [22]. Training in a simulation environment not only reduces hardware damage but also shortens training time thanks to higher simulation speeds. It allows errors to be safely observed and analyzed, which contributes to improving the learning process. Additionally, the reproducible recreation of conditions enables the fair comparison of different algorithms and ensures methodological consistency [23].

2.1. Dynamic Equations of TR-VTOL

The dynamic equations of the aircraft are based on factors such as wing and body geometry, air density, airspeed, and the UAV’s lift force, drag, and directional stability. The thrust forces generated by the motors are calculated using thrust system equations. Based on the linear and angular momentum equations, the force and moment equations of the TR-VTOL UAVs are expressed as Equation (1) [24]:

$$\left[\begin{array}{c}F\\ M\end{array}\right]=\left[\begin{array}{cc}mI& 0\\ 0& J\end{array}\right]\left[\begin{array}{c}{\dot{v}}^B\\ {\dot{\omega }}^B\end{array}\right]+\left[\begin{array}{c}{w}^B\times m{v}^B\\ w^B\times J{w}^B\end{array}\right]$$

(1)

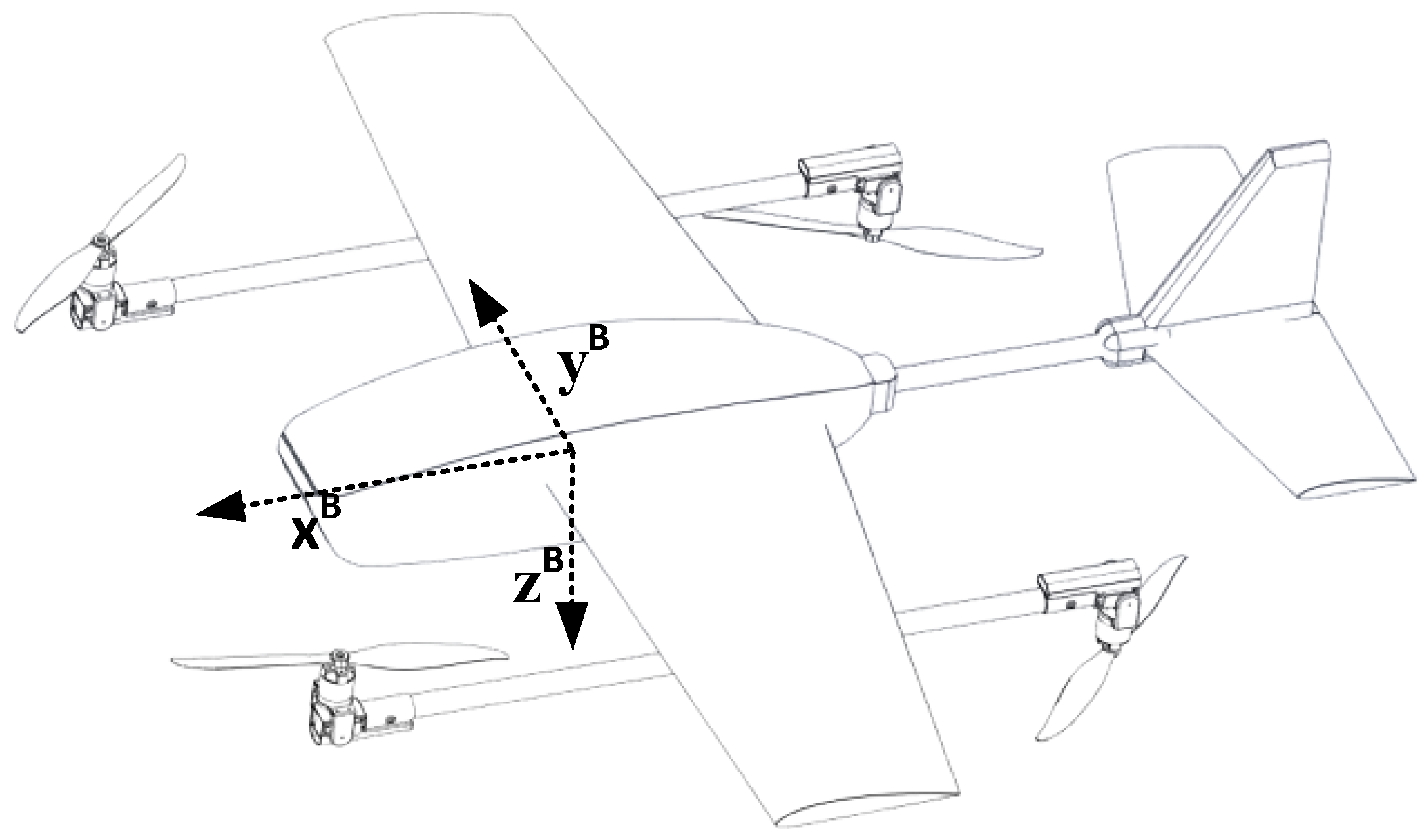
Here, F and M represent the total external force and moment. I is the 3 × 3 identity matrix, J is the inertia matrix, m is the mass, and ${\dot{v}}^B$ and ${\dot{\mathsf{\omega }}}^{\mathrm{B}}$ are the linear and angular accelerations of the UAV in the body frame. The Euler angles indicate the orientation of the body frame with respect to the inertial frame. A schematic of the TR-VTOL UAV employed in this work is shown in Figure 1.

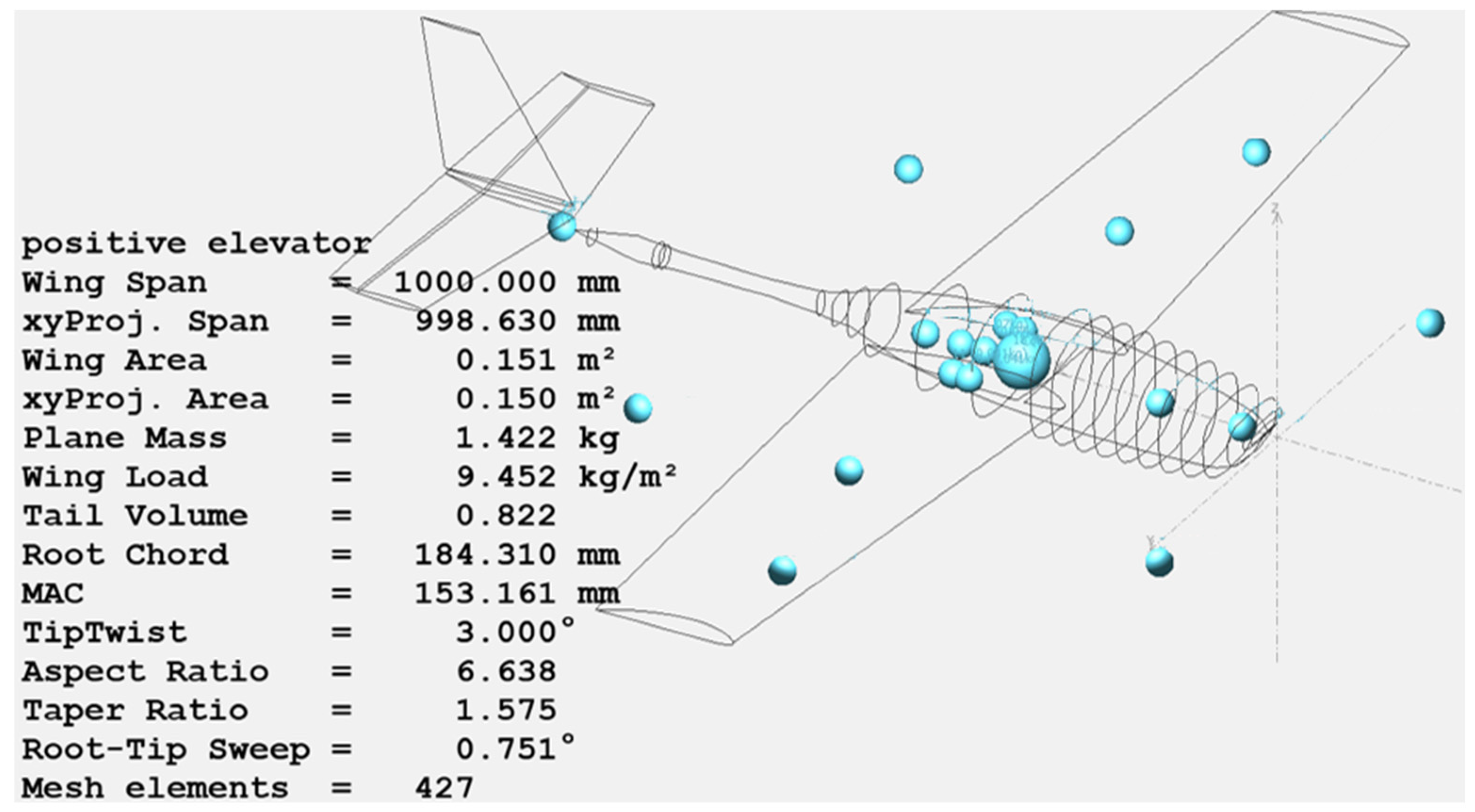
The inertia moments of the UAV were calculated taking into account the masses and positions of all components. Table S1 shows the masses of the main equipment on the TR-VTOL UAV and their x, y, z positions relative to the body coordinate system. Using this information, the contribution of each component to the body inertia was determined, and the total inertia matrix was created. The XFLR5 software (version 6.47) was employed to perform inertia calculations, providing central inertia values by accounting for both the wing–body geometry and the spatial distribution of onboard equipment. Figure 2 shows the visual model of the UAV designed in the XFLR5 environment and the equipment layout. This method allows for a more realistic modelling of UAV dynamics in simulation and control design. The inertia moments of the TR-VTOL UAV were calculated considering the masses and positions of all onboard components. Detailed information on the masses, positions, and the calculation procedure is provided in Figure S1.

The rotational transformation matrix that represents the vehicle’s orientation with respect to the inertial frame, expressed in terms of Euler angles, is presented in Equation (2). In the transformation matrix, the shorthand notations $Ca$ and $S\alpha$ are used to denote $\cos \alpha$ and $\sin \alpha$, respectively.

$$R_B^i=\left[\begin{array}{ccc}C\psi C\theta & C\psi S\theta S\varphi -S\psi C\varphi & C\psi S\theta C\varphi +S\psi S\varphi \\ S\psi C\theta & S\psi S\theta S\varphi +C\psi C\varphi & S\psi S\theta C\varphi -C\psi S\varphi \\ -S\theta & C\theta S\varphi & C\theta C\varphi \end{array}\right]$$

(2)

The total forces acting on the aircraft consist of aerodynamic force ($F_a$), gravity ($F_g$), and propeller thrust force ($F_p$). The total force acting on the UAV in the body frame is expressed in Equation (3):

$$F^B=F_g^B+F_p^B+F_a^B$$

(3)

The gravitational force on body frame, denoted as $F_g^B$, is presented in Equation (4).

$$F_g^B=R_i^B\left[\begin{array}{c}0\\ 0\\ mg\end{array}\right]=\left[\begin{array}{c}-mgS\theta \\ mgC\theta S\varnothing \\ mgC\theta C\varnothing \end{array}\right]$$

(4)

The motors are positioned at four separate points, with the center located at the center of gravity. The TR-VTOL UAV and its motor tilt configurations in hover, transition, and fixed-wing modes are illustrated in Figure 3.

2.1.1. Forces and Moments in Quad Mode

The expression for the force and moment generated by each motor when the vehicle is in quad mode is given in Equations (5)–(9) [25]:

$$F_{p\left(i\right)}=K_f{w}_i^2$$

(5)

$$M_i=K_m{w}_i^2$$

(6)

$$M_x=\left(F_2+F_4-F_1-F_3\right)y$$

(7)

$$M_y=\left(F_1+F_2-F_3-F_4\right)x$$

(8)

$$M_z=\left(F_1+F_4-F_2-F_3\right)c$$

(9)

with $w_i$ being the angular velocity (rotational velocity) of motor number $i$, $K_f$ the thrust coefficient of the propellers, $K_m$ the propeller’s torque coefficient, $x, y, c$ the moment arm length of the TR-VTOL UAV with respect to the y-axis, the x-axis, and the force-moment scaling factor, respectively. $M_x, M_y, M_z$ represent the moments generated with respect to the $\mathrm{x},\mathrm{y},\mathrm{z}$ axes, respectively.

In practice, the coefficients $K_f$ and $K_m$ are typically determined through experimental measurements. Since the present study is simulation-based, with experimental validation planned for a subsequent phase, the thrust force F was obtained using the simplified dynamic thrust model proposed by Gabriel Staples [26], in combination with the specifications of the selected motor–propeller system. The moment coefficient $K_m$ was adopted from a similar motor–propeller study reported in the literature [27], due to its provision of validated data for comparable configurations. The primary focus of this study is on improving the overall control performance of the aircraft; therefore, the net thrust produced by the motor–propeller assembly is employed. Accordingly, the simplified dynamic thrust model forms the basis for evaluating overall aircraft control performance. It should be noted that this approach relies on momentum-based assumptions and neglects certain real-world phenomena, such as installation effects, propeller–wing interactions, and three-dimensional tip losses. In addition, it is acknowledged that the effective thrust coefficient $K_f$ may differ between rotary-wing and fixed-wing flight modes due to variations in inflow conditions, advance ratios, and installation effects. Such efficiency differences have been analytically discussed in the literature [28], where mode-dependent corrections were introduced to capture the influence of propeller–nacelle interactions and forward-flight aerodynamics. In this study, the primary focus is on developing the RL-based control framework. Since the present work is limited to simulations, detailed modeling of propeller efficiency was not pursued. Instead, simplified equations and constant coefficients were adopted to emphasize the control objective, with mode-specific efficiency variations to be considered in future work.

The dynamic thrust equation is provided in Equation (10).

$$F=4.3924\times {10}^{-8}·RPM{\displaystyle \frac{d^{3.5}}{\sqrt{pitch}}}\left(4.234\times {10}^{-4}·RPM·pitch-V_0\right)$$

(10)

where F (N) is the propeller thrust, d (in.) is the propeller diameter, RPM is the rotational speed, pitch (in.) is the propeller pitch, and V₀ (m/s) is the forward flight velocity. The thrust–velocity characteristics of the selected motor–propeller combination are shown in Figure 4.

2.1.2. Forces and Moments in Transition Mode

The motor force and position vectors are shown in Figure 3. In the transition mode, the motor’s rotation angle is denoted as λ. By varying the rotation angle (λ) between 0 and 90 degrees, the vehicle transitions between rotary wing mode and fixed wing mode. The position and rotation vectors of the motors are expressed in Equations (11) and (12), respectively.

$${\widehat{r}}_i={\left[ \begin{array}{ccc}{x}_i& y_i& 0\end{array}\right]}^T$$

(11)

$$r_m^{\left(i\right)}={\left[ \begin{array}{ccc}sin{\lambda }_i& 0& cos{\lambda }_i\end{array}\right]}^T, 0<{\lambda }_i<90 , i=1,\dots ,4$$

(12)

The force vector generated by each motor is given by Equation (13):

$$F_{p\left(i\right)}=F_{p\left(i\right)}{r}_m^{\left(i\right)}$$

(13)

The total motor force is expressed as Equation (14).

$$F_p^B=\sum _{i=1}^4{F}_{p\left(i\right)}$$

(14)

moment generated by each motor is given by Equation (15):

$$M_i={\widehat{r}}_i\times F_p^B$$

(15)

2.1.3. Forces and Moments in Fixed-Wing Mode

The aerodynamic behavior of a fixed-wing UAV is determined by the forces and moments generated as a function of flight conditions and control surface deflections. These forces and moments, which include both longitudinal (lift, drag, pitching moment) and lateral–directional (side force, rolling moment, yawing moment) components, are functions of parameters such as angle of attack, sideslip angle, angular rates, and control surface deflections. These aerodynamic effects are modeled using well-established force and moment equations, which provide the basis for analyzing and controlling the motion of the vehicle [29]. The details of the aerodynamic force and moment equations used in this study are provided below.

Longitudinal Forces and Moments

The longitudinal forces and moments acting on the UAV are described by lift, drag, and pitching moment, which depend on the angle of attack, pitch rate, and elevator deflection. The governing equations are given in Equations (16)–(18).

$$F_{lift}={\displaystyle \frac{1}{2}}\rho V_a^{2}S{C}_L\left(\alpha ,q,{\delta }_e\right)$$

(16)

$$F_{drag}={\displaystyle \frac{1}{2}}\rho V_a^{2}S{C}_D\left(\alpha ,q,{\delta }_e\right)$$

(17)

$$M={\displaystyle \frac{1}{2}}\rho V_a^{2}Sc{C}_m\left(\alpha ,q,{\delta }_e\right)$$

(18)

Here F_lift and F_drag are the lift and drag forces, M is the pitch moment, ρ is the air density, V_a is the relative flow velocity of the aircraft, α is the angle of attack, β is the sideslip angle, q is pitch rate,${ \delta }_e$ is the elevator deflection, $C_L, C_D, C_m$ are the lift, drag, and pitch moment coefficient, S represents the wing surface area, b represents the wing span and c represents the chord length.

Equations (16)–(18) model the contributions of elevator deflection to lift, drag, and aerodynamic moments based on aerodynamic data obtained from the XFLR5 software. These data are incorporated into the dynamic model within the MATLAB/Simulink (version 2023b) environment through prelookup tables. Consequently, variations in elevator deflection yield corresponding changes in forces and moments in a realistic manner, thereby capturing the longitudinal dynamic response of the UAV in the simulation environment. Figure 5 illustrates the implementation of longitudinal forces in the Simulink model and their integration via prelookup tables.

Lateral Forces and Moments

The lateral-directional forces and moments include side force, rolling moment, and yawing moment, depending on sideslip angle, roll rate, and aileron/rudder deflections. The governing equations are given in Equations (19)–(21):

$$Y={\displaystyle \frac{1}{2}}\rho V_a^{2}S{C}_Y\left(\beta ,p,{\delta }_a,{\delta }_r\right)$$

(19)

$$L={\displaystyle \frac{1}{2}}\rho V_a^{2}Sb{C}_I\left(\beta ,p,{\delta }_a,{\delta }_r\right)$$

(20)

$$N={\displaystyle \frac{1}{2}}\rho V_a^{2}Sb{C}_n\left(\beta ,p,{\delta }_a,{\delta }_r\right)$$

(21)

Here, Y is the sideslip force, L, N are the roll and yaw moments, p is the roll rate. ${\delta }_a,{\delta }_r$ are the aileron and rudder deflections, respectively. $C_Y,C_I{,C}_n$ are the sideslip coefficient, roll moment coefficient, yaw moment coefficient, respectively.

In Equations (19)–(21), the contributions of aileron and rudder deflections to roll moment, yaw moment, and side force are modeled using aerodynamic data similar obtained from XFLR5. These data are also transferred into prelookup tables within the Simulink environment. As a result, variations in aileron and rudder deflections lead to realistic calculations of lateral forces and moments, enabling the simulation of the UAV’s lateral dynamic responses. Figure 6 illustrates the integration of lateral force and moment coefficients into the Simulink model.

The parameters used in the mathematical model and the aerodynamic coefficients obtained from the XFLR5 program are listed in

Table 1. Parameters used.

Name	Description	Tunnel
Ixx	Moment of inertia about the X-axis (kg·m2)	0.02
Iyy	Moment of inertia about the Y-axis (kg·m2)	0.027
Izz	Moment of inertia about the Z-axis (kg·m2)	0.046
S	surface area of wing, (m2)	0.151
b	wingspan, (m)	1
c	chord, (m)	0.153
AR	wing aspect ratio	6.638
W	weight, (kg)	1.422
α	angle of attack (deg)	4
V	velocity (m/s)	17.24
CG	33% MAC on thrust line	0.241
CL	lift coefficient	0.596
CD	Drag coefficient	0.04
Cmq	pitch moment due to pitch rate	−0.041
CIp	roll moment due to roll rate	−0.439
CIr	roll moment due to yaw rate	0.330
Cnp	yaw moment due to roll rate	−0.265
Cnr	yaw moment due to yaw rate	−0.048

.

3. RL-Based Multi-Agent SAC Control Framework

RL algorithms are artificial intelligence tools that continuously update policy parameters based on actions, observations, and rewards. The goal of an RL algorithm is to find the optimal policy that maximizes the long-term cumulative reward received during a task. Various models are used for discrete and continuous-time systems. Since the system operates in both continuous action and continuous observation spaces, models suitable for such domains were considered. Research has shown that the DDPG model is widely used in such environments, followed by TD3, PPO, SAC, and TRPO. In this study, the SAC algorithm has been preferred. The SAC model is an algorithm that performs well in complex, continuous-space problems encountered in real-world applications. It utilizes an entropy regulator, which not only maximizes rewards but also increases policy uncertainty, thereby enhancing the exploration process of agents [30]. Thanks to these features, it is commonly used in complex control tasks, robotic applications, and other continuous-space RL scenarios. The model of the algorithm is presented in Equation (22).

$$J\left(\pi \right)=\sum _{t=0}^{T}E\left(s_t,a_t\right)~ {\rho }_{\pi }\left[r\left(s_t,a_t\right)+aH\left(\pi \left(·|s_t\right)\right)\right]$$

(22)

J(π): Objective function measuring the performance of the policy, ρ_π: Distribution of states followed by the policy, r (s_t,a_t): Reward of the action at in state s_t, α: A scaling parameter for the entropy term, γ: Discount factor of future rewards. H (π (·∣s_t)): Entropy of the action distribution of policy π in state s_t.

AC utilizes three networks. These are the state value function (V), the soft Q function and the policy function (π). The state value function is parameterized by ψ, the soft Q function is parameterized by θ and the policy function is parameterized by ϕ.

The state value function calculates the total expected reward from a specific state.

$$J_{\nu }\left(\psi \right)=E_{s_t-D}\left[{\displaystyle \frac{1}{2}}{\left(V_{\mathsf{\psi }}\left(s_t\right)-E_{a_t-{\pi }_{\Phi }}\left[Q_{ϴ}\left(s_t,a_t\right)-log{\pi }_{\Phi }\left(a_t\right|s_t)\right]\right)}^2\right]$$

(23)

$V_{\mathsf{\psi }}\left(s_t\right)$: Estimation of the value function for state $s_t$.

D: Situations in the experience pool (replay buffer).

$Q_{ϴ}\left(s_t,a_t\right)$: Estimation of the Q-value function for a given state and action.

${\pi }_{\Phi }\left(a_t\right|s_t)$: It represents the policy function that has the probability of choosing an action when the situation is given.

The soft Q function parameters are trained to minimize the residuals from the soft Bellman equation shown in Equations (24) and (25).

$$J_Q\left(ϴ\right)=E_{{(s}_t,a_t)-D}\left[{\displaystyle \frac{1}{2}}{\left(V_{ϴ}\left(s_t,a_t\right)-\widehat{Q}\left(s_t,a_t\right)\right)}^2\right]$$

(24)

$$\widehat{Q}\left(s_t,a_t\right)=r\left(s_t,a_t\right)+\gamma E_{s_{t+1~p}}\left[V_{\overline{\psi }}\left(s_{t+1}\right)\right]$$

(25)

$r\left(s_t,a_t\right)$: Instantaneous reward obtained by action a_t in state s_t.

γ: discount factor used to calculate the present value of future rewards.

$V_{\overline{\psi }}\left(s_{t+1}\right)$: It represents the state value function.

The SAC algorithm encourages exploration during policy updates by using an entropy regularizer. However, some SAC variants employ KL Divergence during policy updates to ensure that the new policy does not deviate too far from the old policy Equation (26). KL Divergence is a metric that quantifies the difference between two probability distributions.

$$J_{\pi }\left(\varphi \right)=E_{s_t-D}\left[D_{KL}\left({\pi }_{\varnothing }\left(.|S_t\right){\displaystyle \frac{\mathit{exp}\left(Q_{\theta }\left(s_t,·\right)\right)}{Z_{\theta }\left(s_t\right)}}\right)\right]$$

(26)

$Z_{\theta }\left(s_t\right)$: It is a partition function, it serves to normalize the distribution, although it is generally stubborn, it does not contribute to the gradient according to the new policy, so it is ignored.

$Q_{\theta }\left(s_t,·\right)$: It expresses the action distribution of the Q value function in the s_t case.

For a comprehensive description of the SAC algorithm, including the update rules and implementation details, the reader is referred to Figure S1.

The proposed control strategy employs the Soft Actor-Critic (SAC) algorithm, which uses an actor-critic architecture to optimize policy and value estimation. Detailed algorithmic procedures, including the actor and critic update rules, are provided in Figure S1.

A key feature of SAC is entropy regulation. The policy is trained to maximize the balance between the expected payoff and entropy, which measures the randomness in the policy. This is closely related to the exploration-exploitation tradeoff. Increasing entropy promotes more exploration, thereby accelerating learning. It also helps prevent the policy from prematurely converging to a poor local optimum. The agent used in training consists of two neural networks: the critic and the actor. The structure of the actor and critic networks is depicted in Figure 7. These networks serve as function estimators [31]. The structure of the neural networks in our study is specified as follows: the critic takes the state and action as inputs and outputs a value function that estimates future rewards. The term Time Division Error (TD-error) usually refers to time slot overlaps or timing errors in time division multiplexing systems. The actor network takes the state observed by the agent as input; this state represents information from the environment. The output includes the average action value and the standard deviation of the action.

3.1. Nominal Reference Dynamic Reward

One of the significant challenges in RL is designing the reward function. To shape the reward function effectively and achieve the desired results, a deep understanding of the system and expertise in the relevant field are essential. Additionally, this process involves various optimization problems. In this study, a nominal dynamic reward function was developed to determine rewards and penalties. During the simulation process, parameters such as exceedance rate, rise time, and settling time were updated according to the initial and target values for each iteration. The limits were adjusted based on these parameters in each iteration Figure 8. Within the framework of these established limits, a penalty was applied in the event of a limit violation using the Exterior Penalty Function.

The mathematical formula for the function used to generate penalties in the event of a violation of specific constraints is provided Equation (27).

$$P\left(\overrightarrow{x},w_h,w_g\right)=w_h\sum _{j=1}^l{\left(h_j\left(\overrightarrow{x}\right)\right)}^2+w_g\sum _{i=1}^m{\left(max\left\{0,g_i\left(\overrightarrow{x}\right)\right\}\right)}^2$$

(27)

$\overrightarrow{x}$: Represents decision variables. w_h and w_g: Weight coefficients used in the penalty function. These coefficients determine the contributions of equality and inequality constraints to the penalty function. $h_j\left(\overrightarrow{x}\right)$: Represents the j-th equality constraint. Equality constraints require the system to satisfy a certain condition. $g_i\left(\overrightarrow{x}\right)$: Represents the i-th inequality constraint. Inequality constraints ensure that a system stays within certain limits. ${\sum }_{j=1}^l$ and ${\sum }_{i=1}^m$: Express the sums of equality and inequality constraints. $max\left\{0,g_i\left(\overrightarrow{x}\right)\right\}$: A function used in case of violation of the inequality constraint. If $g_i\left(\overrightarrow{x}\right)$ is greater than zero, the constraint is violated and the penalty is applied; otherwise, the penalty is not applied. This reward function is applied separately to each axis of the aircraft. For example, the reward-penalty algorithm for the pitch angle is shown in Figure S2.

3.2. Overall Control of the TR-VTOL UAV RL Neural Network Implementation System

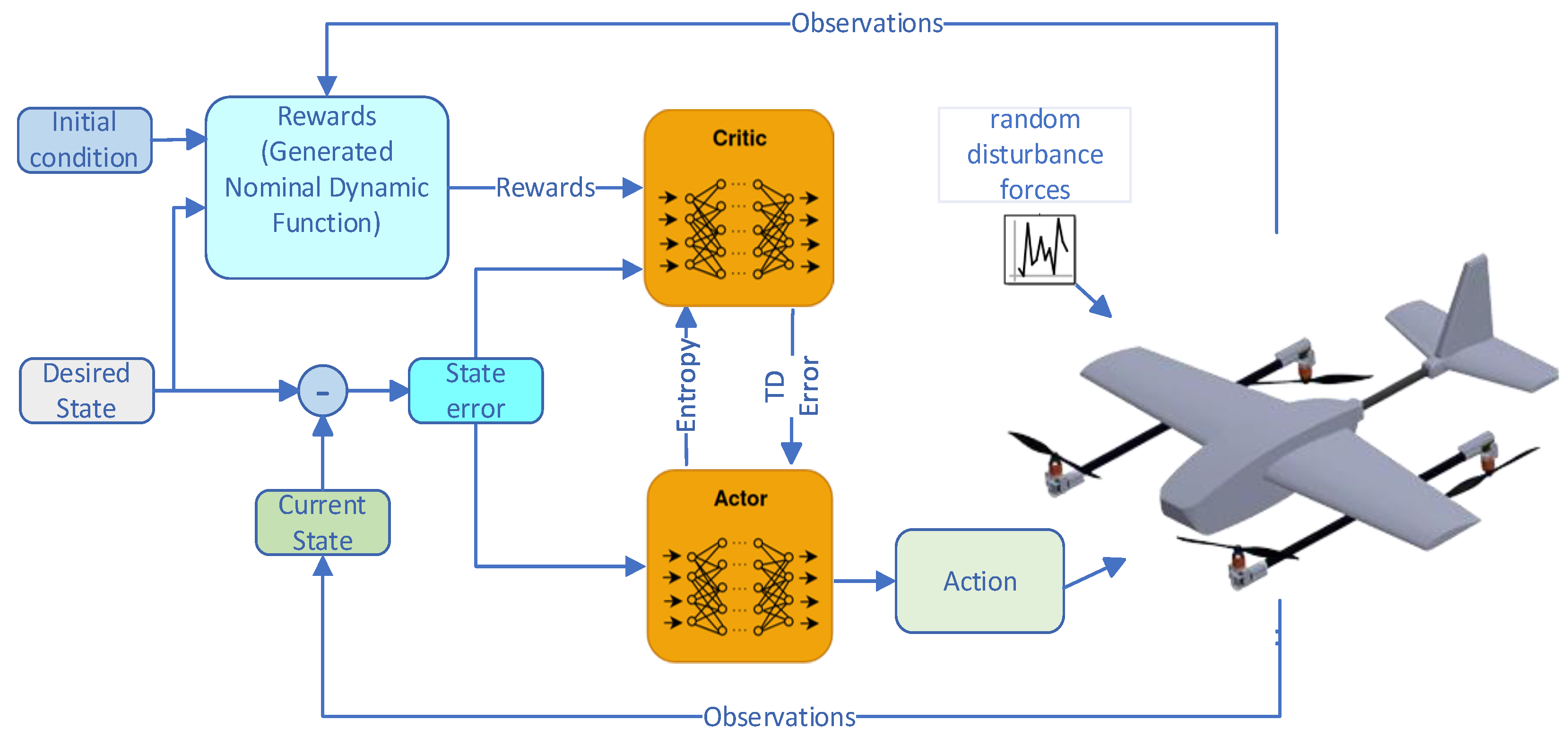
The control architecture of the system with RL is shown in Figure 9. Random desired references and initial conditions for the quad mode and fixed-wing flight mode were generated using a uniform distribution. Specifically, roll angles were sampled independently from [−0.4, 0.4] rad (≈±23°), pitch angles from [−0.3, 0.3] rad (≈±17°), and yaw angles (heading) from [−0.1, 0.1] rad (≈±5.7°). The initial values of roll, pitch, and yaw angles are also randomly selected within the same ranges. This allows moderate roll and pitch variations while keeping heading errors small, avoiding non-physical or infeasible flight states.

During training, an error signal is obtained by comparing randomly generated reference and initial values for the model. The RL agent makes inferences based on the observed values and the reward generated by the nominal dynamic equation, attempting to send the most appropriate command to the aircraft.

To accurately replicate real-world flight conditions during simulation, uniform random external disturbance forces were introduced to emulate the effects of unpredictable environmental interactions. These physical perturbations were applied directly to the UAV body in multiple directions to test the robustness of the control policy under dynamic and uncertain conditions. The quantitative parameters used to characterize these disturbances are summarized in

Table 2. Parameters of Random Disturbance Forces.

Disturbance Type	Applied Axis	Magnitude	Distribution	Purpose
External Force	X, Y, Z (Body Axes)	±2 N	Uniform	Evaluate control policy under physical disturbances

.

Figure 9 illustrates the RL neural network implementation scheme, which includes the actor, critic, entropy, and temporal-difference (TD) error components of the SAC algorithm. As shown, the desired value is compared with the initial value of the model to generate an error signal. The Actor block represents the policy function, which selects actions in different states and improves decision-making by updating policy parameters during training. The critic block represents the Q-value function, estimating the quality of the Actor’s actions. The entropy term in SAC increases policy uncertainty, enabling the policy to explore a broader distribution of actions. The maximum entropy strategy not only maximizes the expected return but also encourages exploration by preventing the policy from becoming overly deterministic, thereby improving the exploration–exploitation balance. The TD error quantifies the discrepancy between the target Q-value and the Critic’s estimate; this error is used to update the critic network. Finally, the RL agent receives a reward signal from the nominal dynamic model, which provides feedback on the quality of the current system state.

4. Simulation Results

To evaluate the effectiveness of the proposed reinforcement learning framework, simulations were conducted for both single-agent and multi-agent implementations of the SAC algorithm. The training was carried out separately for quadcopter and fixed-wing flight modes. At the end of the training process, the controllers were assessed in terms of reward convergence speed and the final reward values achieved. The following subsections present the training outcomes, including the number of episodes and time required for convergence, as well as the corresponding reward evolution for each configuration.

In the single-agent case, training with the SAC algorithm lasted for 2500 episodes, corresponding to approximately 2 h and 21 min of simulation time. The agent achieved an average reward of −1.7, which represents the baseline performance for comparison with the multi-agent approach, as illustrated in Figure 10.

Although improvements were observed with the single-agent SAC algorithm, a multi-agent implementation was adopted to further enhance vehicle stabilization. One of the simulation results obtained from applying the multi-agent SAC algorithm is presented in Figure 11. Notably, the training process was observed to be 98% shorter compared to the single-agent scenario. The corresponding training parameters are summarized in the table below. The multi-agent training lasted 121 episodes, taking 3 min and 56 s, with the average rewards recorded as −0.03, −0.057, and −0.022. Vehicle control was successfully achieved using the RL agents trained in these separate sessions, demonstrating both faster convergence and improved stabilization performance.

The proposed multi-agent Soft Actor-Critic (MA-SAC) controller was trained separately for quad-mode and fixed-wing mode; the controllers provide attitude regulation about the roll, pitch and yaw axes in both modes. Figure 12 shows the roll tracking performance in quad-mode: the desired roll trajectory (reference) is closely tracked by the learned policy, with small transient deviations during setpoint changes and negligible steady-state error.

Figure 13 illustrates the pitch tracking performance in quad-mode. The desired pitch trajectory (reference) is followed closely, with small transient deviations during setpoint changes and negligible steady-state error.

Figure 14 shows the yaw tracking performance in quad-mode. The desired yaw trajectory (reference) is tracked accurately, with minor transient deviations during setpoint changes and minimal steady-state error.

Axis control in fixed wing mode is shown in Figure 15, Figure 16 and Figure 17. Figure 15 illustrates the roll-axis tracking performance of the UAV in fixed-wing mode. As can be seen, the UAV generally follows the commanded roll angle. However, no significant overshoot or delay occurs during setpoint changes. This indicates that, although slight deviations are observed in the roll axis, the control algorithm maintains accuracy and stability.

Figure 13 shows the pitch tracking performance in fixed-wing mode. The UAV accurately follows the desired pitch, staying within a ± ε band without overshoot during setpoint changes.

Figure 17 illustrates the yaw-axis tracking performance of the UAV in fixed-wing mode. As seen, the UAV follows the commanded yaw angle; however, the tracking range is slightly wider compared to the other axes. No significant overshoot is observed during setpoint changes. This indicates that the control algorithm provides stable yaw-axis tracking, but its accuracy is somewhat limited compared to the other axes.

The vertical take-off, transition to horizontal flight, fixed-wing motion, transition back to vertical flight, and vertical landing of the Tilt Rotor fixed-wing UAV were carried out as follows. In Q1, the vehicle performed a vertical take-off in quadcopter mode and reached the target altitude. To achieve the required speed for switching to fixed-wing mode, it accelerated forward while moving horizontally in quadcopter mode during Q2. In Q3, the vehicle maintained stable motion in fixed-wing mode. During Q4, preparations for vertical landing were conducted as the vehicle transitioned back to quadcopter mode. Finally, in Q5, the operation concluded with a vertical landing in quadcopter mode. The entire sequence is illustrated using two complementary visualizations: the altitude (H) profile in Figure 18 and the MATLAB UAV Animation (version 2023b) in Figure 19.

Figure 20 illustrates the fixed-wing motion of the TR-VTOL UAV during circular maneuvers. The vehicle executes smooth and stable turns in response to the commanded roll angles, forming circular paths without following a predefined reference trajectory. This visualization demonstrates the capability of the control system to maintain stability and orientation during continuous maneuvering, with only minor deviations caused by aerodynamic effects.

Beyond qualitative visualizations, a quantitative evaluation of the proposed controller was conducted by comparing its performance with existing approaches in both hover and fixed-wing modes. The following analysis presents detailed results in terms of RMSE, rise time, settling time, and overshoot. In the hover mode, the RMSE values of the roll, pitch, and yaw axes were compared with the AC NN and NTSMC methods [9]. As shown in

Table 3. Analysis of Control Root Mean Square Errors (RMSE) Hover Mode.

Experiments	Proposed (SAC)	(AC NN)	(NTSMC)
RMS Error of roll angle (°)	0.058	0.153	0.484
RMS Error of pitch angle (°)	0.083	0.1758	0.629
RMS Error of yaw angle (°)	0.070	0.311	0.316

, the proposed SAC controller reduced the roll RMSE from 0.153 (AC NN) to 0.058, corresponding to a 62.1% improvement; the pitch RMSE from 0.1758 (AC NN) to 0.083, corresponding to a 52.8% improvement; and the yaw RMSE from 0.311 (AC NN) to 0.070, corresponding to a 77.5% improvement. The percentage improvement was calculated as: (reference−proposed)/reference × 100.

In the fixed-wing flight mode, the multi-agent SAC algorithm was compared with the PPO algorithm [33], a classical PID controller, and the method in [34] under both no-wind and (20 m/s) constant wind conditions. As shown in

Table 4. Analysis of Control Root Mean Square Errors (RMSE) Fixed Wing Mode.

Experiments	Controller	Rise Time (s)		Settling Time (s)		Overshot (%)
		φ	θ	φ	θ	φ	θ
No Wind	Proposed RL (SAC)	0.158	0.103	0.267	0.254	0	0
	PPO RL	0.265	0.661	1.584	1.663	21	24
	PID without RL	1.344	0.228	2.050	1.364	4	17
Constant Wind (20 m/s)	Proposed RL (SAC)	0.084	0.016	0.261	0.267	0	0
	PPO RL	0.166	1.792	2.903	3.280	122	93
	PID without RL	0.930	0.945	3.576	5.256	92	80

, the proposed SAC controller shows improved performance compared to PPO and PID, particularly in terms of settling time and rise time. In the no-wind case, the roll rise time was reduced from 0.265 s (PPO) to 0.158 s (SAC), corresponding to a 40.4% improvement, while the pitch rise time was reduced from 0.661 s (PPO) to 0.103 s (SAC), yielding an 84.4% improvement. Settling times were shortened by more than 80% in both roll and pitch compared with PPO and PID. While the SAC controller reduced rise time and settling time compared to PPO and PID, it did not achieve an improvement in overshoot performance. Instead, SAC maintained a small steady tracking error without exceeding the reference, whereas PPO exhibited overshoot of 21% and 24% for roll and pitch, respectively, and PID without RL showed overshoot of 4% and 17%. Under 20 m/s constant wind, the SAC algorithm maintained stable performance. As shown in Table 4, rise and settling times for the pitch axis were lower than those observed with PPO and PID controllers, while overshoot present in the other controllers was not observed with SAC. These results indicate that the proposed multi-agent SAC model provides stable transient responses under wind conditions.

Overall, the results confirm that the proposed multi-agent SAC controller achieves superior tracking accuracy and transient response compared to baseline methods.

5. Conclusions and Future Work

This study investigated the training of a TR-VTOL UAV using reinforcement learning (RL), emphasizing the importance of algorithm selection, reward function design, and the development of an appropriate training environment. One of the main contributions is the introduction of a nominal dynamic reward function. At each iteration of the training process, reward values were dynamically generated based on varying initial and target conditions. Training across diverse scenarios improved the stabilization performance of the TR fixed-wing UAV.

Another key innovation is the adoption of a multi-agent structure, where a separate agent is assigned to control each axis. This allows control tasks to be distributed among agents, enabling sensor data for each control input to be processed independently and reward values to be generated dynamically. As a result, the agents reached appropriate control values more efficiently during training. Since extensive iterations are required and direct real-world training may risk damaging the aircraft before the RL model is fully learned, the entire training procedure was conducted in a simulation environment.

For future work, the proposed control architecture will be further evaluated under varying wind and turbulence conditions to provide a more comprehensive performance assessment. In addition, real-flight experiments will be carried out to validate the practical applicability of the method. To improve computational efficiency, faster training algorithms and advanced optimization techniques will be investigated. Finally, the proposed approach will be extended to different VTOL configurations to assess its generalization capability in other complex flight tasks.