Research on ATFM Delay Optimization Method Based on Dynamic Priority Ranking
Abstract
1. Introduction
- How can a flight prioritization mechanism be designed to reflect network-wide effects, moving beyond airline-centric or localized strategies? How do different priority strategies affect global network performance, in terms of total delay and delay distribution equity?
- How can an ATFM delay optimization model be developed to effectively capture resource coupling in a multi-resource environment, thereby avoiding local optima and enhancing overall capacity utilization and network efficiency?
- Introduction of an Improved Constrained Position Shifting (CPS) Constraint with Priority Strategies: The study refines the traditional CPS constraint by integrating priority strategies into the model. In alignment with the Target CASA framework, the modified CPS constraint incorporates restricted displacement strategies under different priority levels. Additionally, to investigate the trade-off between efficiency and fairness in the optimization model, three distinct priority strategies are introduced, examining the relationship between priority levels and allowable displacement.
- Development of a Dynamic Priority-Based ATFM Delay Optimization Model for Multi-Resource Scenarios: A Mixed-Integer Linear Programming (MILP) model is formulated to optimize ATFM delay by dynamically adjusting flight priorities across multiple hotspots. By reordering traffic flows passing through congested areas, the model enhances network-wide delay management through an adaptive priority mechanism.
- Enhancement of the Existing FCFS-Based Sequencing Strategy: Building upon the priority-based approach of the UDPP, this study introduces a global priority-setting mechanism that considers network-wide impacts. This mechanism extends beyond single-resource scenarios and is validated in a multi-resource environment to assess its effectiveness.
2. Literature Review
2.1. ATFM Delay Optimization
2.2. Priority-Based ATFM Delay Assignment
3. Methodology
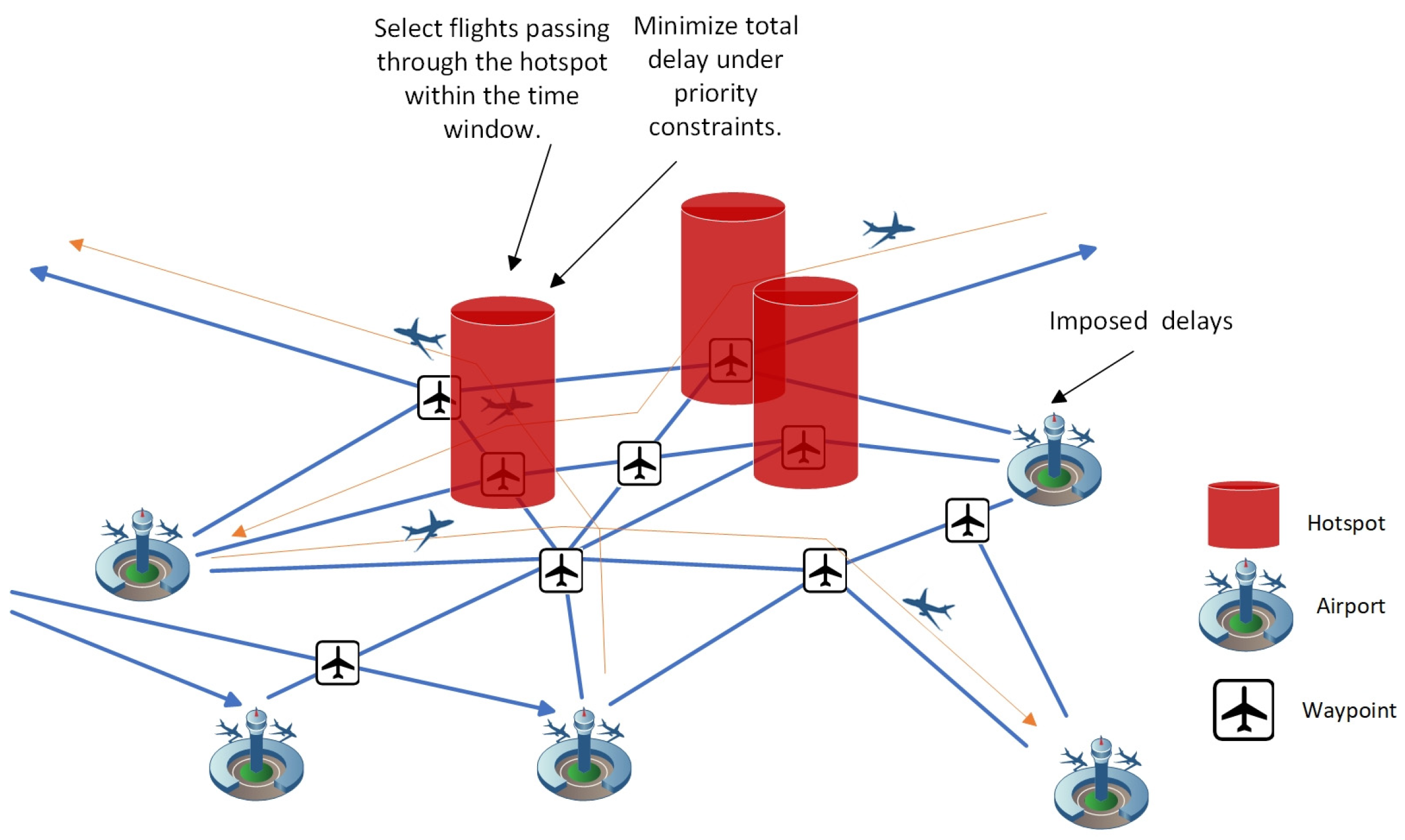
3.1. Demand–Capacity Balancing Network
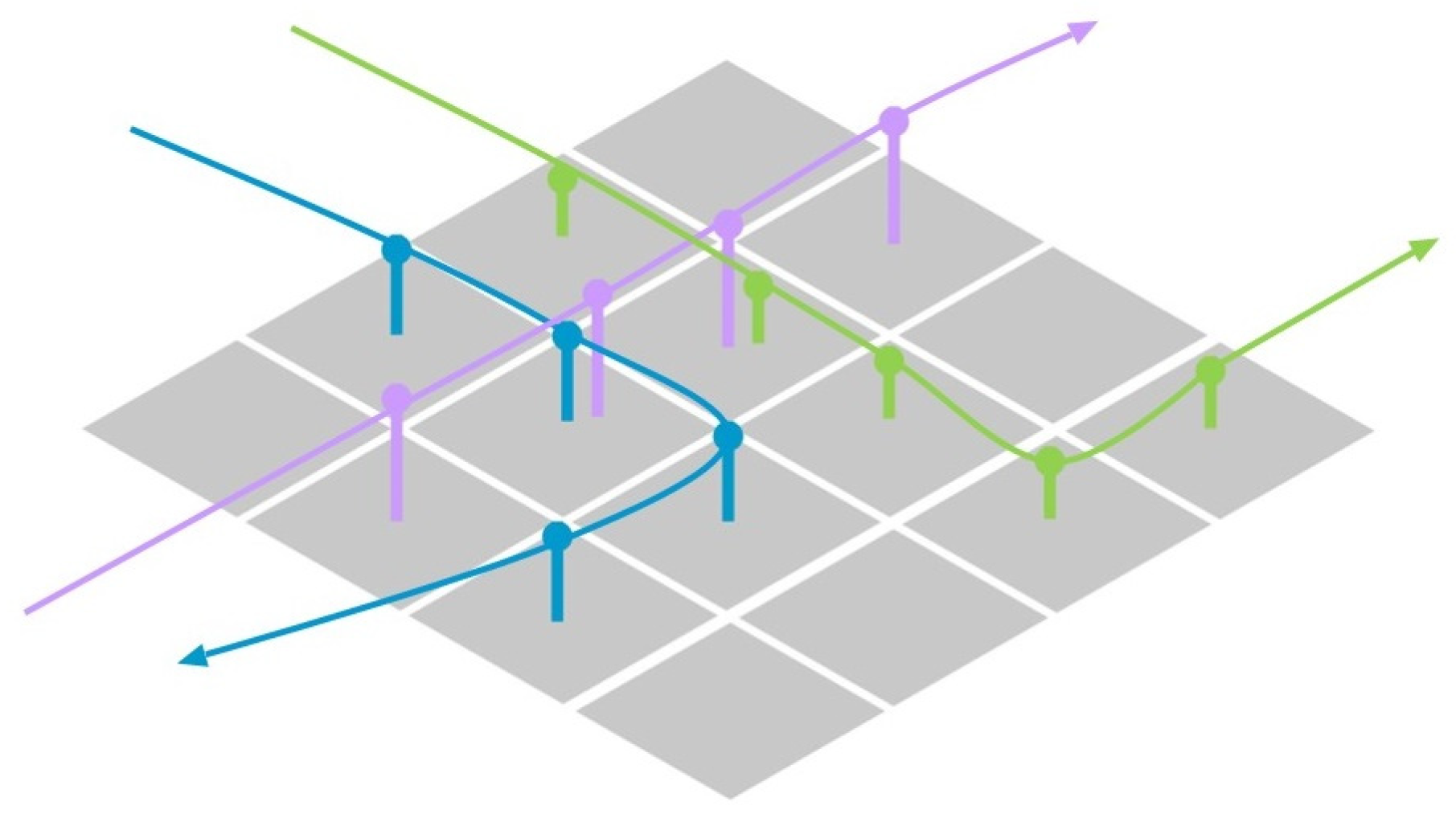
3.2. Delay Conflict Mechanism Under Multi-Resource Constraints
3.3. Dynamic Priority Strategy
3.3.1. Priority Definition
- Congestion level at the departure airport: Represented by the ratio of traffic to capacity at the airport within a given timeframe, this indicator reflects the airport’s ability to handle operations and determines its congestion level. Airport capacity refers to the published departure capacity, while traffic is defined as the unconstrained demand based on flight plans.
- Occurrence of preceding delays: Flights experiencing preceding delays are given higher priority. Preceding delay is determined using the difference between the Scheduled Off-Block Time (SOBT) and the Actual Off-Block Time (AOBT).
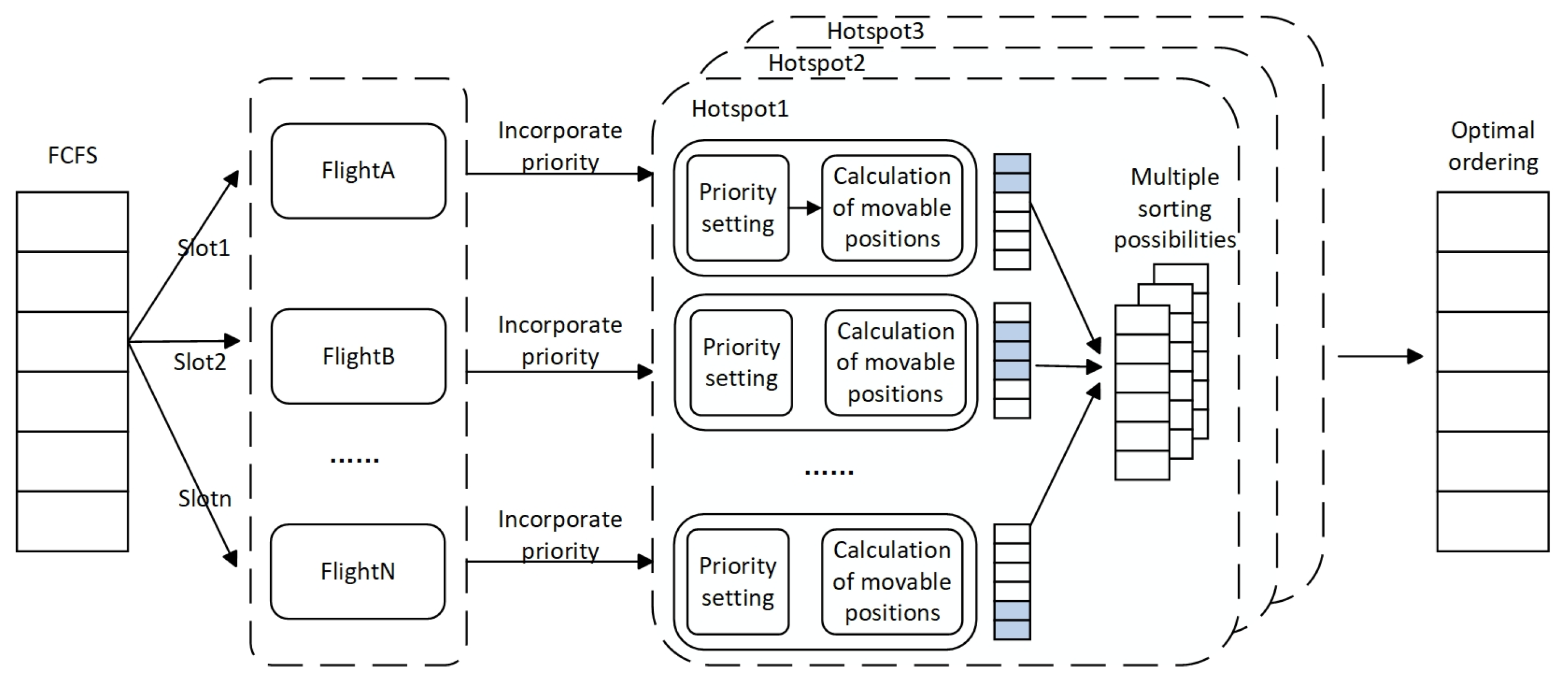
3.3.2. Dynamic Priority Strategy
- Proportional Constrained Position Shift (PCPS)
- 2.
- Exponential Constrained Position Shift (ECPS)
- 3.
- Balanced Constrained Position Shift (BCPS)
4. Dynamic Priority-Based ATFM Delay Optimization Model
- The model’s solution is strictly implementable, with flights adhering to their planned overflight times.
- Flights passing through multiple waypoints may have different delays per segment. To ensure operational reliability, the final delay assigned to a flight in the current iteration is determined by adopting the maximum across the segments.
- It is assumed that cruising time between consecutive waypoints is constant for each flight.
4.1. Variable Definition
4.2. Objective Function
4.3. Constraints
- Network optimization constraints
- 2.
- Sequencing and Scheduling Constraints
- 3.
- Variable Definition and Coupling Constraints
5. Flight Sequence Optimization Algorithm
5.1. Algorithm Principles
- Neighborhood search
- 2.
- Branch-and-bound
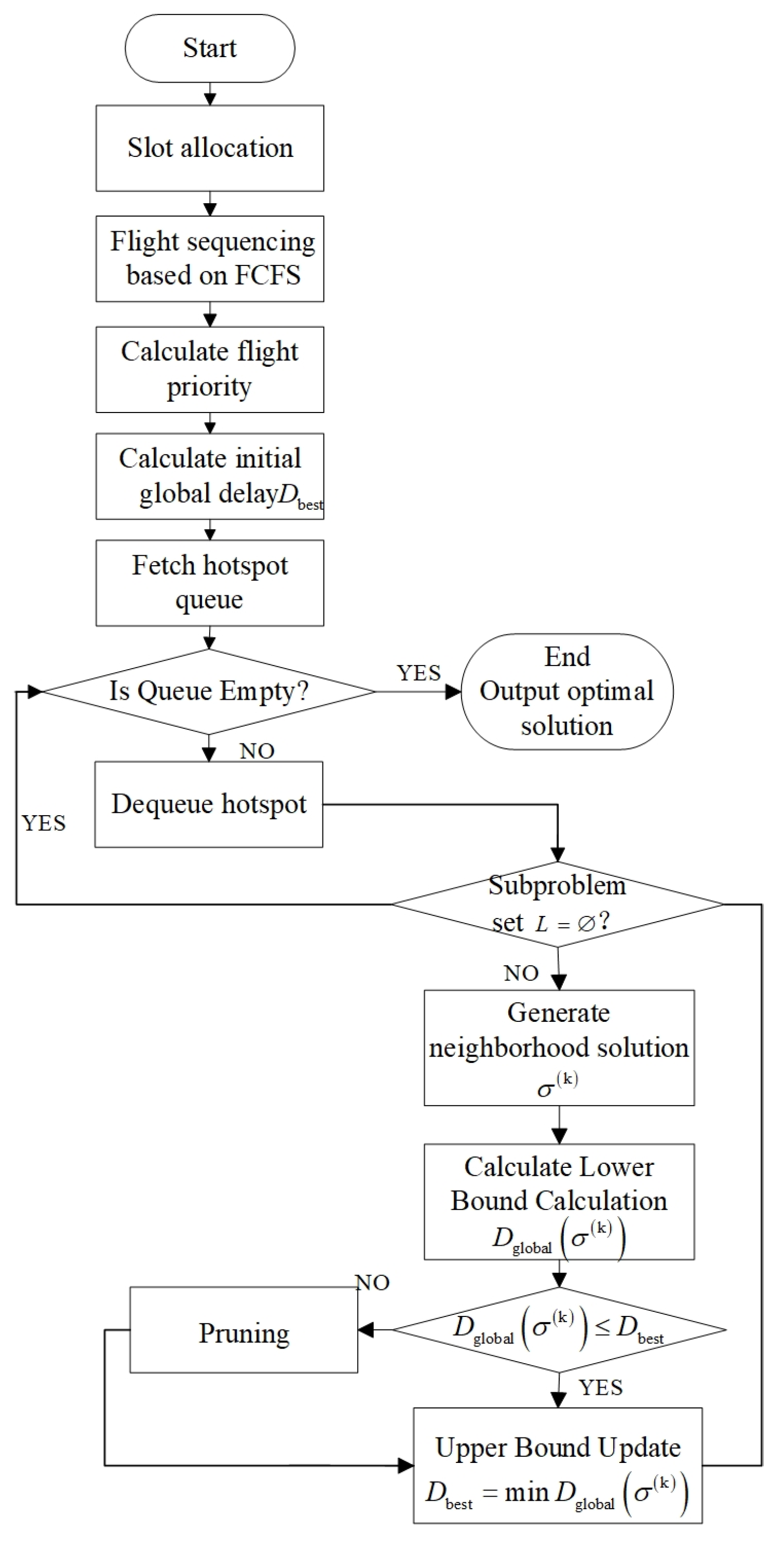
5.2. Algorithm Steps
- 1.
- Initialization
- (i)
- Define variables
- (ii)
- Calculate initial global delay
- 2.
- Hotspot detection
- 3
- Branch-and-Bound
- (i)
- Neighborhood solution generation with constraint checking
- CPS constraint: The reordered flight sequence must remain within the allowable range defined by the Constrained Position Shifting (CPS) constraint. Otherwise, the solution is discarded.
- Minimum separation constraint: After adjusting the flight sequence at the waypoint, the minimum required separation time must be maintained. Otherwise, the solution is discarded.
- (ii)
- Calculate lower bound
- (iii)
- Prune
- (iv)
- Update upper bound
- (v)
- Termination condition and output
6. Validation
6.1. Experimental Setup
6.2. Assessment of Model Performance
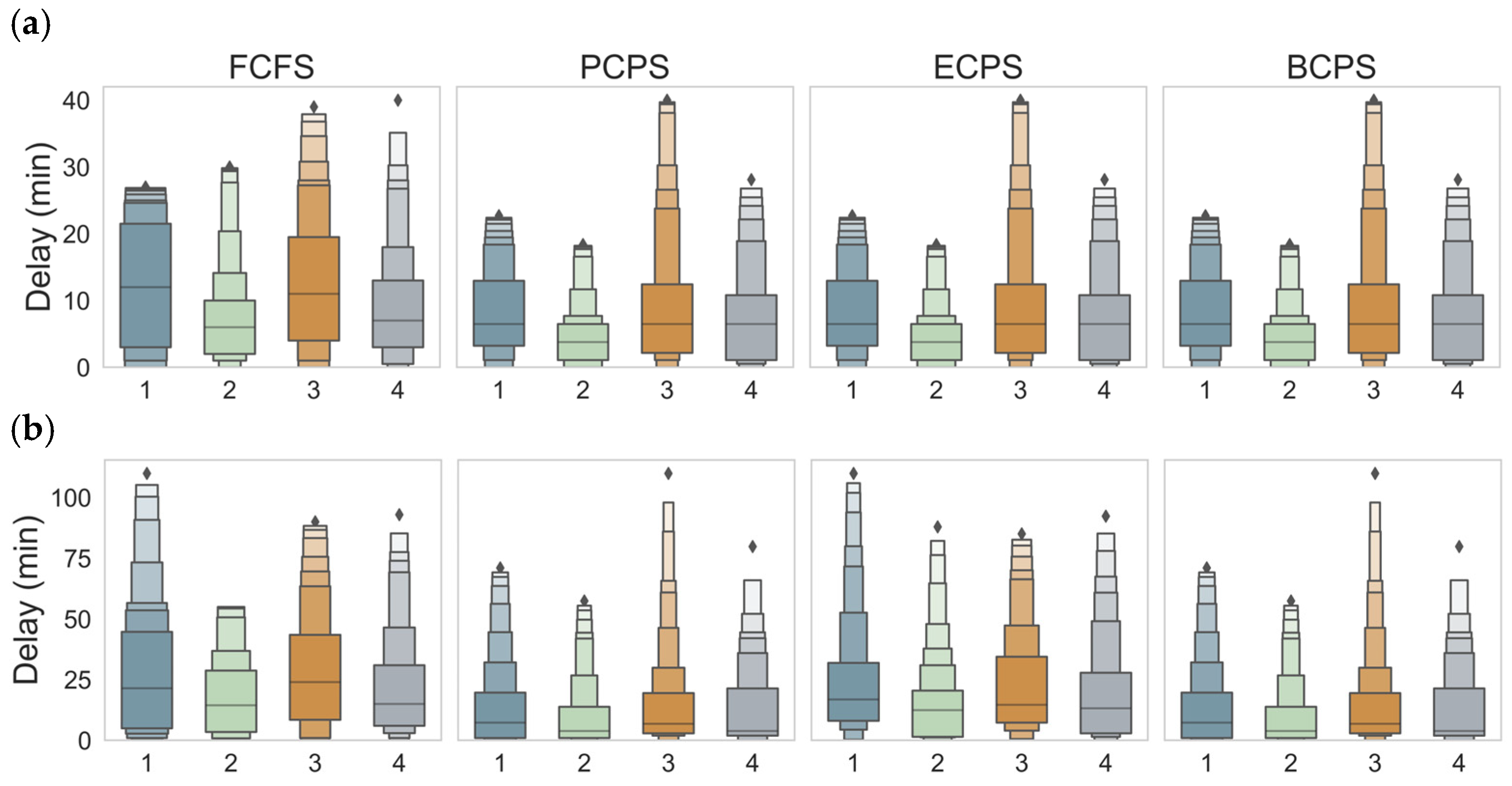
6.2.1. Model Stability Analysis
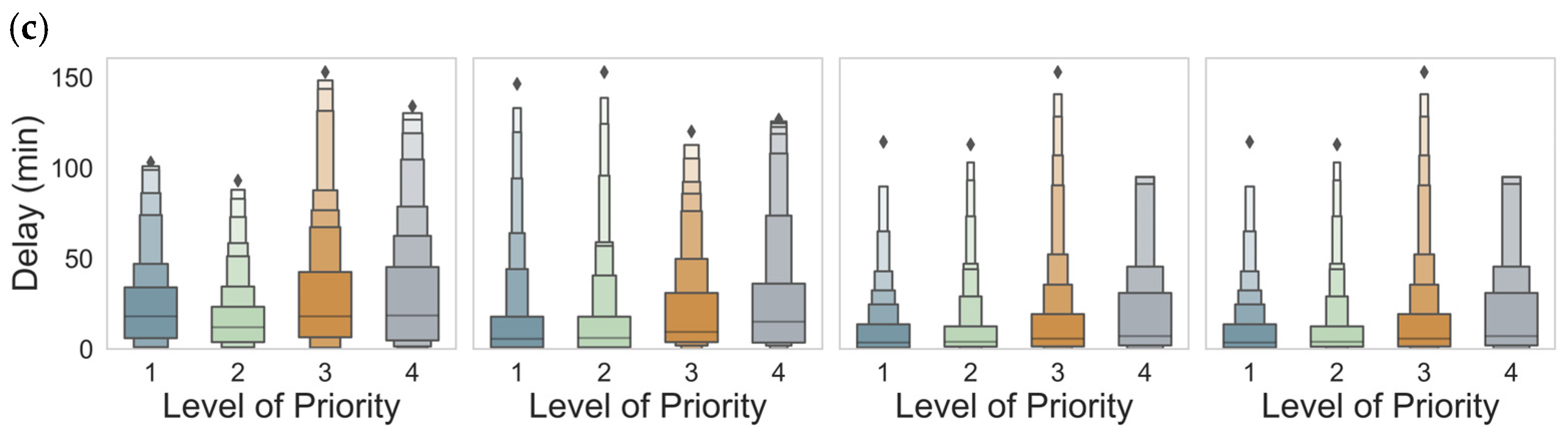
6.2.2. Priority Analysis
6.2.3. Efficiency and Fairness Trade-Off
6.2.4. Effectiveness of Priority Strategies in Different Scenarios
7. Conclusions
- Defining flight priorities based on network-wide effects of delays. Drawing on the core concepts of the target CASA framework, two factors are used to determine flight priority: the traffic level of the departure airport and the presence of preceding delays. A dynamic priority-setting method is proposed to categorize flights into four priority levels. This method introduces new attributes to flights, enabling those with higher value to save more time.
- Establishing three distinct priority strategies and incorporating them into the model using improved CPS constraints. By refining the traditional CPS constraint, the study introduces a method that limits the maximum positional shift K for flights of various priority levels. This allows for adjustments of up to K positions relative to the FCFS sequence. To examine the trade-offs between efficiency and fairness in the optimization model, three priority strategies were developed: PCPS, ECPS, and BCPS.
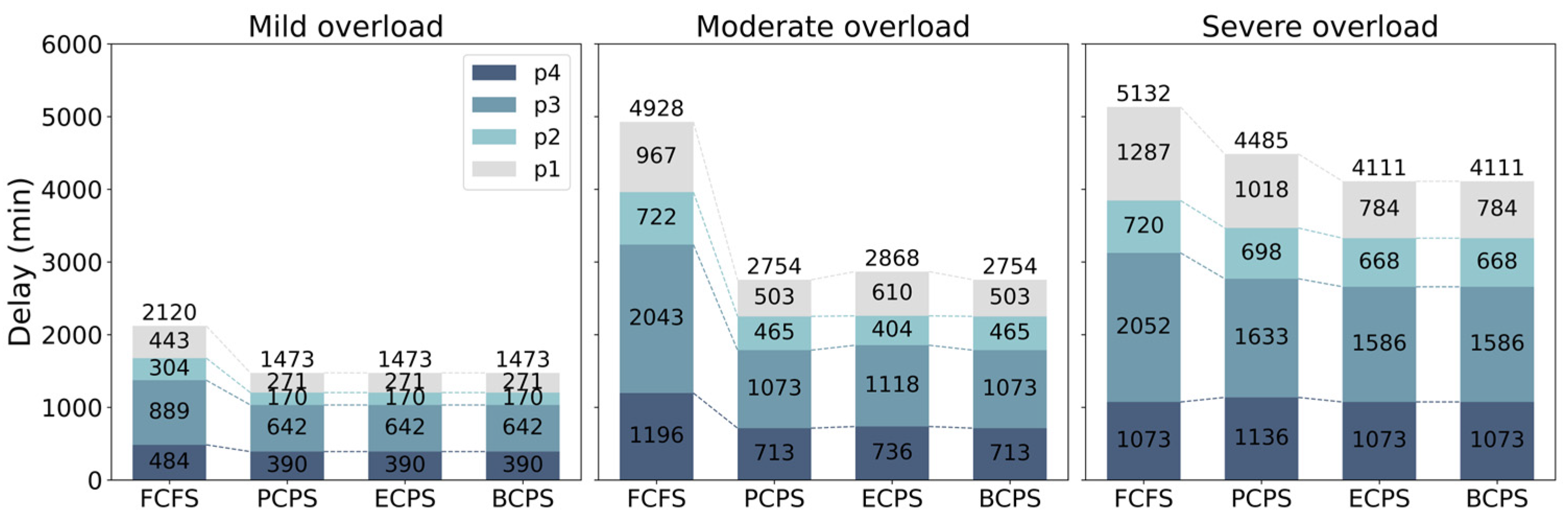
- Developing a dynamic priority-based ATFM delay optimization model. A MILP model was developed to optimize ATFM delays through a dynamic reordering of the air route network’s traffic flows through multiple hotspots. The model demonstrates robust performance in reducing total ATFM delays, redistributing delays across flights, and alleviating demand–capacity imbalances at critical nodes. Validation and testing in various overload scenarios show consistent reductions in total delays, with improvements of 30.5%, 44.1%, and 19.9% under mild, moderate, and severe overload conditions, respectively.
- Exploring the effectiveness of priority strategies under different overload scenarios. A comprehensive evaluation of the three priority strategies was conducted from the perspectives of efficiency and fairness, the delay distribution effects, and computational time. Based on this, the suitable scenarios for each priority strategy were proposed: PCPS is most suitable for light-to-moderate overload scenarios with even flight flow and weak resource competition; ECPS is better suited for severe overload scenarios with a high number of critical flights that require significant optimization of high-priority flight performance; and BCPS, with its more flexible priority adjustment range, balances the optimization needs of different priority flights, making it suitable for complex severe overload scenarios and providing better overall performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AOBT | actual off-block time |
| ATFM | air traffic flow management |
| CASA | Computer-Assisted Slot Allocation |
| CPS | Constrained Position Shifting |
| CTO | calculated time over |
| CTOT | calculated take-off time |
| DCB | demand–capacity balancing |
| ETOs | estimated times over |
| FCFS | First-Come First-Served |
| MPR | Most Penalizing Regulation |
| MILP | Mixed-Integer Linear Programming |
| SOBT | scheduled off-block time |
| TTOT | target take-off time |
| UDPP | User-Driven Prioritization Process |
References
- EUROCONTROL. EUROCONTROL Forecast; EUROCONTROL: Brussels, Belgium, 2023. [Google Scholar]
- Mannino, C.; Nakkerud, A.; Sartor, G. Air traffic flow management with layered workload constraints. Comput. Oper. Res. 2021, 127, 105159. [Google Scholar] [CrossRef]
- Giovanni Lenti. Flow CONOPS; EUROCONTROL: Brussels, Belgium, 2024. [Google Scholar]
- EUROCONTROL. CFMU ATFCM Public Report December 2008; Eurocontrol: Brussels, Belgium, 2009. [Google Scholar]
- SESAR. Sesar Solution PJ07.02 SPR-INTEROP/OSED for V2-Part I; SESAR: Brussels, Belgium, 2007. [Google Scholar]
- SESAR. Step 1 V3 UDPP Validation Report, Optimised Airspace User Operations; Sesar: Brussels, Belgium, 2015. [Google Scholar]
- Gasparin, A.; Castelli, L.; Bolić, T.; Gurtner, G.; Pilon, N. A User-Driven Prioritisation Process implementation and optimisation for ATFM hotspot resolution. Transp. Res. Part C Emerg. Technol. 2025, 170, 104894. [Google Scholar] [CrossRef]
- Pilon, N.; Guichard, L.; Bazso, Z.; Murgese, G.; Carré, M. User-Driven Prioritisation Process (UDPP) from advanced experimental to pre-operational validation environment. J. Air Transp. Manag. 2021, 97, 102124. [Google Scholar] [CrossRef]
- Sesar. 2019 Sesar S.Sesar Solution PJ07.02 SPR-INTEROP/OSED for V2-Part I; SESAR: Brussels, Belgium, 2019. [Google Scholar]
- ICAO GANP PORTAL. Performance Objective; ICAO: Montreal, Canada, 2013. [Google Scholar]
- EUROCONTROL. Network Management Board; EUROCONTROL: Brussels, Belgium, 2012. [Google Scholar]
- ICAO GANP PORTAL. Doc 9971. Manual on Collaborative Decision Making (CDM); ICAO: Montreal, Canada, 2012. [Google Scholar]
- EUROCONTROL. Network Manager Annual Report 2022; EUROCONTROL: Brussels, Belgium, 2023. [Google Scholar]
- ISOBAR. Isobar-Artificial Intelligence Solutions to Meteo-Based DCB Imbalances for Network Operations Planning. Available online: https://www.sesarju.eu/projects/isobar (accessed on 9 January 2025).
- Jacquillat, A.; Odoni, A.R. An Integrated Scheduling and Operations Approach to Airport Congestion Mitigation. Oper. Res. 2015, 63, 1390–1410. [Google Scholar] [CrossRef]
- Bolić, T.; Castelli, L.; Corolli, L.; Rigonat, D. Reducing ATFM s through Strategic Flight Planning. Transp. Res. Part E Logist. Transp. Rev. 2017, 98, 42–59. [Google Scholar] [CrossRef]
- Wang, D.; Zhao, Q. A Simultaneous Optimization Model for Airport Network Slot Allocation under Uncertain Capacity. Sustainability 2020, 12, 5512. [Google Scholar] [CrossRef]
- Presto, F.; Gollnick, V.; Lau, A.; Lütjens, K. Flight Frequency Regulation and its Temporal Implications. Transp. Policy 2022, 116, 106–118. [Google Scholar] [CrossRef]
- Delgado, L.; Prats, X. Simulation of Airborne ATFM Delay and Delay Recovery by Cruise Speed Reduction. In Proceedings of the SESAR Innovation Days, Toulouse, France, 28–30 December 2011. [Google Scholar]
- Prats Menéndez, X.; Hansen, M. Green Delay Programs, Absorbing ATFM Delay by Flying at Minimum Fuel Speed. Air Traffic Manag. Res. Dev. 2011, 2011, 1–8. [Google Scholar]
- Dalmau, R. Predicting the Likelihood of Airspace User Rerouting to Mitigate Air Traffic Flow Management. Transp. Res. Part C Emerg. Technol. 2022, 144, 103869. [Google Scholar] [CrossRef]
- Chen, J.; Pan, S.; Peng, W.; Xu, W. Bilinear Spatiotemporal Fusion Network: An efficient approach for traffic flow prediction. Neural Netw. 2025, 187, 107382. [Google Scholar] [CrossRef]
- Chen, J.; Ye, H.; Ying, Z.; Sun, Y.; Xu, W. Dynamic trend fusion module for traffic flow prediction. Appl. Soft Comput. 2025, 174, 112979. [Google Scholar] [CrossRef]
- Castelli, L.; Corolli, L.; Lulli, G. Critical Flights Detected with Time Windows. Transp. Res. Rec. J. Transp. Res. Board 2011, 2214, 103–110. [Google Scholar] [CrossRef]
- Xu, Y.; Prats, X.; Delahaye, D. Synchronized Demand-capacity Balancing in Collaborative Air Traffic Flow Management. Transp. Res. Part C Emerg. Technol. 2020, 114, 359–376. [Google Scholar] [CrossRef]
- Zhang, Q.; Le, M.; Xu, Y. Collaborative Delay Management Towards Demand-capacity Balancing within User Driven Prioritisation Process. J. Air Transp. Manag. 2021, 91, 102017. [Google Scholar] [CrossRef]
- Barnhart, C.; Bertsimas, D.; Caramanis, C.; Fearing, D. Equitable and Efficient Coordination in Traffic Flow Management. Transp. Sci. 2012, 46, 262–280. [Google Scholar] [CrossRef]
- de Villardi de Montlaur, A.; Delgado, L. Flight and Passenger Efficiency-fairness Trade-off for ATFM Assignment. J. Air Transp. Manag. 2020, 83, 101758. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, Y.; Hu, M. General Multi-agent Reinforcement Learning Integrating Heuristic-based Delay Priority Strategy for Demand and Capacity Balancing. Transp. Res. Part C Emerg. Technol. 2023, 153, 104218. [Google Scholar] [CrossRef]
- Chen, Y.; Hu, M.; Xu, Y.; Yang, L. Locally generalised multi-agent reinforcement learning for demand and capacity balancing with customised neural networks. Chin. J. Aeronaut. 2023, 36, 338–353. [Google Scholar] [CrossRef]
- International Civil Aviation Organization. ICAO EUR Regional Performance Framework Workshop; ICAO: Montreal, QC, Canada, 2018. [Google Scholar]
- Guvercin, M.; Ferhatosmanoglu, N.; Gedik, B. Forecasting flight delays using clustered models based on airport networks. IEEE Trans. Intell. Transp. Syst. 2020, 22, 3179–3189. [Google Scholar] [CrossRef]
- Zhixing, T.; Shan, H.; Songchen, H. Recent progress about flight delay under complex network. Complexity 2021, 2021, 5513093. [Google Scholar] [CrossRef]
- Guo, Z.; Hao, M.; Yu, B.; Yao, B. Detecting Delay Propagation in Regional Air Transport Systems Using Convergent cross Mapping and Complex Network Theory. Transp. Res. Part E Logist. Transp. Rev. 2022, 157, 102585. [Google Scholar] [CrossRef]
- Cai, Q.; Alam, S.; Duong, V.N. A Spatial–temporal Network Perspective for the Propagation Dynamics of Air Traffic Delays. Engineering 2021, 7, 452–464. [Google Scholar] [CrossRef]
- Dear, R.G. The Dynamic Scheduling of Aircraft in the Near Terminal Area. Cambridge, Mass.: Flight Transportation Laboratory; Massachusetts Institute of Technology: Cambridge, UK, 1976. [Google Scholar]
- Balakrishnan, H.; Chandran, B.G. Algorithms for Scheduling Runway Operations Under Constrained Position Shifting. Oper. Res. 2010, 58, 1650–1665. [Google Scholar] [CrossRef]
- Rodríguez-Díaz, A.; Adenso-Díaz, B.; González-Torre, P.L. Minimizing Deviation from Scheduled Times in a Single Mixed-operation Runway. Comput. Oper. Res. 2017, 78, 193–202. [Google Scholar] [CrossRef]
- Bianco, L.; Dell’Olmo, P.; Giordani, S. Scheduling Models for Air Traffic Control in Terminal Areas. J. Sched. 2006, 9, 223–253. [Google Scholar] [CrossRef]
- Malaek, S.M.B.; Naderi, E. A New Scheduling Strategy for Aircraft Landings under Dynamic Position Shifting. In Proceedings of the 2008 IEEE Aerospace Conference, Big Sky, MT, USA, 1–8 March 2008; IEEE: New York, NY, USA, 2008; pp. 1–8. [Google Scholar]
- You, G.; Zhao, Y. A weighted-fair-queuing (WFQ)-based dynamic request scheduling approach in a multi-core system. Future Gener. Comput. Syst. 2012, 28, 1110–1120. [Google Scholar] [CrossRef]
- Kwak, B.J.; Song, N.O.; Miller, L.E. Performance analysis of exponential backoff. IEEE/ACM Trans. Netw. 2005, 13, 343–355. [Google Scholar] [CrossRef]
- Prakash, R.; Piplani, R.; Desai, J. An optimal data-splitting algorithm for aircraft scheduling on a single runway to maximize throughput. Transp. Res. Part C Emerg. Technol. 2018, 95, 570–581. [Google Scholar] [CrossRef]
- Durand, N.; Gianazza, D.; Gotteland, J.B.; Alliot, J.M. Metaheuristics for Air Traffic Management; John Wiley and Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Pawełek, A.; Lichota, P. Tactical and strategic air traffic sequencing with minimum-fuel trajectories. J. Theor. Appl. Mech. 2025, 63, 27–36. [Google Scholar] [CrossRef] [PubMed]

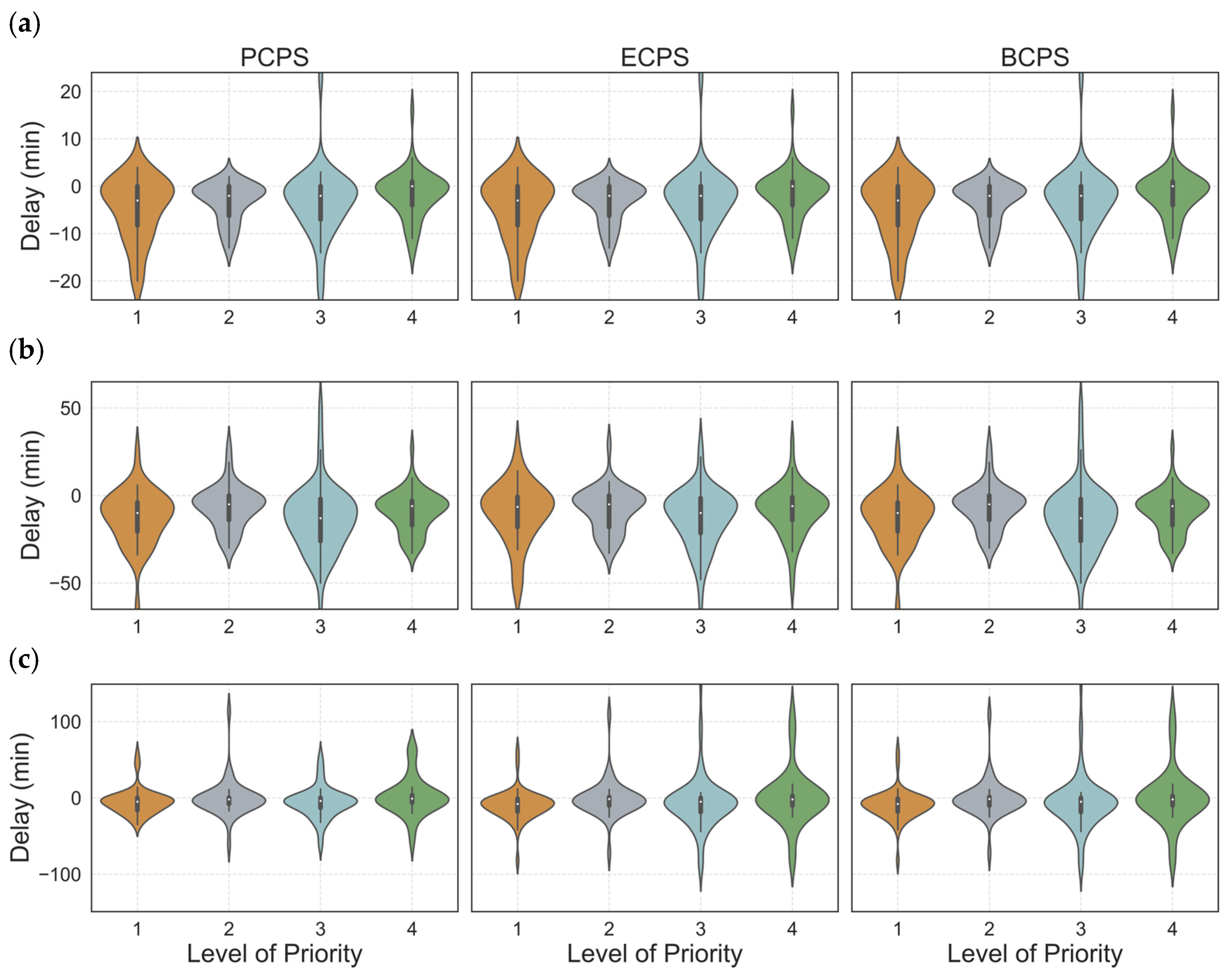
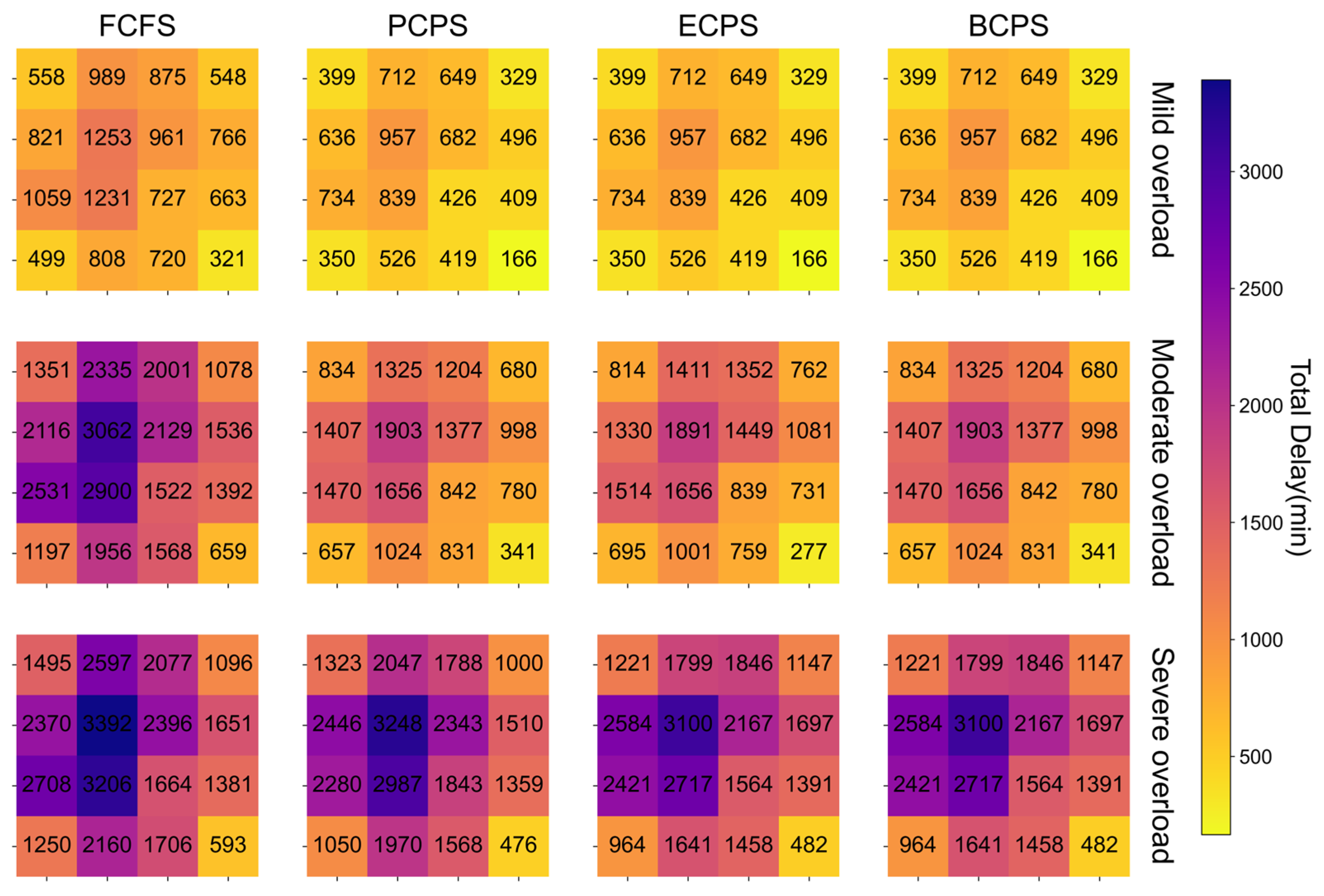

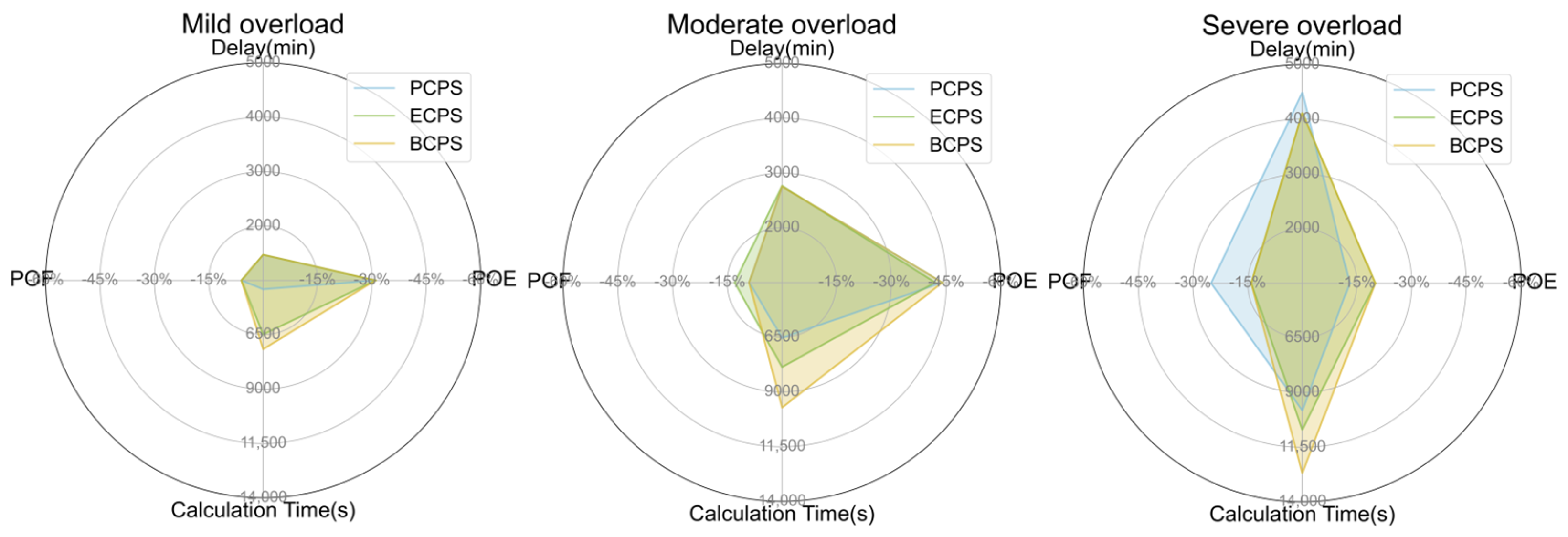
| Priority | Departure Airport Congestion Level | Preceding Flight Delays |
|---|---|---|
| 1 | departing from busy airport | experiencing preceding delays |
| 2 | departing from busy airport | without preceding delays |
| 3 | departing from non-busy airport | experiencing preceding delays |
| 4 | departing from non-busy airport | without preceding delays |
| Priority Strategy | ||
|---|---|---|
| PCPS | ||
| ECPS | ||
| BCPS |
| Constants | Definitions |
|---|---|
| passes | |
| after optimization | |
| , determined by the FCFS rule | |
| Variables | |
| ) | |
| Overload Scenario | Total Number of Congested Waypoints (with at Least One Instance of Congestion) | Average Congestion Duration per Waypoint (Time Windows) | Average Waypoint Load Level |
|---|---|---|---|
| Mild overload | 4 | 2.5 | 1.20 |
| Moderate overload | 6 | 3.5 | 1.28 |
| Severe overload | 7 | 4.1 | 1.44 |
| Overload Scenario | Mean ± SD (Before) | Mean ± SD (After) | Mean Reduction | p-Value |
|---|---|---|---|---|
| Mild overload | 2802 ± 609 | 1631 ± 136 | 1172 | 2.04 × 10−4 |
| Moderate overload | 4228 ± 575 | 2167 ± 496 | 2061 | 1.09 × 10−9 |
| Severe overload | 4813 ± 418 | 3412 ± 913 | 1401 | 4.57 × 10−4 |
| Priority Strategy | PCPS | ECPS | BCPS | |||
|---|---|---|---|---|---|---|
| Overload scenario | POF | POE | POF | POE | POF | POE |
| Mild overload | −6% | −31% | −6% | −31% | −6% | −31% |
| Moderate overload | −9% | −44% | −13% | −42% | −9% | −44% |
| Severe overload | −25% | −13% | −14% | −20% | −14% | −20% |
| Traffic Scenario | Priority Strategy | POE | Delay (min) | POF | Calculation Time (s) |
|---|---|---|---|---|---|
| Mild overload | PCPS | −31% | 1473 | −6% | 4410 |
| ECPS | −31% | 1473 | −6% | 6488 | |
| BCPS | −31% | 1473 | −6% | 7166 | |
| Moderate overload | PCPS | −44% | 2754 | −9% | 6531 |
| ECPS | −42% | 2768 | −13% | 7864 | |
| BCPS | −44% | 2754 | −9% | 9715 | |
| Severe overload | PCPS | −13% | 4485 | −25% | 9807 |
| ECPS | −20% | 4111 | −14% | 10,689 | |
| BCPS | −20% | 4111 | −14% | 12,670 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Li, Y.; Liu, X.; Zhu, J.; Zhao, S. Research on ATFM Delay Optimization Method Based on Dynamic Priority Ranking. Aerospace 2025, 12, 793. https://doi.org/10.3390/aerospace12090793
Zhao Z, Li Y, Liu X, Zhu J, Zhao S. Research on ATFM Delay Optimization Method Based on Dynamic Priority Ranking. Aerospace. 2025; 12(9):793. https://doi.org/10.3390/aerospace12090793
Chicago/Turabian StyleZhao, Zheng, Yanchun Li, Xiaocheng Liu, Jie Zhu, and Siqi Zhao. 2025. "Research on ATFM Delay Optimization Method Based on Dynamic Priority Ranking" Aerospace 12, no. 9: 793. https://doi.org/10.3390/aerospace12090793
APA StyleZhao, Z., Li, Y., Liu, X., Zhu, J., & Zhao, S. (2025). Research on ATFM Delay Optimization Method Based on Dynamic Priority Ranking. Aerospace, 12(9), 793. https://doi.org/10.3390/aerospace12090793






