Numerical Study of the Induction Length Effect on Oblique Detonation Waves
Abstract
1. Introduction
2. Numerical Treatment
3. Results and Discussions
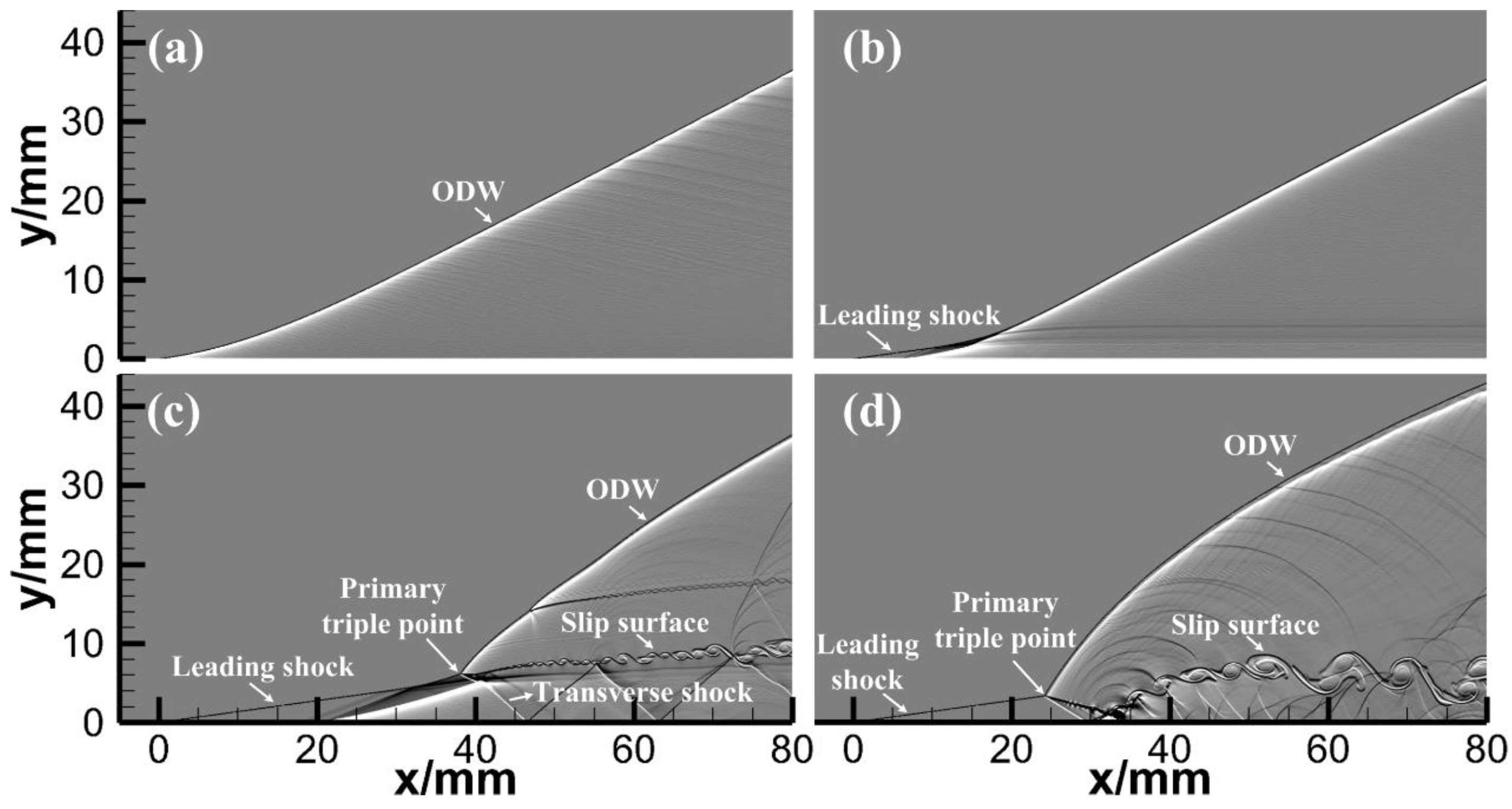
3.1. Effect of the Induction Length on the ODW Structure and Transition Pattern
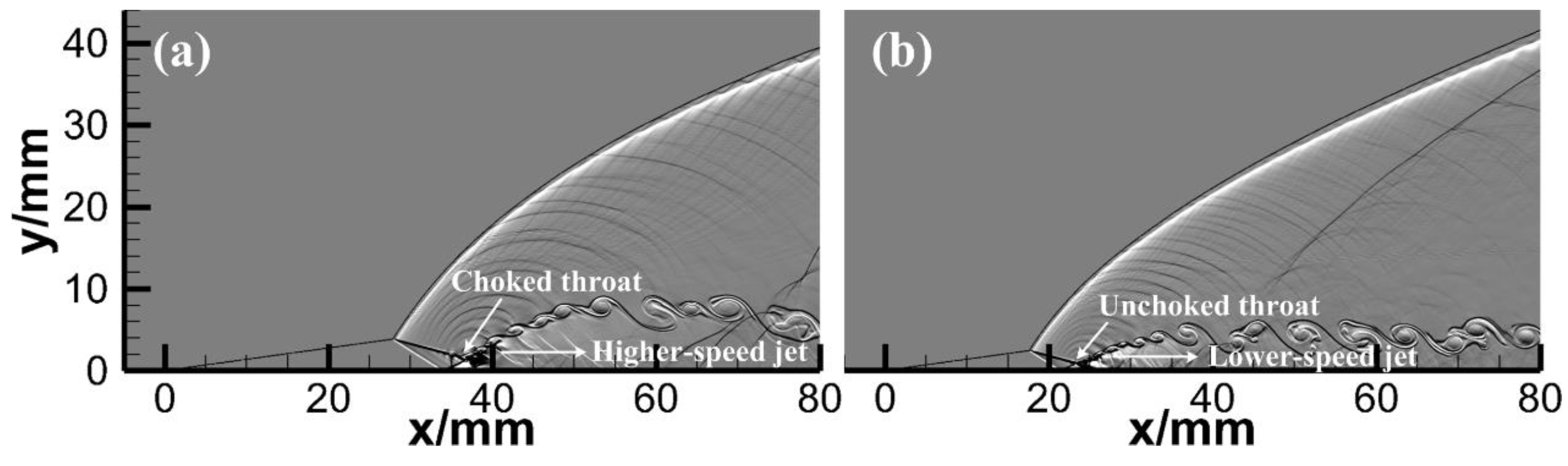
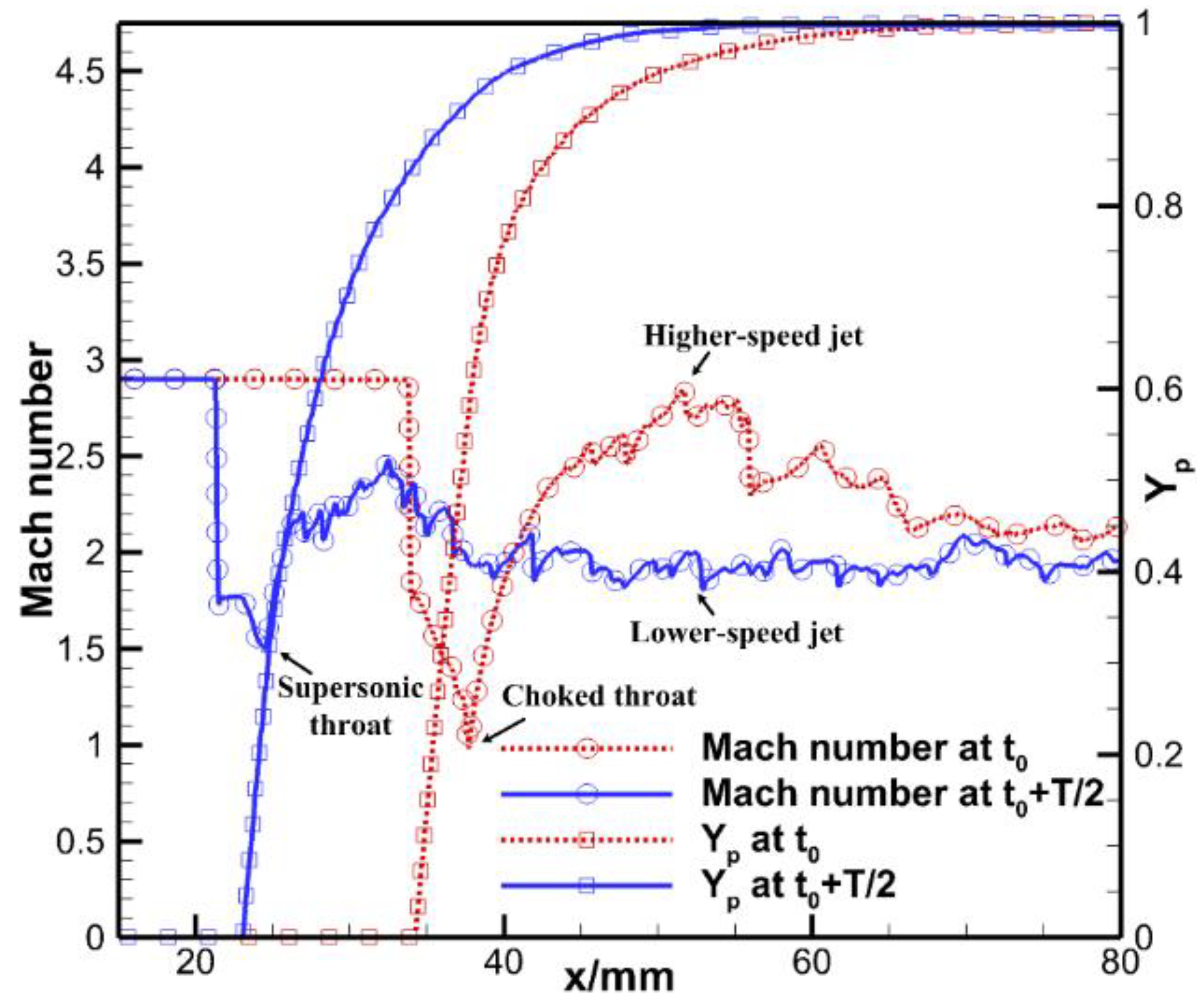
3.2. Oscillatory Motion of the Upstream Primary Triple Point
3.3. Effect of the Induction Length on ODW Hysteresis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jiang, Z.L. Standing oblique detonation for hypersonic propulsion: A review. Prog. Aerosp. Sci 2023, 143, 100955. [Google Scholar] [CrossRef]
- Ostrander, M.; Hyde, M.; Young, M.; Kissinger, R.; Pratt, D. Standing oblique detonation wave engine performance. In Proceedings of the 23rd Joint Propulsion Conference, San Diego, CA, USA, 29 June–2 July 1987. [Google Scholar] [CrossRef]
- Adelman, H.G.; Cambier, J.L.; Menees, G.P.; Balboni, J.A. Analytical and experimental validation of the oblique detonation wave engine concept. In Proceedings of the 26th Aerospace Sciences Meeting, Reno, NV, USA, 11–14 January 1988. [Google Scholar] [CrossRef]
- Zhang, Z.J.; Wen, C.; Yuan, C.K.; Liu, Y.F.; Han, G.L.; Wang, C.; Jiang, Z.L. An experimental study of formation of stabilized oblique detonation waves in a combustor. Combust. Flame 2022, 237, 111868. [Google Scholar] [CrossRef]
- Silva, L.F.F.; Deshaies, B. Stabilization of an oblique detonation wave by a wedge: A parametric numerical study. Combust. Flame 2000, 121, 152–166. [Google Scholar] [CrossRef]
- Wang, A.F.; Zhao, W.; Jiang, Z.L. The criterion of the existence or inexistence of transverse shock wave at wedge supported oblique detonation wave. Acta Mech. Sin. 2011, 27, 611–619. [Google Scholar] [CrossRef]
- Teng, H.H.; Jiang, Z.L. On the transition pattern of the oblique detonation structure. J. Fluid Mech. 2012, 713, 659–669. [Google Scholar] [CrossRef]
- Teng, H.; Tian, C.; Zhang, Y.; Zhou, L.; Ng, H.D. Morphology of oblique detonation waves in a stoichiometric hydrogen-air mixture. J. Fluid Mech. 2021, 913, A1. [Google Scholar] [CrossRef]
- Shi, X.; Xie, H.; Zhou, L.; Zhang, Y. A theoretical criterion on the initiation type of oblique detonation waves. Acta Astronaut. 2022, 190, 342–348. [Google Scholar] [CrossRef]
- Verreault, J.; Higgins, A.J. Initiation of detonation by conical projectiles. Proc. Combust. Inst. 2011, 33, 2311–2318. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Xiang, G.X.; Yu, J.; Jin, K.; Goh, K.B. Accelerated initiation of oblique detonation induced by disturbance in detonative zone. Chin. J. Aeronaut. 2023, 36, 153–164. [Google Scholar] [CrossRef]
- Xiang, G.X.; Zhang, Y.C.; Zhang, C.F.; Kou, Y. Study on initiation mechanism of oblique detonation induced by blunt bump on wedge surface. Fuel 2022, 323, 124314. [Google Scholar] [CrossRef]
- Han, X.; Liu, Y.F.; Zhang, Z.J.; Zhang, W.S.; Yuan, C.K.; Han, G.L.; Jiang, Z.L. Experimental demonstration of forced initiation of kerosene oblique detonation by an on-wedge trip in an ODE model. Combust. Flame 2023, 258, 113102. [Google Scholar] [CrossRef]
- Yang, P.F.; Teng, H.H.; Ng, H.D.; Jiang, Z.L. A numerical study on the instability of oblique detonation waves with a two-step induction–reaction kinetic model. Proc. Combust. Inst. 2019, 37, 3537–3544. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Xiang, G.X.; Gao, X.; Yu, J.; Hu, X.Q.; Xin, Y.R.; Li, D.Y.; Wang, Q. Study on initiation characteristics of oblique detonation induced by hydrogen jets in acetylene-air mixtures. Fuel 2023, 350, 128787. [Google Scholar] [CrossRef]
- Wang, A.F.; Bian, J.; Teng, H.H. Numerical study on initiation of oblique detonation wave by hot jet. Appl. Therm. Eng. 2022, 213, 118679. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, L.; Xiao, B.G.; Yan, Z.H.; Wang, C. Hysteresis phenomenon of the oblique detonation wave. Combust. Flame 2018, 192, 170–179. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, W.Q.; Wang, L.; Xiao, B.G.; Cai, X.D. Oblique detonation initiation by an instantaneous energy source in high-speed wedge flows. AIAA J. 2021, 59, 4794–4799. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, B.G.; Wang, L.; Wang, C. Numerical study of disturbance resistance of oblique detonation waves. Int. J. Aerosp. Eng. 2020, 2020, 8876637. [Google Scholar] [CrossRef]
- Ng, H.D.; Radulescu, M.I.; Higgins, A.J.; Nikiforakis, N.; Lee, J.H.S. Numerical investigation of the instability for one dimensional Chapman-Jouguet detonations with chain-branching kinetics. Combust. Theory Model. 2005, 9, 385–401. [Google Scholar] [CrossRef]
- Deiterding, R. Parallel Adaptive Simulation of Multi-Dimensional Detonation Structures. Ph.D. Dissertation, Brandenburgischen Technischen Universität Cottbus, Cottbus, Germany, 2003. [Google Scholar]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Liu, Y.; Wu, D.; Yao, S.B.; Wang, J.P. Analytical and numerical investigations of wedge-induced oblique detonation waves at low inflow mach number. Combust. Sci. Technol. 2015, 187, 843–856. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, S.; Liu, Y.; Xiang, G. Numerical Study of the Induction Length Effect on Oblique Detonation Waves. Aerospace 2025, 12, 792. https://doi.org/10.3390/aerospace12090792
Sun S, Liu Y, Xiang G. Numerical Study of the Induction Length Effect on Oblique Detonation Waves. Aerospace. 2025; 12(9):792. https://doi.org/10.3390/aerospace12090792
Chicago/Turabian StyleSun, Shilong, Yu Liu, and Gaoxiang Xiang. 2025. "Numerical Study of the Induction Length Effect on Oblique Detonation Waves" Aerospace 12, no. 9: 792. https://doi.org/10.3390/aerospace12090792
APA StyleSun, S., Liu, Y., & Xiang, G. (2025). Numerical Study of the Induction Length Effect on Oblique Detonation Waves. Aerospace, 12(9), 792. https://doi.org/10.3390/aerospace12090792






