1. Introduction
The problem of UAV penetration into the radar air defense area can be modeled as a problem of flight path planning under path constraints, fire threat constraints, and flight time constraints. The purpose of the UAV is to plan a reasonable flight path to complete the task efficiently and ensure its safety [
1]. The path planning of UAV penetration can be divided into static and dynamic path planning according to the dynamic change in the fire threat area [
2]. Static path planning means that the space environment faced by the UAV is unchanged, and the flight path planning is completed before the UAV flies, and the waypoints and routes are loaded. Dynamic path planning means that the space environment faced by the UAV is dynamically changing, and the UAV can realize flight and design by perceiving the environment and adjusting its state [
3,
4]. The problem considered in this paper belongs to dynamic path planning.
In recent years, more and more algorithms have been proposed to solve the path planning problem. The commonly used algorithms include the graph search algorithm [
5], operations research linear programming algorithm [
6,
7], intelligent optimization algorithm [
8,
9], and reinforcement learning algorithm [
10,
11]. The graph search algorithm is one of the classical algorithms of graph theory that can effectively solve the shortest path problem. However, as the environment becomes complicated and the number of nodes increases, the solving efficiency decreases [
12]. The linear programming algorithm is a mathematical method that obtains the extreme value of the objective function under linear constraints. It is widely used in military and engineering technology fields and has the characteristics of simple and efficient calculation. However, in complex space environments, its constraints are not necessarily linear [
13]. In UAV path planning, the genetic algorithm [
14], particle swarm algorithm [
15,
16], ant colony algorithm [
17], and hybrid algorithm [
18,
19] are widely used, but there are also problems with an unclear logical relationship. Reinforcement learning is an algorithm framework that interacts with the environment to obtain feedback and optimize decisions based on it. The core of reinforcement learning is the Markov decision process. In recent years, researchers have mainly used the Q-learning algorithm and the Deep Q-Network (DQN) algorithm for path planning [
20,
21], but the Q-learning algorithm is prone to overfitting, leading to local optimization, and the DQN algorithm has the problem of overestimating the reward function [
22,
23,
24]. In order to solve the above two problems, the DDQN algorithm was introduced in this paper for the path planning of the stealth UAV. Compared with Dueling DQN, DDQN reduces the Q value estimation bias and has better initial performance. Compared with PPO, it has the characteristics of offline learning, is more suitable for a discrete action space, and has low dependence on the environment model. Compared with the DDPG algorithm, the DDQN algorithm is more suitable for discrete action output and has higher sample efficiency, while the DDPG algorithm is suitable for continuous action output. Compared with the MTCS algorithm, the DDQN algorithm has better online optimization ability and less dependence on the environment model, while the MTCS algorithm is based on model search, has high dependence on the model, and has weak online optimization ability [
25].
It is different from the traditional assumption that the RCS of the UAV is constant. The RCS of the stealth UAV from various angles is different, and the angle between the stealth UAV and the radar constantly changes during the flight, resulting in a dynamic change in the detection probability of the radar and the range of the anti-aircraft kill zone. Using the characteristics of the anti-aircraft kill zone, the stealthy UAV penetration into the multi-radar anti-aircraft zone with optimal path planning reaches the mission destination. Compared with existing conventional UAV path planning algorithms based on reinforcement learning [
26], the main innovation of this paper lies in the proposed stealth UAV path planning algorithm. The RCS characteristics of the stealthy UAV designed by our team are significantly different from those of conventional UAVs. At present, most of the research on stealthy UAV path planning is based on the traditional A* algorithm. The RCS value of stealth UAVs varies with the angle of the fuselage. Multiple radars can detect the aircraft from various angles, posing a serious threat to stealth UAVs. To address this issue, reference [
27] proposed an A* algorithm based on the trajectory planning of stealth UAVs. Considering the RCS characteristics of stealth UAVs, reference [
28] proposed an improved A* algorithm, a sparse A* algorithm, and a dynamic A* algorithm, taking into account the feasibility of the trajectory through the radar detection probability, and completed the trajectory planning under three different scenarios. In view of the shortcomings of traditional algorithms in addressing the issue of stealth penetration, and fully considering the requirements of rapidity and safety when planning the flight path, an improved A* algorithm was designed in reference [
29]. Considering the survivability and penetration capability under the deployment of single-base and dual-base radars, reference [
30] proposed an improved A-Star algorithm based on the multi-step search method to achieve the path planning of stealth UAVs in complex scenarios. To balance the average RCS and peak RCS, reference [
31] introduced a detection probability model and a penetration efficiency model and used a gradient-free optimization algorithm based on the genetic algorithm to maximize efficiency. However, the A* algorithm has the characteristics of large computational complexity and being unsuitable for dynamic environments. To address this problem, the continuous turning angle is discretized, the algorithm structure is simplified, and the convergence speed of the reinforcement learning algorithm is improved. Finally, the feasibility of the proposed algorithm was verified by comparing it with the existing algorithms.
The rest of this paper is organized as follows. The DDQN algorithm is introduced in
Section 2, and the mapping relationship between UAV action and reinforcement learning elements is given. In
Section 3, the environment model of this paper is presented, and the stealth UAV penetration algorithm based on DDQN is proposed. In
Section 4, the effectiveness of the proposed algorithm is verified by simulation. Finally,
Section 5 summarizes this paper.
2. DDQN Algorithm
This paper uses the improved DDQN algorithm under the reinforcement learning framework. After obtaining environmental information, the stealth UAV can avoid the air defense zone composed of multiple radars through real-time planning and maneuvering. A stealth UAV is an agent that cruises through the airspace at a constant speed, and the airspace environment is an anti-aircraft kill zone composed of multiple radars. The state information of the agent is its position in a two-dimensional space, the action is the corner direction of the stealth UAV at the path point, and the reward function is designed as a function related to the distance from the stealth UAV to the target point and the safety state.
In the reinforcement learning framework, the state information the stealth UAV perceives is its position in the airspace. According to the state information, the stealth UAV makes decisions according to the reinforcement learning model, and the action is the steering angle of the UAV at the path point. After completing the action, the stealth UAV constantly cruised to the following path point and updated its state information. In this framework, the stealth UAV must estimate the probability of being detected by each radar according to its state before taking action. The radar detection probability is related to the reward function, and the action taken aims to maximize the reward function. The real-time decision-making framework of the stealth UAV is shown in
Figure 1.
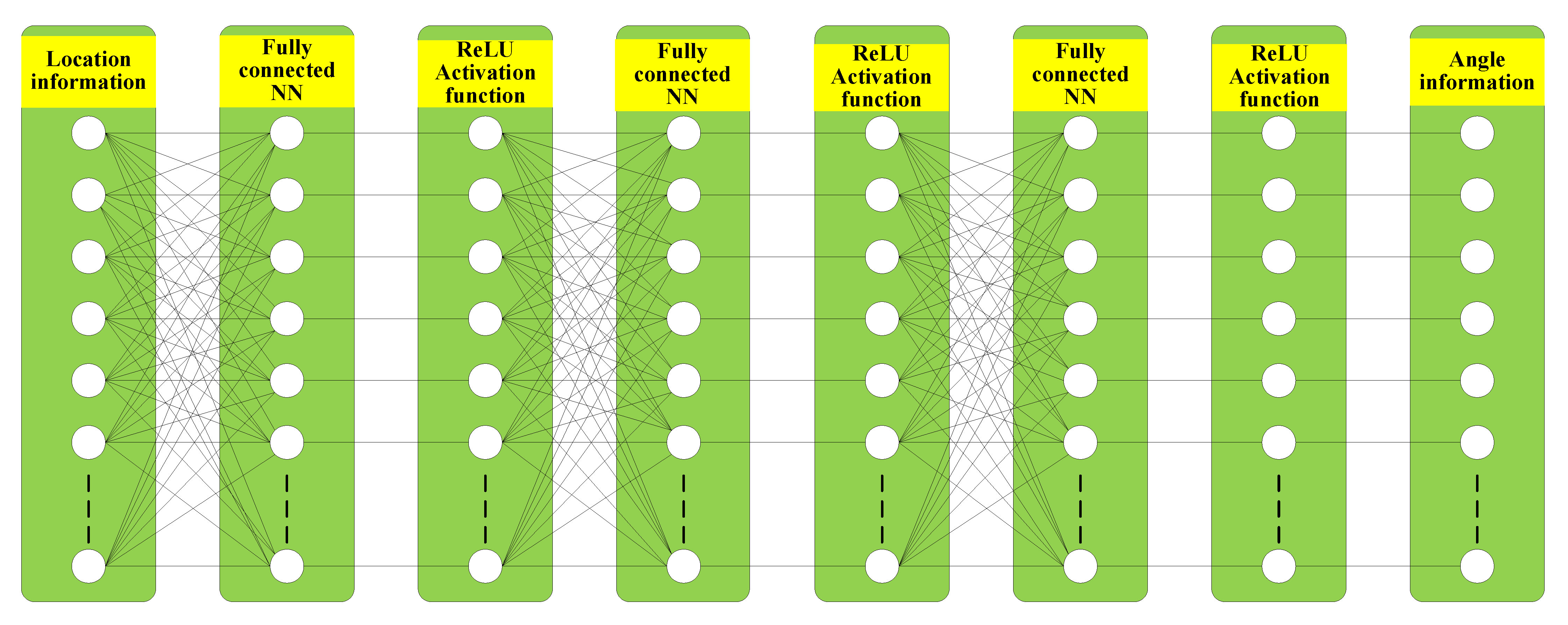
The state space perceived by stealth UAVs is its position in a two-dimensional space. It is not conducive to training because of many states. Therefore, this paper uses the powerful fitting ability of neural networks to fit the Q function through neural networks. The input of the Q-network is the position information
of the stealth UAV, and the output is the angle
of the stealth UAV. In DDQN, the training and target Q-networks have the same structure, with three hidden layers. The hidden layer is the fully connected layer of 128 nodes, and the activation function adopts ReLU. The Q-network architecture is shown in
Figure 2.
In the DQN algorithm, the Q-network loss function is
In order to solve the problem of constantly changing targets and overestimation of the Q value when the network is updated, the DDQN algorithm proposes to use two networks to estimate, that is, one network selects the action with the largest value, and the other network calculates the value. In this case, the loss function is
The state is the position of the stealth UAV. In order to better determine the relative relationship between the various states of the stealth UAV, the initial states of the stealth UAV are set as the origin. The action is the discrete value of the steering angle of the stealth UAV at the path point. The angle is discretized into five fixed values to benefit network training and reduce the amount of data.
The reward function needs to be set to solve the sparse reward problem in stealth UAVs’ path selection. If the target position is set as a positive reward, the stealth UAV will obtain a negative reward for a long time, making searching for the target position difficult. Therefore, this paper sets the reward function as the sum of three sub-reward functions. The three reward functions are the arrival reward
, the detection penalty
, and
.
where Formula (1) represents the positive reward obtained by the stealth UAV for reaching the target position. The positive reward is
, and the positive reward is 0 if the stealth UAV does not reach the target position. Formula (2) represents the relationship between the negative reward obtained by the stealth UAV and the detection probability. When the detection probability is less than 0.5, the reward is 0.
is a maximum value when the detection probability
is detected by radar and destroyed by anti-aircraft fire. When the detection probability
, the path ends. At this time,
is a maximum value, the stealth UAV has been destroyed by anti-aircraft fire, and the rest of the detection probability corresponds to the minimum value of the corresponding level. Equation (3) represents the negative reward obtained when the stealth UAV flies one step, usually set to
. The total reward is set to
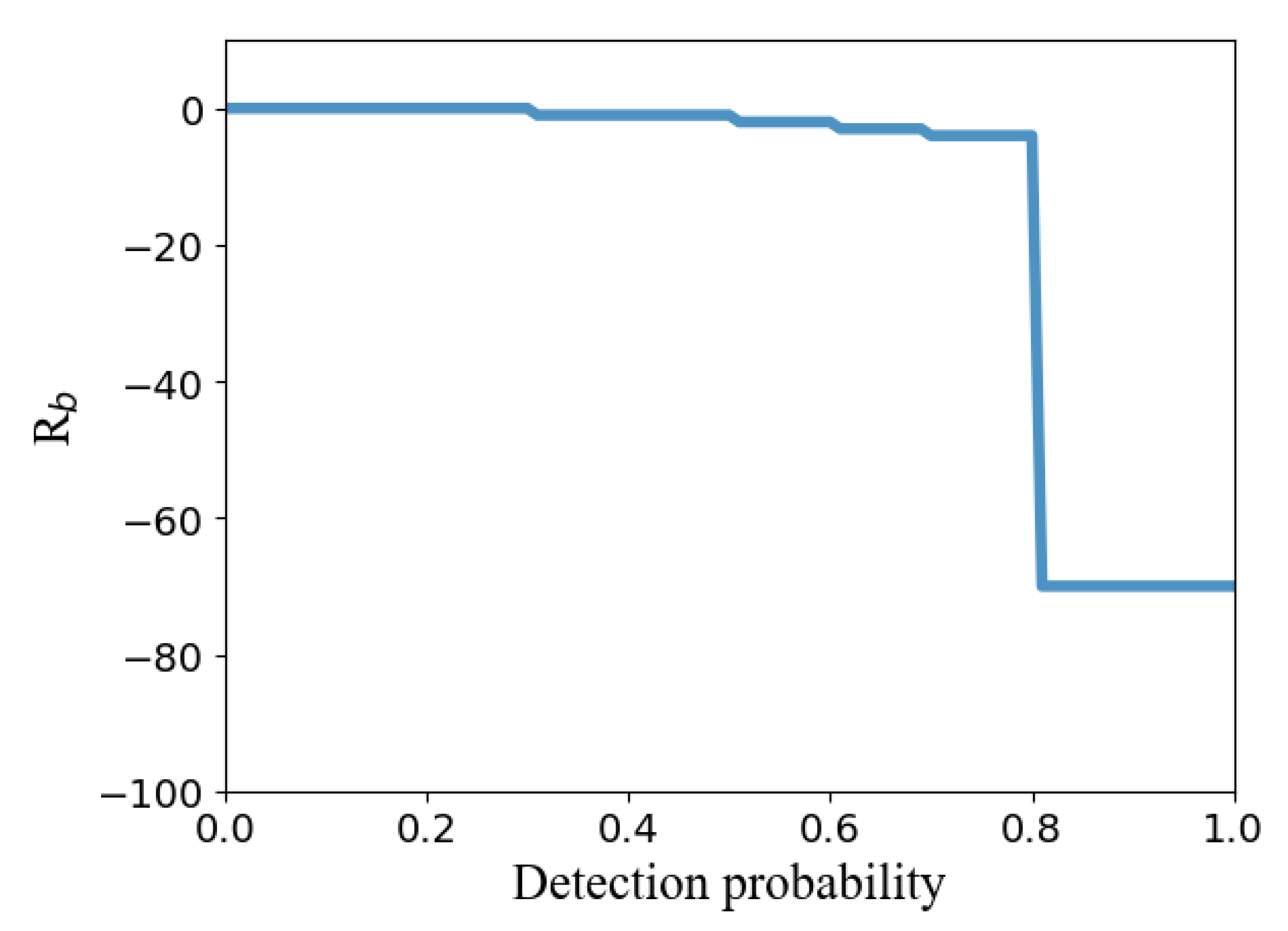
The relationship between the detection penalty and detection probability is shown in
Figure 3. It can be seen that when the radar detection probability is greater than 0.8, the UAV will be greatly penalized. The purpose of the penalty value is to make the stealthy UAV avoid choosing this path node as much as possible. In this paper, the existing penalty value is set based on references [
26,
32] and multiple tests.
The environment will give feedback according to each action of the stealth UAV. If the action is valuable, such as approaching the target and avoiding the threat area, the environment will reward the stealth UAV. If the action is not valuable, such as moving away from the target and entering the threat area, the environment will penalize the stealth UAV.
When the stealth UAV reaches the target location or is shot down by anti-aircraft fire, a round is over. At the end of each round, the sum of the cumulative reward functions of the round is obtained, and the purpose of the stealth UAV is to obtain the maximum sum of the cumulative reward functions per round. The sum of the cumulative reward functions returned can be expressed as
where
means the discount factor.
In order to solve the problem of local optimality in path planning, the design of the reward function should be further clarified. When the anti-aircraft fire shoots down the stealth UAV, the penalty the stealth UAV will obtain is a maximum value, the sum of the discount of the cumulative reward will become small, and the subsequent stealth UAV will not choose this track. When the stealth UAV executes action selection at the path point, the stealth UAV will obtain a penalty value. If the stealth UAV does not fly to the target position by the shortest path, the sum of the discount of the cumulative reward will become smaller, and the subsequent stealth UAV will not choose this track. The local optimum problem in path planning can be solved by integrating the above two constraints.
4. Simulation Results
Stealth UAVs realize state-to-action mapping based on the proposed path planning algorithm, and the settings of each hyperparameter of the algorithm are shown in
Table 1. In terms of specific parameter settings, this paper learned the parameter settings from the literature [
25] and fine-tuned the values of each parameter after multiple simulation tests. The values of each parameter are shown in
Table 1. The learning rate
can effectively balance convergence speed and algorithm stability. The discount factor
represents the weight of future rewards, a discount factor close to 0 indicates more attention to near-term rewards, and a discount factor close to 1 indicates more attention to long-term rewards. The greedy probability
can effectively balance exploration and utilization.
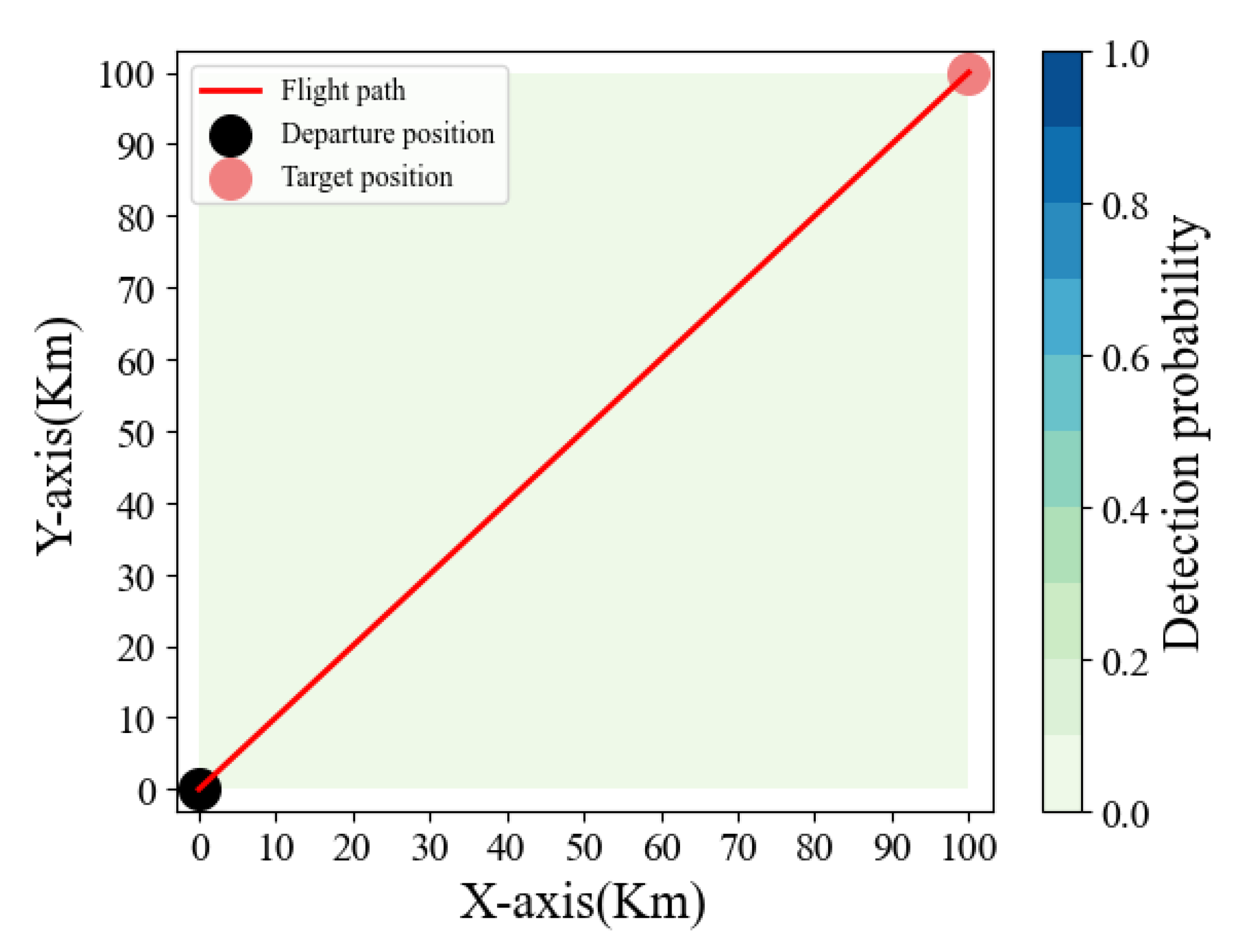
In the pre-training environment, there is no air defense fire unit. Through pre-training, the stealth UAV can find the nearest flight path to the target location, provide prior experience for the subsequent stealth UAV rapid penetration air defense fire unit, and reduce the training time of later training. When there is no anti-aircraft fire unit, the flight path of the stealth UAV is shown in
Figure 5.
From the observation of
Figure 5, we can find no anti-aircraft fire in the airspace. The stealth UAV will fly directly from the starting point to the target position according to the shortest path, verifying the effectiveness of the proposed algorithm in the absence of anti-aircraft fire. Further, the optimization rate of the algorithm can be obtained by observing the relationship between the return of the stealth UAV and the number of turns. The relationship between the return obtained by the stealth UAV and the number of rounds is shown in
Figure 6.
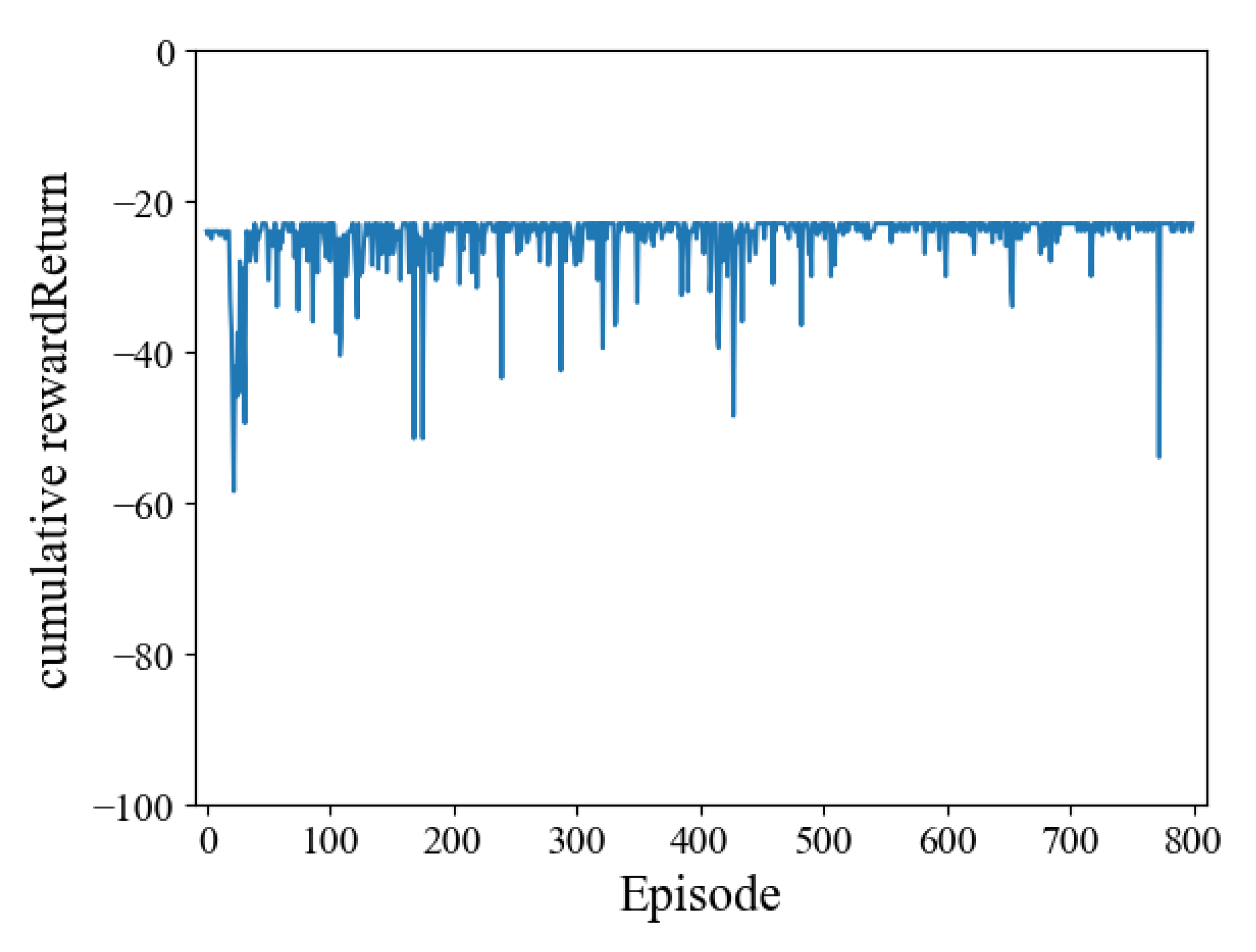
Figure 6 shows that when there is no threat of anti-aircraft fire, the return obtained by stealth drones can converge at a speedy rate. The return fluctuates slightly after convergence because the stealth drone needs to balance the relationship between exploration and utilization, and it will randomly select actions with a probability of
. It helps to find the optimal decision again if the environment changes.
Then, the environment model is changed to include four air defense radars in the airspace. Before the simulation experiment, the parameters of the combat environment between the stealth UAV and the radars are first set. The parameters are shown in
Table 2.
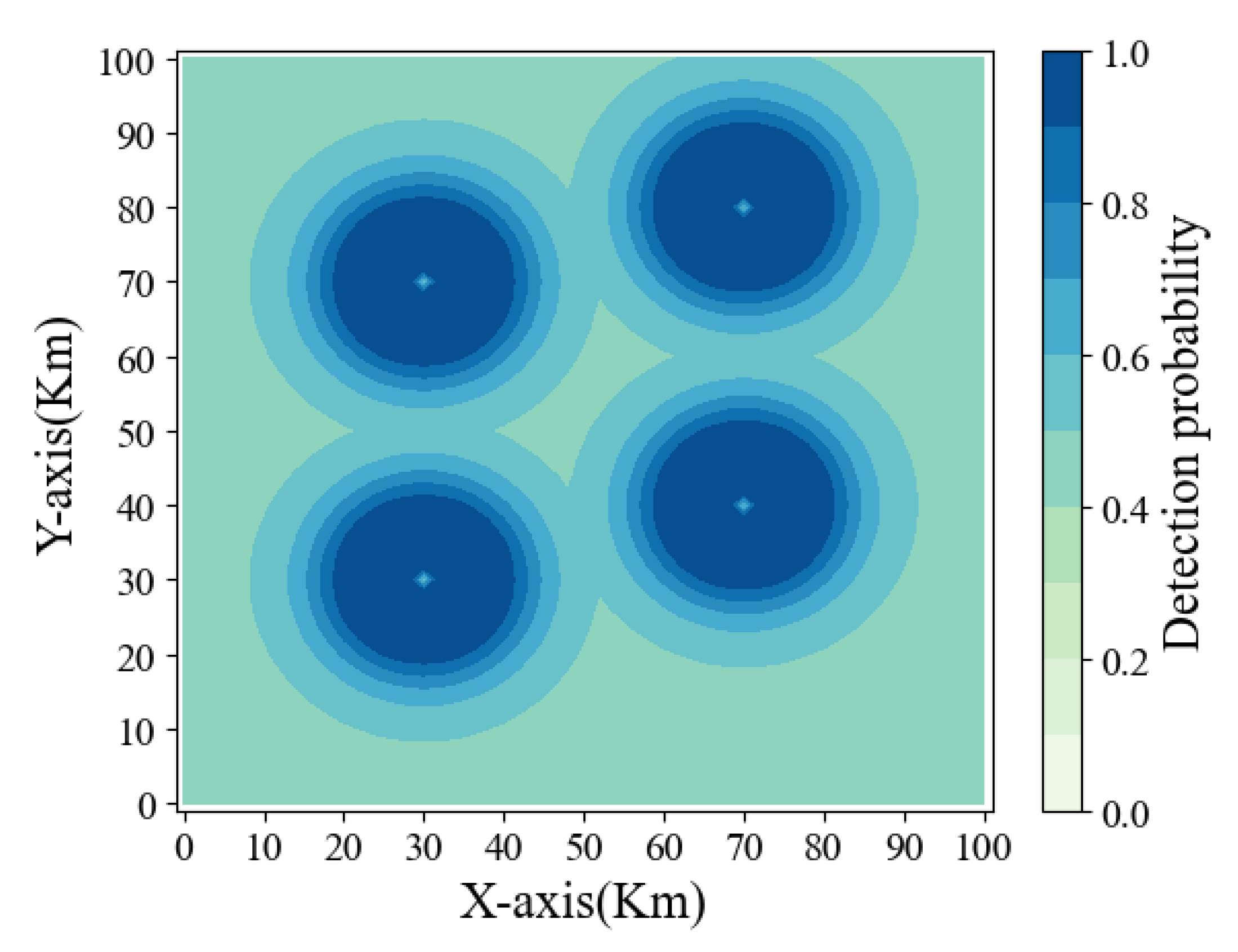
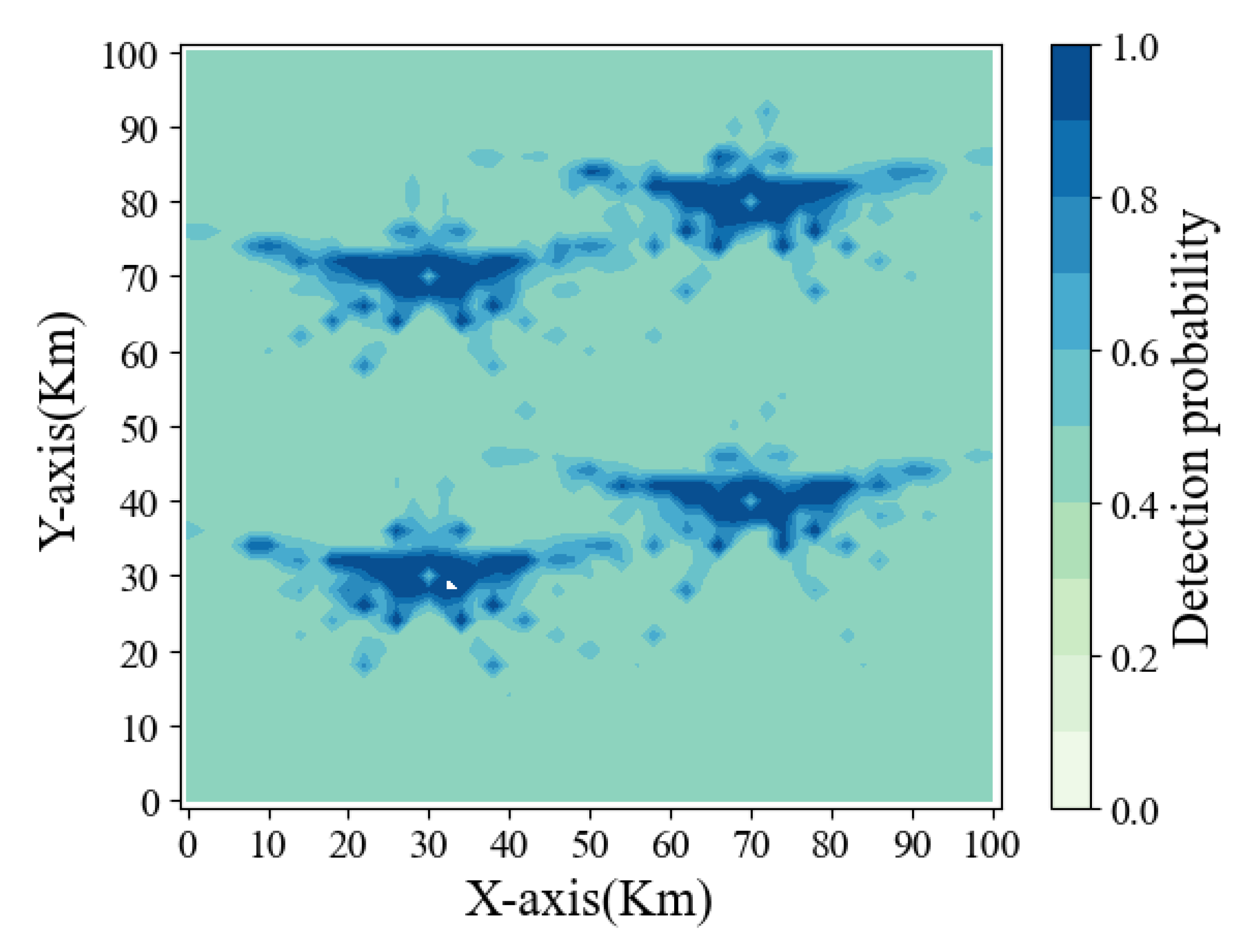
At this time, the radar airspace detection probability is shown in
Figure 7 for the RCS of the stealth UAV.
From the observation of
Figure 7, it can be seen that the probability of the stealth UAV being detected by radar is not only related to the distance but is also closely related to its RCS characteristics because the RCS of stealth UAVs from different angles is different. Based on the model obtained in pre-training, the flight path planning of the stealth UAV is trained again.
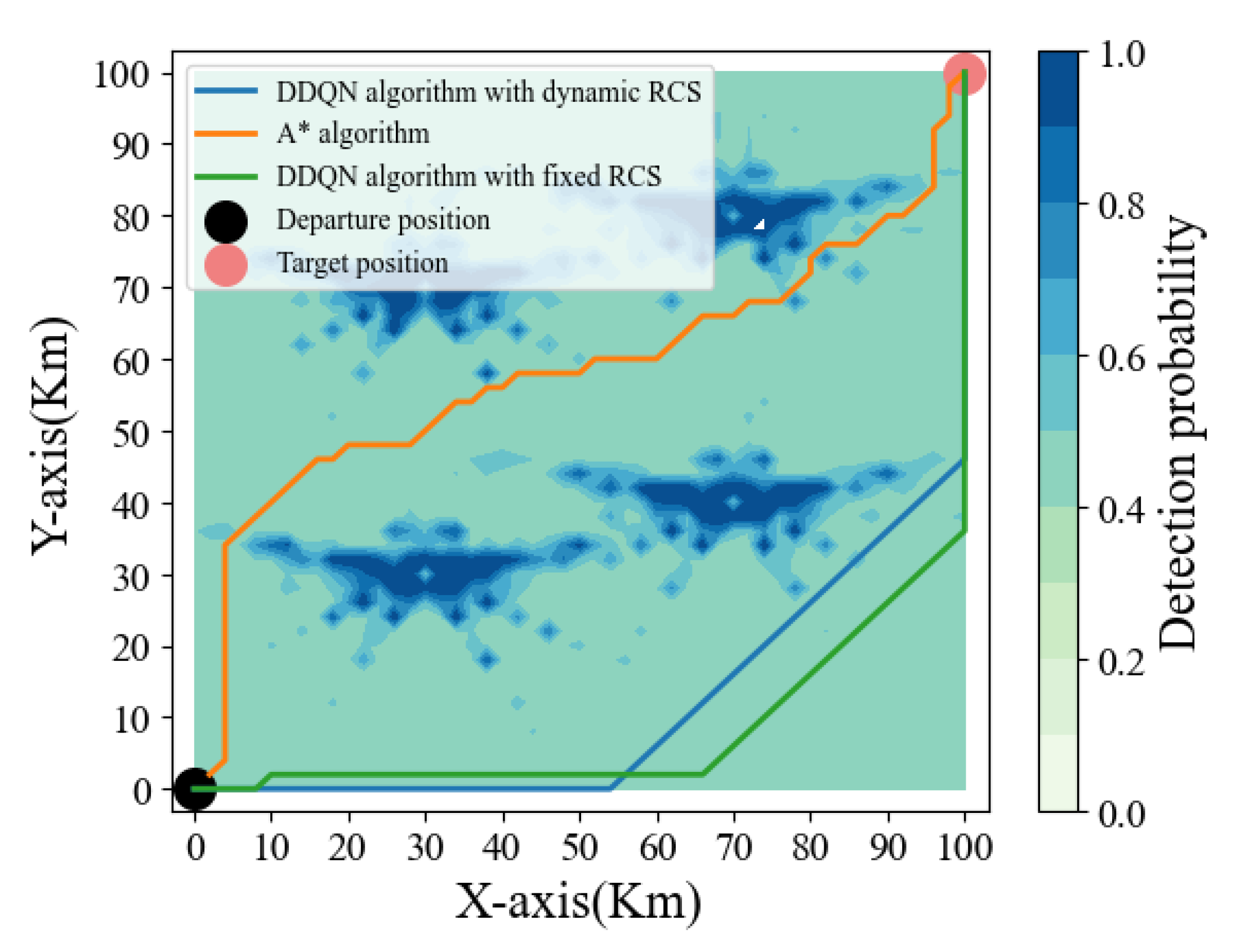
In order to verify the path planning algorithm of a stealth UAV based on a dynamic RCS and DDQN algorithms, the path based on the A* algorithm [
31] and the path based on a fixed RCS and DDQN algorithms are presented simultaneously in the simulation. The simulation results are shown in
Figure 8.
As can be seen from
Figure 6, all three algorithms can effectively avoid the anti-aircraft kill zone and reach the target position. The path length based on the DDQN algorithm with a fixed RCS is
, the path length based on the A* algorithm is
, and the path length based on the DDQN algorithm with a dynamic RCS is
. Although the path based on the DDQN algorithm with a fixed RCS can reach the destination, its path is long and not optimal because it fails to use the RCS characteristics fully. Although the path based on the A* algorithm can reach the destination with a shorter path, there are also problems, such as the path of the A* algorithm taking the diagonal as the reference, lacking the global perception ability, and passing through the threatened area several times. The path of the A* algorithm has many times of turning. Compared with the above two cases, the path based on the DDQN algorithm with a dynamic RCS can effectively overcome the shortcomings of the above two cases and effectively balance the relationship between the path length and fire threat. The stealth UAV can effectively avoid the anti-aircraft kill zone by interacting with the environment and flying to the target location with the shortest path. Finally, the relationship between the return of the stealth drone and the number of rounds is shown in
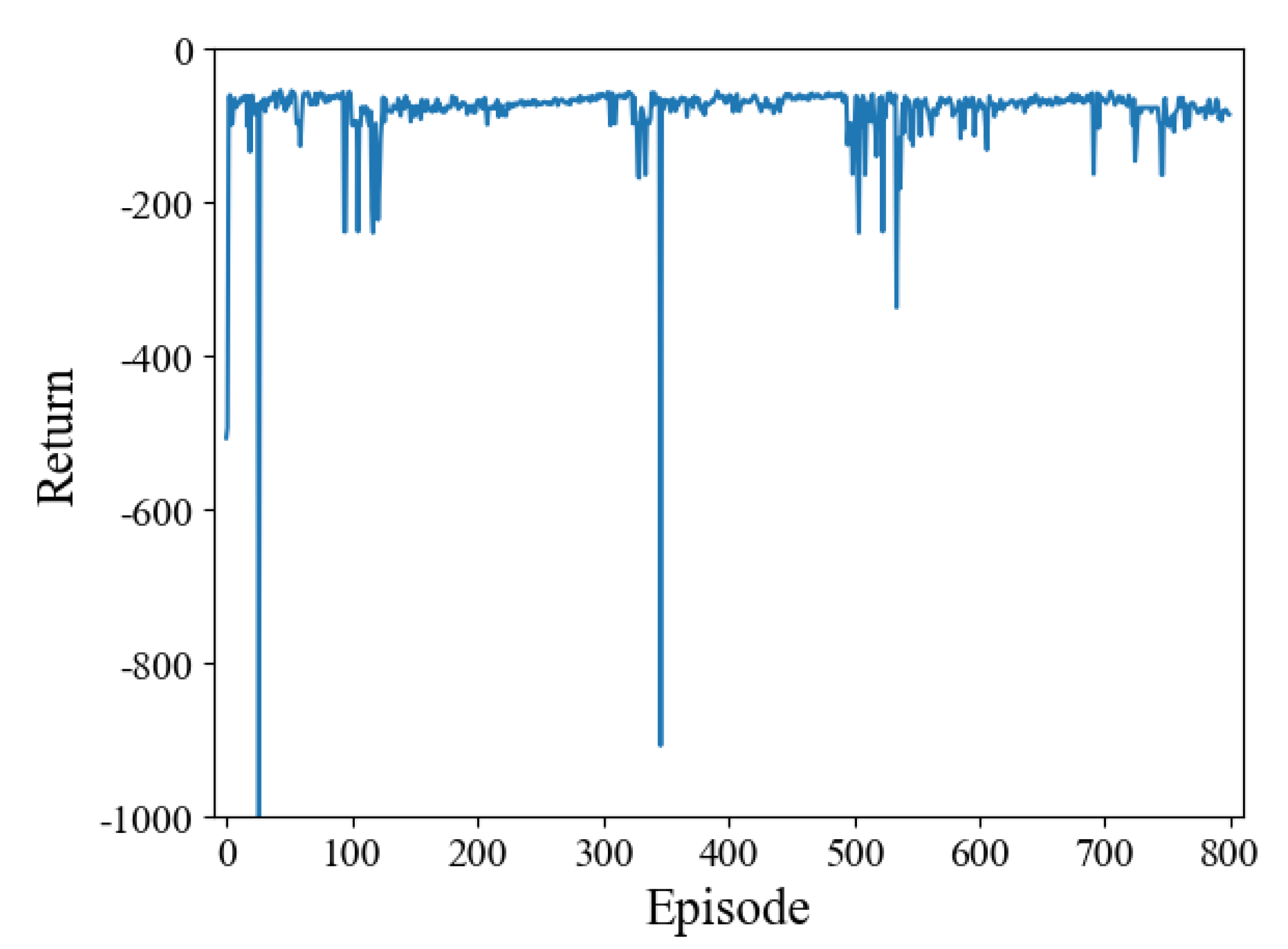
Figure 9.
Figure 9 shows that when four air defense radars are deployed, the return obtained by stealth drones can still converge at a speedy rate. The fluctuation of return is related to the value of the
. When
, the stealth UAV randomly selects actions at each step to explore the entire airspace; when
, the stealth UAV uses the current information to select the action with the greatest reward; when
, the stealth UAV will balance the relationship between exploration and utilization; in this paper, through many experiments,
is set, and the experimental results verify the effectiveness of the proposed algorithm. In summary, this section analyzes the influence of each hyperparameter’s setting on the algorithm’s performance and highlights the proposed algorithm’s advantages through a comparison of path length and convergence speed.