Spectral Emissivity Measurement of Supersonic Nozzles for Radiative Cooling Performance Evaluation
Abstract
1. Introduction
2. Methodology
2.1. Supersonic Nozzle Design and Fabrication
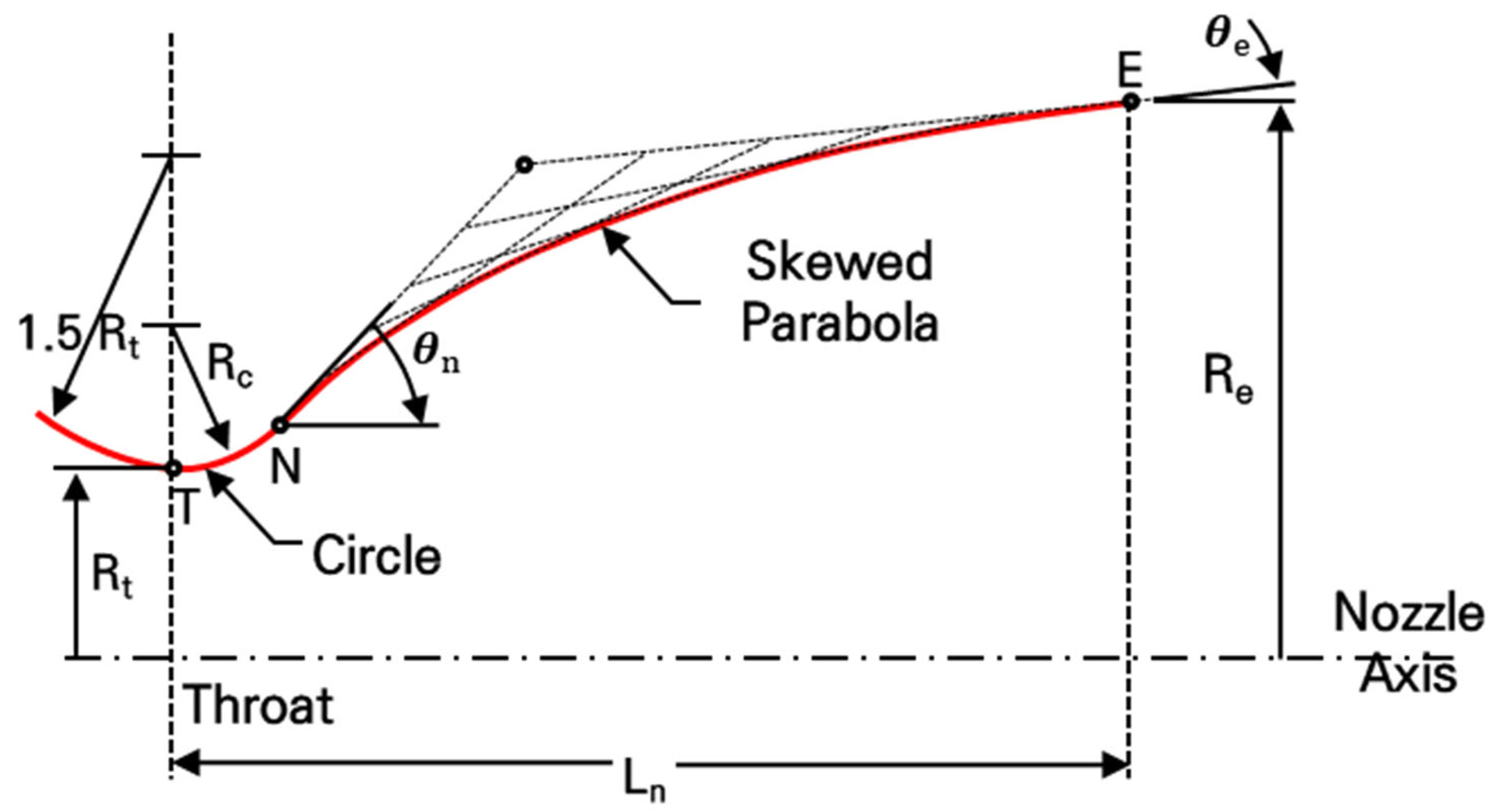
2.1.1. Supersonic Nozzle Design
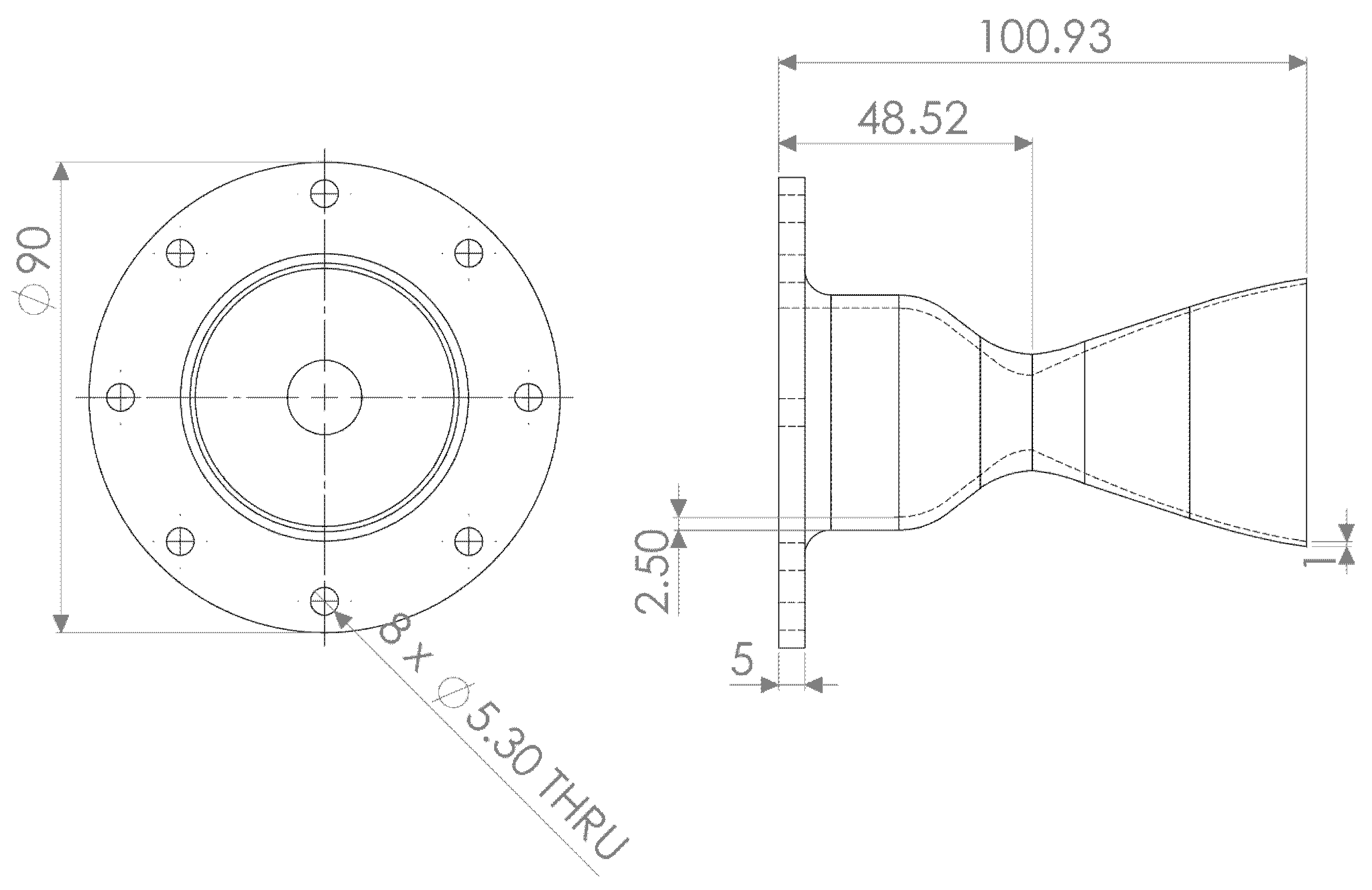
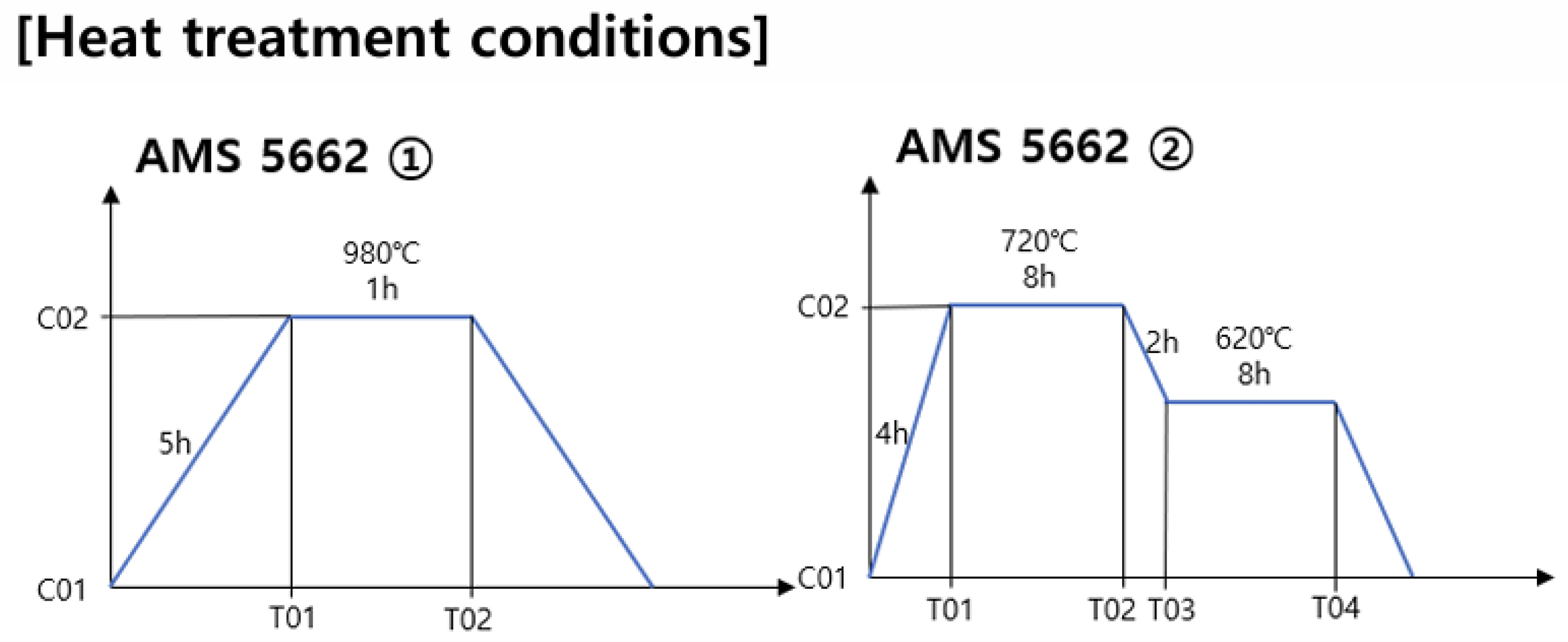
2.1.2. Supersonic Nozzle Fabrication
2.2. Experimental Methodology
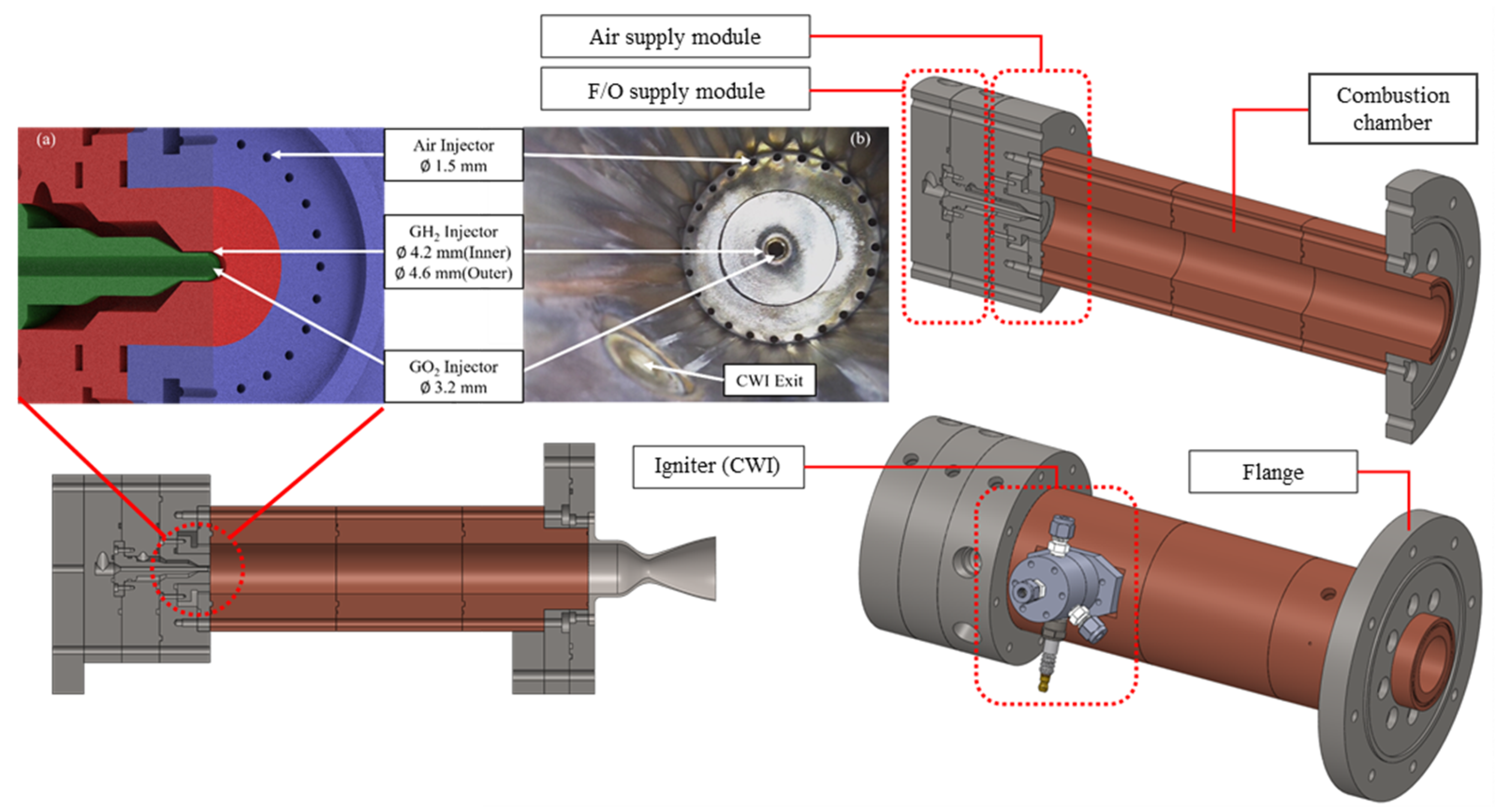
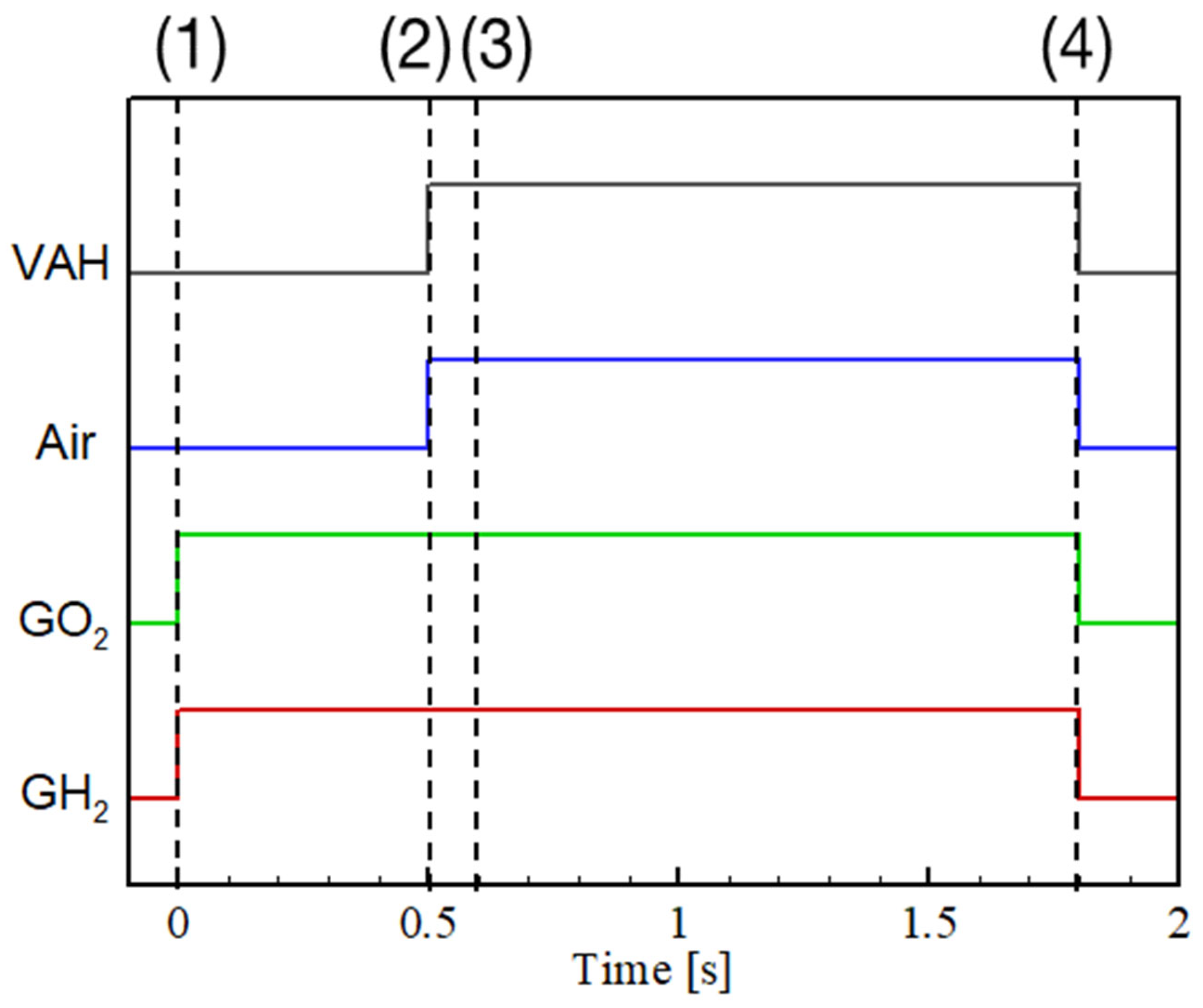
2.2.1. Combustion Test Setup
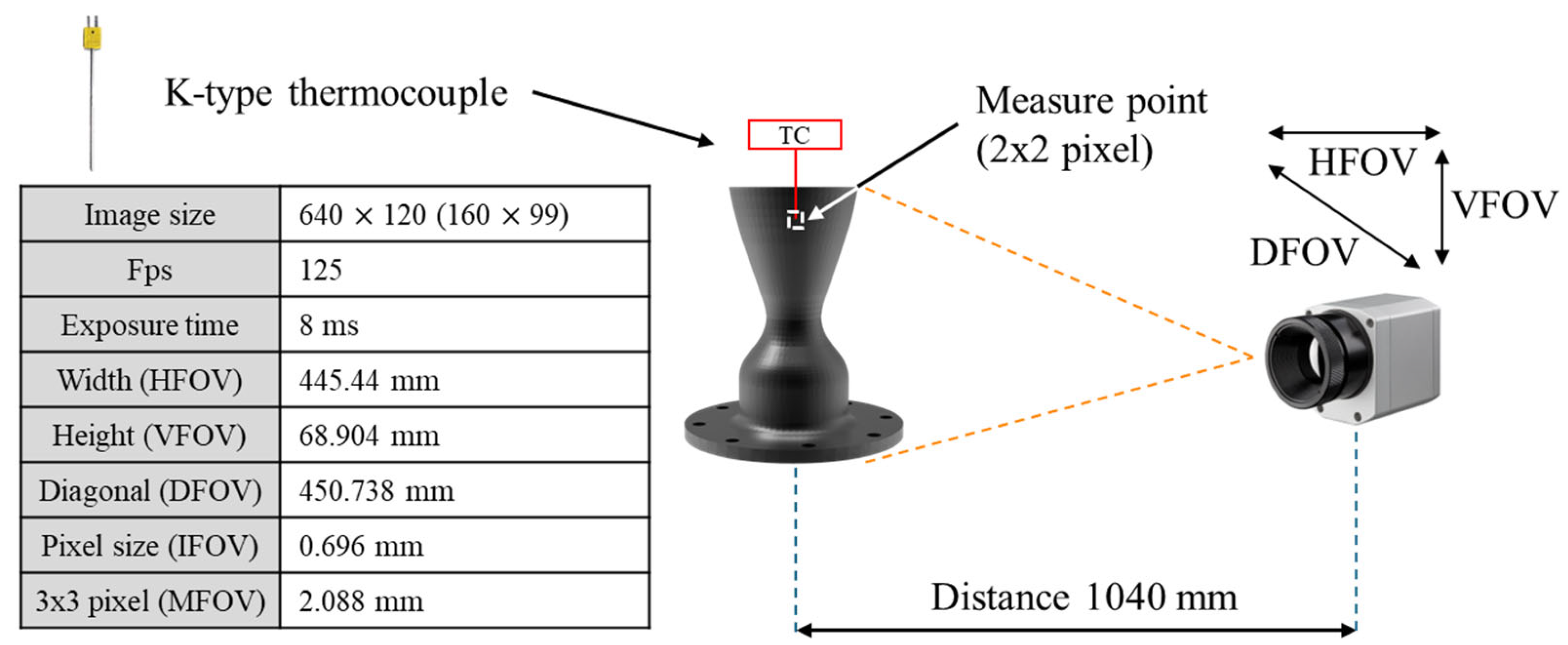
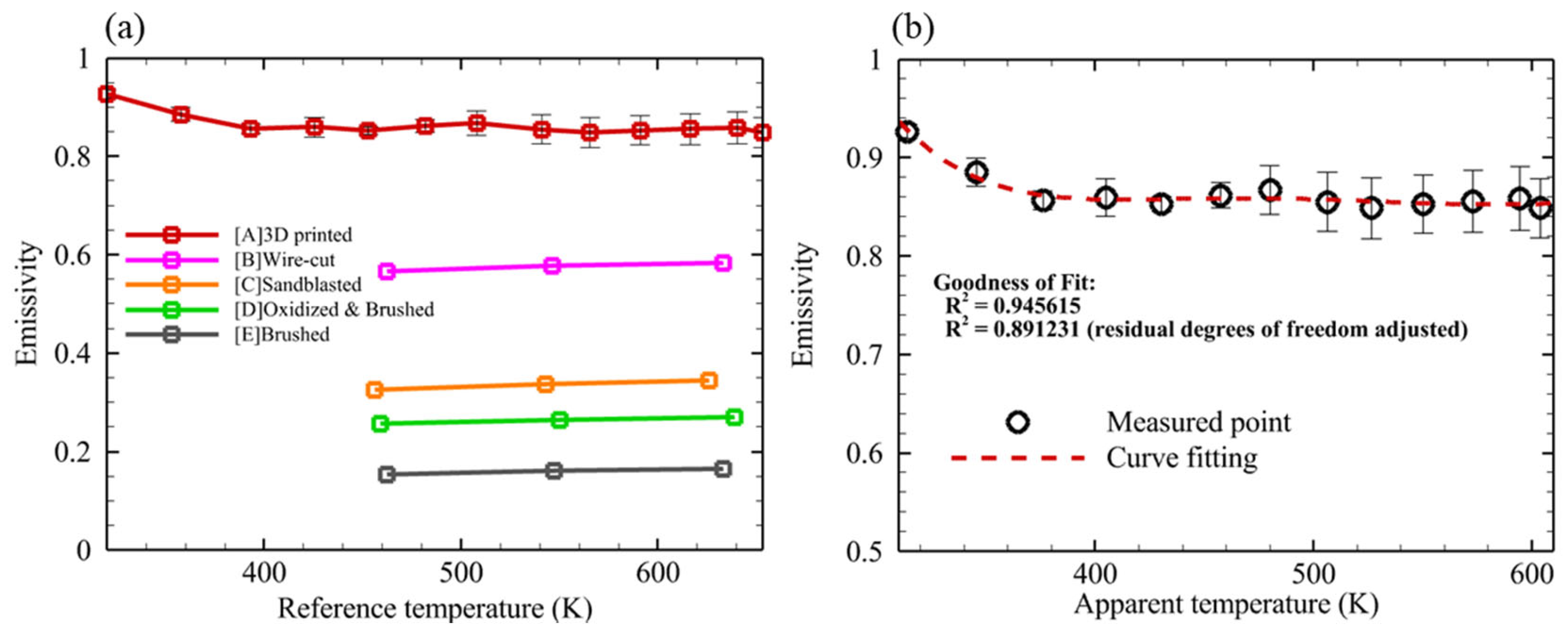
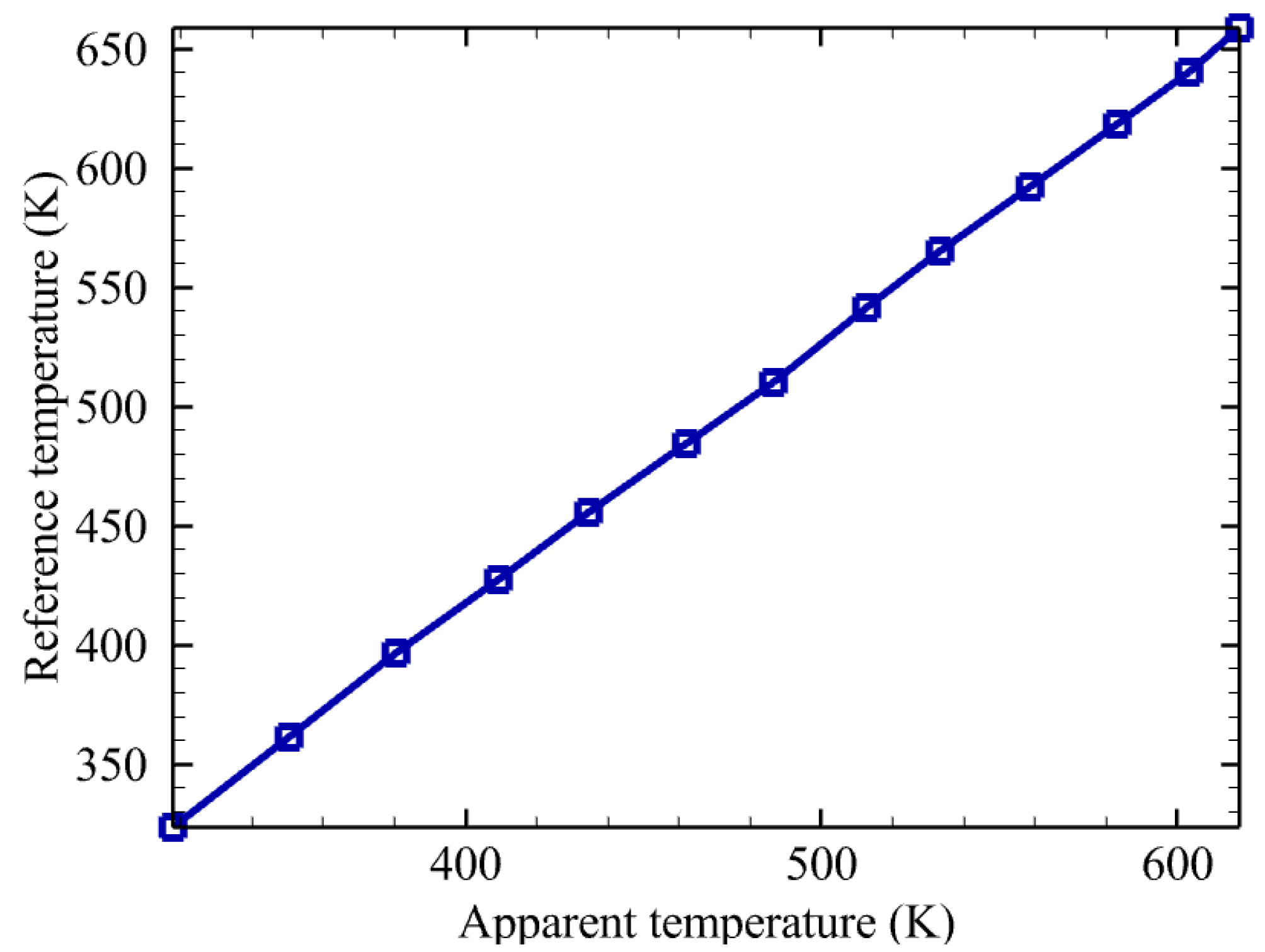
2.2.2. Emissivity Measurement
3. Results and Discussion
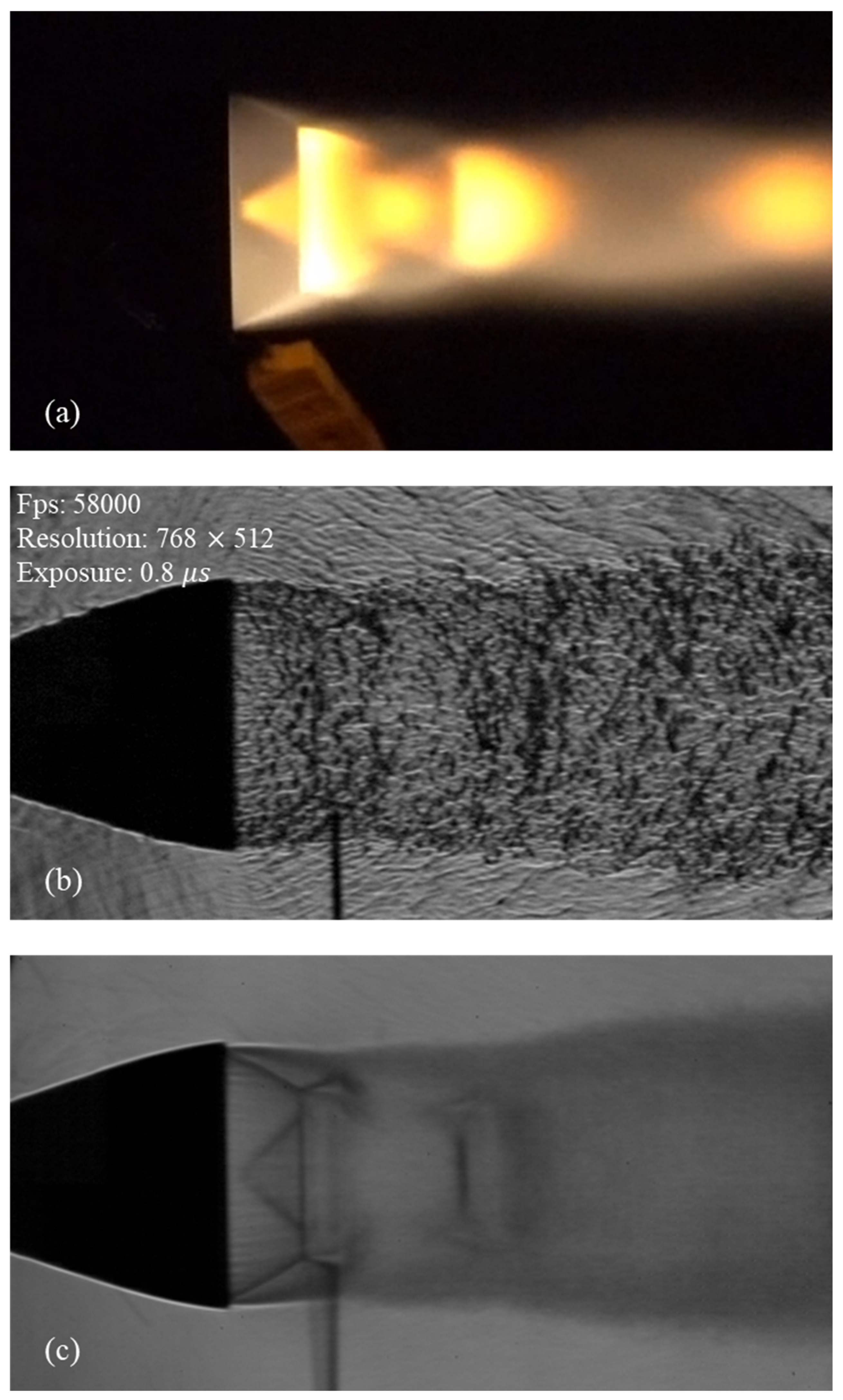
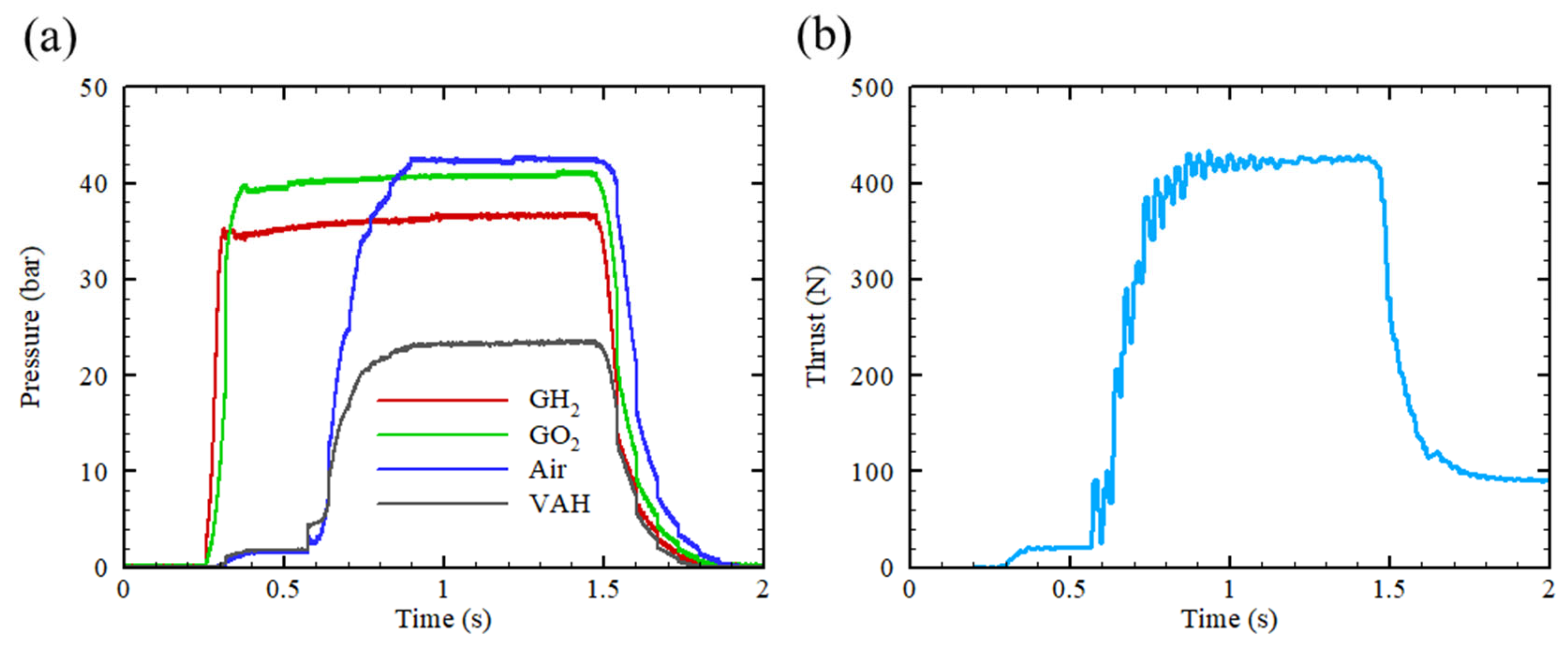
3.1. Hot-Fire Testing of a Supersonic Nozzle Under Flight-like Conditions
3.2. Influence of Emission Angle on 3D-Printed Inconel 718 Emissivity
3.3. Spectral Emissivity Calculation and Emissive Power Distribution of Nozzle Surface
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hou, L.; Fu, P.; Ba, Y. Chemical Mechanism of MMH/NTO and Simulation in a Small Liquid Rocket Engine. Combust. Sci. Technol. 2019, 191, 2208–2225. [Google Scholar] [CrossRef]
- Stechman, R.; Smith, J. Monomethylhydrazine versus hydrazine fuels-Test results using flight qualified 100 LBF and 5 LBF bipropellant engine configurations. In Proceedings of the 19th Joint Propulsion Conference, Seattle, WA, USA, 27–29 June 1983; p. 1257. [Google Scholar]
- Liu, C.; Chen, J.; Han, H.; Wang, Y.; Zhang, Z. A long duration and high reliability liquid apogee engine for satellites. Acta Astronaut. 2004, 55, 401–408. [Google Scholar] [CrossRef]
- Lianbo, Z.; Xu, X. Performance prediction of apogee attitude and orbit control thruster for MMH/NTO hypergolic bipropellant. In Proceedings of the 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Cleveland, OH, USA, 28–30 July 2014; p. 3572. [Google Scholar]
- Krejci, D.; Lozano, P. Space propulsion technology for small spacecraft. Proc. IEEE 2018, 106, 362–378. [Google Scholar] [CrossRef]
- Qin, J.; Zhang, H.; Wang, B. Numerical Investigation on Combustion Instability in a small MMH/NTO Liquid Rocket Engine. In Proceedings of the 52nd AIAA/SAE/ASEE Joint Propulsion Conference, Salt Lake City, UT, USA, 25–27 July 2016; p. 5087. [Google Scholar]
- Zhang, G.; Li, G.; Li, L.; Tang, G. Thermal performance of MMH/NTO rocket thrust chamber based on pintle injector by using liquid film cooling. Appl. Therm. Eng. 2023, 223, 120035. [Google Scholar] [CrossRef]
- Gradl, P.; Tinker, D.C.; Park, A.; Mireles, O.R.; Garcia, M.; Wilkerson, R.; Mckinney, C. Robust metal additive manufacturing process selection and development for aerospace components. J. Mater. Eng. Perform. 2022, 31, 6013–6044. [Google Scholar] [CrossRef]
- Gradl, P.R.; Protz, C.S.; Wammen, T. Additive manufacturing and hot-fire testing of liquid rocket channel wall nozzles using blown powder directed energy deposition inconel 625 and JBK-75 Alloys. In Proceedings of the AIAA Propulsion and Energy 2019 Forum, Indianapolis, IN, USA, 19–22 August 2019; p. 4362. [Google Scholar]
- Tommila, C.D.; Hartsfield, C.R.; Redmond, J.J.; Komives, J.R.; Shelton, T.E. Performance impacts of metal additive manufacturing of very small nozzles. J. Aerosp. Eng. 2021, 34, 04020115. [Google Scholar] [CrossRef]
- Blakey-Milner, B.; Gradl, P.; Snedden, G.; Brooks, M.; Pitot, J.; Lopez, E.; Leary, M.; Berto, F.; du Plessis, A. Metal additive manufacturing in aerospace: A review. Mater. Des. 2021, 209, 110008. [Google Scholar] [CrossRef]
- Blachowicz, T.; Ehrmann, G.; Ehrmann, A. Metal additive manufacturing for satellites and rockets. Appl. Sci. 2021, 11, 12036. [Google Scholar] [CrossRef]
- Moriya, S.; Inoue, T.; Sasaki, M.; Nakamoto, T.; Kimura, T.; Nomura, N.; Kikuchi, K.; Kawasaki, A.; Kato, T.; Masuda, I. Feasibility study on additive manufacturing of liquid rocket combustion chamber. Trans. Jpn. Soc. Aeronaut. Space Sci. Aerosp. Technol. Jpn. 2018, 16, 261–266. [Google Scholar] [CrossRef]
- Coulbert, C.D. Selecting cooling techniques for liquid rockets for spacecraft. J. Spacecr. Rocket. 1964, 1, 129–139. [Google Scholar] [CrossRef]
- Alaruri, S.; Bianchini, L.; Brewington, A. Effective spectral emissivity measurements of superalloys and YSZ thermal barrier coating at high temperatures using a 1.6 μm single wavelength pyrometer. Opt. Lasers Eng. 1998, 30, 77–91. [Google Scholar] [CrossRef]
- Greene, G.; Finfrock, C.; Irvine, T., Jr. Total hemispherical emissivity of oxidized Inconel 718 in the temperature range 300–1000 C. Exp. Therm. Fluid Sci. 2000, 22, 145–153. [Google Scholar] [CrossRef]
- Tanda, G.; Misale, M. Measurement of Total Hemispherical Emittance and Specific Heat of Aluminum and Inconel 718 by a Calorimetric Technique. J. Heat Transf. 2005, 128, 302–306. [Google Scholar] [CrossRef]
- del Campo, L.; Pérez-Sáez, R.B.; González-Fernández, L.; Esquisabel, X.; Fernández, I.; González-Martín, P.; Tello, M.J. Emissivity measurements on aeronautical alloys. J. Alloys Compd. 2010, 489, 482–487. [Google Scholar] [CrossRef]
- Keller, B.P.; Nelson, S.E.; Walton, K.L.; Ghosh, T.K.; Tompson, R.V.; Loyalka, S.K. Total hemispherical emissivity of Inconel 718. Nucl. Eng. Des. 2015, 287, 11–18. [Google Scholar] [CrossRef]
- Leshock, C.E.; Kim, J.-N.; Shin, Y.C. Plasma enhanced machining of Inconel 718: Modeling of workpiece temperature with plasma heating and experimental results. Int. J. Mach. Tools Manuf. 2001, 41, 877–897. [Google Scholar] [CrossRef]
- Pottlacher, G.; Hosaeus, H.; Kaschnitz, E.; Seifter, A. Thermophysical properties of solid and liquidInconel 718 Alloy. Scand. J. Metall. 2002, 31, 161–168. [Google Scholar] [CrossRef]
- Cagran, C.; Reschab, H.; Tanzer, R.; Schützenhöfer, W.; Graf, A.; Pottlacher, G. Normal Spectral Emissivity of the Industrially Used Alloys NiCr20TiAl, Inconel 718, X2CrNiMo18-14-3, and Another Austenitic Steel at 684.5 nm. Int. J. Thermophys. 2009, 30, 1300–1309. [Google Scholar] [CrossRef]
- Schmidt, E.; Eckert, E. Über die Richtungsverteilung der Wärmestrahlung von Oberflächen. Forsch. Auf Dem Geb. Des Ingenieurwesens A 1935, 6, 175–183. [Google Scholar] [CrossRef]
- Li, L.; Wang, F.; Gao, J.; Yu, K.; Wang, L.; Liu, Y. Accurately Measuring the Infrared Spectral Emissivity of Inconel 601, Inconel 625, and Inconel 718 Alloys during the Oxidation Process. Sensors 2024, 24, 5906. [Google Scholar] [CrossRef] [PubMed]
- Rao, G. Exhaust nozzle contour for optimum thrust. J. Jet Propuls. 1958, 28, 377–382. [Google Scholar] [CrossRef]
- Ryu, C.-S.; Lee, K.-O.; Choi, H.-S. Thermo-structural Analysis for Radiation-Cooled Nozzle Extension of Thrust Chamber. In Proceedings of the Korean Society of Propulsion Engineers Conference; 2011; pp. 291–295. Available online: https://koreascience.kr/article/CFKO201132164219425.do (accessed on 26 July 2025).
- Lee, K.-O.; Lim, B.; Kim, D.-J.; Hong, M.; Lee, K. Technology trends in additively manufactured small rocket engines for launcher applications. J. Korean Soc. Propuls. Eng. 2020, 24, 73–82. [Google Scholar] [CrossRef]
- SAE International. AMS 5662: Nickel Alloy, Corrosion and Heat-Resistant, Bars, Forgings, and Rings… Solution Heat Treated; SAE International: Warrendale, PA, USA, 2018. [Google Scholar]
- Sung, B.-K.; Jeong, S.-M.; Choi, J.-Y. Direct-connect supersonic nozzle design considering the effect of combustion. Aerosp. Sci. Technol. 2023, 133, 108094. [Google Scholar] [CrossRef]
- Lee, J.-H.; Lee, E.-S.; Han, H.-S.; Kim, M.-S.; Choi, J.-Y. A study on a vitiated air heater for a direct-connect scramjet combustor and preliminary test on the scramjet combustor ignition. Aerospace 2023, 10, 415. [Google Scholar] [CrossRef]
- Bergman, T.L. Fundamentals of Heat and Mass Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]




| Nickel + Cobalt | Chromium | Molybdenum | Niobium + Tantalum | Cobalt | Aluminum |
|---|---|---|---|---|---|
| 50–55% | 17–21% | 2.8–3.3% | 4.75–5.5% | Max. 1% | 0.2–0.8% |
| Titanium | Carbon | Iron | Manganese | Silicon | Phosphorous |
| 0.65–1.15% | Max. 0.8% | Balance | Max. 0.35% | Max. 0.35% | Max. 0.015% |
| Sulfur | Copper | ||||
| Max. 0.015% | Max. 0.3% | 30 µm |
| B0 | B1 | B2 | B3 | B4 | B5 |
|---|---|---|---|---|---|
| 12.52 | −0.1146 | 0.0004452 | −8.549 × 10−7 | 8.109 × 10−10 | −3.041 × 10−13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, S.-W.; Jo, S.; Sung, B.-K.; Kim, J.-E.; Lee, K.-H.; Mo, G.-U.; Choi, J.-Y. Spectral Emissivity Measurement of Supersonic Nozzles for Radiative Cooling Performance Evaluation. Aerospace 2025, 12, 771. https://doi.org/10.3390/aerospace12090771
Choi S-W, Jo S, Sung B-K, Kim J-E, Lee K-H, Mo G-U, Choi J-Y. Spectral Emissivity Measurement of Supersonic Nozzles for Radiative Cooling Performance Evaluation. Aerospace. 2025; 12(9):771. https://doi.org/10.3390/aerospace12090771
Chicago/Turabian StyleChoi, Su-Wan, Seunghyun Jo, Bu-Kyeng Sung, Jae-Eun Kim, Keon-Hyeong Lee, Gyeong-Ui Mo, and Jeong-Yeol Choi. 2025. "Spectral Emissivity Measurement of Supersonic Nozzles for Radiative Cooling Performance Evaluation" Aerospace 12, no. 9: 771. https://doi.org/10.3390/aerospace12090771
APA StyleChoi, S.-W., Jo, S., Sung, B.-K., Kim, J.-E., Lee, K.-H., Mo, G.-U., & Choi, J.-Y. (2025). Spectral Emissivity Measurement of Supersonic Nozzles for Radiative Cooling Performance Evaluation. Aerospace, 12(9), 771. https://doi.org/10.3390/aerospace12090771







