Uncertainty Quantification of the Impact of High-Pressure Compressor Blade Geometric Deviations on Aero Engine Performance
Abstract
1. Introduction
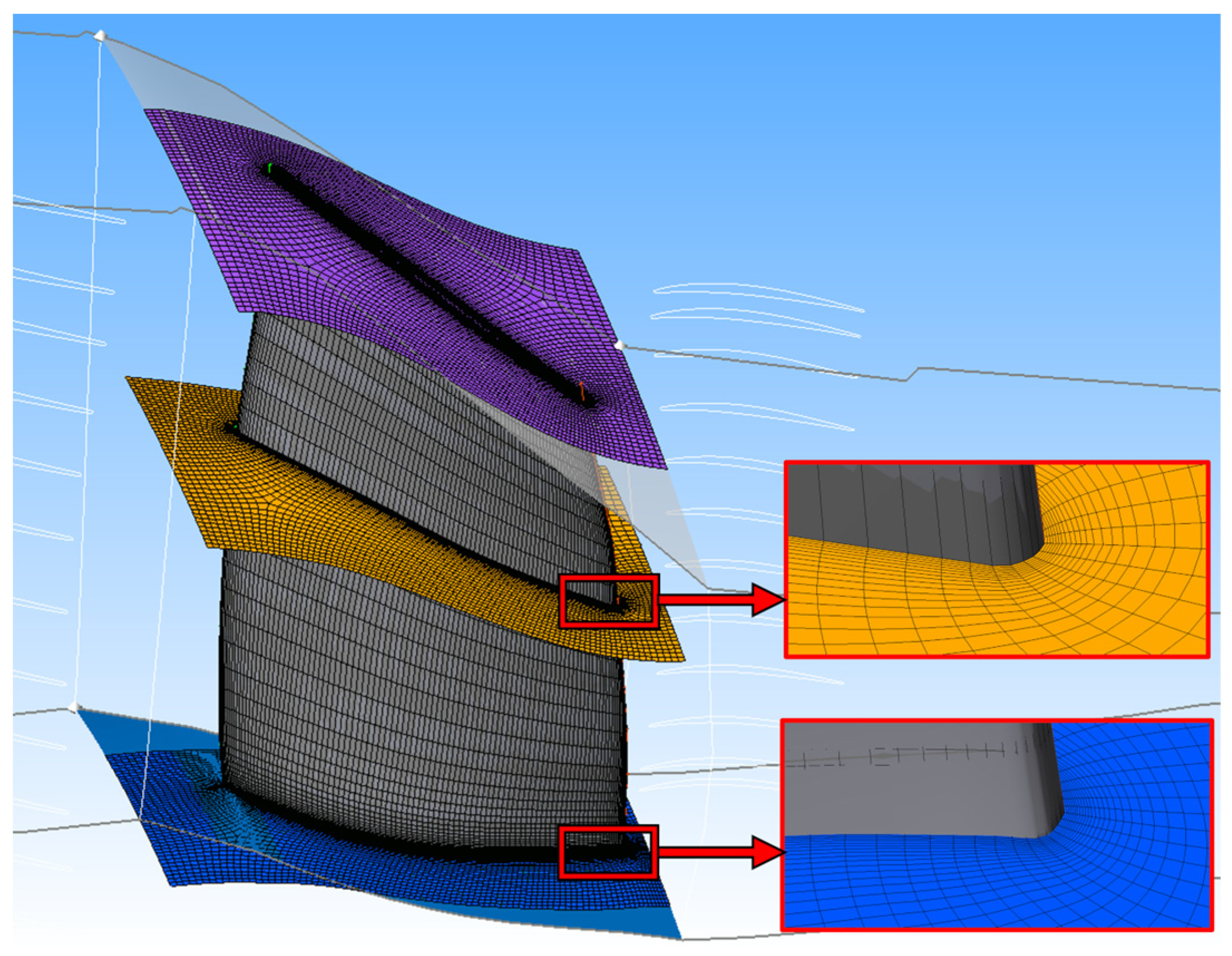
2. Geometric Digital Modeling of HPC
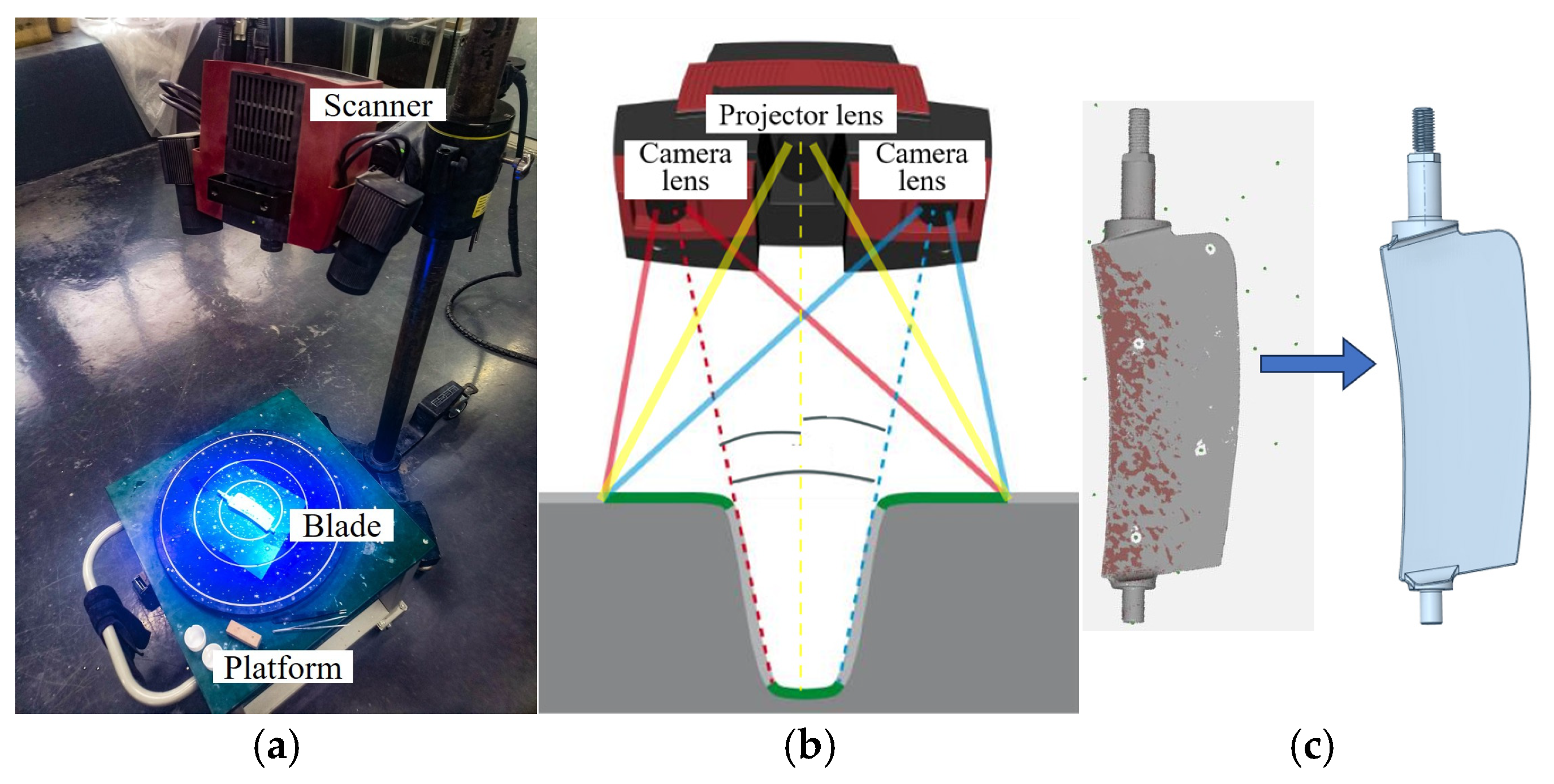
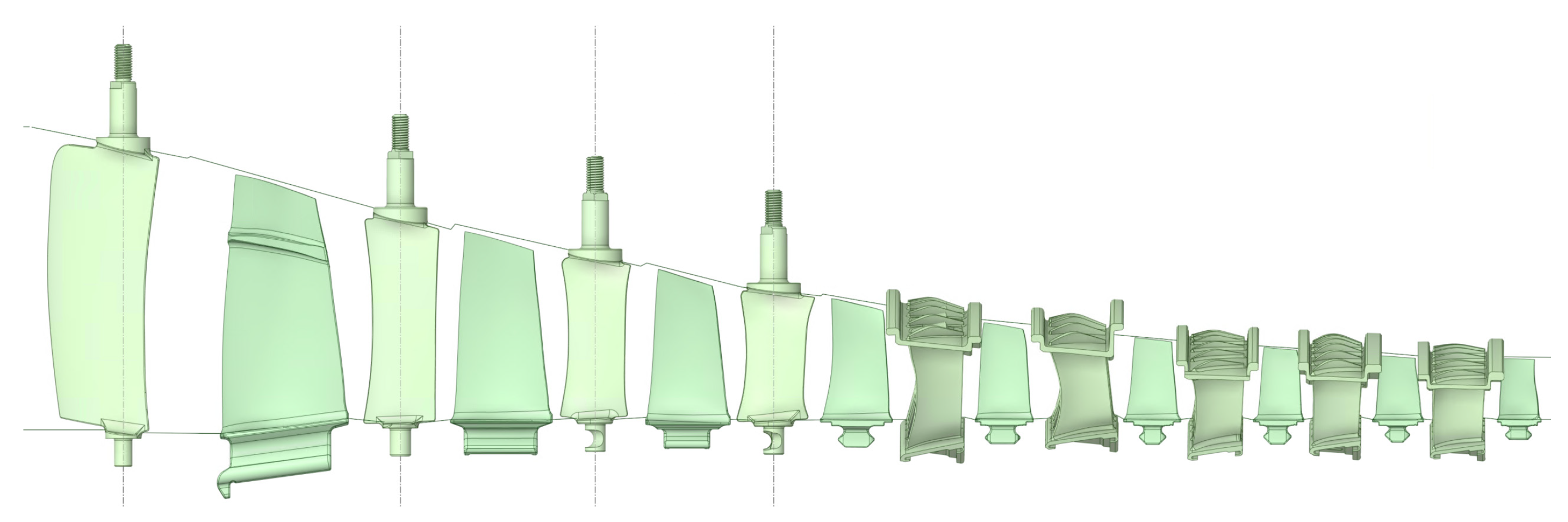
2.1. Reverse Modeling
2.2. Parametric Reconstruction of Blade Geometric Deviations
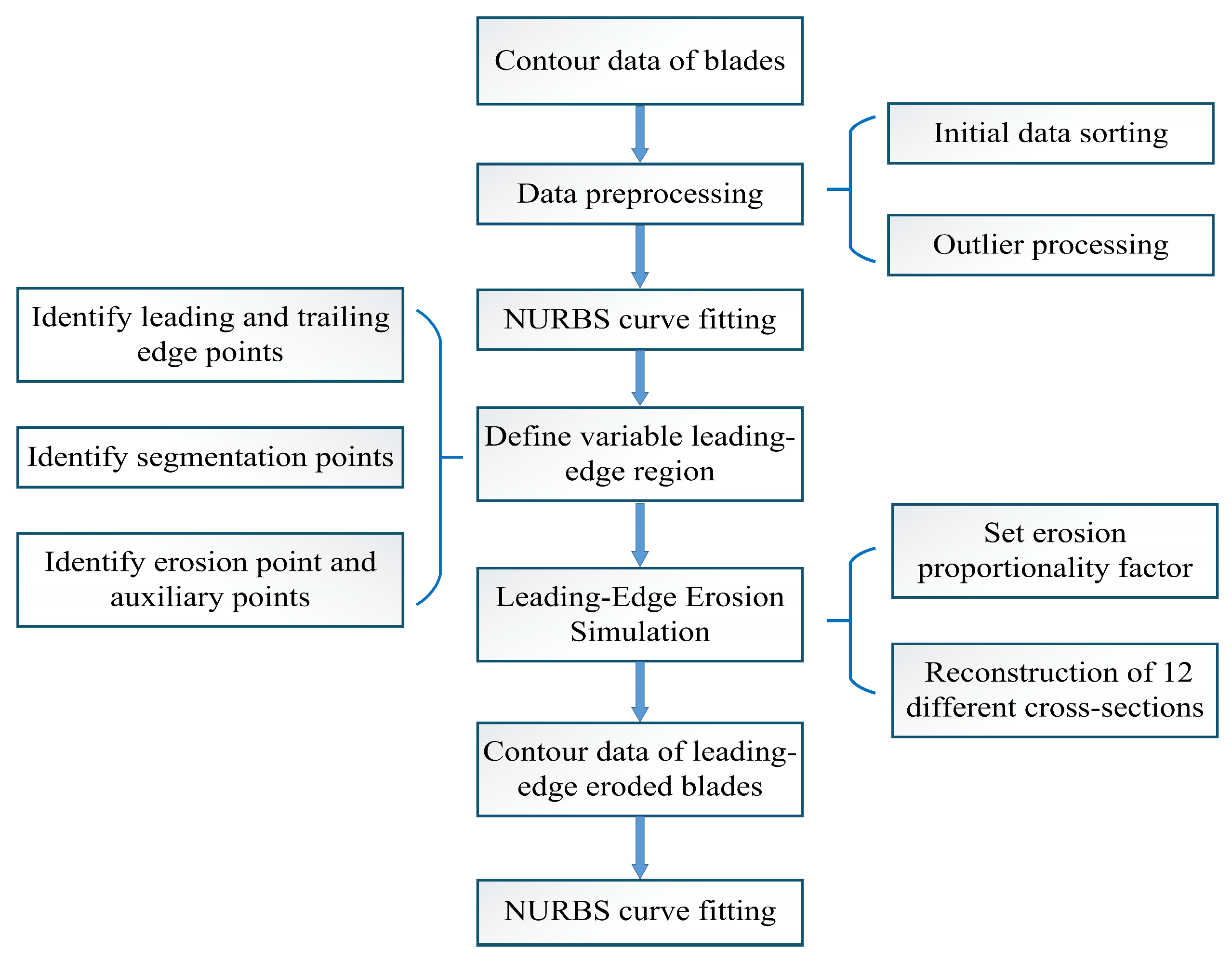
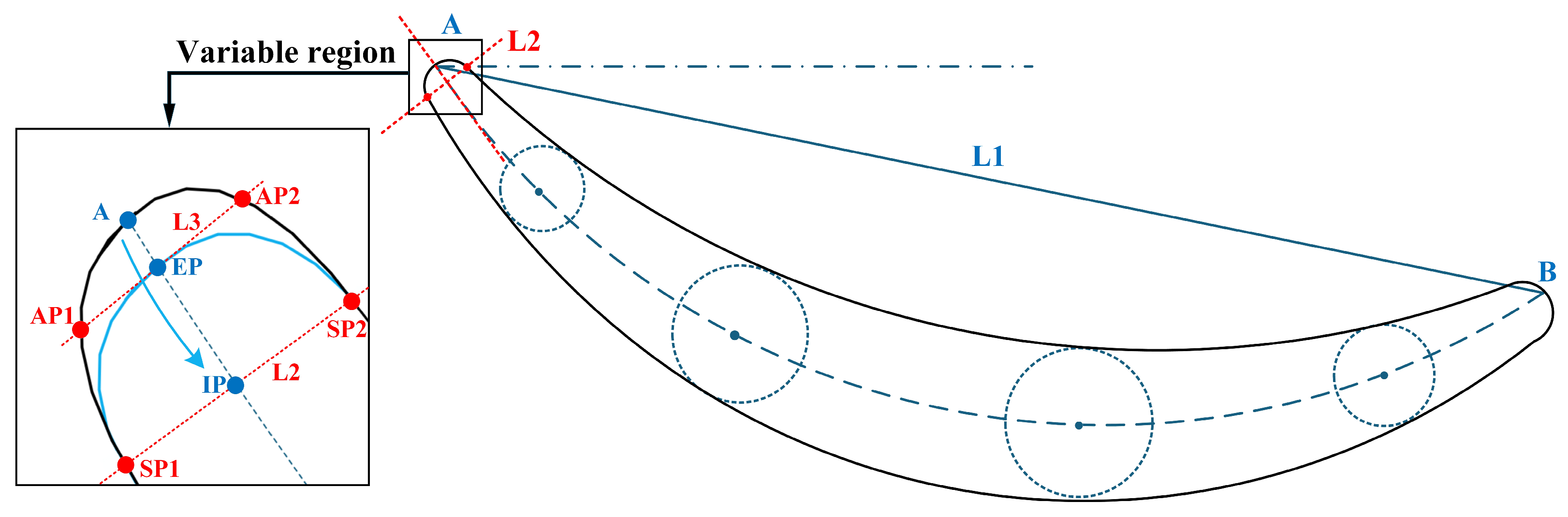
2.2.1. Leading-Edge Erosion
2.2.2. Surface Roughness and Tip Clearance
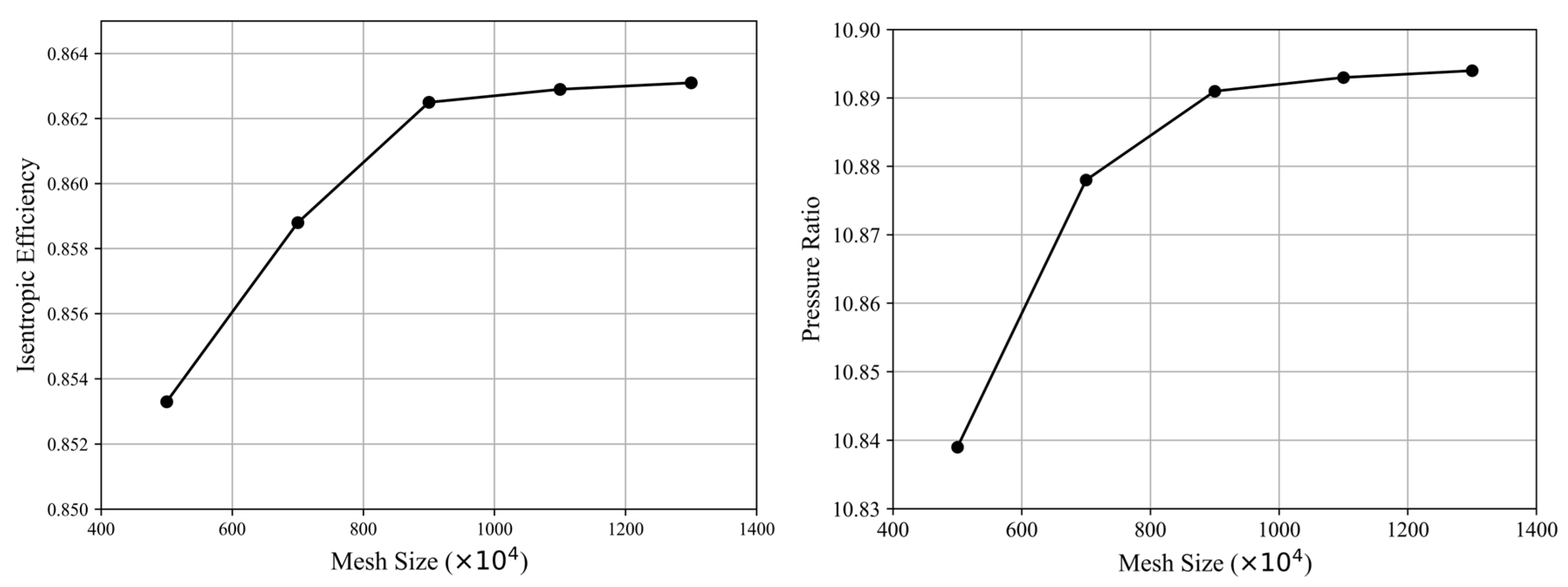
3. Three-Dimensional CFD Simulation
3.1. Automated High-Fidelity Simulation Process
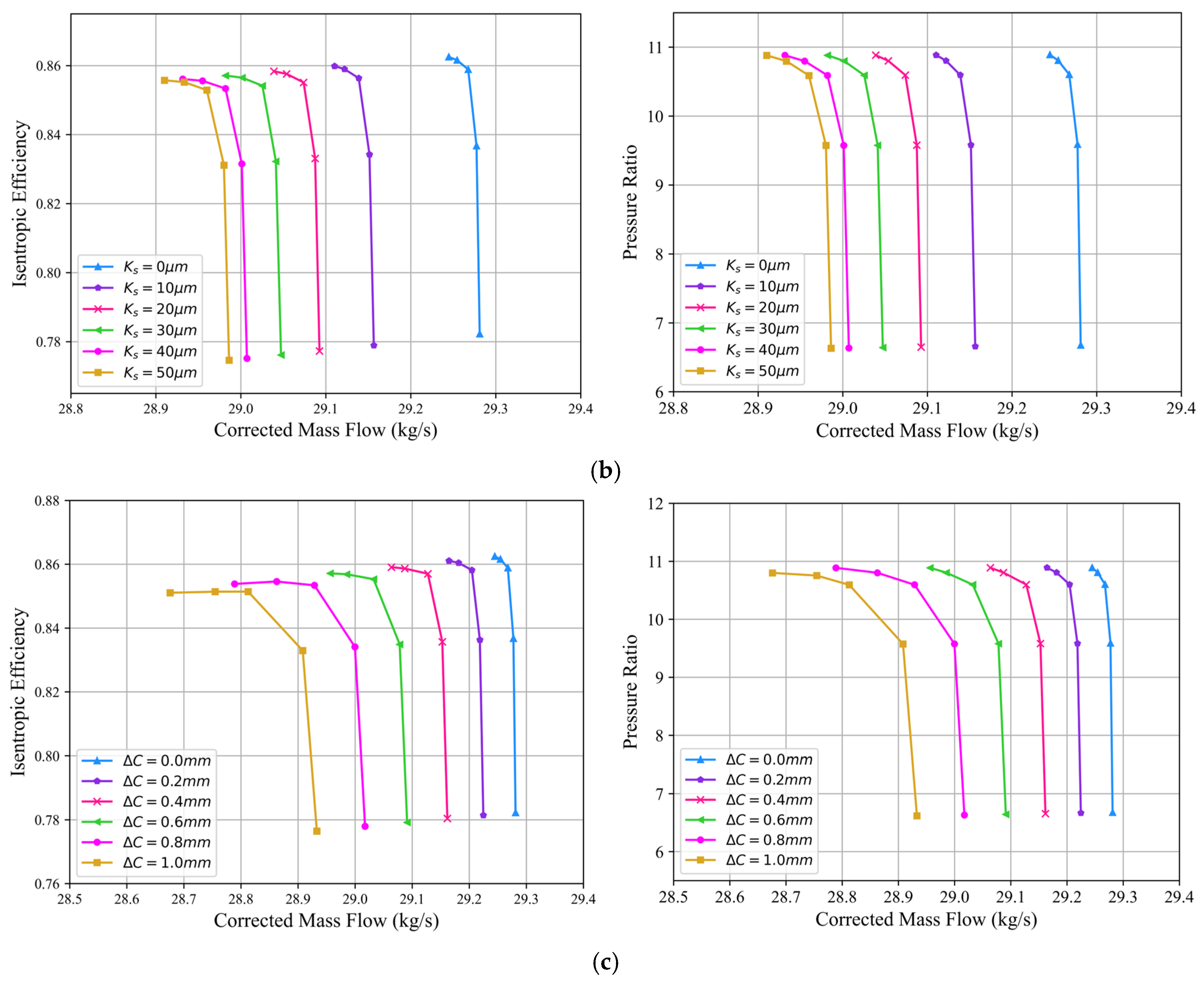
3.2. Simulations of Blade Geometric Deviations
4. Engine Performance Digital Twin Modeling
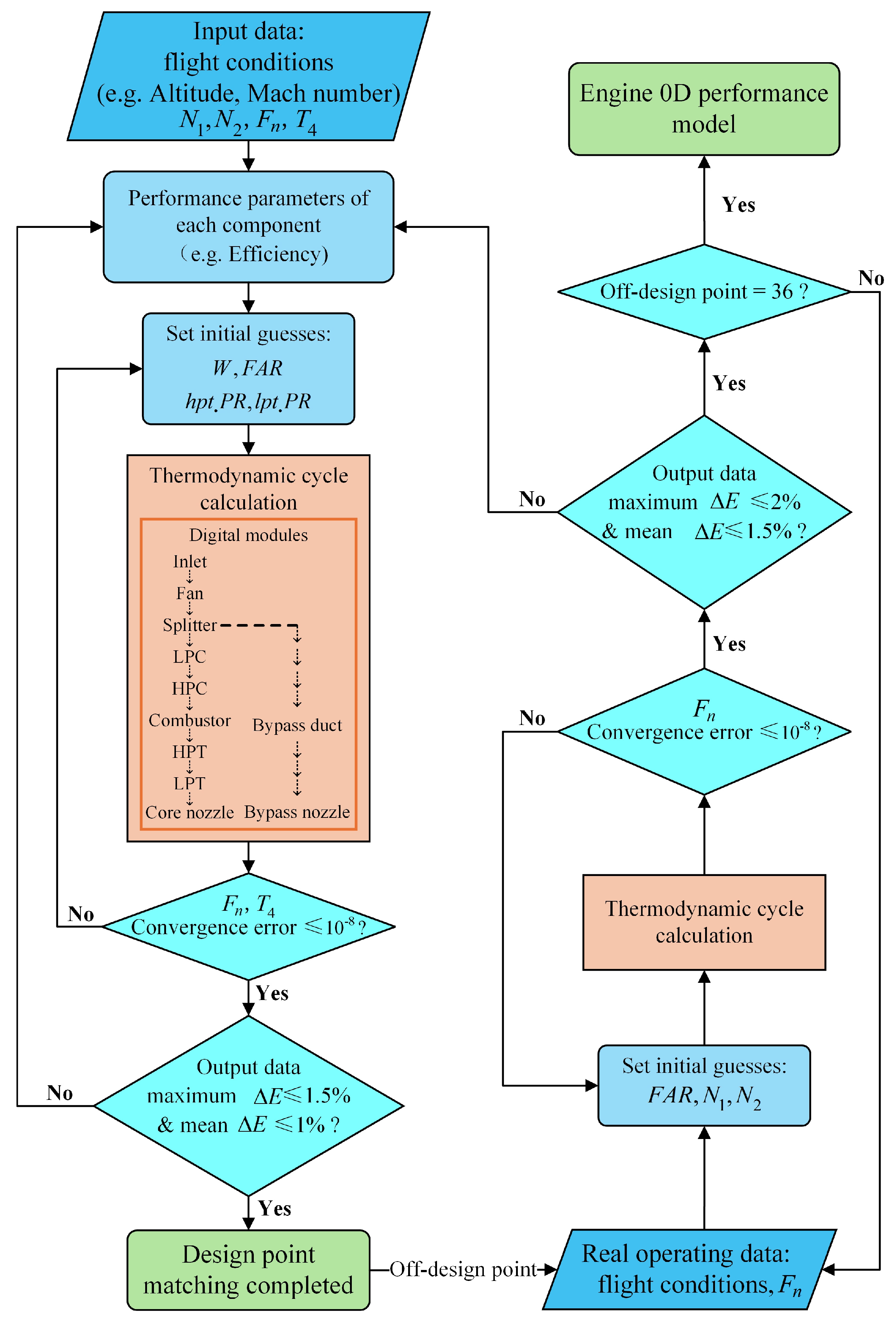
4.1. 0D Performance Modeling Based on Real Operating Data
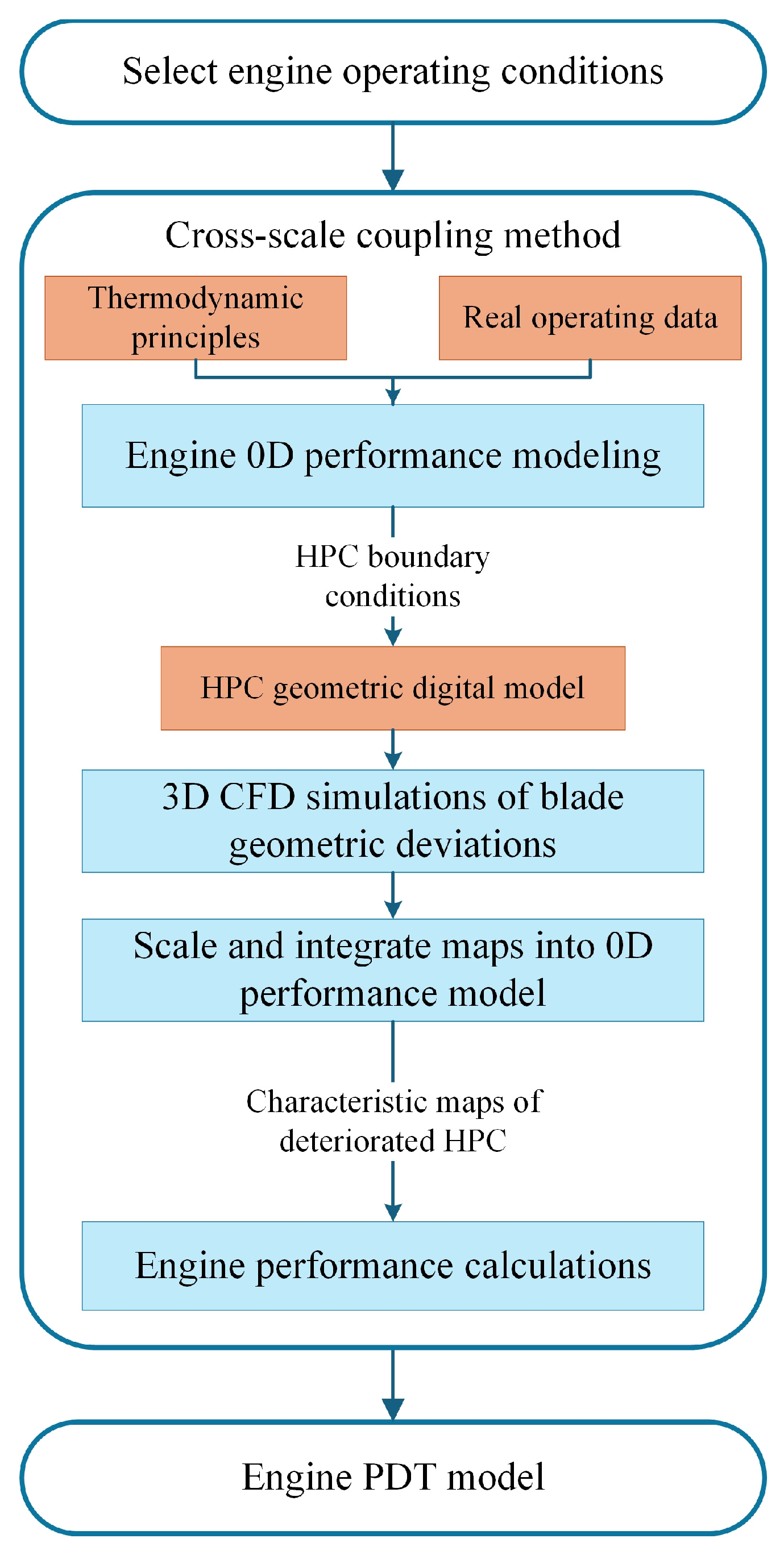
4.2. Cross-Scale Coupling Method
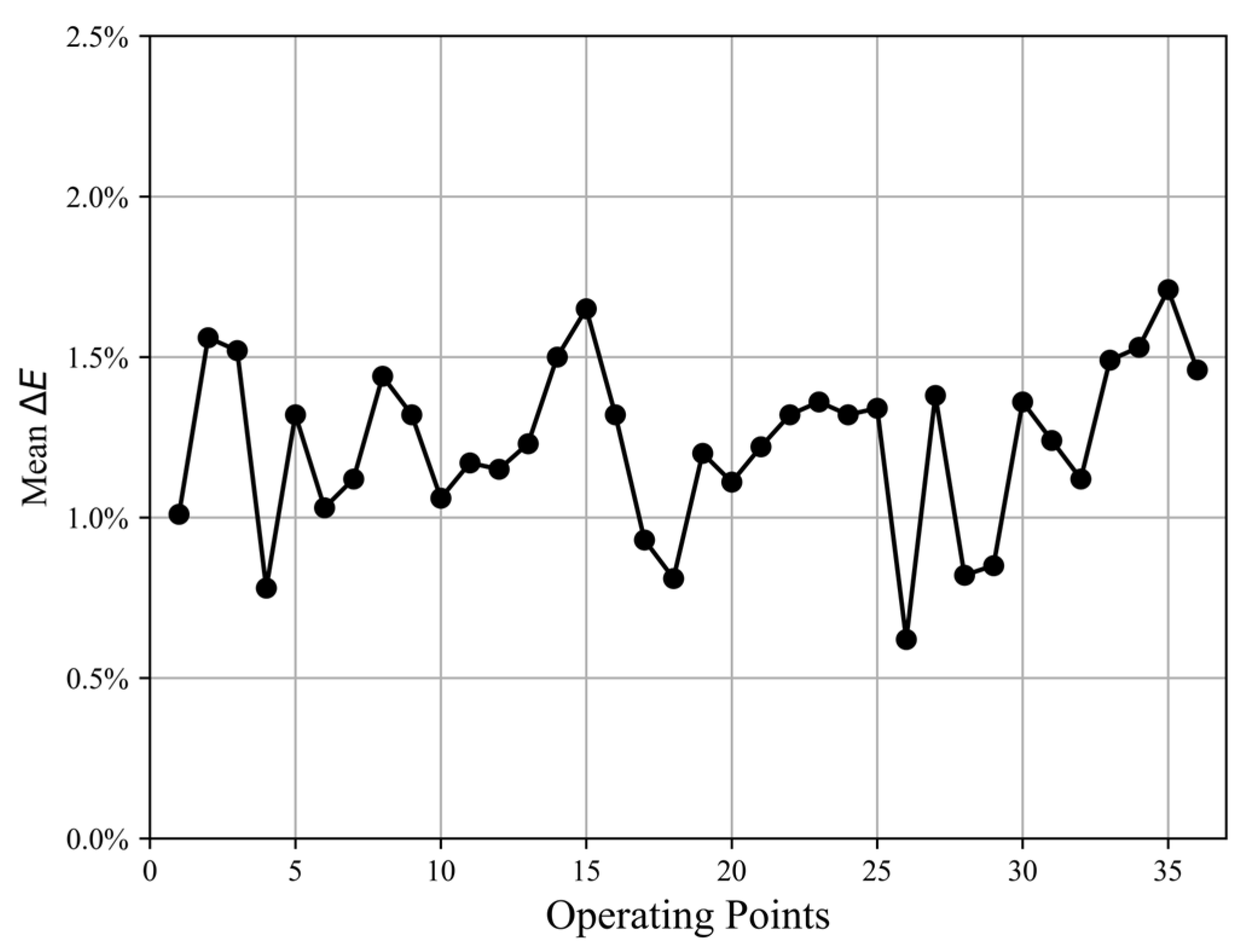
4.3. PDT Modeling and Validation
5. Case Study
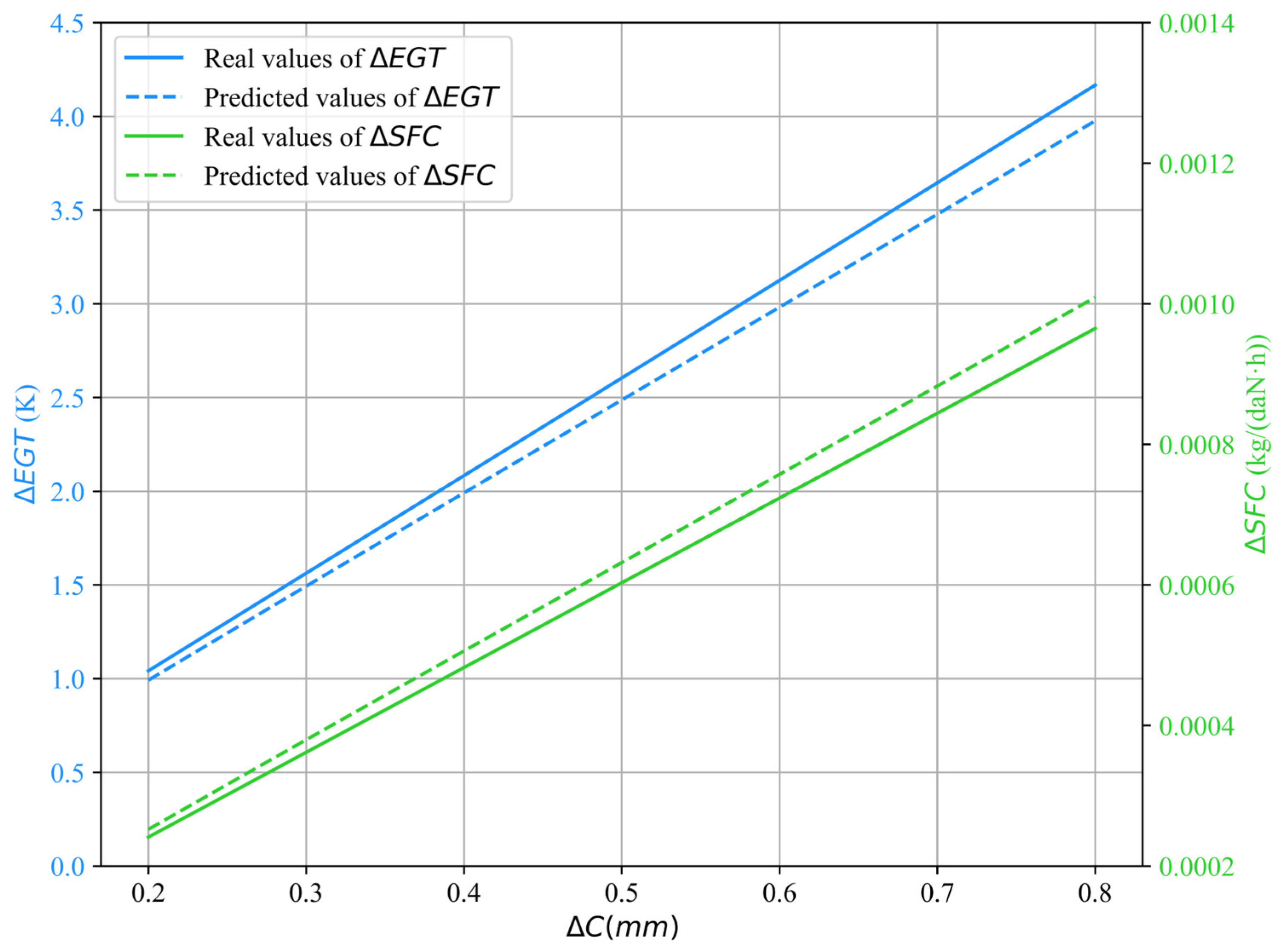
5.1. SVR-Based Surrogate Modeling
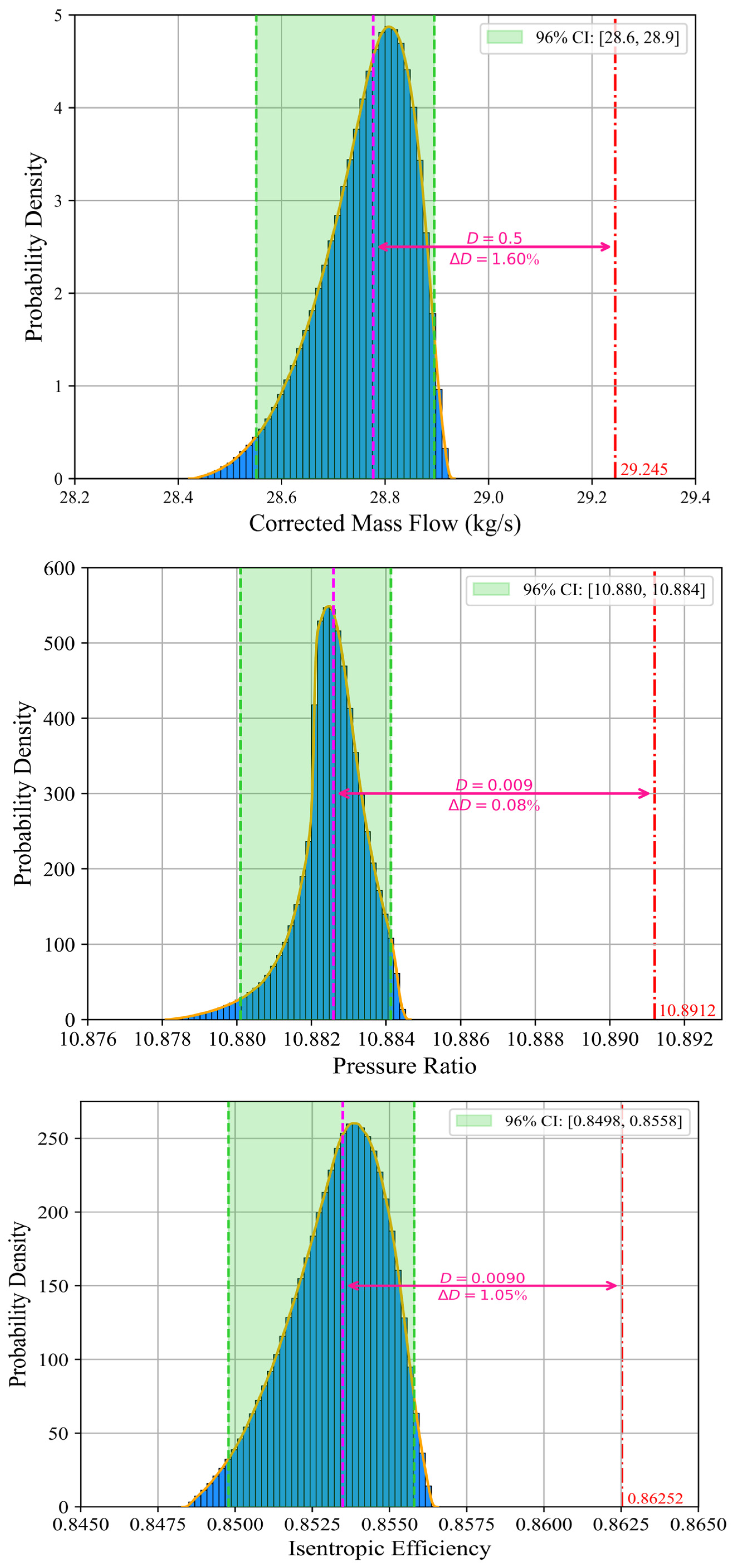
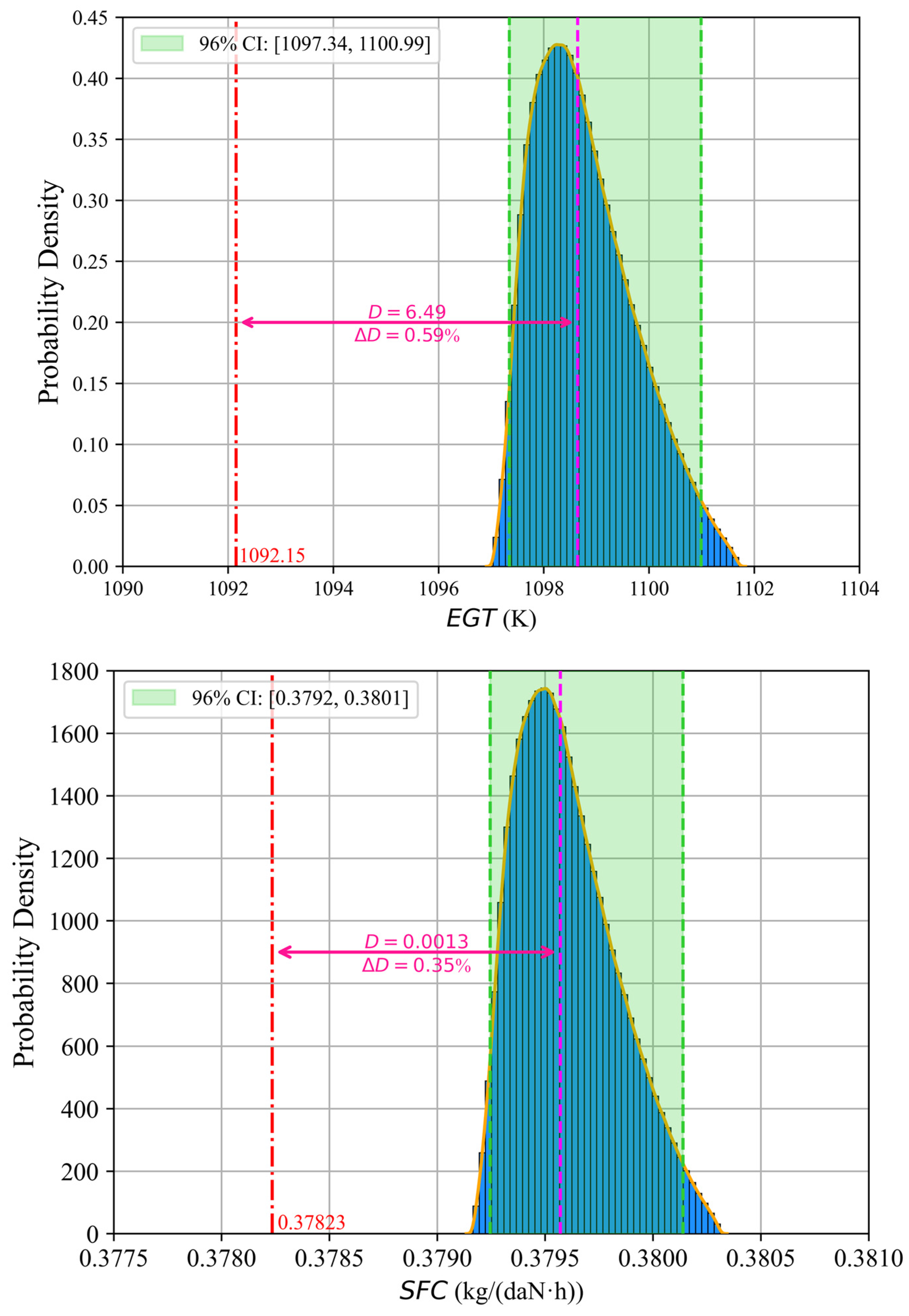
5.2. Uncertainty Quantification of the Impact of Blade Geometric Deviations
6. Conclusions
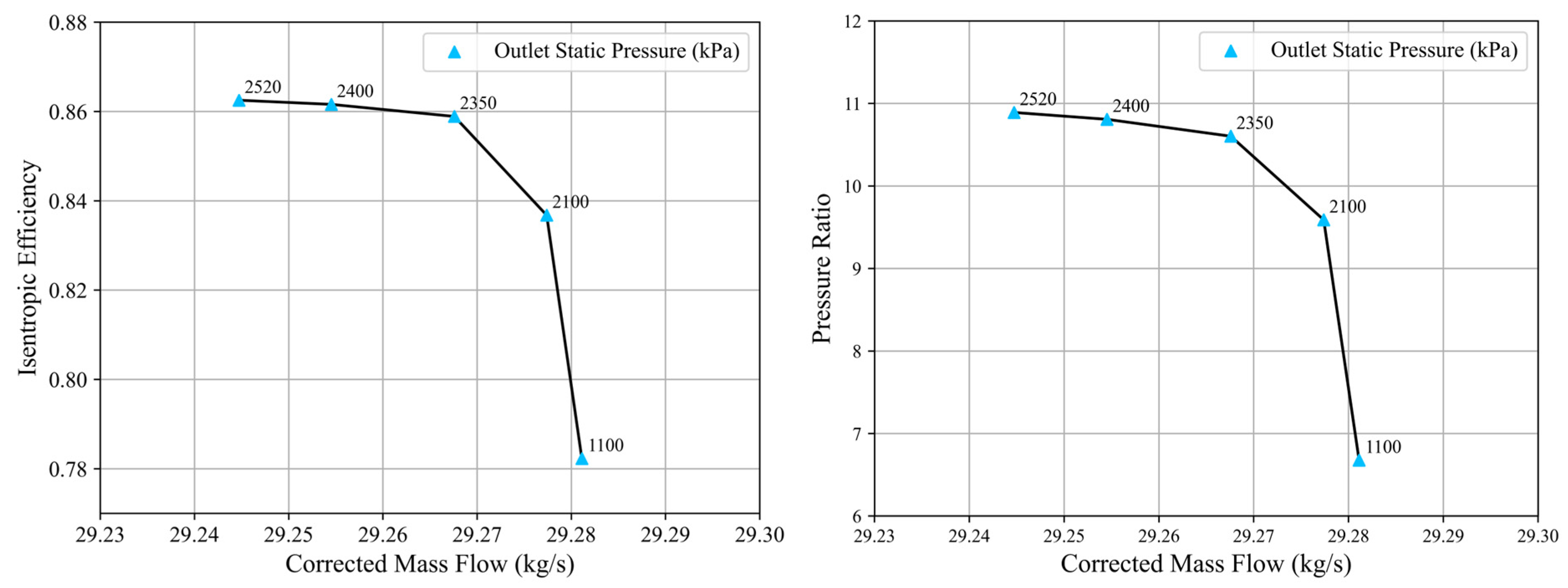
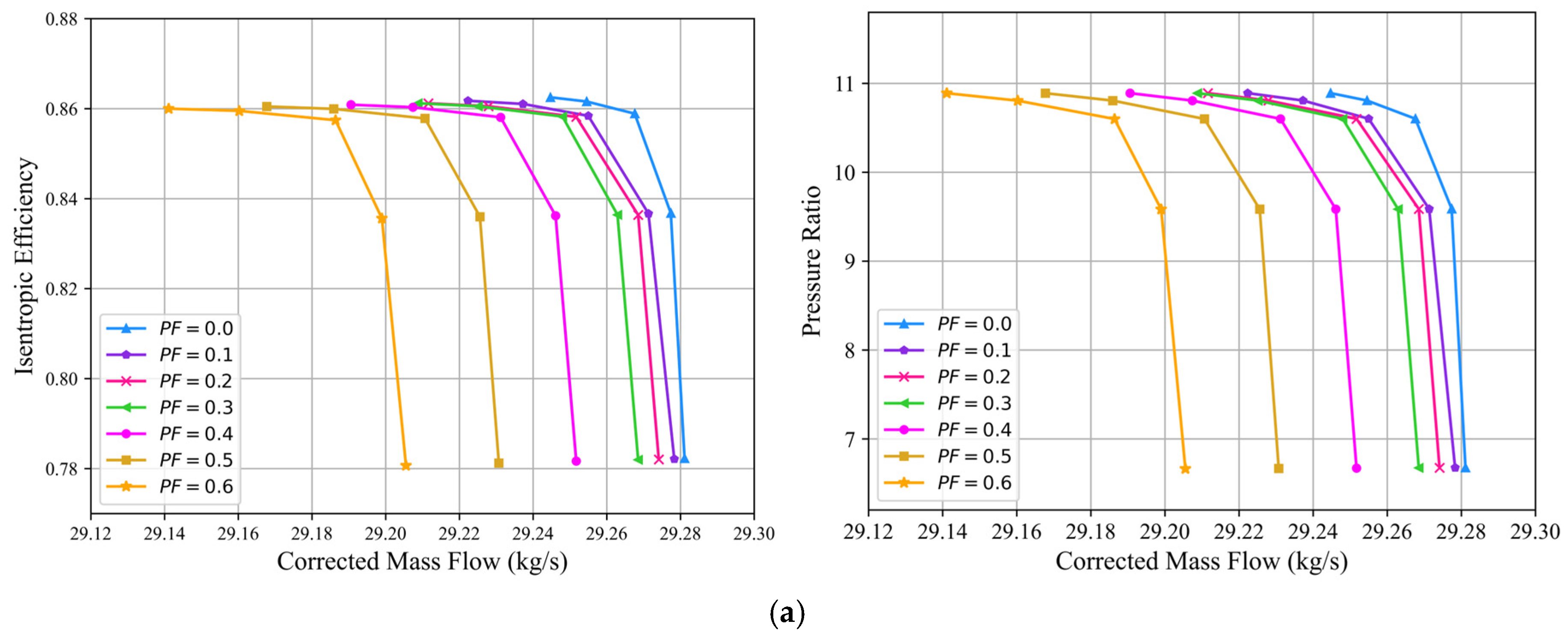
- In the CFD simulations, the HPC mass flow, efficiency, and pressure ratio decrease as the deviation increases. The increase in tip clearance increment from 0 mm to 1.0 mm exerts the most significant impact on HPC aerodynamic performance. Under the boundary condition of maintaining an outlet static pressure of 2520 kPa, the mass flow, efficiency, and pressure ratio decrease by 1.95%, 1.33%, and 0.828%, respectively. When equivalent sand-grain roughness increases from 0 μm to 50 μm, the corresponding reductions are 1.14%, 0.784%, and 0.0845%. In contrast, an increase in the leading-edge erosion proportionality factor from 0 to 0.6 results in only minor decreases of 0.354%, 0.292%, and 0.00826%.
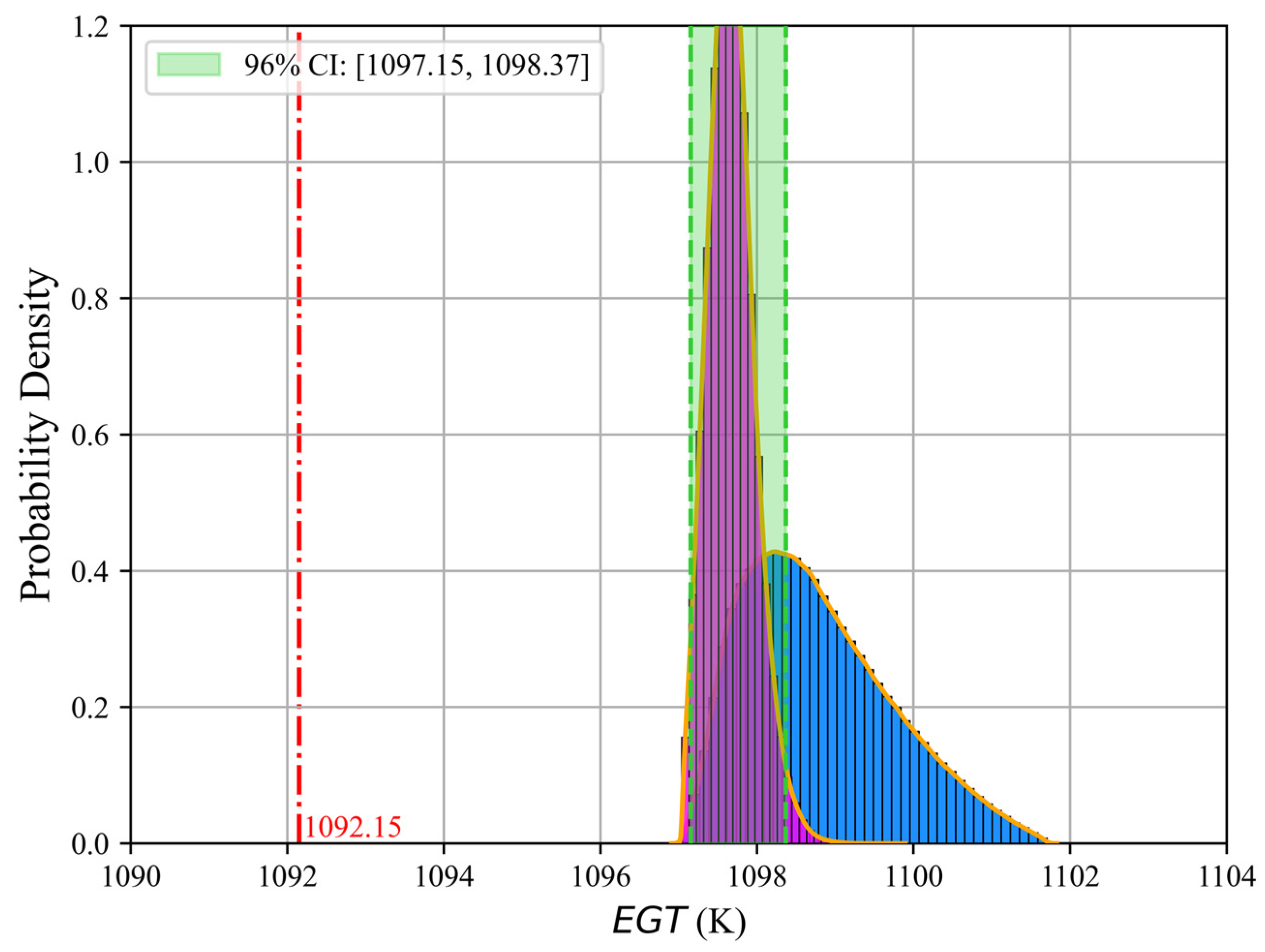
- The developed engine performance model exhibits high accuracy. Among 36 selected operating points, the maximum mean (relative error) between the model outputs and real operating data is 1.71%, with an average value of 1.23%. By integrating the 0D performance model with the HPC geometric digital model, an engine PDT model is developed. The model is validated by comparing the results of simulating the deviation of R1 blades with the relevant manual data.
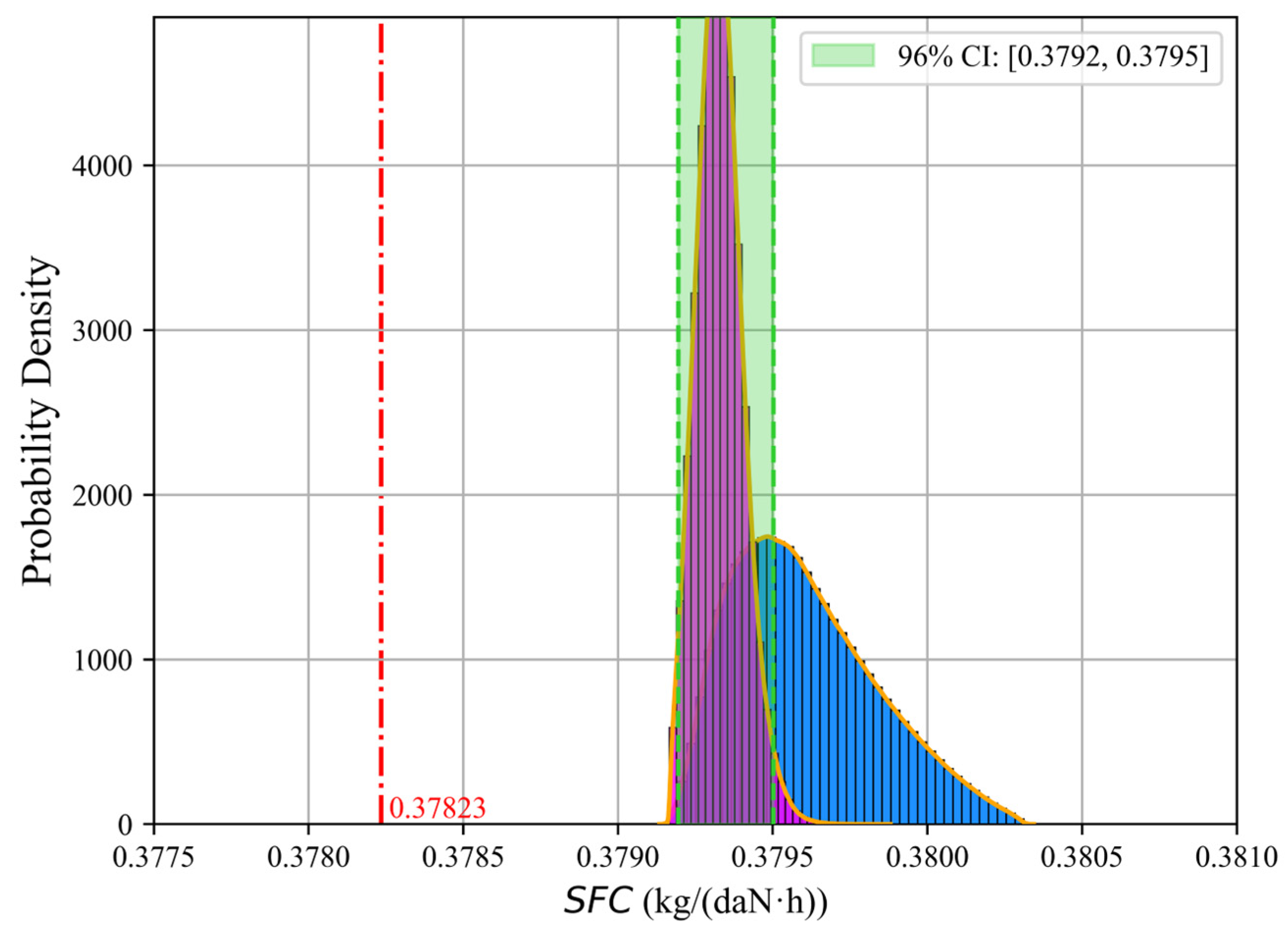
- The impact of combined deviation is analyzed by constructing surrogate models. The sensitivity of pressure ratio to combined deviation is lower than that of efficiency and mass flow, with the median of its degraded probability distribution decreasing by only 0.08% relative to the standard design value. EGT exhibits higher sensitivity than SFC, with its median increasing by 0.59%. The engine performance before and after blade tip repair in the CBM scenario is evaluated, demonstrating that the proposed method based on the PDT model improves maintenance strategies and reduces maintenance costs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CBM | Condition-based maintenance |
| CFD | Computational fluid dynamics |
| CI | Confidence interval |
| EGT | Exhaust gas temperature |
| HPC | High-pressure compressor |
| IGV | Inlet guide vane |
| LHS | Latin hypercube sampling |
| MCS | Monte Carlo simulation |
| MRO | Maintenance, repair, and overhaul |
| NIPC | Non-intrusive polynomial chaos |
| NPSS | Numerical propulsion system simulation |
| NURBS | Non-uniform rational B-spline |
| OEM | Original equipment manufacturer |
| PDT | Performance digital twin |
| SFC | Specific fuel consumption |
| SST | Shear stress transport |
| SVR | Support vector regression |
| 0D | Zero-dimensional |
| 3D | Three-dimensional |
| Fuel-to-air ratio | |
| Net thrust | |
| High-pressure turbine pressure ratio | |
| Equivalent sand-grain roughness | |
| Low-pressure turbine pressure ratio | |
| Low-pressure spool speed | |
| High-pressure spool speed | |
| Erosion proportionality factor | |
| Fan inlet total pressure | |
| HPC outlet static pressure | |
| Combustor exit temperature | |
| HPC inlet total temperature | |
| Engine inlet mass flow | |
| Isentropic efficiency | |
| Total-to-total pressure ratio | |
| Total-to-total temperature ratio | |
| Tip clearance increments | |
| Relative error |
References
- Javed, A.; Pecnik, R.; Van Buijtenen, J.P. Optimization of a centrifugal compressor impeller for robustness to manufacturing uncertainties. ASME J. Eng. Gas Turbines Power 2016, 138, 112101. [Google Scholar] [CrossRef]
- Marx, J.; Städing, J.; Reitz, G.; Friedrichs, J. Investigation and analysis of deterioration in high pressure compressors due to operation. CEAS Aeronaut. J. 2014, 5, 515–525. [Google Scholar] [CrossRef]
- Wang, J.Y.; Yang, H.L.; Zhou, K.; Wei, J.; Wen, M.; Zheng, X. Performance dispersion control of a multistage compressor based on precise identification of critical features. Aerosp. Sci. Technol. 2022, 129, 107845. [Google Scholar] [CrossRef]
- Denkena, B.; Nyhuis, P.; Bergmann, B.; Nübel, N.; Lucht, T. Towards an autonomous maintenance, repair and overhaul process: Exemplary holistic data management approach for the regeneration of aero-engine blades. Procedia Manuf. 2019, 40, 77–82. [Google Scholar] [CrossRef]
- Ahmad, R.; Kamaruddin, S. An overview of time-based and condition-based maintenance in industrial application. Comput. Ind. Eng. 2012, 63, 135–149. [Google Scholar] [CrossRef]
- Labib, A.W. A decision analysis model for maintenance policy selection using a CMMS. J. Qual. Maint. Eng. 2004, 10, 191–202. [Google Scholar] [CrossRef]
- Montomoli, F. Uncertainty Quantification in Computational Fluid Dynamics and Aircraft Engines; Springer: Cham, Switzerland, 2015; pp. 1–3. [Google Scholar] [CrossRef]
- Wang, J.; Zheng, X. Review of geometric uncertainty quantification in gas turbines. ASME J. Eng. Gas Turbines Power 2020, 142, 070801. [Google Scholar] [CrossRef]
- Hu, X.; Chen, X.; Parks, G.T.; Yao, W. Review of improved Monte Carlo methods in uncertainty-based design optimization for aerospace vehicles. Prog. Aerosp. Sci. 2016, 86, 20–27. [Google Scholar] [CrossRef]
- Garzon, V.E.; Darmofal, D.L. Impact of geometric variability on axial compressor performance. ASME J. Turbomach. 2003, 125, 692–703. [Google Scholar] [CrossRef]
- Lange, A.; Voigt, M.; Vogeler, K.; Schrapp, H.; Johann, E.; Gümmer, V. Probabilistic CFD simulation of a high-pressure compressor stage taking manufacturing variability into account. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air, Glasgow, UK, 14–18 June 2010; ASME: New York, NY, USA, 2010; pp. 617–628. [Google Scholar] [CrossRef]
- Giebmanns, A.; Schnell, R.; Werner-Spatz, C. A method for efficient performance prediction for fan and compressor stages with degraded blades. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montreal, QC, Canada, 15–19 June 2015; ASME: New York, NY, USA, 2015; p. V02AT37A006. [Google Scholar] [CrossRef]
- Xu, S.; Zhang, Q.; Wang, D.; Huang, X. Uncertainty Quantification of Compressor Map Using the Monte Carlo Approach Accelerated by an Adjoint-Based Nonlinear Method. Aerospace 2023, 10, 280. [Google Scholar] [CrossRef]
- Gong, Y.; Zhang, J.; Xu, D.; Huang, Y. Quantile-based optimization under uncertainties for complex engineering structures using an active learning basis-adaptive PC-Kriging model. Chin. J. Aeronaut. 2025, 38, 103197. [Google Scholar] [CrossRef]
- Shahpar, S.; Seshadri, P.; Parks, G. Leakage uncertainties in compressors: The case of Rotor 37. J. Propuls. Power 2015, 31, 456–466. [Google Scholar] [CrossRef]
- Wang, J.; Wang, B.; Yang, H.; Sun, Z.; Zhou, K.; Zheng, X. Compressor geometric uncertainty quantification under conditions from near choke to near stall. Chin. J. Aeronaut. 2023, 36, 16–29. [Google Scholar] [CrossRef]
- Zhang, H.; Yue, K.; Zhang, Y. Geometric Optimization of Coanda Jet Chamber Fins via Response Surface Methodology. Aerospace 2025, 12, 571. [Google Scholar] [CrossRef]
- Shi, M.; Lv, L.; Sun, W.; Song, X. A multi-fidelity surrogate model based on support vector regression. Struct. Multidiscip. Optim. 2020, 61, 2363–2375. [Google Scholar] [CrossRef]
- He, X.; Zheng, X. Performance improvement of transonic centrifugal compressors by optimization of complex three-dimensional features. Proc. Inst. Mech. Eng. G J. Aerosp. Eng. 2017, 231, 2723–2738. [Google Scholar] [CrossRef]
- Ma, C.; Gao, L.; Cai, Y.; Li, R. Robust optimization design of compressor blade considering machining error. In Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, Charlotte, NC, USA, 26–30 June 2017; ASME: New York, NY, USA, 2017; p. V02CT47A003. [Google Scholar] [CrossRef]
- Kraft, J.; Sethi, V.; Singh, R. Optimization of aero gas turbine maintenance using advanced simulation and diagnostic methods. ASME J. Eng. Gas Turbines Power 2014, 136, 111601. [Google Scholar] [CrossRef]
- Reitz, G.; Friedrichs, J. Impact of front- and rear-stage high pressure compressor deterioration on jet engine performance. Int. J. Turbomach. Propuls. Power 2018, 3, 15. [Google Scholar] [CrossRef]
- Grieves, M.; Vickers, J. Digital twin: Mitigating unpredictable, undesirable emergent behavior in complex systems. In Transdisciplinary Perspectives on Complex Systems; Kahlen, J., Flumerfelt, S., Alves, A., Eds.; Springer: Cham, Switzerland, 2017; pp. 85–113. [Google Scholar] [CrossRef]
- Hu, M.; He, Y.; Lin, X.; Lu, Z.; Jiang, Z.; Ma, B. Digital twin model of gas turbine and its application in warning of performance fault. Chin. J. Aeronaut. 2023, 36, 449–470. [Google Scholar] [CrossRef]
- Xiong, M.L.; Wang, H.W.; Fu, Q.; Xu, Y. Digital twin-driven aero-engine intelligent predictive maintenance. Int. J. Adv. Manuf. Technol. 2021, 114, 3751–3761. [Google Scholar] [CrossRef]
- Gálvez, A.; Iglesias, A. Particle swarm optimization for non-uniform rational B-spline surface reconstruction from clouds of 3D data points. Inf. Sci. 2012, 192, 174–192. [Google Scholar] [CrossRef]
- Reitz, G.; Kellersmann, A.; Schlange, S.; Friedrichs, J. Comparison of sensitivities to geometrical properties of front and aft high pressure compressor stages. CEAS Aeronaut. J. 2018, 9, 135–146. [Google Scholar] [CrossRef]
- Nikuradse, J. Law of flows in rough pipes. NACA Tech. Memo. 1933, 1292. Available online: https://digital.library.unt.edu/ark%3a/67531/metadc63009/ (accessed on 20 August 2025).
- Koch, C.C.; Smith, L.H. Loss sources and magnitudes in axial-flow compressors. ASME J. Eng. Gas Turbines Power 1976, 98, 411–424. [Google Scholar] [CrossRef]
- Gilge, P.; Kellersmann, A.; Friedrichs, J.; Seume, J.R. Surface roughness of real operationally used compressor blade and blisk. Proc. Inst. Mech. Eng. G J. Aerosp. Eng. 2019, 233, 5321–5330. [Google Scholar] [CrossRef]
- Gray, J.S.; Hwang, J.T.; Martins, J.R.R.A.; Moore, K.T.; Naylor, B.A. OpenMDAO: An open-source framework for multidisciplinary design, analysis, and optimization. Struct. Multidiscip. Optim. 2019, 59, 1075–1104. [Google Scholar] [CrossRef]
- Hendricks, E.S.; Gray, J.S. pyCycle: A Tool for Efficient Optimization of Gas Turbine Engine Cycles. Aerospace 2019, 6, 87. [Google Scholar] [CrossRef]
- Claus, R.W.; Evans, A.L.; Lytle, J.K.; Nichols, L. Numerical propulsion system simulation. Comput. Syst. Eng. 1991, 2, 357–364. [Google Scholar] [CrossRef]
- Turner, M.G.; Reed, J.A.; Ryder, R.; Veres, J.P. Multi-fidelity simulation of a turbofan engine with results zoomed into mini-maps for a zero-D cycle simulation. In Proceedings of the ASME Turbo Expo 2004: Power for Land, Sea, and Air, Vienna, Austria, 14–17 June 2004; ASME: New York, NY, USA, 2004; pp. 219–230. [Google Scholar] [CrossRef]
- Pachidis, V.; Pilidis, P.; Templalexis, I.; Barbosa, J.B.; Nantua, N. A de-coupled approach to component high-fidelity analysis using computational fluid dynamics. Proc. Inst. Mech. Eng. G J. Aerosp. Eng. 2007, 221, 105–113. [Google Scholar] [CrossRef]
- Awad, M.; Khanna, R. Support vector regression. In Efficient Learning Machines; Apress: Berkeley, CA, USA, 2015; pp. 154–156. [Google Scholar] [CrossRef]
- Denkena, B.; Boess, V.; Nespor, D.; Floeter, F.; Rust, F. Engine blade regeneration: A literature review on common technologies in terms of machining. Int. J. Adv. Manuf. Technol. 2015, 81, 917–924. [Google Scholar] [CrossRef]

| Geometric Deviations | Mean | Standard Deviation | 99.7% Probability Range |
|---|---|---|---|
| 0.3 | 0.1 | [0, 0.6] | |
| 30 μm | 6.6667 μm | [10 μm, 50 μm] | |
| 0.4 mm | 0.1333 mm | [0 mm, 0.8 mm] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, P.; Sun, J.; Nian, J.; Lu, J.; Liu, Q. Uncertainty Quantification of the Impact of High-Pressure Compressor Blade Geometric Deviations on Aero Engine Performance. Aerospace 2025, 12, 767. https://doi.org/10.3390/aerospace12090767
Tang P, Sun J, Nian J, Lu J, Liu Q. Uncertainty Quantification of the Impact of High-Pressure Compressor Blade Geometric Deviations on Aero Engine Performance. Aerospace. 2025; 12(9):767. https://doi.org/10.3390/aerospace12090767
Chicago/Turabian StyleTang, Pengfei, Jianzhong Sun, Jinchen Nian, Jilong Lu, and Qin Liu. 2025. "Uncertainty Quantification of the Impact of High-Pressure Compressor Blade Geometric Deviations on Aero Engine Performance" Aerospace 12, no. 9: 767. https://doi.org/10.3390/aerospace12090767
APA StyleTang, P., Sun, J., Nian, J., Lu, J., & Liu, Q. (2025). Uncertainty Quantification of the Impact of High-Pressure Compressor Blade Geometric Deviations on Aero Engine Performance. Aerospace, 12(9), 767. https://doi.org/10.3390/aerospace12090767





