1. Introduction
Technologies for satellite life extension, servicing, and the recovery of malfunctioning spacecraft have become increasingly important with the commercialization of low Earth orbit (LEO) satellites and the rapid deployment of large satellite constellations. At the same time, the accumulation of space debris in orbit has significantly heightened the risk of collisions between satellites, drawing global attention to on-orbit servicing (OOS) technologies aimed at mitigating these threats [
1].
OOS encompasses a broad range of operations, including the repair of existing satellites, refueling, attitude stabilization, health monitoring, component replacement, and the active removal of space debris. Successfully executing these tasks requires high-precision relative navigation capabilities to ensure safe and accurate interaction with target objects in space [
2].
Various sensor-based approaches have been investigated for relative navigation between satellites, including Light Detection and Ranging (LiDAR) [
3,
4], Radio Detection and Ranging (RADAR), and vision sensors [
5,
6]. Among these, vision-based image-processing techniques have advantages in hardware compactness, energy efficiency, and information density. Model-Based Tracking (MBT) [
7] has attracted attention as a practical approach for structured objects because it enables a real-time estimation of the relative position and orientation by aligning features extracted from images with a known Computer-Aided Design (CAD) model of the target object.
Despite these advantages, MBT requires an accurate initial pose, making the estimation highly sensitive to initialization. Moreover, performance degradation can occur under real space conditions because of varying illumination, surface reflections, sensor noise, and outliers in the image data. Outliers can significantly distort the pose estimation results, which necessitates robust methods to mitigate their impact. Error minimization techniques based on M-estimators have been widely used to address this, utilizing various weighting functions to suppress the influence of outliers during optimization [
8,
9].
This study utilized Spacecraft Pose Network v2 (SPNv2) [
10], a convolutional neural network-based model, solely for initial pose estimation in MBT, owing to its relatively high computational cost compared to the subsequent MBT process. After initialization, robustness against dynamically varying noise was enhanced using the General Loss function [
11], which continuously adapts its shape via a single parameter within an iteratively reweighted least squares (IRLS) tracking framework.
Building upon this combination of SPNv2-based initialization and IRLS tracking with reweighting explicitly governed by the General Loss function, this study proposes an extended MBT framework. General Loss dynamically adjusts its shape through a single parameter α, enabling continuous adaptation to varying noise characteristics. This approach not only mitigates the dependency on accurate initial poses but also improves robustness under dynamically changing weighting conditions, without relying on fixed weighting functions that suppress the influence of outliers [
8,
9].
To validate the proposed method, this study conducted a comparative evaluation of the General Loss function against seven representative M-estimators, including Tukey [
8,
12], Welsch [
9,
13], and Huber [
14]. A rendezvous profile with the International Space Station (ISS) was simulated in a ROS–Gazebo environment. The relative position and orientation estimation accuracies of each estimator were quantified using the Root Mean Square Error (RMSE) metric.
The results validate the proposed approach, demonstrating that embedding General Loss in the IRLS loop of MBT delivers robust, high-precision relative navigation and shows strong promise for future on-orbit servicing (OOS) missions.
2. Methodology
2.1. Model-Based Tracking Framework Overview
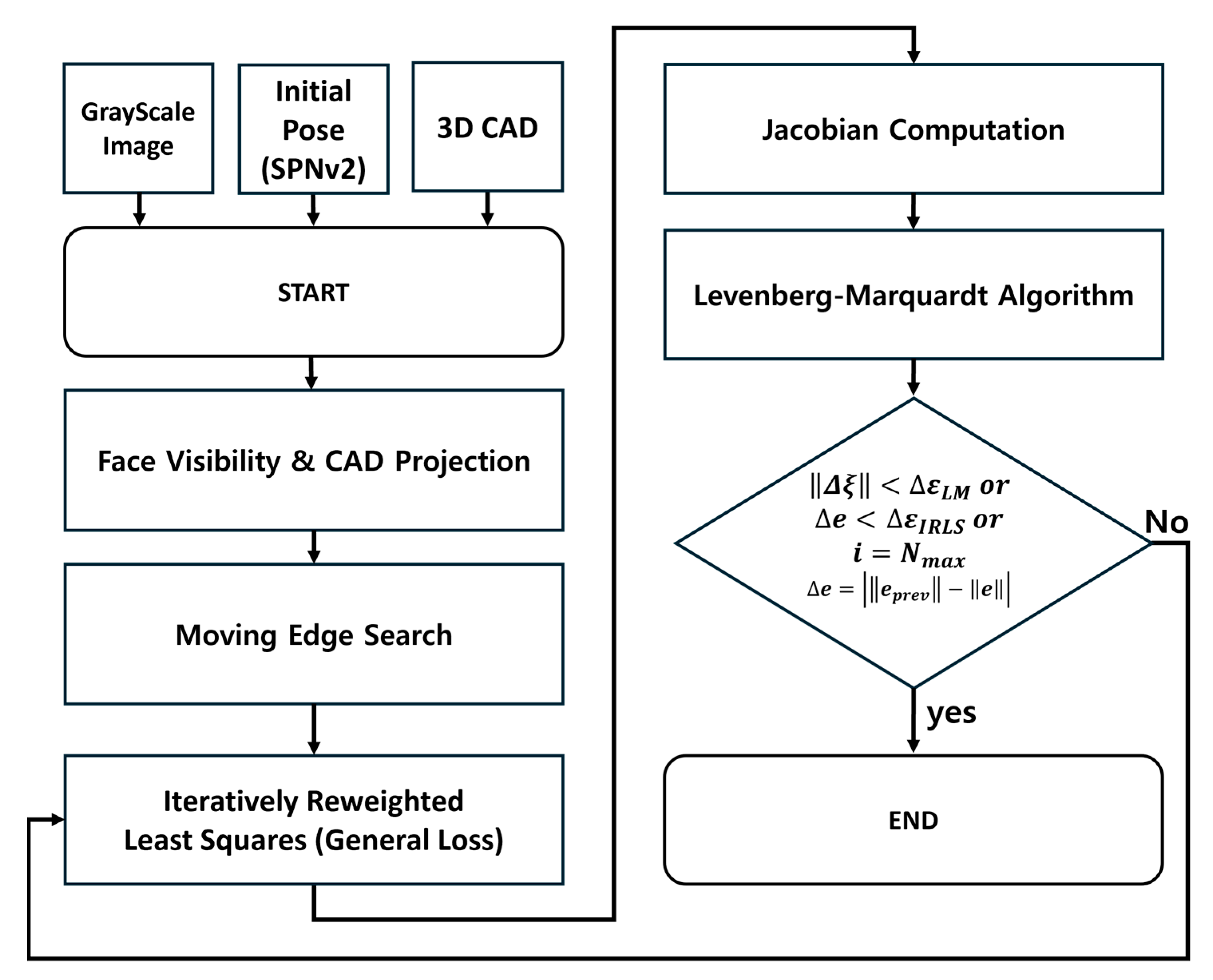
To enhance reproducibility and provide a comprehensive understanding of the overall system, this section outlines the complete pose tracking pipeline used in this study. As illustrated in
Figure 1, the proposed framework consists of two main modules:
Given an input image and a corresponding 3D CAD model of the target spacecraft, the system first estimates an initial relative pose using the proposed SPNv2-based initialization, which provides robust and accurate starting conditions for tracking. Following this initialization, the MBT pipeline begins with the face visibility determination and CAD projection to identify the visible contours of the model in the current view. A moving edge search is then performed to associate these projected contours with the observed image edges.
In each iteration, the process begins with IRLS optimization using the proposed General Loss function to compute robust weights for the current correspondences, ensuring robustness against outliers. The weighted Jacobian matrix is then computed based on these weights, and the Levenberg–Marquardt (LM) algorithm is applied to update the pose estimate. This iterative process continues until the predefined convergence criteria, which combine LM tolerance, IRLS residual variation, and iteration limits, are met. Initial pose estimation was performed using SPNv2 (available at:
https://github.com/tpark94/spnv2, accessed on 2 July 2025), and the subsequent MBT was implemented with ViSP 3.6.1 (Inria, Rennes, France).
2.2. Model-Based Tracking
MBT projects a simplified CAD model onto the image plane based on the provided initial position and orientation. The relative pose is then estimated by minimizing the error () between the observed features () from the camera and the corresponding features () projected from the CAD model. This error minimization can be performed using either the least squares approach or robust M-estimators.
In this study, the feature set is defined as comprising the 16 solar panel edges of the ISS model. These edges are projected from the CAD model and serve as the reference contours for measurement. For each edge, a set of moving edge sites is initialized by uniformly sampling points along the projected contour in the image plane.
Each site stores its 2D location, normal direction, and depth. The local image gradient is then sampled along the contour’s normal direction to build a 1D gradient profile, and the position of maximum gradient magnitude is detected as the observed feature position (
). The error between the projected and observed contours can be mathematically expressed as
where
denotes the intrinsic camera parameters, and
represents the position and orientation of the camera. The projection model
is defined by
and
, and
is the number of considered features. The confidence-weighted error for each feature is expressed by defining the residual as follows:
where
is a diagonal weighting matrix;
, with each
reflecting the confidence of
th feature calculated as follows:
where
denotes the normalized residual defined as
, and
is the influence function derived from the M-estimator. The projection error for that site is then calculated as the signed distance along the contour normal between the model-projected position
and the detected edge position
. This ensures that the residual specifically measures displacement orthogonal to the model edge, making it robust to tangential misalignments. The variation of the residual with respect to the position and orientation can be expressed as
where
denotes the interaction matrix, and
represents the velocity of the virtual camera. Assuming an exponential decay model of the error
, the control law is derived as
where
represents the pseudo-inverse of the weighted interaction matrix
, which is updated at each iteration based on the current weights and estimated depths. The virtual velocity
, corresponding to the differential update of the pose
, converges or the iteration and reaches a maximum number of iterations. At this point, the relative pose between the model and the camera is determined.
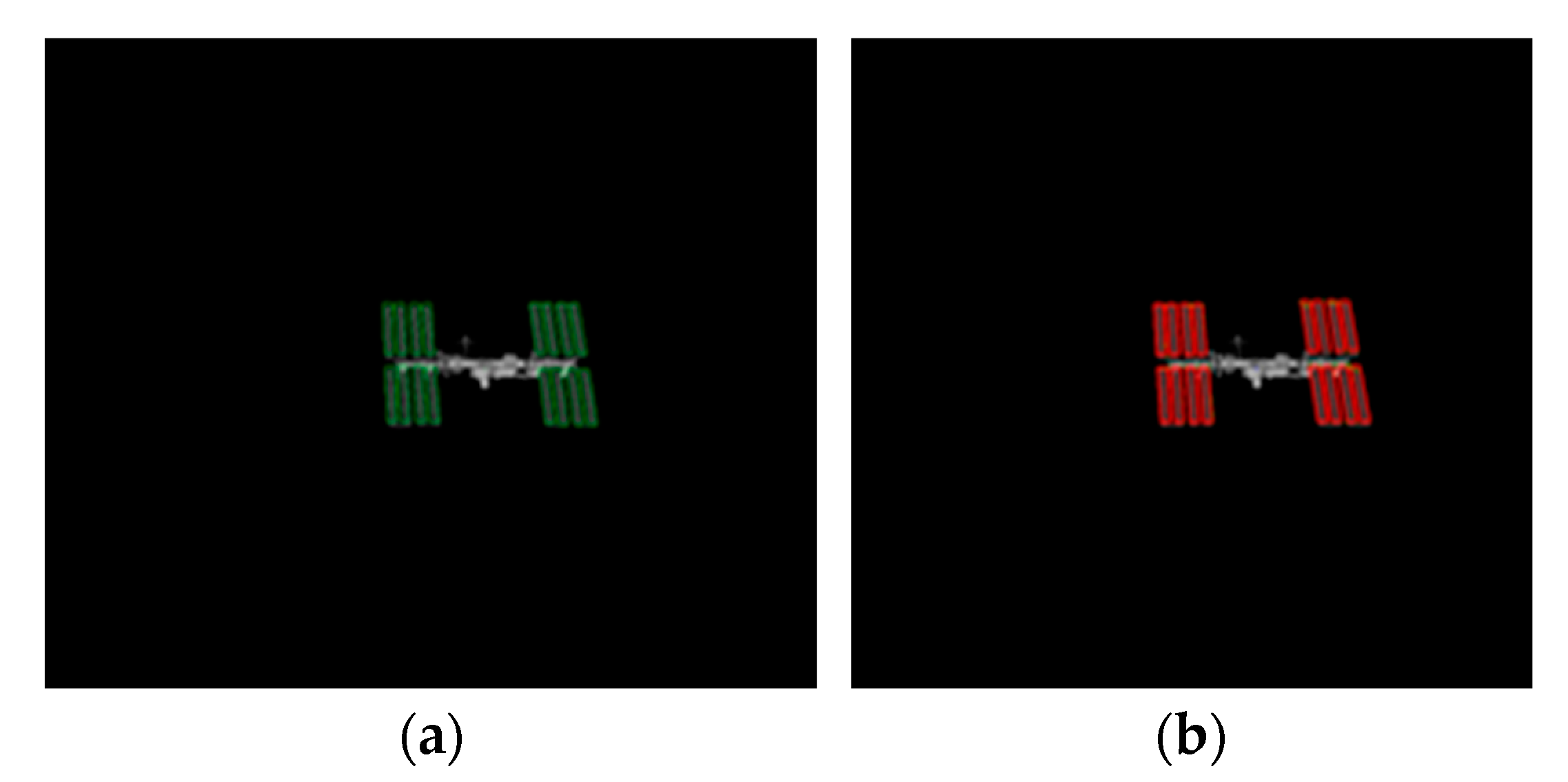
Figure 2a presents the projected initial pose
used to initialize MBT, and
Figure 2b shows the target-tracking and relative-navigation solution produced by MBT.
2.3. SPNv2
SPNv2 is a deep learning model designed to regress the six-DoF (Degrees of Freedom) pose from a single RGB image. The model adopted a Bi-directional Feature Pyramid Network (BiFPN) based on EfficientDet-D3 as its backbone architecture as a two-stage network that combines a heatmap head and a pose regression head.
The Heatmap Head predicts the 2D bounding box and keypoint heatmaps of the satellite from multi-scale feature maps. It generates outputs that include the object presence probability, bounding box classification, and bounding box regression. Subsequently, the Pose Regression Head extracts the region of interest (ROI) and directly regresses the rotation quaternion and translation vector.
A dataset of 20,000 synthetic images was generated in a ROS–Gazebo environment under a simulated ISS rendezvous profile, with positional constraints 100 m x 1000 m and angular constraints . Angle offsets proportional to the relative distance along the x-axis of the camera coordinate frame were introduced to enhance training data diversity.
In addition, randomized visual styles were applied to the dataset, with augmented samples used during training at a 50% probability. This approach enhances the robustness of the model across varying visual environments [
15].
Figure 3 shows the raw dataset collected from the simulation, while
Figure 4 shows the augmented dataset with random visual styles.
2.4. Robust M-Estimator and General Loss Function
The least squares method is commonly used to estimate the position and orientation. On the other hand, this method is sensitive to outliers that significantly degrade the accuracy in the presence of noise or erroneously detected feature points. This study adopted robust estimation methods known as M-estimators to overcome this limitation. M-estimators suppress the influence of outliers by reducing the associated weights as the magnitude of the residual increases, providing stable and accurate estimates.
Specifically, this study used the General Loss function, a generalized robust loss formulation capable of continuously adapting its shape through a single parameter. This adaptability allows the algorithm to maintain robustness against dynamically varying noise conditions. The performance of the proposed MBT framework with General Loss was compared with seven representative robust estimators: Tukey, Welsch, Huber, Cauchy, Talwar, Logistic, and Andrews. The mathematical definitions and characteristics of these estimators are summarized as follows.
2.4.1. Tukey
The Tukey estimator eliminates the influence of outliers by assigning a zero weight to residuals that exceed a predefined threshold c. The loss function and corresponding weight function of the Tukey estimator are defined using Equations (6) and (7):
Although it offers excellent robustness to outliers, the Tukey estimator is sensitive to the initial estimate. An inaccurate initial pose may lead to convergence issues during optimization.
2.4.2. Welsch
The Welsch estimator suppresses the influence of outliers by exponentially decreasing the weight as the residual magnitude increases. The loss function and corresponding weight function of the Welsch estimator are defined as Equations (8) and (9):
Compared to the Tukey estimator, the Welsch estimator handles outliers more moderately and generally offers better convergence stability. Nevertheless, its robustness to such outliers is relatively lower than that of the Tukey estimator because it assigns attenuated weights to extreme outliers rather than zero weights.
2.4.3. Huber
The Huber estimator applies the L2 loss for small residuals and switches to an L1 loss for large residuals, providing a balanced trade-off between estimation accuracy and robustness. Equations (10) and (11) express the loss function and the corresponding weight function of the Huber estimator.
The Huber estimator is computationally efficient and offers stable convergence compared to other estimators. On the other hand, its ability to handle extreme outliers is inferior to that of the Tukey and Welsch estimators.
2.4.4. Cauchy
The Cauchy estimator applies a logarithmic loss function based on the magnitude of the residuals, moderately suppressing the influence of outliers. Although it retains small non-zero weights even for extreme values, minimizing information loss, it does not eliminate the effects of very large outliers. The loss function and corresponding weight function of the Cauchy estimator are defined as Equations (12) and (13):
where
is the scale parameter, and the weighting for each residual is determined by the slope of the influence function
[
16].
2.4.5. Talwar
The Talwar estimator [
17] applies an L2 loss only when the absolute value of the residual is below a certain threshold. Residuals exceeding this threshold are assigned a constant loss value, effectively setting their weights to zero. Although this approach strongly suppresses extreme outliers, it can also eliminate some inliers depending on the choice of the threshold. The loss function and corresponding weight function of the Talwar estimator are defined as Equations (14) and (15).
2.4.6. Logistic
The Logistic estimator suppresses outliers by increasing the loss in a sigmoid-shaped manner based on the magnitude of the residual. The estimator exhibits high convergence stability owing to its smooth influence function
. It is more robust than the Huber estimator, while being more moderate in behavior than the Tukey estimator. The loss function and corresponding weight function of the Logistic estimator are defined as Equations (16) and (17). The weight is given by dividing the influence function
by
, specifically
[
18]
2.4.7. Andrews
The Andrews estimator smoothly increases the loss using a sinusoidal function within a bounded interval and assigns a zero weight outside this range, completely rejecting extreme outliers. Its non-convex shape offers strong robustness against outliers, but it is more prone to convergence issues such as entrapment in local minima. The loss function and corresponding weight function of the Andrews estimator are defined as Equations (18) and (19) [
19]:
2.4.8. General Loss
The General Loss is a robust estimation method that continuously adapts the shape of the loss function based on the residual. Traditional M-estimators, such as Huber and Tukey, use fixed-form loss functions to suppress the influence of outliers. Nevertheless, these fixed functions may not yield optimal performance under varying noise conditions because of their limited adaptability.
In contrast, the General Loss offers a generalized formulation that can smoothly and continuously transition between different loss function shapes using a single parameter. Specifically, it features an adaptive structure in which the loss behavior is adjusted automatically based on the magnitude and distribution of residuals, as controlled by the parameter. The loss function and corresponding weight function of the General Loss are defined in Equations (20) and (21):
where
denotes the residual at each data point;
is a shape-controlling parameter that determines the form of the loss function, and
is a scale parameter that normalizes the residual magnitude.
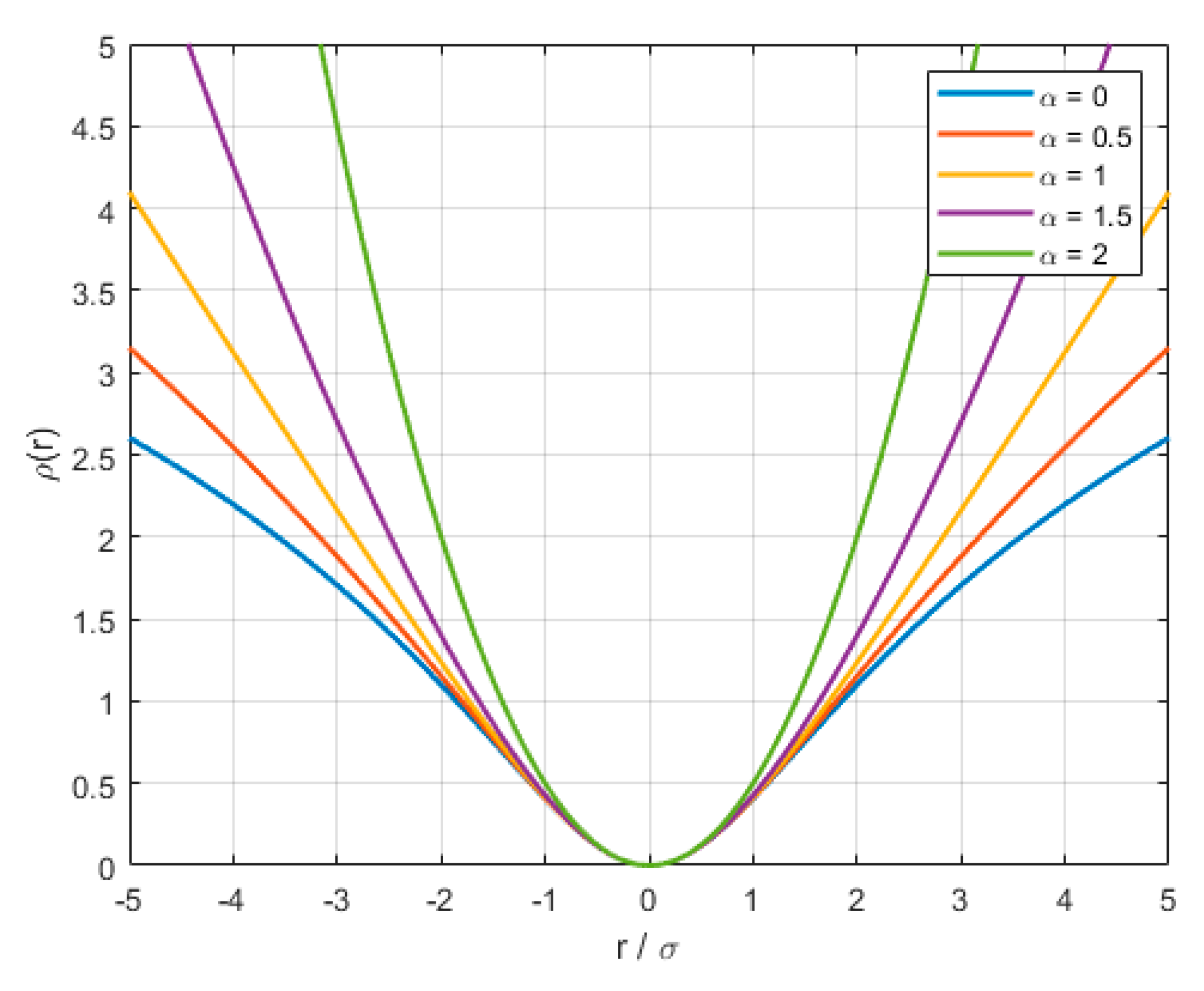
The General Loss function continuously adapts its form based on the residual distribution, determined by a shape-controlling parameter and a scale parameter. The function smoothly transitions among various well-known loss forms, such as the L2 loss (), Charbonnier loss (), Cauchy loss (), and Geman–McClure loss (). The adaptive nature of General Loss provides flexibility in balancing robustness to outliers and the estimation efficiency across diverse noise environments, making it particularly suitable for the relative navigation tasks presented in this study.
The range of
is constrained to [0, 2]. In the original General Loss paper, the adaptation of
was performed through gradient descent over the total loss, implementing an optimization-based adaptive framework. This study adopted a heuristic update strategy based on the difference between the current median residual
and the previous median value
to reduce computational complexity. A gain coefficient
was introduced to modulate this difference, resulting in the update rule defined in Equation (22). Specially, a small change in the median residual leads to a large gain coefficient, allowing rapid adaptation of
. On the other hand, a large change, which may reflect instability in the residual distribution, results in a conservative update. Equation (23) defines a candidate
value that decreases as the residual becomes more outlier-dominated, and Equation (24) blends the old and candidate
using the
to yield a smooth and stable update.
Figure 5 presents the loss function of General Loss for different
values. Furthermore, the coefficient used in Equations (23) and (24) is designed such that the value of
remains within the interval [0, 2], ensuring stable behavior throughout the estimation process:
where
and
denote the lower and upper bounds of the gain coefficient,
and
are threshold values that determine the sensitivity to changes in the residual median,
is a scale parameter that normalizes the residual magnitude,
denotes the estimated scale of the residual, and
and
represent the current and previous median absolute residuals, respectively, and are used to assess temporal changes in the residual distribution for adaptive
update.
The detailed procedure for adapting within the IRLS loop is summarized in Algorithm 1 as pseudocode. This pseudocode outlines the computation of residuals, normalization, influence function weighting, and the adaptive update of based on the current residual distribution.
Algorithm 1 is Pseudocode of the IRLS-based pose refinement algorithm using General Loss.
| Algorithm 1: IRLS-based pose refinement algorithm using General Loss |
| Inputs: image , CAD model , camera intrinsic , initial pose (from SPNv2)
|
| Hyperparameters: scale
, thresholds , , bounds of the gain coefficient , , LM damping , max iteration number , IRLS/LM tolerances , , mapping constant , small constant |
| Outputs: refined pose
|
| Initialize
, ← 0.
|
| repeat |
| Project M with T, determine face visibility, and perform moving edge search to obtain correspondences and residuals {}. |
| Compute residual vector
|
| Compute the median residual
|
|
|
|
| :
|
|
|
|
|
| , |
|
Compute weights:
|
|
|
|
| else if
|
| else:
|
|
|
|
|
|
|
|
|
|
|
| Adapt μ based on the LM gain ratio rule. |
|
|
2.5. Simulation
Simulation Environment
The simulation was conducted in the ROS–Gazebo environment using the 3D model of the ISS provided by NASA. The camera parameters used in the simulation are summarized as follows: focal length parameters,
2463.7618 pixels, and principal point parameters,
pixels. The major specifications of the simulation environment and the system configuration are summarized in
Table 1.
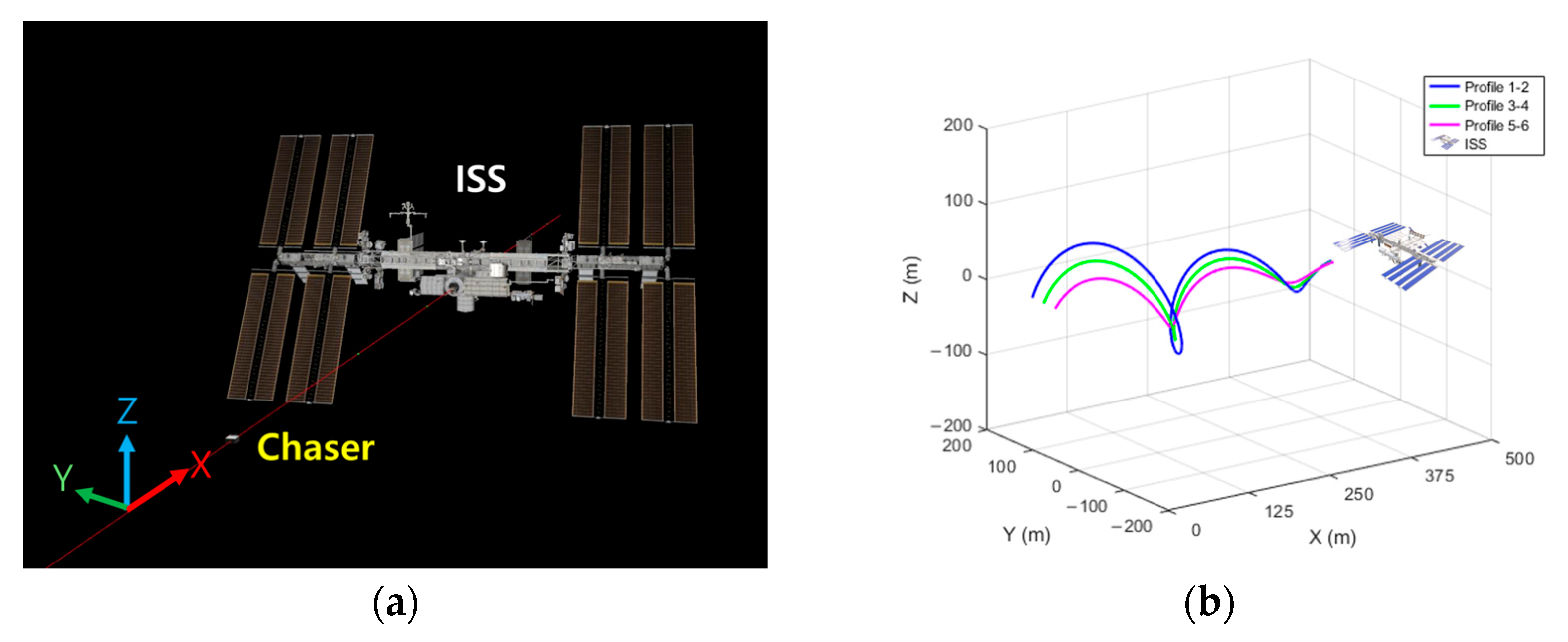
The rendezvous maneuver was simulated by generating a randomized approach corridor and defining a trajectory within this corridor. All data followed the coordinate system shown in
Figure 6a, where the ISS and the chaser are initially separated by a relative distance of 500 m along the x-axis, converging gradually toward 100 m. The positions of the y- and z-axes converge simultaneously from an initial radial offset of 100 m.
The effectiveness of General Loss relative to other robust M-estimators was evaluated under various conditions by comparing the MBT-based relative navigation performance across these six profiles.
Figure 6a shows the simulation environment and coordinate frames, and
Figure 6b presents the trajectory within the approach corridor. To examine the effects of initial estimation errors on the performance of each M-estimator, the initial pose estimates for MBT in each profile were obtained using SPNv2, with a 10° offset applied to the roll axis in profiles 2, 4, and 6.
Table 2 lists the initial position and orientation estimation errors, the applied roll-axis offsets, and the computational time per frame.
Figure 7a (profile 1) and
Figure 7b (profile 2) show the virtual object models generated from these initial poses.
3. Results
Eight M-estimators (Tukey, Welsch, General Loss, Huber, Cauchy, Talwar, Logistic, and Andrews) were applied as weight functions in the MBT framework. Each M-estimator was used independently per frame, with its corresponding weight function applied to the residuals of that frame. The RMSE was calculated for the position (x, y, z) and orientation (roll, pitch, yaw) over the entire simulation interval, and the computation time per frame was also recorded. The RMSE is defined as follows:
where
denotes the MBT result,
is the ground truth from the simulation, and N is the number of frames. The quantitative results for the entire simulation are presented in
Table 3, whereas the errors at the final simulation frame are provided in
Table A1.
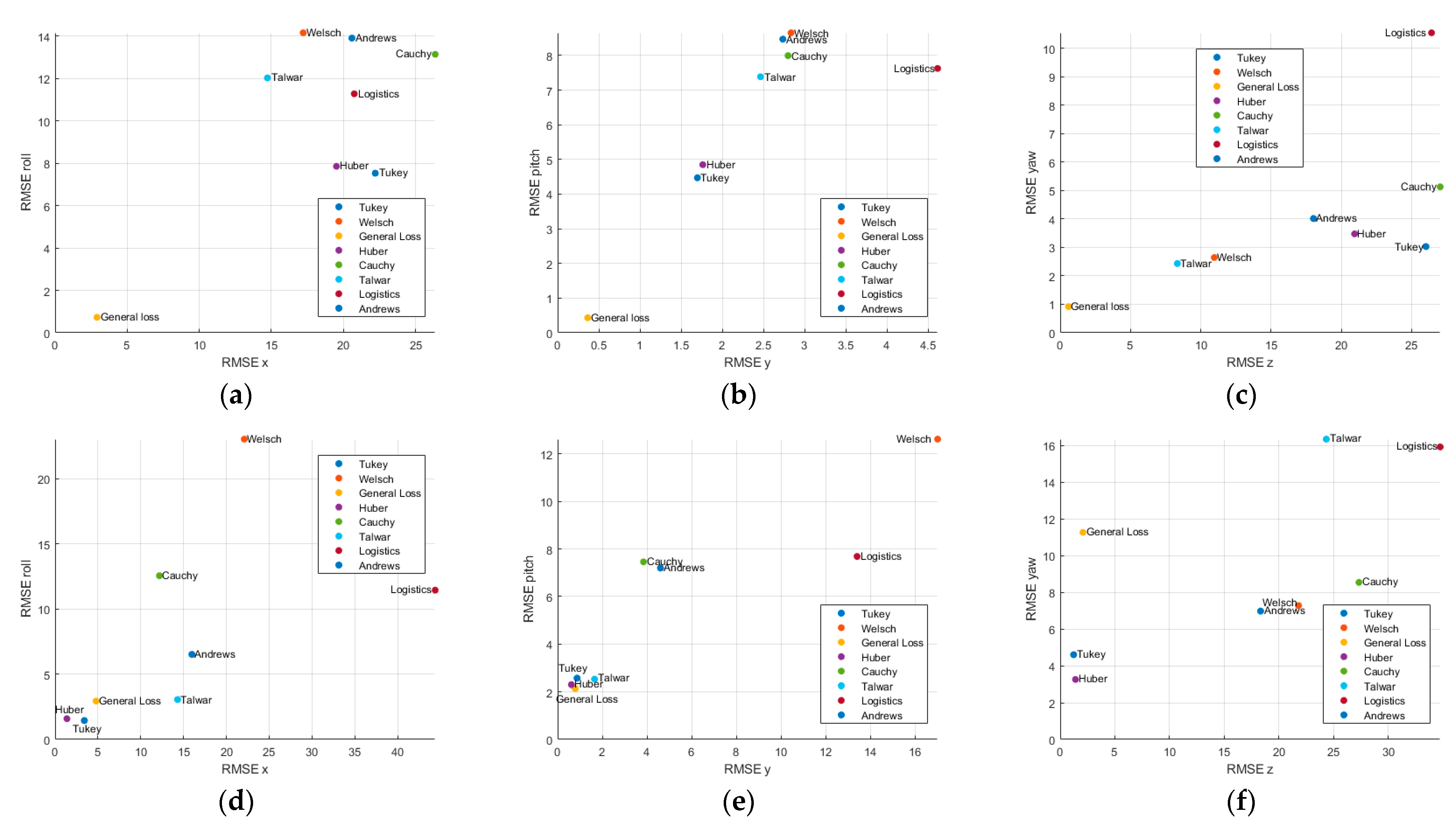
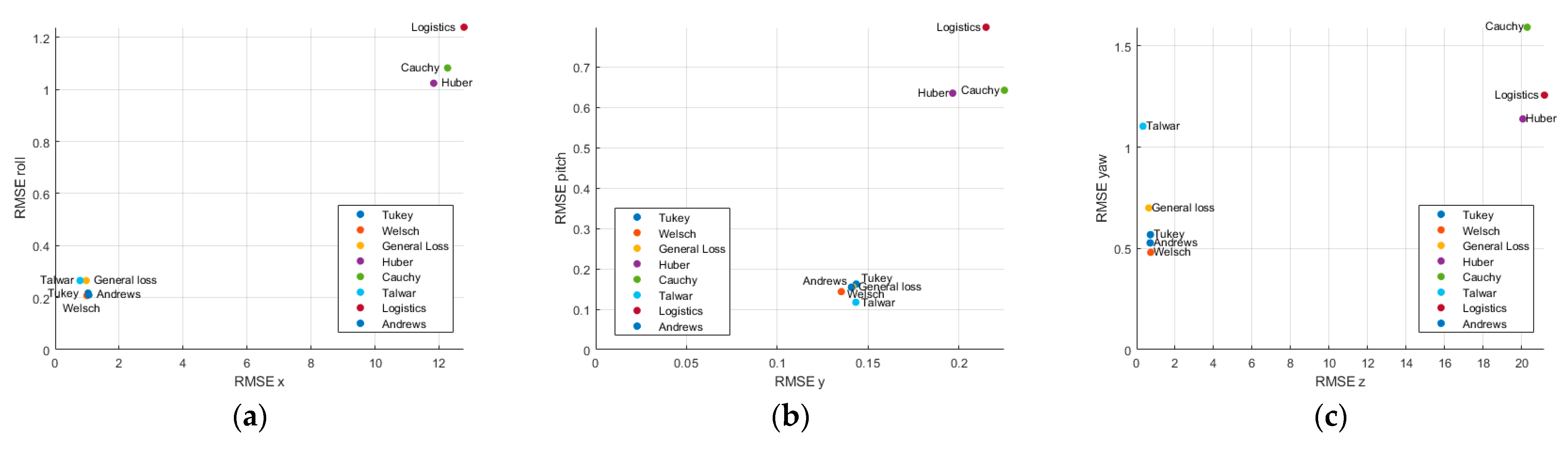
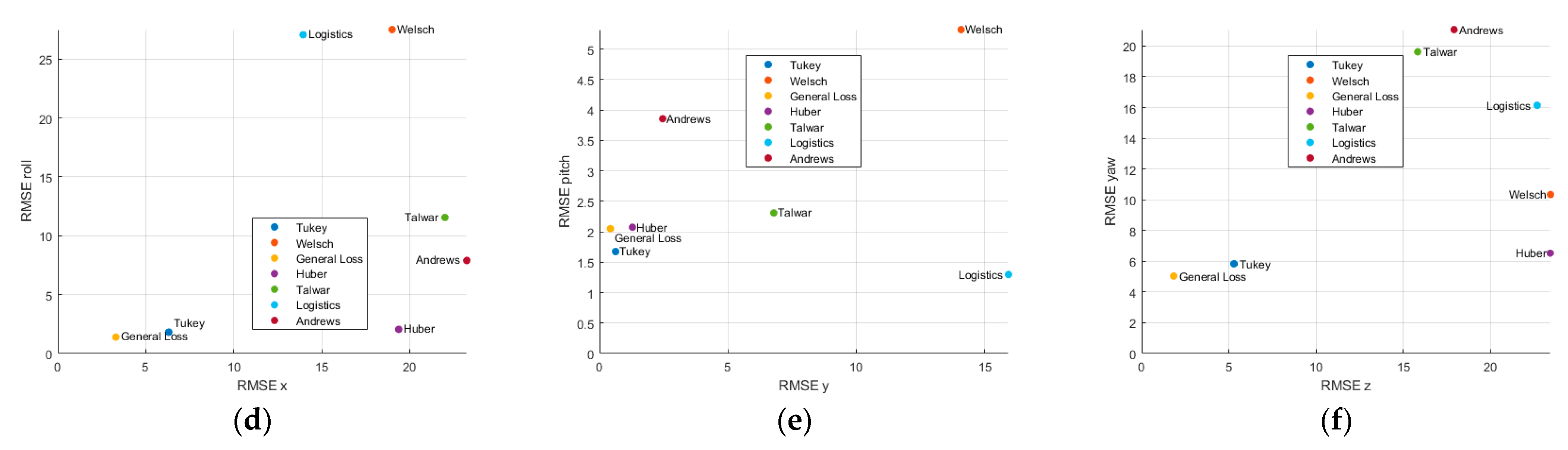
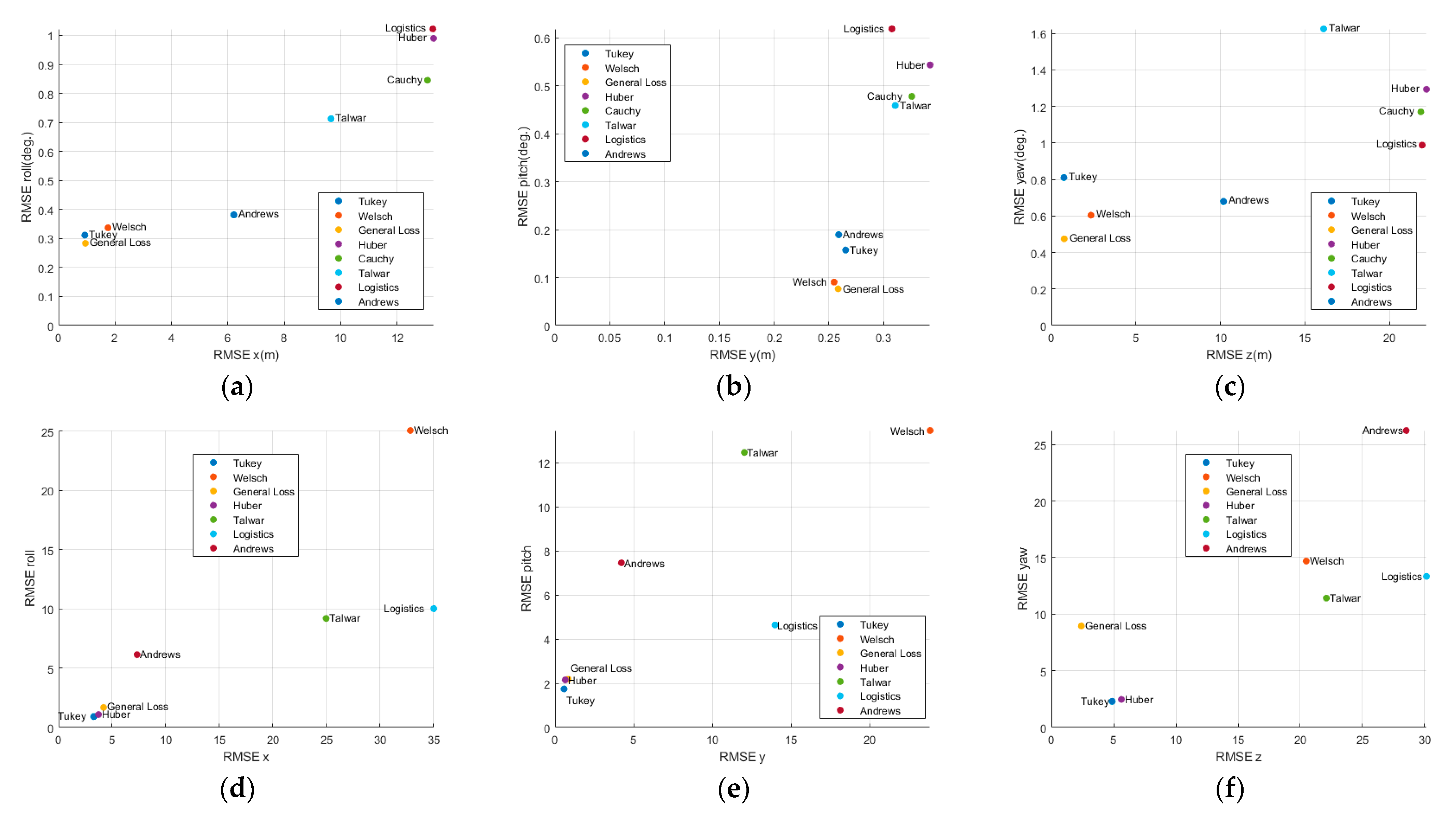
Figure 8,
Figure A1 and
Figure A2 illustrate the estimation errors for each axis, plotting the position RMSE along the x-axis and orientation RMSE along the y-axis to visualize the axis-specific estimation performance.
Profile 1 was conducted under conditions in which only the position of the chaser changed. According to the MBT estimation results, the General Loss and Tukey estimators showed superior performance in position and orientation estimation. In terms of the positional accuracy, the General Loss achieved RMSE values of 1.0133 m (x), 0.2606 m (y), and 0.8554 m (z), significantly outperforming Tukey, which yielded 1.2327 m (x) and 1.4434 m (z).
For orientation estimations, General Loss also provided the most accurate results, achieving RMSEs of 0.3197° (roll), 0.1805° (pitch), and 0.6423° (yaw). Regarding the computational efficiency, Huber (22.8028 ms) and Cauchy (23.1106 ms) showed the fastest computation time per frame, whereas General Loss and Tukey required 51.0111 ms and 26.0755 ms, respectively, representing 123.71% and 14.35% increases relative to Huber. In contrast, Welsch (219.9172 ms), Talwar (114.7814 ms), Logistic (143.7517 ms), and Andrews (201.8872 ms) showed relatively high computational costs.
The lowest estimation errors by axis were observed with General Loss (x-axis), General Loss and Welsch (y-axis), and General Loss (z-axis), as shown in
Figure 8a–c. Overall, General Loss, Welsch, and Tukey consistently ranked among the top-performing estimators for accuracy across all three axes
Profile 2 followed the same trajectory as profile 1, but the chaser continuously tracked the ISS center, involving positional and rotational motion. Tukey showed the best positional accuracy, with RMSE values of 3.2834 m (x), 0.5772 m (y). General Loss also showed competitive performance, achieving RMSE values of 4.1985 m (x), 0.8343 m (y), and 2.4089 m (z). In the orientation estimation, Tukey showed good overall accuracy, with RMSEs of 0.9264° (roll), 1.7462° (pitch), and 2.3079° (yaw).
When transitioning from profile 1 to 2, the computation time increased for most estimators because of the added complexity of simultaneous positional and rotational variations. The most substantial increase was observed for the Huber estimator, which increased by approximately 118.7% (from 22.8028 ms to 49.8701 ms), followed by the Cauchy estimator with a 104.86% increase (from 23.1106 ms to 47.3436 ms). The Tukey and Welsch estimators exhibited moderate increases of 82.59% and 34.12%, respectively. In contrast, the General Loss function showed a relatively modest increase of only 10.74% (from 51.0111 ms to 56.4875 ms). These results suggest that the General Loss estimator maintains stable computational performance even under profile variations, whereas estimators such as Huber and Cauchy are more sensitive to increased complexity, leading to substantial processing time increases.
Across all three axes, General Loss, Tukey, and Huber consistently ranked among the most precise estimators as shown in
Figure 8d–e. These findings align with the profile 1 results (
Table 3) confirming the superior performance of General Loss and Tukey in position-dominant and orientation-dominant profiles.
Profile 3 repeated the position-only trajectory of profile 1 with the displacements in the y-z plane reduced to 75% of their original magnitude. According to the MBT estimation results, the General Loss delivered the most accurate solution on all six degrees of freedom, returning RMSE values of 2.909 m (x), 0.3649 m (y), 0.5905 m (z), 0.7289° (roll), 0.4317° (pitch), and 0.9193° (yaw). Tukey consistently produced the next-lowest error RMSE, whereas Welsch and Cauchy registered z-axis position RMSEs exceeding 10 m.
Profile 4 repeated the position-only trajectory of profile 2 with the displacements in the y–z plane reduced to 75% of their original magnitude. In this profile, Huber achieved the best performance on the two translational axes and one rotational axis, with RMSEs of 1.3870 m (x), 0.6188 m (y), and 3.2513° (yaw). General Loss exhibited a yaw RMSE of 11.2655°, representing a 246% increase relative to Huber’s 3.2513°.
Profile 5 repeated the position-only trajectory of profile 1 with the displacements in the y-z plane reduced to 50% of their original magnitude. Under these benign conditions, all estimators except Huber, Cauchy, and Logistic achieved sub-meter and sub-degree accuracy. Talwar and Welsch achieved the lowest errors across the three positional and three rotational axes, with RMSEs of 0.7776 m (x, Talwar), 0.1353 m (y, Welsch), 0.3322 m (z, Talwar), 0.2171° (roll, Welsch), 0.1172° (pitch, Talwar), and 0.4808° (yaw, Welsch). General Loss demonstrated competitive performance across all axes, achieving RMSE values of 0.9703 m (x), 0.1417 m (y), and 0.6347 m (z) in position and 0.2655° (roll), 0.1550° (pitch), and 0.7000° (yaw) in orientation. Although Talwar and Welsch provided the lowest errors on specific axes, the differences over General Loss remained within a narrow margin of less than 10%, indicating that General Loss maintains robust estimation accuracy under these favorable conditions while ensuring consistent performance across all degrees of freedom.
Profile 6 repeated the position-only trajectory of profile 2 with the displacements in the y-z plane reduced to 50% of their original magnitude. Cauchy failed to achieve model alignment and produced no valid estimate. General Loss showed the greatest overall accuracy, achieving RMSEs of 5.2132 m (x), 0.4000 m (y), 1.5183° (roll), and 3.4539° (yaw). Tukey provided the best z-axis position accuracy at 5.2951 m, while Logistic achieved the lowest RMSE on the pitch axis at 1.2972°. In contrast, Welsch and Logistic once more displayed z-axis errors exceeding 20 m.
4. Discussion
In the discussion, we interpret the profile-wise Errors of General Loss and the seven M-estimators, focusing on profiles 2, 4, and 5. First, in profile 2, Tukey showed the best positional accuracy, with RMSE values of 3.2834 m (x) and 0.5772 m (y). General Loss also showed competitive performance, achieving RMSE values of 4.1985 m (x), 0.8343 m (y), and 2.4089 m (z). In the orientation estimation, Tukey showed good overall accuracy, with RMSEs of 0.9264° (roll), 1.7462° (pitch), and 2.3079° (yaw).
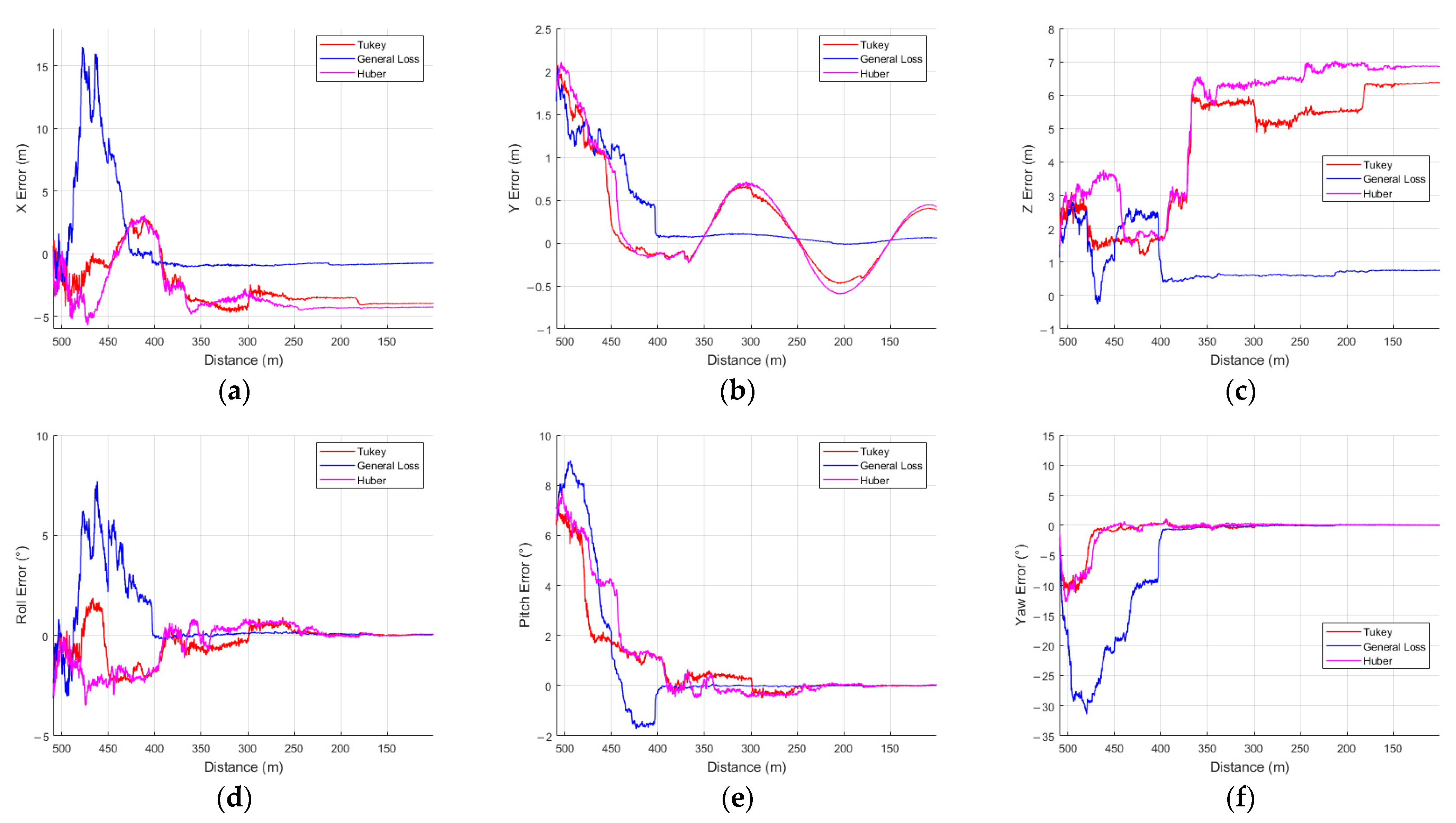
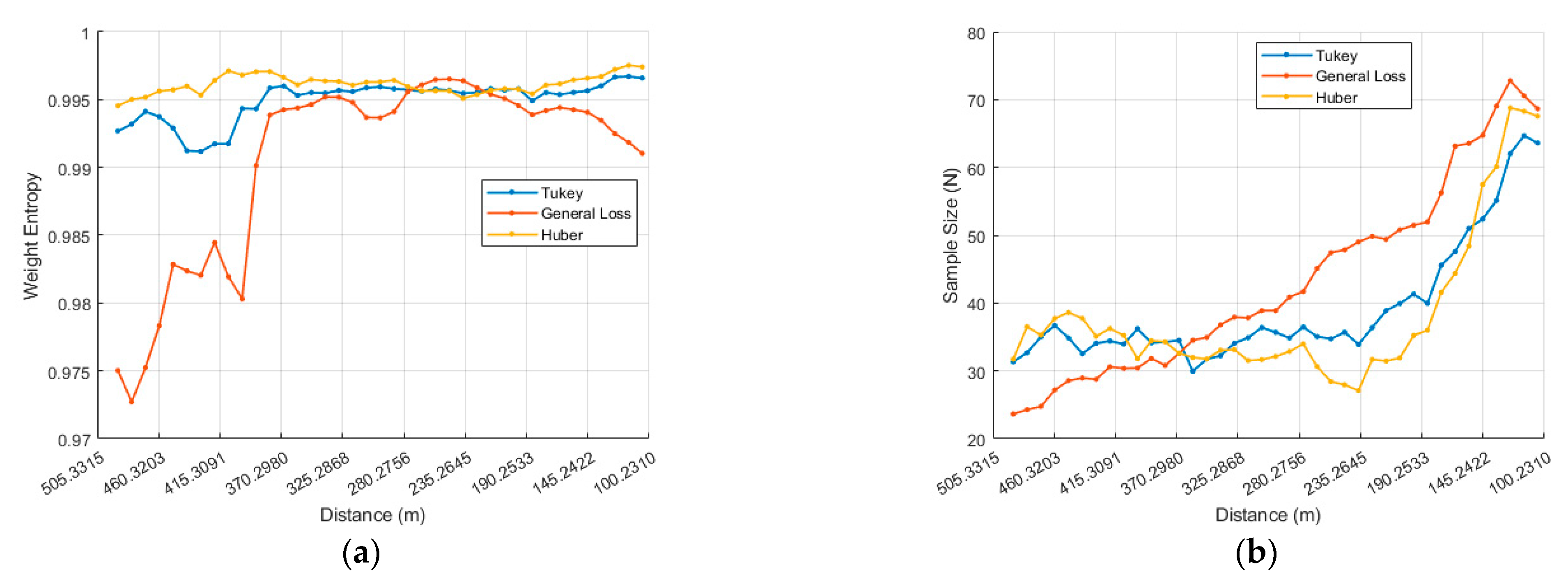
Figure 9a–f shows the error plots with relative distance on the x-axis, comparing three M-estimators (Tukey, General Loss, and Huber) in profile 2.
As
Figure 9a–f illustrates, the General Loss estimator completed model alignment more slowly than Tukey and Huber on every axis except z. However, in
Figure 9c,f, Tukey and Huber each exhibit gross misalignments of approximately 5 m and 6 m, respectively, because the tracker converges exclusively on the left and right edges of the panel, while completely misaligning the top and bottom edges. Consequently, by the end of the simulation, General Loss is the only one of the three estimators that maintains a globally consistent geometric fit, as shown in
Table A1.
Moreover, because the tracker fails to capture the panel’s top and bottom edges, the virtual contour remains locked onto the lateral edges and oscillates along the z-axis, producing a back-and-forth motion that manifests as a sinusoidal signature in the y-axis error.
Despite these tracking slips, the Tukey and Huber estimators still converge and maintain low attitude errors. Even when the central panel is missed, the algorithm stabilizes on the symmetric left- and right-hand faces of the solar-array frame, which provide enough geometric cues to anchor the pose solution.
The larger RMSE of the General Loss estimator on the x and yaw axes stems from a substantial spike in error during the initial pose alignment process. In IRLS, numerical divergence becomes more probable as the Jacobian (
) matrix grows ill-conditioned [
20], and this condition number is strongly linked to the weight entropy [
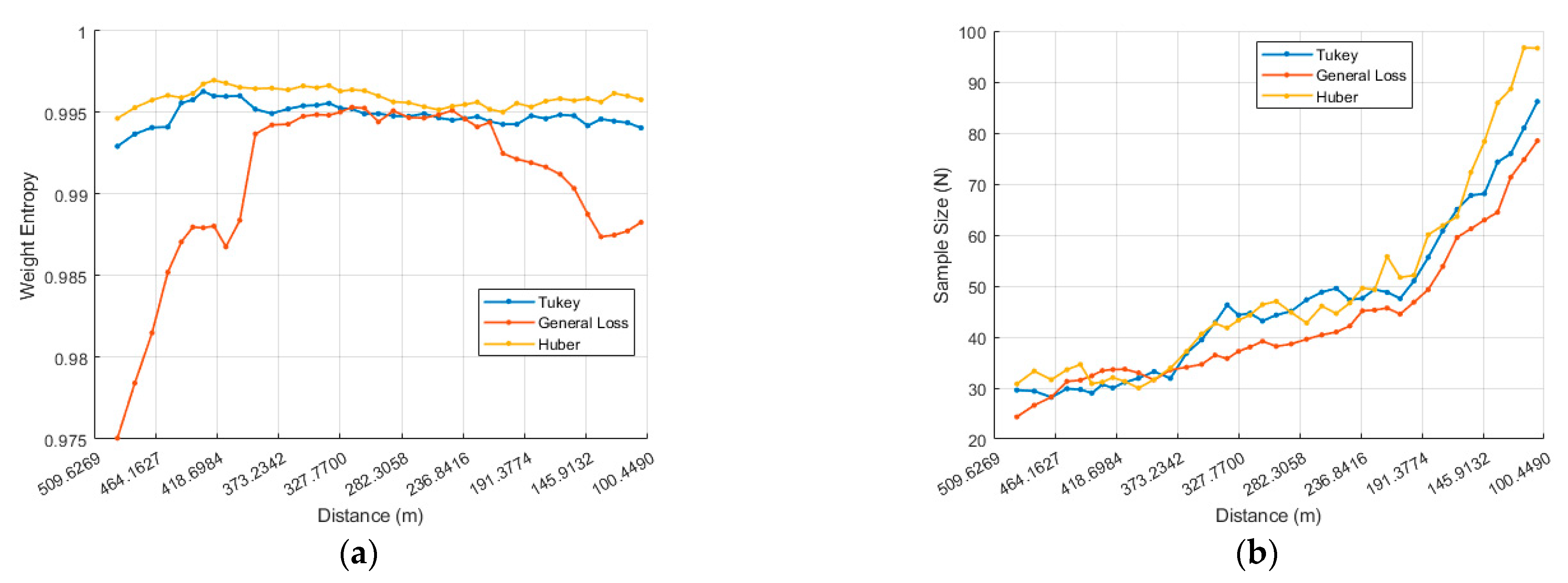
21]. Within the IRLS framework, weight entropy quantifies how evenly the sample weights are distributed. High entropy—i.e., more evenly distributed weights—generally enhances numerical stability and promotes robust convergence. Conversely, low entropy implies that only a few samples carry most of the weight, increasing the risk of instability.
For the ISS MBT experiments, we computed the weight-entropy of the last IRLS iteration at every frame, divided the chaser–ISS separation into 10 m bins, and averaged the weight-entropy within each bin. The resulting profile is plotted in
Figure 7, and weight-entropy is defined in Equation (26).
where
denotes the weight assigned to the
correspondence, obtained from the normalized residual
, and N denotes the number of sample points.
In the numerical results, General Loss starts with a markedly lower weight-entropy than Tukey and Huber. From the first 10 m bin, its entropy increases steadily and reaches a level comparable to Tukey and Huber at about 400 m. This rise in entropy—i.e., more uniformly distributed weights, which enhances numerical stability and supports robust convergence—drives a sharp reduction in six-degree-of-freedom pose estimation errors, culminating in successful model tracking (
Figure 10).
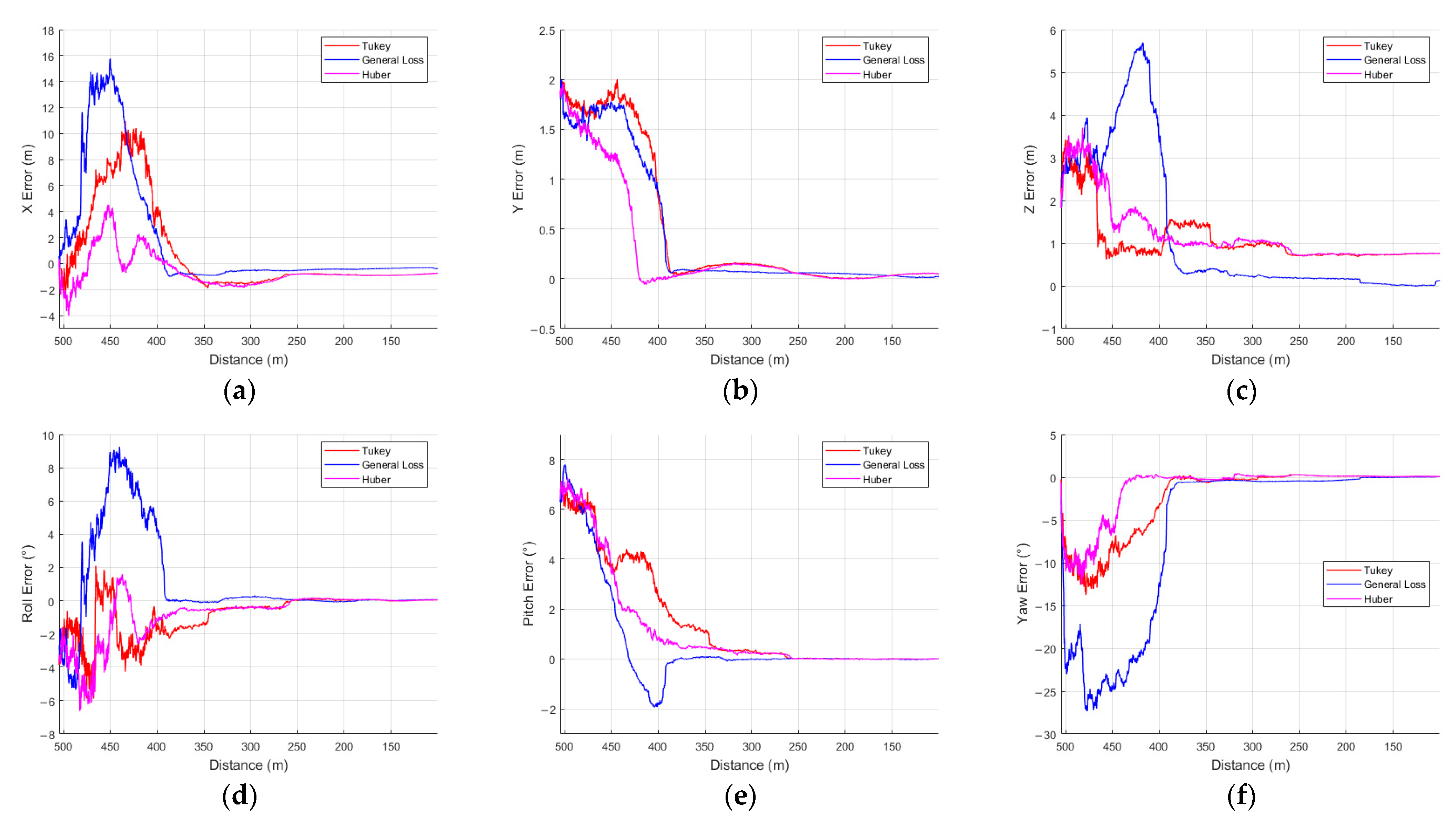
In profile 4, Huber achieved the best performance on the x, y, and yaw axes, with RMSE values of 1.3870 m (x), 0.6188 m (y), and 3.2513° (yaw), respectively. Tukey showed the lowest errors on the z and roll axes, while General Loss achieved the lowest RMSE on the pitch axis.
Figure 11a–f shows the results comparing three M-estimators (Tukey, General Loss, and Huber) in profile 4. As shown in
Figure 11a–f, unlike in profile 2, all three estimators successfully tracked the model throughout the profile. For General Loss, however, large transient errors occurred during model alignment on every axis except for the y and pitch axes.
Following the previous analysis,
Figure 12 shows the weight entropy H as a function of the relative distance. At 500 m, General Loss starts approximately 0.02 lower than Tukey and Huber; it then climbs sharply around 485 m, and by 390 m, all three estimators exhibit nearly identical entropy levels. This behavior corresponds to the divergence observed in the x, z, roll, and yaw axes and the model alignment that occurs near 400 m.
In profile 5, all estimators achieved sub-meter and sub-degree accuracy. Talwar yielded the minimum RMSE on every axis (0.777 m, 0.143 m, and 0.333 m for x, y, and z, respectively, and 0.266°, 0.117°, and 0.701° for roll, pitch, and yaw, respectively)
However, Welsch, Talwar, Logistic, and Andrews estimators exhibited larger position and orientation errors in other profiles. As observed in the tracking results, these three M-estimators, including Welsch, showed significantly higher RMSE values, likely due to incorrect tracking caused by the MBT algorithm occasionally locking onto an unintended ISS solar panel, as shown in
Figure 13a,b. Consequently, the superior accuracy observed for all estimators, particularly for Talwar and Welsch, should be interpreted as a result specific to profile 5 and cannot be generalized to the other profiles.
5. Conclusions
A vision-based MBT approach was used to achieve the high-precision relative navigation required for OOS missions. Specifically, the General Loss function within the MBT framework and its performance was evaluated and compared with seven other robust M-estimators: Tukey, Welsch, Huber, Cauchy, Talwar, Logistic, and Andrews. Simulations were conducted in a ROS–Gazebo environment, emulating a rendezvous profile with the ISS. Six distinct approach profiles, involving different chaser orientations and initial radial offsets (100%, 75%, and 50%), were designed to assess estimator performance under various ISS proximity tracking scenarios. The performance of each estimator was assessed using the RMSE for position (x, y, z) and orientation (roll, pitch, yaw).
Among all M-estimators, General Loss was the only estimator that successfully achieved complete pose alignment across all profiles. In profiles 1, 3, and 6, it provided high accuracy throughout the entire simulation and at the end point (at 100 m relative distance in x-axis), while maintaining stable computational efficiency. In profiles 2, 4, and 5, General Loss exhibited higher RMSE values over some segments compared to other estimators; however, these errors were attributed to the initial offsets applied to the initial poses estimated using SPNv2, which led to transient errors during the pose alignment process. By the end of the simulation, these errors were reduced to the sub-meter and sub-degree levels. The adaptive capability of General Loss to dynamically adjust the loss function shape based on the residual distribution enabled robust performance under various noise conditions and in the presence of outliers. In contrast, the Huber and Cauchy estimators were more sensitive to extreme outliers, resulting in higher estimation errors, while the Welsch and Logistic estimators required longer computational times and showed larger errors. Future research will aim to extend the application of the General Loss-based MBT approach to more challenging conditions, including variable lighting environments, non-standard object geometries, and multi-sensor fusion profiles, with the goal of advancing high-precision and highly reliable relative navigation technologies for real-world OOS missions.





_Zhu.png)



