An Arbitrary Order Virtual Element Method for Free Torsional Vibrations of Beams

Abstract

In this study, a novel arbitrary order Virtual Element Method (p-VEM) for free torsional vibration analysis of beams with negligible warping is presented. This method can serve as an equivalent beam model for slender aerospace structural components. The proposed formulation utilizes a spatial discretization of the primary variable with implicit virtual functions that are approximated with polynomials of arbitrary order p by employing a suitably defined projection operator and degrees of freedom. From the spatial discretization of the weak form of the equations of motion, the semi-discrete equations of motion are obtained, from which stiffness and mass matrices are derived without the need for additional stabilization. The developed formulation is validated through several case studies, which demonstrate that the p-VEM offers higher accuracy and faster convergence rate compared to traditional modeling approaches.

1. Introduction

Many aerospace structures, such as high-aspect-ratio wings and helicopter rotor blades, are often modeled as simplified beam models for conceptual and preliminary design analysis. Prismatic beam elements, assuming constant or linearly variable cross-sectional properties, are commonly used in commercial finite element software. However, accurately modeling beam-type structures with varying structural properties along the spanwise direction may require the use of several beam elements, with a consequent increase in the computational cost. Therefore, there is a growing interest in the development of low-order structural models for slender aerospace structures that employ flexible and accurate beam formulations to significantly reduce the computational cost of analogous full-dimensional models [1].

The Virtual Element Method [2] (VEM) is rapidly emerging as a powerful numerical technique for the approximate solution of partial differential equations with a growing number of applications in the field of computational mechanics, indicating its versatility in different structural applications [3,4,5,6,7,8,9,10,11,12,13,14,15]. While there are several applications of the VEM to the dynamic analysis of two- and three-dimensional structures [16,17,18], formulations specifically developed for trusses and beams have only recently begun to emerge [19,20] in the elastostatic framework and the application of the VEM to the dynamic analysis of one-dimensional structural members is currently limited to a recent space-time formulation that has been presented to model the dynamic response of an elastic bar [21].

This work presents a novel arbitrary order VEM formulation (p-VEM) for analyzing free torsional vibrations of beams. The methodology is applicable to both uniform and nonuniform beams with circular cross-sections, as well as other geometries where warping effects and the coupling of bending and torsion are negligible. The proposed formulation relies on a semi-discretization in space of a weak form of the equation of motion, which is commonly implemented in commercial finite element analysis software. Adopting a virtual element approach, the primary variable of the problem, namely the angular displacement of the cross-section, is spatially discretized using implicit functions. These functions are approximated with polynomials of arbitrary order p through suitably defined degrees of freedom and a projection operator. This approach results in a set of ordinary differential equations in time. The novelty of this work also lies in the development of a consistent mass matrix which has not been previously established within the framework of one-dimensional elements and semi-discretization approaches. Remarkably, this formulation generates stiffness and mass matrices that do not require the inclusion of a stabilization term, which is often necessary in many other VEM formulations. To the best of the author’s knowledge, this is the first arbitrary-order VEM formulation for 1D beam elements in dynamic torsional analysis, using a semi-discretization approach and deriving a consistent mass matrix without stabilization.

While several efficient approaches for the vibration analysis of beams have been proposed in the literature [22,23], the p-VEM formulation presented in this work for free torsional vibrations provides the basis for a flexible and general framework. This framework is well suited for future extensions to more complex geometries, such as thin-walled or composite beams, as well as multiphysics problems.

The rest of this paper is organized as follows: Section 2 provides an overview of the theoretical background and the numerical implementation of the proposed VEM approach; Section 3 presents the results of the numerical tests conducted to validate the method and to assess its efficiency and accuracy; Section 4 discusses these results and offers suggestions for future research.

2. Materials and Methods

This section presents the formulation and implementation of a p-version of the Virtual Element Method (p-VEM) for analyzing the free torsional dynamic behavior of beam structures with negligible warping effects.

2.1. Virtual Element Approximation

The beam is discretized into $n_e$ virtual elements. Each element, denoted with e, has two nodes, at the ends of the beam element as shown in Figure 1. The length of each element is denoted with $L_e$.

For each virtual element e, a local finite element space $V_p\left(e\right)$ is defined to include all polynomials of degree $\le p$, plus other additional unknown functions that might not be polynomials. Therefore, an explicit expression of a function ${\theta }_h\in V_p\left(e\right)$, representing the angular displacement of the cross section within the domain of an element e, is not available. However, with a proper choice of the element degrees of freedom, a projection ${\Pi }_p^{\nabla }{\theta }_h$ of any virtual function ${\theta }_h\in V_p\left(e\right)$ onto a polynomial space ${\mathcal{P}}_p\left(e\right)$ of order p can be computed and used instead of ${\theta }_h$ to formulate the virtual element.

2.1.1. Degrees of Freedom

The degrees of freedom of the element are the nodal values ${\theta }_h\left(0\right)={\theta }_1$ and ${\theta }_h\left(L_e\right)={\theta }_2$, plus, for $p\ge 2$, a set of $p-1$ internal variables, called moments, which are not associated with any node, defined as

$$m_j={\displaystyle \frac{1}{L_e^{j+1}}}{\int }_0^{L_e}{x}^j{\theta }_{h}dx,j=0,\dots ,p-2,$$

(1)

and scaled so that they have the same dimension as nodal rotations. The internal variables defined in Equation (1) are not physical moments in the classical mechanics sense, but instead internal degrees of freedom that provide additional information for constructing higher-order polynomial projections within the VEM framework. The global set of degrees of freedom consists of all nodal displacements, shared by adjacent elements, plus each element’s internal moments, which are local to that element.

2.1.2. Projection Operator

The projection operator ${\Pi }^{\nabla }:V_p\left(e\right)\to {\mathcal{P}}_p\left(e\right)$ maps every virtual function ${\theta }_h\in V_p\left(e\right)$ onto a polynomial ${\Pi }^{\nabla }{\theta }_h\in {\mathcal{P}}_p\left(e\right)$. The operator ${\Pi }^{\nabla }$ is defined for every ${\theta }_h\in V_p\left(e\right)$ by the following orthogonality condition

$${\int }_0^{L_e}\nabla q\left[\nabla {\Pi }^{\nabla }{\theta }_h-\nabla {\theta }_h\right]dx=0,\forall q\in {\mathcal{P}}_p\left(e\right).$$

(2)

The projector definition enforces an orthogonality for the gradients against all polynomial weighting functions q of degree p. In the present one-dimensional setting, the operator ∇ is used to express the first derivative with respect to x, so that $\nabla (·)\equiv {\displaystyle \frac{\partial }{\partial x}}(·)$.

The projection definition is completed by prescribing an additional condition that requires, for every ${\theta }_h\in V_p\left(e\right)$

$${\int }_0^{L_e}\left[{\Pi }^{\nabla }{\theta }_h-{\theta }_h\right]dx=0,$$

(3)

ensuring that ${\Pi }^{\nabla }{\theta }_h$ matches the average of ${\theta }_h$ on the element e.

The first condition in Equation (2) can be reformulated using integration by parts as

$${\int }_0^{L_e}\nabla q\nabla {\Pi }^{\nabla }{\theta }_{h}dx={\left.\nabla q{\theta }_h\right|}_0^{L_e}-{\int }_0^{L_e}\Delta q{\theta }_{h}dx.$$

(4)

where ${\left.(·)\right|}_0^{L_e}$ denotes the evaluation of $(·)$ at the two endpoints $x_1=0$ and $x_2=L_e$ of the element e. The operator $\Delta$ is herein used to express the second derivative with respect to x, so that $\Delta (·)\equiv {\displaystyle \frac{{\partial }^2}{\partial x^2}}(·)$.

For $p\ge 2$, Equation (3) can be written as

$${\int }_0^{L_e}{\Pi }^{\nabla }{\theta }_{h}dx={\int }_0^{L_e}{\theta }_{h}dx.$$

(5)

For $p=1$, instead of evaluating the integrals in Equation (5), the following relation is employed [24]

$$\sum _{n=1}^2{\Pi }^{\nabla }{\theta }_h\left(x_n\right)=\sum _{n=1}^2{\theta }_h\left(x_n\right),$$

(6)

where $x_n$ is the coordinate of node n.

2.2. Computation of the Projection

The two nodal rotations are gathered in the vector

$${\mathit{\theta }}_e=\left[\begin{array}{c}{\theta }_1\\ {\theta }_2\end{array}\right]$$

(7)

The internal moments, defined in Equation (1), are gathered in the vector

$${\mathbf{m}}_e=\left[\begin{array}{c}{m}_0\\ m_1\\ ⋮\\ m_{p-2}\end{array}\right]$$

(8)

which exists only for $p\ge 2$.

All the degrees of freedom of an element are collected in the vector

$${\mathbf{d}}_e=\left[\begin{array}{c}{\mathit{\theta }}_e\\ {\mathbf{m}}_e\end{array}\right]$$

(9)

Since the projection ${\Pi }^{\nabla }{\theta }_h$ is an element of ${\mathcal{P}}_p\left(e\right)$, it can be represented as

$${\Pi }^{\nabla }{\theta }_h=\sum _{i=0}^p{\alpha }_{i+1}{x}^i$$

(10)

where ${\alpha }_i$ are unknown parameters that are computed using the projection operator. The projected rotations, defined in Equation (10), can be expressed in matrix form as

$${\Pi }^{\nabla }{\theta }_h=\mathbf{H}\mathit{\alpha }$$

(11)

where

$$\mathbf{H}=\left[\begin{array}{cccc}1& x& \dots & x^p\end{array}\right],$$

(12)

and the $k+1$ constants are gathered in the array

$$\mathit{\alpha }={\left[\begin{array}{cccc}{\alpha }_1& {\alpha }_2& \dots & {\alpha }_{p+1}\end{array}\right]}^{⊺}.$$

(13)

The gradient of the projected rotations is

$$\nabla {\Pi }^{\nabla }{\theta }_h=\sum _{i=1}^{p}i{\alpha }_{i+1}{x}^{i-1}$$

(14)

which can be expressed in matrix form as

$$\nabla {\Pi }^{\nabla }{\theta }_h={\mathbf{H}}_{\nabla }\widehat{\mathit{\alpha }},$$

(15)

where

$${\mathbf{H}}_{\nabla }=\left[\begin{array}{cccc}1& 2x& \dots & p{x}^{p-1}\end{array}\right],$$

(16)

and

$$\widehat{\mathit{\alpha }}={\left[\begin{array}{cccc}{\alpha }_2& {\alpha }_3& \dots & {\alpha }_{p+1}\end{array}\right]}^{⊺}.$$

(17)

Since q is a polynomial of degree p, its gradient can be expressed in matrix form as

$$\nabla q={\mathbf{H}}_{\nabla }\widehat{\mathit{\beta }},$$

(18)

where

$$\widehat{\mathit{\beta }}={\left[\begin{array}{cccc}{\beta }_2& {\beta }_3& \dots & {\beta }_{p+1}\end{array}\right]}^{⊺}.$$

(19)

Finally, the second derivative of q with respect to x is expressed as

$$\Delta q={\mathbf{H}}_{\Delta }\widehat{\mathit{\beta }},$$

(20)

where, for $p\ge 2$

$${\mathbf{H}}_{\Delta }=\nabla {\mathbf{H}}_{\nabla }=\left[\begin{array}{cccc}0& 2& \dots & (p-1)p{x}^{p-2}\end{array}\right],$$

(21)

since ${\displaystyle \frac{d}{dx}}\left(k{x}^{p-1}\right)=\left(p-1\right)p{x}^{p-2}$.

2.3. Matrix Expressions of the Projector

The matrix form of the first condition defining the projector in Equation (4) is now obtained. The LHS of Equation (4) becomes

$$\begin{array}{cc}\hfill {\int }_0^{L_e}\nabla q\nabla {\Pi }^{\nabla }{\theta }_{h}dx& ={\int }_0^{L_e}{\left({\mathbf{H}}_{\nabla }\widehat{\mathit{\beta }}\right)}^{⊺}{\mathbf{H}}_{\nabla }\widehat{\mathit{\alpha }}dx\hfill \\ \hfill & ={\widehat{\mathit{\beta }}}^{⊺}\widehat{\mathbf{G}}\widehat{\mathit{\alpha }},\hfill \end{array}$$

(22)

where

$$\widehat{\mathbf{G}}={\int }_0^{L_e}{\mathbf{H}}_{\nabla }^{⊺}{\mathbf{H}}_{\nabla }dx={\int }_0^{L_e}\left[\begin{array}{cccc}1& 2x& \dots & p{x}^{p-1}\\ 2x& 4x^2& \dots & 2p{x}^p\\ ⋮& ⋮& \ddots & ⋮\\ p{x}^{p-1}& 2p{x}^p& \dots & p^2{x}^{2p-2}\end{array}\right]dx.$$

(23)

The first term of the RHS of Equation (4) becomes

$$\begin{array}{cc}\hfill {\left.\nabla q{\theta }_h\right|}_0^{L_e}& ={\left.{\left({\mathbf{H}}_{\nabla }\widehat{\mathit{\beta }}\right)}^{⊺}{\theta }_h\right|}_0^{L_e}\hfill \\ \hfill & ={\widehat{\mathit{\beta }}}^{⊺}{\left.{\mathbf{H}}_{\nabla }^{⊺}{\theta }_h\right|}_0^{L_e}\hfill \\ \hfill & ={\widehat{\mathit{\beta }}}^{⊺}\left({\mathbf{H}}_{\nabla }^{⊺}{|}_{L_e}{\theta }_2-{\mathbf{H}}_{\nabla }^{⊺}{|}_0{\theta }_1\right)\hfill \\ \hfill & ={\widehat{\beta }}^{⊺}\mathbf{E}{\mathit{\theta }}_e,\hfill \end{array}$$

(24)

since ${\theta }_h\left(0\right)={\theta }_1$ and ${\theta }_h\left(L_e\right)={\theta }_2$. The $p\times 2$ matrix $\mathbf{E}$ is

$$\mathbf{E}=\left[\begin{array}{cc}-{\mathbf{H}}_{\nabla }^{⊺}{|}_0& {\mathbf{H}}_{\nabla }^{⊺}{|}_{L_e}\end{array}\right]=\left[\begin{array}{cc}-1& 1\\ 0& 2L_e\\ ⋮& ⋮\\ 0& p{L}_e^{p-1}\end{array}\right].$$

(25)

The second term of the RHS of Equation (4) becomes

$$\begin{array}{cc}\hfill -{\int }_0^{L_e}\Delta q{\theta }_{h}dx& =-{\int }_0^{L_e}{\left({\mathbf{H}}_{\Delta }\widehat{\mathit{\beta }}\right)}^{⊺}{\theta }_{h}dx\hfill \\ \hfill & =-{\widehat{\mathit{\beta }}}^{⊺}\left[\begin{array}{c}0\\ 2{\int }_0^{L_e}{\theta }_{h}dx\\ 6{\int }_0^{L_e}x{\theta }_{h}dx\\ ⋮\\ (p-1)p{\int }_0^{L_e}{x}^{p-2}{\theta }_{h}dx\end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{ccccc}0& & & & \\ & 2L_e& & & \\ & & 6L_e^2& & \\ & & & \ddots & \\ & & & & (p-1)p{L}_e^{p-1}\end{array}\right]\left[\begin{array}{c}0\\ m_0\\ m_1\\ ⋮\\ m_{p-2}\end{array}\right]\hfill \\ \hfill & =-{\widehat{\mathit{\beta }}}^{⊺}\mathbf{F}{\mathbf{q}}_e,\hfill \end{array}$$

(26)

where $\mathbf{F}$ is the diagonal matrix

$$\mathbf{F}=\left[\begin{array}{cccc}0& & & \\ & 2L_e& & \\ & & \ddots & \\ & & & (p-1)p{L}_e^{p-1}\end{array}\right],$$

(27)

and ${\mathbf{q}}_e$ is the array of

$${\mathbf{q}}_e={\left[\begin{array}{cccc}0& m_0& \dots & m_{p-2}\end{array}\right]}^{⊺}.$$

(28)

The matrix form of the orthogonal projection of the gradient, defined in Equation (4), then reads

$$\widehat{\mathbf{G}}\widehat{\mathit{\alpha }}=\mathbf{E}{\mathbf{u}}_e-\mathbf{F}{\mathbf{q}}_e,$$

(29)

where the vector of constant coefficients $\widehat{\mathit{\beta }}$ has been simplified on both sides of the equation.

Recasting the RHS of Equation (29) in a more convenient form, the matrix form of the orthogonal projection equation can be rewritten as

$$\widehat{\mathbf{G}}\widehat{\mathit{\alpha }}=\widehat{\mathbf{\Phi }}{\mathbf{d}}_e,$$

(30)

where

$$\widehat{\mathbf{\Phi }}=\left[\begin{array}{cccccc}-1& 1& & & & \\ 0& 2L_e& -2L_e& & & \\ ⋮& ⋮& & \ddots & \\ 0& p{L}_e^{p-1}& & & -(p-1)p{L}_e^{p-1}\end{array}\right],$$

(31)

and ${\mathbf{d}}_e$, defined in Equation (9), is the vector containing all elements’ degrees of freedom.

In order to compute the additional condition for the projector, defined in Equation (5), two different approaches are followed depending on whether $p=1$ or $p\ge 2$.

For $p=1$, by using Equation (12), the LHS of Equation (6) reads

$$\begin{array}{cc}\hfill \sum _{n=1}^2{\Pi }^{\nabla }{\theta }_h\left(x_n\right)& ={\Pi }^{\nabla }{\theta }_h\left(x_1\right)+{\Pi }^{\nabla }{\theta }_h\left(x_2\right)\hfill \\ \hfill & =\mathbf{H}\left(x_1\right)\mathit{\alpha }+\mathbf{H}\left(x_2\right)\mathit{\alpha }\hfill \\ \hfill & =\left[\begin{array}{cc}2& L_e\end{array}\right]\left[\begin{array}{c}{\alpha }_1\\ {\alpha }_2\end{array}\right],\hfill \end{array}$$

(32)

since $x_1=0$ and $x_2=L_e$. The RHS of Equation (6) is

$$\begin{array}{cc}\hfill \sum _{n=1}^2{\theta }_h\left(x_n\right)& ={\theta }_h\left(x_1\right)+{\theta }_h\left(x_2\right)\hfill \\ \hfill & =\left[\begin{array}{cc}1& 1\end{array}\right]\left[\begin{array}{c}{\theta }_1\\ {\theta }_2\end{array}\right],\hfill \end{array}$$

(33)

having used the the identities ${\theta }_h\left(x_1\right)={\theta }_h\left(0\right)={\theta }_1$, ${\theta }_h\left(x_2\right)={\theta }_h\left(L_e\right)={\theta }_2$. Thus, for $p=1$, the second condition defining the projection in Equation (6) becomes

$$\left[\begin{array}{cc}2& L_e\end{array}\right]\left[\begin{array}{c}{\alpha }_1\\ {\alpha }_2\end{array}\right]=\left[\begin{array}{cc}1& 1\end{array}\right]\left[\begin{array}{c}{\theta }_1\\ {\theta }_2\end{array}\right].$$

(34)

For $p\ge 2$, the matrix form of the second condition defining the projection in Equation (5) is

$$\left[{\int }_0^{L_e}\mathbf{H}dx\right]\mathit{\alpha }={\int }_0^{L_e}{\theta }_{h}dx.$$

(35)

The RHS of Equation (35) is computed using Equation (1). After evaluating the integral on the LHS, Equation (35) becomes

$$\left[\begin{array}{cccc}{L}_e& {\displaystyle \frac{L_e^2}{2}}& \dots & {\displaystyle \frac{L_e^{p+1}}{p+1}}\end{array}\right]\left[\begin{array}{c}{\alpha }_1\\ {\alpha }_2\\ ⋮\\ {\alpha }_{p+1}\end{array}\right]=L_e{m}_0.$$

(36)

Equation (34) or Equation (36) can be combined with the system of equations in Equation (30) where it represents the first row. The matrix form of the complete projector equation then is

$$\mathbf{G}\mathit{\alpha }=\mathbf{\Phi }{\mathbf{d}}_e.$$

(37)

The explicit expressions for $\mathbf{G}$ and $\mathbf{\Phi }$ are

$$\mathbf{G}=\left[\begin{array}{cc}2& L_e\\ 0& L_e\end{array}\right],\mathrm{for}p=1,$$

(38)

$$\mathbf{G}=\left[\begin{array}{ccccc}{L}_e& {\displaystyle \frac{L_e^2}{2}}& \dots & \dots & {\displaystyle \frac{L_e^{p+1}}{p+1}}\\ 0& L_e& L_e^2& \dots & L_e^p\\ 0& L_e^2& {\displaystyle \frac{4}{3}}{L}_e^3& \dots & {\displaystyle \frac{2p}{p+1}}{L}_e^{p+1}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& L_e^p& {\displaystyle \frac{2p}{p+1}}{L}_e^{p+1}& \dots & {\displaystyle \frac{p^2}{2p-1}}{L}^{2p-1}\end{array}\right],\mathrm{for}p\ge 2,$$

(39)

$$\mathbf{\Phi }=\left[\begin{array}{cc}1& 1\\ -1& 1\end{array}\right],\mathrm{for}p=1,$$

(40)

$$\mathbf{\Phi }=\left[\begin{array}{ccccc}0& 0& L_e& & \\ -1& 1& 0& & \\ 0& 2L_e& -2L_e& & \\ ⋮& ⋮& & \ddots & \\ 0& p{L}_e^{p-1}& & & -(p-1)p{L}_e^{p-1}\end{array}\right],\mathrm{for}p\ge 2.$$

(41)

The matrix form of the projector can be computed from Equation (37) as

$$\mathbf{\Pi }={\mathbf{G}}^{-1}\mathbf{\Phi }.$$

(42)

The local virtual element approximation of the displacements, defined in Equation (10), can be computed by using the expression for $\mathit{\alpha }$ obtained from Equations (37) and (42) as

$${\Pi }^{\nabla }{\theta }_h(x,t)=\mathbf{H}\alpha =\mathbf{H}\mathbf{\Pi }{\mathbf{d}}_e\left(t\right)={\mathbf{N}}_{\pi }\left(x\right){\mathbf{d}}_e\left(t\right),$$

(43)

where ${\mathbf{N}}_{\pi }=\mathbf{H}\Pi$ is the matrix of the projection of the virtual shape functions.

The matrix form of the projector of the displacement gradients can be computed from Equation (30) as

$$\widehat{\mathbf{\Pi }}={\widehat{\mathbf{G}}}^{-1}\widehat{\mathbf{\Phi }}.$$

(44)

The gradient of the local virtual element approximation of the displacements, defined in Equation (15), can be computed by using the expression for $\widehat{\mathit{\alpha }}$ obtained from Equation (30) as

$$\nabla {\Pi }^{\nabla }{\theta }_h(x,t)={\mathbf{H}}_{\nabla }\widehat{\mathit{\alpha }}={\mathbf{H}}_{\nabla }\widehat{\mathbf{\Pi }}{\mathbf{d}}_e\left(t\right)={\mathbf{B}}_{\pi }\left(x\right){\mathbf{d}}_e\left(t\right),$$

(45)

where ${\mathbf{B}}_{\pi }={\mathbf{H}}_{\nabla }\widehat{\mathbf{\Pi }}$ is the matrix of the projection of the gradient of the virtual shape functions.

2.4. Semi-Discrete Equations of Motion

The semi-discrete equations of motion for the beam element are derived from Hamilton’s principle [25]. For the e-th element, Hamilton’s principle states

$$\delta {\int }_{t_1}^{t_2}\left(T_e-U_e\right)dt=0,$$

(46)

where $t_l$ and $t_2$ represent arbitrary times at which the state of the system is known, $T_e$ is the element kinetic energy and $U_e$ is the element strain energy.

The element strain energy can be written as

$$U_e={\displaystyle \frac{1}{2}}{\int }_0^{L_e}GJ{\left(\nabla {\theta }_h\right)}^{2}dx,$$

(47)

where G and J denote, respectively, the shear modulus and the torsional constant of the beam element cross-section, which might be functions of x.

The kinetic energy of the beam element undergoing pure torsional deformation is

$$T_e={\displaystyle \frac{1}{2}}{\int }_0^{L_e}\rho I_p{\dot{\theta }}_h^{2}dx,$$

(48)

where $\dot{(·)}\equiv {\displaystyle \frac{\partial }{\partial t}}(·)$ and $\rho$ and $I_p$ are, respectively, the mass density and the the polar second moment of area of the beam element cross-section, which might be defined in terms of the x variable.

2.5. Virtual Element Approximation of Energy Functionals

Using the expressions for the projections ${\Pi }^{\nabla }{\theta }_h$ and $\nabla {\Pi }^{\nabla }{\theta }_h$ obtained in Equation (43) and Equation (45), respectively, the local virtual element approximation of energy functionals can be computed.

Using the approximation $\nabla {\theta }_h\approx \nabla {\Pi }^{\nabla }{\theta }_h={\mathbf{B}}_{\pi }{\mathbf{d}}_e$, the element strain energy can be written as

$$\begin{array}{cc}\hfill U_e& ={\displaystyle \frac{1}{2}}{\mathbf{d}}_e^{⊺}\left[{\int }_0^{L_e}GJ{\mathbf{B}}_{\pi }^{⊺}{\mathbf{B}}_{\pi }dx\right]{\mathbf{d}}_e\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}{\mathbf{d}}_e^{⊺}{\mathbf{K}}_e{\mathbf{d}}_e,\hfill \end{array}$$

(49)

where

$${\mathbf{K}}_e={\int }_0^{L_e}GJ{\left({\mathbf{B}}_{\pi }\right)}^{⊺}{\mathbf{B}}_{\pi }dx,$$

(50)

is the element stiffness matrix. It is worth noting that ${\mathbf{K}}_e$ is a $(p+1)\times (p+1)$ symmetric matrix and that its rank is equal to p. Therefore, the matrix has proper rank and does not need to be stabilized because there are no spurious rigid body motions that need to be suppressed.

Using the approximation ${\dot{\theta }}_h\approx {\displaystyle \frac{\partial }{\partial t}}\left({\Pi }^{\nabla }{\theta }_h\right)={\displaystyle \frac{\partial }{\partial t}}\left({\mathbf{N}}_{\pi }{\mathbf{d}}_e\right)={\mathbf{N}}_{\pi }{\dot{\mathbf{d}}}_e$, the element kinetic energy can be written as

$$\begin{array}{cc}\hfill T_e& ={\displaystyle \frac{1}{2}}{\dot{\mathbf{d}}}_e^{⊺}\left[{\int }_0^{L_e}\rho I_p{\mathbf{N}}_{\pi }^{⊺}{\mathbf{N}}_{\pi }dx\right]{\dot{\mathbf{d}}}_e\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}{\dot{\mathbf{d}}}_e^{⊺}{\mathbf{M}}_e{\dot{\mathbf{d}}}_e,\hfill \end{array}$$

(51)

where

$${\mathbf{M}}_e={\int }_0^{L_e}\rho I_p{\left({\mathbf{N}}_{\pi }\right)}^{⊺}{\mathbf{N}}_{\pi }dx,$$

(52)

is the element consistent mass matrix, which is a symmetric, positive-definite matrix and does not require stabilization.

Substituting $T_e$ and $U_e$ in Equation (46), one obtains

$$\delta {\int }_{t_1}^{t_2}\left({\displaystyle \frac{1}{2}}{\dot{\mathbf{d}}}_e^{⊺}{\mathbf{M}}_e{\dot{\mathbf{d}}}_e-{\displaystyle \frac{1}{2}}{\mathbf{d}}_e^{⊺}{\mathbf{K}}_e{\mathbf{d}}_e\right)dt=0.$$

(53)

Performing variation and integrating by parts for time derivatives yields

$${\int }_{t_1}^{t_2}\delta {\mathbf{d}}_e^{⊺}\left(-{\mathbf{M}}_e{\ddot{\mathbf{d}}}_e-{\mathbf{K}}_e{\mathbf{d}}_e\right)dt=0.$$

(54)

Since $\delta {\mathbf{d}}_e\left(t\right)$ is arbitrary, as long as it vanishes at the endpoints, the discretized system of dynamic equilibrium equations for the element are

$${\mathbf{M}}_e{\ddot{\mathbf{d}}}_e+{\mathbf{K}}_e{\mathbf{d}}_e=0.$$

(55)

The global equation of motion is obtained by assembling the element-level matrices (${\mathbf{M}}_e$,${\mathbf{K}}_e$) into global matrices ($\mathbf{M}$,$\mathbf{K}$) by summing contributions from all elements

$$\mathbf{M}\ddot{\mathbf{d}}+\mathbf{K}\mathbf{d}=0,$$

(56)

where $\mathbf{d}$ is the global vector of degrees of freedom.

3. Results

The validation of the proposed p-VEM formulation primarily focuses on demonstrating its efficiency and accuracy in modeling the torsional vibrations of uniform and nonuniform beams with circular cross-sections or other cross-section geometries in which warping displacements can be neglected.

This section presents three case studies aimed at validating the proposed formulation. In each case study, the virtual element mesh is kept fixed (e.g., using a single element for simpler geometries or a few elements for more complex ones) while the polynomial order p of the approximation functions within each element is progressively increased. The results obtained with the p-VEM are compared to those computed using a standard FEM formulation and a mesh of linear interpolation elements commonly implemented in commercial finite element codes. When available, the results are also compared to analytical solutions.

3.1. Free Vibrations of a Uniform Beam

The simplest and fundamental scenario for analyzing free torsional vibrations of a beam occurs when the beam has a uniform cross-section because exact analytical solutions for the natural frequencies and mode shapes of such beams are readily available [26].

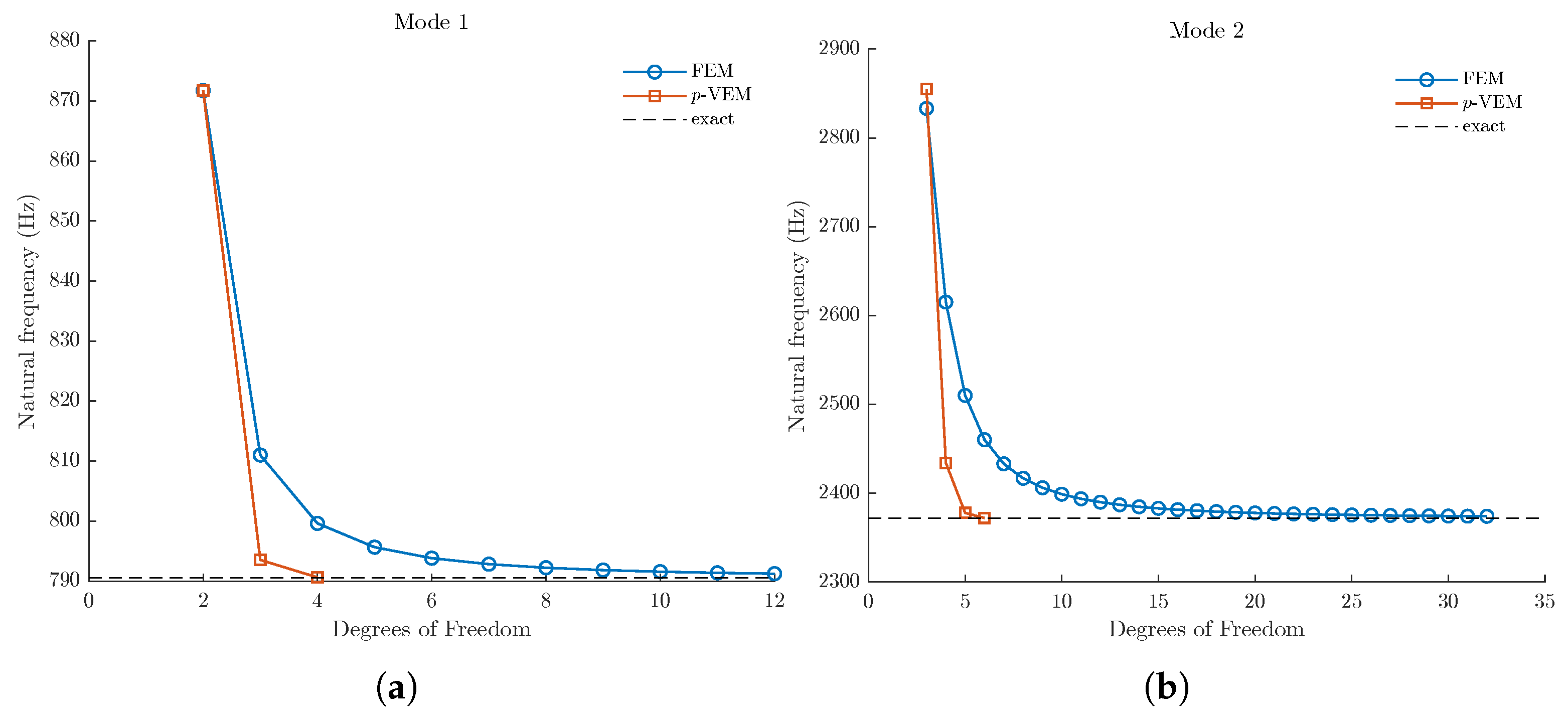
A uniform beam of length $L=1$ m and solid circular cross-section diameter of $d=40$ mm is used to validate the uniform version of the p-VEM beam element herein developed. The material properties of the beam are the shear modulus $G=27$ GPa and the mass density $\rho =2700$ kg/m³. Both Clamped-Free (C-F) and Free-Free (F-F) boundary conditions are considered.

This experiment aims to explore the convergence properties of the proposed p-VEM formulation against a standard FEM approach in approximating the exact natural frequencies. A single p-VEM element of variable order p is used to model the beam. The FEM modeling is done by meshing the beam element with an increasing number of two nodes, linear interpolation elements. For each mode of interest, n, and for both the discretization approaches, convergence is considered reached when the computed natural frequencies exhibit a percentage relative error, $ϵ$, less than $0.1\%$ compared to the analytical solutions.

The convergence plots for the first four (non-zero) modes for the beam with C-F and F-F boundary conditions are shown, respectively, in Figure 2 and Figure 3. The corresponding data are provided in

Table 1. Uniform beam. Torsional natural frequencies (Hz) of the first four modes for the case with C-F boundary conditions.

	Degrees of Freedom	Mode 1	Mode 2	Mode 3	Mode 4
Analytical solution		790.569	2371.708	3952.847	5533.986
FEM	2	871.728
	3	811.013	2833.184
	4	799.628	2615.183	4744.322
	5	795.659	2510.016	4559.525	6593.473
	:	:	:	:	:
	12	791.241	2389.884	4037.255	5766.244
	:		:	:	:
	32		2373.992	3963.427	5563.039
	:			:	:
	52			3956.754	5544.710
	:				:
	72				5539.518
p-VEM	2	871.728
	3	793.537	2855.078
	4	790.623	2434.147	5257.922
	5		2377.849	4192.890	8205.460
	6		2372.095	3995.635	6127.053
	7			3958.532	5676.431
	8			3953.382	5562.850
	9				5538.449

and

Table 2. Uniform beam. Torsional natural frequencies (Hz) of the first four (non-zero) modes for the case with F-F boundary conditions.

	Degrees of Freedom	Mode 1	Mode 2	Mode 3	Mode 4
Analytical solution		1581.139	3162.278	4743.416	6324.555
FEM	2	1743.455
	3	1743.455	3486.910
	4	1653.987	3698.427	5230.365
	5	1622.026	3486.91	5666.368	6973.82
	:	:	:	:	:
	22	1582.614	3174.086	4783.319	6419.291
	:		:	:	:
	42		3165.373	4753.867	6349.339
	:			:	:
	62			4748.136	6335.745
	:				:
	83				6330.746
p-VEM	2	1743.455
	3	1743.455	3898.484
	4	1581.579	3898.484	6564.537
	5		3173.729	6564.537	9814.004
	6		3173.729	4807.045	9814.004
	7		3162.331	4807.045	6521.804
	8			4744.414	6521.804
	9				6331.467
	10				6326.347

. In this initial numerical test, the p-VEM demonstrates significantly faster convergence compared to the standard FEM across all modes and boundary conditions examined. Moreover, the p-VEM consistently shows higher accuracy, with the computed converged natural frequencies being always closer to the analytical solution than those obtained from the standard FEM.

Figure 4 shows the convergence behavior of the proposed p-VEM compared to the standard FEM in predicting the torsional natural frequencies of a uniform beam under Clamped-Free (C-F) boundary conditions. The percentage relative error with respect to the analytical solution is plotted against the number of degrees of freedom for the first four vibration modes. The results show that the p-VEM achieves a higher rate of convergence than the FEM, obtaining highly accurate results (errors below 0.1%) with only a few degrees of freedom. This demonstrates the superior efficiency of the proposed p-VEM formulation in terms of computational cost.

3.2. Free Vibrations of a Stepped Shaft

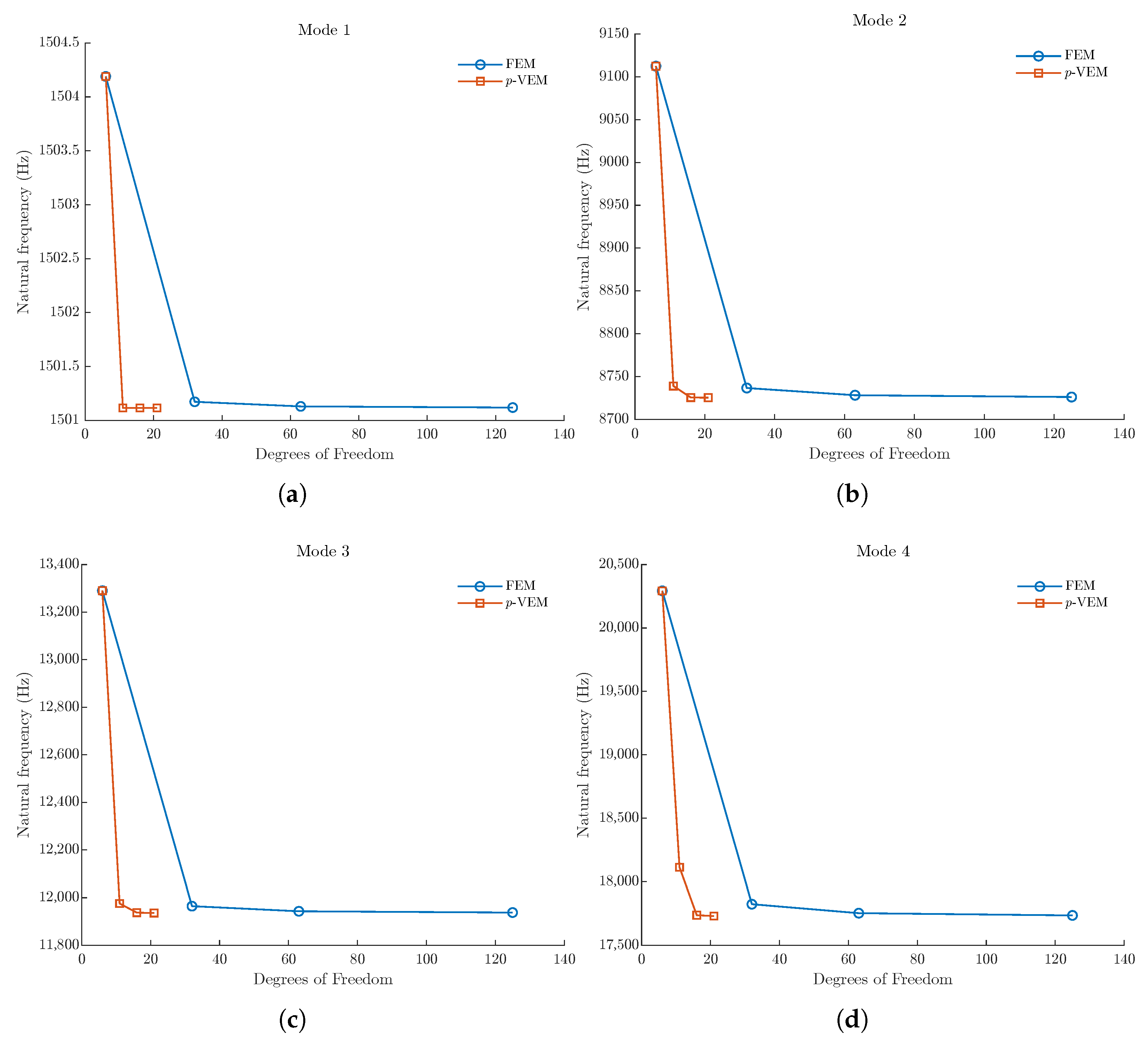
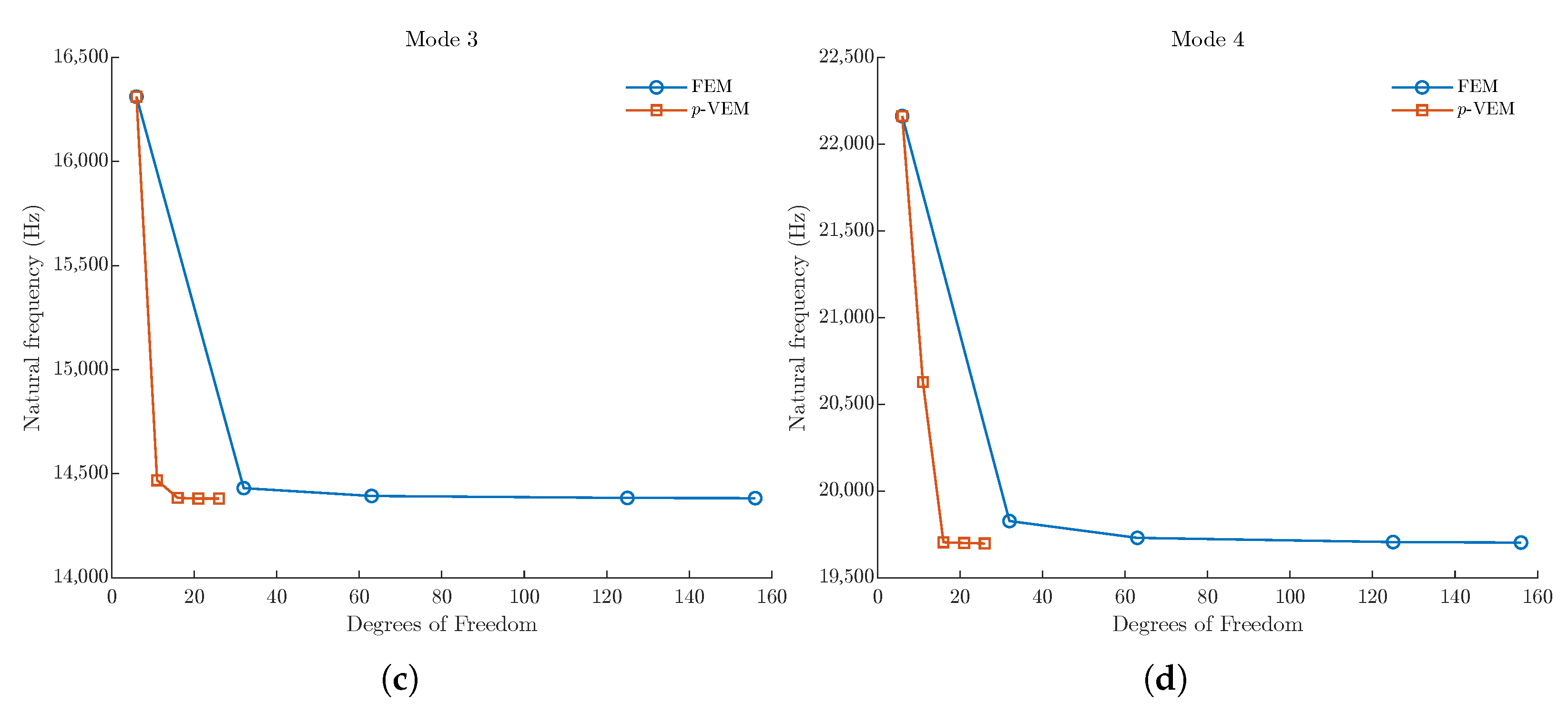
This example considers the free vibrations of an arbitrary stepped shaft. The shaft is composed of five segments with lengths equal to $L_1=60$, $L_2=50$, $L_3=50$, $L_4=80$, and $L_5=70$ mm and cross-section diameters $d_1=30$, $d_2=35$, $d_3=40$, $d_4=50$, and $d_5=40$ mm, shear modulus $G=77$ GPa, and mass density $\rho =7900$ kg/m³.

The p-VEM discretization consists of five beam elements, one per each segment, with variable order p. The FEM modeling is done with a uniform spacing of a variable number of two nodes, linear interpolation beam elements. The first four (non-zero) modes are evaluated under both Clamped-Free (C-F) and Free-Free (F-F) boundary conditions. Convergence is considered achieved when, for all modes of interest, the natural frequencies computed at the current refinement level show a percentage relative error, $ϵ$, of less than $0.1\%$ compared to the previous refinement level.

The convergence analysis results are presented in the plots shown in Figure 5 and Figure 6 for C-F and F-F boundary conditions, respectively. The corresponding data can be found in

Table 3. Stepped shaft. Torsional natural frequencies (Hz) of the first four modes for the case with C-F boundary conditions.

	Degrees of Freedom	Mode 1	Mode 2	Mode 3	Mode 4
FEM	6	1504.190	9112.413	13,290.345	20,293.043
	32	1501.172	8736.626	11,964.616	17,823.957
	63	1501.129	8728.213	11,943.073	17,753.280
	125	1501.118	8726.111	11,937.691	17,735.635
p-VEM	6	1504.190	9112.413	13,290.345	20,293.043
	11	1501.116	8738.970	11,975.678	18,112.791
	16	1501.115	8725.480	11,937.306	17,737.440
	21	1501.115	8725.412	11,935.906	17,730.467

and

Table 4. Stepped shaft. Torsional natural frequencies (Hz) of the first four (non-zero) modes for the case with F-F boundary conditions.

	Degrees of Freedom	Mode 1	Mode 2	Mode 3	Mode 4
FEM	6	6704.330	11,352.034	16,311.649	22,162.214
	32	6533.744	10,499.612	14,430.478	19,826.704
	63	6530.220	10,485.032	14,392.790	19,729.745
	125	6529.340	10,481.389	14,383.377	19,705.547
	156	6529.234	10,480.952	14,382.248	19,702.645
p-VEM	6	6704.330	11,352.034	16,311.649	22,162.214
	11	6530.911	10,513.036	14,467.854	20,628.397
	16	6529.057	10,480.659	14,383.578	19,704.178
	21	6529.046	10,480.181	14,380.280	19,700.137
	26	6529.046	10,480.175	14,380.241	19,697.488

. The analysis of the results indicates that, even for this more complex case study, the p-VEM solution converges considerably faster, in terms of degrees of freedom, than the standard FEM.

3.3. Free Vibrations of a Lifting Surface with Continuously Varying Torsional Stiffness

In this section, the accuracy and efficiency of the proposed p-VEM formulation are further validated with an example involving the analysis of free torsional vibrations of a high-aspect-ratio lifting surface with continuously spanwise varying cross-sectional properties.

The lifting surface has a length that is significantly greater than its width, which in turn is substantially greater than its thickness, resembling a long, very narrow and thin plate (or thin strip) undergoing free torsional vibrations. In this case, using beam elements to create a surrogate model provides a reasonable approximation [27].

The beam has a length of $L=1.2$ m and a solid rectangular cross-section. The dimensions of the root cross-section are a width of $b_0=50$ mm and a height of $h_0=2.5$ mm, while the dimensions at the tip are $b_0=20$ mm and $h_0=1.5$ mm. The material has a density of $\rho =2700$ kg/m³ and a shear modulus of $G=26$ GPa.

The analysis of natural frequency convergence is conducted for the first four torsional modes. The p-VEM discretization consists of a single beam element with varying p-refinement. This is compared to a standard FEM h-refinement approach.

The results of the convergence analysis for both the p-VEM and the FEM are illustrated in the plots presented in Figure 7. The corresponding data are listed in

Table 5. Lifting surface. Torsional natural frequencies (Hz) of the first four modes.

	Degrees of Freedom	Mode 1	Mode 2	Mode 3	Mode 4
FEM	2	150.952
	3	145.222	365.207
	5	143.893	316.358	538.736	825.597
	9	143.487	304.108	488.59	695.393
	17	143.380	300.924	474.337	657.132
	33	143.353	300.122	470.746	647.381
	65	143.346	299.921	469.848	644.943
p-VEM	2	146.263
	3	145.134	330.133
	4	143.347	313.471	576.743
	5	143.344	300.336	508.895	900.890
	6	143.344	299.940	473.940	726.305
	7	143.344	299.860	470.405	661.331
	8	143.344	299.854	469.671	647.647
	9	143.346	299.855	469.553	645.079

. The mode shapes corresponding to the converged p-VEM solution are shown in Figure 8. The FEM model requires a higher number of elements and degrees of freedom to reach a convergent solution. In contrast, the p-VEM is able to accurately represent the torsional vibration of the structure with significantly fewer degrees of freedom and computational costs by using a single beam element and increasing its polynomial order.

4. Discussion

This work introduced and validated an arbitrary order Virtual Element Method (p-VEM) for the analysis of free torsional vibrations of beams. The formulation was specifically developed for the one-dimensional analysis of pure beam torsion, assuming that the effects of cross-sectional warping are negligible.

Three distinct case studies were conducted to assess the method’s accuracy and computational efficiency. In all test cases, the results consistently demonstrated the superior performance of the p-VEM discretization approach over a h-refinement FEM scheme with linear-interpolation elements. The p-VEM achieved high levels of accuracy with significantly fewer degrees of freedom than a comparable FEM model. The capability to obtain highly accurate results from coarse meshes is particularly valuable during the conceptual and preliminary design stages of aerospace structures. The computational efficiency of the p-VEM approach can enable faster design iterations and more extensive parametric studies.

The proposed p-VEM beam element retains the same number of nodal degrees of freedom as the standard FEM’s linear-interpolation element, allowing for straightforward implementation in existing FEM codes. Moreover, the developed formulation produces stable and accurate stiffness and mass matrices without requiring any ad hoc stabilization techniques, thereby simplifying implementation. Within the framework of one-dimensional elements and semi-discretization approaches, the development of a consistent mass matrix represents a key novelty of the present work.

The presented formulation is well suited for the analyses of beam-type structures with solid or closed hollow circular cross-sections or narrow plates but might not be adequate for thin-walled sections where warping deformation is significant. Future work will focus on extending this p-VEM beam framework to include warping deformations and torsion/bending coupling. Additional studies will also investigate the performance of the proposed p-VEM formulation for transient dynamic analyses, comparing its efficiency with established time-integration schemes.

5. Conclusions

This work introduced and validated an arbitrary-order Virtual Element Method (p-VEM) for the analysis of free torsional vibrations of beams with negligible warping effects. The main contributions and achievements of this study can be summarized as follows:

• Novel formulation: to the best of the authors’ knowledge, this is the first arbitrary-order 1D VEM formulation for dynamic torsional problems that uses a consistent mass matrix without requiring stabilization.
• Computational efficiency: the p-VEM approach obtained converged results with one or a few elements of increasing polynomial order, whereas FEM required meshes with numerous elements. This translates into a substantial reduction in computational cost for a target accuracy.
• Robust implementation: the element retains the same number of nodal degrees of freedom as standard FEM beam elements, enabling straightforward integration into existing finite element codes.
• Practical relevance: the proposed formulation contributes to the development of low-order yet accurate structural models for conceptual and preliminary design of slender aerospace components.

Future work will focus on extending this framework to account for cross-sectional warping, torsion–bending coupling, and transient dynamic analyses.