An Ensemble of Heuristic Adaptive Contract Net Protocol for Efficient Dynamic Data Relay Satellite Scheduling Problem

Abstract

Task scheduling in data relay satellite networks (DRSNs) is subject to dynamic disruptions such as resource failures, sudden surges in task demands, and variations in service duration requirements. These disturbances may degrade the performance of pre-established scheduling plans. To improve adaptability and robustness under such uncertainties, this paper presents a dynamic scheduling model for DRSN that integrates comprehensive task constraints and link connectivity requirements. The model aims to maximize overall task utility while minimizing deviations from the original schedule. To efficiently solve this problem, an ensemble heuristic adaptive contract net protocol (EH-ACNP) is developed, which supports dynamic scheduling strategy adaptation and efficient rescheduling through iterative negotiations. Extensive simulation results show that, in scenarios with sudden task surges, the proposed method achieves a 3.1% improvement in yield compared to the state-of-the-art dynamic scheduling algorithm HMCNP, and it also outperforms HMCNP in scenarios involving resource interruptions. Sensitivity analysis further indicates that the algorithm maintains strong robustness when the disposal rate parameter exceeds 0.2. These results highlight the practical potential of the EH-ACNP for dynamic scheduling in complex and uncertain DRSN environments.

1. Introduction

Data relay satellites (DRSs) typically operate in geostationary orbit, providing broad and stable coverage through their antennas to offer long-term and reliable data offloading services to low-Earth orbit (LEO) satellites [1,2,3]. This improves the speed of remote sensing data collection and transmission [4]. However, due to the growing demand for reliable and continuous communication across industries such as telecommunications, defense, and emergency services, the scale of the DRS scheduling problem has increased exponentially [5,6]. This calls for better management of DRS and the development of faster, more flexible scheduling algorithms [1,7,8].

DRSs in China are primarily managed by a centralized ground control center. Users submit their DRS usage requirements in advance to the control center [9,10]. The control center then allocates satellite resources reasonably, considering usage constraints, to generate a usage plan, which is then executed by the DRS through the telemetry and control link [11]. The plans generated in this mode are based on offline predictions of in-orbit resources. However, in practice, due to unpredictable risks such as space debris, solar radiation, and other complex space environmental factors [12,13], both remote sensing satellites (RSSs) and DRSs face the possibility of failures that cannot be predicted. As a result, the satellite control center must adjust the original plan in response to unexpected changes, forming a dynamic transmission plan to improve the resilience of the system [14].

In previous studies on dynamic DRS scheduling, Deng et al. [15] proposed a two-stage, multi-constraint scheduling model for DRSNs. Li et al. [16] developed a unified modeling framework that incorporates multiple types of system disturbances, making it applicable to both dynamic and static scheduling scenarios. Zhao et al. [17] formulated the DRS scheduling problem as a constraint satisfaction problem with multiple constraints. Chen et al. [18] modeled the problem as a Markov decision process, while S. Rojanasoonthon et al. [19] treated it as a mixed-integer programming problem. However, most of these studies focus solely on the utilization constraints of the DRS. In practice, due to antenna pointing losses and free-space path losses, transmission links must be established within the maximum communication cone of the DRS [20,21]. Furthermore, considering the limited transmission power of RSSs, incorporating link budget constraints into DRS scheduling models is both necessary and realistic [22,23].

Dynamic DRS scheduling refers to the process of replanning and adjusting the task transmission schedule of the DRS when the original schedule is affected by resource changes or task disturbances, in order to maintain the overall optimality or near-optimality of the scheduling scheme in a dynamic environment. Regarding scheduling algorithms, Zhai et al. [24] used a rule-based heuristic algorithm to solve the dynamic robust DRS scheduling problem, He et al. [25] applied a stochastic optimization framework to a hybrid dynamic DRS task planning problem, and Dai et al. [26] proposed an adaptive large neighborhood search algorithm with deadline awareness to solve the dynamic relaxation scheduling problem for the DRS. Luo et al. [27] introduced a flexible scheduling mode for the DRS, and Chen et al. [28] used a breakpoint resume method to improve the efficiency of DRS resource scheduling. Li et al. [29] applied an end-to-end reinforcement learning approach to solve the DRS scheduling problem. These studies developed algorithms for traditional DRS control modes, where different parts of the algorithm are tightly coupled, making them suitable for centralized operation on a single machine.

With the development of hardware and software technologies for DRSs, satellites now have the ability for autonomous computation [1,30,31]. The traditional offline control mode of DRS control centers has severely limited the performance of DRSs. Satellites can now autonomously perceive their environment in real-time, and compared to plans generated based on predicted resource information, they can more promptly and accurately respond to risks. Autonomous collaborative planning of the DRS in orbit is the future trend of DRS management [32,33].

The contract net protocol (CNP), as a representative distributed decision-making architecture, exhibits strong scalability, autonomy, and coordination capabilities in dynamic environments [34,35]. In recent years, it has been widely applied to space mission scheduling problems. Xiang et al. [36] introduced a hierarchical disturbance-tolerant CNP for distributed satellite TT&C tasks. Du et al. [37] applied the CNP to the autonomous coordination of RSSs. Yang et al. [32] proposed a multi-agent CNP-based planning framework for imaging missions, while Liu et al. [38] developed a bottom-up CNP structure to coordinate heterogeneous observation resources. Yang et al. [39] also designed a priority-aware variant of the CNP for large-scale constellation mission planning, and Wang et al. [40] combined ant colony optimization with the CNP to address mobile edge computing in space information networks. These studies collectively demonstrate the potential of the CNP in distributed space mission planning. However, most of the existing work focuses on specific task types or static environments, with limited attention to large-scale dynamic DRS scheduling under task and resource disruptions.

In light of these challenges, this paper focuses on the dynamic scheduling problem of the DRS and establishes a dynamic scheduling model that incorporates realistic link budget constraints. To solve this problem, we propose an ensemble heuristic-based adaptive contract net scheduling framework. By introducing a multi-round negotiation mechanism and dynamic strategy adjustment, the framework enables the rapid adaptation of scheduling plans, thereby enhancing the robustness and efficiency of DRS operations under system disturbances. The main contributions of this study are as follows:

(1)

A dynamic DRS scheduling model was established, considering link budget and resource usage constraints, to maximize the benefits of the dynamic adjustment scheme while minimizing disruptions to the original schedule.

(2)

To solve this problem, an ensemble of heuristic adaptive contract net protocols (EH-ACNPs) is proposed. The algorithm coordinates task allocation through multiple rounds of combinatorial auctions, quickly generating a rescheduling plan in disturbance scenarios.

(3)

Compared with current advanced dynamic DRS scheduling algorithms, the proposed method demonstrated excellent performance in experiments involving task disruptions, resource failures, and other scenarios. Sensitivity analysis further confirms its robustness.

The remaining chapters of this paper are organized as follows: Section 2 describes and models the dynamic DRS scheduling problem, Section 3 provides a detailed introduction to the proposed EH-ACNP, Section 4 presents the simulation results, and Section 5 summarizes the main research findings of this paper.

2. Problem Description and Mathematical Model

This section describes the dynamic DRS scheduling problem, establishes model assumptions, and develops both the potential link model for the DRS and the dynamic resource scheduling model for the DRS. The symbols and variables defined in this section are listed in

Table 1. Definitions of main notations.

Parameters	Description
$[S,E]$	Start time and end time of simulation
$R,U,T$	User satellites, DRS antennas, and mission sets
$V_{i,r}$	Set of visible time windows for task i and antenna r
$\left[{vst}_{i,r,q},{vet}_{i,r,q}\right]$	The qth visible time window of task i and antenna r
$\left[{sst}_i,{set}_i\right]$	Service time window of task i
$w_i$	Priority of task i
$d_i$	The shortest transmission time of task i
$\tau$	A certain moment during the simulation, $\tau \in [S,E]$
${\vartheta }_1$,${\vartheta }_2$	Antenna alignment and reset time
$\Xi \left(l,r,\tau \right)$	Logical variable of link connectivity
${\Xi }_E(l,r,\tau )$	Logical variable of visibility constraint
${\Xi }_V(l,r,\tau )$	Logical variable of elevation angle constraint
${\Xi }_P(l,r,\tau )$	Logical variable of power constraint
${\varphi }_{l,r,\tau }$, ${\varpi }_{l,r,\tau }$, $b_{l,r,\tau }$	Elevation angle, central angle, and inter-satellite distance from l to r at $\tau$
${\theta }_{min}$	Minimum communication elevation angle
$R_e$, $h_r$, $h_l$	Earth radius, DRS altitude, and RSS altitude
$P_{max}$	Maximum transmit power of the RSS transmitter
$R_r$, $G_r^R$, $G_l^{\tau }$	DRS antenna receiving sensitivity and gain, RSS antenna gain
${\phi }_{l,\tau }$, ${\phi }_{r,\tau }$, ${\gamma }_{l,\tau }$, ${\gamma }_{r,\tau }$	Latitude and longitude of RSS l and DRS r at $\tau$
Varibles	Description
$x_{i,r,q}$	Assignment decision variable of task i, $x_{i,r,q}\in \{0,1\}$
${st}_{i,r}$	Start execution time of task i, ${st}_{i,r}\in [S,E]$
${et}_{i,r}$	End execution time of task i, ${et}_{i,r}\in [S,E]$

.

2.1. Problem Description

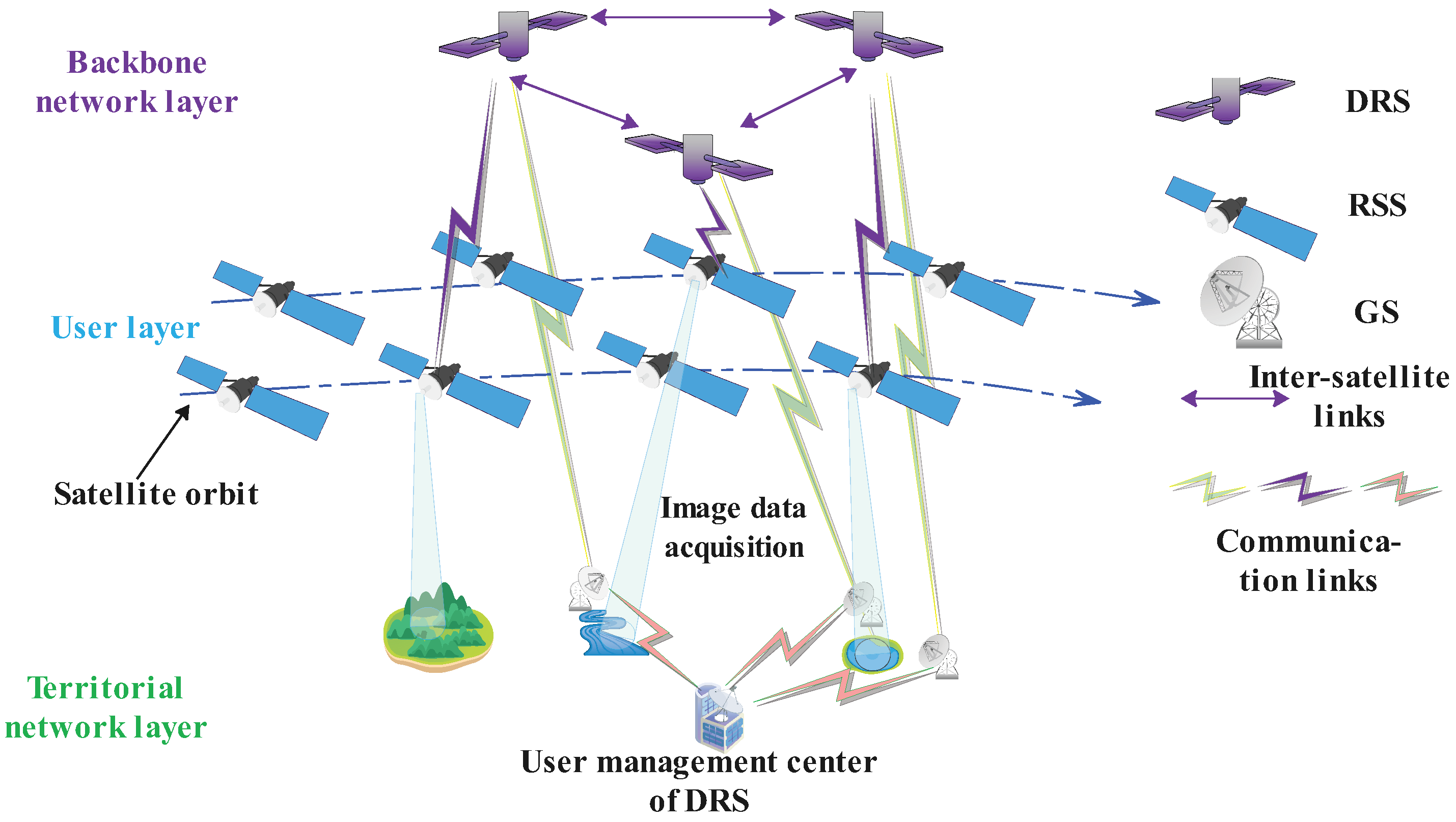
As shown in Figure 1, the DRS plays a crucial role in satellite networks by handling essential data transmission and relay forwarding tasks, ensuring stable communication between ground stations and target satellites such as LEO RSSs and scientific research satellites [41]. However, due to the complex and dynamic in-orbit environment, the system may face uncertainties such as resource disturbances and task disturbances, which can render the original scheduling plan invalid, thereby affecting data transmission stability and task completion rates [36].

Resource disturbances refer to variations in DRS resources, such as link availability, power supply, and storage capacity, caused by unexpected failures or fluctuations in consumption [16]. Task disturbances refer to changes in task parameters such as service time, priority, and data volume due to shifting demands, as well as the emergence of urgent, unplanned tasks [36].

The objective of the dynamic resource scheduling problem for the DRS is to promptly adjust scheduling plans in response to these uncertainties to maximize task fulfillment. In practical applications, significantly modifying the original plan can negatively impact ongoing or upcoming tasks. Therefore, to enhance system stability, dynamic scheduling for DRS should aim to minimize drastic changes to the original schedule while balancing scheduling stability and resource utilization.

In this paper, we aim to maximize task benefits while minimizing scheduling disruptions. Considering engineering constraints such as task service windows, available connection time windows, task execution frequency, and antenna switching time, we establish a dynamic resource scheduling model for DRS and design algorithms for its solution. To simplify the problem without compromising its real-world representation, we introduce the following three model assumptions:

(1)

DRSs employ a single-access technology, meaning they can serve only one user at a time. Additionally, at any given moment, a user satellite can connect to only one DRS and cannot establish simultaneous connections with multiple DRSs [29].

(2)

User satellites do not transmit data directly to the ground via ground stations; instead, they rely solely on DRSs for data forwarding.

(3)

Energy and DRS memory limitations are not considered. The DRSs are assumed to be in geostationary orbit, where continuous sunlight provides a sufficient power supply. Inter-satellite links between relay satellites are stable and reliable, and the inter-satellite topology is relatively fixed. It is also assumed that DRSs primarily forward data rather than storing them for extended periods, enabling real-time data transmission to ground stations [42].

2.2. Potential Connection Link Model

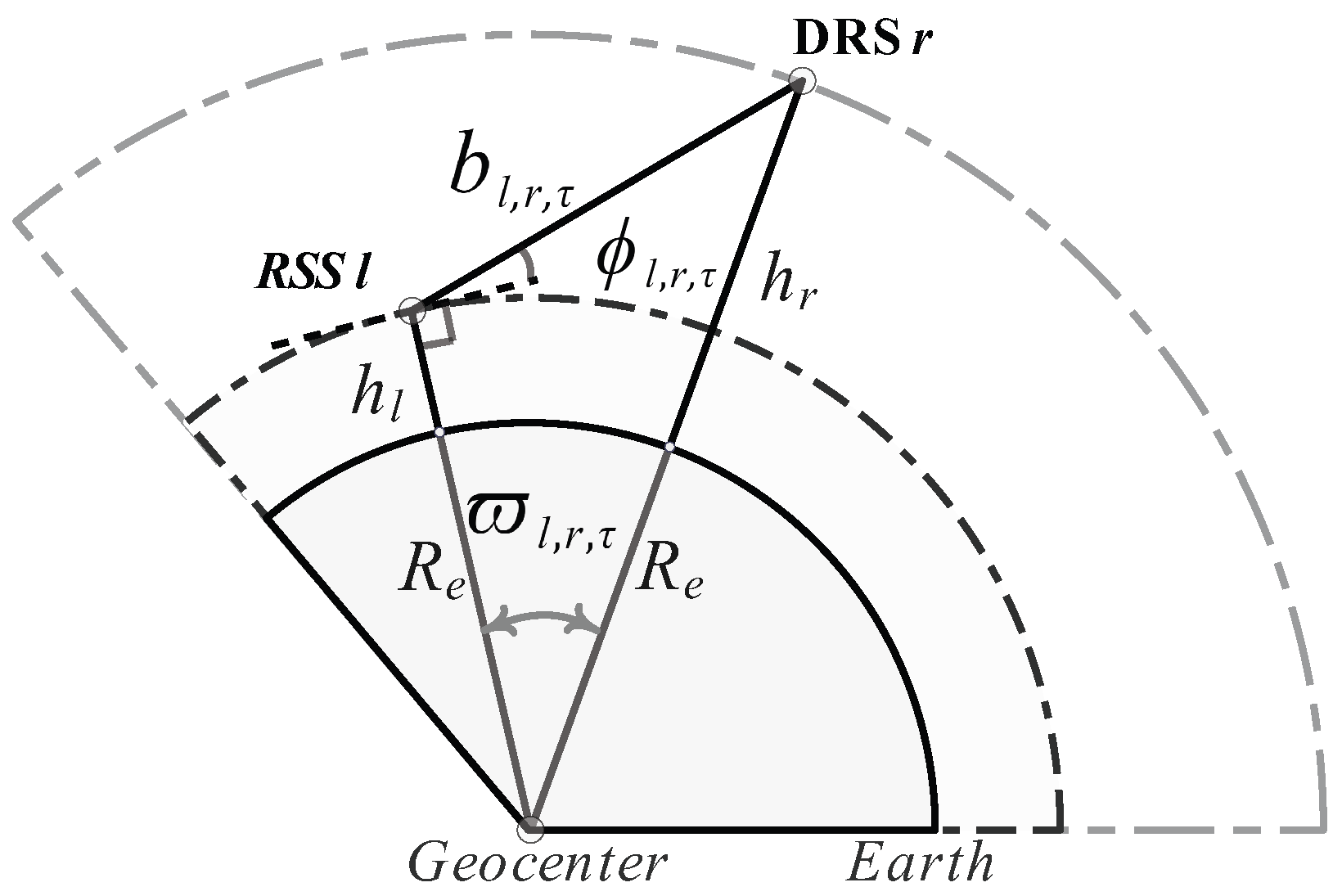
Figure 2 illustrates the geometric relationship between the RSS and the DRS. Let $\tau \in [S,E]$ represent a specific moment in the scheduling cycle, and let $\Xi (l,r,\tau ),$ denote the connectivity variable between the RSS and the DRS. When they are connected at time $\tau$, $\Xi \left(l,r,\tau \right)=1$; otherwise, $\Xi \left(l,r,\tau \right)=0$. The following three constraints apply:

(1) Elevation Angle Constraint: Due to the limited beamwidth of the DRS’s antenna, if the relative elevation angle between the RSS and the DRS is too low, it may exceed the coverage range of the DRS’s antenna [43]. Let ${\Xi }_E(l,r,\tau )$ represent the elevation angle constraint logic variable. When the elevation angle condition is satisfied ${\Xi }_E(l,r,\tau )$, it can be described as follows [23,43]:

$${\Xi }_E(l,r,\tau )=({\varphi }_{l,r,\tau }\ge {\theta }_{min})\wedge ({\varphi }_{r,l,\tau }\ge {\theta }_{min})$$

(1)

In the above equation, ${\varphi }_{l,r,\tau }$ represents the relative elevation angle between the RSS and the DRS at time $\tau$, and ${\theta }_{min}$ is the minimum communication elevation angle. When a connection is possible, the elevation angle should not be smaller than the minimum communication elevation angle. In the figure, by applying the law of sines, the following expression can be obtained:

$${\displaystyle \frac{R_e+h_r}{sin({\varphi }_{l,r,\tau }+\frac{\pi }{2})}}={\displaystyle \frac{b_{l,r,\tau }}{sin{\varpi }_{l,r,\tau }}}$$

(2)

Here, $R_e$ is the Earth’s radius, $h_r$ is the DRS’s orbital altitude, ${\varpi }_{l,r,\tau }$ is the geocentric angle between the satellites, and $b_{l,r,\tau }$ is the inter-satellite distance. From this expression, the elevation angle between the RSS and the DRS can be calculated as

$${\varphi }_{l,r,\tau }=arccos\left({\displaystyle \frac{(R_e+h_r)\sin {\varpi }_{l,r,\tau }}{b_{l,r,\tau }}}\right)$$

(3)

In the above equation, the inter-satellite distance $b_{l,r,\tau }$ can be calculated using the law of cosines, and the geocentric angle ${\varpi }_{l,r,\tau }$ can be obtained by calculating the satellite’s longitude and latitude.

$$\begin{array}{cc}\hfill b_{l,r,\tau }& ={\left({(R_e+h_l)}^2+{(R_e+h_r)}^2-2(R_e+h_l)(R_e+h_r)cos{\varpi }_{l,,\tau }\right)}^{1/2}\hfill \end{array}$$

(4)

$$\begin{array}{c}\hfill {\varpi }_{l,r,\tau }=arccos[sin{\phi }_{l,\tau }sin{\phi }_{r,\tau }+cos{\phi }_{l,\tau }cos{\phi }_{r,\tau }cos({\gamma }_{l,\tau }-{\gamma }_{r,\tau })]\end{array}$$

(5)

(2) Visibility Constraint: The communication link between the RSS and the DRS cannot be obstructed by the Earth, as the signal would be blocked. The maximum distance between the RSS and the DRS occurs when the line connecting the two satellites is tangent to the Earth. Let ${\Xi }_V(l,r,\tau )$ represent the visibility relationship logic variable, which can be described as follows [23,44]:

$$\begin{array}{c}\hfill {\Xi }_V(l,r,\tau )=\left(b_{l,r,\tau }\le \sqrt{{\left(R_e+h_l\right)}^2-R_e^2}\right.\left.+\sqrt{{\left(R_e+h_r\right)}^2-R_e^2}\right)\end{array}$$

(6)

(3) Transmission Power Constraint: Due to free-space path loss, wireless signals attenuate during transmission through the space link. When the RSS and the DRS establish a communication link, the transmitted power, after space attenuation, must be sufficient to meet the minimum demodulation threshold at the receiver, considering the antenna gain. In other words, the antenna’s operating power should be less than the maximum power $P_{max}$. Let ${\Xi }_P(l,r,\tau )$ represent the power constraint logic variable, which can be described as follows:

$${\Xi }_P(l,r,\tau )=(P_{l,r,\tau }\le P_{max})$$

(7)

In the above equation, $P_{l,r,\tau }$ represents the transmission power from l to r at time $\tau$, described $P_{l,r,\tau }$ in decibels, and can be expressed as follows: [44]

$$\left[P_{l,r,\tau }\right]=\left[R_r\right]-\left[G_r^R\right]-\left[G_l^{\tau }\right]+\left[FSL\left(f,b_{l,r,\tau }\right)\right]$$

(8)

$$\left[FSL\left(f,b_{l,r,\tau }\right)\right]=20lg\left(b_{l,r,\tau }\right)+20lg\left(f\right)+32.4$$

(9)

Here, $R_r$ (dB) and $G_r^R$ (dB) represent the receiver sensitivity and gain of the DRS, $G_l^{\tau }$ (dB) is the transmission gain of the RSS, and $FSL\left(f,b_{l,r,\tau }\right)$ is the free-space loss, expressed in terms of the communication frequency and inter-satellite distance.

By employing interval sampling to calculate the connectivity constraints at each simulation time $\tau$, the connection window $\left[{vst}_{i,r,q},{vet}_{i,r,q}\right]$ between the RSS and the DRS can be determined.

$$\Xi \left(l,r,\tau \right)={\Xi }_E\left(l,r,\tau \right)\wedge {\Xi }_V\left(l,r,\tau \right)\wedge {\Xi }_P\left(l,r,\tau \right)$$

(10)

2.3. Mathematical Programming Model

The DRS system consists of multiple DRSs, several user spacecraft, and multiple data transmission tasks. The dynamic resource scheduling problem for the DRS is an optimization problem with multiple complex constraints. To establish the dynamic scheduling model for the DRS, the relevant objects are symbolized, and the related symbols are shown as follows.

In terms of decision variables, the model defines three decision variables: $x_{i,r,q}$, $s{t}_{i,r}$, and $e{t}_{i,r}$. $x_{i,r,q}$ is a binary variable that indicates the execution window assigned to task i. If task i is assigned to the q-th execution window related to the user satellite on antenna r, then $x_{i,r,q}=1$; otherwise, $x_{i,r,q}=0$. $s{t}_{i,r}$ and $e{t}_{i,r}$ are continuous variables representing the start and end times of task i’s execution, respectively.

We aim to maximize task completion benefits and minimize the degree of disruption in the scheduling plan. The objective function $f_1$ represents the total benefits from task completion, while $f_2$ is the dynamic disruption measure, indicating the difference between the dynamic adjustment plan and the original plan. Here, $w_i$ represents the priority of task i, $n_{\mathrm{del}}$ represents the total number of tasks removed from the original plan, and $n_{\mathrm{new}}$ represents the total number of tasks adjusted in the dynamic plan compared to the original plan. ${\lambda }_{\mathrm{del}}$ and ${\lambda }_{\mathrm{new}}$ are the corresponding weights for these two components. The overall objective function is denoted as f, and ${\xi }_1$ and ${\xi }_2$ are the objective coefficients.

$$f_1=\sum _{i\in T}\sum _{r\in R}\sum _{q\in V_{i,r}}{x}_{i,r,q}·w_i$$

(11)

$$f_2={\lambda }_{del}·n_{del}+{\lambda }_{new}·n_{new}$$

(12)

$$max\left(f\right)={\xi }_1·f_1-{\xi }_2·f_2$$

(13)

The model’s relevant constraints mainly include task uniqueness constraints, service duration constraints, service time window constraints, switching time window constraints, and available time window constraints, as detailed below:

(1) Task Uniqueness Constraint: Each task should be transmitted through, at most, one time slot of a single DRS to avoid duplicate transmissions and prevent resource wastage.

$$\sum _{r\in R}\sum _{q\in V_{i,r}}{x}_{i,r,q}\le 1\forall i\in T$$

(14)

(2) Service Duration Constraint: Each task has a different data size and requires sufficient transmission time slots to accommodate its data.

$$e{t}_{i,r}-s{t}_{i,r}\ge d_i\forall i\in T,r\in R$$

(15)

(3) Service Time Window Constraint: Each task must be executed within a specific transmission time window. If the task is not transmitted within the time limit, it becomes invalid and no longer holds transmission significance.

$$x_{i,r,q}·s{t}_{i,r}\ge ss{t}_i\forall i\in T,r\in R$$

(16)

$$x_{i,r,q}·e{t}_{i,r}\le se{t}_i\forall i\in T,r\in R$$

(17)

(4) Switching Time Constraint: A certain amount of time should be reserved between two adjacent transmission tasks executed by a DRS to allow for antenna alignment adjustments, i.e., antenna switching time.

$$\begin{array}{c}\hfill [s{t}_{i,r}-{\vartheta }_1,e{t}_{i,r}+{\vartheta }_2]\cap [s{t}_{j,r}-{\vartheta }_1,e{t}_{j,r}+{\vartheta }_2]=\varnothing \forall i,j\in T,r\in R\end{array}$$

(18)

where ${\vartheta }_1$, ${\vartheta }_2$ represent the antenna alignment time and the reset time of DRSs, respectively.

(5) Available Time Window Constraint: Tasks should be executed within the connectivity time window of the DRS and the user satellite. Users whose connectivity time window is not satisfied should not be assigned transmission time slots.

$$x_{i,r,q}·s{t}_{i,r}\ge vs{t}_{i,r,q}\forall i\in T,r\in R$$

(19)

$$x_{i,r,q}·e{t}_{i,r}\le ve{t}_{i,r,q}\forall i\in T,r\in R$$

(20)

(6) Variable Range Constraints: The following are the range constraints for the relevant variables.

$$x_{i,r,q}\in \{0,1\}\forall i\in T,r\in R,q\in V_{i,r}$$

(21)

$$S\le s{t}_{i,r}\le E\forall i\in T,r\in R$$

(22)

$$S\le e{t}_{i,r}\le E\forall i\in T,r\in R$$

(23)

3. Algorithm Design

This section provides a detailed description of the EH-ACNP algorithm, performs an analysis of its algorithmic complexity, and presents its time complexity.

3.1. Algorithm Framework

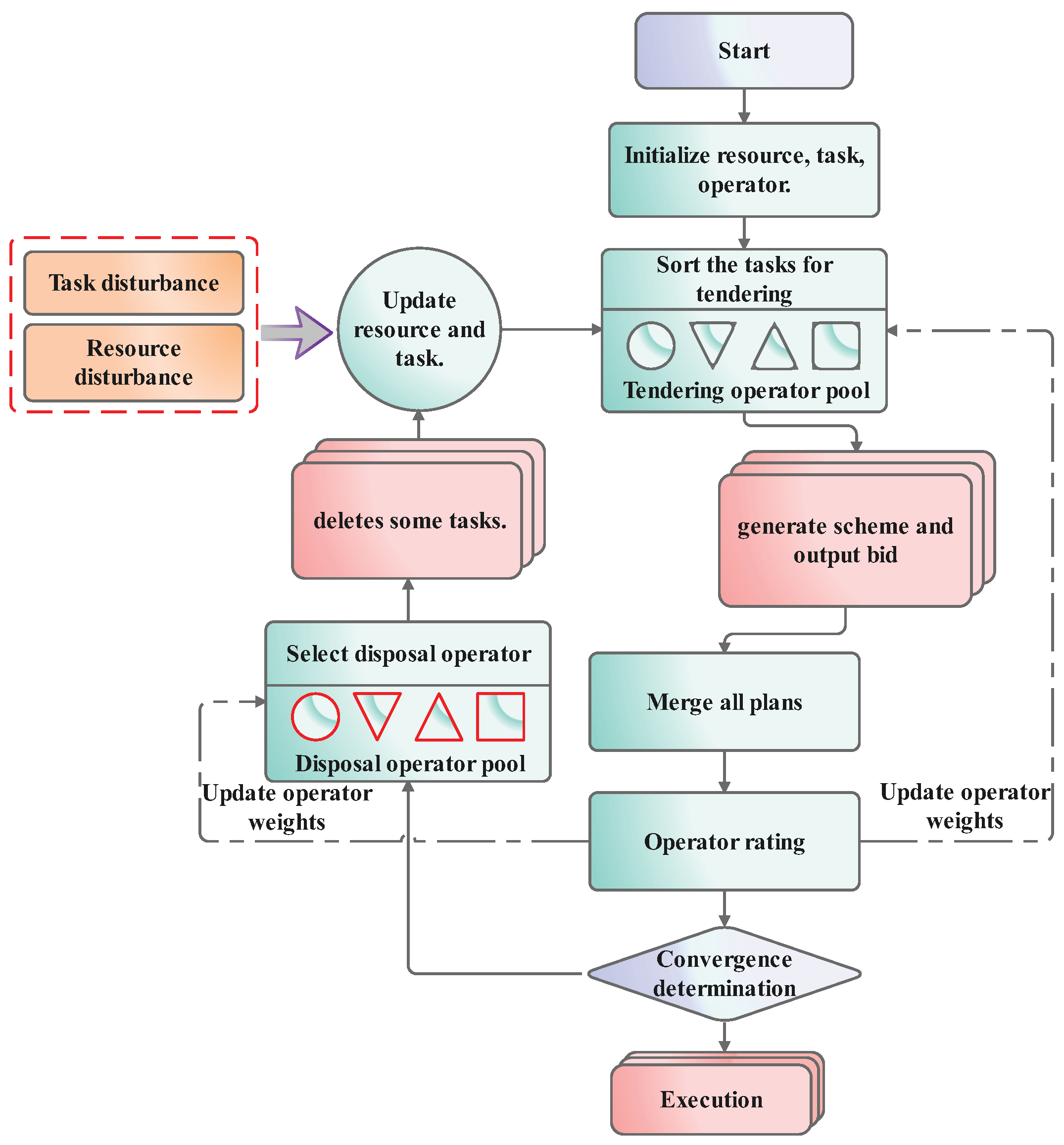
To address the dynamic DRS scheduling problem, we propose an EH-ACNP method. The workflow of the EH-ACNP is shown in Figure 3, and it is implemented using a multi-process concurrent architecture. The EH-ACNP takes as input both task-related information, including the set of user RSSs, the set of tasks, and resource-related information, including the set of DRSs, the set of antennas, and the available time windows for each task.

The EH-ACNP begins by initializing a process pool consisting of one main process and multiple subprocesses, each corresponding to an antenna. It also initializes a task pool managed by the main process, a resource pool managed by each subprocess for its assigned antenna, and an operator pool with initial weights assigned to each operator.

In the EH-ACNP, the main process acts as the centralized tenderer, while the subprocesses act as bidders. The tenderer applies multiple heuristic rules, referred to as bidding operators, to sort the tasks. The tenderer sends bidding requests for each task in the task pool to the bidders. Each bidder uses its bidding algorithm to plan an execution scheme and returns a bid price to the tenderer. The tenderer assigns the task to the bidder offering the highest bid. Once all tasks have been bid on, the tenderer consolidates the plans from all bidders into an overall scheduling scheme, evaluates the improvement of the solution, assigns scores to the operators, and updates their weights accordingly.

After each optimization round, if the solution has not converged, the tenderer selects a disposal operator from the operator pool. The corresponding bidders remove a portion of tasks from its local schedule, return them to the task pool, and update its resource.

The algorithm employs an adaptive operator adjustment strategy to manage the operator pool. The convergence criterion is met if either the objective function shows no improvement in two consecutive iterations or the algorithm reaches the predefined number of iterations. When either condition is satisfied, the algorithm terminates.

3.2. Bidding Operator Pool

The EH-ACNP method designs four bidding operators for sorting the bidding sequence: the maximum weight bidding operator, the minimum conflict degree bidding operator, the efficiency-first bidding operator, and the random bidding operator. This section introduces each of these four operators.

(1) Maximum Weight Bidding Operator: The maximum weight bidding operator refers to the process where the main process sorts the tasks in the task pool in descending order based on task weight, and then sequentially bids the sorted tasks to the child processes. This operator is a greedy operator that prioritizes scheduling tasks with higher weights, which helps achieve the goal of maximizing the scheduling task’s benefit.

(2) Minimum Conflict Degree Bidding Operator: The conflict degree evaluates how much a task conflicts with other tasks. Referring to the definition in the referenced paper [28,45], as shown in the Figure 4, $[a_1,b_1]$ and $[a_2,b_2]$ represent overlapping available transmission time windows, where $a_1$ and $a_2$ are the earliest start times, and $b_1$ and $b_2$ are the latest end times. The colored dashed lines indicate the start times of transmission activities. The conflict degree value is defined as the ratio of the shaded area to the area of the closed rectangle ABCD. This represents the conflict degree of a task within a single available time window, and the task’s conflict degree is defined as the average conflict degree across all its available windows.

The Minimum Conflict Degree First Bidding Operator prioritizes bidding the tasks with the least conflict degree to the child processes. On one hand, tasks with lower conflict degrees have less impact on subsequent tasks, and on the other hand, this increases the chances of successfully scheduling the current task.

(3) Efficiency First Bidding Operator: The efficiency e is defined as the ratio of the task’s time slot length to the task’s weight. It measures the contribution to the overall objective per unit length of the time slot that a task occupies, reflecting marginal utility. The specific formula for calculating efficiency is as follows:

$$e_i={\displaystyle \frac{w_i}{d_i}}$$

(24)

The efficiency first bidding operator sorts the tasks in the task pool in descending order of efficiency values and bids tasks with higher efficiency values to the child processes first. This operator fully exploits the utility of time slots by prioritizing tasks with higher marginal utility, aiming to maximize the scheduling task benefit greedily.

(4) Random Bidding Operator: The random bidding operator refers to the main process shuffling the tasks in the task pool in random order and then bidding them to the child processes according to this random sequence. This operator is a random search operator that introduces more uncertainty into the solution, which is beneficial for exploring the solution space.

3.3. Disposal Operator Pool

The EH-ACNP algorithm designs four disposal operators for sorting the task sequence: the minimum weight disposal operator, the maximum conflict degree disposal operator, the efficiency-first disposal operator, and the random disposal operator. This section introduces each of these four operators.

(1) Minimum Weight Disposal Operator: The minimum weight disposal operator means that each child process sorts the tasks assigned to it by weight and deletes the tasks with lower weights first. These tasks are returned to the main process’s task pool, and their resource usage is released. This operator temporarily removes lower-weight tasks from the solution to increase the possibility of occupying higher-weight tasks.

(2) Maximum Conflict Degree Disposal Operator: The maximum conflict degree disposal operator uses the same definition of conflict degree as described earlier. When this operator is selected, each child process deletes the task with the highest conflict degree, returns it to the main process’s task pool, and releases the resource usage.

(3) Efficiency First Disposal Operator: The efficiency first disposal operator uses the same efficiency definition as in the previous formula. It prioritizes deleting tasks with lower marginal utility to improve the weight contribution of the time slots. This operator helps increase the overall solution benefit.

(4) Random Disposal Operator: The random disposal operator means that each child process randomly deletes tasks assigned to it, in order to enhance the diversity of the solution. This method increases exploration and helps explore the solution space.

3.4. Bidding Algorithm

The bidding algorithm refers to the process in which each subprocess, upon receiving a task bidding request from the main process, develops a feasible execution plan for the task and provides the corresponding bidding price. The pseudocode of the bidding algorithm is shown in Algorithm 1; Steps 1–2 perform a preliminary validity check of the task; Steps 4–5 verify the availability of the current $vtw$; Steps 7–9 remove the time intervals in the $vtw$ that are already occupied to obtain the executable time slot set $S_a$; and Steps 10–17 generate the task execution plan while satisfying constraints such as antenna alignment and adjustment time windows. A schematic of the bidding algorithm is presented in Figure 5. Once the scheduling plan is obtained, the bidding price is calculated according to Equation (25).

$$bid=e^{-s{t}_{i,r}}·w_i$$

(25)

Algorithm 1: Bidding algorithm

3.5. Adaptive Operator Adjustment

The adaptive operator adjustment rule scores operators based on their performance, indirectly adjusting their weights. Specifically, if an operator results in the solution reaching the historical optimum during an iteration, it indicates good performance, and a higher score is rewarded. Conversely, if the operator leads to a solution worse than the previous iteration, it indicates poor performance, and its weight is reduced, resulting in a lower score.

Since each round of bidding computation generates a new solution, using a greedy approach that only accepts better solutions may easily lead to local optima. To encourage the algorithm to explore more, we adopt a simulated annealing criterion to determine whether to update the current solution, which involves gradually lowering a “temperature” parameter to balance exploration and optimization. If the new solution reaches the historical optimum, it is accepted unconditionally. If the new solution is better than the current one, it is also accepted. If the new solution is worse than the current one, the Metropolis criterion is used to accept the new solution with a certain probability [46].

Since we have designed four bidding operators and four bidding-rejecting operators, the operator scoring matrix is represented by a $4\times 4$ matrix $\mathit{Q}\in {\mathbb{R}}^{4\times 4}$, where ${\mathit{Q}}_{xy}$ represents the combination of bidding operator x and bidding-rejecting operator y, with $x,y\in \{1,2,3,4\}$, indexing the bidding and bidding-rejecting operators, respectively. In a given round of computation, if using operators x and y results in the total solution yield reaching the historical optimum, the operators are assigned a score of ${\varrho }_1$. If the solution does not surpass the historical optimum but is better than the current solution, a score of ${\varrho }_2$ is given. If the new solution is worse than the current solution but is accepted as the new solution based on the simulated annealing criterion, a score of ${\varrho }_3$ is assigned. If the new solution is worse than the current solution and is not accepted as the new solution, a score of ${\varrho }_4$ is given. The computation algorithm is as described in the Formula (26).

$${\mathit{Q}}_{xy}={\mathit{Q}}_{xy}+\varrho$$

(26)

After the operator scoring matrix is updated at regular intervals, the corresponding operator weight matrix is updated. $\mathit{G}\in {\mathbb{R}}^{4\times 4}$ represents the operator weight matrix, where ${\mathit{G}}_{xy},x,y\in \{1, 2, 3, 4\}$ are the cross weights of the operator pair, with x being the bidding operator index and y being the bidding-rejecting operator index. $\Gamma \in {\mathbb{R}}^{4\times 4}$ is the operator selection count matrix, where ${\Gamma }_{xy},x,y\in \{1, 2, 3, 4\}$, and each time an operator pair is selected, the corresponding count element ${\Gamma }_{xy}$ is incremented by 1. $\tau$ is the operator weight update cycle. After every $\tau$ updates of the operator scoring matrix, the operator weights are updated with a step size of $F_c$, and the count matrix ${\Gamma }_{xy}$ is reset. The score matrix ${\mathit{Q}}_{xy}$ undergoes a discount decay with a decay factor $\beta$, where $\overline{\mathit{Q}}\in {\mathbb{R}}^{4\times 4}$ is the normalized score matrix. The update formula is as follows:

$$\overline{\mathit{Q}}=1/\Gamma \odot \mathit{Q}$$

(27)

$$\mathit{G}=(1-F_c)\ast \mathit{G}+F_c\ast {\displaystyle \frac{\overline{\mathit{Q}}}{{\sum }_{x=1}^4{\sum }_{y=1}^4{\overline{\mathit{Q}}}_{\mathit{xy}}}}$$

(28)

$$\mathit{Q}=\beta \ast \mathit{Q}$$

(29)

3.6. Algorithm Complexity Analysis

The time complexity of one round of bidding is as follows: For Algorithm 1, its time complexity is $O\left(\left|VTW\right| \times |S_a|\right)$. The value of $\left|VTW\right|$ is related to the simulation cycle length, not the problem size, and is relatively small and finite. The value of $|S_a|$ is also finite and does not increase with the problem size, so the time complexity can be considered $O\left(1\right)$. For Algorithm 2, its time complexity is $O\left(\right|OTW|+|N_C\left|\right)$, where the upper bound of $\left|OTW\right|$ is the total number of tasks $\left|T\right|$, and the upper bound of $|N_C|$ is also $\left|T\right|$. Therefore, the complexity of the bidding algorithm is $O(2\times |T\left|\right)$. In one round of bidding, tasks need to be sorted, which has a time complexity of $O\left(\right|T|\times log|T\left|\right)$. Thus, the total complexity is $O(2\times |T|+|T|\times log|T\left|\right)$.

Algorithm 2: Function FSWA: fetch available slots within window

For the disposal phase, tasks need to be sorted, which has an upper time complexity of $O\left(\right|T|log|T\left|\right)$. A certain proportion of tasks need to be discarded, and the time complexity for this operation is $O(a\times |T\left|\right)$, The overall time complexity of the pruning phase is $O\left(\right|T|\times log|T|+a\times |T\left|\right)$.

The total time complexity of one round of computation is $O(2\times |T|+|T|\times log|T|+|T|\times log|T|+a\times |T\left|\right)\approx O\left(\left|T\right|log\left|T\right|\right)$, and considering the number of generations, the overall time complexity of the proposed algorithm is $O(l_{max}\times |T|log|T\left|\right)$.

4. Simulation Analysis

This section establishes simulation scenarios to validate and analyze the dynamic DRS scheduling problem and the algorithm. The EH-ACNP is compared with current advanced dynamic DRS scheduling algorithms, tested in scenarios of large-scale task arrivals and temporary resource failures. A sensitivity analysis of the EH-ACNP is also conducted to test its robustness.

4.1. Simulation Scenario Setup

The experimental simulation scenario consists of a DRS network made up of 12 DRSs and 29 RSSs, used to validate the proposed algorithm. The parameters of the DRS are as follows: The DRSs are located in geostationary Earth orbit at nominal longitudes of ${98}^{°}$ W, ${75}^{°}$ W, ${65}^{°}$ W, $0^{°}$, ${17}^{°}$, ${53}^{°}$ E, ${65}^{°}$ E, ${75}^{°}$ E, ${85}^{°}$ E, ${90}^{°}$ E, ${102}^{°}$ E, and ${110}^{°}$ E, and are labeled as R1–R12. The parameters for the RSS are based on the Spire satellite orbital data from the CelesTrack website, comprising a total of 29 RSSs. The simulation period is from 12:00:00 on 23 June 2024 to 12:00:00 on 24 June 2024, the link simulation parameters are as in

Table 2. Communication link calculation parameters.

Parameters	f	${\mathit{P}}_{\mathit{max}}$	${\mathit{R}}_{\mathit{g}}$	${\mathit{G}}_{\mathit{g}}^{\mathit{R}}$	${\mathit{G}}_{\mathit{l}}^{\mathit{\tau }}$	${\mathit{\theta }}_{\mathit{min}}$	${\mathit{\vartheta }}_1$	${\mathit{\vartheta }}_2$
Value	$14.2$ GHz	$42.8$ dBm	$-40$ dBm	$34.2$ dB	$42.8$ dB	${10}^{\circ }$	60 s	60 s

, and the link calculations are implemented using the Skyfield v1.47 in Python 3.12.

The initial task scenarios are designed with four different static task scales: 400, 600, 800, and 1000 tasks. The initial task schedules, labeled C1 to C4, are generated using a known efficient algorithm-adaptive variable neighborhood descent algorithm combined with tabu search [28].

To verify the effectiveness of the proposed algorithm in the context of DRS task scheduling under large-scale dynamic burst task disturbances, 100 to 1000 additional task test cases were designed for each of the four static initial scenario sets, resulting in a total of 40 test cases.

The task generation method follows the approach by Li et al. [29], using a normal distribution. The task service time window length has a mean of 5600 s and a standard deviation of 900 s, while the task execution duration has a mean of 540 s and a standard deviation of 360 s.

To verify the effectiveness of the proposed algorithm in a DRS scheduling scenario where DRS resources fail due to external environmental factors, 10 different test cases were created in the C4 scenario, where the static task count is set to 1000. The specific settings for the test scenarios are as

Table 3. Experimental setup for resource disturbance test scenarios.

Experiment ID	Original Test Case	Faulty Resource ID
E1	C4	R1, R3, R7
E2	C4	R2, R6, R9
E3	C4	R3, R4, R10
E4	C4	R2, R4
E5	C4	R6, R8
E6	C4	R1, R7
E7	C4	R5, R9
E8	C4	R1
E9	C4	R3
E10	C4	R5

.

Based on previous research on dynamic resource scheduling for DRSs, the proposed algorithm in this paper is compared and analyzed with four other algorithms: Earliest Deadline First Greed Search (GS) [47], the Improved Contract Net Algorithm (HMCNP) [36], the Preemptive Dynamic Scheduling Algorithm (PDSA) [15], and the Whole Rescheduling Algorithm (WAR) [48].

All algorithms were executed on a computer with a 13th Gen Intel^® Core™ i7-13700 processor at 2.10 GHz and 16 GB of RAM. The algorithms were implemented using Python 3.12. To ensure the reliability of the experimental results, each experiment was repeated 20 times, and the mean and standard deviation of the 20 trial results were calculated.

The EH-ACNP algorithm parameters are divided into two parts: the simulated annealing section and the operator weight management section. The simulated annealing section follows classic parameter settings [49], while the remaining parameters are set as shown in

Table 4. EH-ACNP algorithm parameters.

Parameters	Value
${\varrho }_1$	4
${\varrho }_2$	2
${\varrho }_3$	1
${\varrho }_4$	0.5
$F_c$	0.2
$\beta$	0.2
Maximum iterations	100
Maximum iterations without solution updates	5
Strategy update interval	1

.

4.2. Comparative Analysis of Experiments

4.2.1. Comparative Experiment of Large-Scale Temporary Task Arrivals

Table 5. Numerical results of scheduling benefits under different Burst tasks in test scenario C1.

Number of Burst Tasks	EH-ACNP	GS	PDSA	HMCNP	WAR
100	2305.29	2215.75	2223.21	2275.43	2230.65
200	2833.64	2684.39	2691.85	2818.71	2744.09
300	3317.23	3070.95	3093.34	3235.13	3130.65
400	3696.33	3509.76	3427.67	3569.46	3479.91
500	4067.97	3791.85	3776.92	3918.71	3761.98
600	4432.15	4148.56	4133.64	4275.43	4081.38
700	4691.85	4356.03	4311.27	4535.13	4296.33
800	5085.88	4705.30	4660.50	4876.92	4638.12
900	5330.65	4875.43	4875.43	5151.55	4860.50
1000	5530.65	5060.50	5015.73	5299.31	4978.42

presents the computational results of different algorithms for various burst tasks in the C1 scenario. The EH-ACNP achieved the highest revenue in all experimental groups, with an average revenue improvement of 3.10% compared to the latest HMCNP algorithm. Figure 6 shows the dynamic scheduling solution revenue error bar plot for the EH-ACNP and other comparison algorithms under different burst task scales in test scenario C1. The dots represent the average revenue from repeated experiments in this scenario, and the bars above the dots represent the error. From the figure, it can be observed that the EH-ACNP outperforms the four other algorithms, including the PDSA, in terms of revenue. In scenarios with small-scale task surges, the EH-ACNP maintains a slight advantage, and as the task scale increases, the advantage of the EH-ACNP over the other comparison algorithms grows. This indicates that the EH-ACNP performs excellently in large-scale task burst scenarios. By observing the length of the error bars, it can be seen that the EH-ACNP has shorter error bars compared to the comparison algorithms, indicating that the algorithm performs more stably.

Additionally, Figure 7, Figure 8, and Figure 9 present the results under the initial scenarios C2, C3, and C4, respectively. It can be observed that in cross-scenario comparison experiments, the EH-ACNP consistently achieves the best performance among the various algorithms, demonstrating that the EH-ACNP is adaptable across different scenarios.

The revenue calculation method is a weighted combination of the solution disturbance factor and scheduling revenue. A higher solution revenue indicates that the total weight of the scheduled tasks is maximized, and the solution disturbance is relatively small. This shows that the EH-ACNP can achieve the goal of maximizing task execution weights with minimal adjustments across different dynamic task arrival scenarios.

In summary, GS, due to its greedy search strategy, is prone to becoming trapped in local optima and struggles to find globally optimal solutions. The PDSA prioritizes the scheduling of the earliest-arriving tasks, which helps ensure the execution of high-opportunity tasks but, similarly, faces challenges in escaping local optima. The WAR achieves optimization by globally rescheduling all tasks; however, this results in significant disruption to the original plan, reducing its stability. The HCMCNP, based on the CNP, demonstrates strong coordination capabilities in distributed scheduling and performs better than the aforementioned approaches. Nevertheless, its limitation to a single negotiation round constrains its search depth in the solution space, thereby limiting its optimization capacity.

In contrast, the EH-ACNP algorithm proposed in this study leverages a multi-round collaborative negotiation mechanism, allowing for the flexible exploration of better task assignments among multiple DRSs. This design enhances its ability to avoid local optima. Furthermore, by integrating multiple scheduling strategies with adaptive adjustment capabilities, the algorithm significantly improves system adaptability and scheduling effectiveness under dynamic disturbances. As a result, it can more effectively approximate optimal solutions and demonstrates superior scheduling quality and robustness.

4.2.2. Comparative Experiment of Temporary Resource Failure

Figure 10 presents the computational simulation results of the EH-ACNP compared with GS, the PDSA, the HMCNP, and the WAR across 10 different resource failure scenarios (E1–E10). As shown in the figure, the EH-ACNP and HMCNP algorithms, which adopt a contract net framework, demonstrate a significant advantage over the PDSA, the WAR, and GS. This advantage stems from the contract net framework’s ability to coordinate task allocation among satellites through negotiation, making it more suitable for dynamic scheduling.

In contrast, the PDSA prioritizes tasks with higher scheduling weights, which can easily lead to local optima and hinder effective solution space exploration. GS schedules tasks based on the earliest deadline first, ensuring that the most time-critical tasks are prioritized. This approach helps prevent highly flexible tasks from occupying resources too early, thereby reducing the risk of unschedulable tasks and improving task completion rates to some extent.

The WAR, on the other hand, reschedules the entire plan, which, while potentially leading to a more optimized schedule, significantly alters the initial plan. This drastic adjustment disrupts ongoing or already-prepared tasks, making it impractical for real-world engineering applications.

The EH-ACNP, utilizing contract net-based negotiation, makes incremental adjustments to the schedule, exploring the solution space and increasing the likelihood of finding a better solution. This makes it a reliable approach for dynamic DRS scheduling.

4.3. Sensitivity Analysis Experiment

This section presents a sensitivity analysis of the task disposal rate parameter in the algorithm, conducted under the C4 test scenario. The results are shown in Figure 11. The figure illustrates the variation in scheduling yield as the disposal rate increases from 0.1 to 0.5, with the shaded area representing the standard deviation of multiple independent runs at each disposal rate. Overall, the scheduling yield increases with the disposal rate and levels off in the higher range, exhibiting a clear diminishing marginal return. A low disposal rate limits the algorithm’s exploration and re-optimization capabilities, resulting in insufficient performance and higher variability. In contrast, a high disposal rate maintains a good average yield but offers no significant improvement in gains and may introduce additional computational and negotiation overhead.

Notably, as the disposal rate increases, the standard deviation decreases significantly and stabilizes around 0.18, while reaching its maximum at 0.26, indicating that this range not only improves yield but also enhances solution stability. Considering yield improvement, stability, and computational cost, we recommend setting the disposal rate in the range of 0.18–0.26 under typical load conditions to achieve a better balance between exploration capability and solution stability.

5. Conclusions

This paper investigates the dynamic resource scheduling problem for DRSs, aiming to maximize task completion benefits while minimizing disruptions to the initial schedule. To achieve these objectives, a weighted objective function is employed, considering constraints such as task-resource allocation limitations and link connectivity. A method named EH-ACNP is designed to solve the problem, This method utilizes a multi-round combinatorial auction mechanism for task negotiation and allocation, while integrating dynamic scheduling strategies to improve the algorithm’s adaptability in dynamic environments. The experimental results demonstrate that in real-world scenarios involving unexpected task arrivals and sudden resource failures, the proposed algorithm outperforms existing approaches by achieving superior scheduling outcomes, maximizing task execution benefits while minimizing disruptions to the original plan. Sensitivity analysis further reveals that the algorithm maintains a stable performance under appropriate task disposal rates.

Although the EH-ACNP method shows strong optimization capability in dynamic resource scheduling for data relay satellites, its validation has been limited to a simulation platform and has not yet been tested at an engineering level on-board or in hardware-in-the-loop environments. Future work will validate its real-time performance and applicability in actual hardware or hybrid simulation environments and extend its application to energy power systems and unmanned aerial vehicle task optimization.