Research on Parameter Prediction Model of S-Shaped Inlet Based on FCM-NDAPSO-RBF Neural Network
Abstract
1. Introduction
2. Structural Coupling Design of S-Shaped Inlet Considering Stealth Performance
2.1. The Total Pressure Recovery Coefficient of Inlet
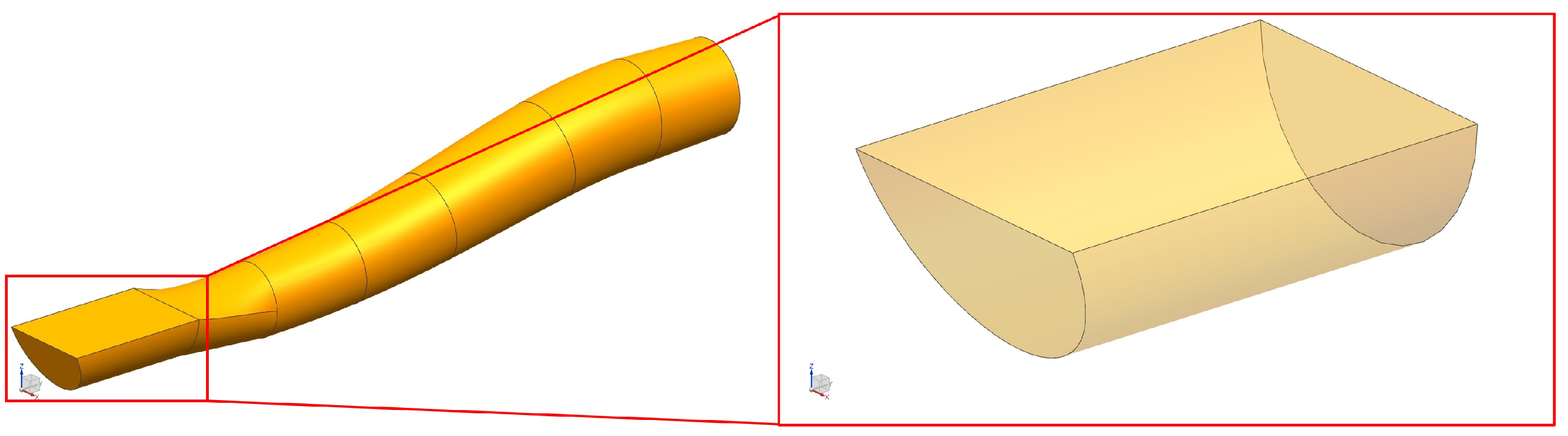
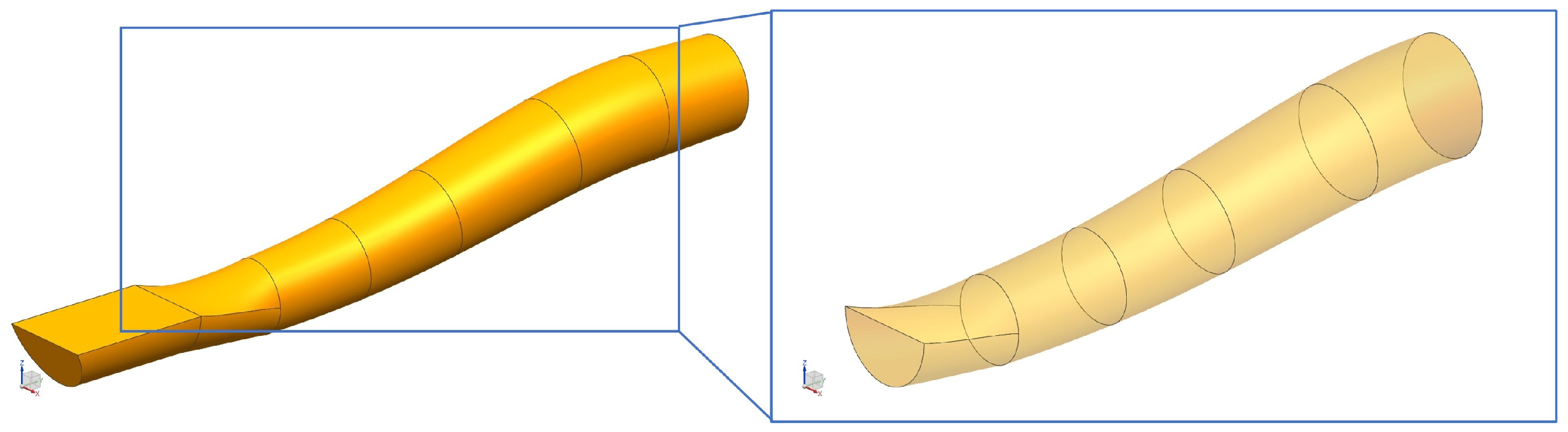
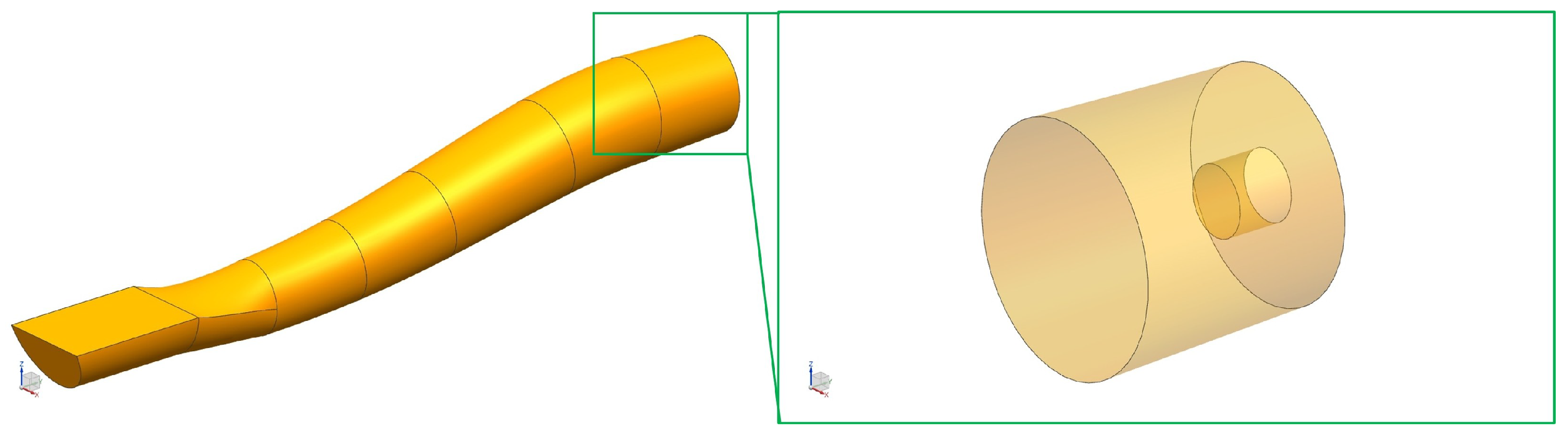
2.2. The S-Shaped Inlet
3. Nonlinear Dynamic Adaptive Particle Swarm Optimization Algorithm
3.1. Standard Particle Swarm Optimization
3.2. Improved Particle Swarm Optimization
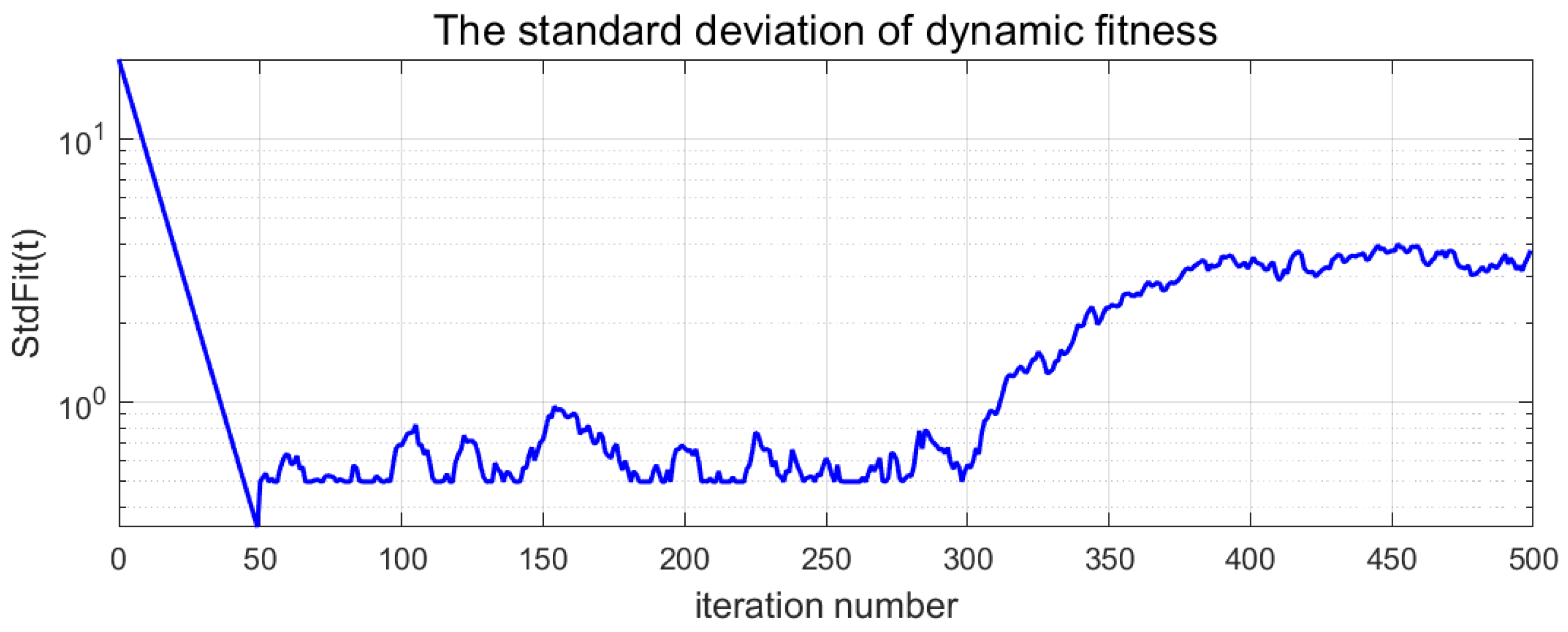
3.3. Dynamic Fitness Standard Deviation Based on Population Convergence State
3.4. Dynamic Adaptation Factor Based on Inertia Weight Change
| Algorithm 1 Nonlinear dynamic adaptive particle swarm optimization algorithm |
| Require: Swarm size N, dimension D, max iterations Require: , , velocity limit Ensure: Global best solution
|
4. Inlet Data Prediction Based on FCM-NDAPSO-RBF Neural Network
4.1. Sample Data Processing
4.2. FCM Based on Feature Vector
4.3. Analysis of Clustering Number
4.4. Radial Basis Function Neural Network
4.5. NDAPSO-RBF Neural Network
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of Symbols
| Total pressure recovery coefficient | |
| Total pressure of the outlet airflow of the inlet | |
| Total pressure of the free unperturbed airflow | |
| The maximum value of the total pressure of the airflow at the outlet section of the inlet | |
| The minimum value of the total pressure of the airflow at the outlet section of the inlet | |
| The average total pressure of the total area of the inlet outlet | |
| The distortion coefficient | |
| Q | The air quality flow |
| The fluid density | |
| A | The size of the corresponding cross-sectional area |
| The longitudinal coordinate of center line of the diffuser | |
| H | The longitudinal offset of the diffuser |
| The transverse coordinate of the diffuser centerline | |
| The length of the diffuser | |
| The inlet area of the diffuser | |
| The outlet area of the diffuser. | |
| The individual optimal solution | |
| The global optimal solution | |
| The velocity of the particle i at the iteration k | |
| w | Inertia weight in PSO |
| , | Learning factor |
| , | Random numbers |
| The individual optimal position of the particle i | |
| The globa optimal position of the particle i | |
| The position of the particle i at the iteration k | |
| The fixed inertia weight | |
| The time-varying inertia weight | |
| , | The maximum and minimum inertia weights |
| The maximum number of iterations | |
| t | The current number of iterations |
| The population evolution fitness index function | |
| The standard deviation of the fitness of the current population particles | |
| The random disturbance term | |
| The random disturbance term | |
| The random disturbance term | |
| D | The goodness of fit between the particle position distribution and the normal distribution |
| The nonlinear feature mapping activation function | |
| b | The fixed adaptation factor |
| Δ w | Amplitude |
| g | Global best position |
| The time-varying adaptation factor | |
| R | The diffusion radius |
| The later oscillation energy | |
| The medium-term oscillation energy | |
| B | The sample data |
| The clustering sample before normalization | |
| The minimum value in the clustering sample | |
| The maximum value in the clustering sample | |
| The normalized clustering sample | |
| The inverse normalized predictive value | |
| The normalized predictive value | |
| J | The objective function |
| c | The number of clusters |
| c | The number of clusters |
| m | The fuzzy coefficient |
| The membership degree of the sample j in the class i | |
| The central distance between the two points of the sample j and the cluster center i | |
| Input contraction mapping | |
| The cluster center | |
| modulus | |
| The similarity relationship between the i-th cluster and the j-th cluster | |
| The intra-cluster diameter of the i-th cluster | |
| The average of all cluster similarities | |
| The tightness within each data point cluster and the separation between clusters | |
| The average distance between each data point and all other points in the cluster | |
| The average distance between each data point and all points in the nearest neighbor cluster | |
| RBF activation function | |
| The extended width factor | |
| The connection weight from the hidden layer | |
| The center position of the hidden layer node | |
| e | The output bias |
| Diffusion interval | |
| FCM | Fuzzy C-Means |
| PSO | Particle Swarm Optimization |
| NDAPSO | Nonlinear Dynamic Adaptive Particle Swarm Optimization |
| RBF | Radial Basis Function |
| RBFNN | Radial Basis Function Neural Network |
| RMSE | Root Mean Square Error |
| RANS | Reynolds Averaged Navier–Stokes Equation |
| AMPC | Adaptive Model Predictive Control |
| LDIW | Linear Decreasing Control Strategy |
| DB | DB Value |
| CH | CriterionValue |
References
- Xiang, G.; Hong, Z.; Wenjian, D.; Jiaqi, W. Investigation of Aerodynamic and Electric Scattering Characteristics of Double S-shaped Intake with Different Inlet Shapes. Comput. Simul. 2018, 35, 35–39. [Google Scholar]
- Zeng, L.; Hu, J.; Pan, D.; Li, J.; Shao, X. Multi-points and multi-objective optimization design of subsonic UAV S-shaped inlet. J. Propuls. Technol. 2021, 42, 495. [Google Scholar]
- Liu, X.; Liu, W.; Zhao, Y. Navier–Stokes predictions of dynamic stability derivatives for air-breathing hypersonic vehicle. Acta Astronaut. 2016, 118, 262–285. [Google Scholar] [CrossRef]
- Belaidouni, H.; Samardžić, M.; Živković, S.; Kozić, M. Computational fluid dynamics and experimental data comparison of a missile-model roll derivative. J. Spacecr. Rocket. 2017, 54, 672–682. [Google Scholar] [CrossRef]
- Ronch, A.D.; Vallespin, D.; Ghoreyshi, M.; Badcock, K. Evaluation of dynamic derivatives using computational fluid dynamics. AIAA J. 2012, 50, 470–484. [Google Scholar] [CrossRef]
- Liu, J.; Li, C.; Teng, P.; Tang, B.; Cao, Y. Actual-Calibration Technique of Gas Flowmeters in Inlet Wind Tunnel Test. J. Propuls. Technol. 2023, 44, 174. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, Y. Data-driven exhaust gas temperature baseline predictions for aeroengine based on machine learning algorithms. Aerospace 2022, 10, 17. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, J.; Cheng, J.; Xiang, H. Aerodynamic optimization of transonic rotor using radial basis function based deformation and data-driven differential evolution optimizer. Aerospace 2022, 9, 508. [Google Scholar] [CrossRef]
- Zhang, Y.; Zheng, H.; Xu, J.; Wang, Z. Radial basis function model-based adaptive model predictive control for trajectory tracking of a clapping-wing micro air vehicle. Aerospace 2023, 10, 253. [Google Scholar] [CrossRef]
- Wei, J.; Zheng, Q.; Yan, W.; Jiang, B. Dynamic particle swarm optimization-radial function extremum neural network method of HCF probability analysis for compressor blade. Int. J. Fatigue 2023, 176, 107900. [Google Scholar] [CrossRef]
- Wu, Y.; Sun, G.; Tao, J. An improved multi-objective particle swarm optimization method for rotor airfoil design. Aerospace 2023, 10, 820. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings, IEEE World Congress on Computational Intelligence (Cat. No. 98TH8360), Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Li, R.; Guo, Y.; Nguang, S.K.; Chen, Y. Takagi-Sugeno fuzzy model identification for turbofan aero-engines with guaranteed stability. Chin. J. Aeronaut. 2018, 31, 1206–1214. [Google Scholar] [CrossRef]
- Pan, M.; Wang, H.; Huang, J. T–S Fuzzy Modeling for Aircraft Engines: The Clustering and Identification Approach. Energies 2019, 12, 3284. [Google Scholar] [CrossRef]
- Zheng, R.; Qi, K.; Zhang, Q.; Xiao, Z.; Liu, H. Integrated investigation of aerodynamic shape and stealth performance for supersonic vehicle with “X” sawtooth lip inlet. J. Propuls. Technol. 2017, 38, 2471. [Google Scholar]
- Yu, X.; Zhao, M. A study on stealth technology in UAV inlet design. Flight Dyn.-Xian 2007, 25, 69. [Google Scholar]
- Shi, L.; Guo, R. Electromagnetic scattering of a submerged inlet. Acta Aeronaut. Et Astronaut. Sin. 2008, 29, 1098–1104. [Google Scholar]
- Lee, C.; Boedicker, C. Subsonic diffuser design and performance for advanced fighter aircraft. In Proceedings of the Aircraft Design Systems and Operations Meeting, Colorado Springs, CO, USA, 14–16 October 1985; p. 3073. [Google Scholar]
- Zhang, J.; Zhan, H.; Mi, B. Study on Aerodynamic Design of the Front Auxiliary Inlet. Aerospace 2023, 10, 700. [Google Scholar] [CrossRef]
- Jia, W.; Li, G.; Liu, T.; Kong, Q.; Ding, S. Numerical Analysis of the Effect of S-Shaped Duct Key Geometry Parameters on the Inlet Distortion of Distributed Ducted Fans. Aerospace 2025, 12, 316. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, Z.; Xu, X. Area and centerline distribution on stealth design of S-shaped inlet. J. Syst. Simul. 2019, 30, 2999–3006. [Google Scholar]

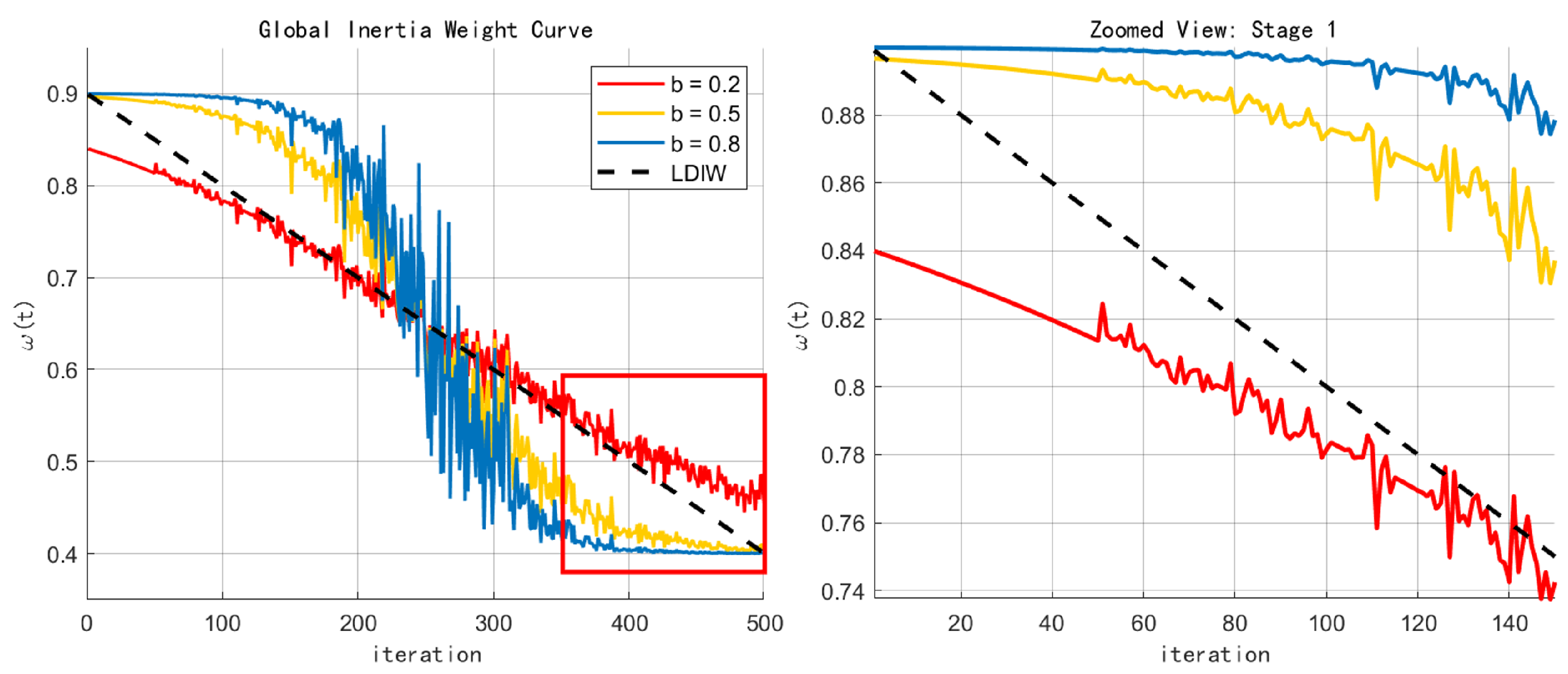
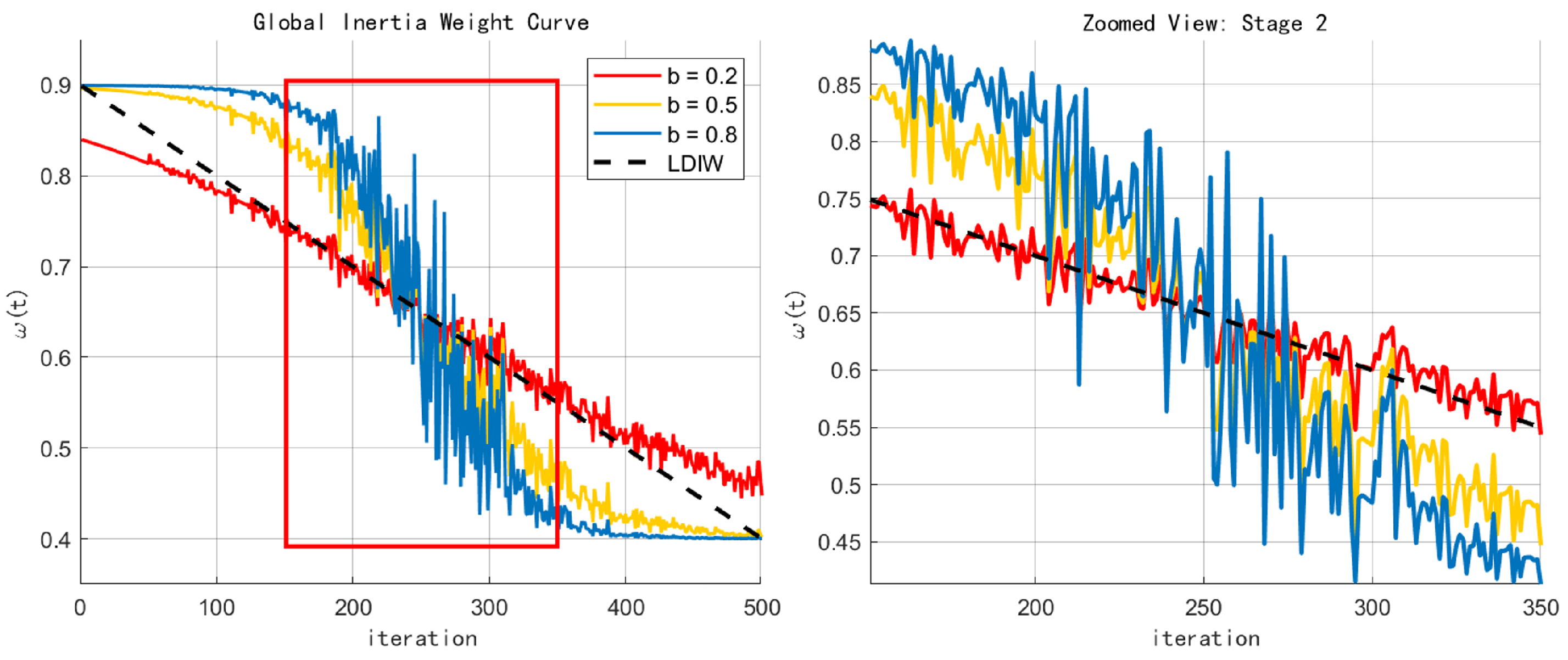
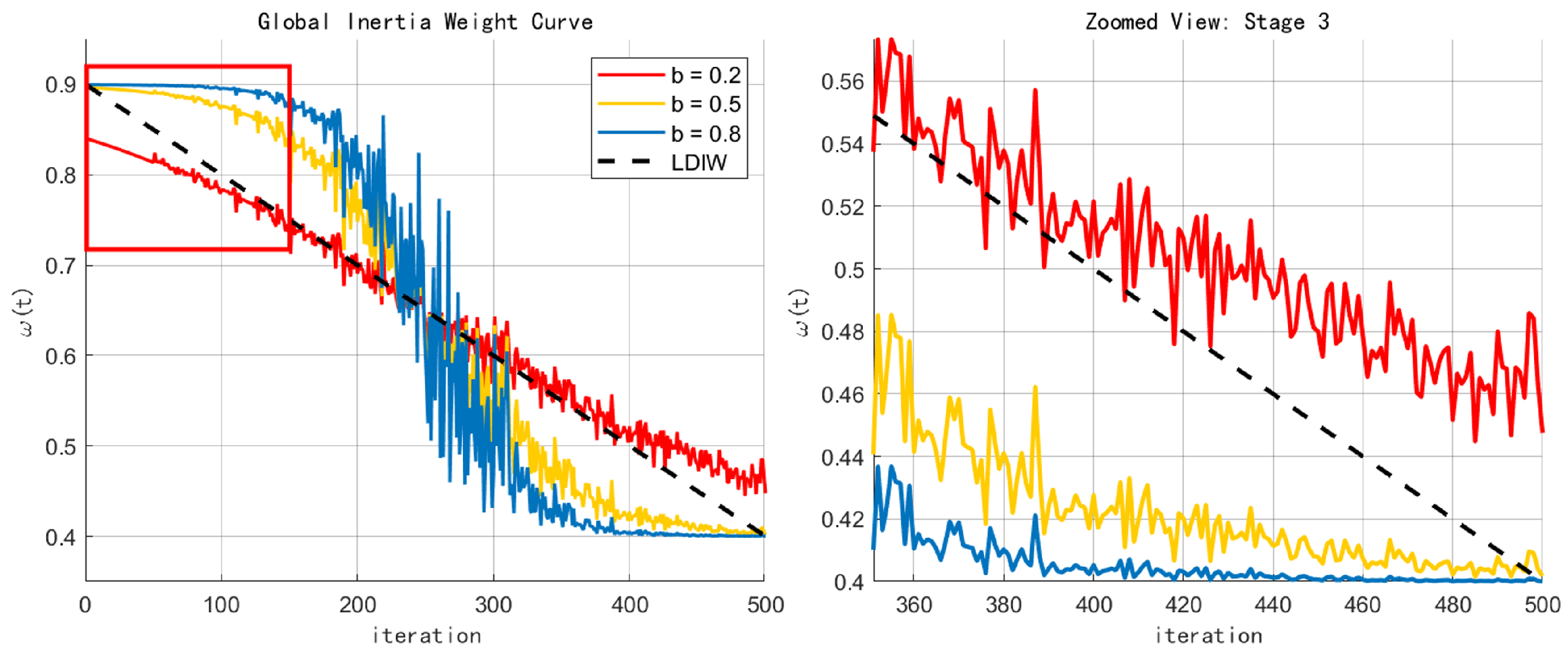
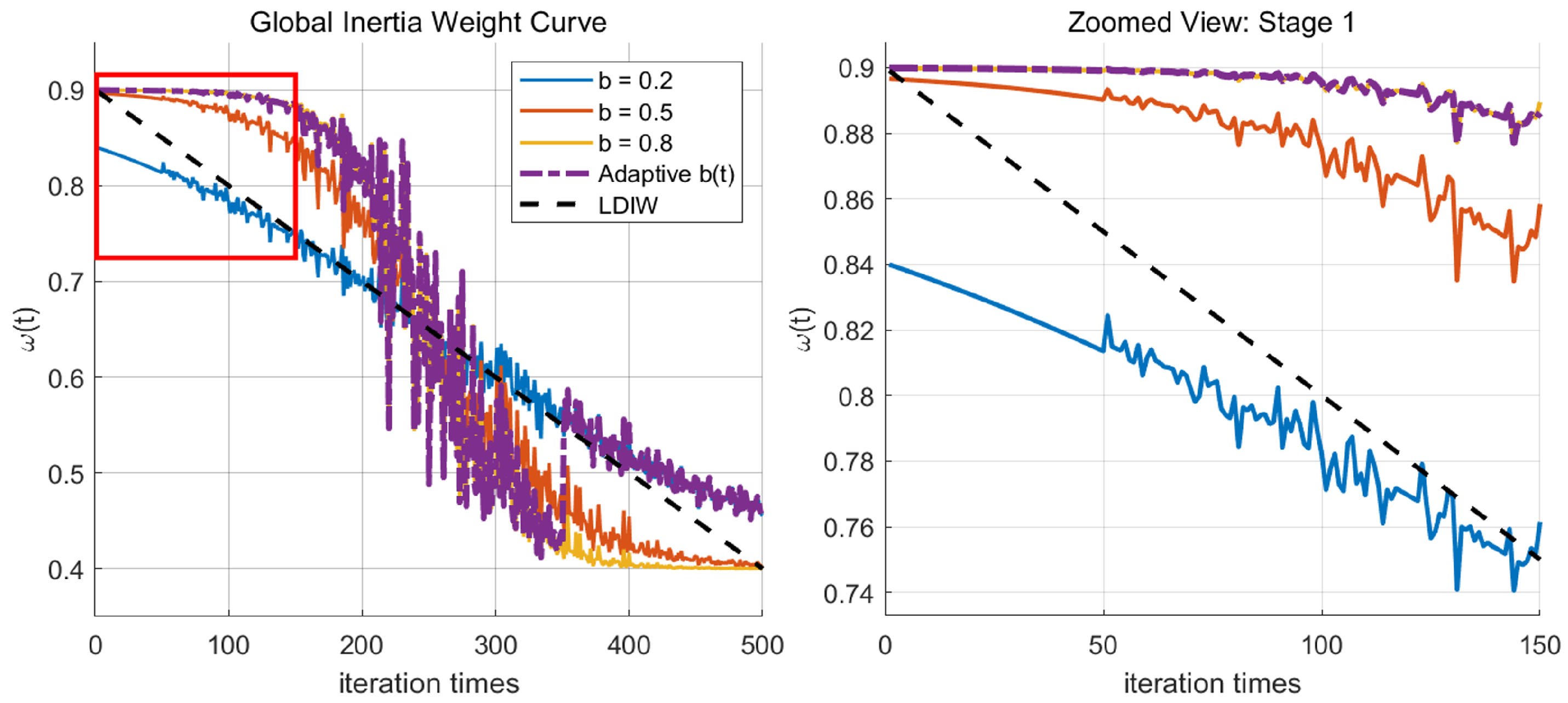
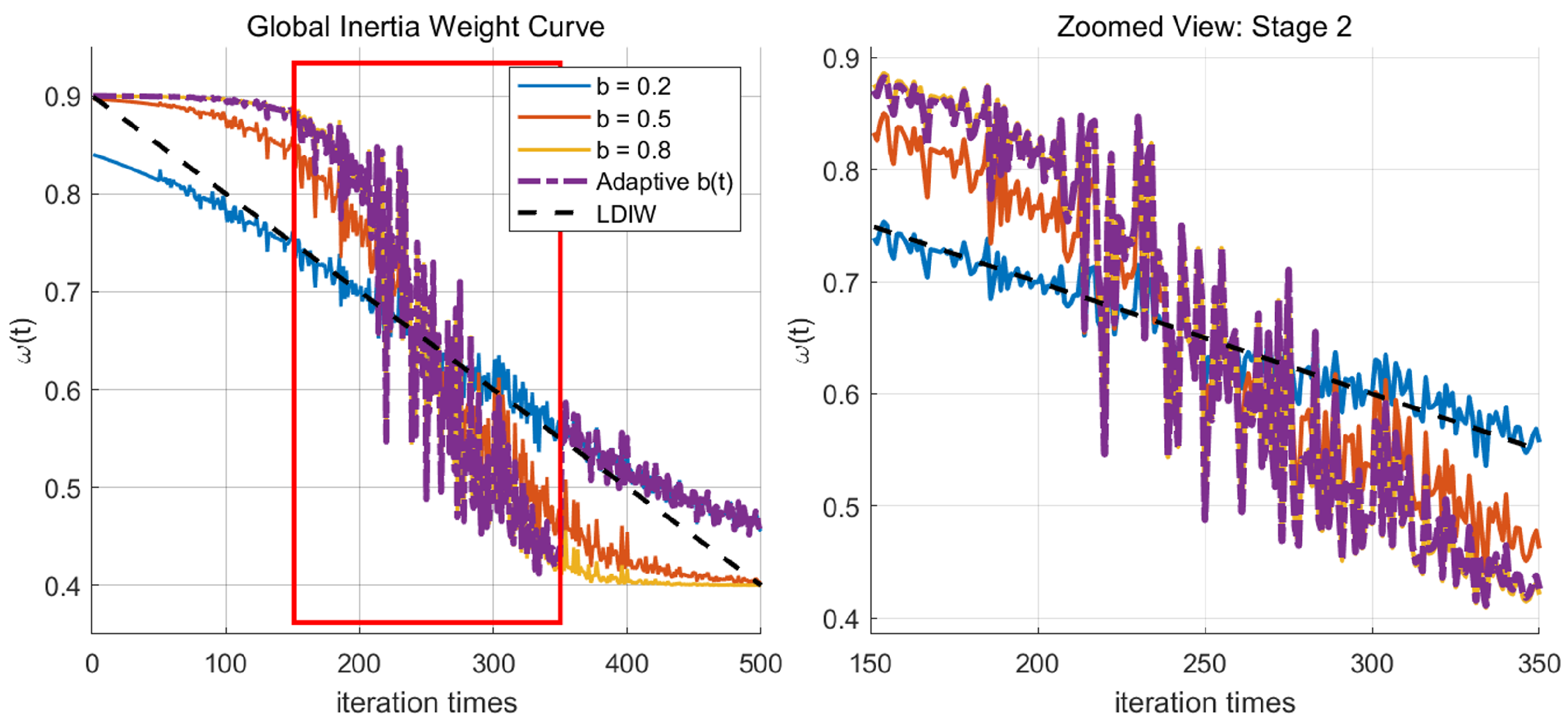
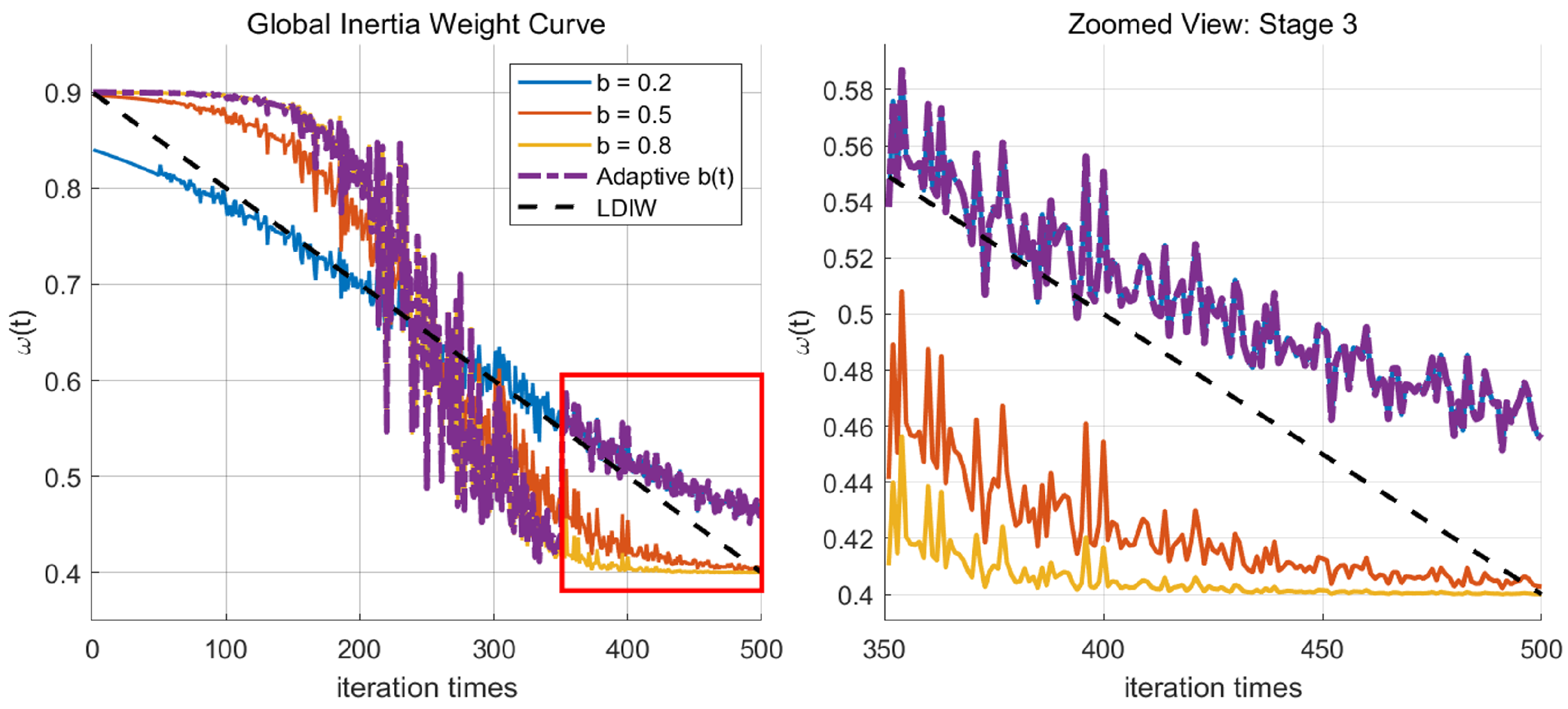


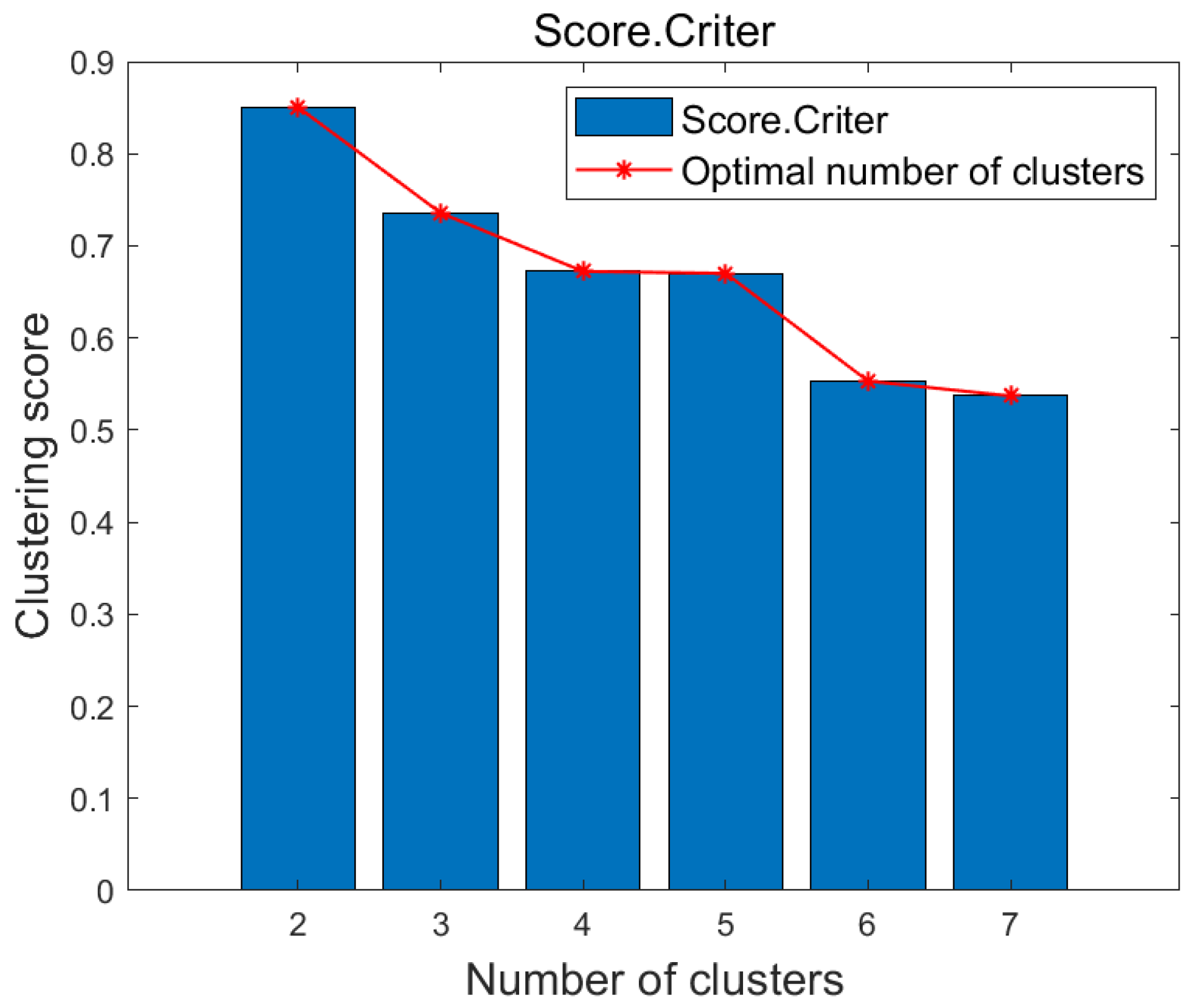
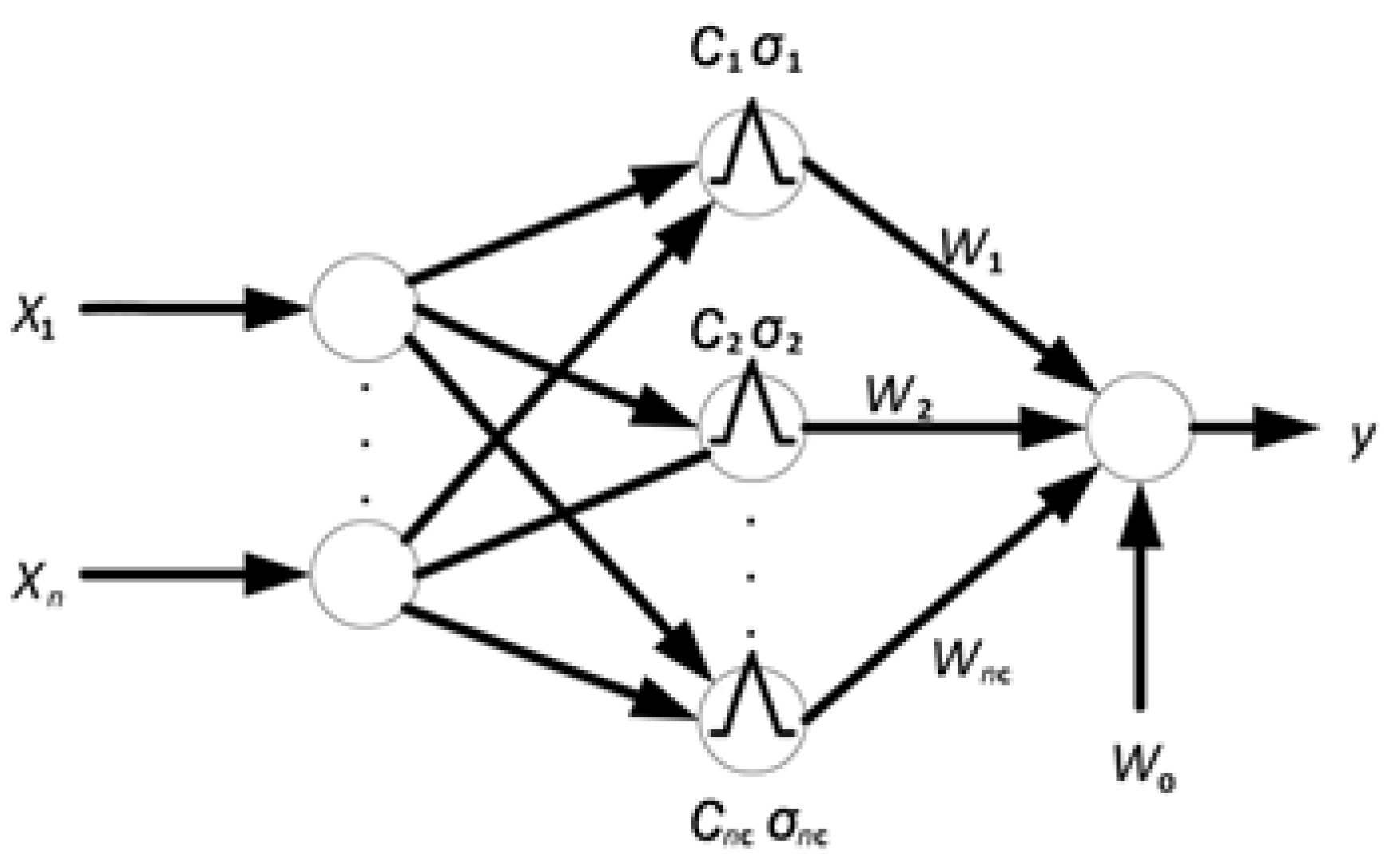

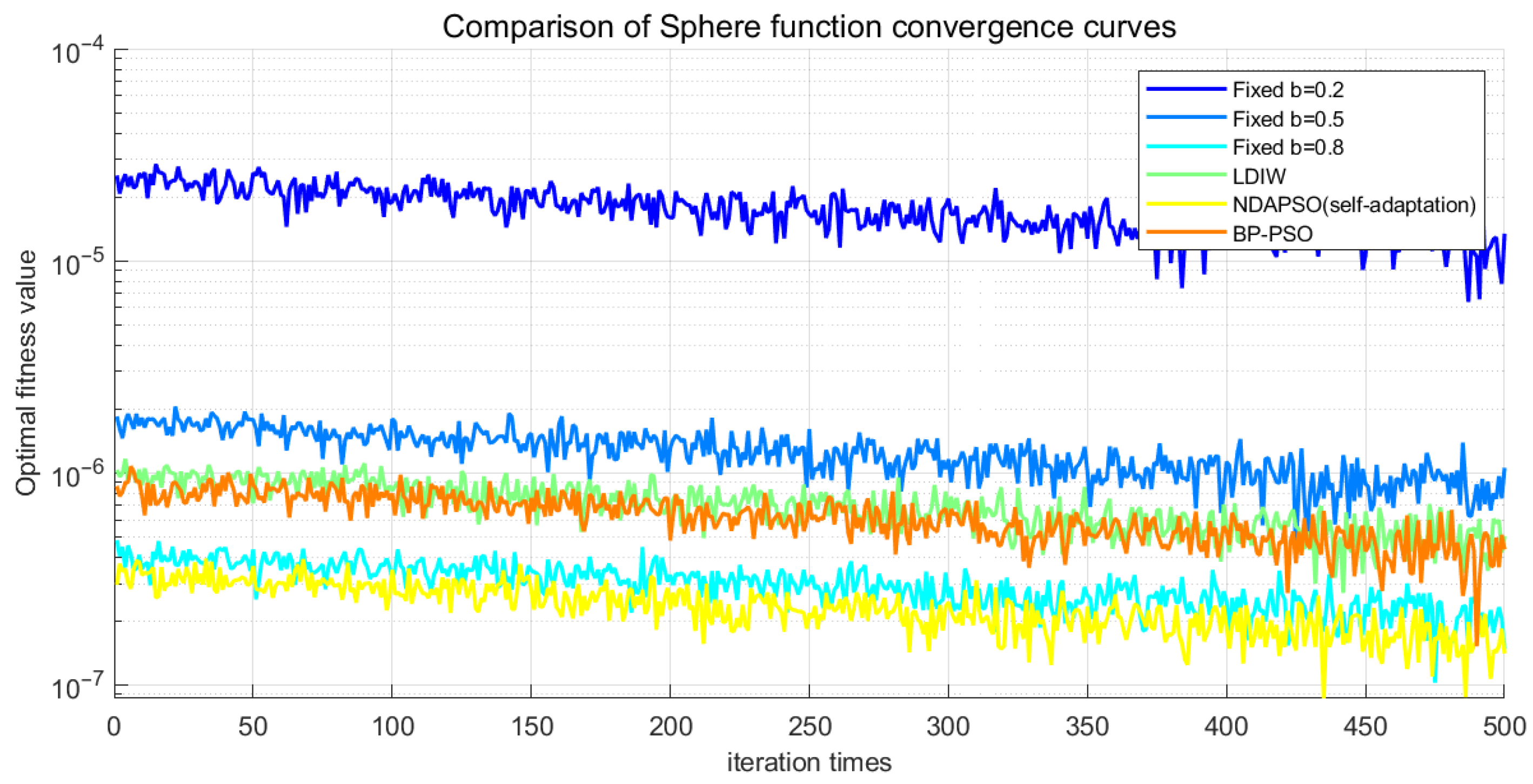

| Parameter | Average Diffusion Radius | Peak Coverage | Attenuation Rate of Inertia Weight |
|---|---|---|---|
| Parameter | Convergence Precision | Multi-Peak Success Rate | Disturbance |
|---|---|---|---|
| Parameter | Convergence Precision | Peak Coverage | Disturbance |
|---|---|---|---|
| 0 |
| Algorithm | Number of Successes | Number of Failures |
|---|---|---|
| 92 | 8 | |
| 86 | 14 | |
| 64 | 14 | |
| 71 | 29 | |
| 51 | 49 | |
| 68 | 32 |
| Number of Mesh Units | Sample Number | Characteristic Number |
|---|---|---|
| 351 | 34 | |
| 373 | 30 | |
| 569 | 57 | |
| 683 | 70 |
| Traditional PSO-BP/s | Traditional PSO-RBF/s | NDAPSO-RBF/s | Speed-Up Ratio |
|---|---|---|---|
| Item | Configuration Parameter |
|---|---|
| Operating system | Windows 11 64-Bit |
| CPU | Intel Core i7-12700H (14 Cores, 20 Threads, 2.3 GHz) (Intel, Santa Clara, CA, USA) |
| RAM | 16 GB DDR4 3200 MHz |
| GPU | NVIDIA RTX 3070 GPU (NVIDIA, Santa Clara, CA, USA) |
| Programming language/environment | MATLAB R2023a/Python 3.10 + NumPy/SciPy/PyTorch |
| Simulation algorithm running environment | MATLAB built-in function + custom function (PSO, NAPSO, BP-PSO module) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Y.; Xiao, L.; Zhang, X.; Hu, J.; Li, J. Research on Parameter Prediction Model of S-Shaped Inlet Based on FCM-NDAPSO-RBF Neural Network. Aerospace 2025, 12, 748. https://doi.org/10.3390/aerospace12080748
Wei Y, Xiao L, Zhang X, Hu J, Li J. Research on Parameter Prediction Model of S-Shaped Inlet Based on FCM-NDAPSO-RBF Neural Network. Aerospace. 2025; 12(8):748. https://doi.org/10.3390/aerospace12080748
Chicago/Turabian StyleWei, Ye, Lingfei Xiao, Xiaole Zhang, Junyuan Hu, and Jie Li. 2025. "Research on Parameter Prediction Model of S-Shaped Inlet Based on FCM-NDAPSO-RBF Neural Network" Aerospace 12, no. 8: 748. https://doi.org/10.3390/aerospace12080748
APA StyleWei, Y., Xiao, L., Zhang, X., Hu, J., & Li, J. (2025). Research on Parameter Prediction Model of S-Shaped Inlet Based on FCM-NDAPSO-RBF Neural Network. Aerospace, 12(8), 748. https://doi.org/10.3390/aerospace12080748






