Acceleration Command Tracking via Hierarchical Neural Predictive Control for the Effectiveness of Unknown Control
Abstract
1. Introduction
2. Problem Formulation
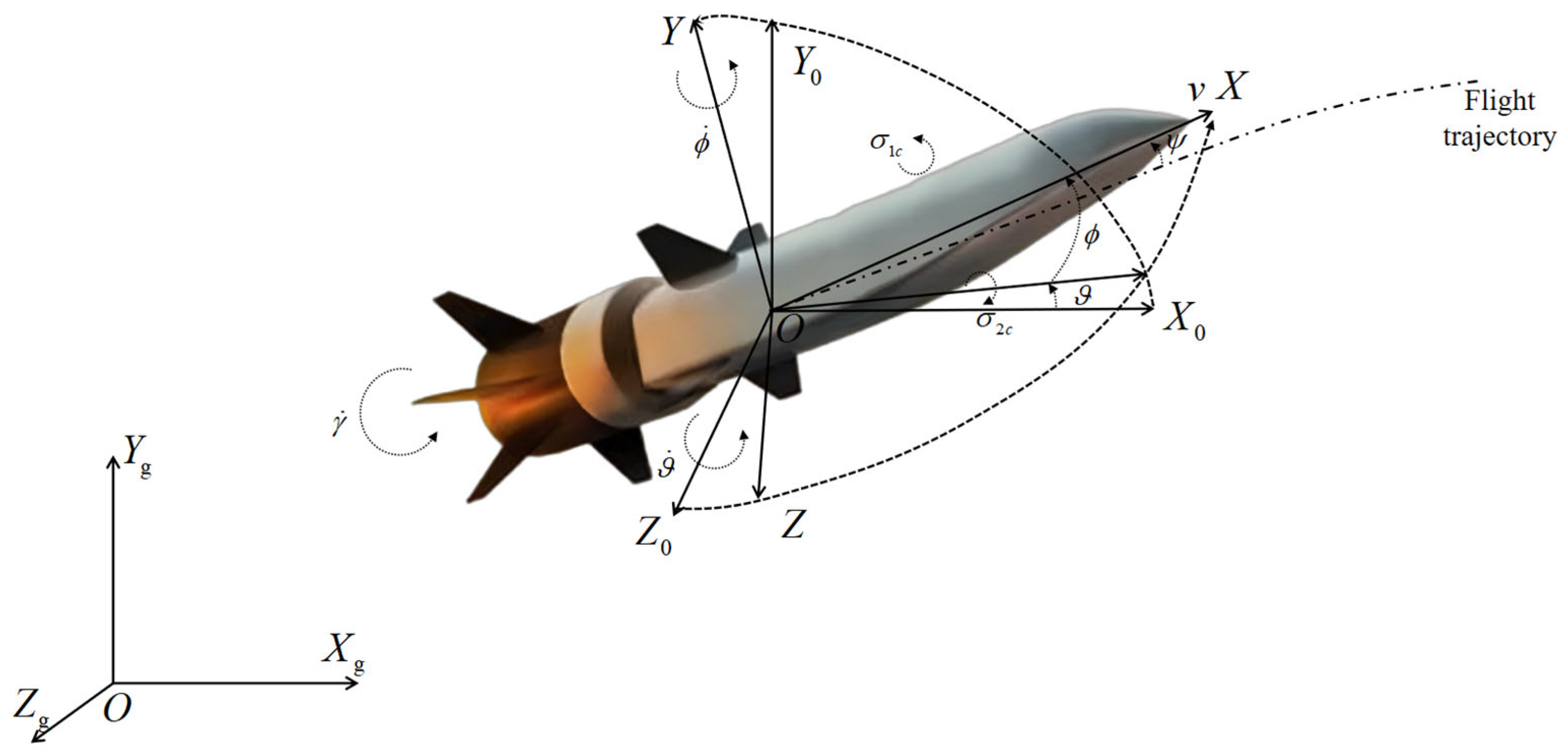
2.1. Description of the SV Dynamics Problem
2.2. Control Problem and Model Description
3. Dual-Layer Control Method Based on NN-MPC
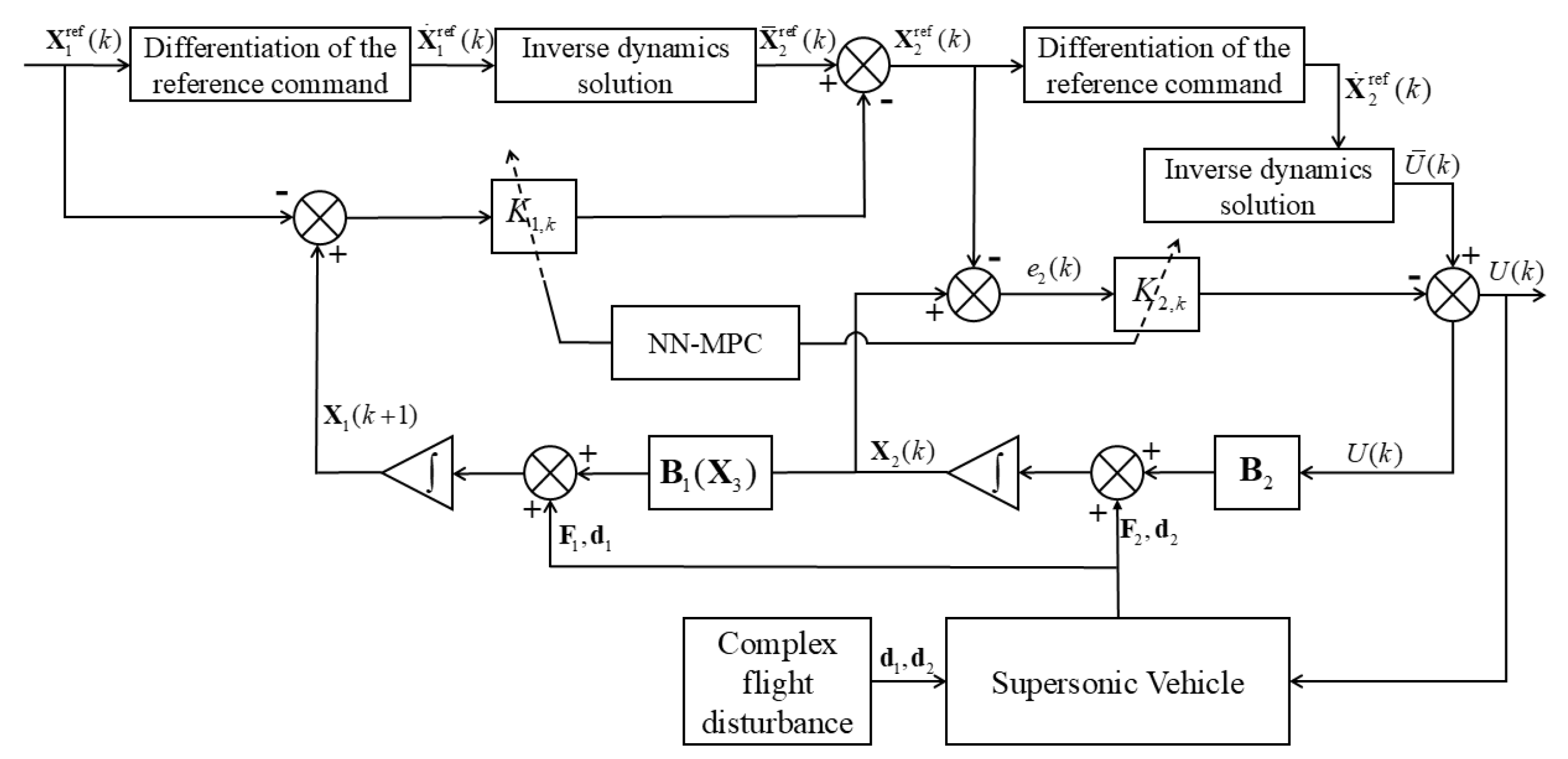
3.1. Control Framework
3.2. Neural Network Optimization
3.3. Algorithm Implementation Procedure
| Algorithm 1. Pseudo-code for the execution of the proposed method | |
| 1: | Input: |
| 2: | Output: , , |
| 3: | Initialize parameter , , , , , . Configure the algorithm parameters , etc. |
| 4: | For do |
| 5: | Acceleration subsystem |
| 6: | Calculate the acceleration error using Equation (14) |
| 7: | For do |
| 8: | Generate perturbation paths based on the transition probability , and compute using Equation (18) |
| 9: | Estimate the predicted cost through Equations (37)–(39) |
| 10: | Update the acceleration layer dataset |
| 11: | Optimize the gain using Equations (37)–(42), and generate the angular velocity virtual control quantity |
| 12: | repeat |
| 13: | Update the gain matrix of the acceleration subsystem in Step 11 |
| 14: | until optimality is achieved |
| 15: | End for |
| 16: | Angular velocity subsystem |
| 17: | Calculate the acceleration error using Equation (15) |
| 18: | For do |
| 19: | Generate perturbation paths based on the transition probability and compute using Equation (19) |
| 20: | Estimate the predicted cost through Equations (37)–(39) |
| 21: | Update the acceleration layer dataset |
| 22: | Optimize the gain using Equations (37)–(42) |
| 23: | |
| 24: | repeat |
| 25: | Update the gain matrix of the acceleration subsystem in step 22 |
| 26: | until optimality is achieved |
| 27: | End for |
| 28: | Update the system state using Equations (10)–(11) |
| 29: | End for |
4. Stability Analysis
5. Experimental Results and Analysis
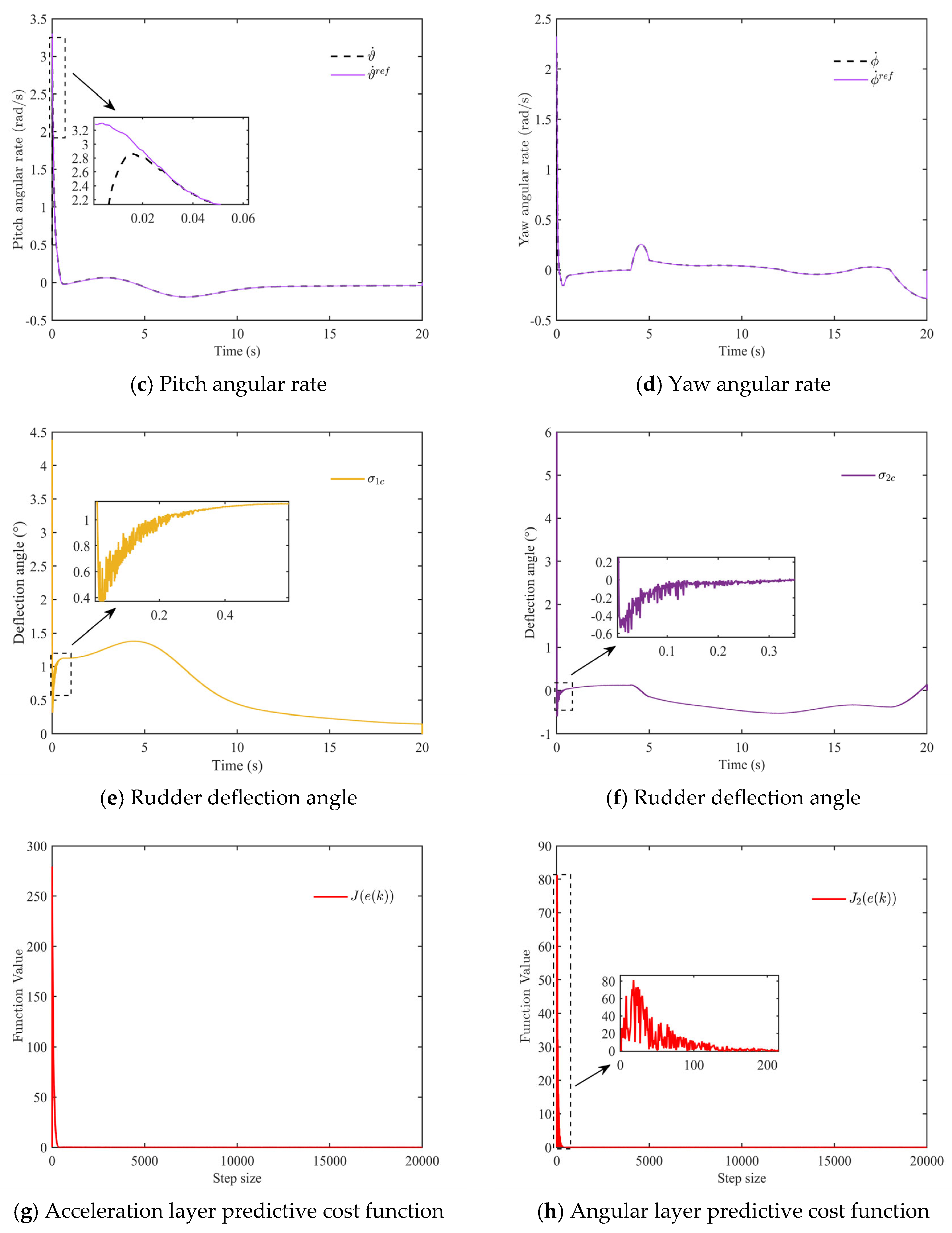
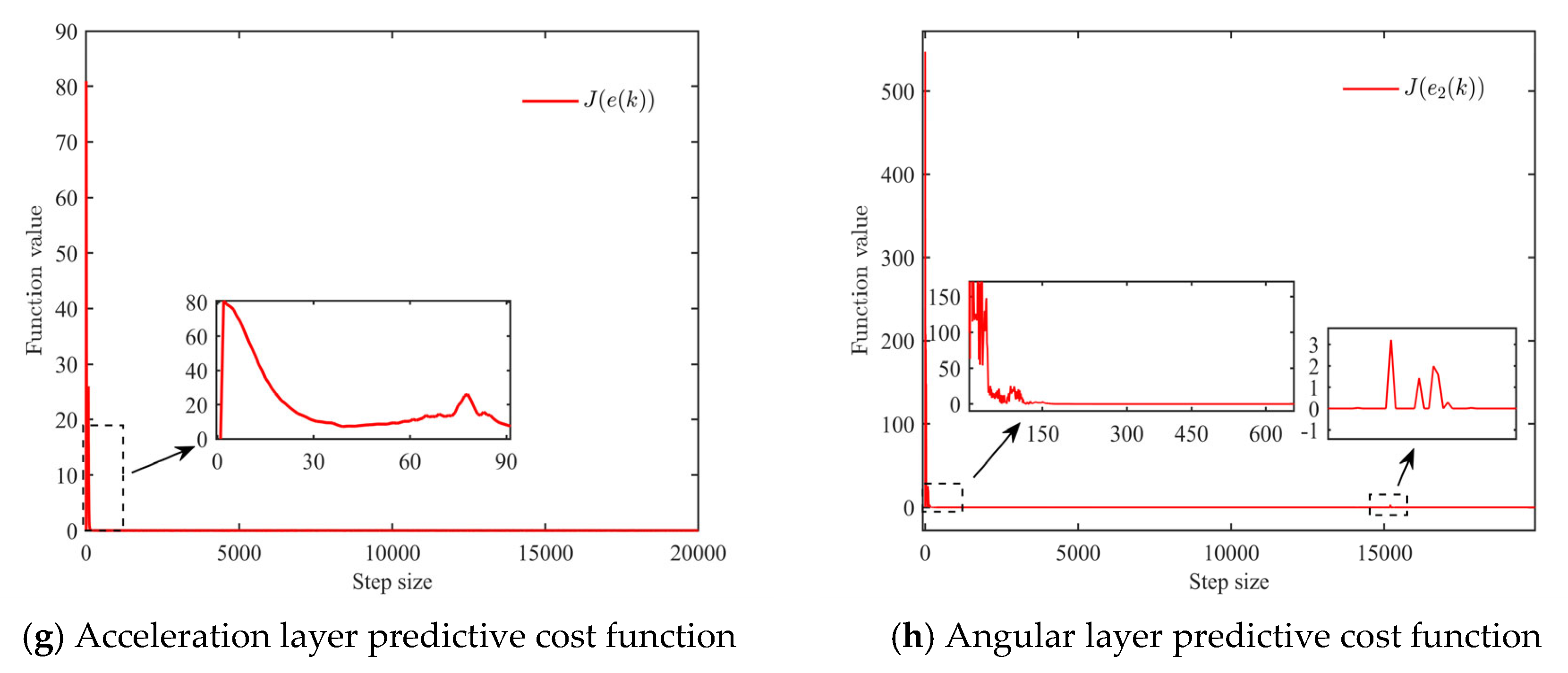
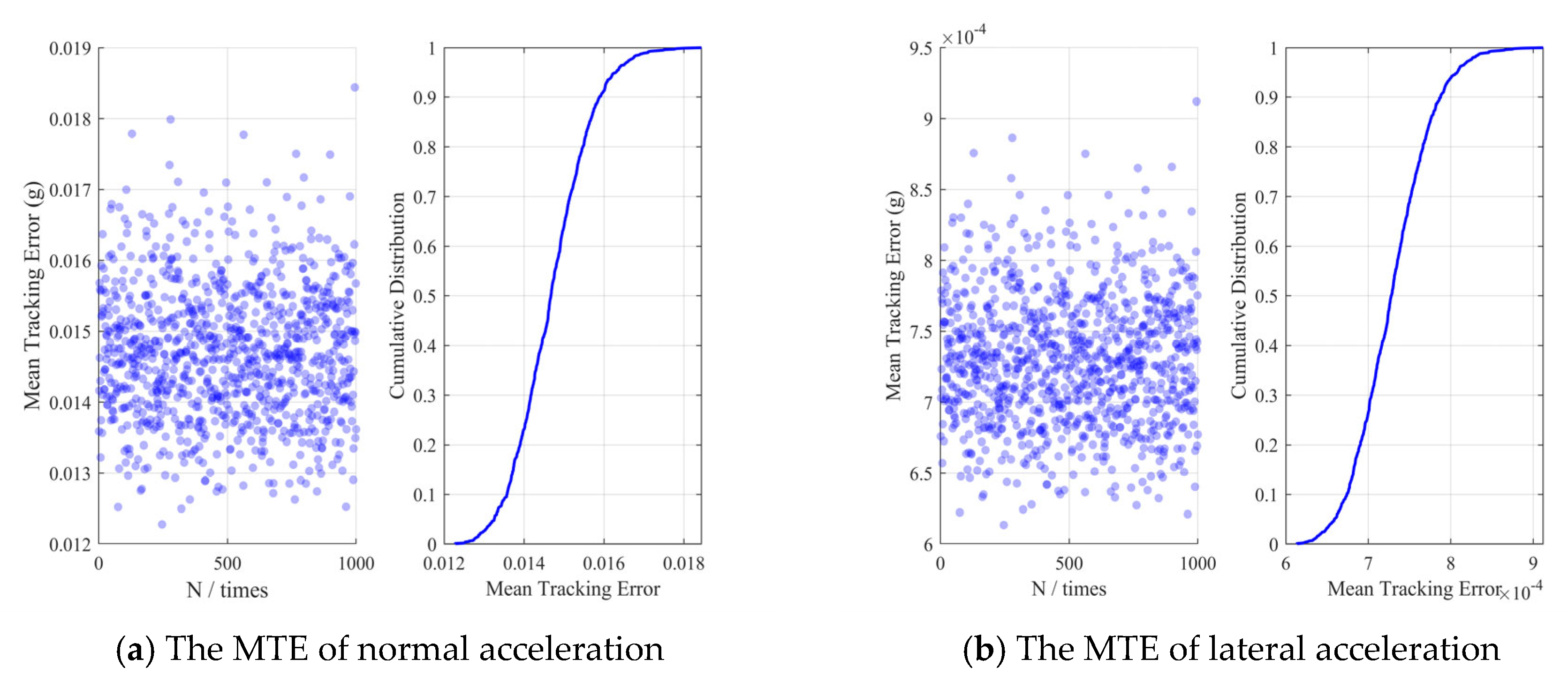
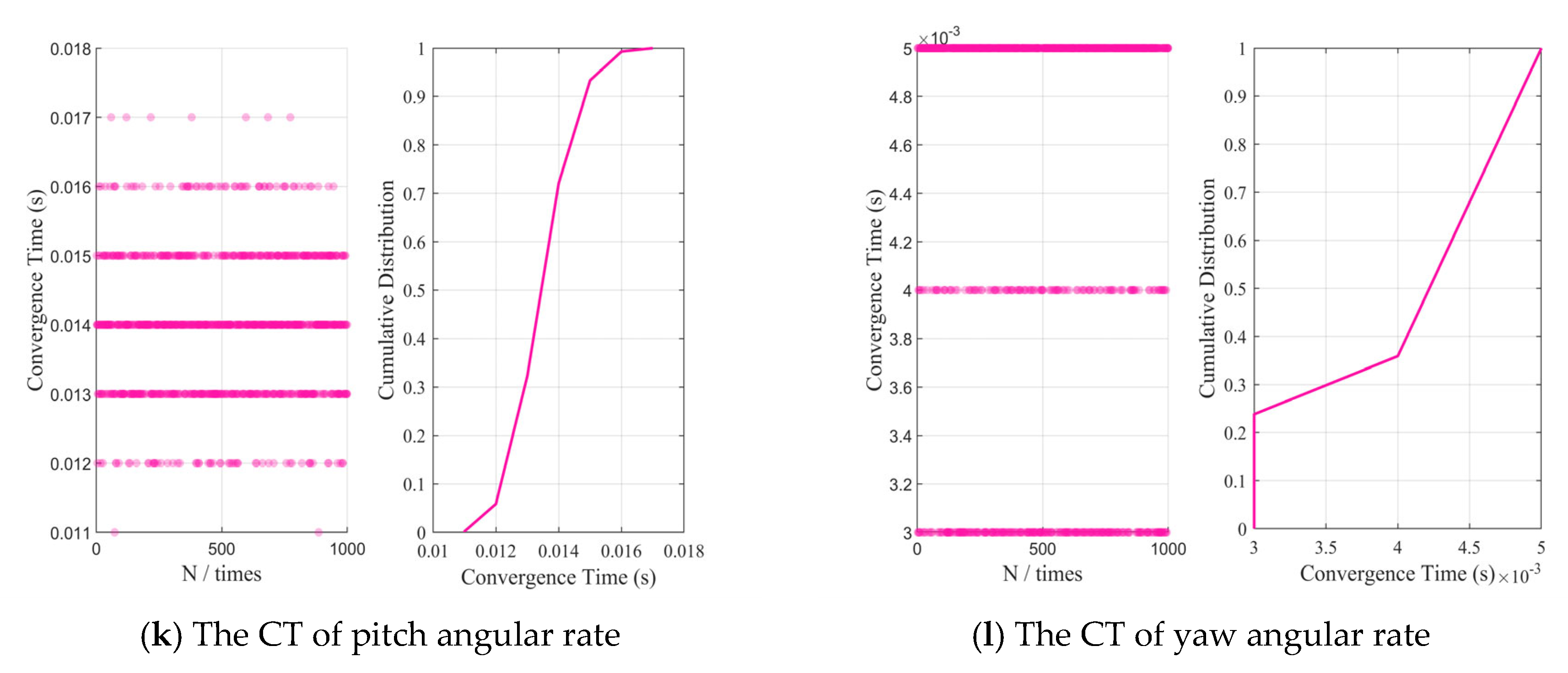
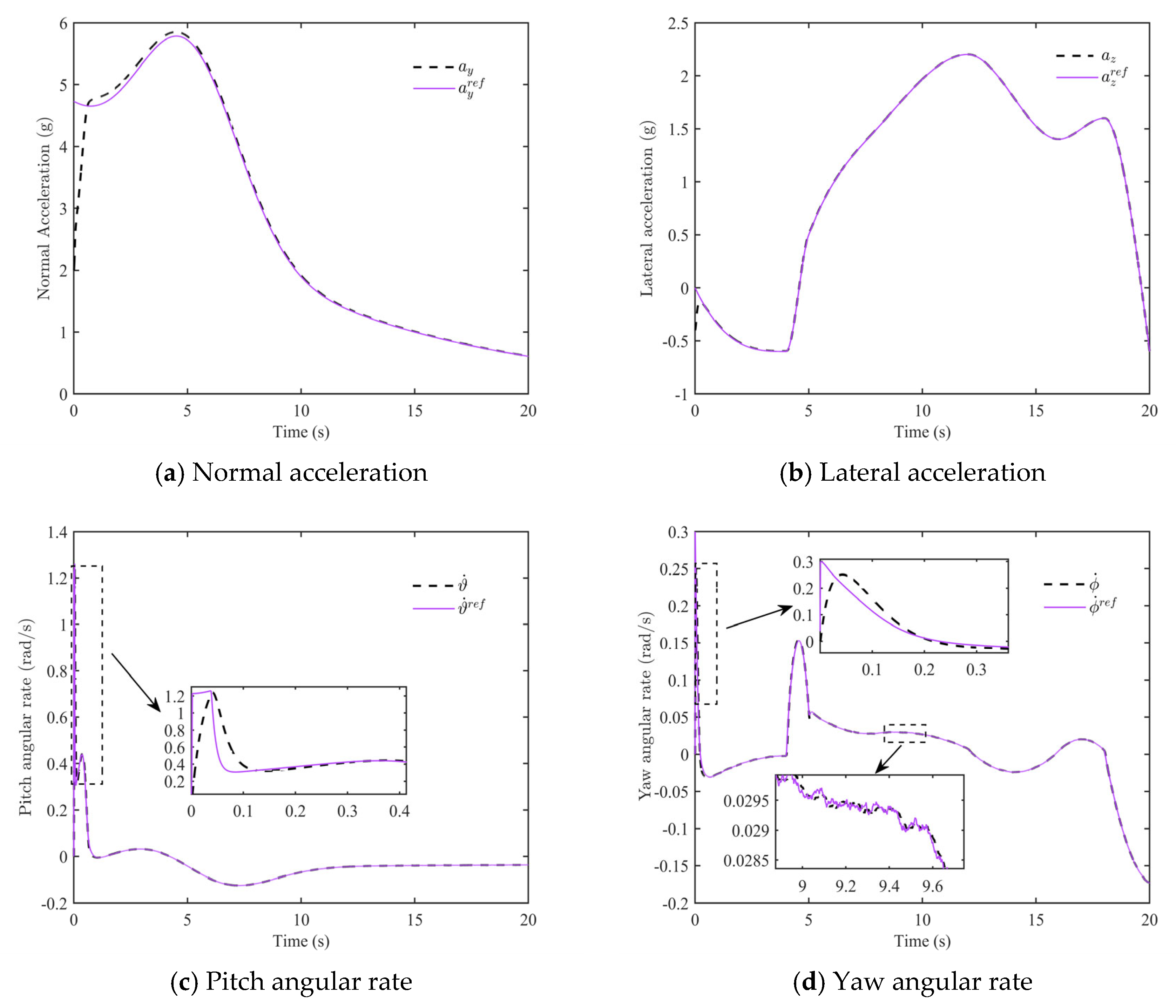
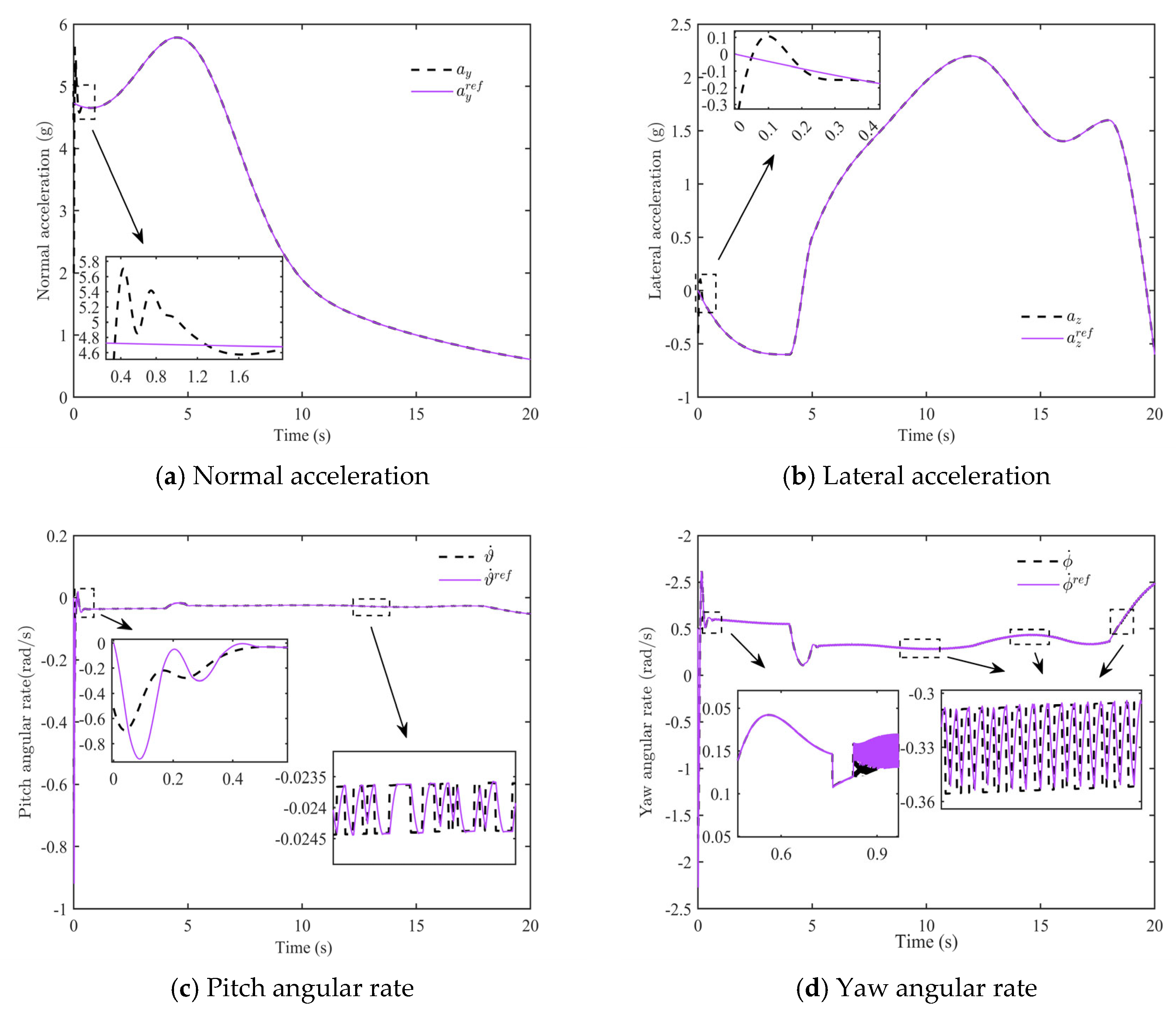
5.1. Performance Evaluation of the Proposed Method
5.2. Performance Comparison
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| NN-MPC | Neural Network Model Predictive Control |
| SV | Supersonic Vehicle |
| SMC | Sliding Mode Controllers |
| MARC | Model Adaptive Reference Control |
| MPC | Model Predictive Control |
| DSC | Dynamic Surface Control |
| TLC | Trajectory Linearization Control |
| ISMC | Improved Sliding Mode Control |
| ESO | Extended State Observer |
| PID | Proportional Integral Derivative |
| NN | Neural Networks |
| MTE | Mean Tracking Error |
| DRR | Disturbance Rejection Ratio |
| CT | Convergence Time |
References
- Xu, Q.; Chang, S.; Wang, Z. Acceleration autopilot design for gliding guided projectiles with less measurement information. Aerosp. Sci. Technol. 2018, 77, 256–264. [Google Scholar] [CrossRef]
- Zhao, L.; Shi, Z.; Zhu, Y. Acceleration autopilot for a guided spinning rocket via adaptive output feedback. Aerosp. Sci. Technol. 2018, 77, 573–584. [Google Scholar] [CrossRef]
- Xu, Q.P.; Chang, S.J.; Wang, Z.Y. Composite-Efficiency-Factor-Based Trajectory Optimization for Gliding Guided Projectiles. J. Spacecr. Rocket. 2018, 55, 66–76. [Google Scholar] [CrossRef]
- Shi, Z.; Zhao, L.; Liu, Z. Variational method based robust adaptive control for a guided spinning rocket. Chin. J. Aeronaut. 2021, 34, 164–175. [Google Scholar] [CrossRef]
- Zouaoui, S.; Elajrami, M.; Kouider, B. Easy Tracking of UAV Using PID Controller. Period. Polytech. Transp. Eng. 2019, 47, 171–177. [Google Scholar] [CrossRef]
- Mohamed, E.; Zouaoui, S.; Kouider, B. Drone Control using the Coupling of the PID Controller and Genetic Algorithm. Komunikacie 2021, 3, 75–82. [Google Scholar]
- Eltayeb, A.; Rahmat, M.; Basri, M.; Eltoum, M.; Mahmoud, M. Integral Adaptive Sliding Mode Control for Quadcopter UAV Under Variable Payload and Disturbance. IEEE Access 2022, 10, 94754–94764. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, J.Y.; Wang, X.M.; Jia, F.X. A guidance and control design with reduced information for a dual-spin stabilized projectile. Def. Technol. 2024, 33, 494–505. [Google Scholar] [CrossRef]
- Whitehead, B.; Bieniawski, S. Model Reference Adaptive Control of a Quadrotor UAV. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Tornoto, ON, Canada, 2–5 August 2010. [Google Scholar]
- Nguyen, N. Model-Reference Adaptive Control; Advanced Textbooks in Control and Signal Processing; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Faulwasser, T.; Findeisen, R. Nonlinear Model Predictive Control for Constrained Output Path Following. IEEE Trans. Autom. Control 2016, 61, 1026–1039. [Google Scholar] [CrossRef]
- Hanover, D.; Foehn, P.; Sun, S.; Kaufmann, E.; Scaramuzza, D. Performance, Precision, and Payloads: Adaptive Nonlinear MPC for Quadrotors. IEEE Robot. Autom. Lett. 2022, 7, 690–697. [Google Scholar] [CrossRef]
- Zou, Y.; Zheng, Z. A Robust Adaptive RBFNN Augmenting Backstepping Control Approach for a Model-Scaled Helicopter. IEEE Trans. Control Syst. Technol. 2015, 23, 2344–2352. [Google Scholar] [CrossRef]
- Huang, J. Global Tracking Control of Strict-Feedback Systems Using Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 1714–1725. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q.; Wang, Z.; Zhen, Z. Adaptive neural network finite time control for quadrotor UAV with unknown input saturation. Nonlinear Dyn. 2019, 98, 1973–1998. [Google Scholar] [CrossRef]
- Sun, C.Y.; Mu, C.X.; Yu, Y. Some control problems for near space hypersonic vehicles. Acta Autom. Sin. 2013, 39, 1901–1913. [Google Scholar] [CrossRef]
- Mu, C.X.; Zong, Q.; Tian, B.L.; Xu, W. Continuous sliding mode controller with disturbance observer for hypersonic vehicles. IEEE CAA J. Autom. Sin. 2015, 2, 45–55. [Google Scholar] [CrossRef]
- Chunodkar, A.; Akella, M. Switching angular velocity observer for rigid-body attitude stabilization and tracking control. J. Guid. Control Dyn. 2014, 37, 869–878. [Google Scholar] [CrossRef]
- Shen, Y.C.; Yu, J.Q.; Luo, G.C.; Ai, X.L.; Jia, Z.Y.; Chen, F.Z. Observer-based adaptive sliding mode backstepping output-feedback DSC for spin-stabilized rudder-controlled projectiles. Chin. J. Aeronaut. 2017, 30, 1115–1126. [Google Scholar] [CrossRef]
- Tang, P.; Zhang, F.; Ye, J.; Lin, D. An integral TSMC-based adaptive fault-tolerant control for quadrotor with external disturbances and parametric uncertainties. Aerosp. Sci. Technol. 2021, 109, 106415. [Google Scholar] [CrossRef]
- Tang, P.; Lin, D.; Zheng, D.; Fan, S.; Ye, J. Observer based finite-time fault tolerant quadrotor attitude control with actuator faults. Aerosp. Sci. Technol. 2020, 104, 105968. [Google Scholar] [CrossRef]
- Xu, W.; Qu, S.; Zhao, L.; Zhang, H. An improved adaptive sliding mode observer for middle-and high-speed rotor tracking. IEEE Trans. Power. Electron. 2020, 36, 1043–1053. [Google Scholar] [CrossRef]
- Liu, F.; Wang, S.Y.; Chao, T.; Yang, M. Adaptive saturated tracking control for solid launch vehicles in ascending based on differential inclusion stabilization. Def. Technol. 2023, 26, 157–179. [Google Scholar] [CrossRef]
- Yu, J.; Luo, G.; Mei, Y. Surface-to-air missile autopilot design using LQG/LTR gain scheduling method. Chin. J. Aeronaut. 2011, 24, 279–286. [Google Scholar] [CrossRef]
- Yan, X.Y.; Li, K.Y.; Yang, S.X. The control method of spinning missile based on dynamic inversion. J. Proj. Rocket. Missiles Guid. 2009, 29, 83–86. [Google Scholar]
- Liu, Y.; Zhu, J. Regular perturbation analysis for trajectory linearization control. In Proceedings of the American Control Conference, New York, NY, USA, 9–13 July 2007; pp. 3053–3058. [Google Scholar]
- Xue, Y.L.; Jiang, C.S. Trajectory linearization control of an aerospace vehicle based on RBF neural network. J. Syst. Eng. Electron. 2008, 19, 799–805. [Google Scholar] [CrossRef]
- Mu, D.; Wang, G.; Fan, Y.; Qiu, B.; Sun, X. Adaptive course control based on trajectory linearization control for unmanned surface vehicle with unmodeled dynamics and input saturation. Neurocomputing 2019, 330, 1–10. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, X.G.; Yang, J.; Wang, Z.Y. Acceleration tracking control for a spinning glide guided projectile with multiple disturbances. Chin. J. Aeronaut. 2020, 33, 3405–3422. [Google Scholar] [CrossRef]
- Pane, Y.; Nageshrao, S.; Kober, J.; Babuska, R. Reinforcement learning based compensation methods for robot manipulators. Eng. Appl. Artif. Intell. 2019, 78, 236–247. [Google Scholar] [CrossRef]
- Kim, J.; Shim, H.; Yang, I. On improving the robustness of reinforcement learning-based controllers using disturbance observer. In Proceedings of the IEEE 58th conference on decision and control (CDC), Nice, France, 11–13 December 2019; pp. 847–852. [Google Scholar]
- Bakshi, N. Model Reference Adaptive Control of Quadrotor UAVs: A Neural Network Perspective. In Adaptive Robust Control Systems; IntechOpen: London, UK, 2018. [Google Scholar]
- He, N.; Ma, K.; Li, H.; Li, Y. Resilient Self-Triggered Model Predictive Control of Discrete-Time Nonlinear Cyberphysical Systems Against False Data Injection Attacks. IEEE Intell. Transp. Syst. Mag. 2024, 16, 23–36. [Google Scholar] [CrossRef]
- Yang, B.; He, F.; Yao, Y. MPC-based design of on-off control law of the attitude control thruster. In Proceedings of the 27th Chinese Control Conference, Kunming, China, 16–18 July 2008; pp. 539–543. [Google Scholar]
- Ollerenshaw, D.; Costello, M. Model Predictive Control of a Direct Fire Projectile Equipped with Rudders. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, San Francisco, CA, USA, 15–18 August 2005. 5818. [Google Scholar]
- Li, K.; Yang, S.; Zhao, L. Stability of spinning missiles with an acceleration autopilot. J. Guid. Control Dyn. 2012, 35, 774–786. [Google Scholar] [CrossRef]
- Wang, P.X.; Rui, X.T.; Yu, H.L.; Wang, G.P.; Chen, D.Y. Adaptive control of track tension estimation using radial basis function neural network. Def. Technol. 2021, 17, 1423–1433. [Google Scholar] [CrossRef]





| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 34.2 | 0.462 | ||
| 0.120 | 34.54 | ||
| 1.54 | 14.796 | ||
| 0.01131 | 0.272 | ||
| 0.088 | −3.376 | ||
| 4.02 | 0.354 | ||
| 480 | 6.862 | ||
| 0.017 | 2.378 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 0.01 | 10 | ||
| 0.05 | 100 | ||
| 0.1 | 10 | ||
| 8.0 | 0.1 | ||
| 6.0 | 10 | ||
| 800 | 0.1 |
| Parameter | Value | Parameter | Value | ||
|---|---|---|---|---|---|
| TLC controller based on ISMC-ESO | |||||
| STD | 0.01 | ISMC | 0.1 | ||
| 12 | 0.1 | ||||
| 2 | 5 | ||||
| 1 | 3 | ||||
| Model-assisted ESO | 25 | 3 | |||
| 35 | 1.5 | ||||
| SMC | |||||
| 5 | 0.5 | ||||
| 0.35 | 10 | ||||
| 4 | 4 | ||||
| 0.01 | 0.2 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Ming, C.; Wang, H.; Peng, T. Acceleration Command Tracking via Hierarchical Neural Predictive Control for the Effectiveness of Unknown Control. Aerospace 2025, 12, 689. https://doi.org/10.3390/aerospace12080689
Yang Z, Ming C, Wang H, Peng T. Acceleration Command Tracking via Hierarchical Neural Predictive Control for the Effectiveness of Unknown Control. Aerospace. 2025; 12(8):689. https://doi.org/10.3390/aerospace12080689
Chicago/Turabian StyleYang, Zhengpeng, Chao Ming, Huaiyan Wang, and Tongxing Peng. 2025. "Acceleration Command Tracking via Hierarchical Neural Predictive Control for the Effectiveness of Unknown Control" Aerospace 12, no. 8: 689. https://doi.org/10.3390/aerospace12080689
APA StyleYang, Z., Ming, C., Wang, H., & Peng, T. (2025). Acceleration Command Tracking via Hierarchical Neural Predictive Control for the Effectiveness of Unknown Control. Aerospace, 12(8), 689. https://doi.org/10.3390/aerospace12080689






