A Hybrid Deep Learning Architecture for Enhanced Vertical Wind and FBAR Estimation in Airborne Radar Systems

Abstract

Accurate prediction of the F-factor averaged over one kilometer (FBAR), a critical wind shear metric, is essential for aviation safety. A central F-factor is used to compute FBAR. i.e., compute the value of FBAR at a point using a spatial interval beginning 500 m prior to the point and ending 500 m beyond the point. Traditional FBAR estimation using the Vicroy method suffers from limited vertical wind speed (W${\phantom{,}}_h$) accuracy, particularly in complex, non-idealized atmospheric conditions. This foundational study proposes a hybrid CNN-BiLSTM-Attention deep learning architecture that integrates spatial feature extraction, sequential dependency modeling, and attention mechanisms to address this limitation. The model was trained and evaluated on data generated by the industry-standard Airborne Doppler Weather Radar Simulation (ADWRS) system, using the DFW microburst case (C1-11) as a benchmark hazardous scenario. Following safety assurance principles aligned with SAE AS6983, the proposed model achieved a W${\phantom{,}}_h$ estimation RMSE (root-mean-squared deviation) of $0.623$ $\mathrm{m} {\mathrm{s}}^{-1}$ (vs. Vicroy’s $14.312$ $\mathrm{m} {\mathrm{s}}^{-1}$) and a correlation of 0.974 on 14,524 test points. This subsequently improved FBAR prediction RMSE by 98.5% (0.0591 vs. 4.0535) and MAE (Mean Absolute Error) by 96.1% (0.0434 vs. 1.1101) compared to Vicroy-derived values. The model demonstrated a 65.3% probability of detection for hazardous downdrafts with a low 1.7% false alarm rate. These results, obtained in a controlled and certifiable simulation environment, highlight deep learning’s potential to enhance the reliability of airborne wind shear detection for civil aircraft, paving the way for next-generation intelligent weather avoidance systems.

1. Introduction

Low-level wind shear, characterized by rapid changes in wind speed and/or direction below 600 $\mathrm{m}$ (2000 $\mathrm{ft}$) AGL, poses a critical threat to aviation safety, particularly during takeoff and landing [1,2]. The F-factor, averaged over a one-kilometer radial distance (FBAR) (a key metric derived from airborne weather radar), quantifies wind shear intensity along the flight path [3,4]. Accurate FBAR prediction is therefore paramount for pilot situational awareness and timely avoidance maneuvers. The core scientific challenge addressed in this paper is the accurate estimation of vertical wind speed (W${\phantom{,}}_h$), which is a primary limiting factor in the reliability of current FBAR predictions [5].

Traditional techniques for W${\phantom{,}}_h$ estimation, notably the Vicroy method [6], rely on physics-based empirical models. These models often use simplified assumptions, such as axisymmetry in wind fields (e.g., microbursts), and employ empirical K-factors that may not adapt to the diverse and rapidly evolving spatio-temporal characteristics of real-world wind shear. Consequently, the Vicroy method can struggle to capture the true complexity of atmospheric turbulence and non-linear interactions, leading to significant errors in W${\phantom{,}}_h$ estimation, especially in non-idealized wind shear events [7]. This study demonstrates that a data-driven deep learning approach can more effectively model these complex relationships, overcoming the limitations of models reliant on simplified physics.

Recent advances in deep learning offer powerful tools for learning complex patterns from data [8,9]. In meteorology, CNNs and LSTMs have shown promise for spatio-temporal tasks [10,11]. While some studies have applied ML to vertical velocity estimation from ground-based radar [12] or general wind forecasting [13], a significant research opportunity remains. Specifically, the application of a hybrid architecture combining CNNs, Bidirectional LSTMs, and Attention mechanisms to directly estimate W${\phantom{,}}_h$ from airborne radar scan line data for the explicit purpose of improving FBAR prediction has not been fully explored.

This paper proposes a novel hybrid CNN-BiLSTM-Attention deep learning architecture to address this challenge. The primary objective is to significantly improve W${\phantom{,}}_h$ estimation accuracy from simulated airborne radar I/Q data, leading to more reliable FBAR predictions. This work is aligned with the advancement of intelligent avionics for civil aircraft. Furthermore, the development methodology is consciously aligned with the safety assurance principles of emerging standards like SAE AS6983 [14], considering a Design Assurance Level (DAL) C context, which is crucial for integrating machine learning into safety-critical aeronautical systems.

The main contributions of this paper are as follows: (1) The design and rigorous evaluation of a hybrid CNN-BiLSTM-Attention model for enhanced W${\phantom{,}}_h$ estimation. (2) A comprehensive quantitative comparison of the proposed model’s performance against the Vicroy method and other ML approaches on a challenging simulated benchmark dataset. (3) An illustration of how deep learning development can align with the principles of emerging safety assurance standards.

This paper is structured as follows: Section 2 reviews related work. Section 3 details the data generation, model architecture, training, FBAR calculation, and safety considerations. Section 4 presents experimental results. Section 5 discusses the implications, and Section 6 provides conclusions and future work.

2. Related Work

The challenge of low-level wind shear and its impact on aviation has been a subject of extensive research and operational concern for decades. This section reviews key literature pertinent to wind shear hazard characterization, traditional and AI-based estimation techniques, and the evolving landscape of safety assurance for AI in aviation.

2.1. Wind Shear Hazard Characterization and the F-Factor

The F-factor, representing the rate of change of aircraft specific energy due to wind variations, is a cornerstone in modern wind-shear-alerting systems [4]. A positive F-factor indicates performance-decreasing shear. The operational relevance of the 1 km averaged version (FBAR) is underscored by its adoption in airborne wind-shear-warning systems and regulatory standards like RTCA DO-220A [3]. The historical context is well documented in ICAO’s Manual on low-level wind shear [1] and by Arbuckle et al. [5]. Foundational work by Etkin [2] also detailed the broader effects of turbulent wind on flight.

2.2. Vertical Wind (W${\phantom{,}}_h$) Estimation Techniques

Estimating W${\phantom{,}}_h$ is crucial for accurate F-factor calculation. The Vicroy method [6] provides physics-based empirical models to estimate W${\phantom{,}}_h$ from along-beam radial velocity shear ($d{V}_r/dr$) and signal correlation ($R_{corr}$). These models typically assume a relationship of the form $d{W}_h/dz\approx -K·(d{V}_r/dr)$, where $d{W}_h/dz$ is the vertical gradient of vertical wind, and K is an empirical factor (often K = 2 for $d{V}_r/dr>0$ and $R_{corr}\ge 0.9$; K = 1, otherwise). This formulation is derived from theoretical considerations of microburst dynamics, which often assume an idealized, axisymmetric flow structure. W${\phantom{,}}_h$ is then obtained by integrating $d{W}_h/dz$ along the radar beam. While effective in many scenarios, the Vicroy method’s performance can be limited when encountering real-world wind shear events that deviate significantly from these idealized assumptions—a key motivation for exploring data-driven alternatives.

2.3. Machine Learning in Meteorology and Radar Applications

The application of ML to meteorological problems has gained significant traction. ConvLSTM, introduced by Shi et al. [10], explicitly models spatio-temporal correlations and has proven effective in precipitation nowcasting, as benchmarked in [11]. More recent works have incorporated attention mechanisms into ConvLSTM frameworks for various forecasting tasks.

Specific to vertical air motion, Chase et al. (2024) [12] employed U-Nets to estimate maximum vertical velocity from 3D radar reflectivity fields, highlighting both the potential and challenges of ML. Other applications include wind speed forecasting for energy production [13] and specialized CNNs for wind interval prediction [15]. General surveys on deep learning in weather prediction [16,17] provide comprehensive overviews. However, the application of a hybrid CNN-BiLSTM-Attention model for direct W${\phantom{,}}_h$ estimation from airborne radar scan line data to improve FBAR prediction for civil aircraft remains a relatively underexplored area.

2.4. AI Certification and Safety Assurance in Aviation

Integrating AI/ML into safety-critical aerospace systems presents unique V&V challenges not fully addressed by standards like DO-178C [18]. The SAE G-34 committee’s AS6983 standard [14] is a key initiative, establishing a dedicated Machine Learning Development Lifecycle (MLDL) [19]. This standard emphasizes data management rigor, model validation, robustness, and explainability, all of which are crucial for ensuring that AI contributions to safety are verifiable and trustworthy.

3. Materials and Methods

The methodological framework of this study is designed to address the core scientific problem of accurately estimating vertical wind speed (W${\phantom{,}}_h$) from airborne radar data to improve FBAR predictions. This involves a multi-stage process encompassing high-fidelity data simulation, extraction of relevant radar features, the design and optimization of a novel deep learning architecture, and a comparative evaluation against traditional and alternative machine learning techniques, all while considering aviation safety assurance principles. Figure 1 provides a high-level overview of this process.

3.1. Data Generation and Preprocessing

The foundation of this study is a robust dataset derived from sophisticated simulations, ensuring access to both realistic radar measurements and corresponding ground truth atmospheric conditions.

3.1.1. Simulation Environment and Atmospheric Data

The foundation of this research rests upon simulated radar In-phase and Quadrature (I/Q) data, generated using the Airborne Doppler Weather Radar Simulation (ADWRS) system. ADWRS is a simulation tool developed by NASA and widely accepted by the aviation community for system evaluation and certification support [3]. The atmospheric conditions, including the critical DFW test case, were sourced from the “Windshear Database for Forward-Looking Systems Certification” [20], a publicly accessible resource developed specifically for this purpose.

For this study, we focused on the Dallas–Fort Worth (DFW) microburst event of 2 August 1985 (identified as Scenario C1-11), a scenario compliant with RTCA DO-220A [3]. This event, extensively analyzed by Fujita [21], is a widely recognized and challenging benchmark for evaluating airborne radar performance due to its severe, non-axisymmetric characteristics. The high-resolution numerical simulation of this event in the certification database provides the ground truth for all atmospheric variables, including the target vertical wind component (W${\phantom{,}}_h$). ADWRS processes these atmospheric data files with defined radar parameters and flight paths to produce the I/Q data, forming the basis for our feature engineering.

3.1.2. Input Feature Engineering

A set of 10 distinct features was engineered from the raw ADWRS outputs for each range gate along a radar scan line. This feature extraction aimed to provide the model with comprehensive information about the radar returns and their local context:

• range_m: The distance from the radar to the center of the range gate (m).
• altitude_m: The altitude of the range gate above ground level (m).
• u_r: The mean radial velocity (m/s) estimated via Pulse Pair Processing (PPP).
• duds: The along-beam shear of radial velocity (s⁻¹), calculated as the gradient of u_r using a 5-point Ordinary Least Squares (OLS) fit.
• R_corr: The correlation coefficient from the 5-point OLS fit.
• ref_gt: The ground truth reflectivity (dBZ) interpolated from the atmospheric database.
• u_r_lag1, duds_lag1: Radial velocity and shear at the preceding range gate.
• u_r_lead1, duds_lead1: Radial velocity and shear at the succeeding range gate.

The inclusion of lagged and lead features provides a localized spatial context (a 3-gate window, approx. 150 $\mathrm{m}$) for each prediction.

3.1.3. Target Variable

The target variable is the ground truth vertical wind speed (W${\phantom{,}}_h$) in $\mathrm{m} {\mathrm{s}}^{-1}$ (positive upwards), sourced directly from the DFW case data and interpolated to the precise spatio-temporal coordinates of each radar range gate.

3.1.4. Data Structuring, Splitting, and Normalization

Final data preparation for model training involved several key steps:

• Sequence Generation: Data from individual scan lines were formed into sequences of length 173 (maximum observed gates). Shorter sequences were padded with 0.0, and target W${\phantom{,}}_h$ values were padded with NaNs, which were masked during loss calculation.
• Data Splitting Strategy: The dataset was split based on unique radar scan identifiers. A stratified sampling approach was employed, categorizing scans based on the presence of significant downdrafts (W${\phantom{,}}_h$ < $-4.0$ $\mathrm{m} {\mathrm{s}}^{-1}$). The test set consisted of 2 scan scenarios, with one specifically chosen for containing the critical benchmark event to ensure evaluation under hazardous conditions. A validation set of 1 scan scenario was similarly selected. The final test set comprised 14,524 individual gate-level data points.
• Normalization: All 10 input features were standardized using a scaler fitted only on the training set data.

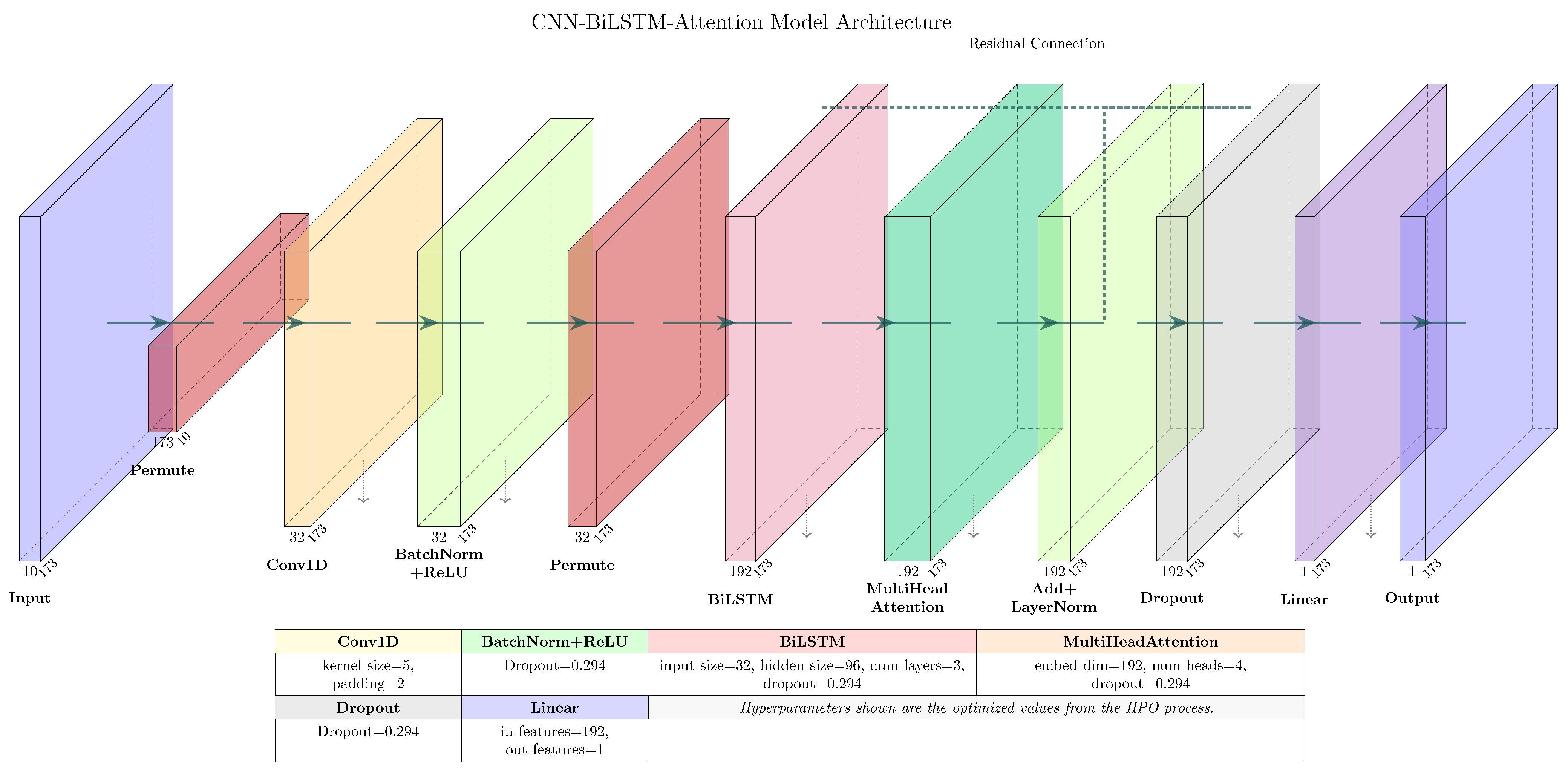
3.2. Proposed CNN-BiLSTM-Attention Model Architecture

The proposed model is a hybrid neural network designed to exploit the spatio-temporal nature of radar scan line data. The architecture, depicted in Figure 2, consists of the following key components:

• Input Layer: Accepts sequences of shape (batch_size, sequence_length = 173, num_features = 10).
• 1D Convolutional Block: A 1D CNN extracts local spatial features.
  • A Conv1d layer with 32 channels and a kernel size of 5 is followed by BatchNorm1d, ReLU, and Dropout (rate 0.2940). The convolutional operation at position l for output channel j is given by

    $$Y_{l,j}=\sigma \left(b_j+\sum _{i=1}^{C_{in}}\sum _{m=1}^k{W}_{j,i,m}·X_{l+m-1,i}\right),$$

    (1)

    where X is the input sequence, W is the kernel, b is bias, and $\sigma$ is the ReLU activation.
• Bidirectional LSTM Layers: Three layers of Bidirectional LSTMs (LSTM) capture long-range dependencies. The core operations at each step t are [22]

  $$\begin{array}{ccc}\hfill i_t& =\sigma (W_i[h_{t-1},x_t]+b_i)\hfill & \hfill (\mathrm{Input}\mathrm{gate})\\ \hfill f_t& =\sigma (W_f[h_{t-1},x_t]+b_f)\hfill & \hfill (\mathrm{Forget}\mathrm{gate})\\ \hfill o_t& =\sigma (W_o[h_{t-1},x_t]+b_o)\hfill & \hfill (\mathrm{Output}\mathrm{gate})\\ \hfill {\tilde{C}}_t& =tanh(W_C[h_{t-1},x_t]+b_C)\hfill & \hfill (\mathrm{Candidate}\mathrm{cell}\mathrm{state})\\ \hfill C_t& =f_t\odot C_{t-1}+i_t\odot {\tilde{C}}_t\hfill & \hfill (\mathrm{Cell}\mathrm{state})\\ \hfill h_t& =o_t\odot tanh\left(C_t\right)\hfill & \hfill (\mathrm{Hidden}\mathrm{state})\end{array}$$

  (2)
  • Each LSTM layer has 96 hidden units per direction, and the final hidden state is $H_t=[\overrightarrow{h_t};\overleftarrow{h_t}]$.
  • Dropout (rate 0.2940) is applied between LSTM layers.
• Multi-Head Self-Attention Layer: An attention mechanism dynamically weighs the importance of different parts of the sequence.
  • Using queries (Q), keys (K), and values (V) projected from the BiLSTM hidden states, the scaled dot-product attention is [23]

    $$\mathrm{Attention}(Q,K,V)=\mathrm{softmax}\left({\displaystyle \frac{Q{K}^T}{\sqrt{d_k}}}\right)V$$

    (3)
  • A MultiheadAttention layer with 4 attention heads is used.
• Residual Connection and Normalization: The attention output is added to its input (the LSTM output), forming a residual connection, followed by layer normalization.
• Output Layer: A final Dropout and a Linear layer together map features to a single output, i.e., the predicted W${\phantom{,}}_h$.

This hierarchical architecture is designed to first learn local spatial features (CNN), then model sequential dependencies (BiLSTM), and finally re-weight representations based on contextual relevance (Attention).

3.3. Model Training and Hyperparameter Optimization

The model was trained to minimize Mean Squared Error (MSE), $L_{MSE}={\displaystyle \frac{1}{N}}\sum {(y_{true}-y_{pred})}^2$, using the Adam optimizer [24]. Hyperparameter optimization (HPO) was conducted using Ray Tune [25] with the ASHA scheduler over 100 trials. The best HPO trial achieved a validation MSE of 0.1189.

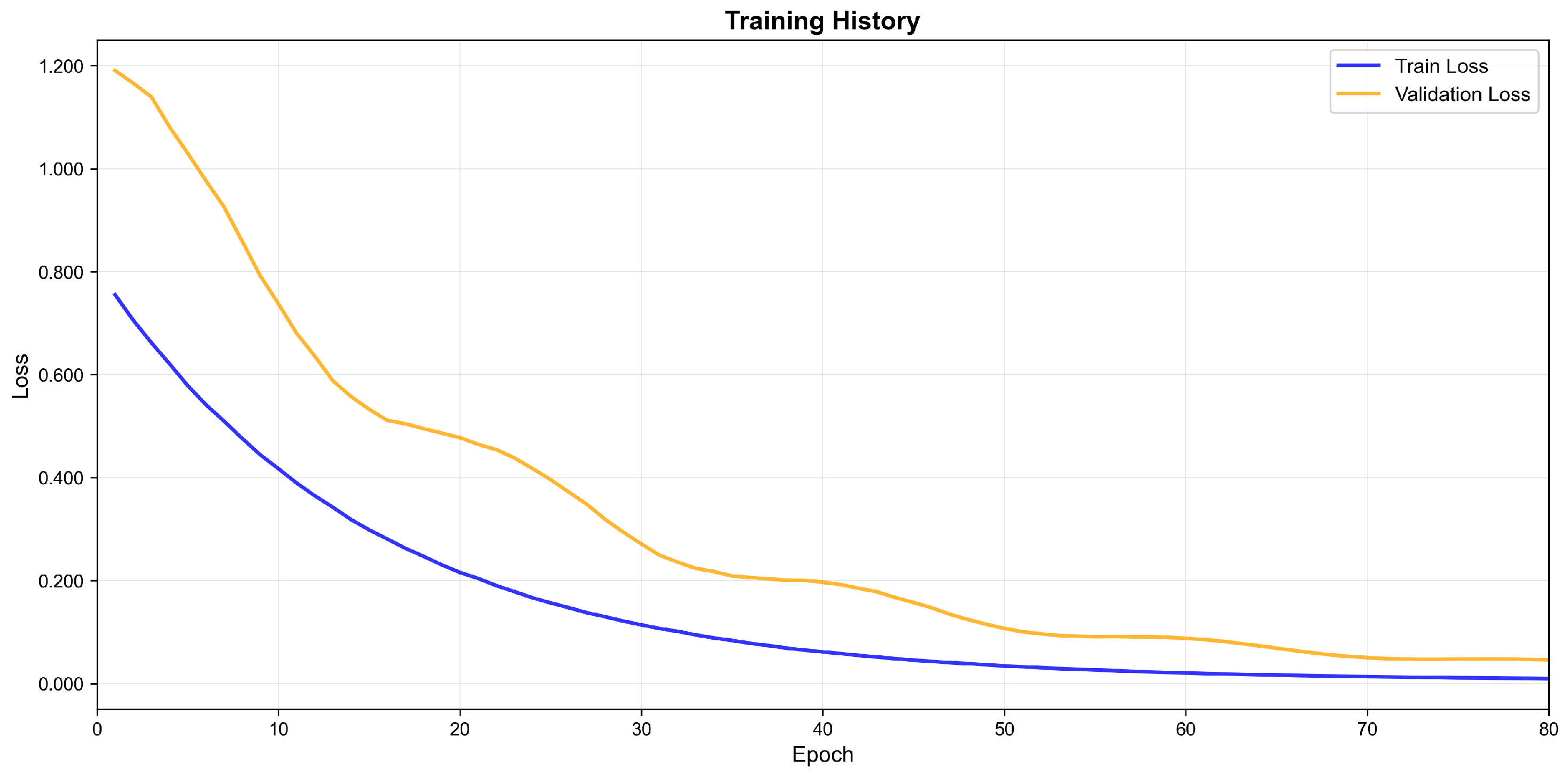
The final model, using optimized hyperparameters (e.g., learning rate 0.000606, 3 LSTM layers, 96 hidden units), was trained for up to 150 epochs with an early stopping patience of 30 epochs. Figure 3 shows the training and validation loss curves.

Ablation Study of Key Hyperparameters

The HPO process systematically explored the hyperparameter space.

Table 1. Impact of hyperparameter variations on validation loss (MSE) during HPO. Baseline (optimal) validation loss ≈ 0.1189.

Parameter Varied	Setting (Trial ID Suffix)	Validation Loss (MSE)
Baseline (Optimal HPO-Derived)	As per Section 3.2	0.1189
LSTM Hidden Size (per dir.)	64 (_002)	3.8785
	192 (_000)	0.2354
LSTM Layers	1 (_001)	0.2291
	2 (_010, Conv.Ch = 48, Drop = 0.1455)	0.8356
Residual Connections	False (_004)	16.5227

shows that deviations from the optimal set generally led to increased validation loss, confirming the effectiveness of HPO and the model’s sensitivity to key architectural choices.

3.4. FBAR Calculation Method

The instantaneous F-factor is given by [3,7]

$$F={\displaystyle \frac{1}{g}}{\displaystyle \frac{d{U}_h}{dt}}-{\displaystyle \frac{W_h}{V_{TAS}}}$$

(4)

where g is gravity, $U_h$ is horizontal wind speed, $d{U}_h/dt$ is horizontal wind change rate, $W_h$ is vertical wind speed, and $V_{TAS}$ is true airspeed ( 150 $\mathrm{kt}$). F-factor values are then averaged over a 1 $\mathrm{k}$$\mathrm{m}$ sliding window to produce FBAR.

3.5. Baseline and Alternative Machine Learning Methods

To benchmark performance, the proposed model was compared against the following:

• Vicroy Method (Baseline): A traditional physics-based empirical method [6].
• MLP-Enhanced Vicroy: An MLP predicts an adaptive K-factor for the Vicroy equation.
• MLP-Corrected Vicroy: An MLP predicts a correction term for the Vicroy output.
• Direct W${\phantom{,}}_h$ MLP: An MLP directly predicts W${\phantom{,}}_h$ from radar features.
• Physics-Informed ConvLSTM: A ConvLSTM with a loss term incorporating a simplified continuity equation.
• Spatio-Temporal Transformer: A Transformer-based architecture using self-attention.

3.6. Safety Assurance Considerations

The model development and evaluation were conducted with consideration for the principles of the emerging SAE AS6983 standard [14], targeting a Design Assurance Level (DAL) C context.

• Data Management (AS6983 Sec 6): We used a controlled, traceable data source (ADWRS) with documented scenarios (e.g., C1-11). Data preprocessing, including feature extraction (see step1_extract_features.py) and NaN handling (see step2_prepare_comprehensive_data.py), was codified for reproducibility. A stratified splitting strategy (see step3b_prepare_conv-lstm_data.py) ensured the test set contained operationally relevant hazardous conditions, fulfilling data representativeness requirements.
• Model Design and Training (AS6983 Sec 7.1): The architecture was deliberately chosen for its suitability for spatio-temporal radar data. A systematic HPO process using Ray Tune was employed to find optimal parameters, which were documented (see best_hyperparameters_ray.json). The final training utilized a robust methodology with early stopping based on validation loss to prevent overfitting.
• Model V&V (AS6983 Sec 7.2, 7.3): Performance was rigorously verified on an independent test set using predefined metrics (RMSE, MAE, POD, FAR), as implemented in our evaluation scripts (see step5b_evaluate_raytune.py). The stratified test set guaranteed verification under the most critical conditions defined in our dataset.
• Lifecycle Data (AS6983 Sec 8): All key artifacts of the Machine Learning Development Lifecycle (MLDL)—including data processing scripts, model architecture definitions, training logs, HPO results, and evaluation reports (see evaluation_metrics.txt)—were systematically managed. This structured approach provides a foundation for the traceability and review required in a certified environment.

4. Results

4.1. Experimental Setup

The CNN-BiLSTM-Attention model was evaluated on a test set of 14,524 gate-level data points from two ADWRS scan scenarios. FBAR performance was compared on a subset of 2105 points corresponding to the direct flight path within the wind field.

4.2. Vertical Wind (W${\phantom{,}}_h$) Estimation Performance

Table 2. W${\phantom{,}}_h$ Estimation regression performance on the full test set (N = 14,524 points).

Method	RMSE (m s${\phantom{,}}^{-1}$)	MAE (m s${\phantom{,}}^{-1}$)	Correlation
Proposed Model (CNN-BiLSTM-Attention)	0.6233	0.3254	0.9736
Vicroy Method	14.3120	11.7693	0.1377

summarizes the W${\phantom{,}}_h$ estimation performance. The proposed model dramatically improves upon the Vicroy method. The unusually high RMSE for the Vicroy method is a confirmed result for this experiment and is attributed to the challenging nature of the DFW C1-11 test case. Its complex, non-axisymmetric wind fields deviate significantly from the idealized assumptions underpinning the Vicroy model’s empirical K-factors, thereby highlighting the method’s known limitations in such conditions and reinforcing the need for more adaptive models.

Figure 4 shows the strong agreement between the model’s predictions and the ground truth. Some underestimation of strong updrafts is noted, which may be due to their relative rarity in the training data and the nature of the MSE loss function.

Classification performance for strong downdrafts (W${\phantom{,}}_h$ < $-4.0$ $\mathrm{m} {\mathrm{s}}^{-1}$) is presented in

Table 3. Proposed model W${\phantom{,}}_h$ classification performance for strong downdrafts (W${\phantom{,}}_h$ < $-4.0$ $\mathrm{m} {\mathrm{s}}^{-1}$) on the test set (N = 14,524 points).

Metric	TP	FN	FP	TN	Value
CSI	1262	671	22	12,569	0.6455
POD					0.6529
FAR					0.0171

.

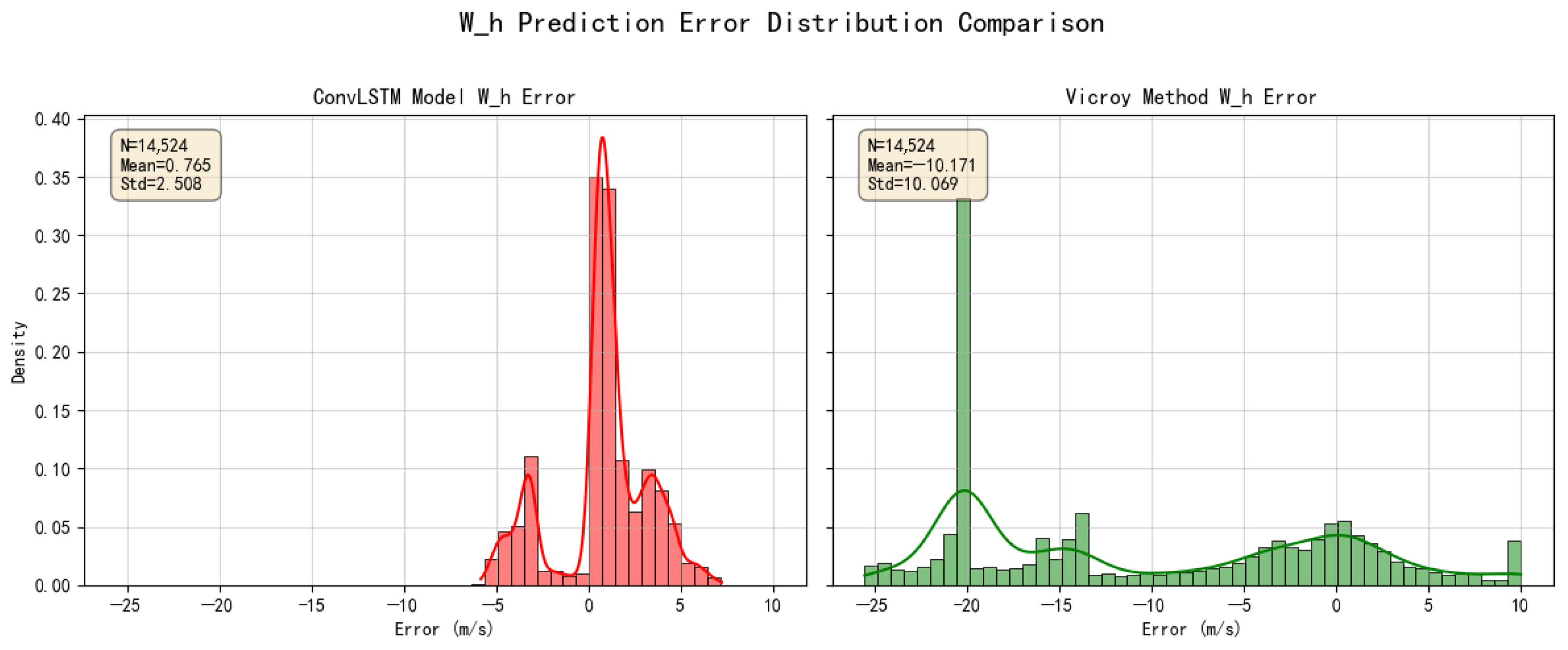
The model achieves a POD of 65.3% with a very low FAR of 1.7%. Error distributions (Figure 5) show the proposed model’s errors are smaller and more centered around zero than Vicroy’s.

Qualitative examples (Figure 6) illustrate the model’s ability to track W${\phantom{,}}_h$ variations along scan lines, capturing the general trend and magnitude of vertical winds.

4.3. FBAR Prediction Performance of the Proposed Model

Enhanced W${\phantom{,}}_h$ accuracy significantly improves FBAR predictions (

Table 4. FBAR prediction performance comparison (N = 2105 points from center line, within wind field of test scans).

FBAR Source (Wh Estimate from)	RMSE	MAE	Correlation
Proposed Model (CNN-BiLSTM-Attention)	0.0591	0.0434	0.8876
Vicroy Method	4.0535	1.1101	0.0801
Improvement (RMSE)	98.54%
Improvement (MAE)	96.09%

, N = 2105 center-line points).

The model reduces FBAR RMSE by 98.5% and MAE by 96.1%. Profile plots (Figure 7 and Figure 8) visually confirm this.

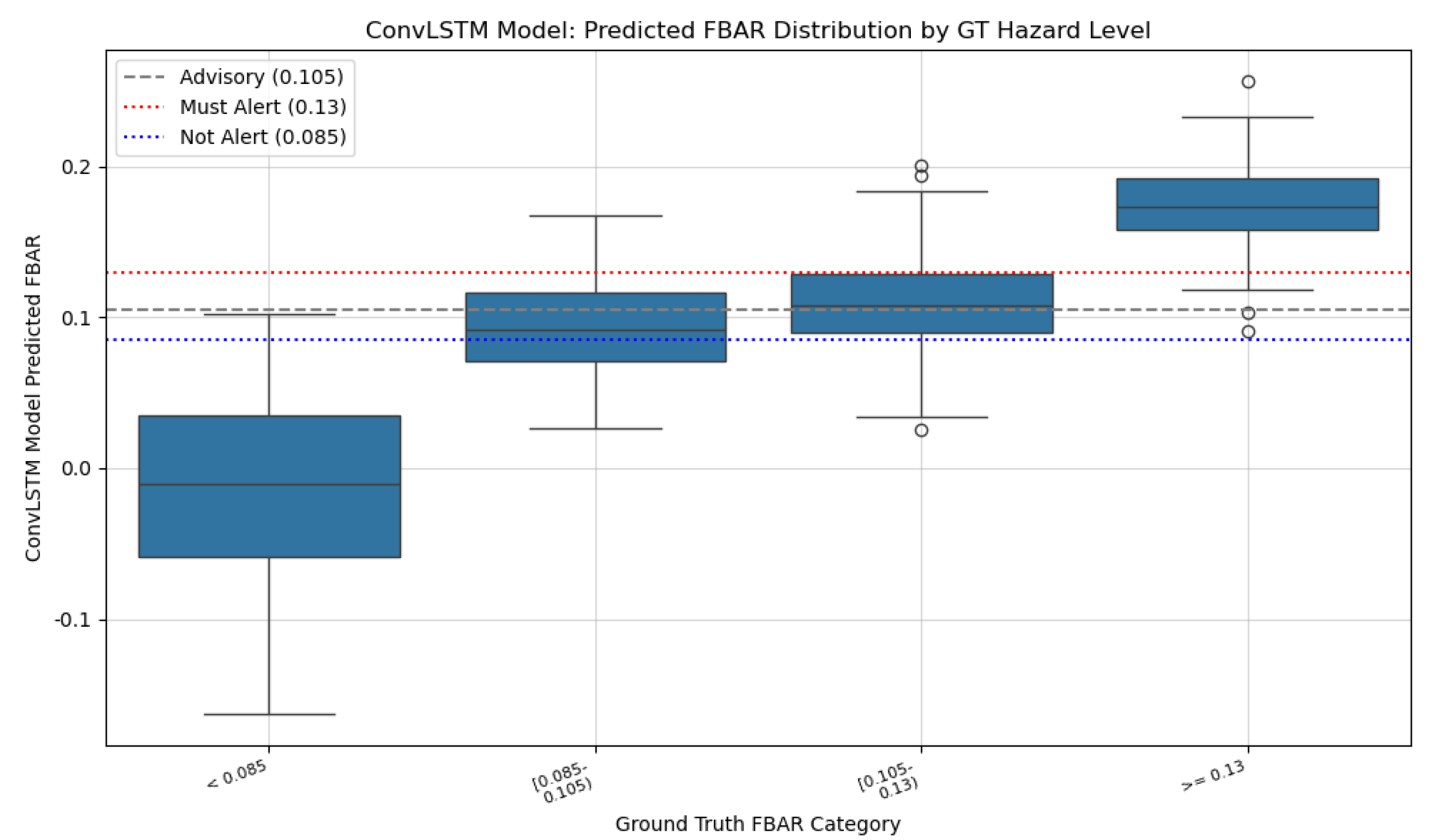
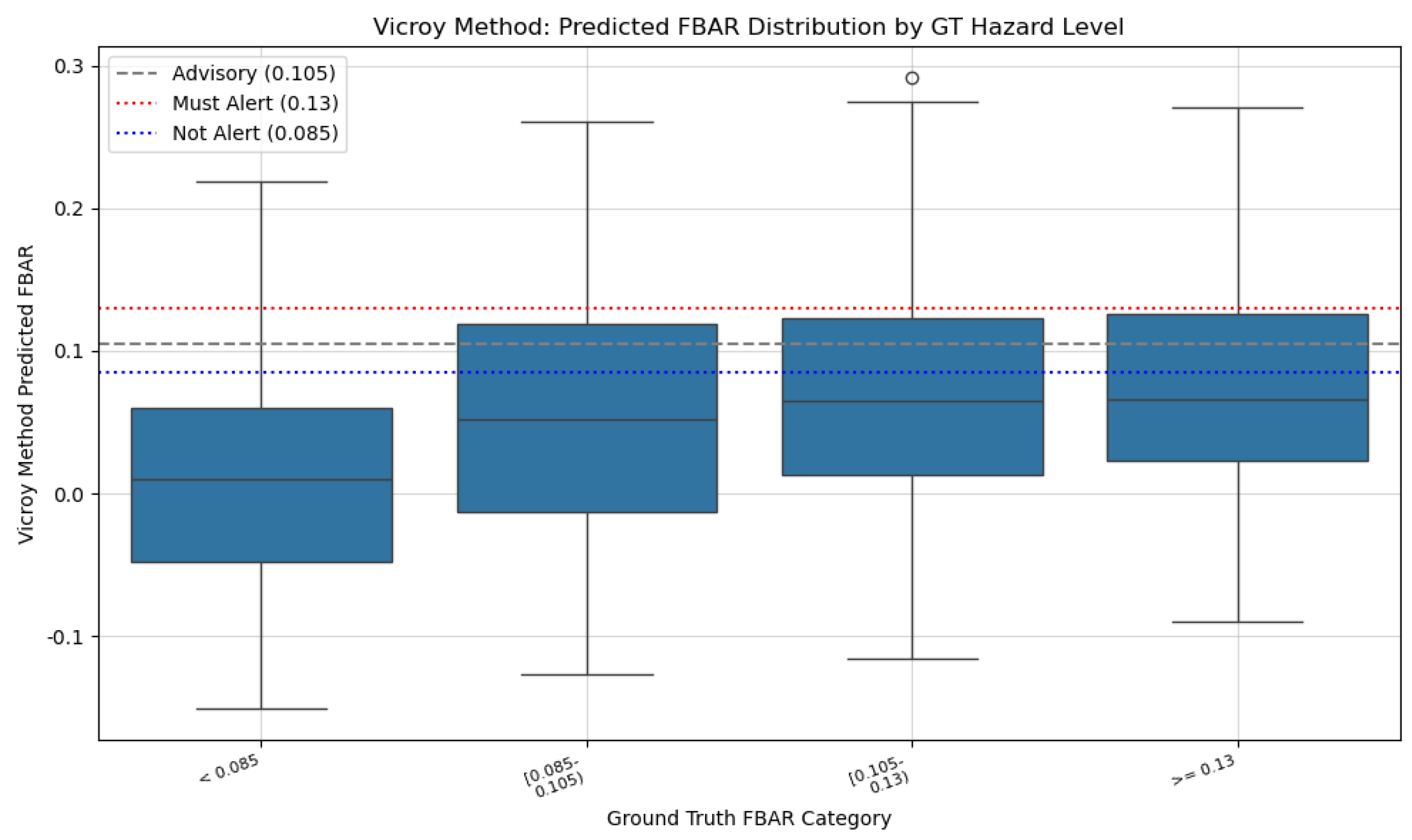
FBAR threshold analysis (Figure 9 and Figure 10) shows the proposed model’s superior classification of FBAR values into hazard categories.

4.4. Performance Comparison with Alternative Machine Learning Methods

A comparative analysis was conducted against alternative ML approaches, as detailed in Section 3.5. Performance is summarized in

Table 5. W${\phantom{,}}_h$ Estimation performance comparison: Proposed model vs. alternative ML methods and Vicroy baseline ^a.

Method	RMSE (m s${\phantom{,}}^{-1}$)	MAE (m s${\phantom{,}}^{-1}$)	Correlation	N (Points)
Vicroy Method (Baseline)	14.3120	11.7693	0.1377	14,524
MLP-Enhanced Vicroy (K-Factor)	10.4716	9.1959	0.0803	204
MLP-Corrected Vicroy ($\Delta W_h$)	7.8752	6.7209	−0.0230	204
Direct $W_h$ MLP (+Ref)	0.8845	0.6445	0.7009	204
Physics-Informed ConvLSTM	0.3763	0.3202	0.7869	1254
Spatio-Temporal Transformer	1.2516	1.1642	0.9100	1010
Proposed CNN-BiLSTM-Attention Model	0.6233	0.3254	0.9736	14,524

^a N (points) for alternative methods reflects their evaluation on specific test subsets as configured in their respective, independent evaluation scripts. This provides a valuable performance benchmark, though a direct one-to-one comparison on the exact same point set for all methods was not part of this study’s scope.

for W${\phantom{,}}_h$ and

Table 6. FBAR prediction performance comparison: Proposed model vs. selected advanced ML methods and Vicroy baseline.

FBAR Source (W${\phantom{,}}_{\mathit{h}}$ Estimate from)	RMSE	MAE	Correlation	N (Points)
Vicroy Method (Baseline)	4.0535	1.1101	0.0801	2105
Physics-Informed ConvLSTM	0.0604	0.0444	0.8903	1952
Spatio-Temporal Transformer	0.0555	0.0306	0.9014	1093
Proposed CNN-BiLSTM-Attention Model	0.0591	0.0434	0.8876	2105

for FBAR.

5. Discussion

The collective results strongly support the hypothesis that a well-designed deep learning model can significantly enhance W${\phantom{,}}_h$ estimation, leading to substantially more accurate FBAR predictions. The proposed model’s RMSE of $0.623$ $\mathrm{m} {\mathrm{s}}^{-1}$ for W${\phantom{,}}_h$ (vs. Vicroy’s $14.312$ $\mathrm{m} {\mathrm{s}}^{-1}$) on the full test set underscores this. The hierarchical structure of the proposed model, processing local features with CNNs (convolutional neural networks), sequential context with BiLSTMs (Bidirectional Long Short-Term Memory), and salient feature weighting with Attention, appears particularly effective. It likely learns to identify precursor patterns in the radar data that are indicative of vertical air motion—relationships that are difficult to encapsulate in fixed empirical rules like those in the Vicroy method. Any perceived differences between the model’s derived F-factor profiles and the raw DFW wind field database are expected, as the model processes simulated radar returns (which include effects like volume averaging) and calculates a derived, smoothed hazard metric (FBAR), rather than directly reporting instantaneous wind speeds. The model’s success suggests an ability to learn a more nuanced and data-adaptive mapping from radar observables to the underlying vertical wind field than is possible with pre-defined physical simplifications. This inherent flexibility as a data-driven pattern-recognition engine suggests the architecture is highly adaptable for other complex atmospheric phenomena, such as turbulence. Unlike traditional methods that rely on rigid, phenomenon-specific rules (e.g., axisymmetry), the proposed model could be retrained on datasets with turbulence metrics (e.g., Eddy Dissipation Rate) to learn their unique radar signatures, offering a versatile tool for a wider range of aviation hazards.

The comparative analysis with alternative machine learning architectures consistently demonstrated the superior or highly competitive performance of the proposed HPO-tuned CNN-BiLSTM-Attention model. While other advanced architectures like the Spatio-Temporal Transformer also surpassed the Vicroy baseline significantly, the proposed model excelled in the fundamental task of W${\phantom{,}}_h$ prediction. This superior W${\phantom{,}}_h$ estimation is crucial, as it forms the physical basis for FBAR calculation; a model that better understands the underlying vertical wind field is theoretically more likely to produce robust FBAR values across a wider range of conditions.

However, the Spatio-Temporal Transformer model, despite strong FBAR performance, exhibited limitations. A key observation was the spatial sparsity of its underlying W${\phantom{,}}_h$ predictions, generating valid estimates for only a small fraction of range gates in the test cases. This sparsity subsequently limited the spatial coverage of the derived FBAR. This contrasts with the proposed CNN-BiLSTM-Attention model, which provides more continuous predictions. This behavior suggests the Transformer architecture might be more sensitive to the completeness of input data windows. In operational scenarios where continuous hazard assessment is critical, this characteristic would need significant improvement.

The model’s compatibility with “clear-air” conditions is demonstrated by its training on entire scan lines, which inherently include not only the high-reflectivity hazardous core but also the surrounding non-hazardous periphery. By learning from these complete sequences, the architecture learns to associate the low-signal characteristics of benign regions with safe, near-zero FBAR outputs. This ability to distinguish non-hazardous clean-air areas from hazardous cores is a key advantage that effectively mitigates the risk of false alerts in the regions adjacent to a weather event.

Despite successes, the proposed model shows some underestimation of peak updrafts and relies on simulated data. From a safety assurance perspective, the systematic development process (HPO, independent testing, documented lifecycle artifacts) aligns with AS6983 principles, providing a foundation for trustworthy ML systems in avionics. The low FAR for hazardous W${\phantom{,}}_h$ detection is operationally encouraging for future integration into civil aircraft safety systems. Furthermore, this foundational study focused on performance with high-quality, complete data; the model’s resilience to missing or incorrect individual inputs has not yet been systematically tested. However, we hypothesize that the architecture, which utilizes a comprehensive set of 10 features and an Attention mechanism, may offer greater robustness than methods reliant on fewer inputs. The model could theoretically learn to down-weigh anomalous data points based on the surrounding spatio-temporal context, a hypothesis that requires rigorous verification.

6. Conclusions

This paper has presented a novel CNN-BiLSTM-Attention deep learning model that demonstrates a transformative improvement in estimating vertical wind speed (W${\phantom{,}}_h$) from simulated airborne radar data, directly enhancing the accuracy of F-Factor Along Track (FBAR) predictions. Compared to the traditional Vicroy method, the proposed model reduced W${\phantom{,}}_h$ estimation RMSE from $14.312$ $\mathrm{m} {\mathrm{s}}^{-1}$ to $0.623$ $\mathrm{m} {\mathrm{s}}^{-1}$. This translated to a 98.5% reduction in FBAR RMSE, showcasing the model’s ability to learn complex, non-linear relationships from radar signatures that empirical models cannot capture. The scientific contribution lies in demonstrating that a hybrid architecture, systematically optimized, can significantly outperform established methods in a complex geophysical estimation task critical to aviation safety.

A significant aspect of this research was the deliberate effort to align the model’s development with the principles of the emerging SAE AS6983 standard. This included systematic data management, robust model design, and comprehensive verification, providing a blueprint for developing and validating ML systems for safety-critical aeronautical applications. The success of this approach underscores the potential for advanced AI to power the next generation of intelligent, data-informed avionics in civil aircraft.

While the results are highly promising, future work is needed to advance the model towards operational readiness:

• Validation on Real-World Airborne Radar Data: This is the most critical next step. Acquiring and evaluating the model on actual flight data are essential to assess its robustness to real-world factors like sensor noise, clutter, and atmospheric variability not present in the simulation.
• Expansion and Diversification of Training Data: The training dataset should be expanded with more ADWRS scenarios representing diverse meteorological phenomena (e.g., gust fronts, different microburst types) and dynamic flight conditions (e.g., varying aircraft attitudes) to enhance generalization.
• Refinement of Model and Training Process: Explore alternative loss functions (e.g., Huber loss, quantile loss) to improve prediction of rare, extreme events and reduce sensitivity to outliers. Conduct formal statistical significance testing to bolster performance claims.
• Explainability, Robustness, and Uncertainty Quantification: To address the critical safety risk of “dangerous residuals” (large prediction errors under specific conditions), a multi-faceted V&V (Verification and Validation) strategy is planned. This includes systematic corner-case testing with simulated sensor noise and edge-of-the-envelope flight conditions. Implementing Explainable AI (XAI) techniques is essential to perform root cause analysis on any significant errors found during testing [26]. Critically, our future work will focus on uncertainty quantification (UQ), enabling the model to output not just a prediction but also a confidence level. This allows the system to flag or disregard low-confidence estimates, providing a crucial safety layer for certification.
• Operational Feasibility Study: Assess computational requirements (inference time, memory) for on-board implementation on representative avionics hardware. This includes exploring model optimization techniques like pruning and quantization.

In conclusion, this research provides compelling evidence that specifically designed deep learning methodologies can revolutionize airborne wind shear detection for civil aviation. The substantial improvements in hazard prediction, coupled with a safety-conscious development process, pave the way for a new generation of more reliable and effective weather avoidance systems, significantly enhancing global aviation safety.