A DSP–FPGA Heterogeneous Accelerator for On-Board Pose Estimation of Non-Cooperative Targets

Abstract

The increasing presence of non-cooperative targets poses significant challenges to the space environment and threatens the sustainability of aerospace operations. Accurate on-orbit perception of such targets, particularly those without cooperative markers, requires advanced algorithms and efficient system architectures. This study presents a hardware–software co-design framework for the pose estimation of non-cooperative targets. Firstly, a two-stage architecture is proposed, comprising object detection and pose estimation. YOLOv5s is modified with a Focus module to enhance feature extraction, and URSONet adopts global average pooling to reduce the computational burden. Optimization techniques, including batch normalization fusion, ReLU integration, and linear quantization, are applied to improve inference efficiency. Secondly, a customized FPGA-based accelerator is developed with an instruction scheduler, memory slicing mechanism, and computation array. Instruction-level control supports model generalization, while a weight concatenation strategy improves resource utilization during convolution. Finally, a heterogeneous DSP–FPGA system is implemented, where the DSP manages data pre-processing and result integration, and the FPGA performs core inference. The system is deployed on a Xilinx X7K325T FPGA operating at 200 MHz. Experimental results show that the optimized model achieves a peak throughput of 399.16 GOP/s with less than 1% accuracy loss. The proposed design reaches 0.461 and 0.447 GOP/s/DSP48E1 for two model variants, achieving a 2× to 3× improvement over comparable designs.

1. Introduction

Non-cooperative targets refer to spacecraft that lack external identification markers and cannot actively transmit information [1]. Their motion trajectories are highly uncertain, posing substantial risks to the operational safety of on-orbit spacecraft. To enhance the autonomy and robustness of space missions, the demand for tasks such as space debris removal and on-orbit servicing is rapidly increasing, placing stricter requirements on onboard computing systems. Representative missions, including ESA’s TECSAS and DEOS [2], NASA’s MEV [3,4] and RSGS [5], and OHB Sweden’s PRISMA [6], have identified autonomous rendezvous with non-cooperative targets in the absence of auxiliary information as a critical research focus. The core challenge lies in perceiving and estimating the relative pose of targets without fiducial markers or prior models [7].

In practical engineering applications, the European Space Agency has identified machine learning as the preferred technological approach for addressing the challenges of pose estimation for non-cooperative spacecraft targets [8]. Traditional image-based algorithms face significant limitations in feature extraction and stability due to factors such as varying illumination conditions in space, low contrast, and constrained viewing angles. With the rapid advancement of deep learning, convolutional neural networks (CNNs) have achieved remarkable progress in object detection [9], semantic segmentation [10], and pose estimation [11], offering effective support for intelligent perception in spaceborne scenarios.

For non-cooperative target pose estimation, current mainstream approaches can be broadly categorized into two paradigms: hybrid modular approaches and end-to-end methods. Hybrid approaches typically involve multiple stages, including target region extraction, keypoint prediction, and pose estimation based on 2D–3D keypoint correspondences. In contrast, end-to-end methods employ unified neural network architectures that directly regress the complete pose representation from image inputs, bypassing intermediate steps and commonly using loss functions based on pose errors for optimization. For example, Phisannupawong et al. [12] developed an efficient pose-estimation network for non-cooperative spacecraft based on an improved GoogLeNet architecture, introducing a weighted Euclidean loss to enhance prediction accuracy. Sharma et al. [13] proposed the Spacecraft Pose Network, which comprises a five-layer convolutional backbone and three branch modules that jointly regress the pose vector. Furthermore, Musallam et al. [14] were the first to incorporate SE(2)-equivariant structures into pose regression tasks. They designed a lightweight model, E-PoseNet, which effectively integrates geometric priors of camera motion and demonstrates superior accuracy and feature efficiency across multiple benchmark datasets.

In the domain of spatial perception, various advanced technological pathways have been developed, including vision-based servo control strategies [15] and autonomous navigation and manipulation for orbital robotic systems [16]. Among these, high-fidelity simulation and validation methods tailored for space applications play a critical role in supporting algorithm development and system testing, particularly in the field of optical visual simulation [17].

Several representative platforms have been widely adopted for the validation of vision-based algorithms. Notable examples include Stanford University’s TRON platform [18] and the robotic arm simulation system developed by the German Aerospace Center (DLR) [19]. These platforms construct high-fidelity visual scenes through realistic lighting and physical modeling, enabling rigorous validation of navigation and recognition algorithms. For the construction of high-quality synthetic image datasets, image synthesis has become the mainstream approach. Common tools such as Unreal Engine, Blender [20], and SurRender [21] support diverse lighting and material simulations, allowing the generation of large-scale, multi-scene, and multi-illumination image datasets. These datasets are extensively used in training pose-estimation and object-detection models.

To enhance pose-estimation accuracy and system generalizability, Duarte et al. [22] proposed an AI-based monocular pose-estimation method and established a co-simulation environment using MATLAB/Simulink and Blender. This setup enabled the generation of multi-scene docking images and the execution of closed-loop simulations with robotic arms and vision sensors. Kaaniche et al. [23] introduced a 3D visual servoing approach that integrates neural network-based pose estimation with differential flatness control, and evaluated its performance using a simulation platform built on the RVCTOOLS toolbox. Shinhye et al. [24] developed a virtual simulation environment in Unreal Engine 4 capable of replicating structural, lighting, and viewpoint variations. They generated keypoint-annotated synthetic images and integrated air bearings, a spacecraft simulator, and an optical motion capture system to form a comprehensive hardware-in-the-loop experimental platform for real-time image acquisition and pose-estimation validation.

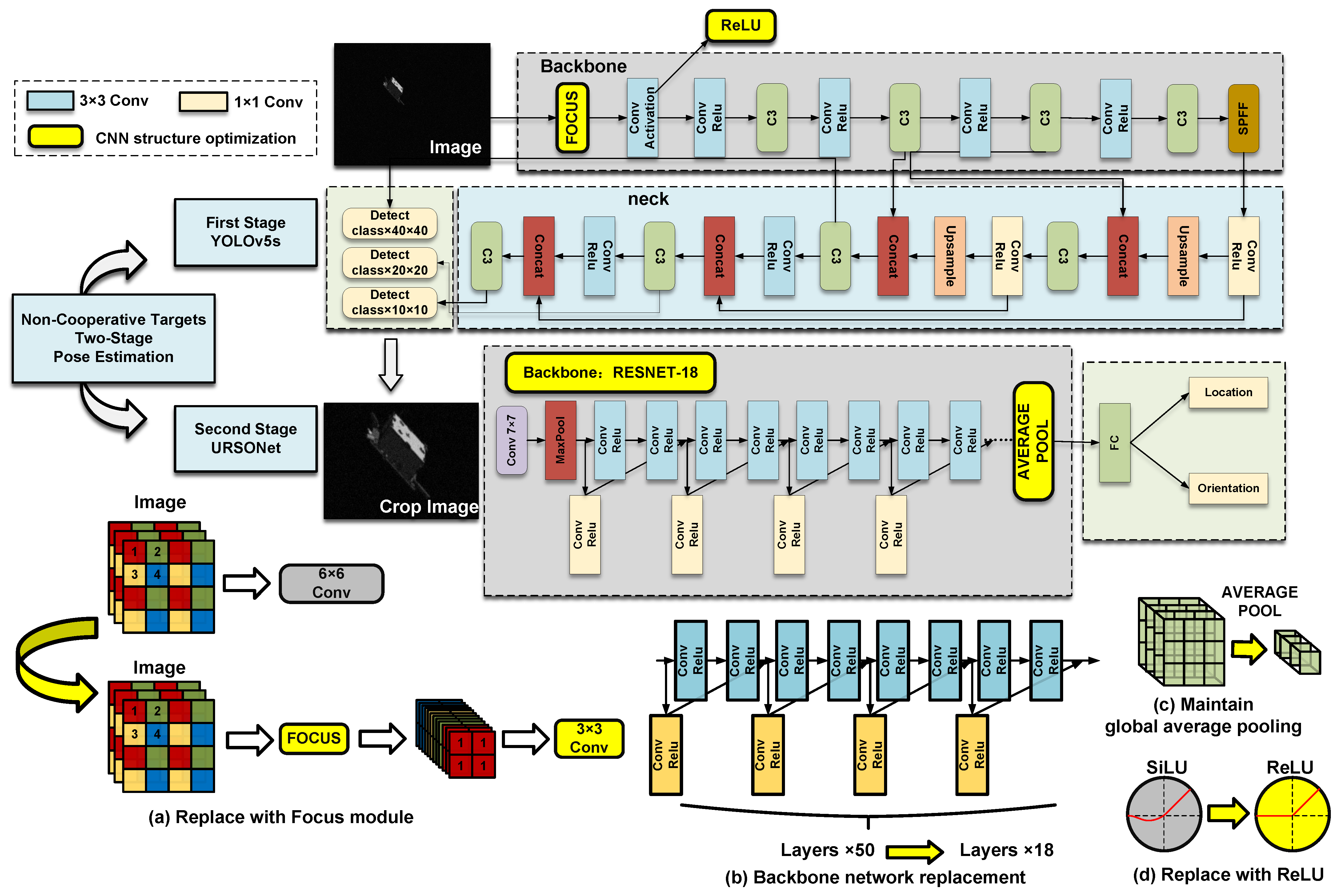
In on-orbit servicing tasks involving non-cooperative targets, developing an intelligent perception system with high robustness and real-time performance is essential for accurately acquiring target position and pose parameters, which are critical for ensuring the successful execution of the mission pipeline. This perception process can be divided into two stages: the first involves determining the existence of the target and performing coarse spatial localization, which is essentially a small-object detection task; the second stage refines this result by regressing the target’s position and pose within the extracted region. To address this, a two-stage CNN-based perception framework is proposed. The first stage employs a lightweight object detection network for rapid localization, while the second stage uses deep feature encoding to regress the target’s pose parameters.

Given the stringent constraints on power consumption and computational resources in spaceborne computing platforms [25,26], the integration of efficient hardware acceleration into neural network design is essential. Traditional spaceborne platforms typically operate within a power envelope of 20 W, while high-performance systems such as SpaceVPX [27] can reach up to 80 W. The third-generation CubeSat standard [28,29,30] specifies a power range of 8–46 W.

In the context of neural network acceleration, GPUs are unsuitable for space applications due to excessive power consumption, and ASICs lack the reconfigurability [31,32] required for model updates. In contrast, FPGAs offer a favorable balance between flexibility and power efficiency, enabling dynamic model adaptation under the evolving demands of space environments. This makes FPGAs an ideal acceleration platform for onboard intelligent perception tasks.

Numerous studies have demonstrated the feasibility of accelerating CNNs on FPGAs, as summarized in

Table 1. The acceleration platforms, models, tasks, and throughput of different neural network accelerators on FPGA.

	Electronics [33]	IEEE IOTJ [34]	Remote Sensing [35]	Remote Sensing [36]
Platform	XC7Z035	XC7Z045	XC7VLX	XC7VX690T
Model	YOLO	U-Net like	YOLO, VGG, ResNet	DeepLab
Task	Object Detection	Segmentation	Object Detection	Segmentation
Performance (GOP/s)	111.5	198.16	386.7, 344.4, 182.3	184.19

. Zhang et al. [33] proposed an optimized implementation of the YOLO network for hardware deployment, presenting a dedicated architecture tailored for remote-sensing object detection. This design, mapped onto an FPGA, achieves a throughput of up to 111.5 GOP/s. Chen et al. [34] developed an efficient accelerator based on a lightweight, low-bandwidth convolutional structure. By adopting a fully pipelined architecture, their design achieves 198.16 GOP/s when executing inference on a UNet-like network. Ni et al. [35] presented algorithm–hardware co-optimization that enabled the deployment of YOLOv2, VGG-16, and ResNet-34 on FPGAs, achieving average throughputs of 386.74 GOP/s, 344.44 GOP/s, and 182.34 GOP/s, respectively. Guo et al. [36] introduced a customized accelerator for spacecraft image segmentation based on the DeepLab algorithm, reaching 184.19 GOP/s using 16-bit quantization. While these designs demonstrate high throughput, they are tailored for specific vision tasks and require complete FPGA reconfiguration when switching models, limiting their applicability in the diverse and dynamic task environments characteristic of spaceborne computing tasks.

However, CNN computation also involves a substantial number of non-convolutional operations, including input data conditioning and output result integration, which must be executed in coordination with general-purpose processors. In recent years, CPU–FPGA heterogeneous platforms have seen significant advances [37,38,39]. However, under spaceborne constraints, DSP–FPGA architectures offer greater advantages in terms of power efficiency and radiation tolerance. Digital Signal Processors (DSPs), architected specifically for signal processing tasks, provide high computational efficiency and low power consumption, making them well-suited for embedded heterogeneous systems.

Based on the aforementioned requirements and analysis, this study proposes a two-stage perception framework and a dedicated hardware acceleration scheme for spaceborne pose estimation of non-cooperative targets. The main contributions are as follows:

• We propose a two-stage pose-estimation framework for non-cooperative targets, incorporating lightweight optimization of the employed networks. In the object detection stage, the YOLOv5s model is utilized, with a Focus module introduced in the initial layer to enhance feature extraction efficiency and ReLU adopted as the activation function. For pose estimation, the framework employs the URSONet architecture with ResNet18 as the backbone. To reduce computational complexity, global average pooling is applied before the fully connected layers. Moreover, to improve hardware adaptability, the model is further optimized through batch normalization fusion, INT8 linear quantization, and ReLU function fusion.
• To support the proposed pose-estimation framework for non-cooperative targets, a prototype FPGA accelerator for CNN models is designed and implemented. The accelerator integrates an instruction scheduling unit and adopts an instruction-driven control mechanism to enable compatible inference across multiple CNN models, thereby avoiding frequent FPGA reconfiguration. A memory slicing mechanism is introduced to manage on-chip data flow efficiently, enabling parallel-pipelined processing across multiple channels. In addition, a weight concatenation strategy is employed to maximize the utilization of the adder tree array, significantly enhancing the acceleration performance of core convolution operations.
• The data conditioning and result integration are deployed on a TMS320C6678 DSP, while the core inference components of the YOLOv5s and URSONet models are mapped onto an XC7K325T FPGA. The FPGA operates at 200 MHz with a measured power consumption of 7.241 W, achieving a peak throughput of 399.16 GOP/s. Under this configuration, the YOLOv5s model reaches an inference speed of 64.43 FPS, and the URSONet model achieves 62.31 FPS, corresponding to energy efficiencies of 8.898 FPS/W and 8.605 FPS/W, respectively.

2. Two-Stage Pose Estimation Framework for Non-Cooperative Targets

2.1. Algorithm Framework

In spaceborne missions, pose estimation of non-cooperative targets is a critical component for enabling autonomous rendezvous and manipulation. Constrained by mission-specific requirements and the limited onboard computational resources, the servicing spacecraft relies on onboard vision sensors to capture images of the target and performs real-time processing on embedded platforms.

Regression-based object detection methods offer a favorable balance between detection speed and accuracy, making them well-suited for real-time applications [40,41,42,43,44,45,46]. Since the emergence of the YOLOv4 [43] algorithm, the SSD [40] family has exhibited significantly slower inference speeds compared to the YOLO series. The YOLO models achieve faster inference while maintaining high detection accuracy. Among them, YOLOv7 [46] demonstrates outstanding performance in both inference speed and detection accuracy; however, its large number of parameters poses challenges for deployment on resource-constrained edge devices.

Considering the application scenario in this study involves detecting only non-cooperative targets—with far fewer categories than those in the COCO [47] dataset—we trained and compared several YOLO models on our custom dataset, SPEED-DET2k (SPEED [48]). The results are presented in

Table 2. Performance of YOLO series models on the SPEED-DET2k dataset (Performance evaluated using ONNX TOOL. Computational complexity refers to the number of multiplication and addition operations during convolution).

Model	Parameter	mAP@0.5	Complexity (GOPS)
YOLOv3-tiny	8.27 M	80.19%	1.734
YOLOv5s	6.69 M	81.82%	2.175
YOLOv7	34.79 M	84.44%	13.63

. Although the YOLOv5s model exhibits lower accuracy compared to YOLOv7, the latter contains approximately 5× more parameters and has about 6.3× higher computational complexity. To strike a balance between detection performance and model size, this study ultimately selects YOLOv5s as the detection model for non-cooperative targets and further optimizes it to meet the inference requirements of the target hardware platform.

Once the non-cooperative target is effectively detected, its attitude is subsequently estimated. In this stage, URSONet [11] is employed as the pose-estimation model. URSONet is an end-to-end regression network built upon a ResNet backbone. It incorporates two fully connected branches: one regresses the 3D position based on a relative error minimization objective, while the other adopts a soft classification strategy by discretizing the attitude into a 3D histogram of Euler angles. A Gaussian kernel is used to generate a soft-label probability distribution for the ground-truth attitude. The network outputs a probability distribution over the discretized angular bins. Finally, a weighted least squares fitting is performed on this distribution to obtain a continuous quaternion-based pose-estimation result.

Based on the above process, we propose a two-stage pose-estimation framework, as illustrated in Figure 1. The proposed framework achieves a coarse-to-fine cooperative optimization from object detection to attitude regression. In the first stage, a lightweight object detection network, YOLOv5s, is employed to rapidly capture and coarsely localize the non-cooperative target. In the second stage, the URSONet network is employed to estimate the attitude of the non-cooperative target within the cropped image.

2.2. Algorithm Optimization

CNN-based algorithmic frameworks face practical constraints during deployment in onboard space environments, including limited computational resources and strict power consumption requirements. To address these challenges, hardware-aware optimization of neural network models is essential to enable efficient deployment on FPGA platforms. A series of optimization strategies tailored for neural network models are adopted in this study to effectively reduce inference complexity, minimize resource consumption, and enhance processing speed.

During the training of CNN algorithms, batch normalization is commonly introduced to accelerate convergence and effectively mitigate overfitting. Batch normalization layers are typically placed after convolutional layers to normalize their outputs, thereby stabilizing feature distributions. However, during inference, the independent computation of batch normalization introduces additional computational overhead. To address this, the first optimization strategy adopted in this work is the fusion of convolution and batch normalization operations, which reduces operator complexity and improves inference efficiency.

During the inference stage, the batch normalization operation is formulated as Equation (1).

$$\mathrm{BN}\left(y\right)=\gamma ·{\displaystyle \frac{y-\mu }{\sqrt{{\sigma }^2+ϵ}}}+\beta$$

(1)

where y denotes the output of the convolutional layer, $\mu$ and ${\sigma }^2$ represent the mean and variance, respectively, $ϵ$ is a small constant to prevent division by zero, and $\gamma$ and $\beta$ are learnable scaling and shifting parameters.

To achieve the fusion of the two operations, batch normalization is directly applied to the output of the convolutional layer as Equation (2).

$$\mathrm{BN}(W\ast x+b)=\gamma ·{\displaystyle \frac{W\ast x+b-\mu }{\sqrt{{\sigma }^2+ϵ}}}+\beta$$

(2)

By rearranging the expression, the fused weight $\tilde{W}$ and fused bias $\tilde{b}$ can be derived as Equations (3) and (4).

$$\tilde{W}={\displaystyle \frac{\gamma }{\sqrt{{\sigma }^2+ϵ}}}·W$$

(3)

$$\tilde{b}={\displaystyle \frac{\gamma }{\sqrt{{\sigma }^2+ϵ}}}·(b-\mu )+\beta$$

(4)

Another optimization strategy is model quantization. Previous studies [49,50] have shown that quantization can significantly reduce computational overhead by lowering data precision, while largely preserving model accuracy. In this work, 8-bit quantization is employed to optimize the model, aiming to achieve a favorable trade-off among energy efficiency, resource consumption, and inference performance, thereby enhancing overall execution efficiency. In the quantized computation, feature maps are quantized to the UINT8 format, while weights are quantized to the INT8 format. The quantized operation can be expressed as Eqution (5).

$$\begin{array}{cc}\hfill X_q& =\mathrm{round}\left({\displaystyle \frac{X}{S_X}}\right)+Z_X\hfill \\ \hfill W_q& =\mathrm{round}\left({\displaystyle \frac{W}{S_W}}\right)+Z_W\hfill \end{array}$$

(5)

Here, X denotes the feature map, W the weights, $S_X$ and $S_W$ the scaling factors for features and weights, respectively, $Z_X$ and $Z_W$ the corresponding zero-point offsets, and $X_q$ and $W_q$ the quantized representations of the feature map and weights.

During quantization, the convolution operation can be fused with the ReLU activation function to further reduce computational overhead during inference. The ReLU function is defined as Equation (6).

$$\mathrm{ReLU}\left(y\right)=\left\{\begin{array}{cc}y,\hfill & y>0\hfill \\ 0,\hfill & y\le 0\hfill \end{array}\right.$$

(6)

After the convolution operation, a clipping step is required to constrain the output within the quantized range. In the floating-point domain, the ReLU activation is computed as $\max (0,Y)$, while in the quantized domain, it becomes $\max (Y_q,Z_Y)$. Therefore, the ReLU function can be fused into the convolution operation, and the subsequent clipping operation becomes Equation (7).

$$Y_q=min\left(max\left(\mathrm{round}\left({\displaystyle \frac{S_X·S_W}{S_Y}}·y\right)+Z_Y,Z_Y\right),255\right)$$

(7)

Here, $Y_q$ denotes the quantized output, $S_Y$ represents the scaling factor of the output and $Z_Y$ represents the zero-point offset of the output.

For the YOLOv5s architecture, we introduce a modification to its first layer by replacing it with a Focus module, as illustrated in Figure 1a. In the original YOLOv5s, the first layer employs a large 6 × 6 convolution kernel for feature extraction, resulting in a high computational cost. The Focus module, in contrast, performs slicing and channel concatenation on the input image, dividing the original three-channel image into four spatial sub-regions and concatenating them along the channel dimension. This operation reduces the spatial resolution of the feature map while enhancing channel-wise feature representation. It effectively decreases the kernel size required in subsequent convolutional layers and is better suited for hardware-efficient inference. In our design, the slicing and concatenation operations of this module are mapped to the DSP module, further improving overall computational efficiency. Additionally, to align with the post-quantization ReLU fusion strategy described in Equation (7), the SiLU activation function is replaced with ReLU, as shown in Figure 1d.

We conducted a performance comparison of the YOLOv5s model with respect to two factors: the choice of activation function and the use of the Focus module. The experimental results are presented in

Table 3. Performance comparison of YOLOv5s with various optimizations (dataset: SPEED-DET2k).

Optimization			mAP@0.5		Complexity (GOPS)
SiLU	ReLU	Focus	FP32	INT8
✓			81.82%	81.80%	2.175
	✓		81.46%	81.77%	1.985
	✓	✓	81.66%	81.43%	1.985

The check mark indicates that the activation function or structure has been selected or implemented.

. Additionally, we compared the mAP@0.5 of three model variants under FP32 and INT8 quantization. The accuracy loss was found to be less than 1%, demonstrating the feasibility of model quantization.

For the URSONet architecture, we first replace its original backbone network, ResNet50, with a more lightweight ResNet18, as illustrated in Figure 1b, to better accommodate resource-constrained applications with strict real-time requirements. ResNet18 contains fewer parameters and offers faster inference, making it more suitable for deployment on platforms with limited computational resources, such as FPGAs. Moreover, the global average pooling layer that was removed in the original URSONet is retained in our design, as shown in Figure 1c. This structure effectively reduces the dimensionality of the feature representation while significantly decreasing the computational cost of the subsequent fully connected layers. Models corresponding to different numbers of discretized orientation bins are trained and evaluated, and the relevant experimental results are summarized in

Table 4. URSONet model size and complexity under different bin settings (using average pooling before fully connected layers).

Bins	Parameter	Complexity (GOPS)
4	10.69 M	≈3.716
8	10.91 M	3.716
12	11.50 M	3.717
16	12.65 M	3.718
24	17.42 M	3.723

.

In summary, YOLOv5s-ReLU-Focus is selected as the inference network for the object detection task, while URSONet-ResNet18 is employed for pose estimation. The detailed inference performance of both models on the validation dataset will be evaluated and analyzed in Section 4.

3. System Architecture of the DSP–FPGA Heterogeneous Accelerator

3.1. Algorithmic Flow of the DSP

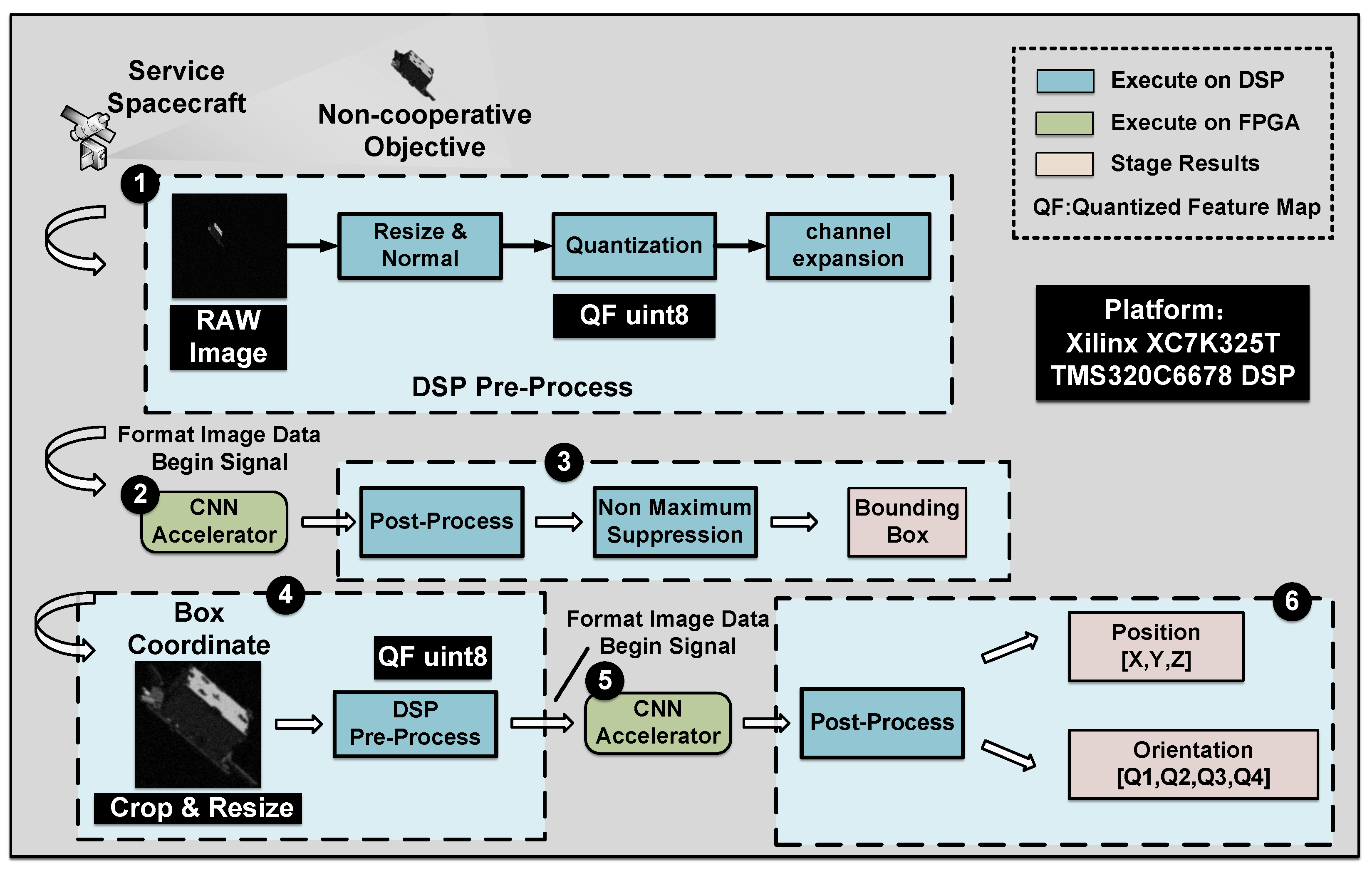
The acceleration flow of the DSP component in the proposed DSP–FPGA heterogeneous accelerator is illustrated in Figure 2.

The captured raw image is first resized to a fixed resolution compatible with the model input requirements of the YOLOv5s (Step 1). The Resize and Normal modules standardize the input image in terms of scale and value to meet the model requirements. Specifically, the Resize operation employs bilinear interpolation to adjust the image to a fixed resolution, ensuring consistency in network input size. The Normal operation linearly maps pixel values from the [0, 255] range to [0, 1], preserving the data distribution used during training and thereby maintaining inference accuracy and consistency. The Quantization module maps floating-point values to 8-bit integers based on the quantization rule defined in Equation (5). The Channel Expansion module increases the number of input image channels to 32 by zero-padding the additional channels. This design aligns the input data format with the hardware accelerator, ensuring compatibility with the channel-wise parallel architecture of the FPGA computing units.

Upon receiving the inference start signal, the FPGA executes the main body of the neural network using a predefined 512-bit instruction to accelerate inference (Step 2). The inference results of the YOLO model are then transmitted back to the DSP via the SRIO interface.

The DSP post-processing module (Step 3) first applies the Sigmoid activation function to the detection outputs from the three scales produced by the FPGA, yielding normalized class confidence scores and bounding box parameters. It then decodes the activated outputs by converting relative offsets into absolute bounding box coordinates in the image space and extracts the associated confidence scores for target filtering and final result generation. The Non-Maximum Suppression (NMS) module eliminates redundant candidate boxes with low confidence or high overlap, retaining only the most confident and spatially distinct detections. This enhances the accuracy and uniqueness of the final detection results.

Based on the final detection results, regions containing non-cooperative targets are cropped from the original image, producing target-focused images with a higher object-to-background ratio to improve the accuracy and robustness of feature extraction in the subsequent pose-estimation stage.

For the cropped images, the same pre-processing steps as those used in the YOLOv5s model are applied (Step 4). The pre-processed images are then fed into the FPGA, which accelerates the inference of the pose-estimation network (Step 5).

The resulting output vector is transmitted back to the DSP via the SRIO interface and includes both the position vector and the orientation distribution of the target. The position vector is directly output without requiring further decoding or coordinate transformation. The orientation vector represents a probabilistic histogram of the target’s pose. A Softmax operation is first applied to obtain a normalized probability distribution. The final quaternion-based pose is then derived via weighted averaging (Algorithm 1), where the probabilities are used to construct a covariance matrix over the set of candidate quaternions. The eigenvector corresponding to the largest eigenvalue of this matrix is extracted to effectively fuse the directional probabilities into a single pose estimate (Step 6).

Algorithm 1 Weighted quaternion average

Require: Predicted quaternions $\{Q_1,Q_2,\dots ,Q_N\}$, confidence weights $\{w_1,w_2,\dots ,w_N\}$ Ensure: Averaged quaternion $q_{\mathrm{avg}}$     Initialize matrix $A\leftarrow {\mathbf{0}}_{4\times 4}$     for $i=1$ to N do         $A\leftarrow A+w_i·Q_i{Q}_i^{\top }$     end for     Perform eigen-decomposition: $A=V\mathsf{\Lambda }{V}^{-1}$     Let $q_{\mathrm{avg}}\leftarrow$ eigenvector of A with the largest eigenvalue     Normalize: $q_{\mathrm{avg}}\leftarrow q_{\mathrm{avg}}/\parallel q_{\mathrm{avg}}\parallel$     return $q_{\mathrm{avg}}$

3.2. Architecture of the FPGA-Based Hardware Accelerator

As shown in Figure 3, the model trained in PyTorch 1.8.0 is first converted into ONNX format and then quantized using ONNX Runtime. The model weights are quantized to 8-bit signed integers, while bias parameters are quantized to 32-bit signed integers, resulting in a quantized ONNX model. During the Parameter Extract stage, quantized weights and biases (denoted as $Q_W$ and $Q_B$) are extracted layer by layer and saved as binary files. The weight data $Q_W$ is then reformatted according to the requirements of the FPGA computing units, following the layout defined in Algorithm 2. In the Instruction Compile stage, a corresponding 512-bit control instruction is designed for each operator in the ONNX model. Finally, the quantized weights are stored in the onboard SDRAM of the FPGA, while the bias parameters and compiled instructions are loaded into the on-chip BRAM.

Algorithm 2 Parameter Extract: Aligned Weight Packing for FPGA format

Require: Weight tensor $W\in {\mathbb{Z}}^{M\times N\times K\times K}$ Ensure: Packed stream with 32-channel alignment     $W_T\leftarrow \mathrm{reshape}\left(\mathrm{transpose}(W,(0,2,3,1))\right)$     $T\leftarrow \mathrm{length}\left(W_T\right)$     $N_{32}\leftarrow ⌈{\displaystyle \frac{N}{32}}⌉\times 32$     $offset\leftarrow 0$, $remain\leftarrow T$, $s\leftarrow 0$     while $remain>0$ do        $l\leftarrow min(32,N-s)$        $v\leftarrow W_T[offset:offset+l]$        Pad v with zeros to length 32 if $l<32$        $offset\leftarrow offset+l$        $s\leftarrow 0$ if $s+32\ge N$ else $s+32$        $remain\leftarrow remain-l$     end while

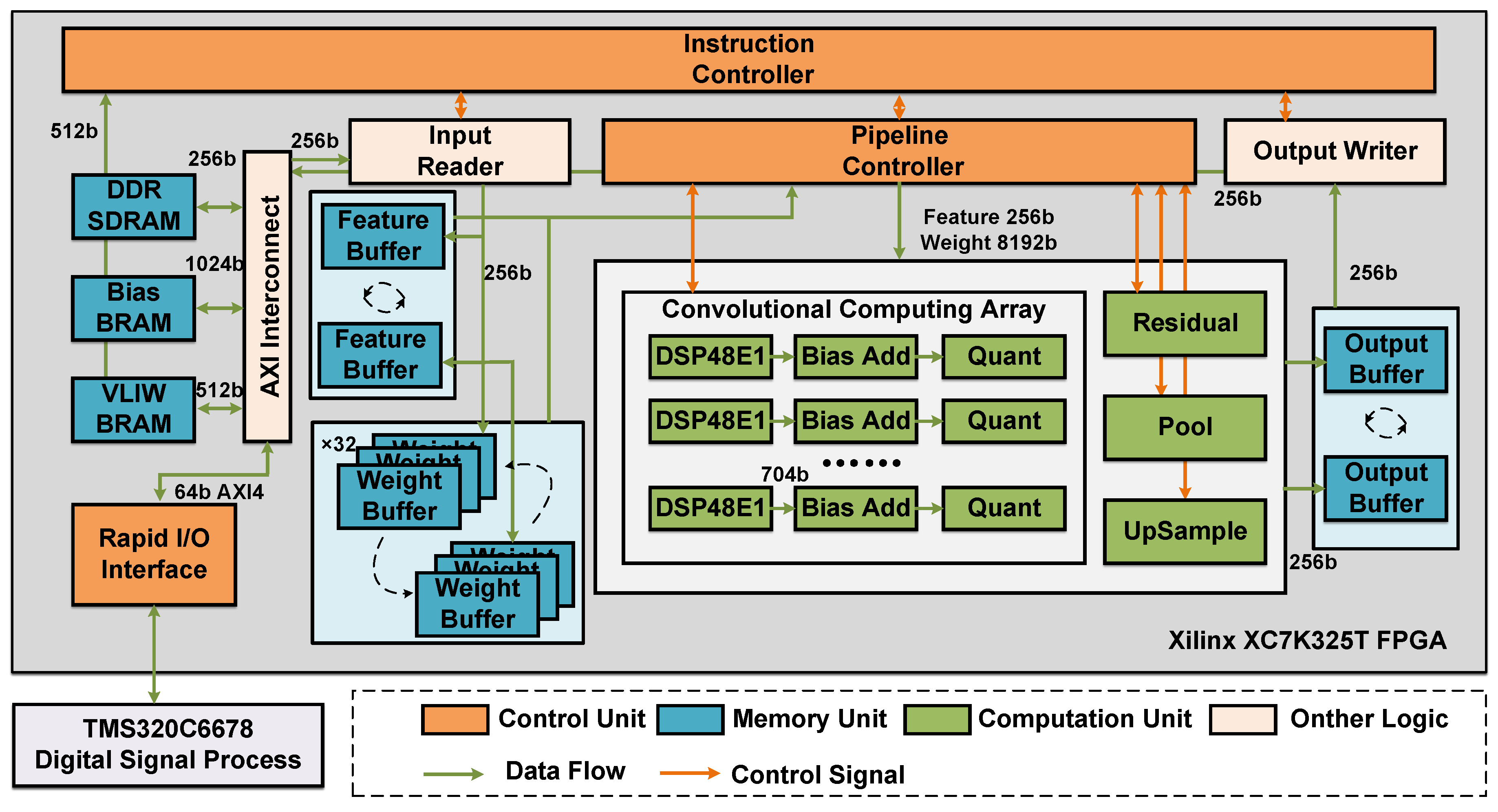
As illustrated in Figure 4, the FPGA hardware accelerator is composed of three main components: a control unit, a memory unit, and a computation unit. These units operate collaboratively to enable efficient data processing and computational acceleration.

The control unit consists of an instruction controller and a pipeline controller. The instruction controller reads instructions from the instruction memory, decodes them, and generates the corresponding control signals. It is responsible for synchronizing and coordinating the operation of various modules to ensure the orderly execution of neural network inference. The pipeline controller breaks down complex logic operations into multiple stages, reducing latency in each stage and ensuring stable system operation at high clock frequencies. The RapidI/O interface module is responsible for data communication with heterogeneous DSP devices, enabling efficient data exchange and instruction transmission.

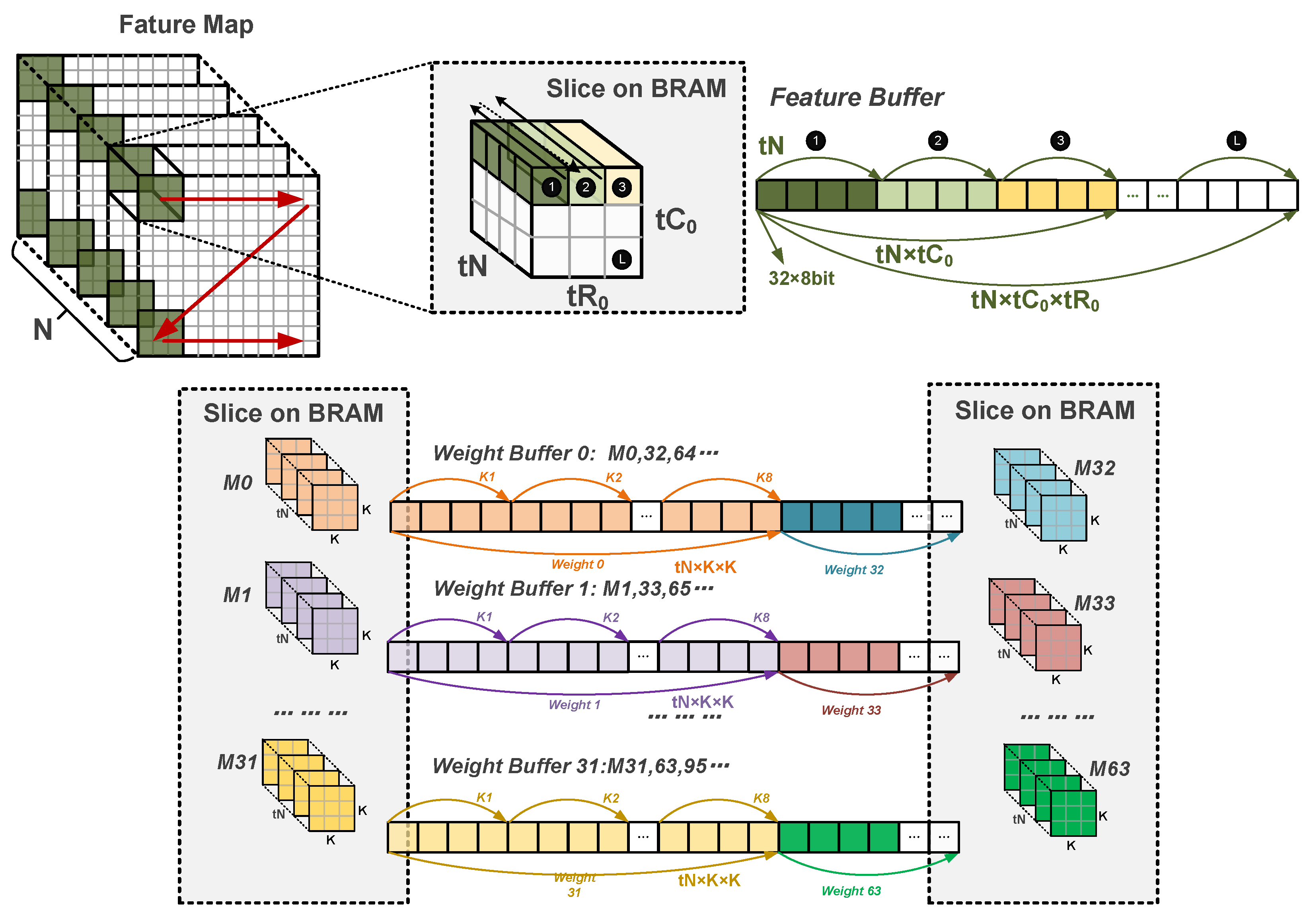
The memory unit consists of off-chip DDR SDRAM and on-chip BRAM. The BRAM is organized into several functional units, including a bias buffer, an instruction buffer, two feature buffers, sixty-four weight buffers, and two output buffers. The AXI Interconnect module facilitates communication between the memory unit and on-chip logic. Data required for computation, such as feature maps and weights, are fetched from the DDR via the AXI bus and processed by the Input Reader module, which slices the data and loads it into the on-chip Feature Buffers and Weight Buffers. Computation results stored in the Output Buffers are sliced and written back to the DDR via the Output Writer module through the AXI bus. To optimize data access and computation efficiency, all on-chip buffers adopt a ping-pong buffering scheme, which minimizes idle time in the convolution computing array and significantly enhances overall system performance.

The computation unit comprises the convolution computing array along with several functional modules responsible for post-processing, including the convolution array module, bias addition module, quantization module, pooling module, residual connection module, and upsampling module. The convolution computing array consists of a DSP48E1 array and an adder tree array, designed to perform the multiply-accumulate operations in convolution. To maximize the utilization of limited on-chip DSP48E1 resources, the design adopts a resource-sharing strategy to enhance both resource efficiency and parallelism of multiply-accumulate operations. To further improve computational throughput, the array employs a DoubleMAC weight concatenation scheme, in which two 8-bit weights are combined into a 25-bit input and multiplied with an 8-bit feature map value. This enables two multiplication operations per cycle within a single DSP48E1 unit without additional resources overhead, thereby fully exploiting its bit-width capacity.

The bias addition module performs element-wise addition of the accumulated convolution result with the corresponding bias values. The quantization module compresses the output to 8-bit signed integers to meet the requirements of subsequent storage and computation. The pooling module uses max pooling or average pooling for downsampling, and outputs the maximum or average value within each window. The residual connection module adds the outputs of two convolution layers on a pixel-wise and channel-wise basis to preserve feature information. The upsampling module restores the spatial resolution of feature maps by doubling their width and height using nearest-neighbor interpolation.

3.2.1. Control Unit Design

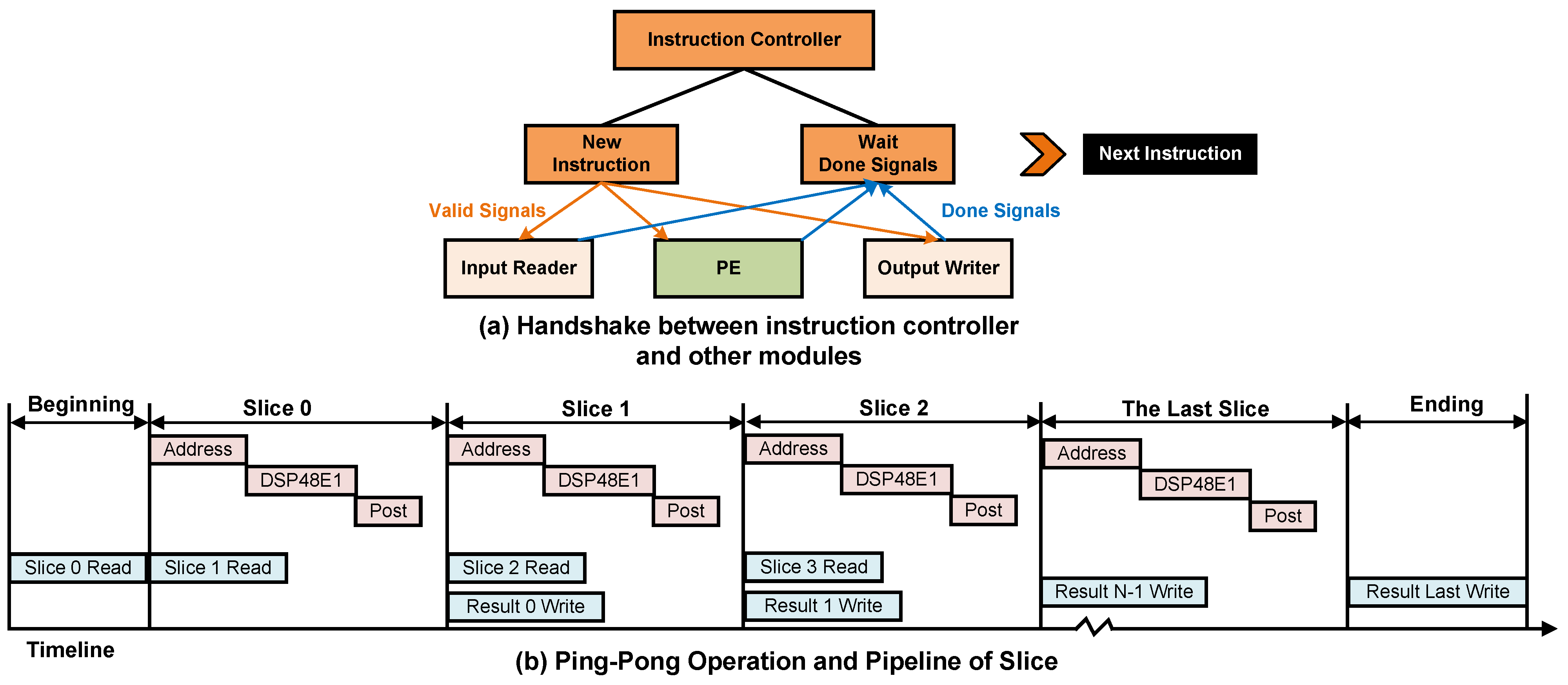
As shown in Figure 5a, the instruction controller is primarily responsible for generating handshake signals to control the Input Reader, Processing Element (PE), and Output Writer. When a new instruction begins decoding, the controller sends valid signals to each module, indicating the start of execution. Upon receiving the valid signal, each module performs its designated operation. Once the current instruction is completed, each module returns a Done signal. After receiving Done signals from all modules, the instruction controller proceeds to fetch and execute the next instruction.

In the control module of the FPGA accelerator, the pipeline controller serves as the core component. It is responsible for coordinating the data-read, computation, and write-back processes within the on-chip BRAM across the entire computation module. Once the data slices loaded from DDR are written into BRAM, all subsequent read and computation operations are scheduled and managed by the pipeline controller.

The pipeline controller is designed with a three-stage hierarchy. The first stage is the BRAM address generation pipeline, responsible for producing read addresses. The second stage is the computation pipeline of the DSP48E1 array, which performs the core multiply-accumulate operations. The third stage is the post-convolution processing pipeline, which carries out operations such as bias addition and quantization. The close coordination among these three pipeline stages enables efficient on-chip data flow, thereby achieving fast operator-level inference acceleration.

To further improve throughput, an on-chip ping-pong buffering mechanism, as illustrated in Figure 5b, is introduced into the pipeline control process. While the current data slice is being processed, the controller pre-fetches the next slice from DDR and concurrently writes back the results of the previous slice to DDR. This enables parallel execution of data loading, computation, and write-back processes, thereby enhancing overall processing efficiency.

3.2.2. Memory Unit Design

The majority of data in convolution operations is concentrated in the input feature maps and convolution weights, with total data sizes typically reaching several megabytes. For instance, in a spacecraft satellite target detection model, the weights occupy 6.67 MB, while the quantized and channel-expanded feature maps reach 3.125 MB. However, the Xilinx XC7K325T FPGA  (Xilinx is an FPGA design and manufacturing company headquartered in San Jose, CA, USA. It has long focused on the development of programmable logic devices and adaptive computing platforms, with a significant influence in the field of high-performance reconfigurable computing.) is equipped with only 445 on-chip BRAM blocks of 36 Kb each, yielding a theoretical total capacity of approximately 1.95 MB. This is insufficient to store all weights and feature maps of the entire network simultaneously. Therefore, the system adopts a slicing strategy to load data into the FPGA progressively and on demand.

The data slices required for each layer’s computation are scheduled by the instruction controller. The on-chip logic dynamically partitions and accesses the corresponding data segments, enabling block-wise management of both feature maps and weights. This mechanism not only reduces reliance on external pre-processing but also simplifies the data preparation process prior to FPGA input, thereby enhancing the overall efficiency of data handling within the system.

The feature buffer has a width of 256 bits, capable of storing 32 channel values for a single pixel. In convolution operations, the feature map is first sliced along the channel dimension. If the last slice contains fewer than 32 channels, zero-padding is applied to complete the block. After storing all channel values for a given pixel, the next pixel in the column direction is stored. Once a column is filled, storage proceeds to the next row of pixels. The storage order in the feature buffer follows the sequence of depth (channel), column, and row dimensions.

The weight buffer also has a width of 256 bits, storing 32 channel values of convolutional kernels. The convolution operations primarily involve 1 × 1 and 3 × 3 kernels (excluding the first layer of ResNet), which are relatively small in size. A total of 32 small-capacity BRAMs are used to store the weights, with each kernel assigned to a weight buffer according to a modulo-32 mapping based on its index (e.g., M33, representing the 33rd output channel, is stored in Weight Buffer 1). Within each weight buffer, the input channels of the convolution kernel are stored first, followed by the two spatial dimensions of the kernel. Once 32 kernels are stored, the process loops back to the first weight buffer, continuing the modulo-32 storage pattern.

The output buffer follows the same storage format as the feature buffer, storing data in the order of depth (channel), column, and row dimensions. The sliced storage format of the on-chip buffers is illustrated in Figure 6.

3.2.3. Convolutional Array Design

The convolution operations in the proposed algorithm model primarily involve 1 × 1 and 3 × 3 kernels, both computed using a convolution array built with Xilinx DSP48E1 hard cores. The convolution array consists of 16 adder tree structures, each comprising 32 DSP48E1 units that perform multiply-accumulate operations.

To achieve more efficient utilization of on-chip DSP48E1 hard cores, the convolution array adopts the DoubleMAC design scheme [51], as illustrated in Figure 7b. This design leverages the maximum multiplication capability of DSP48E1—supporting up to 25-bit × 18-bit operations—by adjusting the multiplier width to 25 bits, thereby enabling two 8-bit fixed-point multiplications within a single DSP48E1 unit. Accordingly, feature maps are quantized to 8-bit unsigned integers, while weights are quantized to 8-bit signed integers. This approach effectively doubles the computational efficiency of DSP48E1 resources, significantly improving hardware utilization and reducing overall resource consumption.

$$\begin{array}{cc}\hfill A\times B& =(-a_{n-1}·2^{n-1}+\sum _{i=0}^{n-2}{a}_i·2^i)·B\hfill \\ \hfill & =(a_{n-1}·(2^{n-1}-2^n)+\sum _{i=0}^{n-2}{a}_i·2^i)·B\hfill \\ \hfill & =(a_{n-1}·2^{n-1}+\sum _{i=0}^{n-2}{a}_i·2^i)·B-a_{n-1}·2^n·B\hfill \\ \hfill & =A^{\prime }·B-a_{n-1}·2^n·B\hfill \\ \hfill & =A^{\prime }·B-(a_{n-1}<<n)·B\hfill \end{array}$$

(8)

After splicing the weights, the $ResultLow$ part needs to be corrected. This is because the lower 8-bit data, when concatenated, are treated as unsigned numbers for multiplication. To ensure the accuracy of the computed results, correction through subtraction is required after the computation. The correction operation follows Equation (8), where $A=a_{n-1}\dots a_1{a}_0$ represents a n-bit signed integer. It is represented in complement form, where $a_{n-1}$ denotes the sign bit. Thus, $A=-a_{n-1}·2^{n-1}+{\sum }_{i=0}^{n-2}{a}_i·2^i$. B is a n-bit unsigned integer, and $A^{\prime }={\sum }_{i=0}^{n-1}{a}_i·2^i$ represents the value of A interpreted as an unsigned number.

Figure 7c illustrates the correction process for the multiplication of −5 and 7. In the DSP48E1, −5 in the lower-weight position is interpreted as 251 due to two’s complement representation, resulting in an intermediate product of 1757. To apply the correction, the sign bit 1 of −5 is bit-wise ANDed with each bit of 7; the result is then left-shifted by 8 bits and subtracted from 1757, yielding the correct result of −35.

Based on the principle of Equation (8) and the structural characteristics of the DSP48E1 hard core, we designed the hardware circuit illustrated in Figure 7d. Specifically, two signed 8-bit weight values are concatenated to form a 25-bit wide input, which is fed into the DSP48E1 input port. Since the feature map data is unsigned, a leading zero is appended to form a 9-bit input to ensure that the multiplier correctly interprets the data as unsigned. The multiplication produces a 34-bit output due to the 9-bit multiplicand, which introduces additional high-order bits in the result. This output is then split into two valid 16-bit partial results. For the correction of the lower-weight term, the sign bit is extracted and bit-wise ANDed with the feature map data; the result is left-shifted by 8 bits and subtracted from the lower partial product to achieve correction. This structure enables two weight multiplications with a single DSP48E1 unit, thereby doubling computational efficiency.

Figure 8 illustrates the architecture of the designed convolution computing array, which integrates a total of 512 DSP48E1 hard cores. Each row of DSP48E1 units constitutes a convolution array group, with each group comprising 32 DSP48E1 units and producing the convolution results of two kernels. Each DSP48E1 receives a 25-bit input formed by concatenating two 8-bit signed quantized weights, along with an 8-bit unsigned quantized feature map input. After slicing by the storage module, the feature map data is loaded into the Feature Buffer, while the weight data is distributed across 32 Weight Buffers. The 256-bit feature map is divided into 32 registers, each holding 8-bit data. The weight data comprises 8192 bits, corresponding to 32 convolution kernels, each with 256 bits of quantized weights. Each convolution array group is equipped with 64 registers to store the 32-channel weights for two convolution kernels. The 32-channel feature map data is broadcast to 16 convolution array groups, enabling parallel convolution computation between the 32 channels and 32 kernels.

The computation process of the convolutional array can be formalized as Algorithm 3, which systematically describes the mapping and computational flow among the input feature maps, weights, and output feature maps.

DSP48E1-based multiplication pipeline: Taking $\mathrm{DSP}48\mathrm{E}1(0,i)$ as an example (where $i=0,1,2,\dots ,31$), each unit in this array group reads the corresponding 32-channel feature map data from registers $Re{g}_0$ to $Re{g}_{31}$, where $Re{g}_i$ is mapped one-to-one with $\mathrm{DSP}48\mathrm{E}1(0,i)$. The weight data are fetched from $WRe{g}_0$ and $WRe{g}_{16}$, concatenated in DoubleMAC mode to form a 25-bit input, and fed into the DSP48E1. Within the DSP48E1, the feature map and weight inputs undergo multiplication; the high part of the product is stored in register $R_1$, while the low part is stored in register $R_0$. The low part is further corrected through a post-processing operation, and then both $R_0$ and $R_1$ are forwarded to the subsequent adder tree array for accumulation.

Adder tree for partial sum accumulation: The adder tree array performs pair-wise additions on the multiplication results stored in the 32 registers. Through 16 groups of adder trees, 32 intermediate results are generated, representing the partial sums of 32 channels at a single pixel location. Taking a convolution kernel window as the processing unit, if not all input channels have been processed or the current kernel window has not been fully traversed, partial sums are retained in the Reg registers and accumulated iteratively in subsequent cycles. In each cycle, new multiplication results are added to the stored partial sums. Once all input channels and all positions within the kernel window have been processed, no further accumulation is performed, and the current result is output. This output corresponds to the complete convolution results of the 32 kernels across all input channels.

Bias Addition Operation: After the convolutional multiply-accumulate operations are completed, bias addition is performed. The bias values are pre-stored in the on-chip Bias BRAM as 32-bit integers, totaling 1024 bits, and are individually added to the convolution outputs of the 32 channels to complete the bias addition process.

Quantization with rounding and clamping: Following bias addition, quantization is applied to compress the results into an 8-bit representation. This process combines multiplication and bit-shifting operations to enhance hardware efficiency.

Algorithm 3 Convolutional Array Operation Pipeline

Require: $F_{\mathrm{in}}\in {\mathbb{Z}}^{32\times 3\times 3}$, $W\in {\mathbb{Z}}^{32\times 32\times 3\times 3}$, bias $b\in {\mathbb{Z}}^{32}$, scale factor $\lambda$ Ensure: $F_{\mathrm{out}}\in {\mathbb{Z}}^{32\times 1\times 1}$    // Stage I: DSP48E1-based multiplication pipeline    for $i=0$ to 15 do       for $j=0$ to 31 do         for $t=0$ to 8 do            $(u_t,v_t)\leftarrow (\lfloor t/3\rfloor ,tmod3)$            $R(i,j,t)\leftarrow F_{\mathrm{in}}(j,u_t,v_t)·W(i,j,u_t,v_t)$            $R(i+16,j,t)\leftarrow F_{\mathrm{in}}(j,u_t,v_t)·W(i+16,j,u_t,v_t)$         end for       end for    end for    // Stage II: Adder tree for partial sum accumulation    for $i=0$ to 31 do       Flatten $R(i,j)$ to $r_k$, $k=0\dots 31$       for $k=0$ to 7 do         // Clock Cycle 01         $L0\_a\left(k\right)=r_{4k}+r_{4k+1}$,   $L0\_b\left(k\right)=r_{4k+2}+r_{4k+3}$         // Clock Cycle 02         $L1\left(k\right)=L0\_a\left(k\right)+L0\_b\left(k\right)$       end for       for $k=0$ to 1 do         // Clock Cycle 03         $L2\_a\left(k\right)=L1\left(4k\right)+L1(4k+1)$,   $L2\_b\left(k\right)=L1(4k+2)+L1(4k+3)$         // Clock Cycle 04         $L3\left(k\right)=L2\_a\left(k\right)+L2\_b\left(k\right)$       end for       // Clock Cycle 05       $P_{\mathrm{sum}}\left(i\right)=L3\left(0\right)+L3\left(1\right)$    end for    // Stage III–IV: Add bias and Quantization with rounding and clamping    // where δ is the rounding offset (e.g., $\delta =0.5$ for round-to-nearest)    for $i=0$ to 31 do       $y\leftarrow ⌊{\displaystyle \frac{(P_{\mathrm{sum}}\left(i\right)+b\left(i\right))·\lambda }{2^{32}}}+\delta ⌋$       $F_{\mathrm{out}}(i,1,1)\leftarrow min(255,max(0,y))$    end for

4. Experimental Evaluation

4.1. Experimental Setup

Hardware Implementation Tools: The accelerator is developed using Verilog Hardware Description Language (HDL). The PC-based development environment is equipped with an Intel Core i9-13800K processor (Intel is a CPU manufacturer headquartered in Santa Clara, CA, USA. It has long been dedicated to the research and production of general-purpose processor architectures.) and 64 GB of RAM. The Electronic Design Automation (EDA) tool utilized throughout the design and implementation process is Xilinx Vivado 2018.3, while functional simulations are conducted using ModelSim 10.6d. Under a clock frequency of 200 MHz, the design is successfully deployed on a Xilinx XC7K325T FPGA chip.

Algorithm Training Tools and Datasets: The training of the neural network model is conducted using the PyTorch framework, with input image dimensions of 320 × 320. The training is carried out on a PC equipped with an NVIDIA RTX 4080 GPU (NVIDIA is a GPU manufacturer headquartered in Santa Clara, CA, USA, specializing in the development of high-performance graphics computing and parallel processing architectures.) and 32 GB of RAM. During both training and testing on the GPU, the data type employed is Float32. Post-training quantization is performed using the ONNX Runtime framework.

The datasets employed in this study are as follows:

• SPEED-DET2k Dataset: This dataset consists of 2000 satellite images randomly selected from the SPEED dataset, all with a resolution of 1280 × 720. Among them, 1800 images are used for training and 200 for testing. The dataset is primarily used for the first-stage non-cooperative target detection task.
• SPEED Dataset: The SPEED [48] dataset is specifically designed for spacecraft pose-estimation tasks and was created by the Stanford Space Rendezvous Laboratory (SLAB). It contains 15,300 satellite images along with corresponding pose annotations, with 12,000 images used for training and 3300 for testing.
• UESD Dataset: The UESD [52] dataset is constructed using Unreal Engine 4 to simulate space scenarios and includes 33 high-quality, optimized 3D satellite models. A total of 10,000 satellite images with diverse backgrounds are generated. This dataset is primarily intended for component-level segmentation and recognition tasks. In this work, it is used to evaluate the generalization capability of the proposed model.

Algorithm Hyperparameter: During training, various data augmentation strategies are employed to enhance the model’s adaptability to complex space imaging environments. Specifically, image hue adjustments are used to simulate varying lighting conditions; random rotations within ±15° improve angular robustness, and random horizontal flipping and scaling operations simulate image acquisition from different perspectives and scales.

Baseline: To evaluate the performance of the accelerator, a comparative analysis was conducted across three distinct computing platforms. The AMD Ryzen 7 4800H CPU (AMD is a CPU manufacturer headquartered in Sunnyvale, CA, USA, primarily engaged in the design and development of high-performance computing, graphics processing, and embedded system chips.) was selected as a representative mobile general-purpose processor, and the NVDIA GTX 1080Ti served as a mid-range consumer-grade accelerator. The remaining FPGA-based platform was used as a comparable hardware accelerator. Inference speed on the CPU and GPU was measured using software-based counters, while that of our accelerator was measured via hardware performance counters.

4.2. Model Performance Evaluation

Figure 9 illustrates the visualized detection results of the YOLOv5s object detection model under different scenarios, including variations in pose, noise perturbation, and illumination conditions. The test images are selected from two public datasets, SPEED and UESD. All detection results are obtained through model inference, with bounding boxes, class labels, and corresponding confidence scores annotated in the figure.

The first two columns show the detection performance of the model under varying satellite poses. Despite significant differences in attitude, the model accurately localizes the targets, with confidence scores consistently around 80%, indicating that YOLOv5s exhibits strong robustness to pose variations.

The middle two columns evaluate the detection stability of the model under different noise levels. To simulate potential interference from transmission or sensor noise in space imagery, Gaussian noise was added to the test images with ten predefined noise levels, where the variance increases progressively from 0.005 to 2.56. The figure displays five representative noise levels. The results show that as the noise intensity increases, the detection confidence gradually decreases, while the localization accuracy and size of the bounding boxes remain relatively stable. This indicates that the model demonstrates strong robustness to low and moderate levels of noise. Noticeable detection failure occurs only under extremely high noise conditions with large variance, suggesting that the model possesses a certain degree of noise tolerance and is capable of adapting to variations in image quality encountered in practical scenarios.

The last two columns reflect the model’s detection performance under varying illumination conditions. To simulate challenging lighting environments such as overexposure and low-light scenarios, image brightness was systematically increased and decreased across ten levels. Experimental results show that the model exhibits stronger robustness to lighting variations compared to noise perturbations, with smaller fluctuations in confidence scores and stable bounding box predictions. Even under the most severe low-light condition, the model maintains a confidence score of approximately 0.8. Although high-intensity illumination introduces some degradation, the overall detection accuracy remains within an acceptable range. These results indicate that YOLOv5s retains reliable detection capability under complex lighting disturbances.

Figure 10 presents the visualized prediction results of the URSONet pose-estimation model on the SPEED dataset. The model adopts a lightweight ResNet18 as the backbone and employs a discretization strategy with 16 bins to regress the target’s orientation angles. The first three columns display randomly selected test samples, illustrating the predicted target center and overlaid pose axes. Statistical analysis shows that under standard testing conditions, the model achieves an average position error of 0.63 m and an average Euler angle error of 5.4°, indicating high pose-estimation accuracy in regular scenarios.

Case 3 further evaluates the model’s robustness under noise interference. Gaussian noise with a variance of 0.04 was added to the test images. The experimental results show that although image quality deteriorates, the model’s average position error increases only to 1.06 m, and the average angular error rises to 9.6°, both remaining within acceptable limits. The predicted bounding boxes and pose axes do not exhibit significant deviation or failure, indicating that URSONet maintains stable inference performance under moderate noise conditions and demonstrates strong noise resilience.

Case 4 and Case 5 illustrate the pose-estimation results under different illumination conditions, corresponding to enhanced and reduced brightness, respectively. The results indicate that the model maintains strong robustness against lighting variations, with position errors comparable to those under standard conditions and only minor fluctuations in orientation angle errors. Notably, the model performs slightly better under low-light conditions than in high-brightness scenarios.

4.3. Accelerator Performance Analysis

This section provides an analysis of the implementation details of the accelerator and evaluates its performance.

Figure 11 shows the resource utilization of the proposed accelerator on the Xilinx XC7K325T FPGA. The primary consumption of logic resources is concentrated in the LUTs. Aside from the AXI interconnect logic, the convolution computing array accounts for the largest share of resource usage. A total of 512 DSP48E1 units are employed in the array to enable parallel convolution and multiply-accumulate operations across multiple channels. The distribution of LUT usage among the different logic modules is illustrated in Figure 11b.

In terms of memory resources, the main overhead of the accelerator lies in the on-chip block memory (BRAM). The buffers required for convolution computation constitute the primary source of memory consumption. To support highly parallel convolution operations, the system allocates 32 small-capacity weight buffer units, which occupy a significant portion of the BRAM resources. The BRAM usage distribution across different memory modules is shown in Figure 11c.

For power evaluation, we employed the dynamic power analysis tools provided by Vivado to model and estimate the overall system power consumption. Additionally, the power distribution across functional modules was analyzed in detail. The total power breakdown is summarized in

Table 5. The dynamic power consumption of the XC7K325T chip. In addition, there is GTX-related power consumption and static power consumption.

Clock	Signals	Logic	BRAM	DSP
0.649 W	2.016 W	1.322 W	0.978 W	1.016 W
PLL	MMCM	PHASER	I/O	XADC
0.212 W	0.217 W	0.282 W	0.545 W	0.004 W
Total	7.241 W

The bolded parts indicate the sources of dynamic power consumption.

. Specifically, the Signals and Logic components primarily reflect dynamic power associated with circuit switching activities, including transitions in combinational logic and sequential elements. The BRAM and DSP components correspond to power consumption from on-chip memory resources and DSP48E1 hard blocks during computation.

Among all functional modules, power consumption is primarily concentrated in the PE, the DDR controller, and the SRIO controller. The DDR and SRIO controllers are Xilinx-provided IP cores, whose power profiles are relatively fixed. Therefore, detailed analysis focuses on the core processing unit. The power analysis reveals that the PE consumes a total of 4.056 W. Within it, the convolutional array constructed from DSP48E1 blocks accounts for the largest share at 2.128 W. The pooling module and residual structure module consume 0.657 W and 0.512 W, respectively. The high power consumption in these modules is mainly attributed to post-processing quantization operations, which introduce additional multipliers and lead to a significant increase in dynamic power. Additionally, the pipeline control module also contributes noticeably to power consumption due to the overhead of managing multi-stage control signals under high-frequency operation. Overall, convolutional computations and the associated quantization logic constitute the primary sources of dynamic power consumption in the system.

The Roofline model [53] is used to describe the maximum achievable computation speed under the constraints of bandwidth and computational power on a hardware platform. $TT{R}_c$ represents the theoretical peak throughput of the computation array, while $TT{R}_b$ denotes the theoretical peak throughput that the memory unit can provide. The total throughput P that the hardware platform can deliver is expressed as Equation (9):

$$P=min(TT{R}_c,TT{R}_b)$$

(9)

According to the design of the convolutional array, it consists of M groups of adder tree arrays, with each adder tree utilizing N DSP48E1 units. By concatenating two weights, each DSP48E1 unit can simultaneously perform two sets of multiply-accumulate operations. When the FPGA operates at a clock frequency of $Freq$ (in Hz), the theoretical peak throughput of the convolutional array, $TT{R}_c$, can be expressed as Equation (10):

$$TT{R}_c=2\times 2\times M\times N\times Freq$$

(10)

In this study, the FPGA operates at a clock frequency of 200 MHz, employing 16 groups of adder tree arrays, with each group using 32 DSP48E1 units. $TT{R}_c$ is 409.6 GOP/s. Figure 12 presents the Roofline model analysis for the YOLOv5s and URSONet models. The vertical axis represents throughput, while the horizontal axis denotes computational intensity. The intersection point of the memory bandwidth and peak compute lines on the x-axis indicates the upper bound of achievable computational intensity. In the figure, the closer a layer’s point is to the Roofline boundary, the higher the hardware utilization. For layers with high computational density, the accelerator’s performance approaches the theoretical limit.

In this work, the integrated logic analyzer (ILA) was used for cycle statistics. The final inference time was calculated by combining the number of cycles with the clock frequency, allowing the estimation of the actual throughput during the inference process.

The calculated average convolution throughput of YOLOv5s is 284.02 GOP/s, with an inference latency of 15.52 ms, incurring an additional 6.56 ms compared to the theoretical latency. For URSONet, the average convolution throughput is 240.83 GOP/s, with an inference latency of 16.05 ms and an additional latency of 7.09 ms over the theoretical value.

Figure 13 and Figure 14 illustrate the variations in throughput and calculation quantity across convolutional layers in the YOLOv5s and ResNet18 models, respectively. The x-axis represents the layer index, while the left y-axis shows the throughput in GOP/s and the right y-axis indicates the actual calculation quantity in MOP. The light green bars represent the throughput of 1 × 1 convolutions, and the light blue bars correspond to 3 × 3 convolutions (with a 7 × 7 convolution in the first layer of ResNet18). Experimental results show that 3 × 3 convolutions generally execute faster, as the accelerator operates in a compute-bound region. Due to pipeline stalls in the on-chip convolution array during some cycles, the average throughput of 1 × 1 convolutions is lower than that of 3 × 3 convolutions. With model quantization and optimized FPGA hardware design, the proposed accelerator achieves near-peak theoretical throughput in layers with high computational demand. The YOLOv5s model reaches peak throughput and calculation quantity at the second convolutional layer, while the ResNet18 model peaks at the fifth layer. In layers with lower computational demand and smaller kernel sizes, underutilization of the convolution array leads to some performance degradation.

4.4. Comparison with Other Platforms and Related Works

In aerospace applications, energy efficiency is a critical constraint. This work compares the energy efficiency of the proposed FPGA-based accelerator with other general-purpose hardware platforms.

Table 6. Energy efficiency comparison with general computing platforms.

Model	Platform	Precision (Bit)	Latency (ms)	FPS	Power (W)	Efficiency (FPS/W)
YOLOv5s	CPU	Float32	13.904	71.92	54.0	1.332
	GPU	Float32	5.625	177.78	184.2	0.965
	FPGA	Int8	15.521	64.43	7.241	8.898
URSONet	CPU	Float32	14.31	69.86	54.0	1.294
	GPU	Float32	6.419	155.79	184.2	0.846
	FPGA	Int8	16.05	62.31	7.241	8.605

presents the energy efficiency of the YOLOv5s and URSONet models tested on an AMD Ryzen 7 4800H CPU, an NVIDIA GTX 1080Ti GPU, and a Xilinx XC7K325T FPGA. The inference portion includes only the core neural network computation, excluding pre-processing and post-processing. Experimental results show that, for the YOLOv5s object detection task, the FPGA achieves a 6.68× improvement in energy efficiency over the CPU and a 9.22× improvement over the GPU. For the pose-estimation task, the FPGA offers an 6.65× energy efficiency gain over the CPU and a 10.17× gain over the GPU.

For object detection tasks, numerous studies have implemented CNN inference acceleration on various FPGA platforms. However, significant differences exist among these accelerators in terms of model quantization strategies, chip selection, and resource utilization. Given that the core computation in CNNs is convolution, the primary resource consumed is the on-chip DSP48E1 blocks. Therefore, this work does not use overall throughput as the sole metric for evaluating accelerator performance. Instead, we introduce Computational Efficiency (CE, GOP/s/DSP48E1) as a key indicator of computational efficiency, providing a more accurate reflection of resource utilization.

Table 7. Comparison with other object detection accelerators.

	Work [54]	Work [55]	Work [56]	Ours	Work [57]	Work [58]	Ours
Model	YOLOv3-tiny	YOLOv3-tiny	YOLOv3-tiny	YOLOv3-tiny	YOLOv5s	YOLOv5s	YOLOv5s
Resolution	-	320 × 320	416 × 416	320 × 320	512 × 512	640 × 640	320 × 320
Precision (bit)	18	8	8/16	8	8	16	8
FPGA Platform	VC707	Nexys A7	VCU110	KC705	VC709	VC709	KC705
Technology (nm)	28	28	20	28	28	28	28
Frequency (MHz)	200	100	220	200	180	200	200
DSPs used	2304	240	1780	512	920	1024	512
LUTs used	48,500	58,100	127,000	102,182	158,555	166,000	102,182
FFs used	140,012	58,100	-	87,826	-	228,000	87,826
BRAMs used	141	185	2090.5	245	528	1094	245
Power (W)	4.81	2.203	15.4	7.241	9.759	14.662	7.241
Throughput (GOP/s)	460.80	95.08	418.9	285.1	406.1	394.4	236.4
CE (GOP/s/DSP)	0.2	0.3960	0.2353	0.5568	0.4414	0.3852	0.4617
EE (GOP/s/W)	95.80	43.15	27.20	39.373	41.61	28.899	32.647

compares our proposed accelerators with other FPGA-based object detection implementations [54,55,56,57,58]. Our design achieves a throughput of 285.1 GOP/s for YOLOv3-tiny and 236.4 GOP/s for YOLOv5s. For inference acceleration of the YOLOv3-tiny model, compared to reference [54], the number of DSP48E1 units used in this study and in [54] are 512 and 2,304, respectively, yet the computational efficiency of this study is 2.77× higher. Compared to reference [55], the number of DSP48E1 units used in this study is 2.13× greater, but the throughput achieved is approximately 3× higher. For reference [56], the computational efficiency of this study shows an improvement of 135.3%. Regarding the inference acceleration of the YOLOv5s model, compared to reference [57], similar computational efficiency is achieved, but with lower consumption of resources such as LUTs and BRAM. Compared to reference [58], the computational efficiency is improved by 1.19×.

Table 8. Comparison with other ResNet accelerators.

	Work [59]	Work [60]	Work [61]	Work [62]	Work [63]	Ours
Model	ResNet-18	ResNet-18	ResNet-18	ResNet-34	ResNet-50	ResNet-18
Precision (bit)	16	8	8	-	16	8
FPGA Platform	VC709	ZC706	SX660	Zynq7045	GX1150	KC705
Frequency (MHz)	200	200	170	100	240	200
DSPs used	514	818	512	392	3036	512
LUTs used	168,930	100,200	102,600	-	286,000	102,182
BRAMs used	483.5	708	465	-	2356	245
Power (W)	6.931	7.31	4.6	6.511	-	7.241
Throughput (GOP/s)	153.14	124.9	89.088	57.02	599.61	228.65
CE (GOP/s/DSP)	0.2979	0.152	0.174	0.1455	0.198	0.447
EE (GOP/s/W)	22.09	17.09	19.37	8.76	-	31.577

presents a comprehensive comparison of our proposed accelerator with other ResNet accelerators reported in recent works [59,60,61,62,63]. Our design achieves a throughput of 228.65 GOP/s, significantly outperforming other 8-bit implementations such as [60]’s 124.9 GOP/s and [61]’s 89.088 GOP/s, and surpassing the 16-bit design in [59]’s 153.14 GOP/s. In terms of CE (GOP/s/DSP48E1), our design attains 0.447, the highest among all compared methods, indicating more efficient utilization of DSP48E1 resources.

In addition, our method demonstrates strong competitiveness in terms of hardware resource utilization and power efficiency, requiring only 102,182 LUTs and 245 BRAMs, with a total power consumption of 7.241 W. Considering that energy consumption is a critical factor in space applications, we introduce the Energy Efficiency (EE, GOP/s/W) metric to evaluate the computational throughput per unit of power.

According to our calculations, the proposed accelerator achieves an EE of 32.647 for object detection tasks and 31.577 for ResNet acceleration. Notably, the EE achieved for ResNet is the highest among comparable accelerators, and the value for object detection is also at a competitive level. It is worth emphasizing that the designed accelerator not only delivers high energy efficiency for the two aforementioned tasks but also exhibits excellent generality. It supports the entire pose-estimation pipeline while being compatible with various CNN models, demonstrating a high degree of adaptability that task-specific accelerators typically lack.

Finally, the non-cooperative target pose-estimation pipeline, as illustrated in Figure 2, was executed on a heterogeneous platform comprising a TMS320C6678 DSP and an XC7K325T FPGA.

Table 9. End-to-End time statistics of the DSP–FPGA heterogeneous system (input image size is 1000 × 1000).

Task	Process	Platform	Latency (ms)
Object Detection	Pre-Process	DSP	336.3
	YOLOv5s	FPGA	15.52
	Post-Process	DSP	211.4
Pose Estimation	Pre-Process	DSP	149.76
	URSONet	FPGA	16.05
	Post-Process	DSP	13.54
Total			742.57

presents the end-to-end latency breakdown of the proposed DSP–FPGA heterogeneous system for a two-stage intelligent perception task comprising object detection and pose estimation. The total system latency is 742.57 ms, which includes both DSP-side pre-processing and post-processing operations, as well as FPGA-accelerated inference. For the object detection stage using YOLOv5s, the FPGA contributes only 15.52 ms to the overall latency. Similarly, in the pose-estimation stage using URSONet, the FPGA inference latency is 16.05 ms. These results demonstrate that the FPGA accelerators achieve high-speed inference, while the overall system performance is bounded by the DSP stages, indicating potential for further optimization in data preparation and result parsing. The clear division of labor between the DSP and FPGA components validates the effectiveness of our heterogeneous design in balancing computational load and maximizing platform compatibility.

5. Conclusions and Future Work

This paper presents a two-stage algorithmic framework for the pose estimation of non-cooperative targets, consisting of a object detection stage followed by a pose-estimation stage. The overall pipeline is implemented using a lightweight YOLOv5s network for detection and a URSONet-based network for pose estimation. To enhance real-time performance under resource-constrained conditions, the proposed method is accelerated using a DSP–FPGA heterogeneous architecture. A custom RTL-level hardware accelerator is designed to support the complete pose-estimation process efficiently. The accelerator is deployed on a Xilinx XC7K325T FPGA operating at 200 MHz, demonstrating its performance under near real-world resource-limited scenarios.

The primary advantage of this study lies in the integration of INT8 quantization with model architecture optimization, enabling efficient software–hardware co-acceleration. Hardware evaluations show that the accelerator achieves a peak throughput of 399.16 GOP/s, approaching its theoretical limit. In practical deployments, the accelerator yields average throughputs of 236.4 GOP/s for YOLOv5s and 228.65 GOP/s for ResNet18, representing a 2–3× performance improvement over existing comparable solutions. The accelerator is designed with strong model compatibility, allowing flexible deployment across various network architectures without the need for hardware reconfiguration. Future work will focus on exploring more efficient algorithmic structures to fully exploit the accelerator’s adaptability and scalability in complex application scenarios.

The main limitations of the proposed method can be analyzed from the perspective of algorithm–hardware co-design. On the algorithmic side, adopting backbone networks from the MobileNet family could further reduce computational complexity while maintaining acceptable accuracy. In particular, the use of depth-wise separable convolutions offers potential for improved efficiency and inference speed when combined with dedicated hardware designs, without increasing DSP48E1 resource consumption. On the hardware side, the current design does not yet incorporate multi-core DSP collaboration, and the pipeline coordination between the DSP and FPGA remains suboptimal. Efficiently organizing DSP data flow and enabling parallel pipelined-processing between the two processing units represent important directions for future research.

Moreover, all experiments in this study were conducted in ground-based environments. For deployment in actual space conditions, further engineering validation is required. For instance, single-event upsets (SEUs) caused by radiation in space may lead to computational errors, which must be carefully addressed during the design phase. From an architectural perspective, incorporating fault-tolerant mechanisms such as triple modular redundancy (TMR) and self-refreshing circuits could enhance system reliability and robustness under high-radiation conditions.