Abstract
The ability to collaborate with new teammates, adapt to unfamiliar environments, and engage in effective planning is essential for multi-drone agents within unmanned combat systems. This paper introduces DETEAMSK (Model-based Reinforcement Learning by Decoupling the Identification of Teammates and Tasks), a model-based reinforcement learning method in intelligent top-level planning and decisions designed for ad hoc teamwork among multi-drone agents. It specifically addresses integrated reconnaissance and strike missions in urban combat scenarios under varying conditions. DETEAMSK’s performance is evaluated through comprehensive, multidimensional experiments and compared with other baseline models. The results demonstrate that DETEAMSK exhibits superior effectiveness, robustness, and generalization capabilities across a range of task domains. Moreover, the model-based reinforcement learning approach offers distinct advantages over traditional models, such as the PLASTIC-Model, and model-free approaches, like the PLASTIC-Policy, due to its unique “dynamic decoupling identification” feature. This study provides valuable insights for advancing both theoretical and applied research in model-based reinforcement learning methods for multi-drone systems.
1. Introduction
In multi-drone systems, achieving efficient and robust coordination and collaboration among drone agents is essential. This challenge is known as multi-drone agent ad hoc teamwork, which requires developing drone agents capable of spontaneously cooperating and collaborating with other team members without prior coordination, which is vital for tasks such as cooperative navigation, pursuit and encirclement, communication, and joint training [,,].
In the multi-drone agent ad hoc teamwork, each individual drone agent within the swarm can follow a set of tacit rules to perform its specific duties while coordinating with others, autonomously completing designated tasks, and must shift from a local perspective to a global perspective within the operational feedback loop of “Observation (O)-Orientation (O)-Decision (D)-Action (A) (OODA).” They must consider both their own behavior and that of other drones in order to generate the optimal individual response, ensuring that the team works in harmony to achieve the task objectives. The key issue for this is to enhance the generalization capability, robustness and efficiency of the multi-drone ad hoc teamwork (shown in Figure 1 and Figure 2) [,,,,].
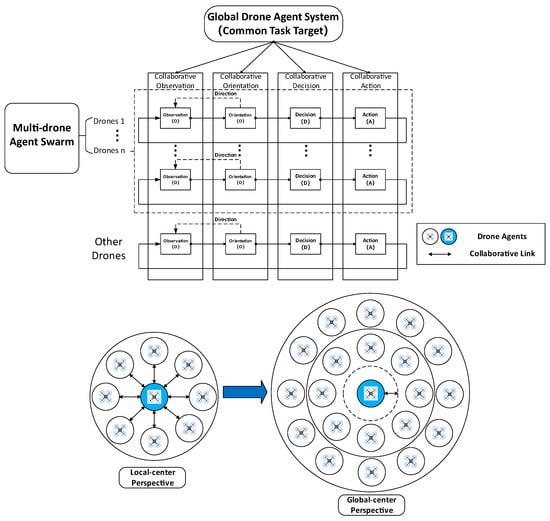
Figure 1.
The smart multi-drone agent swarm ad hoc teamwork.
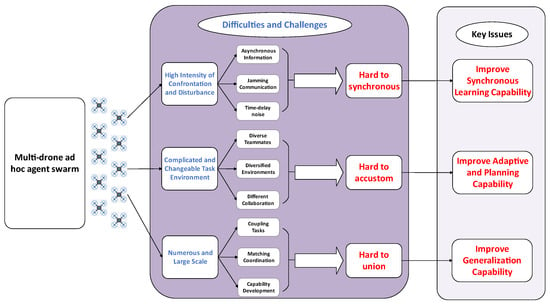
Figure 2.
Difficulties, challenges and key issues of the smart multi-drone agent swarm ad hoc teamwork.
The ability to adapt to new environments and cooperate stably and efficiently with new teammates in unknown conditions (especially without any pre-coordination with the team members and environment) to achieve tasks is so important for humans and autonomous agents; this can be called ad hoc teamwork (AHT). Also known as the online immediate cooperation of a multi-agent system, this is an important area of sub-research in multi-agent cooperation. In the problem of ad hoc teamwork, the agents can cooperate and collaborate with unknown teammates in unfamiliar environments to fulfill a common goal without pre-coordination conditions (such as a shared task, communication protocol or joint training). The teammates can make their own contributions to the teamwork [,,,,]. Traditional reinforcement learning emphasizes learning how to interact with the environment from the perspective of an individual agent to maximize rewards. The agent’s action decision mainly relies on feedback from the given environment (as illustrated in Figure 3a); when the agent of a team interacts with the external environment, it is generally assumed that the teammates are known to it. Then, the agent makes action decisions based on the joint actions of the internal team and the feedback from the given environmental conditions by seperately modeling teammates and the environment for learning (as shown in Figure 3b); the ad hoc teamwork can be seen as the “upgraded dimensional issue” of the former two, focusing on how the agents adjust their behavior to achieve teamwork and common goals with maximum rewards when both teammates and the environment are in random states (depicted in Figure 3c). It is evident that the ad hoc teamwork is a higher-level, more complex and more challenging reinforcement learning problem. The focus of the ad hoc teamwork is to train an autonomous agent to coordinate with a group of unfamiliar teammates without prior coordination while adapting to the external environment. The trained agent is called the learner. The learner needs to acquire two fundamental abilities through training: first, to fully infer the team dynamics and understand the teammates to achieve collaboration and second, to learn how to take actions within the environment to maximize reward returns. The learner’s teammates possess the ability to complete common task objectives with it [,].
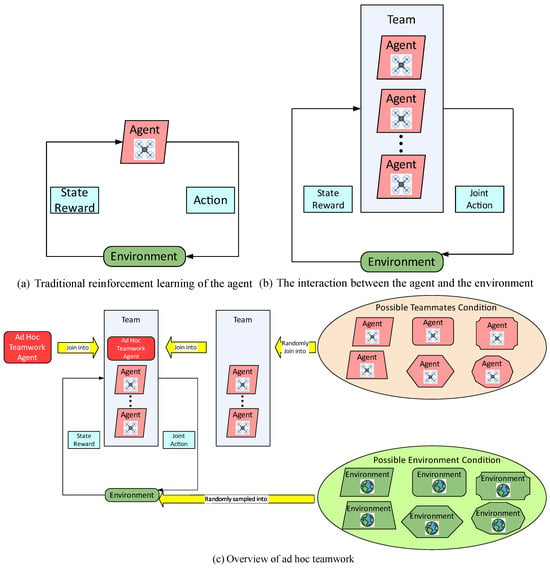
Figure 3.
The ad hoc teamwork viewed as the agent.
Thus, ad hoc teamwork reinforcement learning should be on the research frontline. It aims to comprehensively coordinate between the cooperation relationship of the ad hoc team and the changes in the outside environment based on different team types under diverse observation conditions, which can be generalized mainly into three perspectives in current research: environmental observation, external situational changes, and internal coordination types [,,,].
- (i)
- Observation of the environment: This perspective examines the performance of ad hoc teams under complex environmental conditions, encompassing both fully observable and partially observable scenarios [,]. In fully observable scenarios, agents have complete knowledge of the environment and reward structure. Conversely, in partially observable scenarios, agents must predict these factors based on limited information [,,,].
- (ii)
- External situation changes: This perspective examines how ad hoc teams adapt to various external challenges to enhance coordination stability and robustness. In this context, the team is considered a unit interacting with its environment, encompassing scenarios such as potential attackers [], coordination with teammates [], dynamic environments [], and few-shot teamwork [].
- (iii)
- Internal coordination types: This perspective examines the self-coordination styles of ad hoc teams, categorized into closed-type and open-type [,]. In closed-type teams, members remain constant and aim to observe and learn the known behaviors of their teammates to predict future actions and enhance coordination [,,,]. In open-type teams, the team composition varies over time, requiring more complex analysis for coordination [,,,]. This perspective primarily studies how diverse ad hoc teams achieve efficient coordination.
Studies in these sectors are frequently conducted with a comprehensive approach, taking into account the existing context to propose effective ad hoc team reinforcement learning methods, as indicated in Figure 4.
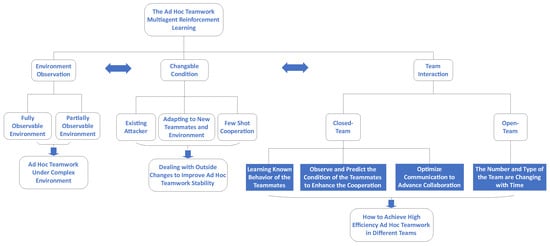
Figure 4.
Outline of ad hoc teamwork reinforcement learning research.
This paper aims to investigate more effective methods from an intelligent top-level planning and decision-making perspective to enhance efficiency, robustness, and generalization capability for closed-type ad hoc multi-drone teams operating in fully observable environments.
This study is structured into seven sections. Section 1 introduces the study, Section 2 reviews related works, and Section 3 provides the necessary background. Section 4 details the DETEAMSK algorithm method, while Section 5 describes the experiments conducted. Section 6 discusses the findings, and Section 7 concludes the study and outlines future work.
2. Related Works
Teammates and environments are pivotal elements that multi-drone ad hoc team agents must manage to achieve effective coordination [,,,,,]. Nevertheless, adapting to varying external conditions poses a significant challenge for these agents, as mismatches between teammates and environments are common. To address this issue, several studies have been conducted. Barrett et al. [] introduced two algorithms: PLASTIC-Model (Planning and Learning to Adapt Swiftly to Teammates to Improve Cooperation-Model) and PLASTIC-Policy (Planning and Learning to Adapt Swiftly to Teammates to Improve Cooperation-Policy) that are also mentioned in references [,,]. The former is a model-based reinforcement learning algorithm that leverages known teammate models as a decision reference library, along with dynamic environment models, to make predictions for decision-making []. The latter is a model-free reinforcement learning algorithm, wherein the ad hoc agent learns various policies within its own library, comparing collaboration objects to previously known teammate policies without modeling the transition and reward information related to the environment [,,]. However, each algorithms possesses distinct limitations: PLASTIC-Model necessitates comprehensive models of teammates and environments, which are not always feasible, while PLASTIC-Policy struggles to match policies effectively across different environments. To address these limitations, Ribeiro et al. [] proposed TEAMSTER (Task and tEAMmate identification through modelbaSed reinforcemenT lEaRning), a novel model-based reinforcement learning method that simultaneously utilizes teammate and environment models to learn dynamic external conditions without coupling limitations. This enables the ad hoc agent to adapt swiftly to new conditions.
However, TEAMSTER’s performance has been evaluated only in relatively simple and small-sized team and in and from limited experimental scenarios and perspectives. Besides the training mechanism of the model network architecture, the dynamic programming method and the action exploration and exploitation policy of the reinforcement learning are also singular, raising concerns about its generalization capability, robustness and high efficiency for large-sized teams under more complicated task environments with longer interactions. Furthermore, its mechanism requires updates to enhance its comprehensive effectiveness across diverse tasks and scenarios.
To recap, and based on prior studies, this paper aims to address existing research limitations by introducing a novel model-based reinforcement learning method, DETEAMSK (moDEl-based reinforcement learning by decoupling the identification of TEAMmates and TaSKs), which is updated based on TEAMSTER. A multi-agent collaborative dynamic planning and learning framework was designed, and the generalization capability, robustness and high efficiency of the ad hoc teamwork are optimized with the model network architecture, dynamic programming and the action exploration and exploitation policy by decoupling teammates and environments through innovative algorithmic mechanisms. We evaluate the approach across more diversified and complex tasks and scenarios.
3. Background
The problem of the closed-type ad hoc teamwork is modeled as a multiagent Markov decision problem () [], described as a 6-tuple M = (N,,A,,,) following the approach in the literature []:
N is the total number of the agents in the ad hoc team;
is the (countable) set of the states of the environment, while denotes the states that vary as the time step goes up;
A is the joint action space. Each element in represents the individual action set of agent n related to the other agents and embodies one of the elements in . denotes the individual action of the agent as the time step goes up;
are the transition probabilities corresponding to different joint actions ;
is the expected reward when the ad hoc team reach state with the action a;
is the discount factor in the interval [0, 1).
The ad hoc team’s goal is to make a decision regarding the optimal joint policy matching each state with a joint action , which computes
for each state to the maximum. in (1) is the random reward given to the ad hoc team as time goes by, which can also be denoted as
in this case.
Solving this MMDP problem means finding the most proper computation of the action-value function that can satisfy the following equation:
Meanwhile, we can obtain the optimal joint policy from Equations (3) and (4) by computing with some dynamic planning algorithm methods such as MCTS [,,], Q-learning [,,], etc.
Basing on the assumption above, some variables can be defined as a supplementary explanation to the MMDP tuple M: is the joint action of the teammates with as the corresponding policy, and the transition probabilities of the MDP can be computed as
for every x, , and .
Then, we can transfer the MMDP problem to an MDP by only considering a 5-tuple, as defined in Equation (6):
where the elements in Equation (6) have been defined before. Furthermore,
for every , and .
In our study, the ad hoc teamwork within a Multi-Agent Markov Decision Process (MMDP) can be optimized by considering the action of a single agent. The transition function is determined by integrating the behaviors of the teammates and the environment. This approach allows us to concentrate on the impact of the ad hoc agent’s individual actions on the team’s performance, thereby providing a more precise and streamlined decision analysis process for our research. Thus, the ad hoc teamwork of MMDP can be viewed as a standard MDP from the perspective of a single agent’s action. The problem can be resolved if the teammates’ actions, denoted as , their corresponding policy , the environment’s dynamic transition probabilities , and the reward are known. These can be addressed using dynamic planning or standard reinforcement learning algorithms. However, in our assumptions, these elements are unknown to the ad hoc agent. Therefore, the solution relies on the prior experience and knowledge acquired by the ad hoc agent through coordination and collaboration with the team. The framework for modeling and analysis on the closed-type team ad hoc teamwork is shown in Figure 5.
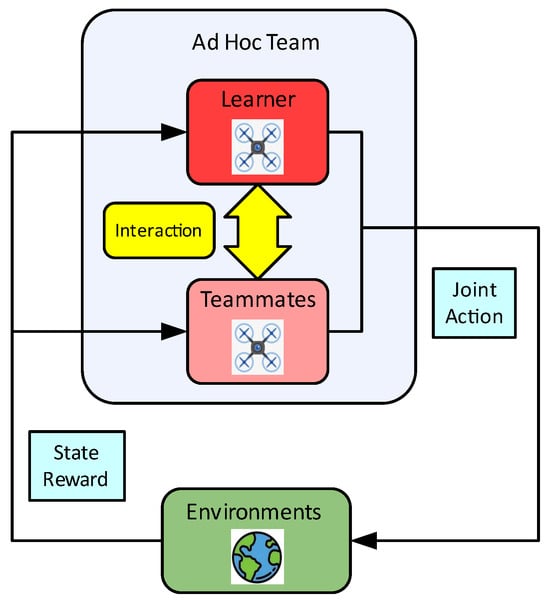
Figure 5.
Framework for modeling and analysis of the closed-type team ad hoc teamwork.
4. The DETEAMSK Algorithm Method
In this section, we introduce our algorithm, DETEAMSK (moDEl-based reinforcement learning by decoupling the identification of TEAMmates and TaSKs), which is an enhancement of the TEAMSTER algorithm []. This method is designed to improve the generalization capability, robustness and efficiency in the ad hoc teamwork. DETEAMSK comprises three key components: (i) teammate behavior identification; (ii) task environment identification; and (iii) action planning and learning. These components are relatively independent yet connected, working together to provide optimal action decision-making for the agent.
For each run timestep t, DETEAMSK initializes a new teammate library T to store policies trained offline using historical datasets from previous team interactions. It then compares the current team policy with the previous one to determine if it has been encountered before. During this process, the teammate identification model analyzes the current team’s characteristics and sets a belief . This belief is used to update the library to and form a new model (Lines 2–4, 9 and 11 of Algorithm 1).
Simultaneously, the ad hoc agent monitors the current state of the teamwork. It employs the environment identification model E to learn environmental changes based on the current state and team actions , utilizing the belief . This leads to the creation of a new model (Lines 5, 6 and 10 of Algorithm 1).
DETEAMSK then selects optimal actions using the action planning and learning mechanism , which is based on the current state , and the models and . The belief is subsequently updated to . This process repeats over time (Lines 7–8, and 12–13 of Algorithm 1).
Initially, the teammate library T is empty, and the environment identification model E is a blank slate, making DETEAMSK function as a basic model-based reinforcement learning system. Once action selection is completed, DETEAMSK transitions to standard model-based reinforcement learning, enhanced by its module functions.
| Algorithm 1: DETEAMSK pseudo-code description |
| Basic Algorithm Models: Teammate Identification Model , Environment Identification Model E, Action Planning and Learning Mechanism 1. First runtime: t = 0 2. Set teammate module 3. Set the regarding belief of the current team to build new 4. Repeat 1–3 above 5. Observe the current state 6. 7. 8. Select and execute and continue to observe 9. Update to 10. Update to 11. Update to 12. 13. Run until is to the end |
The primary operational mechanism of DETEAMSK is illustrated in Figure 6 and a summary of the DETEAMSK main work loop in pseudo-code is presented in Algorithm 1.
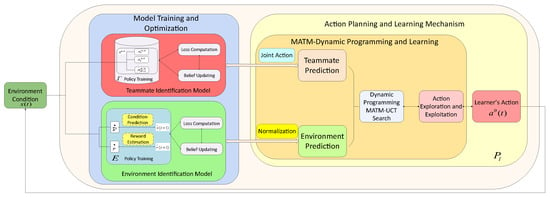
Figure 6.
Architecture of the ad hoc agent DETEAMSK.
4.1. Teammate Behavior Identification
The Teammate Identification Model () is configured as a feedforward neural network, enabling the ad hoc agent to learn the joint actions of other teammates by computing optimized action policies, denoted as . These policies are represented by categorical distributions and are updated through the belief during interactions at each time step t. The input to the neural network comprises the state features observed by the ad hoc drone agent n, while the output is a probability distribution over the individual actions of agent n. The activation function Relu [,] and optimizers Rmsprop, Adamw, SGD [,], and Adam [,] are used for training the feedforward neural network. The core function of this model is to minimize the belief update loss caused by the learner’s individually generated action policy, which is incentivized based on the teammate’s joint action policies during interaction. This, in turn, achieves the highest degree of team behavior alignment and maximizes team collaboration efficiency. It can help the learner identify similar teams by quickly and effectively learning from them, as well as predicting the next actions based on observed behaviors with the prior experience and knowledge obtained by interacting with the team.
4.2. Task Environment Identification
The Environment Identification Model (E) is also structured as a feedforward neural network similar to the teammate identification model. This model allows the ad hoc agent to adapt to the dynamic external environment at each run timestep t. It utilizes the current state and the joint action of the team, informed by the updated belief from the teammate identification model . This model is intricately linked to the action planning and learning mechanism, as the dynamic changes in the transition probabilities and rewards are reflected from it and utilized for action planning and learning. The inputs include features, , which represent the current state of the agent n (e.g., distance from other agents) and its actions. The outputs are the probabilities of agent n moving in four directions or remaining stationary, along with two scalars indicating the reward. The activation function Relu [,] and optimizers Rmsprop, Adamw, SGD [,], and Adam [,] are used for training the feedforward neural network. The core function of this model is to minimize the belief update loss that arises from the learner predicting the next state and rewards based on state transition probabilities during interactions. This allows for effective adaptation to dynamic environmental changes.
Based on the above analysis, it can be concluded that the teammate identification model and the environment identification model can maximize the elimination of cross-linked coupling effects between the team and the environment. This enables the learner, in the process of ad hoc teamwork, to dynamically learn the internal and external conditions of the team at different time stages, thereby maintaining sensitivity and timeliness in the overall situation.
4.3. Action Planning and Learning
Action Planning and Learning Mechanism (): This module functions as a multi-agent collaborative action selection and generation mechanism; the learner uses an updated teammate identification model and environment identification model at each run timestep t to inform their next action . Dynamic planning algorithms such as UCT [,,,] and value iteration [] can be applied to obtain the optimal action decision.
At each run timestep t, the learner will complete action decision-making and execution through the action planning and learning mechanism based on the updated condition of the teammate identification model and environment identification model (Lines 6–7 of Algorithm 1). The action planning and learning mechanism can be primarily divided into three components: the multi-agent collaborative dynamic planning and learning framework, dynamic programming, and reinforcement learning exploration and exploitation.
4.3.1. Multi-Agent Collaborative Dynamic Programming and Learning Framework
The multi-agent collaborative dynamic programming and learning framework proposed in our research involves such modules as teammate behavior modeling, joint action space design, dynamic environment prediction, reward normalization, and dynamic planning algorithms. Teammate behavior modeling involves dynamically predicting the actions of teammates, for which promising results have been shown in the literature []. Combined with the learning outcomes of the teammate identification model, this approach predicts and generates joint actions based on the teammates’ current states, thereby enhancing the adaptive process within the team. The joint action space design draws on the definition of multi-agent joint actions in the literature [], integrating the learner’s actions with those of teammates to better reflect the relationship between individual and team behaviors. By modeling and predicting team joint actions, the learner can more accurately adjust its adaptive behavior decision. Dynamic environment prediction, as proposed in references [,], is implemented here based on the outcomes of the environment identification model. This approach primarily involves predicting environmental uncertainties by learning state transitions and reward feedback, which significantly improves the learner’s adaptability to the environment. Reward normalization, inspired by the method presented in reference [], simplifies complex into binary 0-1 values to streamline problem-solving. For dynamic planning, the study adopts the Monte Carlo tree series algorithms mentioned in the literature [], using simulation-based predictions for decision-making searches. This reduces reliance on real environments and enhances decision-making accuracy.
4.3.2. Multi-Agent Collaborative Dynamic Programming MATM-UCT Search
As one of the most popular algorithms in Monte Carlo Tree Search, the Upper Confidence Bound for Trees (UCT) method demonstrates superior performance in large state and action space, and is thus widely used []. This study designs a Multi-Agent TeaMwork UCT algorithm (MATM-UCT) as the primary method within the multi-agent collaborative dynamic programming Monte Carlo Tree Search framework. It constructs the search tree through rollout expansion, combining this with the teammate identification model and environment identification model to use various reinforcement learning policies (such as the greedy policy, the -greedy policy [], the Boltzman policy [,], linear annealing policy [,], etc.) to estimate the action with the highest reward value in the current environmental state . This is fed back to the learner to assist its action decision-making response. The main work loop of MATM-UCT is summarized in the pseudo-code shown in Algorithm 2.
| Algorithm 2: MATM-UCT pseudo-code description |
| 1. Function: generates actions with dynamic programming 2. For at current timestep t, repeat: 3. Predict the joint action of teammates 4. Predict the environment condition 5. Compute and Normalize the reward 6. Select, expand, rollout, backup 7. Exploring and exploitation Policy () 8. Return |
4.3.3. Reinforcement Learning Exploration and Exploitation
After modeling study and dynamic programming, the learner will employ an exploration and exploitation policy to carry out the reinforcement learning process of action selection. Based on the varying degrees of exploration and exploitation of action rewards, some common policies have been introduced and analyzed in references [,], such as the greedy policy, the -greedy policy, the Boltzman policy and the linear annealing policy. The greedy policy consistently selects the action with the highest reward at any given moment, exhibiting minimal exploration and a strong degree of determinism, making it suitable for simple and fixed environments. The -greedy policy introduces randomness based on the greedy policy, balancing action selection and exploitation through a probability parameter, which is more effective in identifying optimal actions under relatively complex environmental conditions, as detailed in references [,]. References [,,] mention that the fundamental concept of the Boltzmann policy is similar to that of the -greedy policy; however, it selects actions based on a temperature parameter, providing enhanced stability. When the temperature parameter is high, the action selection becomes more randomized, emphasizing exploration; conversely, when it is low, it aligns more closely with the greedy policy, focusing on exploitation. The linear annealing policy is suitable for hyperparameter adjustments (such as for the exploration rate) within a specified timeframe in reinforcement learning and is also applicable in more complex environmental scenarios, facilitating a gradual transition from exploration to the selection of optimal actions. Related discussions can be found in references [,,]. This study conducts an analysis and discussion of the impact of different reinforcement learning action exploration policies on algorithm performance under various conditions.
Through action planning and learning, the learner will take the action and continue to focus on the joint action of teammates. The environmental state and reward feedback (Lines 7 and 8 of Algorithm 1) complete the belief updates and state transitions, while simultaneously updating the teammate identification model and environment identification model (Lines 9–11 of Algorithm 1), so that the whole ad hoc teamwork is achieved. The entire process will repeat in cycles until the environmental state terminates (Lines 12 and 13 of Algorithm 1).
5. Experiments
This section elaborates on the experiments conducted in our study, detailing their settings such as scenarios, teams, domains, and tasks in Section 5.1, the methodology used in Section 5.2, and the results obtained in Section 5.3.
5.1. Settings
In our experiments, we focus on urban combat scenarios involving drone swarms in cooperative navigation, pursuit and encirclement.
In cooperative navigation, each drone in the swarm operates as an ad hoc agent with a specific algorithm to execute the missions. The collective mission goal of the drone swarm is to achieve coordinated navigation through aerial movement, reaching their respective sets of destination landmarks as quickly as possible to perform integrated reconnaissance and strike missions. During this process, the ad hoc learner must observe the relative positions and distances to the other agents and their target landmarks, avoiding obstacles, hazardous facilities, and potential collisions that could hinder their mission achievement, and receive different rewards based on their task completion status (such as proximity to the target). The mission concludes when all ad hoc agents have reached their designated target landmarks. Three distinct classical urban combat task domains with different scale characteristics are chosen for our study: the Center Base District (CBD), the Sparse Discrete Cross-street District (SAD), and the Multi-falling Building District (MFD), as illustrated in Figure 7a–c.
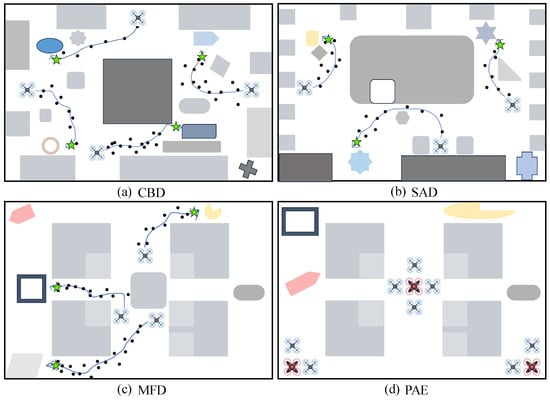
Figure 7.
The figure illustrates four classical urban-combat task domains for ad hoc drone swarm agents. Green stars denote the final destinations. The blue curves with arrowheads indicate the movement trajectories of the ad hoc drone agents. Black dots signify potential expanded states of the agents [,,,,].
In pursuit and encirclement (PAE), the common goal of the drone swarm is for every four or two drones to cooperate in capturing an enemy drone. The domains are described as a gridded circular area, divided into two types, 5 × 5 and 10 × 10, as shown in Figure 7d. At each run timestep, the enemy drone will randomly move to an adjacent grid cell with a certain probability, while our drones will move in one of four directions—up, down, left, or right—to an adjacent grid cell, avoiding collisions with each other and the enemy drone (i.e., moving to the same grid cell at the same time). The task ends when the enemy drone is surrounded on all four sides.
Four distinct drone swarm teams are prepared to execute the task:
Reconnaissance-Sensitive Team (): Agents in this team prioritize minimizing the total distance from the target landmark during reconnaissance tasks, moving strategically towards objectives.
Strike-Priority Team (): Agents in this team opt for the shortest path to the target landmark to efficiently complete quick attack tasks.
Adaptive Response Team (): Agents in this team select their path probabilistically, based on changes in reconnaissance and strike scenarios, favoring paths with shorter total distances.
Integrated Reconnaissance-Strike Team (): This mixed team comprises agents from each of the previous team types (–). It possesses both offensive and defensive capabilities, is highly maneuverable in all directions, and is responsible for carrying out the core reconnaissance and strike missions.
5.2. Methodology
5.2.1. Baseline Algorithm Methods
To assess the effectiveness of DETEAMSK, we selected seven algorithmic methods as comparison baselines. Several of these methods have also been employed in previous studies, as referenced in the literature []:
PLASTIC-Model (perfect + perfect E + MATM-UCT): The architecture, akin to DETEAMSK, integrates a learned teammate identification model and an exact environment identification model. It employs MATM-UCT for dynamic programming.
DE Learns Team (learned +perfect E + MATM-UCT): The architecture, which is similar to DETEAMSK, incorporates a learned teammate identification model and an exact environment identification model, with MATM-UCT being utilized for dynamic programming.
DE Learns Environment (perfect +learned E + MATM-UCT): The architecture, analogous to DETEAMSK, integrates a learned environment identification model and a precise teammate identification model, employing MATM-UCT for dynamic programming.
PLASTIC-Policy: PLASTIC-Policy is a model-free reinforcement learning method that incorporates a policy library, similar to the teammate library in DETEAMSK. This method employs a Q-function learned through interactions with teams that are congruent with their respective environments.
Random Policy: A method in which an ad hoc drone agent selects an action based on a random probability.
UCT-Model: This is a MATM-UCT method for multi-agent collaboration without learning models.
Original teammate: The ad hoc teammates as described above in four different teams.
5.2.2. Evaluation Procedures
The experiment is structured based on the DETEAMSK foundational work loop and the procedures defined in TEAMSTER []. Initially, the ad hoc agent is sequentially deployed within each team to learn and gather prior knowledge and experience, serving as a pre-training process. Subsequently, the agent interacts with all teams to assess coordination performance. Each team, as described in Section 5.1, comprises three members, while team is specifically formed to test the scalability and extensiveness of the ad hoc agent’s teamwork in more challenging scenarios. In addition, we analyze the architecture and mechanisms of DETEAMSK with various optimizations in the feedforward neurual network and action exploration and exploitation policies, as well as its asymptotic convergence performances. All tasks are executed for each type of agent within the baselines across four distinct task domains, with eight trials conducted through eight subexperiments.
5.2.3. Experiment Items
(i) Stand ad hoc task evaluation experiment
The experiment was conducted according to the methodology described in Section 5.2.2. In the cooperative navigation task, the total number of ad hoc agents in CBD, SAD, and MFD is N = 4. This means that, within the corresponding task areas, the learner has three teammates from four corresponding teams. In the pursuit and encirclement task, the total number of ad hoc agents was four, with a total of five (including one enemy drone agent).
(ii) Method mechanism optimization evaluation experiment
This experiment focuses on examining the optimization effects of different model architectures and planning policies on the performance of DETEAMSK with the three sub-modules of DETEAMSK from multiple perspectives based on item (1). For the three different sub-parts of the DETEAMSK, we have used various models and methods with architectures and hyperparameters to improve and optimize the algorithm in our study. All details are summarized in Appendix A.
(iii) Performance convergence evaluation experiment
To assess the comprehensive asymptotic robustness and effectiveness of the ad hoc agent, we set the training timesteps as three times those in items (1) and (2) with the other procedures kept as before; then, we evaluated the performances in various task domains.
5.3. Results
5.3.1. Stand Ad Hoc Task Evaluation
The pre-training reinforcement learning processes of four ad hoc agents (DETEAMSK, DE Learns Team, DE Learns Environment, and PLASTIC-Policy) across four task domains are illustrated in Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15.
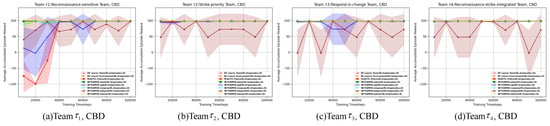
Figure 8.
The pre-training reinforcement learning process of each ad hoc drone agent on the CBD domain. The shaded areas of colors are the confidence interval of 95%.

Figure 9.
The pre-training reinforcement learning process of each ad hoc drone agent on the SAD domain. The shaded areas of colors are the confidence interval of 95%.

Figure 10.
The pre-training reinforcement learning process of each ad hoc drone agent on the MFD domain. The shaded areas of colors are the confidence interval of 95%.
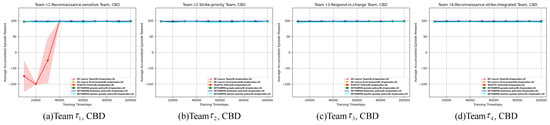
Figure 11.
The pre-training reinforcement learning process of each ad hoc drone agent on the CBD domain. The shaded areas of colors are the confidence interval of 95%.

Figure 12.
The pre-training reinforcement learning process of each ad hoc drone agent on the SAD domain. The shaded areas of colors are the confidence interval of 95%.
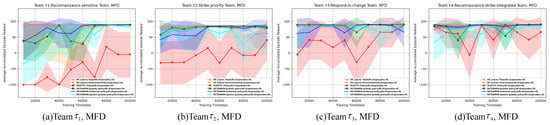
Figure 13.
The pre-training reinforcement learning process of each ad hoc drone agent on the MFD domain. The shaded areas of colors are the confidence interval of 95%.

Figure 14.
The pre-training reinforcement learning process of each ad hoc drone agent on the PAE (5 * 5) domain. The shaded areas of colors are the confidence interval of 95%.
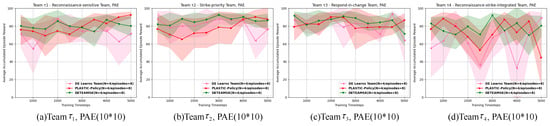
Figure 15.
The pre-training reinforcement learning process of each ad hoc drone agent on the PAE (10 * 10) domain. The shaded areas of colors are the confidence interval of 95%.
First, for the cooperative navigation, shown in Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13, initially, it is evident that during the pre-training process, the general tendencies of the four ad hoc agents remain relatively stable across the learning processes of the previous three teams. Overall, DETEAMSK demonstrates superior performance in three distinct task domains, outperforming other agents in most scenarios and particularly excelling in the CBD domain. Even in complex domains such as SAD and MFD, DETEAMSK maintains a relatively stable trend and swiftly converges to final values with minimal steady-state errors, despite some fluctuations in the SAD domain. During the learning of , DETEAMSK’s advantages are less pronounced, especially in the CBD domain; however, it continues to perform relatively well in more complex environments like SAD and MFD compared to others. While this is a satisfactory outcome for achieving complex missions, there remains room for improvement. The other two ablations perform adequately, whereas PLASTIC-Policy consistently underperforms, particularly in complex environments. This suggests that model-based reinforcement learning is superior to model-free approaches in terms of complex mission response and adaptability.
Then, we evaluated the interaction processes of the four teams, as shown in Table A5, Table A6, Table A7, Table A8, Table A9 and Table A10 (detailed in Appendix A). In interactions with through , DETEAMSK consistently outperforms other agents, achieving relatively high rewards. When interacting with , the accumulated episode rewards of the team are the highest in the CBD task domain, exhibiting minimal variance, and are also strong in the MBA domain with low variance. Notably, across both task domains, consistently surpasses to , indicating that the ad hoc agent effectively leverages accumulated knowledge and experience from prior training and interactions to enhance coordination in challenging scenarios. Performance in the CBD and MFD domains is satisfactory; however, in the SAD domain, performance declines with lower rewards and greater variance compared to the other two domains. There are even downward trends in performance after learning and , likely due to the adaptation process required for a more diverse set of teammates, necessitating further improvement.
5.3.2. Method Mechanism Optimization Evaluation
Also, in our study on optimizing feedforward neural networks, we compared the Adam optimizer with three alternatives: SGD, RMSprop, and AdamW, as shown in Figure 8, Figure 9 and Figure 10 (in Figure 8, Figure 9 and Figure 10, the legends from top to bottom are, respectively, DE Learns Team (N = 4/episodes = 8), DE Learns Environment (N = 4/episodes = 8), PLASTIC-Policy(N = 4/episodes = 8), DETEAMSK-adam (N = 4/episodes = 8), DETEAMSK-sgd (N = 4/episodes = 8), DETEAMSK-rmsprop (N = 4/episodes = 8), DETEAMSK-adagrad (N = 4/episodes = 8), DETEAMSK-adamw (N = 4/episodes = 8)), and Table A5, Table A6 and Table A7 (detailed in Appendix A). Our findings indicate that, for simple tasks, such as those in the CBD domain, SGD, RMSprop, or AdamW can be viable alternatives, offering a performance comparable to Adam. The AdamW optimizer performs well on both simple and medium-sized tasks, such as those in the CBD and MFD domains, but is less effective for large-scale tasks like SAD. From a comprehensive perspective, particularly for medium-sized and large tasks like SAD and MFD, the RMSprop optimizer is preferred due to its comparable or superior performance relative to Adam, notably in terms of stability and faster convergence during the pre-training process.
Then, we evaluated the action exploration and exploitation policy in reinforcement learning, as shown in Figure 11, Figure 12 and Figure 13 (in Figure 11, Figure 12 and Figure 13, the legends from top to bottom are, respectively, DE Learns Team (N = 4/episodes = 8), DE Learns Environment (N = 4/episodes = 8), PLASTIC-Policy (N = 4/episodes = 8), DETEAMSK-greedy policy (N = 4/episodes = 8), DETEAMSK- boltzman policy (N = 4/episodes = 8), DETEAMSK-epsilon greedy policy (N = 4/episodes = 8), DETE- AMSK-adagrad (N = 4/episodes = 8), DETEAMSK-adamw (N = 4/episodes = 8)). Table A8, Table A9 and Table A10 (detailed in the Appendix A) present the pre-training process and the reward evaluation of the interaction. It can be observed that the Boltzmann policy can serve as an alternative optimization choice, as it performs well in most cases and even outperforms the -greedy policy in certain scenarios, both during reinforcement learning pre-training and interaction processes. The -greedy policy is suitable for simple or medium-task regions, such as CBD and MFD, but its performance is unstable and suboptimal in a sparse-task region like SAD.
For the pursuit and encirclement, as shown in Figure 14 and Figure 15 (in Figure 14 and Figure 15, the legends from top to bottom are, respectively, DE Learns Team (N = 4/episodes = 8), PLASTIC-Policy (N = 4/episodes = 8), DETEAMSK (N = 4/episodes = 8)) and Table A11 and Table A12 (detailed in Appendix A), we can see that DETEAMSK is able to maintain a relatively stable performance; however, adapting to environmental changes remains its weakness. The performance of model-free methods is even less impressive compared to model-based ones, which is also in line with expectations. These tendencies are more obvious, especially at larger scales. When the scale of the task domain expands, it can be observed that DETEAMSK and its ablation methods maintain stable and good performances during the reinforcement learning pre-training process. However, during interactive collaboration, its performance is inferior to its two ablation methods, with DE Learns Team performing the best, achieving the highest reward value and the smallest variance, followed by PLASTIC-Model, and then DE Learns Environment. This indicates that environmental factors pose a significant challenge to the ad hoc teamwork learner in competitive tasks. The model-free method continues to perform the worst, suggesting that the effectiveness of prior knowledge and experience matched with previous states is lower in competitive environments, and its adaptability needs further enhancement.
5.3.3. Performance Convergence Evaluation
Figure 16, Figure 17, Figure 18 and Figure 19 (in Figure 16, Figure 17, Figure 18 and Figure 19, the legends from top to bottom are, respectively, DE Learns Team (N = 4/episodes = 8), DE Learns Environment (N = 4/episodes = 8), PLASTIC-Policy (N = 4/episodes = 8), DETEAMSK-adam (N = 4/episodes = 8)) and Table A13, Table A14, Table A15 and Table A16 (detailed in Appendix A) indicate that, in most cases, DETEAMSK can converge on the final values with small steady-state errors; it performs especially well in the CBD task domain. In the MFD domain, the performances are good, while the SAD are the worst. For the previous 100,000 timesteps, the performances of CBD and MFD are similar to those in standard ad hoc evaluation, which shows the stability of DETEAMSK on the simple and medium-sparse environment; however, for the SAD, which is more irregularly shaped with sparse obstacles and buildings, the performances are prone to be more unstable with much fluctuation, which is worse than the standard ad hoc ones. Furthermore, DETEAMSK converges faster than PLASTIC-Policy both on the CBD and MFD domains, whether in 100,000 or 300,000 training timesteps; however, on the SAD, for the previous 100,000 training timesteps in the standard ad hoc evaluation, DETEAMSK converges faster than PLASTIC-Policy with higher rewards. Conversely, in this round, the opposite trend is reflecting. Before the 25th evaluation checkpoint (training timestep 250,000), for the training in four teams, PLASTIC-Policy outperforms DETEAMSK; almost at the training timestep 250,000, DETEAMSK reluctantly equals PLASTIC-Policy or outperforms it a little for just a short period, before significantly dropping in amplitudes and becoming the inferior of the two. For the team, the two agents converge on the same point at timestep 275,000 again and then DETEAMSK takes the lead. By the end of the interaction, both of the two agents converge on similar asymptotic performances. The other two ablations of DETEAMSK keep average performances as before. The analysis indicates that whether the training timestep is short or long, the environment adaptability of DETEAMSK with more teammates requires large optimization.
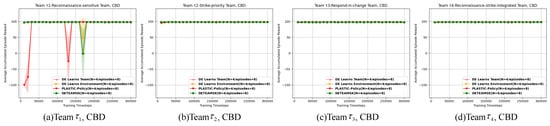
Figure 16.
The pre-training reinforcement learning process of each ad hoc drone agent on the CBD domain. The shaded areas of colors are the confidence interval of 95%.

Figure 17.
The pre-training reinforcement learning process of each ad hoc drone agent on the SAD domain. The shaded areas of colors are the confidence interval of 95%.
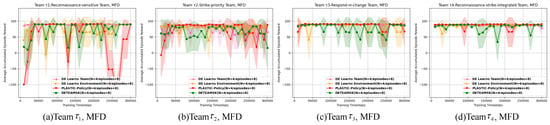
Figure 18.
The pre-training reinforcement learning process of each ad hoc drone agent on the MFD domain. The shaded areas of colors are the confidence interval of 95%.

Figure 19.
The pre-training reinforcement learning process of each ad hoc drone agent on the PAE (10 * 10) domain. The shaded areas of colors are the confidence interval of 95%.
6. Discussions
The results of our experiments facilitate an analysis of the performance of ad hoc drone swarm agents in urban combat tasks.
First, several factors significantly influence the evaluation of the algorithmic method:
- (i)
- Environment scalability. Whether in cooperative or competitive tasks, DETEAMSK demonstrates significant effects in simple domain tasks, such as the CBD domain, by yielding more stable learning curves, higher accumulated average rewards, and lower variances. However, its performance in more complex domains is less favorable and could benefit from further optimization. In the SAD and MFD task domains, DETEAMSK’s learning processes exhibit greater fluctuations and lower evaluated rewards with increased variances. This may be attributed to the challenges of learning in high-dimensional, dynamic environments. Further research is warranted to explore the impact of environmental factors.
- (ii)
- Interaction complexity. The ad hoc agent exhibits an enhanced and more consistent performance when collaborating with teammates of the same category during both the learning and interaction processes. While the agent generally performs effectively after engaging with a simple-class team, some instability may still be observed. To further evaluate the generalizability of DETEAMSK, it is crucial to increase the diversity of interactions.
- (iii)
- Internal method architecture. Several components within the architecture of DETEAMSK can be optimized to enhance its overall performance, including the optimizer, the action exploration and exploitation policy, the hyperparameters, etc. Our experiments suggest that Rspromp is effective for DETEAMSK across various domain tasks when used as the optimizer in feedforward neural networks. For simpler environments, SGD is appropriate, while AdamW is suitable for small to medium-sized task domains. Investigating more advanced methods is crucial to further improve DETEAMSK.
Second, the model-based reinforcement learning method, DETEAMSTER, along with its two ablations, demonstrates superiority over model-free approaches such as PLASTIC-Model in most scenarios. This holds true during both the learning stages and the evaluation of interactions. DETEAMSTER effectively addresses the limitations of PLASTIC-Policy in aligning policies with dynamic environments.
Third, in general perspectives, although worse than the perfect set-up of a PLASTIC model, DETEAMSTER has made progress in further exploring the idea of the method of PLASTIC-Model by introducing the “learning model”, which is free of the restrictions on known teams or tasks. It is more practical in real combat scenarios.
7. Conclusions and Future Work
In this study, we conducted a series of investigations into the model-based reinforcement learning algorithm DETEAMSK to assess its applicability across various task domains and perspectives. We also compared its performance with other baseline methods to evaluate its effectiveness. DETEAMSK exhibited good generalization capability, robustness and high efficiency in simple task domains and performed well in large and complex environments, frequently surpassing model-free methods and, in some instances, approaching the performance of optimal baseline setups. DETEAMSK enables agents to better leverage prior knowledge and experience and adapt more efficiently to team interactions and environmental changes across different task scenarios, thereby enhancing the effectiveness of the ad hoc teamwork. This underscores the advantages of the “dynamic learning of teammates and tasks” inherent to the method.
The most notable breakthrough of this study is the exploration and application of various optimized techniques, combined with multidimensional experiments, to evaluate the generalization capability, robustness and high efficiency of DETEAMSK in diversified tasks and scenarios. Nonetheless, further research is necessary. Future work should concentrate on enhancing the method [], exploring more challenging application fields (e.g., continuous or high-dimensional environments) [], partial observation scenarios [,], strategic maneuver situations [], diverse behaviors in dynamically changing ad hoc agent environments [], communication applications such as flying ad hoc networks [] and equipment application research []. These areas warrant deeper exploration. Furthermore, rather than merely optimizing existing metrics, the focus should be on proposing more creative performance indicators to evaluate the overall effectiveness of the methods. The experimental algorithm evaluation metrics proposed in this study are based on relatively classical domains, and future developments can further introduce new evaluation dimensions to derive more representative and valuable conclusions.
In addition to simulation validation, physical experiments can also be conducted, making the evaluation more concrete and observable, and the conclusions more comprehensive and accurate. The combination of simulations and physical experiments enhances the persuasiveness, allowing the research findings of this paper to be better integrated with practical applications.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/aerospace12070635/s1.
Author Contributions
Conceptualization, P.X.; methodology, P.X.; software, P.X.; validation, P.X.; formal analysis, P.X.; investigation, P.X.; resources, L.H. and Q.Y.; data curation, P.X.; writing—original draft preparation, P.X.; writing—review and editing, P.X.; visualization, P.X. and Y.Z.; supervision, Y.Z.; project administration, P.X. and Y.Z.; funding acquisition, Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article/Supplementary Materials. Further inquiries can be directed to the corresponding authors.
Acknowledgments
The author would like to thank Zhang Yu for their instruction and support, as well as Hao Le and Yan Qilin for their work on this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Appendix A.1. Hyperparameters and Architectures Used in Experiments

Table A1.
Hyperparameters used for the MATM-UCT planner (shared by DETEAMSK, DE Learns Team, DE Learns Environment and PLASTIC-Model).
Table A1.
Hyperparameters used for the MATM-UCT planner (shared by DETEAMSK, DE Learns Team, DE Learns Environment and PLASTIC-Model).
| Task Domain | Total Iterations | Maximum Rollout Depth | UCB Exploration | Discount Factor |
|---|---|---|---|---|
| CBD | 150 | 15 | 0.95 | |
| SAD | 150 | 15 | 0.95 | |
| MFD | 150 | 15 | 0.95 | |
| PAE | 300 | 5 | 0.95 |

Table A2.
Network training architecture, action exploration and exploitation policy and hyperparameters used for the teammate identification model and environment identification model (for DETEAMSK, PLASTIC-Model and PLASTIC-Policy) in cooperative navigation task domains.
Table A2.
Network training architecture, action exploration and exploitation policy and hyperparameters used for the teammate identification model and environment identification model (for DETEAMSK, PLASTIC-Model and PLASTIC-Policy) in cooperative navigation task domains.
| Model | Optimizer | Learning Rate | Hidden Layers | Hidden Units per Layer | Activation Function | Exploration and Exploitation Policy |
|---|---|---|---|---|---|---|
| Transition | Adam/Sgd /Rmsprop /Adagrad /Adamw | 0.001 | 2 | 512 | ReLu | Greedy Policy |
| Rewards | Adam/Sgd /Rmsprop /Adagrad /Adamw | 0.01 | 1 | 64 | ReLu | Greedy Policy |
| Teammate Identification | Adam/Sgd /Rmsprop /Adagrad /Adamw | 0.001 | 2 | 48 | ReLu | Greedy Policy |

Table A3.
Network training architecture, action exploration and exploitation policy and hyperparameters used for the teammate identification model and environment identification model (for DETEAMSK, PLASTIC-Model and PLASTIC-Policy) in cooperative navigation task domains.
Table A3.
Network training architecture, action exploration and exploitation policy and hyperparameters used for the teammate identification model and environment identification model (for DETEAMSK, PLASTIC-Model and PLASTIC-Policy) in cooperative navigation task domains.
| Model | Optimizer | Learning Rate | Hidden Layers | Hidden Units per Layer | Activation Function | Exploration and Exploitation Policy |
|---|---|---|---|---|---|---|
| Transition | Adam | 0.001 | 2 | 256 | ReLu | Linear Annealing Policy |
| Rewards | Adam | 0.001 | 2 | 256 | ReLu | Linear Annealing Policy |
| Teammate Identification | Adam | 0.001 | 2 | 48 | ReLu | Linear Annealing Policy |

Table A4.
Training architecture used for PLASTIC-Policy’s DQNs and the linear annealing policy of DETEAMSK.
Table A4.
Training architecture used for PLASTIC-Policy’s DQNs and the linear annealing policy of DETEAMSK.
| Task Domain | Adam Learning Rate | Hidden Layers | Hidden Units per Layer | Activation Function | Initial Exploration Rate | Final Exploration Rate | Initial Random Steps | Final Exploration Step | Target Update Frequency (Steps) |
|---|---|---|---|---|---|---|---|---|---|
| CBD | 0.001 | 2 | 512 | ReLu | 1.00 | 0.05 | 15000 | 250000 | 4 |
| SAD | 0.001 | 2 | 512 | ReLu | 1.00 | 0.05 | 15000 | 250000 | 4 |
| MFD | 0.001 | 2 | 512 | ReLu | 1.00 | 0.05 | 15000 | 250000 | 4 |
| PAE | 0.001 | 2 | 64 | ReLu | 0.50 | 0.05 | 0 | 5000 | 1 |
Appendix A.2. The Average Accumulated Reward Values of the Ad Hoc Teamwork Interaction of DETEAMSK and Other Baseline Algorithms

Table A5.
The average accumulated episode reward values in each trial computed for each ad hoc drone agent after learning through interaction with teams on the CBD domain.
Table A5.
The average accumulated episode reward values in each trial computed for each ad hoc drone agent after learning through interaction with teams on the CBD domain.
| Baseline | Eval on | Eval on | Eval on | Eval on |
|---|---|---|---|---|
| Original Teammate | 98.000(±0.000) | 98.000(±0.000) | 97.750(±1.750) | ∖ |
| Radom Policy | 83.000(±39.000) | 83.000(±39.000) | 83.000(±39.000) | 83.000(±39.000) |
| UCT -Model | 97.750(±0.750) | 98.000(±0.000) | 97.750(±1.750) | 97.875(±0.875) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK-Adam | 97.875(±0.875) | 98.000(±0.000) | 97.875(±0.875) | 97.750(±1.750) |
| DETEAMSK-Sgd | 96.750(±8.750) | 97.625(±1.625) | 97.125(±2.125) | 97.500(±0.500) |
| DETEAMSK-Rmsprop | 98.000(±0.000) | 97.875(±0.875) | 97.750(±1.750) | 98.000(±0.000) |
| DETEAMSK-Adagrad | 84.875(±85.875) | 96.375(±5.375) | 72.375(±73.375) | 71.875(±72.875) |
| DETEAMSK-Adamw | 98.000(±0.000) | 97.875(±0.875) | 97.750(±1.750) | 98.000(±0.000) |
| PLASTIC-Policy | 98.000(±0.000) | 98.000(±0.000) | 98.000(±0.000) | 98.000(±0.000) |
| DE Learns Team | 97.750(±0.750) | 97.750(±0.750) | 97.625(±0.625) | 97. 750(±0.750) |
| DE Learns Environment | 98.000(±0.000) | 97.625(±1.625) | 97.750(±1.750) | 98.000(±0.000) |
| PLASTIC-Model | 97.875(±0.875) | 98.000(±0.000) | 97.750(±0.750) | 97.750(±1.750) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK-Adam | 98.000(±0.000) | 97.875(±0.875) | 98.000(±0.000) | 98.000(±0.000) |
| DETEAMSK-Sgd | 97.750(±0.750) | 97.875(±0.875) | 97.625(±1.625) | 97.875(±0.875) |
| DETEAMSK-Rmsprop | 97.750(±0.750) | 97.625(±0.625) | 97.625(±1.625) | 97.875(±0.875) |
| DETEAMSK-Adagrad | 96.875(±1.875) | 71.250(±72.250) | 96.875(±1.125) | 72.375(±73.375) |
| DETEAMSK-Adamw | 97.750(±0.750) | 98.000(±0.000) | 97.750(±1.750) | 97.625(±1.625) |
| PLASTIC-Policy | 98.000(±0.000) | 98.000(±0.000) | 97.750(±1.750) | 98.000(±0.000) |
| DE Learns Team | 98.000(±0.000) | 97.750(±0.750) | 97.625(±1.625) | 97.625(±1.625) |
| DE Learns Environment | 97.750(±0.750) | 97.875(±0.875) | 97.750(±0.750) | 98.000(±0.000) |
| PLASTIC-Model | 98.000(±0.000) | 97.875(±0.875) | 98.000(±0.000) | 97.625(±1.625) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK-Adam | 97.875(±0.875) | 97.375(±2.375) | 97.750(±0.750) | 98.000(±0.000) |
| DETEAMSK-Sgd | 97.125(±1.125) | 97.375(±1.375) | 97.375(±1.375) | 97.500(±1.500) |
| DETEAMSK-Rmsprop | 97.875(±0.875) | 97.875(±0.875) | 97.750(±1.750) | 98.000(±0.000) |
| DETEAMSK-Adagrad | 96.500(±1.500) | 85.000(±86.000) | 96.875(±1.125) | 96.625(±1.375) |
| DETEAMSK-Adamw | 97.625(±0.625) | 97.875(±0.875) | 97.750(±1.750) | 97.875(±0.875) |
| PLASTIC-Policy | 98.000(±0.000) | 98.000(±0.000) | 98.000(±0.000) | 98.000(±0.000) |
| DE Learns Team | 97.875(±0.875) | 97.750(±0.750) | 97.750(±1.750) | 98.000(±0.000) |
| DE Learns Environment | 97.875(±0.875) | 97.750(±0.750) | 97.500(±1.500) | 97.750(±1.750) |
| PLASTIC-Model | 98.000(±0.000) | 97.875(±0.875) | 97.875(±0.875) | 98.000(±0.000) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK-Adam | 98.000(±0.000) | 97.875(±0.000) | 97.875(±0.875) | 97.625(±1.625) |
| DETEAMSK-Sgd | 97.000(±5.000) | 97.875(±5.000) | 97.750(±0.750) | 97.625(±0.625) |
| DETEAMSK-Rmsprop | 98.000(±0.000) | 97.750(±0.000) | 97.750(±1.750) | 97.625(±0.625) |
| DETEAMSK-Adagrad | 72.625(±73.625) | 80.875(±73.625) | 84.375(±85.375) | 83.500(±84.500) |
| DETEAMSK-Adamw | 97.750(±1.750) | 97.875(±1.750) | 98.000(±0.000) | 97.875(±0.875) |
| PLASTIC-Policy | 98.000(±0.000) | 98.000(±0.000) | 98.000(±0.000) | 98.000(±0.000) |
| DE Learns Team | 98.000(±0.00) | 97.875(±0.000) | 97.375(±2.375) | 97.625(±0.625) |
| DE Learns Environment | 97.875(±0.875) | 97.750(±0.875) | 98.000(±0.000) | 97.625(±1.625) |
| PLASTIC-Model | 98.000(±0.000) | 97.875(±0.000) | 98.000(±0.000) | 98.000(±0.000) |

Table A6.
The average accumulated episode reward values in each trial computed for each ad hoc drone agent after learning through interaction with teams on the SAD domain.
Table A6.
The average accumulated episode reward values in each trial computed for each ad hoc drone agent after learning through interaction with teams on the SAD domain.
| Baseline | Eval on | Eval on | Eval on | Eval on |
|---|---|---|---|---|
| Original Teammate | 90.000(±2.000) | 83.000(±0.000) | 89.875(±1.875) | ∖ |
| Radom Policy | 78.250(±39.250) | 54.875(±49.875) | 67.250(±48.250) | 53.750(±51.750) |
| UCT -Model | 89.125(±1.875) | 84.500(±5.500) | 89.375(±2.375) | 88.750(±2.250) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK-Adam | 78.750(±79.750) | 74.375(±75.375) | 91.625(±3.625) | 75.500(±76.500) |
| DETEAMSK-Sgd | 22.750(±71.250) | 32.750(±56.250) | 33.875(±58.125) | 22.000(±70.000) |
| DETEAMSK-Rmsprop | 92.000(±7.000) | 76.250(±77.250) | 75.000(±76.000) | 83.625(±27.625) |
| DETEAMSK-Adagrad | 45.875(±46.875) | −1.000(±0.000) | 29.750(±63.250) | 42.000(±44.000) |
| DETEAMSK-Adamw | 88.250(±17.250) | 52.125(±53.125) | 85.125(±26.125) | 33.250(±58.750) |
| PLASTIC-Policy | 81.000(±82.000) | 66.000(±67.000) | 92.250(±3.250) | 56.000(±57.000) |
| DE Learns Team | 92.375(±6.375) | 74.375(±75.375) | 91.625(±3.625) | 75.500(±76.500) |
| DE Learns Environment | 79.000(±80.000) | 73.125(±74.125) | 88.750(±8.750) | 80.875(±81.875) |
| PLASTIC-Model | 91.750(±3.750) | 59.125(±60.125) | 91.125(±5.125) | 78.750(±79.750) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK-Adam | 78.750(±79.750) | 74.375(±75.375) | 91.625(±3.625) | 75.500(±76.500) |
| DETEAMSK-Sgd | 22.750(±71.250) | 32.750(±56.250) | 33.875(±58.125) | 22.000(±70.000) |
| DETEAMSK-Rmsprop | 92.000(±7.000) | 76.250(±77.250) | 75.000(±76.000) | 83.625(±27.625) |
| DETEAMSK-Adagrad | 45.875(±46.875) | −1.000(±0.000) | 29.750(±63.250) | 42.000(±44.000) |
| DETEAMSK-Adamw | 88.250(±17.250) | 52.125(±53.125) | 85.125(±26.125) | 33.250(±58.750) |
| PLASTIC-Policy | 81.000(±82.000) | 66.000(±67.000) | 92.250(±3.250) | 56.000(±57.000) |
| DE Learns Team | 92.375(±6.375) | 74.375(±75.375) | 91.625(±3.625) | 75.500(±76.500) |
| DE Learns Environment | 79.000(±80.000) | 73.125(±74.125) | 88.750(±8.750) | 80.875(±81.875) |
| PLASTIC-Model | 91.750(±3.750) | 59.125(±60.125) | 91.125(±5.125) | 78.750(±79.750) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK-Adam | 64.625(±65.625) | 62.125(±63.125) | 88.750(±19.750) | 72.375(±73.375) |
| DETEAMSK-Sgd | 33.875(±60.125) | 29.750(±59.250) | 29.750(±59.250) | 61.250(±62.250) |
| DETEAMSK-Rmsprop | 81.250(±76.250) | 75.250(±76.250) | 75.250(±76.250) | 66.000(±67.000) |
| DETEAMSK-Adagrad | 26.125(±63.875) | −1.000(±0.000) | −1.000(±0.000) | 28.875(±63.125) |
| DETEAMSK-Adamw | 80.735(±81.735) | 63.500(±64.500) | 65.125(±66.125) | 33.250(±58.750) |
| PLASTIC-Policy | 63.000(±64.000) | 65.000(±66.000) | 86.750(±8.750) | 79.125(±80.125) |
| DE Learns Team | 92.750(±2.750) | 62.125(±63.125) | 88.750(±19.750) | 72.375(±73.375) |
| DE Learns Environment | 90.500(±4.500) | 76.750(±77.750) | 92.250(±3.250) | 77.750(±78.750) |
| PLASTIC-Model | 91.375(±4.375) | 75.250(±76.250) | 91.750(±8.750) | 78.875(±79.875) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK-Adam | 58.625(±59.625) | 76.250(±77.250) | 81.250(±52.250) | 67.750(±68.750) |
| DETEAMSK-Sgd | 10.875(±83.125) | 43.250(±83.125) | 32.625(±59.375) | 44.500(±47.500) |
| DETEAMSK-Rmsprop | 80.375(±81.375) | 75.250(±8.375) | 88.500(±12.500) | 77.125(±78.125) |
| DETEAMSK-Adagrad | 5.500(±45.500) | 21.500(±45.500) | 29.875(±49.125) | 15.500(±76.500) |
| DETEAMSK-Adamw | 88.000(±9.000) | 42.875(±9.000) | 68.250(±69.250) | 56.250(±57.250) |
| PlASTIC-Policy | 88.500(±8.500) | 87.750(±8.750) | 78.875(±79.875) | 78.375(±79.375) |
| DE Learns Team | 87.750(±4.750) | 76.250(±77.250) | 81.250(±52.250) | 67.750(±68.750) |
| DE Learns Environment | 87.625(±17.625) | 87.750(±5.750) | 89.375(±4.625) | 78.250(±79.250) |
| PLASTIC-Model | 91.750(±4.750) | 74.500(±75.500) | 89.000(±26.000) | 77.250(±78.250) |

Table A7.
The average accumulated episode reward values in each trial computed for each ad hoc drone agent after learning through interaction with teams on the MFD domain.
Table A7.
The average accumulated episode reward values in each trial computed for each ad hoc drone agent after learning through interaction with teams on the MFD domain.
| Baseline | Eval on | Eval on | Eval on | Eval on |
|---|---|---|---|---|
| Original Teammate | 90.000(±2.000) | 83.000(±0.000) | 89.875(±1.875) | ∖ |
| Radom Policy | 78.250(±39.250) | 54.875(±49.875) | 67.250(±48.250) | 53.750(±51.750) |
| UCT -Model | 89.125(±1.875) | 84.500(±5.500) | 89.375(±2.375) | 88.750(±2.250) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK-Adam | 90.375(±2.375) | 87.125(±4.125) | 90.125(±2.125) | 88.500(±3.500) |
| DETEAMSK-Sgd | 83.375(±29.375) | 72.125(±73.125) | 71.125(±72.125) | 64.250(±41.250) |
| DETEAMSK-Rmsprop | 89.625(±1.625) | 69.875(±66.875) | 90.625(±0.625) | 86.250(±18.250) |
| DETEAMSK-Adagrad | 48.250(±49.250) | 52.750(±53.750) | 72.750(±73.750) | 21.250(±66.750) |
| DETEAMSK-Adamw | 88.250(±1.750) | 68.250(±69.250) | 89.750(±1.750) | 88.625(±2.625) |
| PLASTIC-Policy | 44.375(±46.625) | 31.250(±57.750) | −1.000(±0.000) | 55.000(±56.000) |
| DE Learns Team | 89.875(±1.875) | 78.875(±14.875) | 89.250(±1.750) | 88.250(±2.750) |
| DE Learns Environment | 89.625(±1.625) | 84.750(±5.250) | 89.375(±2.375) | 89.000(±2.000) |
| PLASTIC-Model | 90.375(±2.375) | 72.75(±73.750) | 89.000(±2.000) | 88.125(±2.875) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK-Adam | 88.125(±7.125) | 84.750(±5.250) | 79.000(±80.000) | 86.750(±3.250) |
| DETEAMSK-Sgd | 37.375(±51.625) | 74.875(±52.875) | 53.625(±54.625) | 49.875(±50.875) |
| DETEAMSK-Rmsprop | 88.500(±14.500) | 71.625(±72.625) | 88.000(±5.000) | 87.250(±4.250) |
| DETEAMSK-Adagrad | 48.875(±49.875) | 58.250(±59.250) | 53.625(±54.625) | 46.250(±47.250) |
| DETEAMSK-Adamw | 86.625(±21.625) | 76.625(±30.625) | 89.125(±3.125) | 80.125(±40.250) |
| PLASTIC-Policy | 78.250(±79.250) | 32.000(±57.000) | 44.875(±46.125) | 67.125(±68.125) |
| DE Learns Team | 88.875(±2.125) | 83.750(±15.750) | 89.125(±9.125) | 88.750(±2.250) |
| DE Learns Environment | 89.000(±2.000) | 85.625(±4.375) | 90.125(±2.125) | 87.875(±4.875) |
| PlASTIC-Model | 90.125(±2.125) | 81.875(±21.875) | 89.125(±1.875) | 87.875(±6.875) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK-Adam | 90.000(±2.000) | 83.625(±6.625) | 89.750(±1.750) | 88.750(±5.750) |
| DETEAMSK-Sgd | 66.750(±67.750) | 60.125(±61.125) | 60.000(±61.000) | 68.500(±69.500) |
| DETEAMSK-Rmsprop | 89.250(±1.750) | 79.125(±24.125) | 88.375(±2.375) | 89.000(±3.000) |
| DETEAMSK-Adagrad | 74.875(±75.875) | 40.375(±42.625) | 42.000(±48.000) | 56.000(±57.000) |
| DETEAMSK-Adamw | 89.250(±1.250) | 82.500(±8.500) | 90.125(±2.125) | 84.625(±31.625) |
| PLASTIC-Policy | 89.625(±2.625) | 53.375(±54.375) | 55.875(±56.875) | 76.625(±77.625) |
| DE Learns Team | 89.125(±1.875) | 81.000(±12.000) | 89.750(±1.750) | 89.125(±1.875) |
| DE Learns Environment | 89.500(±1.500) | 83.875(±6.125) | 88.875(±9.875) | 90.000(±2.000) |
| PLASTIC-Model | 88.875(±2.125) | 84.750(±5.250) | 89.500(±1.500) | 87.375(±6.375) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK-Adam | 88.375(±5.375) | 83.500(±6.500) | 88.250(±12.250) | 89.125(±3.125) |
| DETEAMSK-Sgd | 54.750(±55.750) | 58.750(±55.750) | 26.125(±64.875) | 78.625(±23.625) |
| DETEAMSK-Rmsprop | 88.375(±2.625) | 67.500(±2.625) | 88.125(±7.125) | 89.000(±5.000) |
| DETEAMSK-Adagrad | 45.500(±46.500) | 44.125(±46.500) | 55.750(±56.750) | 63.000(±64.000) |
| DETEAMSK-Adamw | 89.625(±1.625) | 83.125(±1.625) | 89.250(±1.750) | 88.750(±2.250) |
| PLASTIC-Policy | 78.750(±79.750) | 74.500(±75.500) | 78.000(±79.000) | 76.750(±77.750) |
| DE Learns Team | 88.625(±2.375) | 82.500(±10.500) | 89.375(±1.625) | 89.500(±1.500) |
| DE Learns Environment | 89.000(±2.000) | 84.750(±5.250) | 89.250(±2.250) | 88.625(±2.375) |
| PLASTIC-Model | 90.000(±2.000) | 82.125(±7.875) | 89.000(±4.000) | 83.625(±36.625) |

Table A8.
The average accumulated episode reward values in each trial computed for each ad hoc drone agent after learning through interaction with teams on the PAE (5 * 5) domain.
Table A8.
The average accumulated episode reward values in each trial computed for each ad hoc drone agent after learning through interaction with teams on the PAE (5 * 5) domain.
| Baseline | Eval on | Eval on | Eval on | Eval on |
|---|---|---|---|---|
| Original Teammate | 91.125(±6.125) | 92.000(±6.000) | 95.500(±3.500) | ∖ |
| Radom Policy | 76.750(±23.250) | 72.000(±34.000) | 20.875(±170.875) | 31.000(±181.000) |
| UCT-Model | 91.250(±14.250) | 94.375(±5.375) | 92.625(±6.625) | ∖ |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK | 90.750(±7.750) | 91.125(±8.875) | 80.500(±23.500) | 88.875(±24.875) |
| PLASTIC-Policy | 91.375(±7.625) | 76.375(±48.375) | 84.875(±19.875) | 82.875(±23.875) |
| DE Learns Team | 91.250(±17.250) | 90.625(±15.625) | 93.250(±9.250) | 93.500(±9.500) |
| DE Learns Environment | 88.375(±17.375) | 85.875(±24.875) | 83.875(±17.875) | 78.250(±40.250) |
| PLASTIC-Model | 96.125(±2.125) | 87.750(±21.750) | 81.875(±23.875) | 87.000(±13.000) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK | 91.625(±8.625) | 91.750(±91.750) | 89.250(±30.250) | 78.875(±26.875) |
| PLASTIC-Policy | 90.125(±17.125) | 90.125(±18.125) | 82.125(±13.125) | 82.000(±17.000) |
| DE Learns Team | 91.000(±7.000) | 93.500(±7.500) | 94.125(±9.125) | 93.125(±13.125) |
| DE Learns Environment | 85.875(±18.875) | 90.250(±9.250) | 92.125(±18.125) | 85.625(±19.625) |
| PLASTIC-Model | 91.000(±2.125) | 96.000(±9.000) | 96.000(±5.000) | 90.000(±25.000) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK | 90.875(±9.875) | 89.750(±13.750) | 93.000(±9.000) | 86.375(±29.375) |
| PLASTIC-Policy | 91.875(±7.875) | 88.000(±16.000) | 87.875(±34.875) | 71.875(±58.875) |
| DE Learns Team | 93.750(±6.750) | 94.000(±5.000) | 95.250(±3.750) | 90.375(±21.375) |
| DE Learns Environment | 91.125(±17.125) | 86.625(±21.625) | 89.375(±8.625) | 73.125(±25.125) |
| PLASTIC-Model | 94.250(±8.250) | 96.375(±3.375) | 94.750(±6.750) | 90.500(±10.500) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK | 90.250(±11.250) | 91.375(±22.375) | 89.125(±27.125) | 87.125(±21.125) |
| PLASTIC-Policy | 72.125(±24.875) | 89.000(±12.000) | 70.875(±70.875) | 85.750(±12.750) |
| DE Learns Team | 89.625(±1.625) | 69.875(±66.875) | 90.625(±0.625) | 86.250(±18.250) |
| DE Learns Environment | ∖ | ∖ | ∖ | ∖ |
| PLASTIC-Model | ∖ | ∖ | ∖ | ∖ |

Table A9.
The average accumulated episode reward values in each trial computed for each ad hoc drone agent after learning through interaction with teams on the PAE (10 * 10) domain.
Table A9.
The average accumulated episode reward values in each trial computed for each ad hoc drone agent after learning through interaction with teams on the PAE (10 * 10) domain.
| Baseline | Eval on | Eval on | Eval on | Eval on |
|---|---|---|---|---|
| Original Teammate | 82.750(±17.750) | 73.375(±53.375) | 14.125(±164.125) | ∖ |
| Radom Policy | −86.000(±164.000) | −129.375(±144.375) | −94.875(±186.875) | −121.875(±196.875) |
| UCT-Model | 88.125(±8.125) | 66.750(±27.250) | 73.875(±22.125) | ∖ |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK | −30.250(±119.750) | 4.125(±154.125) | −36.500(±119.500) | −94.625(±128.625) |
| PLASTIC-Policy | 20.000(±170.0) | −54.750(±132.75) | −92.625(±180.625) | 7.625(±157.625) |
| DE Learns Team | 76.750(±15.750) | 53.125(±203.125) | 40.500(±49.500) | 22.000(±172.000) |
| DE Learns Environment | 11.625(161.625) | −109.375(±162.375) | −58.250(±135.250) | −96.250(±172.250) |
| PLASTIC-Model | 91.125(±5.875) | 27.500(±177.500) | 27.000(±177.000) | −96.250(±172.250) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK | 34.375(±61.375) | −13.500(±136.500) | 4.375(±154.375) | −30.000(±120.000) |
| PLASTIC-Policy | 10.625(±160.625) | −98.625(±187.625) | −136.625(±93.625) | −67.625(±117.625) |
| DE Learns Team | 73.000(±30.000) | 43.750(±193.75) | 72.000(±18.000) | 64.375(±46.375) |
| DE Learns Environment | −60.750(±148.75) | −33.000(±117.000) | 16.000(±166.000) | −134.875(±105.875) |
| PLASTIC-Model | 86.750(±12.750) | 68.750(±49.750) | 64.500(±36.500) | −134.875(±105.875) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK | −20.750(±129.250) | −35.125(±125.125) | 4.500(±154.500) | −105.875(±160.875) |
| PLASTIC-Policy | −9.375(±140.625) | −92.375(±139.375) | −9.000(±141.000) | −106.625(±186.625) |
| DE Learns Team | 85.125(±8.875) | 72.375(±21.625) | 75.625(±45.625) | 71.875(±71.875) |
| DE Learns Environment | −69.375(±131.375) | −23.375(±126.625) | −43.750(±139.750) | −33.500(±121.500) |
| PLASTIC-Model | 88.250(±21.250) | 68.125(±72.125) | 74.750(±62.750) | −33.500(±121.500) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK | 2.500(±152.500) | −46.375(±140.375) | −12.000(±138.000) | −34.875(±115.125) |
| PLASTIC-Policy | −56.125(±131.125) | −32.250(±129.250) | −47.750(±141.750) | −88.125(±142.125) |
| DE Learns Team | 80.500(±19.500) | 50.000(±200.000) | 35.750(±66.750) | 71.125(±94.125) |
| DE Learns Environment | ∖ | ∖ | ∖ | ∖ |
| PLASTIC-Model | ∖ | ∖ | ∖ | ∖ |

Table A10.
The average accumulated episode reward values in each trial computed for each ad hoc drone agent after learning through interaction with teams on the CBD domain.
Table A10.
The average accumulated episode reward values in each trial computed for each ad hoc drone agent after learning through interaction with teams on the CBD domain.
| Baseline | Eval on | Eval on | Eval on | Eval on |
|---|---|---|---|---|
| Original Teammate | 98.000(±0.000) | 98.000(±0.000) | 97.750(±1.750) | ∖ |
| Radom Policy | 83.000(±39.000) | 83.000(±39.000) | 83.000(±39.000) | 83.000(±39.000) |
| UCT-Model | 97.750(±0.750) | 98.000(±0.000) | 97.750(±1.750) | 97.875(±0.875) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK-Greedy policy | 97.875(±0.875) | 98.000(±0.000) | 97.875(±0.875) | 97.750(±1.750) |
| DETEAMSK-Boltzman policy | 97.875(±0.875) | 98.000(±0.000) | 97.625(±1.625) | 98.000(±0.000) |
| DETEAMSK-Epsilon greedy policy | 96.875(±1.125) | 95.250(±5.250) | 96.875(±1.875) | 95.625(±3.625) |
| PLASTIC-Policy | 98.000(±0.000) | 98.000(±0.000) | 98.000(±0.000) | 98.000(±0.000) |
| DE Learns Team | 97.750(±0.750) | 97.750(±0.750) | 97.625(±0.625) | 97.750(±0.750) |
| DE Learns Environment | 98.000(±0.000) | 97.625(±1.625) | 97.750(±1.750) | 98.000(±0.000) |
| PLASTIC-Model | 97.875(±0.875) | 98.000(±0.000) | 97.750(±0.750) | 97.750(±1.750) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK-Greedy policy | 98.000(±0.000) | 97.875(±0.875) | 98.000(±0.000) | 98.000(±0.000) |
| DETEAMSK-Boltzman policy | 97.875(±0.875) | 98.000(±0.000) | 98.000(±0.000) | 97.625(±1.625) |
| DETEAMSK-Epsilon greedy policy | 95.750(±2.750) | 97.125(±2.125) | 95.000(±13.000) | 84.000(±85.000) |
| PLASTIC-Policy | 98.000(±0.000) | 98.000(±0.000) | 97.750(±1.750) | 98.000(±0.000) |
| DE Learns Team | 98.000(±0.000) | 97.750(±0.750) | 97.625(±1.625) | 97.625(±1.625) |
| DE Learns Environment | 97.750(±0.750) | 97.875(±0.875) | 97.750(±0.750) | 98.000(±0.000) |
| PLASTIC-Model | 98.000(±0.000) | 97.875(±0.875) | 98.000(±0.000) | 97.625(±1.625) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK-Greedy policy | 97.875(±0.875) | 97.375(±2.375) | 97.750(±0.750) | 98.000(±0.000) |
| DETEAMSK-Boltzman policy | 98.000(±0.000) | 97.750(±0.750) | 97.625(±1.625) | 98.000(±0.000) |
| DETEAMSK-Epsilon greedy policy | 96.125(±4.125) | 95.875(±2.875) | 95.500(±3.500) | 96.000(±4.000) |
| PLASTIC-Policy | 98.000(±0.000) | 98.000(±0.000) | 98.000(±0.000) | 98.000(±0.000) |
| DE Learns Team | 97.875(±0.875) | 97.750(±0.750) | 97.750(±1.750) | 98.000(±0.000) |
| DE Learns Environment | 97.875(±0.875) | 97.750(±0.750) | 97.500(±1.500) | 97.750(±1.750) |
| PLASTIC-Model | 98.000(±0.000) | 97.875(±0.875) | 97.875(±0.875) | 98.000(±0.000) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK-Greedy policy | 98.000(±0.000) | 97.875(±0.000) | 97.875(±0.875) | 97.625(±1.625) |
| DETEAMSK-Boltzman policy | 98.000(±0.000) | 97.875(±0.000) | 97.750(±1.750) | 97.750(±1.750) |
| DETEAMSK-Epsilon greedy policy | 95.875(±3.875) | 96.375(±3.875) | 97.700(±3.000) | 95.875(±9.875) |
| PLASTIC-Policy | 98.000(±0.000) | 98.000(±0.000) | 98.000(±0.000) | 98.000(±0.000) |
| DE Learns Team | 98.000(±0.000) | 97.875(±0.000) | 97.375(±2.375) | 97.625(±0.625) |
| DE Learns Environment | 97.875(±0.875) | 97.750(±0.875) | 98.000(±0.000) | 97.625(±1.625) |
| PLASTIC-Model | 98.000(±0.000) | 97.875(±0.000) | 98.000(±0.000) | 98.000(±0.000) |

Table A11.
The average accumulated episode reward values in each trial computed for each ad hoc drone agent after learning through interaction with teams on the SAD domain.
Table A11.
The average accumulated episode reward values in each trial computed for each ad hoc drone agent after learning through interaction with teams on the SAD domain.
| Baseline | Eval on | Eval on | Eval on | Eval on |
|---|---|---|---|---|
| Original Teammate | 90.000(±2.000) | 83.000(±0.000) | 89.875(±1.875) | ∖ |
| Radom Policy | 78.250(±39.250) | 54.875(±49.875) | 67.250(±48.250) | 53.750(±51.750) |
| UCT-Model | 89.125(±1.875) | 84.500(±5.500) | 89.375(±2.375) | 88.750(±2.250) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK-Greedy policy | 78.750(±79.750) | 74.375(±75.375) | 91.625(±3.625) | 75.500(±76.500) |
| DETEAMSK-Boltzman policy | 90.125(±21.125) | 53.500(±54.500) | 90.750(±4.750) | 64.625(±65.625) |
| DETEAMSK-Epsilon greedy policy | 91.250(±3.250) | 27.875(±58.125) | 71.000(±72.000) | 53.375(±54.375) |
| PLASTIC-Policy | 81.000(±82.000) | 66.000(±67.000) | 92.250(±3.250) | 56.000(±57.000) |
| DE Learns Team | 92.375(±6.375) | 74.375(±75.375) | 91.625(±3.625) | 75.500(±76.500) |
| DE Learns Environment | 79.000(±80.000) | 73.125(±74.125) | 88.750(±8.750) | 80.875(±81.875) |
| PLASTIC-Model | 91.750(±3.750) | 59.125(±60.125) | 91.125(±5.125) | 78.750(±79.750) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK-Greedy policy | 90.125(±1.875) | 86.625(±6.625) | 76.875(±77.875) | 77.500(±78.500) |
| DETEAMSK-Boltzman policy | 90.125(±2.125) | 73.625(±57.625) | 87.875(±8.875) | 90.250(±7.250) |
| DETEAMSK-Epsilon greedy policy | 73.625(±74.625) | 62.875(±63.875) | 71.875(±72.875) | 68.750(±57.750) |
| PLASTIC-Policy | 87.000(±11.000) | 65.500(±66.500) | 47.500(±48.500) | 71.750(±72.750) |
| DE Learns Team | 90.250(±4.250) | 86.625(±6.625) | 76.875(±77.875) | 77.500(±78.500) |
| DE Learns Environment | 90.500(±3.500) | 86.875(±10.875) | 87.375(±17.375) | 85.750(±17.750) |
| PLASTIC-Model | 91.875(±5.875) | 87.375(±7.375) | 91.125(±6.125) | 66.250(±67.250) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK-Greedy policy | 64.625(±65.625) | 62.125(±63.125) | 88.750(±19.750) | 72.375(±73.375) |
| DETEAMSK-Boltzman policy | 94.000(±2.250) | 62.875(±63.875) | 92.250(±2.250) | 73.875(±74.875) |
| DETEAMSK-Epsilon greedy policy | 70.375(±56.375) | 53.375(±54.375) | 72.250(±73.250) | 47.000(±48.000) |
| PLASTIC-Policy | 63.000(±64.000) | 65.000(±66.000) | 86.750(±8.750) | 79.125(±80.125) |
| DE Learns Team | 92.750(±2.750) | 62.125(±63.125) | 88.750(±19.750) | 72.375(±73.375) |
| DE Learns Environment | 90.500(±4.500) | 76.750(±77.750) | 92.250(±3.250) | 77.750(±78.750) |
| PLASTIC-Model | 91.375(±4.375) | 75.250(±76.250) | 91.750(±8.750) | 78.875(±79.875) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK-Greedy policy | 58.625(±59.625) | 76.250(±77.250) | 81.250(±52.250) | 67.750(±68.750) |
| DETEAMSK-Boltzman policy | 94.000(±7.750) | 56.375(±7.750) | 90.000(±11.000) | 87.375(±10.375) |
| DETEAMSK-Epsilon greedy policy | 86.500(±12.500) | 48.625(±12.500) | 83.000(±33.000) | 78.375(±41.375) |
| PLASTIC-Policy | 88.500(±8.500) | 87.750(±8.750) | 78.875(±79.875) | 78.375(±79.375) |
| DE Learns Team | 87.750(±4.750) | 76.250(±77.250) | 81.250(±52.250) | 67.750(±68.750) |
| DE Learns Environment | 87.625(±17.625) | 87.750(±5.750) | 89.375(±4.625) | 78.250(±79.250) |
| PLASTIC-Model | 91.750(±4.750) | 74.500(±75.500) | 89.000(±26.000) | 77.250(±78.250) |

Table A12.
The average accumulated episode reward values in each trial computed for each ad hoc drone agent after learning through interaction with teams on the MFD domain.
Table A12.
The average accumulated episode reward values in each trial computed for each ad hoc drone agent after learning through interaction with teams on the MFD domain.
| Baseline | Eval on | Eval on | Eval on | Eval on |
|---|---|---|---|---|
| Original Teammate | 90.000(±2.000) | 83.000(±0.000) | 89.875(±1.875) | ∖ |
| Radom Policy | 78.250(±39.250) | 54.875(±49.875) | 67.250(±48.250) | 53.750(±51.750) |
| UCT-Model | 89.125(±1.875) | 84.500(±5.500) | 89.375(±2.375) | 88.750(±2.250) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK-Greedy policy | 90.375(±2.375) | 87.125(±4.125) | 90.125(±2.125) | 88.500(±3.500) |
| DETEAMSK-Boltzman policy | 88.750(±2.250) | 57.875(±58.875) | 80.250(±24.250) | 87.000(±18.000) |
| DETEAMSK-Epsilon greedy policy | 88.750(±1.250) | 79.625(±18.625) | 89.750(±1.750) | 86.625(±4.375) |
| PLASTIC-Policy | 44.375(±46.625) | 31.250(±57.750) | −1.000(±0.000) | 55.000(±56.000) |
| DE Learns Team | 89.875(±1.875) | 78.875(±14.875) | 89.250(±1.750) | 88.250(±2.750) |
| DE Learns Environment | 89.625(±1.625) | 84.750(±5.250) | 89.375(±2.375) | 89.000(±2.000) |
| PLASTIC-Model | 90.375(±2.375) | 72.750(±73.750) | 89.000(±2.000) | 88.125(±2.875) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK-Greedy policy | 88.125(±7.125) | 84.750(±5.250) | 79.000(±80.000) | 86.750(±3.250) |
| DETEAMSK-Boltzman policy | 83.625(±18.625) | 74.750(±17.750) | 77.625(±75.625) | 77.375(±22.375) |
| DETEAMSK-Epsilon greedy policy | 89.375(±5.375) | 84.875(±5.125) | 88.500(±3.500) | 87.875(±4.875) |
| PLASTIC-Policy | 78.250(±79.250) | 32.000(±57.000) | 44.875(±46.125) | 67.125(±68.125) |
| DE Learns Team | 88.875(±2.125) | 83.750(±15.750) | 89.125(±9.125) | 88.750(±2.250) |
| DE Learns Environment | 89.000(±2.000) | 85.625(±4.375) | 90.125(±2.125) | 87.875(±4.875) |
| PLASTIC-Model | 90.125(±2.125) | 81.875(±21.875) | 89.125(±1.875) | 87.875(±6.875) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK-Greedy policy | 90.000(±2.000) | 83.625(±6.625) | 89.750(±1.750) | 88.750(±5.750) |
| DETEAMSK-Boltzman policy | 66.375(±67.375) | 72.250(±58.250) | 75.375(±76.375) | 84.625(±18.625) |
| DETEAMSK-Epsilon greedy policy | 86.750(±14.750) | 79.500(±16.500) | 88.250(±11.250) | 87.250(±4.250) |
| PLASTIC-Policy | 89.625(±2.625) | 53.375(±54.375) | 55.875(±56.875) | 76.625(±77.625) |
| DE Learns Team | 89.125(±1.875) | 81.000(±12.000) | 89.750(±1.750) | 89.125(±1.875) |
| DE Learns Environment | 89.500(±1.500) | 83.875(±6.125) | 88.875(±9.875) | 90.000(±2.000) |
| PLASTIC-Model | 88.875(±2.125) | 84.750(±5.250) | 89.500(±1.500) | 87.375(±6.375) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK-Greedy policy | 88.375(±5.375) | 83.500(±6.500) | 88.250(±12.250) | 89.125(±3.125) |
| DETEAMSK-Boltzman policy | 77.250(±78.250) | 65.125(±78.250) | 68.250(±69.250) | 77.750(±40.750) |
| DETEAMSK-Epsilon greedy policy | 88.375(±2.625) | 56.875(±2.625) | 86.875(±16.875) | 83.125(±46.125) |
| PLASTIC-Policy | 78.750(±79.750) | 74.500(±75.500) | 78.000(±79.000) | 76.750(±77.750) |
| DE Learns Team | 88.625(±2.375) | 82.500(±10.500) | 89.375(±1.625) | 89.500(±1.500) |
| DE Learns Environment | 89.000(±2.000) | 84.750(±5.250) | 89.250(±2.250) | 88.625(±2.375) |
| PLASTIC-Model | 90.000(±2.000) | 82.125(±7.875) | 89.000(±4.000) | 83.625(±36.625) |

Table A13.
The average accumulated episode reward values in each trial computed for each ad hoc drone agent after learning through interaction with teams on the CBD domain.
Table A13.
The average accumulated episode reward values in each trial computed for each ad hoc drone agent after learning through interaction with teams on the CBD domain.
| Baseline | Eval on | Eval on | Eval on | Eval on |
|---|---|---|---|---|
| Original Teammate | 98.000(±0.000) | 98.000(±0.000) | 97.750(±1.750) | ∖ |
| Radom Policy | 83.000(±39.000) | 83.000(±39.000) | 83.000(±39.000) | 83.000(±39.000) |
| UCT-Model | 97.750(±0.750) | 98.000(±0.000) | 97.750(±1.750) | 97.875(±0.875) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK | 97.750(±0.750) | 97.875(±0.875) | 97.875(±0.875) | 97.750(±0.750) |
| PLASTIC-Policy | 98.000(±0.000) | 98.000(±0.000) | 98.000(±0.000) | 98.000(±0.000) |
| DE Learns Team | 98.000(±0.000) | 98.000(±0.000) | 97.750(±0.750) | 97.875(±0.875) |
| DE Learns Environment | 97.875(±0.875) | 97.750(±1.750) | 97.625(±1.625) | 97.875(±0.875) |
| PLASTIC-Model | 98.000(±0.000) | 98.000(±0.000) | 97.500(±1.500) | 98.000(±0.000) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK | 97.750(±0.750) | 98.000(±0.000) | 97.875(±0.875) | 97.875(±0.875) |
| PLASTIC-Policy | 98.000(±0.000) | 98.000(±0.000) | 98.000(±0.000) | 98.000(±0.000) |
| DE Learns Team | 98.000(±0.000) | 98.000(±0.000) | 97.625(±1.625) | 98.000(±0.000) |
| DE Learns Environment | 98.000(±0.000) | 98.000(±0.000) | 97.625(±1.625) | 98.000(±0.000) |
| PLASTIC-Model | 97.875(±0.875) | 98.000(±0.000) | 97.750(±0.750) | 97.750(±0.750) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK | 97.500(±2.500) | 97.875(±0.875) | 97.875(±0.875) | 98.000(±0.000) |
| PLASTIC-Policy | 98.000(±0.000) | 98.000(±0.000) | 97.750(±1.750) | 98.000(±0.000) |
| DE Learns Team | 98.000(±0.000) | 97.750(±0.750) | 97.375(±1.375) | 97.875(±0.875) |
| DE Learns Environment | 98.000(±0.000) | 97.750(±0.750) | 97.625(±1.625) | 97.875(±0.875) |
| PLASTIC-Model | 97.875(±0.875) | 98.000(±0.000) | 98.000(±0.000) | 97.625(±1.625) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK | 98.000(±0.750) | 97.500(±0.750) | 98.000(±0.000) | 97.750(±0.750) |
| PLASTIC-Policy | 98.000(±0.000) | 98.000(±0.000) | 97.750(±1.750) | 98.000(±0.000) |
| DE Learns Team | 97.750(±0.750) | 97.875(±0.750) | 98.000(±0.000) | 97.750(±0.750) |
| DE Learns Environment | 97.500(±1.500) | 97.875(±1.500) | 97.375(±1.375) | 97.875(±0.875) |
| PLASTIC-Model | 97.875(±0.875) | 98.000(±0.875) | 97.875(±0.875) | 97.875(±0.875) |

Table A14.
The average accumulated episode reward values in each trial computed for each ad hoc drone agent after learning through interaction with teams on the SAD domain.
Table A14.
The average accumulated episode reward values in each trial computed for each ad hoc drone agent after learning through interaction with teams on the SAD domain.
| Baseline | Eval on | Eval on | Eval on | Eval on |
|---|---|---|---|---|
| Original Teammate | 93.000(±1.000) | 87.375(±2.375) | 92.250(±2.250) | ∖ |
| Radom Policy | 58.125(±24.875) | 51.250(±40.250) | 52.375(±38.625) | 45.250(±40.250) |
| UCT-Model | 82.125(±63.125) | 87.625(±2.625) | 90.750(±8.750) | 90.250(±5.250) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK | 44.375(±49.625) | 19.000(±71.000) | 58.000(±59.000) | 49.250(±50.250) |
| PLASTIC-Policy | 81.500(±82.500) | 55.250(±56.250) | 81.125(±82.125) | 66.500(±67.500) |
| DE Learns Team | 80.500(±81.500) | 72.125(±73.125) | 91.375(±7.375) | 64.875(±65.875) |
| DE Learns Environment | 44.875(±49.125) | 52.250(±53.250) | 44.000(±50.000) | 31.750(±59.250) |
| PLASTIC-Model | 93.500(±1.500) | 72.000(±73.000) | 88.500(±23.500) | 85.125(±26.125) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK | 22.375(±70.625) | 43.250(±44.750) | 79.125(±80.125) | 43.750(±48.250) |
| PLASTIC-Policy | 92.625(±1.375) | 77.250(±78.250) | 79.750(±80.750) | 91.250(±6.250) |
| DE Learns Team | 91.000(±6.000) | 76.000(±77.000) | 89.625(±3.625) | 98.000(±0.000) |
| DE Learns Environment | 45.750(±48.250) | 12.125(±60.875) | 42.375(±49.625) | 36.625(±55.375) |
| PLASTIC-Model | 89.625(±4.625) | 84.750(±4.750) | 91.375(±3.375) | 55.625(±56.625) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK | 45.625(±48.375) | 21.875(±69.125) | 65.125(±66.125) | 54.250(±55.250) |
| PLASTIC-Policy | 92.875(±1.125) | 76.875(±77.875) | 92.875(±1.125) | 78.500(±79.500) |
| DE Learns Team | 92.000(±8.000) | 64.500(±65.500) | 92.500(±2.500) | 79.125(±80.125) |
| DE Learns Environment | 28.750(±63.250) | 41.625(±46.375) | 45.125(±48.875) | 62.875(±63.875) |
| PLASTIC-Model | 92.750(±1.750) | 86.875(±5.875) | 92.750(±1.250) | 76.375(±77.375) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK | 63.875(±64.875) | 50.000(±64.875) | 52.625(±53.625) | 34.125(±59.875) |
| PLASTIC-Policy | 92.625(±1.375) | 76.250(±1.375) | 79.625(±80.625) | 79.875(±80.875) |
| DE Learns Team | 90.750(±5.750) | 76.750(±5.750) | 80.125(±81.125) | 74.500(±75.500) |
| DE Learns Environment | 55.000(±56.000) | 50.875(±56.000) | 46.250(±47.750) | 62.625(±63.625) |
| PLASTIC-Model | 89.125(±9.125) | 76.625(±9.125) | 91.000(±7.000) | 77.500(±78.500) |

Table A15.
The average accumulated episode reward values in each trial computed for each ad hoc drone agent after learning through interaction with teams on the MFD domain.
Table A15.
The average accumulated episode reward values in each trial computed for each ad hoc drone agent after learning through interaction with teams on the MFD domain.
| Baseline | Eval on | Eval on | Eval on | Eval on |
|---|---|---|---|---|
| Original Teammate | 90.000(±2.000) | 83.000(±0.000) | 89.875(±1.875) | ∖ |
| Radom Policy | 78.250(±39.250) | 54.875(±49.875) | 67.250(±48.250) | 53.750(±51.750) |
| UCT-Model | 89.125(±1.875) | 84.500(±5.500) | 89.375(±2.375) | 88.750(±2.250) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK | 88.625(±11.625) | 84.750(±20.750) | 78.000(±79.000) | 88.375(±5.375) |
| PLASTIC-Policy | 90.875(±0.875) | 88.125(±5.125) | 90.500(±0.500) | 79.000(±80.000) |
| DE Learns Team | 90.000(±6.000) | 84.250(±6.250) | 84.750(±29.750) | 87.125(±11.125) |
| DE Learns Environment | 77.750(±78.750) | 74.250(±55.250) | 83.500(±30.500) | 89.000(±6.000) |
| PLASTIC-Model | 88.375(±2.625) | 73.250(±68.250) | 90.000(±2.000) | 88.125(±4.125) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK | 78.000(±79.000) | 58.875(±59.875) | 74.625(±75.625) | 73.000(±74.000) |
| PLASTIC-Policy | 90.500(±0.500) | 86.625(±4.375) | 78.750(±79.750) | 90.375(±2.375) |
| DE Learns Team | 85.500(±9.500) | 76.750(±27.500) | 89.875(±2.875) | 83.000(±16.000) |
| DE Learns Environment | 87.000(±11.000) | 83.000(±17.000) | 90.000(±5.000) | 84.125(±22.125) |
| PLASTIC-Model | 89.125(±2.625) | 83.875(±6.125) | 78.375(±66.375) | 89.875(±1.875) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK | 77.250(±78.250) | 82.250(±9.250) | 89.875(±3.875) | 87.875(±6.875) |
| PLASTIC-Policy | 89.625(±1.625) | 75.625(±76.625) | 90.375(±0.625) | 88.750(±3.750) |
| DE Learns Team | 88.625(±2.375) | 65.750(±66.750) | 89.500(±3.500) | 88.375(±2.625) |
| DE Learns Environment | 87.000(±10.000) | 86.000(±7.000) | 77.000(±78.000) | 82.375(±16.375) |
| PLASTIC-Model | 88.375(±88.375) | 84.250(±5.750) | 89.625(±3.625) | 88.250(±7.250) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK | 87.750(±13.750) | 77.625(±13.750) | 89.250(±3.250) | 88.625(±9.625) |
| PLASTIC-Policy | 89.000(±3.000) | 87.875(±3.000) | 89.000(±4.000) | 90.125(±2.125) |
| DE Learns Team | 89.875(±1.875) | 85.000(±1.875) | 88.875(±4.875) | 86.250(±13.250) |
| DE Learns Environment | 83.625(±42.625) | 74.250(±42.625) | 90.625(±0.625) | 74.375(±75.375) |
| PLASTIC-Model | 89.250(±1.750) | 79.750(±1.750) | 88.875(±2.125) | 86.625(±6.625) |

Table A16.
The average accumulated episode reward values in each trial computed for each ad hoc drone agent after learning through interaction with teams on the PAE (10 * 10) domain.
Table A16.
The average accumulated episode reward values in each trial computed for each ad hoc drone agent after learning through interaction with teams on the PAE (10 * 10) domain.
| After Learning | Eval on | Eval on | Eval on | Eval on |
|---|---|---|---|---|
| DETEAMSK | 25.500(±175.500) | −49.125(±125.125) | 17.000(±167.000) | −8.750(±141.250) |
| PLASTIC-Policy | 17.625(±167.625) | −63.625(±157.625) | −62.875(±121.875) | −69.000(±142.000) |
| DE Learns Team | 80.000(±15.000) | 62.750(±98.750) | 51.875(±59.875) | 46.500(±45.500) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK | 49.625(±60.625) | −28.500(±121.500) | −3.750(±146.250) | −15.750(±134.250) |
| PLASTIC-Policy | 35.750(±185.750) | −102.250(±153.250) | −130.250(±138.250) | −100.500(±192.500) |
| DE Learns Team | 70.250(±27.750) | 64.375(±51.375) | 51.250(±47.250) | 69.625(±60.625) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK | 55.625(±34.625) | −63.000(±152.000) | −82.500(±174.500) | −47.750(±139.750) |
| PLASTIC-Policy | −87.000(±138.000) | −67.375(±157.375) | −94.375(±167.375) | −93.250(±159.250) |
| DE Learns Team | 86.750(±12.750) | 66.500(±51.500) | 67.375(±60.375) | 63.750(±59.750) |
| After Learning | Eval on | Eval on | Eval on | Eval on |
| DETEAMSK | 24.625(±174.625) | 24.375(±174.375) | −56.875(±125.875) | −6.625(±143.375) |
| PLASTIC-Policy | −57.750(±142.750) | −69.125(±161.125) | −83.875(±88.875) | −94.250(±188.250) |
| DE Learns Team | 79.500(±32.500) | 62.750(±30.750) | 57.375(±50.375) | 80.000(±17.000) |
References
- Bekmezci, I.; Sahingoz, O.K.; Temel, Ş. Flying ad-hoc networks (FANETs): A survey. Ad Hoc Netw. 2013, 11, 1254–1270. [Google Scholar] [CrossRef]
- Kamel, B.; Oussama, A. Cooperative Navigation and Autonomous Formation Flight for a Swarm of Unmanned Aerial Vehicle. In Proceedings of the 2021 5th International Conference on Vision, Image and Signal Processing (ICVISP), Kuala Lumpur, Malaysia, 18–20 December 2021; pp. 212–217. [Google Scholar]
- Shen, L.C.; Niu, Y.F.; Zhu, H.Y. Theories and methods of autonomous cooperative control for multiple UAVs. Sci.-Technol. Publ. 2013, 50–56. [Google Scholar]
- Zou, L.Y.; Zhang, M.Z.; Rong, M. Analysis of intelligent unmanned aircraft systems swarm concept and main development trend. Tactical Missile Technol. 2019, 5, 1–11. [Google Scholar]
- Hu, X. The Science of War: Understanding the Scientific Foundations and Thinking Methods of War; Science Press. 2018. Available online: https://fx.gfkd.chaoxing.com/detail_38502727e7500f26645e6677ee9b5d50f085fb46afe9a5921921b0a3ea25510134114c969f2eae5c338fa974ce0cee956c2520ce8449a34547b9173ffddc58c1fc5334fd739e739d0891d1a62223f3f3 (accessed on 1 December 2021).
- Zhang, B.C.; Liao, J.; Kuang, Y.; Zhang, M.; Zhou, S.L.; Kang, Y.H. Research status and development trend of the United States UAV swarm battlefield. Aero Weapon. 2020, 27, 7–12. [Google Scholar]
- Niu, Y.F.; Shen, L.C.; Li, J.; Wang, X. Key scientific problems in cooperation control of unmanned-manned aircraft systems. Sci. Sin. Inform. 2019, 49, 538–554. [Google Scholar] [CrossRef]
- Wang, Y.C.; Liu, J.G. Evaluation methods for the autonomy of unmanned systems. Chin. Sci. Bull. 2012, 57, 3409–3418. [Google Scholar] [CrossRef]
- Mirsky, R.; Carlucho, I.; Rahman, A.; Fosong, E.; Macke, W.; Sridharan, M.; Stone, P.; Albrecht, S.V. A survey of ad hoc teamwork research. In Proceedings of the European Conference on Multi-Agent Systems, Düsseldorf, Germany, 14–16 September 2022; Springer International Publishing: Cham, Switzerland, 2022; pp. 275–293. [Google Scholar]
- Bowling, M.; McCracken, P. Coordination and adaptation in impromptu teams. In Proceedings of the AAAI 2005, Pittsburgh, PA, USA, 9–13 July 2005; Volume 5, pp. 53–58. [Google Scholar]
- Rovatsos, M.; Wolf, M. Towards social complexity reduction in multiagent learning: The adhoc approach. In Proceedings of the 2002 AAAI Spring Symposium on Collaborative Learning Agents, Palo Alto, CA, USA, 25–27 March 2002; pp. 90–97. [Google Scholar]
- Stone, P.; Kaminka, G.; Kraus, S.; Rosenschein, J. Ad hoc autonomous agent teams: Collaboration without pre-coordination. In Proceedings of the AAAI Conference on Artificial Intelligence, Atlanta, GA, USA, 11–15 July 2010; Volume 24, pp. 1504–1509. [Google Scholar]
- Yuan, L.; Zhang, Z.; Li, L.; Guan, C.; Yu, Y. A survey of progress on cooperative multi-agent reinforcement learning in open environment. arXiv 2023, arXiv:2312.01058. [Google Scholar] [CrossRef]
- Barrett, S.; Rosenfeld, A.; Kraus, S.; Stone, P. Making friends on the fly: Cooperating with new teammates. Artif. Intell. 2017, 242, 132–171. [Google Scholar] [CrossRef]
- Barrett, S.; Stone, P. Cooperating with unknown teammates in complex domains: A robot soccer case study of ad hoc teamwork. In Proceedings of the AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; Volume 29. [Google Scholar]
- Barrett, S.; Stone, P. An analysis framework for ad hoc teamwork tasks. In Proceedings of the 11th International Conference on Autonomous Agents and Multiagent Systems-Volume 1, Valencia, Spain, 4–8 June 2012; pp. 357–364. [Google Scholar]
- Barrett, S.; Stone, P.; Kraus, S. Empirical evaluation of ad hoc teamwork in the pursuit domain. In Proceedings of the 10th International Conference on Autonomous Agents and Multiagent Systems-Volume 2, Taipei, Taiwan, 2–6 May 2011; pp. 567–574. [Google Scholar]
- Barrett, S. Making Friends on the Fly: Advances in Ad Hoc Teamwork; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Melo, F.S.; Sardinha, A. Ad hoc teamwork by learning teammates’ task. Auton. Agents Multi-Agent Syst. 2016, 30, 175–219. [Google Scholar] [CrossRef]
- Gu, P.; Zhao, M.; Hao, J.; An, B. Online ad hoc teamwork under partial observability. In Proceedings of the International Conference on Learning Representations, Online, 3–7 May 2021. [Google Scholar]
- Dodampegama, H.; Sridharan, M. Knowledge-based reasoning and learning under partial observability in ad hoc teamwork. Theory Pract. Log. Program. 2023, 23, 696–714. [Google Scholar] [CrossRef]
- Fujimoto, T.; Chatterjee, S.; Ganguly, A. Ad hoc teamwork in the presence of adversaries. arXiv 2022, arXiv:2208.05071. [Google Scholar] [CrossRef]
- Santos, P.M.; Ribeiro, J.G.; Sardinha, A.; Melo, F.S. Ad hoc teamwork in the presence of non-stationary teammates. In Proceedings of the EPIA Conference on Artificial Intelligence, Virtual, 7–9 September 2021; Springer International Publishing: Cham, Switzerland, 2021; pp. 648–660. [Google Scholar]
- Ribeiro, J.G.; Rodrigues, G.; Sardinha, A.; Melo, F.S. TEAMSTER: Model-based reinforcement learning for ad hoc teamwork. Artif. Intell. 2023, 324, 104013. [Google Scholar] [CrossRef]
- Fosong, E.; Rahman, A.; Carlucho, I.; Albrecht, S.V. Few-shot teamwork. arXiv 2022, arXiv:2207.09300. [Google Scholar] [CrossRef]
- Chandrasekaran, M.; Eck, A.; Doshi, P.; Soh, L. Individual planning in open and typed agent systems. In Proceedings of the Thirty-Second Conference on Uncertainty in Artificial Intelligence, New York, NY, USA, 25–29 June 2016; pp. 82–91. [Google Scholar]
- Ribeiro, J.G.; Faria, M.; Sardinha, A.; Melo, F.S. Helping people on the fly: Ad hoc teamwork for human-robot teams. In Proceedings of the Progress in Artificial Intelligence: 20th EPIA Conference on Artificial Intelligence, EPIA 2021, Virtual Event, 7–9 September 2021; Proceedings 20. Springer International Publishing: Cham, Switzerland, 2021; pp. 635–647. [Google Scholar]
- Ribeiro, J.G.; Martinho, C.; Sardinha, A.; Melo, F.S. Assisting unknown teammates in unknown tasks: Ad hoc teamwork under partial observability. arXiv 2022, arXiv:2201.03538. [Google Scholar] [CrossRef]
- Rahman, M.A.; Hopner, N.; Christianos, F.; Albrecht, S.V. Towards open ad hoc teamwork using graph-based policy learning. In Proceedings of the International Conference on Machine Learning, PMLR, Online, 18–24 July 2021; pp. 8776–8786. [Google Scholar]
- Rahman, A.; Carlucho, I.; Höpner, N.; Albrecht, S.V. A general learning framework for open ad hoc teamwork using graph-based policy learning. J. Mach. Learn. Res. 2023, 24, 1–74. [Google Scholar]
- Rahman, M.A. Advances in Open ad Hoc Teamwork and Teammate Generation. 2023. Available online: https://era.ed.ac.uk/handle/1842/40567 (accessed on 15 May 2023).
- Eck, A.; Shah, M.; Doshi, P.; Soh, L.K. Scalable decision-theoretic planning in open and typed multiagent systems. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 7127–7134. [Google Scholar]
- Jameson, S.; Franke, J.; Szczerba, R.; Stockdale, S. Collaborative autonomy for manned/unmanned teams. In Proceedings of the Annual Forum Proceedings-American Helicopter Society, Grapevine, TX, USA, 1–3 June 2005; American Helicopter Society, Inc.: Fairfax, VA, USA, 2005; Volume 61, p. 1673. [Google Scholar]
- Martinez, S. UAV cooperative decision and control: Challenges and practical approaches (shima, t. and rasmussen, s.; 2008) [bookshelf]. IEEE Control Syst. Mag. 2010, 30, 104–107. [Google Scholar]
- Zhu, S.; Wang, D.; Low, C.B. Cooperative control of multiple UAVs for moving source seeking. In Proceedings of the 2013 International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 28–31 May 2013; pp. 193–202. [Google Scholar]
- Neves, A.; Sardinha, A. Learning to Cooperate with Completely Unknown Teammates. In Proceedings of the EPIA Conference on Artificial Intelligence, Lisbon, Portugal, 31 August–2 September 2022; Springer International Publishing: Cham, Switzerland, 2022; pp. 739–750. [Google Scholar]
- Sutton, R.S. Reinforcement Learning: An Introduction; A Bradford Book; 2018. Available online: https://www.cambridge.org/core/journals/robotica/article/abs/robot-learning-edited-by-jonathan-h-connell-and-sridhar-mahadevan-kluwer-boston-19931997-xii240-pp-isbn-0792393651-hardback-21800-guilders-12000-8995/737FD21CA908246DF17779E9C20B6DF6 (accessed on 13 July 2025).
- Kocsis, L.; Szepesvári, C. Bandit based monte-carlo planning. In Proceedings of the European Conference on Machine Learning, Berlin, Germany, 18–22 September 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 282–293. [Google Scholar]
- Browne, C.B.; Powley, E.; Whitehouse, D.; Lucas, S.M.; Cowling, P.I.; Rohlfshagen, P.; Tavener, S.; Perez, D.; Samothrakis, S.; Colton, S. A survey of monte carlo tree search methods. IEEE Trans. Comput. Intell. AI Games 2012, 4, 1–43. [Google Scholar] [CrossRef]
- Gray, R.C.; Zhu, J.; Ontañón, S. Beyond UCT: MAB Exploration Improvements for Monte Carlo Tree Search. In Proceedings of the 2023 IEEE Conference on Games (CoG), Boston, MA, USA, 21–24 August 2023; pp. 1–8. [Google Scholar]
- Watkins, C.J.C.H. Dayan P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar]
- Watkins, C.J.C.H. Learning from delayed rewards. Robot. Auton. Syst. 1989. Available online: https://d1wqtxts1xzle7.cloudfront.net/50360235/Learning_from_delayed_rewards_20161116-28282-v2pwvq-libre.pdf?1479337768=&response-content-disposition=inline%3B+filename%3DLearning_from_delayed_rewards.pdf&Expires=1752568841&Signature=XNY6TdtsZ5zJIhAg5ztgppa3YkIA3r3HJIlgAqyxL9lGL~WYcjzuNKvMlBr4P2OsT8LrucS8A6zelmuCGVCB8l-u~4DL0bMM1XWUMG2Z0ee7WRnJNBMIx6eL8IBpHrpS-ZVYCLMierFuOMinOojOA6rPwByqDDgYKAxvtELo04AnBOUdU9TIOOT7V-lA1HXH1qxPxA6Cch2mzGoAtHD5zeVppGma4ooslHfY2DDC0aUw-2mWPwy98Ei4IlS3gxfoTa8hsE5jVXK4rOanJ7WPIOzfnyhA8OEKEzZLR0-DVE5Q6dD16HScrtTvdIqPfWD1HBvUHsArlV4VspjywznzEg__&Key-Pair-Id=APKAJLOHF5GGSLRBV4ZA (accessed on 13 July 2025).
- Kalman, B.L.; Kwasny, S.C. Why tanh: Choosing a sigmoidal function. In Proceedings of the [Proceedings 1992] IJCNN International Joint Conference on Neural Networks, Baltimore, MD, USA, 7–11 June 1992; Volume 4, pp. 578–581. [Google Scholar]
- Agarap, A.F. Deep learning using rectified linear units (relu). arXiv 2018, arXiv:1803.08375. [Google Scholar]
- Shi, N.; Li, D. Rmsprop converges with proper hyperparameter. In Proceedings of the International Conference on Learning Representation, Online, 3–7 May 2021. [Google Scholar]
- Zou, F.; Shen, L.; Jie, Z.; Zhang, W.; Liu, W. A sufficient condition for convergences of adam and rmsprop. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 11127–11135. [Google Scholar]
- Kingma, D.P. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Yourdshahi, E.S.; Pinder, T.; Dhawan, G.; Marcolino, L.S.; Angelov, P. Towards large scale ad-hoc teamwork. In Proceedings of the 2018 IEEE International Conference on Agents (ICA), Singapore, 28–31 July 2018; pp. 44–49. [Google Scholar]
- Csáji, B.C.; Monostori, L. Value function based reinforcement learning in changing Markovian environments. J. Mach. Learn. Res. 2008, 9, 1679–1709. [Google Scholar]
- Albrecht, S.V.; Stone, P. Autonomous agents modelling other agents: A comprehensive survey and open problems. Artif. Intell. 2018, 258, 66–95. [Google Scholar] [CrossRef]
- Deisenroth, M.P.; Neumann, G.; Peters, J. A survey on policy search for robotics. Found. Trends Robot. 2013, 2, 1–142. [Google Scholar]
- Guestrin, C.; Koller, D.; Parr, R.; Venkataraman, S. Efficient solution algorithms for factored MDPs. J. Artif. Intell. Res. 2003, 19, 399–468. [Google Scholar] [CrossRef]
- Kaelbling, L.P.; Littman, M.L.; Moore, A.W. Reinforcement learning: A survey. J. Artif. Intell. Res. 1996, 4, 237–285. [Google Scholar] [CrossRef]
- Szepesvári, C. Algorithms for Reinforcement Learning; Springer Nature: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Bellemare, M.G.; Naddaf, Y.; Veness, J.; Bowling, M. The arcade learning environment: An evaluation platform for general agents. J. Artif. Intell. Res. 2013, 47, 253–279. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Buşoniu, L.; Babuška, R.; De Schutter, B. Multi-agent reinforcement learning: An overview. In Innovations in Multi-Agent Systems and Applications-1; Springer: Berlin/Heidelberg, Germany, 2010; pp. 183–221. [Google Scholar]
- Kool, W.; Van Hoof, H.; Welling, M. Attention, learn to solve routing problems! arXiv 2018, arXiv:1803.08475. [Google Scholar]
- Melo, F.S.; Veloso, M. Learning of coordination: Exploiting sparse interactions in multiagent systems. In Proceedings of the 8th International Conference on Autonomous Agents and Multiagent Systems-Volume 2, Budapest, Hungary, 10–15 May 2009; pp. 773–780. [Google Scholar]
- Hu, Y.; Gao, Y.; An, B. Learning in Multi-agent Systems with Sparse Interactions by Knowledge Transfer and Game Abstraction. In Proceedings of the AAMAS 2015, Istanbul, Turkey, 4–8 May 2015; pp. 753–761. [Google Scholar]
- Melo, F.S.; Sardinha, A.; Belo, D.; Couto, M.; Faria, M.; Farias, A.; Gambôa, H.; Jesus, C.; Kinarullathil, M.; Lima, P.; et al. Project INSIDE: Towards autonomous semi-unstructured human–robot social interaction in autism therapy. Artif. Intell. Med. 2019, 96, 198–216. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Andrejczuk, E.; Cao, Z.; Zhang, J. Aateam: Achieving the ad hoc teamwork by employing the attention mechanism. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 7095–7102. [Google Scholar]
- Lowe, R.; Wu, Y.I.; Tamar, A.; Harb, J.; Pieter Abbeel, O.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Zhang, Y.; Zavlanos, M.M. Cooperative Multiagent Reinforcement Learning With Partial Observations. IEEE Trans. Autom. Control 2023, 69, 968–981. [Google Scholar] [CrossRef]
- Fernandez, R.; Asher, D.E.; Basak, A.; Sharma, P.K.; Zaroukian, E.G.; Hsu, C.D.; Dorothy, M.R.; Kroninger, C.M.; Frerichs, L.; Rogers, J.; et al. Multi-Agent Coordination for Strategic Maneuver with a Survey of Reinforcement Learning; tech. rep.; US Army Combat Capabilities Development Command, Army Research Laboratory: 2021. Available online: https://apps.dtic.mil/sti/html/trecms/AD1154872/ (accessed on 1 December 2021).
- Albrecht, S.V.; Ramamoorthy, S. Comparative evaluation of MAL algorithms in a diverse set of ad hoc team problems. In Proceedings of the 11th International Conference on Autonomous Agents and Multiagent Systems-Volume 1, Valencia, Spain, 4–8 June 2012; pp. 349–356. [Google Scholar]
- Arafat, M.Y.; Moh, S. A Q-learning-based topology-aware routing protocol for flying ad hoc networks. IEEE Internet Things J. 2021, 9, 1985–2000. [Google Scholar] [CrossRef]
- Yoo, J.; Jang, D.; Kim, H.J.; Johansson, K.H. Hybrid reinforcement learning control for a micro quadrotor flight. IEEE Control Syst. Lett. 2020, 5, 505–510. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).