A Rapid Method for Heat Transfer Coefficient Prediction on the Icing Surfaces of Aircraft Wings Based on a Partitioned Boundary Layer Integral Model
Abstract
1. Introduction
2. Computational Methodology
2.1. Approximate Solution for Wing Surface Heat Transfer Coefficient
- (1)
- Stagnation Region Treatment
- (2)
- Non-Stagnation Region Treatment
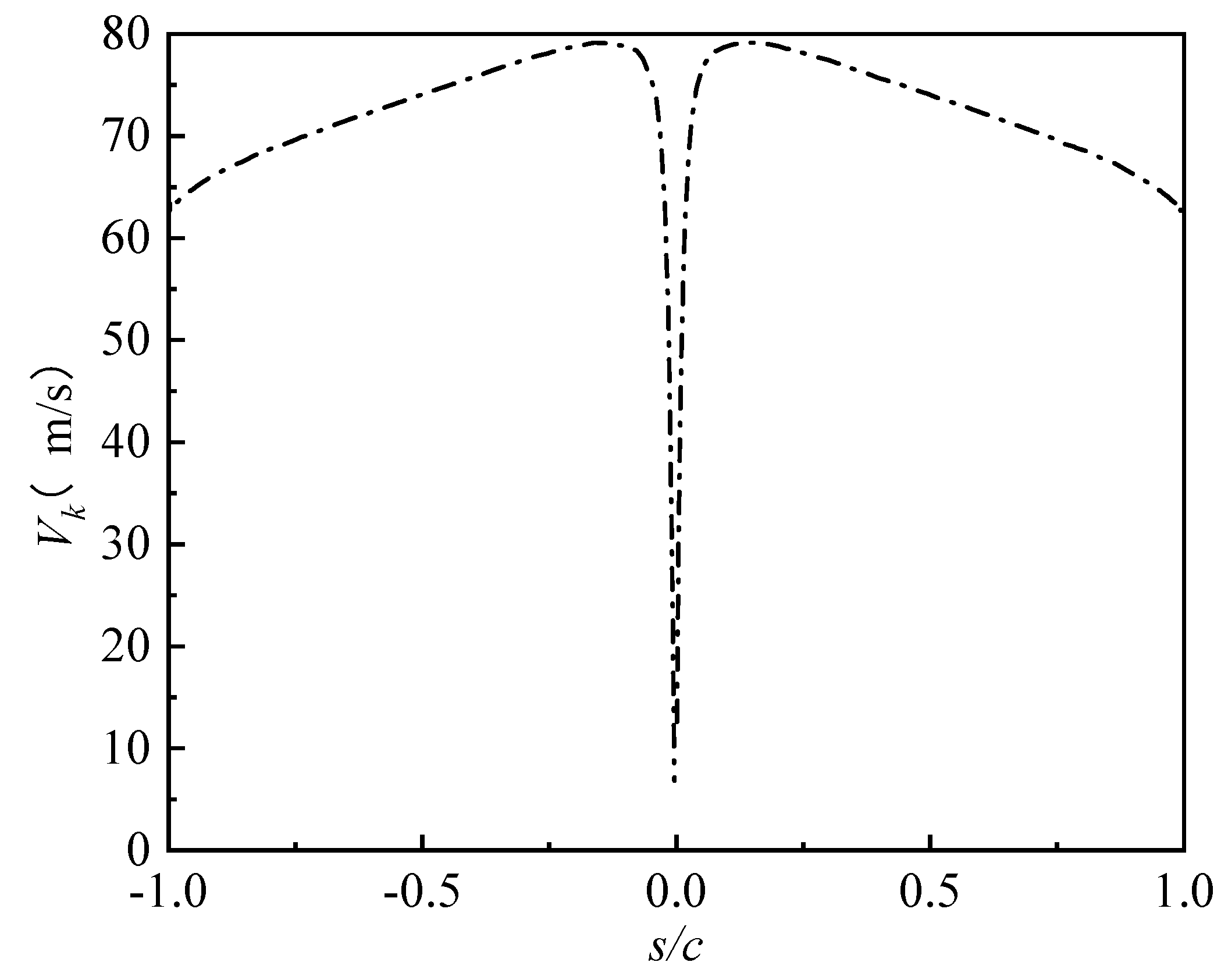
2.2. Roughness Reynolds Number
- Ks denotes the surface roughness height (varying spatially along the airfoil);
- Vk represents the airflow velocity at the roughness element height.
- = dynamic viscosity of water;
- u = horizontal component of velocity;
- y = film thickness.
- (1)
- Roughness of Water Droplets and Fine Flow Areas
- Cd = 0.44—the drag coefficient (constant for spherical beads);
- Ab is the frontal area exposed to airflow.
- eb is the bead height (equilibrium vertical dimension);
- θc is the surface contact angle.
- (2)
- Roughness Demarcation Method Based on Critical Friction Coefficient
- (a)
- Boundary Between Water Film and Droplets
- (b)
- Boundary Between Droplets and Overflow Streams
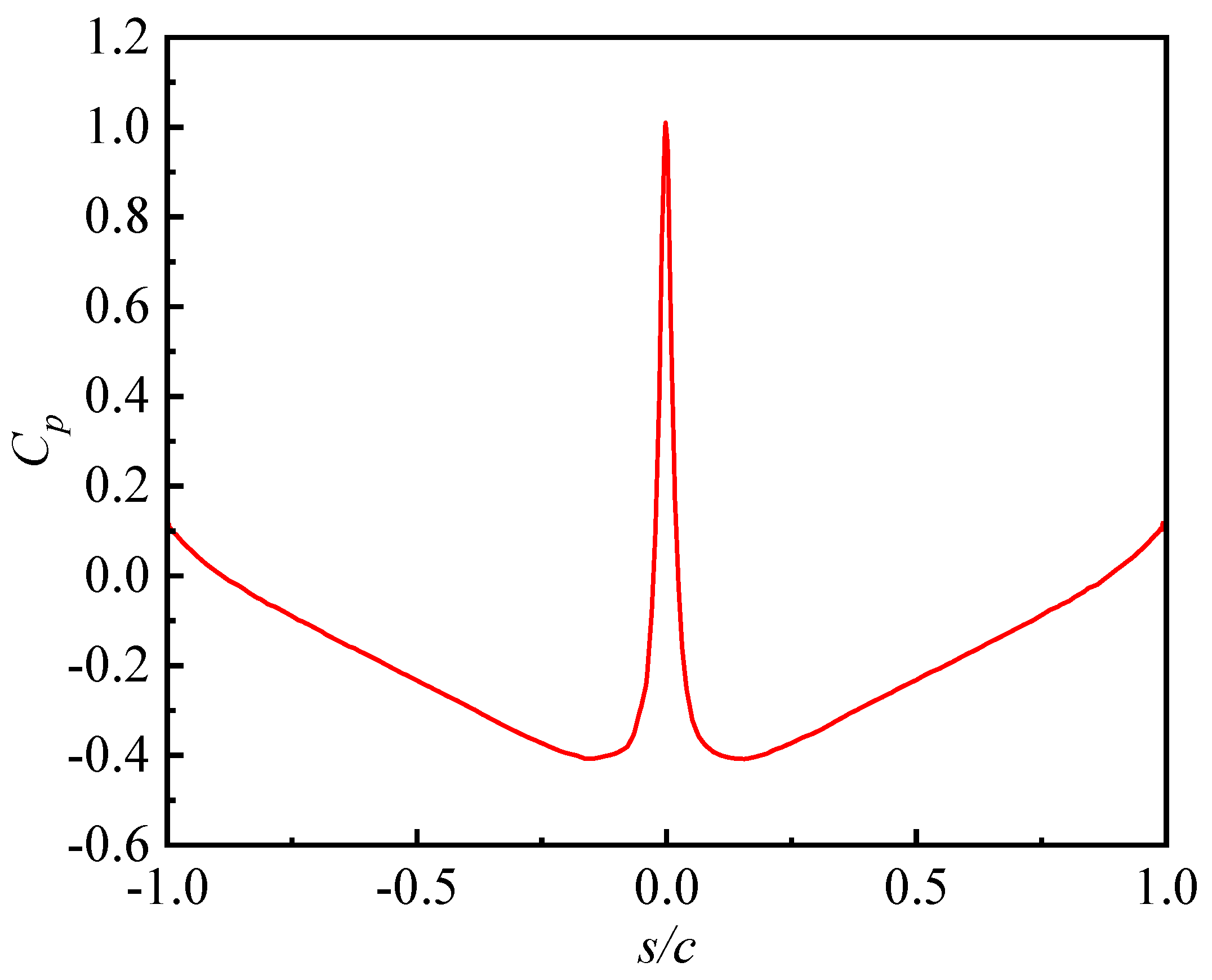
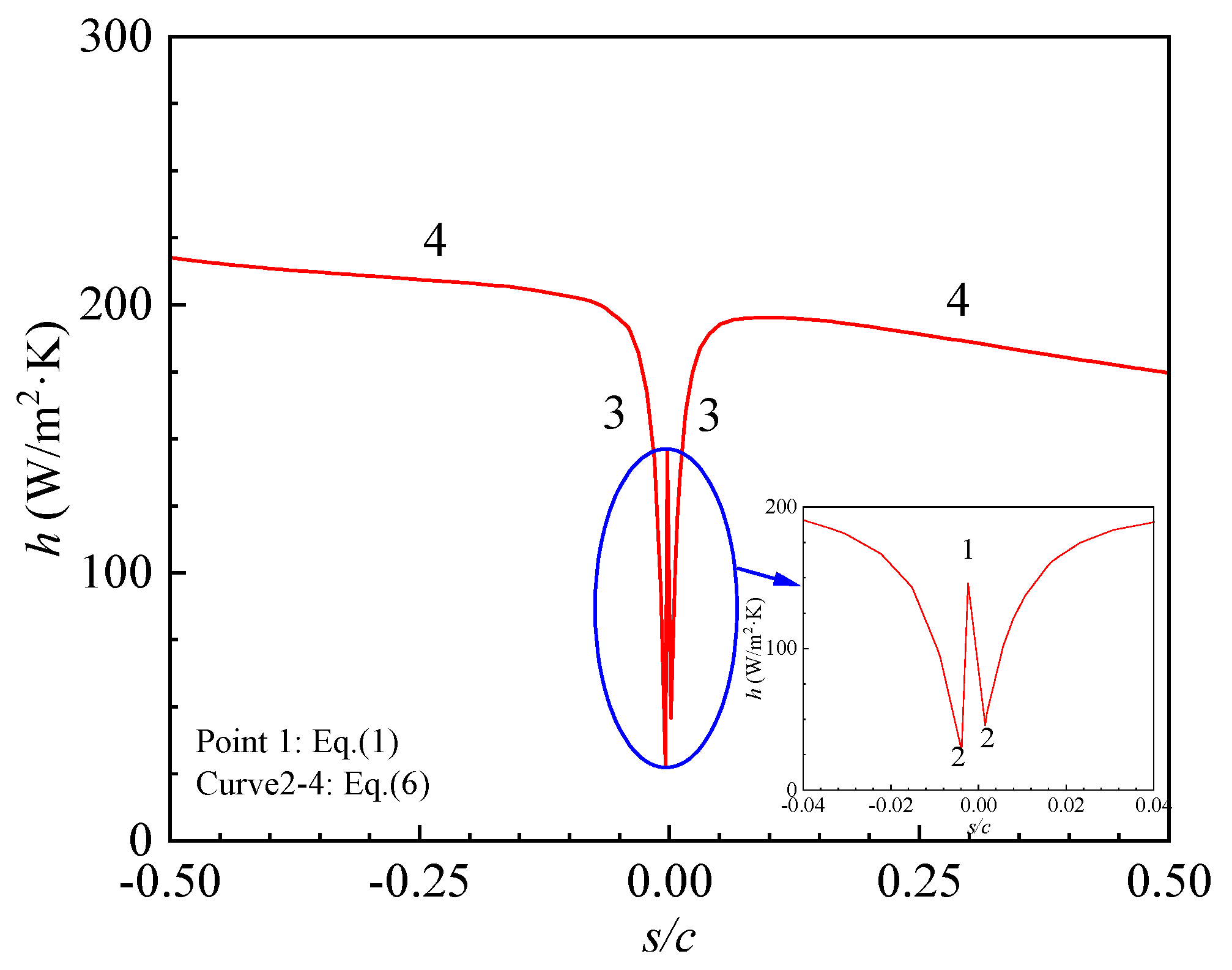
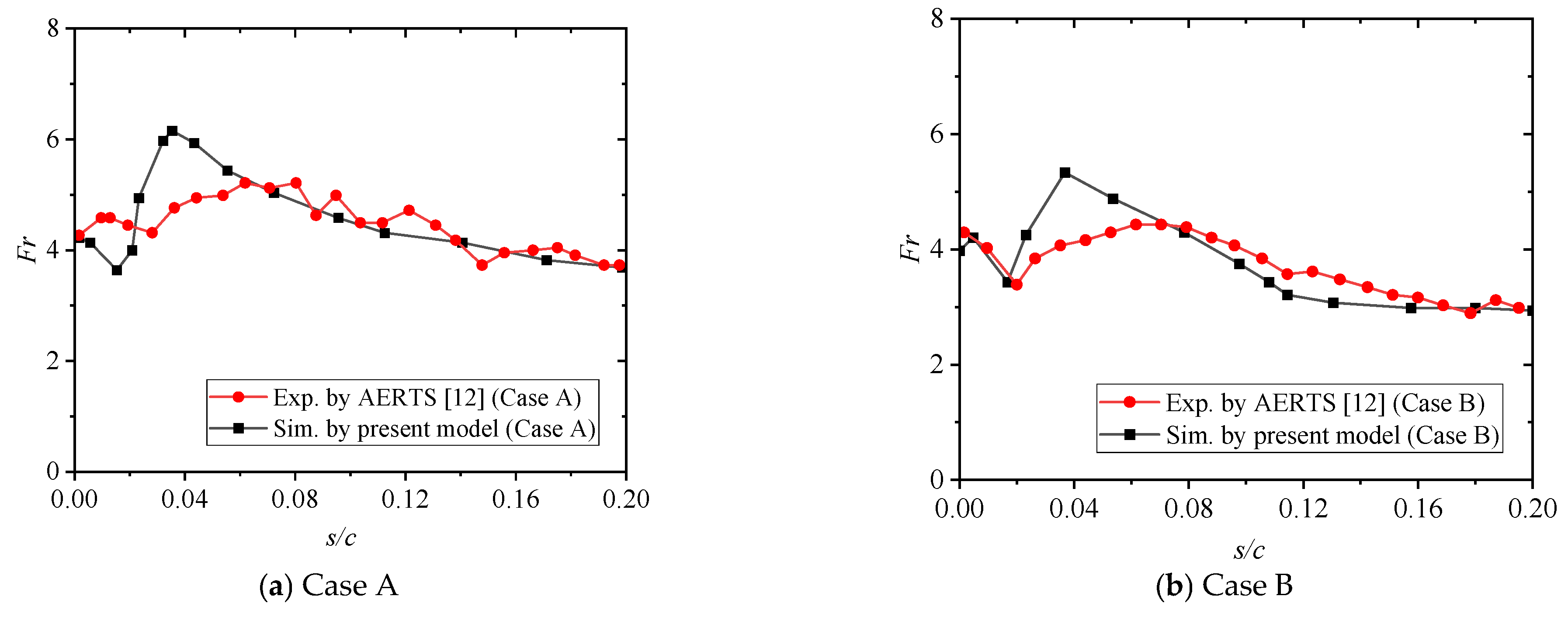
3. Results and Discussion
- T0 = freestream temperature (°C);
- V0 = freestream velocity (m/s);
- C0 = isobaric specific heat capacity of air (J/kg·°C).
4. Conclusions
- (1)
- A method for the rapid prediction of the heat transfer coefficient on icing surfaces of aircraft wings based on a partitioned rough-wall boundary layer integral approach was proposed. It enables calculation of the heat transfer coefficient through airfoil geometry without the need for CFD computations.
- (2)
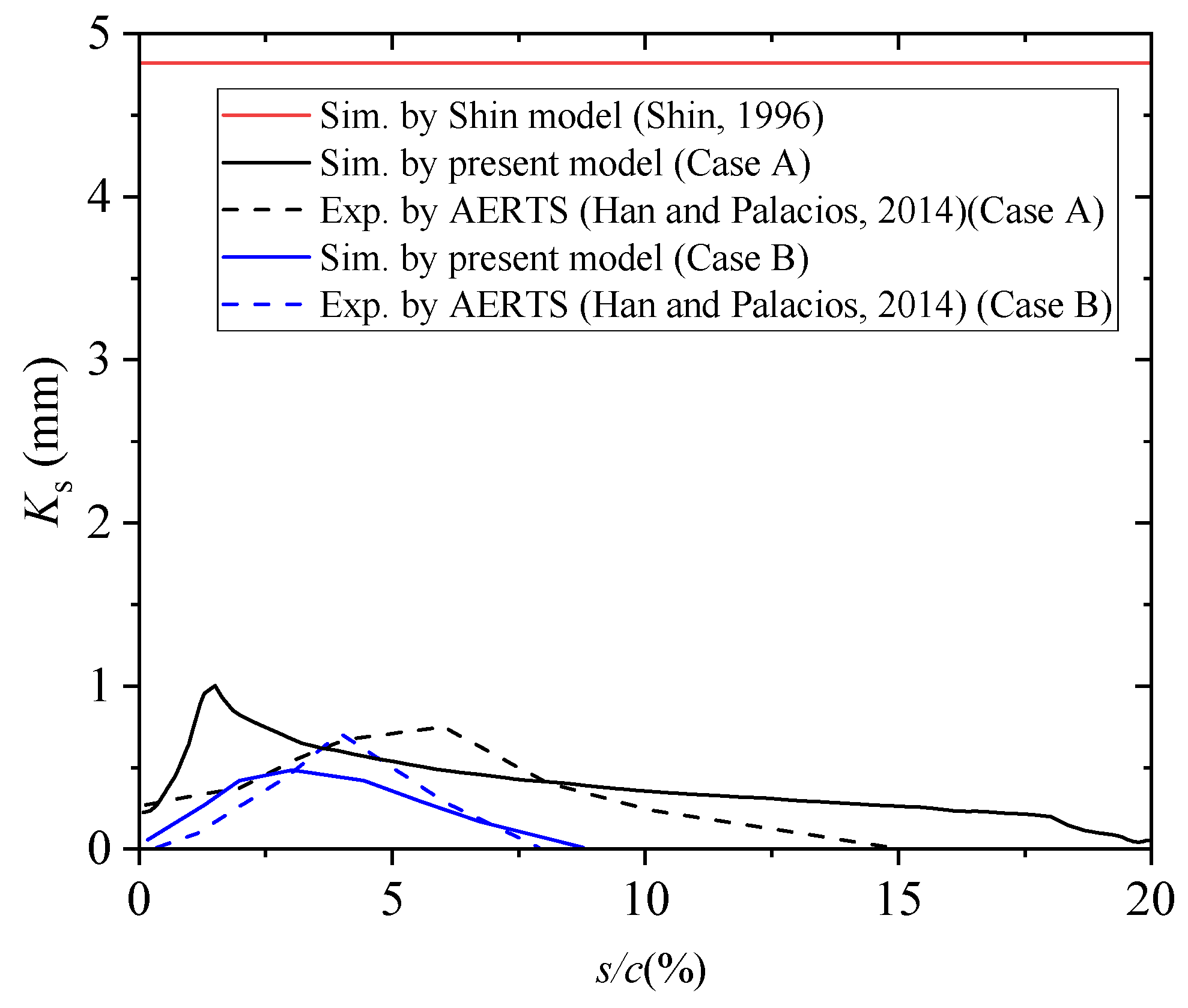
- Three distinct hydrodynamic regimes—a hydraulically smooth zone (water film), a transitionally rough zone (water beads), and a fully rough zone (rivulets)—are categorized by the partitioned theory method based on droplet dynamics. Each regime exhibits specific equivalent sand grain roughness heights. This framework enables determination of the relative magnitude between roughness Reynolds number and critical Reynolds number, thereby mapping the Ks distribution over the aerodynamic surface.
- (3)
- Incorporating local roughness effects, the refined boundary layer integral method computes convective heat transfer coefficients along the wing surface. Compared to conventional approaches, the boundary layer transition is identified at the 0.1 chordwise station (0.1 s/c).
- (4)
- The convective heat transfer distribution over the NACA0012 airfoil is quantitatively characterized by the proposed method. It shows that prediction accuracy for heat transfer coefficients shows measurable improvement.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| C | Isobaric specific heat capacity | Greek symbols | |
| Cd | Drag coefficient | β | Water droplet collection efficiency |
| Cf | Friction coefficient | λ | Thermal conductivity |
| Cp | Pressure coefficient | μ | Dynamic viscosity |
| c | Chord length of the airfoil | ρ | Density |
| Fd | Drag force | τi | Shear stress on the water film |
| Capillary force | |||
| h | Heat transfer coefficient | Subscripts | |
| Ks | Surface roughness height | ave | Average |
| Pr | Prandtl number | c | Critical |
| Re | Reynolds number | D | Cylinder diameter |
| Rek | Roughness Reynolds number | w | Water |
| S | Surface distance from stagnation point of the leading edge of the airfoil | 0 | Air |
| T | Temperature | Abbreviation | |
| u | Horizontal component of velocity | AoA | Angle of attack |
| V | Velocity | MVD | Median volume diameter |
| y | Film thickness | NACA | National Advisory Committee for Aeronautics |
References
- Bragg, M.B.; Broeren, A.P.; Blumenthal, L.A. Iced-airfoil aerodynamics. Prog. Aerosp. Sci. 2005, 41, 323–362. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Q.; Yi, X.; Chen, N.; Ren, J.; Li, W. An anti-icing scaling method for wind tunnel tests of aircraft thermal ice protection system. Chin. J. Aeronaut. 2024, 37, 1–6. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Q.; Wang, Q.; Guo, X.; Bu, X.; Yi, X. Investigations on Optimization and Verification of Nacelle Hot Air Anti-Icing System in a Large Icing Wind Tunnel. Aerosp. Sci. Technol. 2025, 163, 110312. [Google Scholar] [CrossRef]
- Aliaga, C.N.; Aubé, M.S.; Baruzzi, G.S.; Habashi, W.G. FENSAP-ICE-Unsteady: Unified in-flight icing simulation methodology for aircraft, rotorcraft, and jet engines. J. Aircr. 2011, 48, 119–126. [Google Scholar] [CrossRef]
- Verdin, P.G.; Charpin, J.P. Multi-stepping ice prediction on cylinders and other relevant geometries. J. Aircr. 2013, 50, 871–878. [Google Scholar] [CrossRef]
- Cao, Y.; Ma, C.; Zhang, Q.; Sheridan, J. Numerical simulation of ice accretions on an aircraft wing. Aerosp. Sci. Technol. 2012, 23, 296–304. [Google Scholar] [CrossRef]
- Lavoie, P.; Pena, D.; Hoarau, Y.; Laurendeau, E. Comparison of thermodynamic models for ice accretion on airfoils. Int. J. Numer. Methods Heat Fluid Flow. 2018, 28, 1004–1030. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuan, X.; Xiong, J.; Bu, X. An Electro-thermal De-icing Model and Simulation Analysis Considering Ice Shedding. Trans. Nanjing Univ. Aeronaut. Astronaut. 2025, 42, 162–177. [Google Scholar]
- Ferro, C.G.; Pietrangelo, F.; Maggiore, P. Heat exchange performance evaluation inside a lattice panel using CFD analysis for an innovative aerospace anti-icing system. Aerosp. Sci. Technol. 2023, 141, 108565. [Google Scholar] [CrossRef]
- Yakhya, S.; Ernez, S.; Morency, F. Computational fluid dynamics investigation of transient effects of aircraft ground deicing jets. J. Thermophys. Heat Transf. 2019, 33, 117–127. [Google Scholar] [CrossRef]
- Ozcer, I.A.; Baruzzi, G.S.; Reid, T.; Habashi, W. FENSAP-ICE: Numerical prediction of ice roughness evolution, and its effects on ice shapes. SAE Tech. Pap. 2011. [Google Scholar] [CrossRef]
- Bayeux, C.; Radenac, E.; Villedieu, P. Theory and validation of a 2D finite-volume integral boundary-layer method for icing applications. AIAA J. 2019, 57, 1092–1112. [Google Scholar] [CrossRef]
- Harry, R.; Radenac, E.; Blanchard, G.; Villedieu, P. Heat Transfer modeling by integral boundary-layer methods towards icing applications. In Proceedings of the AIAA AVIATION 2021 FORUM, VIRTUAL EVENT, 2–6 August 2021. [Google Scholar]
- Ruff, G.A.; Berkowitz, B.M. Users Manual for the NASA Lewis Ice Accretion Prediction Code (LEWICE); Sverdrup Technology, Inc.: Brook Park, OH, USA, 1990. [Google Scholar]
- Shin, J. Characteristics of surface roughness associated with leading-edge ice accretion. J. Aircr. 1996, 33, 316–321. [Google Scholar] [CrossRef]
- Hansman Jr, R.J.; Turnock, S.R. Investigation of surface water behavior during glaze ice accretion. J. Aircr. 1989, 26, 140–147. [Google Scholar] [CrossRef]
- Han, Y.; Palacios, J. Transient heat transfer measurements of surface roughness due to ice accretion. In Proceedings of the 6th AIAA Atmospheric and Space Environments Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar]
- Steiner, J.; Bansmer, S. Ice roughness and its impact on the ice accretion process. In Proceedings of the 8th AIAA Atmospheric and Space Environments Conference, Washington, DC, USA, 13–17 June 2016. [Google Scholar]
- Mcclain, S.T.; Vargas, M.; Tsao, J.; Broeren, A.; Lee, S. Ice accretion roughness measurements and modeling. In Proceedings of the European Conference for Aeronautics and Space Sciences (EUCASS), Milan, Italy, 3–6 July 2017. [Google Scholar]
- Yamaguchi, K.; Hansman, R.J., Jr. Heat transfer on accreting ice surfaces. J. Aircr. 1992, 29, 108–113. [Google Scholar] [CrossRef]
- Martinelli, R.C. An Investigation of Aircraft Heaters: VIII-A Simplified Method for the Calculation of the Unit Thermal Conductance Over Wings. National Advisory Committee for Aeronautics. 1943. Available online: https://ntrs.nasa.gov/citations/19930092970 (accessed on 14 July 2025).
- Goldstein, K.; Novoselac, A. Convective heat transfer in rooms with ceiling slot diffusers (RP-1416). HVACR Res. 2010, 16, 629–655. [Google Scholar] [CrossRef]
- Blasius, H. Grenzschichten in Flüssigkeiten Mit Kleiner Reibung; Druck von BG Teubner: Leipzig, Germany, 1907. [Google Scholar]
- Kolev, N.I. Multiphase Flow Dynamics; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Department of Transportation; FAA. 14 CFR Appendix O to Part 25—Supercooled Large Drop Icing Conditions; FAA: Washington, DC, USA, 2014. [Google Scholar]
- Özgen, S.; Canıbek, M. Ice accretion simulation on multi-element airfoils using extended Messinger model. Heat Mass Transf. 2009, 45, 305–322. [Google Scholar] [CrossRef]
- Rodič, P. Modelna Podobnost in Vpliv Modelnega Merila na Prenos Rezultatov Fizičnega Hidravličnega Modela na Prototip: Magistrsko Delo [na Spletu]. Master’s Thesis, Ljubljana, Slovenia, 2016. Available online: https://repozitorij.uni-lj.si/IzpisGradiva.php?lang=slv&id=88894 (accessed on 15 July 2025).
- Shin, J.; Berkowitz, B.; Chen, H.; Cebeci, T. Prediction of ice shapes and their effect on airfoil performance. In Proceedings of the Aerospace Sciences Meeting, Reno, NV, USA, 7–10 January 1991. [Google Scholar]
- Guo, W.; Shen, H.; Li, Y.; Feng, F.; Tagawa, K. Wind tunnel tests of the rime icing characteristics of a straight-bladed vertical axis wind turbine. Renew. Energy 2021, 179, 116–132. [Google Scholar] [CrossRef]
- Wen, T.; Agarwal, R.K. A new extension of wray-agarwal wall distance free turbulence model to rough wall flows. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Ignatowicz, K.; Morency, F.; Beaugendre, H. Sensitivity study of ice accretion simulation to roughness thermal correction model. Aerospace 2021, 8, 84. [Google Scholar] [CrossRef]
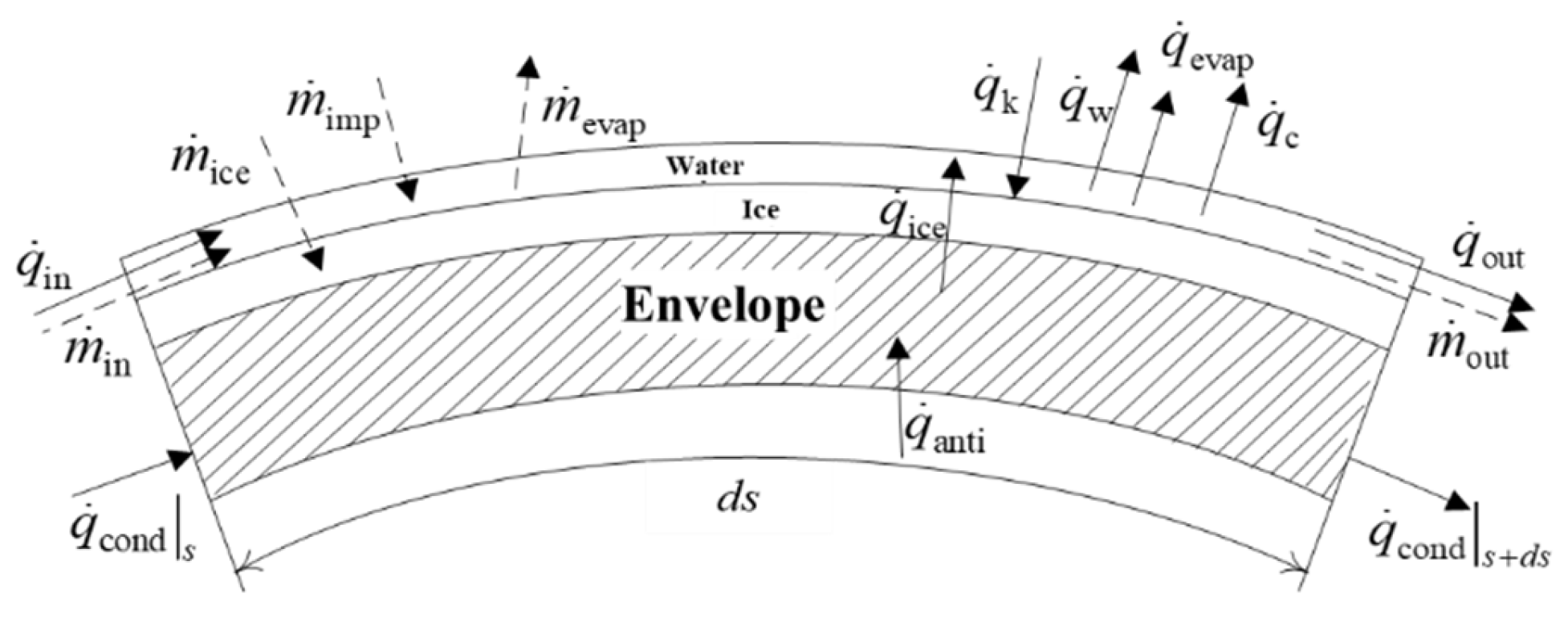

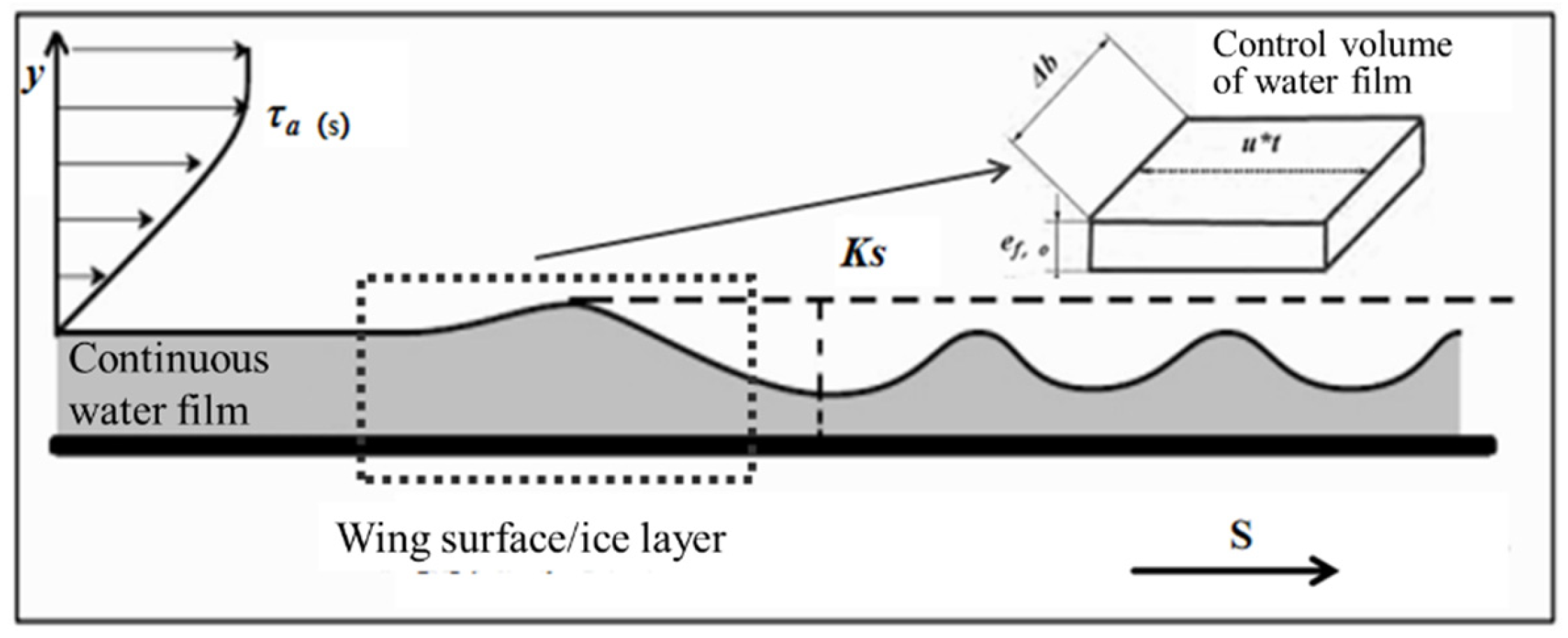
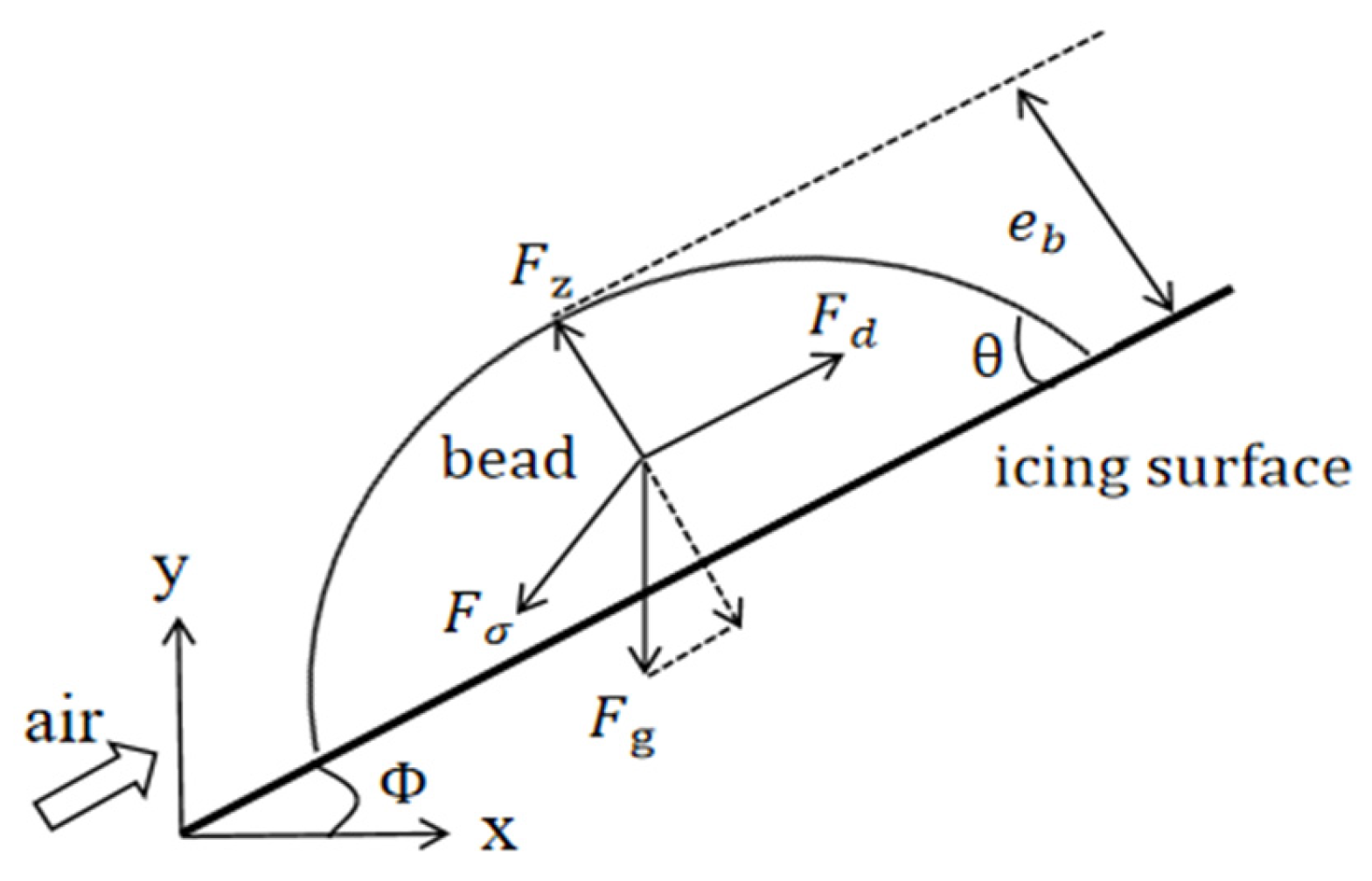



| Parameter | Case A | Case B |
|---|---|---|
| Airfoil | NACA0012 | NACA0012 |
| Characteristic length, m | 0.5334 | 0.5334 |
| Angle of attack (AoA), ° | 0 | 0 |
| Velocity, m/s | 66.7 | 66.7 |
| Temperature, °C | −3.6 | −5.86 |
| LWC, g/m3 | 1.7 | 1.0 |
| Droplet median volume diameter (MVD), μm | 30 | 20 |
| Time, s | 100 | 100 |
| xupper | yupper | xlower | ylower |
|---|---|---|---|
| 0.000 | 0.000 | 0.000 | 0.000 |
| 0.054 | 0.037 | 0.086 | −0.044 |
| 0.114 | 0.049 | 0.146 | −0.053 |
| 0.174 | 0.055 | 0.206 | −0.057 |
| 0.234 | 0.058 | 0.266 | −0.059 |
| 0.294 | 0.059 | 0.326 | −0.059 |
| 0.354 | 0.059 | 0.386 | −0.058 |
| 0.414 | 0.057 | 0.446 | −0.055 |
| 0.474 | 0.054 | 0.506 | −0.052 |
| 0.534 | 0.050 | 0.566 | −0.048 |
| 0.594 | 0.045 | 0.626 | −0.043 |
| 0.654 | 0.040 | 0.686 | −0.037 |
| 0.714 | 0.034 | 0.746 | −0.031 |
| 0.774 | 0.028 | 0.806 | −0.025 |
| 0.834 | 0.021 | 0.866 | −0.018 |
| 0.894 | 0.014 | 0.926 | −0.010 |
| 0.954 | 0.006 | 0.986 | −0.002 |
| 1.000 | 0.000 | 1.000 | 0.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Zhang, D.; Cheng, Z.; Feng, J.; Sun, B.; Chen, J.; Xie, J. A Rapid Method for Heat Transfer Coefficient Prediction on the Icing Surfaces of Aircraft Wings Based on a Partitioned Boundary Layer Integral Model. Aerospace 2025, 12, 634. https://doi.org/10.3390/aerospace12070634
Wang L, Zhang D, Cheng Z, Feng J, Sun B, Chen J, Xie J. A Rapid Method for Heat Transfer Coefficient Prediction on the Icing Surfaces of Aircraft Wings Based on a Partitioned Boundary Layer Integral Model. Aerospace. 2025; 12(7):634. https://doi.org/10.3390/aerospace12070634
Chicago/Turabian StyleWang, Liu, Dexin Zhang, Zikang Cheng, Jiaxin Feng, Bo Sun, Jianye Chen, and Junlong Xie. 2025. "A Rapid Method for Heat Transfer Coefficient Prediction on the Icing Surfaces of Aircraft Wings Based on a Partitioned Boundary Layer Integral Model" Aerospace 12, no. 7: 634. https://doi.org/10.3390/aerospace12070634
APA StyleWang, L., Zhang, D., Cheng, Z., Feng, J., Sun, B., Chen, J., & Xie, J. (2025). A Rapid Method for Heat Transfer Coefficient Prediction on the Icing Surfaces of Aircraft Wings Based on a Partitioned Boundary Layer Integral Model. Aerospace, 12(7), 634. https://doi.org/10.3390/aerospace12070634