Optimal Midcourse Guidance with Terminal Relaxation and Range Convex Optimization
Abstract
1. Introduction
- (1)
- A dual-channel controlled midcourse guidance model for interceptors is established in the range domain, avoiding the linear dependence of time-domain control and eliminating the need for terminal time prediction.
- (2)
- A novel terminal relaxation technique is proposed to overcome the strict terminal selection requirements in optimal problem solving. Based on the maximum principle, it has been proven that the convexified second-order cone problem is equivalent to the original nonconvex problem, and simulations have verified the robustness of the algorithm.
- (3)
- An initial guess trajectory generation method is presented, and the performance of three discretization approaches—TM, fourth-order Runge–Kutta (RK4), and pseudospectral discretization—is compared.
2. Optimal Midcourse Guidance Problem in Range Domain
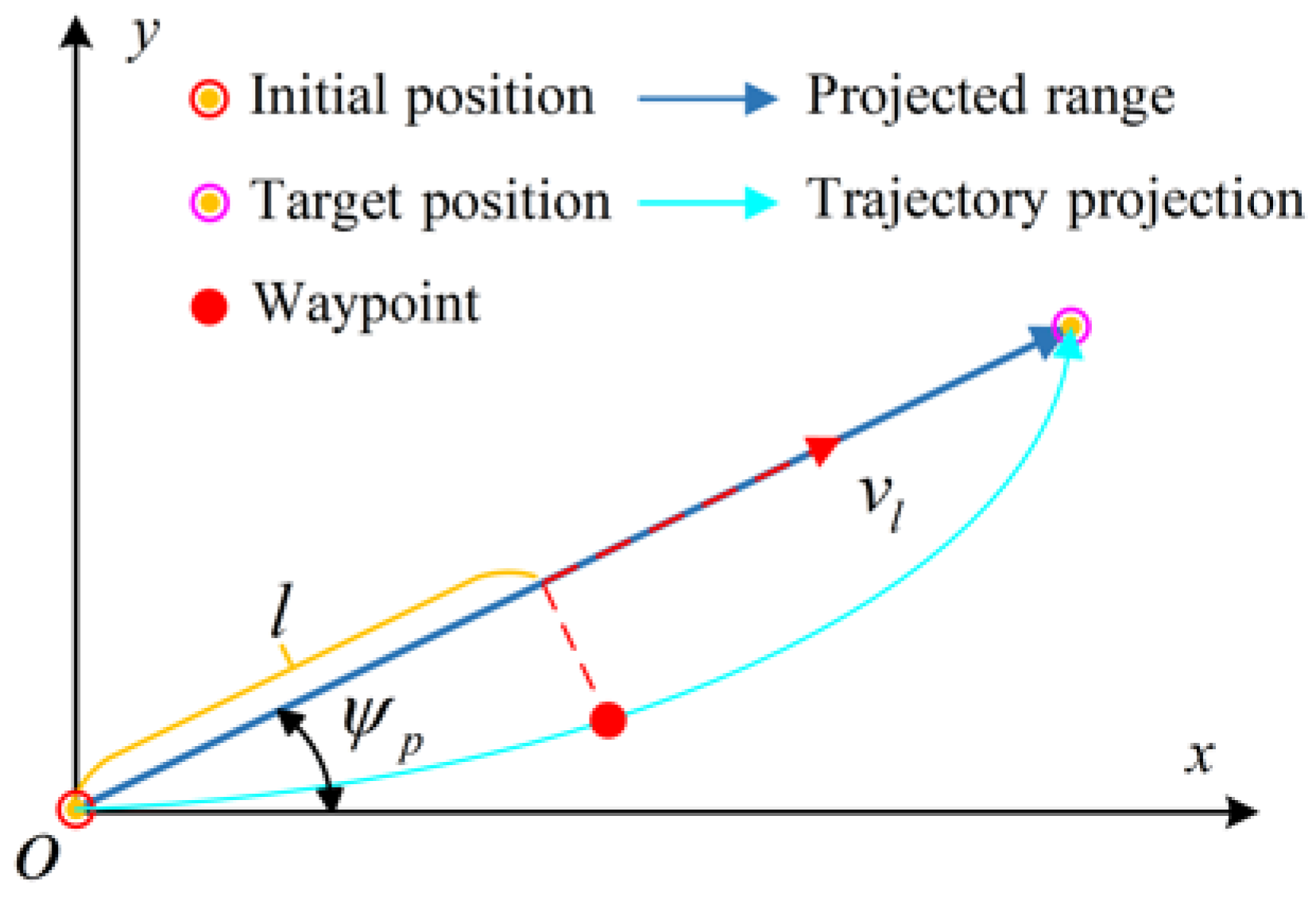
2.1. Dynamics Model in Range Domain
2.2. Boundary Constraints and Process Constraints
2.3. Formulation of the Optimal Control Problem
3. SOCP Formulation
3.1. Linearization
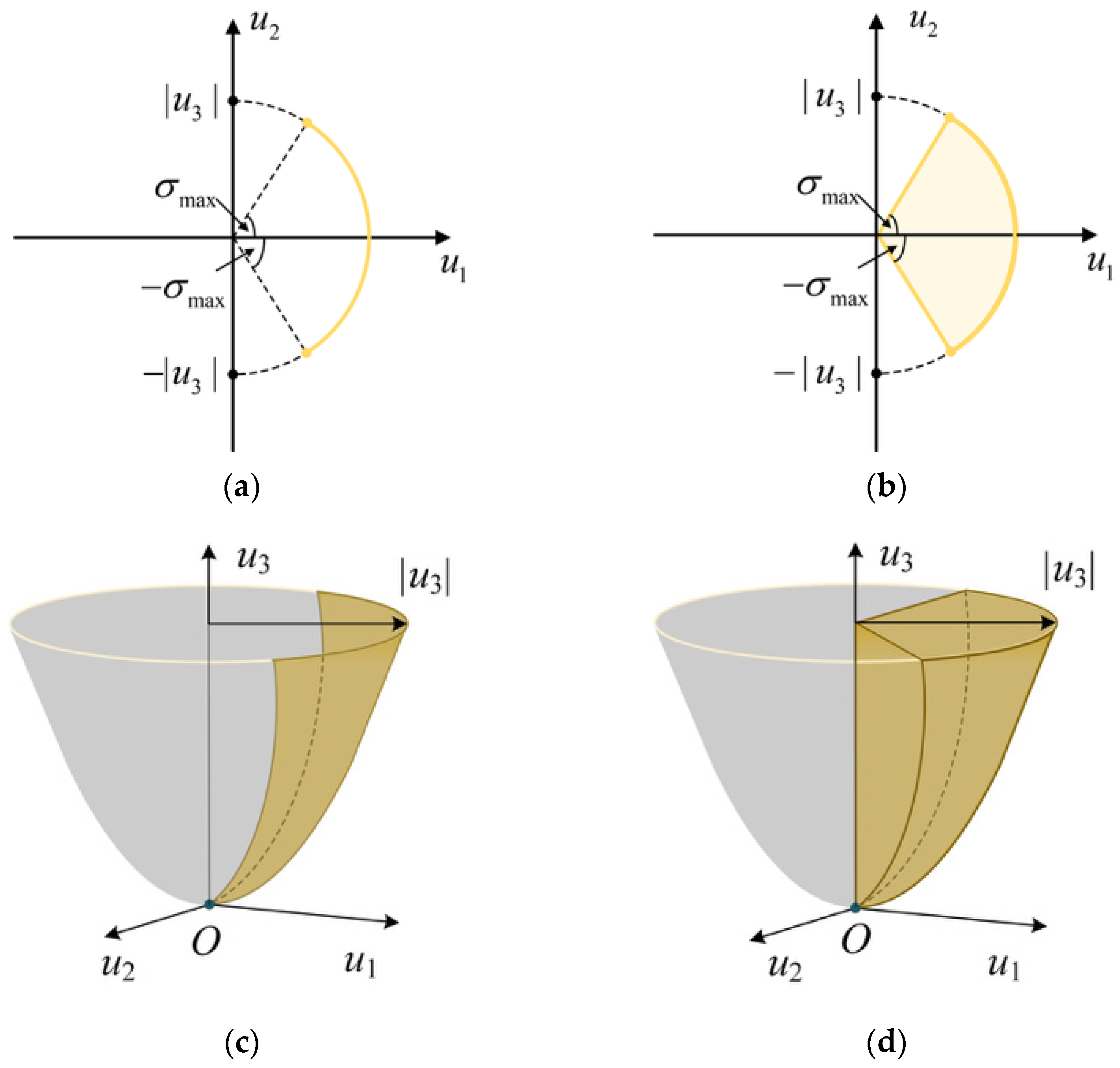
3.2. Relaxation of Control Constraints
3.3. Relaxation Accuracy Assurance
4. Iterative Solution
4.1. RK4
4.2. Initial Guess Trajectory Generation Method and Iterative Algorithm
| Algorithm 1. Solve the original problem P0 |
| Input: Initial guess trajectory , trust region , convergence region , Outout: and |
| While 1 do If || Solve problem P4 to obtain and ; Else Solve problem P3 to obtain and ; End if |
| If then return and ; Else ; ; End if End While |
5. Numerical Simulation
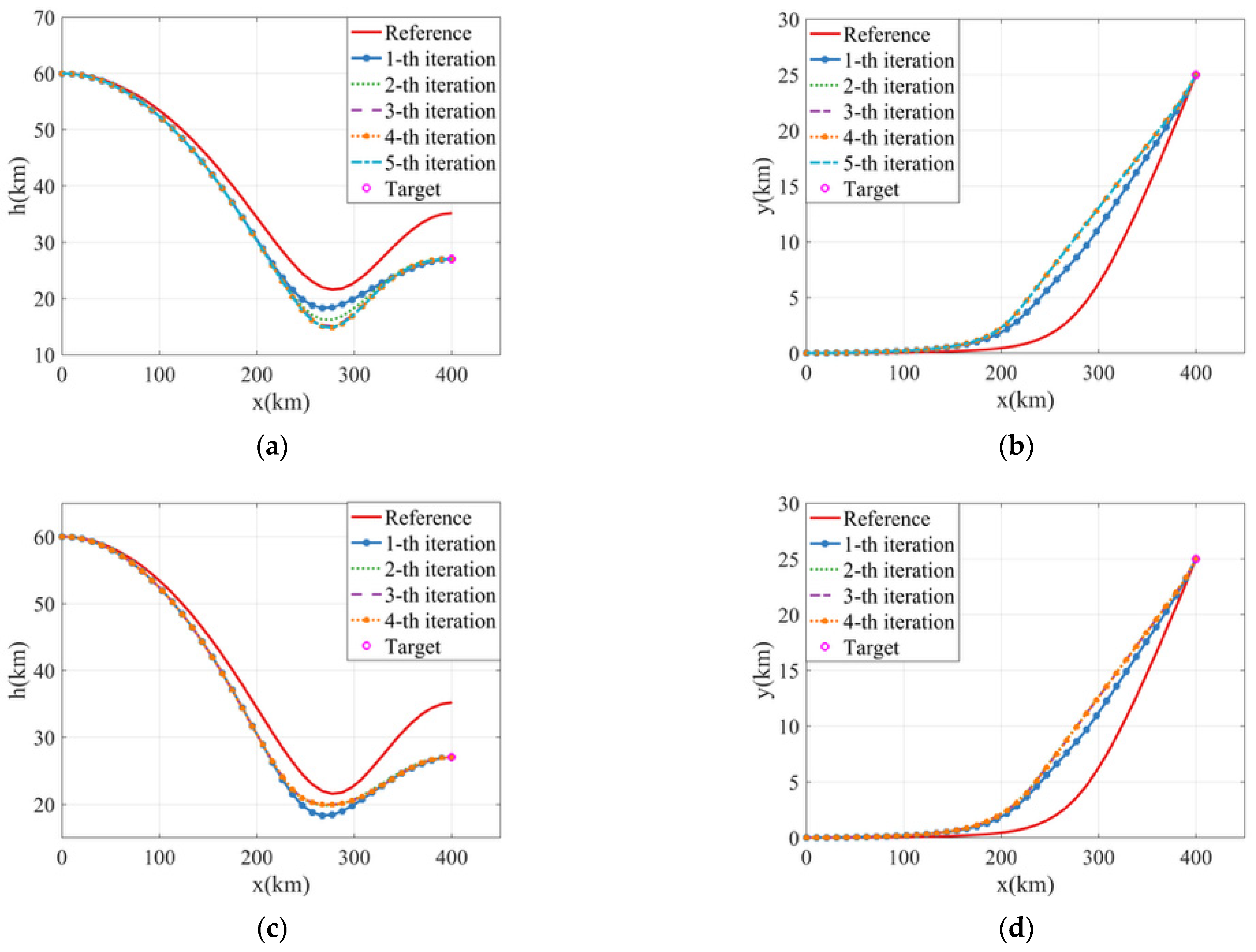
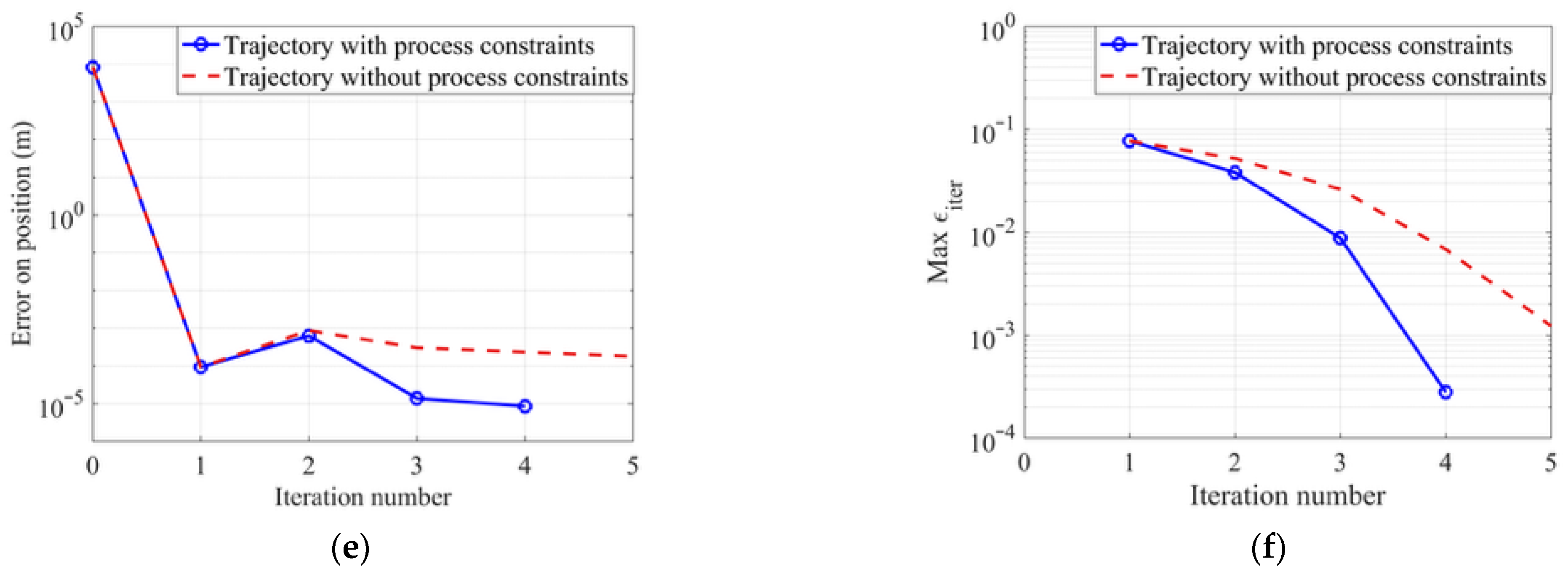
5.1. Convergence Mode of the Proposed Algorithm
5.2. Method Performance Comparison
5.3. Validation of the Proposed Algorithm
5.4. The Effect of Interpolation Method and the Number of Discrete Points
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of Theorem 1
Appendix B. Proof of Theorem 3
- (1)
- The nontriviality condition:
- (2)
- The costate differential equation:
- (3)
- The stationary conditions:
- (4)
- The complementary slack conditions:
- (5)
- The transversality conditions used in the proof are as follows:
References
- Malyuta, D.; Yu, Y.; Elango, P.; Açıkmeşe, B. Advances in trajectory optimization for space vehicle control. Annu. Rev. Control 2021, 52, 282–315. [Google Scholar] [CrossRef]
- Bu, X.W.; Lv, M.L.; Lei, H.M.; Cao, J. Fuzzy neural pseudo control with prescribed performance for waverider vehicles: A fragility-avoidance approach. IEEE Trans. Cybern. 2023, 53, 4986–4999. [Google Scholar] [CrossRef]
- Kim, B.; Lee, C.-H. Optimal midcourse guidance for dual-pulse rocket using pseudospectral sequential convex programming. J. Guid. Control Dyn. 2023, 46, 1425–1436. [Google Scholar] [CrossRef]
- Zhou, C.; He, L.; Yan, X.; Meng, F.; Li, C. Active-set pseudospectral model predictive static programming for midcourse guidance. Aerosp. Sci. Technol. 2023, 134, 108137. [Google Scholar] [CrossRef]
- Wan, S.X.; Chang, X.F.; Li, Q.C.; Yan, J. Suboptimal midcourse guidance with terminal-angle constraint for hypersonic target interception. Int. J. Aerosp. Eng. 2019, 2019, 6161032. [Google Scholar] [CrossRef]
- Calise, A.J. Adaptive finite time intercept guidance. J. Guid. Control Dyn. 2023, 46, 1975–1980. [Google Scholar] [CrossRef]
- Shin, H.S.; Li, K.B. An improvement in three-dimensional pure proportional navigation guidance. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 3004–3014. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, Q.; Liang, Z.; Li, P.; Ren, Z.; Zheng, Y. Fractional calculus guidance algorithm in a hypersonic pursuit-evasion game. Def. Sci. J. 2017, 67, 688–697. [Google Scholar] [CrossRef]
- Liu, S.; Yan, B.; Liu, R.; Dai, P.; Yan, J.; Xin, G. Cooperative guidance law for intercepting a hypersonic target with impact angle constraint. Aeronaut. J. 2022, 126, 1026–1044. [Google Scholar] [CrossRef]
- Liu, S.; Yan, B.; Zhang, T.; Dai, P.; Liu, R.; Yan, J. Three-dimensional cooperative guidance law for intercepting hypersonic targets. Aerosp. Sci. Technol. 2022, 129, 107815. [Google Scholar] [CrossRef]
- Yao, D.; Xia, Q. Finite-Time Convergence Guidance Law for Hypersonic Morphing Vehicle. Aerospace 2024, 11, 680. [Google Scholar] [CrossRef]
- Xi, A.; Cai, Y. A nonlinear finite-time robust differential game guidance law. Sensors 2022, 22, 6650. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Jing, W.; Gao, C. Online midcourse guidance method for boost phase interception via adaptive convex programming. Aerosp. Sci. Technol. 2021, 118, 107037. [Google Scholar] [CrossRef]
- Chai, R.; Tsourdos, A.; Savvaris, A.; Chai, S.; Xia, Y.; Chen, C.P. Review of advanced guidance and control algorithms for space/aerospace vehicles. Prog. Aerosp. Sci. 2021, 122, 100696. [Google Scholar] [CrossRef]
- Liu, G.; Feng, W.; Yang, K.; Zhao, J. Hybrid QPSO and SQP algorithm with homotopy method for optimal control of rapid cooperative rendezvous. J. Aerosp. Eng. 2019, 32, 04019030. [Google Scholar] [CrossRef]
- Ann, S.; Lee, S.; Kim, Y.; Ahn, J. Midcourse guidance for Exoatmospheric Interception Using Response Surface based trajectory shaping. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 3655–3673. [Google Scholar] [CrossRef]
- Kasmi, H.; Laporte, S.; Mongeau, M.; Vidosavljevic, A.; Delahaye, D. Holistic approach for vehicle trajectory optimization using optimal control. J. Veh. 2023, 60, 1302–1313. [Google Scholar]
- Chai, R.; Savvaris, A.; Tsourdos, A.; Chai, S.; Xia, Y. A review of optimization techniques in spacecraft flight trajectory design. Prog. Aerosp. Sci. 2019, 109, 100543. [Google Scholar] [CrossRef]
- Dennis, M.E.; Hager, W.W.; Rao, A.V. Computational method for optimal guidance and control using adaptive Gaussian quadrature collocation. J. Guid. Control Dyn. 2019, 42, 2026–2041. [Google Scholar] [CrossRef]
- Luo, C.X.; Zhou, C.J.; Bu, X.W. Multi-Missile Phased Cooperative Interception Strategy for High-Speed and Highly Maneuverable Targets. IEEE Trans. Aerosp. Electron. Syst. 2025, 61, 1971–1996. [Google Scholar] [CrossRef]
- Zhou, C.; Yan, X.; Ban, H.; Tang, S. Generalized Newton Iteration based MPSP Method for Terminal Constrainted Guidance. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 9438–9450. [Google Scholar] [CrossRef]
- Mondal, S.; Padhi, R. Angle-constrained terminal guidance using quasi-spectral model predictive static programming. J. Guid. Control Dyn. 2018, 41, 783–791. [Google Scholar]
- Chai, R.; Tsourdos, A.; Savvaris, A.; Chai, S.; Xia, Y. Solving constrained trajectory planning problems using biased particle swarm optimization. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 1685–1701. [Google Scholar] [CrossRef]
- Li, W.L.; Li, J.; Li, N.B.; Shao, L.; Li, M.J. Online trajectory planning method for midcourse guidance phase based on deep reinforcement learning. Aerospace 2023, 10, 441. [Google Scholar] [CrossRef]
- Li, H.; Wang, J.; Tao, H.; Lin, D. Near-Optimal Impact-Vector-Control Guidance. J. Guid. Control Dyn. 2024, 47, 1965–1972. [Google Scholar] [CrossRef]
- Kada, B.; Ansari, U.; Bajodah, A.H. Highly maneuvering target interception via robust generalized dynamic inversion homing guidance and control. Aerosp. Sci. Technol. 2020, 99, 105749. [Google Scholar] [CrossRef]
- Annam, C.; Ratnoo, A.; Ghose, D. Singular-perturbation-based guidance of pulse motor interceptors with look angle constraints. J. Guid. Control Dyn. 2021, 44, 1356–1370. [Google Scholar] [CrossRef]
- Wang, Z. A survey on convex optimization for guidance and control of vehicular systems. Annu. Rev. Control 2024, 57, 100957. [Google Scholar] [CrossRef]
- Kayama, Y.; Howell, K.C.; Bando, M.; Hokamoto, S. Low-thrust trajectory design with successive convex optimization for libration point orbits. J. Guid. Control Dyn. 2022, 45, 623–637. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, H.-B.; Xie, L.; Tang, G.-J.; Bao, W.-M. An improved solution method via the pole-transformation process for the maximum-crossrange problem. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2020, 234, 1491–1506. [Google Scholar] [CrossRef]
- Niu, G.; Wu, L.; Gao, Y.; Pun, M.-O. Unmanned aerial vehicle (UAV)-assisted path planning for unmanned ground vehicles (UGVs) via disciplined convex-concave programming. IEEE Trans. Veh. Technol. 2022, 71, 6996–7007. [Google Scholar] [CrossRef]
- Mousavi, S.M.A.; Moshiri, B.; Heshmati, Z. On the distributed path planning of multiple autonomous vehicles under uncertainty based on model-predictive control and convex optimization. IEEE Syst. J. 2020, 15, 3759–3768. [Google Scholar] [CrossRef]
- Liu, X.; Shen, Z.; Lu, P. Exact convex relaxation for optimal flight of aerodynamically controlled missiles. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1881–1892. [Google Scholar] [CrossRef]
- Yang, R.; Liu, X.; Song, Z. Rocket landing guidance based on linearization-free convexification. J. Guid. Control Dyn. 2024, 47, 217–232. [Google Scholar] [CrossRef]
- Ma, S.; Yang, Y.; Tong, Z.; Yang, H.; Wu, C.; Chen, W. Improved sequential convex programming based on pseudospectral discretization for entry trajectory optimization. Aerosp. Sci. Technol. 2024, 152, 109349. [Google Scholar] [CrossRef]
- Wang, Z.; Grant, M.J. Autonomous entry guidance for hypersonic vehicles by convex optimization. J. Spacecr. Rocket. 2018, 55, 993–1006. [Google Scholar] [CrossRef]
- Liu, X.; Lu, P.; Pan, B. Survey of convex optimization for aerospace applications. Astrodynamics 2017, 1, 23–40. [Google Scholar] [CrossRef]
- Wang, Q.; Li, S.; Zhang, Y.; Cheng, M. Spacecraft Close Proximity to Noncooperative Target Based on Pseudospectral Convex Method. J. Aerosp. Eng. 2024, 37, 04024034. [Google Scholar] [CrossRef]
- Zhou, X.; He, R.-Z.; Zhang, H.-B.; Tang, G.-J.; Bao, W.-M. Sequential convex programming method using adaptive mesh refinement for entry trajectory planning problem. Aerosp. Sci. Technol. 2021, 109, 106374. [Google Scholar] [CrossRef]
- Liu, X. Convergence-guaranteed trajectory planning for a class of nonlinear systems with nonconvex state constraints. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 2243–2256. [Google Scholar] [CrossRef]
- Tang, G.; Jiang, F.; Li, J. Fuel-optimal low-thrust trajectory optimization using indirect method and successive convex programming. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2053–2066. [Google Scholar] [CrossRef]
- Wang, Z.; Lu, Y. Improved sequential convex programming algorithms for entry trajectory optimization. J. Spacecr. Rocket. 2020, 57, 1373–1386. [Google Scholar] [CrossRef]
- Liu, X.; Shen, Z.; Lu, P. Entry trajectory optimization by second-order cone programming. J. Guid. Control Dyn. 2016, 39, 227–241. [Google Scholar] [CrossRef]
- NASA. U.S. Standard Atmosphere, 1976; NASA Technical Memorandum X-74335; NASA: Washington, DC, USA, 1976.
- Li, H.F. Guidance and Control Technology for Hypersonic Vehicles; China Astronautic Publishing House: Beijing, China, 2012. [Google Scholar]
- Domahidi, A.; Chu, E.; Boyd, S. ECOS: An SOCP solver for embedded systems. In Proceedings of the 2013 European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 3071–3076. [Google Scholar]
- Wächter, A.; Biegler, L.T. On the Implementation of a Primal-Dual Interior Point Filter Line Search Algorithm for Large-Scale Nonlinear Programming. Math. Program 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Hartl, R.F.; Sethi, S.P.; Vickson, R.G. A survey of the maximum principles for optimal control problems with state constraints. SIAM Rev. 1995, 37, 181–218. [Google Scholar] [CrossRef]
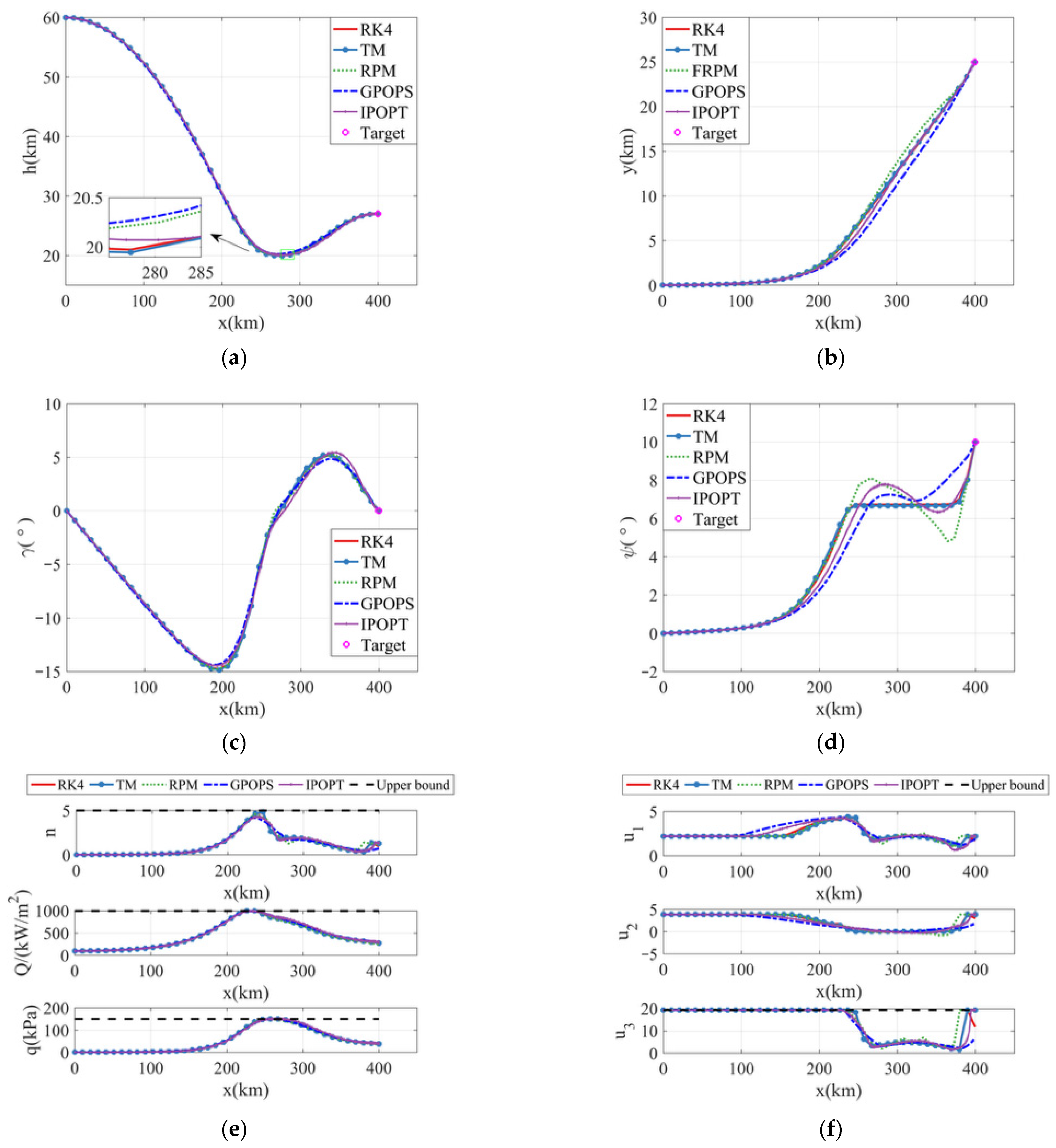
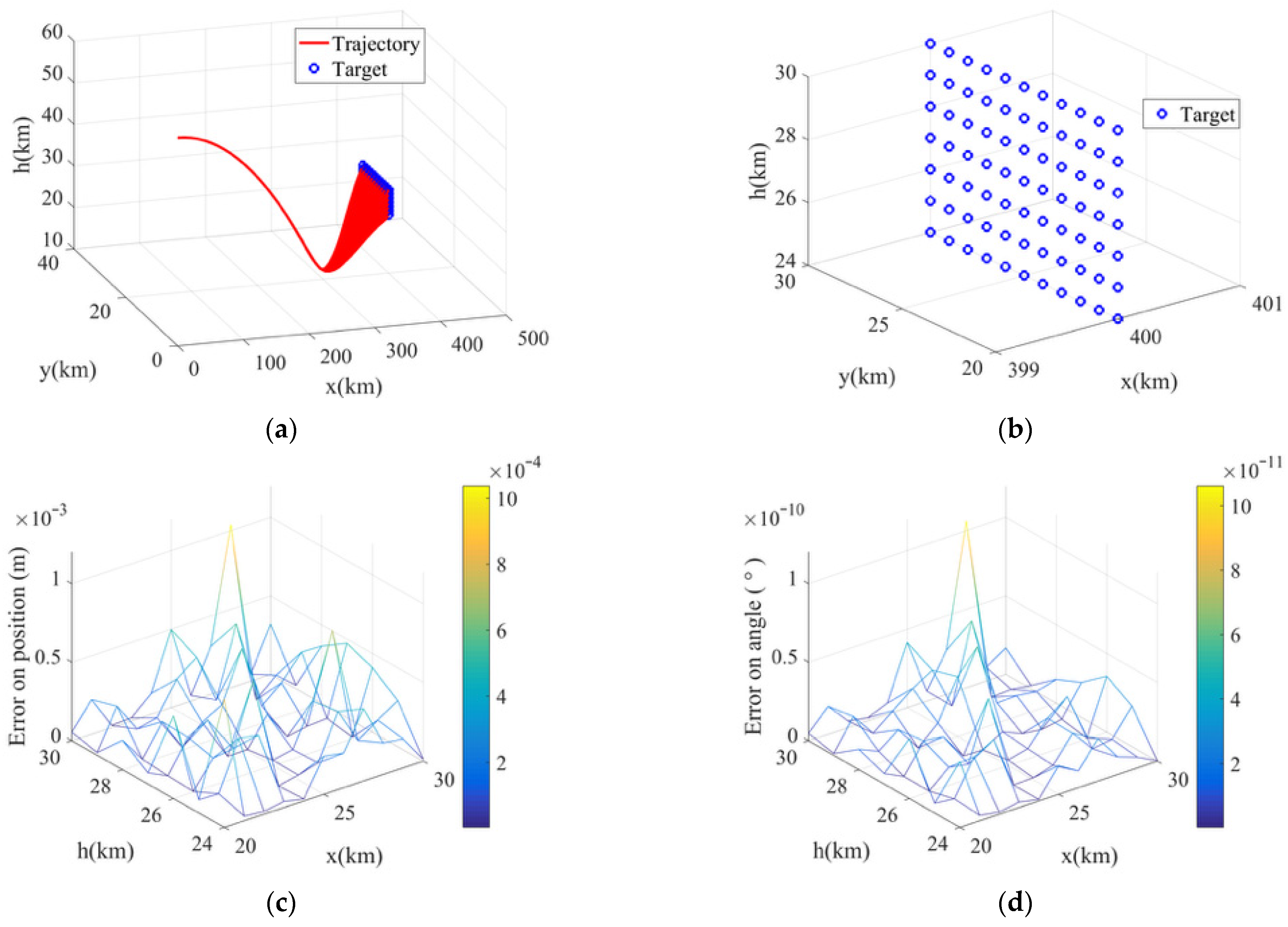
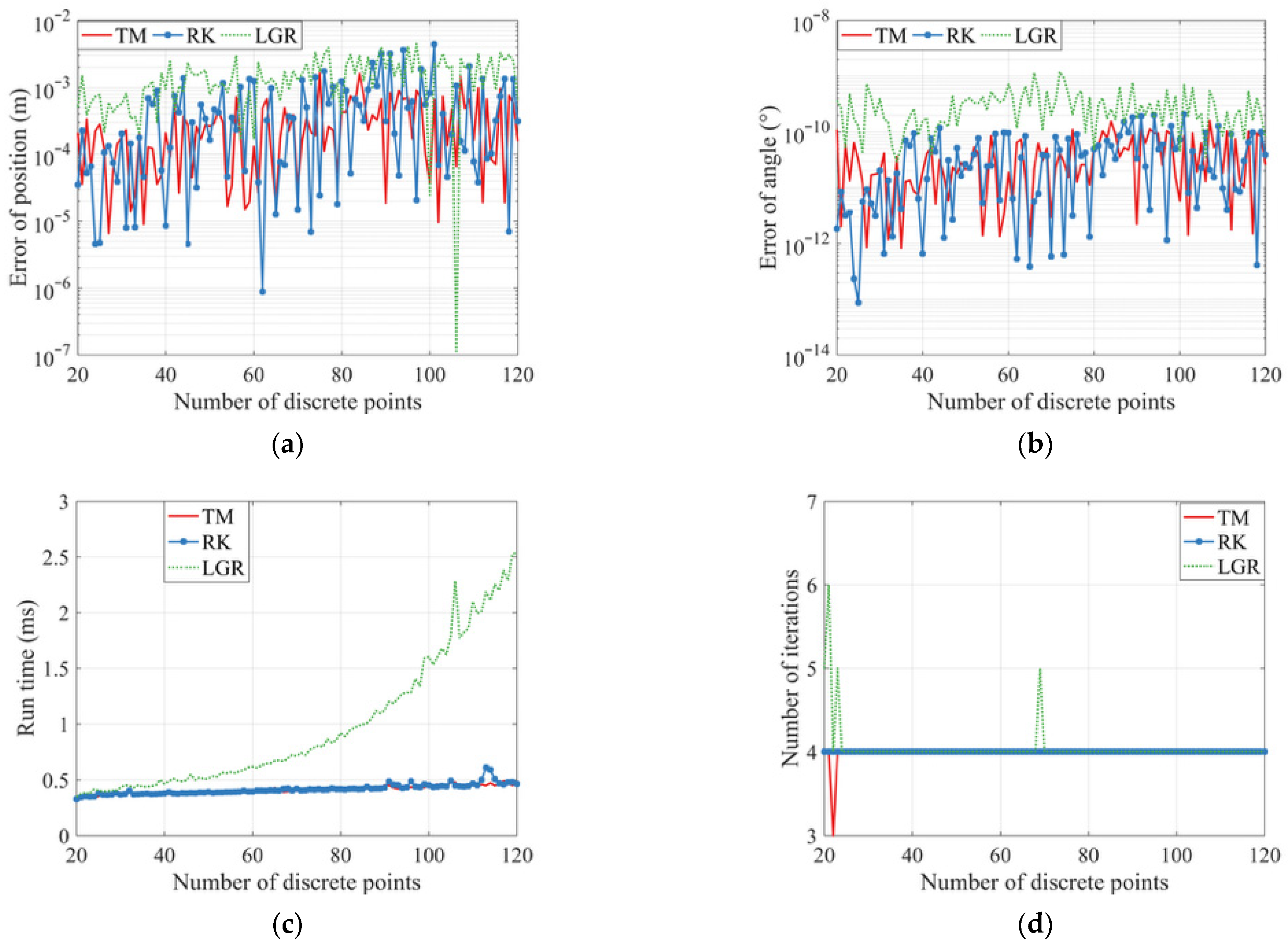
| Process Constraints | Run Time (ms) | Number of Iterations | Error on Position (m) | Error on Angle (°) |
|---|---|---|---|---|
| No | 1638.0 | 5 | 5.6 × 10−5 | 8.0 × 10−12 |
| Yes | 1511.6 | 4 | 9.6 × 10−5 | 6.0 × 10−12 |
| Method | Run Time (ms) | Number of Iterations | Error on Position (m) | Error on Angle (°) |
|---|---|---|---|---|
| RK4 | 1511.6 | 4 | 8.5 × 10−6 | 6.5 × 10−13 |
| TM | 1468.2 | 4 | 2.1 × 10−4 | 1.9 × 10−11 |
| RPM | 1858.2 | 4 | 9.4 × 10−4 | 1.5 × 10−10 |
| GPOPS | 4814.6 | \ | 0 | 0 |
| IPOPT | 5338.3 | \ | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Zhang, J.; Ye, J.; Shao, L.; Bu, X. Optimal Midcourse Guidance with Terminal Relaxation and Range Convex Optimization. Aerospace 2025, 12, 618. https://doi.org/10.3390/aerospace12070618
Li J, Zhang J, Ye J, Shao L, Bu X. Optimal Midcourse Guidance with Terminal Relaxation and Range Convex Optimization. Aerospace. 2025; 12(7):618. https://doi.org/10.3390/aerospace12070618
Chicago/Turabian StyleLi, Jiong, Jinlin Zhang, Jikun Ye, Lei Shao, and Xiangwei Bu. 2025. "Optimal Midcourse Guidance with Terminal Relaxation and Range Convex Optimization" Aerospace 12, no. 7: 618. https://doi.org/10.3390/aerospace12070618
APA StyleLi, J., Zhang, J., Ye, J., Shao, L., & Bu, X. (2025). Optimal Midcourse Guidance with Terminal Relaxation and Range Convex Optimization. Aerospace, 12(7), 618. https://doi.org/10.3390/aerospace12070618







