Abstract
An aircraft that has been carefully optimized for a single flight condition will tend to perform poorly at other flight conditions. For aircraft such as long-haul airliners, this is not necessarily a problem, since the cruise condition so heavily dominates a typical mission. However, other aircraft, such as Unmanned Aerial Vehicles (UAVs), may be expected to perform well at a wide range of flight conditions. Morphing systems may be a solution to this problem, as they allow the aircraft to adapt its shape to produce optimum performance at each flight condition. This study proposes an aerodynamic optimization framework for morphing airfoils by integrating Principal Component Analysis (PCA) for geometric dimensionality reduction and deep learning (DL) for surrogate modeling, alongside an optimization-guided data augmentation strategy. By employing PCA, the geometric dimensionality of airfoil surfaces is reduced from 24 to 18 design variables while preserving 100% shape fidelity, thus establishing a compressed morphing parameterization space. A Multi-Island Genetic Algorithm (MIGA) efficiently explores the reduced design space, while iterative retraining of the surrogate model enhances prediction accuracy, particularly in high-performance regions. Additionally, Shapley Additive Explanation (SHAP) analysis reveals interpretable correlations between principal component modes and aerodynamic performances. Experimental results show that the optimized airfoil achieves a 54.66% increase in low-speed cruise lift-to-drag ratio and 10.90% higher climb lift compared to the baseline. Overall, the proposed framework not only enhances the adaptability of morphing airfoils across various low-speed flight conditions but also facilitates targeted surrogate refinement and efficient data acquisition in high-performance regions.
1. Introduction
In recent years, the widespread use of UAVs and the development of general aviation have greatly advanced the progress of aerodynamic shape optimization (ASO), driving it towards higher levels of efficiency, intelligence, and multi-mission capability. For the ASO problem, the main challenges are the expensive computational cost during the optimization process and the number of design variables. Moreover, conventional fixed-wing designs face inherent limitations that hinder their ability to achieve optimal aerodynamic performance across various low-speed flight conditions. Therefore, the development of efficient optimization methods for ASO problems in aircraft design is of great interest and necessity.
A typical ASO process consists of four stages: shape parameterization, mesh creation or deformation, flow solution, and optimization algorithm [1]. The dimensionality of design variables in the optimization process is directly linked to the number of parameterized variables. The shape parameterization stage plays a crucial role in determining optimization efficiency [2,3]. The Free-Form Deformation technique [4] allows flexible manipulation of geometric surfaces by displacing control points to alter the surface mesh. However, it generally requires a large number of design variables and lacks clear geometric interpretability. The Class-Shape Transformation (CST) [5] parameterization method offers strong shape control capabilities. It is characterized by low design dimensionality, high adaptability, and excellent geometric accuracy. Wang et al. [6] introduced an enhanced CST method by incorporating B-spline basis functions to overcome limitations in local expressiveness and shape adjustment capability. However, this modification significantly increased the number of design variables.
An effective way of overcoming the shortcoming that too many design variables can greatly decrease the optimization efficiency is to reduce the number of design variables via dimension reduction techniques. This can be realized by using the PCA technique. Cinquegrana et al. [7] applied PCA-based airfoil parameterization for aerodynamic layout optimization and introduced an adaptive optimization method for design variables. Oyama et al. [8,9] used PCA on the optimized airfoil dataset to reduce dimensionality and conducted reverse analysis to assess the influence of individual modes on aerodynamic characteristics. Yu et al. [10] introduced a PCA-based airfoil parameterization method and examined how various factors impact the effectiveness of PCA modeling. Asouti et al. [11] used the PCA technique to better guide the application of evolution operators and train metamodels in Metamodel-Assisted Evolutionary Algorithms.
In the flow solution stage, employing surrogate models [12,13] or neural networks [14,15,16] as alternatives to computational fluid dynamics is regarded as an effective approach to enhance optimization efficiency. The revolutionary application of Artificial Intelligence (AI) in fields like natural language processing has demonstrated its substantial potential in transforming aircraft design. A key AI-based approach is the development of intelligent prediction models for aerodynamic parameters, which function as surrogate models to establish precise relationships between aerodynamic characteristics and aircraft shape parameters. These models allow for rapid aerodynamic evaluations, significantly speeding up and enhancing the efficiency of the design process [17]. As advancements in design technologies progress rapidly and integrate more quickly, utilizing intelligent methodologies to streamline the design cycle has become a crucial trend in the development of morphing aircraft.
To achieve multi-mission capability, the concept of morphing wings has gained significant attention as a promising method. Morphing wings are capable of adjusting their shape in response to changing flight conditions, thereby enabling optimal aerodynamic performance across various flight missions. This paper primarily focuses on the optimization of airfoils with variable camber and thickness. As morphing mechanisms become increasingly complex, with higher deformation dimensionality and greater demands for high-fidelity modeling in morphing aircraft, it is essential to develop parameterization techniques with reduced dimensionality and high geometric accuracy.
In traditional passive sampling approaches, a batch of airfoils is typically generated in a single step using methods like Latin Hypercube Sampling (LHS) [18] or random sampling. These samples are then evaluated through aerodynamic simulations, and a surrogate model is trained based on this fixed dataset. However, this approach has several drawbacks: the design space is often extensive, with regions corresponding to high performance being sparsely covered. As a result, the trained model may lack sufficient sample support in high-performance regions, leading to prediction errors. In contrast, purely grid-based or large-scale random sampling methods tend to generate numerous low-performance samples, leading to unnecessary simulation costs and computational inefficiencies.
To overcome the limitations outlined above, this study proposes an aerodynamic optimization framework that combines PCA with DL. An optimization-guided data augmentation strategy is introduced, where the initial surrogate model is used to guide the search for high-performance airfoil candidates within reduced iterations. These candidates are then evaluated through high-fidelity aerodynamic simulations, which provide accurate coefficients for retraining the predictive model, thereby improving its reliability in performance-critical regions. Finally, SHAP analysis is applied to quantitatively evaluate the contribution of each principal component to the predicted aerodynamic coefficients, thus enhancing the interpretability of optimization results.
2. Methodology
Figure 1 illustrates the proposed optimization framework for airfoil design, which integrates deep learning with an optimization-guided data augmentation loop. The process starts by constructing an initial airfoil database through a Design of Experiments (DoE) approach, where airfoil geometries are parameterized via PCA, and their aerodynamic coefficients are calculated using XFOIL. These samples are used to train an initial surrogate model, built on a deep neural network (DNN). Utilizing this model as a performance estimator, a MIGA is employed to identify candidate airfoils with potentially superior lift or lift-to-drag ratios. The selected candidates are then evaluated through high-fidelity XFOIL simulations, and the validated samples are added to the training dataset. The surrogate model is retrained using this augmented dataset, thereby improving its predictive accuracy, particularly in high-performance regions of the design space. Finally, the airfoil optimization process commences.
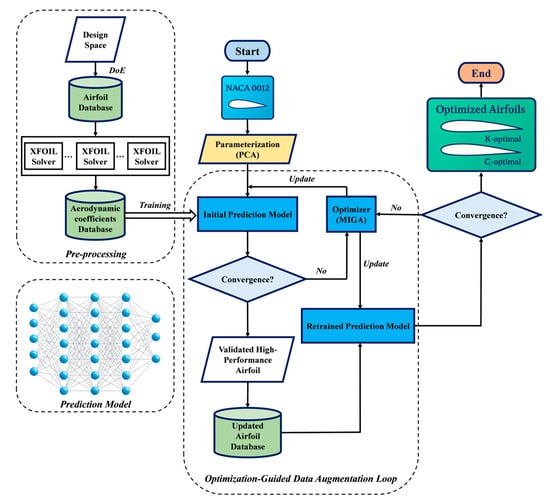
Figure 1.
Flowchart of airfoil optimization based on optimization-guided data augmentation loop.
- Step 1: the PCA method is employed to parameterize the input airfoil.
- Step 2: import the airfoil parameters into the DL-based prediction model and obtain the aerodynamic coefficients.
- Step 3: update the design variables using the optimization algorithm.
- Step 4: use a short-term MIGA run to produce high-performance candidate airfoils, and then employ XFOIL to obtain accurate aerodynamic coefficients. Incorporate these new data points into the training set and retrain the DL model.
- Step 5: determine whether the new airfoil satisfies the convergence condition. If so, output the final airfoil; if not, repeat steps 2 and 3.
The following subsections provide a detailed description of the surrogate model based on optimization-guided data augmentation loop for predicting aerodynamic coefficients of airfoils, as well as the optimization algorithm for airfoil design.
2.1. Parameterization Method
2.1.1. CST Parameterization Method
CST [5] not only reduces the number of optimization parameters but also keeps the airfoil surface smooth. The method approximates the airfoil geometry using polynomials. The upper surface of an airfoil is described as
and the lower surface of an airfoil is described as
where and denote the dimensionless values of the x-axis and y-axis, respectively. The subscripts u and l represent the upper and lower surfaces of the airfoil, respectively. and are the thickness ratios of the upper and lower surfaces of the airfoil trailing edge. The class function C() is defined as
where the parameters and are related to the geometric shape of the airfoil. For a general class of geometric shapes, = 0.5 and = 1.0. The shape function equations are as follows:
where the shape functions for Bernstein polynomials of order n are defined as
in which and are the required parameters for optimization. The order is 12 in the present paper; so, there are 24 design parameters that control the airfoil shape.
2.1.2. PCA Dimensionality Reduction Method
PCA [19,20] is a multivariable analysis method, which can reduce the number of variables. PCA is implemented on the basis of a database, and its idea is to transform the original set of parameters into a new set with a lower dimension while preserving the intrinsic information of the original data.
Assume that the size of the database is n, and the dimension of the input data is m. The input data can be written in the form of a matrix, as follows:
PCA for the database is implemented as per the following procedures.
- (1)
- Obtain a new matrix as follows:
It is obvious that the mean value of the elements in the vector (i = 1, 2, …, m) is zero.
- (2)
- Calculate the covariance matrix of DA:
- (3)
- Calculate eigenvectors (i = 1, 2, …, m) and the corresponding eigenvalues (i = 1, 2, …, m) of matrix C through
Then, rank the eigenvalues from largest to smallest as , , …, , where the corresponding eigenvectors are , , …, .
- (4)
- Calculate the contribution rate of each principal component:
Then, calculate the cumulative contribution rate of the principal components:
Select the largest p (p < m) principal components through
In this study, q is set to be 1 to transform the original input data into a lower dimension.
- (5)
- Generate the new dataset using the largest p principal components:
The PCA airfoil parameterization modeling process studied in this paper is illustrated in Figure 2.

Figure 2.
Flowchart for PCA parametrization.
2.2. Deep Neural Network
A DNN is a model composed of multiple layers of interconnected neurons, where each layer contains several neurons that learn to establish complex mappings between inputs and outputs. Figure 3 presents a schematic diagram of a single neuron. The output of the neuron is defined as:
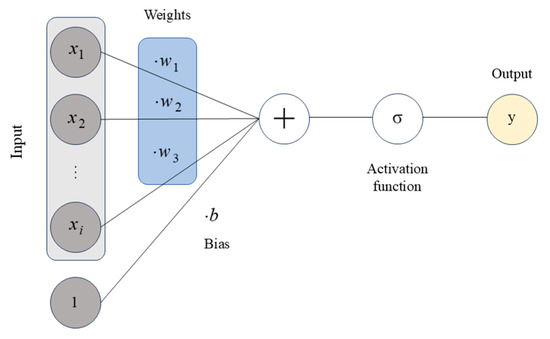
Figure 3.
Input and output structure of one neuron.
In the equation, represents the input to the neuron; denotes the weights corresponding to each input; b represents the bias; and σ is the activation function.
2.3. Optimization Method
2.3.1. Multi-Island Genetic Algorithm
The MIGA [21] is used to optimize the airfoil. This algorithm has better global optimization ability and faster computational efficiency than the Genetic Algorithm (GA). The algorithm divides a large population into several subpopulations called islands. On each island, the traditional GA is applied for subpopulation evolution. The GA is inspired by the survival of the fittest during natural selection. First, the object is encoded for optimization in the solution domain. The algorithm then generates high-quality solutions through genetic operators such as selection, crossover, and mutation. A large population is used to search for the optimal solution [22].
2.3.2. Optimization Objective and Constraint Conditions
The optimization procedure focuses on two key flight conditions: climb and low-speed cruise. During the climb phase, enhancing lift is necessary to support efficient upward motion. During the low-speed cruise phase, the goal is to maximize the lift-to-drag ratio. Achieving this improves aerodynamic performance, lowers fuel consumption, and increases the aircraft’s operational range. The optimization variables include PCA weights for both the upper and lower surfaces. These variables consist of 18 components in total. The first 9 components correspond to PCA weights for the upper surface, while the remaining 9 components represent PCA weights for the lower surface. The airfoil designed in this study is intended for a typical military UAV and features a chord length of 600 mm. The boundary conditions and optimization objectives corresponding to two flight states are summarized in Table 1.

Table 1.
Design points and objectives for the airfoil.
The optimization enforces two-level thickness constraints:
1. Local Constraints: At 11 chordwise positions χ∈{0.1, 0.2, 0.3, 0.4, 0.45, 0.5, 0.55, 0.6, 0.7, 0.8, 0.9}:
2. Global Constraint: maximum thickness:
2.4. Optimization-Guided Data Augmentation
To expand the high-quality training set for the surrogate model, the MIGA is executed 100 times, with each run initialized using a distinct pseudo-random seed k∈{1,…,100}. At the start of each restart, the default Pseudo-Random Number Generator engines in both the Python 3.9.13 random module and the NumPy library are reseeded using the same value k. This setup ensures that the processes of initialization, crossover, mutation, and reproduction follow a unique path. Each path corresponds to a specific realization of the Markov chain [23].
Each restart generates ten loosely coupled islands, with each island consisting of 30 individuals. The evolutionary process is then carried out for exactly 10 generations. This island-based structure enables the algorithm to explore multiple regions of the search space in parallel while keeping the communication overhead between islands relatively low. Each individual in the population is represented by a stacked vector that encodes the design variables used in the optimization process.
Let denote the upper-surface and lower-surface PCA coefficients of the i-th individual, respectively. Each individual is thus represented by an 18-dimensional vector formed by stacking these two components. The optimization process is therefore conducted within this 18-dimensional PCA coefficient space.
All candidate airfoils were subsequently evaluated using XFOIL to obtain accurate aerodynamic coefficients. The corresponding surrogate model predictions were then replaced with these high-fidelity simulation results. This correction step compensates for the surrogate model’s limited accuracy in regions associated with high aerodynamic performance. The validated samples were added to the original training dataset and used to retrain the neural network. Using the retrained surrogate model, a final round of global optimization was conducted to identify the optimal airfoil geometry with enhanced reliability in aerodynamic predictions. By introducing targeted high-performance samples and refining the distribution of training data, the approach effectively mitigated the original model’s deficiencies in critical subspaces of the design space.
3. Results
3.1. Data Preparation for the DNN
3.1.1. Analysis Based on PCA
The airfoil upper and lower surface grid data points were each set to 140. PCA was then applied to the sampled airfoil shapes. The eigenvalues obtained from the analysis were ranked in descending order based on the amount of variance they captured. Figure 4 shows the variation of the top ten eigenvalues, while Figure 5 illustrates the contribution rates of the modes corresponding to these eigenvalues.

Figure 4.
Top ten eigenvalues.
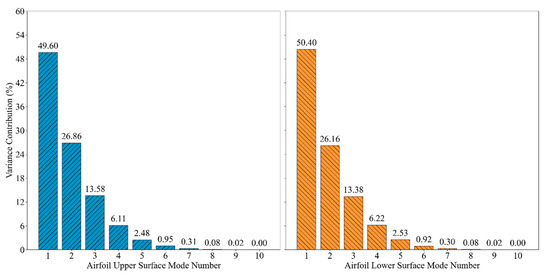
Figure 5.
Contribution of the top ten modes.
As shown in Figure 5, the cumulative contribution of the first nine principal modes reaches 100% for both the upper and lower surfaces of the airfoil. This indicates that these nine modes are sufficient to fully represent the original geometric space. From the perspective of dimensionality reduction, when the goal is to preserve complete shape information, the PCA-based parameterization method reduces the number of design variables required to describe a single airfoil surface from 12 to 9. This represents a reduction in dimensionality compared to the CST parameterization approach.
Five airfoils were randomly resampled from the design space and used as test airfoils for fitting accuracy and error analysis. Figure 6 illustrates the shapes of these test airfoils, where c represents the airfoil’s chord length, x denotes the coordinate along the chord direction, and y represents the coordinate along the thickness direction. The horizontal axis corresponds to the normalized chordwise position, while the vertical axis corresponds to the normalized thickness distribution.
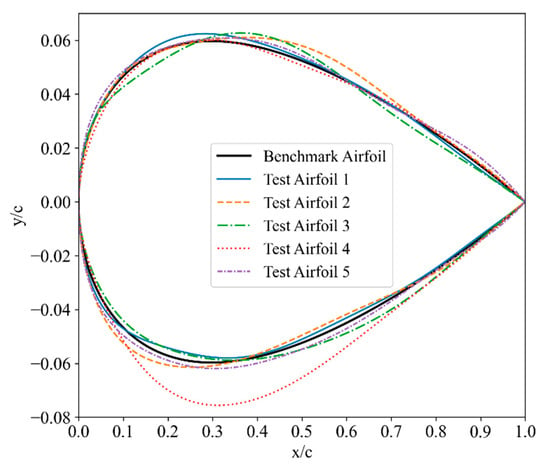
Figure 6.
Test and benchmark airfoils.
The first 3 to 10 principal modes were individually employed to represent the test airfoils. During the fitting stage, the upper and lower surface data of each airfoil were projected onto the principal component space. This projection yielded a set of principal component coefficients for each surface. These coefficients were obtained by solving a system of linear equations through the least squares method [24]. Using this method, the projection coefficients corresponding to each test airfoil were accurately computed within the principal component space, allowing precise reconstruction of the original airfoil shapes.
In the equation, F(α) denotes the reconstructed airfoil grid point data obtained through the fitting procedure. The variable represents the actual grid point data of the airfoil being fitted. The objective function defined in Equation (22) quantifies the fitting accuracy. Figure 7 shows the variation of the fitting accuracy of the test airfoils with the number of principal modes. Figure 8 presents the fitting error between the actual and fitted data for the upper surface of the test airfoils when the first nine modes are used for characterization. In this paper, the fitting accuracy is defined as the sum of the squared differences between the fitted data and the actual data across all grid points. This measure is cumulative. The fitting error refers to the individual difference at each grid point between the actual and reconstructed data. This value is evaluated at a single point.

Figure 7.
Fitting accuracy varying with the number of modes.
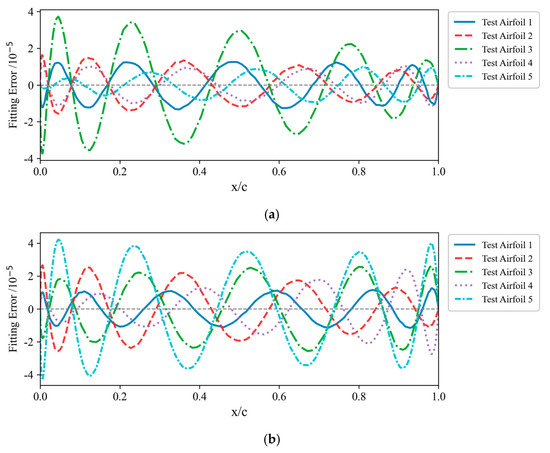
Figure 8.
Fitting errors of the upper and lower surfaces using 9 modes: (a) upper surface and (b) lower surface.
From Figure 7, it can be seen that three modes ensure a fitting accuracy on the order of 10−4. From Figure 8, it can be observed that when the first nine modes are used for fitting, the fitting error at any grid point on the upper and lower surface of the airfoil is within 5 × 10−5. Reference [25] points out that in practical applications, the fitting error of the normalized airfoil surface grid points must meet the ‘typical wind tunnel tolerance.’ Specifically, the geometric error of the airfoil should not exceed 0.0004 at 0–20% of the chord length and 0.0008 at 20–100% of the chord length for the airfoil representation to be considered within an acceptable accuracy range. The detailed derivation of this conclusion can be found in Reference [26]. From Figure 8, it can be seen that when nine modes are used for characterization, the geometric fitting error falls within the ‘typical wind tunnel tolerance’ range.
To analyze the effect of each mode on the geometric shape, using test airfoil 1 as an example, the coefficients corresponding to each of the first nine modes were perturbed during the fitting process (upper surface coefficients were increased by 0.1, and lower surface coefficients were decreased by 0.1). Figure 9 shows the results after perturbing each mode.
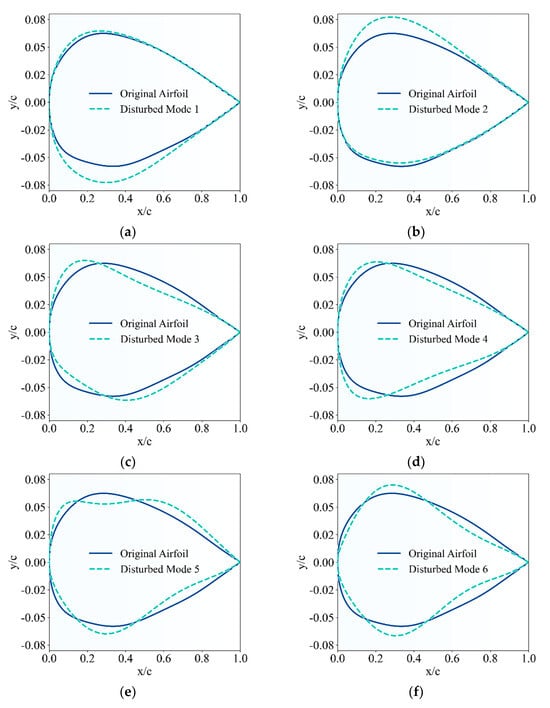
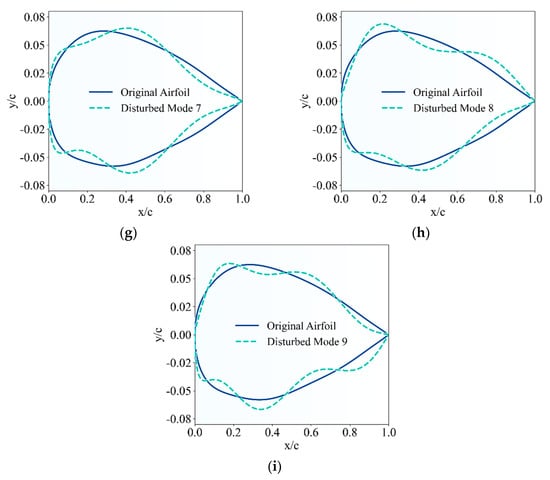
Figure 9.
Disturbing influences of the first nine modes: (a) Mode 1; (b) Mode 2; (c) Mode 3; (d) Mode 4; (e) Mode 5; (f) Mode 6; (g) Mode 7; (h) Mode 8; and (i) Mode 9.
From Figure 9, it can be observed that Mode 1 and Mode 2 correspond to the thickness deformation mode of the airfoil. Mode 3 and Mode 4 correspond to the axial displacement modes at the maximum thickness locations on the upper and lower surfaces, respectively. Modes 5 through 9 correspond to the extrusion modes of the airfoil surfaces.
3.1.2. Computation of Aerodynamic Coefficients
We selected the classical NACA0012 airfoil as the baseline. Airfoil samples were generated using the LHS method within the design domain. This design domain was defined by allowing a ±5% variation in all CST parameters. A total of 1500 airfoil samples were produced and used to construct the training dataset for the neural network. To maintain consistency between training and testing phases, an additional 150 test samples were uniformly generated within the same design space. Prior to training, mean-variance normalization was applied to the dataset:
where x represents the original data; μ denotes the mean of the sample data; δ signifies the standard deviation of the sample data; and x∗ indicates the normalized data.
The geometries of all the airfoils obtained through sampling are shown in Figure 10.

Figure 10.
Airfoil dataset.
In the current study, for fast simulation of the aerodynamic performance of the airfoil, the open software XFOIL 6.99 was chosen to calculate the flow around an airfoil [27]. The software was developed based on a flow panel method, combining an integral boundary layer formula. Unrealistic airfoil geometries were excluded from the dataset. At the same time, non-convergent aerodynamic computation results associated with these geometries were also removed. As a result, the finalized airfoil database and the corresponding flow field database were constructed with a strict one-to-one correspondence, thereby providing a dependable dataset for subsequent analysis.
Since the aerodynamic coefficient training dataset of the DNN is generated using the XFOIL method, it is essential to validate the accuracy of the numerical simulation of the airfoil flow field. The NACA0012 airfoil described was selected as the validation case [28]. The computational conditions are as follows: Ma = 0.3; Re = 3 × 106; and the angle of attack ranges from 0° to 9° in increments of 1°. Figure 11a indicates that the lift coefficients obtained from the analysis are close to the experimental data for angles of attack ranging from 0° to 9°. Figure 11b indicates that the lift and drag results from the analysis are in good agreement with the experimental results.
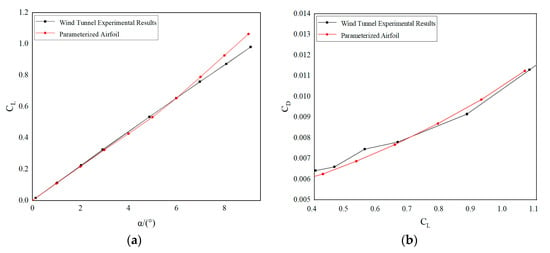
Figure 11.
Lift and drag characteristics at different angles of attack: (a) lift coefficient at different angles of attack and (b) lift and drag coefficients.
3.2. Training Results and Performance of the DNN Model
In this study, hyperparameter optimization was carried out using the Bayesian search strategy implemented in Keras Tuner. The final model architecture selected through this process was an MLP with a single hidden layer containing 4032 neurons. The activation function applied to each neuron was the Rectified Linear Unit. The optimizer was Nesterov-accelerated Adaptive Moment Estimation, with an initial learning rate set to 0.001. An exponential decay schedule with a decay factor of 0.5 was applied every 500 training epochs. During training, the mean squared error (MSE) was used as the loss function to update the weights and biases of the neurons via backpropagation. The definition of MSE is as follows:
where and y are the predicted and true values of the airfoil aerodynamic coefficients, respectively, and m is the number of samples. The prediction performance was evaluated using two metrics: root mean square error (RMSE) and mean relative error (MRE), defined as follows:
As shown in Table 2, the RMSE and MRE for both K and CL exhibit a clear nonmonotonic trend with increasing mode numbers. Specifically, the errors decrease initially, reach minima at Mode 9, and subsequently increase for higher modes. This pattern suggests that Mode 9 represents an optimal balance between retaining sufficient physical information and avoiding noise amplification from redundant modes.

Table 2.
Initial prediction of different modes.
The variance contribution analysis shown in Figure 5 indicates that the first six principal modes account for the majority of the geometric variability within the dataset. In contrast, Modes 7 through 12 exhibit relatively low variance contributions. Although the variance of Modes 7 to 9 is small, these modes capture fine-scale geometric details that play an important role in flow behavior. When included in the MLP model, they contribute to improved prediction accuracy by refining the representation of subtle aerodynamic features. However, the addition of modes beyond Mode 9 introduces signals dominated by noise. This results in a noticeable increase in prediction errors. Such behavior reflects the bias–variance tradeoff principle [29]: lower-variance modes enhance model flexibility but require strict control to prevent overcomplexity.
The combined analysis of performance metrics and variance contributions justifies the selection of nine principal component modes for each airfoil surface. The initial model was trained using the original dataset. In contrast, the retrained model was developed based on the dataset augmented through the optimization-guided data augmentation process.
Figure 12 compares the distributions of K and CL between the initial and retrained models across training and testing datasets. The optimization-guided data augmentation increased the number of samples in high-performance regions.

Figure 12.
Comparison of the predicted K and CL distributions for the initial and retrained models on training and testing datasets: (a) for K and (b) for CL.
Table 3 presents a comparison between the predictive performance of the initial and retrained models, evaluated on the same testing dataset. The evaluation metrics include the coefficients of R2, RMSE, and MRE. For the parameter K, retraining leads to an increase in R2 to 0.992, along with reductions in RMSE and MRE to 0.634 and 0.0123, respectively. For the parameter CL, retraining similarly improves R2 to 0.993, while RMSE and MRE decrease to 3.92 × 10−3 and 2.92 × 10−3. These results indicate an enhancement in predictive accuracy, particularly in regions of high aerodynamic performance.

Table 3.
Comparison of initial and retrained model prediction results for the same testing datasets.
Figure 13 illustrates the distributions of relative errors in the predicted K and CL for the initial and retrained models on the testing dataset. These results confirm that the optimization-guided data augmentation and retraining strategy effectively reduces prediction errors in critical aerodynamic performance metrics.

Figure 13.
Distribution of relative errors in aerodynamic coefficient predictions from the initial and retrained model: (a) for K and (b) for CL.
3.3. Optimization Results
A large population size can improve the search quality of the GA and prevent premature convergence. However, it also increases the computational cost of evaluating individual fitness, thereby slowing down the convergence speed. To balance search accuracy and computational efficiency, appropriate parameter settings must be chosen. The GA is configured with 10 islands, each containing 10 individuals, and runs for 400 generations. The interval of migration is 10 with a 1.0 crossover rate and 0.05 mutation rate. The rate of migration is set to 0.1, the relative tournament size is 0.5, and the elite size is 0.5 [30].
Figure 14 illustrates the convergence histories of K and CL during aerodynamic shape optimization using CST and PCA parameterization methods. Figure 14a,b display the results for each method. The PCA-based approach demonstrates a faster convergence rate. It reaches near-optimal fitness values within a smaller number of generations. While PCA reduces the dimensionality of the design space, it still achieves final optimization results that are comparable to those obtained using the CST method.
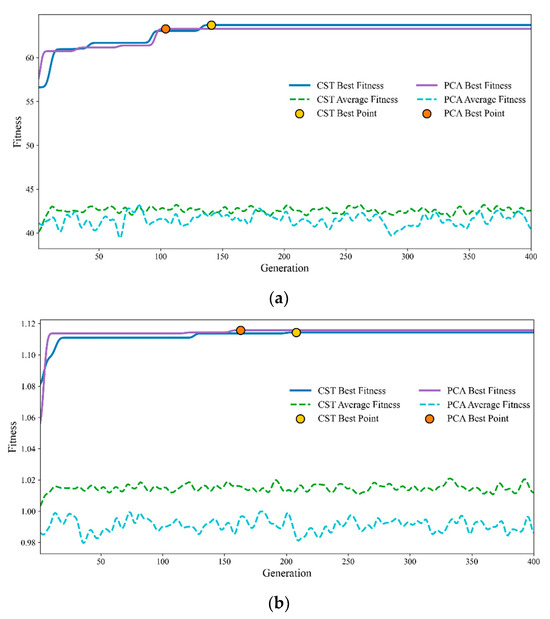
Figure 14.
Convergence history of airfoil optimization: (a) K and (b) CL.
The changes in aerodynamic force coefficients before and after optimization are summarized in Table 4. It can be observed that at design point No. 1, the K of the optimized airfoil increased by 54.66%, while at design point No. 2, the CL increased by 10.90%. These outcomes indicate that, relative to the baseline airfoil NACA0012, the optimized airfoil demonstrates enhanced aerodynamic performance under both low-speed cruise and takeoff conditions. The results also suggest that the use of PCA-based parameterization helps accelerate the optimization process. At the same time, it preserves optimization effectiveness while reducing the complexity of the design space.

Table 4.
Comparison of aerodynamic coefficients between the baseline airfoil and the optimized airfoil.
Figure 15 illustrates the surface coefficients and their corresponding bounds for the optimized airfoil shapes based on PCA and CST parameterizations. Subfigures (a) and (b) show the results corresponding to the optimal values of K and CL obtained through the PCA-based representation. Subfigures (c) and (d) present the results derived using the CST-based approach. In all cases, the optimized coefficients for both the upper and lower surfaces lie within the specified bounds. This confirms that the shape optimization process successfully complied with the predefined geometric constraints. Table 5 presents the PCA coefficients of each optimized design point, which are used to reconstruct the airfoil geometries for the upper and lower surfaces.
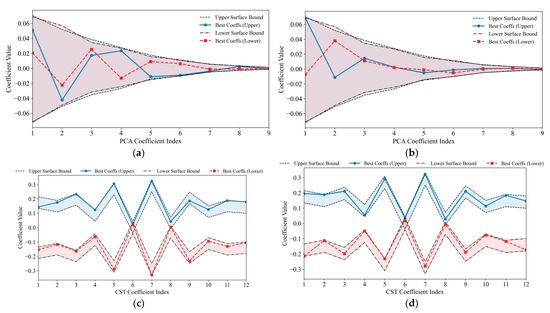
Figure 15.
Surface coefficients and bounds for the optimized airfoil obtained using PCA and CST parameterizations: (a) PCA-optimal K; (b) PCA-optimal CL; (c) CST-optimal K; and (d) CST-optimal CL.

Table 5.
Optimized PCA coefficients for the upper and lower surfaces of selected design points.
Figure 16 presents a comparison of the geometric profiles between the baseline airfoil NACA0012 and the optimized airfoils. For the baseline airfoil, the maximum relative thickness is 0.120, located at 0.309c, and the relative camber is zero. For optimized airfoil 1, the maximum relative thickness is 0.134 at 0.326c, and the maximum relative camber is 0.00605, occurring at 0.822c. For optimized airfoil 2, the maximum relative thickness is 0.128 at 0.273c, with a maximum relative camber of 0.00730 located at 0.495c.

Figure 16.
Comparison of optimized airfoil and NACA0012 airfoil shapes: (a) optimized airfoil 1 and (b) optimized airfoil 2.
The surface pressure coefficient distributions of the baseline and optimized airfoils are shown in Figure 17. Here, Cp denotes the pressure coefficient. Under the conditions of design point No. 2, the optimized airfoil demonstrates several notable aerodynamic features when compared to the baseline configuration. On the upper surface, the optimized airfoil exhibits a broader suction peak distribution, an expanded pressure difference contribution region, and a reduced adverse pressure gradient. These combined effects lead to an increase in the lift coefficient CL.

Figure 17.
Comparison of pressure coefficients between the baseline airfoil and the optimized airfoil.
3.4. Outcome Analysis of Explainable Strategies for Airfoil Optimization
Neural networks are black boxes with strong prediction performance, but there are shortcomings in explaining the potential mechanisms of the data. Aiming at improving the interpretability of the “black box” model, the SHAP method is employed to explore the impact of input features on the neural network model [31,32,33]. The Shapley value fundamentally quantifies the marginal contribution of individual input features to the model output. It is calculated as follows [34]:
where is a feature of sample x, n is the number of samples, {x1, x2, …, xn} is a set of input features, S is a subset that does not contain feature , and is the prediction of features in set S. The Shapley value assigned to each feature is used to construct the following additive interpretation model function:
When > 0, a positive effect occurs as the predicted value is higher than the baseline value under the influence of feature . When < 0, feature has a negative effect and causes the predicted value to be lower than the baseline value. The SHAP method not only takes the impact of a single feature into account but also considers the impact of feature combinations and synergistic effects between features that may exist.
In this study, two SHAP implementation strategies are employed and systematically compared. The first approach is Kernel SHAP, which is a model-agnostic approximation technique. It can be applied to any black-box predictive model. Reference [35] demonstrates that when using a weighted linear regression model as the local surrogate and selecting an appropriate kernel function, the resulting regression coefficients closely approximate the SHAP values. The second approach is Deep SHAP, which is a model-specific method tailored for deep neural networks. This technique integrates backpropagated gradients with reference-based input perturbations to efficiently compute SHAP values [36].
SHAP-Based Visualization Analysis
To clarify the role of each principal component mode in influencing the aerodynamic performance of the optimized airfoil, a SHAP-based local interpretability framework is applied. Unlike global sensitivity analysis, this method emphasizes the contribution of individual features to a specific optimized instance. This allows for a more direct understanding of how lift enhancement is achieved as captured by the predictive model. Since the primary focus of this study is on the physical interpretation of the final optimal design, global SHAP visualizations are not included.
Figure 18 presents a comparison of SHAP attributions across principal components for the final optimized models used to predict K and CL. PC refers to the principal components derived from PCA. In the model predicting K, PC4 shows the strongest positive contribution. PC3 has a negative influence. This suggests that multiple components work together to improve aerodynamic efficiency. In the model predicting CL, PC1 and PC2 make the most significant contributions. This indicates that variations in the first two components are primarily responsible for lift enhancement. The similarity in attribution patterns between Kernel SHAP and Deep SHAP supports the reliability of Deep SHAP in approximating contribution values and interpreting deep neural networks.
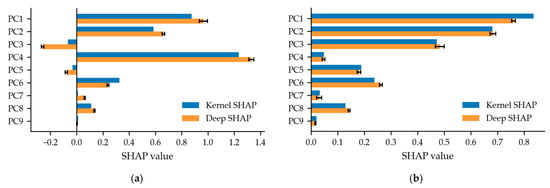
Figure 18.
Attribution analysis of principal components using Kernel SHAP and Deep SHAP: (a) K prediction and (b) CL prediction.
Figure 19 displays the generational progression of SHAP contributions for predicting K and CL throughout the MIGA optimization process. As optimization proceeds, the cumulative SHAP values for each principal component exhibit distinct and stable trends. For K, PC1 and PC4 maintain a dominant influence across generations. For CL, PC1, PC2, and PC3 consistently play leading roles. This is consistent with the trend in Figure 18.
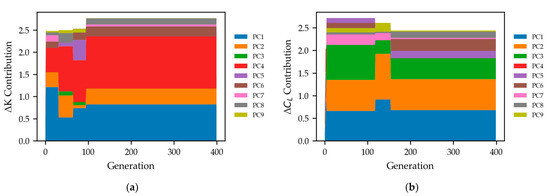
Figure 19.
Generation-wise evolution of SHAP contributions for principal components: (a) for K prediction and (b) for CL prediction.
To further support the global attribution patterns and the mode evolution observed throughout the optimization process, Figure 20 provides a local SHAP waterfall plot for the final optimized airfoil design. These plots illustrate how each principal component contributes additively from the baseline output to the final model prediction. For the coefficient K, Modes 4, 1, and 2 are found to make the most significant positive contributions. For CL, Modes 1, 2, and 3 are identified as the primary contributors to performance enhancement. This instance-level explanation is consistent with the global attribution results shown in Figure 18 and the mode progression trends depicted in Figure 19.

Figure 20.
SHAP waterfall plots by modal grouping: (a) for K and (b) for CL.
4. Discussion
(1) The airfoil parameterization approach based on PCA serves two main purposes. First, it reduces the dimensionality of the design variables. Second, it retains the essential geometric characteristics required for accurate airfoil representation. However, selecting an insufficient number of principal modes may limit the ability to capture complex geometric features. This reduction in expressiveness can negatively impact the model’s predictive accuracy. On the other hand, incorporating too many modes may introduce components dominated by noise. These components do not contribute meaningful information and may degrade prediction performance.
(2) The aerodynamic surrogate model for airfoils integrates deep learning with PCA. This combination enables efficient dimensionality reduction of the input geometry. At the same time, it preserves a high level of predictive accuracy in modeling aerodynamic performance.
(3) After the initial training phase of the machine learning model, a GA is applied to explore a wider range of airfoil candidates that are predicted to exhibit high aerodynamic performance. These predicted high-performance airfoils are subsequently evaluated using XFOIL to obtain more accurate aerodynamic coefficients. The refined samples are then used to enrich the dataset with targeted high-performance data. This approach reduces the inefficiency associated with purely random sampling and helps alleviate the bias introduced by insufficient data in regions of high aerodynamic quality.
(4) The interpretability workflow employs a combination of visualization tools to construct a clear and organized local explanation system. These tools include waterfall plots, stacked contribution charts, comparative bar plots, and SHAP correlation diagrams. Together, they provide detailed insight into the prediction behavior of the surrogate model. This structured framework is used to support the evaluation of the model’s reliability in specific prediction scenarios.
Author Contributions
Conceptualization, A.G. and H.W.; methodology, A.G. and J.W.; software, A.G.; validation, A.G., J.W. and H.W.; formal analysis, A.G.; investigation, J.W. and M.Z.; resources, A.G.; data curation, A.G.; writing—original draft preparation, A.G.; writing—review and editing, A.G. and J.W.; visualization, M.Z.; supervision, H.W.; project administration, H.W.; funding acquisition, H.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Key Science and Technology Project Plan of Shanxi Province, grant numbers 202301120401010 and 202101120401007.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
Author Miao Zhang was employed by the company Shanghai Aircraft Design and Research Institute. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Appendix A
To assess the consistency and robustness of Deep SHAP in interpreting neural network outputs, a comparative analysis was carried out against Kernel SHAP. This evaluation was performed using the final optimized airfoil. The comparison was conducted under two prediction tasks: the aerodynamic coefficients K and CL.
As illustrated in Figure A1, SHAP values for the optimized sample were calculated across the nine principal component modes. Deep SHAP was applied using five independently generated background sets, with each set containing 512 data points. In parallel, Kernel SHAP values were computed using the same background size and 2048 Monte Carlo samples. To maintain consistency between upper and lower surface contributions, the SHAP values corresponding to each mode were summed across both surfaces. This resulted in a unified nine-dimensional representation for the interpretability analysis.
For Figure A1a, Deep SHAP showed strong alignment with Kernel SHAP, achieving a Pearson correlation of 0.990. Table A1 summarizes the error metrics across five background sets, where MAE remains below 0.083 and correlation consistently exceeds 0.989. A mode-wise comparison in Table A2 reveals that dominant modes such as Mode 1 and Mode 4 exhibit small standard deviations, indicating high attribution reliability.
For Figure A1b, a similarly high degree of consistency was observed, with a Pearson correlation of 0.997. Table A3 reports that the MAE across background sets is as low as 0.014–0.022, and the RMSE remains below 0.033. Table A4 provides the mode-level attribution comparison, where key Modes 1–3 demonstrate small discrepancies and low variance, supporting the robustness of Deep SHAP even under different reference baselines.
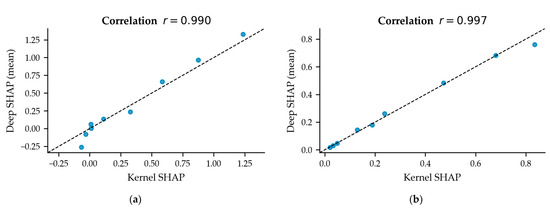
Figure A1.
Attribution consistency analysis between Deep SHAP and Kernel SHAP: (a) for K prediction and (b) for CL prediction.

Table A1.
Error statistics for K prediction.
Table A1.
Error statistics for K prediction.
| Background Set | MAE | RMSE | Pearson Correlation |
|---|---|---|---|
| 1 | 0.0666 | 0.0825 | 0.9904 |
| 2 | 0.0742 | 0.0888 | 0.9908 |
| 3 | 0.0770 | 0.0922 | 0.9903 |
| 4 | 0.0820 | 0.1015 | 0.9899 |
| 5 | 0.0761 | 0.0914 | 0.9892 |

Table A2.
Mode-wise attribution comparison for K.
Table A2.
Mode-wise attribution comparison for K.
| Mode | Kernel SHAP | Deep SHAP * | Standard Deviation |
|---|---|---|---|
| 1 | 0.874561 | 0.965154 | 0.030648 |
| 2 | 0.584151 | 0.661414 | 0.009638 |
| 3 | −0.066276 | −0.259167 | 0.009274 |
| 4 | 1.235204 | 1.328859 | 0.019508 |
| 5 | −0.031033 | −0.078686 | 0.008764 |
| 6 | 0.326275 | 0.238011 | 0.006862 |
| 7 | 0.009486 | 0.062211 | 0.005123 |
| 8 | 0.111857 | 0.135941 | 0.004369 |
| 9 | 0.012600 | 0.003142 | 0.002314 |
* Deep SHAP values represent the mean across five independently sampled background sets.

Table A3.
Error statistics for CL prediction.
Table A3.
Error statistics for CL prediction.
| Background Set | MAE | RMSE | Pearson Correlation |
|---|---|---|---|
| 1 | 0.0148 | 0.0232 | 0.9976 |
| 2 | 0.0202 | 0.0325 | 0.9945 |
| 3 | 0.0215 | 0.0301 | 0.9956 |
| 4 | 0.0198 | 0.0292 | 0.9958 |
| 5 | 0.0150 | 0.0265 | 0.9969 |

Table A4.
Mode-wise attribution comparison for CL.
Table A4.
Mode-wise attribution comparison for CL.
| Mode | Kernel SHAP | Deep SHAP * | Standard Deviation |
|---|---|---|---|
| 1 | 0.835384 | 0.760385 | 0.007422 |
| 2 | 0.680771 | 0.683107 | 0.010299 |
| 3 | 0.472347 | 0.483651 | 0.016891 |
| 4 | 0.048717 | 0.047090 | 0.005351 |
| 5 | 0.188648 | 0.179598 | 0.006754 |
| 6 | 0.237636 | 0.262005 | 0.005217 |
| 7 | 0.032899 | 0.030293 | 0.009542 |
| 8 | 0.129278 | 0.142899 | 0.003263 |
| 9 | 0.020385 | 0.016269 | 0.002031 |
* Deep SHAP values represent the mean across five independently sampled background sets.
References
- Zhang, C.; Chen, H.; Xu, X.; Duan, Y.; Wang, G. A data-driven metric-based proper orthogonal decomposition method with Shapley Additive Explanations for aerodynamic shape inverse design optimization. Adv. Eng. Inform. 2025, 65, 103277. [Google Scholar] [CrossRef]
- Castonguay, P.; Nadarajah, S. Effect of shape parameterization on aerodynamic shape optimization. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8 January–11 January 2007; p. 59. [Google Scholar]
- Zhang, C.; Duan, Y.; Chen, H.; Lin, J.; Xu, X.; Wang, G.; Liu, S. Efficient aerodynamic shape optimization with the metric-based POD parameterization method. Struct. Multidiscip. Optim. 2023, 66, 140. [Google Scholar] [CrossRef]
- Liu, B.; Liang, H.; Han, Z.-H.; Yang, G. Surrogate-based aerodynamic shape optimization of a morphing wing considering a wide Mach-number range. Aerosp. Sci. Technol. 2022, 124, 107557. [Google Scholar] [CrossRef]
- Kulfan, B.M. Universal parametric geometry representation method. J. Aircr. 2008, 45, 142–158. [Google Scholar] [CrossRef]
- Wang, X.; Cai, J.; Qu, K.; Liu, C. Airfoil optimization based on improved CST parametric method and transition model. Acta Aeronaut. Astronaut. Sin. 2015, 36, 449–461. [Google Scholar]
- Cinquegrana, D.; Iuliano, E. Investigation of adaptive design variables bounds in dimensionality reduction for aerodynamic shape optimization. Comput. Fluids 2018, 174, 89–109. [Google Scholar] [CrossRef]
- Oyama, A.; Nonomura, T.; Fujii, K. Data mining of Pareto-optimal transonic airfoil shapes using proper orthogonal decomposition. J. Aircr. 2010, 47, 1756–1762. [Google Scholar] [CrossRef]
- Oyama, A.; Verburg, P.; Nonomura, T.; Hoeijmakers, H.; Fujii, K. Flow field data mining of Pareto-optimal airfoils using proper orthogonal decomposition. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4 January–7 January 2010; p. 1140. [Google Scholar]
- Jing, Y.; Jiang, A.; Liang, L.; Xiaojun, W.; Yewei, G.; Shenshen, L. PCA aerodynamic geometry parametrization method. Acta Aeronaut. Astronaut. Sin. 2024, 45, 129125. [Google Scholar]
- Asouti, V.G.; Kyriacou, S.A.; Giannakoglou, K.C. PCA-enhanced metamodel-assisted evolutionary algorithms for aerodynamic optimization. In Application of Surrogate-Based Global Optimization to Aerodynamic Design; Springer: Berlin/Heidelberg, Germany, 2016; pp. 47–57. [Google Scholar]
- Li, J.; Bouhlel, M.A.; Martins, J.R. Data-based approach for fast airfoil analysis and optimization. AIAA J. 2019, 57, 581–596. [Google Scholar] [CrossRef]
- Xue, D.; Li, Y.; Zhang, H.; Tong, X.; Gao, B.; Yu, J. Reliability-based robust optimization design for tolerance of aerospace thin-walled components based on surrogate model. Adv. Eng. Inform. 2024, 62, 102754. [Google Scholar] [CrossRef]
- Du, B.; Shen, E.; Wu, J.; Guo, T.; Lu, Z.; Zhou, D. Aerodynamic Prediction and Design Optimization Using Multi-Fidelity Deep Neural Network. Aerospace 2025, 12, 292. [Google Scholar] [CrossRef]
- Zhang, C.; Hu, Z.; Shi, Y.; Xu, G. Fast aerodynamic prediction of airfoil with trailing edge flap based on multi-task deep learning. Aerospace 2024, 11, 377. [Google Scholar] [CrossRef]
- Suarez, G.; Özkaya, E.; Gauger, N.R.; Steiner, H.-J.; Schäfer, M.; Naumann, D. Nonlinear Surrogate Model Design for Aerodynamic Dataset Generation Based on Artificial Neural Networks. Aerospace 2024, 11, 607. [Google Scholar] [CrossRef]
- Chen, S.; Jia, M.; Liu, Y.; Gao, Z.; Xiang, X. Deformation modes and key technologies of aerodynamic layout design for morphing aircraft: Review. Acta Aeronaut. Astronaut. Sin. 2024, 45, 629595. [Google Scholar]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 2000, 42, 55–61. [Google Scholar] [CrossRef]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Jun, T.; Gang, S.; Liqiang, G.; Xinyu, W. Application of a PCA-DBN-based surrogate model to robust aerodynamic design optimization. Chin. J. Aeronaut. 2020, 33, 1573–1588. [Google Scholar]
- Scrucca, L. On some extensions to GA package: Hybrid optimisation, parallelisation and islands evolution. arXiv 2016, arXiv:1605.01931. [Google Scholar]
- Liu, J.; Chen, R.; Lou, J.; Hu, Y.; You, Y. Deep-learning-based aerodynamic shape optimization of rotor airfoils to suppress dynamic stall. Aerosp. Sci. Technol. 2023, 133, 108089. [Google Scholar] [CrossRef]
- Matsumoto, M.; Nishimura, T. Mersenne twister: A 623-dimensionally equidistributed uniform pseudo-random number generator. ACM Trans. Model. Comput. Simul. 1998, 8, 3–30. [Google Scholar] [CrossRef]
- Abdi, H. The method of least squares. Encycl. Meas. Stat. 2007, 1, 530–532. [Google Scholar]
- Masters, D.A.; Taylor, N.J.; Rendall, T.; Allen, C.B.; Poole, D.J. Geometric comparison of aerofoil shape parameterization methods. AIAA J. 2017, 55, 1575–1589. [Google Scholar] [CrossRef]
- Kulfan, B.; Bussoletti, J. “Fundamental” parameteric geometry representations for aircraft component shapes. In Proceedings of the 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Portsmouth, VA, USA, 6 September–8 September 2006; p. 6948. [Google Scholar]
- Drela, M. XFOIL: An analysis and design system for low Reynolds number airfoils. In Proceedings of the Low Reynolds Number Aerodynamics: Proceedings of the Conference, Notre Dame, IN, USA, 5–7 June 1989; pp. 1–12. [Google Scholar]
- Kai, X.; Fuhai, D. Optimization method of aerodynamic characteristics for variable thickness wing. J. Dalian Univ. Technol. 2024, 64, 368–375. [Google Scholar]
- Geman, S.; Bienenstock, E.; Doursat, R. Neural networks and the bias/variance dilemma. Neural Comput. 1992, 4, 1–58. [Google Scholar] [CrossRef]
- Song, X.; Wang, L.; Luo, X. Airfoil optimization using a machine learning-based optimization algorithm. In Proceedings of the Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2022; p. 012009. [Google Scholar]
- Ni, M.; Wei, Z.; Deng, W.; Tao, H.; Ren, G.; Gan, X. Enhancing Multi-Hole Pressure Probe Data Processing in Turbine Cascade Experiments Using Structural Risk Minimization Principle. Aerospace 2024, 11, 973. [Google Scholar] [CrossRef]
- Nanyonga, A.; Wasswa, H.; Joiner, K.; Turhan, U.; Wild, G. Explainable Supervised Learning Models for Aviation Predictions in Australia. Aerospace 2025, 12, 223. [Google Scholar] [CrossRef]
- Xie, Y.; Pongsakornsathien, N.; Gardi, A.; Sabatini, R. Explanation of Machine-Learning Solutions in Air-Traffic Management. Aerospace 2021, 8, 224. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, L.; Yao, M.; Zhang, J. Neural network models and shapley additive explanations for a beam-ring structure. Chaos Solitons Fractals 2024, 185, 115114. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4768–4777. [Google Scholar]
- Chen, H.; Lundberg, S.M.; Lee, S.-I. Explaining a series of models by propagating Shapley values. Nat. Commun. 2022, 13, 4512. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).