Entry Guidance for Hypersonic Glide Vehicles via Two-Phase hp-Adaptive Sequential Convex Programming
Abstract
1. Introduction
- Objective reformulation of NFZ avoidance. We replace hard NFZ constraints with a single objective—maximizing NFZ-avoidance capability—thereby ensuring progressive trajectory refinement even when full avoidance is unattainable.
- Soft-trust-region shrinkage. We introduce a dynamic penalty-weight strategy that contracts the trust region, controls linearization errors, and promotes stable convergence.
- Objective-sensitivity-driven mesh refinement. In Stage I, we leverage adjoint-based sensitivity of the performance objective to drive targeted mesh adaptation, avoiding unnecessary refinement in low-impact regions.
2. Problem Formulation
2.1. Dynamics
- r is the nondimensional radial distance, defined by r = 1 + H, with H the nondimensional altitude.
- θ and φ are longitude and latitude, respectively.
- V is the nondimensional Earth-relative speed.
- γ and ψ are the flight-path angle and heading angle, respectively.
- ω is the nondimensional Earth rotation rate.
- σ is the bank angle.
2.2. Control Variable Selection
2.3. Optimal Control Problem
3. Convexification and Discretization
3.1. Convexification
3.1.1. Dynamics Linearization
3.1.2. Path-Constraint Convexification
3.1.3. NFZ-Constraint Convexification
3.1.4. Objective Reformulation
3.2. Discretization and Approximation
4. Entry Guidance Method
4.1. Shrinking-Trust-Region Strategy
4.2. Adaptive Mesh Refinement
4.2.1. Phase I: Sensitivity-Driven Mesh Refinement
- If any :
- If for all i but :
- If all :
4.2.2. Phase II: Residual-Driven Mesh Refinement
- If βy < βmax and Ny ≤ Nmax:
- Otherwise:
| Algorithm 1. hp-Adaptive SCP Workflow | |
| Step | Procedure |
| 1 Initialization | Set initial guess X(0), iteration index k = 1, and algorithm parameters (e.g., penalty bounds, error tolerances). Initialize a uniform mesh with Y(0) segments and N(0) collocation points per segment. |
| 2 Problem Selection | If this is an initial trajectory or mission parameters have changed: Solve Problem P3 using the two-stage strategy (Steps 3–10).If replanning due to tracking deviation without mission change: Solve Problem P5 using the single-stage hard-trust-region strategy (Steps 7–10). |
| —Sensitivity-Driven Refinement Phase (for P3)— | |
| 3 | Solve P3 with the current mesh and penalty C3 to obtain X(k). |
| 4 | If the trust-region convergence criterion (56) is satisfied, freeze C3 and proceed to Step 7; otherwise, continue. |
| 5 | Evaluate scaled adjoint sensitivities (Equation (64)). If , subdivide; else if , increase polynomial order; otherwise, retain current mesh. |
| 6 | Set k ← k + 1, update C3 ← min(k3C3, C3,max), and return to Step 3. |
| —Residual-Driven Refinement Phase (for both P3 and P5)— | |
| 7 | Solve the active problem (P3 or P5) to get X(k). |
| 8 | Estimate local discretization errors (Equation (68)). If all segments satisfy , terminate. Otherwise, proceed. |
| 9 | Compute the curvature ratio βy (Equation (70)) of the dominant state. If βy > βmax or Ny > Nmax, subdivide the segment; otherwise, increase its polynomial order. |
| 10 | Set k ← k + 1, then return to Step 7. |
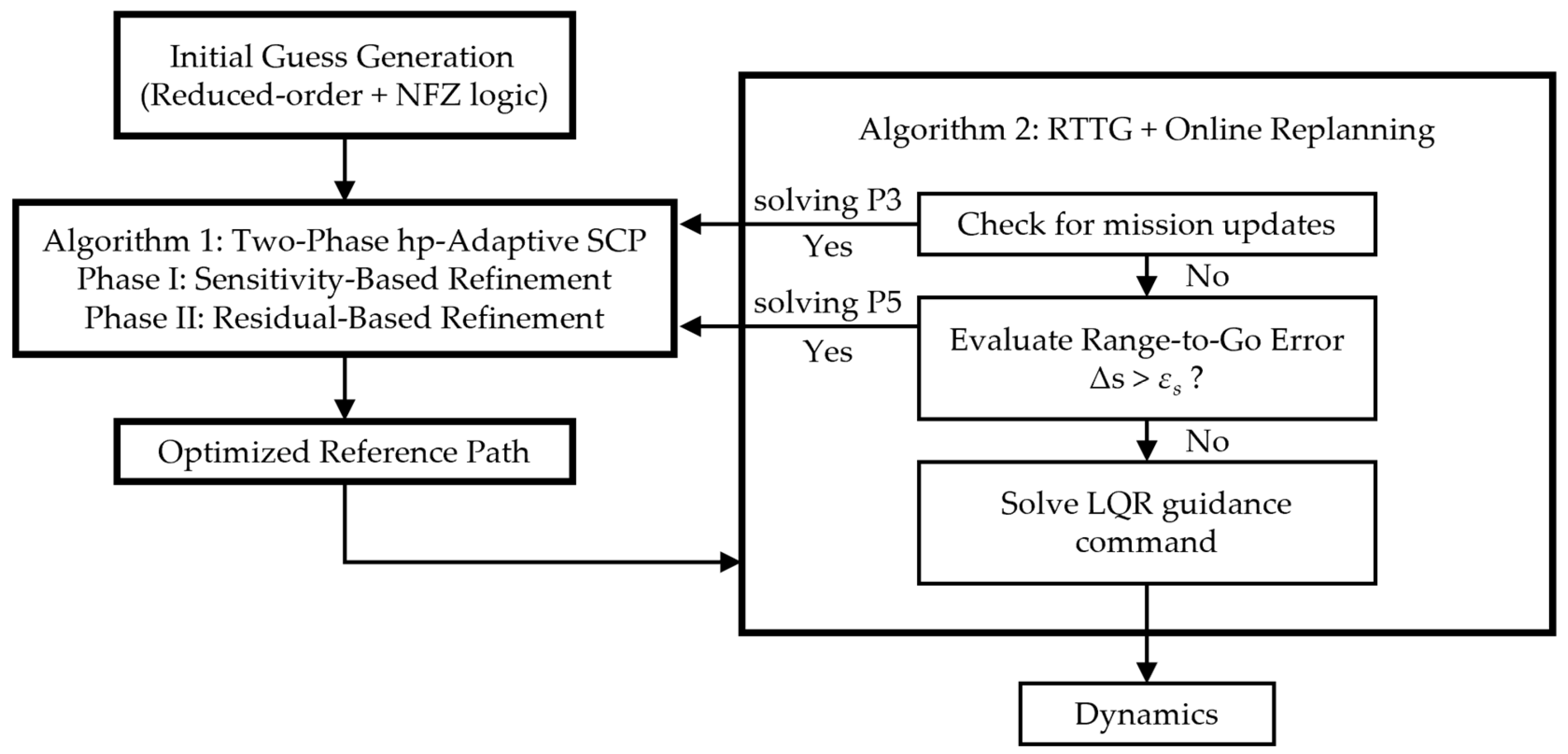
4.3. Reference-Trajectory-Tracking Guidance (RTTG) Algorithm
4.3.1. Initial Guess Generation
4.3.2. Trajectory Tracking and Online Correction
| Algorithm 2. RTTG with Online Reference Trajectory Updates | |
| Step | Procedure |
| 1 | Initialize vehicle states, constraints, and all relevant parameters. Generate an initial reference guess. |
| 2 | Compute the reference trajectory via Algorithm 1 (solving Problem P3). |
| 3 | If t ≥ tf, terminate guidance; otherwise, proceed to Step 4. |
| 4 | Check for mission updates (e.g., NFZ changes). If applicable, return to Step 2; otherwise, continue. |
| 5 | Evaluate the RTG deviation ∆s. If ∆s > εs, recompute the trajectory by solving Problem P5. |
| 6 | Apply the LQR guidance command via Equation (73), and return to Step 3. |
5. Results and Analysis
5.1. Simulation Conditions
5.2. Influence of the Soft-Trust-Region Weight
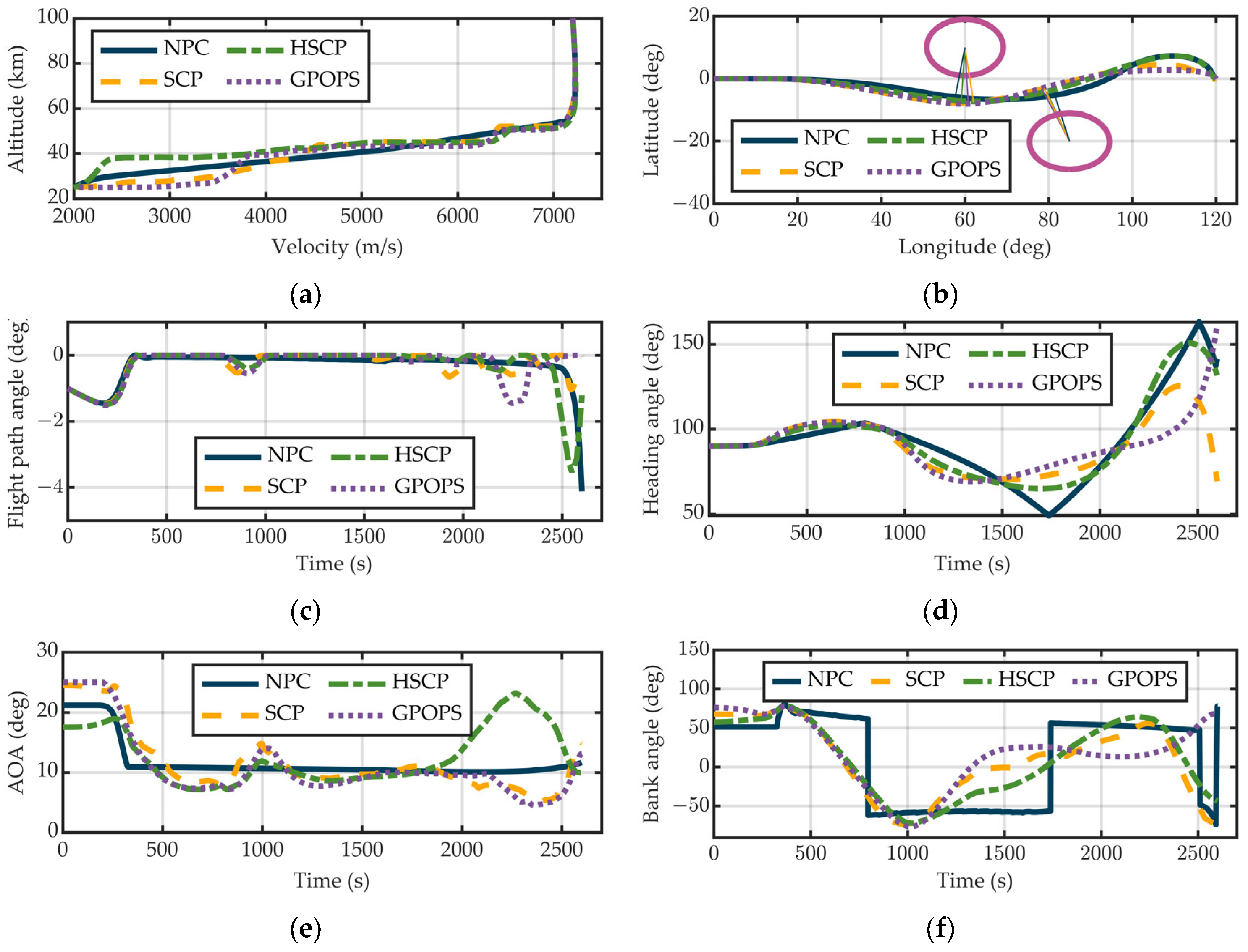
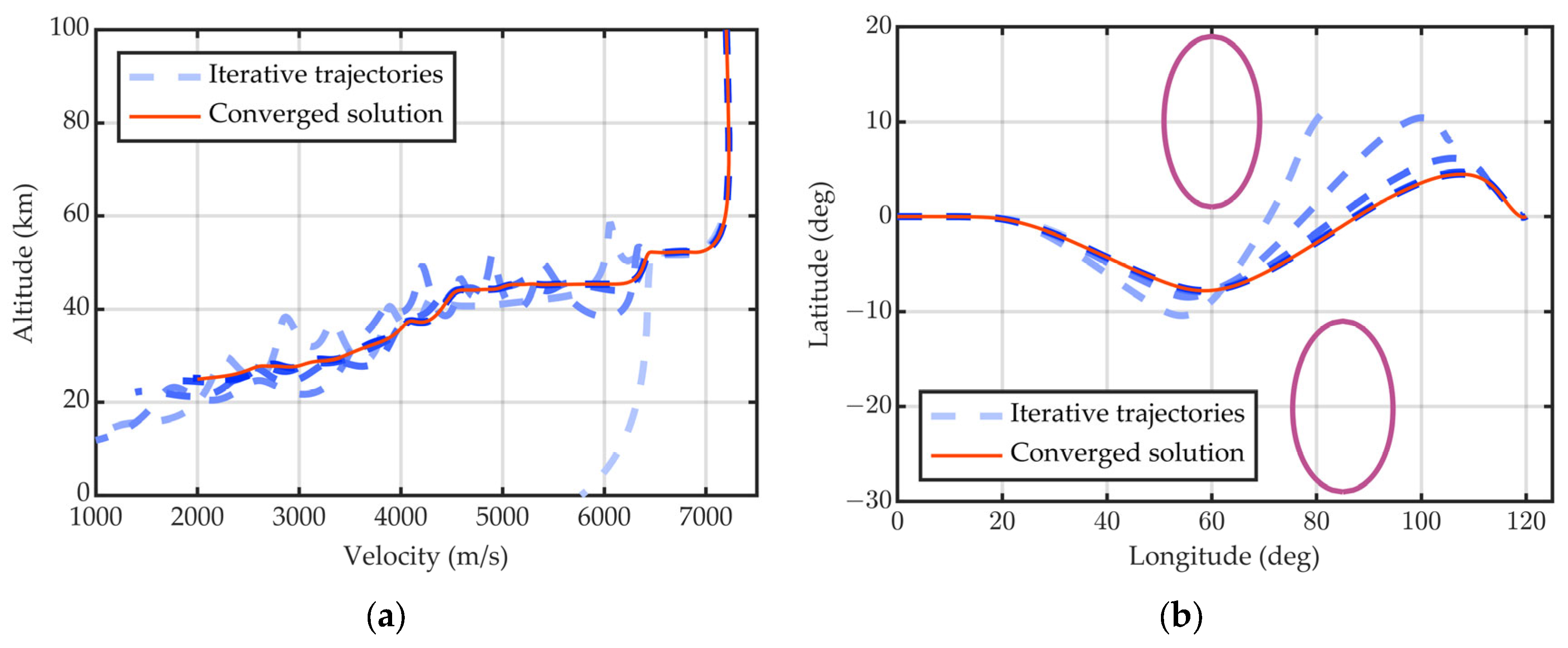
5.3. Nominal-Case Reference Trajectory
- Two variants are considered:
- SCP—the default first-order soft-trust-region formulation (Problem P3).
- HSCP—a fourth-order soft-trust-region formulation obtained by replacing P3 with P4 and setting C3 = 10−3 and C3,max = 100.
- For comparison, we also include the following:
- NPC—the numerically predicted-corrected guess described in Section 4.3.1.
- GPOPS—the global optimum computed off-line with GPOPS-II [38].
- Comparative results are illustrated in Figure 5.
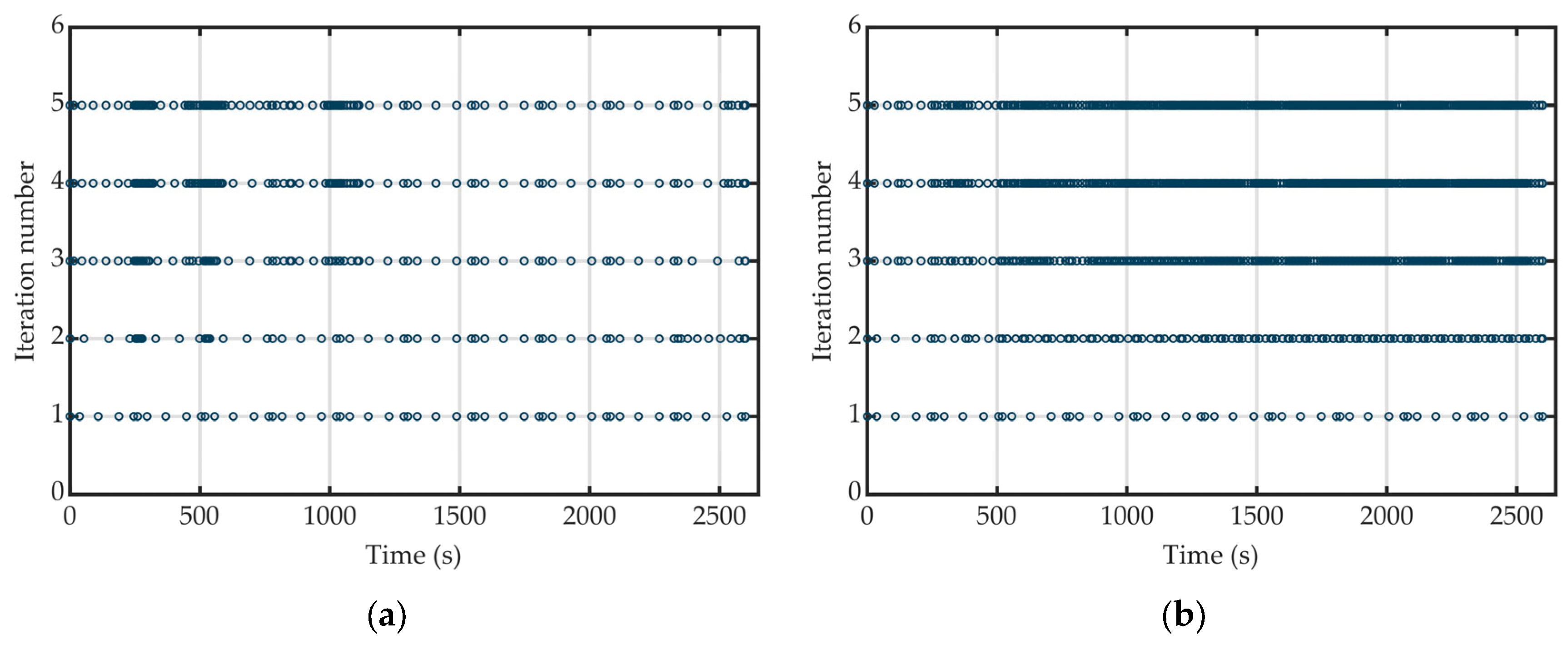
- sensitivity-based refinement (proposed),
- residual-based refinement (baseline).
- Sensitivity strategy: average 100 nodes·per iteration, total CPU time = 1.23 s.
- Residual strategy: average 334 nodes·per iteration, total CPU time = 3.86 s.
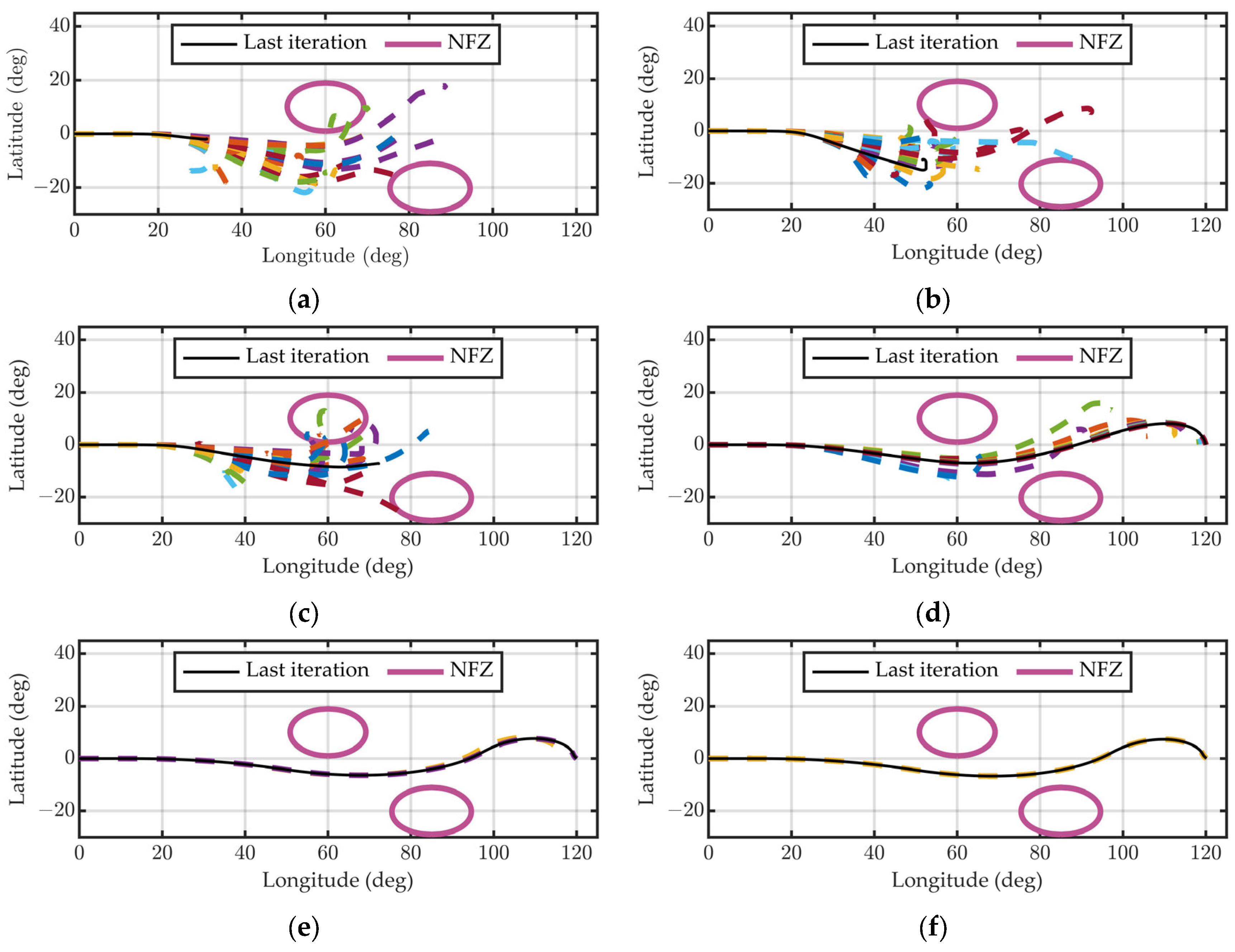
- Iterations 1–3—the coarse 50-node grid under-resolves the dynamics; integrated ground-track errors exceed 1000 km.
- Progressive refinement—as hp-adaptation concentrates points in sensitive segments, the mismatch contracts rapidly.
- Final mesh—with 181 nodes, the maximum deviations shrink to altitude = 277 m, velocity = 5.5 m/s, and RTG = 3.8 km.
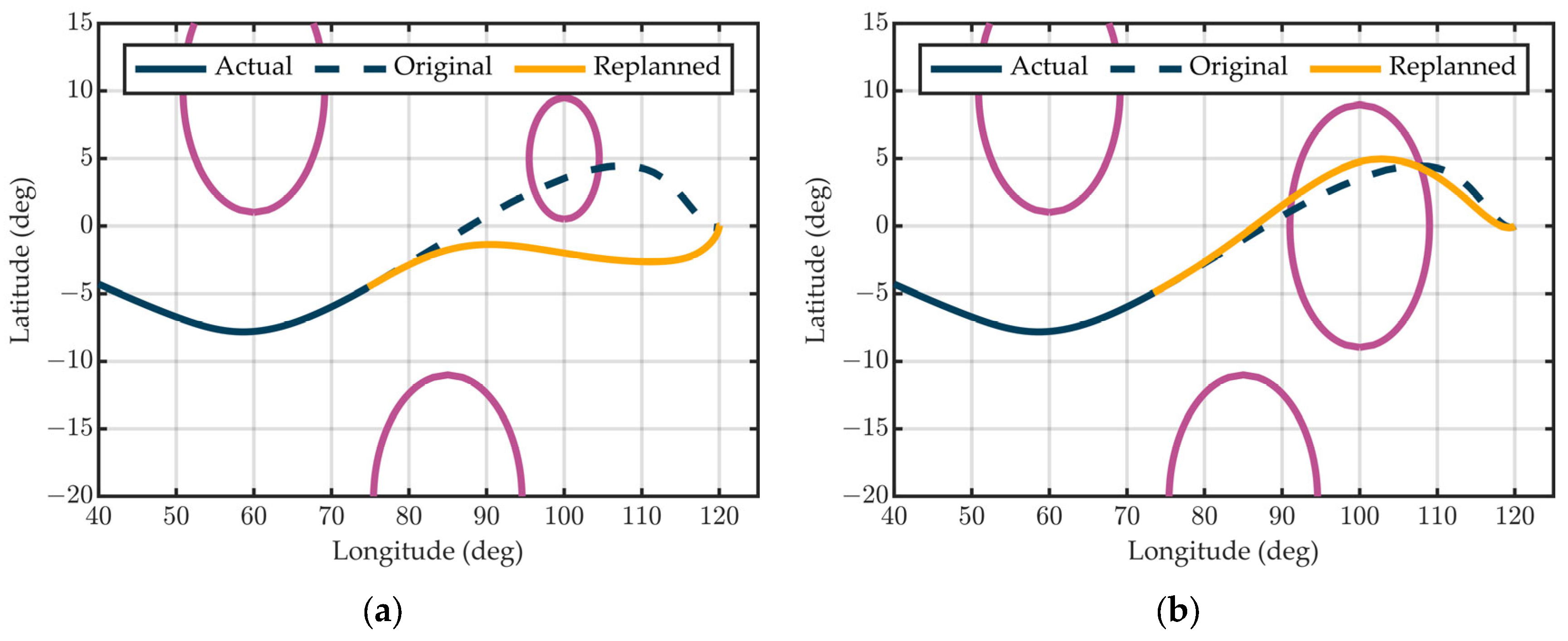
- Scenario 1—modest obstacle (Figure 9a)
- Scenario 2—large obstacle (Figure 9b)
5.4. Computational Performance and Complexity
5.5. Sensitivity Study on Initial Guess Quality
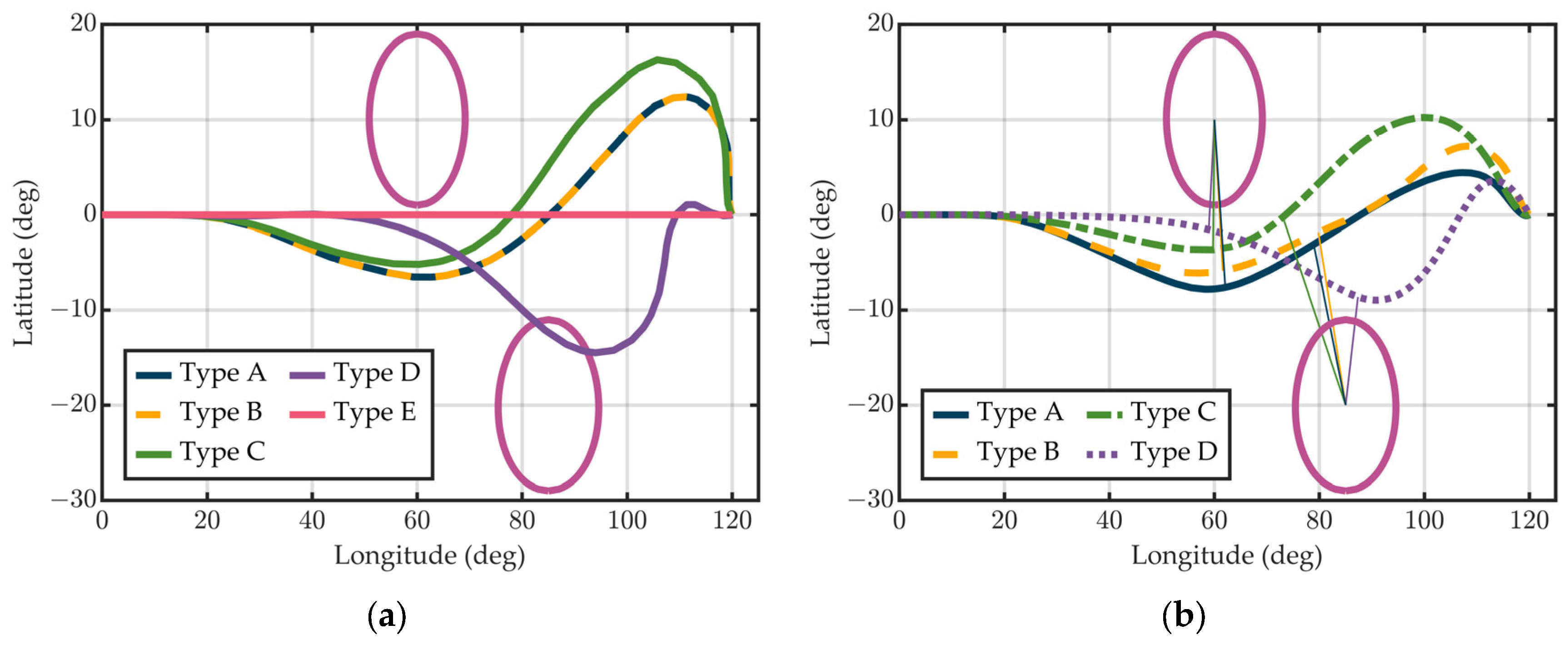
- (A)
- (B)
- Perturbed Trajectory (H + ψ): Gaussian noise added to the initial altitude and heading profile of the proposed method.
- (C)
- Perturbed Trajectory (All States): Random perturbations applied to all state variables along the trajectory.
- (D)
- Degraded Trajectory: Initialization using [39] only, without considering NFZ constraints.
- (E)
- Straight-Line Trajectory: A naively constructed trajectory by linearly interpolating all state variables from the initial point to the terminal point.
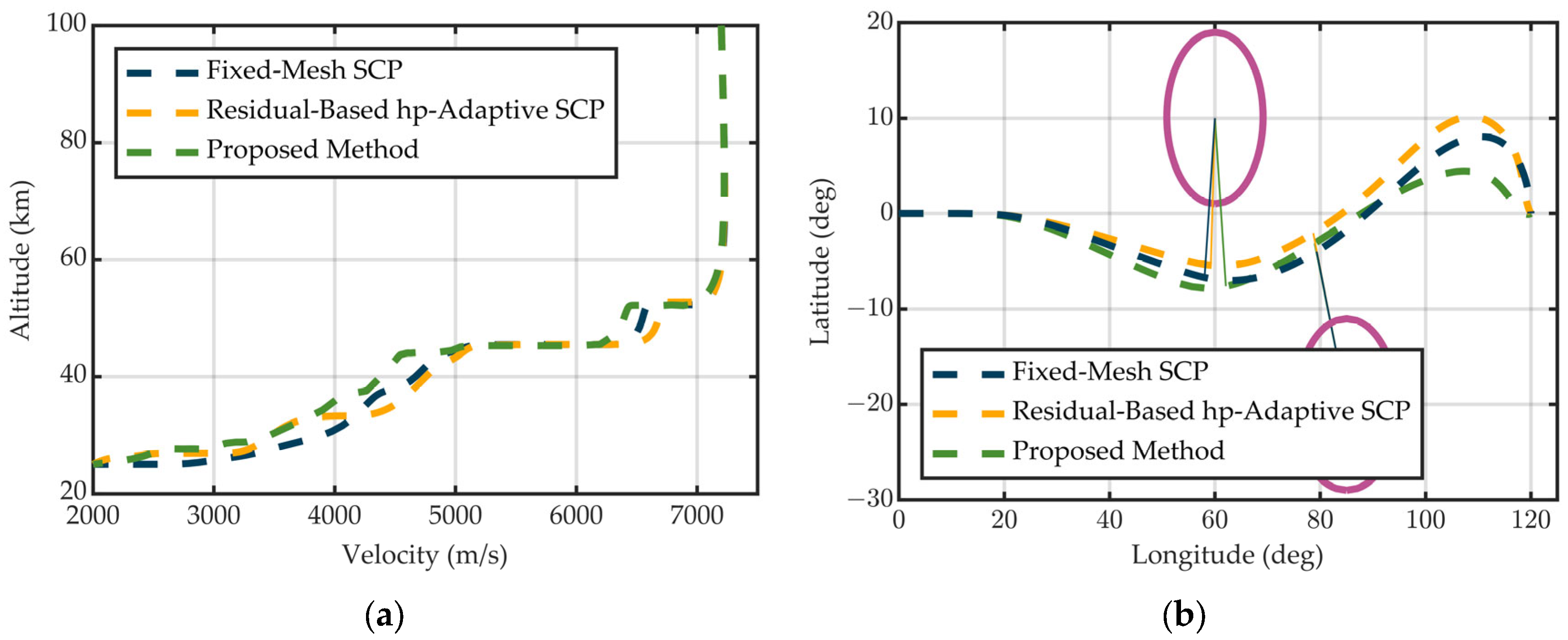
5.6. Comparison with Alternative SCP-Based Methods
- Fixed-Mesh SCP: A single-stage SCP algorithm employing a fixed pseudospectral mesh of 10 segments with 20 LGR points per segment (201 total nodes). The soft-trust-region weight is held constant at C3 = 10−2, corresponding to the moderate-penalty configuration from Section 5.2.
- Residual-Based hp-Adaptive SCP: An hp-refined variant using residual-driven mesh adaptation at all iterations. This method applies the same initial mesh and refinement logic as Phase II of our proposed method, but without separating the linearization and discretization error handling.
- Proposed Method: The two-phase strategy introduced in this paper, using sensitivity-guided refinement in Phase I and residual-driven refinement in Phase II, with dynamic trust-region weights to balance global exploration and local convergence.
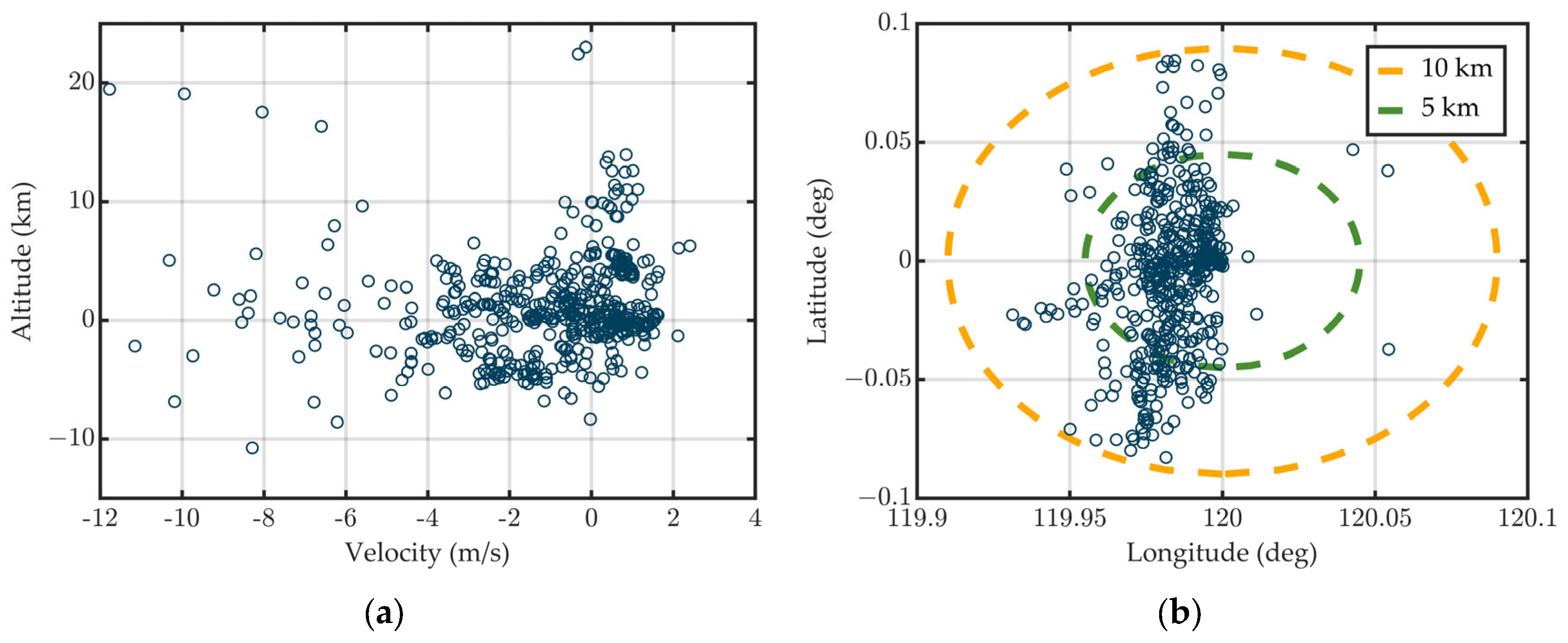
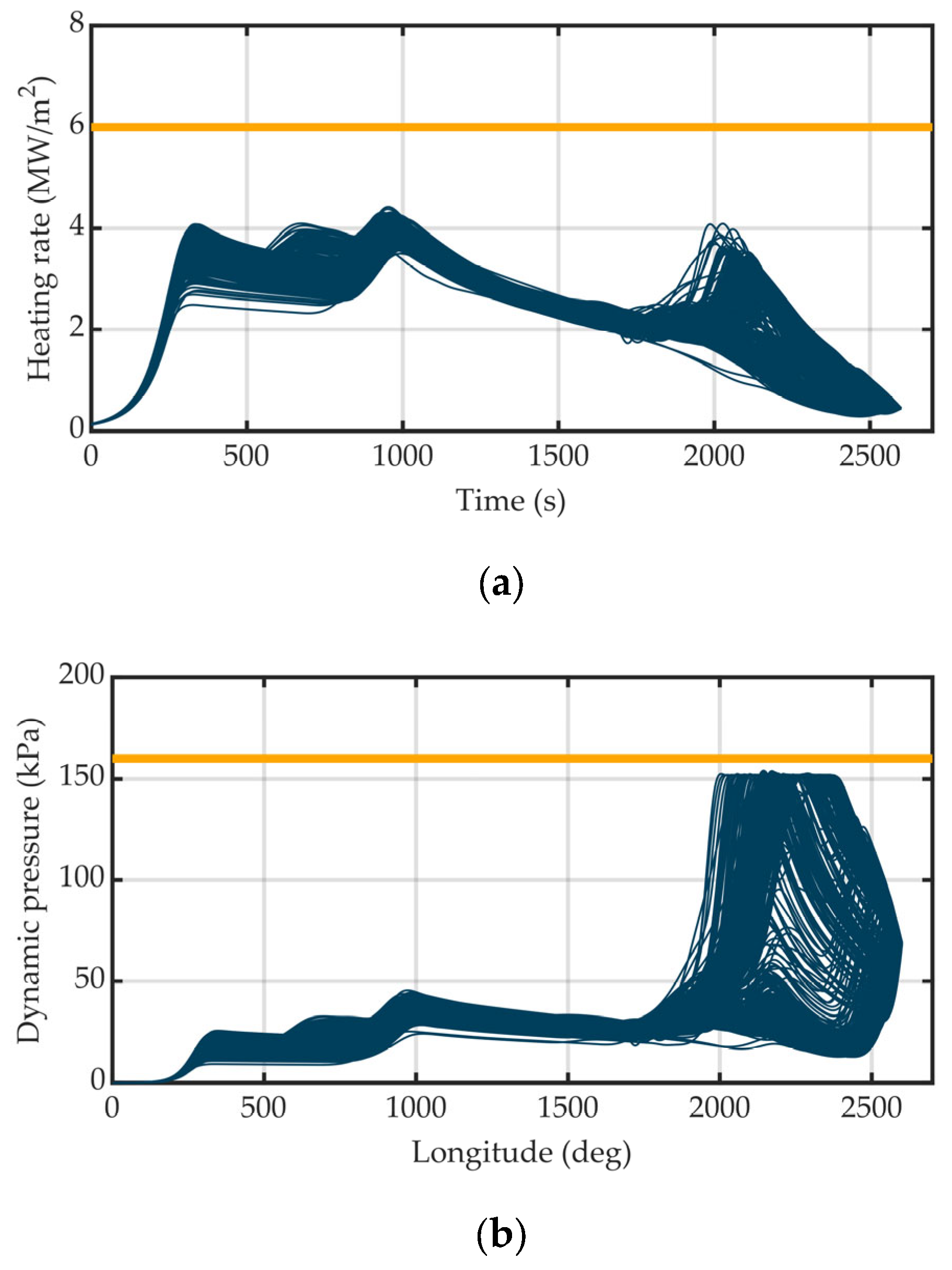
5.7. Monte Carlo Assessment with Dispersed Parameters
- Altitude ±25 m (≈0.1% of nominal).
- Velocity ±12 m/s (≈0.6% of nominal).
- Down-range ±10 km (≈0.07% of total range).
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lu, P. Entry guidance: A unified method. J. Guid. Contr. Dyn. 2014, 37, 713–728. [Google Scholar] [CrossRef]
- Yu, W.; Yang, J.; Chen, W. Entry guidance based on analytical trajectory solutions. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 2438–2466. [Google Scholar] [CrossRef]
- Guo, Y.; Li, X.; Zhang, H.; Wang, L.; Cai, M. Entry guidance with terminal time control based on quasi-equilibrium glide condition. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 887–896. [Google Scholar] [CrossRef]
- Liu, Z.; Zheng, G.; Zhang, B.; Wei, J.; Huang, H.; Yan, J. Predictor-corrector reentry guidance for hypersonic glide vehicles based on high-precision analytical solutions. Aerosp. Sci. Technol. 2024, 155, 109545. [Google Scholar] [CrossRef]
- Liang, Z.; Lv, C.; Zhu, S. Lateral entry guidance with terminal time constraint. IEEE Trans. Aerosp. Electron. Syst. 2022, 59, 2544–2553. [Google Scholar] [CrossRef]
- Wang, H.; Guo, J.; Wang, X.; Li, X.; Tang, S. Time-coordination entry guidance using a range-determined strategy. Aerosp. Sci. Technol. 2022, 129, 107842. [Google Scholar] [CrossRef]
- Yao, D.; Xia, Q. Predictor-corrector guidance for a hypersonic morphing vehicle. Aerospace 2023, 10, 795. [Google Scholar] [CrossRef]
- Dukeman, G. Profile-following entry guidance using linear quadratic regulator theory. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Monterey, CA, USA, 5–8 August 2002. [Google Scholar] [CrossRef]
- Mease, K.D.; Chen, D.T.; Teufel, P.; Schönenberger, H. Reduced-order entry trajectory planning for acceleration guidance. J. Guid. Contr. Dyn. 2002, 25, 257–266. [Google Scholar] [CrossRef]
- Guo, J.; Wu, X.; Tang, S. Autonomous gliding entry guidance with geographic constraints. Chin. J. Aeronaut. 2015, 28, 1343–1354. [Google Scholar] [CrossRef]
- Wang, X.; Guo, J.; Tang, S.; Qi, S.; Wang, Z. Entry trajectory planning with terminal full states constraints and multiple geographic constraints. Aerosp. Sci. Technol. 2019, 84, 620–631. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, Y.; Peng, S.; Tang, G.; Bao, W. Entry trajectory generation with complex constraints based on three-dimensional acceleration profile. Aerosp. Sci. Technol. 2019, 91, 231–240. [Google Scholar] [CrossRef]
- Wang, Z.; Grant, M.J. Autonomous entry guidance for hypersonic vehicles by convex optimization. J. Spacecr. Rockets 2018, 55, 993–1006. [Google Scholar] [CrossRef]
- Wu, Y.; Yao, J.; Qu, X. An adaptive reentry guidance method considering the influence of blackout zone. Acta Astronaut. 2018, 142, 253–264. [Google Scholar] [CrossRef]
- Sana, K.S.; Hu, W. Hypersonic reentry trajectory planning by using hybrid fractional-order particle swarm optimization and gravitational search algorithm. Chin. J. Aeronaut. 2021, 34, 50–67. [Google Scholar] [CrossRef]
- Kabganian, M.; Hashemi, S.M.; Roshanian, J. Multidisciplinary design optimization of a re-entry spacecraft via Radau pseudospectral method. Appl. Mechanics 2022, 3, 1176–1189. [Google Scholar] [CrossRef]
- Ma, S.; Yang, Y.; Yang, H.; Chen, W. Trajectory optimization of hypersonic vehicle considering the quasi-static assumption of pitch motion. Aerosp. Sci. Technol. 2024, 146, 108969. [Google Scholar] [CrossRef]
- Mu, L.; Cao, S.; Wang, B.; Zhang, Y.; Feng, N.; Li, X. Pseudospectral-based rapid trajectory planning and feedforward linearization guidance. Drones 2024, 8, 371. [Google Scholar] [CrossRef]
- Acikmese, B.; Ploen, S.R. Convex programming approach to powered descent guidance for Mars landing. J. Guid. Contr. Dyn. 2007, 30, 1353–1366. [Google Scholar] [CrossRef]
- Açıkmeşe, B.; Blackmore, L. Lossless convexification of a class of optimal control problems with non-convex control constraints. Automatica 2011, 47, 341–347. [Google Scholar] [CrossRef]
- Liu, X.; Shen, Z. Rapid smooth entry trajectory planning for high lift/drag hypersonic glide vehicles. J. Optim. Theory Appl. 2016, 168, 917–943. [Google Scholar] [CrossRef]
- Liu, X.; Shen, Z.; Lu, P. Solving the maximum-crossrange problem via successive second-order cone programming with a line search. Aerosp. Sci. Technol. 2015, 47, 10–20. [Google Scholar] [CrossRef]
- Liu, X.; Shen, Z.; Lu, P. Entry trajectory optimization by second-order cone programming. J. Guid. Contr. Dyn. 2016, 39, 227–241. [Google Scholar] [CrossRef]
- Wang, Z.; Grant, M.J. Constrained trajectory optimization for planetary entry via sequential convex programming. J. Guid. Contr. Dyn. 2017, 40, 2603–2615. [Google Scholar] [CrossRef]
- Zhao, D.; Song, Z. Reentry trajectory optimization with waypoint and no-fly zone constraints using multiphase convex programming. Acta Astronaut. 2017, 137, 60–69. [Google Scholar] [CrossRef]
- Xie, L.; He, R.; Zhang, H.; Tang, G. Oscillation phenomenon in trust-region-based sequential convex programming for the nonlinear trajectory planning problem. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 3337–3352. [Google Scholar] [CrossRef]
- Pei, P.; Fan, S.; Wang, W.; Lin, D. Online reentry trajectory optimization using modified sequential convex programming for hypersonic vehicle. IEEE Access 2021, 9, 23511–23525. [Google Scholar] [CrossRef]
- Wang, Z.; Lu, Y. Improved sequential convex programming algorithms for entry trajectory optimization. J. Spacecr. Rockets 2020, 57, 1373–1386. [Google Scholar] [CrossRef]
- Dong, C.; Xie, L.; He, R.; Zhang, H. Sequential convex programming without penalty function for reentry trajectory optimization problem. Acta Astronaut. 2024, 225, 402–416. [Google Scholar] [CrossRef]
- Xie, L.; Zhou, X.; Zhang, H.; Tang, G. Higher-order soft-trust-region-based sequential convex programming. J. Guid. Contr. Dyn. 2023, 46, 2199–2206. [Google Scholar] [CrossRef]
- Wang, J.; Cui, N.; Wei, C. Rapid trajectory optimization for hypersonic entry using a pseudospectral-convex algorithm. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 5227–5238. [Google Scholar] [CrossRef]
- Ma, S.; Yang, Y.; Tong, Z.; Yang, H.; Wu, C.; Chen, W. Improved sequential convex programming based on pseudospectral discretization for entry trajectory optimization. Aerosp. Sci. Technol. 2024, 152, 109349. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, J.; Jiang, J.; Liang, H. Reentry trajectory planning for hypersonic vehicles via an improved sequential convex programming method. Aerosp. Sci. Technol. 2024, 149, 109130. [Google Scholar] [CrossRef]
- Zhou, X.; He, R.; Zhang, H.; Tang, G.; Bao, W. Sequential convex programming method using adaptive mesh refinement for entry trajectory planning problem. Aerosp. Sci. Technol. 2021, 109, 106374. [Google Scholar] [CrossRef]
- Zhang, T.; Su, H.; Gong, C. Hp-adaptive RPD based sequential convex programming for reentry trajectory optimization. Aerosp. Sci. Technol. 2022, 130, 107887. [Google Scholar] [CrossRef]
- Liu, Z.; Cui, N.; Du, L.; Pu, J. Sequential convex programming for reentry trajectory optimization utilizing modified hp-adaptive mesh refinement and variable quadratic penalty. Aerospace 2024, 11, 785. [Google Scholar] [CrossRef]
- Garg, D.; Hager, W.W.; Rao, A.V. Pseudospectral methods for solving infinite-horizon optimal control problems. Automatica 2011, 47, 829–837. [Google Scholar] [CrossRef]
- Patterson, M.A.; Rao, A.V. GPOPS-II: A MATLAB software for solving multiple-phase optimal control problems using hp-adaptive Gaussian quadrature collocation methods and sparse nonlinear programming. ACM Trans. Math. Softw. 2014, 41, 1–37. [Google Scholar] [CrossRef]
- Liu, X.; Li, X.; Zhang, H.; Zhu, L.; Huang, H. Entry guidance with terminal time constraint based on reduced-order dynamics. IEEE Trans. Aerosp. Electron. Syst. 2024, in press. [Google Scholar] [CrossRef]
- Liang, Z.; Liu, S.; Li, Q.; Ren, Z. Lateral entry guidance with no-fly zone constraint. Aerosp. Sci. Technol. 2017, 60, 39–47. [Google Scholar] [CrossRef]
- Brunner, C.W.; Lu, P. Skip entry trajectory planning and guidance. J. Guid. Contr. Dyn. 2008, 31, 1210–1219. [Google Scholar] [CrossRef]
- Phillips, T.H. A common aero vehicle (CAV) model, description, and employment guide. Schafer Corp. AFRL AFSPC 2003, 27, 1–12. [Google Scholar]
- CVX: Matlab Software for Disciplined Convex Programming. Available online: https://cvxr.com/cvx (accessed on 17 May 2025).
- MOSEK ApS. MOSEK Optimization Suite (Version 10.1). Available online: https://www.mosek.com (accessed on 17 May 2025).





| State | H (km) | θ (deg) | ϕ (deg) | V (m/s) | γ (deg) | ψ (deg) | α (deg) | σ (deg) |
|---|---|---|---|---|---|---|---|---|
| x0 | 120 | 0 | 0 | 7200 | −1 | 90 | \ 1 | \ |
| xf | 25 | 120 | 0 | 2000 | \ | \ | \ | \ |
| xmin | 25 | −180 | −90 | 2000 | -5 | 0 | 5 | −80 |
| xmax | 120 | 180 | 90 | 7500 | 0 | 360 | 25 | 80 |
| NFZ No. | Center (θ, ϕ) (deg) | Radius (km) |
|---|---|---|
| NFZ 1 | (60, 10) | 1000 |
| NFZ 2 | (85, −20) | 1000 |
| Trajectory | NPC | SCP | HSCP | GPOPS |
|---|---|---|---|---|
| NFZ 1 (km) | 780.0 | 974.4 | 909.7 | 1015.2 |
| NFZ 2 (km) | 682.6 | 990.4 | 867.6 | 1015.2 |
| Initial Guess Type | Converged? | Total Iterations | Time (s) | Minimum Distance to NFZ 1 (km) | Minimum Distance to NFZ 2 (km) |
|---|---|---|---|---|---|
| (A) Proposed Method | Yes | 7 | 2.01 | 974.4 | 990.4 |
| (B) Perturbed H + ψ | Yes | 8 | 2.04 | 774.6 | 1096.2 |
| (C) Perturbed All States | Yes | 8 | 3.16 | 520.2 | 1552.7 |
| (D) Degraded (No NFZ) | Yes | 10 | 3.91 | 289.6 | 291.1 |
| (E) Straight-Line | No | – | – | – | – |
| Initial Guess Type | Max Altitude Error (m) | Max Velocity Error (m/s) | Max RTG Error (km) |
|---|---|---|---|
| (A) Proposed Method | 277 | 5.5 | 3.8 |
| (B) Perturbed H + ψ | 114 | 3.4 | 1.6 |
| (C) Perturbed All States | 292 | 11.5 | 4.5 |
| (D) Degraded (No NFZ) | 379 | 19.2 | 5.8 |
| Parameter | H0 (km) | θ0 (deg) | φ0 (deg) | V0 (m/s) | γ0 (deg) | ψ0 (deg) | m | ρ | CL | CD |
|---|---|---|---|---|---|---|---|---|---|---|
| 3-sigma | 1 | 0.5 | 0.5 | 20 | 0.1 | 0.5 | 5% | 10% | 10% | 10% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Li, X.; Zhang, H.; Huang, H.; Wu, Y. Entry Guidance for Hypersonic Glide Vehicles via Two-Phase hp-Adaptive Sequential Convex Programming. Aerospace 2025, 12, 539. https://doi.org/10.3390/aerospace12060539
Liu X, Li X, Zhang H, Huang H, Wu Y. Entry Guidance for Hypersonic Glide Vehicles via Two-Phase hp-Adaptive Sequential Convex Programming. Aerospace. 2025; 12(6):539. https://doi.org/10.3390/aerospace12060539
Chicago/Turabian StyleLiu, Xu, Xiang Li, Houjun Zhang, Hao Huang, and Yonghui Wu. 2025. "Entry Guidance for Hypersonic Glide Vehicles via Two-Phase hp-Adaptive Sequential Convex Programming" Aerospace 12, no. 6: 539. https://doi.org/10.3390/aerospace12060539
APA StyleLiu, X., Li, X., Zhang, H., Huang, H., & Wu, Y. (2025). Entry Guidance for Hypersonic Glide Vehicles via Two-Phase hp-Adaptive Sequential Convex Programming. Aerospace, 12(6), 539. https://doi.org/10.3390/aerospace12060539






