Prediction of Airfoil Icing and Evaluation of Hot Air Anti-Icing System Effectiveness Using Computational Fluid Dynamics Simulations
Abstract
1. Introduction
2. Calculation Methods and Validation Cases
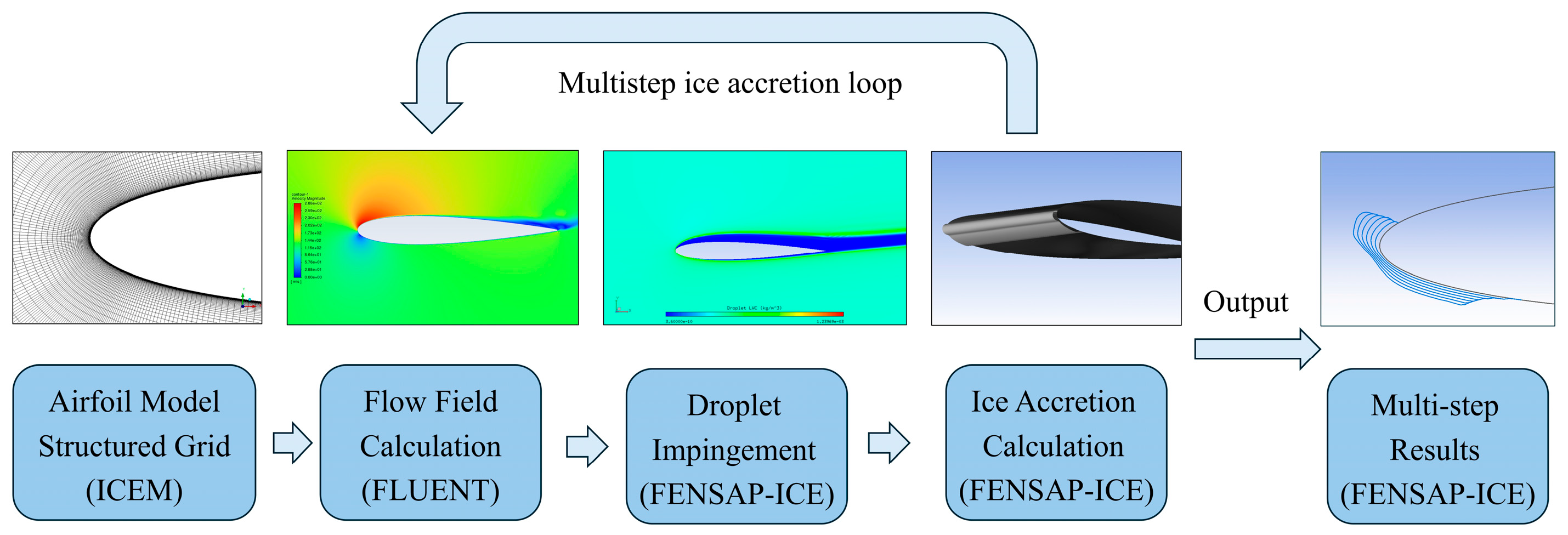
2.1. Computational Approaches
Multistep Computation
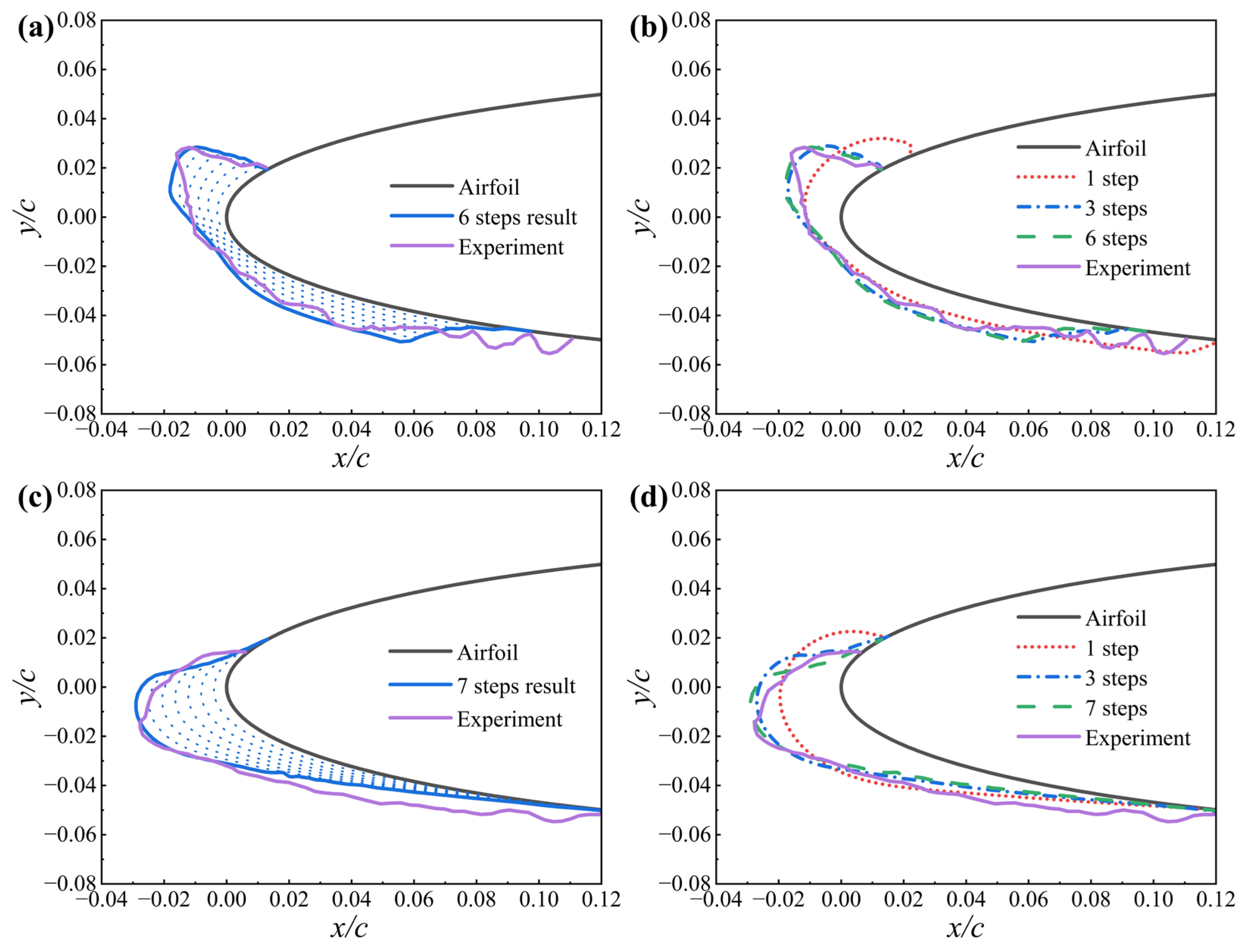
2.2. Example Analysis and Validation
3. Icing Conditions and Calculation Results
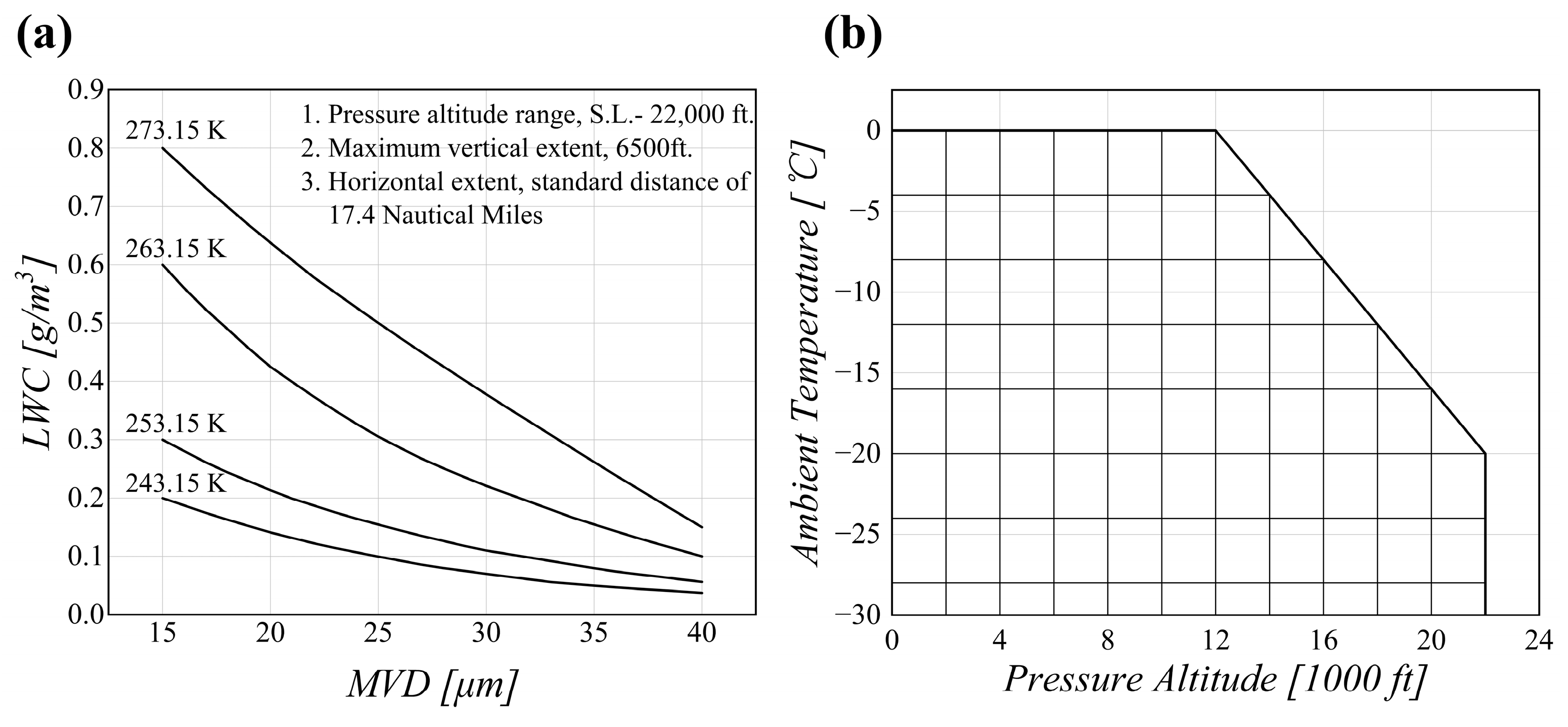
3.1. Icing Meteorological Conditions
3.2. Flight Phases and Flight Conditions
3.3. Icing Conditions for Each Flight Phase
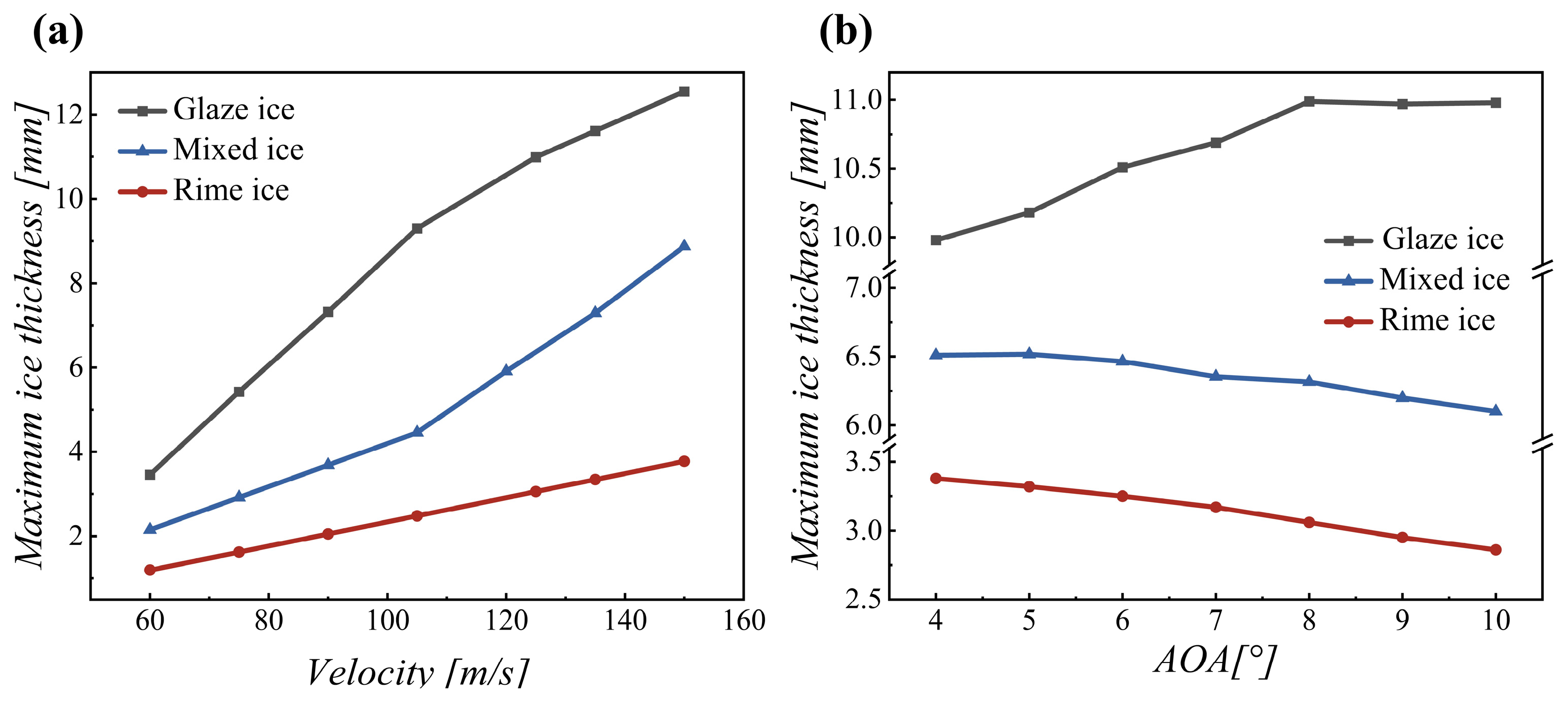
3.3.1. Influences of the Airspeed and Angle of Attack
3.3.2. Airfoil Icing Conditions
3.4. Icing Simulation Results
4. Ice Thickness Prediction Model Development and Verification
4.1. Ice Thickness Prediction Models Based on CFD Data
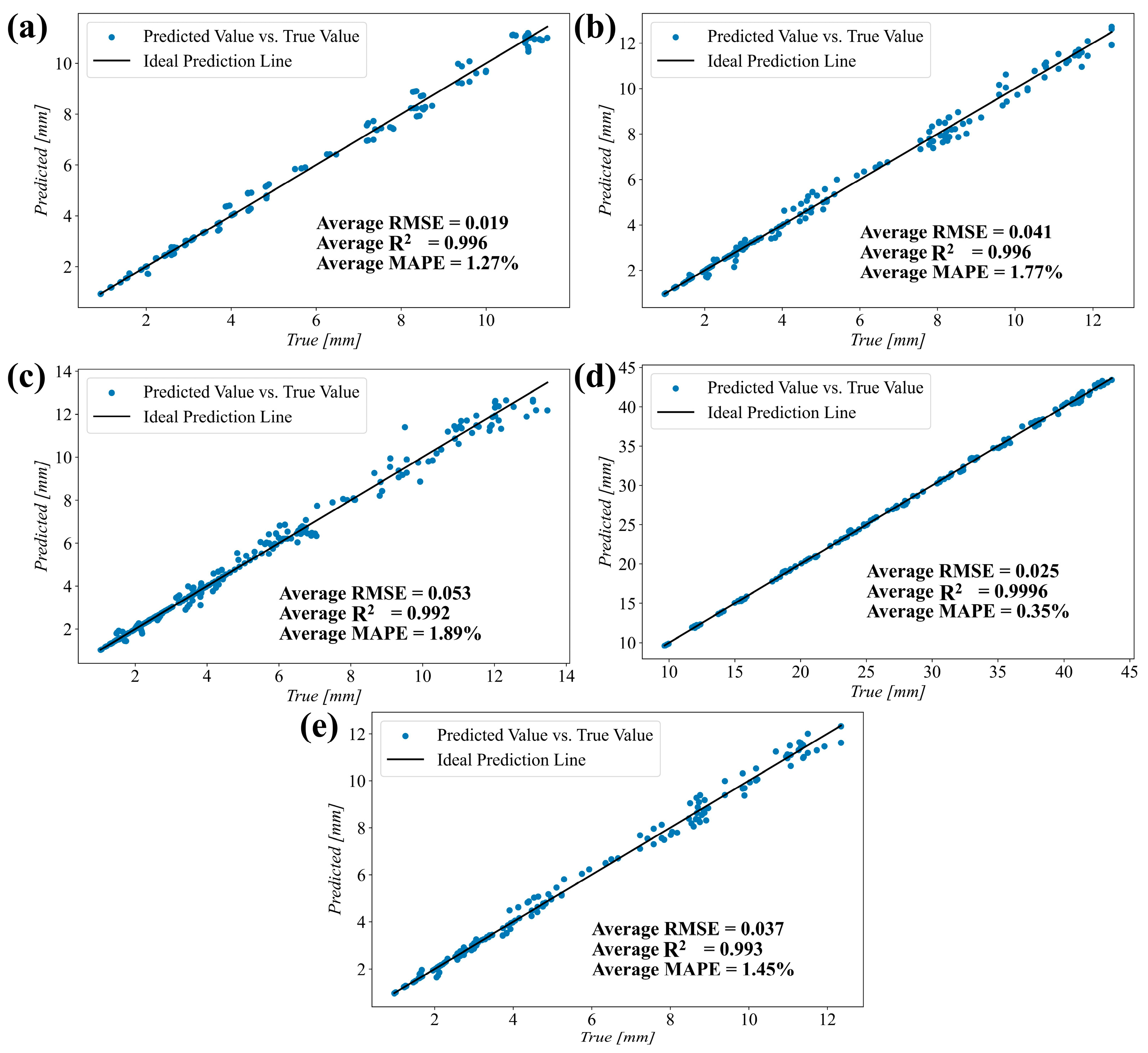
4.2. Performance Evaluation and Error Analysis
5. Piccolo Tube Hot Air Anti-Icing System
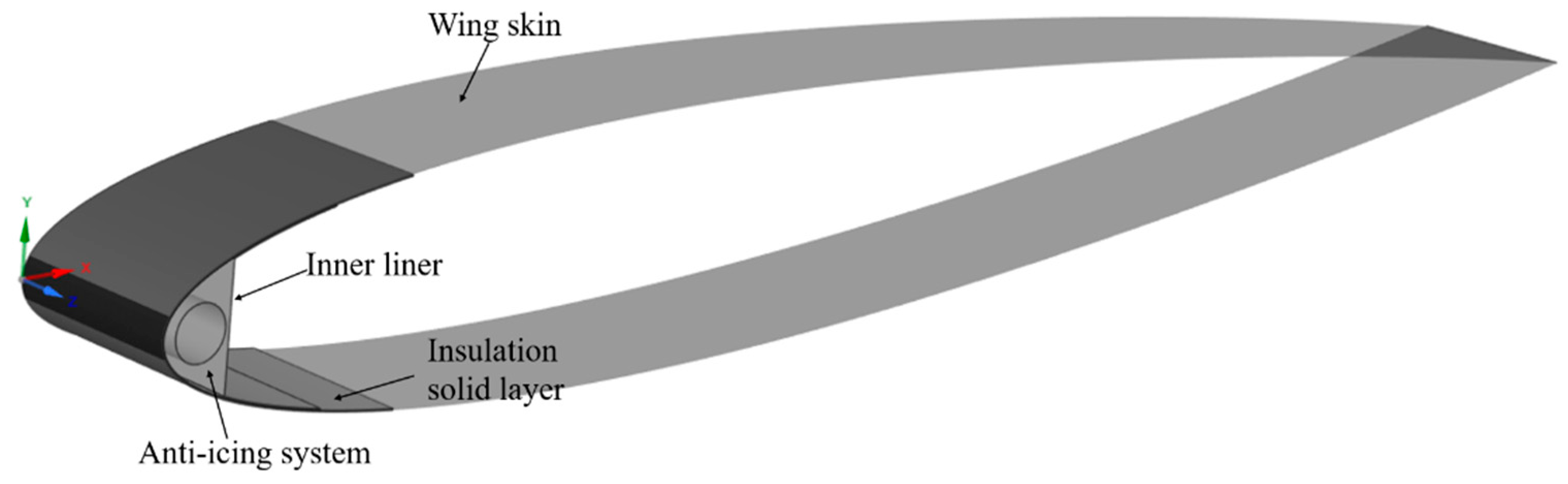
5.1. Numerical Calculation Models
5.2. Validation of the Test Case
5.3. Validation of the Effectiveness of the Anti-Icing System Under Severe Icing Conditions
5.3.1. Severe Icing Conditions
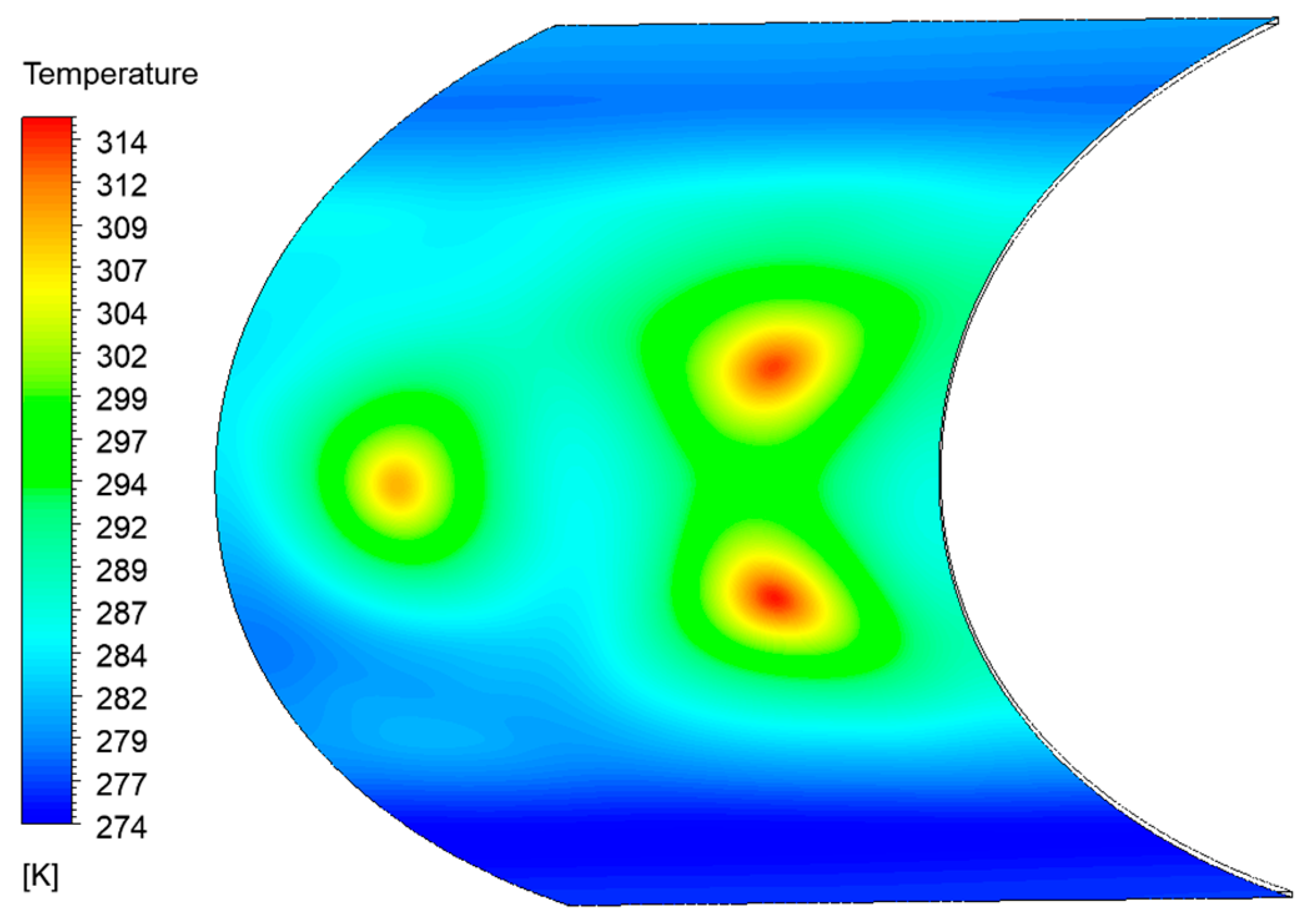
5.3.2. Calculation Results and Discussion
5.3.3. Analysis of the Effectiveness of the Anti-Icing System
6. Conclusions
- (1)
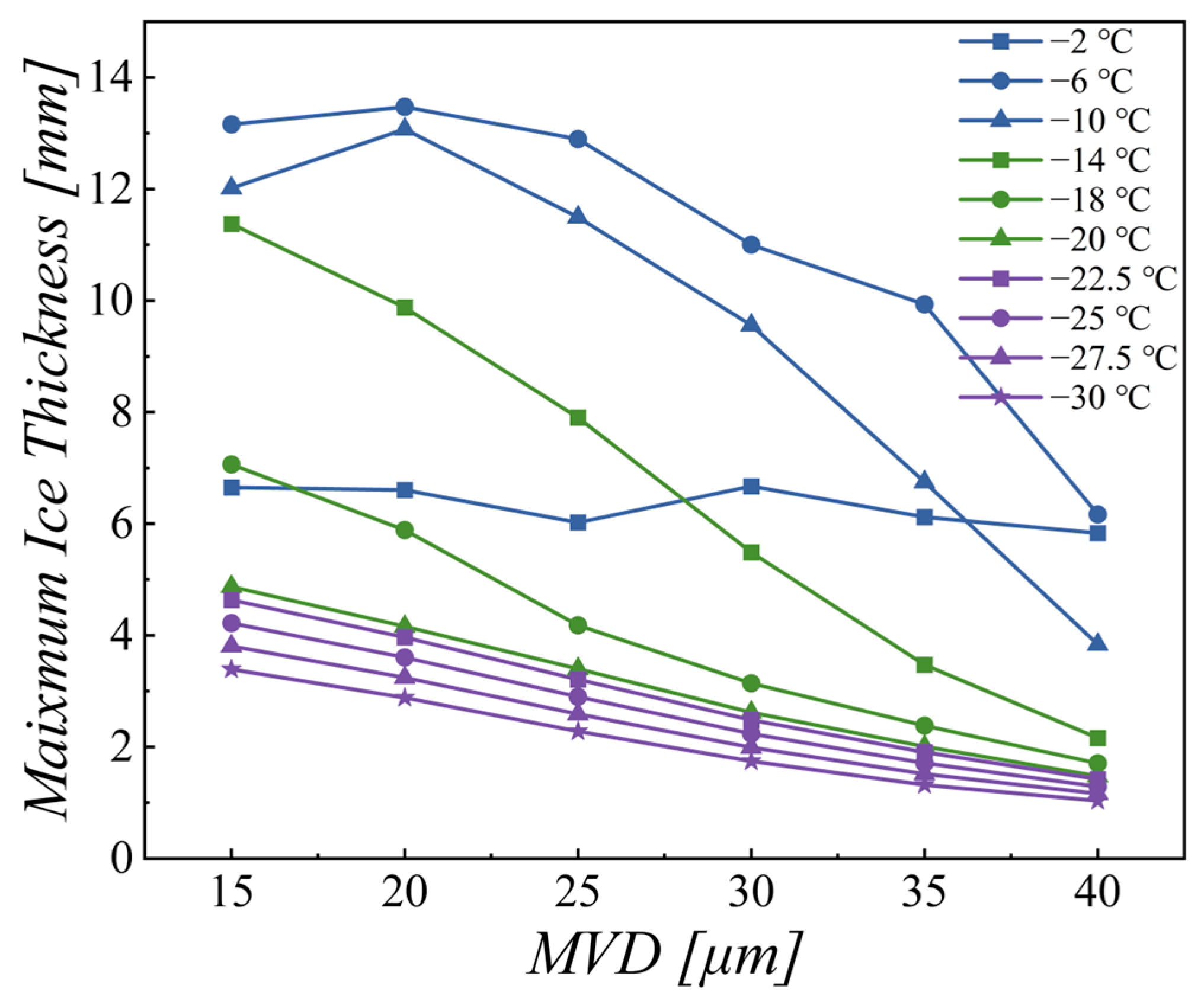
- Under a constant external airspeed and AOA, the ice shape and maximum thickness are influenced by the temperature, MVD, and LWC. The temperature primarily affects the ice shape, the MVD mainly influences the icing area, and the LWC largely influences the ice thickness. With decreasing temperature, the ice shape transitions from angular glaze ice to rime ice with a smooth surface. The icing area and thickness under glaze ice conditions are affected by both the MVD and LWC. At a temperature of −2 °C, the maximum icing area occurs at an MVD of 20 μm, and the ice thicknesses under different MVD values vary between 6 and 7 mm. At temperatures of −6 °C and −10 °C, the maximum ice thickness occurs at an MVD of 20 μm. At other temperatures, as the MVD increases, the icing area gradually increases. An increase in the MVD is associated with a decrease in the LWC, leading to a decrease in the maximum icing thickness.
- (2)
- The icing results were classified into five flight phases (takeoff, climbing below 10,000 ft, climbing above 10,000 ft, holding, and approach/landing) and three ice types (glaze ice, mixed ice, and rime ice), resulting in a total of 15 datasets. Each icing calculation was treated as an isolated event. A quadratic polynomial regression model was applied to fit 80% of the data, with the remaining 20% reserved for testing. The test results demonstrated the high accuracy of the model, with the average relative error remaining below 3%. By inputting the icing condition parameters, these models provide rapid predictions of maximum ice thickness within an acceptable error margin compared with CFD calculations.
- (3)
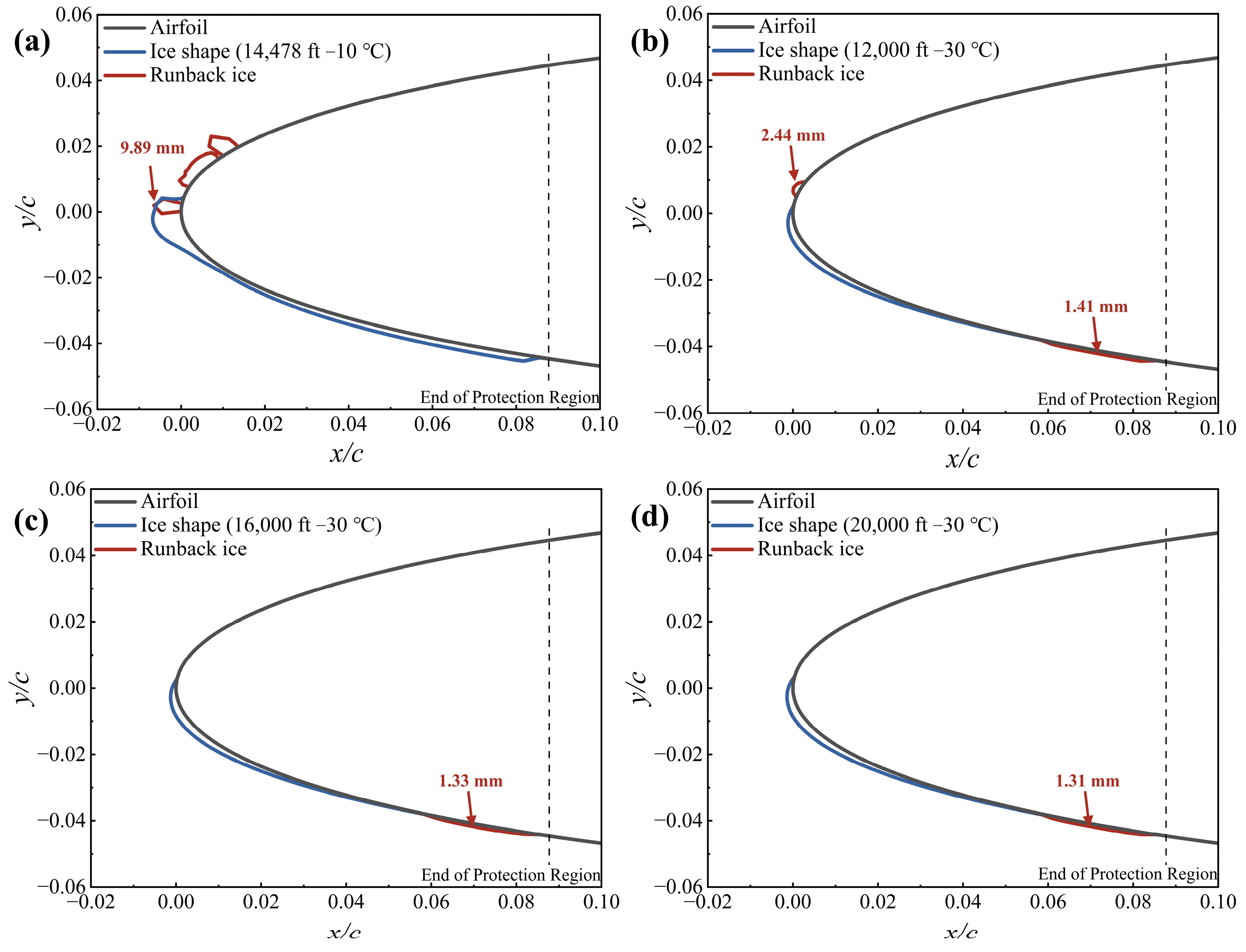
- The anti-icing performance was validated by calculating the anti-icing capability of the proposed system under the most severe external flow icing conditions. An internal hot air anti-icing system incorporating a piccolo tube structure under the airfoil skin was modeled. The most severe icing conditions occurred when the ambient temperature was lowest and the ice was thickest, with the latter conditions derived from the prediction models. The hot air anti-icing system performed effectively under most icing conditions, particularly at temperatures above −10 °C. However, at a high climbing speed of 154.3 m/s during specific phases such as the takeoff phase and prolonged exposure during the holding phase, the system may face challenges in maintaining effective anti-icing performance, resulting in runback ice with a maximum thickness exceeding 5 mm.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| y+ | Dimensionless distance to the wall |
| μt | Turbulent viscosity |
| μ | Kinetic viscosity |
| I | Turbulence intensity |
| H | Altitude |
| V∞ | Airspeed |
| T0 | Ambient temperature |
| True value | |
| Predicted value | |
| Mean of the true values | |
| Hot air mass flow rate | |
| Hot air inlet temperature | |
| mu | Unheated total ice mass |
| mh | Heated total ice mass |
Abbreviations
| CFD | Computational fluid dynamics |
| CHT | Conjugate heat transfer |
| LWC | Liquid water content |
| MVD | Median volumetric diameter |
| FAR | Federal Aviation Regulation |
| RANS | Reynolds-averaged Navier–Stokes equation |
| SST | Shear stress transport |
| AOA | Angle of attack |
| ICAO | International Civil Aviation Organization |
| MSE | Mean square error |
| MAPE | Mean absolute percentage error |
Appendix A
Appendix A.1. Polynomial Regression
Appendix A.2. Polynomial Coefficient Data
| Flight Phase | Ice Type | 1 | x1 | x2 | x3 | x4 |
|---|---|---|---|---|---|---|
| Takeoff | Glaze | 384.4159 | 0.7945 | 12.1233 | −14.007 | −707.3222 |
| Mixed | 14.0647 | 0.2289 | 2.0822 | 0.4305 | 121.8727 | |
| Rime | 1.5975 | −0.032 | −0.1422 | −0.1609 | 19.1868 | |
| Climbing below 10,000 ft | Glaze | 303.3042 | 0.228 | 8.2574 | −11.0277 | −549.6192 |
| Mixed | 15.4574 | −0.095 | 2.7835 | 0.8029 | 152.1168 | |
| Rime | 1.0561 | 0.0054 | −0.1391 | −0.1352 | 20.9728 | |
| Climbing above 10,000 ft | Glaze | 193.5477 | −2.5864 | 3.3641 | −5.5387 | −294.6683 |
| Mixed | 125.972 | −0.0726 | 7.358 | −2.2136 | −66.1643 | |
| Rime | 4.1092 | 0.0122 | −0.0593 | −0.1958 | 18.2349 | |
| Holding | Glaze | 211.381 | 0.1236 | 5.2253 | −6.788 | −362.0233 |
| Mixed | 114.4934 | −0.0839 | 1.5344 | −3.0998 | −140.5761 | |
| Rime | 45.6082 | 0.0763 | −0.4387 | −2.1194 | 3.2703 | |
| Approach and landing | Glaze | 359.8611 | 0.3235 | 11.4168 | −13.0325 | −666.1164 |
| Mixed | 55.5489 | −0.1298 | 3.7192 | −0.7565 | 52.2447 | |
| Rime | 1.0434 | 0.005 | −0.1415 | −0.1377 | 20.8362 |
| Flight Phase | Ice Type | ||||
|---|---|---|---|---|---|
| Takeoff | Glaze | −0.0018 | 0.0288 | 0.1264 | 328.8846 |
| Mixed | 0.0081 | 0.0285 | −0.0131 | −90.5186 | |
| Rime | 0.0012 | −0.0022 | 0.0019 | −20.8271 | |
| Climbing below 10,000 ft | Glaze | −0.0003 | −0.005 | 0.0999 | 252.4877 |
| Mixed | 0.0042 | 0.0336 | −0.0209 | −117.2068 | |
| Rime | 0 | −0.0021 | 0.0016 | −20.1184 | |
| Climbing above 10,000 ft | Glaze | 0.1095 | −0.0941 | 0.0395 | 131.4334 |
| Mixed | −0.0003 | 0.0688 | −0.001 | −8.8369 | |
| Rime | −0.0001 | −0.0018 | 0.0018 | −18.3447 | |
| Holding | Glaze | 0.0001 | 0.0125 | 0.0541 | 158.1472 |
| Mixed | −0.0018 | −0.0386 | 0.017 | 41.3202 | |
| Rime | −0.0005 | −0.015 | 0.0208 | −54.4345 | |
| Approach and landing | Glaze | −0.0037 | 0.028 | 0.1168 | 310.9552 |
| Mixed | 0.0022 | 0.038 | −0.0058 | −58.2327 | |
| Rime | 0 | −0.0022 | 0.0017 | −20.2136 |
| Flight Phase | Ice Type | ||||||
|---|---|---|---|---|---|---|---|
| Takeoff | Glaze | 0.0005 | −0.017 | −0.7545 | −0.2403 | −12.9427 | 13.1868 |
| Mixed | 0.0024 | −0.0051 | −0.1582 | −0.0292 | 1.4258 | −2.7716 | |
| Rime | −0.0005 | 0.0004 | 0.1994 | 0.0002 | 0.5854 | 0.4797 | |
| Climbing below 10,000 ft | Glaze | −0.0041 | −0.0047 | −0.1257 | −0.1631 | −9.3107 | 10.2246 |
| Mixed | 0.0023 | 0.0014 | 0.4366 | −0.0407 | 1.12 | −4.0122 | |
| Rime | 0.0001 | −0.0001 | 0.1126 | 0.0003 | 0.5264 | 0.4123 | |
| Climbing above 10,000 ft | Glaze | 0.0495 | −0.0010 | −0.1862 | −0.0961 | −5.7943 | 4.2874 |
| Mixed | −0.0074 | −0.0014 | 0.0649 | −0.1096 | −4.3194 | −1.4623 | |
| Rime | 0.0001 | −0.0002 | 0.101 | −0.0009 | 0.4602 | 0.2757 | |
| Holding | Glaze | 0.0155 | −0.0001 | 0.3749 | −0.1004 | −6.1764 | 8.4468 |
| Mixed | −0.0072 | 0.0008 | 0.3468 | −0.046 | −2.6114 | 3.6869 | |
| Rime | −0.0004 | −0.0018 | 0.6548 | −0.0081 | 2.3469 | 5.5221 | |
| Approach and landing | Glaze | 0.001 | −0.0056 | −0.2068 | −0.2245 | −12.3401 | 12.4056 |
| Mixed | −0.0004 | 0.0023 | 0.3918 | −0.0591 | −0.1521 | −2.1118 | |
| Rime | 0.0001 | −0.0001 | 0.1135 | 0.0003 | 0.5312 | 0.4285 |
Appendix B
Appendix C



References
- Gent, R.W.; Dart, N.P.; Cansdale, J.T. Aircraft icing. Phil. Trans. R. Soc. A 2000, 358, 2873–2911. [Google Scholar] [CrossRef]
- Bragg, M.B.; Broeren, A.P.; Blumenthal, L.A. Iced-airfoil aerodynamics. Prog. Aerosp. Sci. 2005, 41, 323–362. [Google Scholar] [CrossRef]
- Lampton, A.; Valasek, J. Prediction of icing effects on the lateral/directional stability and control of light airplanes. Aerosp. Sci. Technol. 2012, 23, 305–311. [Google Scholar] [CrossRef]
- Xie, L.; Liang, H.; Zong, H.; Liu, X.; Li, Y. Multipurpose distributed dielectric-barrier-discharge plasma actuation: Icing sensing, anti-icing, and flow control in one. Phys. Fluids 2022, 34, 071701. [Google Scholar] [CrossRef]
- Su, Q.; Chang, S.; Song, M.; Zhao, Y.; Dang, C. An experimental study on the heat transfer performance of a loop heat pipe system with ethanol-water mixture as working fluid for aircraft anti-icing. Int. J. Heat Mass Transf. 2019, 139, 280–292. [Google Scholar] [CrossRef]
- Dong, W.; Zheng, M.; Zhu, J.; Lei, G.; Zhao, Q. Experimental investigation on anti-icing performance of an engine inlet strut. J. Propuls. Power 2017, 33, 379–386. [Google Scholar] [CrossRef]
- Cao, Y.; Ma, C.; Zhang, Q.; Sheridan, J. Numerical simulation of ice accretions on an aircraft wing. Aerosp. Sci. Technol. 2012, 23, 296–304. [Google Scholar] [CrossRef]
- Janjua, Z.A.; Turnbull, B.; Hibberd, S.; Choi, K. Mixed ice accretion on aircraft wings. Phys. Fluids 2018, 30, 270101. [Google Scholar] [CrossRef]
- Addy, H.E.; Potapczuk, M.G., Jr.; Sheldon, D.W. Modern airfoil ice accretions. In Proceedings of the 35th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1997. AIAA Paper 97-0174. [Google Scholar] [CrossRef]
- Shin, J.; Bond, T.H. Results of an icing test on a NACA 0012 airfoil in the NASA Lewis icing research tunnel. In Proceedings of the 30th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992; p. 647. [Google Scholar] [CrossRef]
- Bowden, D.T.; Gensemer, A.G.; Sheen, C.A. Engineering Summary of Airframe Icing Technical Data; FAA Technical Report ADS-4; Federal Aviation Administration: Washington, DC, USA, 1963.
- Messinger, B.L. Equilibrium temperature of an unheated icing surface as a function of air speed. J. Aeronaut. Sci. 1953, 20, 29–42. [Google Scholar] [CrossRef]
- Myers, T.G. Extension to the Messinger model for aircraft icing. AIAA J. 2001, 39, 211–218. [Google Scholar] [CrossRef]
- Hedde, T.; Guffond, D. ONERA three-dimensional icing model. AIAA J. 1995, 33, 1038–1045. [Google Scholar] [CrossRef]
- Szilder, K.; Lozowski, E.P. Simulation of airfoil icing with a novel morphogenetic model. J. Aerosp. Eng. 2005, 18, 102–110. [Google Scholar] [CrossRef]
- Prince Raj, L.; Lee, J.W.; Myong, R.S. Ice accretion and aerodynamic effects on a multi-element airfoil under SLD icing conditions. Aerosp. Sci. Technol. 2019, 85, 320–333. [Google Scholar] [CrossRef]
- Lynch, F.T.; Khodadoust, A. Effects of ice accretion on aircraft aerodynamics. Prog. Aerosp. Sci. 2001, 37, 669–767. [Google Scholar] [CrossRef]
- Miranda, L.R.; Elliott, R.D.; Baker, W.M. A Generalized Vortex Lattice Method for Subsonic and Supersonic Flow Applications; NASA Contractor Report 2865; NASA: Washington, DC, USA, 1977.
- Erickson, L.L. Panel Methods: An Introduction; NASA Technical Paper 2995; NASA: Washington, DC, USA, 1990.
- Boelens, O.J. CFD analysis of the flow around the X-31 aircraft at high angle of attack. Aerosp. Sci. Technol. 2012, 20, 38–51. [Google Scholar] [CrossRef]
- Durst, F.; Miloievic, D.; Schönung, B. Eulerian and Lagrangian predictions of particulate two-phase flows: A numerical study. Appl. Math. Model. 1984, 8, 101–115. [Google Scholar] [CrossRef]
- Ghenai, C.; Lin, C.X. Verification and validation of NASA LEWICE 2.2 icing software code. J. Aircr. 2006, 43, 1253–1258. [Google Scholar] [CrossRef]
- Trontin, P.; Kontogiannis, A.; Blanchard, G.; Villedieu, P. Description and assessment of the new ONERA 2D icing suite IGLOO2D. In Proceedings of the 9th AIAA Atmospheric and Space Environments Conference, Denver, CO, USA, 5–9 June 2017; p. 3417. [Google Scholar] [CrossRef]
- Aliaga, C.N.; Aubé, M.S.; Baruzzi, G.S.; Habashi, W.G. FENSAP-ICE-Unsteady: Unified in-flight icing simulation methodology for aircraft, rotorcraft, and jet engines. J. Aircr. 2011, 48, 119–126. [Google Scholar] [CrossRef]
- Fossati, M.; Habashi, W.G. Multiparameter analysis of aero-icing problems using proper orthogonal decomposition and multidimensional interpolation. AIAA J. 2013, 51, 946–960. [Google Scholar] [CrossRef]
- Xia, Y.; Li, T.; Wang, Q.; Yue, J.; Peng, B.; Yi, X. A rapid prediction method for water droplet collection coefficients of multiple airfoils based on incremental learning and multi-modal dynamic fusion. Phys. Fluids 2024, 36, 103313. [Google Scholar] [CrossRef]
- Strijhak, S.; Ryazanov, D.; Koshelev, K.; Ivanov, A. Neural network prediction for ice shapes on airfoils using icefoam simulations. Aerospace 2022, 9, 96. [Google Scholar] [CrossRef]
- Federal Aviation Administration. Part 25-Airworthiness Standards: Transport Category Airplanes; Federal Aviation Regulations; Federal Aviation Administration: Washington, DC, USA, 2013.
- Massegur, D.; Clifford, D.; Da Ronch, A.; Lombardi, R.; Panzeri, M. Low-dimensional models for aerofoil icing predictions. Aerospace 2023, 10, 444. [Google Scholar] [CrossRef]
- Li, S.; Qin, J.; He, M.; Paoli, R. Fast evaluation of aircraft icing severity using machine learning based on XGBoost. Aerospace 2020, 7, 36. [Google Scholar] [CrossRef]
- Yang, Q.; Zheng, H.; Guo, X.; Dong, W. Experimental validation and tightly coupled numerical simulation of hot air anti-icing system based on an extended mass and heat transfer model. Int. J. Heat Mass Transf. 2023, 217, 124645. [Google Scholar] [CrossRef]
- Silva, G.; Silvares, O.; Zerbini, E. Airfoil anti-ice system modeling and simulation. In Proceedings of the 41st AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 2003; p. 734. [Google Scholar] [CrossRef]
- Yang, Q.; Guo, X.; Zheng, H.; Dong, W. Single-and multi-objective optimization of an aircraft hot-air anti-icing system based on Reduced Order Method. Appl. Therm. Eng. 2023, 219, 119543. [Google Scholar] [CrossRef]
- Abdelghany, E.S.; Farghaly, M.B.; Almalki, M.M.; Sarhan, H.H.; Essa, M.E.-S.M. Machine Learning and IoT Trends for Intelligent Prediction of Aircraft Wing Anti-Icing System Temperature. Aerospace 2023, 10, 676. [Google Scholar] [CrossRef]
- Lee, J.; Jo, H.; Choe, H.; Lee, D.; Jeong, H.; Lee, H.; Kweon, J.; Lee, H.; Myong, R.S.; Nam, Y. Electro-thermal heating element with a nickel-plated carbon fabric for the leading edge of a wing-shaped composite application. Compos. Struct. 2022, 289, 115510. [Google Scholar] [CrossRef]
- Jung, S.K.; Prince Raj, L.; Rahimi, A.; Jeong, H.; Myong, R.S. Performance evaluation of electrothermal anti-icing systems for a rotorcraft engine air intake using a meta model. Aerosp. Sci. Technol. 2020, 106, 106174. [Google Scholar] [CrossRef]
- Shin, J.; Bond, T.H. Experimental and Computational Ice Shapes and Resulting Drag Increase for a NACA 0012 Airfoil; National Aeronautics and Space Administration: Washington, DC, USA, 1992.
- Fortin, G.; Ilinca, A.; Laforte, J.L.; Brandi, V. Prediction of 2D airfoil ice accretion by bisection method and by rivulets and beads modeling. In Proceedings of the 41st AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 2003; p. 1076. [Google Scholar] [CrossRef]
- Airbus Customer Services. Getting to Grips with Aircraft Performance; Flight Operations Support & Line Assistance; Airbus S.A.S.: Toulouse, France, 2002. [Google Scholar]
- International Civil Aviation Organization. 8168 OPS/611 Aircraft Operations: Procedures for Air Navigation Services-Volume II Construction of Visual and Instrument Flight Procedures; ICAO: Montréal, QC, Canada, 2006. [Google Scholar]
- Cao, Y.; Tan, W.; Wu, Z. Aircraft icing: An ongoing threat to aviation safety. Aerosp. Sci. Technol. 2018, 75, 353–385. [Google Scholar] [CrossRef]
- Cao, Y.; Yuan, K.; Li, G. Effects of ice geometry on airfoil performance using neural networks prediction. Aircr. Eng. Aerosp. Technol. 2011, 83, 266–274. [Google Scholar] [CrossRef]
- Wright, W. An evaluation of jet impingement heat transfer correlations for piccolo tube application. In Proceedings of the 42nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 5–8 January 2004; p. 62. [Google Scholar] [CrossRef]
- Hannat, R.; Morency, F. Numerical validation of conjugate heat transfer method for anti-/de-icing piccolo system. J. Aircr. 2014, 51, 104–116. [Google Scholar] [CrossRef]
- Papadakis, M.; Wong, S.H.; Yeong, H.W.; Wong, S.C.; Vu, G. Icing tunnel experiments with a hot air anti-icing system. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008; p. 444. [Google Scholar] [CrossRef]
- Guo, Z.; Zheng, M.; Yang, Q.; Guo, X.; Dong, W. Effects of flow parameters on thermal performance of an inner-liner anti-icing system with jets impingement heat transfer. Chin. J. Aeronaut. 2021, 34, 119–132. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, J. Influence of environment parameters on anti-icing heat load for aircraft. J. Aerosp. Power 2021, 36, 8–14. [Google Scholar] [CrossRef]
- Mısır, O.; Akar, M. Efficiency and core loss map estimation with machine learning based multivariate polynomial regression model. Mathematics 2022, 10, 3691. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- Chen, N.; Ji, H.; Cao, G.; Hu, Y. A three-dimensional mathematical model for simulating ice accretion on helicopter rotors. Phys. Fluids 2018, 30, 083602. [Google Scholar] [CrossRef]
- Nwachukwu, A.; Jeong, H.; Pyrcz, M.; Lake, L.W. Fast evaluation of well placements in heterogeneous reservoir models using machine learning. J. Petrol. Sci. Eng. 2018, 163, 463–475. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, C.; Zhang, H.; Li, Y.; Wang, L. Prediction of undrained shear strength using extreme gradient boosting and random forest based on Bayesian optimization. Geosci. Front. 2021, 12, 469–477. [Google Scholar] [CrossRef]


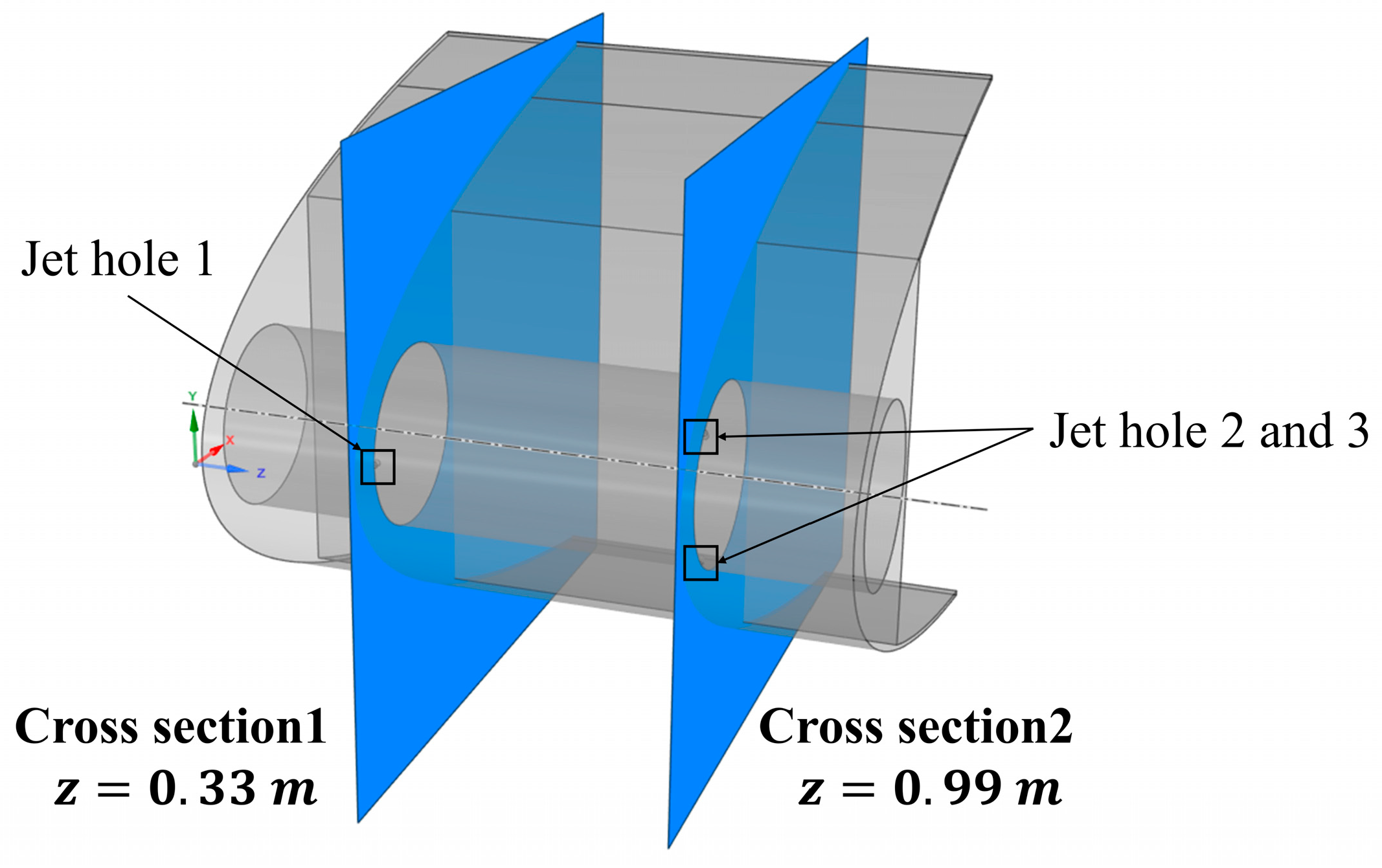
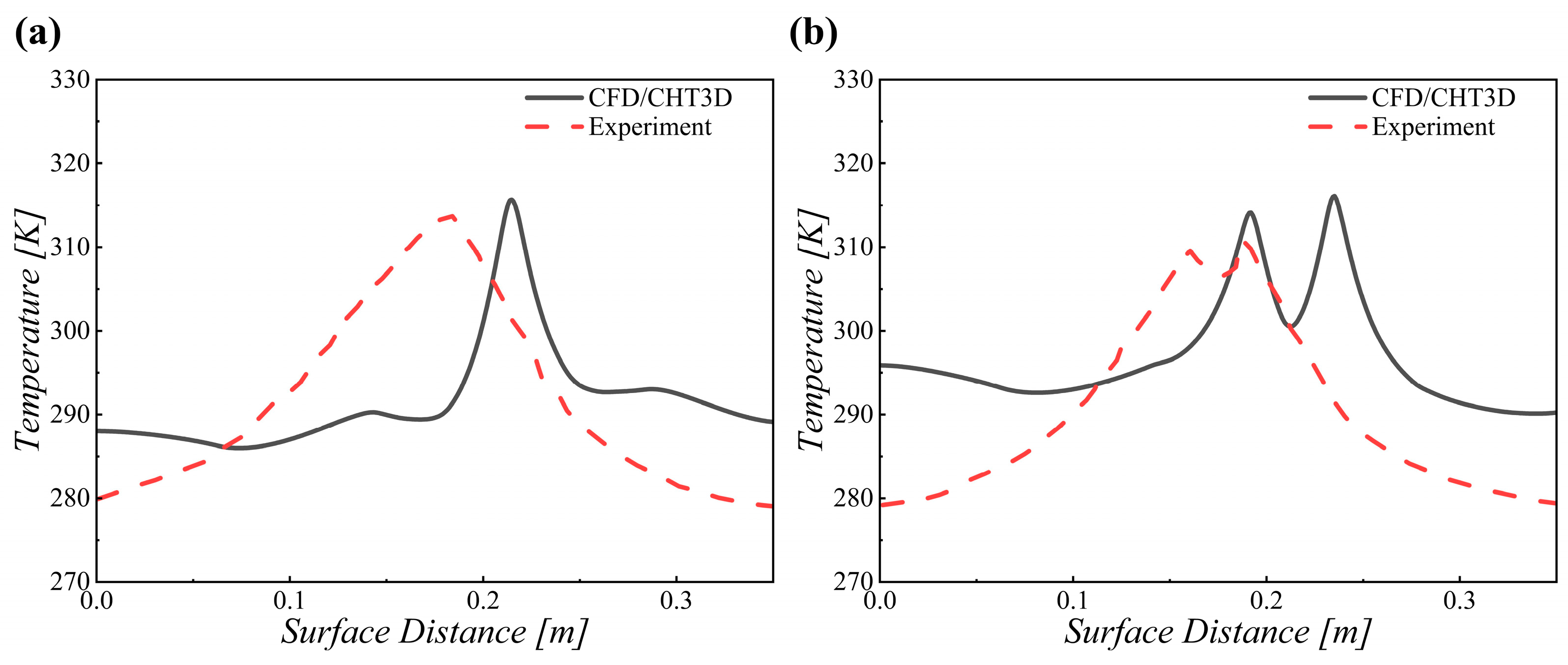
| Case | AOA (°) | (m/s) | LWC (g/m3) | MVD (μm) | (°C) |
|---|---|---|---|---|---|
| 1 | 4.0 | 67.05 | 1.0 | 20 | −2.22 |
| 2 | 4.0 | 102.82 | 0.55 | 20 | −26.11 |
| Flight Phase | Altitude (ft) | Airspeed (m/s) |
|---|---|---|
| Takeoff | ||
| Climbing below 10,000 ft | ||
| Climbing above 10,000 ft | ||
| Holding | ||
| Approach and landing | (initial approach) (final approach) (landing) |
| Flight Phase | (1000 ft) | (m/s) | (°C) | (μm) | (g/m3) | (s) |
|---|---|---|---|---|---|---|
| Takeoff | 0, 0.75, 1.5 | 125 | −2, −6, −10 | 15 20 25 30 35 40 | Determined on the basis of temperature and MVD in the continuous maximum icing envelope | 258 |
| 0, 0.75, 1.5 | −10, −14, −18 | |||||
| 0, 0.75, 1.5 | −20, −25, −30 | |||||
| Climbing below 10,000 ft | 1.5, 5.5, 9.5 1.5, 5.5, 9.5 1.5, 5.5, 9.5 | 128.6 | −2, −6, −10 −10, −14, −18 −20, −25, −30 | 250 | ||
| Climbing above 10,000 ft | 11, 12, 13 11, 14, 17 12, 16, 20 | 154.3 | −2, −6, −10 −10, −14, −18 −20, −25, −30 | 210 | ||
| Holding | 11, 12, 13 | 136.3 | −2, −6, −10 | 2700 | ||
| 11, 14, 17 | −10, −14, −18 | |||||
| 12, 17, 22 | −20, −25, −30 | |||||
| Approach and landing | 2, 6, 10 | 123.5 | −2, −6, −10 | 260 | ||
| 2, 6, 10 | −10, −14, −18 | |||||
| 2, 6, 10 | −20, −25, −30 |
| Flight Phase | Ice Type | |||
|---|---|---|---|---|
| Takeoff | Glaze | 0.0404 | 0.9900 | 1.63% |
| Mixed | 0.0163 | 0.9975 | 1.87% | |
| Rime | 0.000113 | 0.999835 | 0.31% | |
| Climbing below 10,000 ft | Glaze | 0.1026 | 0.9893 | 2.93% |
| Mixed | 0.0211 | 0.9985 | 2.13% | |
| Rime | 0.000098 | 0.999896 | 0.24% | |
| Climbing above 10,000 ft | Glaze | 0.1074 | 0.9806 | 2.71% |
| Mixed | 0.0513 | 0.9952 | 2.78% | |
| Rime | 0.000049 | 0.999961 | 0.18% | |
| Holding | Glaze | 0.0527 | 0.9993 | 0.50% |
| Mixed | 0.0199 | 0.9996 | 0.33% | |
| Rime | 0.0034 | 0.999946 | 0.21% | |
| Approach and landing | Glaze | 0.0976 | 0.9792 | 2.46% |
| Mixed | 0.0140 | 0.9989 | 1.63% | |
| Rime | 0.000107 | 0.999887 | 0.25% |
| Parameter | Unit | Value | |
|---|---|---|---|
| Flight conditions | m/s | 59.2 | |
| AOA | ° | 3 | |
| K (°C) | 268.21 (−4.94) | ||
| Icing conditions | MVD | μm | 29 |
| LWC | g/m3 | 0.87 | |
| Time | min | 22.5 | |
| Hot air conditions | g/s | 0.327 | |
| K | 449.817 |
| Flight Phase | Case | H (ft) | V∞ (m/s) | T0 (°C) | (μm) | (g/m3) | (s) |
|---|---|---|---|---|---|---|---|
| Takeoff | 1 | 1500 | 125 (243 kt) | −10 | 17.3 | 0.5137 | 258 |
| 2 | 0 | −30 | 15 | 0.2 | |||
| 3 | 750 | −30 | 15 | 0.2 | |||
| 4 | 1500 | −30 | 15 | 0.2 | |||
| Climbing below 10,000 ft | 5 | 10,000 | 128.6 (250 kt) | −8.30 | 20.66 | 0.4453 | 250 |
| 6 | 1500 | −30 | 15 | 0.2 | |||
| 7 | 5500 | −30 | 15 | 0.2 | |||
| 8 | 9500 | −30 | 15 | 0.2 | |||
| Climbing above 10,000 ft | 9 | 14,478 | 154.3 (300 kt) | −10 | 17.85 | 0.4948 | 210 |
| 10 | 12,000 | −30 | 15 | 0.2 | |||
| 11 | 16,000 | −30 | 15 | 0.2 | |||
| 12 | 20,000 | −30 | 15 | 0.2 | |||
| Holding | 13 | 13,344 | 136.3 (265 kt) | −2.69 | 21.85 | 0.5294 | 2700 |
| 14 | 12,000 | −30 | 15 | 0.2 | |||
| 15 | 17,000 | −30 | 15 | 0.2 | |||
| 16 | 22,000 | −30 | 15 | 0.2 | |||
| Approach and landing | 17 | 10,000 | 123.5 (240 kt) | −7.34 | 21.89 | 0.4322 | 260 |
| 18 | 2000 | −30 | 15 | 0.2 | |||
| 19 | 6000 | −30 | 15 | 0.2 | |||
| 20 | 10,000 | −30 | 15 | 0.2 |
| Flight Phase | Case | Unheated Ice Mass (10−2 kg) | Heated Ice Mass (10−2 kg) | Anti-Icing Efficiency | Maximum Ice Thickness (mm) |
|---|---|---|---|---|---|
| Takeoff | 1 | 5.23 | 0 | 100% | 0 |
| 2 | 1.6 | 0.573 | 64.19% | 5.11 | |
| 3 | 1.62 | 0.579 | 64.26% | 4.32 | |
| 4 | 1.65 | 0.587 | 64.42% | 4.39 | |
| Climbing below 10,000 ft | 5 | 6.9 | 0 | 100% | 0 |
| 6 | 1.67 | 0.631 | 62.22% | 3.08 | |
| 7 | 1.8 | 0.64 | 64.44% | 2.42 | |
| 8 | 1.94 | 0.665 | 65.72% | 1.78 | |
| Climbing above 10,000 ft | 9 | 6.84 | 1.78 | 73.98% | 9.89 |
| 10 | 2.2 | 0.73 | 66.82% | 2.44 | |
| 11 | 2.35 | 0.527 | 77.57% | 1.33 | |
| 12 | 2.52 | 0.544 | 78.41% | 1.31 | |
| Holding | 13 | 104.96 | 0 | 100% | 0 |
| 14 | 23.84 | 8.49 | 64.39% | 17.07 | |
| 15 | 25.99 | 8.41 | 67.64% | 16.51 | |
| 16 | 28.19 | 8.01 | 71.59% | 16.09 | |
| Approach and landing | 17 | 7.14 | 0 | 100% | 0 |
| 18 | 1.64 | 0.579 | 64.70% | 4.38 | |
| 19 | 1.77 | 0.614 | 65.31% | 2.12 | |
| 20 | 1.91 | 0.635 | 66.75% | 1.73 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, Y.; Wang, Z.; Su, J.; Yao, J.; Wang, H. Prediction of Airfoil Icing and Evaluation of Hot Air Anti-Icing System Effectiveness Using Computational Fluid Dynamics Simulations. Aerospace 2025, 12, 492. https://doi.org/10.3390/aerospace12060492
Niu Y, Wang Z, Su J, Yao J, Wang H. Prediction of Airfoil Icing and Evaluation of Hot Air Anti-Icing System Effectiveness Using Computational Fluid Dynamics Simulations. Aerospace. 2025; 12(6):492. https://doi.org/10.3390/aerospace12060492
Chicago/Turabian StyleNiu, Yifan, Zhiqiang Wang, Jieyao Su, Jiawei Yao, and Hainan Wang. 2025. "Prediction of Airfoil Icing and Evaluation of Hot Air Anti-Icing System Effectiveness Using Computational Fluid Dynamics Simulations" Aerospace 12, no. 6: 492. https://doi.org/10.3390/aerospace12060492
APA StyleNiu, Y., Wang, Z., Su, J., Yao, J., & Wang, H. (2025). Prediction of Airfoil Icing and Evaluation of Hot Air Anti-Icing System Effectiveness Using Computational Fluid Dynamics Simulations. Aerospace, 12(6), 492. https://doi.org/10.3390/aerospace12060492





