Broadband Dynamic Sensitivity Analysis of a Euler–Bernoulli Beam Under Thermal Load Using the Efficient Wave-Based Method
Abstract
1. Introduction
2. Theoretical Basis
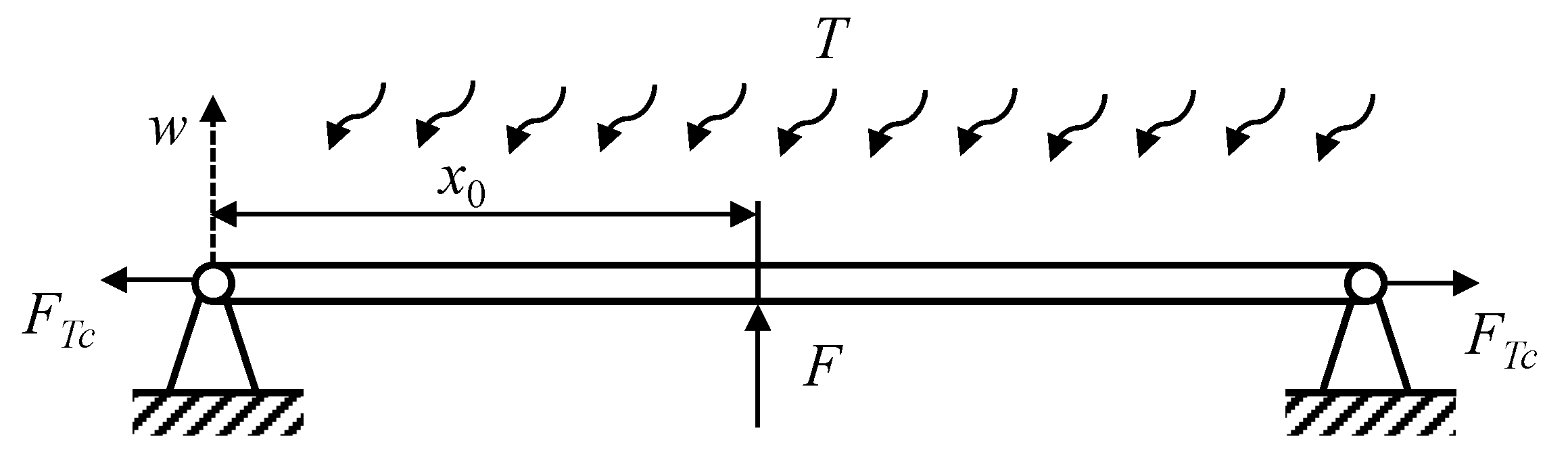
2.1. Problem Definition
2.2. Dynamic Response Prediction Using the Wave-Based Method
2.3. Design Sensitivity Analysis
3. Numerical Simulations
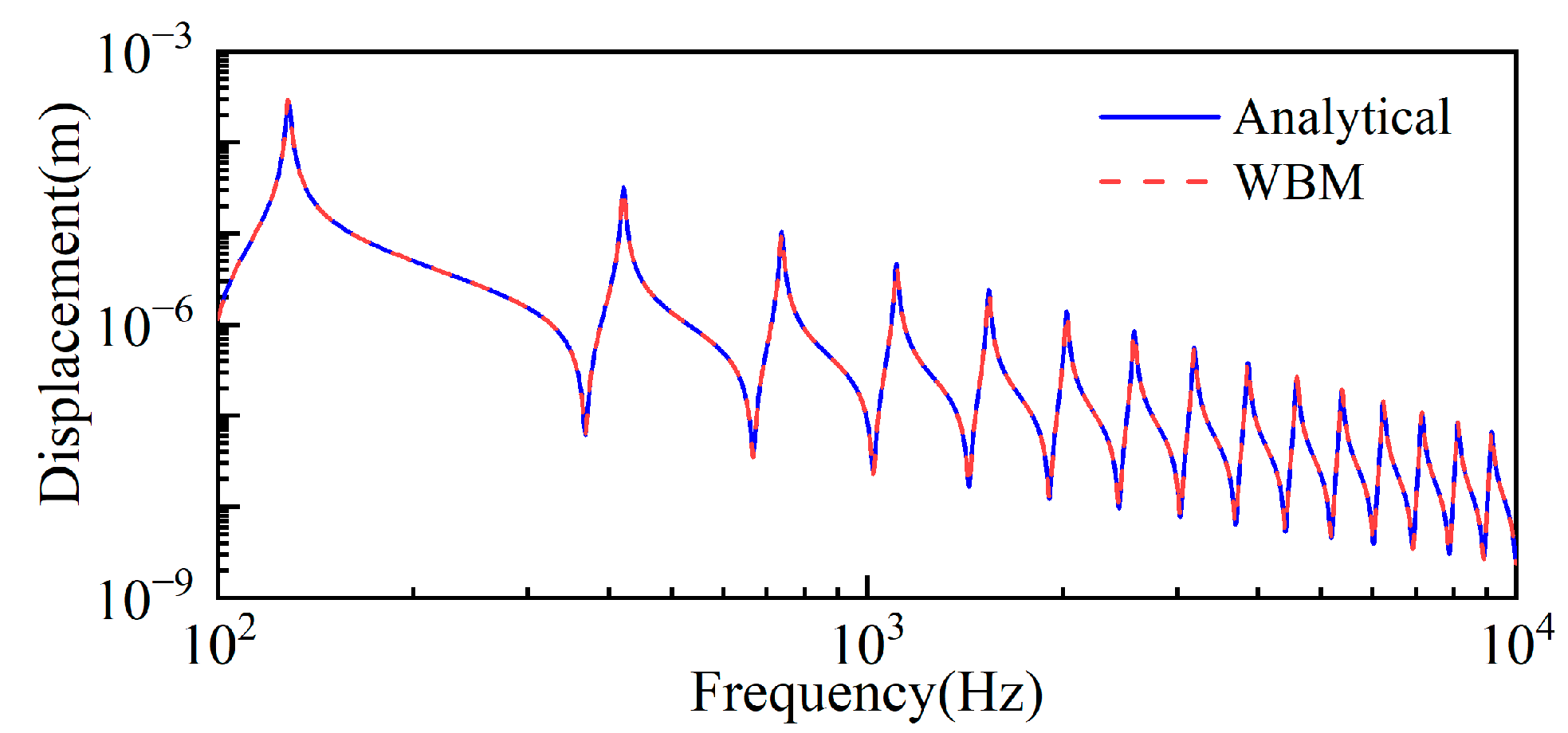
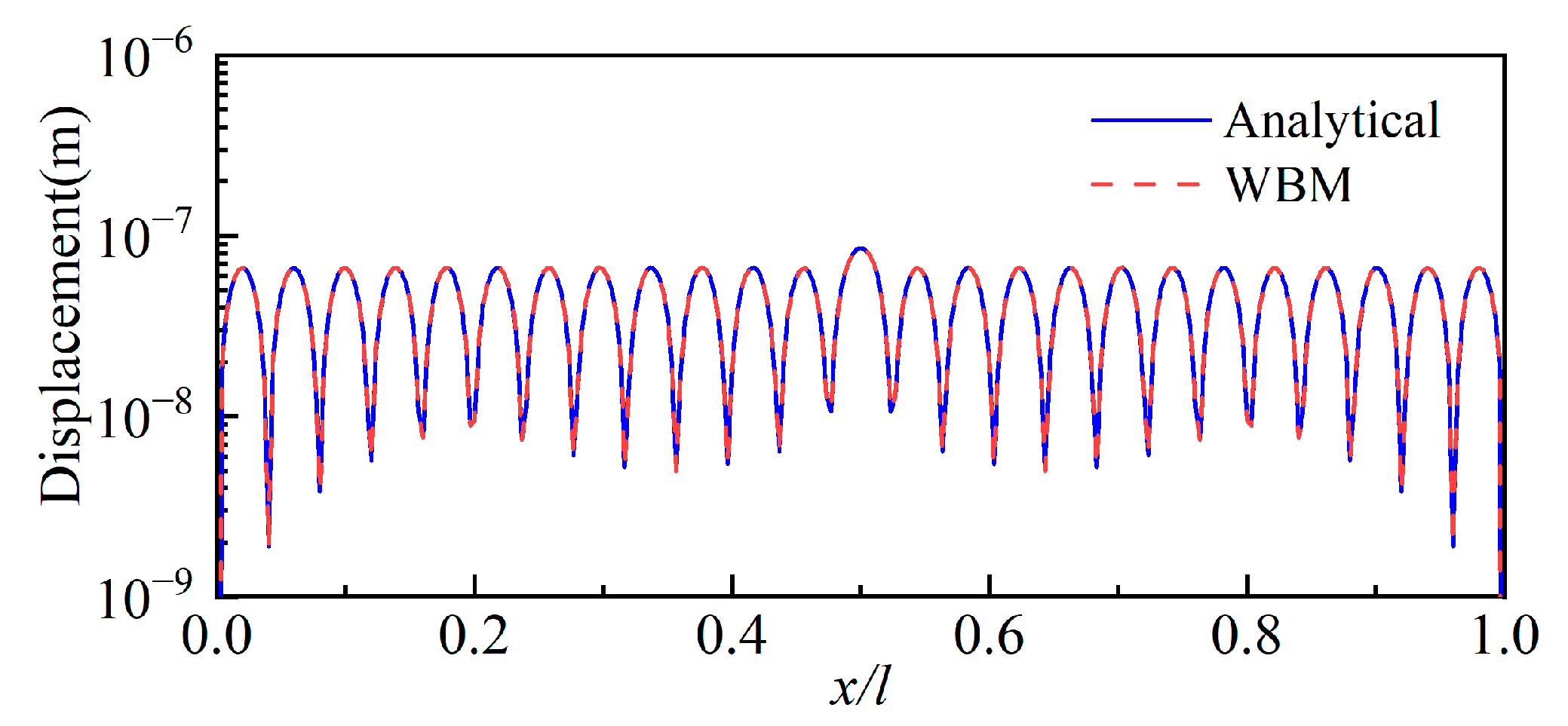
3.1. Validation Cases
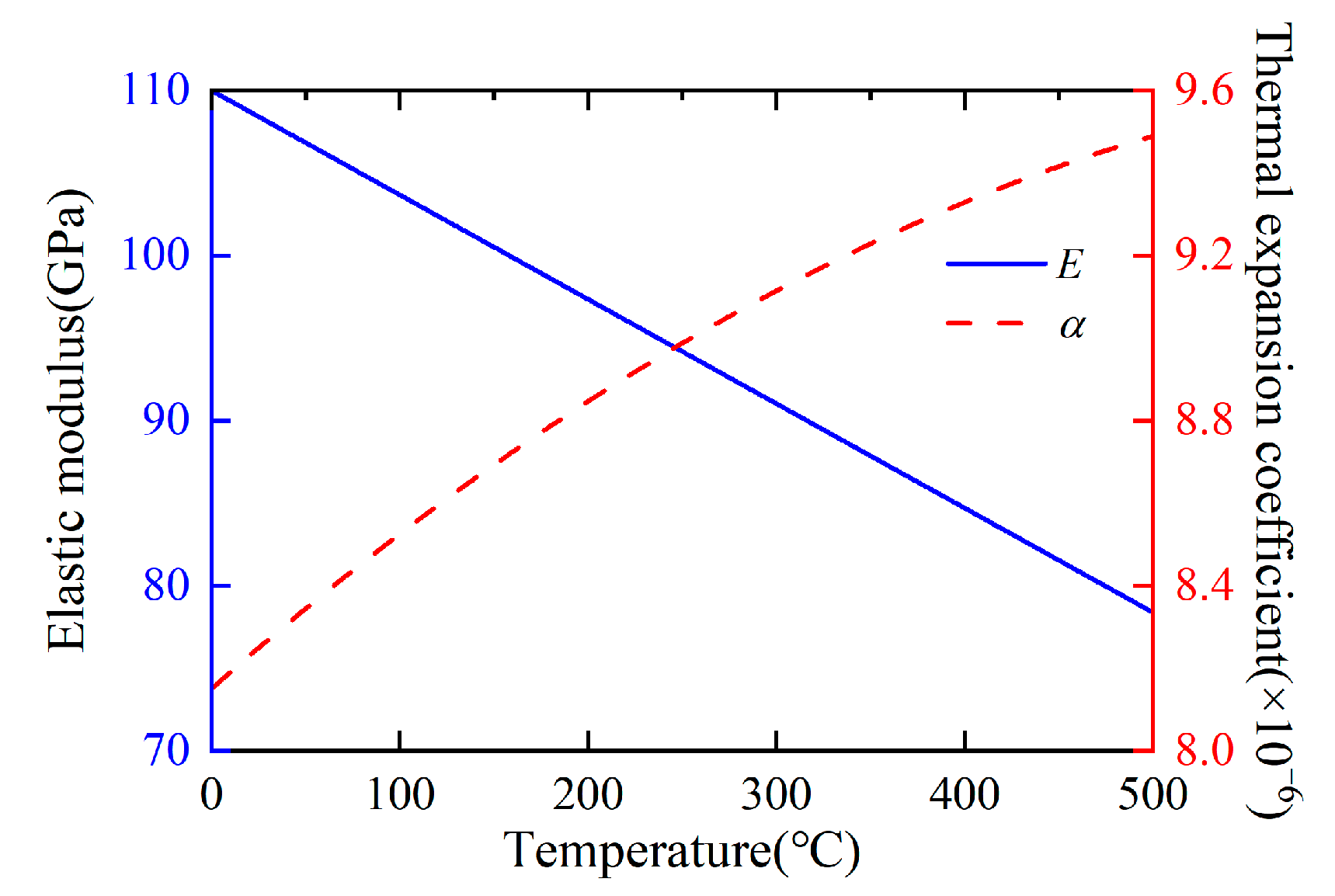
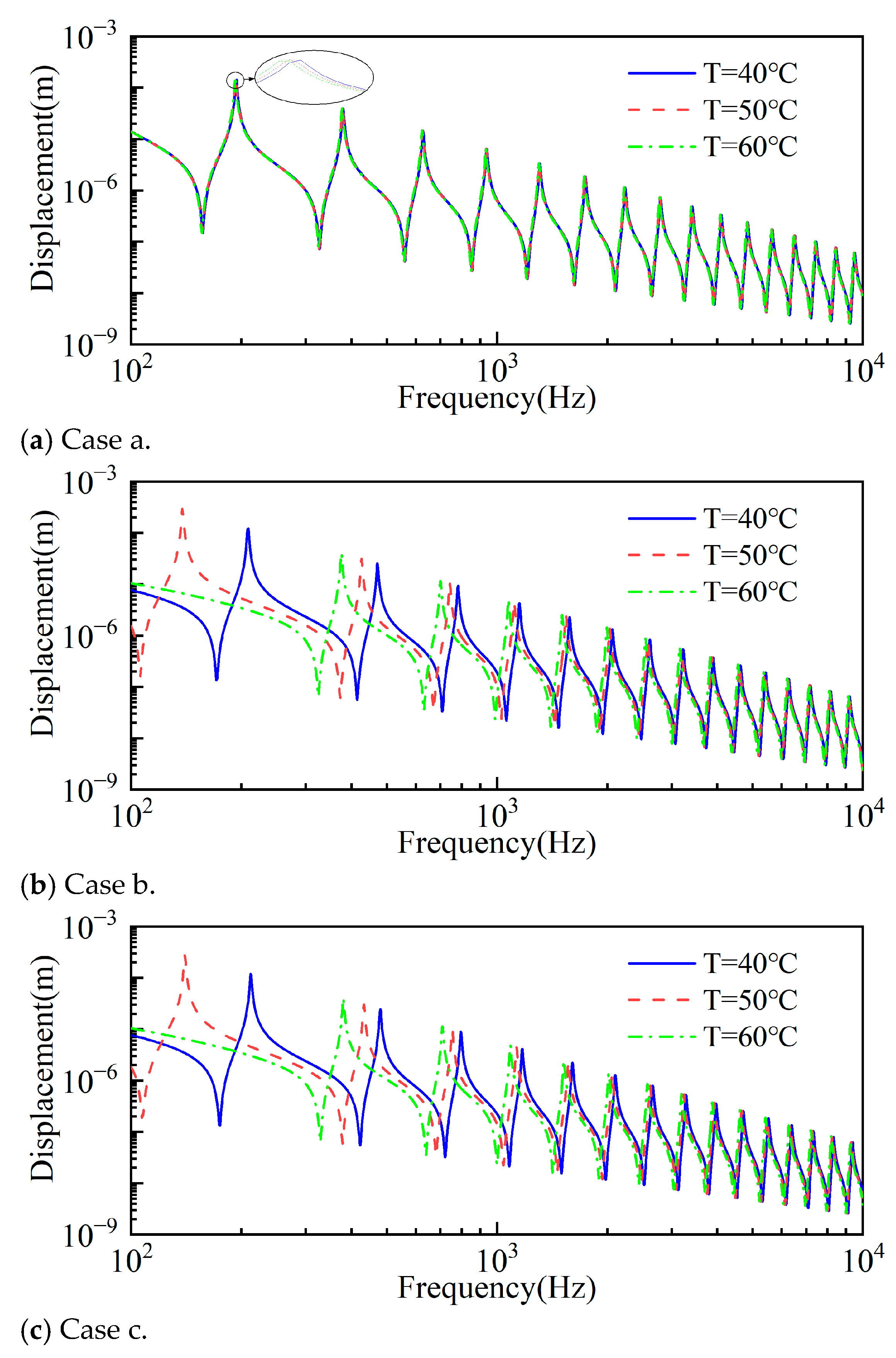
3.2. Thermal Effect on the Broadband Dynamic Responses
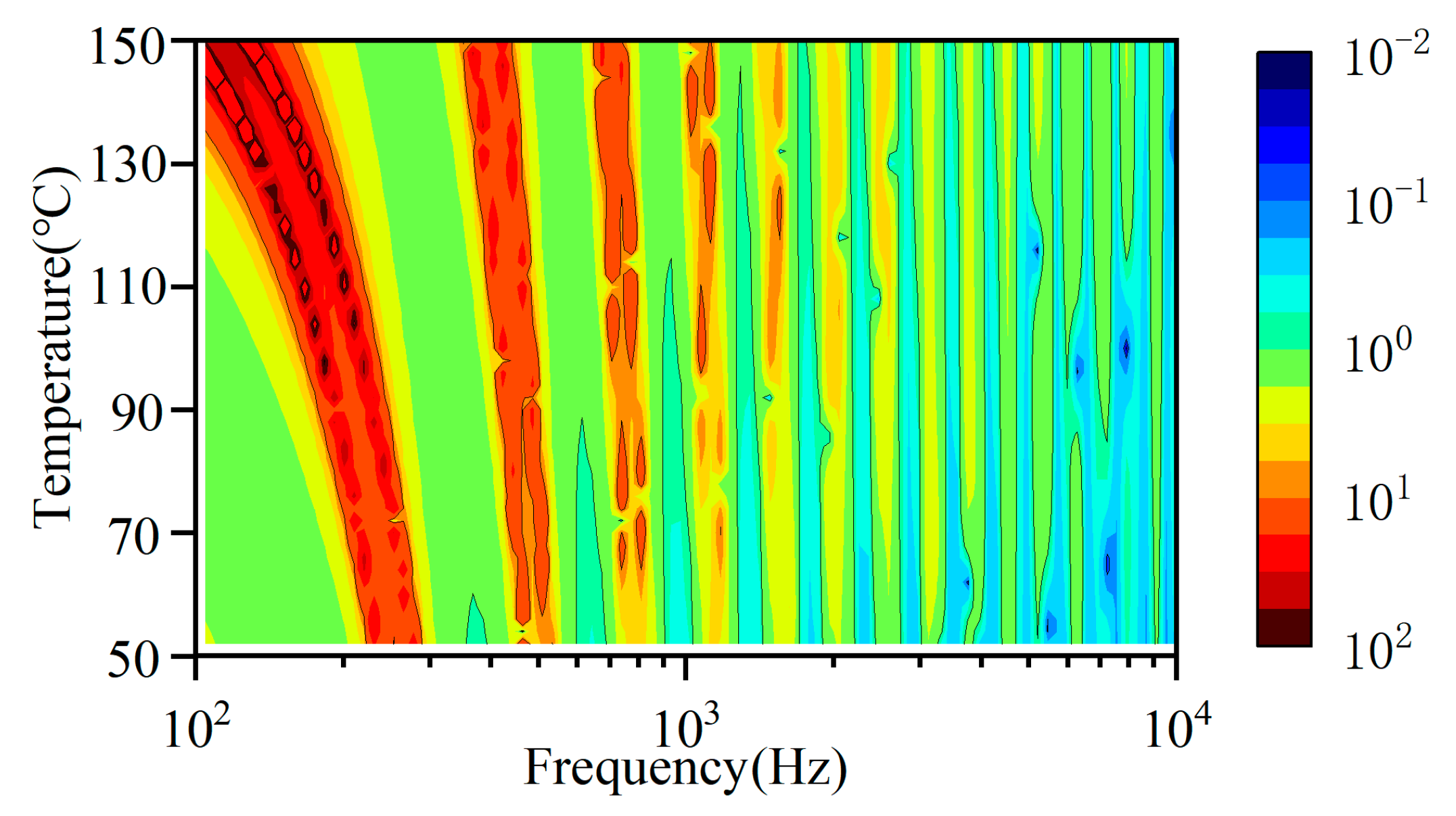
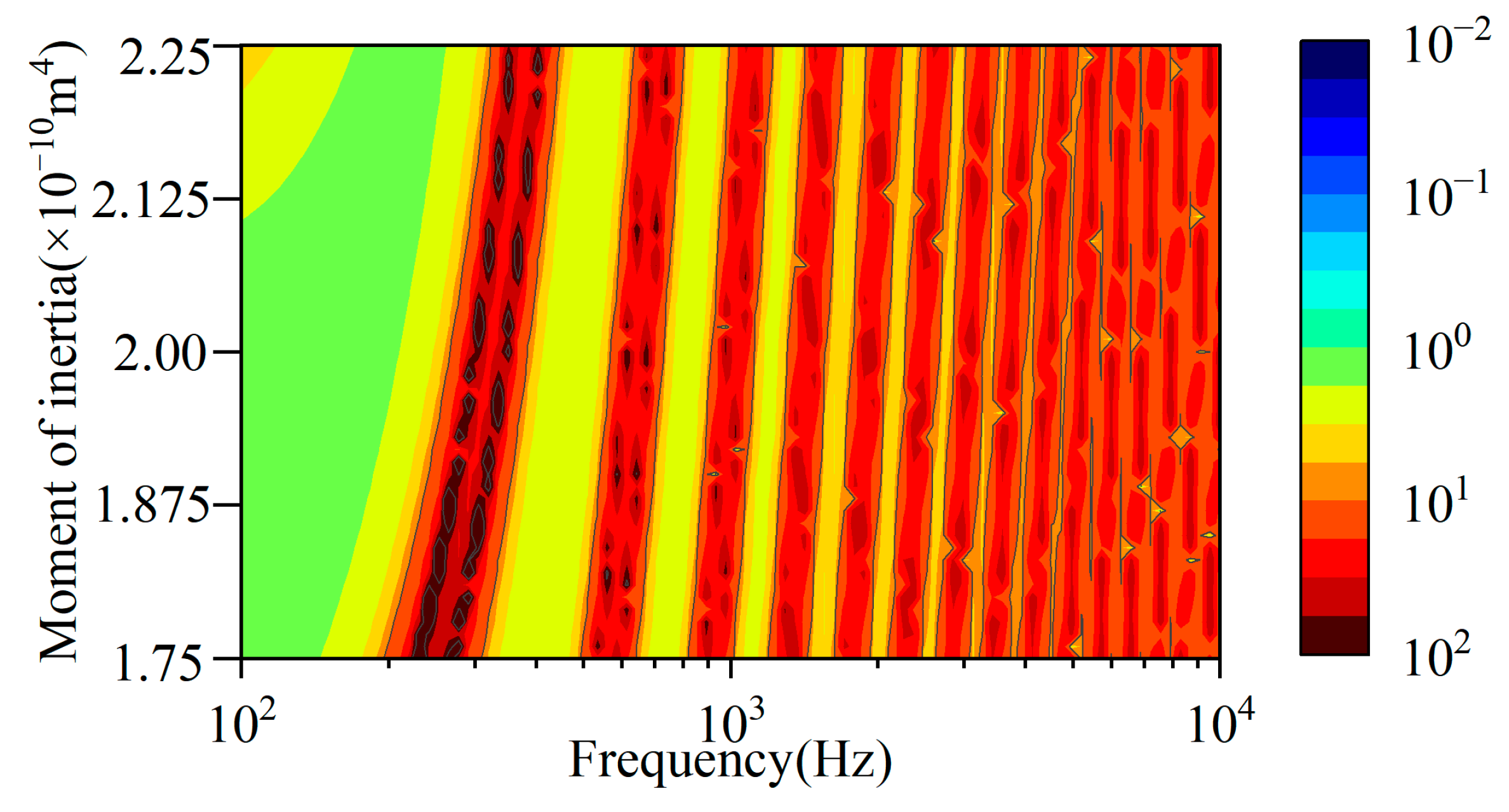
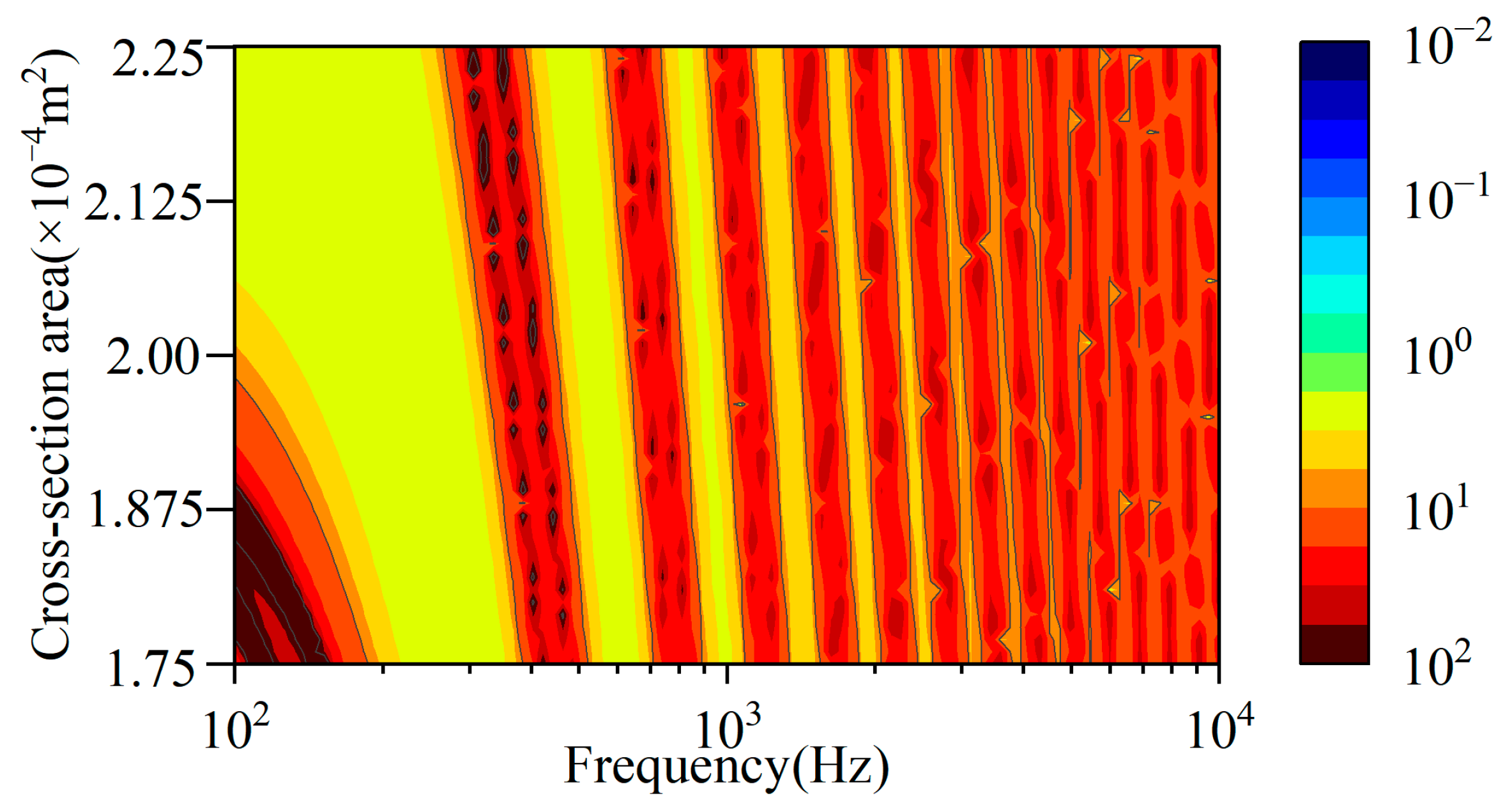
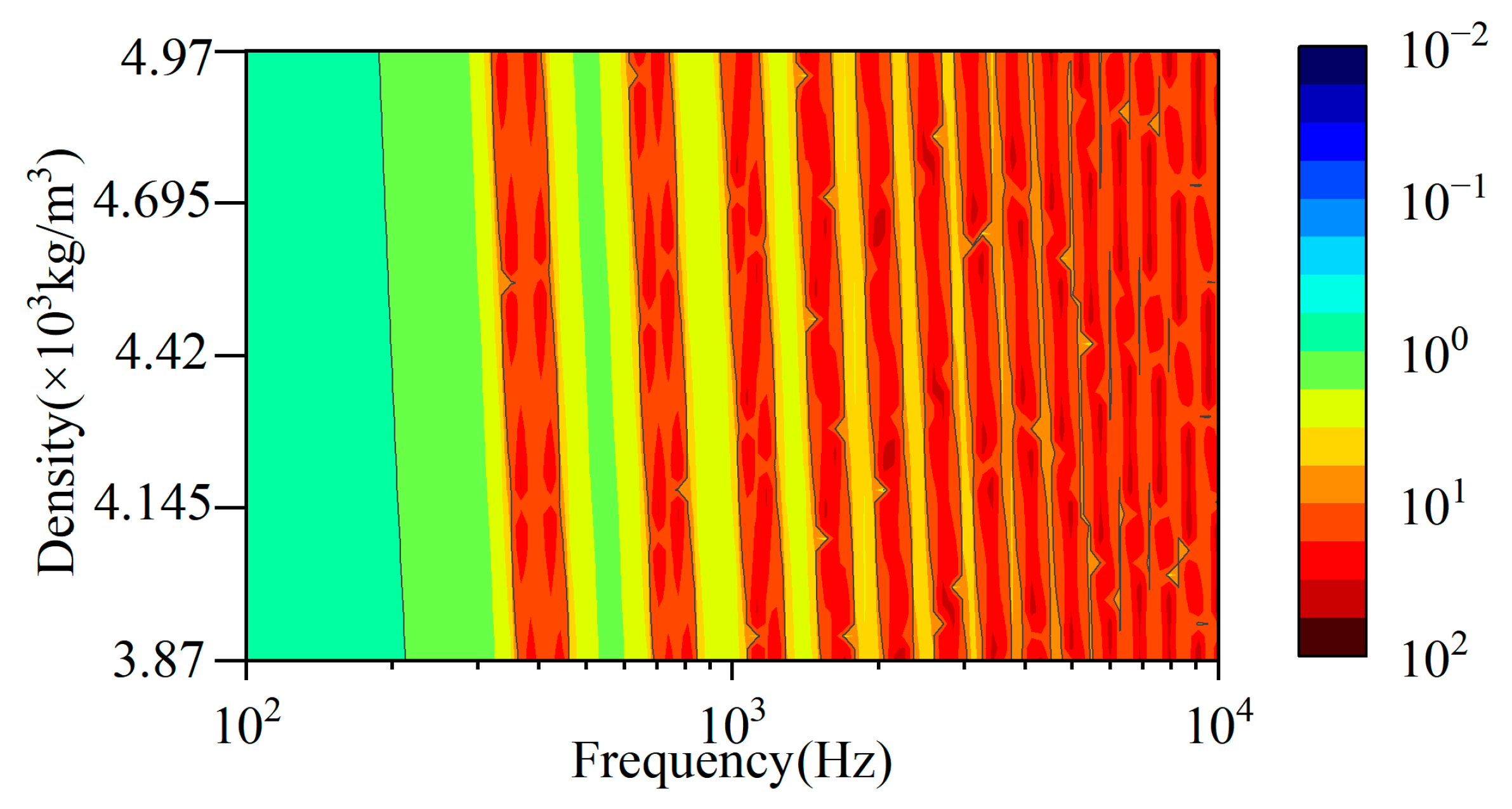
3.3. Global Sensitivity Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, Z.; Yang, Z.; Gu, Y.; Guo, S. An energy flow model for high-frequency vibration analysis of two-dimensional panels in supersonic airflow. Appl. Math. Model. 2019, 76, 495–512. [Google Scholar] [CrossRef]
- Cardoso, R.P. A new beam element which blends the Euler-Bernoulli beam theory with idealised transverse shear flows for aircraft structural analysis. Thin-Walled Struct. 2020, 157, 107118. [Google Scholar] [CrossRef]
- Fleischmann, D.; Könözsy, L. On a novel approximate solution to the inhomogeneous Euler–Bernoulli equation with an application to aeroelastics. Aerospace 2021, 8, 356. [Google Scholar] [CrossRef]
- Su, W.; King, C.K.; Clark, S.R.; Griffin, E.D.; Suhey, J.D.; Wolf, M.G. Dynamic beam solutions for real-time simulation and control development of flexible rockets. J. Spacecr. Rockets 2017, 54, 403–416. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, Z.; Guo, N.; Zhang, G. An energy finite element method for high frequency vibration analysis of beams with axial force. Appl. Math. Model. 2018, 61, 521–539. [Google Scholar] [CrossRef]
- Deckers, E.; Atak, O.; Coox, L.; D’amico, R.; Devriendt, H.; Jonckheere, S.; Koo, K.; Pluymers, B.; Vandepitte, D.; Desmet, W. The wave based method: An overview of 15 years of research. Wave Motion 2014, 51, 550–565. [Google Scholar] [CrossRef]
- Lainer, M.; Taddei, F.; Müller, G. A Wave Based Method for the analysis of a fully and partially saturated halfspace under harmonic loading. Comput. Struct. 2023, 283, 107040. [Google Scholar] [CrossRef]
- Sun, L.; Chen, Z.; Zhang, S.; Chu, L. A wave based method for two-dimensional time-harmonic elastic wave propagation in anisotropic media. Appl. Math. Lett. 2021, 120, 107292. [Google Scholar] [CrossRef]
- Wu, B.; Fan, W.; Xu, Z.; Zhang, Z.; Jin, G. Topology optimization of damping material layout in coupled vibro-acoustic system using hybrid finite element-wave based method. Struct. Multidiscip. Optim. 2021, 64, 3819–3834. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, X.; Wang, X. An analytical dynamic stiffness formulation for highly accurate broadband vibro-acoustic response analysis. Appl. Math. Model. 2025, 145, 116128. [Google Scholar] [CrossRef]
- Jonckheere, S.; Vandepitte, D.; Desmet, W. A Wave Based approach for the dynamic bending analysis of Kirchhoff plates under distributed deterministic and random excitation. Comput. Struct. 2015, 156, 42–57. [Google Scholar] [CrossRef]
- Mahi, A.; Bedia, E.A.; Tounsi, A.; Mechab, I. An analytical method for temperature-dependent free vibration analysis of functionally graded beams with general boundary conditions. Compos. Struct. 2010, 92, 1877–1887. [Google Scholar] [CrossRef]
- Zhou, K.; Hu, Z.; Hua, H. Investigations on the aero-thermo-elastic characteristics of arbitrary polygon built-up structures in supersonic airflow. Int. J. Mech. Sci. 2021, 196, 106300. [Google Scholar] [CrossRef]
- Geng, Q.; Li, H.; Li, Y. Dynamic and acoustic response of a clamped rectangular plate in thermal environments: Experiment and numerical simulation. J. Acoust. Soc. Am. 2014, 135, 2674–2682. [Google Scholar] [CrossRef]
- Demir, Ç.; Civalek, Ö. A new nonlocal FEM via Hermitian cubic shape functions for thermal vibration of nano beams surrounded by an elastic matrix. Compos. Struct. 2017, 168, 872–884. [Google Scholar] [CrossRef]
- Chen, Q.; Fei, Q.; Li, Y.; Wu, S.; Zhang, P. Prediction of statistical energy analysis parameters in thermal environment. J. Spacecr. Rockets 2019, 56, 687–694. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, H.; Zhu, D.; Kong, X. The thermal effects on high-frequency vibration of beams using energy flow analysis. J. Sound Vib. 2014, 333, 2588–2600. [Google Scholar] [CrossRef]
- Chen, Q.; Ma, W.; Fei, Q.; Devriendt, H.; Desmet, W. An efficient wave based method for the mid-frequency transverse vibration analysis of a thermal beam with interval uncertainties. Aerosp. Sci. Technol. 2021, 110, 106438. [Google Scholar] [CrossRef]
- Lainer, M.; Müller, G. Implementation of a Timoshenko beam within an elastodynamic halfspace modeled by the Wave Based Method. J. Phys. Conf. Ser. 2024, 2647, 082004. [Google Scholar] [CrossRef]
- He, D.; Shi, D.; Wang, Q.; Ma, C. Wave propagation in magneto-electro-thermo-elastic nanobeams based on nonlocal theory. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 601. [Google Scholar] [CrossRef]
- Chen, Q.; Fei, Q.; Devriendt, H.; Wu, S.; Pluymers, B.; Desmet, W. The dynamic bending analysis of plates under thermal load using an efficient wave-based method. Thin-Walled Struct. 2020, 149, 106421. [Google Scholar] [CrossRef]
- Chen, Q.; Fei, Q.; Devriendt, H.; Wu, S.; Pluymers, B.; Desmet, W. Investigation of thermal effects on the steady-state vibrations of a rectangular plate-cavity system subjected to harmonic loading and static temperature loads using a Wave Based Method. Wave Motion 2021, 104, 102748. [Google Scholar] [CrossRef]
- Chen, Q.; Ma, H.; Lu, F.; Fei, Q. Wave based method for mid-frequency dynamic analysis of structures with fuzzy uncertainties under the thermal environment. Structures 2023, 57, 105038. [Google Scholar] [CrossRef]
- Liu, G.; Lu, Z.R.; Wang, L.; Liu, J.K. A new semi-analytical technique for nonlinear systems based on response sensitivity analysis. Nonlinear Dyn. 2021, 103, 1529–1551. [Google Scholar] [CrossRef]
- Rouco, P.; Orgeira-Crespo, P.; Gonzalez, G.D.R.; Aguado-Agelet, F. Airfoil Optimization and Analysis Using Global Sensitivity Analysis and Generative Design. Aerospace 2025, 12, 180. [Google Scholar] [CrossRef]
- Xiang, R.; van Schie, S.P.; Scotzniovsky, L.; Yan, J.; Kamensky, D.; Hwang, J.T. Automating adjoint sensitivity analysis for multidisciplinary models involving partial differential equations. Struct. Multidiscip. Optim. 2024, 67, 146. [Google Scholar] [CrossRef]
- Li, S.; Yin, J.; Jiang, X.; Zhang, Y.; Wang, H. A novel reduced basis method for adjoint sensitivity analysis of dynamic topology optimization. Eng. Anal. Bound. Elem. 2024, 162, 403–419. [Google Scholar] [CrossRef]
- Tortorelli, D.A.; Michaleris, P. Design sensitivity analysis: Overview and review. Inverse Probl. Eng. 1994, 1, 71–105. [Google Scholar] [CrossRef]
- Callejo, A.; Bauchau, O.A.; Diskin, B. Adjoint method for the sensitivity analysis of composite beam cross-sections. Comput. Struct. 2019, 213, 100–111. [Google Scholar] [CrossRef]
- Saltelli, A.; Aleksankina, K.; Becker, W.; Fennell, P.; Ferretti, F.; Holst, N.; Li, S.; Wu, Q. Why so many published sensitivity analyses are false: A systematic review of sensitivity analysis practices. Environ. Model. Softw. 2019, 114, 29–39. [Google Scholar] [CrossRef]
- Koo, K.; D’Amico, R.; Pluymers, B.; Desmet, W. Design sensitivity analysis and optimization of frequency averaged input power using the residue theorem. Comput. Struct. 2014, 145, 58–71. [Google Scholar] [CrossRef]
- Lewandowski, R.; Łasecka-Plura, M. Design sensitivity analysis of structures with viscoelastic dampers. Comput. Struct. 2016, 164, 95–107. [Google Scholar] [CrossRef]
- Jung, J.; Hyun, J.; Goo, S.; Wang, S. An efficient design sensitivity analysis using element energies for topology optimization of a frequency response problem. Comput. Methods Appl. Mech. Eng. 2015, 296, 196–210. [Google Scholar] [CrossRef]
- Zhu, R.; Fei, Q.; Jiang, D.; Cao, Z. Dynamic Sensitivity Analysis Based on Sherman–Morrison–Woodbury Formula. AIAA J. 2019, 57, 4992–5001. [Google Scholar] [CrossRef]
- Wang, X.; Li, X.; Yue, Z.S.; Yu, R.P.; Zhang, Q.C.; Du, S.F.; Yang, Z.K.; Han, B.; Lu, T.J. Optimal design of metallic corrugated sandwich panels with polyurea-metal laminate face sheets for simultaneous vibration attenuation and structural stiffness. Compos. Struct. 2021, 256, 112994. [Google Scholar] [CrossRef]
- Chavan, A.T.; Manik, D.N. Sensitivity analysis of vibro-acoustic systems in statistical energy analysis framework. Struct. Multidiscip. Optim. 2010, 40, 283. [Google Scholar] [CrossRef]
- Patil, V.H.; Manik, D.N. Sensitivity analysis of a two-plate coupled system in the statistical energy analysis (SEA) framework. Struct. Multidiscip. Optim. 2019, 59, 201–228. [Google Scholar] [CrossRef]
- Koo, K.; Pluymers, B.; Desmet, W. Acoustic impedance sensitivity approach for defining absorbing material layout using the wave based method. J. Sound Vib. 2020, 483, 115471. [Google Scholar] [CrossRef]
- Koo, K.; Pluymers, B.; Desmet, W.; Wang, S. Vibro-acoustic design sensitivity analysis using the wave-based method. J. Sound Vib. 2011, 330, 4340–4351. [Google Scholar] [CrossRef]
- Penna, R.; Feo, L.; Lovisi, G.; Fabbrocino, F. Application of the higher-order Hamilton approach to the nonlinear free vibrations analysis of porous FG nano-beams in a hygrothermal environment based on a local/nonlocal stress gradient model of elasticity. Nanomaterials 2022, 12, 2098. [Google Scholar] [CrossRef]
- Penna, R.; Feo, L.; Lovisi, G.; Fabbrocino, F. Hygro-thermal vibrations of porous FG nano-beams based on local/nonlocal stress gradient theory of elasticity. Nanomaterials 2021, 11, 910. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Tang, H.; Yan, H.; Chen, Q. Broadband Dynamic Sensitivity Analysis of a Euler–Bernoulli Beam Under Thermal Load Using the Efficient Wave-Based Method. Aerospace 2025, 12, 475. https://doi.org/10.3390/aerospace12060475
Zhang X, Tang H, Yan H, Chen Q. Broadband Dynamic Sensitivity Analysis of a Euler–Bernoulli Beam Under Thermal Load Using the Efficient Wave-Based Method. Aerospace. 2025; 12(6):475. https://doi.org/10.3390/aerospace12060475
Chicago/Turabian StyleZhang, Xudong, Hao Tang, Hao Yan, and Qiang Chen. 2025. "Broadband Dynamic Sensitivity Analysis of a Euler–Bernoulli Beam Under Thermal Load Using the Efficient Wave-Based Method" Aerospace 12, no. 6: 475. https://doi.org/10.3390/aerospace12060475
APA StyleZhang, X., Tang, H., Yan, H., & Chen, Q. (2025). Broadband Dynamic Sensitivity Analysis of a Euler–Bernoulli Beam Under Thermal Load Using the Efficient Wave-Based Method. Aerospace, 12(6), 475. https://doi.org/10.3390/aerospace12060475





