Comparative Study of Sphere Decoding Algorithm and FCS-MPC for PMSMs in Aircraft Application
Abstract
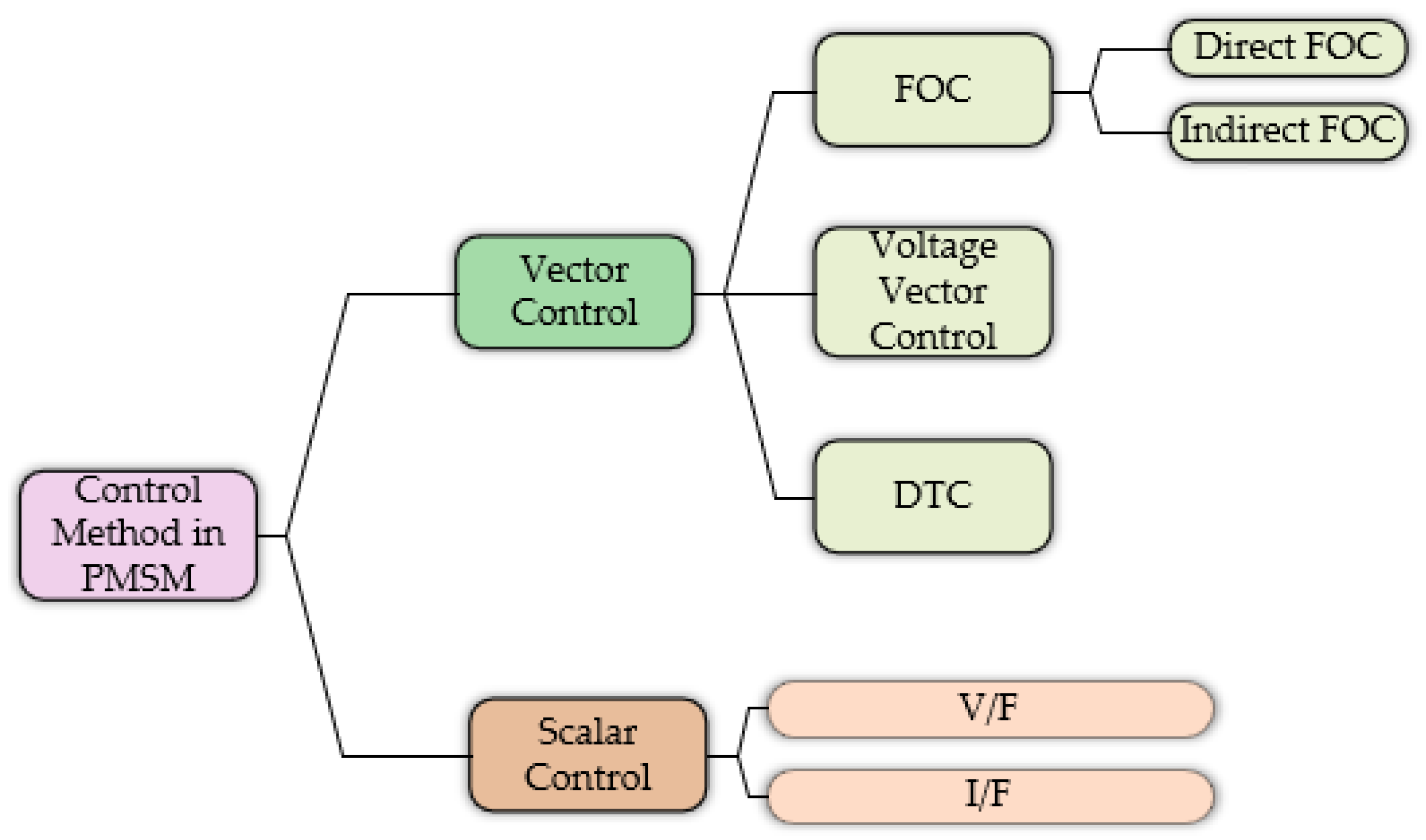
1. Introduction
2. Problem Formulation for LPH PMSM Control
2.1. Performance Metrics
2.1.1. Total Harmonic Distortion (THD)
2.1.2. Switching Frequency
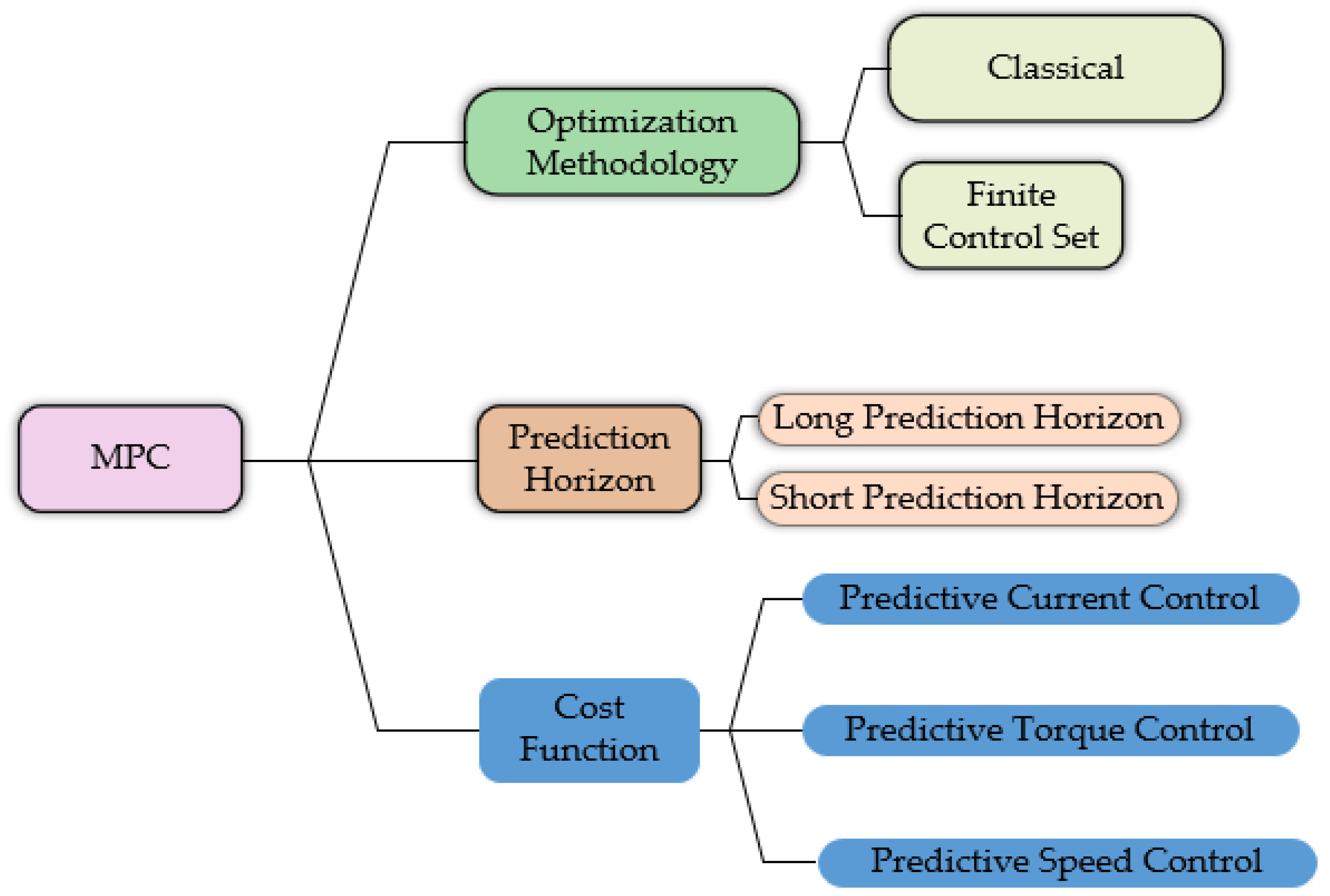
2.2. Model Predictive Control Formulation for PMSM Drive
2.2.1. SPMSM Mathematical Model
- and are the currents on the d- and q-axis, respectively;
- is the stator resistance;
- and are the d-axis and q-axis inductances;
- is the electrical angular speed of the rotor;
- is the permanent magnet flux linkage;
- and are the d-axis and q-axis voltage inputs;
- and are the electrical torque and load torques;
- n, p, and B are the inertia, pole pairs, and load viscous friction coefficient.
2.2.2. Model Predictive Current Control
2.3. Long Prediction Horizon MPC Formulation for PMSM Drive
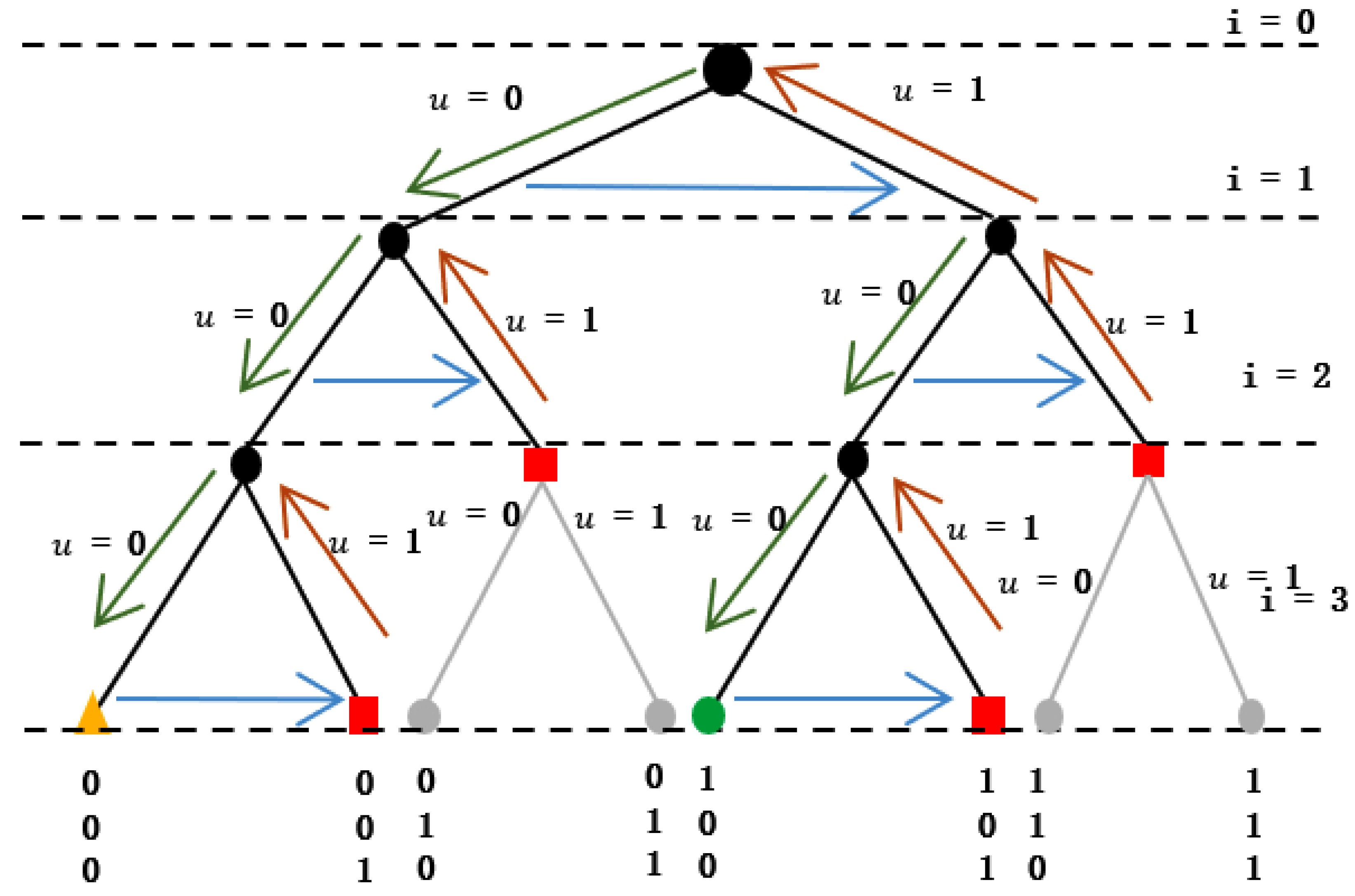
2.4. Sphere Decoding Algorithm Implementation for the PMSM Drive
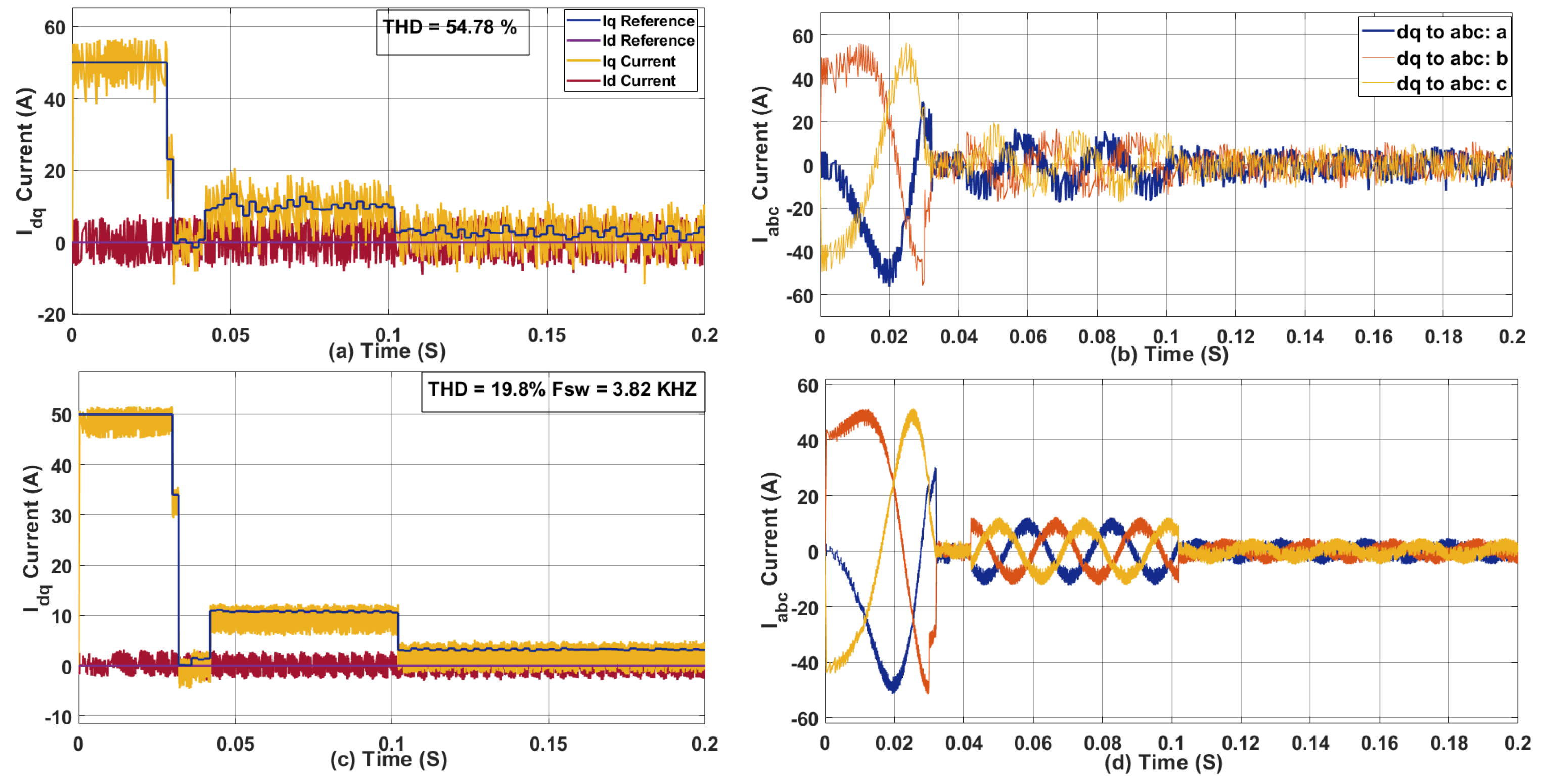
3. Simulation Results and Comparison
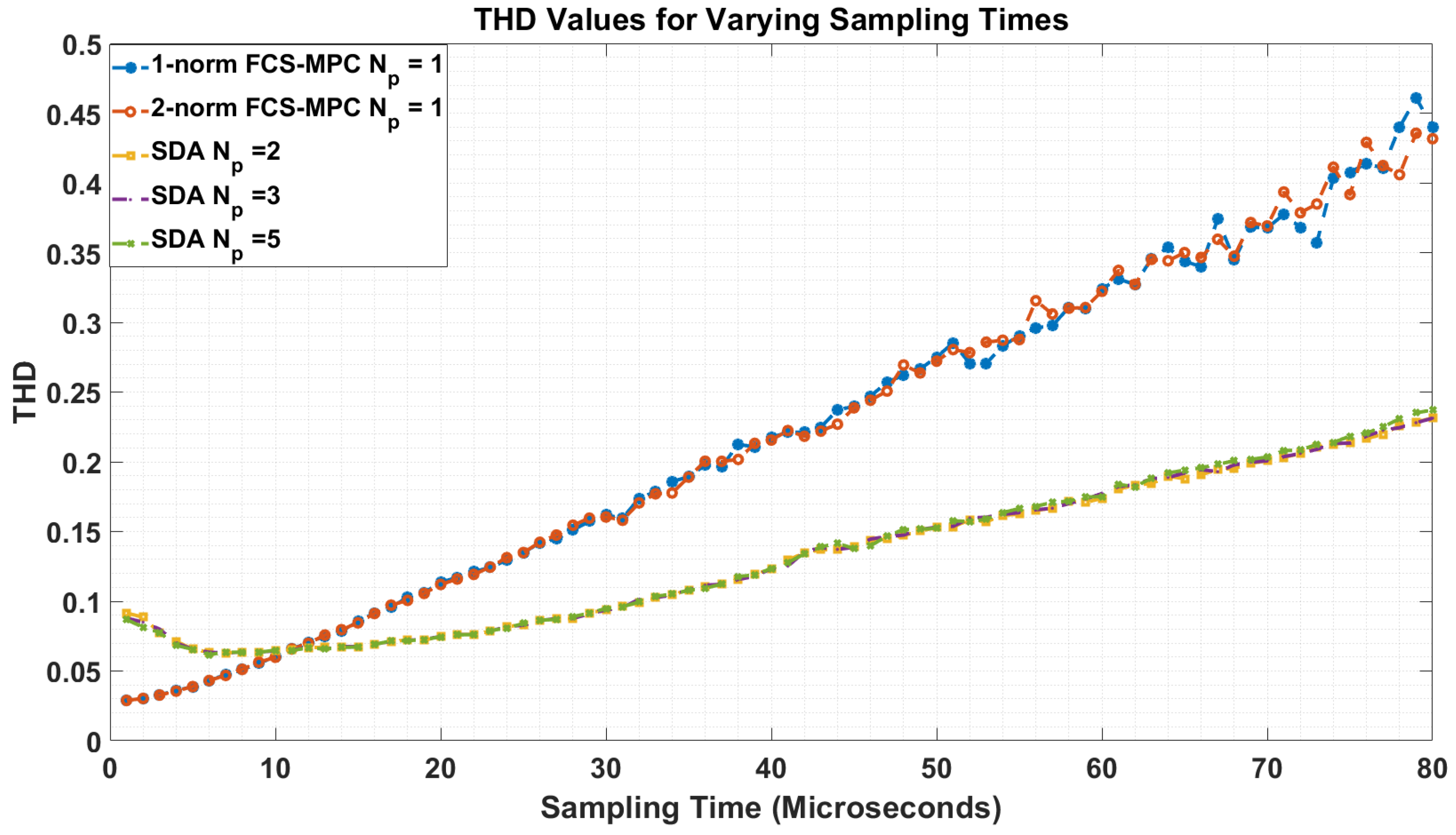
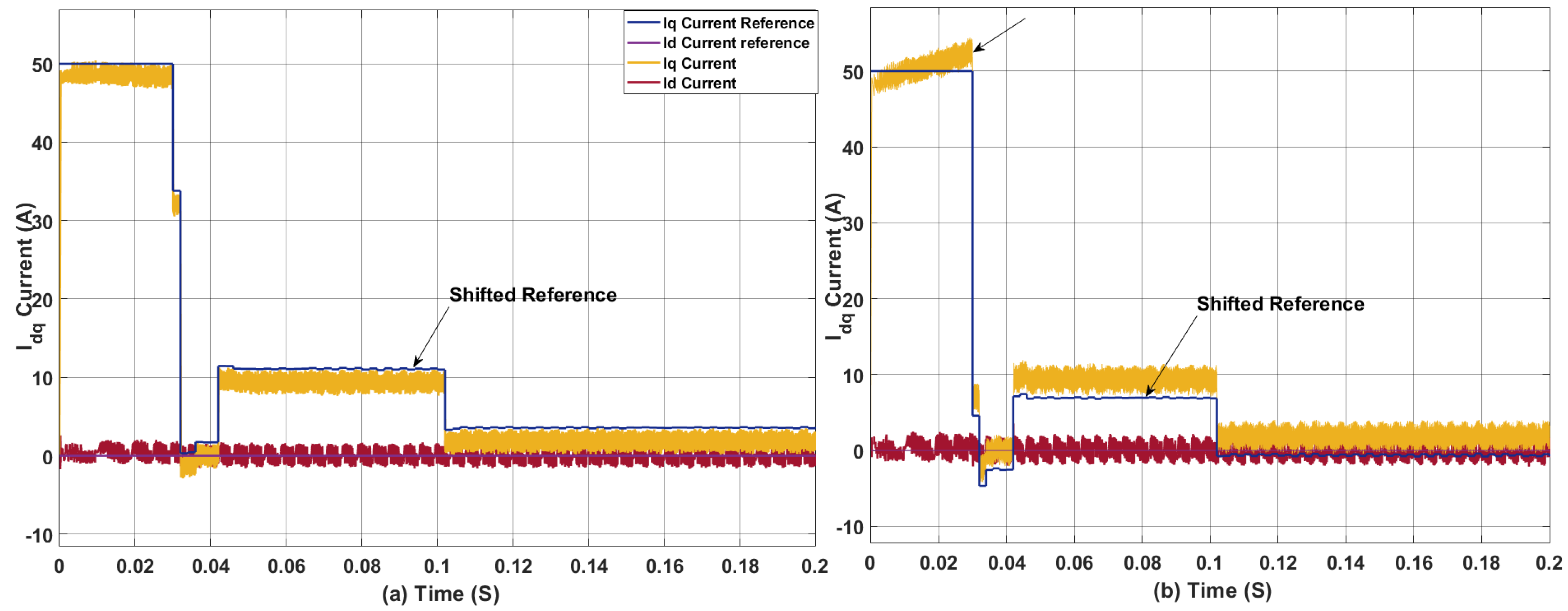
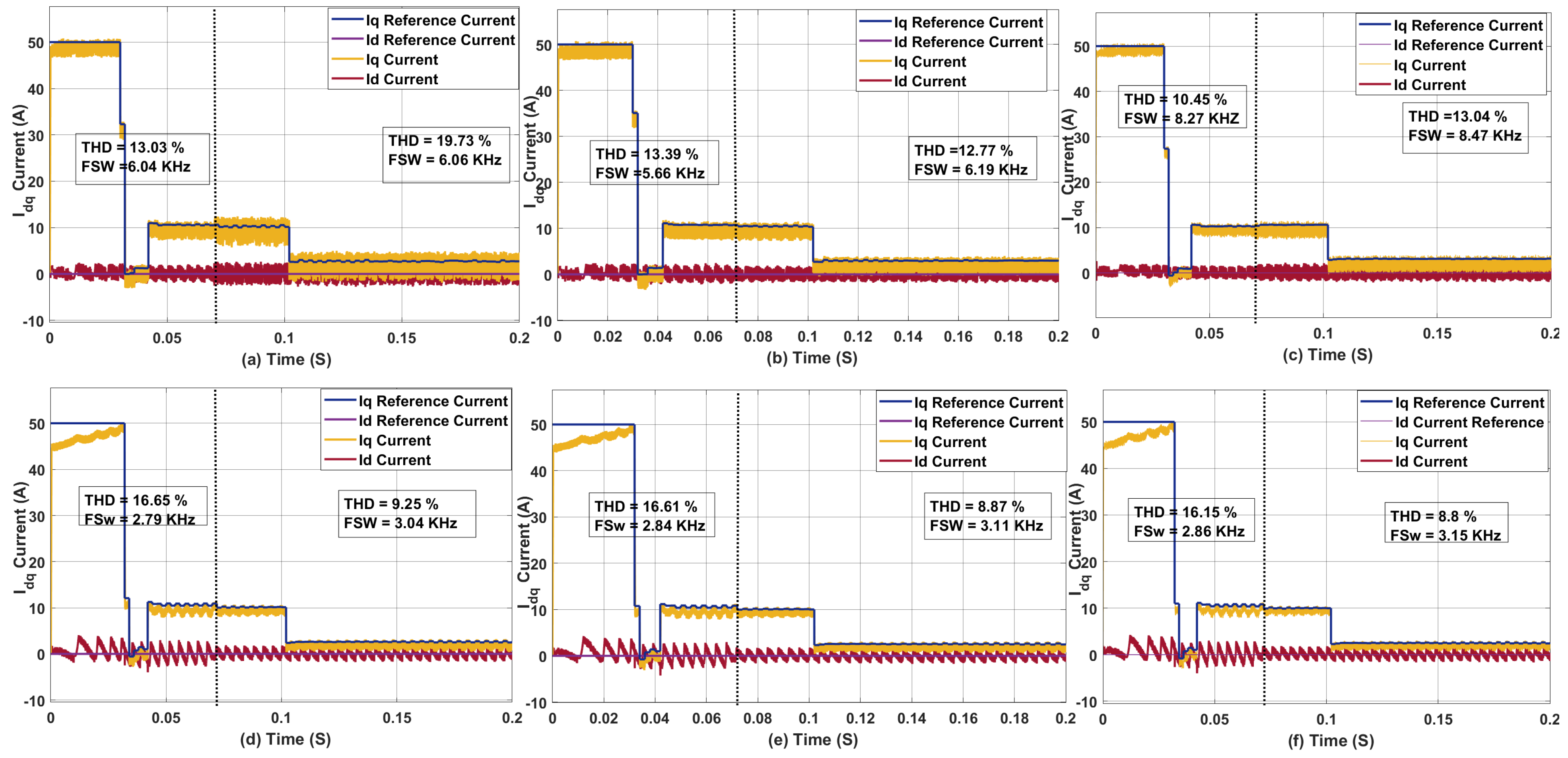
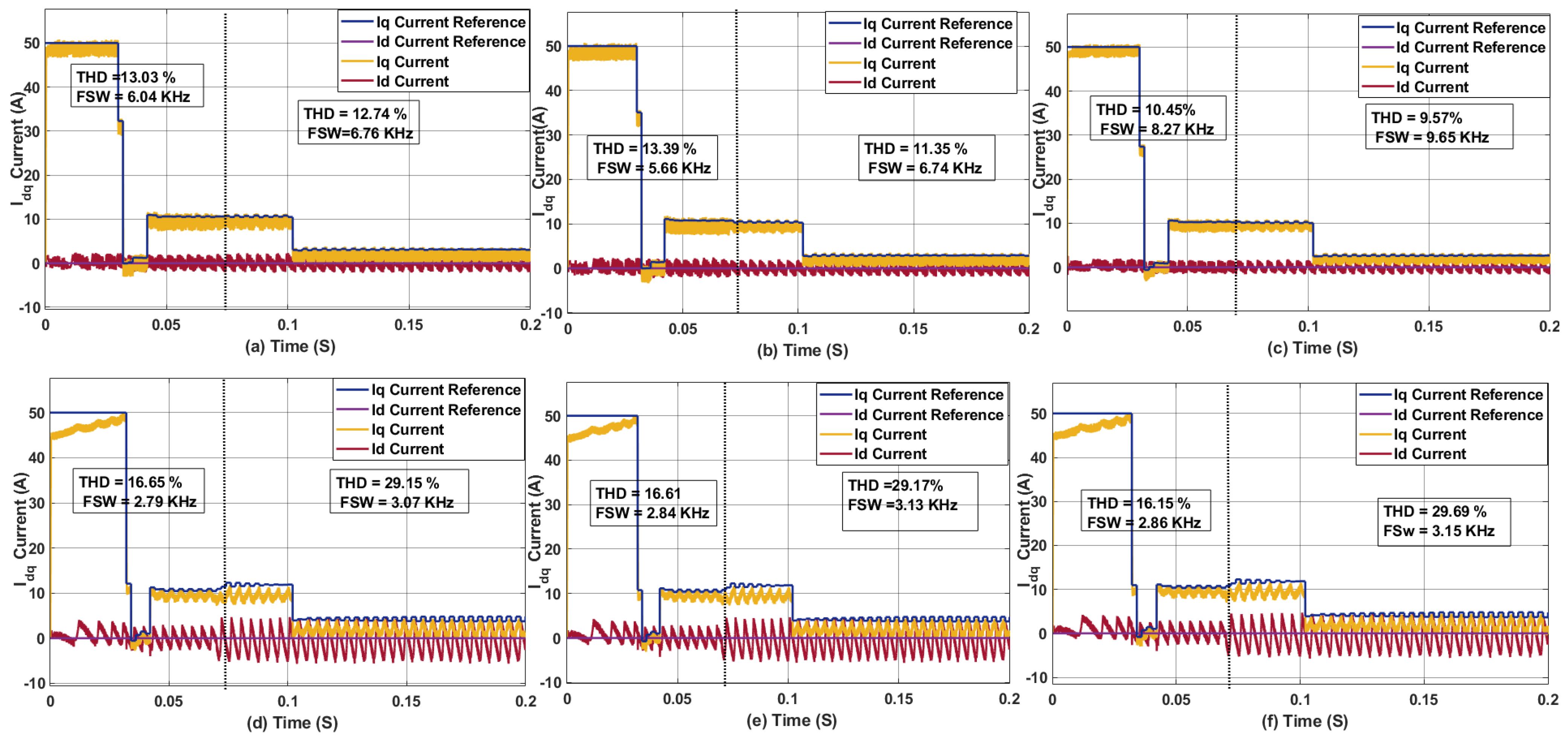
3.1. Effect of Sampling Time on Sphere Decoding Algorithm for PMSM
3.2. Effect of Weighing Factor on THD and Average Switching Frequency
3.3. Sphere Decoding Algorithm for
3.4. Computational Time
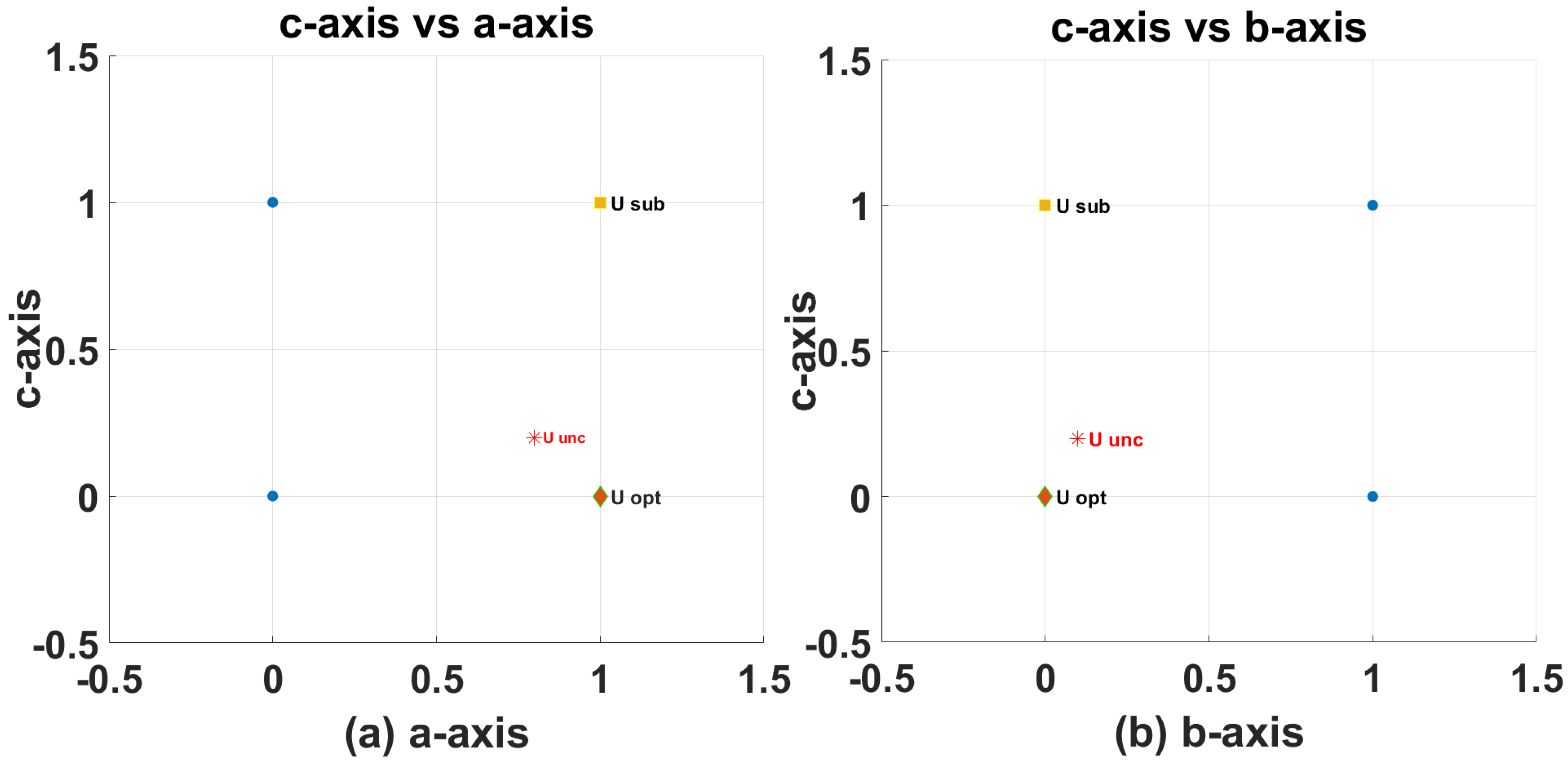
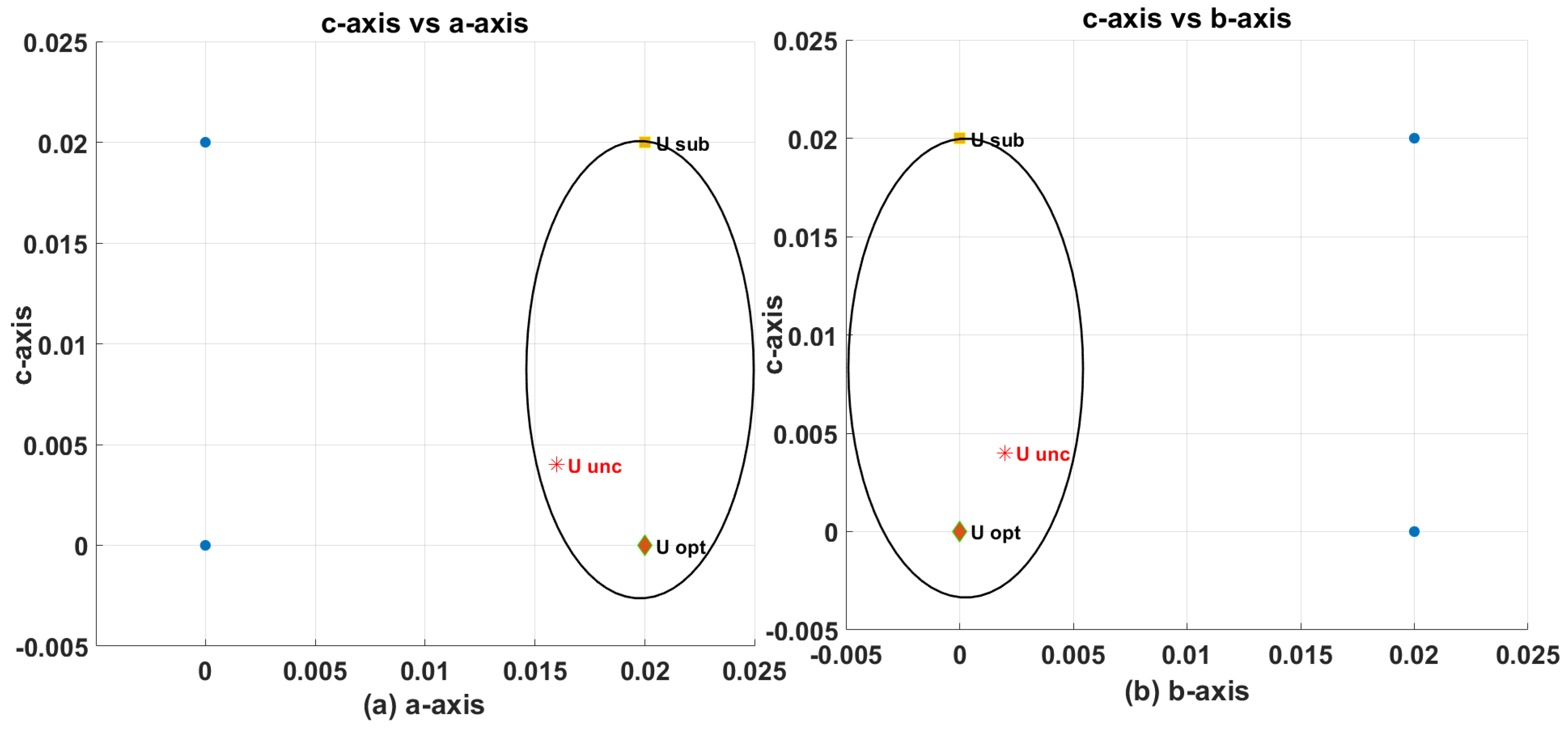
3.5. Effect of Parameter Mismatch on Long Prediction Horizon MPC
3.5.1. Resistance Mismatch
3.5.2. Flux Mismatch
3.5.3. Inductance Mismatch
3.6. Effect of Nonlinear Inductance on SDA for PMSM
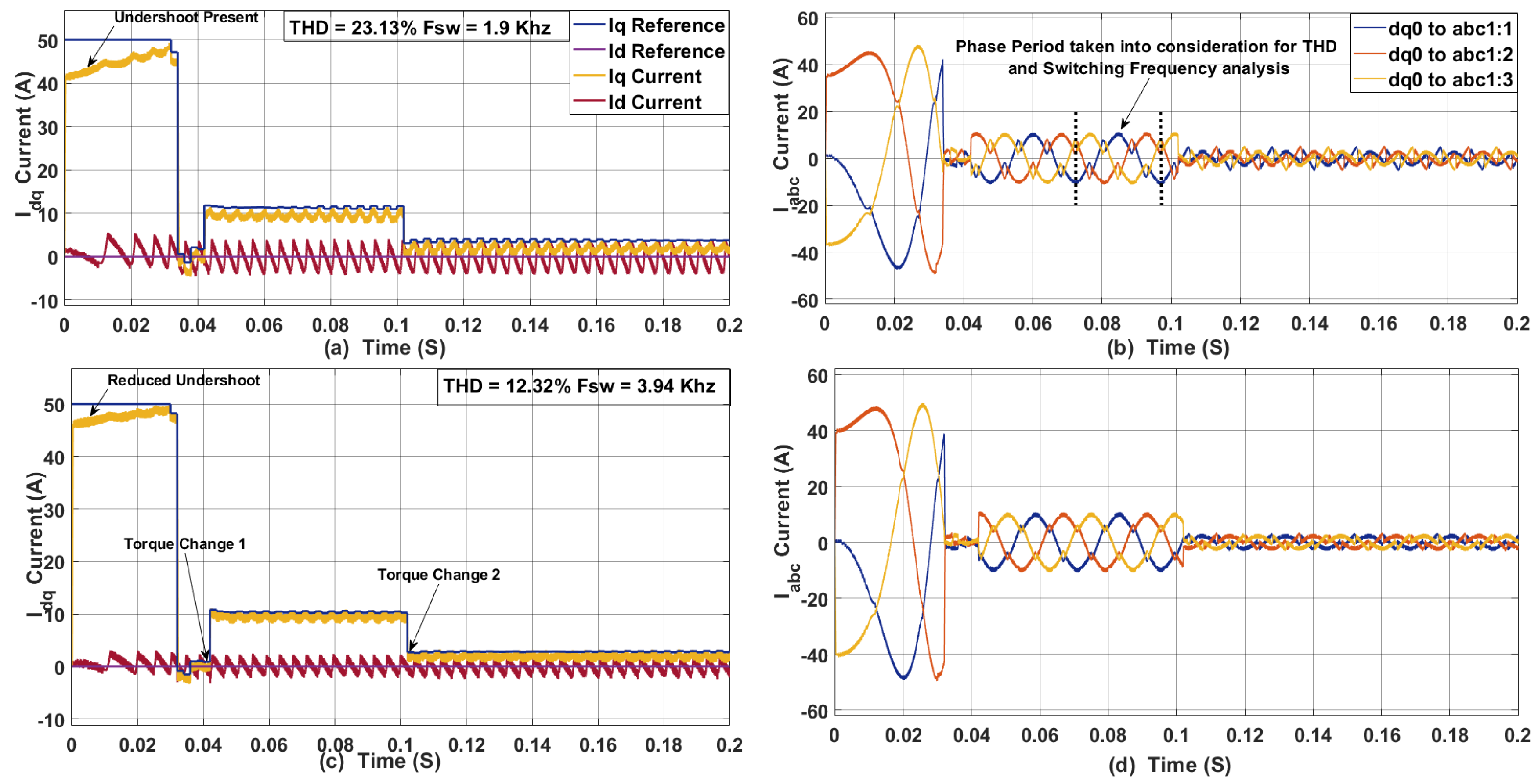
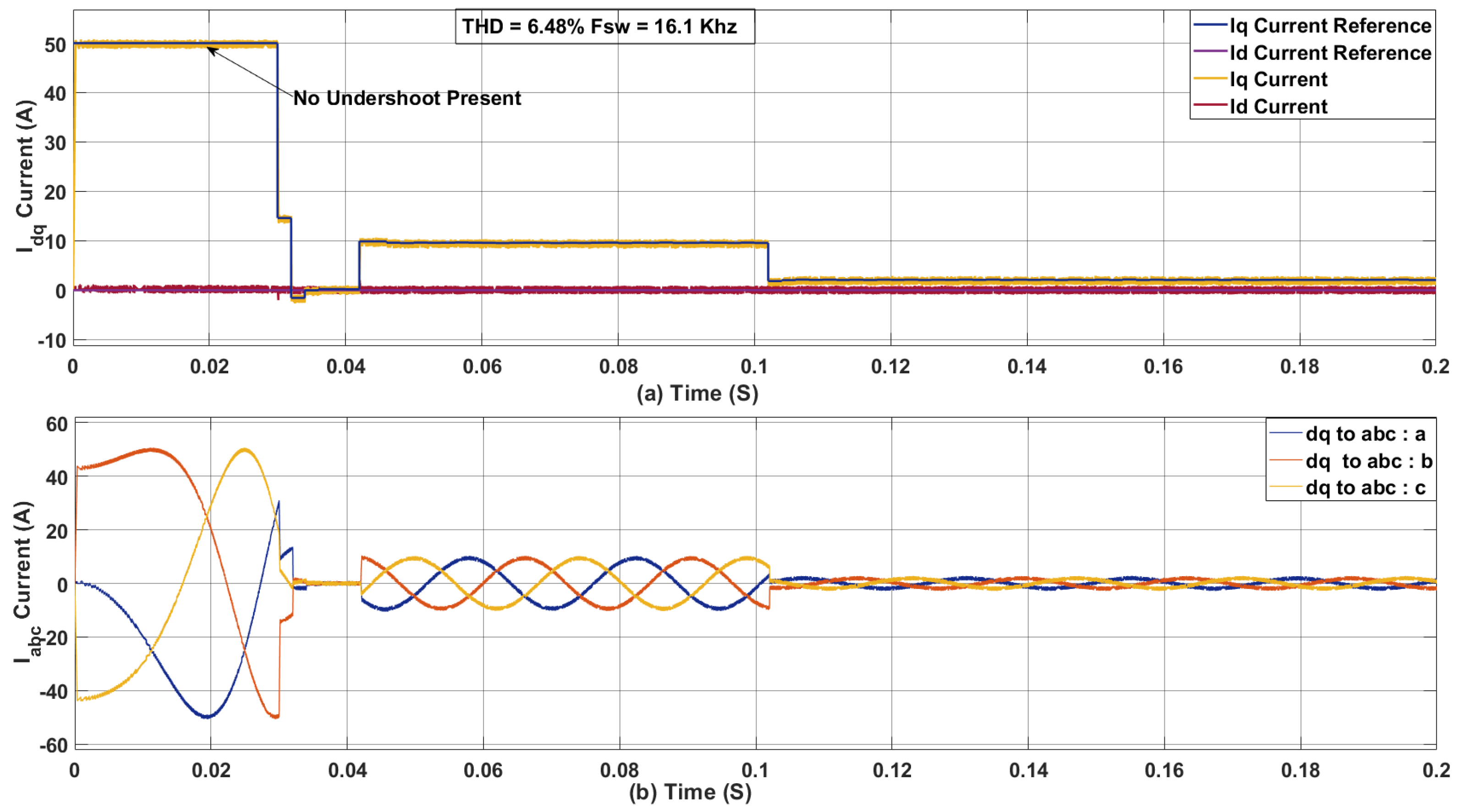
3.7. Coupled Effect of Sampling Time, Control Effort, and Inductance Mismatch on the PMSM Drive
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Weimer, J. Electrical power technology for the more electric aircraft. In Proceedings of the [1993 Proceedings] AIAA/IEEE Digital Avionics Systems Conference, Fort Worth, TX, USA, 25 October 2005–28 October 1993; pp. 445–450. [Google Scholar]
- Liao, C.; Bianchi, N.; Zhang, Z. Recent Developments and Trends in High-Performance PMSM for Aeronautical Applications. Energies 2024, 17, 6199. [Google Scholar] [CrossRef]
- Finken, T.; Felden, M.; Hameyer, K. Comparison and design of different electrical machine types regarding their applicability in hybrid electrical vehicles. In Proceedings of the 2008 18th International Conference on Electrical Machines, Vilamoura, Portugal, 6–9 September 2008; pp. 1–5. [Google Scholar] [CrossRef]
- Ford, A. Brushless generators for aircraft—A review of current developments. Proc. IEE Part A Power Eng. 1962, 109, 437–452. [Google Scholar] [CrossRef]
- Pardo-Vicente, M.A.; Guerrero, J.M.; Platero, C.A.; Sánchez-Férnandez, J.A. Contactless Rotor Ground Fault Detection Method for Brushless Synchronous Machines Based on an AC/DC Rotating Current Sensor. Sensors 2023, 23, 9065. [Google Scholar] [CrossRef] [PubMed]
- Strobl, S. Field Oriented Control (FOC) of Permanent Magnet Synchronous Machine (PMSM). 2021. Available online: https://imperix.com/doc/implementation/field-oriented-control-of-pmsm (accessed on 28 March 2024).
- Aguilera, R.P.; Acuna, P.; Konstantinou, G.; Vazquez, S.; Leon, J.I. Chapter 2—Basic Control Principles in Power Electronics: Analog and Digital Control Design. In Control of Power Electronic Converters and Systems; Blaabjerg, F., Ed.; Academic Press: Cambridge, MA, USA, 2018; pp. 31–68. [Google Scholar] [CrossRef]
- Zhang, Z.; Dragicevic, T.; Li, Y.; Wang, Y.; Zheng, C.; Leng, M.; Rodriguez, J. Chapter 4–Model predictive control of power converters, motor drives, and microgrids. In Control of Power Electronic Converters and Systems; Blaabjerg, F., Ed.; Academic Press: Cambridge, MA, USA, 2021; pp. 101–124. [Google Scholar] [CrossRef]
- Rodriguez, J.; Pontt, J.; Silva, C.A.; Correa, P.; Lezana, P.; Cortes, P.; Ammann, U. Predictive Current Control of a Voltage Source Inverter. IEEE Trans. Ind. Electron. 2007, 54, 495–503. [Google Scholar] [CrossRef]
- Matias Aguirre, M.; Vazquez, S.; Wilson-Veas, A.H.; Kouro, S.; Rojas, C.A.; Leon, J.I.; Franquelo, L.G. Extended Period Control Approach FCS-MPC for Three Phase NPC Power Converters. IEEE Trans. Power Electron. 2025, 40, 4927–4937. [Google Scholar] [CrossRef]
- Vazquez, S.; Rodriguez, J.; Rivera, M.; Franquelo, L.G.; Norambuena, M. Model Predictive Control for Power Converters and Drives: Advances and Trends. IEEE Trans. Ind. Electron. 2017, 64, 935–947. [Google Scholar] [CrossRef]
- Gade, C.R.; W, R.S. Control of Permanent Magnet Synchronous Motor Using MPC–MTPA Control for Deployment in Electric Tractor. Sustainability 2022, 14, 12428. [Google Scholar] [CrossRef]
- Murali, A.; Wahab, R.S.; Gade, C.S.R.; Annamalai, C.; Subramaniam, U. Assessing Finite Control Set Model Predictive Speed Controlled PMSM Performance for Deployment in Electric Vehicles. World Electr. Veh. J. 2021, 12, 41. [Google Scholar] [CrossRef]
- Li, X.; Yang, Q.; Tian, W.; Karamanakos, P.; Kennel, R. A Dual Reference Frame Multistep Direct Model Predictive Current Control With a Disturbance Observer for SPMSM Drives. IEEE Trans. Power Electron. 2022, 37, 2857–2869. [Google Scholar] [CrossRef]
- Dorfling, T.; Mouton, H.; Geyer, T.; Karamanakos, P. Long-Horizon Finite-Control-Set Model Predictive Control With Nonrecursive Sphere Decoding on an FPGA. IEEE Trans. Power Electron. 2019, 69, 7520–7531. [Google Scholar] [CrossRef]
- Karamanakos, P.; Geyer, T. Guidelines for the Design of Finite Control Set Model Predictive Controllers. IEEE Trans. Power Electron. 2020, 35, 7434–7450. [Google Scholar] [CrossRef]
- Zafra, E.; Granado, J.; Lecuyer, V.B.; Vazquez, S.; Alcaide, A.M.; Leon, J.I.; Franquelo, L.G. Computationally Efficient Sphere Decoding Algorithm Based on Artificial Neural Networks for Long-Horizon FCS-MPC. IEEE Trans. Ind. Electron. 2024, 71, 39–48. [Google Scholar] [CrossRef]
- Geyer, T.; Quevedo, D.E. Multistep Finite Control Set Model Predictive Control for Power Electronics. IEEE Trans. Power Electron. 2014, 29, 6836–6846. [Google Scholar] [CrossRef]
- Zafra, E.; Vazquez, S.; Alcaide, A.M.; Franquelo, L.; Leon, J.; Pérez, E. K-Best Sphere Decoding Algorithm for Long Prediction Horizon FCS-MPC. IEEE Trans. Ind. Electron. 2021, 69, 7571–7581. [Google Scholar] [CrossRef]
- Akinwumi, J.O.; Gao, Y.; West, G.T.; Ruiz, H.S. Optimisation Algorithms in Multi-Step Prediction Horizon MPC for Two-Level Inverters. In Proceedings of the 2024 International Symposium on Electrical, Electronics and Information Engineering (ISEEIE), Leicester, UK, 26–28 September 2024; pp. 115–122. [Google Scholar] [CrossRef]
- Lin, C.K.; Liu, T.H.; Yu, J.t.; Fu, L.C.; Hsiao, C.F. Model-Free Predictive Current Control for Interior Permanent-Magnet Synchronous Motor Drives Based on Current Difference Detection Technique. IEEE Trans. Ind. Electron. 2014, 61, 667–681. [Google Scholar] [CrossRef]
- Lin, C.K.; Yu, J.t.; Lai, Y.S.; Yu, H.C. Improved Model-Free Predictive Current Control for Synchronous Reluctance Motor Drives. IEEE Trans. Ind. Electron. 2016, 63, 3942–3953. [Google Scholar] [CrossRef]
- Yuan, X.; Zhang, S.; Zhang, C. Improved Model Predictive Current Control for SPMSM Drives with Parameter Mismatch. IEEE Trans. Ind. Electron. 2019, 67, 852–862. [Google Scholar] [CrossRef]
- Ortombina, L.; Karamanakos, P.; Zigliotto, M. Robustness Analysis of Long-Horizon Direct Model Predictive Control: Permanent Magnet Synchronous Motor Drives. In Proceedings of the 2020 IEEE 21st Workshop on Control and Modeling for Power Electronics (COMPEL), Aalborg, Denmark, 9–12 November 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Geyer, T.; Quevedo, D.E. Multistep direct model predictive control for power electronics — Part 2: Analysis. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 1162–1169. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, Z. Multi-Stage Series Model Predictive Control for PMSM Drives. IEEE Trans. Veh. Technol. 2021, 70, 6591–6600. [Google Scholar] [CrossRef]
- Jeong, I.; Hyon, B.J.; Nam, K. Dynamic Modeling and Control for SPMSMs With Internal Turn Short Fault. IEEE Trans. Power Electron. 2013, 28, 3495–3508. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, J.; Wang, S.; Guo, Y.; Xu, W. Nonlinear Magnetic Model of Surface Mounted PM Machines Incorporating Saturation Saliency. IEEE Trans. Magn. 2009, 45, 4684–4687. [Google Scholar] [CrossRef]
- Mohamed, I.S.; Rovetta, S.; Do, T.D.; Dragicevic, T.; Diab, A.A.Z. A Neural-Network-Based Model Predictive Control of Three-Phase Inverter With an Output LC Filter. IEEE Access 2019, 7, 124737–124749. [Google Scholar] [CrossRef]
- Bi, E.; Yang, J.; Liu, Y.; Wang, X. Multistep finite-control-set model predictive control of active power filter. IOP Conf. Ser. Earth Environ. Sci. 2020, 617, 012039. [Google Scholar] [CrossRef]
- Xia, C.; Liu, T.; Shi, T.; Song, Z. A Simplified Finite-Control-Set Model-Predictive Control for Power Converters. IEEE Trans. Ind. Inform. 2014, 10, 991–1002. [Google Scholar] [CrossRef]
- Narimani, M.; Wu, B.; Yaramasu, V.; Cheng, Z.; Zargari, N.R. Finite Control-Set Model Predictive Control (FCS-MPC) of Nested Neutral Point-Clamped (NNPC) Converter. IEEE Trans. Power Electron. 2015, 30, 7262–7269. [Google Scholar] [CrossRef]
- Karamanakos, P.; Geyer, T.; Kennel, R. On the Choice of Norm in Finite Control Set Model Predictive Control. IEEE Trans. Power Electron. 2018, 33, 7105–7117. [Google Scholar] [CrossRef]
- Zheng, C.; Dragicevic, T.; Blaabjerg, F. Current-Sensorless Finite-Set Model Predictive Control for LC-Filtered Voltage Source Inverters. IEEE Trans. Power Electron. 2020, 35, 1086–1095. [Google Scholar] [CrossRef]
- Kouro, S.; Cortes, P.; Vargas, R.; Ammann, U.; Rodriguez, J. Model Predictive Control—A Simple and Powerful Method to Control Power Converters. IEEE Trans. Ind. Electron. 2009, 56, 1826–1838. [Google Scholar] [CrossRef]
- Geyer, T. Model Predictive Control of High Power Convertersand Industrial Drives; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2016; pp. 1–545. [Google Scholar] [CrossRef]
- Acuna, P.; Rojas, C.A.; Baidya, R.; Aguilera, R.P.; Fletcher, J.E. On the Impact of Transients on Multistep Model Predictive Control for Medium-Voltage Drives. IEEE Trans. Power Electron. 2019, 34, 8342–8355. [Google Scholar] [CrossRef]
- Agrell, E.; Eriksson, T.; Vardy, A.; Zeger, K. Closest point search in lattices. IEEE Trans. Inf. Theory 2002, 48, 2201–2214. [Google Scholar] [CrossRef]
- Zafra, E.; Vazquez, S.; Geyer, T.; Aguilera, R.P.; Franquelo, L.G. Long Prediction Horizon FCS-MPC for Power Converters and Drives. IEEE Open J. Ind. Electron. Soc. 2023, 4, 159–175. [Google Scholar] [CrossRef]
- Karamanakos, P.; Geyer, T.; Kennel, R. Suboptimal search strategies with bounded computational complexity to solve long-horizon direct model predictive control problems. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 334–341. [Google Scholar] [CrossRef]
- Luo, G.; Zhang, R.; Chen, Z.; Tu, W.; Zhang, S.; Kennel, R. A Novel Nonlinear Modeling Method for Permanent-Magnet Synchronous Motors. IEEE Trans. Ind. Electron. 2016, 63, 6490–6498. [Google Scholar] [CrossRef]







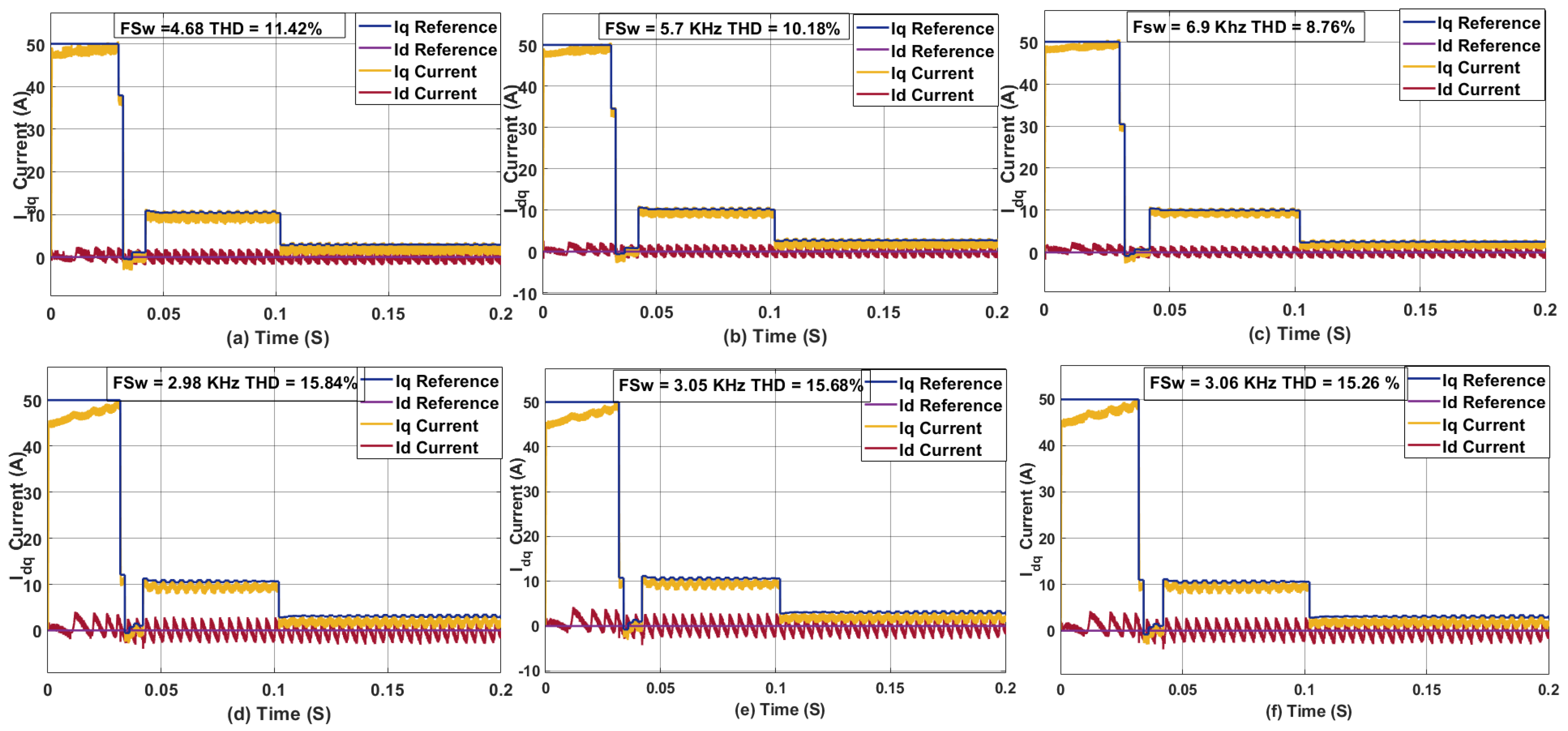
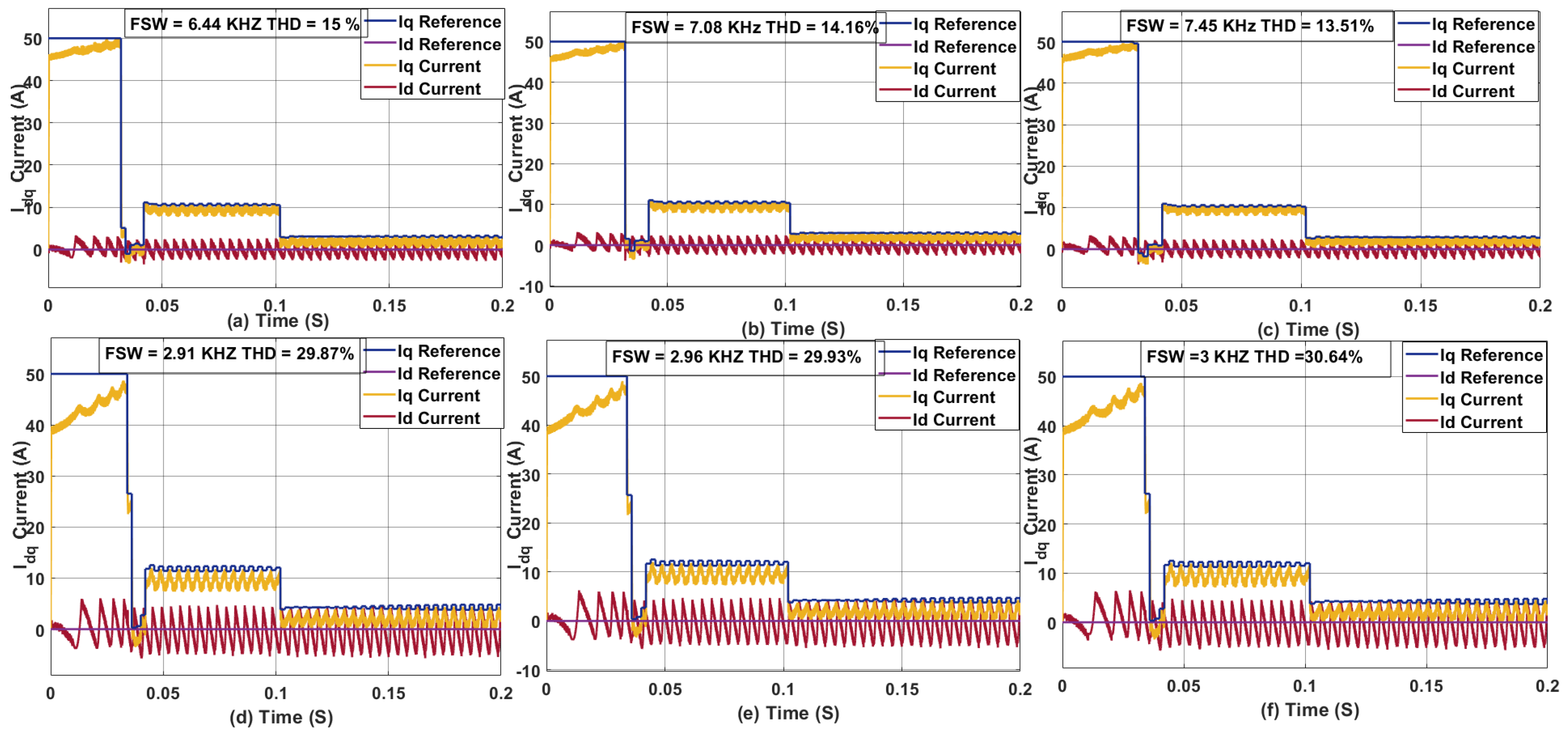

| Sampling Time s | Sampling Frequency (KHz) | Switching Frequency (KHz) | THD (%) |
|---|---|---|---|
| 20 | 50 | 9.87 | 10.67 |
| 40 | 25 | 4.94 | 21.16 |
| 80 | 12.5 | 2.51 | 41.85 |
| Sampling Time s | Sampling Frequency (KHz) | Switching Frequency (KHz) | THD (%) |
|---|---|---|---|
| 20 | 50 | 9.84 | 10.75 |
| 40 | 25 | 4.76 | 21.04 |
| 80 | 12.5 | 2.39 | 42.32 |
| Optimization Algorithm | ||||
|---|---|---|---|---|
| FCS-MPC | 5.63–16 | - | - | - |
| SDA | 4.5–11 | 46–69 | 50–57 | 55–57 |
| Prediction Horizon | 5 × | 0.2 × | 10 × |
|---|---|---|---|
| 2-Step | 12.97 (6.995 | 13.01 (7.034 | 13.13 (6.97 |
| 3-Step | 13.00 (6.545 | 12.99 (6.547 | 13.38 (6.325 |
| 5-Step | 10.15 (9.543 | 10.08 (9.543 | 10.14 (9.3607 |
| Prediction Horizon | 0.1 × | 0.5 × | 2 × | 5 × |
|---|---|---|---|---|
| 2-Step | 13.05 (6.98 | 12.81 (7.0282 | 12.69 (7.0051 KHz) | 13.07 (7.0355 |
| 3-Step | 13.10 (6.585 | 13.22 (6.6065 | 13.19 (6.5679 | 13.13 (6.5767 |
| 5-Step | 10.27 (9.4064 | 9.97 (9.5314 | 9.70 (9.4994 | 10.07 (9.4714 |
| Prediction Horizon | 0.1 × | 0.5 × | 2 × | 5 × |
|---|---|---|---|---|
| 2-Step | 29.72 (1.58 | 12.85 (8.4147 | 18.37 (4.4052 KHz) | 39.60 (3.108 KHz) |
| 3-Step | 29.67 (1.62 | 11.20 (10.448 | 12.48 (7.0995 KHz) | 22.22 (4.3292 |
| 5-Step | 29.37 (1.6717 | 9.57 (13.647 | 13.20 (7.0751 | 12.09 (7.3826 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akinwumi, J.O.; Gao, Y.; Yuan, X.; Vazquez, S.; Ruiz, H.S. Comparative Study of Sphere Decoding Algorithm and FCS-MPC for PMSMs in Aircraft Application. Aerospace 2025, 12, 458. https://doi.org/10.3390/aerospace12060458
Akinwumi JO, Gao Y, Yuan X, Vazquez S, Ruiz HS. Comparative Study of Sphere Decoding Algorithm and FCS-MPC for PMSMs in Aircraft Application. Aerospace. 2025; 12(6):458. https://doi.org/10.3390/aerospace12060458
Chicago/Turabian StyleAkinwumi, Joseph O., Yuan Gao, Xin Yuan, Sergio Vazquez, and Harold S. Ruiz. 2025. "Comparative Study of Sphere Decoding Algorithm and FCS-MPC for PMSMs in Aircraft Application" Aerospace 12, no. 6: 458. https://doi.org/10.3390/aerospace12060458
APA StyleAkinwumi, J. O., Gao, Y., Yuan, X., Vazquez, S., & Ruiz, H. S. (2025). Comparative Study of Sphere Decoding Algorithm and FCS-MPC for PMSMs in Aircraft Application. Aerospace, 12(6), 458. https://doi.org/10.3390/aerospace12060458









