Unsteady Numerical Investigation into the Impact of Isolator Motion on High-Mach-Number Inlet Restart via Throat Adjustment

Abstract

This paper focuses on exploring the variable throat-assisted restart method for high-Mach-number inlets. A two-dimensional adjustable throat hypersonic inlet was designed, and unsteady numerical simulations were carried out on its restart process, which was triggered by unstart induced by excessive back pressure and assisted by throat adjustment. The Chimera grid technique was used for grid generation, and the simulations were performed on the ARI_CFD platform. Results show that during the throat adjustment restart process, different flow states emerged with an increase in adjustment height. Specifically, when the adjustment height was too low, an unstarted flow state existed; within a specific height range (with lower and upper critical heights of 1.190 and 1.196, respectively, in this study), a fully restarted flow state occurred; and when the height was too high, an off-design flow state induced by the separation region in the internal contraction section occurred. The geometric adjustment time and throat adjustment angle also had a significant impact on the restart process. Shorter adjustment times and larger adjustment angles expanded the adjustment interval for full restart, as the rotation of the isolator helps reduce the resistance of the separation bubble’s downstream movement on the compression surface, thereby facilitating the full restart of the inlet.

1. Introduction

In an air-breathing ramjet engine, the inlet is a crucial aerodynamic component tasked with capturing and compressing air. Its working state significantly impacts the overall propulsion system’s performance. Generally, the inlet has two working states: started and unstarted. The main reasons for inlet non-starting are low incoming flow Mach numbers [1], excessive internal contraction ratio of the inlet [2], high back pressure [3], thermal throat, etc. When the inlet fails to start, the captured flow rate drops sharply, and spillage drag and pressure-difference drag increase substantially, deteriorating the propulsion system performance, reducing thrust rapidly, and potentially damaging the aircraft structure. Thus, the inlet start/unstart issue has always attracted extensive attention. Based on the approximately inviscid assumption, Kantrowitz and Donaldson proposed two limits for the self-starting contraction ratio [4]. Specifically, if the inlet’s internal contraction ratio is less than the Kantrowitz limit, self-starting can be achieved without external help. However, if it exceeds the isentropic limit, self-starting becomes unfeasible.

To balance compression efficiency and starting performance, the inlet’s internal contraction ratio is often designed within the dual-solution region [5,6,7,8,9]. Therefore, when the inlet fails to start, additional technical measures are needed to restart it. Currently, the main auxiliary restart technical means include suction [10,11], plasma control and magnetohydrodynamic control [12], active jet control [13], vortex generator control [14], and variable geometry adjustment control [15,16]. Since variable geometry adjustment can coordinate various moving parts during flight, adjust the compression wave system and internal contraction ratio in real time to meet the compression requirements of incoming flow at different Mach numbers, and ensure high-performance compression and starting at various flight Mach numbers, variable-geometry-assisted inlet restart technology has been widely applied. Currently, adjustable inlets are mainly achieved by rotating [17,18], translating [19] the lip cowl, or adjusting the throat [20,21,22]. When the inlet fails to start, whether by adjusting the lip or changing the throat, restart is achieved by reducing the internal contraction ratio. With the gradual ingestion of the separation region in front of the lip and the continuous changes in the complex wave structure, the flow evolution during the restart process is highly complex. After the geometric adjustment of the inlet is completed, different flow states can exist, such as the unstarted flow state induced by large-scale flow separation in front of the lip and the restarted flow state with the separation region completely ingested. In addition, our research group previously discovered that when the cowl rotation angle is between the upper and lower critical angles, an off-designed flow state induced by a medium- and small-scale separation region within the contraction section will occur [15]. Jin Yi from Nanjing University of Aeronautics and Astronautics also observed the existence of this non-designed flow state in experiments [16,23]. Although this flow state does not affect the inlet’s flow capture, it reduces the inlet’s total pressure recovery. Therefore, the evolution process of the flow field structure of this flow state deserves attention.

In the field of variable geometry inlet, lip adjustment and throat adjustment are two equally important methods. Although previous studies by our research group on rotating lips have revealed the existence of off-design flow states, it remains unclear whether off-design flow states will occur during throat adjustment and under what conditions they will occur. On the other hand, currently, most of the adjustment schemes for the throat of hypersonic inlets adopt the strategy of translating the isolator [20,21,22]. Whether the motion form and law of the isolator can avoid the occurrence of the off-design flow state and its influence on the flow characteristics requires further research.

In response to the above-mentioned issues, this paper designs a two-dimensional hypersonic inlet with an adjustable throat. Aiming to investigate the inlet non-start phenomenon caused by excessive back pressure, an unsteady numerical simulation study on the adjustable-throat-assisted restart process is carried out. Through the coordinated movement of multiple components, the translation and rotation of the throat isolator are achieved, and the influence of the isolator’s movement form and law on the inlet–restart process is analyzed in detail.

2. Variable Geometry Scheme for Inlet

2.1. Inlet Model

Figure 1 depicts the geometric details of a typical two-dimensional mixed-compression inlet model featuring an adjustable throat. The design conditions for this inlet are a Mach number of 4.0, an angle of attack of 0°, and a flight altitude of 24 km.

The inlet comprises a main structure, a throat adjustment mechanism on the compression surface side, and a cowl. The main structure consists of a first-stage compression surface and a second-stage compression surface. The throat adjustment mechanism is made up of a third-stage compression surface, an isolator, a diffuser, a horizontal sliding section, and two actuators that drive the mechanical movements of these components. In the design state, the isolator is horizontally positioned.

The throat height $H_t$ is 34.39 mm, the inlet exit height is 70 mm, and the internal contraction ratio is 1.5, falling within the dual-solution region, which means that when the flow field in front of the inlet is “clean” (without obvious disturbances or shock wave interference), the airflow can smoothly enter the inlet and achieve starting. When the flow field in front of the inlet is “severe” (with interfering shock waves and separation vortices), the inlet cannot achieve self-starting. For the remaining detailed dimensions of the inlet, refer to

Table 1. Parameters of the inlet.

Parameter	Valve
${\theta }_1$	5.79°
${\theta }_2$	14.10°
${\theta }_3$	23.89°
${\theta }_4$	14.10°
Point A (mm)	(236.53, 23.99)
Point B (mm)	(381.52, 60.42)
Point C (mm)	(661.88, 165.61)
Point D (mm)	(801.88, 165.61)
Point E (mm)	(1101.88, 110.00)
Point F (mm)	(1151.88, 110.00)
Point G (mm)	(509.87, 173.69)
Isolator length (mm)	140
Inlet total length (mm)	1251.88

.

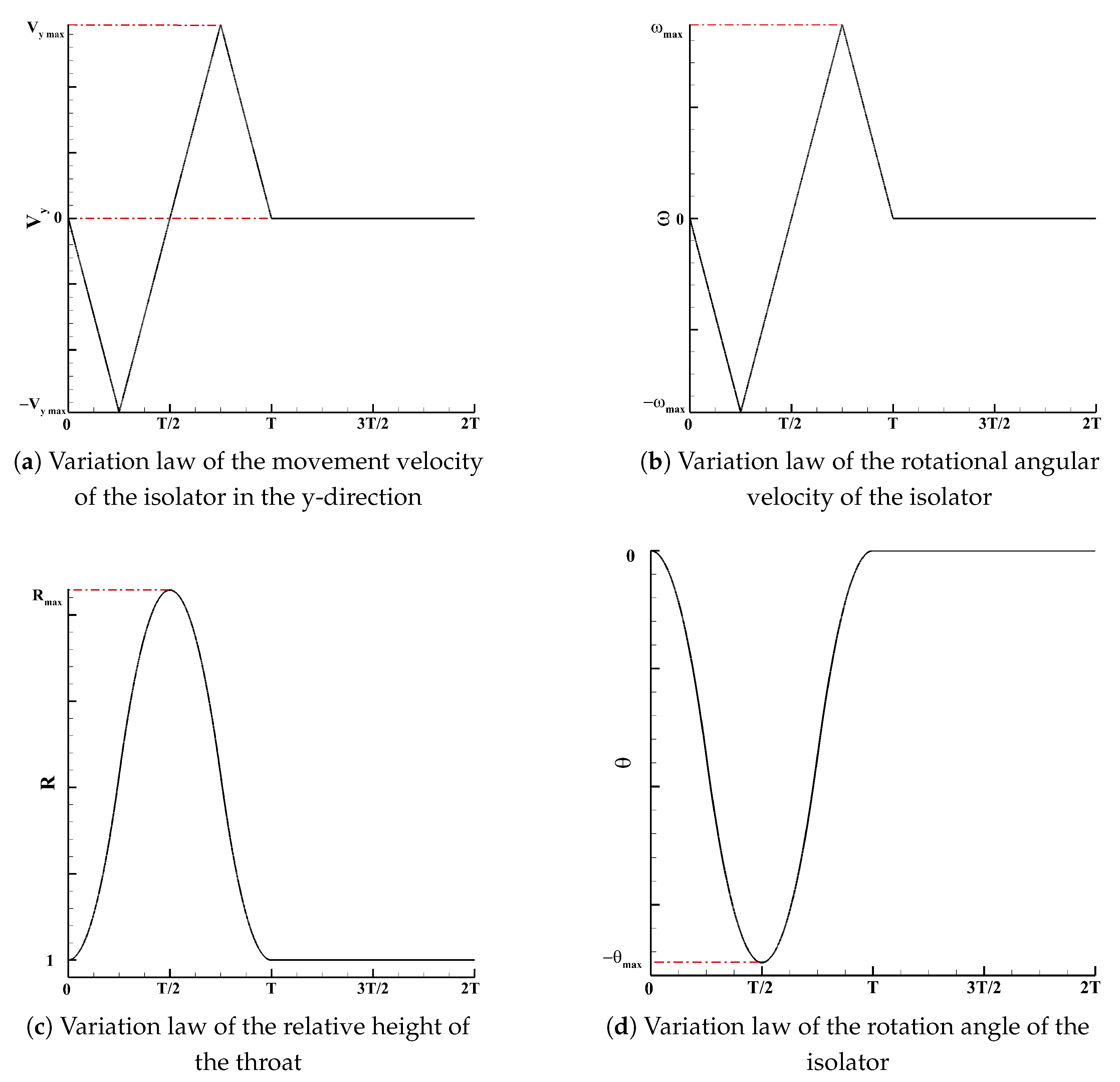
2.2. Throat Adjustment Mechanism

As depicted in Figure 1, hinge connections are located at points B, C, D, and E, while a sliding connection is positioned at point F. The adjustment of the throat is primarily accomplished by a four-bar linkage mechanism. The overall degree of freedom of the throat adjustment mechanism is 2. Consequently, through the coordinated operation of actuator 1 and actuator 2, the translation or rotation of the isolator can be effectively achieved.

During numerical simulations, the motion law of the isolation section is explicitly defined, and the remaining moving components move in strict accordance with the established motion and geometric constraints. To guarantee the convenience and precision of the calculation process, a 0.5 mm gap is deliberately set at the hinge and sliding connection positions between different components.

The velocity of the isolator’s movement in the y-direction is denoted as $V_y$, $V_y$ denotes the vertical velocity component of the isolator, describing its translational motion along the y-axis during geometric adjustment, the rotational angular velocity of the isolator around point C is $\omega$, and the relative height is R, which can be expressed as

$$\begin{array}{c}\hfill R={\displaystyle \frac{H_t^{\prime }}{H_t}}\end{array}$$

(1)

where $H_t^{\prime }$ represents the throat height during the geometric adjustment process, and the angle between the isolator and the x-axis is $\theta$. In the initial design state, $V_y=0$, $\omega =0$, $R=1$, and $\theta =0^{\circ }$.

The throat height difference is generated by the vertical translation of the isolator driven by actuator 1, which changes the geometric distance between the compression surface and the cowl. The four-bar linkage ensures smooth motion, while actuator 2 can adjust the isolator’s rotation angle during translation. In order to avoid abrupt acceleration and deceleration of the isolator during the geometric adjustment, the isolator is designed to move with a uniformly variable motion. Figure 2 presents a schematic illustration of the isolator motion law throughout the entire geometric adjustment period T. The movement velocity $V_y$ and angular velocity $\omega$ both become zero at three specific moments: $t=0$ (start time), $t=T/2$ (the relative height R and angle $\theta$ each reach their maximum values, namely the throat adjustment height $R_{max}$ and the throat adjustment angle ${\theta }_{max}$) and $t=T$ (the inlet profile reverts to its original state). Then, the calculation is continued for a period of time to observe whether obvious changes occur in the flow field structure.

3. Numerical Method and Validation

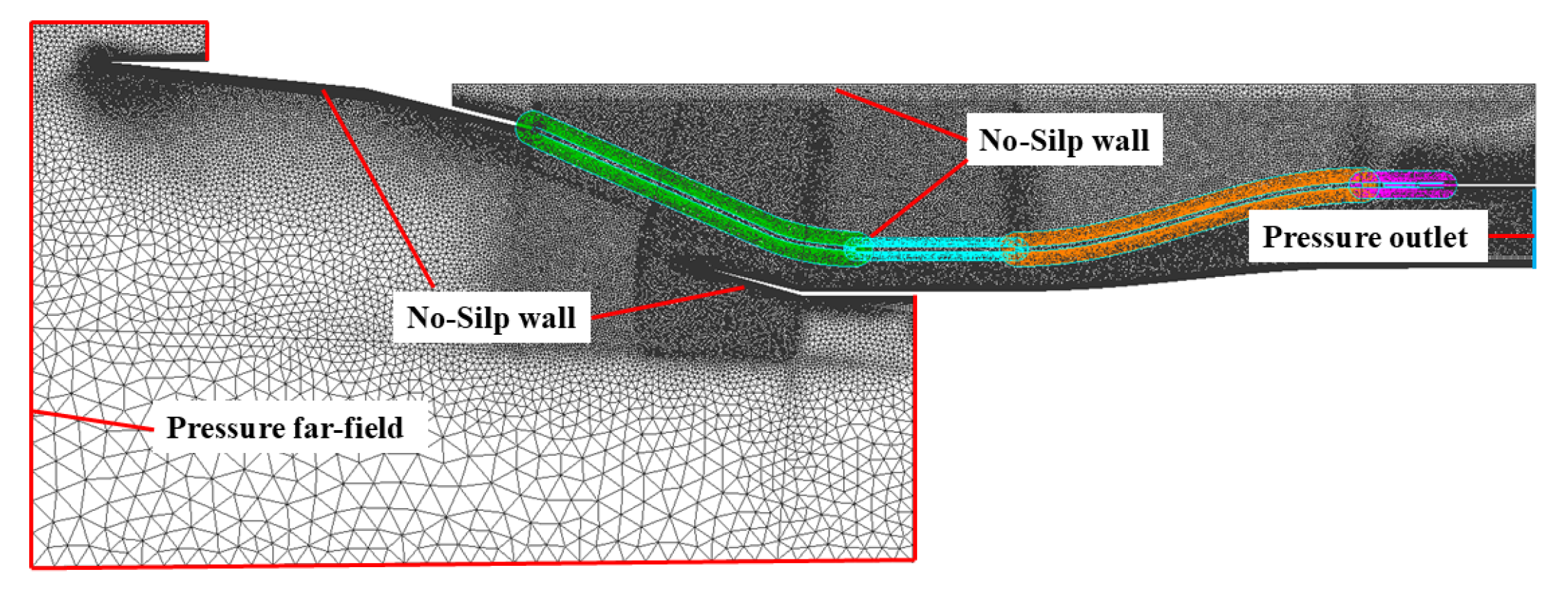
3.1. Chimera Grid

The overset grid technique [15] merges multiple grid blocks through hole-cutting and interpolation methods. It then implements corresponding motion control strategies for different grid blocks, enabling the dynamic simulation of multi-body relative motion.

As illustrated in Figure 3 and Figure 4, the inlet grid is divided into background grids and moving component grids. The moving component grids comprise the third-stage compression surface (colored green), the isolator (colored blue), the diffuser (colored orange), and the horizontal sliding section (colored purple). These moving component grids will cut away the redundant portions within the background grids to generate a complete grid, as presented in Figure 5.

The first-layer grid height of 0.01 mm ensures y ≈ 1 at the design condition, suitable for resolving the viscous sublayer with the SA model. To better analyze a more realistic flow state, the grids inside the inlet are refined appropriately. This refinement ensures that the flow characteristics can be captured more accurately, providing a more reliable basis for subsequent simulations and analyses.

3.2. Numerical Simulation Setup

This study employs the ARI_CFD numerical simulation platform, which is independently developed by the AVIC Aerodynamics Research Institute, to carry out numerical simulation research on the dynamic aerodynamic characteristics of hypersonic inlet throat adjustment.

The two-dimensional unsteady Reynolds-Averaged Navier–Stokes (RANS) equations are used as the basic governing equations. These equations describe the conservation of mass, momentum, and energy for a fluid flow. Mathematically, the continuity equation is

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial \rho }{\partial t}}+\nabla ·\left(\rho \mathbf{v}\right)=0\end{array}$$

(2)

where $\rho$ is the density of the fluid, t is time, $\mathbf{v}$ is the velocity vector.

The momentum equation is

$$\begin{array}{c}\hfill \rho \left({\displaystyle \frac{\partial \mathbf{v}}{\partial t}}+\left(\mathbf{v}·\nabla \right)\mathbf{v}\right)=\rho f-\nabla p+\mu {\nabla }^2\mathbf{v}+\left(\mu +\lambda \right)\nabla \left(\nabla ·\mathbf{v}\right)\end{array}$$

(3)

where p is the pressure, f is the gravitational force, and $\mu$ and $\lambda$ are the first and second viscosity coefficients, respectively.

The energy equation can be written as

$$\begin{array}{c}\hfill \rho \left({\displaystyle \frac{\partial e}{\partial t}}+\nabla ·e\mathbf{v}\right)=\rho f\mathbf{v}+Q-\nabla ·q+\nabla ·\left(\mathbf{v}·\tau -p\mathbf{v}\right)\end{array}$$

(4)

In the formula, e is the total energy per unit mass, including internal energy and kinetic energy. Q is the external energy source term for heat conduction $q=-k\nabla T$, k is the thermal conductivity coefficient, and T is the temperature; $\tau$ is the viscous stress tensor.

The SA model was selected for its balance of computational efficiency and accuracy in hypersonic flows with shock–boundary layer interactions, as validated in prior studies [15]. Its transport equation is

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial }{\partial t}}\left(\rho \tilde{v}\right)+{\displaystyle \frac{\partial }{\partial x_i}}\left(\rho \tilde{v}{u}_i\right)=G_v+{\displaystyle \frac{1}{{\sigma }_{\tilde{v}}}}\left[{\displaystyle \frac{\partial }{\partial x_j}}\left\{(\mu +\rho \tilde{v}){\displaystyle \frac{\partial \tilde{v}}{\partial x_j}}\right\}+C_{b2}\rho {\left({\displaystyle \frac{\partial \tilde{v}}{\partial x_j}}\right)}^2\right]-Y_v\end{array}$$

(5)

In the above formula, $G_v$ represents the generation term of turbulent viscosity. $Y_v$ is the destruction term of turbulent viscosity caused by the obstruction of the airflow near the wall surface and the reasons related to viscosity. ${\sigma }_{\tilde{v}}$ and $C_{b2}$ are constants. For a detailed introduction to this turbulence model, please refer to Reference [24]. For the spatial discretization of inviscid terms, the second-order accurate Roe scheme is implemented, while the second-order central difference scheme is adopted for viscous terms.

The far-field boundary condition is set as the Riemann non-reflective condition, ensuring that disturbances such as pressure waves propagating from the interior of the computational domain to the far-field boundary can pass through the boundary without reflection, avoiding the generation of non-physical reflected waves at the boundary. For supersonic flow, the inflow value is taken as the free-stream value, and the outflow value is interpolated from the field. For subsonic and transonic flows, the Riemann invariants are processed as follows:

$$\begin{array}{c}\hfill \begin{array}{c}{R}_{\infty }={\overrightarrow{V}}_{\infty }·\overrightarrow{n}-{\displaystyle \frac{2c_{\infty }}{\gamma -1}}\\ R_{inner}={\overrightarrow{V}}_{inner}·\overrightarrow{n}+{\displaystyle \frac{2c_{inner}}{\gamma -1}}\end{array}\Rightarrow \begin{array}{c}{\overrightarrow{V}}_0·\overrightarrow{n}={\displaystyle \frac{1}{2}}\left(R_{\infty }+R_{inner}\right)\\ c_0={\displaystyle \frac{\gamma -1}{4}}\left(R_{inner}-R_{\infty }\right)\end{array}\end{array}$$

(6)

From this, we can obtain $u_0$ and $v_0$; additionally,

$$\begin{array}{c}\hfill \begin{array}{c}{\rho }_0={\left({\displaystyle \frac{c_0^2{S}_0}{\gamma }}\right)}^{{\displaystyle \frac{1}{\gamma -1}}}\end{array}\end{array}$$

(7)

$$\begin{array}{c}\hfill \begin{array}{c}{p}_0={\displaystyle \frac{c_0^2{\rho }_0}{\gamma }}\end{array}\end{array}$$

(8)

$$\begin{array}{c}\hfill \begin{array}{c}{E}_0={\displaystyle \frac{V_0^2}{2}}+{\displaystyle \frac{p_0}{{\rho }_0\left(\gamma -1\right)}}\end{array}\end{array}$$

(9)

where, $S_0={\displaystyle \frac{{\rho }_{\infty }^{\gamma }}{p_{\infty }}}\left({\overrightarrow{V}}_0·\overrightarrow{n}<0\right)$ or $S_0={\displaystyle \frac{{\rho }_{inner}^{\gamma }}{p_{inner}}}\left({\overrightarrow{V}}_0·\overrightarrow{n}>0\right)$.

The subscript ∞ represents the far-field value of the flow field at the boundary, the subscript 0 represents the boundary value, and the subscript $inner$ represents the value of the grid cell adjacent to the boundary.

The pressure outlet condition is applied at the inlet and outlet, and a no-slip adiabatic wall is used for the physical surface. This is because the focus of our research is to explore the influence of the isolator’s motion on the restart of a high-Mach-number inlet through throat adjustment. Given the complexity of the flow physical phenomena involved in this process, such as shock wave–boundary layer interactions, flow separation, and reattachment, we need to simplify certain aspects to isolate the key factors. The adiabatic wall assumption is a commonly used and well-studied boundary condition in hypersonic flow research [25,26]. It enables us to focus on the overall flow field changes caused by the throat adjustment and the isolator’s motion, without making the problem overly complicated by the additional heat transfer effects at the wall. During numerical solution, the flow field is directly solved up to the wall surface, and the height of the first layer of the grid near the wall is 0.01 mm to ensure that $y+\approx 1$ for boundary layer resolution. The gas is assumed to be an ideal gas, so we used the equation of state $p=\rho RT$, where R is the specific gas constant for air. The thermophysical properties of air, such as specific heat at constant pressure $C_p$ and specific heat at constant volume $C_v$, were set according to the standard values for air at the given flight altitude (24 km in our study).

In unsteady calculations, the implicit LU-SGS time-marching method is adopted. Drawing on the previous research findings of our research group [15], the time step is determined to be 1 ms. By introducing sub-iterations, a relatively high-precision solution in the time domain is achieved, with the number of sub-iteration steps set to 50. The free-stream Mach number is 4.0, and the calculation altitude is 24 km.

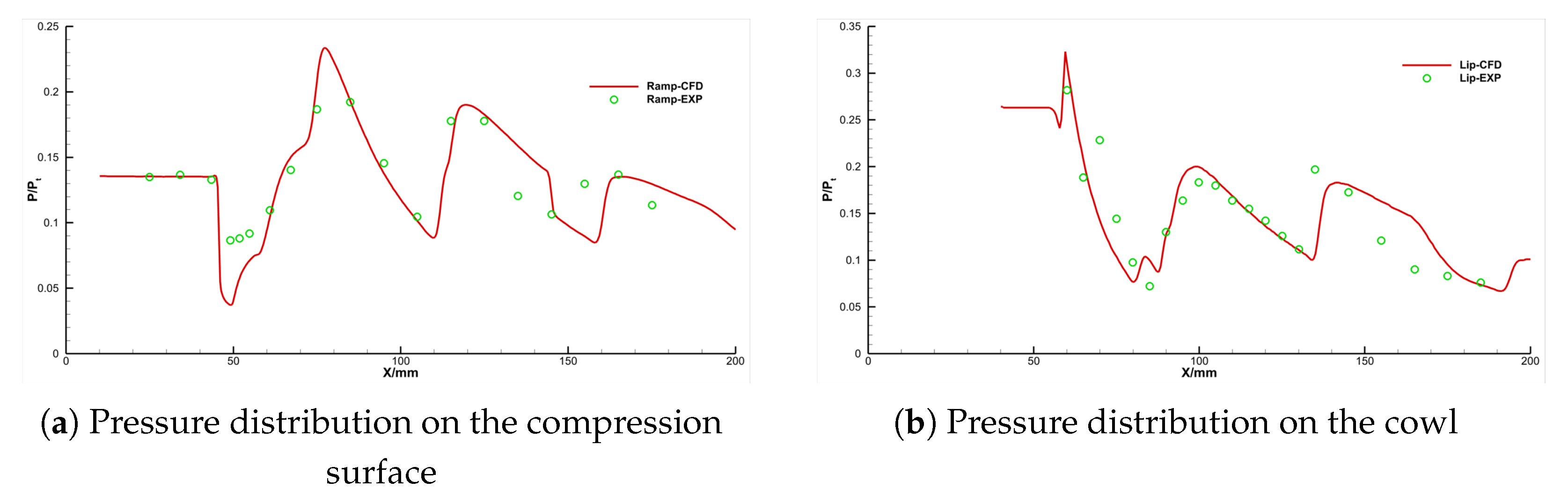
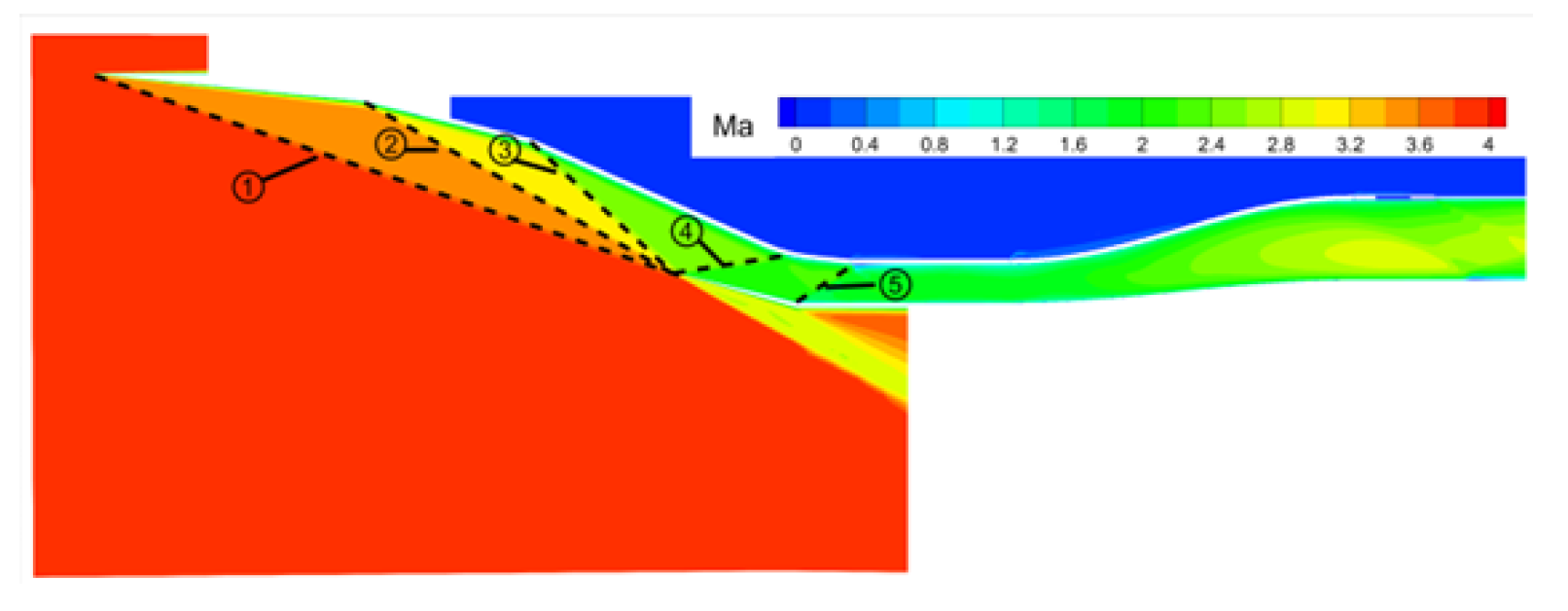
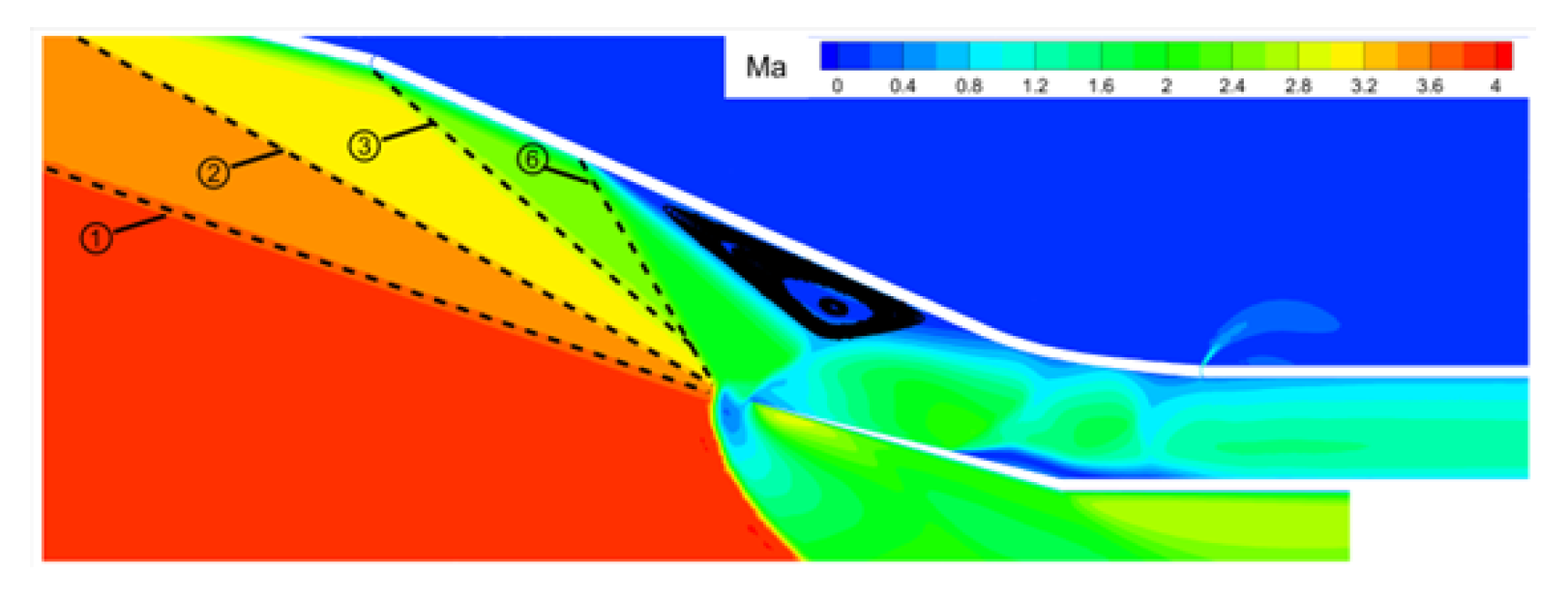
3.3. Validation

In hypersonic inlets, multiple shock wave reflections commonly occur, and the shock wave–boundary layer interaction renders the flow highly complex. The inlet model from Reference [27] is chosen for numerical simulation and compared with experimental data. Under the experimental conditions, the incoming flow has a Mach number of 2.5, a total pressure of 5.6 bar, and a total temperature of 295 K.

Figure 6 shows the comparison of pressure distributions on the compression surface side and the lip sidewall between the experimental and numerical results in this paper. Evidently, the wall pressure distributions of the experimental and calculated results are remarkably close, and the positions of the extreme and inflection points of the curves are accurately predicted, effectively reproducing the internal flow field of the two-dimensional inlet with separation regions and shock wave reflections. Figure 7 presents the comparison between the color experimental schlieren in reference [27] and the numerical schlieren of this paper’s calculation. It can be seen that the flow field distributions of the experimental and numerical results are essentially identical. The calculation results have successfully captured the wave system structure in the flow field, with the positions and reflections of the lip shock wave, separation shock wave, and reattachment shock wave being very similar in both the experimental and calculated results.

Moreover, the overset grid method, a key technology of the ARI_CFD platform, has yielded reliable results in dynamic numerical simulations of numerous multi-body relative motions, such as weapon release and variable geometry inlet/exhaust systems. Its reliability has been fully validated in previous studies [28,29,30] and will not be elaborated on further here.

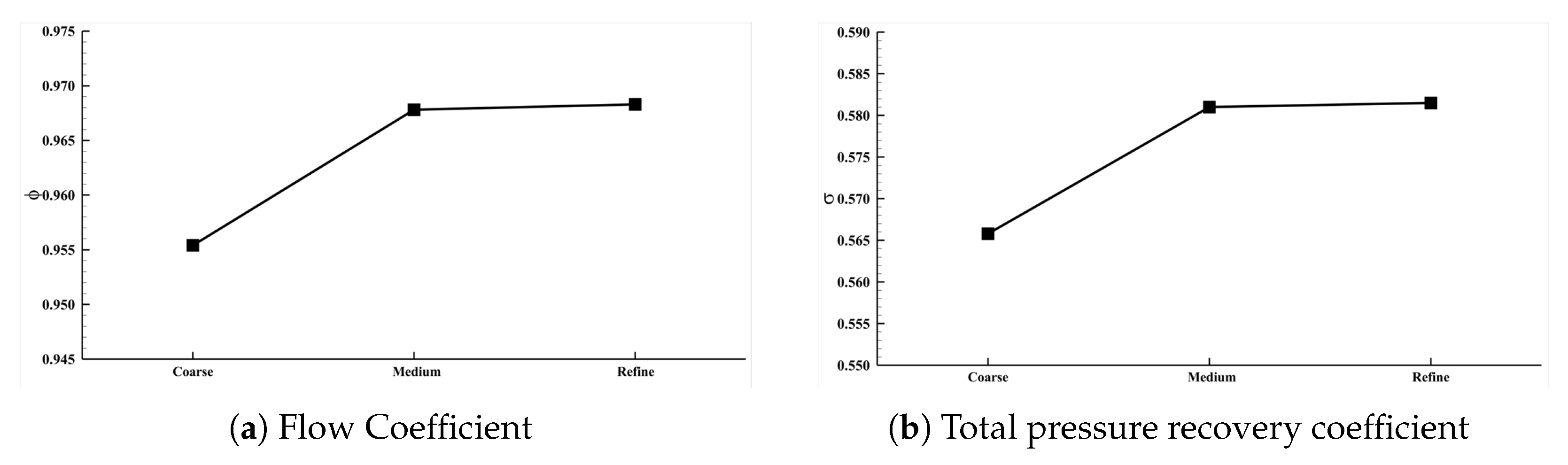
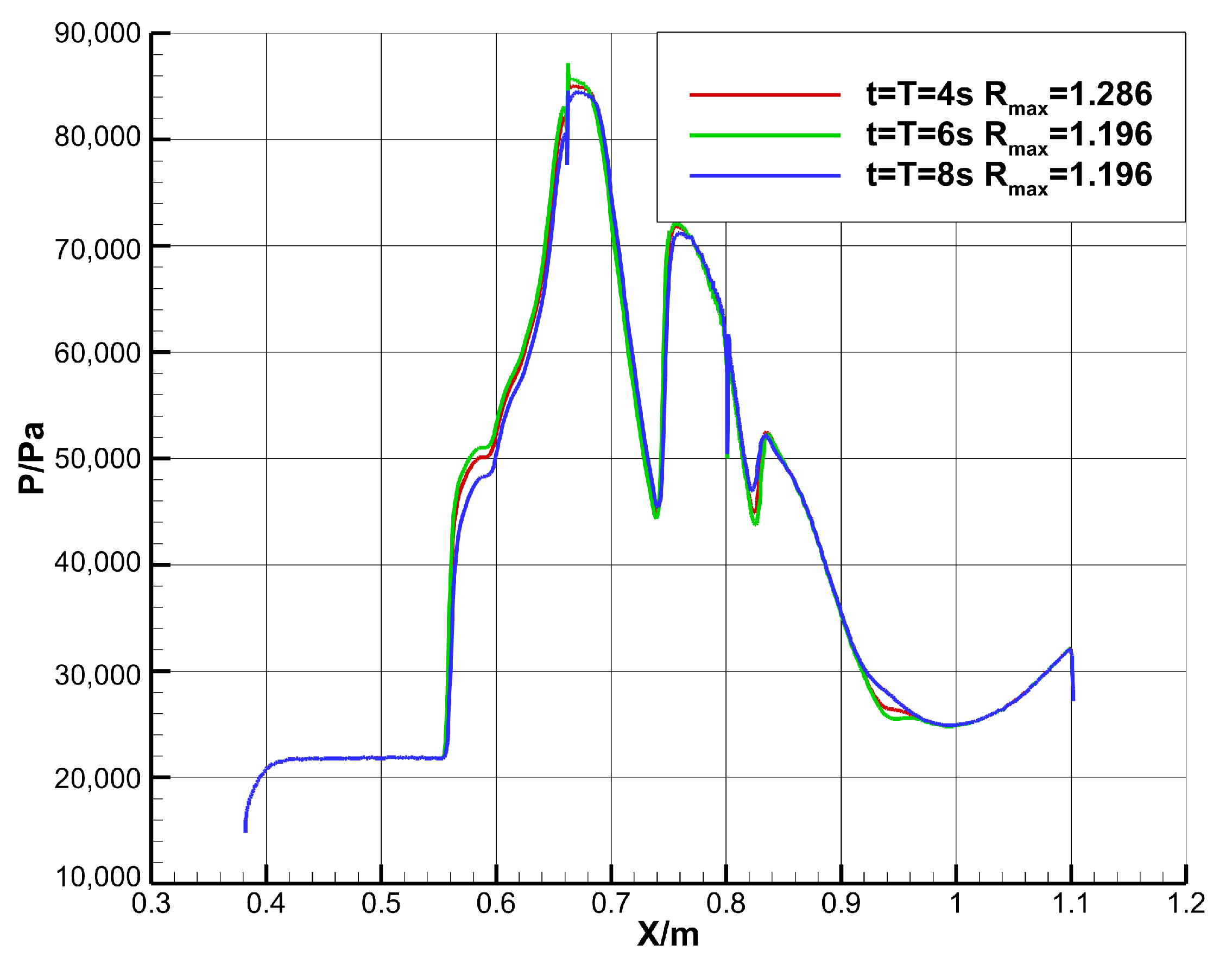
3.4. Grid Convergence Analysis

To balance computational efficiency and the accuracy of numerical simulation, the numerical calculation results of fine, medium, and coarse grids under the inlet design point conditions are compared. This is to verify the impact of grid density on the calculation results and determine the appropriate number of computational grids. The grid parameters are shown in

Table 2. Parameters of the mesh.

Grid Density	Cell Number
Coarse	100672
Medium	282828
Refine	420619

.

Figure 8 illustrates the changes in the flow coefficient and the total pressure recovery coefficient at the outlet. These are under the inlet through-flow condition with a Mach number of 4.0 at an altitude of 24 km, as related to the grid quantity. The results clearly show that as the grid quantity rises, the calculation results gradually converge. The data obtained from fine grids and medium grids show a high level of consistency, with the grid convergence error reaching the magnitude of 1‰. In order to reduce the overall computational burden during the numerical simulation process, the medium grid size is selected for subsequent calculations.

4. Research on the Restart of the Inlet Assisted by Adjusting the Throat

4.1. Self-Starting Performance of the Inlet

Numerical calculations were carried out with the given boundary conditions, Figure 9 depicts the flow field structure in the through-flow state at the inlet’s design point. It mainly comprises the external compression shock waves ① ② ③, the lip incident shock wave ④, and the internal channel corner shock wave ⑤. The three shock waves on the inlet’s external compression surface intersect in front of the lip. There is no apparent flow separation inside the inlet. At this moment, the total pressure recovery coefficient and the flow coefficient at the inlet outlet are 0.5810 and 0.9678, respectively.

The definitions of the inlet performance parameters are as follows:

• Total pressure recovery coefficient $\sigma$:

  $$\sigma ={\displaystyle \frac{P_{t,\mathrm{outlet}}}{P_{t,\mathrm{freestream}}}}$$

  (10)

  where $P_{t,\mathrm{outlet}}$ is the total pressure at the inlet outlet obtained by the flow averaging method, and $P_{t,\mathrm{freestream}}$ is the free-stream total pressure. This parameter quantifies the efficiency of pressure recovery through the inlet.
• Flow coefficient $\phi$:

  $$\phi ={\displaystyle \frac{{\dot{m}}_{\mathrm{captured}}}{{\dot{m}}_{\mathrm{freestream},\mathrm{inlet}\mathrm{area}}}}$$

  (11)

  where ${\dot{m}}_{\mathrm{captured}}$ is the mass flow rate captured by the inlet, and ${\dot{m}}_{\mathrm{freestream}\mathrm{inlet}\mathrm{area}}$ is the free-stream mass flow rate through the inlet’s frontal area. This reflects the inlet’s ability to capture free-stream flow.

The inlet unstart induced by the downstream engine’s abnormal operation is simulated by increasing the inlet’s back pressure. Based on the inlet’s through-flow calculation results, the back pressure at the inlet outlet is gradually increased until the terminal shock wave is pushed out of the lip and the inlet enters the unstart state. Subsequently, the back pressure is decreased to the through-flow state. The final flow field structure is presented in Figure 10. The results indicate that the inlet cannot restart spontaneously. There is a large-scale flow separation on the compression surface, which induces the generation of the separation shock wave ⑥. Flow choking occurs near the lip and the inlet throat. An obvious compression/expansion wave system structure exists near the throat. Meanwhile, a stable spillage wave system structure is present in front of the lip. At this time, the total pressure recovery coefficient and the flow coefficient at the inlet outlet are 0.3809 and 0.8706, respectively, both of which are significantly lower compared to the performance at the design point.

4.2. Research on Numerical Calculation of Throat Adjustment

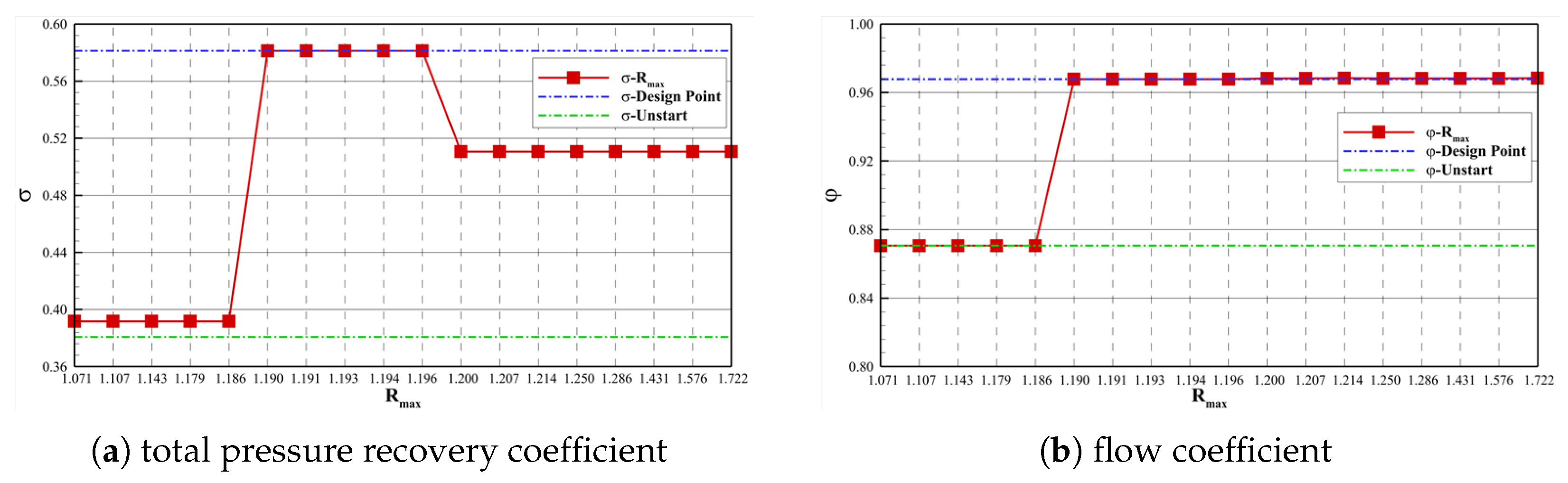
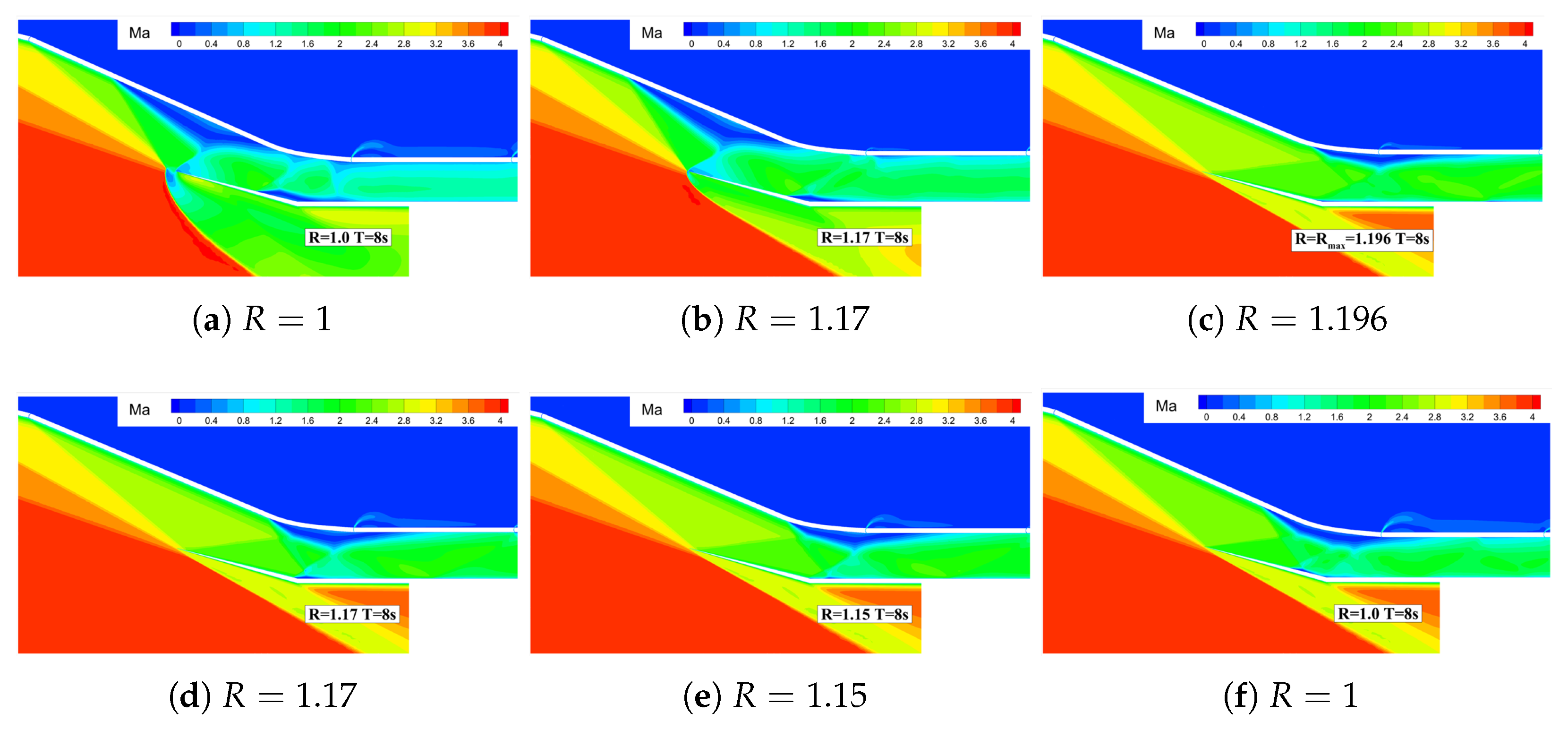
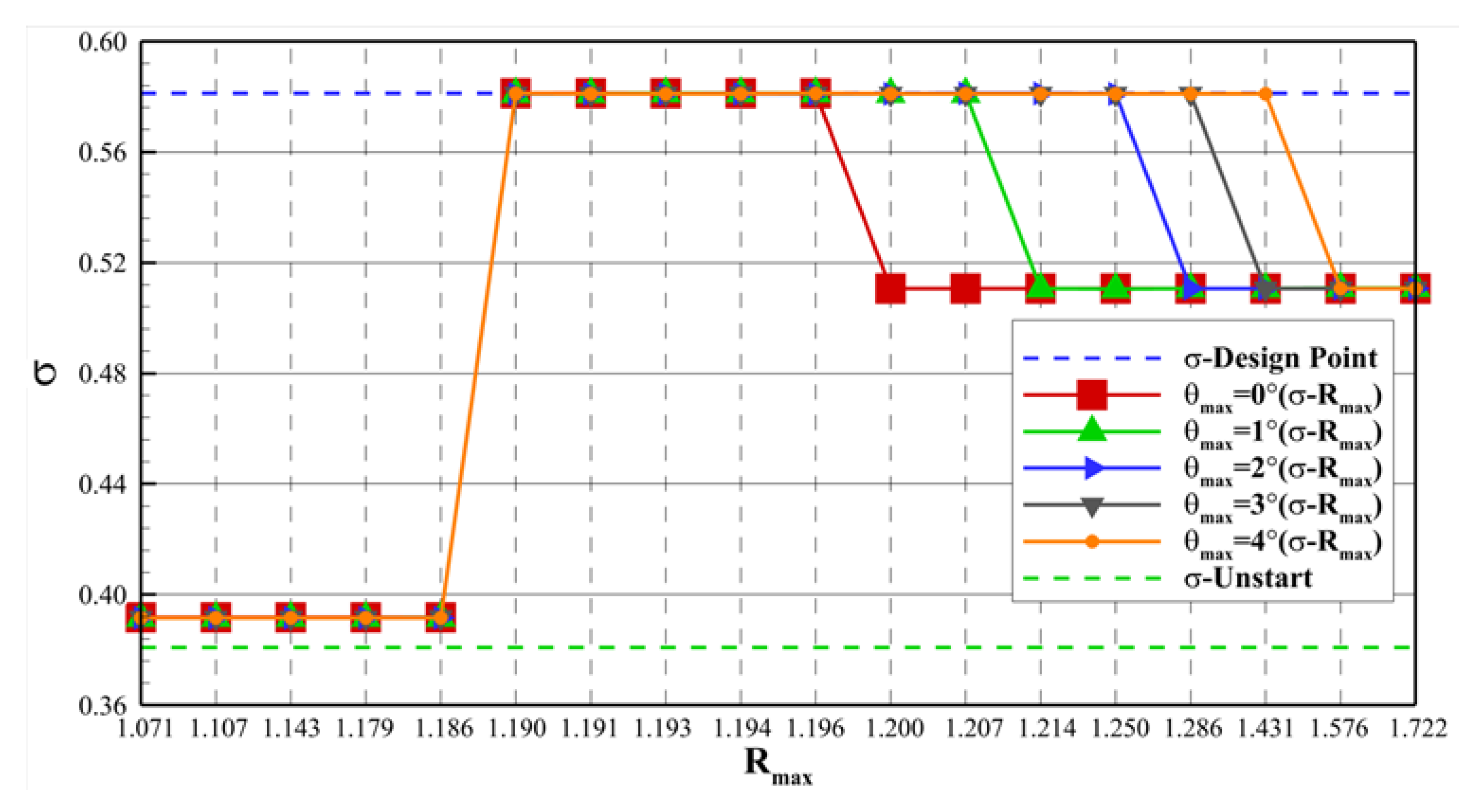
4.2.1. Influence of Throat Adjustment Height

In this section, the unstarted flow field at the inlet serves as the initial flow field for unsteady calculations. Considering the motion law of the isolator (CD), unsteady numerical simulations are carried out to study the variable-throat-assisted starting process. Specific $T=4\mathrm{s}$ and ${\theta }_{max}=0^{\circ }$ are set, and various values of $R_{max}$ are chosen to explore the impact of the throat adjustment height on the evolution of the inlet’s dynamic adjustment flow field structure and the outlet performance parameters.

Table 3. Calculation condition table of throat wall translation.

Case	T	${\mathit{\theta }}_{max}$	${\mathit{R}}_{max}$	Case	T	${\mathit{\theta }}_{max}$	${\mathit{R}}_{max}$
1	4 s	$0^{\circ }$	1.071	10	4 s	$0^{\circ }$	1.196
2	4 s	$0^{\circ }$	1.107	11	4 s	$0^{\circ }$	1.200
3	4 s	$0^{\circ }$	1.143	12	4 s	$0^{\circ }$	1.207
4	4 s	$0^{\circ }$	1.179	13	4 s	$0^{\circ }$	1.214
5	4 s	$0^{\circ }$	1.186	14	4 s	$0^{\circ }$	1.250
6	4 s	$0^{\circ }$	1.190	15	4 s	$0^{\circ }$	1.286
7	4 s	$0^{\circ }$	1.191	16	4 s	$0^{\circ }$	1.431
8	4 s	$0^{\circ }$	1.193	17	4 s	$0^{\circ }$	1.576
9	4 s	$0^{\circ }$	1.194	18	4 s	$0^{\circ }$	1.722

details the specific parameters of each adjustment scheme.

Figure 11 illustrates the calculated results of the total pressure recovery coefficient $\sigma$ and the flow coefficient $\phi$ at the inlet outlet after the geometric adjustment of each scheme is completed. The results indicate that under $R_{max}<1.190$, both the total pressure recovery coefficient and the flow coefficient are lower than their values at the design point. When $1.190\le R_{max}\le 1.196\mathrm{s}$ is met, the total pressure recovery coefficient and the flow coefficient are identical to those at the design point. For $R_{max}>1.196$, the flow coefficient remains the same as that at the design point, while the total pressure recovery coefficient is lower. Through in-depth analysis, it is found that the above three results are in one-to-one correspondence with the three distinct flow states that occur in the inlet during the adjustment process: the unstarted flow state (stable spillage shock wave system exists in front of the cowl, both the total pressure recovery coefficient and the flow coefficient are lower than the design-point values, the power system cannot work properly), the fully restarted flow state (the separation bubble on the compression surface is fully entrained into the downstream of the throat by the main flow, the total pressure recovery coefficient and the flow coefficient are both equal to the design-point values, the power system can work properly), and the off-design flow state induced by the separation region in the internal contraction section (the flow coefficient is equal to the design-point value, but the total pressure recovery coefficient is lower than the design-point value, and the power system is capable of operation; however, its performance remains suboptimal). The following elaborates on the specific reasons for the occurrence of different flow states in the inlet:

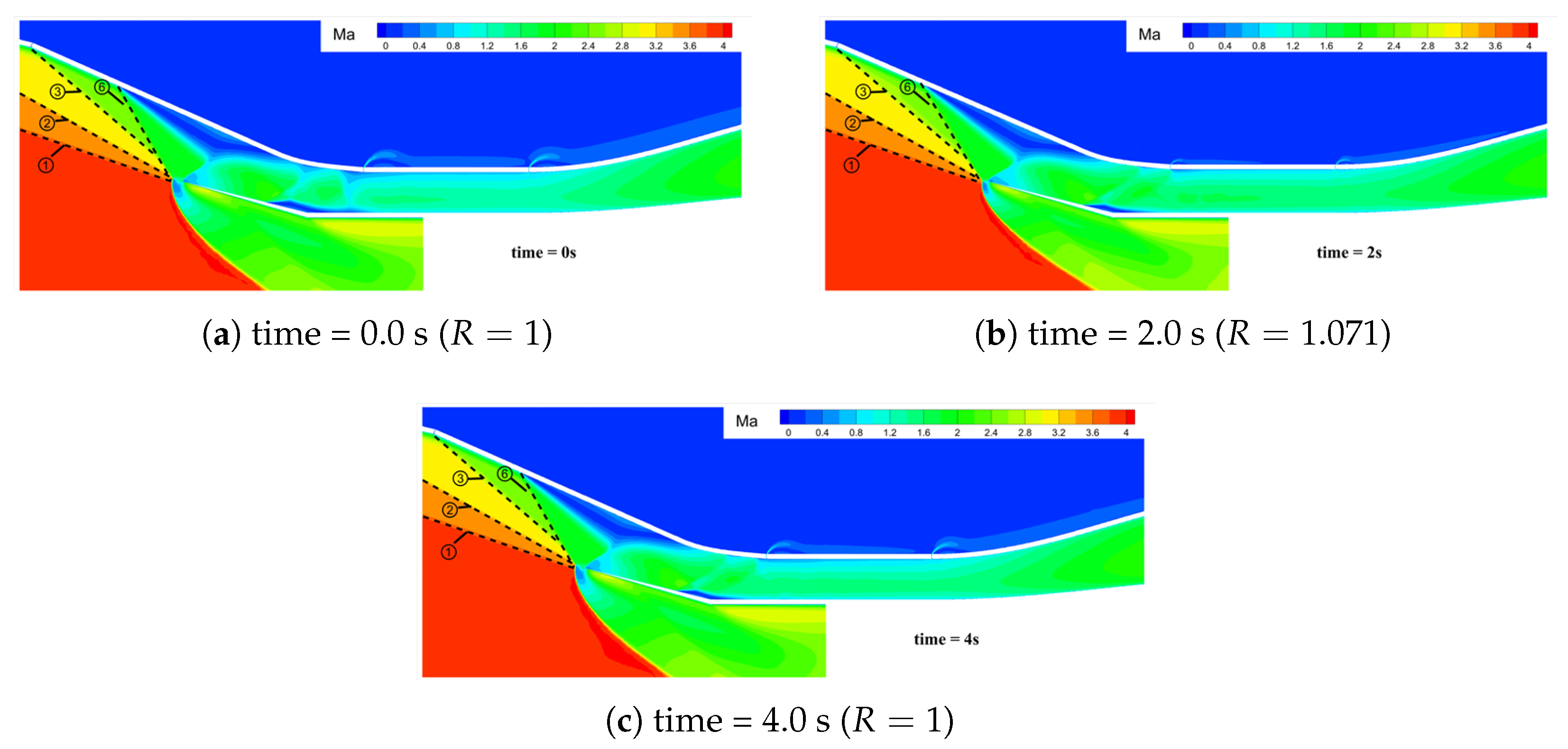
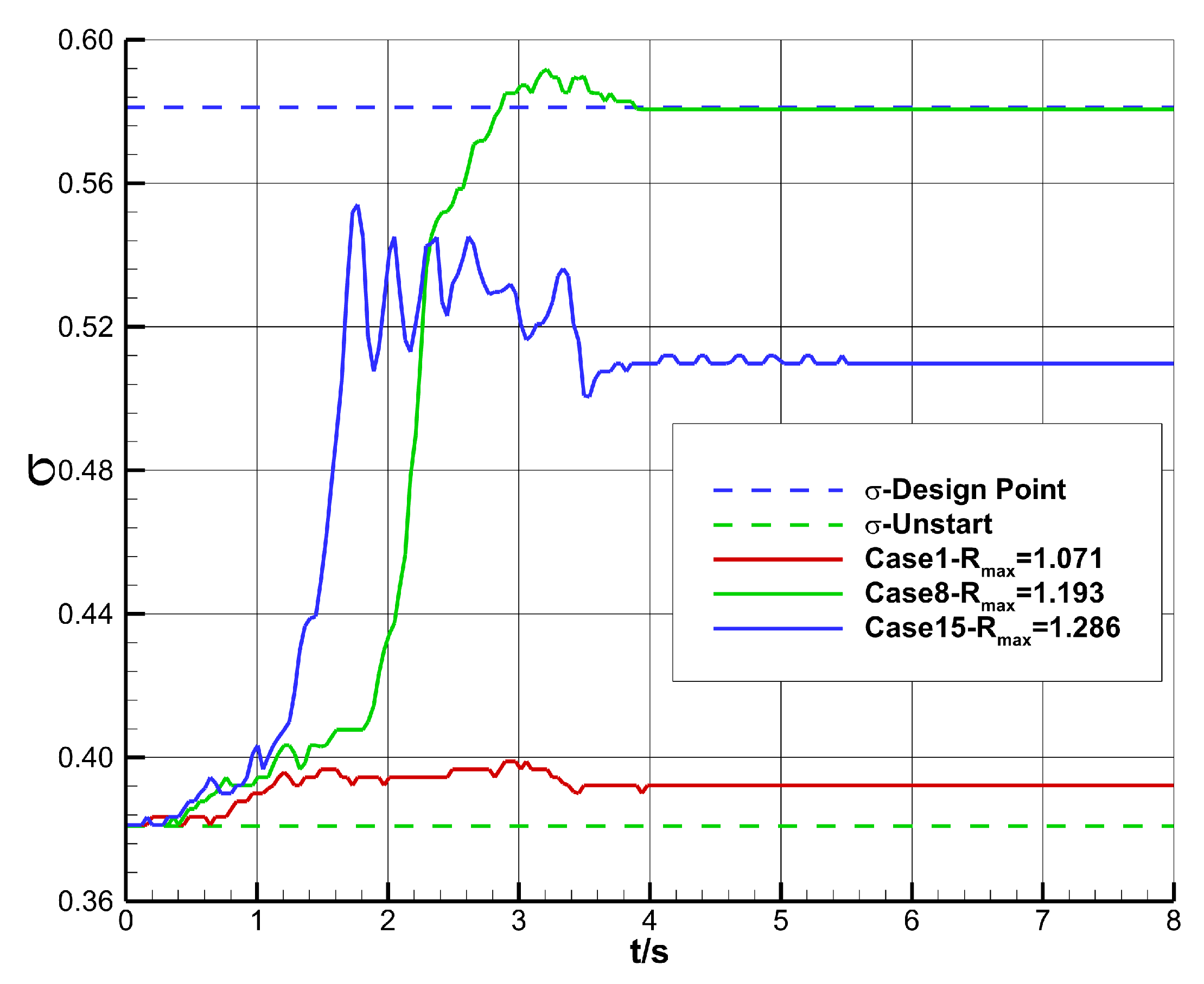
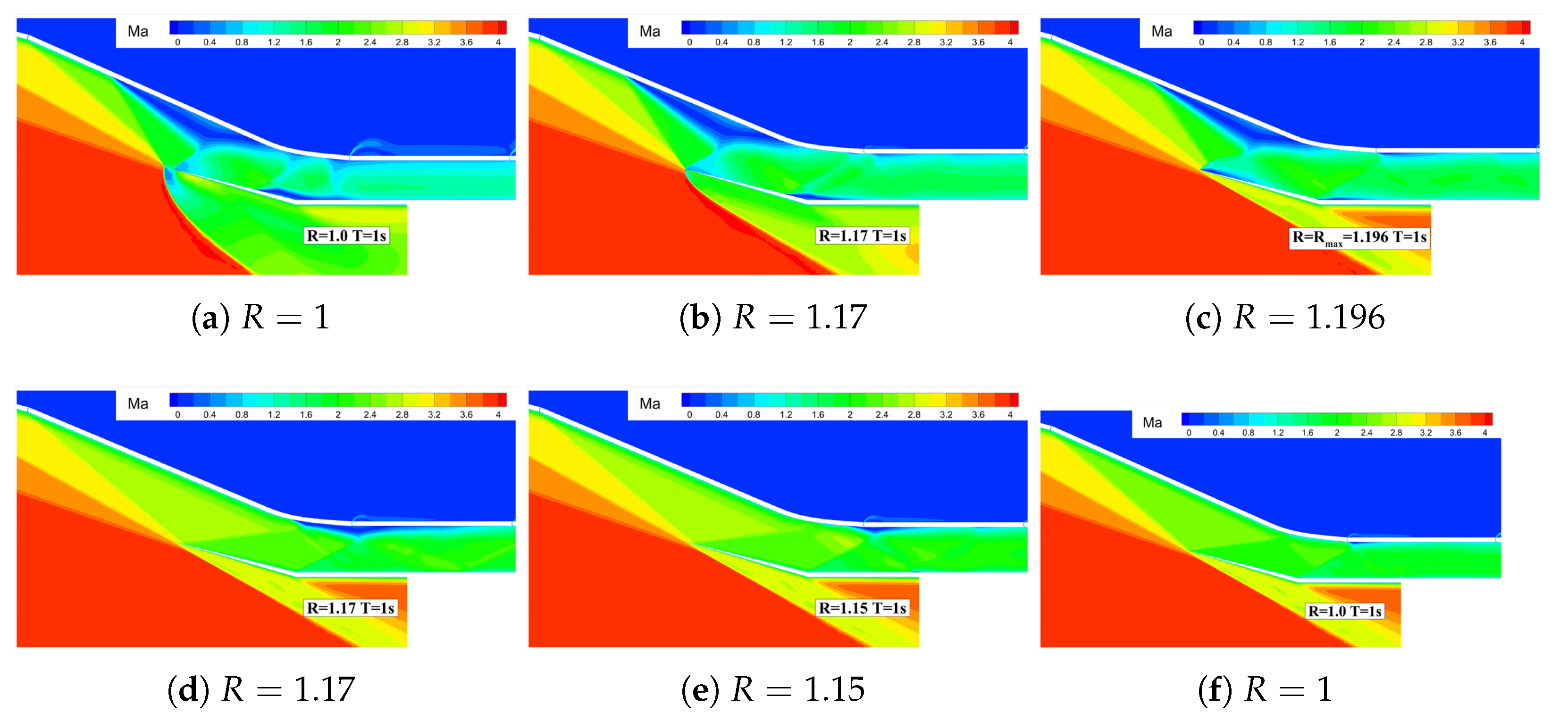
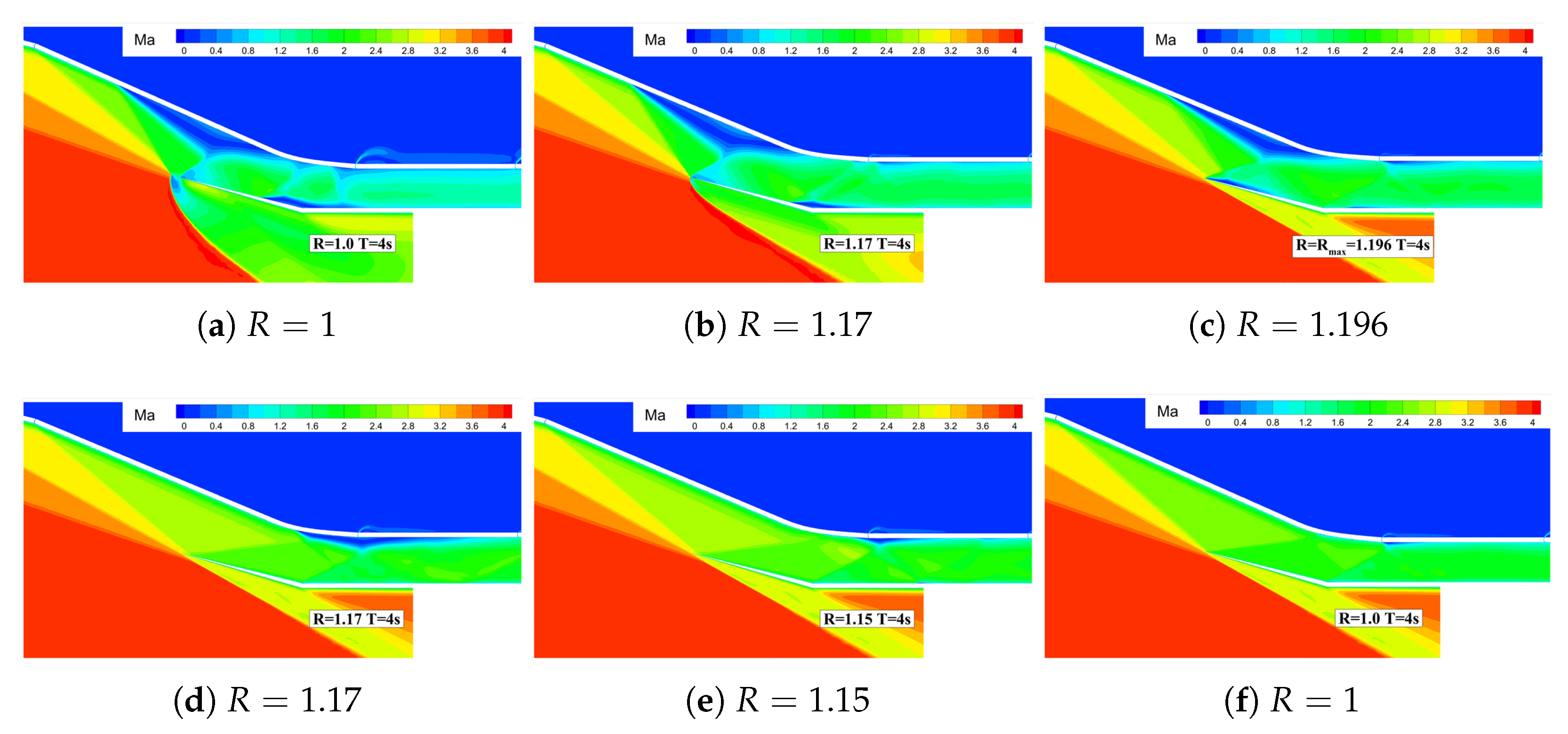
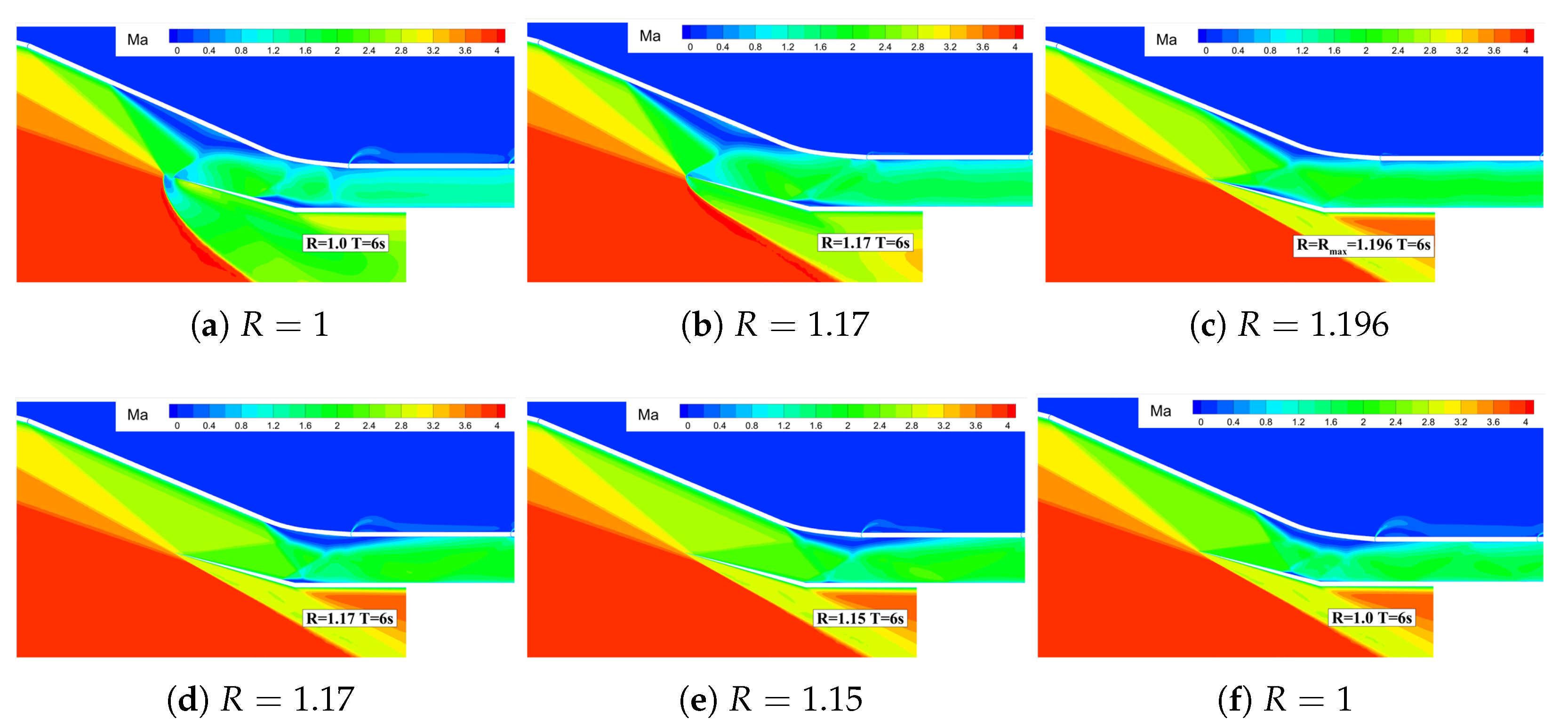
• Unstarted flow state
  When the parameter $R_{max}<1.190$, the inlet is incapable of restarting. As depicted in Figure 12, exemplified by Case 1, it demonstrates the temporal variation of the Mach number distribution within the inlet. At $t=0.0\mathrm{s}$, it represents the initial non-started flow field of the inlet. At $t=2.0\mathrm{s}$, the throat height reaches its peak value, alleviating the choking near the throat to a certain extent. However, choking persists near the inlet, the aerodynamic throat remains intact, and the captured mass flow rate of the inlet still exceeds the maximum flow rate that the inlet can accommodate at this instant. Thus, the spillage wave system structure in front of the inlet remains stable. At $t=4.0\mathrm{s}$, the inlet profile returns to its original configuration, and the inlet fails to restart. Moreover, due to the attenuation of the compression/expansion wave system structure near the throat and the reduction in flow losses, the total pressure recovery coefficient increases compared to that prior to the geometric adjustment.

  Figure 12. Mach number contours during throat wall movement ($R_{max}=1.071$).

  Figure 12. Mach number contours during throat wall movement ($R_{max}=1.071$).
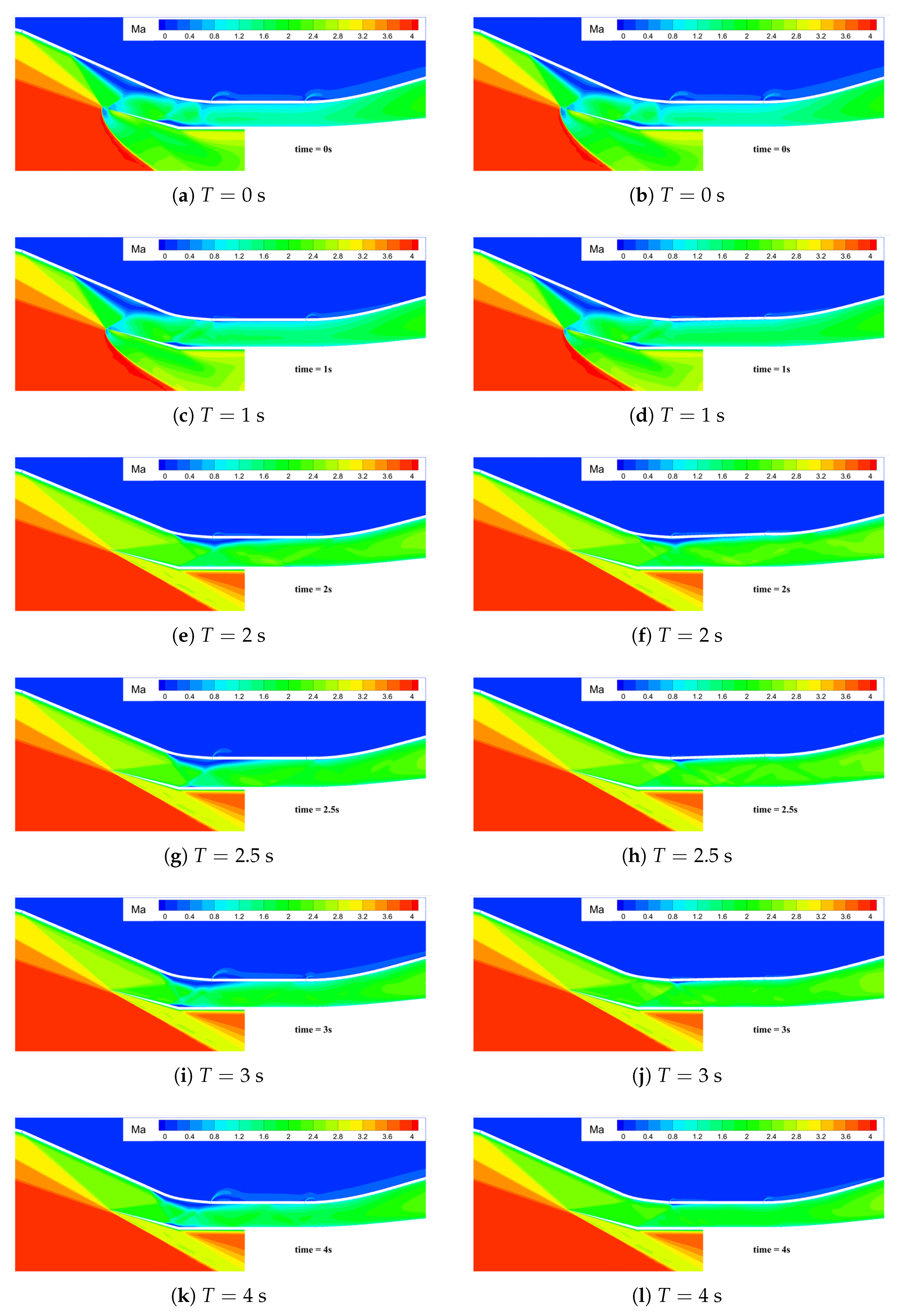
• Fully restarted flow state
  When $1.190\le R_{max}\le 1.196$, the inlet fully restarts. As shown in Figure 13, taking Case 8 as an example, it depicts the temporal variation of the Mach number distribution in the inlet. From 0.0 to 2.0 s, as the throat height increases, flow choking gradually dissipates, and the spillage in front of the inlet progressively decreases. At $t=2.0\mathrm{s}$, the inlet spillage completely vanishes. Simultaneously, the separation region gradually moves downstream. From 2.0 to 4.0 s, the throat height gradually decreases. Due to the enhanced flow capacity of the inlet, the separation region moves further downstream. At $t=2.25\mathrm{s}$, the separation region is completely swallowed. However, at this moment, a small separation is observed at the shoulder position of the profile. This is because as the throat height increases, the third-stage compression angle decreases, leading to an increase in the Mach number in front of the corner shock wave ⑤ and an intensification of the shock wave intensity. Under the influence of this shock wave, a small separation occurs at the shoulder. Subsequently, as the throat height gradually decreases, the intensity of the corner shock wave ⑤ weakens, the separation region gradually shrinks, and the inlet restarts.

  Figure 13. Mach number contours during throat wall movement ($R_{max}=1.193$).

  Figure 13. Mach number contours during throat wall movement ($R_{max}=1.193$).
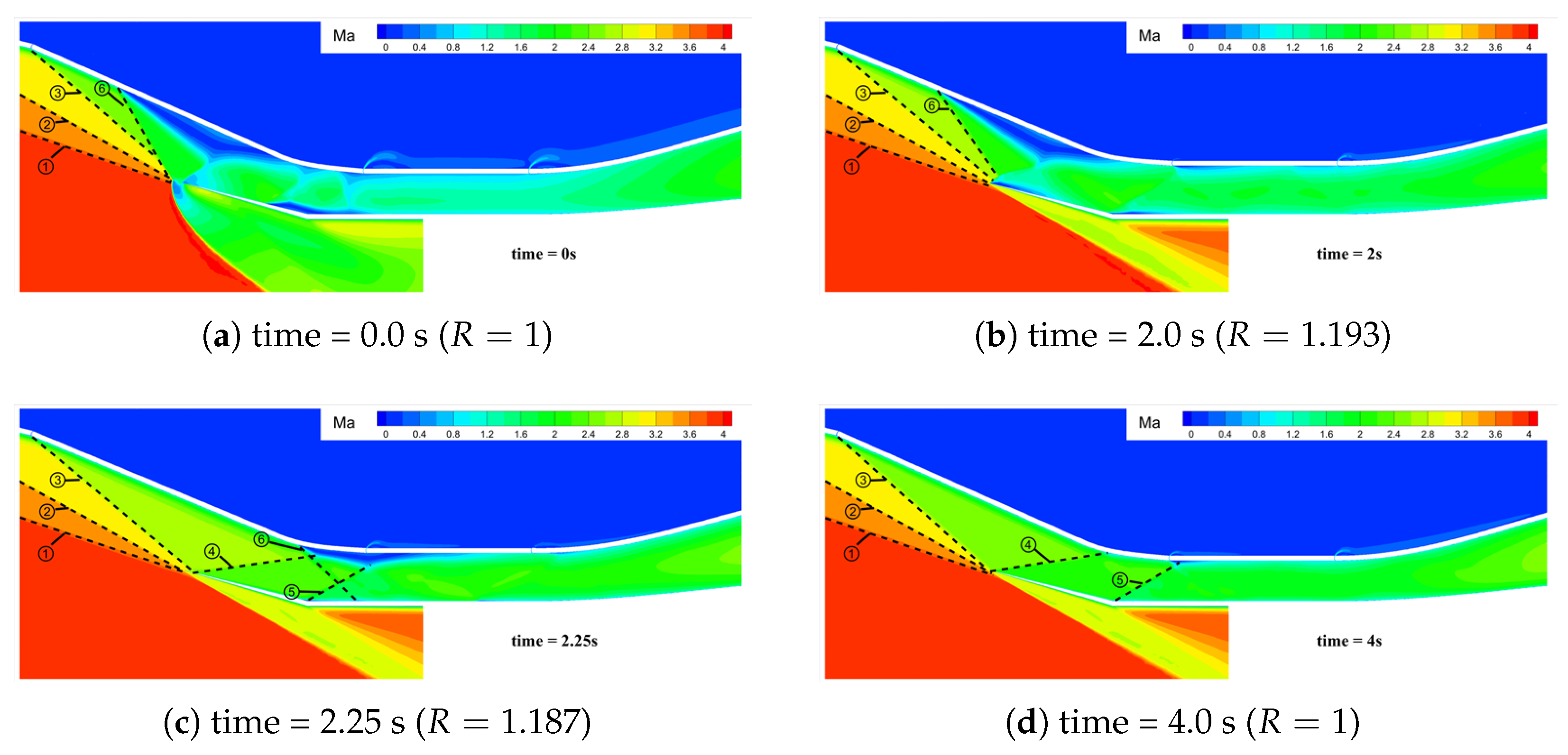
• Off-design flow state induced by the separation region in the internal contraction section
  When the parameter $R_{max}>1.196$, the inlet experiences an off-design flow state induced by the separation region within the internal contraction section. The following delves into the reasons underlying the stable existence of this off-design flow state.
  Figure 14, exemplified by Case 15, depicts the time-dependent variation of the Mach number distribution in the inlet. Within the 0 to 2s interval, as the throat height gradually increases, the spillage in front of the lip vanishes completely at $t=1.30\mathrm{s}$, and the separation region gradually migrates downstream. By $t=1.65\mathrm{s}$, the separation region is fully engulfed. Influenced by the corner shock wave ⑤, a minor flow separation emerges at the shoulder of the profile. With a further increase in the throat height, the intensity of the corner shock wave ⑤ keeps growing. At $t=1.85\mathrm{s}$, it becomes clear that the separation region expands substantially, resulting in the strengthening of the separation shock wave ⑥ The separation shock wave ⑥ triggers a small-scale flow separation near the corner of the cowl and intersects and interferes with the separation shock wave ⑦ at the corner, forming a local Mach-stem structure. At $t=2.0\mathrm{s}$, the throat height reaches its peak, enhancing the inlet’s flow capacity and reducing the separation region on the compression surface to some extent. Nevertheless, at this moment, the separation shock wave ⑦ at the corner and the reattachment shock wave ⑧ are incident downstream of the separation region on the compression surface, preventing the separation region on the compression surface from further downstream movement. From 2.0 to 4.0 s, the throat height gradually decreases until it reverts to its original state. The pressure downstream of the throat rises, and the separation region on the compression surface is gradually pushed upstream into the internal contraction section. The separation shock wave ⑦ at the corner, the reattachment shock wave ⑧, and the corner shock wave ⑤ precisely align downstream of the separation region on the compression surface, thereby forming a stable self-sustaining wave system structure, as illustrated in Figure 14f.

Figure 14. Mach number contours during throat wall movement ($R_{max}=1.286$).

Figure 14. Mach number contours during throat wall movement ($R_{max}=1.286$).

Figure 15 illustrates the time-dependent variations of total pressure recovery coefficients for Cases 1, 8, and 15. The results depicted in the curves indicate that upon completion of geometric adjustment ($t=T$), all flow fields converge to a stable state. It is important to emphasize that during off-design flow conditions, minor fluctuations in the total pressure recovery coefficient are observed, which can be attributed to small-scale oscillations within the separation zone of the internal contraction section. Notwithstanding these transient fluctuations, the coefficient ultimately achieves stabilization, and no qualitative alterations in the flow field structure are detected.

In conclusion, when restarting the inlet via throat adjustment, a larger adjustment height is not always advantageous. As the adjustment height increases, the inlet successively experiences an unstarted flow state, a fully restarted flow state, and an off-design flow state induced by the separation region in the internal contraction section. Here, the lower critical height $R_{max down}$ is defined as 1.190 and the upper critical height $R_{max up}$ as 1.196. The adjustment range between the upper and lower critical heights is the interval within which the inlet can fully restart. Only when the throat adjustment height lies within this interval can the inlet achieve full restart.

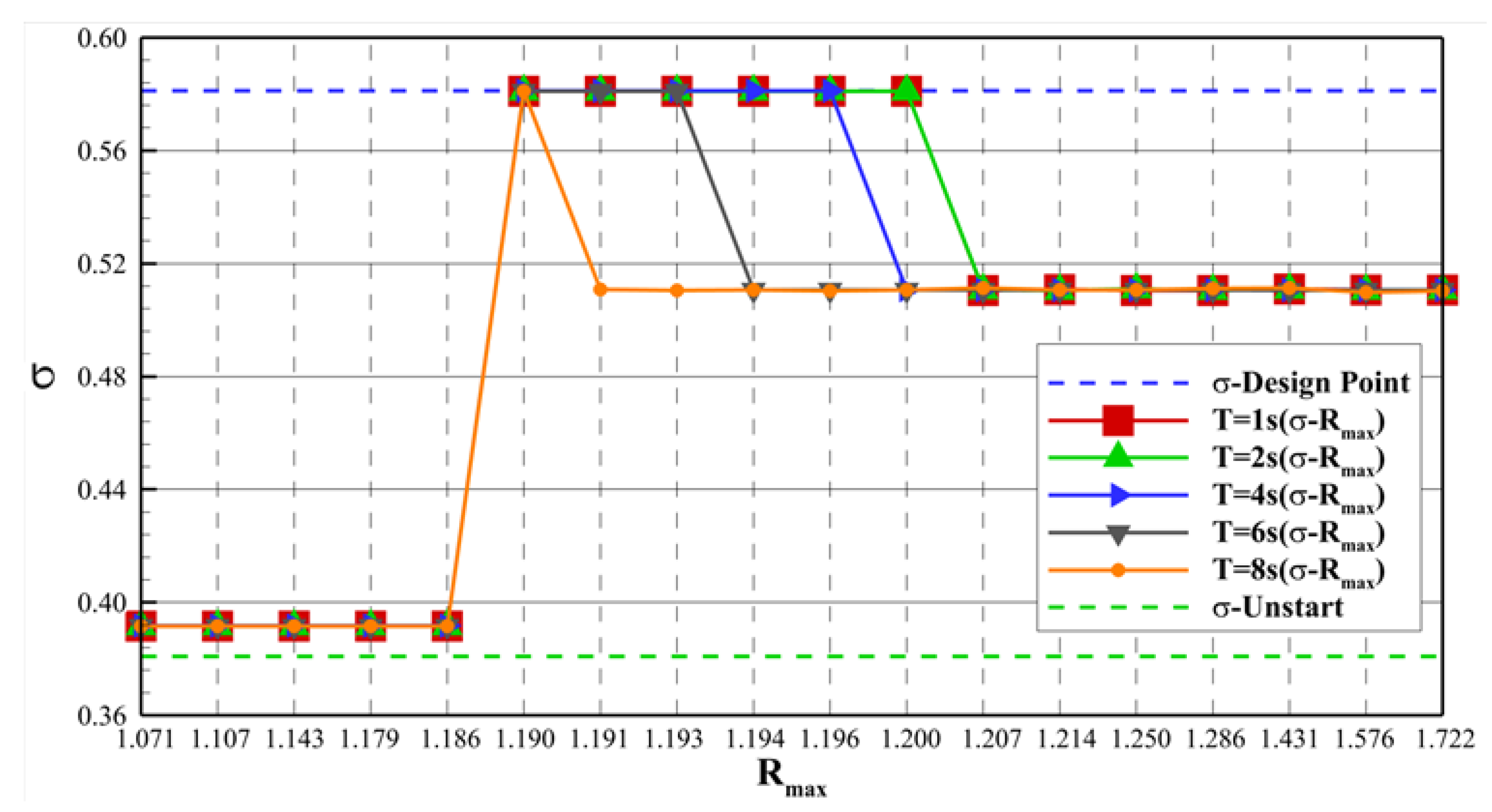
4.2.2. Influence of Geometric Adjustment Time

In this section, the adjustment height $R_{max down}$ and adjustment angle ${\theta }_{max}$ are the same as those in Section 4.2.1. Set $T=1\mathrm{s}$, $2\mathrm{s}$, $4\mathrm{s}$, $6\mathrm{s}$, and $8\mathrm{s}$ to analyze the influence of the throat adjustment time on the evolution of the flow field structure during the inlet’s dynamic adjustment and on the upper and lower critical heights. Figure 16 shows the calculated total pressure recovery coefficients of each adjustment scheme under different adjustment times. The results indicate that the geometric adjustment time significantly affects the adjustment interval for the inlet to fully restart. Generally, as the adjustment time decreases, the lower critical height remains constant, the upper critical height gradually increases, and the adjustment interval range progressively expands. The following analyzes the specific reasons.

Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21 depict the variation in the Mach number distribution with the relative height R under the conditions of $R_{max}=1.196$, ${\theta }_{max}=0^{\circ }$, and $T=1\mathrm{s}$, $2\mathrm{s}$, $4\mathrm{s}$, $6\mathrm{s}$, and $8\mathrm{s}$. When the relative height R gradually increases from 1 to $R_{max}$, the adjustment time has a negligible effect on the flow field structure. The only difference among various schemes is that the longer the adjustment time, the farther downstream the separation region on the compression surface moves. When the relative height R gradually decreases from $R_{max}$ to 1, the adjustment time significantly impacts the flow field structure:

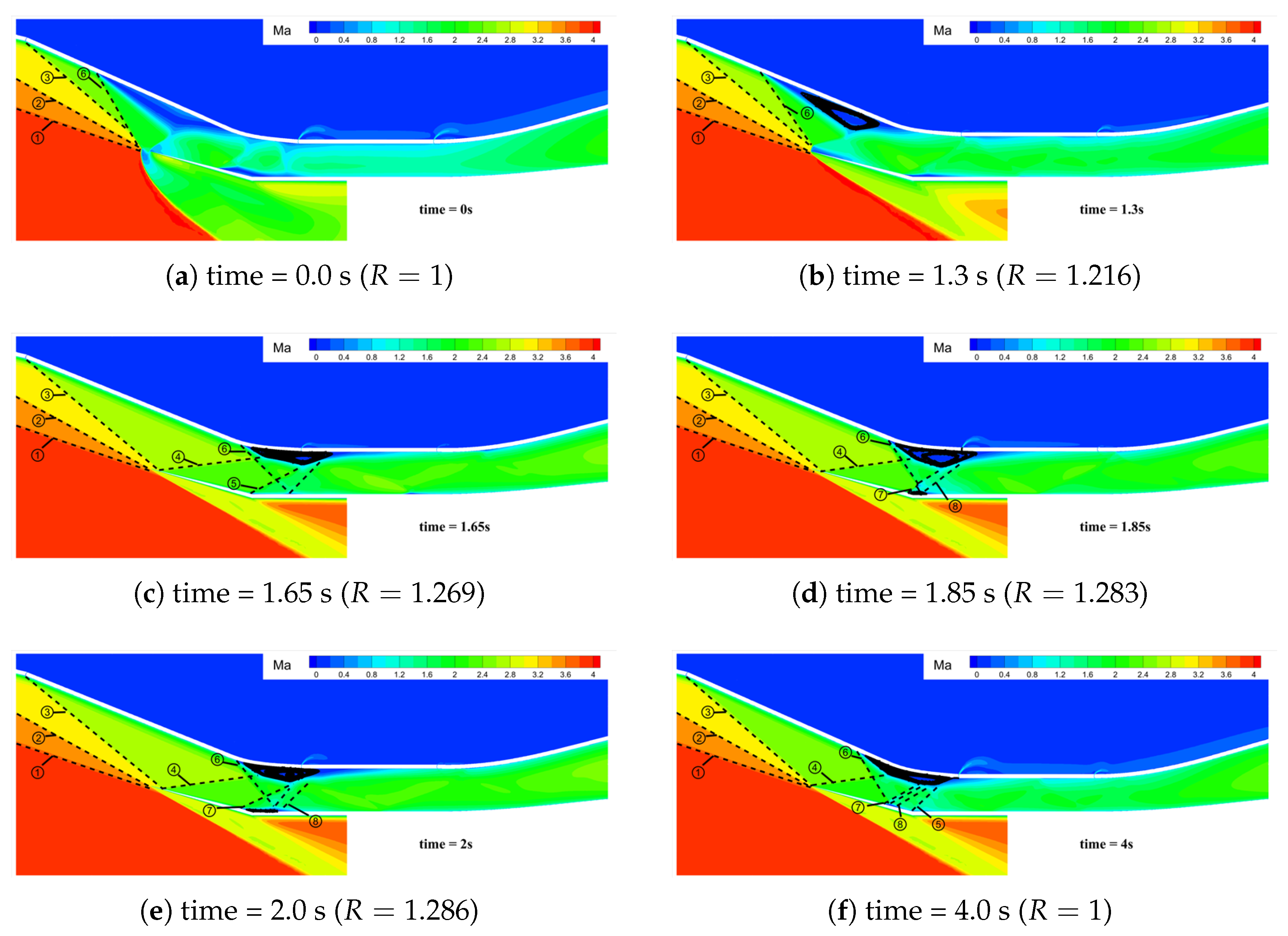
• When $T\le 4\mathrm{s}$, although influenced by the corner shock wave, flow separation occurs at the shoulder position of the profile. As the relative height R gradually decreases, the intensity of the corner shock wave gradually weakens, and this separation region gradually shrinks until the inlet finally returns to the fully restarted state.
• When $T>4\mathrm{s}$, due to the increase in the adjustment time, the flow separation at the shoulder position of the profile develops more fully. It can be observed that the separation region expands significantly and is gradually pushed upstream, finally forming the stable self-sustaining wave system structure described above, the off-design flow state induced by the separation region in the internal contraction section.

Figure 22 shows the pressure distribution on the compression surface side at time $t=T$ for three schemes with $T=4\mathrm{s}$, $R_{max}=1.286$, $T=6\mathrm{s}$, $R_{max}=1.196$ and $T=8\mathrm{s}$, $R_{max}=1.196$. It can be seen that although the geometric adjustment time and adjustment height differ, the final flow field structures of the off-design flow state are very similar, so their total pressure recovery coefficients are basically the same.

4.2.3. Influence of Throat Adjustment Angle

In this section, the adjustment height $R_{max}$ and time T are set to be identical to those in 4.2.1. The adjustment angles ${\theta }_{max}$ are set at $1^{\circ }$, $2^{\circ }$, $3^{\circ }$ and $4^{\circ }$. The influence of the throat adjustment angle on the evolution of the flow field structure during the dynamic adjustment of the inlet and the upper and lower critical heights is analyzed. Figure 23 shows the calculated total pressure recovery coefficients for each adjustment scheme under different adjustment angles. The results indicate that as the adjustment angle increases, the lower critical height remains constant, the upper critical height gradually rises, and the adjustment interval range gradually expands. The following is an analysis of the specific reasons.

Figure 24 depicts the temporal variation of the Mach number distribution for two schemes with $R_{max}=1.214$ and ${\theta }_{max}=0^{\circ }$ and $2^{\circ }$, respectively. From 0 to 2.0 s, the flow fields of the two schemes exhibit minimal difference. At 2.0 s, the corner shock waves in both schemes trigger a relatively extensive flow separation on the compression surface. Between 2 and 4 s, the throat height gradually decreases. For the scheme with ${\theta }_{max}=0^{\circ }$, an off-design flow state emerges within the inlet. Conversely, for the ${\theta }_{max}=2^{\circ }$ scheme, as the isolator rotates and the downstream of the throat is an expanding duct, the favorable pressure gradient increases. This allows the separation region on the compression surface to continue moving downstream. At 4.0 s, the flow separation on the compression surface vanishes completely, and the inlet restarts.

In conclusion, the rotation of the isolator can, to some extent, decrease the resistance to the downstream movement of the separation bubble on the compression surface, alleviate the negative influence of the corner shock wave, and facilitate the full restart of the inlet.

5. Conclusions

Numerical simulations were employed to comprehensively analyze the flow field structures and basic performances of the inlet under the design point conditions and in the unstarted flow state. Subsequently, unsteady numerical simulations were implemented to investigate the variation patterns of the inlet’s flow field structure and performance parameters during the dynamic adjustment process of variable-throat-assisted restart. The impact of the isolator’s movement law on the start characteristics of the inlet was also analyzed, and the following primary conclusions were derived:

(1)

Throat Adjustment Height: The throat adjustment height is crucial for the restart of high-Mach-number inlets. There are lower and upper critical heights. Only when the adjustment height is within the interval between these two critical values (1.190–1.196 in this research) can the inlet fully restart. Outside this interval, the inlet will be in an unstarted or off-design flow state, which deteriorates the total pressure recovery coefficient and flow coefficient at the inlet and outlet.

(2)

Geometric Adjustment Time: The geometric adjustment time has a significant influence on the inlet’s restart. As the adjustment time decreases, the lower critical height remains unchanged, while the upper critical height increases, and the adjustment interval for full restart expands. This is because different adjustment times lead to different degrees of flow separation development during the adjustment process, thereby affecting the final flow state of the inlet.

(3)

Throat Adjustment Angle: The throat adjustment angle also affects the inlet restart. As the adjustment angle increases, the lower critical height remains constant, the upper critical height rises, and the adjustment interval widens. The rotation of the isolator can mitigate the negative impact of the corner shock wave and reduce the resistance of the separation bubble on the compression surface moving downstream, which is beneficial to the full restart of the inlet.