The Three-Dimensional Transient Simulation of Cross-Shaped Grains in Hybrid Rocket Motors
Abstract
1. Introduction
2. Transient Model Construction Process
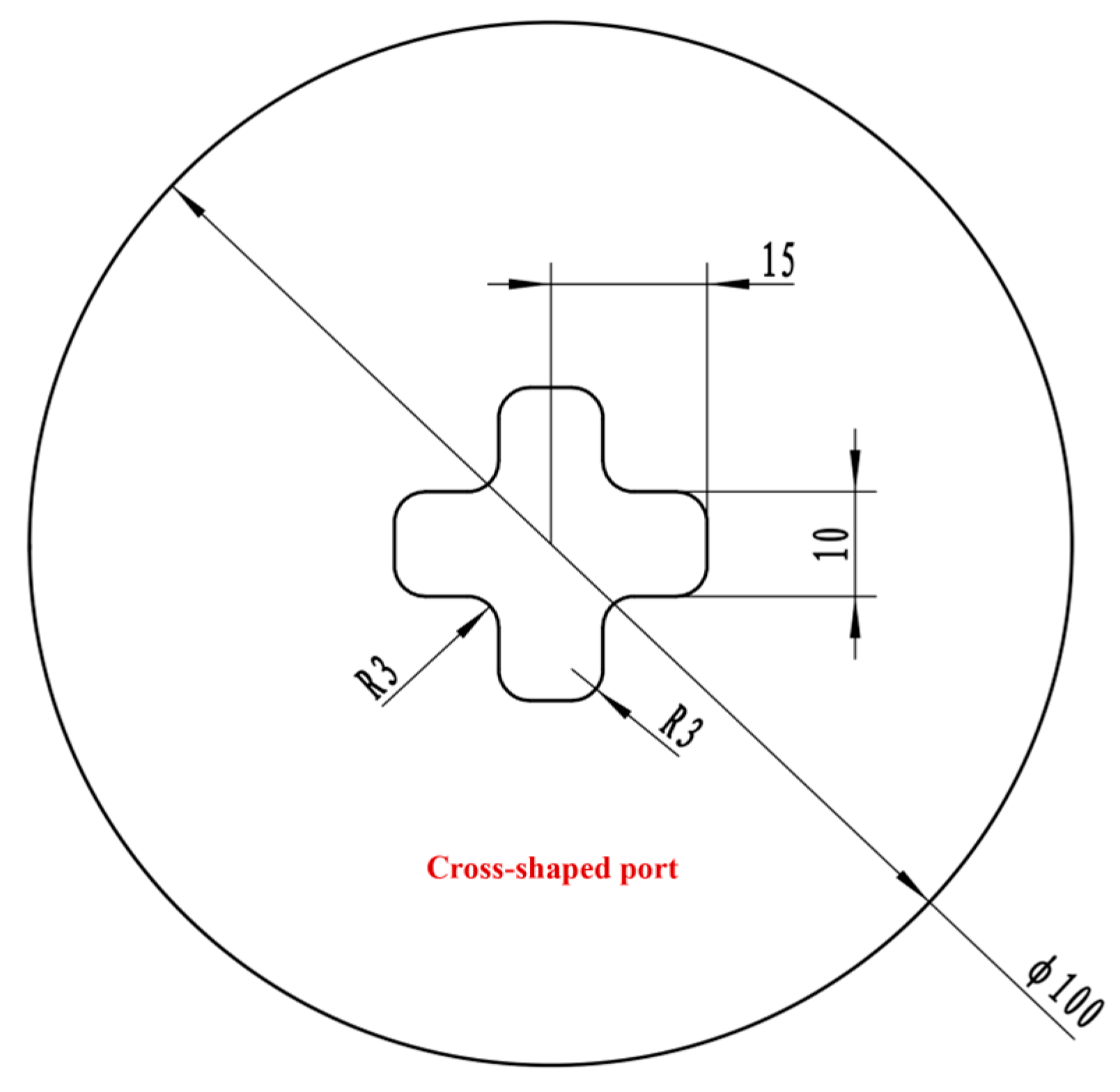
2.1. Introduction to the Motor Structure
2.2. Numerical Modeling
2.2.1. Governing Equations
2.2.2. Turbulent Model
2.2.3. Regression Rate Model
2.2.4. Chemical Reaction Model
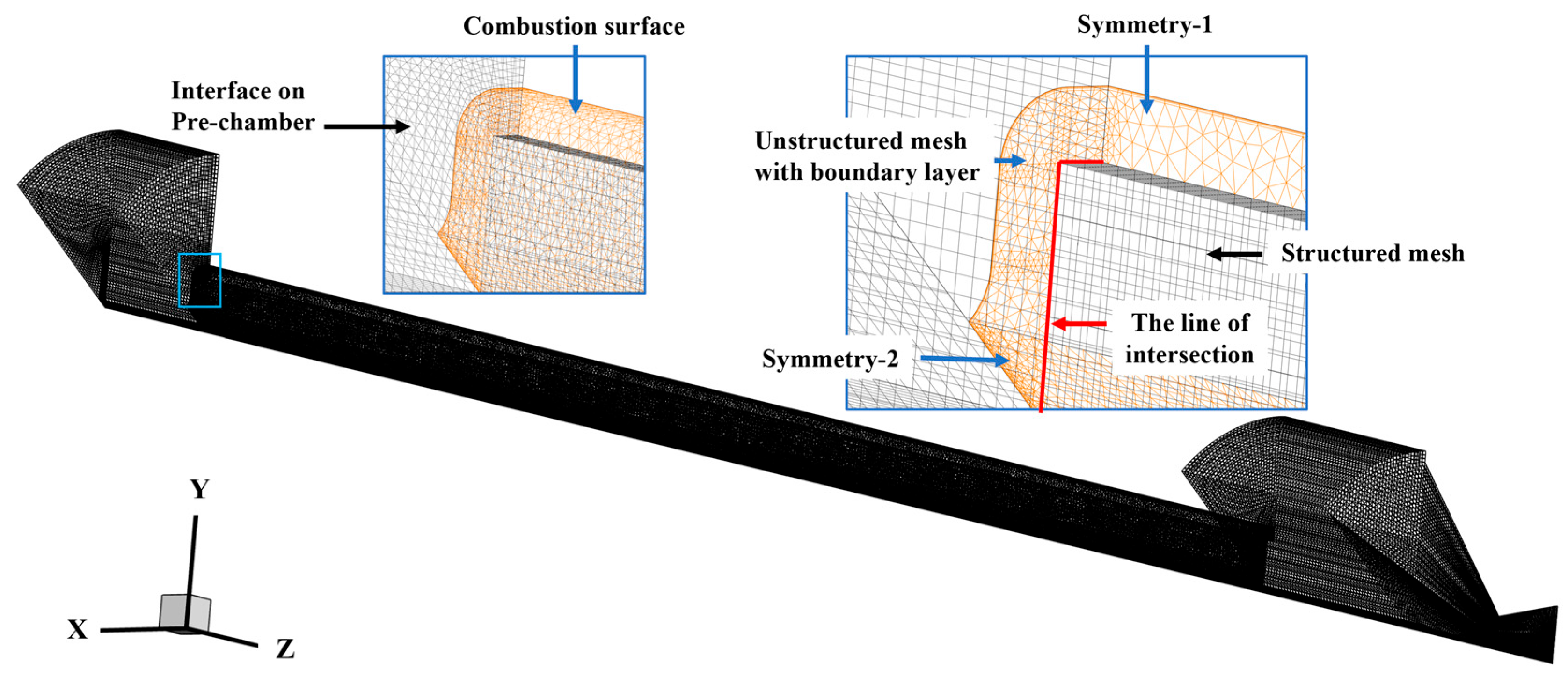
2.2.5. Computational Grids
2.2.6. Simplified and Updated Model for the Combustion Surface Based on the Dynamic Mesh Technique
2.3. Operating Conditions
3. Setup for Validation Experiment
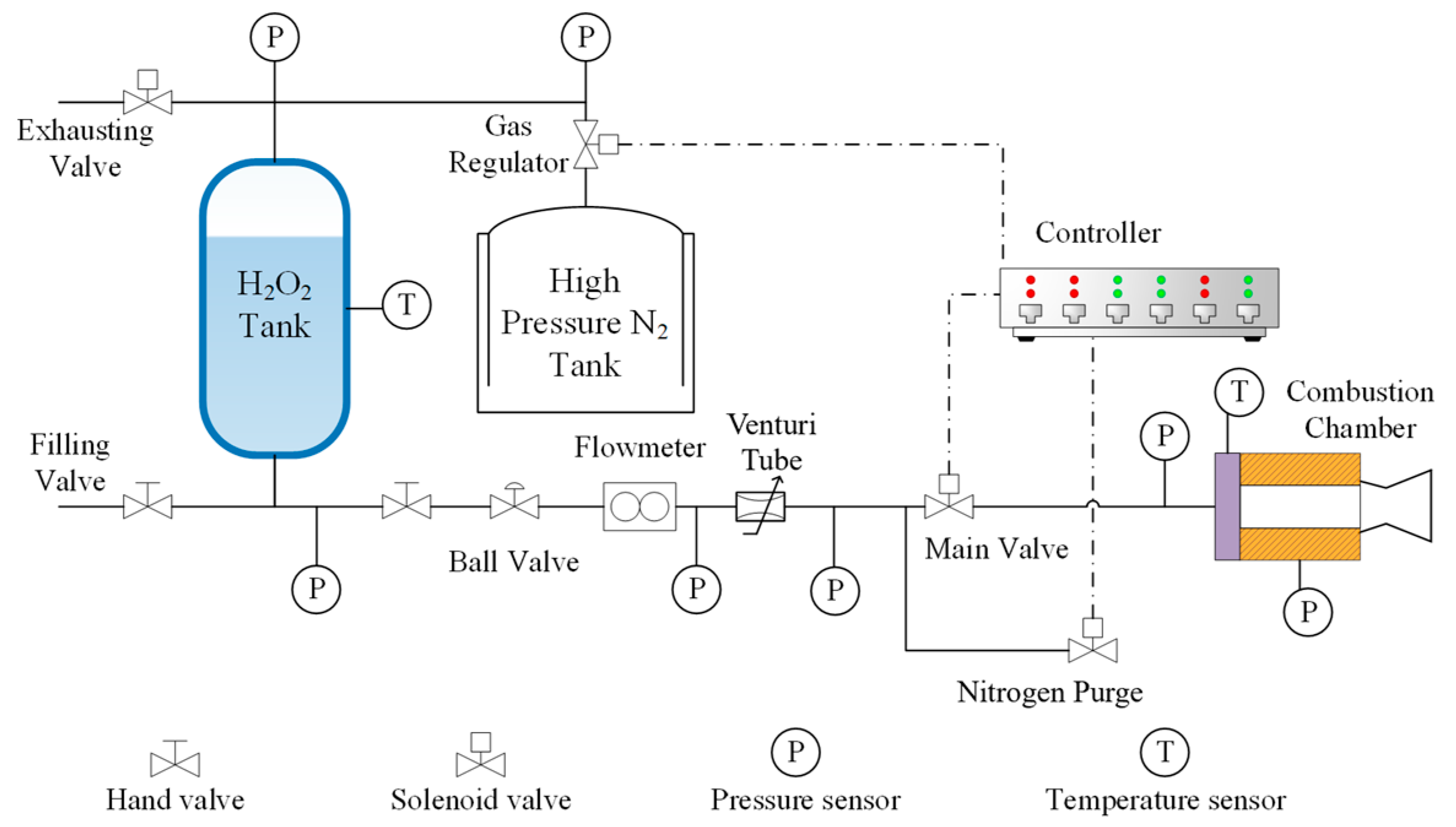
3.1. Supplying System for Hydrogen Peroxide
3.2. Test Platform of This Hybrid Rocket Motor
4. Results and Discussions
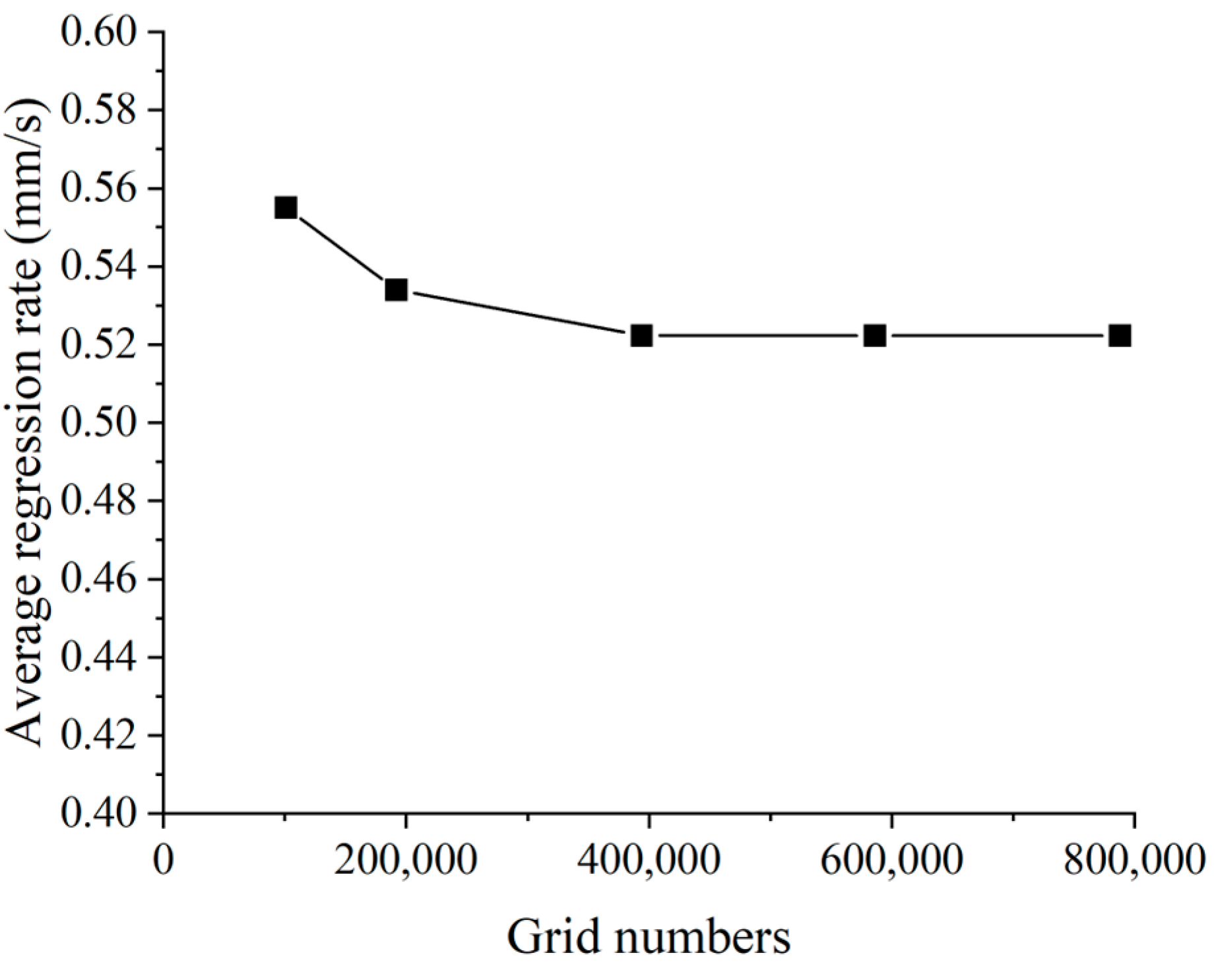
4.1. Grid Independence Verification
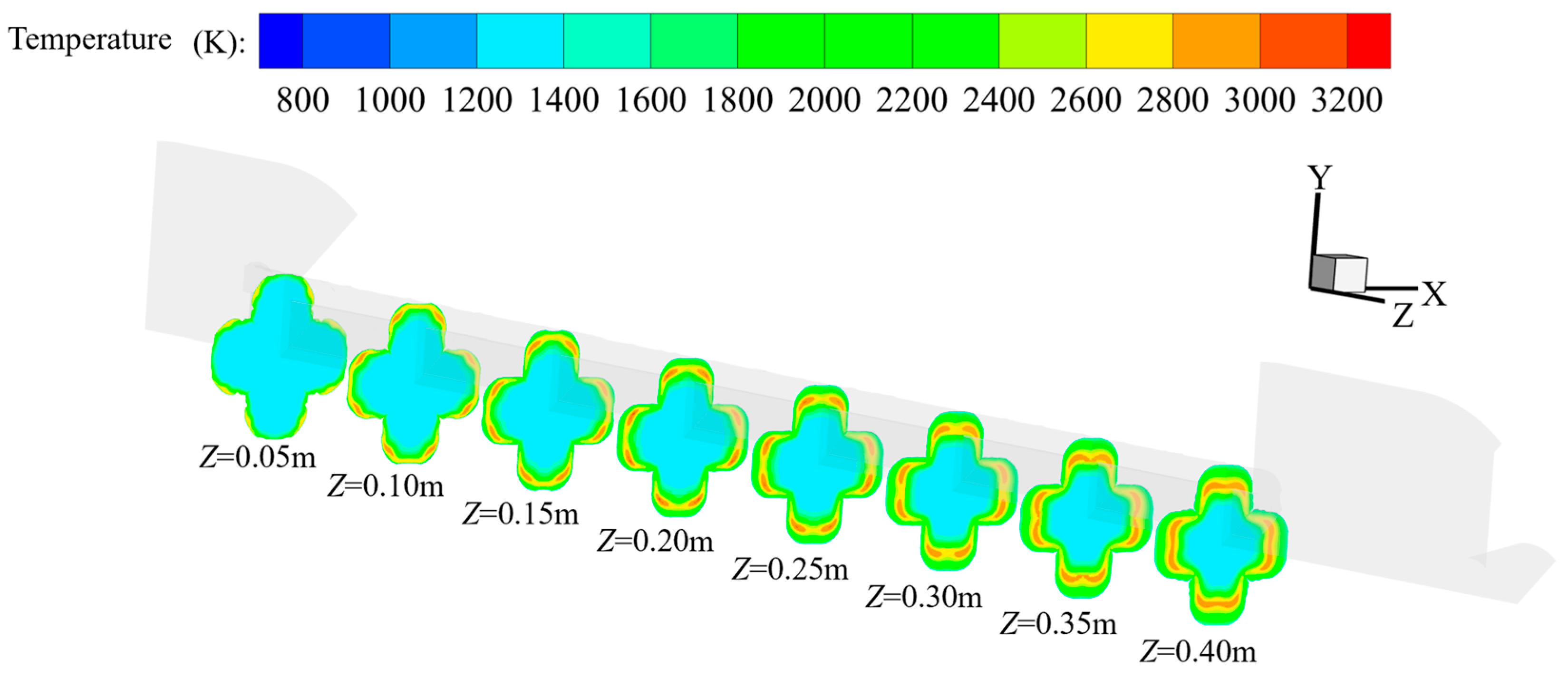
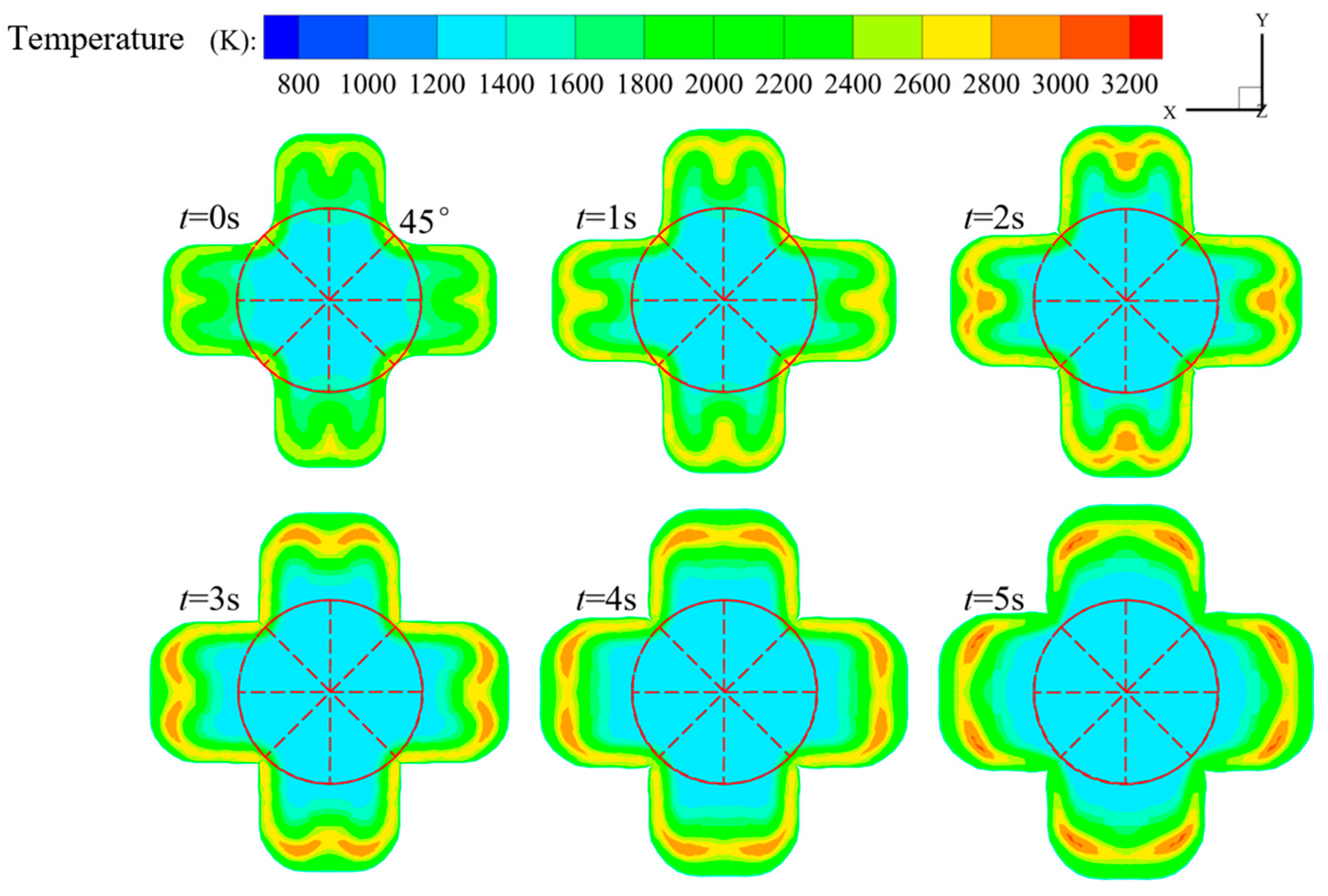
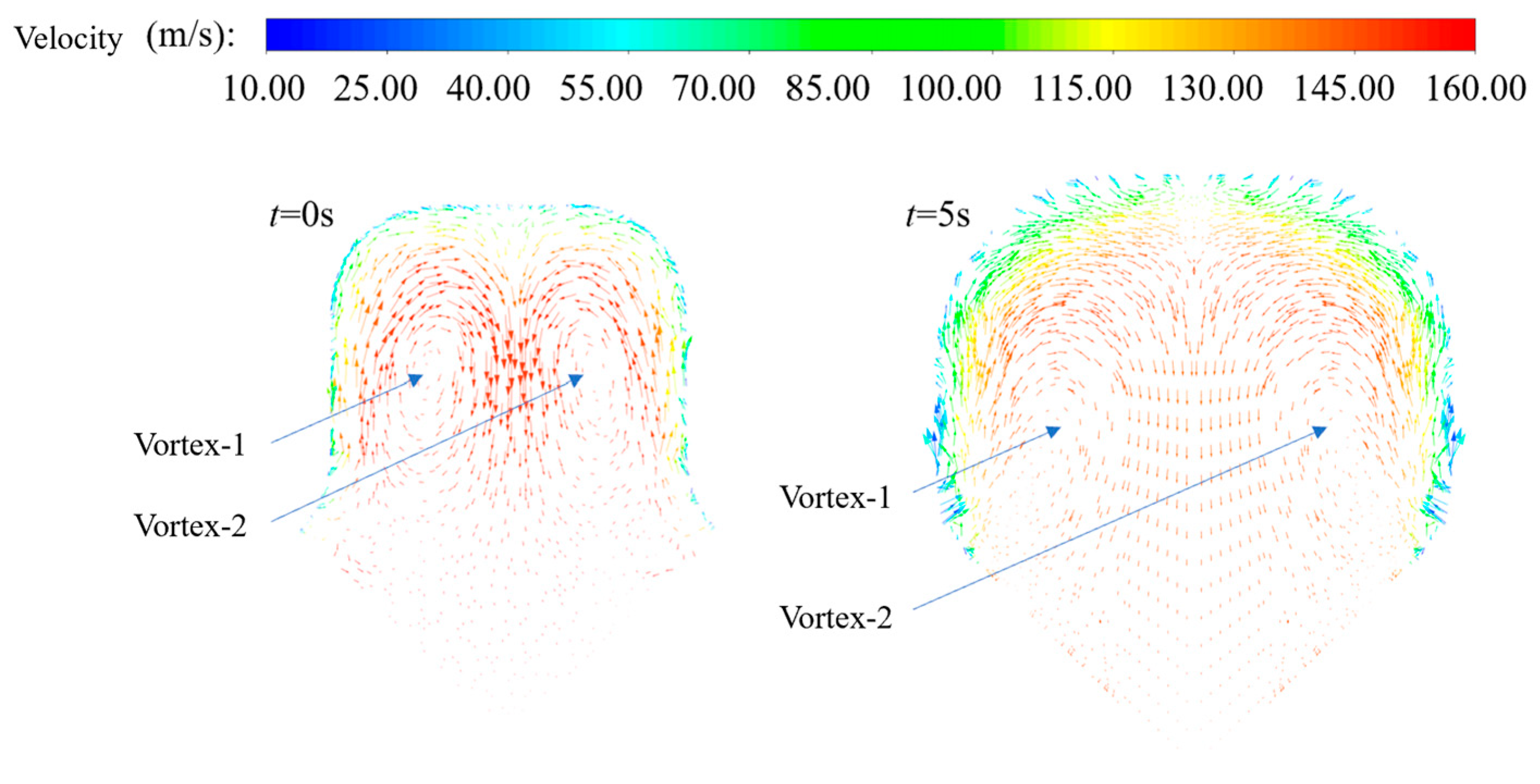
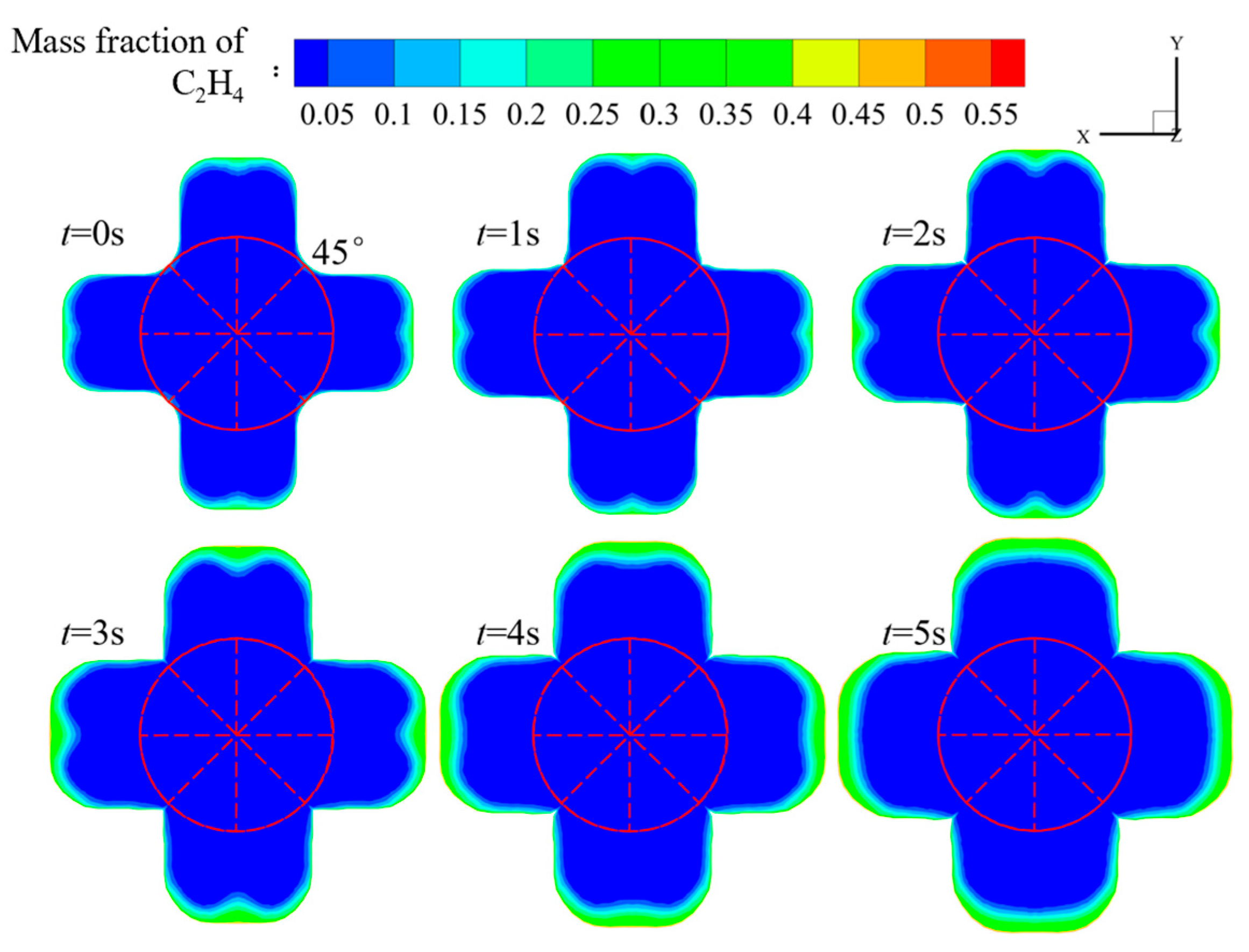
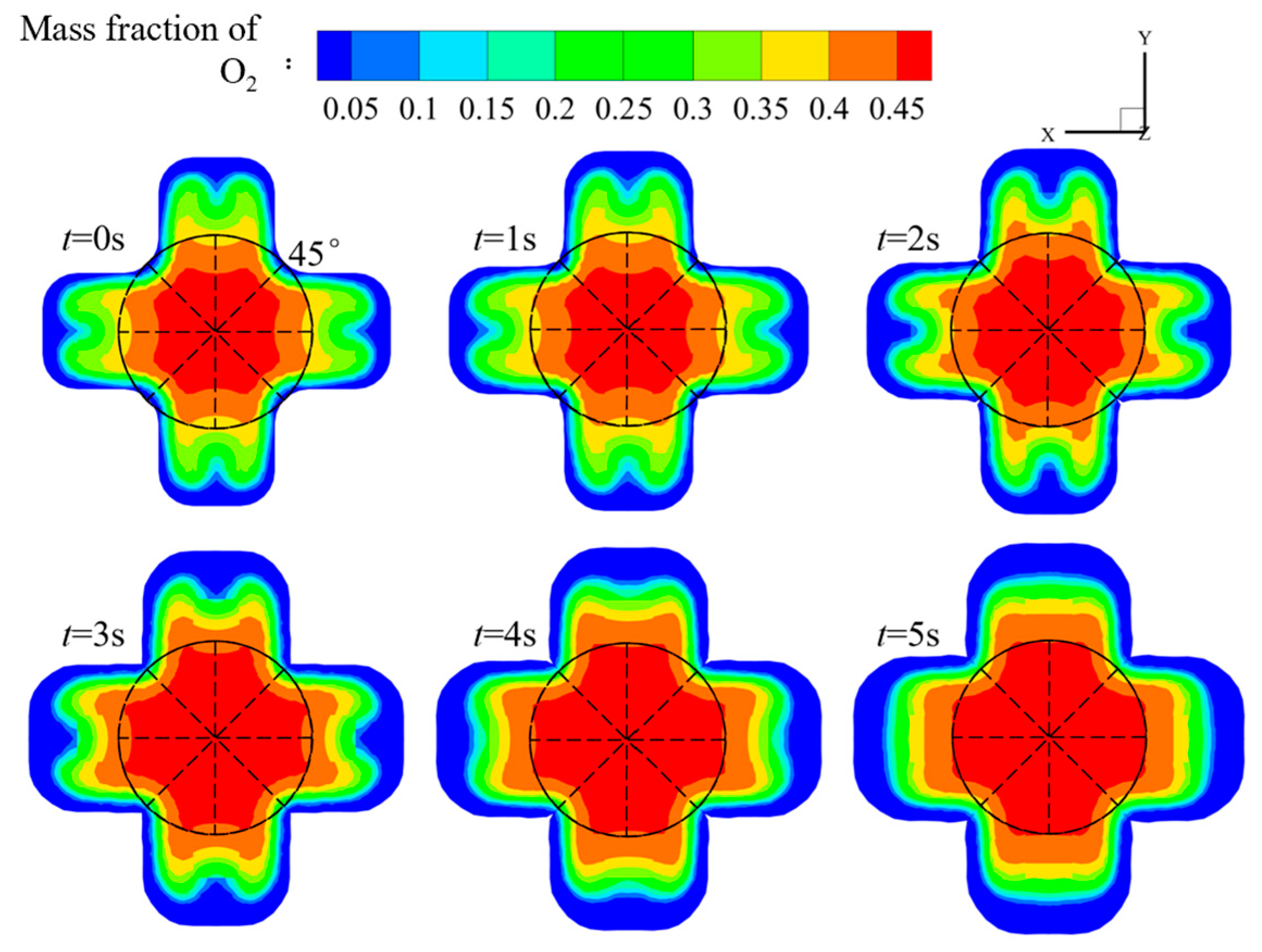
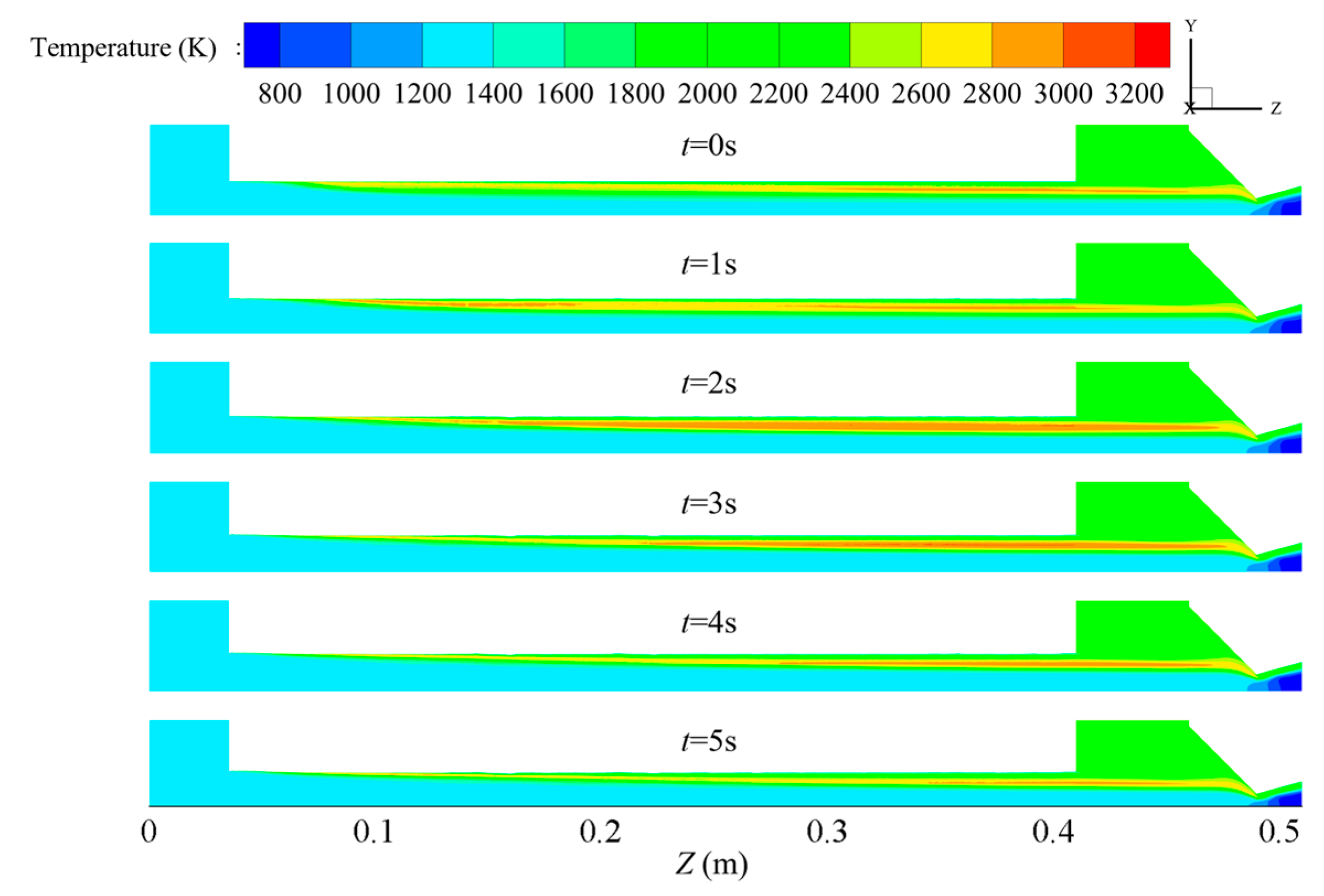
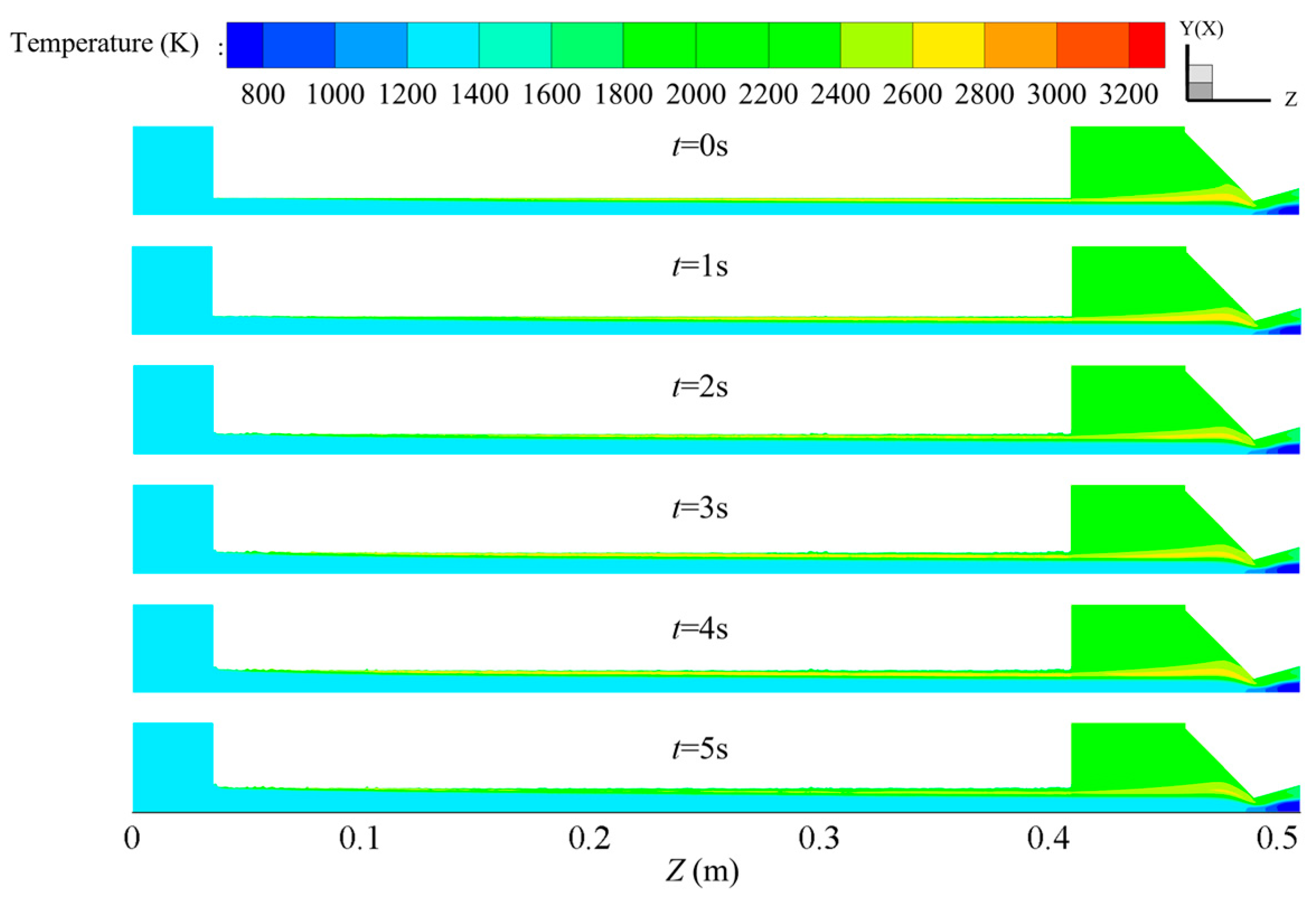
4.2. Flow Field Analysis of Cross-Shaped Grain
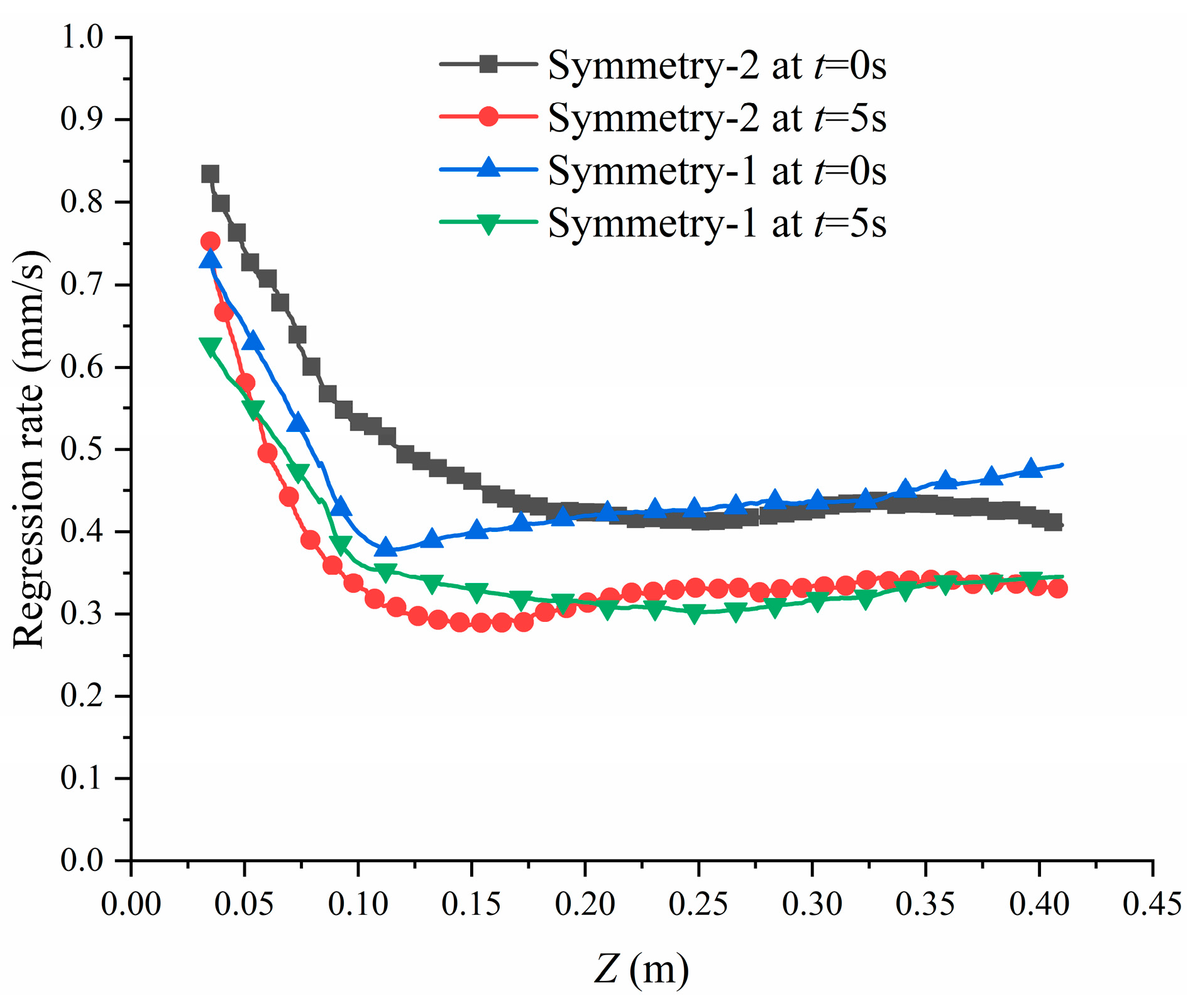
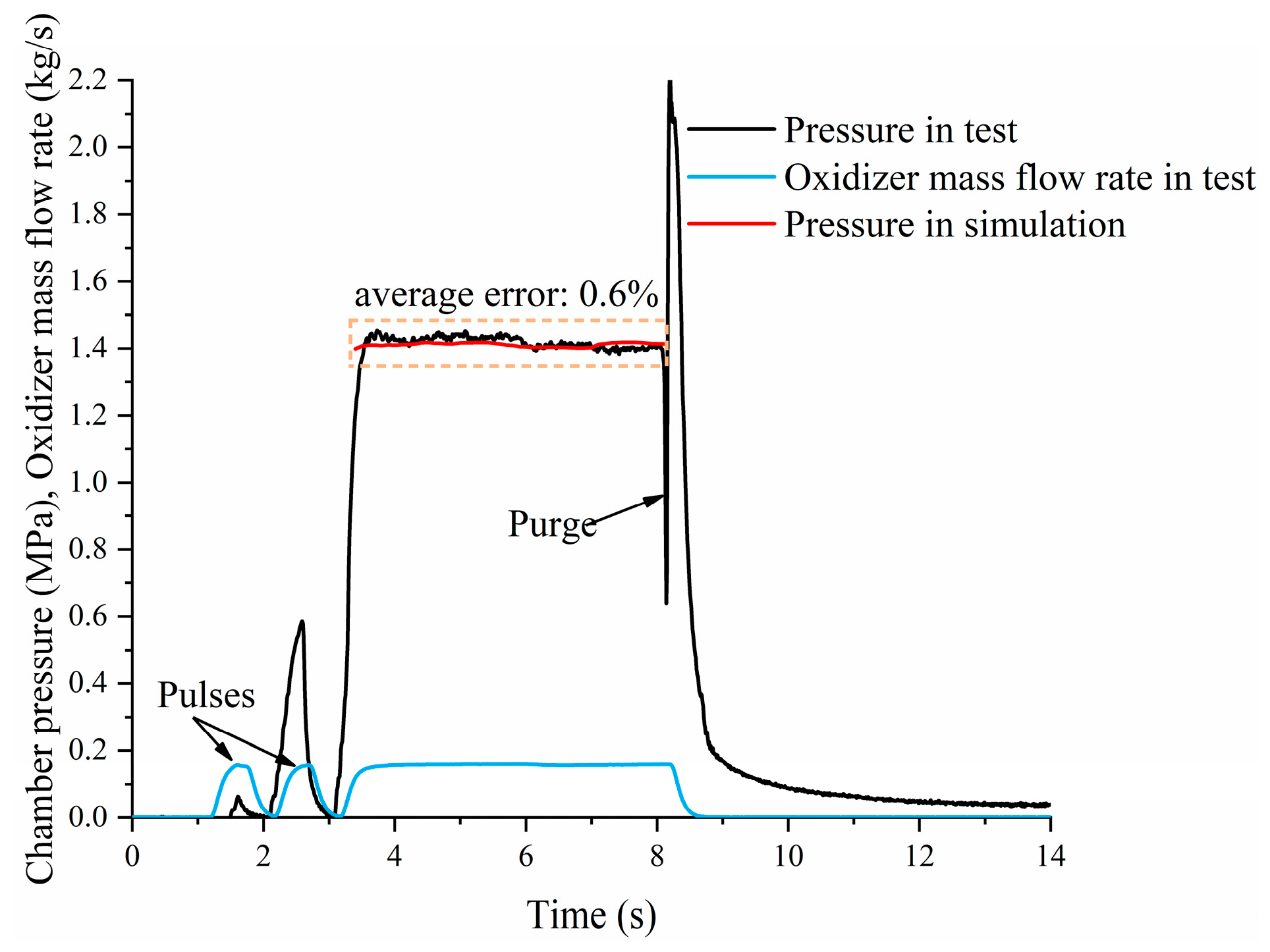
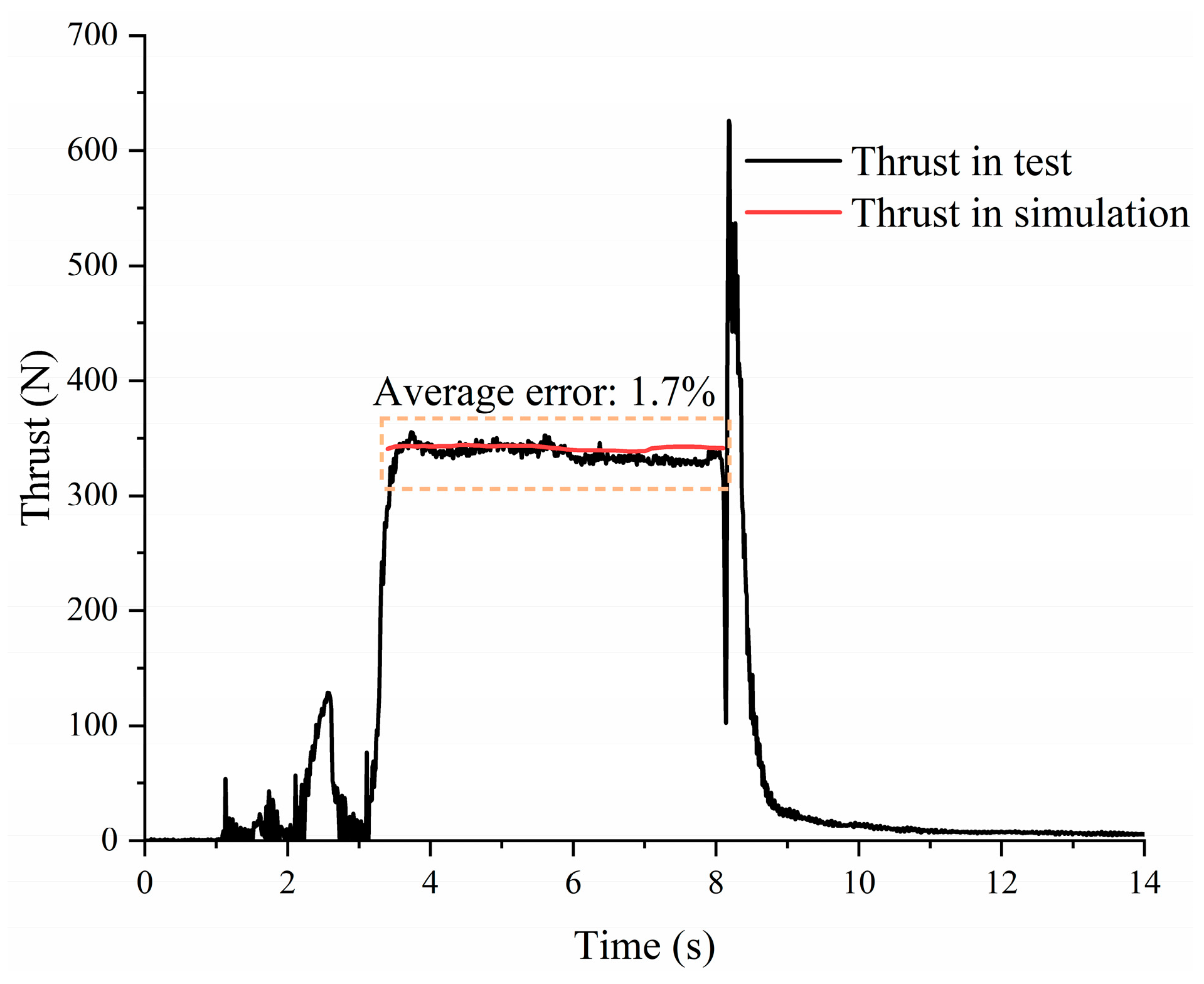
4.3. Verification and Performance Parameters Analysis
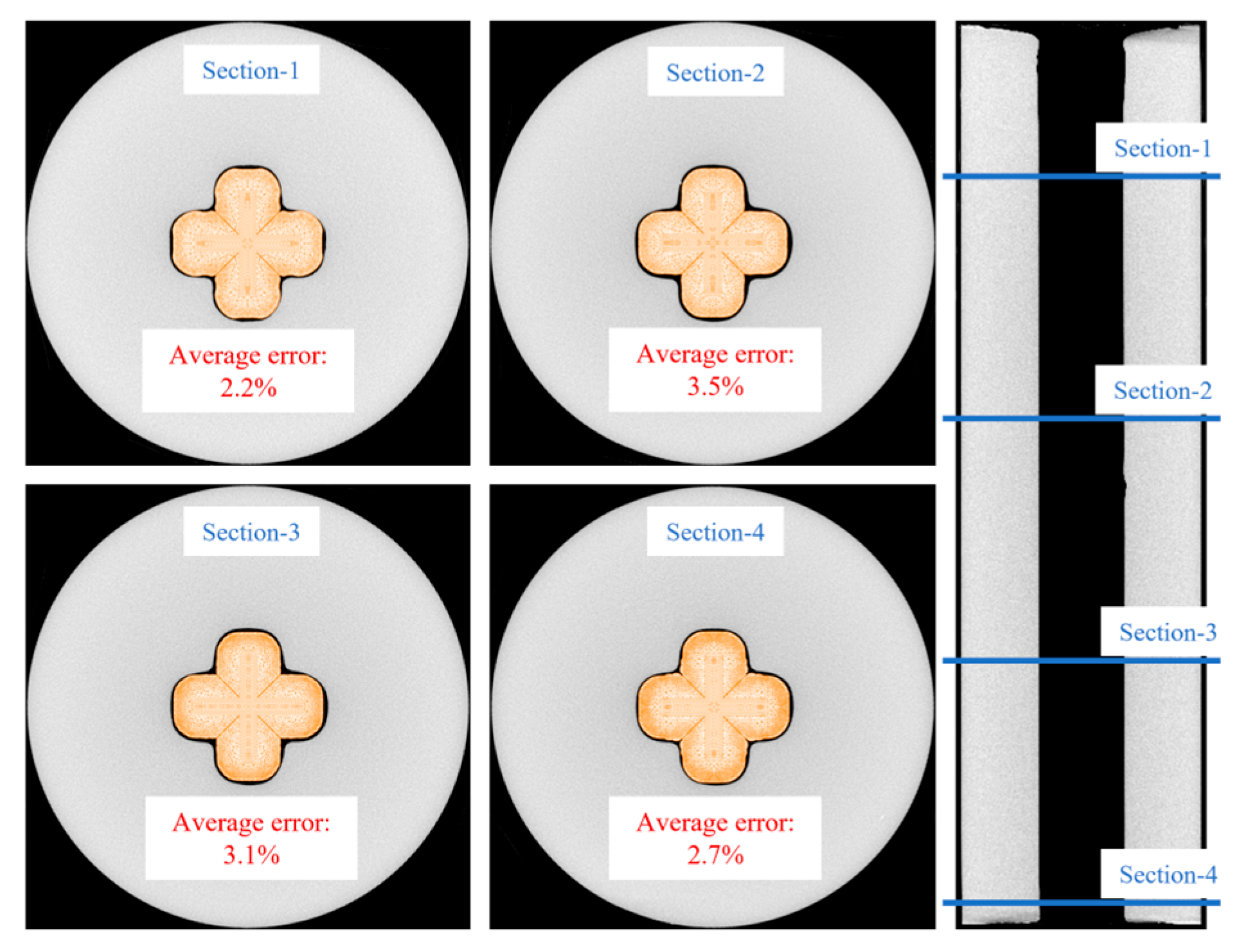
4.4. Comparison of the Combustion Surface After Test and Simulation Results
5. Conclusions
- (1)
- A new, simplified, and updated model for the combustion surface based on the dynamic mesh technique was proposed. When the distance between the nodes on the combustion surface and the symmetrical plane is less than 0.01 mm, the nodes shift to the symmetrical plane, negating the function of adding source items to adjacent grids.
- (2)
- The changes in the flow field structure and performance parameters during the operation of a cross-shaped grain in hybrid rocket motors were obtained. Notably, as the port expands, the high-temperature zone inside it changes from an “m” shape to an “n” shape. This occurs because the distance between the vortices on both sides of the symmetry plane gradually increases.
- (3)
- The deviations in chamber pressure and thrust from the simulation and test were less than 0.6% and 1.7%, respectively. The deviation between the simulated port area and the CT-scanned port area after the test was less than 3.5%. This indicates that the three-dimensional dynamic model of cross-shaped grains demonstrates good accuracy in performance parameters and combustion surface distribution.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, B.N. Understanding and outlook on EDLA technology. Aerosp. Return Remote Sens. 2018, 39, 36–44. [Google Scholar]
- Cai, G.B. Development and Application of Hybrid Rocket Motor Technology: Overview and Prospect. J. Propuls. Technol. 2012, 33, 831. [Google Scholar]
- Sutton, O.G.P. Biblarz, Rocket Propulsion Elements, 9th ed.; John Wiley & Sons: New York, NY, USA, 2016. [Google Scholar]
- Taylor, T.S. Introduction to Rocket Science and Engineering; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Karp, A.C.; Jens, E.T. Hybrid Rocket Propulsion Design Handbook; Academic Press: London, UK, 2023. [Google Scholar]
- Newlands, R.M. The Science and Design of the Hybrid Rocket Engine; Lulu.com: Raleigh, NC, USA, 2017. [Google Scholar]
- Luo, J.X.; Zhang, Z.L.; Lin, X.; Wang, Z.Z.; Kun, W.; Zhou, G.X.; Zhang, S.H.; Li, F.; Yu, X.L.; Wu, J. Flame Dynamics in the Combustion Chamber of Hybrid Rocket Using Multiangle Chemiluminescence. J. Propuls. Power 2023, 39, 482–491. [Google Scholar] [CrossRef]
- Wang, R.; Lin, X.; Wang, Z.; Wu, K.; Zhang, Z.; Luo, J.; Li, F.; Yu, X. Combustion Characteristics of a Swirl-Radial-Injection Composite Fuel Grain with Applications in Hybrid Rockets. Aerospace 2023, 10, 759. [Google Scholar] [CrossRef]
- Wei, T.; Cai, G.; Tian, H.; Jiang, X. Experiment and Numerical Research on Regression Rate of Hybrid Rocket Motor with Single-port Wagon Wheel Fuel Grain. Acta Astronaut. 2023, 207, 265–282. [Google Scholar] [CrossRef]
- Meng, X.; Gao, J.; Tian, H.; Niu, X.; Chen, R.; Cai, G. Study on the dynamic numerical simulation of flow and combustion in hybrid rocket motors based on a discrete phase model. Acta Astronaut. 2014, 215, 156–167. [Google Scholar] [CrossRef]
- Meng, X.; Tian, H.; Chen, X.; Jiang, X.; Wang, P.; Wei, T.; Cai, G. Numerical simulation of combustion surface regression based on Butterworth filter in hybrid rocket motor. Acta Astronaut. 2023, 202, 400–410. [Google Scholar] [CrossRef]
- Antoniu, A.; Akyuzlu, K.M. A physics based comprehensive mathematical model to predict motor performance in hybrid rocket propulsion systems. In Proceedings of the 41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Tucson, AZ, USA, 10–13 July 2005; p. 3541. [Google Scholar]
- Tian, H.; Li, Y.; Zeng, P. Transient Simulation of Regression Rate on Thrust Regulation Process in Hybrid Rocket Motor. Chin. J. Aeronaut. 2014, 27, 1343–1351. [Google Scholar] [CrossRef]
- Zhang, S.; Hu, F.; Wang, D.; Okolo, N.P.; Zhang, W. Numerical Simulations on Unsteady Operation Processes of N2O/HTPB Hybrid Rocket Motor with/without Diaphragm. Acta Astronaut. 2017, 136, 115–124. [Google Scholar] [CrossRef]
- Di Martino, G.D.; Mungiguerra, S.; Carmicino, C.; Savino, R.; Cardillo, D.; Battista, F.; Invigorito, M.; Elia, G. Two-Hundred-Newton Laboratory-Scale Hybrid Rocket Testing for Paraffin Fuel-Performance Characterization. J. Propuls. Power 2019, 35, 224–235. [Google Scholar] [CrossRef]
- Gallo, G.; Carmicino, C.; Mungiguerra, S.; Di Martino, G.D.; Savino, R. An Improvement of the Gas-surface Interaction and Entrainment Models for Paraffin-based Fuels in Hybrid Rocket Engines. In Proceedings of the AIAA Propulsion and Energy 2020 Forum, Online, 17 August 2020; p. 3760. [Google Scholar]
- Migliorino, M.T.; Gubernari, G.; Bianchi, D.; Nasuti, F.; Cardillo, D.; Battista, F. Numerical Simulations of Fuel Shape Change in Paraffin-Oxygen Hybrid Rocket Engines. In Proceedings of the AIAA AVIATION 2022, Chicago, IL, USA, 27 June–1 July 2022; p. 3563. [Google Scholar]
- Meng, X.; Tian, H.; Niu, X.; Zhu, H.; Gao, J.; Cai, G. Long-Duration Dynamic Numerical Simulation of Combustion and Flow in Hybrid Rocket Motors Considering Nozzle Erosion. Aerospace 2024, 11, 318. [Google Scholar] [CrossRef]
- Meng, X.; Tian, H.; Jiang, X.; Wei, T.; Cai, G. Experimental and numerical investigation on thermochemical erosion and mechanical erosion of carbon-based nozzles in hybrid rocket motors. Aerosp. Sci. Technol. 2024, 148, 109097. [Google Scholar] [CrossRef]
- Motoe, M.; Shimada, T. Numerical Simulations of Combustive Flows in a Swirling-Oxidizer-Flow-Type Hybrid Rocket. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014; p. 0310. [Google Scholar]
- Betelin, V.; Kushnirenko, A.; Smirnov, N.; Nikitin, V.; Tyurenkova, V.; Stamov, L. Numerical Investigations of Hybrid Rocket Engines. Acta Astronaut. 2018, 144, 363–370. [Google Scholar] [CrossRef]
- Smirnov, N.; Betelin, V.; Nikitin, V.; Stamov, L.; Altoukhov, D. Accumulation of Errors in Numerical Simulations of Chemically Reacting Gas Dynamics. Acta Astronaut. 2015, 117, 338–355. [Google Scholar] [CrossRef]
- Meng, X.; Tian, H.; Yu, R.; Lu, Y.; Gu, X.; Tan, G.; Cai, G. Three-dimensional numerical simulation of hybrid rocket motor based on dynamic mesh technology. Aerosp. Sci. Technol. 2023, 141, 108573. [Google Scholar] [CrossRef]
- Li, X.; Tian, H.; Yu, N.; Cai, G. Three-dimensional Numerical Simulation of Two-phase Flow in Hybrid Rocket Motor. In Proceedings of the 49th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, San Jose, CA, USA, 14–17 July 2013; p. 3893. [Google Scholar]
- Li, C.; Cai, G.; Tian, H. Numerical analysis of combustion characteristics of hybrid rocket motor with multi-section swirl injection. Acta Astronaut. 2016, 123, 26–36. [Google Scholar] [CrossRef]
- Shih, T.-H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A New k-ε Eddy Viscosity Model for High Reynolds Number Turbulent Flows: Model Development and Validation. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Zou, X.; Wang, N.; Han, L.; Bai, T.; Xie, K. Numerical Investigation on Regression Rate and Thrust Regulation Behaviors of a Combined Solid Rocket Motor with Aluminum-based Fuel. Aerosp. Sci. Technol. 2021, 119, 107102. [Google Scholar] [CrossRef]
- Shan, F.; Hou, L.; Piao, Y. Combustion Performance and Scale Effect from N2O/HTPB Hybrid Rocket Motor Simulations. Acta Astronaut. 2013, 85, 1–11. [Google Scholar] [CrossRef]
- Durand, J.; Raynaud, F.; Lestrade, J.-Y.; Anthoine, J. Turbulence Modeling Effects on Fuel Regression Rate in Hybrid Rocket Numerical Simulations. J. Propuls. Power 2019, 35, 1127–1142. [Google Scholar] [CrossRef]
- Baurle, R.A.; Eklund, D.R. Analysis of Dual-Mode Hydrocarbon Scramjet Operation at Mach 4-6.5. J. Propuls. Power 2002, 18, 990–1002. [Google Scholar] [CrossRef]
- Zhang, S.; Hu, F.; Zhang, W. Numerical Investigation on the Regression Rate of Hybrid Rocket Motor with Star Swirl Fuel Grain. Acta Astronaut. 2016, 127, 384–393. [Google Scholar] [CrossRef]
- Gurunadhan, M.D.P.; Baran, A.; Menon, S.K. Numerical Simulation of Combustion in a Hybrid Rocket with Liquefying Fuels. In Proceedings of the AIAA Propulsion and Energy 2019 Forum, Indianapolis, IN, USA, 19–22 August 2019; p. 4415. [Google Scholar]






| No. | Reaction | Parameters | ||
|---|---|---|---|---|
| A | b | Ta | ||
| 1 | 2.10 × 1014 | 0.0 | 18,015.3 | |
| 2 | 3.48 × 1011 | 2.0 | 10,134.9 | |
| 3 | 3.00 × 1020 | −1.0 | 0 | |
| Parameter | Value |
|---|---|
| Inner diameter of pre-chamber/mm | 80 |
| Length of pre-chamber/mm | 35 |
| Length of grain/mm | 375 |
| Length of post-chamber/mm | 50 |
| Diameter of nozzle throat/mm | 15 |
| Expansion area ratio of nozzle | 3 |
| Position (mm) | Area in Simulation (mm2) | Area in Test (mm2) | Error (%) |
|---|---|---|---|
| 100 | 719.7 | 736.1 | 2.2 |
| 200 | 720.1 | 746.7 | 3.5 |
| 300 | 739.3 | 763.3 | 3.1 |
| 400 | 745.5 | 766.4 | 2.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, X.; Huang, H.; Chen, Y.; Yao, M.; Wang, J.; Tian, H. The Three-Dimensional Transient Simulation of Cross-Shaped Grains in Hybrid Rocket Motors. Aerospace 2025, 12, 429. https://doi.org/10.3390/aerospace12050429
Meng X, Huang H, Chen Y, Yao M, Wang J, Tian H. The Three-Dimensional Transient Simulation of Cross-Shaped Grains in Hybrid Rocket Motors. Aerospace. 2025; 12(5):429. https://doi.org/10.3390/aerospace12050429
Chicago/Turabian StyleMeng, Xiangyu, Huihuang Huang, Yifei Chen, Mingsen Yao, Jianyuan Wang, and Hui Tian. 2025. "The Three-Dimensional Transient Simulation of Cross-Shaped Grains in Hybrid Rocket Motors" Aerospace 12, no. 5: 429. https://doi.org/10.3390/aerospace12050429
APA StyleMeng, X., Huang, H., Chen, Y., Yao, M., Wang, J., & Tian, H. (2025). The Three-Dimensional Transient Simulation of Cross-Shaped Grains in Hybrid Rocket Motors. Aerospace, 12(5), 429. https://doi.org/10.3390/aerospace12050429







