1. Introduction
The rapid advancements in energy technologies are driving modern power devices toward higher levels of compactness and integration. This development involves high levels of power consumption and hence requires high-performance cooling technologies. Heat exchangers play a critical role in various industrial fields, such as chemical engineering [
1], aerospace [
2], and nuclear energy [
3]. Heat exchangers enable the recovery of waste heat and further improve thermal effectiveness. In the field of micro gas turbines, adding a heat exchanger (recuperator) between the compressor and the turbine can potentially increase the overall thermal efficiency of the system from 15–20% to 30% or even higher. Given the compact size of micro gas turbines, to ensure their compactness, heat exchangers are predominantly designed in a circular configuration [
4].
Conventional heat exchangers employed in micro gas turbines are predominantly of the plate–fin and primary surface types; studies have also been conducted to modify their internal structures to enhance their thermal performances [
5]. However, conventional designs are still impeded by their large size and heavy weight. In addition, these heat exchangers have areas with low specific heat transfer. Furthermore, constrained by manufacturing techniques, conventional fabrication methods are incapable of producing complex structures, which significantly limit innovation and design possibilities for heat exchangers. Highly complex structures with large surface areas are required to improve the compactness and thermal effectiveness of heat exchangers.
The development of additive manufacturing (AM) technologies has significantly expanded the design possibilities for compact heat exchangers. AM, commonly known as 3D printing, is a transformative manufacturing process that builds objects layer by layer from digital models, enabling the creation of complex geometries that are difficult to achieve with conventional methods. AM has made it possible to fabricate porous media with customized topological structures, particularly those inspired by nature, such as triply periodic minimal surfaces (TPMSs), which have garnered significant attention due to their superior thermal–mechanical performances [
6]. TPMS structures were first discovered in the 19th century by Schwarz [
7]. These structures, characterized by an overall mean curvature of zero, exhibit periodicity in three-dimensional space with smooth and continuous surfaces [
8]. TPMSs can be classified into two types: solid (skeletal) networks and sheet networks [
9,
10]. The sheet-based TPMS structures are particularly notable for their ability to partition three-dimensional space into two non-interconnected channels, which can independently accommodate cold and hot fluids, making these structures suitable for two-fluid heat exchanger designs. AM technologies have been used to fabricate TPMS structures for various fields, such as mechanical components, heat sinks, heat exchangers, and fluid mixers [
11,
12,
13]. The mechanical performance of sheet-based TPMSs also outperforms various lattice designs, which further confirms the usability of the heat exchanger application [
14].
The flow and heat transfer performance of different TPMS topologies have been intensively investigated to find the optimal model, with various studies showing that the TPMS heat exchangers provide better heat transfer performances than conventional designs. Femmer et al. [
15] investigated the performance of heat exchangers based on Diamond, Gyroid, Primitive, and I-WP TPMS structures and compared them with conventional flat-plate and hollow-tube structures. The results showed that the performance of TPMS heat exchangers exceeded those of hollow-tube and flat-plate designs by an order of magnitude, demonstrating superior heat transfer characteristics. Among these, the Diamond structure exhibited the best heat transfer performance under its inherent pressure loss. Reynolds et al. [
16] manufactured a series of TPMS heat exchangers and found that the Nusselt numbersof Gyroid heat exchangers is 112% higher than that of straight tubes, while their friction factor is the lowest among various TPMS structures. Yan et al. [
17] conducted simulations of five Lattice structures; they demonstrated that, within the Reynolds number range of 200–500, the overall heat transfer performances of the Gyroid, Diamond, and I-WP structures improved by 90% compared to printed circuit heat exchanger (PCHE). Huang et al. [
18] investigated the thermal–hydraulic performance of Diamond, Fischer–Koch S, and PCHE through numerical simulations. The TPMS heat exchanger demonstrated a fourfold increase in power-to-weight ratio while reducing the volume by half compared to PCHE, highlighting the significant potential of TPMS heat exchangers for further space and weight savings in aerospace applications. Wang et al. [
19] addressed the demand for highly efficient heat exchangers in advanced nuclear systems by designing two types of heat exchangers based on I-WP and Primitive structures; the numerical simulation results indicated that the TPMS heat exchangers achieved a total heat transfer rate approximately 2–3 times higher than that of PCHE while reducing the volume by half.
The configurations of the TPMS structures, such as porosity, unit cell size, and even material, have shown a significant influence on heat transfer effectiveness. Mahmoud et al. [
20] fabricated four heat exchanger prototypes based on Gyroid structures by controlling lattice thickness and porosity. The study revealed that thinner lattice structures and stretched TPMS channels help reduce pressure loss. However, it also pointed out that lattice thicknesses below 0.2 mm should be avoided during 3D printing to prevent leakage. Cheng et al. [
21] examined the correlations between flow resistance and heat transfer coefficients for four TPMS structures within the Reynolds number range of 10–129 and porosity range of 0.2–0.8. The results showed that the I-WP structure achieved the highest heat transfer performance per unit flow resistance, which was 1.9 times that of the Diamond structure. Tang et al. [
22] observed that the superior convective heat transfer performance of the Diamond structure compared to other TPMS structures is due to its lack of “through-holes” in its geometry, which increases fluid disturbances. Liang et al. [
23] fabricated three types of heat exchangers: Diamond, Gyroid, and Primitive. The experimental results demonstrated that the Diamond structure exhibited a higher heat transfer rate compared to the Gyroid and Primitive structures. It was observed that the surface area-to-volume ratio of TPMS units increases exponentially as the unit size decreases, suggesting potential improvements in compactness and thermal performance. Liang et al. [
24] designed three cross-flow Diamond heat exchangers with different unit sizes but identical porosity. Experimental results revealed that smaller unit sizes tend to induce large-scale bifurcation flow, thereby enhancing heat transfer effectiveness, albeit at the cost of increased pressure loss. Similarly, Gao et al. [
25] found that smaller lattice sizes lead to more uniform temperature distributions and higher effectiveness but also result in greater pressure loss.
The flow and heat transfer performance of different TPMS heat exchanger materials have also been studied. Gao et al. [
26] fabricated two Diamond heat exchangers with identical structures using pure copper and 316 L stainless steel, respectively. Experimental results showed that the convective heat transfer coefficient of the pure copper TPMS heat exchanger was approximately 1.17–1.33 times higher than that of the 316 L stainless steel counterpart, indicating that pure copper is a promising candidate material for next-generation heat exchangers. Qian et al. [
27] fabricated three pure copper heat exchangers based on Primitive, Gyroid, and Fischer–Koch S structures. Their findings also confirmed that the copper heat exchangers exhibited higher volumetric heat transfer rates. Among these, the Fischer–Koch S structure demonstrated significantly superior heat transfer performance compared to the other two. However, its complex internal channels, which continuously alter the flow direction, resulted in poorer temperature uniformity and significantly higher pressure losses than those of the Gyroid structure [
28].
Although there has been extensive research on TPMS heat exchangers, most studies have primarily focused on investigating the flow and heat transfer characteristics of a few representative TPMS structures, such as 4 × 4 × 4 or 1 × 1 × n. However, these dimensions are far from meeting the size requirements necessary for industrial heat exchangers. Moreover, these studies often employ large lattice sizes, which result in lower compactness and fail to fully utilize the inherent high compactness of TPMS structures.
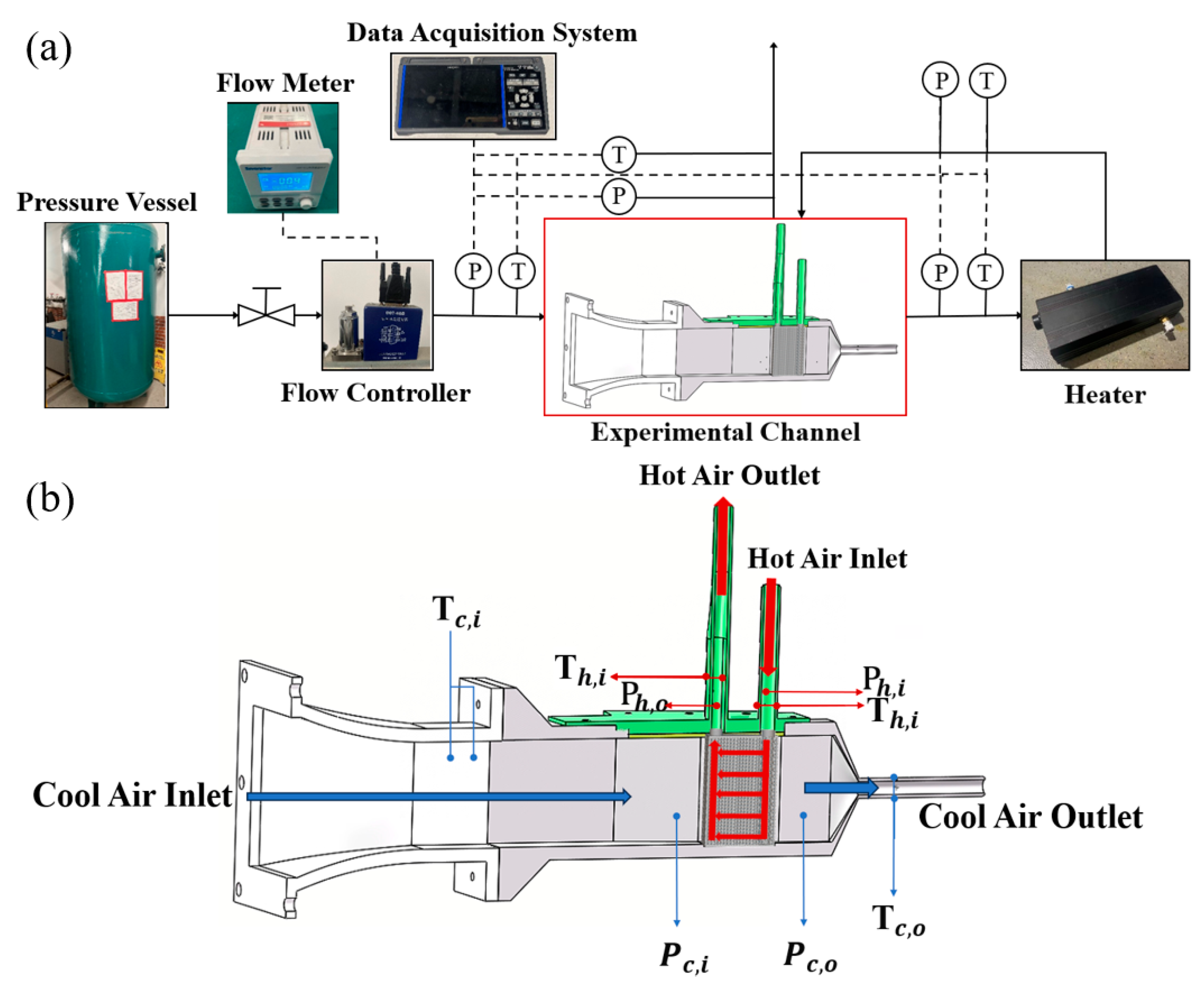
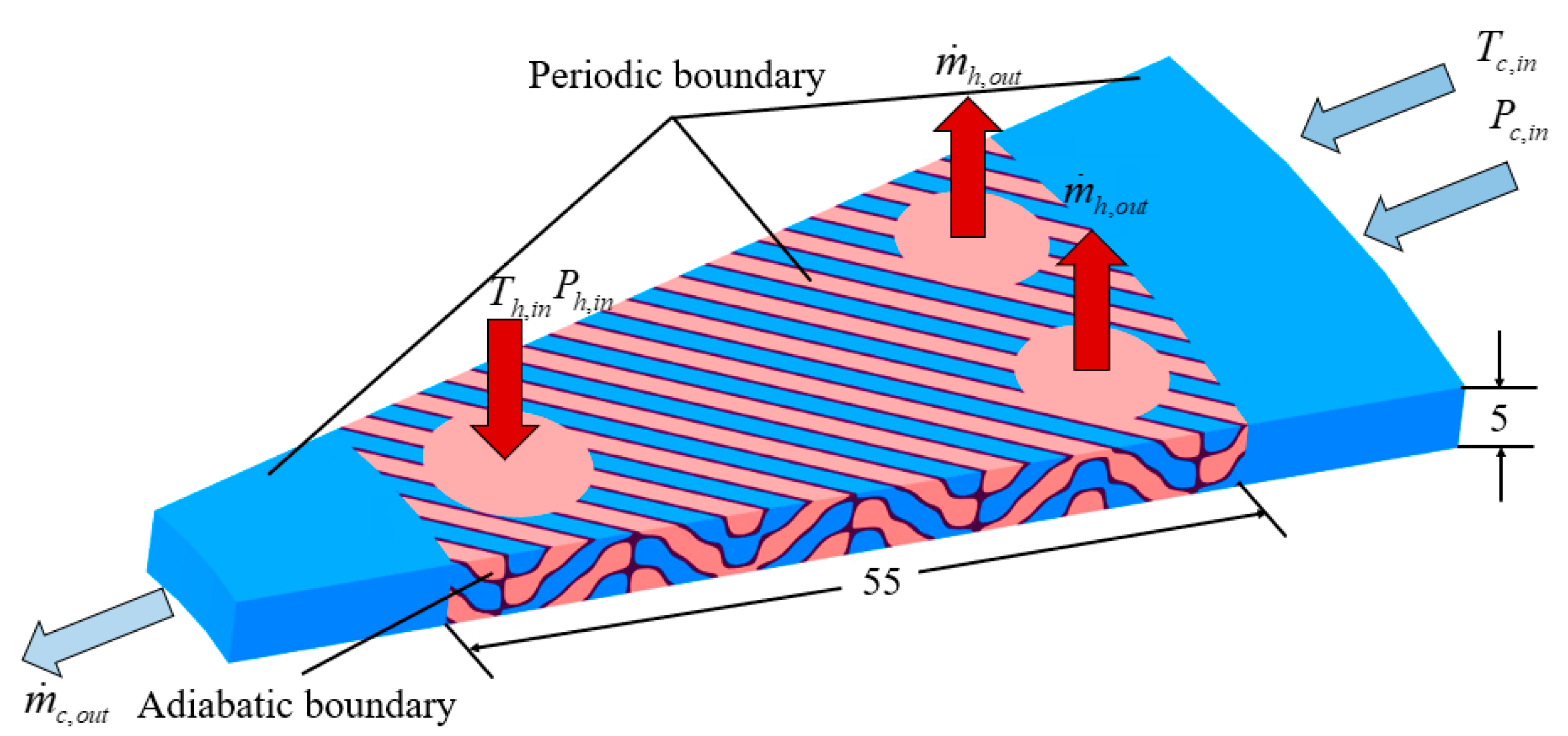
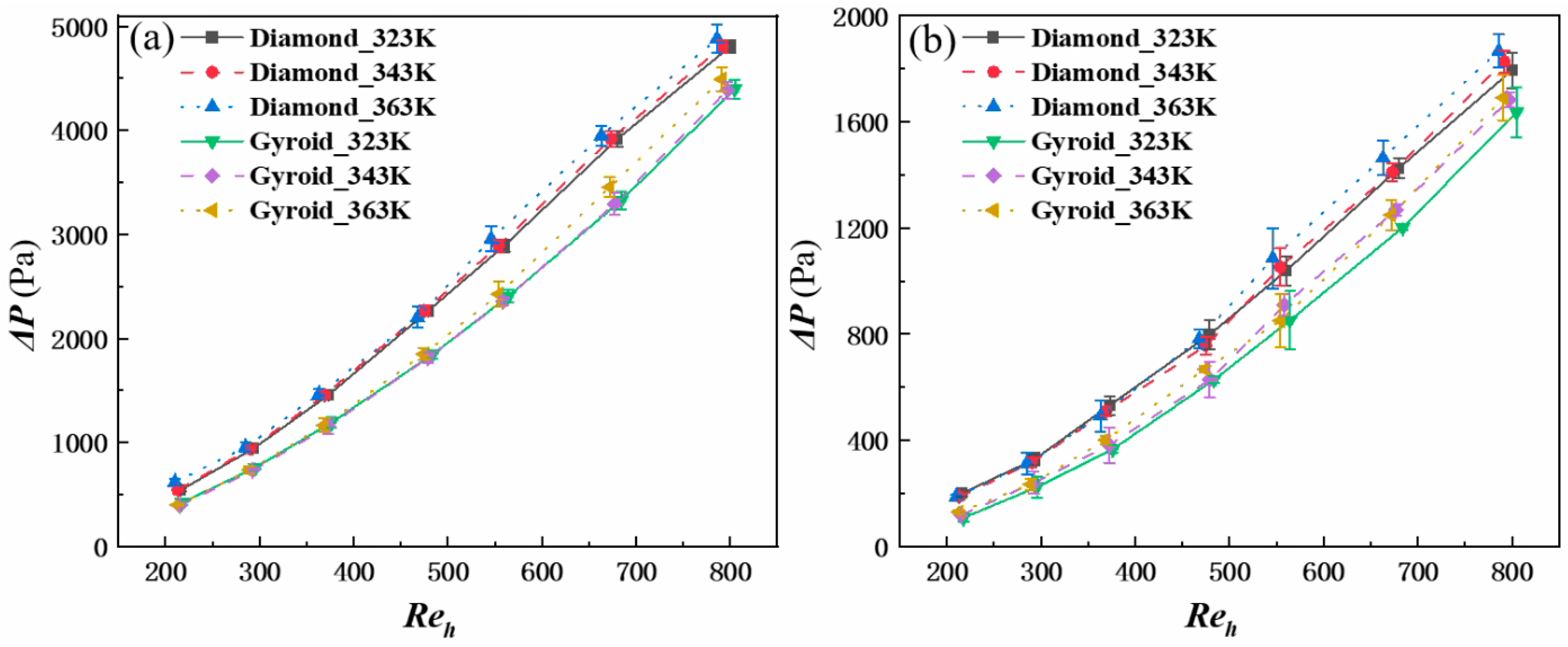
In this study, to address the demand for highly efficient and compact heat exchangers in micro gas turbines, an annular TPMS-based heat exchanger is proposed, leveraging additive manufacturing technology. This design can be directly installed on the outer side of the combustion chamber, significantly reducing the required installation space. Two modular prototypes of the annular heat exchangers were fabricated, which comprise a large number of lattice units with smaller lattice sizes, aligning with the requirements for industrial compact heat exchangers. The heat transfer performance of the heat exchangers was investigated through steady-state experiments, and their performance was compared with those of existing heat exchangers and other TPMS designs. Additionally, numerical simulations of the TPMS heat exchanger were conducted to further elucidate the mechanisms of heat transfer enhancement. This study aims to address the lack of data on the flow and heat transfer performance of compact heat exchangers with large-scale lattices.