Optimization of Flight Scheduling in Urban Air Mobility Considering Spatiotemporal Uncertainties
Abstract
1. Introduction
2. Conflict Identification Model Incorporating Flight Uncertainty
2.1. Initial Flight Plan Generation
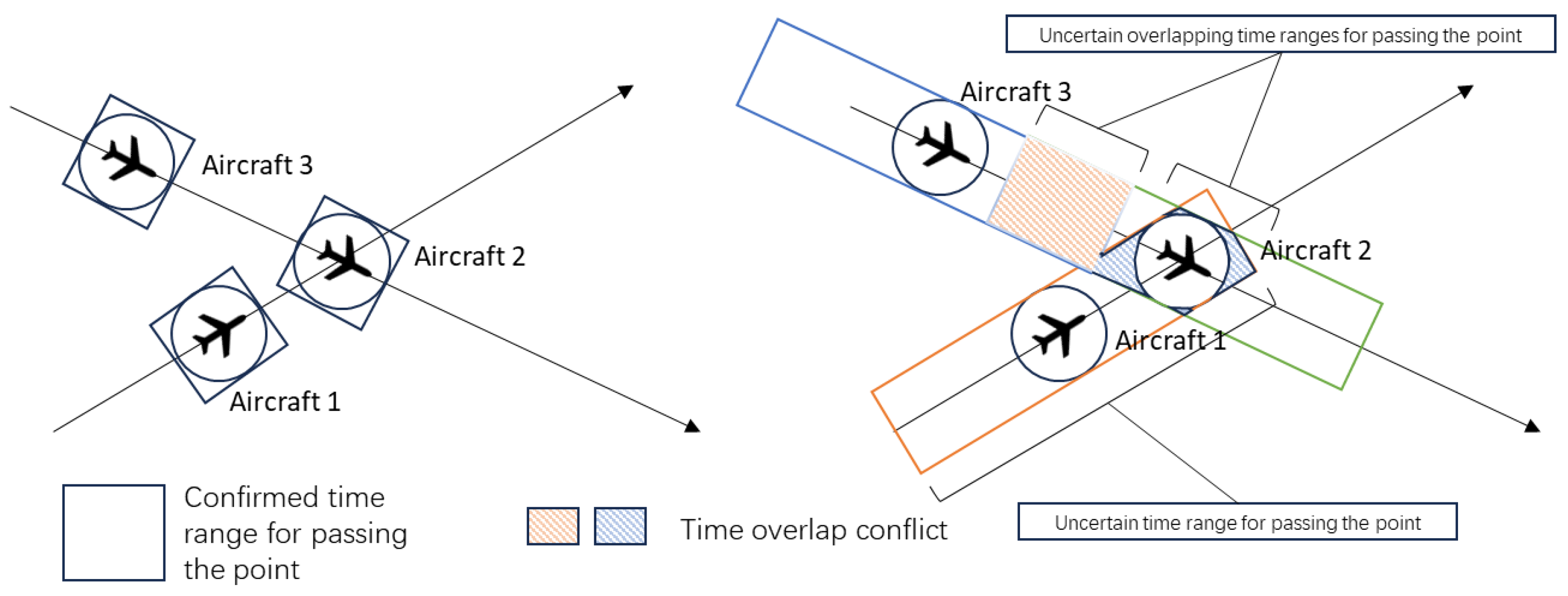
2.2. Uncertainty Principle
- (1)
- Confidence Interval and Temporal Boundaries
- (2)
- Preceding and Succeeding Interval Bounds
- (3)
- Latent Conflict Detection Model
- (4)
- Mathematical Derivation of Conflict Probability
3. Critical Flight Plan Identification
3.1. Critical Flight Plan Identification Methodology
- (1)
- Eigenvector Centrality
- (2)
- PageRank Algorithm
- (3)
- Degree Centrality
- (4)
- Betweenness Centrality
3.2. Critical Flight Plan Identification Methodology Validation
4. Flight Plan Optimization Strategy
4.1. Development of Flight Plan Optimization Model
4.1.1. Optimization Objective
4.1.2. Adjustment Strategies
- Speed-Only Adjustment
- Departure Time-Only Adjustment
- Joint Departure Time and Speed Adjustment
Advanced departure + increased speed → potential total time reduction
4.1.3. Model Constraints
4.2. Staged Optimization Solution
- (1)
- Critical Plan Prioritization
- (2)
- Non-Critical Plan Local Optimization
4.3. Optimization Solution Based on Artificial Lemming Algorithm
- (1)
- Long-Distance Migration (Global Exploration via Brownian Motion)
- (2)
- Burrowing (Local Refinement Toward Global Optimum)
- (3)
- Foraging (Spiral Search Strategy)
- (4)
- Predator Evasion (Flight Exploration)
- (5)
- Energy Factor for Behavioral Transition
5. Simulation Experiments
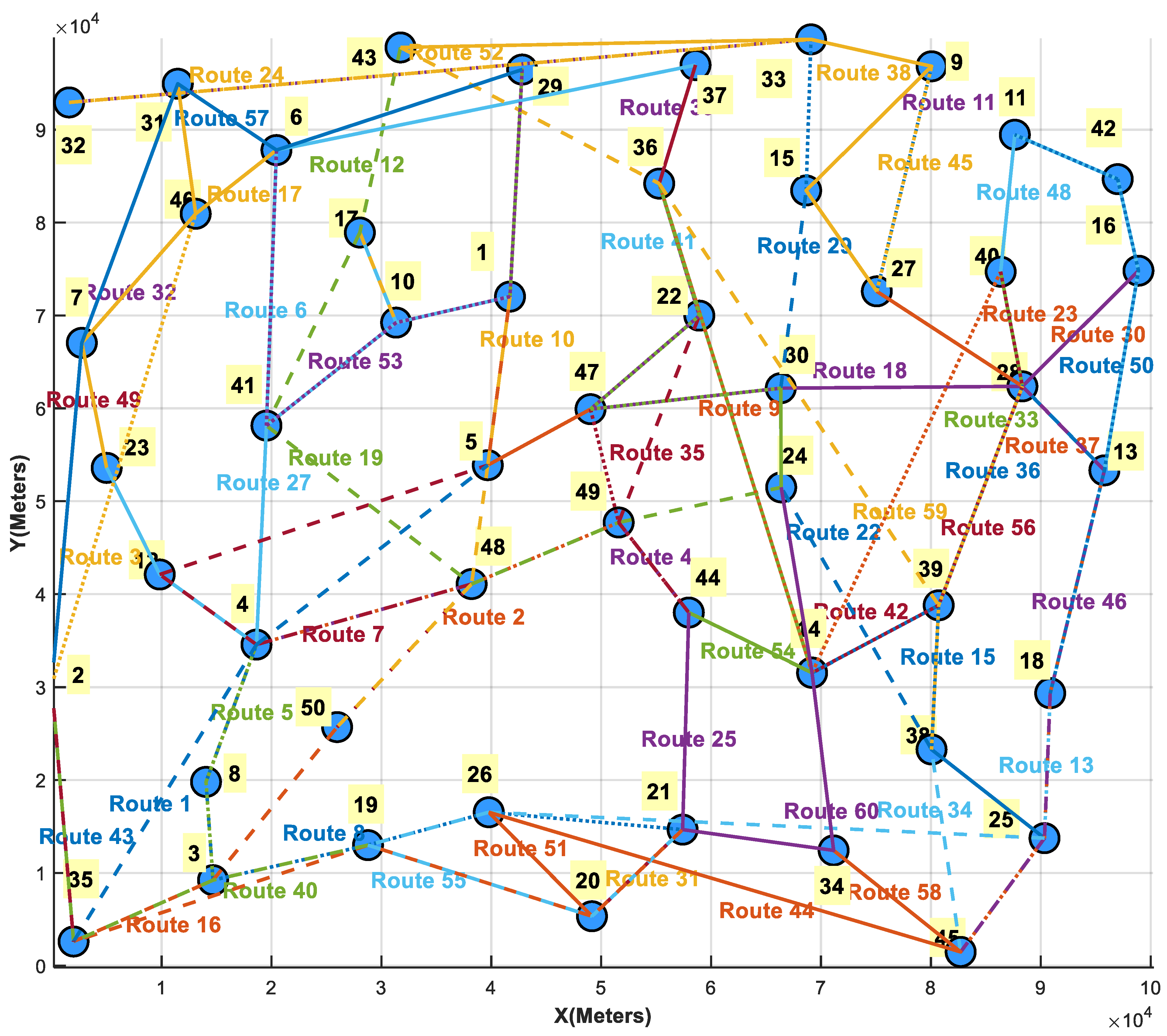
5.1. Design of the Simulation Experiment Environment
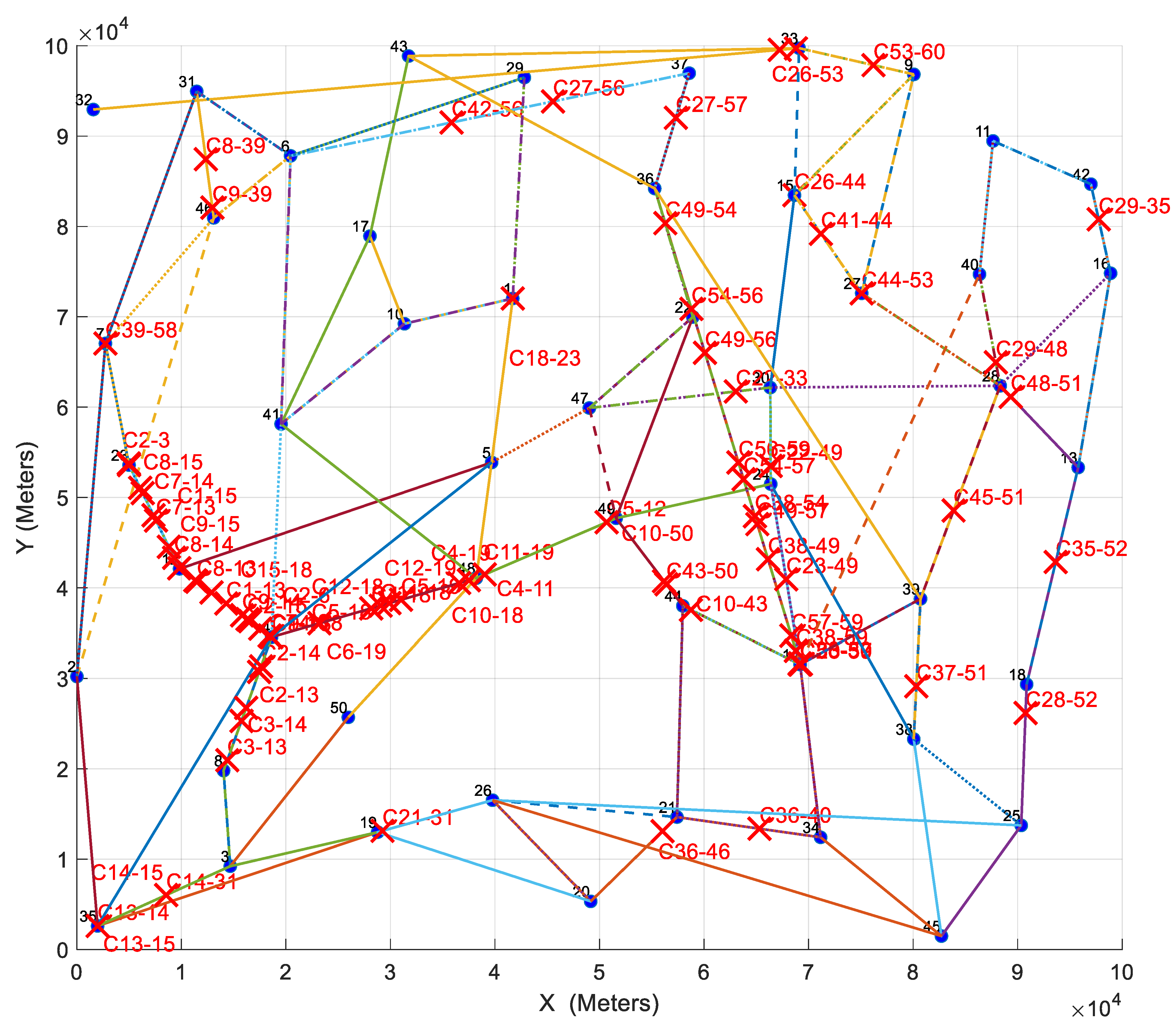
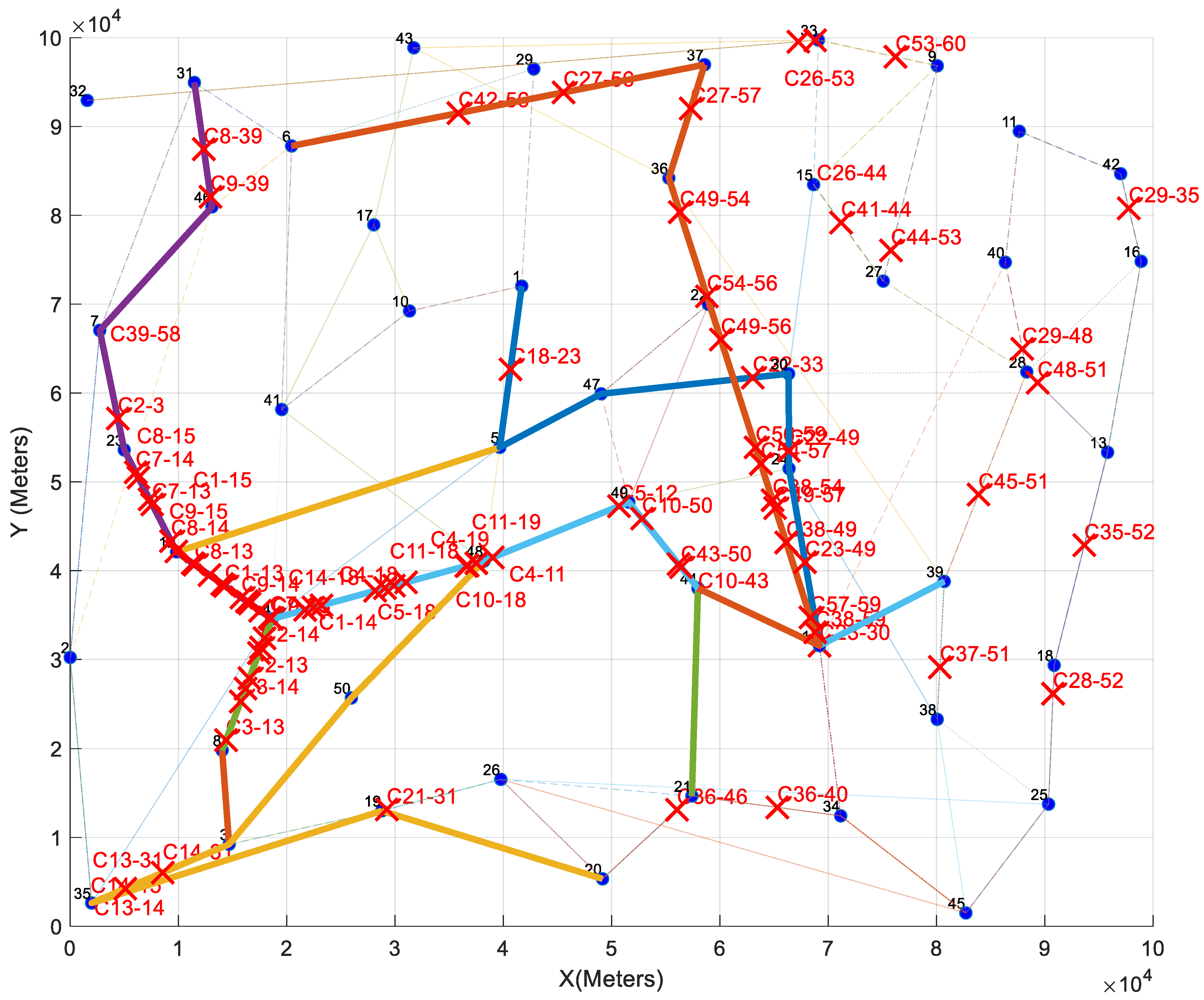
5.2. Conflict Identification Based on Uncertainty Principle
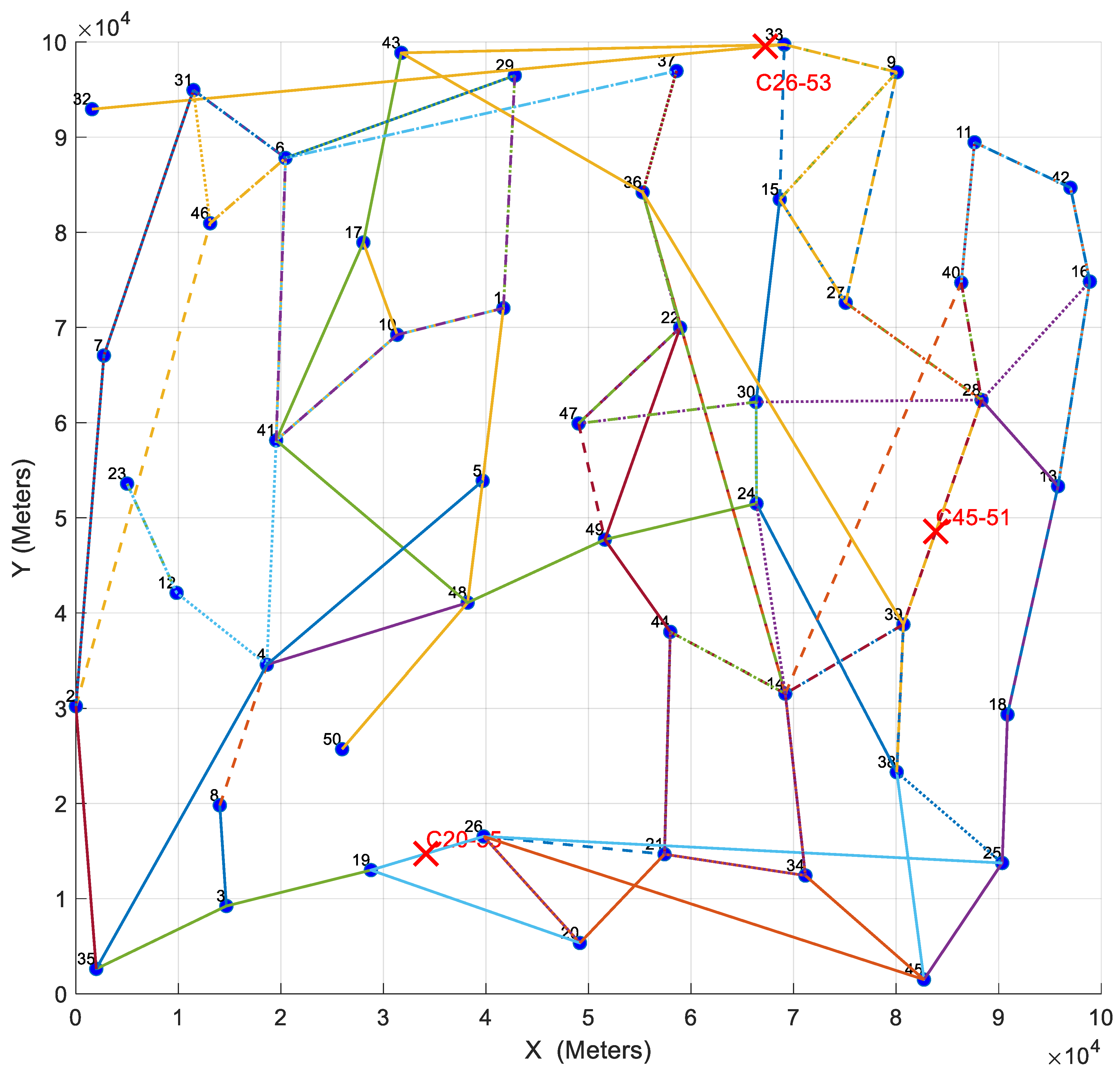
5.3. Critical Flight Plan Identification
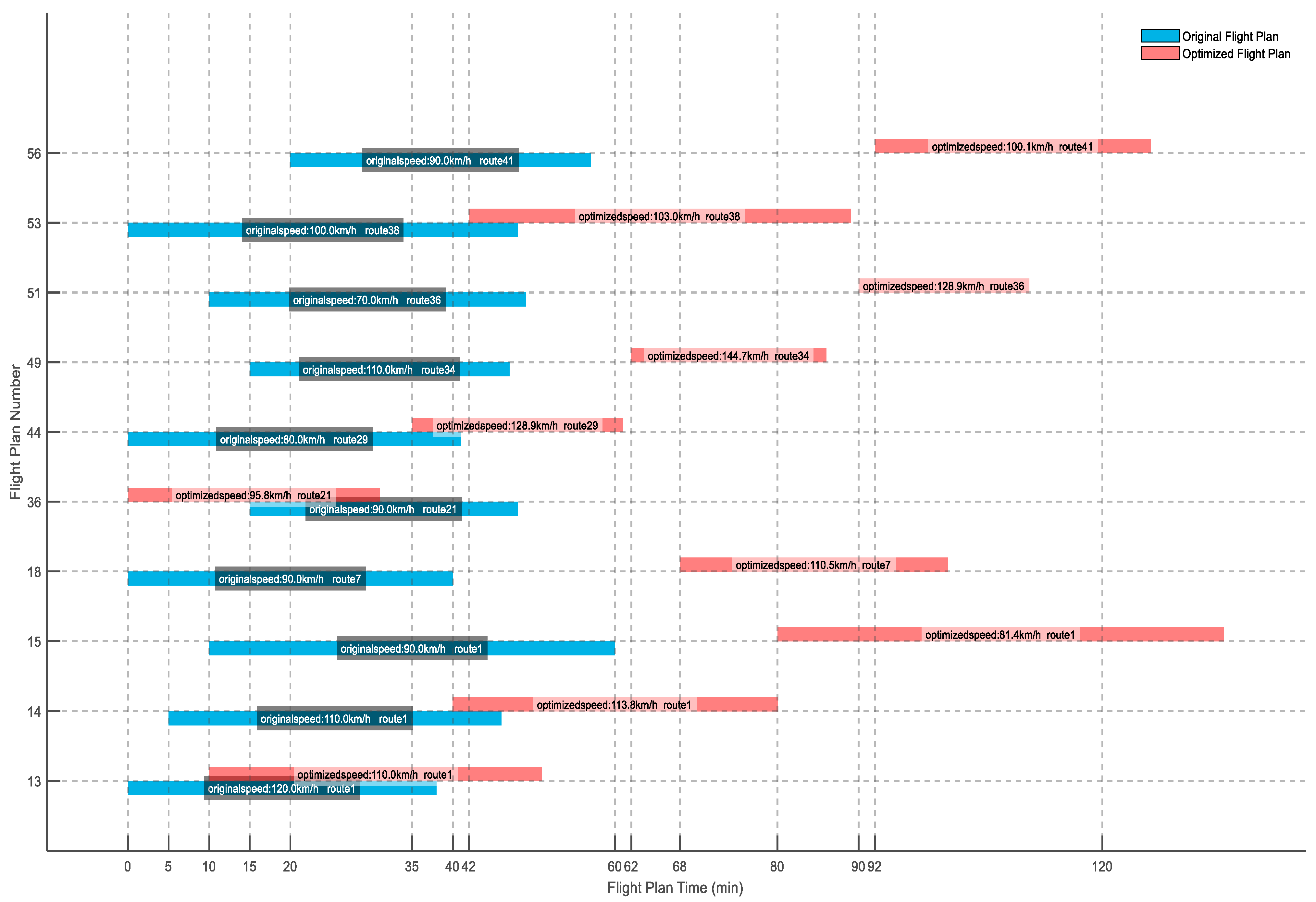
5.4. Staged Flight Plan Optimization
Optimization Algorithm Parameter Settings
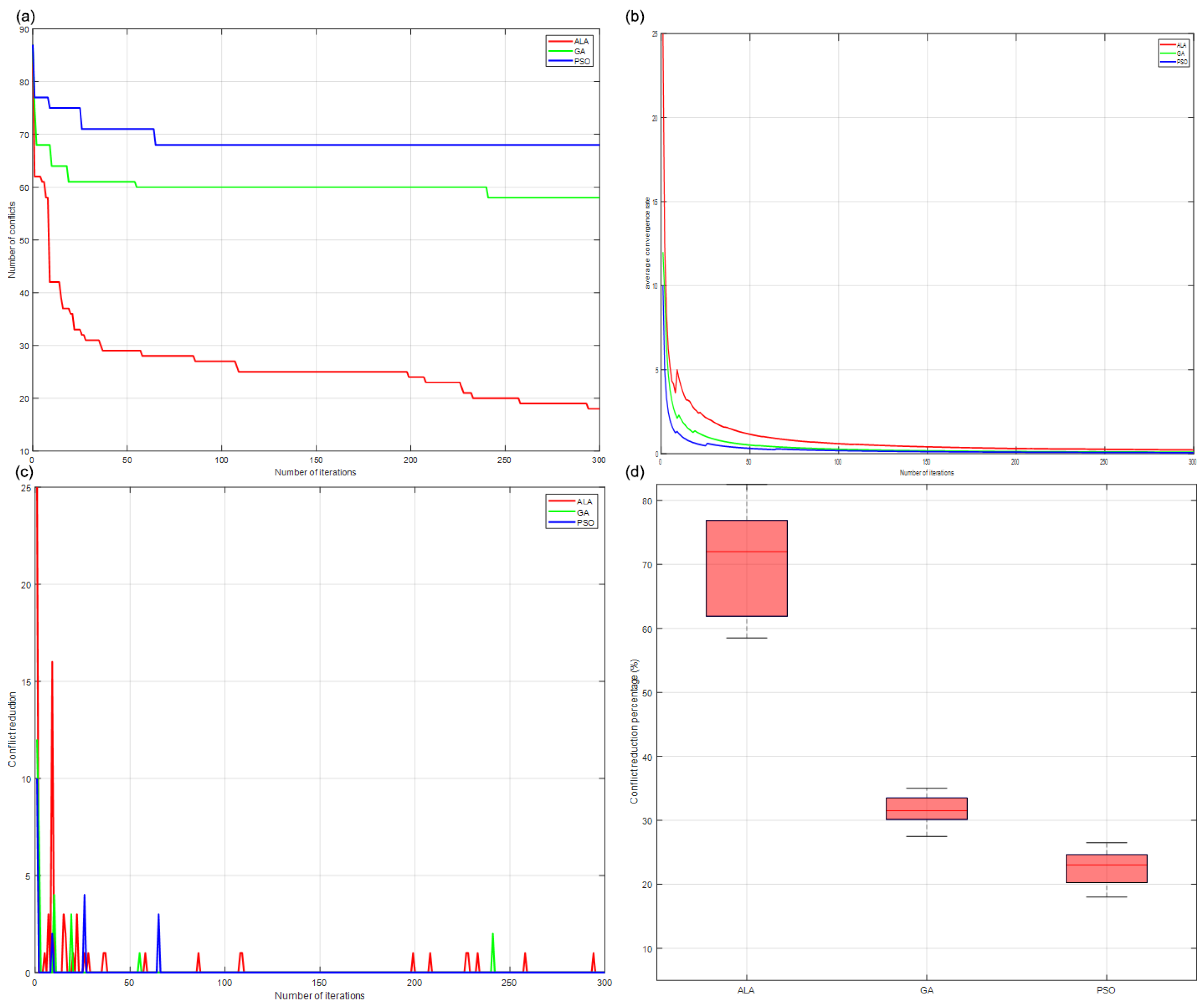
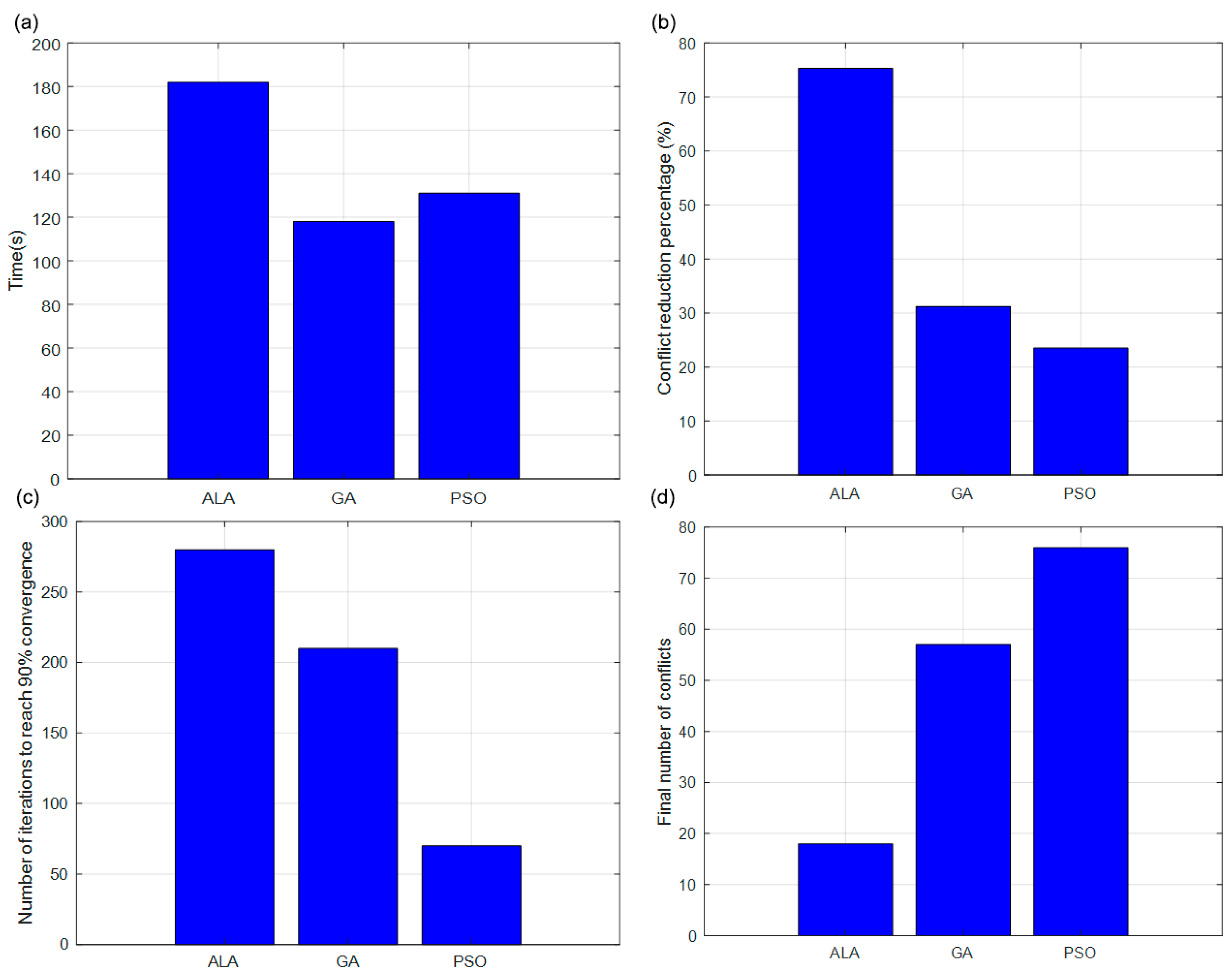
6. Optimization Algorithm Comparative Analysis
6.1. ALA Algorithm Comparison
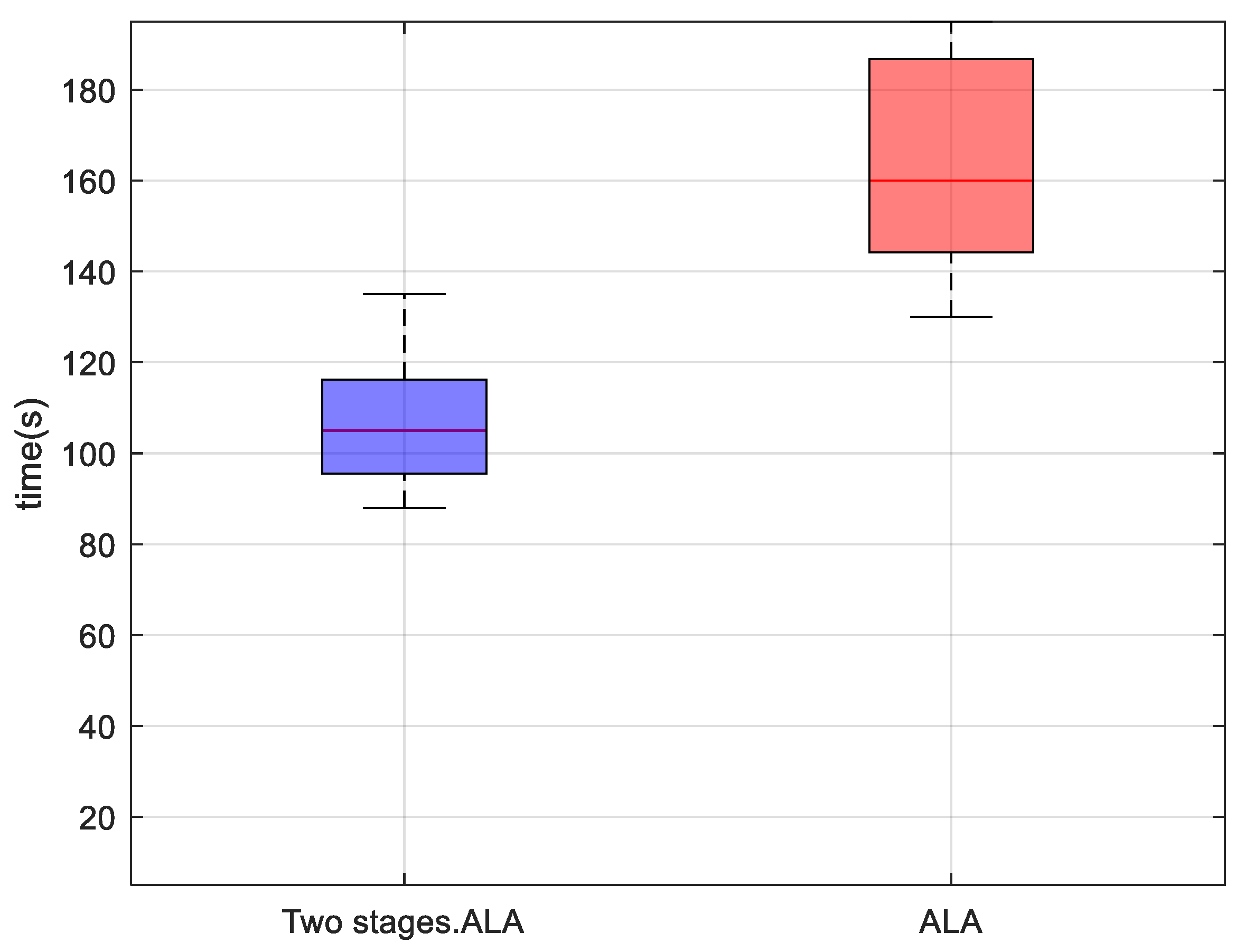
6.2. Analysis of the Effects of the Two-Stage Algorithm
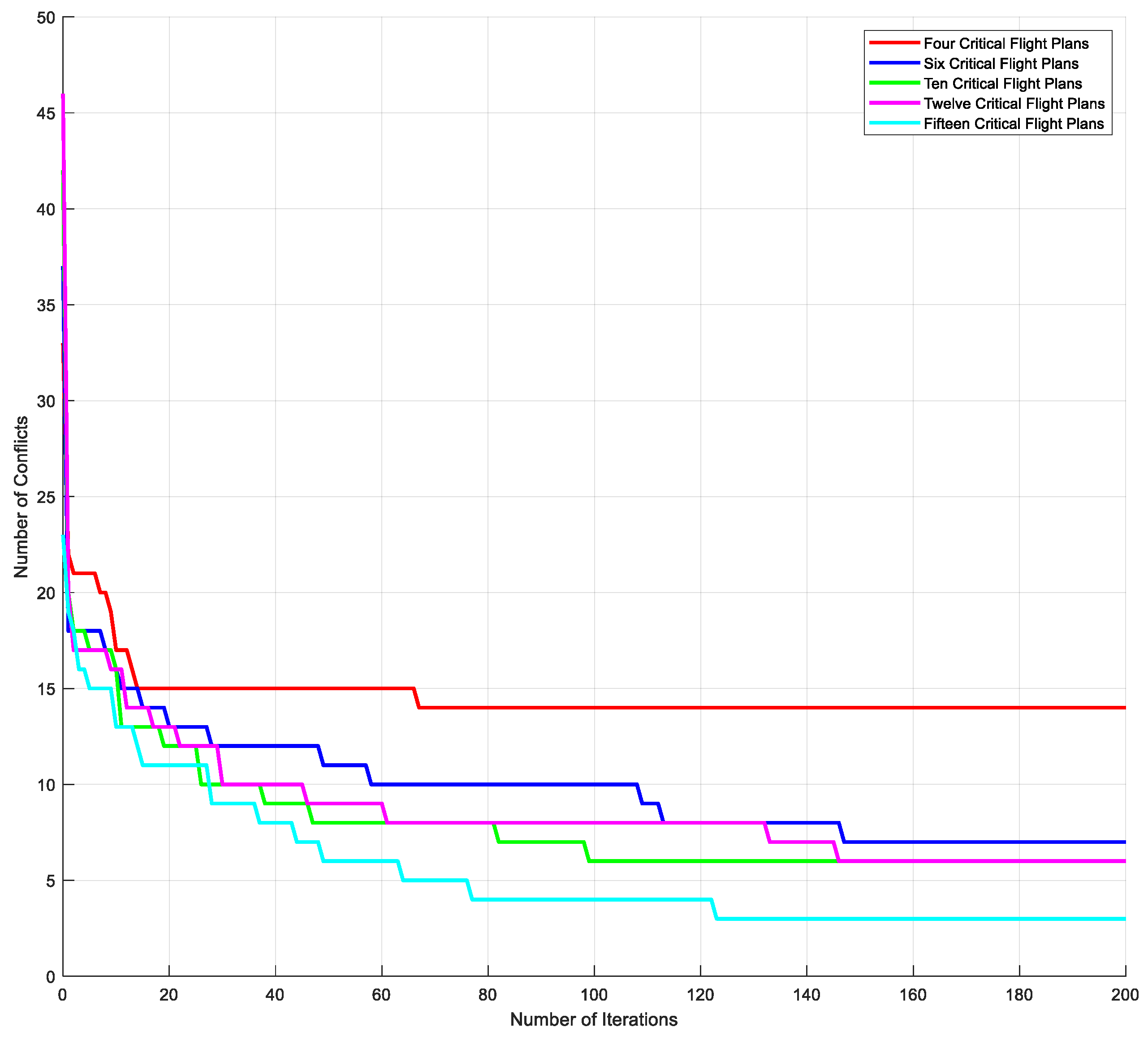
6.3. Analysis of the Influence of Critical Plans
7. Conclusions
- (1)
- Uncertainty-Driven Conflict Detection Model: By incorporating probabilistic distribution characteristics of aircraft time-over-point errors, a conflict detection model based on four-dimensional trajectory confidence interval overlap is constructed. This model significantly enhances the ability to identify latent conflicts in real-world operations, expanding detection scope and improving flight plan robustness when compared with traditional deterministic methods (fixed time interval checks).
- (2)
- Critical Plan Identification Using Complex Network Theory: A conflict complex network is established with flight plans as nodes and conflict relationships as edges. Multi-dimensional indicators including PageRank centrality and degree centrality are integrated to accurately identify critical flight plans that decisively impact network stability. This method is validated through node removal experiments, providing a quantitative basis for optimization strategy prioritization.
- (3)
- Staged Optimization Strategy and ALA Algorithm Application: A two-stage conflict resolution algorithm is proposed:
- First stage: Synchronous optimization of departure times and speeds for critical plans (spatiotemporal co-optimization).
- Second stage: Velocity-only adjustments for non-critical plans (single-variable optimization) to avoid cascading delays from departure time perturbations.
- This strategy reduces algorithm runtime by 59% when compared with single-stage global optimization. The artificial lemming algorithm (ALA)-based multi-objective optimization algorithm demonstrates significant advantages, including fast convergence and superior solution quality, effectively solving multi-objective hybrid nonlinear programming problems.
- Flight plan optimization for urban air mobility (UAM) can better balance the limited airspace resources against the surge in flight plans, enabling as many flight plans as possible to be implemented as required. The proposed phased optimization strategy allows targeted adjustments to flight plans—for example, minimizing changes to high-priority plans (e.g., search and rescue, emergency relief), thus providing theoretical support and solutions for dynamic scheduling in high-density airspace scenarios.
- Development Stage and Route Constraints: The core of this study is designed for the initial development phase of UAM, under the key assumption that autonomous flight technologies are not yet fully mature, requiring operations within a fixed, pre-defined route network. While this simplifies conflict prediction and management, it limits the algorithm’s direct applicability to more free-flight environments.
- Limitations in Optimization Dimensions: Current optimization methods primarily focus on adjusting flight plan departure times and aircraft speeds, excluding the optimization of flight paths themselves. When conflicts are predicted, integrating path planning capabilities—such as executing local route diversions or altitude layer adjustments in conflict-prone areas—would offer more diverse and flexible conflict resolution means. Collaborative optimization across multiple dimensions (time, speed, spatial path) is expected to enable more precise, less disruptive conflict solutions, thereby accommodating safer and more efficient operations for a larger number of flight plans.
- Needs for Future Enabling Technologies: With technological advancements, future UAM will trend toward flexible, non-fixed-route free-flight modes. In such scenarios, achieving efficient plan optimization and dynamic adjustment (especially with path optimization) will require more than just pre-planning. It will depend on the mature application of real-time on-board or ground-based conflict detection and resolution (CD&R) systems, as well as advanced airspace dynamic surveillance technologies (e.g., more precise positioning, communication, and data sharing capabilities) to address rapidly changing air traffic conditions.
- Limitations in Validation Methods: The effectiveness of the proposed optimization method is currently validated primarily at the theoretical and simulation levels, using a small-scale flight plan dataset. While MATLAB and other simulation software were used to test the algorithm’s feasibility and basic performance, real urban traffic flow data or real-world scenario experiments have not yet been employed. The complexity of the real world—including communication delays, navigation errors, sudden weather conditions, and non-cooperative targets—may significantly impact the algorithm’s practical performance, especially after introducing path optimization, where sensitivity to environmental factors is likely to increase.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ALA | Artificial lemming algorithm |
| UAM | Urban air mobility |
| eVTOL | Electric vertical takeoff and landing |
| UTM | Unmanned aircraft system traffic management |
| ADS-B | Automatic dependent surveillance broadcast system |
| UAS | Unmanned aircraft systems |
| TOP | Time-over-point |
| PSO | Particle swarm optimization |
| GA | Genetic algorithm |
References
- Rajendran, S.; Srinivas, S. Air taxi service for urban mobility: A critical review of recent developments, future challenges, and opportunities. Transp. Res. Part E Logist. Transp. Rev. 2021, 143, 102090. [Google Scholar] [CrossRef]
- The Future of Vertical Mobility: Sizing the Market for Passenger, Inspection, and Goods Services Until 2035. Available online: https://www.readkong.com/page/the-future-of-sizing-the-market-for-passenger-inspection-5278425 (accessed on 26 March 2025).
- Urban Air Mobility Flying Cars: Investment Implications of Autonomous Urban Air Mobility. Available online: https://www.morganstanley.com/ideas/autonomous-aircraft (accessed on 26 March 2025).
- Swadesir, L.; Bil, C. Urban air transportation for Melbourne metropolitan area. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019; p. 3572. [Google Scholar]
- Bai, C.Y.; Guo, Y.Z.; Liu, X.C.; Wang, Y.F.; Wang, J.Z.; Qin, Q.H. Research progress of collsion safety characteristics of civil light and small UAVs. Acta Aeronaut. Astronaut. Sin. 2022, 43, 137–153. [Google Scholar]
- UTM Concept of Operations Version 2.0. Available online: https://www.faa.gov/researchdevelopment/trafficmanagement/utm-concept-operations-version-20-utm-conops-v20 (accessed on 26 March 2025).
- Liang, J.; Yang, K.; Tan, C.; Wang, J.; Yin, G. Enhancing High-Speed Cruising Performance of Autonomous Vehicles Through Integrated Deep Reinforcement Learning Framework. IEEE Trans. Intell. Transp. Syst. 2025, 26, 835–848. [Google Scholar] [CrossRef]
- Wu, P.; Yang, X.; Wei, P.; Chen, J. Safety Assured Online Guidance with Airborne Separation for Urban Air Mobility Operations in Uncertain Environments. IEEE Trans. Intell. Transp. Syst. 2022, 23, 19413–19427. [Google Scholar] [CrossRef]
- Zhang, J.F.; Ge, T.T.; Chen, Q.; Wang, F. 4D Trajectory Prediction and Uncertainty Analysis for Departure Aircraft. J. Southwest Jiaotong Univ. 2016, 51, 800–806. [Google Scholar]
- Liang, Z.; Chaovalitwongse, W.A.; Elsayed, E.A. Sequence assignment model for the flight conflict resolution problem. Transp. Sci. 2014, 48, 334–350. [Google Scholar] [CrossRef]
- Zuo, J.P.; Xie, H.P.; Zhou, H.W.; Peng, S.P. Research on scheduling problem of intersection flight considering priority. Aeronaut. Comput. Tech. 2014, 181, 593–603. [Google Scholar]
- Takeichi, N. Nominal flight time optimization for arrival time scheduling through estimation/resolution of delay accumulation. Transp. Res. Part C Emerg. Technol. 2017, 77, 433–443. [Google Scholar] [CrossRef]
- Zhang, Y.; Su, R.; Li, Q.; Cassandras, C.G.; Xie, L. Distributed flight routing and scheduling for air traffic flow management. Trans. Intell. Transp. Syst. 2017, 18, 2681–2692. [Google Scholar] [CrossRef]
- Sacharny, D.; Henderson, T.C.; Marston, V.V. Lane-Based Large-Scale UAS Traffic Management. IEEE Trans. Intell. Transp. Syst. 2022, 23, 18835–18844. [Google Scholar] [CrossRef]
- De Oliveira, Í.R.; Altus, S.; Tiourine, S.; Neto, E.C.P.; Leite, A.; De Azevedo, F.C. Stochastic Flight Plan Optimization. In Proceedings of the 2023 IEEE/AIAA 42nd Digital Avionics Systems Conference (DASC), Barcelona, Spain, 1–5 October 2023; pp. 1–8. [Google Scholar] [CrossRef]
- Su, Y.; Xu, Y.; Inalhan, G. A comprehensive flight plan risk assessment and optimization method considering air and ground risk of UAM. In Proceedings of the 2022 IEEE/AIAA 41st Digital Avionics Systems Conference (DASC), Portsmouth, VA, USA, 18–22 September 2022; pp. 1–10. [Google Scholar] [CrossRef]
- Pang, B.; Low, K.H.; Lv, C. Adaptive conflict resolution for multi-UAV 4D routes optimization using stochastic fractal search algorithm. Transp. Res. Part C Emerg. Technol. 2022, 139, 103666. [Google Scholar] [CrossRef]
- Dai, W.; Pang, B.; Low, K.H. Conflict-free four-dimensional path planning for urban air mobility considering airspace occupancy. Aerosp. Sci. Technol. 2021, 119, 107154. [Google Scholar] [CrossRef]
- Haba, R.; Mano, T.; Ueda, R.; Ebe, G.; Takeda, K.; Terabe, M.; Ohzeki, M. Routing and scheduling optimization for urban air mobility fleet management using quantum annealing. Sci. Rep. 2025, 15, 4326. [Google Scholar] [CrossRef] [PubMed]
- Shihab, S.A.M.; Wei, P.; Ramirez, D.S.J.; Mesa-Arango, R.; Bloebaum, C. By schedule or on demand?—A hybrid operation concept for urban air mobility. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019; p. 3522. [Google Scholar]
- Wei, Z. Research of an Improved Flight Plan Adjustment Method. Informatiz. Res. 2018, 44, 13–17. [Google Scholar]
- Sun, G.; Wang, Y.; Yu, H.; Guizani, M. Proportional Fairness-Aware Task Scheduling in Space-Air-Ground Integrated Networks. IEEE Trans. Serv. Comput. 2024, 17, 4125–4137. [Google Scholar] [CrossRef]
- Kim, J.; Nam, G.; Min, D.; Kim, N.M.; Lee, J. Safety Risk Assessment Based Minimum Separation Boundary for UAM Operations. In Proceedings of the 2023 IEEE/AIAA 42nd Digital Avionics Systems Conference (DASC), Barcelona, Spain, 1–5 October 2023. [Google Scholar] [CrossRef]
- Shi, M.T. Research on the Flight Delay Propagation in Aviation Network Under Uncertainty Factor. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2017. [Google Scholar]
- Sallan, J.M.; Lordan, O. Air Route Networks Through Complex Networks Theory; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Xiao, Y.; Cui, H.; Khurma, R.A.; Castillo, P.A. Artificial lemming algorithm: A novel bionic meta-heuristic technique for solving real-world engineering optimization problems. Artif. Intell. Rev. 2025, 58, 84. [Google Scholar] [CrossRef]
- Wu, M.; Wang, Z.; Gan, X.; Yang, G.; Wen, X. Identification of key flight conflict nodes based on complex network theory. J. Northwestern Polytech. Univ. 2020, 38, 279–287. [Google Scholar] [CrossRef]
- Pang, B.; Low, K.H.; Duong, V.N. Chance-constrained UAM traffic flow optimization with fast disruption recovery under uncertain waypoint occupancy time. Transp. Res. Part C Emerg. Technol. 2024, 161, 104547. [Google Scholar] [CrossRef]
- Solá, L.; Romance, M.; Criado, R.; Flores, J.; García del Amo, A.; Boccaletti, S. Eigenvector centrality of nodes in multiplex networks. arXiv 2013, arXiv:1305.7445. [Google Scholar] [CrossRef] [PubMed]
- Langville, A.N.; Meyer, C.D. Deeper inside pagerank. Internet Math. 2004, 1, 335–380. [Google Scholar] [CrossRef]



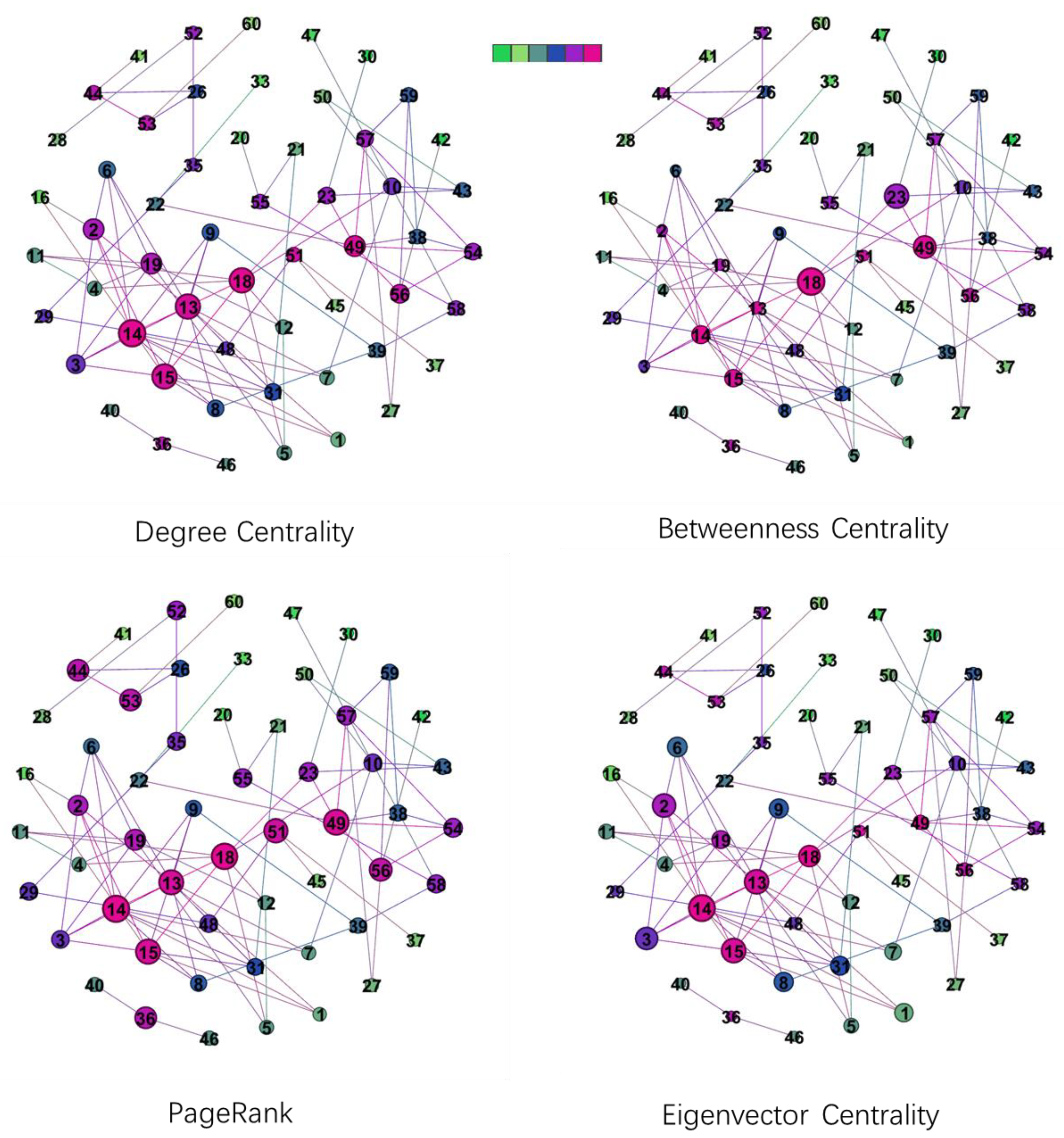
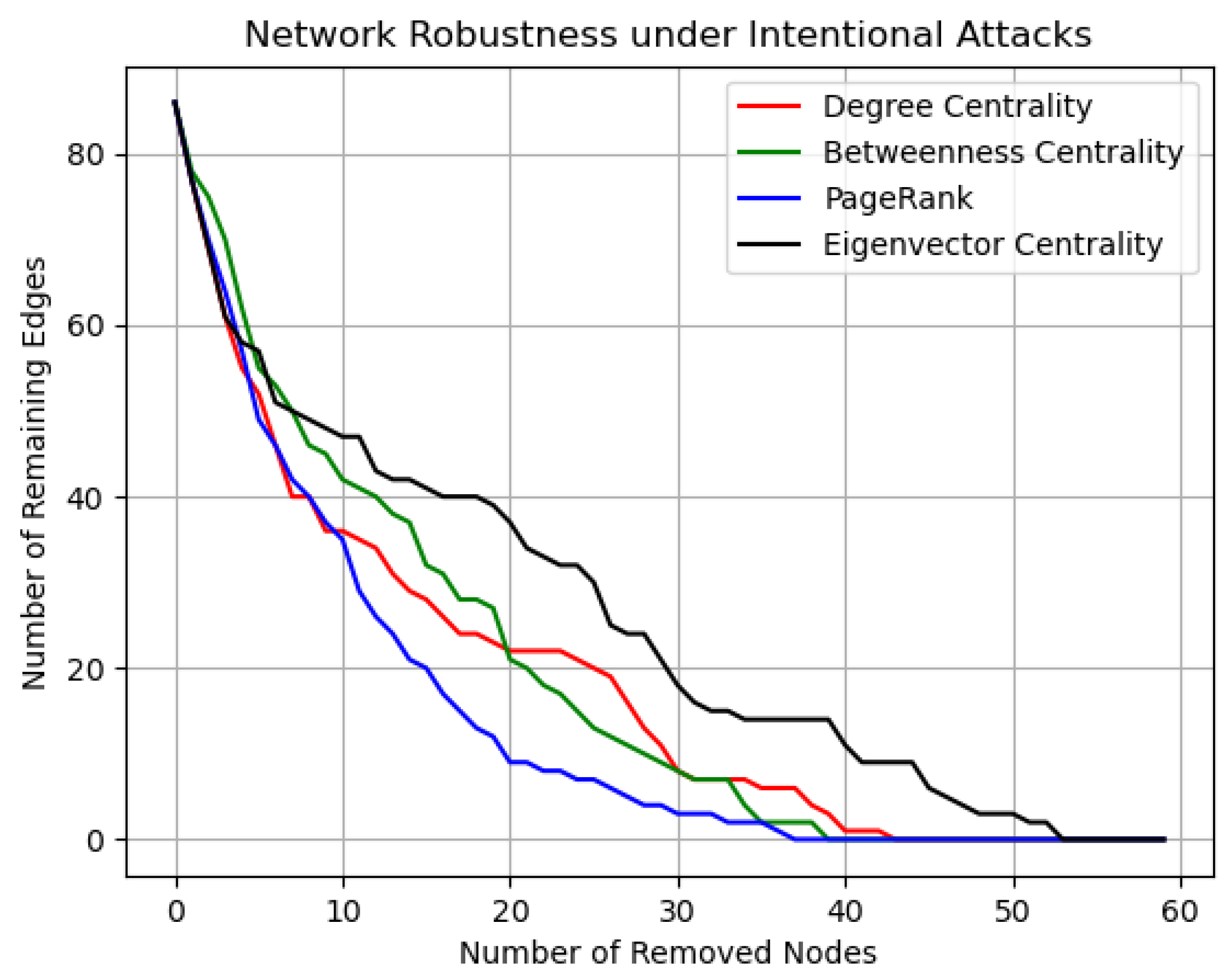


| Degree Centrality | Betweenness Centrality | PageRank | Eigenvector Centrality | |
|---|---|---|---|---|
| 1 | 14 | 18 | 14 | 14 |
| 2 | 18 | 23 | 18 | 15 |
| 3 | 15 | 49 | 49 | 13 |
| 4 | 13 | 14 | 15 | 2 |
| 5 | 49 | 15 | 13 | 3 |
| 6 | 19 | 31 | 51 | 18 |
| 7 | 2 | 39 | 56 | 6 |
| 8 | 56 | 56 | 36 | 8 |
| 9 | 3 | 21 | 44 | 9 |
| 10 | 23 | 10 | 53 | 31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, L.; Wu, M.; Wen, X.; Zhou, Z.; Tian, Q. Optimization of Flight Scheduling in Urban Air Mobility Considering Spatiotemporal Uncertainties. Aerospace 2025, 12, 413. https://doi.org/10.3390/aerospace12050413
Meng L, Wu M, Wen X, Zhou Z, Tian Q. Optimization of Flight Scheduling in Urban Air Mobility Considering Spatiotemporal Uncertainties. Aerospace. 2025; 12(5):413. https://doi.org/10.3390/aerospace12050413
Chicago/Turabian StyleMeng, Lingzhong, Minggong Wu, Xiangxi Wen, Zhichong Zhou, and Qingguo Tian. 2025. "Optimization of Flight Scheduling in Urban Air Mobility Considering Spatiotemporal Uncertainties" Aerospace 12, no. 5: 413. https://doi.org/10.3390/aerospace12050413
APA StyleMeng, L., Wu, M., Wen, X., Zhou, Z., & Tian, Q. (2025). Optimization of Flight Scheduling in Urban Air Mobility Considering Spatiotemporal Uncertainties. Aerospace, 12(5), 413. https://doi.org/10.3390/aerospace12050413






