Task Allocation Method for Emergency Active Debris Removal Based on the Fast Elitist Non-Dominated Sorting Genetic Algorithm

Abstract

Active space debris removal is now integral to modern space exploration. In order to address the problem of a heterogeneous satellite swarm with different payloads carrying out the emergency active removal of space debris, this paper proposes a Multi-type Chromosome Fast Elitist Non-Dominated Sorting Genetic Algorithm (MC-NSGA-II). The algorithm is designed to enable the satellite swarm to execute multiple coupled tasks in succession with improved optimization efficiency. An arbitrary execution order may result in deadlock, where one or more satellites become trapped in an infinite waiting loop. In order to address the heterogeneous problem of satellites and task coupling constraints, a multi-type chromosome coding strategy is developed. To evaluate different allocation strategies, three optimization objectives—time consumption, fuel consumption, and task balance—are introduced. To align with the multi-type chromosome coding strategy, two distinct sorting methods are developed for crossover and mutation operations, ensuring that all offspring individuals meet the constraints. Additionally, the algorithm incorporates a dynamic parameter-setting strategy to enhance solution efficiency. Finally, comparative simulations validate the effectiveness and superiority of the proposed method. The results show that the high-quality solution search ability of the MC-NSGA-II algorithm is 23.07% higher than that of the standard NSGA-II algorithm.

1. Introduction

With continuous progress being made in the field of human space exploration, the quantity of orbital debris has seen a dramatic rise [1]. During the initial phase of space activities, the relatively small number of spacecrafts caused the dangers of space debris to be largely overlooked. The seriousness of this issue only gained widespread attention after D.J. Kessler and B.G. Cour-Palais introduced the concept of the “Kessler Syndrome” [2]—a theoretical scenario where collisions among sizable debris fragments could trigger a chain reaction, leading to a densely packed field of orbital debris encircling the Earth. This escalating concentration of space junk now represents a substantial and growing hazard to spacecraft, affecting both their launch processes and extended operational life. Statistics from the European Space Agency (ESA) indicate that over 630 incidents have occurred in orbit, each playing a role in the worsening debris problem. As a result, implementing active debris removal strategies has become essential for maintaining the viability of future space missions.

Space debris is typically categorized into three classes—large debris (greater than 100 mm in diameter), medium debris (10–100 mm), and small debris (less than 10 mm). While shielding technologies [3] offer effective protection against small debris, they are inadequate for protecting satellites against medium and large objects. As such, the active removal of medium- and large-sized debris has emerged as a central focus of current efforts. Current strategies for active debris removal fall broadly into two categories—contact-based and contactless methods. Contact-based approaches involve direct physical interaction with debris, employing technologies including robotic arms [4] or tether-nets [5], among others. These methods offer high precision but are often time-consuming. In contrast, contactless techniques [6], including ion beams or laser ablation [7], alter the orbital trajectories of debris without direct contact. These methods are more suitable for large-scale space debris removal missions.

Task planning for multi-target debris removal has become a focal point in contemporary research. To address the challenges of solution sparsity and entrapment in local optima that are inherent in large-scale debris removal mission planning, Xia et al. [8] proposed a new hierarchical exploration artificial bee colony (HEABC) optimization algorithm. Bonnal et al. [9] employed a weighted coefficient method to formulate a single-objective optimization problem that integrates delta-v and mission duration in order to enable the removal of multiple debris targets. As the volume of orbital debris continues to grow, the limitations of single-satellite operations—particularly in terms of removal technique and efficiency—have stimulated growing research into multi-satellite mission planning frameworks. For instance, Zhao et al. [10] applied a simulated annealing algorithm to address task scheduling for multi-service satellites operating across space–ground hybrid zones. Similarly, Jing et al. [11] investigated task planning for multiple servicing spacecraft (SSCs) involved in the clearance of geostationary orbit (GEO) debris. These spacecrafts, initially deployed within the GEO belt, must rendezvous with debris located at diverse orbital altitudes and inclinations, redirect them to graveyard orbits, and subsequently return to their initial positions. In another study, Missel J and Mortari D [12] employ a genetic algorithm to optimize the trajectory of a Sling-Sat-based Space Sweeper system, aiming to complete the mission in under six months.

While the aforementioned studies primarily address long-term removal strategies for low-threat debris, scenarios involving multiple debris objects that pose imminent risks to high-value spacecraft require urgent removal strategies. In such cases, the deployment of highly maneuverable swarms of micro-nano satellites presents a promising approach for rapid threat mitigation. Recent research has increasingly focused on emergency debris removal strategies. For instance, Zhou et al. [13] proposed a task planning method based on an improved reinforcement learning framework with online optimization to improve mission efficiency and facilitate rapid debris removal under strict time constraints. Similarly, Yang et al. [14] introduced a “multi-satellite to multi-debris” task allocation strategy designed for time-sensitive scenarios, in which multiple spacecraft coordinate to remove multiple debris targets within a limited operational timeframe.

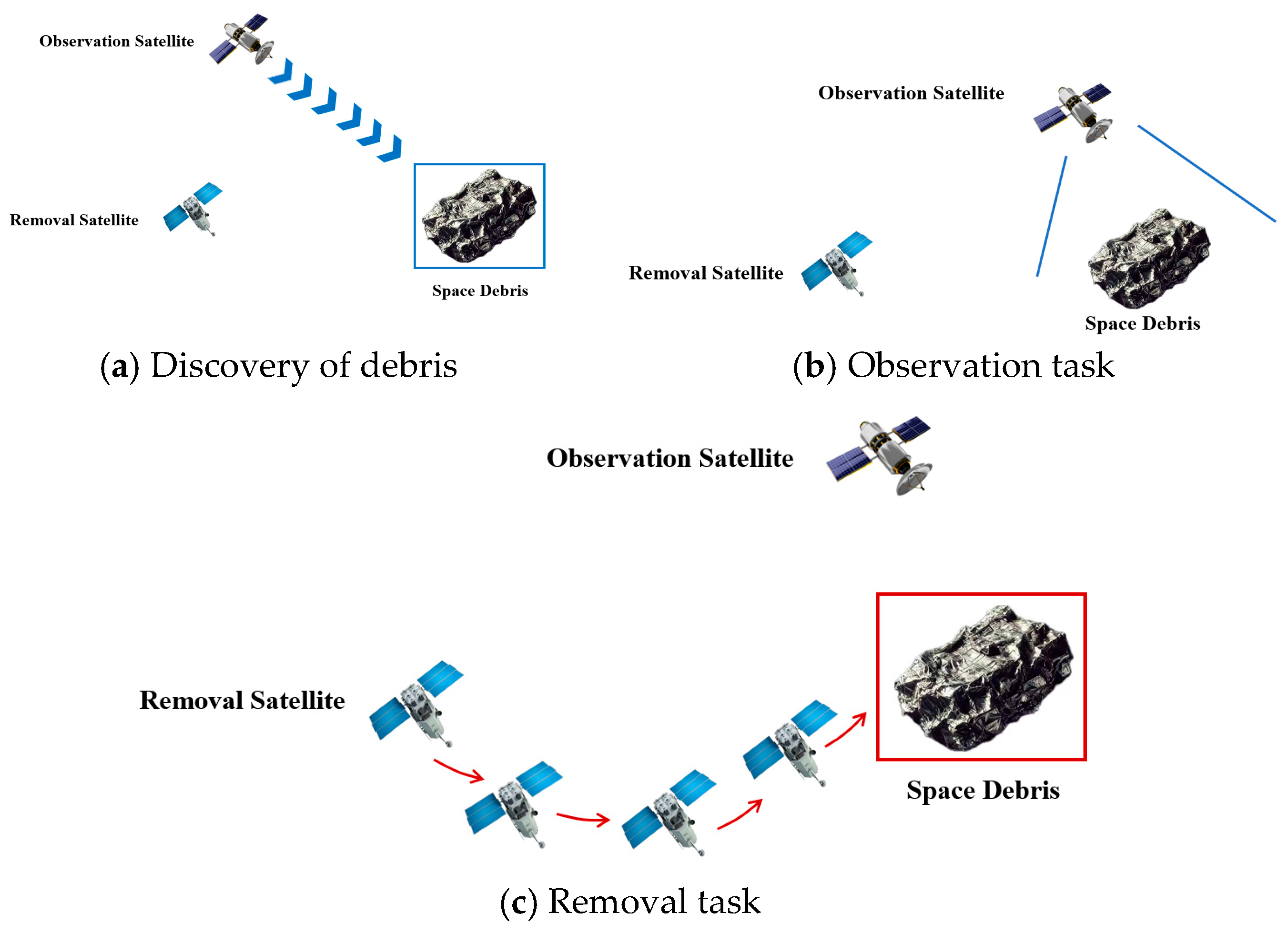
Given that space debris consists of non-cooperative objects, emergency removal missions involving multiple debris targets often lack precise prior positional information. Consequently, the initial step involves dispatching observation satellites to maneuver into close proximity in order to acquire accurate location data. Subsequently, removal satellites perform contactless debris removal at close range. Assigning observation and removal functions to a single satellite imposes considerable burdens on its payload capacity. In contrast, a heterogeneous satellite swarm—featuring complementary payload configurations—can effectively fulfill these operational requirements. Through coordinated operation, such swarms are capable of executing complex tasks with enhanced efficiency and adaptability. However, many current methods do not take into account heterogeneity [15,16].

The task allocation problem in a heterogeneous satellite swarm can be formulated as a multi-objective optimization problem with task coupling constraints. In general, solution methods can be categorized into two types—conventional methods and biologically inspired optimization methods. Conventional methods, such as dynamic programming (DP) [17] and mixed integer linear programming (MILP) [18], can yield optimal solutions but lead to prohibitive computational complexity when handling large-scale allocation problems. In order to reduce the computational complexity of algorithms, biologically inspired optimization methods have been widely employed, including particle swarm optimization (PSO) [19,20], ant colony optimization (ACO) [21], genetic algorithm (GA) [22,23], and simulated annealing (SA) [24]. These methods are more effective than traditional algorithms because they do not rely heavily on gradient information. However, these optimization methods may generate numerous infeasible solutions after the introduction of task coupling constraints, and random task allocation may result in deadlock.

A multi-type chromosome-encoding scheme [25] is introduced to improve the Fast Elitist Non-Dominated Sorting Genetic Algorithm for multi-objective optimization—NSGA-II [26]—and the MC-NSGA-II is constructed to solve the proposed heterogeneous satellite task allocation problem. The main contributions of this paper are summarized as follows: (1) A mathematical model of the “observation–removal” mission for multiple space debris by heterogeneous satellite swarms is formulated, including the mathematical model of mission coupling constraints and the objective function for evaluating the task allocation results. (2) The MC-NSGA-II algorithm is introduced, along with a multi-type chromosome-encoding scheme designed to produce feasible chromosomes that comply with the constraints of satellite heterogeneity and task coupling. Two distinct sorting methods are designed for crossover and mutation operations to ensure that all offspring individuals are feasible solutions. (3) A hybrid mutation mechanism consisting of two mutation operators, based on the task exchange strategy and allocation information mutation, is proposed to enhance the algorithm’s local search capability. (4) A dynamic parameter adjustment strategy is introduced to modify the populations for crossover and mutation, which, in turn, improves the overall efficiency of the algorithm.

The structure of this paper is outlined as follows. In Section 2, the problem of heterogeneous satellite missions is introduced. Section 3 offers an in-depth explanation of the proposed algorithm, covering chromosome encoding, genetic operations, and the dynamic adjustment strategy. Section 4 showcases the simulation results and provides a comparison between the proposed algorithm and other existing ones. Finally, Section 5 wraps up the paper.

2. Problem Statements

This paper tackles the issue of cooperative task allocation, considering satellite heterogeneity and the constraints related to task coupling. A heterogeneous satellite swarm performs “observation–removal” missions on multiple space debris. As shown in Figure 1, removal satellites require accurate location information from observation satellites to perform tasks.

2.1. Task Model

The task model involves multiple space debris in space, hereinafter referred to as targets. The target set is defined as follows:

$$T=\{T_1,T_2,\dots ,T_{N_T}\}$$

(1)

where $T_j$$(i=1,2,3,\dots ,N_T)$ represents the jth target debris and $N_T$ is the total number of targets.

In this mission, the observation and removal tasks need to be carried out in sequence for each target. The task type set is defined as follows:

$$M_T=\{R,I\}$$

(2)

where $R$ and $I$ represent observation and removal tasks.

Remark 1. 

The task coupling constraints capture the following two key aspects:

(1) 

Only when both tasks ($R$, $I$) are completed can the mission of a specific target be considered. Based on Equations (1) and (2), each target undergoes $\left|M_T\right|=2$ tasks, while the overall number of tasks is $N_t=N_T\cdot \left|M_T\right|=2N_T$.

(2) 

The sequence of task execution is governed by strict priority constraints, where task $I$ can only be executed after task $R$.

2.2. Satellite Model

The multi-satellite system consists of three types of satellites—an observation satellite, a removal satellite, and a multifunctional satellite. The satellite set is defined as follows:

$$A=\{A_1,A_2,\dots ,A_{N_A}\}$$

(3)

where $A_i$$(i=1,2,3,\dots ,N_A)$ denotes the ith satellite and $N_A$ represents the number of satellites.

Remark 2. 

Satellite heterogeneity reflects the following two parts:

(1) 

Different types of satellites have distinct capabilities—observation satellites are limited to performing observation tasks, removal satellites are dedicated to removal tasks, and multifunctional satellites can perform all tasks. Correspondingly, we record the set of satellites with different capabilities as follows:

$$A_R=\left\{\begin{array}{l}{a}_1,a_2,\dots ,a_{N_{A_R}},a_{N_{A_R}+1},\hfill \\ a_{N_{A_R}+2},\dots ,a_{N_{A_R}+N_{A_C}}\hfill \end{array}\right\}$$

(4)

$$A_I=\left\{\begin{array}{l}{a}_1,a_2,\dots ,a_{N_{A_I}},a_{N_{A_I}+1},\hfill \\ a_{N_{A_I}+2},\dots ,a_{N_{A_I}+N_{A_C}}\hfill \end{array}\right\}$$

(5)

where $N_{A_R}$, $N_{A_I}$, and $N_{A_C}$ denote the number of observation, removal, and multifunctional satellites, respectively.

(2) 

The fuel-carrying capacity varies across different satellites. The maximum speed increment ($\Delta V$) provided by the fuel carried by the observation satellite is $\Delta V_R$, while the maximum speed increment ($\Delta V$) provided by the fuel of the removal and multifunctional satellites is $\Delta V_I$.

2.3. Lambert Double Pulse Approach

By solving the Lambert problem [27], the satellite employs a double-pulse approach to complete the task. The solution to the Lambert problem primarily involves determining both the initial and terminal velocities required for orbital transfer between two points ($P_1$ and $P_2$), ensuring the spacecraft reaches the target within a given flight time. The Lambert theorem outlines the conditions necessary for such an orbital transfer, and the approach process is depicted in Figure 2.

2.4. Formulation of Optimization Problem

This section formulates the model constraints and optimization objectives based on the two fundamental models—the task model and the satellite model.

2.4.1. Constraint Conditions

$X_{ik}$ is defined as the matrix of task allocation results, derived from both the task model and the satellite model. The parameters are defined as follows:

$$X_{ik}=\left\{\begin{array}{ll}1,\hfill & \mathrm{allocate} \mathrm{task} M_k \mathrm{to} A_i\hfill \\ 0,\hfill & \mathrm{else}\hfill \end{array}\right.$$

(6)

where $M_k$ is the set of all tasks, $k=\{1,2,3,\dots ,N_t\}$, and $i=\{1,2,3,\dots ,N_A\}$.

Allocation constraint: During the task process, each task must be performed by only one satellite, but each satellite can perform many tasks if it has the necessary quality and resources.

$${\displaystyle \sum _{i=1}^{N_A}{X}_{ik}}=1,\forall k\in N_t$$

(7)

As shown in Equation (7), each task $k$ needs to be performed by one satellite.

Capability constraint: The capabilities of each satellite must be aligned with the requirements of its assigned task. The capability parameter $Q_k$ is defined to assess the quality of task execution. If $Q_k=0$, it indicates that the task $k$ is not performed correctly.

$$Q_k={\displaystyle \sum _{i=1}^{N_A}{X}_{ik}}{P}_{ik}>0,\forall k\in N_t$$

(8)

Here, $P_{ik}$ is the satellite’s capability matrix for each task.

Fuel consumption constraint: To ensure the satellite’s survival in space, the fuel consumed by each satellite during task execution must not exceed the total fuel it carries.

$${\displaystyle \sum _{j=1}^{N_T}{\displaystyle \sum _{m=1}^2{f}_{ij}^m\cdot X_{ij}^m}}\le F_i,\forall i\in N_A$$

(9)

Here, $f_{ij}^m$ represents the fuel consumed by the satellite $A_i$ to perform task $m$ on the target $T_j$; $F_i$ represents the total fuel carried by the satellite $A_i$.

Task coupling constraint: When tasks are coupled, a specific execution order must be followed. The removal task of the target must be executed only after the observation task is completed.

$$t_{T_j}^R<t_{T_j}^I$$

(10)

Here, $t_{T_j}^m$ represents the time when task $m$ on the target $T_j$ is performed.

2.4.2. Optimization Objectives

In the task allocation model, three optimization objectives are established to assess various allocation plans—task completion time, fuel consumption, and fuel consumption balance.

Task completion time: As a key optimization objective, task completion time is commonly employed in task allocation. To maximize task execution efficiency, the task completion time should be minimized.

$$\min J_1={\max }_{A_i\in A}{t}_{A_i}$$

(11)

$$t_{A_i}={\displaystyle \sum _{i=1}^{N_A}{\displaystyle \sum _{j=1}^{N_T}{\displaystyle \sum _{m=1}^2{X}_{ij}^m{t}_{ij}^m}}}$$

(12)

Here, $t_{ij}^m$ represents the time required for the satellite $A_i$ to perform task $m$ to the target $T_j$.

Fuel consumption: Fuel consumption refers to the sum of the total satellite fuel consumption after the completion of the mission. By reducing the optimization of fuel consumption, fuel resources can be saved to the greatest extent without affecting the successful completion of the task. According to the Tsiolkovsky rocket equation [28], velocity increment $\Delta v_{ij}^m$ can be converted into fuel consumption $f_{ij}^m$, as follows:

$$f_{ij}^m=F_i\cdot \left(1-e^{-{\displaystyle \frac{\Delta v_{ij}^m}{\omega }}}\right)$$

(13)

where $\omega$ represents the speed at which the satellite engine ejects fuel. It can be seen from Equation (13) that the speed increment $\Delta v_{ij}^m$ required for the satellite to perform the task is proportional to the consumed fuel $f_{ij}^m$; therefore, the fuel consumption can be expressed by the speed increment.

$$\min J_2={\displaystyle \sum _{i=1}^{N_A}{\displaystyle \sum _{j=1}^{N_T}{\displaystyle \sum _{m=1}^2{X}_{ij}^m\Delta v_{ij}^m}}}$$

(14)

Fuel consumption balance: Fuel depletion represents the end of this satellite’s life. It is necessary to avoid excessive consumption by certain satellites. To evaluate the balance of task allocation, the fuel consumption balance index is employed for optimization. This index measures the variance in the proportion of fuel consumption for each satellite relative to the total fuel it carries.

$$\min J_3={\displaystyle \frac{1}{N_A}}{\displaystyle \sum _{i=1}^{N_A}{\left(\frac{{\displaystyle \sum _{j=1}^{N_T}{\displaystyle \sum _{m=1}^2{X}_{ij}^m}}\Delta v_{ij}^m}{\Delta V_i}-\frac{1}{N_A}{\displaystyle \sum _{i=1}^{N_A}\frac{{\displaystyle \sum _{j=1}^{N_T}{\displaystyle \sum _{m=1}^2{X}_{ij}^m}}\Delta v_{ij}^m}{\Delta V_i}}\right)}^2}$$

(15)

3. Optimization Algorithm

To address the issues outlined in Section 2, this paper introduces MC-NSGA-II, an enhancement of NSGA-II. This paper enhances chromosome coding, objective function computation, and genetic operations. Furthermore, a dynamic parameter-setting strategy during the iterative process is proposed. The complete algorithmic process is shown in Figure 3.

3.1. Multi-Type Chromosome Encoding

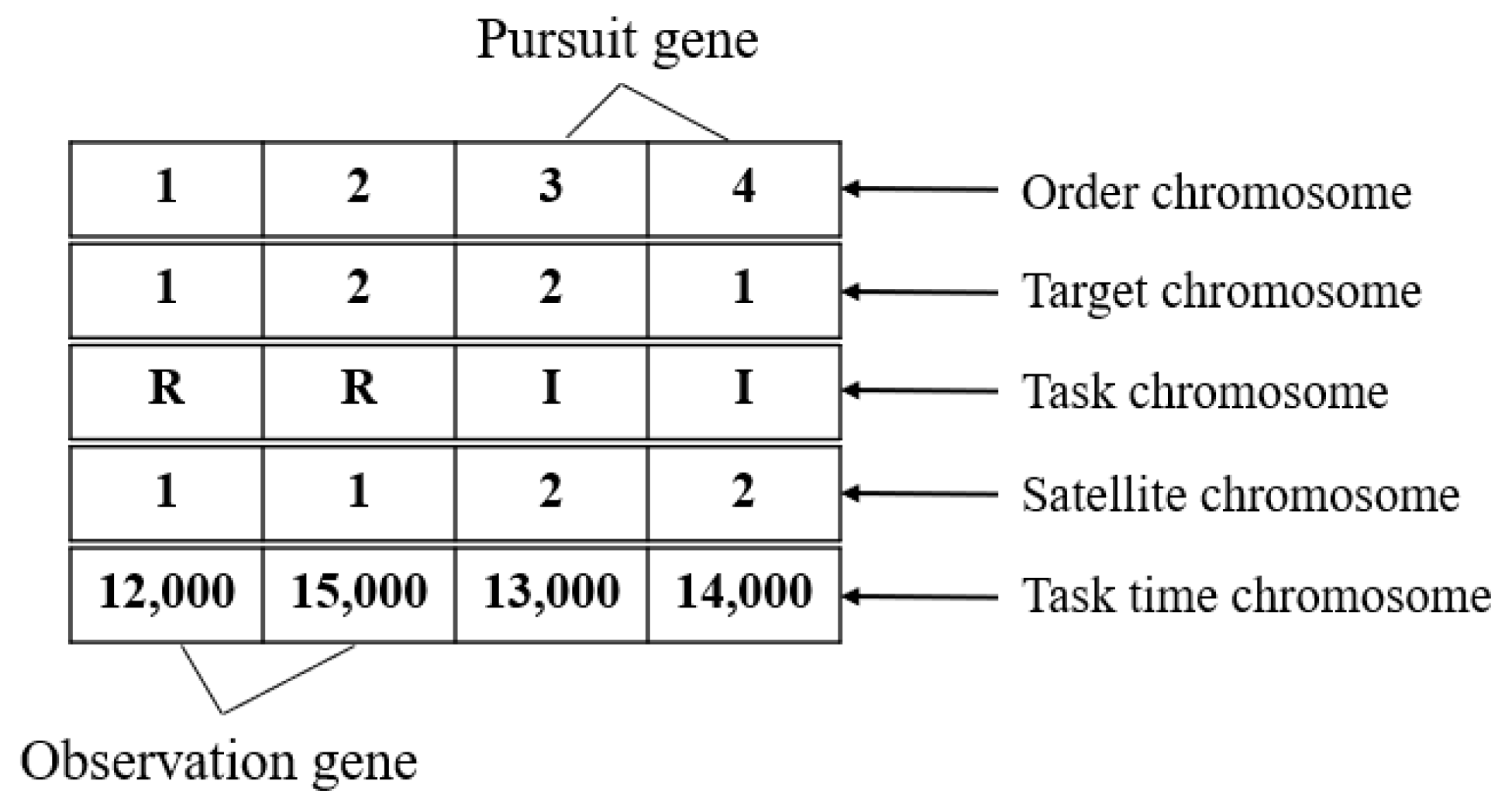
Multi-type chromosome encoding plays a pivotal role in the algorithm. As shown in Figure 4, each individual is represented by a matrix consisting of five chromosomes—the order chromosome, the target chromosome, the task type chromosome, the satellite chromosome, and the task time chromosome. Each column of the matrix represents the assignment of a satellite to a specific task on a target within a designated task time.

Order chromosomes are used to determine the order in which each satellite performs tasks, not the order in which all tasks are performed. The target chromosome is a member of set $T=\{T_1,T_2,\dots ,T_{N_T}\}$. The task type chromosome is a specific task indicator, where R and I represent observation tasks and removal tasks, respectively. The satellite chromosome is selected from set $A=\{A_1,A_2,\dots ,A_{N_A}\}$. The task time chromosome represents the random time selected in the $[t_{\min },t_{\max }]$ interval as the time when the satellite approaches the target to perform the task.

If the satellite performing the previous task has a later access time on the same target compared to the satellite performing the subsequent task, the latter must wait for the former to arrive and complete its assigned task. However, an arbitrary execution order of tasks may result in an infinite waiting cycle, leading to a deadlock.

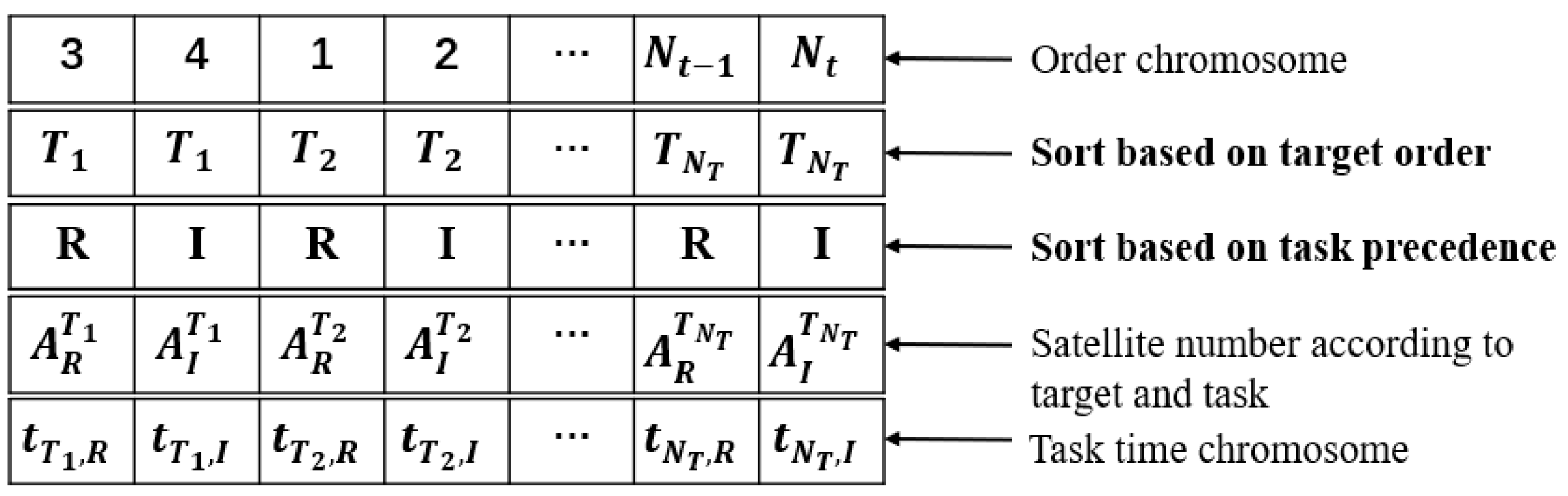
To satisfy the coupling constraints of tasks and to prevent deadlocks, a target-based multi-type chromosome-encoding method is proposed. Initially, the task execution order for the first row of chromosomes is generated, and $N_t=N_T\cdot \left|M_T\right|=2N_T$ targets are randomly assigned to the second row. Subsequently, the genes are arranged in ascending order based on the target number, as shown in Figure 5. The third row is organized based on the execution order of the task coupling constraints, and satellites with execution capabilities are matched according to the information in the second and third rows. The final row represents the task time. The multi-type chromosomes generated by this encoding scheme naturally avoid deadlock situations.

As shown in Figure 5, the multi-type chromosome meets the task coupling constraints. Firstly, the satellites assigned in each gene (line 4) possess the necessary capabilities for performing the task (line 3). Furthermore, the execution order of tasks R and I demonstrates that they are not only executed but they are also carried out sequentially. Consequently, the multi-type chromosomes satisfy the task coupling constraints outlined in Section 2.4.

3.2. Population Initialization

By employing the multi-type chromosome-encoding strategy outlined, the population initialization procedure is designed to ensure the feasibility of the genetic operation. The initialization step is the sequential creation of $N_p$ individuals containing order chromosomes, target chromosomes, task type chromosomes, satellite chromosomes, and task time chromosomes in order.

3.3. Fitness Calculation

The three optimization objectives outlined in Section 2 serve as the objective function for calculating fitness.

$$f_i=\min J_i,i=1,2,\cdots ,M$$

(16)

Here, $M$ is the number of objective functions.

The satellite-based chromosome is derived by rearranging the satellite-based multi-chromosomes, as shown in Figure 6.

It is assumed that when two tasks for a target are performed by the same satellite, both tasks can be completed simultaneously, meaning that only the time and fuel consumption required for the first task need to be calculated.

3.4. Genetic Operation

Genetic operations are a key component of the optimization algorithm, encompassing chromosome selection, elite chromosome retention, crossover, and mutation operations. The roulette wheel selection technique is applied to select parent chromosomes for the mating pool, ensuring that chromosomes with superior fitness values have a higher probability of being chosen. The elite retention operator is applied to retain the $N_e$ parental chromosomes with the highest dominance level in the offspring population. This paper proposes a method to modify the crossover and mutation operators based on the multi-type chromosome-encoding strategy. All offspring chromosomes generated adhere to the task coupling constraints of the task allocation model, ensuring the optimization efficiency of the crossover and mutation operations.

3.4.1. Crossover Operation

The crossover operation swaps genetic information between two selected parent chromosomes, resulting in the creation of two offspring chromosomes. The purpose is to enhance the global search capability through the exchange of information. In the proposed MC-NSGA-II algorithm, a two-point crossover operator is used to produce $N_{cr}<N_p-N_e$ offspring chromosomes. An example of the crossover process is shown in Figure 7.

As depicted in Figure 7, the target-based chromosome is derived before the crossover between the two parent chromosomes, ensuring that the information in the second and third rows remains unchanged after the crossover. This operation alters the execution order (line 1), the satellite (line 4), and the task time (line 5), while the satellite, after the exchange, still retains the ability to perform the task. This operation satisfies both the task coupling constraint and the satellite capability constraint.

3.4.2. Mutation Operation

The mutation operation’s goal is to enhance local search capability by introducing variations in the gene. In this paper, two mutation operators for producing $N_{mu}=N_p-N_e-N_{cr}$ offspring chromosomes are proposed.

(a)

Mutation based on the task exchange strategy: In addition to the task execution time, the number of feasible solutions of other decision variables is limited. Therefore, this paper proposes a mutation operator to exchange the allocation information. Figure 8 shows an implementation example.

As shown in Figure 8, the chromosomes are reordered based on the priority order of the third-line task type, and the task allocation information is exchanged accordingly. The mutation process only swaps the allocation of the selected task, ensuring that the offspring chromosome remains in compliance with the task coupling constraint.

(b)

Allocation information mutation: A mutation site is chosen randomly, and the satellite assigned to the mutation site undergoes mutation. The implementation is shown in Figure 9.

As illustrated in Figure 9, the satellite at the mutation site has undergone mutation. The satellite sets with distinct capabilities are labeled as $A_R$ and $A_I$, respectively. If multiple capable satellites exist in the corresponding satellite set, one is randomly selected.

3.4.3. Dynamic Setting Strategy

A dynamic setting for the genetic operations is introduced. The proposed MC-NSGA-II algorithm adjusts the number of offspring chromosomes produced by crossover and mutation in each iteration.

The offspring population was made up of $N_e$ chromosomes generated through the elite operation, $N_{cr}$ chromosomes produced by the crossover operation, and $N_{mu}$ chromosomes produced by the mutation operation. The subjective selection of parameters $N_e$, $N_{cr}$, and $N_{mu}$ will affect the performance of the algorithm. In order to avoid this problem, the proposed dynamic setting strategy dynamically adjusts the parameters $N_{cr}$ and $N_{mu}$ according to the iteration time.

$$N_{cr}=\mathrm{int}\left[\left(N_p-N_e\right)\cdot e^{\left(-{\displaystyle \frac{N_{\mathrm{iter}}}{N_i}}\right)}\right]$$

(17)

Here, $N_{\mathrm{iter}}$ and $N_i$ represent the current number of iterations and the total number of iterations, respectively.

In the early stages of iteration, the crossover population is relatively large and the genetic operations emphasize improving the algorithm’s global search capability. As the iteration progresses, the mutation population increases, with genetic operations focusing on enhancing local search capability, thus speeding up the algorithm’s convergence.

4. Simulations and Analysis

According to the multi-objective optimization algorithm proposed in Section 3, the task allocation problem is simulated to verify the proposed MC-NSGA-II algorithm.

The satellite swarm is required to perform observation and removal tasks on multiple targets. The effectiveness of the proposed algorithm is demonstrated by solving the task allocation problem using the MC-NSGA-II algorithm and analyzing the resulting task allocations. Furthermore, the simulation employs several multi-objective optimization algorithms to address the same problem. By comparing the non-dominated solutions, the superiority of the enhanced NSGA-II algorithm is demonstrated.

4.1. The Simulation Settings

In the mission window of [0, 50,000 s], suppose that the satellite swarm consists of three heterogeneous satellites—observation satellites, removal satellites, and multifunctional satellites. The swarm target comprises multiple space debris. The mission involves the satellites performing observation and removal tasks on each debris in turn. The initial parameters are presented in

Table 1. Initial parameters of satellites.

Serial Number	Type	X/ (km)	Y/ (km)	Z/ (km)	Vx/ (km/s)	Vy/ (km/s)	Vz/ (km/s)	$\Delta \mathit{V}$/ (m/s)
1	observation	−6760.4	41463	13.968	−3.0401	−0.4957	0.00696	200
2	removal	−6767.6	41462	13.985	−3.0400	−0.4962	0.00696	300
3	multifunctional	−6774.8	41460	14.002	−3.0400	−0.4967	0.00696	300

and

Table 2. Initial parameters of targets.

Serial Number	X/(km)	Y/(km)	Z/(km)	Vx/(km/s)	Vy/(km/s)	Vz/(km/s)
1	−7032.3	41576	15.607	−3.0315	−0.5128	0.00743
2	−6959.7	41588	13.228	−3.0324	−0.5074	0.00638
3	−7104.9	41563	15.202	−3.0306	−0.5180	0.00716
4	−6996.0	41582	16.071	−3.0320	−0.5101	0.00770
5	−7177.4	41551	14.235	−3.0297	−0.5233	0.00662

.

4.2. Effectiveness Analysis

To demonstrate the effectiveness of the proposed algorithm, this paper conducts task allocation experiments in three scenarios and analyzes the task allocation results from each scenario.

A.

Scenario I (three satellites on two targets)

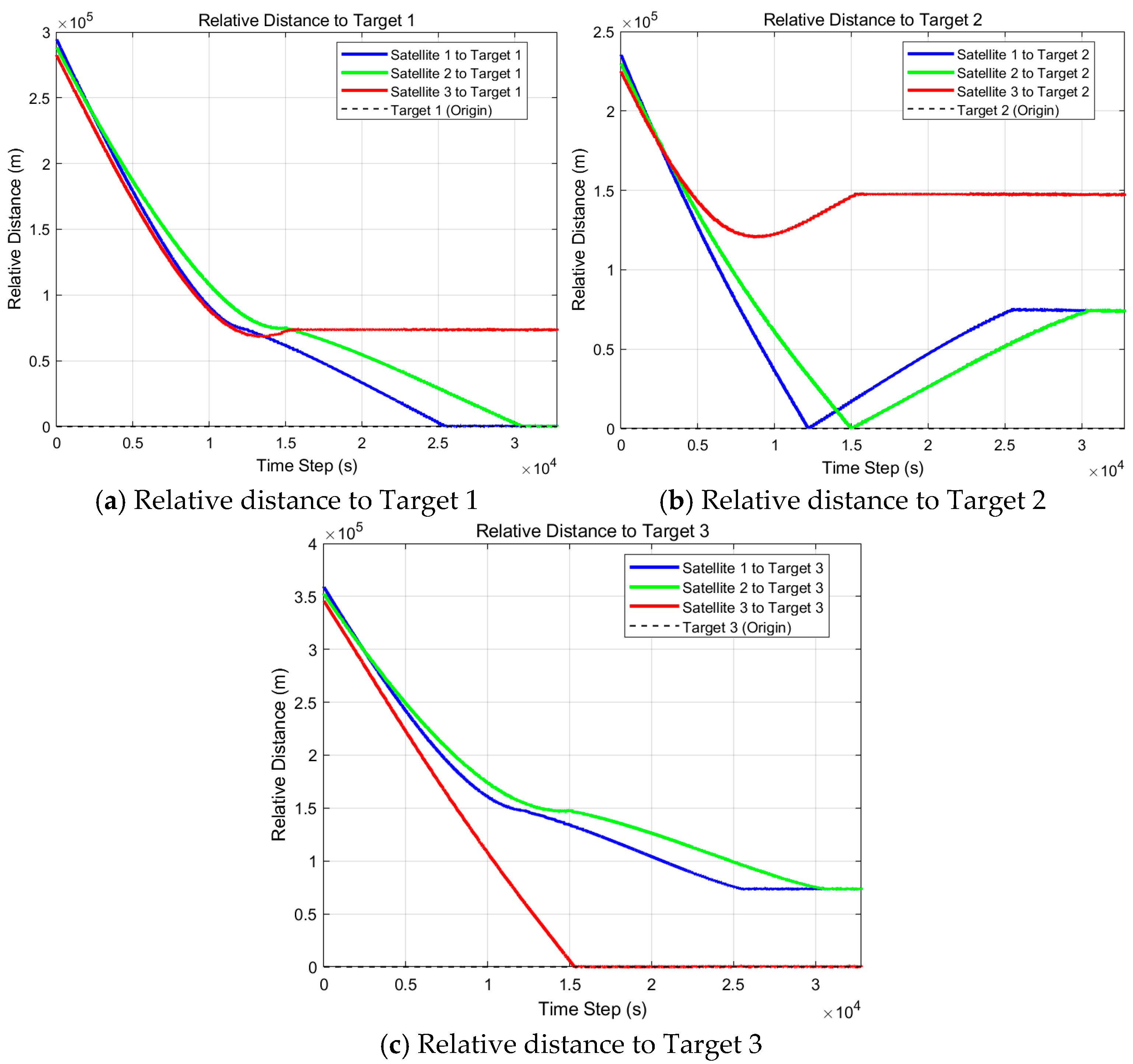
Scenario I consists of the three satellites shown in Table 1 and two targets selected from Table 2. The task allocation results are shown in

Table 3. Scenario I task allocation result.

Order	2	4	1	3
Target	1	1	2	2
Type	R	I	R	I
Satellite	1	2	3	3
Task time	13,500	15,000	16,000	16,000

, and the orbit simulation result is shown in Figure 10.

From Table 3, the task allocation results of the satellites (shown in

Table 4. Task allocation results based on satellites in Scenario I.

Satellite	Order	Target	Type	$\mathbf{Total} \Delta \mathit{v}$/(m/s)	Execution Time/s
1	1	1	R	29	13,500
2	3	1	I	24	15,000
3	2	2	R	18	16,000
	4	2	I

) and the task completion results based on the targets (shown in

Table 5. Task allocation results based on targets in Scenario I.

Target	Type	Execution Satellite	Completion Time/s
1	R	1	13,500
	I	2	15,000
2	R	3	16,000
	I	3	16,000

) can be obtained, respectively.

As shown in Table 4, Satellite No. 1 performs observation tasks on Target No. 1, Satellite No. 2 performs removal tasks on Target No. 1, and Satellite No. 3 performs both observation and removal tasks on Target No. 2. The execution results satisfy the allocation, fuel consumption, and capacity constraints described in Equations (7)–(9). As shown in Table 5, the observation task for each target is performed before the removal task, satisfying the task coupling constraint outlined in Equation (10).

B.

Scenario II (three satellites on three targets)

Scenario II is composed of the three satellites in Table 1 and three targets selected from Table 2. The task allocation results are shown in

Table 6. Scenario II task allocation result.

Order	3	6	2	4	1	5
Target	1	1	2	2	3	3
Type	R	I	R	I	R	I
Satellite	1	2	1	2	3	3
Task time	13,300	15,500	12,200	15,000	15,300	15,300

, and the orbit simulation result is shown in Figure 11.

From Table 6, the task allocation results of the satellites (shown in

Table 7. Task allocation results based on satellites in Scenario II.

Satellite	Order	Target	Type	$\mathbf{Total}\Delta \mathit{v}$/(m/s)	Execution Time/s
1	3	2	R	39	25,500
	6	1	R
2	2	2	I	31	30,500
	4	1	I
3	1	3	R	30	15,300
	5	3	I

) and the task completion results based on the targets (shown in

Table 8. Task allocation result based on targets in Scenario II.

Target	Type	Execution Satellite	Completion Time/s
1	R	1	25,500
	I	2	30,500
2	R	1	12,200
	I	2	15,000
3	R	3	15,300
	I	3	15,300

) can be obtained, respectively.

As shown in Table 7, Satellite No. 1 performs observation tasks on Targets No. 2 and No. 1, respectively; Satellite No. 2 performs removal tasks on Targets No. 2 and No. 1, respectively; and Satellite No. 3 performs both observation and removal tasks on Target No. 3. The execution results satisfy the allocation, fuel consumption, and capacity constraints described in Equations (7)–(9). As shown in Table 8, the observation task for each target is performed before the removal task, satisfying the task coupling constraint outlined in Equation (10).

C.

Scenario III (three satellites on five targets)

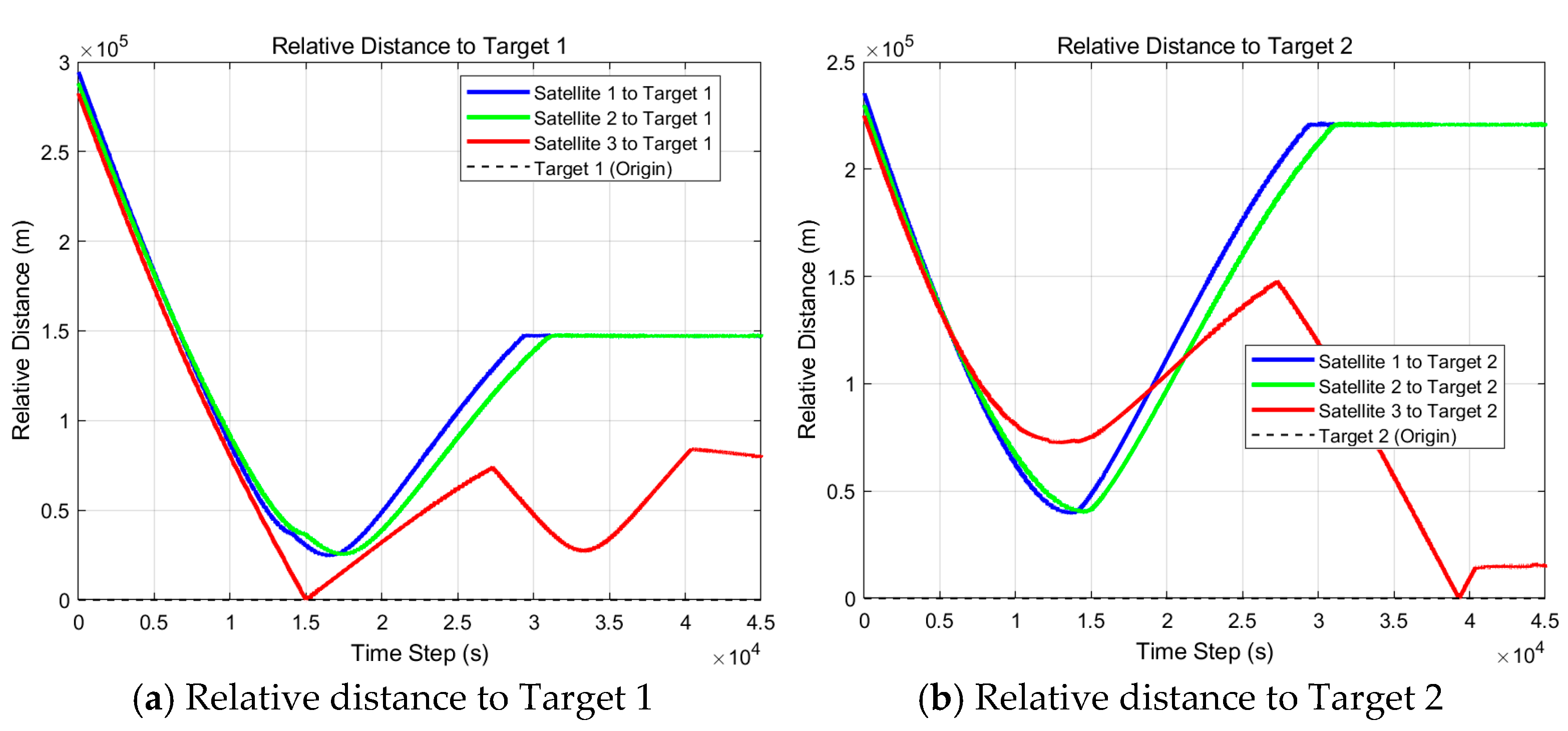
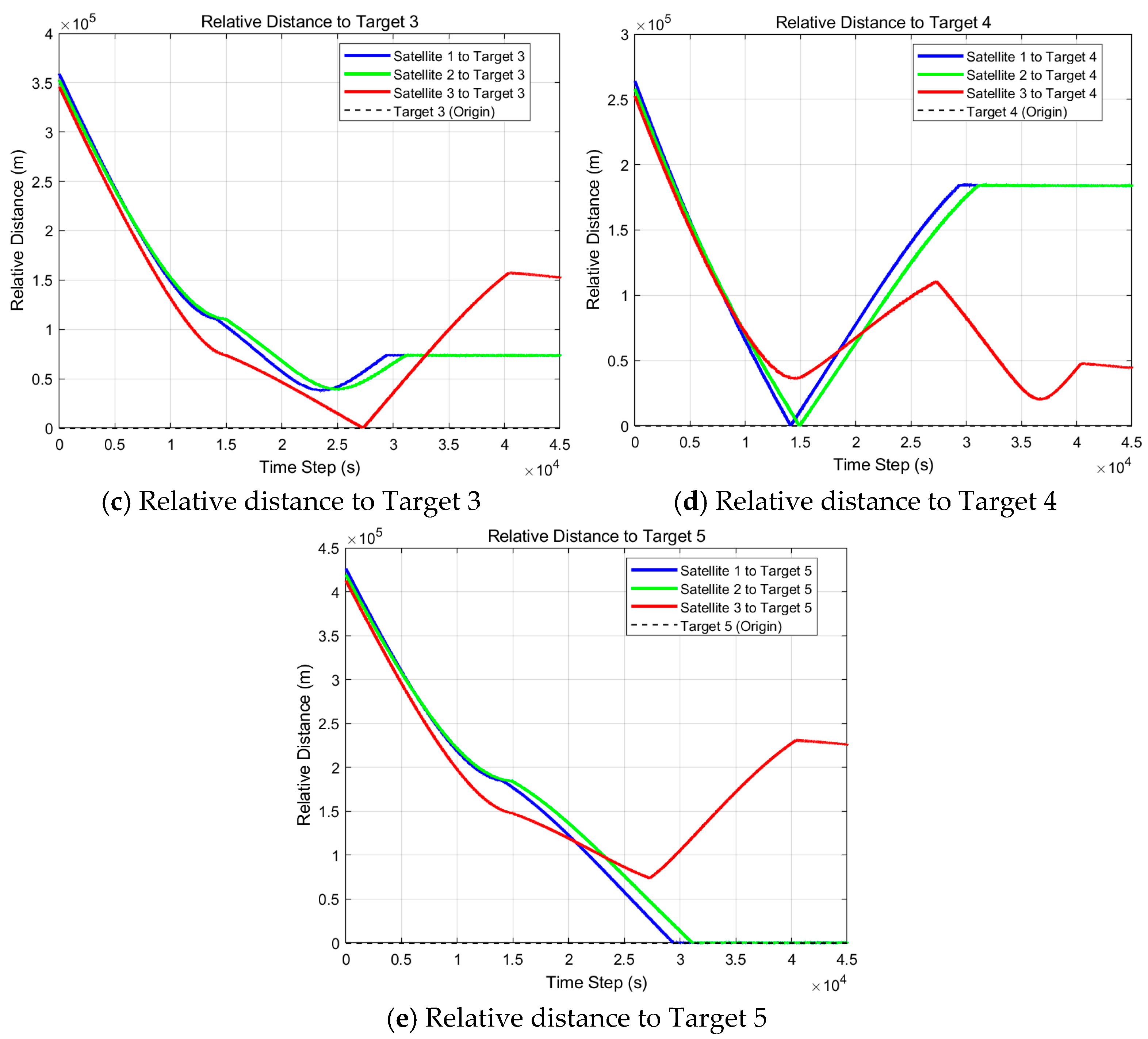
Scenario III is composed of three satellites and five targets. The task allocation result is shown in

Table 9. Scenario III task allocation results.

Order	1	2	7	10	4	5	3	8	6	9
Target	1	1	2	2	3	3	4	4	5	5
Type	R	I	R	I	R	I	R	I	R	I
Satellite	3	3	3	3	3	3	1	2	1	2
Task time	15,000	15,000	13,100	13,100	12,300	12,300	14,100	14,900	15,300	16,200

, and the orbit simulation results are shown in Figure 12.

From Table 9, the task allocation results of the satellite (shown in

Table 10. Task allocation results based on satellites in Scenario III.

Satellite	Order	Target	Type	$\mathbf{Total}\Delta \mathit{v}$/(m/s)	Execution Time/s
1	3	4	R	51	29,400
	6	5	R
2	8	4	I	47	31,100
	9	5	I
3	1	1	R	63	40,400
	4	3	R
	7	2	R
	2	1	I
	5	3	I
	10	2	I

) and the task completion results based on the target (shown in

Table 11. Task allocation results based on targets in Scenario III.

Target	Type	Execution Satellite	Completion Time/s
1	R	3	15,000
	I	3	15,000
2	R	3	40,400
	I	3	40,400
3	R	3	27,300
	I	3	27,300
4	R	1	14,100
	I	2	16,200
5	R	1	29,400
	I	2	31,100

) can be obtained, respectively.

It can be seen from Table 10 that the task allocation plan is as follows:

$$\begin{gathered} A_1:(T_4,R,14100s)\to (T_5,R,15300s) \\ {A}_2:(T_4,I,14900s)\to (T_5,I,16200s) \\ {A}_3:(T_1,RI,15000s)\to (T_3,RI,12300s)\to (T_2,RI,13100s) \end{gathered}$$

As shown in Table 10, Satellite No. 1 performs observation tasks on Targets No. 4 and No. 5 in turn; Satellite No. 2 performs removal tasks on Targets No. 4 and No. 5 in turn; and Satellite No. 3 performs both observation and removal tasks on Targets No. 1, No. 3, and No. 2 in turn. The execution results satisfy the allocation, fuel consumption, and capacity constraints described in Equations (7)–(9). As shown in Table 11, the observation task for each target is performed before the removal task, satisfying the task coupling constraint outlined in Equation (10).

Through the simulation experiments of Scenarios I–III, we can conclude that it is feasible to use MC-NSGA-II to solve the problem of task allocation for heterogeneous satellite swarm, satisfying the relevant constraints.

4.3. Comparative Analysis

To demonstrate the superiority of the proposed MC-NSGA-II algorithm, 100 Monte Carlo simulations are conducted for various algorithms under the conditions of Scenario II. When the Pareto front is unknown, the virtual ideal solution set $S^{*}$ is constructed to evaluate the algorithm’s performance. Two performance indices are proposed to evaluate these algorithms—inversion generation distance (IGD) and hypervolume (HV).

Five algorithms are compared—the multi-objective ant colony algorithm (MOACO) [29], the multi-objective particle swarm optimization (MOPSO) [30], the multi-objective evolutionary algorithm based on decomposition (MOEA/D) [31], the standard NSGA-II [26], and the MC-NSGA-II. The core idea of MOACO is to utilize the cooperative behavior of ants to construct a solution set that satisfies the requirements of multiple objectives during the search process. The MOPSO introduces the dominance relation and the external repository as the basis for comparison. MOEA/D is an evolutionary algorithm based on scalar functions. The standard NSGA-II enhances GA by incorporating the non-dominated sorting operation. The basic parameters are provided in

Table 12. Basic parameter for algorithms.

Algorithm	Parameter Setting
MOACO	$N_{ants}=100,\alpha =1,\beta =2,k_1=0.03$
MOPSO	$rep=50,\omega =1.2,C_1,C_2=2$
MOEA/D	$P_c=0.7,P_m=0.3,T=20,Z=(0,0,0)$
NSGA-II	$P_c=0.7,P_m=0.3$
MC-NSGA-II	$N_p=100$

.

All these algorithms are tested with the same population size and maximum number of iterations. The population size is set to 100, and the maximum number of iterations is 100. Each algorithm is executed independently 100 times, and the mean and standard deviation of IGD and HV are recorded for comparison.

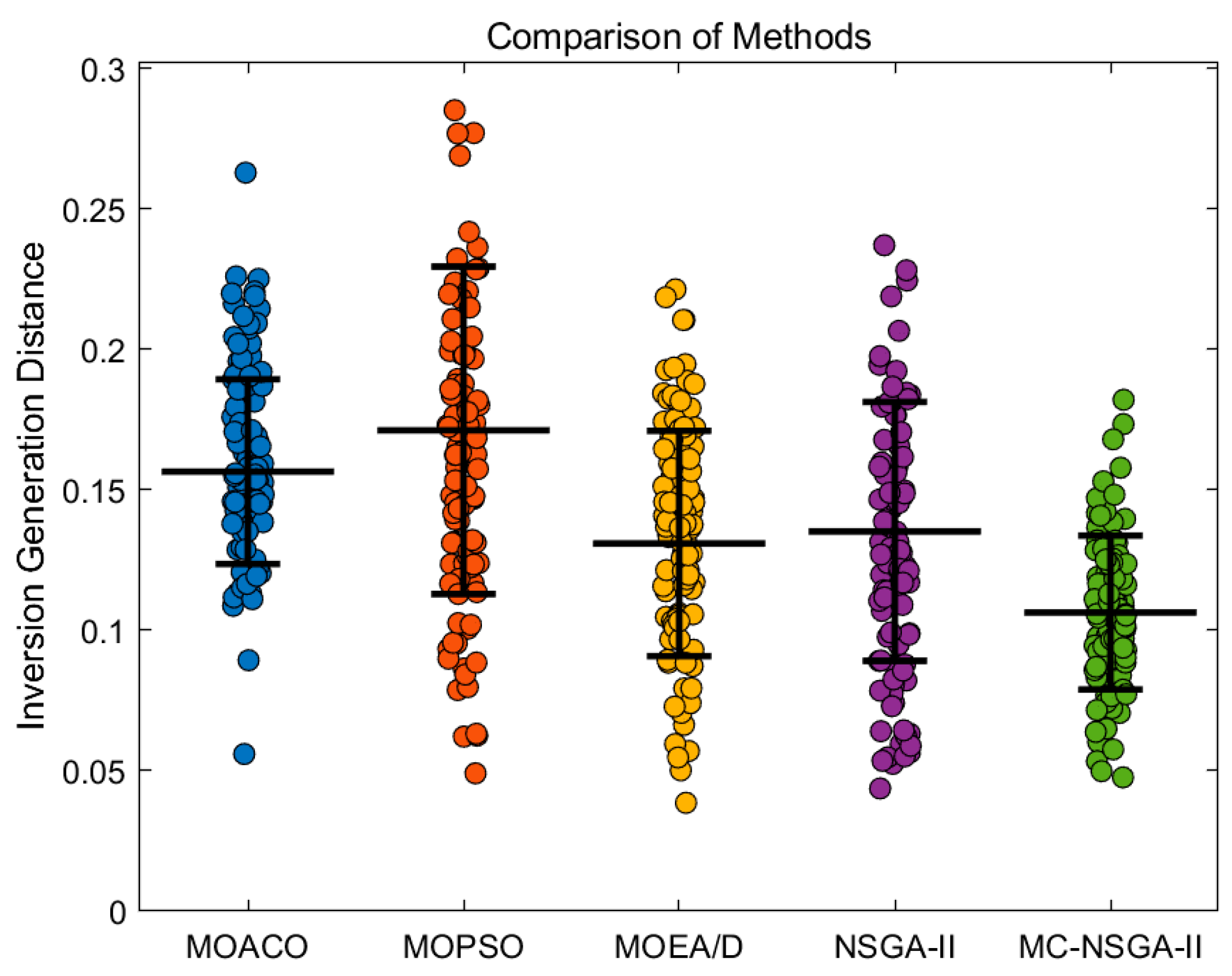
The IGD metric is employed to assess both the proximity and distribution uniformity between the algorithm-generated non-dominated solution set and the true Pareto optimal front. Figure 13 illustrates the IGD for these algorithms. MC-NSGA-II performs the best among all algorithms by virtue of the lowest IGD mean, which implies that MC-NSGA-II’s ability to find the optimal solution is the strongest. NSGA-II also has a strong ability to find high-quality solutions, but the stability of evolutionary operations is poor. The MC-NSGA-II outperforms the standard NSGA-II by 23.07%. By improving the coding method, as well as the genetic and mutation operations, the efficiency of searching for the effective solution set is enhanced, resulting in satisfactory convergence.

The HV metric is utilized to evaluate the quality of non-dominated solution sets, reflecting both solution diversity and approximation accuracy. Figure 14 displays the HV index of each algorithm. The MC-NSGA-II improves the weight of mutation operation in the later stage of the algorithm through dynamic genetic operation settings, so as to improve the diversity of understanding while stabilizing convergence. MC-NSGA-II has the highest average value of HV, which means that the MC-NSGA-II algorithm has the strongest space exploration capability. At the same time, the HV values of MOEA/D and NSGA-II are also higher than those of the other algorithms, except MC-NSGA-II, highlighting the effectiveness of genetic operations in finding feasible solutions.

Based on the above analysis, the MC-NSGA-II improves the ability of finding high-quality feasible solutions. This is achieved through a novel gene coding method, dynamic genetic operation parameter control, and an improved crossover and mutation strategy. The improved algorithm enhances the random search capability of the standard NSGA-II.

5. Conclusions

To address emergency debris removal scenarios involving a swarm of space debris and a heterogeneous satellite swarm equipped with diverse payloads, this paper proposes the MC-NSGA-II. The main conclusions are as follows.

A mathematical model is constructed to represent the heterogeneous satellite swarm while considering task coupling constraints. To evaluate different allocation strategies effectively, three optimization objectives are introduced. Multi-type chromosome encoding is proposed to address task coupling constraints, generate feasible solutions that satisfy these constraints, and improve the efficiency of searching for effective solution sets. Improved genetic operators are designed to generate feasible solutions. In addition, the algorithm introduces dynamic parameter control and a hybrid mutation mechanism. By comparing it with other algorithms, the effectiveness of the improved algorithm is demonstrated. The results show that the high-quality solution search ability of the MC-NSGA-II algorithm is 23.07% higher than that of the standard NSGA-II algorithm.

Furthermore, the dynamic positioning problem can be explored further. Considering the failure of some satellites or other unexpected events, rolling optimization is used to solve the reallocation strategy.