Abstract
To address the trade-off between safety levels and operational efficiency in the Bay Area, this study proposes a Multi-Stand Grouped Operations method based on deep reinforcement learning under the consideration of the safety domain. The full-process operation of aircraft within the Bay Area is analyzed to identify key operational spots. Safety domains are then established based on path conflicts arising from aircraft movements and safety conflicts caused by minimum separation distances and wake vortex effects. These domains are used to define corresponding safe operating spaces and construct an optimized operational model for the Bay Area. A multi-agent reinforcement learning algorithm is employed to solve the model, deriving an optimized stand allocation plan and Multi-Stand Grouped Operations strategy. To evaluate the effectiveness of the optimization, real flight data from the northwest Bay Area of Terminal 2 at Guangzhou Baiyun Airport are used for validation. Compared to the original stand allocation scheme, the optimized stand allocation and Multi-Stand Grouped Operations strategy reduce aircraft delay times by 62.45%, demonstrating that the proposed model effectively enhances operational efficiency in the Bay Area.
1. Introduction
As the demand for quality services among air passengers continues to rise, higher requirements are being placed on the contact stand. The Bay Area, which can provide more contact stands, is key to improving the bridge docking rate. The Bay Area primarily consists of stands and taxiway corridors, and their coordinated operation is crucial to overall efficiency. However, due to the complexity of aircraft movements within the Bay Area and the significant interdependencies between stands, optimizing operational procedures in the Bay Area has become a critical challenge that the industry urgently needs to address. During peak flight hours at busy airports, ramp congestion and aircraft rollout conflicts occur from time to time, resulting in ever-increasing flight delays. There are two main types of aircraft rollout conflicts: (1) neighboring aircraft rollout conflicts; (2) non-neighboring aircraft rollout conflicts with their taxiing forward rollout aircraft in the taxiing process [1]. Meanwhile, as airport airside operations transition from digitization to intelligent management, the traditional sequential single-aircraft pushback method is no longer sufficient to meet peak-hour operational demands. The Bay Area has become a major bottleneck in airport efficiency, requiring urgent optimization.
The Civil Aviation Administration has issued relevant regulations on apron layout and aircraft operation rules on the apron. At present, some studies have focused on optimizing the apron layout, planning stand arrangements and taxiway settings to improve apron operation efficiency. For example, Hagspihl et al. [2] established a mixed-integer programming model to plan the apron layout, aiming to minimize the number of aircraft assigned to remote stands. Wang et al. [3] planned the remote apron stand layout and taxiway configuration with the objective of maximizing the number of stands. Li M. et al. [4] constructed an evaluation index system for the spatial efficiency of Bay Area apron areas from the two perspectives of apron design and operation, and applied it to the calculation of domestic Bay Area. The results show that the proposed system can effectively evaluate the spatial efficiency of Bay Area with different layouts.
Current research on the optimization of Bay Area operations at domestic and international airports primarily focuses on two aspects: stand allocation optimization and operational procedure optimization.
Regarding stand allocation optimization, Burke et al. [5] set fuel consumption reduction and economic cost minimization as two primary optimization objectives and proposed two airport surface operation strategies. By improving the stand allocation strategy, they optimized the departure queue sequence and reduced unnecessary aircraft delays before takeoff. Diepen et al. [6] proposed a column generation algorithm and developed a two-stage model to analyze the robustness of stand allocation. Cheng et al. [7] established a stand allocation model and evaluated the performance of three metaheuristic algorithms: Genetic Algorithm (GA), Tabu Search (TS), and Simulated Annealing (SA). Zoutendijk, M. [8] applied Mixture Density Networks (MDNs) and Random Forest Regression to predict flight delays at European airports. They further integrated probabilistic forecasting into a stochastic stand allocation problem, achieving up to a 74% reduction in conflicting flights compared to deterministic gate assignment models. Xue Y. [9] introduced a safety-based apron grouped operation rule, developed a constraint model, and optimized the model using Genetic Algorithm (GA) to achieve a balanced distribution of stand idle time. Liu Y. [10] considered factors such as bridge docking rate, passenger walking distance and stand conflict, and proposed a multi-objective stand allocation collaborative optimization model. Bagamanova et al. [11] focused on the robustness of slot allocation, proposed an innovative allocation method to mitigate the impact of flight delays on overall operations, and validated it with simulation tools. Karsu et al. [12] established a mixed-integer planning model with the optimization objectives of minimizing the total walking distance of passengers and minimizing the number of flights assigned to the remote seats, and solved the problem by using a branch-and-bound algorithm, which effectively protects the rights and interests of passengers. She et al. [13] investigated the slot allocation problem of flights under different operating states, transformed the preferences of airport operators into scores as the optimization objective, and considered the robustness problem caused by flight delays at the same time, and they designed a two-phase Monte Carlo-based NSGA-II algorithm for effective solution.
Regarding operational procedure optimization, Wouter van Lingen [14] analyzed the impact of gate pit-stops on flight delays and operational efficiency. By integrating the Electronic Taxiing System (ETS) into the modeling of aircraft arrival and departure states, they demonstrated the effectiveness of gate pit-stops in improving operational efficiency. Li Z. [15] constructed a dynamic waiting point model and used a two-layer simulated annealing algorithm to reduce stand delay time. Yu Q. [16] proposed a Bay Area operation optimization strategy under apron control handover conditions. Based on the analysis of Bay Area configurations, they developed a particle swarm optimization algorithm to minimize total pushback time within the Bay Area. Chang Y. [17] established a flight conflict detection algorithm for the Bay Area, based on airport Bay Area usage rules and historical flight data nodes, providing support for air traffic controllers in scheduling adjustments. Yang T. [18] proposed an airport airside Bay Area optimization model, which introduced stand-related factors and quantified structural parameters. Using a dynamic grouping method, they effectively improved airport airside operational efficiency. Shi Z. et al. [19] investigated operational restrictions specific to Beijing Daxing Airport’s Bay Area configuration, analyzing the impact of aircraft conflicts within the Bay Area. Liu Y. [20] designed a U-shaped apron operation program, including exclusive, zonal shared, and globally shared modes. Through multi-dimensional evaluation metrics and classification-based assessments, the global sharing mode significantly increased apron capacity and improved operational efficiency at complex airports.
From the above studies, it can be seen that the optimization of stand allocation in the Bay Area has only improved the turnover rate and utilization of stands. In terms of optimizing operational procedures, it has merely reduced the number of conflicts within the Bay Area and enhanced the operational efficiency of a single aircraft, and it has optimized zonal grouping within the existing stand allocation. However, these improvements have had a limited impact on the overall operational efficiency of the Bay Area.
Deep reinforcement learning has been widely applied in path planning. Dai S. [21] designed an efficient path planning framework for multi-unmanned vehicle systems using deep reinforcement learning, and introduced an improved twin-delayed deep deterministic policy gradient (TD3) algorithm, enabling effective exploration in unknown environments and efficient collaborative obstacle avoidance and encirclement. Si P. [22] proposed a multi-agent deep reinforcement learning UAV path planning framework that employs the proximal policy optimization (PPO) algorithm and network pruning to improve training efficiency, verifying its effectiveness under different parameter configurations. Y. Guan [23] proposed a collaborative multi-UAV trajectory design method based on multi-agent proximal policy optimization (MAPPO) to enhance RF/FSO channel throughput, demonstrating that MAPPO outperforms state-of-the-art deep reinforcement learning (DRL) methods in RF resource allocation efficiency. Liu, X. [24] designed a comprehensive reward function based on the angle, speed, altitude, distance, and damage in the missile attack area for unmanned combat aerial vehicles (UCAVs), utilizing the centralized training and decentralized execution paradigm to enhance UAV decision-making capabilities and algorithm training efficiency. Kang H. [25] further improved training efficiency by introducing state normalization and action masking strategies. Wei, D. [26] addressed the challenge of sparse and stochastic rewards in UAV agents’ learning to search for unknown dynamic targets by proposing the OC-MAPPO method, which provides stable and continuous rewards for agents. Ming C. [27] proposed an online multi-agent proximal policy optimization (O-MAPPO) scheme to enhance energy efficiency while satisfying task execution, power consumption, computation, and time constraints. Simulation results show that O-MAPPO significantly outperforms benchmark algorithms in robustness and stability.
This paper proposes a deep reinforcement learning-based Multi-Stand Grouped Operations method to enhance the Bay Area’s capability to simultaneously operate multiple aircraft, thereby improving the overall operational efficiency of the Bay Area. The specific innovations are as follows:
- Proposed a Multi-Stand Grouped Operations method based on a safety threshold, constructing a secure operational space for aircraft in the Bay Area;
- Developed an optimization model for the Bay Area based on the Multi-Stand Grouped Operations method;
- Employed the MAPPO algorithm to derive optimal slip-in and pushback strategies, enabling distributed decision-making;
- Provided a reference model for the Airport Operations Center (AOC) in stand allocation, facilitating stand reallocation and multi-stand marshalling operations to reduce flight delays and enhance Bay Area operational efficiency.
2. Current Status of the Analysis of the Composition and Operational Characteristics of the Facilities in the Airport Bay Area
2.1. Comprehensive Analysis of Aircraft Operational Processes in the Bay Area
Aircraft operating in the Bay Area generally follow four main processes: slip-in process, entry process, pushback process, and taxi-out process. Arrival flights must complete the slip-in process to enter the assigned stand, while departure flights undergo a pushback process followed by a taxi-out process to exit the Bay Area. These processes are illustrated in Figure 1.
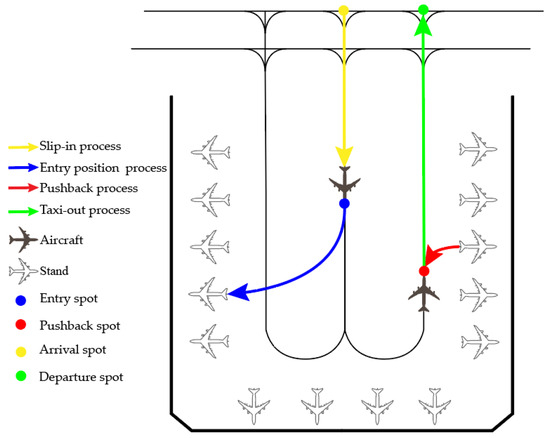
Figure 1.
Comprehensive analysis of aircraft operations in the Bay Area.
- Slip-in process. The slip-in process refers to the aircraft taxiing from the Bay Area’s arrival spot to the designated entry spot, which corresponds to the assigned stand. The entry spot is a virtual point on the taxiway where the aircraft transitions from taxiway operation to stand operation;
- Entry process. The entry process involves taxiing the aircraft from the entry spot to the designated stand;
- Pushback process. The pushback process refers to the aircraft being towed by a pushback tug from the stand to the designated pushback spot;
- Taxi-out process. The taxi-out process is the phase where the aircraft taxis from the pushback spot to the Bay Area exit point in preparation for departure.
2.2. Analysis of Stand Types and Pushback Process in the Bay Area
The stands in the Bay Area can be divided into three types according to their location—pier stand, terminal stand and corner stand. The stand release procedure is mainly reflected in the release flow; the release flow of the stand is related to the direction of travel of the taxiway at its location and nearby. The traditional release method at the airport is a one-sided release mode. In order to maximize the number of grouped flights, the terminal stand can adopt a two-sided release mode. Taking the three-aisle Bay Area as an example, we can describe the following steps:
- Pier stand and pushback process
Pier stands are stands located in the terminal building’s finger section and close to the outside of the taxiway. The closer a pier stand is to the outside of the Bay Area, the less impact it will have on the Bay Area when it is pushed out;
- Terminal stand and pushback process
The bottom stand refers to the stand in the main part of the terminal building. There are two main procedures for pushing out the bottom stand, as shown in Figure 2 as ‘red push’ and ‘blue push’. Generally, the method with the shortest taxiway after pushing out is selected, and the choice will also be based on the activities of the stands on both sides;
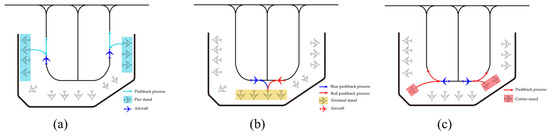
Figure 2.
Diagram of stand types and pushback procedures in the Bay Area: (a) represents the pier stand and its pushback procedure; (b) represents the bottom stand and its pushback procedure; (c) represents the corner stand and its pushback procedure.
- Corner stand and pushback process
A corner stand is a stand between a bottom stand and a pier stand. When pushing out an aircraft from a corner stand, it will have a huge impact on other stands in the Bay Area. The pushback procedures for a corner stand are similar to those for pier stands.
2.3. Classification of Flight Types and Their Operational Characteristics in the Bay Area
Flights are categorized into originating flights, transit flights, and overnight flights based on their operational tasks. While definitions may vary across airports, their operational procedures within the Bay Area remain consistent. This document adopts 00:00–24:00 as the standard time reference for flight classification, defined as follows.
- Originating flights
- Refers to departing flights that arrived the previous day and depart after 00:00 (inclusive).
- Their operations in the Bay Area primarily involve pushback and taxi-out procedures.
- Overnight flights
- Their Bay Area operations include the slip-in and entry processes.
- These flights may be towed to a remote stand for overnight parking.
- Transit flights
- Excluding originating and overnight flights, all other flights are categorized as transit flights, which include both arrival and departure operations.
- Their Bay Area procedures typically consist of the slip-in, entry, pushback, and taxi-out processes.
- Transit flights are further classified into the following:Short-transit flights—Flights with a transit time of less than 4 h.Long-transit flights—Flights with a transit time of more than 4 h.
Due to longer layovers, arrival aircraft may be towed to a remote stand. Before departure, they may be relocated to a stand in the Bay Area or pushed back directly from the remote stand. The analysis of the operation procedures for various types of flights in the Bay Area is shown in Figure 3.
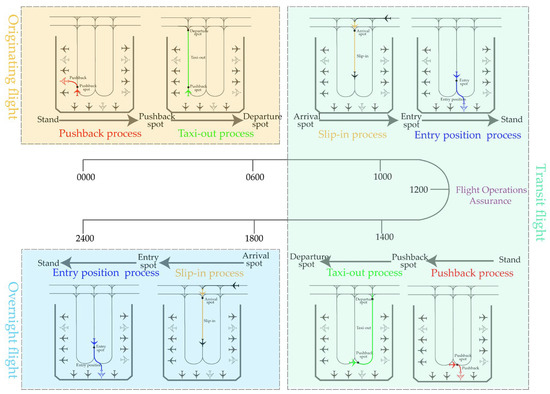
Figure 3.
Analysis of the flight operation procedures in the Bay Area.
2.4. Flight Conflict Analysis for the Bay Area
In the current operation mode of aircraft within the terminal Bay Area of airports, the typical strategy is a “single aircraft pushback one by one” approach. In practical airport operations, only one aircraft is allowed to operate within the Bay Area at any given time, ensuring that there is no conflict between aircraft. However, flight delays often result from potential conflicts caused by the inability to meet the demand for the simultaneous operation of multiple aircraft within the same time period. To enable simultaneous aircraft operations, this section analyzes the causes of flight conflicts. Based on the operational processes, flight conflicts can be mainly categorized into two main types—one is path conflicts during flight operations; the other is safety conflicts caused by wake turbulence and safety distance requirements.
- Path conflicts
Path conflicts are categorized based on the minimum safe distance between aircraft on the apron and the trajectory changes associated with different operational processes.
The entry process involves a path transition from the taxiway to the stand. The pushback process involves a path transition from the stand to the taxiway. The slip-in and taxi-out processes do not involve any path changes, as both occur entirely on the taxiway. Since both the slip-in and taxi-out processes take place on the taxiway, they are considered within the same category. In total, six types of path conflicts occur between flights, as illustrated in Figure 4.
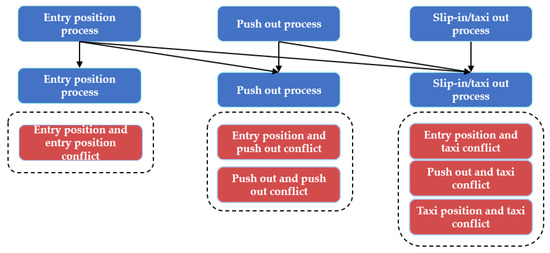
Figure 4.
Analysis of flight conflicts in the Bay Area.
- 2.
- Safety conflicts caused by wake turbulence and minimum safety distance
The impact range of wake turbulence under idle engine thrust varies depending on aircraft type and wind speed conditions. For ease of calculation, the wake turbulence impact area is approximated as a rectangle, with the width equal to the aircraft’s wingspan and the length corresponding to the wake turbulence effect distance under upwind conditions.
2.5. Multi-Stand Grouped Operations Based on Safety Domain
“Flight formation” refers to grouping multiple flights within the Bay Area that meet the safe operating conditions in the stand and taxiway within the same defined period of time to achieve the simultaneous operation of multiple aircraft within the group; “stand formation” refers to grouping stands in the Bay Area that do not affect each other’s operations into a group, so that aircraft in the same group can operate at the same time to improve the operational efficiency of the Bay Area. However, both are limited by the gate assignment of flights in the Bay Area and the safe operation of aircraft. Therefore, this paper proposes safety thresholds for each operation process based on the path conflicts and safety spacing conflicts generated between the aircraft’s various operating processes in the Bay Area, and proposes a Multi-Stand Grouped Operations method based on safety thresholds.
In the entire aircraft operation process, the entry stand is the process from the entry spot to the stand, and the path changes from the taxiway to the stand. According to the envelope generated by considering the safety spacing and the wake impact range during aircraft operation, the safety domain of the entry stand is constructed. Due to the influence of the wake, the safety zone is relatively large, which will cause conflicts with other safety domains and make it difficult for aircraft to operate at the same time. The pushback process is the process from the stand to the pushback spot. The path changes from the stand to the taxiway. The safety domain of the pushback process is constructed based on the envelope line generated by considering the safe distance during aircraft operation. In the pushback process, the aircraft is pushed out by the trailer, there is no influence of the wake blast, and the pushback processes at different stands can be run simultaneously; the slip-in process and taxi out process are the processes that occur from the arrival spot to the entry spot and from the pushback spot to the departure spot, respectively, and the path does not change between them. Considering the wake blast, the safety threshold during taxiway operation is constructed by referring to the principle of automatic railway blocking, as shown in Figure 5.
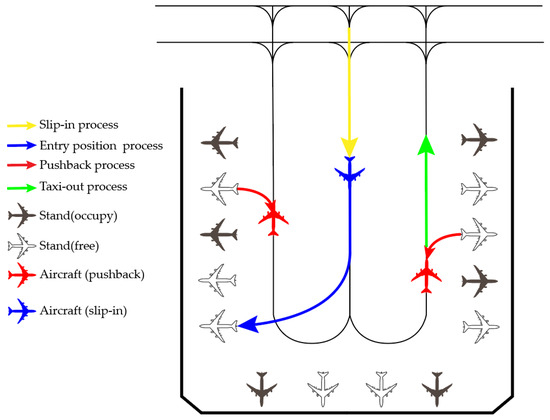
Figure 5.
Multi-Stand Grouped Operation’s mechanism.
Due to the conflict between the safety thresholds of each operation process in static space, when initially grouping stands, there are many possibilities for the number of groups and the number of stands in a group. Through aircraft parking reallocation and dynamic operation, an optimal Multi-Stand Grouped Operation strategy for the Bay Area is obtained, which enables multiple flights in the Bay Area to operate simultaneously with different operation processes, so as to improve the operation efficiency of the Bay Area.
In the actual stand allocation process, taking Guangzhou Baiyun Airport as an example, the airport AOC (Airport Operations Control Center) duty officers initially perform the pre-allocation of stands for all flights at around 7 p.m. on the night before operation. During the actual operation on the following day, the duty officers conduct secondary allocation based on the real-time operation status of flights. The proposed multi-stand grouped operation method is applied after the pre-allocation of flights. It focuses on the reallocation of flights assigned within the bay area and proposes a Multi-Stand Grouped Operation strategy to provide decision-making support for the secondary allocation conducted by the duty officers.
It should be noted that this study has not incorporated the impact of human scheduling behaviors on conflict avoidance into the modeling analysis. Therefore, it is assumed that the dispatcher performs the secondary stand allocation strictly following the proposed Multi-Stand Grouped Operations method, in order to explore and evaluate the effectiveness of this method in improving the operational efficiency of the Bay Area.
3. Construction of an Optimization Model for the Operation of the Terminal Bay Area
This chapter builds upon the previously proposed Multi-Stand Grouped operation method and constructs the corresponding safety operational spaces, including the Taxiway Corridor Safety Space, Stand Entry Safety Space, and Stand Pushback Safety Space. Based on the complete operational procedures of originating flights, overnight flights, and transit flights within the Bay Area, these processes are represented through their respective safety spaces. Task modeling is then performed, and a Bay Area operational optimization model is developed by integrating stand allocation with the occupancy time of each safety space.
3.1. Basic Model Assumptions
The following basic assumptions are made for the model:
- Since this study focuses on the optimization of aircraft operations within the Bay Area, it is assumed that the arrival and departure times of flights are known. Congestion on taxiways between the Bay Area exit and the runway is not considered, nor are delays of flights outside the Bay Area. The availability of stands within the Bay Area is fixed, with no consideration of stand failures or the activation of combined stands. Towing operations within the Bay Area are also excluded;
- To ensure the general applicability and accuracy of the model, it is assumed that the stand occupancy time (including guaranteed parking times) is fixed, with specific durations determined based on the operational conditions of the airport. Additionally, the entry and pushback routes for each stand are fixed. Aircraft operate within the Bay Area along the designated Taxiway Corridor, Stand Entry Streamline, and Stand Pushback Streamline. Finally, flight priority within the Bay Area is not considered, and sequencing is based on the scheduled arrival and departure times.
3.2. Environmental Modelling and Construction of Safe Operating Spaces
The Bay Area environment is modeled based on its facilities, including stands, stand entry spots, pushback spots, the taxiway corridor, stand arrival spots, and stand departure spots. Based on these key points, the Bay Area is divided into different operational zones, including the stand zone, taxiway corridor zone, and Bay Area entrance and exit zone.
Based on the entire process of flights operating in the Bay Area and the types of flight conflicts, the space for the safe operation of flights in different operating processes is constructed, including the Taxiway Corridor Safety Space (TCSS), Stand Entry Safety Space (SESS) and Stand Pushback Safety Space (SESS).
Assuming that the distance between adjacent taxiways in the Bay Area is , the length of the largest aircraft type is , the wingspan is , the minimum safe distance is , and the length of the wake impact range is . Among these, compared to , the is longer, and when considering both the minimum safe distance and the wake impact range in the same direction at the same time, the minimum safe distance can be ignored. is the m-th stand in the Bay Area (m = 1, 2, …, M); is the n-th Taxiway Corridor Safety Space (n = 1,2, … N); is the Stand Pushback Safety Space corresponding to ; is the Stand Entry Safety Space corresponding to .
3.2.1. Taxiway Corridor Safety Space
The taxiway corridor is divided into multiple continuous Taxiway Corridor Safety Spaces based on conflicts arising from the slip-in and taxi-out processes, as well as the pushback and entry processes, as presents in Figure 6 for details.
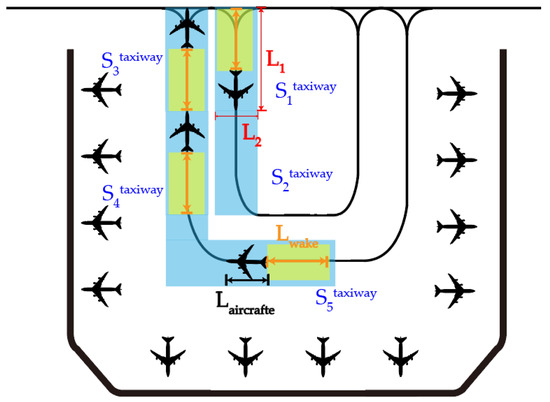
Figure 6.
Schematic of Taxiway Corridor Safety Space.
To ensure that an aircraft operating at any position within the n-th (where n > 2) Taxiway Corridor Safety Space does not affect the operation of another aircraft at any position within the (n − 2)-th Taxiway Corridor Safety Space, the spatial separation must prevent wake vortex interference. Based on the direction of aircraft movement along the taxiway, it is necessary that when an aircraft has just entered the n-th Taxiway Corridor Safety Space, the wake turbulence influence range does not extend to the end of the (n − 2)-th Taxiway Corridor Safety Space.
Therefore, the required length of the Taxiway Corridor Safety Space is calculated as .
When the distance L between taxiway corridor T1 and taxiway corridor T2 is greater than or equal to the sum of and , the Bay Area allows aircraft on taxiway corridor T1 and taxiway corridor T2 to operate simultaneously. The condition for an aircraft to enter Taxiway Corridor Safety Space is that there are no aircraft in Taxiway Corridor Safety Space . When the distance L between T1 and T2 is less than the sum of and , the condition for entering is that there are no aircraft in and .
3.2.2. Stand Entry Safety Space
When the stand for an incoming aircraft is confirmed to be , the area formed by the path taken by the aircraft in the entry stand from the entry spot to the stand, taking into account the impact of its wake and the safety distance, forms the safe area for the aircraft to slip into the stand. The area affected by the wake of the aircraft when it slips in from to is a sector formed by the aircraft’s path. However, this sector will not affect the area that the aircraft cannot reach during operation. For the sake of calculation, a rectangle is formed based on the sector, from the taxiway to the stand, to form the Stand Entry Safety Space . See Figure 7 for details.
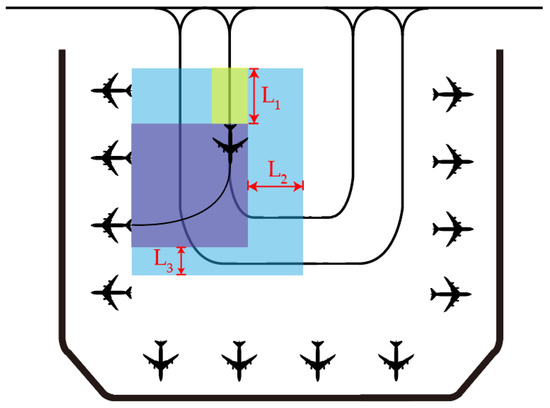
Figure 7.
Schematic of Stand Entry Safety Space.
Let and denote the maximum lateral and longitudinal distances, respectively, that are affected by wake turbulence during stand entry, and let represent the required safety clearance for the aircraft’s wings during stand entry. It is assumed that ,
The operational rules are as follows. For an aircraft that needs to complete stand entry, only one aircraft may operate within the same Stand Entry Safety Space at any given time. If the Stand Entry Safety Space of a given stand overlaps with the Safety Operational Space of another aircraft currently in operation, the aircraft must wait at the Entry Point or in the preceding Taxiway Corridor Safety Space.
3.2.3. Stand Pushback Safety Space
During the pushback process, an aircraft leaving the airport in stand needs to be towed from the stand to pushback spot by a tow truck. The area formed by the path from to is the safety domain for pushing out from this stand. Only the minimum safe distance of the aircraft is considered at this time, and the influence range of the wake vortex is not considered. The area formed by the path from to is the fan-shaped area formed by the aircraft sweeping past, but the area affected by the fan shape is an area that cannot be reached during aircraft operation. For convenience of calculation, a rectangle is formed based on the fan shape, from the taxiway to the stand, to finally form the Stand Pushback Safety Space , as shown in Figure 8.
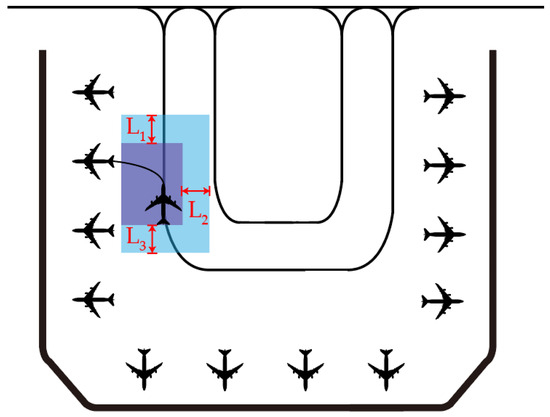
Figure 8.
Schematic of Stand Pushback Safety Space.
, , and represent the safety distances required for the aircraft’s wings or fuselage in the lateral and longitudinal directions during pushback.
Figure: .
The operational rules are as follows. For an aircraft that needs to complete pushback, only one aircraft is allowed to operate within the same Pushback Safety Space at any given time; if the Pushback Safety Space overlaps with the Safety Operational Space of another aircraft currently in operation, the aircraft must wait at the stand.
3.3. Task Modelling
To capture the operational status of all flights within the Bay Area over a given time period, a task modeling approach is employed. First, based on the chronological order of flight arrivals and departures, the i-th arriving flight and the j-th departing flight are defined. Here is the i-th arrival task performed by the aircraft (i = 1, 2, …, I); is the j-th departure task performed by the aircraft (j = 1, 2, …, J);
Next, by matching aircraft identifiers, a correspondence is established among originating flights, transit flights, overnight flights, arriving flights, and departing flights. An originating flight corresponds to one departing flight; a transit flight corresponds to one arriving flight and one departing flight; and an overnight flight corresponds to one arriving flight. These are then divided into arrival tasks and departure tasks, where an originating flight completes a departure task, a transit flight completes an arrival task, and an overnight flight completes an arrival task.
Arrival task. When an aircraft performs an arrival task, it first undergoes gate assignment. The aircraft moves from its stand to arrival spot , arrives at entry spot , and completes stand entry. At this point, the aircraft must complete its operations within the corresponding Taxiway Corridor Safety Space and Stand Entry Safety Space, thereby fulfilling its arrival task.
Departure task. When an aircraft performs an arrival task, it needs to be pushed out from its stand to parking pushback spot , taxi through the taxiway to departure spot , and then leave the Bay Area. At this point, the aircraft must complete its operation within the corresponding Pushback Safety Space and Taxiway Corridor Safety Space, thereby fulfilling its departure task.
3.4. Decision Variables
To represent the assigned stand for arriving flights, the stand location for departing flights, and the safety operation spaces traversed by each flight, the following decision variables are defined:
, the decision variable corresponding to whether arrival flight is operating at . If it is operating at , the value is 1; otherwise, the value is 0.
, the decision variable corresponding to whether arrival flight operates at . If it operates at , the value is 1; otherwise, the value is 0.
, the decision variable corresponding to whether arrival flight is assigned to stand . If it is assigned to stand , the value is 1; otherwise, the value is 0.
, the decision variable corresponding to whether departure flight operates at . If it operates at , the value is 1; otherwise, the value is 0.
, the decision variable corresponding to whether departure flight operates at . If it operates at , the value is 1; otherwise, the value is 0.
, whether the guaranteed stand of the departure flight is the decision variable corresponding to , and if the guaranteed position is , it is 1, otherwise it is 0.
, the decision variable corresponding to whether is occupied at time t. If it is occupied or assigned a gate assignment, the value is 1; otherwise, the value is 0. is the time step t (t = 1, 2, …, T) for the aircraft to operate in the Bay Area, and by time step T, all flight tasks are completed (the same notation applies hereinafter).
, the decision variable corresponding to whether is occupied at time t. If it is occupied, the value is 1; otherwise it is 0.
, the decision variable corresponding to whether is occupied at time t. If it is occupied, the value is 1; otherwise, it is 0.
, the decision variable corresponding to whether is occupied at time t. If it is occupied, the value is 1; otherwise, it is 0.
3.5. Objective Function
The optimization of operations in the Bay Area mainly involves two aspects. From the perspective of aircraft operations, except for the fixed flight guarantee time, the shorter the total operating time of all aircraft in the Bay Area, the shorter the waiting time for aircraft, and the better the optimization effect. From the perspective of flight operations, the shorter the total delay time of all flights in the Bay Area, the better the optimization effect. Therefore, the objective function is proposed.
Objective Function (1) minimizes the total operating time of all flights in the Bay Area. The total operating time is defined as the sum of the taxiway running time and the stand entry time for arriving flights, plus the sum of the pushback time from the stand and the taxiway running time for departing flights, minus the simultaneous operation time of aircraft in the Bay Area (i.e., the time during which multiple safety spaces are occupied concurrently). To prevent the minimization of operating time from leading to increased flight delays, objective Function (2) is introduced to minimize the delay time of all departing flights, where the delay time is defined as the difference between the actual departure time corresponding to the departure task and the scheduled departure time.
Here, is the planned departure time corresponding to the aircraft performing departure task ; is the actual departure time corresponding to the aircraft performing departure task ; is the operating time of the arrival flight assigned to stand from the stand arrival spot to the entry spot; is the operating time of the departure flight from the pushback spot to the departure point; is the time required for the aircraft to complete its operation within the safety space allocated to stand ; is the time required for the aircraft to complete its operation within the Stand Pushback Safety Space allocated to stand ; is the simultaneous operation time of aircraft in the Bay Area (the time when multiple safety spaces are occupied simultaneously).
3.6. Constraints
3.6.1. Constraints on Stands
Only one aircraft can be parked at a stand at the same time. Therefore, at any time step t, the following constraint must be satisfied:
Each arrival flight must be assigned a stand. Therefore, the following constraint must be satisfied:
3.6.2. Constraints on Taxiway Corridor Safety Space
Only one aircraft can be operated in each Taxiway Corridor Safety Space at the same time. Therefore, at any time step t, the following constraint must be satisfied:
3.6.3. Constraints on Stand Pushback Safety Space
Only one aircraft can operate in each Stand Pushback Safety Space at the same time, so the constraint needs to be satisfied at any time step t,
3.6.4. Constraints on Stand Entry Safety Space
Only one aircraft can operate in each Stand Entry Safety Space at the same time, so the constraint needs to be satisfied at any time step t,
3.6.5. Safety Space Conflict Constraint
When an aircraft is ready to enter the Taxiway Corridor Safety Space, it must satisfy the constraint that there is no aircraft in the safety space for the next Taxiway Corridor Safety Space. The constraint that needs to be satisfied is
When there is a spatial conflict between any two safety spaces within any set in , including conflicts in static space between the Stand Entry Safety Space and Stand Pushback Safety Space of the same stand, as well as conflicts in static space between the Stand Entry Safety Space and Stand Pushback Safety Space of adjacent stands, the following constraint must be satisfied:
The Stand Entry Safety Space of stand has a static spatial conflict with the adjacent Taxiway Corridor Safety Space, and its Stand Pushback Safety Space also has a static spatial conflict with the adjacent Taxiway Corridor Safety Space. These spaces respectively form and , and the following constraint must be satisfied:
4. Design of a Multi-Stand Grouped Operations Method for the Bay Area Based on the MAPPO Algorithm
To address the optimization problem of Multi-Stand Grouped Operations in the Bay Area, this chapter models each originating flight, transit flight, and overnight flight as an individual agent. Specifically, the originating flight agent is responsible for completing the departure task, the overnight flight agent completes the arrival task, and the transit flight agent completes both the arrival and departure tasks. The operational process is illustrated in Figure 9.
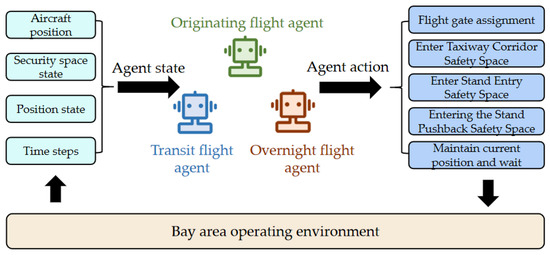
Figure 9.
Operational process of flight agents in the Bay Area.
First, the agent obtains state information from the environment, including the operational status of safety spaces, stand status, and time steps. Then, based on the observed state, the agent utilizes an artificial neural network trained by the MAPPO algorithm to make action decisions, such as stand allocation, entering a safety space, or waiting in place. Subsequently, the agent executes the selected action and interacts with the environment. After the action is completed, the agent re-observes the environmental state and repeats the above process in a loop. The following sections provide a detailed description of the agent’s state space, action space, reward function for training, and the overall training process.
4.1. Partially Observable Markov Decision Process
4.1.1. Global State Space
The state space defines all possible states of the aircraft in the Bay Area. Each state is characterized by the following:
- Aircraft position—the coordinates of the aircraft in the current taxiway space and its movement state in the Bay Area;
- Safe operating space state—records whether each safe operating space is occupied, ensuring that each safe operating space can only accommodate one aircraft at any time step;
- Stand status—records whether each stand is occupied;
- Time step—indicates the current time step t, and is used to track the entire time series of the completion of all aircraft tasks in the Bay Area.
4.1.2. Action Space
The action space defines all possible operations of the aircraft in the Bay Area. Considering that aircraft operations involve constant acceleration and deceleration, the action space of the stand in each safe operating space in the Bay Area is continuous. In order to discretize the continuous space, this paper assumes that the stand’s actions are continuous when operating in each safe operating space, and the stand’s action space for switching safe operating spaces is discrete. Each aircraft can choose the following actions at each time step t:
- Flight gate assignment—positions need to be allocated for transit and overnight flights before their arrival;
- Enter Taxiway Corridor Safety Space—all aircraft choose whether to enter the Taxiway Corridor Safety Space on the taxiway;
- Enter Stand Entry Safety Space—when an aircraft is at the entry spot and preparing to execute the entry process, it determines whether it can enter the Stand Entry Safety Space for the target stand;
- Entering the Stand Pushback Safety Space—when the aircraft is about to execute the pushing out process at its stand, it determines whether it can enter the Stand Pushback Safety Space of its own stand;
- Maintain current position and wait—determine whether to continue taxiing along the current taxiway space or remain stationary in the current taxiway and wait for the next time step.
4.1.3. Reward Function
The reward function defines the rewards that an aircraft receives under different states and actions. In order to minimize the total operation time of aircraft, the reward function in this study was designed based on the operational characteristics of aircraft movements in the Bay Area, combined with expert knowledge and practical experience from airport operations. The specific reward settings are as follows:
Positive reward —When the aircraft starts to move, it can get the time for the aircraft to reach the target point without obstruction. If the aircraft reaches the target point within the specified time, a positive reward is given;
Positive reward —A positive reward is given when the aircraft successfully reaches the target stand or safe operating space, indicating the effectiveness of the scheduling strategy. Set ;
Negative reward —When an aircraft violates safe operating rules (e.g., two aircraft in the same safe process space), a negative reward is given;
Time consumption reward —The more time is consumed waiting, the lower the reward value. By introducing a negative time reward, aircraft are encouraged to complete the scheduling task as quickly as possible. Set for each time step.
In summary, the number of rewards for is
In order to verify the robustness of the reward settings, a sensitivity analysis was conducted by adjusting the key reward values (e.g., increasing or decreasing conflict penalty by 50%) to observe the changes in learning performance and delay reduction. The experimental results show that although the training speed varied slightly, the optimal operation strategy and the delay reduction trend remained consistent, indicating that the reward function design is reasonable and robust.
4.1.4. State Transition
—State transition is determined by the current state, the selected action and the states of other aircraft. Each state transition needs to consider whether the safety spaces for the taxiway and position are occupied by other aircraft, and update the corresponding state representation. State transition describes the probability of an aircraft transferring from one state to the next. Since scheduling in the Bay Area is affected by the states of multiple aircraft, and the occupation of taxiways and positions. The following rules need to be considered in the state transition process:
Taxiway transfer rules—Whether an aircraft can move from one Taxiway Corridor Safety Space to the next depends on whether the next Taxiway Corridor Safety Space is occupied.
Position assignment and pushing out rules—Whether an aircraft can enter or pushback a position depends on whether the Stand Entry Safety Space or the Stand Pushback Safety Space is occupied by other aircraft.
Environment state update—After each state transition, the status of all safety operation spaces and stands in the Bay Area is updated to ensure that all constraints in the model, such as the exclusivity of safety operation spaces, are satisfied.
4.1.5. Policy Representation and Objective Function
The policy describes the optimal action, a, to be executed in each state. The objective of the optimal policy is to maximize the cumulative reward,
4.2. MAPPO Algorithm Design
The MAPPO algorithm adopts a centralized training and decentralized execution (CTDE) multi-agent deep reinforcement learning (MADARL) framework, as illustrated in Figure 10. During training, at time step t, agent i selects an action a based on its local observation and interacts with the environment to receive reward . All agents share a centralized value network, which takes global information , joint actions , and joint rewards as inputs, and outputs the loss function to update the policy network. Once the training process is complete, the agents no longer require the centralized value network, and can independently make decisions [28]. In the Bay Area, aircraft agents experience significant operational conflicts, leading to a competitive relationship. However, as each agent must complete its assigned flight tasks, a cooperative relationship also exists. MAPPO is well-suited to address this scenario.
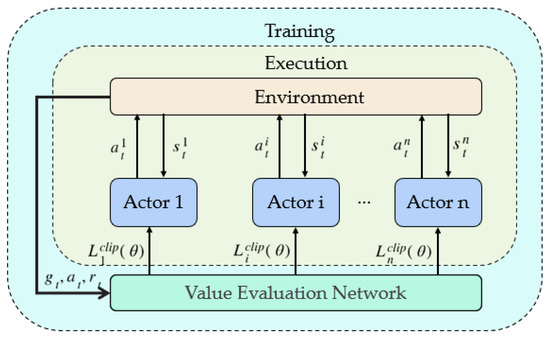
Figure 10.
The framework diagram of the MAPPO algorithm.
4.2.1. Optimization Goal
represents the probability ratio of the old and new policies.
is the advantage function, which represents the improvement of the current policy relative to the baseline policy,
where is the state-action value function, which represents the cumulative reward when an action is executed in state and the current policy is continued. is the clipping range, which is used to limit the magnitude of the policy update.
The advantage function measures the advantage of the current policy. If it is greater than 0, it means that the action has great advantages and the policy can be further optimized; otherwise, the policy should reduce the probability of the action.
4.2.2. Algorithm Implementation Steps
- Initialize the policy network and value network: Construct a deep neural network consisting of an input layer, a hidden layer and an output layer. The policy network is used to generate a probability distribution of individual actions, and the value network is used to estimate the value of the state.
- Sample interaction data: Interact with the environment, execute a series of actions in the Bay Area dispatch model, and record the state, action, reward and state transition at each time step.
- Calculate the advantage function: The advantage function is calculated using the time difference method.
- Update the policy network: Policy updates are performed using a clipped target function to limit the range of policy changes.
- Update the value network: The value network is updated by minimizing the mean square error (MSE) to ensure that the model accurately evaluates the value of the current state.
5. Instance Validation
The Northwest Bay Area of T2 of Guangzhou Baiyun Airport is selected as the research object to verify the validity of the constructed formation model. The Bay Area consists of 14 class C machine stands, numbered 256–269, and the taxiway type is double U-channel, with four taxiways, following the operation mode of ‘in the middle and out on both sides’. The numbering of the stands has been set as 1–14.
A coordinate system was established with the stand entry spot of GATE 04 as the origin and the direction of Taxiway 2 as the Y-axis. Based on the actual spatial layout of the airport Bay Area, the coordinates of each stand and taxiway were determined according to the distances between stands and the distances between taxiways. All stands for category C aircraft were assumed to have the same rectangular shape, and the coordinates of each stand are represented by its center point and the four corner points. The Baiyun Airport Bay Area layout model is shown in Figure 11.
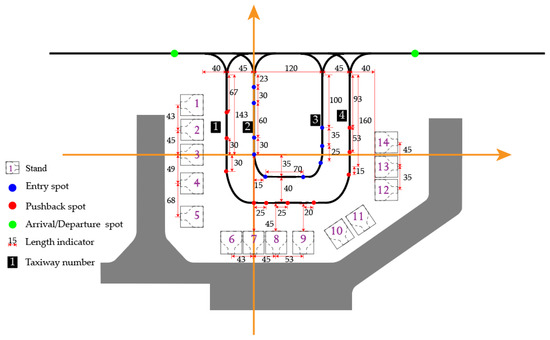
Figure 11.
Baiyun Airport Bay Area layout model.
For calculation convenience, the stands on the same side, including concourse stands, bottom stands, and corner stands, were parallelized and normalized with respect to their distances from the terminal building. The specific coordinates of some stands are shown in Table 1. The coordinates of key operational points, including arrival spots, departure spots, stand entry points, and pushback waiting points for certain stands, are shown in Table 2.

Table 1.
Coordinates of stands in the Bay Area.

Table 2.
Coordinates of key spots in the Bay Area.
Six taxiway safety spaces were constructed, some of which are shown in Table 3; there are also 14 gate entry safety spaces, some of which are shown in Table 4, and 14 gate pushback safety spaces, some of which are shown in Table 5.

Table 3.
Coordinates of part of the Taxiway Corridor Safety Space.

Table 4.
Some of the coordinates of the Stand Entry Safety Space.

Table 5.
Some of the coordinates of the Stand Pushback Safety Space.
To optimize the allocation of flights operating in and out of the Bay Area on a selected day in 1 July 2023 (00:00–24:00), a total of 158 flights were considered after excluding one canceled flight. Filtering the flights based on aircraft registration numbers revealed that some aircraft operated 3–4 flights during this period. To streamline the analysis, these aircraft were renumbered accordingly. The final dataset included 71 transit flights, 10 originating flights, and six overnight flights. Specific details of some flights and aircraft are shown in Table 6.

Table 6.
Partial flight and aircraft information in the Bay Area.
In the early training stage, a grid search was conducted within reasonable ranges to identify appropriate values. During subsequent training, fine-tuning was applied based on training stability, convergence curves, and the performance of the test results. The hyperparameter settings of the model are shown in Table 7, and the reward curve after 200 training rounds is shown in Figure 12. The model training in this study was conducted on a hardware platform equipped with an RTX 3080 GPU (10GB) and an Intel i9-12900K CPU. The RTX 3080 GPU was manufactured by ASUS, Shanghai, China, and the i9-12900K CPU was manufactured by Intel, Chengdu, China. Under 200 training episodes, the average total training time of the MAPPO model was approximately 42.5 min, with each episode taking about 0.51 s on average. The breakdown of computational resource consumption for different modules is shown in Table 8. The final solution is obtained, and the experimental results are analyzed, which mainly include the following three aspects.

Table 7.
Model hyperparameter settings.
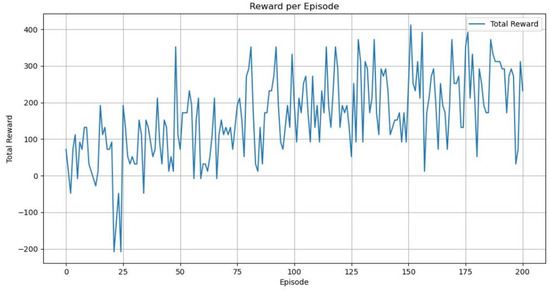
Figure 12.
Schematic diagram of the reward curve for algorithm training.

Table 8.
Model training time.
- Results of gate assignment
By solving the algorithm, the 158 flights allocated to the Bay Area are reasonably allocated to the stands in the Bay Area; the results of the stand allocation of the original scheme and the optimized stand allocation of the Multi-Stand Grouped Operations are shown in Table 9, and the Gantt chart of the gate assignment is shown in Figure 13.

Table 9.
Flight allocation before and after optimization of positions.
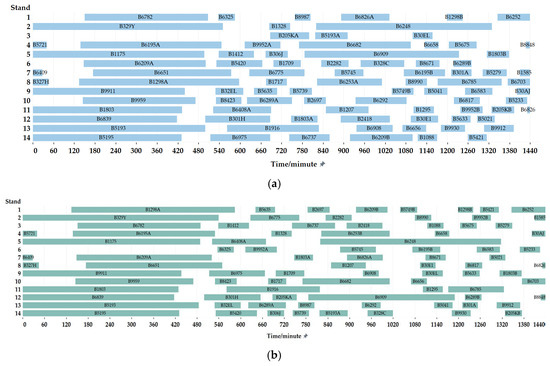
Figure 13.
Bay Area stand allocation Gantt chart. (a) Represents the original stand allocation Gantt chart; (b) represents the stand allocation Gantt chart after Multi-Stand Grouped Operation optimization in the Bay Area.
Among them, the pier stands under the optimized allocation plan have a total of 89 flights allocated, with an average of 12.71 flights per stand; the terminal stands have 46 flights allocated, with an average of 11.5 flights per stand; the corner stands have 23 flights allocated, with an average of 7.67 flights per stand. Compared with the original allocation plan, the pier stands have 20 more flights allocated, the bottom gate assignment flights decreased by 8, and the corner gate assignment flights decreased by 12. The main reasons are as follows.
Under the optimized allocation plan, a total of 89 flights were assigned to pier stands, with an average of 12.71 flights per stand. Terminal stands were allocated 46 flights, with an average of 11.5 flights per stand, while corner stands were assigned 23 flights, averaging 7.67 flights per stand. Compared to the original allocation scheme, the number of flights assigned to pier stands increased by 20, while terminal stands saw a reduction by 8 flights, and corner stands experienced a decrease by 12 flights. The primary reasons for these changes are as follows.
Pier stands, located near the outer edge of the Bay Area, allow for slip-in and pushback operations with minimal impact on other stands. The closer a stand is to the outer edge, the shorter the slip-in and pushback times. Consequently, more short-transit flights were allocated to concourse stands in the optimized plan, leading to an increase in their assigned flights.
Corner stands, on the other hand, significantly affect nearby pier stands and terminal stands during aircraft entry and pushback operations. As a result, the optimized plan allocated more long-transit flights to corner stands, reducing their total number of assigned flights.
Although terminal stands have a relatively lower impact on surrounding stands during entry and pushback, their location at the base of the concourse results in longer slip-in and pushback distances. Therefore, the number of flights assigned to base stands was reduced in the optimized plan.
- 2.
- Delay time
The delay time of each aircraft after the optimization of Multi-Stand Grouped Operation is obtained based on the time node of each aircraft completing its task during training, as shown in Figure 14. To verify the effectiveness of the proposed optimization method, this study conducted a paired t-test to statistically analyze the flight delay times before and after optimization. The results show that the average flight delay time under the original stand allocation scheme was 34.26 min with a variance of 772.53, while after implementing the “Multi-Stand Grouped Operations” optimization, it was reduced to 12.86 min with a variance of 436.63, representing a reduction of approximately 62.45%. The p-value of the paired t-test was 1.69 × 10⁻¹³, indicating that the reduction in delay time is statistically significant. During the entire day, only one flight experienced an increase in delay time, while the delay times of all other flights were reduced.
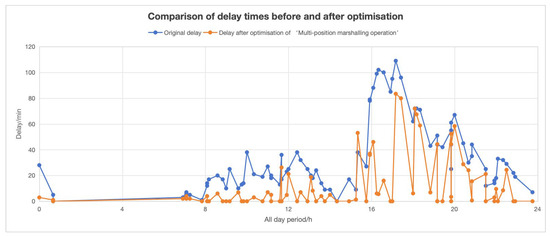
Figure 14.
Delay time comparison before and after optimization.
To further test the robustness of the model under different operational conditions, the flight data on July 2 were selected for validation. Considering the difference in the number of flights between the two days, a comparison was made based on the average flight delay time per hour within the same time period. Detailed results are shown in Figure 15.
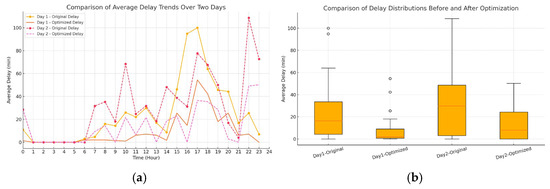
Figure 15.
Analysis of hourly average flight delay time over two days. (a) Comparison of hourly average flight delay time over two days; (b) boxplot of overall average flight delay time for two days.
For Day 1, the average delay time before optimization was 25.47 min with a standard deviation of 28.37 min, while after optimization, the average delay time was reduced to 7.16 min with a standard deviation of 11.33 min. For Day 2, the average delay time before optimization was 28.04 min with a standard deviation of 32.01 min, while after optimization, it was reduced to 9.17 min with a standard deviation of 12.53 min.
In addition, paired t-tests were conducted to evaluate the statistical significance of the delay reduction. The p-value for Day 1 was 0.000278, and for Day 2 it was 0.0000224, both of which are far less than 0.001, indicating highly significant differences between the pre-optimization and post-optimization results. In summary, the proposed Multi-Stand Grouped Operations method can effectively reduce the average flight delay time in the Bay Area on different days, demonstrating stable optimization performance with strong statistical significance.
- 3.
- Multi-Stand Grouped Operation plan
In each training round, the start and end times of each stand corresponding to safe operating space are recorded. The simultaneous operating status of intelligent bodies is obtained based on the simultaneous occupation of safe operating space. The stands of intelligent bodies are grouped according to their simultaneous operating status, and the stands within a group can be marshalled together, including pushback and pushback, pushback and entry position, slip-in and slip-in, taxi-out and taxi-out, and slip-in and slip-out. The influence of wake turbulence is not considered when pushing out positions, the safety space for pushing out positions is small, and pushing out–pushing out simultaneous operation is more common. Multi-Stand Grouped Operations involves pushing out more stands. The stands in each time period after optimization are shown in Table 10.

Table 10.
Multi-Stand Grouped Operation.
Among the 158 flights operating in the Bay Area, Multi-Stand Grouped Operations were conducted 46 times, including 5 instances of three-stand grouped operations and 41 instances of two-stand grouped operations. Within these Multi-Stand Grouped Operations, pushback operations were carried out 28 times, with 5 instances involving three-stand grouped operations and 23 instances involving two-stand grouped operations.
Based on this grouping arrangement, stands that appeared in multiple groups were reclassified into a single group. If the corresponding safety operational space of the stands within the group did not present static conflicts, the grouping was finalized. However, if static conflicts existed within the safety operational space, the stand with the highest grouping frequency was selected as the final grouping stand, while the remaining stands were reassigned for further grouping. The final groupings obtained were as follows: {1,6,9,13}, {2,8,12}, {3,7,17}, {4,10}, and {5,11}. Flights assigned to stands within the same group could operate simultaneously. Based on the final grouping arrangement, the grouped operations ultimately achieved 100% execution efficiency.
6. Conclusions
Considering the optimization of Multi-Stand Grouped Operations in the Bay Area, aircraft are divided into starting flights, transit flights and overnight flights based on their attributes, such as the transit time of the flight. Tasks are divided into arrival and departure tasks according to the flight’s operating process in the Bay Area, and the corresponding task process. Key operating nodes are divided and a safe operating space is constructed based on the operating characteristics and conflict types of flights in the Bay Area, and an optimization model for operations in the Bay Area is established. To solve the model, the aircraft is regarded as an agent, and the decision-making process of the Multi-Stand Grouped Operation of the stand can be modelled as a partially observed Markov decision process, which specifies the action space and state space of the stand and sets the reward function. The optimization problem of Multi-Stand Grouped Operation in the Bay Area is solved based on the MAPPO algorithm. The results show that considering gate assignment for the optimization of Multi-Stand Grouped Operation in the Bay Area can reduce delays and improve operational efficiency in the Bay Area.
However, the airside of an airport is an integrated system, and the operation of the airport surface is a complex engineering system involving the coordination of aircraft, ground vehicles, airfield infrastructure, and airport facilities. It is also closely related to the operation of various subsystems, including runways, taxiways, and stands. This study focuses only on the optimization of a single bay area, which may limit its applicability to the overall airside operation. In future research, the proposed method could be extended to incorporate runway-taxiway systems and jointly optimize the operations of multiple bay areas across the entire terminal, aiming to comprehensively improve the operational efficiency of the airport airside. Moreover, this study does not consider the influence of human scheduling behavior. In future work, human factor modeling or the integration of simulation systems to capture the behavior of airside controllers and dispatchers could be explored, so as to further enhance the practicality and adaptability of the proposed model.
Author Contributions
Conceptualization, J.O. and C.Z.; methodology, J.O.; software, C.Z.; validation, X.T.; investigation, J.O. and C.Z.; resources, J.O.; data curation, C.Z. and X.T.; writing—review and editing, J.O. and C.Z.; visualization, X.T.; supervision, J.Z.; project administration, J.Z.; funding acquisition, J.O. All authors have read and agreed to the published version of the manuscript.
Funding
This study is supported by the National Natural Science Foundation of China Civil Aviation Joint Research Fund (Project Approval Number: U2333204) and the Civil Aviation Joint Fund Supporting Project (Project Approval Number: 3122024PT03).
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy reasons.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Tang, X.; Zhu, J. Research on Aircraft Pushback Procedures at Busy Airports. In Proceedings of the 8th National Academic Conference for Young Scholars in Transportation, Shanghai, China, 30 October 2009. [Google Scholar]
- Hagspihl, T.; Kolisch, R.; Fontaine, P.; Schiffels, S. Apron layout planning–Optimal positioning of aircraft stands. Transp. Res. Part B Methodol. 2023, 179, 102854. [Google Scholar] [CrossRef]
- Wang, L.; Tang, Y.; Zhang, G.; Kang, W.; Zhuang, Y.; Su, Z. Research on airport apron planning strategy in emergency situations. J. Air Transp. Manag. 2024, 117, 102592. [Google Scholar] [CrossRef]
- Li, M.; Yao, L.; He, Y. Evaluation of Spatial Efficiency of U-shaped Apron Area Based on Norm Grey Relational Analysis and Dynamic Efficacy Coefficient Method. Sci. Technol. Eng. 2024, 24, 4336–4342. [Google Scholar]
- Atkin, J.A.D.; Burke, E.K.; Greenwood, J.S. A comparison of two methods for reducing take-off delay at London Heathrow airport. J. Sched. 2011, 14, 409–421. [Google Scholar] [CrossRef]
- Diepen, G.; Akker, J.M.V.D.; Hoogeveen, J.A.; Smeltink, J.W. Finding a robust assignment of flights to gates at Amsterdam Airport Schiphol. J. Sched. 2012, 15, 703–715. [Google Scholar] [CrossRef]
- Cheng, C.; Ho, S.C.; Kwan, C.L. The use of meta-heuristics for airport gate assignment. Expert Syst. Appl. 2012, 39, 12430–12437. [Google Scholar] [CrossRef]
- Zoutendijk, M.; Mitici, M. Probabilistic Flight Delay Predictions Using Machine Learning and Applications to the Flight-to-Gate Assignment Problem. Aerospace 2021, 8, 152. [Google Scholar] [CrossRef]
- Xue, Y.; Zhou, H.; Jiang, Z.; Cai, F. Optimization Research on Stand Allocation for U-Shaped Aprons. Aeronaut. Comput. Technol. 2022, 52, 59–63. [Google Scholar]
- Liu, Y.; Liu, J.; Tian, W. Collaborative optimization of gate assignment in complex apron operation mode. J. Harbin Univ. Commer. (Nat. Sci. Ed.) 2023, 39, 619–627. [Google Scholar]
- Bagamanova, M.; Mota, M.M. A multi-objective optimization with a delay-aware component for airport stand allocation. J. Air Transp. Manag. 2020, 83, 101757. [Google Scholar] [CrossRef]
- Özlem, K.; Meral, A.; Kerem, A. Exact and heuristic solution approaches for the airport gate assignment problem. Omega 2021, 103, 102422. [Google Scholar]
- She, Y.; Zhao, Q.; Guo, R.; Yu, X. A robust strategy to address the airport gate assignment problem considering operators’ preferences. Comput. Ind. Eng. 2022, 168, 108100. [Google Scholar] [CrossRef]
- van Lingen, W.; Roling, P. Modelling the effects of gate planning on apron congestion. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019; American Institute of Aeronautics and Astronautics Inc.(AIAA): Reston, CA, USA, 2019; pp. 1–10. [Google Scholar]
- Li, Z.; Zhu, X.; Zhang, T. Optimal design of push-back spot in single-aisle U-shaped apron area of large airports. Sci. Technol. Eng. 2023, 23, 12744–12752. [Google Scholar]
- Yu, Q. Research on Operation Optimization of U-Shaped Area of Terminal Building Based on Aircraft Control Transfer; Civil Aviation University of China: Tianjin, China, 2020. [Google Scholar] [CrossRef]
- Chang, Y.; Wang, X.; Li, P. Research on Airport Bay Conflict Detection Algorithm Based on Data Analysis. Aeronaut. Comput. Technol. 2022, 52, 61–64, 69. [Google Scholar]
- Yang, T.; Ouyang, J. Airside Cul-de-sac operational optimization in hub-airport. China Transp. Rev. 2023, 45, 46–52. [Google Scholar]
- Shi, Z.; Yang, Z. Research on operation mode optimization of Beijing Daxing International Airport Cul-de-sac apron. China Transp. Rev. 2023, 45, 182–186. [Google Scholar]
- Liu, Y.; Hu, M.; Yin, J.; Su, J.; Wang, S.; Zhao, Z. Optimization design and performance evaluation of u-shaped area operation procedures in complex apron. Aerospace 2023, 10, 161. [Google Scholar] [CrossRef]
- Dai, S.; Wang, Y.; Shang, C. Multi-unmanned vehicle collaborative path planning method based on deep reinforcement learning. J. Beijing Univ. Aeronaut. Astronaut. 2025, 1–12. [Google Scholar] [CrossRef]
- Si, P.; Wu, B.; Yang, R.; Li, M.; Sun, Y. UAV Path Planning Based on Multi-Agent Deep Reinforcement Learning. J. Beijing Univ. Technol. 2023, 49, 449–458. [Google Scholar]
- Guan, Y.; Zou, S.; Li, K.; Ni, W.; Wu, B. MAPPO-Based Cooperative UAV Trajectory Design with Long-Range Emergency Communications in Disaster Areas. In Proceedings of the 2023 IEEE 24th International Symposium on a World of Wireless, Mobile and Multimedia Networks (WoWMoM), Boston, MA, USA, 12–15 June 2023; pp. 376–381. [Google Scholar] [CrossRef]
- Liu, X.; Yin, Y.; Su, Y.; Ming, R. A multi-UCAV cooperative decision-making method based on an MAPPO algorithm for beyond-visual-range air combat. Aerospace 2022, 9, 563. [Google Scholar] [CrossRef]
- Kang, H.; Chang, X.; Mišić, J.; Mišić, V.B.; Fan, J.; Liu, Y. Cooperative UAV Resource Allocation and Task Offloading in Hierarchical Aerial Computing Systems: A MAPPO-Based Approach. In Proceedings of the IEEE Internet of Things Journal, San Antonio, TX, USA, 15 June 2023; Volume 10, pp. 10497–10509. [Google Scholar] [CrossRef]
- Wei, D.; Zhang, L.; Liu, Q.; Chen, H.; Huang, J. UAV Swarm Cooperative Dynamic Target Search: A MAPPO-Based Discrete Optimal Control Method. Drones 2024, 8, 214. [Google Scholar] [CrossRef]
- Cheng, M.; Zhu, C.; Lin, M.; Wang, J.-B.; Zhu, W.-P. An O-MAPPO scheme for joint computation offloading and resources allocation in UAV assisted MEC systems. Comput. Commun. 2023, 208, 190–199. [Google Scholar] [CrossRef]
- Xu, M.; Yu, D.; Zhao, L.; Guo, C. Autonomous Driving Decision at Unsignalized Intersections Based on MAPPO. J. Jilin Univ. (Inf. Sci. Ed.) 2024, 42, 790–798. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).