Abstract
This study presents an improved methodology for celestial triangulation optimization in spacecraft navigation, addressing limitations in existing approaches. While current methods like Linear Optimal Sine Triangulation (LOST) provide statistically optimal solutions for position estimation using multiple celestial body observations, their performance can be compromised by suboptimal measurement pair selection. The proposed approach, called the Improved-LOST algorithm, introduces a systematic method for evaluating and selecting optimal measurement pairs based on a Cramér–Rao Lower-Bound (CRLB) analysis. Through theoretical analysis and numerical simulations on translunar trajectories, this study demonstrates that geometric configuration significantly influences position estimation accuracy, with error variances varying by orders of magnitude depending on observation geometry. The improved algorithm outperforms conventional implementations, particularly in scenarios with challenging geometric configurations. Simulation results along a translunar trajectory using various celestial body combinations show that the systematic selection of measurement pairs based on CRLB minimization leads to enhanced estimation accuracy compared to arbitrary pair selection. The findings provide valuable insights for autonomous navigation system design and mission planning, offering a quantitative framework for assessing and optimizing celestial triangulation performance in deep space missions.
1. Introduction
Space exploration relies on accurate and reliable navigation to ensure the success of interplanetary missions. As spacecraft travel farther from Earth, autonomous navigation becomes increasingly important to enhance mission robustness and reduce operational costs, while long communication delays make real-time ground-based control challenging for certain mission phases. These fundamental limitations, combined with challenges such as gravitational perturbations and position uncertainties, have driven the development of autonomous navigation systems. Such systems enable spacecraft to determine their position and trajectory independently through onboard measurements and computations, reducing reliance on continuous ground support while enhancing mission efficiency and reliability [1]. Among these autonomous capabilities, advanced onboard navigation techniques, particularly vision-based methods, have emerged as promising solutions to overcome these limitations and further improve spacecraft autonomy. These systems effectively complement traditional Inertial Measurement Units (IMUs), which suffer from error accumulation over time, by providing absolute or relative measurements. Navigation systems utilizing vision-based measurements are implemented either as a Vision-aided Inertial Navigation System (VINS), which integrates camera and inertial data, or as standalone Optical Navigation (OPNAV) in spacecraft navigation applications [2,3].
Various OPNAV techniques have been developed to address different mission requirements and operational constraints. In proximity operations, optical and LIDAR-based systems provide accurate position estimation [4,5]. For missions around celestial bodies, Terrain Relative Navigation (TRN) enables precise orbital and landing maneuvers by utilizing and tracking identifiable surface features [6,7,8,9,10]. Navigation methods utilizing visible limbs of celestial bodies [3,11,12] and apparent planetary disk measurements provide alternative positioning techniques [13,14,15,16]. For deep-space missions, where these optical navigation methods may lose effectiveness, alternative techniques such as stellar spectra shift [17] and aberration of starlight (StarNAV) [18] have been proposed. In addition, a notable method, celestial triangulation provides a fundamental approach for autonomous spacecraft localization by utilizing line-of-sight (LoS) measurements of two or more celestial bodies whose locations are known [19,20,21,22,23,24,25,26]. This technique represents a resection case of the triangulation problem, where the positions of two vertices (celestial bodies) are known, and the third vertex (observer) position is to be determined. This technique is a direct application of classical triangulation principles where conventional ranging methods are impractical. By measuring the angular separation between multiple celestial bodies and leveraging their known positions, an observer can estimate their own position. Celestial triangulation has been extensively studied for interplanetary exploration, offering a reliable solution for autonomous navigation in deep space. Furthermore, the triangulation concept is not limited to celestial observation applications, but is also widely used in many photogrammetry [27,28,29], computer vision [30,31,32], and navigation [13,33,34] applications. The celestial triangulation principle can also be implemented using sequential measurements of individual bodies over time integrated with dynamic estimators, rather than requiring simultaneous multi-body observations [35,36].
While triangulation remains a fundamental technique in navigation and positioning systems, it remains an active area of research, with recent advances focusing on position estimation accuracy through improved algorithmic approaches. In the absence of measurement noise, the triangulation is straightforward; however, measurement noise introduces significant challenges [37]. Research has addressed these challenges through two distinct strategies: selective approaches that identify and use only the most geometrically favorable celestial body pairs, and comprehensive methods that incorporate all available measurements with appropriate statistical weighting.
Optimal beacon selection methods have demonstrated that carefully chosen pairs of celestial bodies can yield navigation accuracy comparable to using multiple beacons [38]. These approaches utilize figures of merit that identify pairs minimizing position uncertainty based on geometric considerations and measurement statistics. Studies have shown that position accuracy achievable with different asteroid combinations can vary by orders of magnitude, depending on the selection criteria [20]. Further research has analyzed how different tracking frequencies and measurement errors affect estimation performance, confirming that proper beacon selection can compensate for limitations in observation frequency [39].
While the beacon selection methods focus on identifying the best subset of measurements, complementary studies have emphasized developing algorithms that can optimally utilize all available measurements simultaneously. Conventional methods, such as the Direct Linear Transform (DLT), provide exact geometric solutions, while unweighted least-squares approaches are computationally efficient; however, both fail to yield statistically optimal estimates when dealing with noisy measurements [25]. To achieve statistically optimal solutions, Hartley and Sturm’s method provides a non-iterative approach by formulating the triangulation problem as the solution to a sixth-degree polynomial [30]. While this approach ensures optimality for two measurements, its extension to three or more simultaneous observations becomes computationally impractical due to the increasing complexity of polynomial root-finding [40,41]. To overcome these computational challenges, the Linear Optimal Sine Triangulation (LOST) method has been proposed as a statistically optimal, non-iterative alternative [25]. The method reformulates the triangulation problem as an optimally weighted DLT, achieving the same error covariance as Hartley and Sturm’s approach for two measurements, while significantly reducing computational complexity, making it more suitable for scenarios involving multiple simultaneous observations . However, the weighting terms in LOST depend on the unknown ranges and in this case, it is suggested that calculating these ranges from any possible triangulation (even a random one) would yield the same localization performance. This assumption overlooks the strong dependence of triangulation accuracy on the geometric configuration between the observer and observed bodies. When poorly conditioned geometries are used for range calculations, the method may yield suboptimal estimates despite its theoretical optimality. This limitation in measurement pair selection presents an opportunity to enhance the algorithm’s performance through systematic optimization.
This study presents an improved methodology for triangulation localization that addresses the limitations in the LOST method. The proposed approach, called Improved-LOST, introduces a systematic method for evaluating and selecting optimal measurement pairs for initial range calculations in the LOST algorithm based on a Cramér–Rao Lower-Bound (CRLB) analysis, ensuring more reliable position estimates. While the LOST method suggests arbitrary selection of measurement pairs for unknown range calculations used in its weighting scheme, our analysis demonstrates that this selection significantly impacts the final estimation accuracy. The primary contributions of this work include (1) a comprehensive analysis of how geometric configurations influence triangulation accuracy, (2) the development of a CRLB-based metric for rating triangulation and LOST’s performance, and (3) an enhanced LOST algorithm that incorporates optimal measurement pair selection. Through theoretical analysis and numerical simulations, this study demonstrates that the proposed improvements yield more accurate position estimates compared to arbitrary measurement pair selection, particularly in scenarios with challenging geometric configurations which is very possible in interplanetary space missions. The improved method achieves enhanced estimation accuracy with computationally affordable additional steps.
The remainder of this paper is organized as follows. Section 2 describes the measurement model and error characteristics for celestial observations, followed by a detailed examination of triangulation principles and the LOST algorithm. The theoretical foundation for utilizing CRLB as a geometric performance metric and the proposed Improved-LOST algorithm are also presented in this section. Section 3 analyzes the relationship between geometric configurations and estimation accuracy, evaluates their effect on LOST’s performance, and presents simulation results demonstrating the effectiveness of the Improved-LOST method in realistic space navigation scenarios. The implications of the findings, practical implementation considerations, and potential directions for future research are discussed in Section 4.
2. Materials and Methods
2.1. Measurement and Error Model
Accurate position estimation based on celestial triangulation in interplanetary missions depends critically on the reliability of LoS measurements. These measurements form the foundation for triangulation. In an ideal scenario, without measurement errors, two LoS vectors would provide exact geometric constraints that yield a precise position determination. However, real-world measurements are subject to various error sources that affect the accuracy of the triangulation solution. LoS measurements are unit vectors pointing from the spacecraft towards the certain reference points of the observed objects. These vectors are susceptible to measurement errors and errors due to reference point calculations.
The measured LoS unit vector can be modeled as the sum of the true direction vector and the noise vector , ignoring other deterministic errors and only accounting for the noise.
The measurement error is assumed to follow a zero-mean Gaussian distribution
where the error covariance matrix with the Quest Measurement Model (QMM) [42] can be expressed using an isotropic direction uncertainty model
where represents the standard deviation of the pointing error in radians, and is the identity matrix. This formulation ensures that the noise covariance is orthogonal to the direction of the true LoS vector, preserving its unit length, i.e., both true and noisy LoS vectors are constrained to be unit vectors. The Gaussian noise model provides a robust basis for quantifying the impact of the errors on position estimates via celestial triangulation. This error model accounts for the following:
- The sensor noise in the optical measurements;
- Stochastic attitude determination uncertainties;
- Stochastic centroiding errors in detecting celestial body centers.
The model assumes that systematic errors such as sensor biases, misalignment of instruments, and temperature effects have been compensated and the instruments are properly calibrated, leaving only random measurement noise. This assumption is critical for the subsequent development of optimal triangulation methods.
2.2. Triangulation
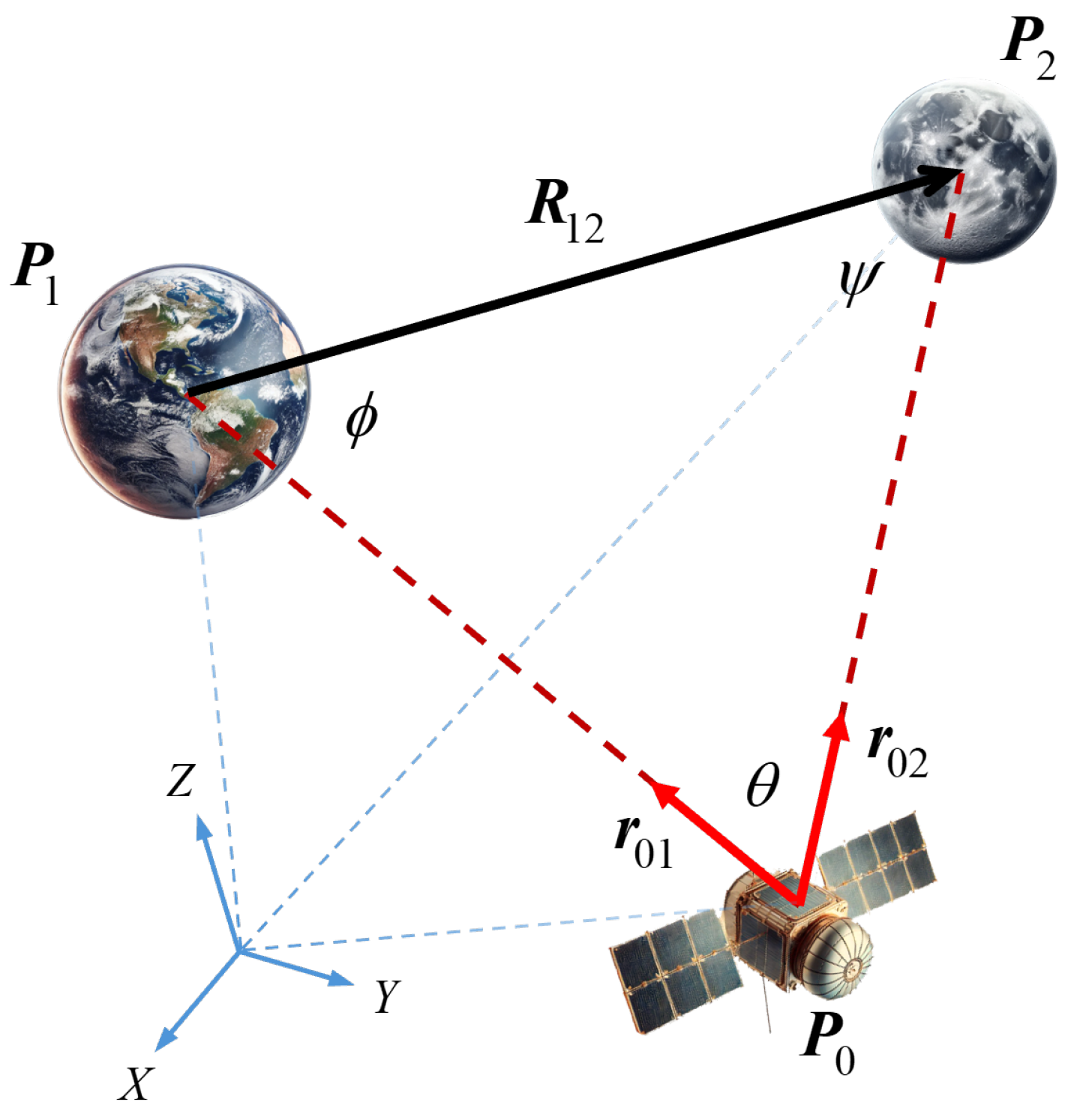
Triangulation is a fundamental geometric technique widely utilized in various disciplines, including spacecraft navigation. In this method, the spacecraft measures LoS unit vectors towards two celestial bodies whose positions are known. This represents a resection case of triangulation, where the positions of celestial bodies form the known vertices, and the spacecraft position is to be determined, as shown in Figure 1.
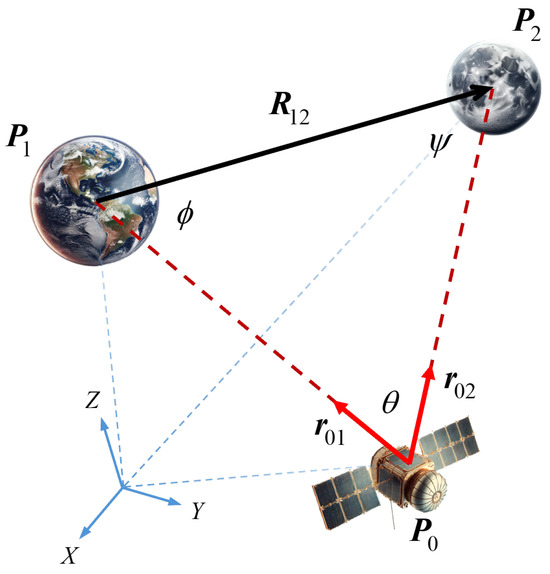
Figure 1.
Triangulation geometry for celestial navigation. The spacecraft at forms a triangle with two bodies at and , expressed in the inertial reference frame (ECI). represents the relative position vector between bodies, while and are line-of-sight (LoS) unit vectors from spacecraft to observed bodies. Interior angles , , and define the geometric configuration of the triangulation.
In celestial triangulation problem, the known quantities include the angular separations between celestial bodies observed from the spacecraft and their relative positions in a reference frame. Although the proposed methods are valid in any consistent reference frame, this study adopted the Earth-Centered Inertial (ECI) frame as the inertial reference frame. The spacecraft’s attitude, and consequently the camera orientations, was assumed to be known through star tracker measurements. This approach eliminates the need for direct range measurements, which are often infeasible or imprecise in long-range interplanetary missions. The solution to the triangulation is based on the principles of the law of sines, which relates the known angles and range to the unknown ranges. The unknown range , from the spacecraft at location to the first body at , can be calculated as:
where is the range between two bodies, and and are the interior angles at vertices and , respectively. The sine terms given in Equation (4) can be computed using cross products of the unit vectors:
where and are the unit LoS measurements towards first and second bodies, and is the unit direction vector from the first to the second body:
Finally, by combining these relations, the relative position vectors from the spacecraft to each celestial body are expressed as:
2.3. Mutliple (n > 2) Observations
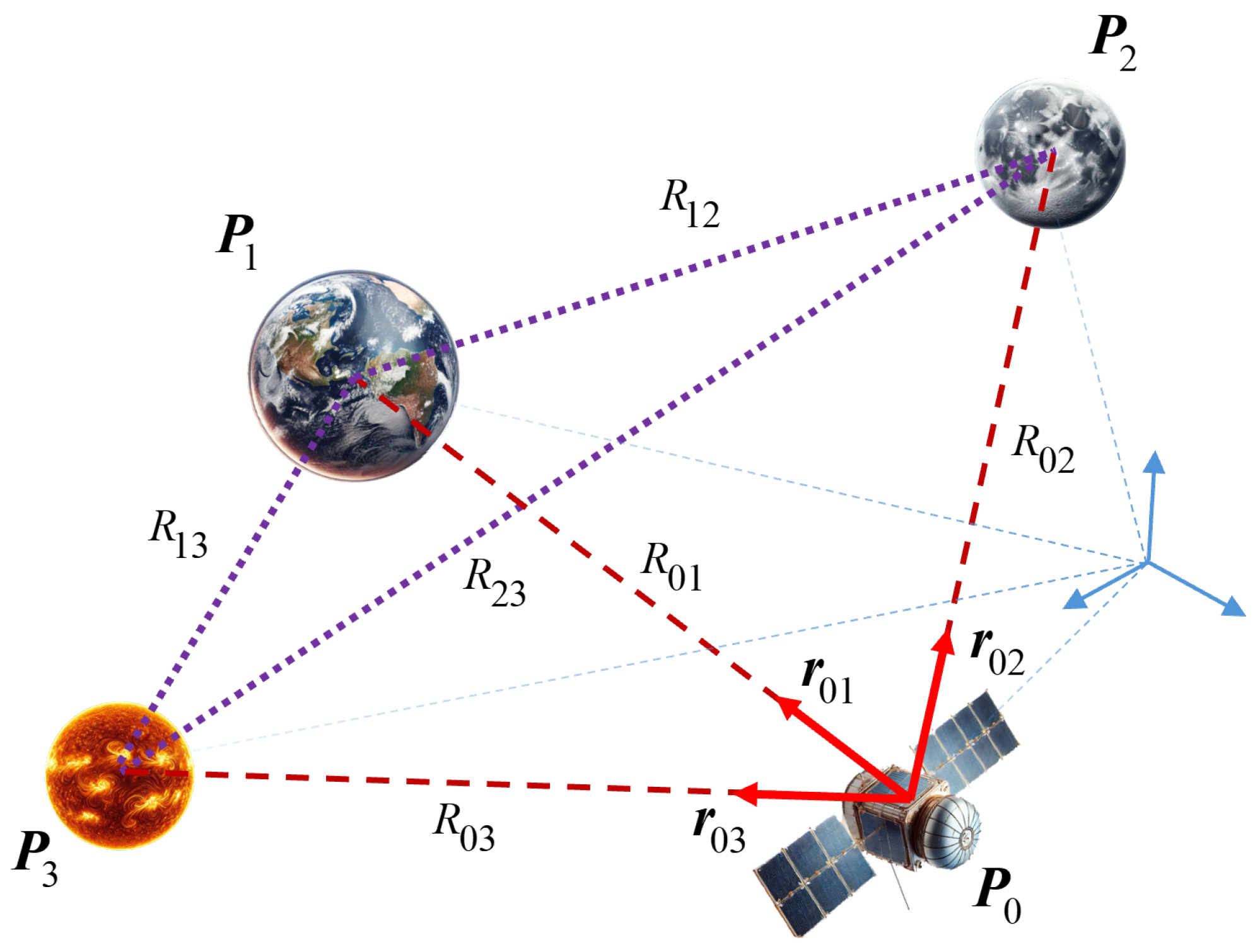
In the fields of photogrammetry and computer vision, utilizing multiple observations enhances the stability of the reconstruction process and mitigates the risk of unstable configurations that often arise when relying solely on two observations [31]. In particular, in the expanse of solar space, celestial bodies serve as critical reference points for spacecraft navigation. While basic triangulation utilizes observations of two celestial bodies, spacecraft are likely to have simultaneous visibility of more than two celestial bodies using multiple or wide-angle cameras and other sensors. This scenario presents an opportunity to enhance navigation accuracy. Each triangle provides an independent geometric constraint on the spacecraft’s location as illustrated in Figure 2, potentially leading to more robust and accurate position determination. The utilization of these multiple geometric constraints necessitates an optimal approach to combine the triangulation solutions effectively.
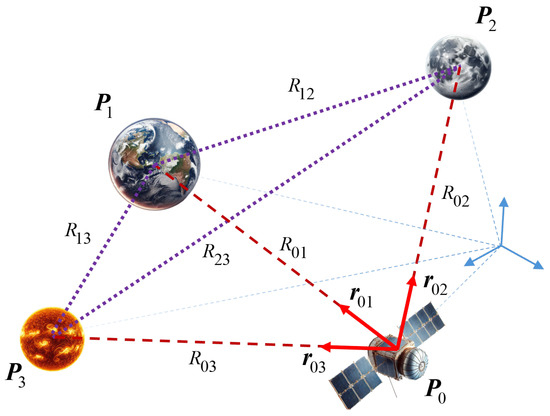
Figure 2.
Geometric configuration showing triangulation possibilities with observed celestial bodies. The ranges represent the known ranges between celestial bodies at and with respect to the inertial frame, while represent the unknown ranges from the spacecraft to each object.
There exist triangles in total, where of them are primary triangles at whose vertices is located the celestial body of interest. To calculate the range from the spacecraft to a celestial body of interest, any primary triangle formed with another body can be used, which can be formularized as:
where is the unknown position vector from the spacecraft to the body, is the known position vector from the to the celestial body, and , are the measured unit LoS vectors.
2.4. Linear Optimal Sine Triangulation (LOST) Method
Optimal triangulation methods aim to estimate an unknown location by minimizing errors associated with LoS measurements. Many popular approaches, such as conventional least-squares-based techniques or the DLT, are often not statistically optimal, as they fail to consider the covariance-weighted measurement residuals, leading to suboptimal results when compared to Maximum Likelihood Estimation (MLE) approaches [26]. MLE solutions, while statistically optimal, are often computationally demanding. For instance, in case of object observation, solving the MLE framework requires addressing a polynomial with 47 roots, making the process complex and resource-intensive [40].
In a recent study, Henry and Christian devised the LOST method [25], which offers statistically optimal solutions while addressing computational challenges associated with more than two observations through a non-iterative approach. The LOST method applies the law of sines twice to derive the cost function used for obtaining the MLE solution. The derivation begins first by identifying the residual in the noisy measurements, which originates from the errors in the LoS measurements.
The error covariance in the position calculations is defined as:
where the noise covariance is defined as:
The final form of the error covariance becomes:
The cost function for location to be minimized is:
After applying the first differential condition and equating the term to zero for the necessary condition, the following equation is obtained:
Finally, after applying QR factorization [25,43], the following system of equations are obtained.
The measurement error standard deviation , the unknown ranges , noisy measurements, and locations of the observed bodies with respect to any reference frame are stacked into the devised equation system for each observation, respectively. It can be solved by the least-squares method. To determine the unknown ranges, the law of sines is again applied between selected pairs of measurements.
The method’s primary contribution lies in applying the MLE framework to the DLT algorithm while utilizing the law of sines for measurement covariance determination. This approach acknowledges the fundamental importance of proper measurement weighting in estimation problems, a consideration that traces back to Fisher’s early work on statistical estimation methods [25].
2.5. Cramér–Rao Lower Bound as a Geometric Performance Metric
In the context of triangulation, the CRLB serves as a valuable tool for evaluating estimation accuracy, whether in basic two-body observation or multiple-body () observations, by quantifying how different measurement combinations and geometric configurations affect the estimation performance. When analyzing the LOST method’s approach of arbitrary range selection between celestial bodies, this method can reveal whether specific combinations of measurements yield solutions closer to the theoretical optimum or not. This theoretical framework becomes particularly relevant when considering that different geometric configurations between the spacecraft and observed celestial bodies can significantly impact estimation accuracy.
The CRLB is a fundamental concept in estimation theory that establishes the theoretical lower limit for the error variance of unbiased estimators, providing a measure of the maximum achievable accuracy of a system based on its known statistical properties. This bound is expressed through the inverse of the Fisher Information Matrix (FIM), which captures the sensitivity of measurement observations with respect to the parameters being estimated. The FIM quantifies this relationship through the expected curvature of the log-likelihood function, effectively measuring how much information the observable data contain about the unknown parameters. It is important to emphasize that the CRLB of the error variance is only valid in the case of unbiased estimators [44,45].
For the celestial triangulation problem, the measurement model consists of noisy LoS unit vectors , from the observation location to the ith body. For two-body observations, the CRLB implies that the covariance of an unbiased estimator is bounded by [44,45]:
The FIM, , is expressed through the expectation of the partial derivatives of the log-likelihood function:
The conditional density function for an observation follows a multivariate normal distribution:
where the error covariance matrix, , was previously defined in Equation (3). Since the measurements are independent, the joint likelihood function is obtained by multiplying their individual conditional density functions:
Then, the log-likelihood function becomes:
which can also be expressed by a simpler form as given in the following equation, which includes constant terms that disappear in the derivation process.
Using a denominator layout for the Jacobian vector/matrix, the partial derivatives are calculated as follows (a more detailed derivation is given in Appendix A):
Finally, the FIM, , is calculated to be:
The minimum limit for the error variance of the position estimation by two-body observation triangulation obtained by the CRLB becomes:
The factor 1/2 in the error variance expression in Equation (26) is introduced to compensate for the factor 1/2 used in the multivariate normal density function (Equation (20)). Multiplication of this factor with the trace of the inverse FIM ensures the correct mathematical relationship in the resulting CRLB for the error variance in the position estimation. The error variance in the position estimation for any unbiased estimator cannot be lower than this bound, making it an ideal metric for evaluating the potential performance of different triangulation configurations. Section 3.1 demonstrates how the position estimation error variance varies with different triangulation configuration for two-body observations.
The CRLB approach integrates the random measurement model described in Section 2.1, providing a bound on the error variance of position estimation for an unknown observer location. The CRLB-based performance metric can be extended to more than two simultaneous observations by incorporating the independent measurement contributions to the FIM, especially if there is a need to avoid comprehensive methods due to computational resource constraints in space missions. For n observed celestial bodies, the FIM becomes the sum of individual measurement contributions:
where each measurement’s contribution is appropriately weighted by its individual geometry and accuracy , allowing the justification of measurement accuracy differences. While the CRLB-based metric requires ranges, by using this method, we demonstrate how it optimizes the comprehensive LOST method (called as Improved-LOST) to obtain the optimal position estimation. The ranges calculated by the Improved-LOST method (or simply retrieved from the accompanying navigation filter) can then be used in the CRLB metric for multiple observation cases, enabling the selection of optimal observation pairs, triples, or larger sets to be used for navigation. This approach may help to alleviate the computational burden on onboard resources while maintaining estimation accuracy. The method provides a quantitative assessment of incremental accuracy improvements when introducing additional measurements, allowing the evaluation of whether selected configurations approach the theoretical accuracy bound or if supplementary observations would yield diminishing returns.
To contextualize our approach relative to existing work, it is worth examining how various studies in deep-space LoS navigation have employed different methods to evaluate beacon selection and estimate position accuracy. Broschart et al. [20] developed a geometric framework to assess spacecraft localization accuracy using LoS measurements from distant objects. Their approach constructed an information matrix from partial derivatives of angular observations, which, when inverted, yielded a position covariance matrix and a closed-form expression for estimation uncertainty with two observations. This formulation related the geometric configuration to achievable accuracy, providing a quantitative figure of merit where smaller covariance values indicated more favorable triangulation conditions. Franzese and Topputo [38] developed a figure of merit based on a covariance analysis that considered both the geometry matrix and input errors, defining optimal beacon selection criteria by minimizing the trace of the solution error covariance matrix. Their approach was scenario-dependent and incorporated both the angle between beacons and their relative geometry to determine which pair of visible beacons provided the smallest achievable error. Casini et al. [39] introduced a semi-analytical method for assessing geometric observability through information matrix analysis. By examining the eigenvalues and trace of the inverse covariance matrix, their approach quantified how geometric factors (such as de-phasing, separation angles, and inter-body distances) affected navigation performance. The CRLB-based figure of merit defined in Equations (25) and (26) differs from these approaches by establishing theoretical limits on estimation accuracy based on the FIM, though all methods fundamentally examine the covariance or error analysis.
The CRLB-based approach offers several advantages. It provides a theoretical lower bound on estimation error regardless of the specific estimation algorithm used, it has a clear theoretical foundation in estimation theory, and it can be readily extended to handle multiple observations through the FIM. Some existing methods provide closed-form solutions but are limited to two observations, and others emphasize angular separation through projection matrices; the CRLB-based approach quantifies the influence of both measurement noise characteristics and geometric configuration on achievable estimation accuracy. While some semi-analytical approaches incorporate dynamic evolution through state transition matrices but require more complex computation, the CRLB-based approach combines theoretical robustness with computational practicality by directly incorporating measurement noise characteristics and range-dependent scaling within a compact 3 × 3 inverse operation. Additionally, a remarkable advantage of this approach is that it enables the quantitative assessment of incremental accuracy improvements when introducing additional measurements, allowing the evaluation of whether selected beacon configurations approach the theoretical accuracy bound or if supplementary observations would yield diminishing returns. However, the CRLB approach has limitations as well. It assumes unbiased estimators and typically Gaussian measurement noise, which may not accurately reflect conditions when dealing with systematic errors. It requires prior knowledge of measurement noise statistics to be accurately computed, though this limitation is not unique to the CRLB-based approach.
2.6. Improved-LOST Algorithm
The LOST algorithm requires the calculation of unknown ranges for its implementation. While the method incorporates all available measurements in its final least-squares solution, the accuracy of the weights applied to these measurements depends critically on the initial range estimates. While the method suggests that any arbitrary selection of measurement pairs would yield similar performance, our analysis indicates that the selection of measurement pairs for range calculation may considerably impact the estimation accuracy, particularly with poorly conditioned geometric configurations. This section introduces a systematic approach for selecting optimal measurement pairs, leveraging the CRLB analysis to minimize error variance in position estimation. By identifying measurement pairs that contribute to the most reliable geometric configurations, the proposed method enhances the robustness and accuracy of triangulation localization.
The proposed methodology addresses a key limitation in the original LOST implementation. Rather than randomly selecting measurement pairs to calculate the unknown ranges that are the weighting terms of Equation (17), this approach evaluates the error variance of possible triangulation configurations using the CRLB analysis. By identifying the configurations that minimize the theoretical error bound, the method ensures that initial range calculations are optimally chosen for improved accuracy in the LOST algorithm.
The theoretical basis for this optimization approach stems from the relationship between triangulation geometry and estimation accuracy. When multiple celestial bodies are observed, each pair of observations forms a potential triangulation configuration with different geometric properties. The CRLB for each configuration provides a quantitative measure of the best achievable estimation accuracy under those geometric conditions. For a system with n observed celestial bodies, there exist possible triangulation configurations. Each configuration’s CRLB value given in Equation (26), derived from its FIM, represents the theoretical minimum variance achievable for position estimation using that specific pair of observations. Based on this theoretical foundation, the Algorithm 1 presents the step-by-step procedure for selecting optimal measurement pairs and calculating initial ranges based on CRLB minimization, leading to an Improved-LOST implementation.
| Algorithm 1: Improved-LOST |
|
The Improved-LOST algorithm systematically evaluates all possible triangulation configurations through the CRLB analysis, replacing the arbitrary selection process of the original method. By evaluating the CRLB values of triangulation configurations, the algorithm identifies the geometric arrangement that theoretically promises the lowest estimation error variance. This comprehensive evaluation ensures that initial ranges are calculated using the most favorable geometric configurations, leading to more accurate position estimates while maintaining computational efficiency of the LOST algorithm. The approach transforms what was previously an arbitrary choice into an optimized selection process grounded in estimation theory.
The Improved-LOST algorithm combines CRLB-based measurement selection with comprehensive utilization of all available measurements. It prevents performance degradation from additional measurements through two key approaches: selecting optimal geometric configurations for initial range calculations based on CRLB minimization and incorporating all available measurements in the statistically optimal weighted least-squares solution. This approach preserves the theoretical information gain from each added measurement while mitigating potential issues from ill-conditioned observations. As a result, the algorithm maximizes the benefit of all available observations without compromising estimation accuracy.
3. Results
3.1. Effect of Triangulation Geometry on Error Variance
Position estimation accuracy in triangulation exhibits significant sensitivity to the geometric configuration between the observer and observed bodies. This dependency manifests through two primary factors: the angular separation between LoS vectors and the relative distances to the observed bodies. To quantify these relationships systematically, a comprehensive analysis was conducted using the CRLB-based framework, evaluating theoretical error variances across various observation locations relative to two fixed reference objects.
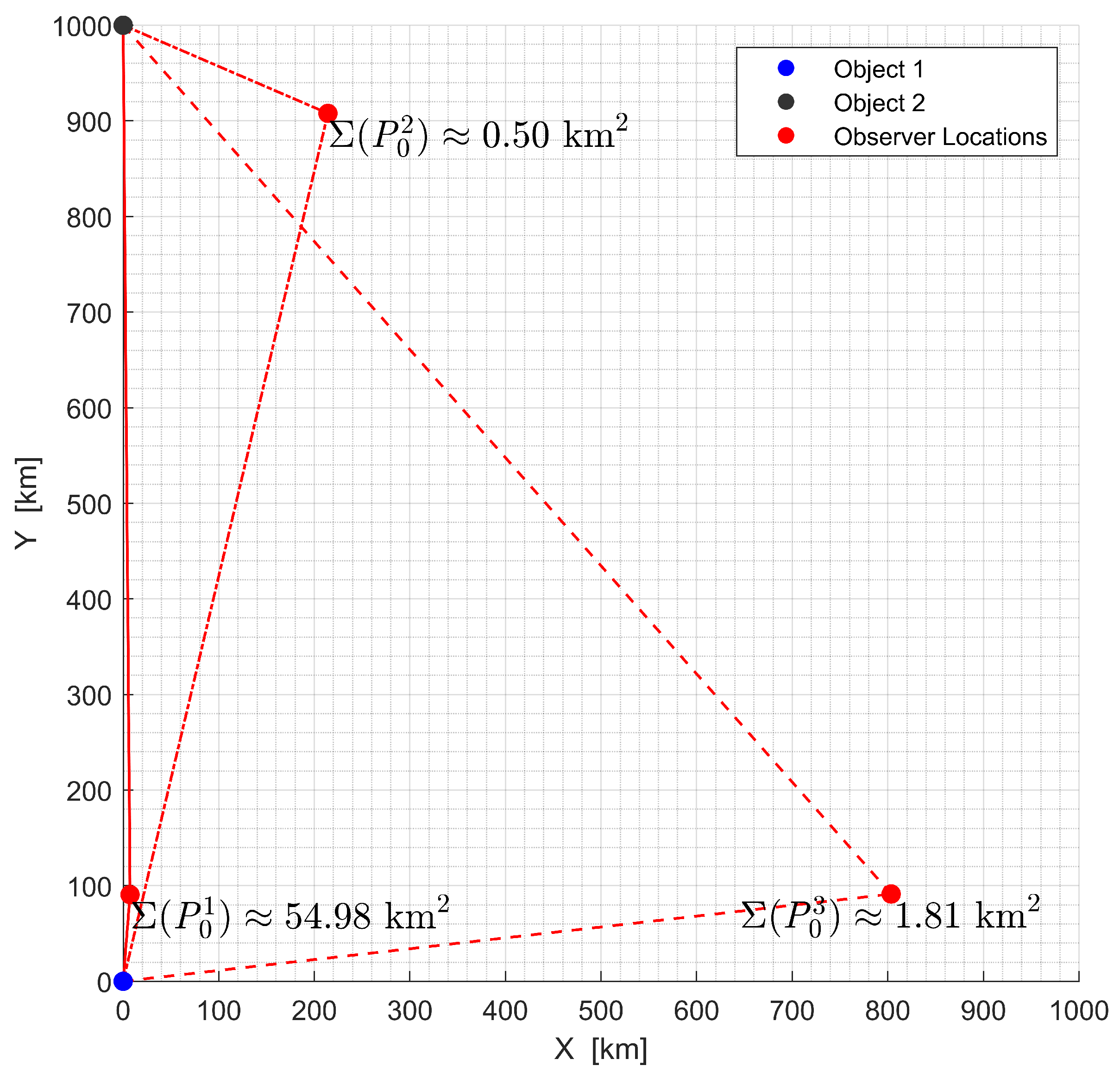
Figure 3 illustrates how the triangulation geometry affects the position estimation accuracy. In this analysis, two objects were positioned at given fixed locations. For simplicity and without loss of generality, it was assumed all the vertices of the triangles lay on the same plane (). The observer positions, marked in red as , , and , established three different geometric configurations with varying angles and distances relative to the reference objects. The analysis utilized LoS measurements with uniform standard deviations for measurement errors.
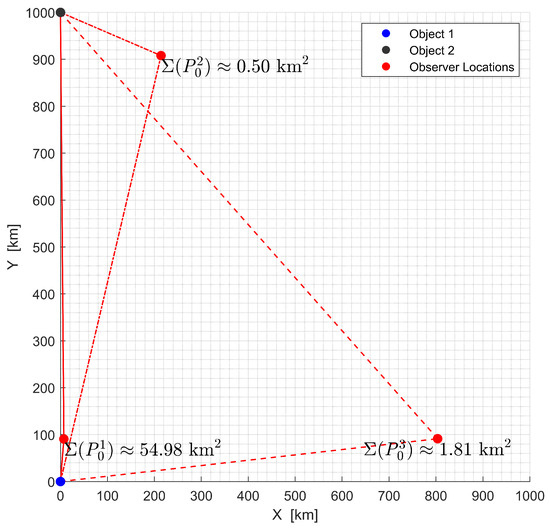
Figure 3.
Effect of triangulation geometry on position estimation error variance at different observer locations relative to two fixed objects.
The error variance at each observation point was computed using the CRLB-based metric derived in Section 2.5, which provides a theoretical limit on the estimation uncertainty. A comparison of the uncertainties of locations and revealed an important characteristic of triangulation geometry. For this example, the error variance at (54.98 km2) was larger by more than two orders of magnitude than at (0.5 km2), despite being positioned closer to both objects. This finding suggests that proximity to observed objects alone may not necessarily lead to improved estimation accuracy in all cases. The geometric configuration between the observer and the observed objects appears to have a significant influence on estimation performance.
These findings motivated a more comprehensive analysis of geometric configurations to identify optimal observation conditions. The analysis revealed that certain geometric arrangements consistently produced lower CRLB values, suggesting the existence of optimal observation regions that could be systematically identified and utilized for improved navigation accuracy.
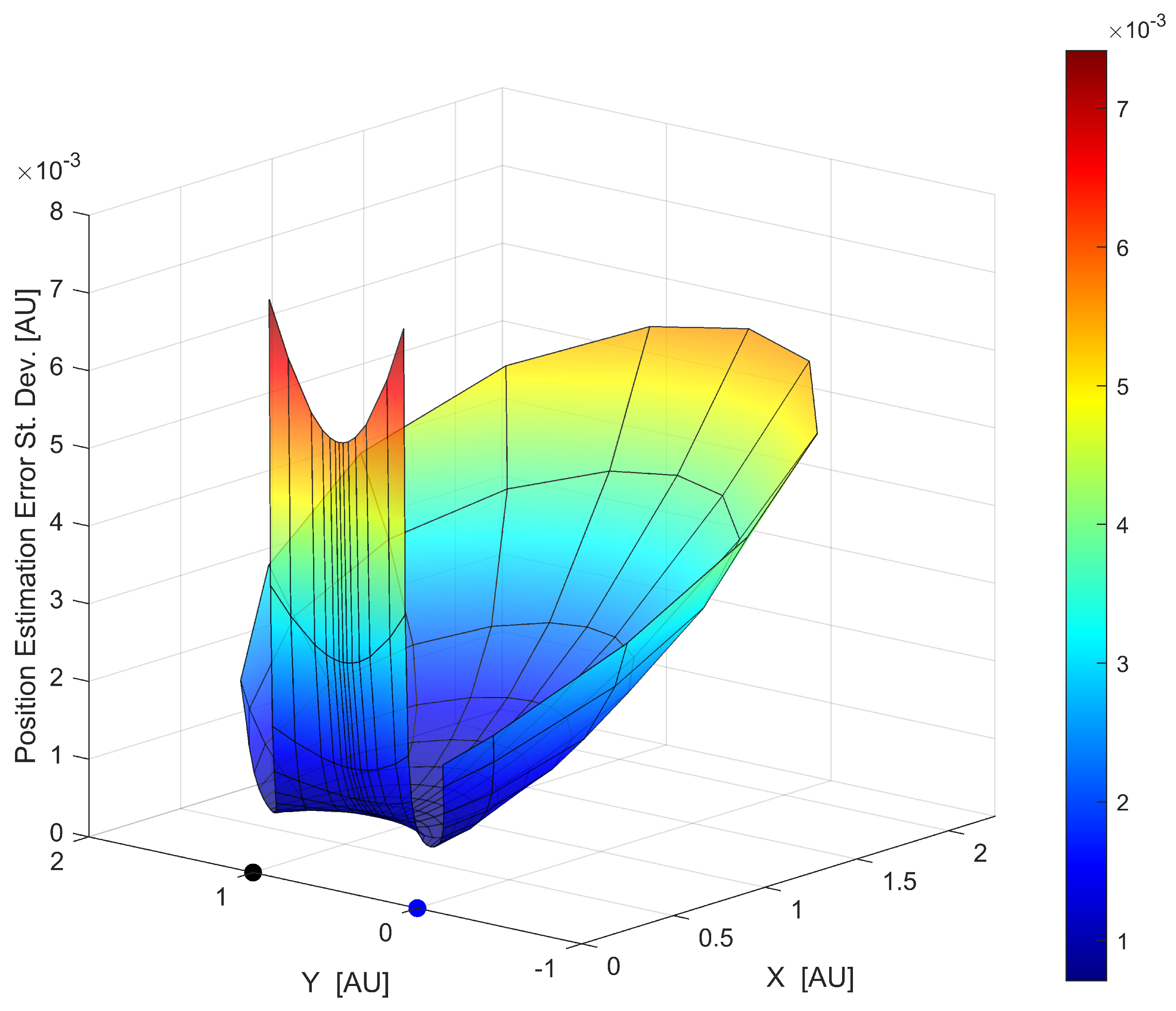
To further analyze the relationship between geometric configuration and estimation accuracy, a comprehensive evaluation was conducted across multiple observation points. Figure 4 and Figure 5 illustrate that analysis through different visualizations of the position error standard deviation distribution obtained by the CRLB analysis.
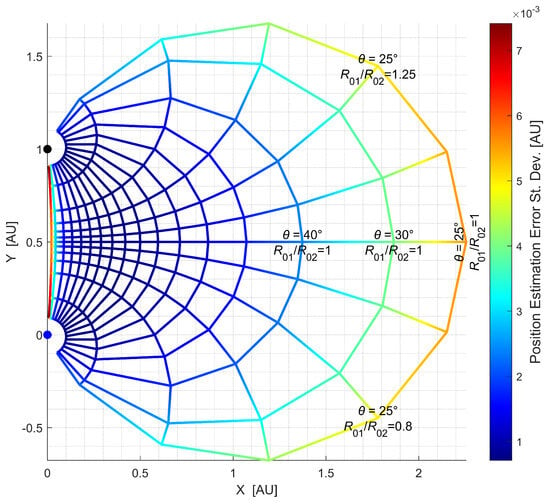
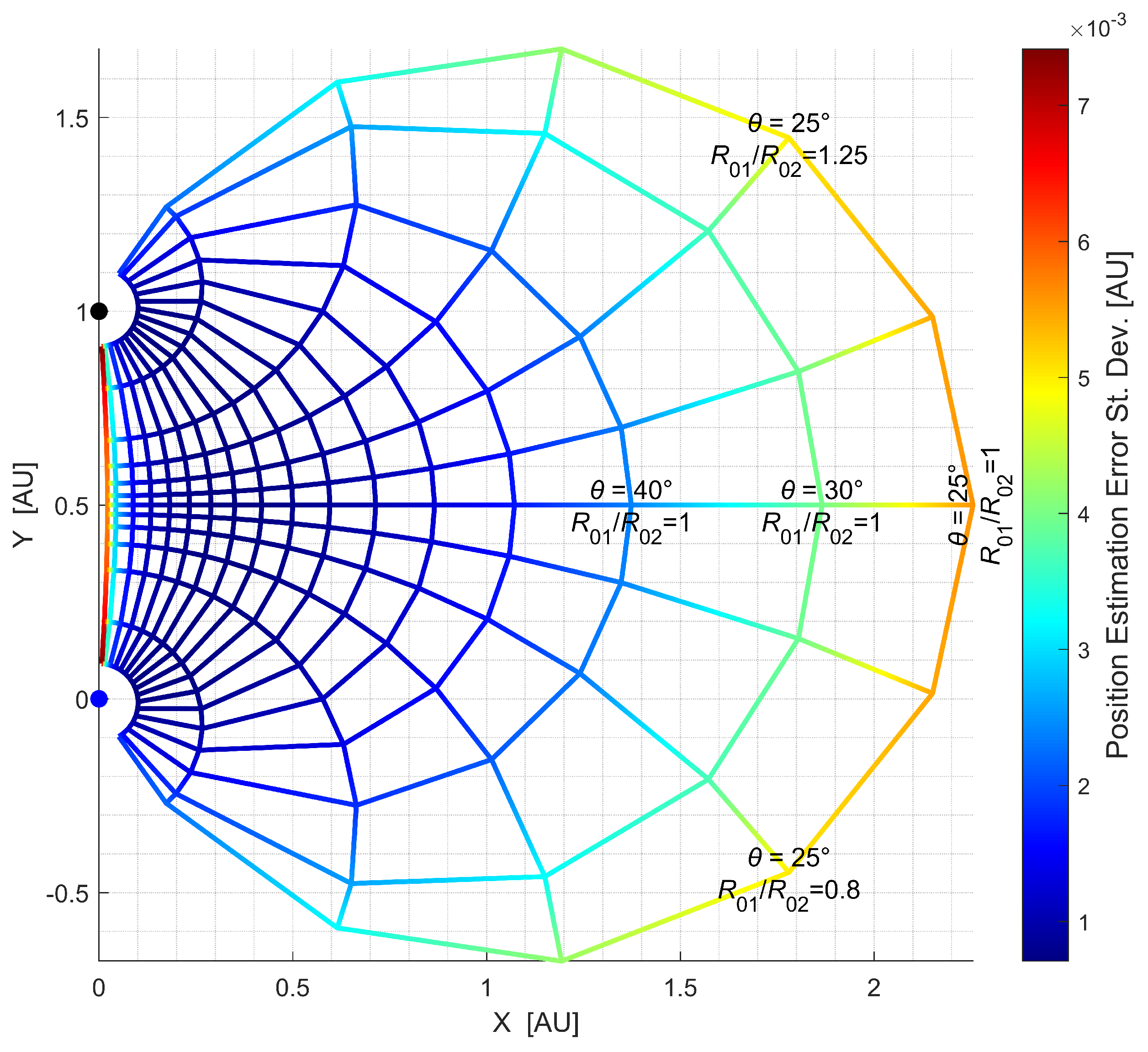
Figure 4.
Position estimation error standard deviation contour plot across different observation locations relative to two fixed objects.
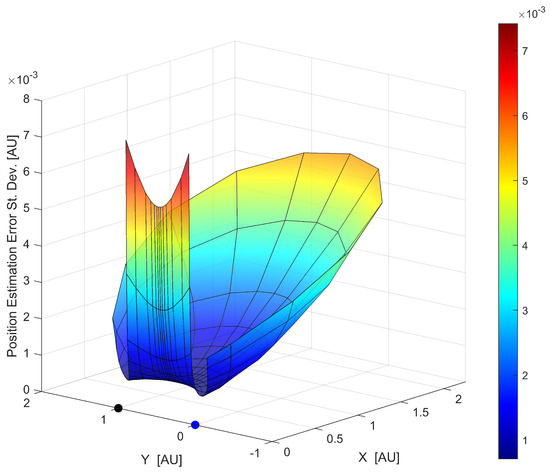
Figure 5.
Three-dimensional surface plot showing the position estimation error standard deviation across different observation locations relative to two fixed objects.
Figure 4 presents a contour plot displaying the position estimation error standard deviation distribution, computed as the square root of the CRLB values across different observation locations (as previously stated, for simplicity, the triangles were assumed to be in the same plane). The two reference objects were fixed at their positions on the Y-axis. The plot uses a color-coded mesh grid where each intersection point represents a potential observation location. The colors indicate the magnitude of the error variance according to the scale bar on the right. The grid lines help visualize how the error variance changes continuously across the observation space. The radial lines represent different observation angles between the two LoS vectors, ranging from 25° to 175° (regular 10° increments from 30° to 170°). The concentric arcs represent varying ratios of distances ranging from 0.1 to 10, i.e., varying and angles as shown in Figure 1.
Figure 5 provides a three-dimensional surface plot of the same error standard deviation distribution, offering additional insight into the magnitude of and variation in estimation uncertainty across different observation locations. The X and Y axes represent the spatial coordinates of potential observation points, while the Z-axis shows the corresponding error standard deviation.
The analysis revealed several key findings about the relationship between triangulation geometry and estimation accuracy. The error variance exhibited strong dependence on the angle between LoS vectors. Observations made at extremely acute or obtuse angles ( approaching 0° or 180°) generally resulted in higher error variances, while configurations near right angles tended to yield lower uncertainties. This result is consistent with prior findings in optical navigation, where the optimal position accuracy was achieved when the angular separation between LoS vectors was near 90°, as demonstrated by Broschart et al. [20] and further confirmed in double-planet scenarios by Casini et al. [39]. Mortari and Conway [46] similarly observed that error peaks occurred at observation points with unfavorable angular geometry, especially in scenarios with limited planet visibility or when observable celestial bodies had small angular separation. Andreis et al. [36] further reinforced this principle, emphasizing that triangulation accuracy deteriorated significantly when LoS vectors approached parallel alignment. The proposed CRLB-based analysis provided a quantitative framework that not only confirmed these geometric insights but also precisely quantified the error variances across different configurations. This aligns with findings from Franzese and Topputo [24,38], whose research demonstrated that optimal beacon selection strategies could reduce navigation error and standard deviation by at least an order of magnitude compared to non-optimized approaches. Our analysis demonstrated similar patterns of improvement. Additionally, the ratio of ranges from observer to the objects, , also influenced estimation accuracy, and its influence varied based on the angle, showing different trends for acute and obtuse angles.
The error variance distribution showed clear triangulation patterns, with certain regions consistently yielding lower uncertainties. This result suggested that optimal observation locations existed and could be identified through CRLB analysis. These findings challenged a key assumption of the LOST method, which suggests arbitrary selection of measurement pairs for unknown ranges. Our analysis showed that geometric configuration significantly impacted estimation accuracy in triangulation localization. This motivated the development of an improved selection strategy based on CRLB minimization, devised in the Section 2.6 and analyzed in the subsequent section. The error distribution maps established through that analysis provide a theoretical foundation for optimizing observation strategies in celestial navigation.
3.2. Effect of Triangulation Geometry on LOST Performance
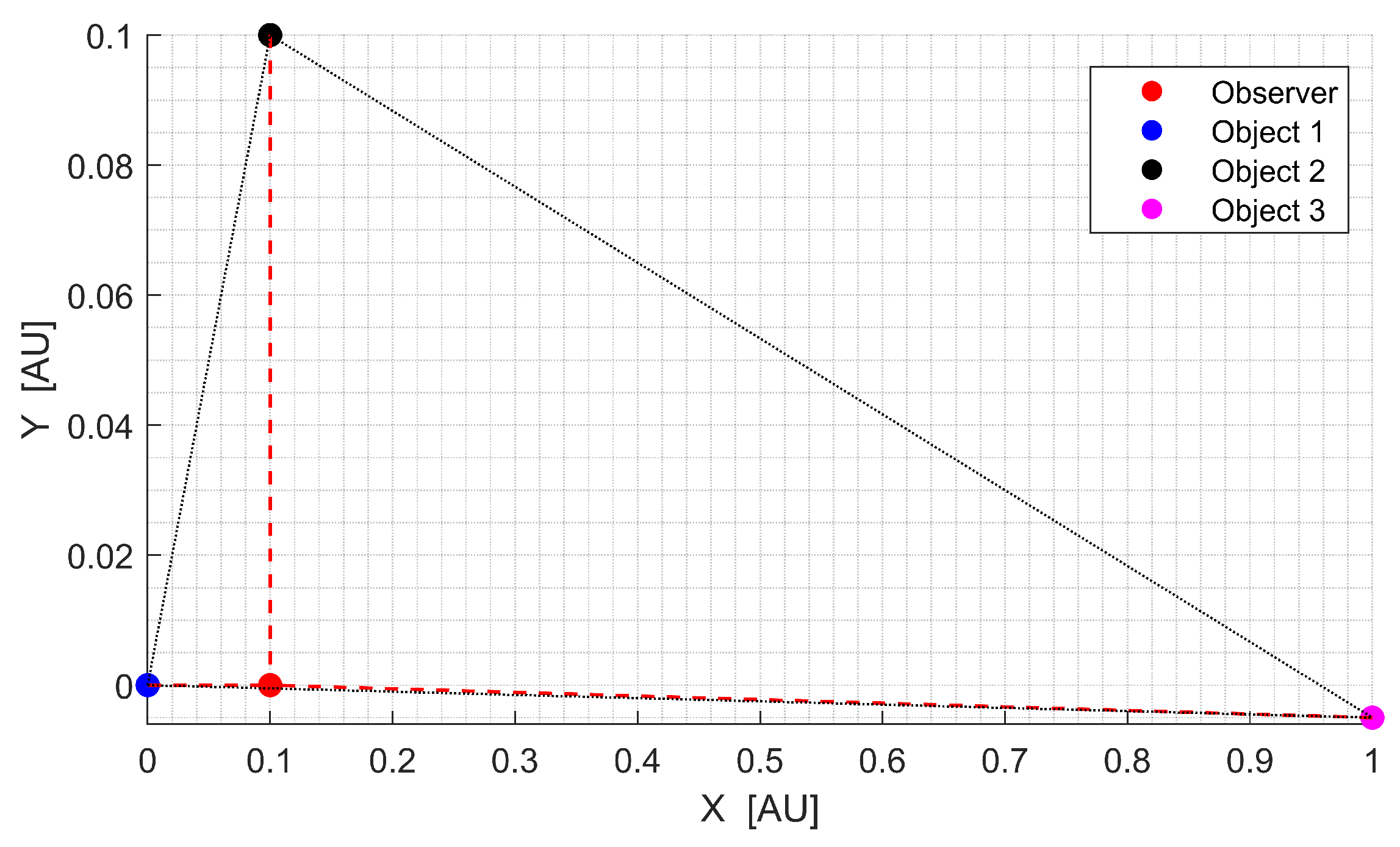
To investigate the impact of triangulation geometry on the LOST algorithm’s performance, an body observation scenario was analyzed, as shown in Figure 6. This example consisted of three observed objects forming three different triangles with varying geometric properties. Among these, two triangles exhibited favorable geometry with lower CRLB values, while one triangle showed poorly conditioned geometric triangulation configuration resulting in an increased CRLB value.
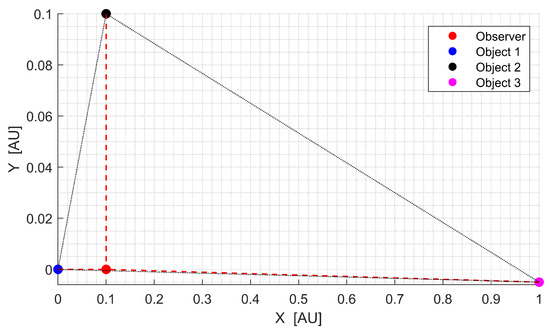
Figure 6.
LOST analysis for observations: spatial configuration for evaluating geometric conditioning effects.
The spatial configuration of the observer and observed objects noticeably influences the triangulation performance. In this example, the observer’s position was AU, while the three observed objects were located at AU, AU, and AU in an XY coordinate frame. This setup formed three distinct triangles, , , and , each exhibiting different geometric properties. This configuration, while somewhat simplified, approximated potential situations in interplanetary navigation where celestial bodies may be distributed at considerably different distances from the observer while still satisfying the visibility constraints.
While the ranges from the observer to each object, , , and , were of similar order of magnitude, the CRLB values for triangles , , and showed significant disparity. Triangle exhibited a substantially higher CRLB value compared to the other triangulations, indicating its geometric configuration was particularly susceptible to measurement errors. This geometric sensitivity becomes a crucial consideration when selecting which triangles to use for calculating the initial ranges required by the LOST algorithm.
The effect of the initial range selection on the performance of the LOST method was investigated through Monte Carlo simulations. Two different approaches for calculating the initial ranges were compared.
Case 1: the initial ranges were calculated using triangles with minimum CRLB values (Improved-LOST approach), prioritizing the use of triangles with favorable geometry.
Case 2: the initial ranges were calculated using triangles with maximum CRLB values (worst-case scenario) via LOST, intentionally incorporating ranges calculated from geometrically disadvantaged triangle configurations.
A comprehensive Monte Carlo analysis was conducted with 500 independent simulation runs. In each run, 10,000 noisy LoS vectors were generated according to the measurement error model described in Section 2.1, and the observation location was computed by using the LOST algorithm for both cases. The noisy vectors followed a zero-mean Gaussian distribution with standard deviation rad for each observation.
The Monte Carlo simulation results demonstrated a remarkable difference in performance between the two range calculation approaches. The Improved-LOST approach (Case 1) consistently outperformed the worst-case scenario with LOST (Case 2) across all evaluation metrics. The minimum position error variance increased by approximately 66.9% when using poorly conditioned triangles compared to the optimal selection. Similarly, the standard deviation of the position error increased by 29.2%, and the mean position error increased by 20.1%, rising from 14,437.7 km with the Improved-LOST method to 17,336.4 km in the worst-case scenario.
This performance difference demonstrates how triangle selection impacts estimation accuracy, even when using the same underlying algorithm. The magnitude of this impact varies with geometric configuration; more extreme geometric disparities would likely produce even larger performance differences. This finding suggests that the selection of triangles for initial range calculations in the LOST algorithm can significantly influence the final position estimation accuracy, even when the underlying algorithm remains unchanged. In scenarios with additional measurements, the performance disparity between methods could potentially increase, as additional measurements provide more opportunities for ranges to be calculated from ill-conditioned triangles. Additionally, as indicated by the CRLB formulations in Equations (25) and (26), the magnitude of these error variances scales with both the ranges of geometric configurations and measurement uncertainties, but the relative performance improvement from optimal triangle selection remains consistent across different measurement scenarios.
3.3. Celestial Triangulation Simulation
The performance of the Improved-LOST algorithm was evaluated through extensive numerical simulations using a translunar trajectory. The trajectory parameters were adopted from [47], with the spacecraft traveling from a 400 km Earth parking orbit to a 100 km polar lunar parking orbit. The simulation incorporated observations of three celestial bodies in two different examples to estimate the position of the spacecraft. The simulation spanned ∼1.16 days with a time step of s. At each time step, for each observed celestial body, 2000 noisy unit LoS vectors were generated according to the error model described in Section 2.1 with a standard deviation rad for each observation. To ensure statistical significance, the process was repeated with 200 runs, and the error variances for each step of the simulations were averaged. The two examples were as follows:
- Example 1: observed celestial bodies were the Earth, the Moon, and Jupiter;
- Example 2: observed celestial bodies were the Earth, the Moon, and Uranus.
At each example, two cases were analyzed:
- Case 1: initial ranges were calculated using triangles with minimum CRLB values (Improved-LOST);
- Case 2: initial ranges were calculated using triangles with maximum CRLB values (worst case LOST).
To focus on the performance analysis of the proposed algorithm, ideal observation conditions were assumed throughout the simulation, where all celestial bodies remained consistently visible to the spacecraft’s optical sensors. While this assumption simplified the analysis by eliminating visibility constraints that would occur in real mission scenarios, it allowed for a direct comparison of the triangulation performance between different geometric configurations.
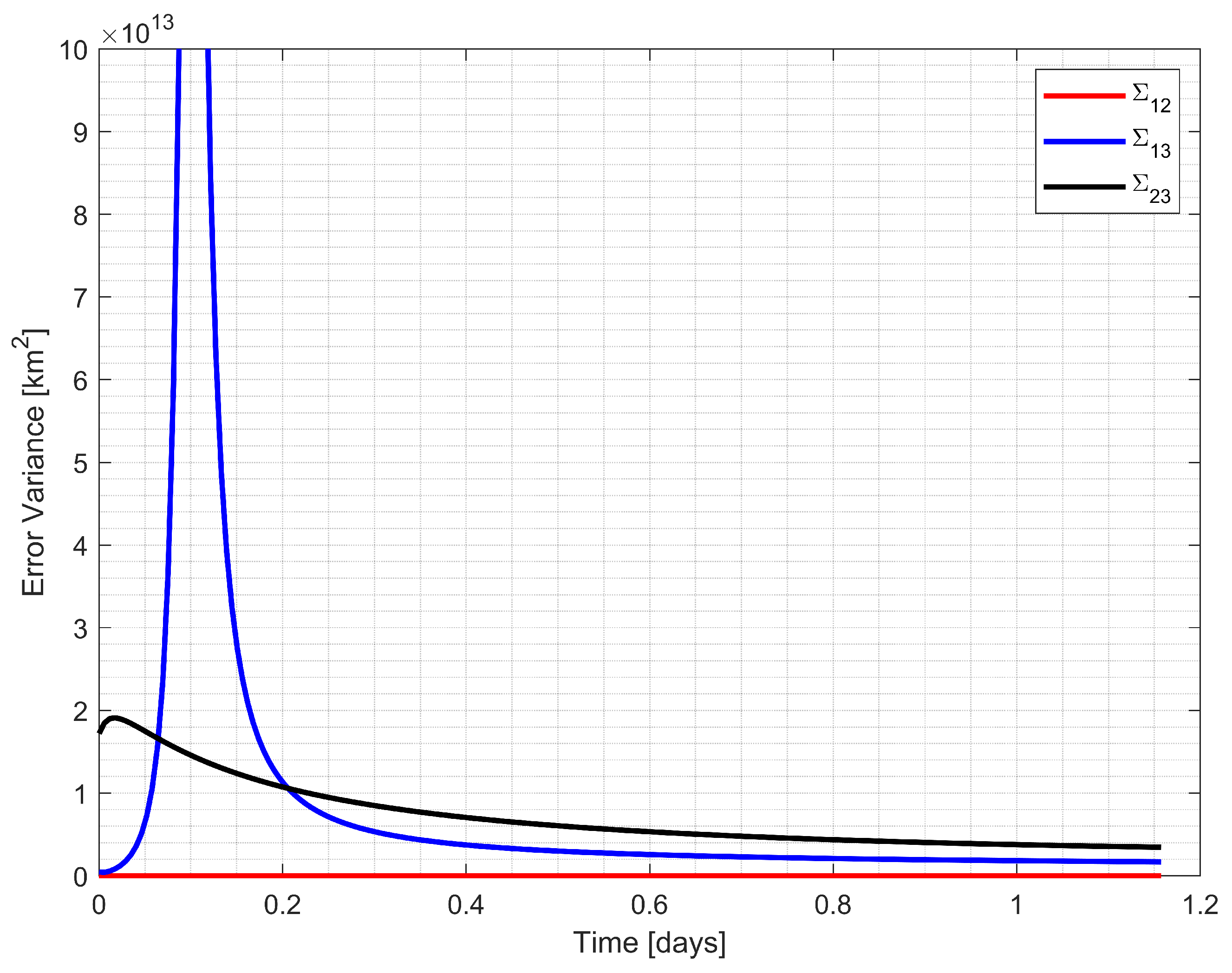
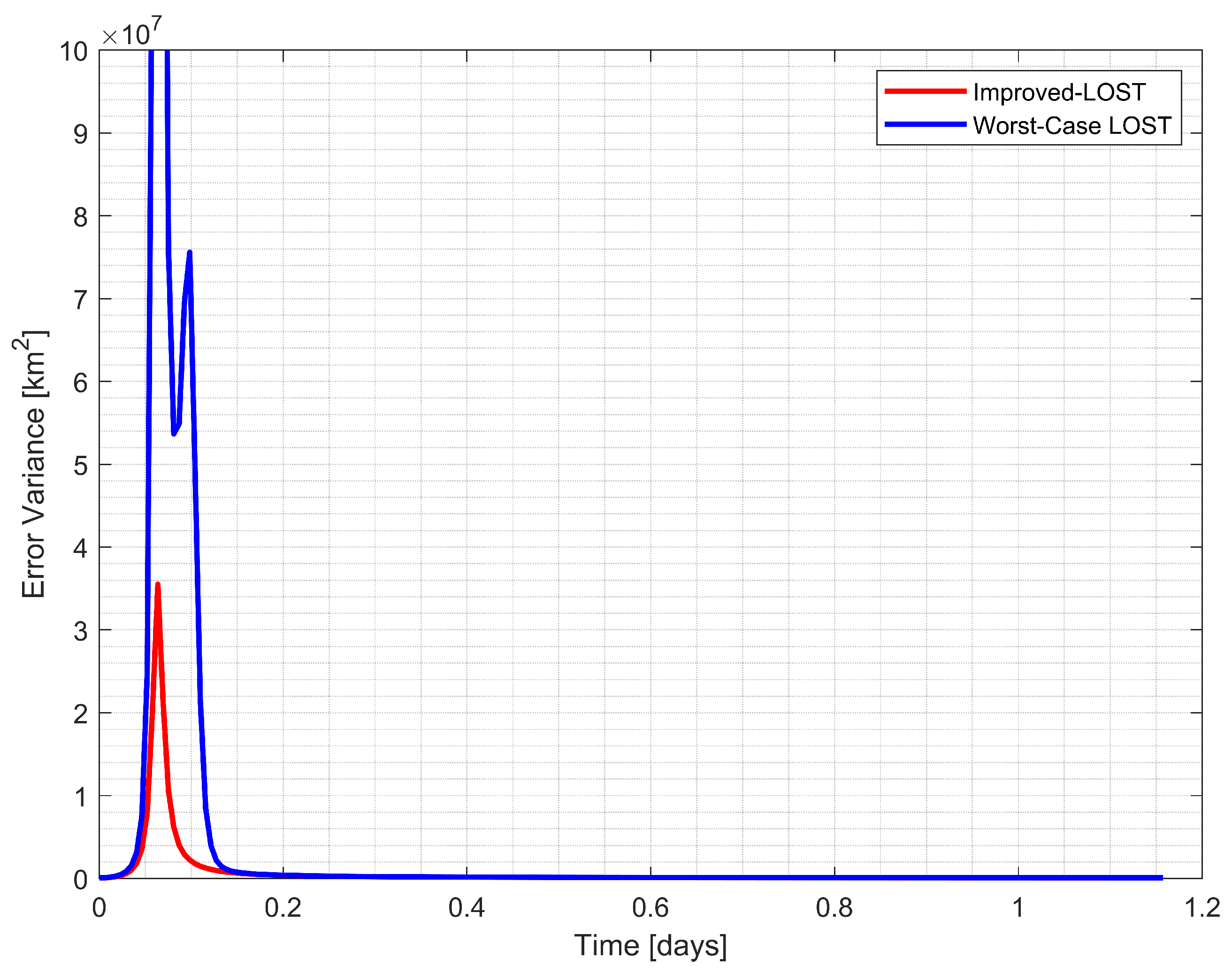
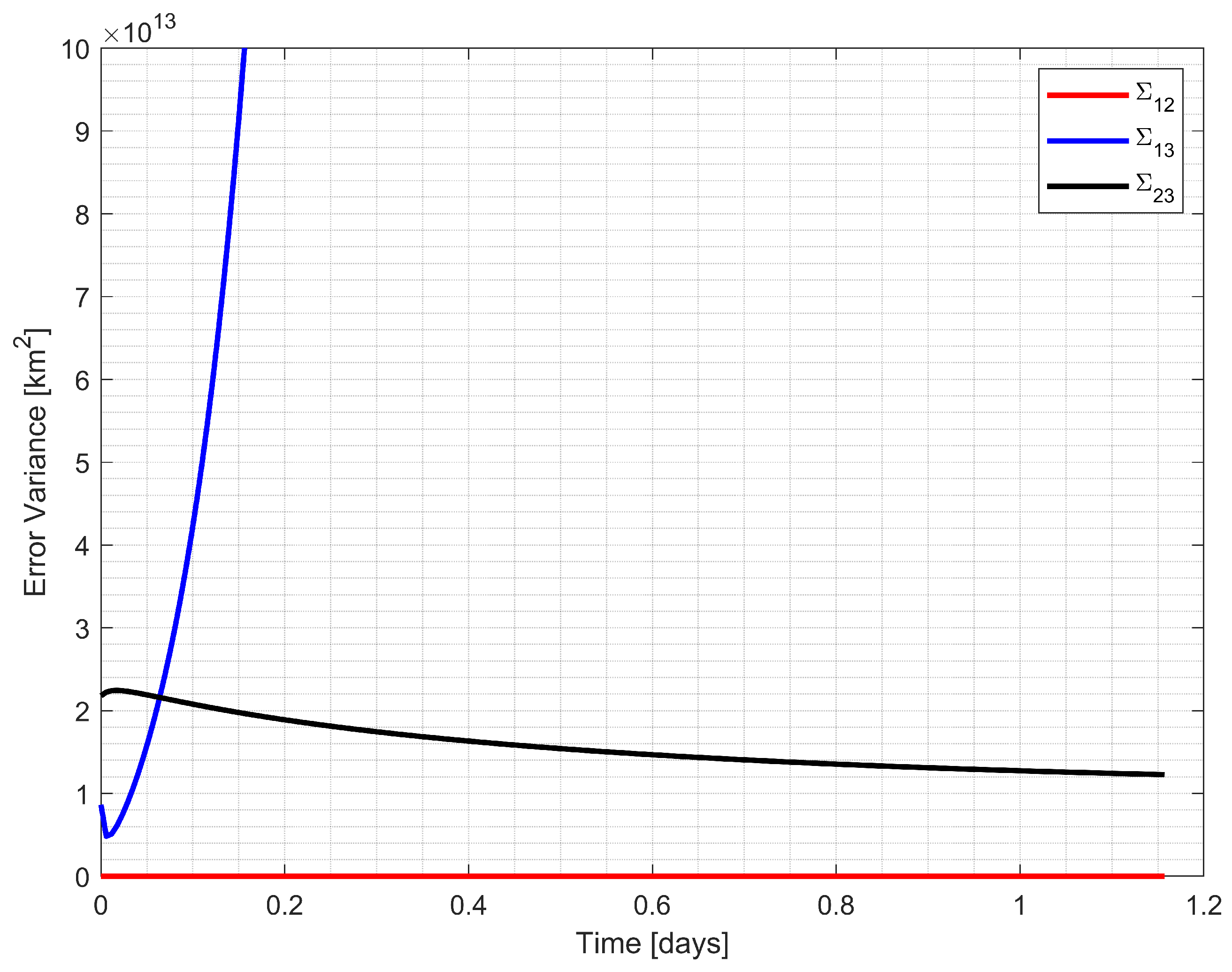
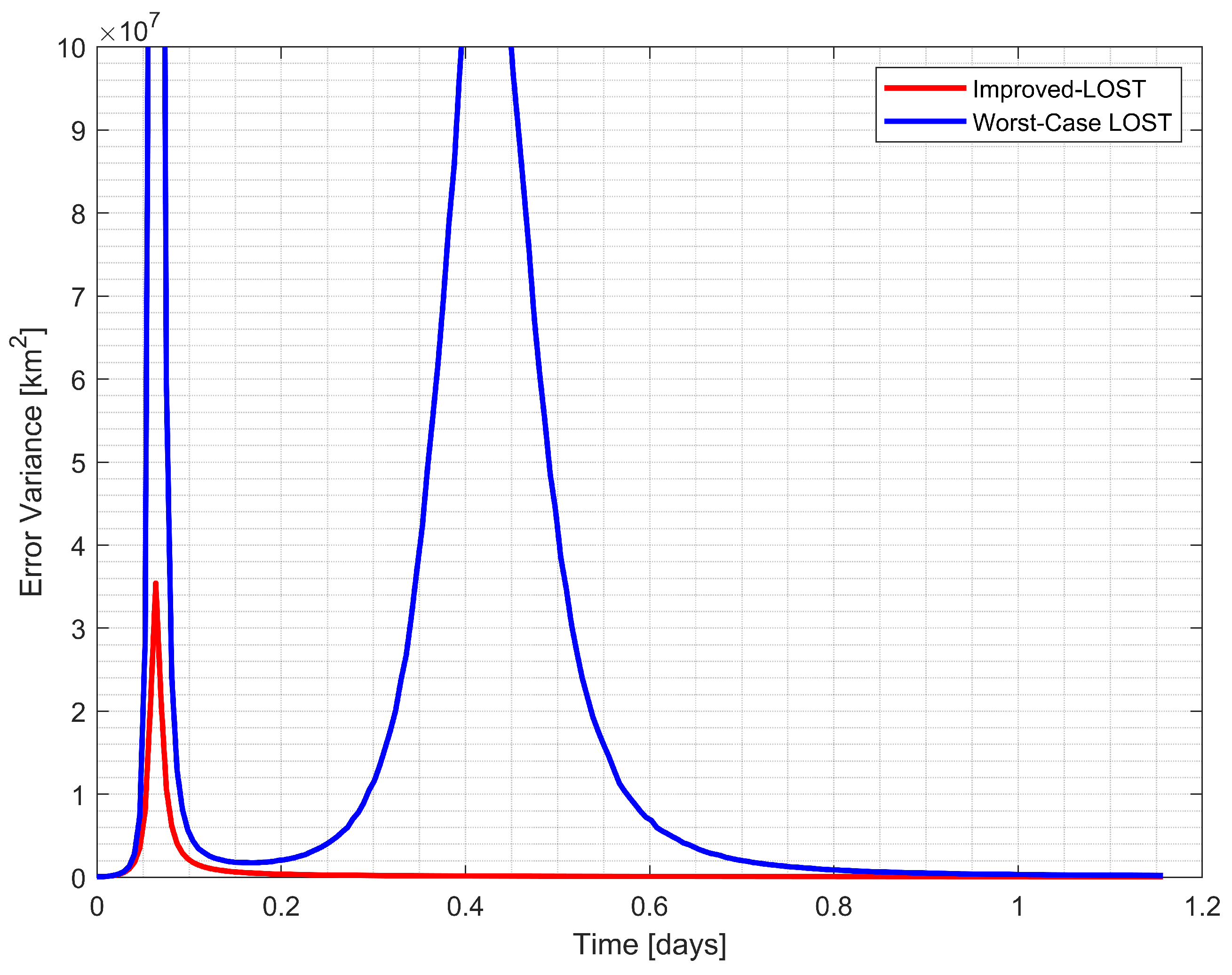
The simulation results are presented in Figure 7, Figure 8, Figure 9 and Figure 10. Figure 7 and Figure 9 illustrate the CRLB values for three possible triangulations, while Figure 8 and Figure 10 demonstrate the performance comparison between the Improved-LOST algorithm and the LOST method using ill-conditioned triangles for calculating the initial ranges, which were the weighting terms in the least-square solution of the LOST equation. Figure 7 and Figure 8 show the results for Example 1 (Earth–Moon–Jupiter observations), while Figure 9 and Figure 10 present the results for Example 2 (Earth–Moon–Uranus observations).
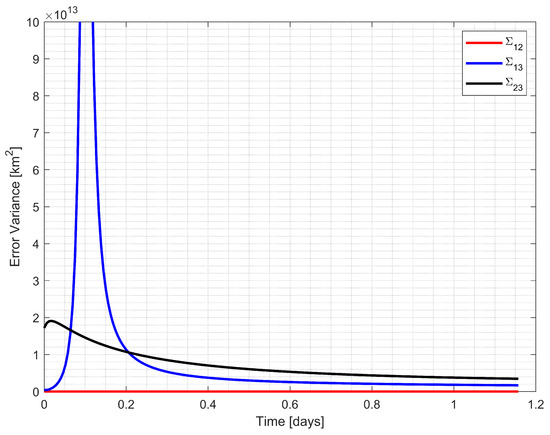
Figure 7.
CRLB values for three possible triangulation configurations using the Earth, the Moon, and Jupiter observations.
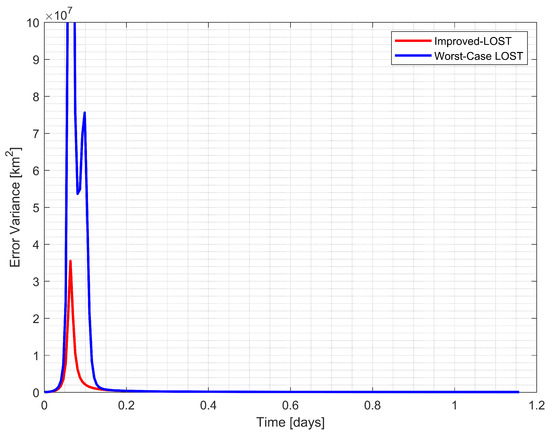
Figure 8.
Comparison of position estimation error variance between Improved-LOST and worst case scenario using the Earth, the Moon, and Jupiter observations.
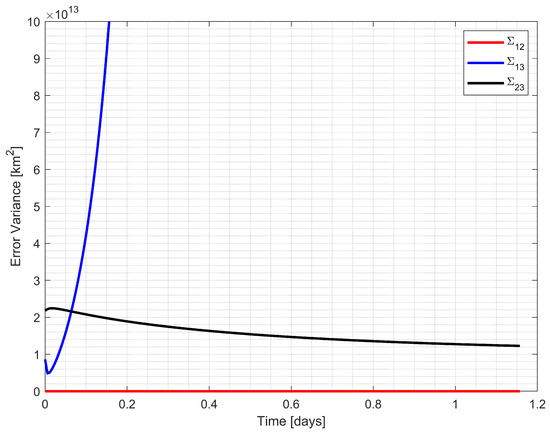
Figure 9.
CRLB values for three possible triangulation configurations using the Earth, the Moon, and Uranus observations.
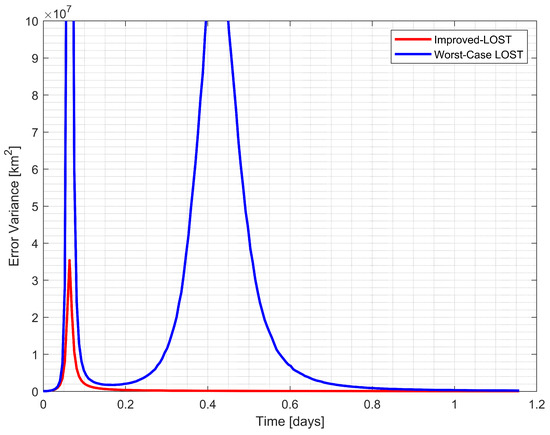
Figure 10.
Comparison of position estimation error variance between Improved-LOST and worst case scenario using the Earth, the Moon, and Uranus observations.
In Example 1, Figure 7 illustrates the CRLB values for three possible triangulations (, , and ) formed by the observed celestial bodies. The triangulation between spacecraft, the Earth, and the Moon () consistently demonstrated the lowest error variance throughout the trajectory, indicating the most favorable geometric configuration. Figure 8 compares the position estimation error variances between the Improved-LOST algorithm and the worst-case scenario with LOST. The Improved-LOST technique, which utilized the triangles with minimum CRLB values, maintained significantly lower error variances compared to the worst-case scenario, particularly during the initial phase of the trajectory where the error variance peaked.
Example 2 exhibited even more pronounced differences in performance. As shown in Figure 9, the CRLB values for different triangulations displayed greater disparity, with the spacecraft–Earth–Moon triangulation () again providing the most favorable configuration. Figure 10 reveals that the worst-case scenario produced substantially higher error variances, especially during the middle portion of the trajectory where a significant spike in error variance was observed. In contrast, the Improved-LOST algorithm maintained consistently low error variances throughout the simulation period.
These results demonstrate the critical importance of proper triangle selection in celestial navigation applications. The Improved-LOST algorithm’s systematic approach to selecting triangulations based on minimum CRLB values proved to be crucial for maintaining reliable position estimates. This is particularly significant in celestial navigation scenarios where various geometric configurations are possible, and poor triangle selection can lead to substantially degraded performance. The results emphasize that leaving the selection of triangles to chance could result in suboptimal navigation solutions, highlighting the necessity of a methodical approach to triangle selection as implemented in the Improved-LOST algorithm.
4. Discussion
4.1. Summary of Key Findings
The analysis of triangulation optimization revealed several significant findings. First, the geometric configuration between the observer and observed bodies substantially influences position estimation accuracy, with error variances varying by orders of magnitude depending on the observation geometry. This was demonstrated through a comprehensive CRLB analysis in Section 3.1, which showed that triangles with nearly right angles between LoS vectors typically yielded lower error variances compared to those with acute or obtuse angles. Notably, the analysis established that proximity to observed bodies did not necessarily correlate with improved estimation accuracy; instead, the relative geometric configuration proved to be the dominant factor in determining estimation performance.
A key contribution of this research was the development of a systematic method for evaluating and rating triangulation performance using the CRLB analysis introduced in Section 2.5. This approach provided a quantitative metric for assessing the potential accuracy of different geometric configurations before performing the position estimation. By computing CRLB values for all possible triangles formed by multiple celestial body observations, the method enabled the selection of optimal measurement pairs, leading to more reliable position estimates.
A notable limitation was identified in the LOST method regarding its range calculation approach. Despite its systematic MLE framework, the method’s assumption that arbitrary selection of measurement pairs would yield similar performance was found to be suboptimal, particularly in cases with extreme geometric configurations. The Monte Carlo simulations validated that the Improved-LOST algorithm consistently outperformed scenarios using suboptimal triangle selections with the classical LOST method, with more pronounced improvements in cases with greater disparity in CRLB values among possible triangulations.
4.2. Interpretation of Results and Comparison with Existing Methods
The observed relationship between triangulation geometry and estimation accuracy can be interpreted through both geometric and statistical perspectives. In the geometric context, when the LoS vectors are close to being either parallel or anti-parallel, the triangulation problem becomes ill-conditioned. This occurs because small measurement errors can lead to large variations in the estimated position.
From a statistical viewpoint, the CRLB analysis provides mathematical justification for these geometric observations. The FIM, which quantifies the amount of information each measurement configuration provides about the unknown position, becomes nearly singular for poor geometric configurations. This mathematical behavior manifests in the significantly higher CRLB values observed for such configurations, directly translating to increased estimation uncertainty. The analysis revealed that the information content of measurements was maximized when the geometric configuration allowed for optimal observability in all spatial directions.
Research on optimal beacon selection has explored various methodologies to identify favorable geometric configurations. Various studies [20,23,24,38,39] have focused on selecting the most advantageous subset of observations for navigation. These approaches typically develop figures of merit based on minimizing position solution covariance or error expressions, selecting the celestial body pairs that yield the smallest expected uncertainty region. A common finding across these studies is that carefully chosen pairs of celestial bodies can yield navigation accuracy comparable to using more beacons simultaneously. These studies also reveal that position accuracy can vary by orders of magnitude depending on the selection criteria, and that proper geometric configuration can effectively compensate for limitations in observation frequency or measurement quality. These selective methods offer advantages in computational simplicity and robustness against poor measurements, as they deliberately exclude unfavorable geometric configurations. However, they inherently disregard potentially useful information and redundancy, which may reduce robustness in dynamic environments where beacon visibility and geometry constantly evolve.
In comparison to these selective approaches, comprehensive methods such as least-squares, DLT, and other triangulation techniques aim to utilize all available measurements simultaneously. Rather than discarding potentially valuable information from additional observations, these methods incorporate all measurements into their solution framework. This approach maximizes information usage and provides natural redundancy, enhancing fault tolerance when one measurement is degraded or lost. However, without proper handling of measurement quality, this approach can potentially degrade accuracy when poorly conditioned observations are given equal weight to well-conditioned ones. The recently proposed LOST method addresses this limitation by implementing a statistically optimal weighting scheme that accounts for the varying quality of each observation. This approach bridges the gap between selective methods which prioritize only the most favorable measurement pairs, and traditional comprehensive methods, which incorporate all measurements without accounting for their relative quality. As a result, it maximizes the information content of the full observation set while reducing the influence of unfavorable geometric configurations. The choice between selective and comprehensive methods ultimately depends on mission-specific constraints such as computational resources, the variability of beacon geometry, and expected measurement quality. Selective methods may be preferable in resource-constrained missions where processing efficiency is critical, whereas comprehensive approaches like LOST provide greater robustness in scenarios where beacon visibility is unpredictable or measurement quality varies significantly.
While the LOST method provides a systematic approach through the MLE framework and least-squares solution of Equation (17), it faces a significant limitation. The coefficients in these equations depend on ranges that are themselves unknown variables. When the LOST method was proposed, it was suggested to calculate unknown ranges through triangulation using randomly selected pairs of measurements, with the assertion that any selection scheme would yield similar performance. However, this assumption of arbitrary range selection leaves a critical gap in the method’s optimization framework, potentially leading to suboptimal solutions in practice. The assertion that the choice of measurement pairs has negligible impact on the MLE solution cannot guarantee optimal performance, especially in cases where the geometric configuration plays a crucial role in measurement accuracy. This limitation presents an opportunity for improvement in the method’s implementation.
The varying performance of the LOST algorithm with different triangle selections can be attributed to the propagation of initial range estimation errors through the algorithm. When initial ranges are calculated using poorly conditioned triangles, the errors in these initial estimates affect the accuracy of the least-squares solution of Equation (17), despite the algorithm’s MLE framework. This finding explains why the original LOST method’s assumption about arbitrary triangle selection being equally valid does not hold in practice.
The translunar trajectory simulation results further reinforce these findings. The improved performance observed when using triangles with lower CRLB values stems from better initial range estimates propagating through the estimation process. The more pronounced improvement in the Earth–Moon–Uranus (Figure 7 and Figure 8) configuration compared to the Earth–Moon–Jupiter case (Figure 9 and Figure 10) can be attributed to the greater geometric diversity among possible triangulations in the former scenario. This suggests that the benefits of optimal triangle selection become more important as the geometric distribution of observed bodies becomes more extreme. The simulation examples using the Earth, the Moon, and the planets were deliberately selected to represent realistic deep-space navigation scenarios with geometric disparities. While the Earth and Moon consistently provided the most favorable geometry in our translunar example, the algorithm’s systematic framework remains valuable for missions where optimal configurations vary throughout the trajectory or where visibility constraints limit observation options. In practical applications, these findings may translate to significant advantages for autonomous space navigation systems, particularly during mission phases where communication delays prevent real-time Earth-based control. By systematically evaluating and selecting optimal triangulation configurations, the Improved-LOST method enhances position estimation reliability across various mission scenarios. This CRLB-based approach also provides mission planners with a quantitative tool to assess expected navigation performance along proposed trajectories, especially during critical phases such as orbital insertions and planetary approaches. The method’s capability to adaptively select optimal configurations becomes especially valuable as visibility and geometric conditions evolve throughout different mission phases.
4.3. Limitations and the Challenges
The Improved-LOST algorithm demonstrated enhanced performance in celestial triangulation, though several practical considerations deserve attention. One key aspect is the computational requirements of the method. For n observed celestial bodies, the algorithm computes and evaluates CRLB values for possible triangulations. This computational cost increases quadratically with the number of observed bodies. However, since this calculation is performed only once per position estimation cycle and modern spacecraft computers have significant processing capabilities, the computational overhead remains manageable for typical applications with three to five celestial body observations.
Implementation considerations arise from the study’s assumptions about observational conditions. The analysis presented in this work was based on ideal visibility of multiple () celestial bodies throughout a trajectory. In actual mission scenarios, several environmental factors may influence celestial body visibility, such as solar glare, occultation effects, limited sensor field of view, and operational constraints of optical sensors. These factors would need to be incorporated into the mission planning phase when implementing the algorithm. Despite these practical limitations, the CRLB-based evaluation remains effective with varying numbers of observations. Although the derived CRLB metric is specifically formulated for the two-observation case, it can be used for multiple observations. Even with just a single visible celestial body, the method can provide valuable metrics for selecting optimal bodies to track when integrated with dynamic estimators. With two or more observations, it enables the assessment of potential estimation uncertainty, facilitating informed decision-making about the reliability of position estimates. The CRLB analysis can also quantify the potential accuracy improvements gained by increasing the number of tracked celestial bodies, helping optimize resource allocation in onboard systems. Moreover, the Improved-LOST technique operates under the same foundational assumptions as the original LOST method, maintaining its core functionality while enhancing performance through optimized observation selection for initial range calculations.
Despite these practical limitations, the CRLB-based evaluation remains effective even with minimal observations (). Even with just two visible observables, the method provides valuable metrics for assessing potential estimation uncertainty, enabling informed decision-making about the reliability of position estimates. Moreover, the Improved-LOST technique operates under the same foundational assumptions as the original LOST method, maintaining its core functionality while enhancing performance through optimized triangle selection for initial range calculations.
The method’s dependence on ephemeris data represents another important consideration. Position estimation accuracy correlates with the precision of celestial body position data used in the calculations. Contemporary ephemeris databases, such as the JPL Development Ephemerides DE440/441 [48], offer remarkable accuracy for celestial body positions. The lunar orbit is known to submeter accuracy through lunar laser ranging data, while inner planet orbits are determined to subkilometer accuracy using radio-tracking measurements from orbiting spacecraft. For outer planets like Jupiter and Saturn, position accuracy is in the range of tens of kilometers [49]. Various other factors also affect the final precision of the position estimation, with their significance varying by condition. While planetary ephemeris uncertainties become significant only near celestial bodies, other factors such as light aberration and light’s time of flight affect the position estimation precision, particularly for distant bodies. These effects have been extensively analyzed in previous literature [19,36] and can be appropriately addressed within the LOST framework [26].
4.4. Recommendations for Future Work
Future research directions emerge from both theoretical foundations and practical considerations in celestial navigation. Four primary areas warrant further investigation.
First, computational optimization of the algorithm deserves attention. While the current implementation’s computational requirements remain manageable for typical applications with three to five celestial bodies, scenarios involving more frequent position updates or limited computational resources could benefit from enhanced efficiency. This could enable real-time implementation in resource-constrained environments or scenarios requiring high-frequency navigation updates.
Second, the application of triangulation algorithms to use other objects for navigation scenarios presents another research direction. Future studies could investigate navigation using small celestial bodies such as asteroids or artificial satellites, where geometric configurations evolve more rapidly and unpredictably compared to planetary bodies. These investigations would need to address challenges such as irregular body shapes, uncertain ephemerides, and rapidly changing observation geometries. Research in this area could be particularly relevant for future asteroid exploration missions or space debris tracking applications.
Third, analysis of varying measurement uncertainties across different celestial bodies offers another direction for investigation. It could be examined how measurement uncertainties vary based on physical characteristics (size, albedo, atmospheric effects), observer–target distance, and environmental conditions affecting sensor performance. For instance, observations of planets with atmospheres might exhibit different error characteristics, while measurements of asteroids could be affected by irregular shape and variable albedo. These factors could enhance position estimation accuracy in diverse navigation scenarios.
Fourth, mission trajectory optimization based on CRLB-based metrics presents another research direction with potential cost-saving benefits. The CRLB-based figure of merit could be integrated into trajectory design algorithms to identify paths that maintain favorable geometric configurations throughout the mission. This approach could help balance traditional optimization criteria such as fuel efficiency and time constraints with navigation accuracy requirements. This could enable the use of simpler, less expensive sensors like optical cameras instead of more costly navigation instruments. Such integration could lead to more robust and cost-effective mission designs that ensure reliable position estimation throughout critical mission phases while reducing overall mission costs.
5. Conclusions
This study presented the Improved-LOST methodology for celestial triangulation optimization, addressing limitations in existing approaches. The research demonstrated that geometric configuration significantly influenced position estimation accuracy in celestial triangulation, with error variances varying by orders of magnitude depending on observation geometry. The proposed Improved-LOST algorithm, which incorporates CRLB-based triangle selection, consistently outperformed conventional implementations in simulation studies. Key findings revealed that proximity to observed celestial bodies did not necessarily correlate with improved estimation accuracy. Instead, the relative geometric configuration between the observer and observed objects proved to be the dominant factor in determining estimation performance. The systematic CRLB-based evaluation method developed in this study provides a quantitative metric for assessing potential estimation accuracy before performing position calculations. Notably, this metric remains valuable even in scenarios with minimal observations (), offering insights into position uncertainty.
Author Contributions
Conceptualization, methodology, validation, investigation, and writing—original draft preparation, A.M.; review and editing, supervision, H.E.S. and U.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available within the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
A. Muratoglu thanks TUBITAK 2214-A International Doctoral Research Fellowship Programme for supporting his researches at Institute for Photogrammetry and Geoinformatics, University of Stuttgart. He also thanks Michael Cramer for his valuable conversations about photogrammetric techniques. This work was carried out as a part of the Ph.D. thesis in Aerospace Engineering at Middle East Technical University by A. Muratoglu under the supervision of H. E. Söken.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| QMM | Quest Measurement Model |
| LoS | Line-of-sight |
| DLT | Direct Linear Transform |
| MLE | Maximum Likelihood Estimation |
| LOST | Linear Optimal Sine Triangulation |
| CRLB | Cramér–Rao Lower Bound |
| FIM | Fisher Information Matrix |
Nomenclature
The following symbols and operators are used in this manuscript:
| True LoS unit vector | |
| Noisy LoS unit vector | |
| Noise vector | |
| Error covariance matrix with QMM model | |
| Standard deviation of the pointing error | |
| Position vector of the observer with respect to the inertial frame | |
| Position vector of ith body with respect to the inertial frame | |
| Noisy unit LoS measurement from observer to the ith body | |
| Position vector from observer to ith body | |
| Range between observer and ith body | |
| Position vector from ith to jth body | |
| Noise vector in the LoS measurement | |
| Residual vector due to noise in the position calculation of | |
| Error covariance matrix of the residual vector | |
| Error covariance matrix of the noise vector, | |
| Error variance of position estimation computed from | |
| Triangle formed by -- at vertices | |
| Skew-symmetric matrix | |
| Expectation | |
| Probability density function | |
| Likelihood function |
Appendix A. Derivations
Derivation of Fisher Information Matrix for Two-Body Observation
In this section, the FIM for a two-body observation is derived to assess the theoretical lower bound of estimation errors in celestial triangulation. The derivation follows the classical Fisher Information approach, where the sensitivity of the log-likelihood function with respect to the estimated parameters is analyzed. The FIM, , is given in Equation (19). The given in Equation (22) represents the log-likelihood function of the observed noisy LoS vector, , conditioned on the true observation location .
To compute the FIM, the derivative of the log-likelihood function with respect to the spacecraft position, is required. Using the denominator layout for the Jacobian vector/matrix, this derivative can be expressed as:
where is the measurement noise in the LoS vector.
The partial derivation of the log-likelihood function with respect to is:
where represents the error covariance matrix of the LoS measurements. Using the geometric relationship between the spacecraft and the observed body, the unit LoS vector can be expressed as:
where is the position vector of the observed ith body. Taking the derivative of with respect to , we obtain:
Thus, the derivative of the noise term with respect to becomes:
Finally, substituting Equations (A3) and (A6) into Equation (A1), we obtain:
The FIM, , can now be computed as:
Since the observations are independent, covariance matrices for cross-measurement terms are zero.
By expanding the expectation operator and using the properties of the error covariance matrix, we arrive at the final expression for the FIM, given in the following equation:
This result provides a fundamental lower bound on the achievable accuracy of position estimation using two-body observations. The inverse of the FIM represents the CRLB, which quantifies the minimum attainable error covariance for an unbiased estimator.
This derivation plays a crucial role in understanding the limitations of the triangulation approach and serves as a benchmark for assessing the optimality of different triangulation methods. The implications of this result for multi-body observations and triangulation optimization techniques are further discussed in the main text.
References
- Wood, L.J.; Bhaskaran, S.; Border, J.S.; Byrnes, D.V.; Cangahuala, L.A.; Ely, T.A.; Folkner, W.M.; Naudet, C.J.; Owen, W.M.; Riedel, J.E.; et al. Navigation and Mission Design Technologies for Future Planetary Science Missions. In Advances in the Astronautical Sciences, Proceedings of the Guidance and Control 2013, American Astronautical Society, Breckenridge, CO, USA, 1–6 February 2013; Univelt: San Diego, CA, USA, 2013; Volume 149, pp. 577–597. [Google Scholar]
- Hesch, J.A.; Kottas, D.G.; Bowman, S.L.; Roumeliotis, S.I. Consistency analysis and improvement of vision-aided inertial navigation. IEEE Trans. Robot. 2013, 30, 158–176. [Google Scholar] [CrossRef]
- Christian, J.A. A tutorial on horizon-based optical navigation and attitude determination with space imaging systems. IEEE Access 2021, 9, 19819–19853. [Google Scholar] [CrossRef]
- Opromolla, R.; Fasano, G.; Rufino, G.; Grassi, M. A review of cooperative and uncooperative spacecraft pose determination techniques for close-proximity operations. Prog. Aerosp. Sci. 2017, 93, 53–72. [Google Scholar] [CrossRef]
- McKee, P.D. Autonomous Navigation in Deep Space Using Optical Measurements of Unresolved Planets and Stars. Ph.D. Thesis, Rensselaer Polytechnic Institute, Troy, NY, USA, 2022; p. 11. [Google Scholar]
- Johnson, A.; Aaron, S.; Chang, J.; Cheng, Y.; Montgomery, J.; Mohan, S.; Schroeder, S.; Tweddle, B.; Trawny, N.; Zheng, J. The lander vision system for mars 2020 entry descent and landing. In Proceedings of the 40th Annual AAS Guidance and Control Conference, Breckenridge, CO, USA, 2–8 February 2017; AAS: Washington, DC, USA, 2017. [Google Scholar]
- Maass, B.; Woicke, S.; Oliveira, W.M.; Razgus, B.; Krüger, H. Crater navigation system for autonomous precision landing on the moon. J. Guid. Control Dyn. 2020, 43, 1414–1431. [Google Scholar] [CrossRef]
- Christian, J.A.; Hong, L.; McKee, P.; Christensen, R.; Crain, T.P. Image-based lunar terrain relative navigation without a map: Measurements. J. Spacecr. Rocket. 2021, 58, 164–181. [Google Scholar] [CrossRef]
- Chen, Z.; Jiang, J. Crater detection and recognition method for pose estimation. Remote Sens. 2021, 13, 3467. [Google Scholar] [CrossRef]
- Johnson, A.E.; Cheng, Y.; Trawny, N.; Montgomery, J.F.; Schroeder, S.; Chang, J.; Clouse, D.; Aaron, S.; Mohan, S. Implementation of a Map Relative Localization System for Planetary Landing. J. Guid. Control Dyn. 2023, 46, 618–637. [Google Scholar] [CrossRef]
- Rebordão, J. Space optical navigation techniques: An overview. In Proceedings of the 8th Iberoamerican Optics Meeting and 11th Latin American Meeting on Optics, Lasers, and Applications, Porto, Portugal, 22–26 July 2013; SPIE: Bellingham, WA, USA, 2013; Volume 8785, pp. 29–48. [Google Scholar] [CrossRef]
- Christian, J.A. Accurate planetary limb localization for image-based spacecraft navigation. J. Spacecr. Rocket. 2017, 54, 708–730. [Google Scholar] [CrossRef]
- Adams, V.H.; Peck, M.A. Interplanetary optical navigation. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, San Diego, CA, USA, 4–8 January 2016. [Google Scholar] [CrossRef]
- Adams, V.H.; Peck, M.A. Lost in space and time. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar] [CrossRef]
- Franzese, V.; Di Lizia, P.; Topputo, F. Autonomous optical navigation for lumio mission. In Proceedings of the 2018 Space Flight Mechanics Meeting, AIAA, Kissimmee, FL, USA, 8–12 January 2018; p. 1977. [Google Scholar] [CrossRef]
- Franzese, V.; Di Lizia, P.; Topputo, F. Autonomous optical navigation for the lunar meteoroid impacts observer. J. Guid. Control Dyn. 2019, 42, 1579–1586. [Google Scholar] [CrossRef]
- Chen, X.; Sun, Z.; Zhang, W.; Xu, J. A novel autonomous celestial integrated navigation for deep space exploration based on angle and stellar spectra shift velocity measurement. Sensors 2019, 19, 2555. [Google Scholar] [CrossRef]
- Christian, J.A. StarNAV: Autonomous optical navigation of a spacecraft by the relativistic perturbation of starlight. Sensors 2019, 19, 4064. [Google Scholar] [CrossRef] [PubMed]
- Raymond Karimi, R.; Mortari, D. Interplanetary autonomous navigation using visible planets. J. Guid. Control Dyn. 2015, 38, 1151–1156. [Google Scholar] [CrossRef]
- Broschart, S.B.; Bradley, N.; Bhaskaran, S. Kinematic approximation of position accuracy achieved using optical observations of distant asteroids. J. Spacecr. Rocket. 2019, 56, 1383–1392. [Google Scholar] [CrossRef]
- Bradley, N.; Olikara, Z.; Bhaskaran, S.; Young, B. Cislunar navigation accuracy using optical observations of natural and artificial targets. J. Spacecr. Rocket. 2020, 57, 777–792. [Google Scholar] [CrossRef]
- Hinga, M. Cis-lunar autonomous navigation via implementation of optical asteroid angle-only measurements. In Proceedings of the 21st Advanced Maui Optical and Space Surveillance Technologies (AMOS) Conference, Maui, HI, USA, 15–18 September 2020. [Google Scholar]
- Franzese, V.; Topputo, F.; Ankersen, F.; Walker, R. Deep-space optical navigation for M-ARGO mission. J. Astronaut. Sci. 2021, 68, 1034–1055. [Google Scholar] [CrossRef]
- Franzese, V.; Topputo, F. Deep-space optical navigation exploiting multiple beacons. J. Astronaut. Sci. 2022, 69, 368–384. [Google Scholar] [CrossRef]
- Henry, S.; Christian, J.A. Absolute triangulation algorithms for space exploration. J. Guid. Control Dyn. 2023, 46, 21–46. [Google Scholar] [CrossRef]
- Henry, S.; Christian, J.A. Analytical methods in triangulation-based celestial localization. J. Astronaut. Sci. 2023, 70, 37. [Google Scholar] [CrossRef]
- Fraser, C.S.; Brown, D. Industrial photogrammetry: New developments and recent applications. Photogramm. Rec. 1986, 12, 197–217. [Google Scholar] [CrossRef]
- Easa, S.M. Space resection in photogrammetry using collinearity condition without linearisation. Surv. Rev. 2010, 42, 40–49. [Google Scholar] [CrossRef]
- Luhmann, T.; Robson, S.; Kyle, S.; Boehm, J. Close-Range Photogrammetry and 3D Imaging, 3rd ed.; Walter de Gruyter GmbH & Co. KG: Berlin, Germany, 2023; pp. 5–6, 24–25. [Google Scholar] [CrossRef]
- Hartley, R.I.; Sturm, P. Triangulation. Comput. Vis. Image Underst. 1997, 68, 146–157. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003; pp. 11–14. [Google Scholar] [CrossRef]
- Gan, S.; Zhang, X.; Zhuge, S.; Ning, C.; Zhong, L.; Li, Y. A Multi-View Vision System for Astronaut Postural Reconstruction with Self-Calibration. Aerospace 2023, 10, 298. [Google Scholar] [CrossRef]
- Madsen, C.B.; Andersen, C.S. Optimal landmark selection for triangulation of robot position. Robot. Auton. Syst. 1998, 23, 277–292. [Google Scholar] [CrossRef]
- Kaplan, G.H. Angles-Only Navigation: Position and Velocity Solution from Absolute Triangulation. Navigation 2011, 58, 187–201. [Google Scholar] [CrossRef][Green Version]
- Polle, B.; Frapard, B.; Gil-Fernandez, J.; Milic, E.; Graziano, M.; Rebordao, J.; Motrena, P. Autonomous navigation for interplanetary missions performance achievements based on real and flight images. In Proceedings of the 6th International ESA Conference on Guidance, Navigation and Control Systems, Loutraki, Greece, 17–20 October 2005; ESA Publications Division: Noordwijk, The Netherlands, 2006. [Google Scholar]
- Andreis, E.; Panicucci, P.; Topputo, F. Autonomous Vision-Based Algorithm for Interplanetary Navigation. J. Guid. Control Dyn. 2024, 47, 1792–1807. [Google Scholar] [CrossRef]
- Chen, L.; Liu, C.; Li, Z.; Kang, Z. A New Triangulation Algorithm for Positioning Space Debris. Remote Sens. 2021, 13, 4878. [Google Scholar] [CrossRef]
- Franzese, V.; Topputo, F. Optimal beacons selection for deep-space optical navigation. J. Astronaut. Sci. 2020, 67, 1775–1792. [Google Scholar] [CrossRef]
- Casini, S.; Cervone, A.; Monna, B.; Gill, E. On line-of-sight navigation for deep-space applications: A performance analysis. Adv. Space Res. 2023, 72, 2994–3008. [Google Scholar] [CrossRef]
- Stewénius, H.; Schaffalitzky, F.; Nistér, D. How hard is 3-view triangulation really? In Proceedings of the Tenth IEEE International Conference on Computer Vision (ICCV’05), Beijing, China, 17–21 October 2005; IEEE: Piscataway, NJ, USA, 2005; Volume 1, pp. 686–693. [Google Scholar] [CrossRef]
- Nasiri, S.M.; Hosseini, R.; Moradi, H. The optimal triangulation method is not really optimal. IET Image Process. 2023, 17, 2855–2865. [Google Scholar] [CrossRef]
- Shuster, M.D.; Oh, S.D. Three-axis attitude determination from vector observations. J. Guid. Control 1981, 4, 70–77. [Google Scholar] [CrossRef]
- Golub, G.H.; Van Loan, C.F. Matrix Computations, 4th ed.; JHU Press: Baltimore, MD, USA, 2013; pp. 305–306. [Google Scholar]
- Crassidis, J.L.; Junkins, J.L. Optimal Estimation of Dynamic Systems, 2nd ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2012; pp. 76–79. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Li, X.R.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation; John Wiley & Sons: Hoboken, NJ, USA, 2001; pp. 109–110. [Google Scholar]
- Mortari, D.; Conway, D. Single-point position estimation in interplanetary trajectories using star trackers. Celest. Mech. Dyn. Astron. 2017, 128, 115–130. [Google Scholar] [CrossRef]
- Muratoglu, A.; Söken, H.E.; Tekinalp, O. Visual Navigation for Lunar Missions Using Sequential Triangulation Technique. Eng. Proc. 2025, 90, 27. [Google Scholar] [CrossRef]
- Park, R.S.; Folkner, W.M.; Williams, J.G.; Boggs, D.H. The JPL planetary and lunar ephemerides DE440 and DE441. Astron. J. 2021, 161, 105. [Google Scholar] [CrossRef]
- Folkner, W.M.; Williams, J.G.; Boggs, D.H.; Park, R.S.; Kuchynka, P. The planetary and lunar ephemerides DE430 and DE431. Interplanet. Netw. Prog. Rep. 2014, 196, 42–196. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).