Rigid–Flexible Coupled Dynamics Modeling and Trajectory Compensation for Overhead Line Mobile Robots
Abstract
1. Introduction
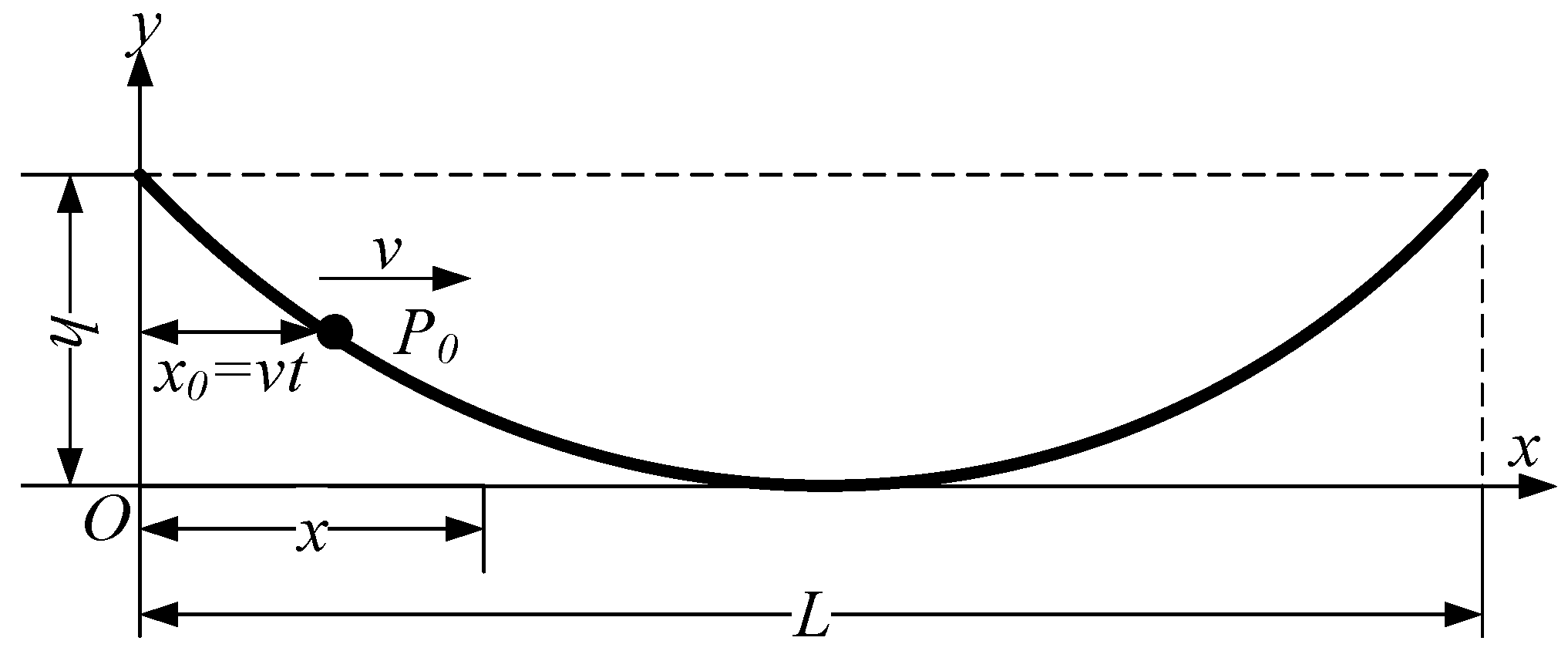
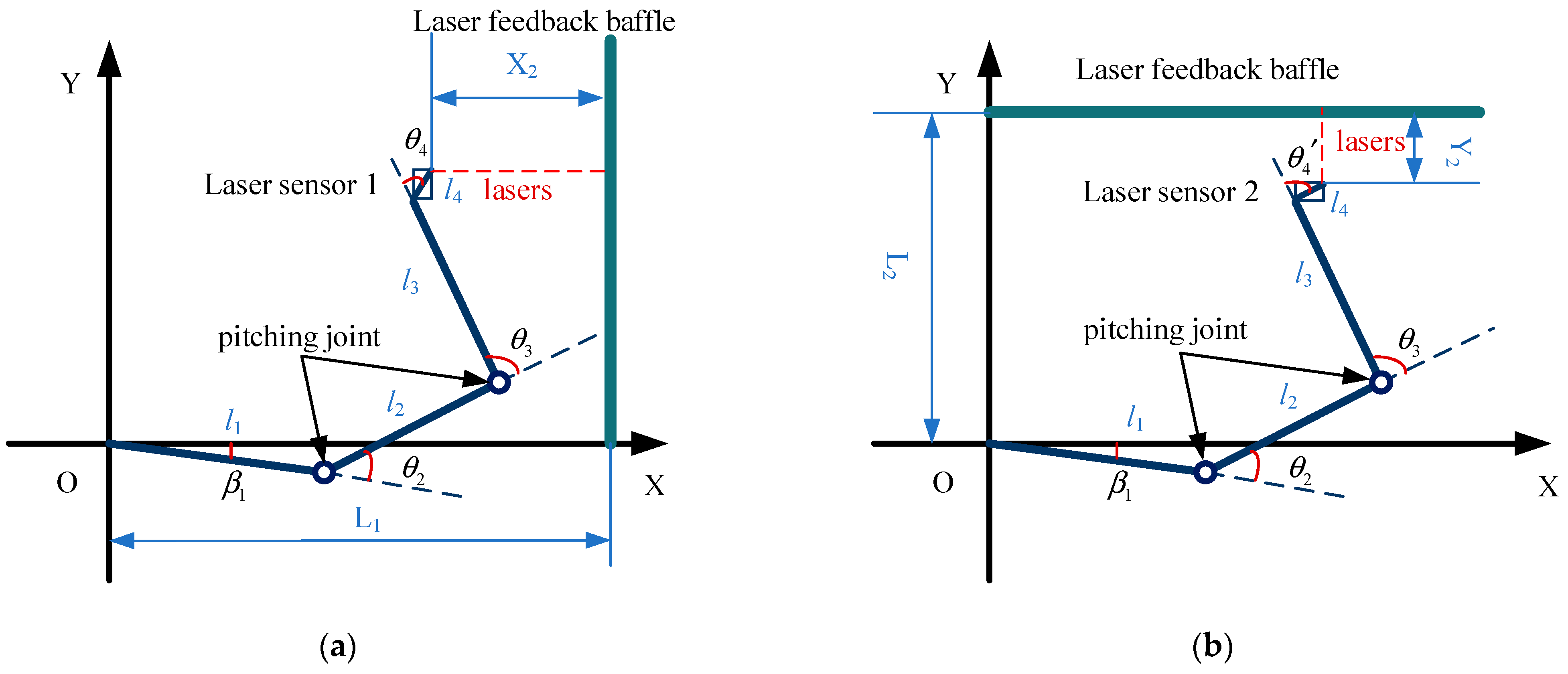
2. Kinematic Analysis
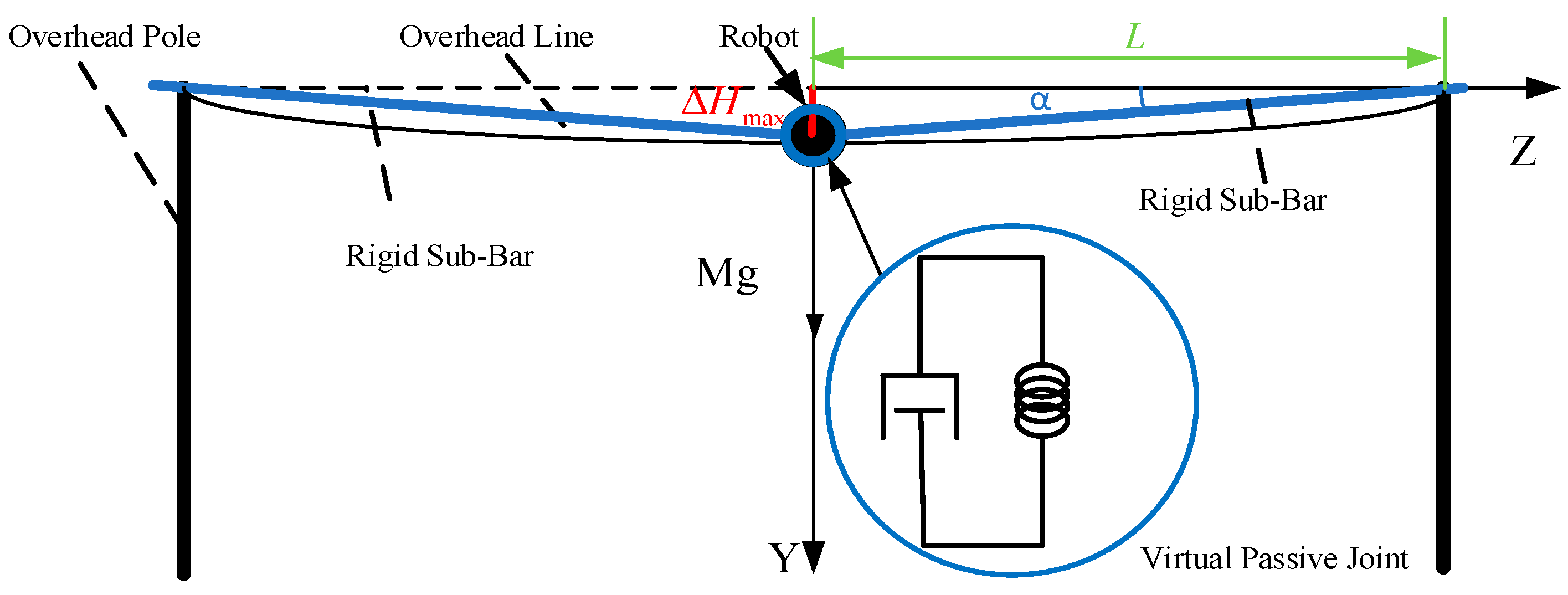
3. Rigid–Flexible Coupling Dynamic Analysis
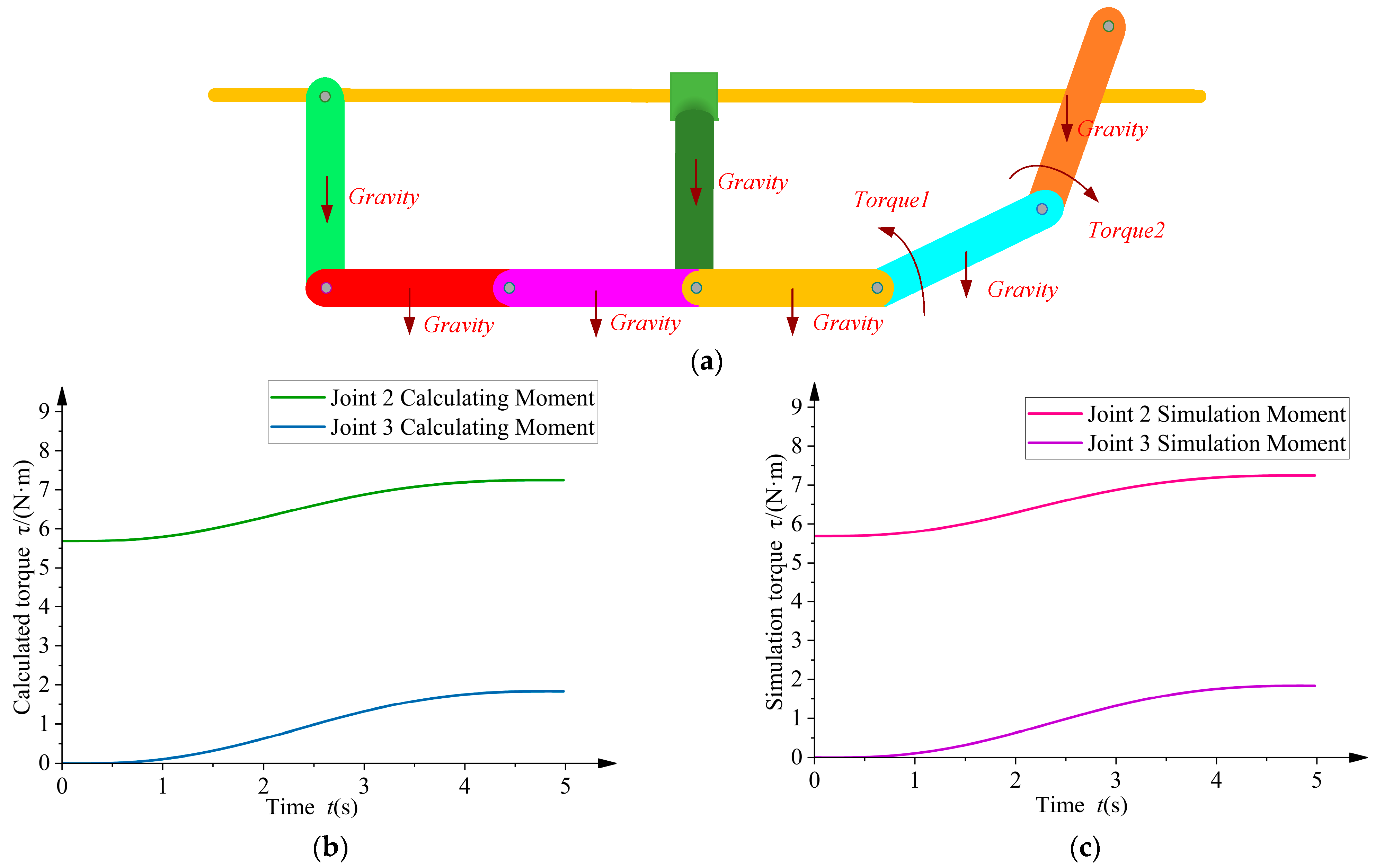
3.1. Rigid Dynamics
3.2. Rigid–Flexible Coupling Dynamics
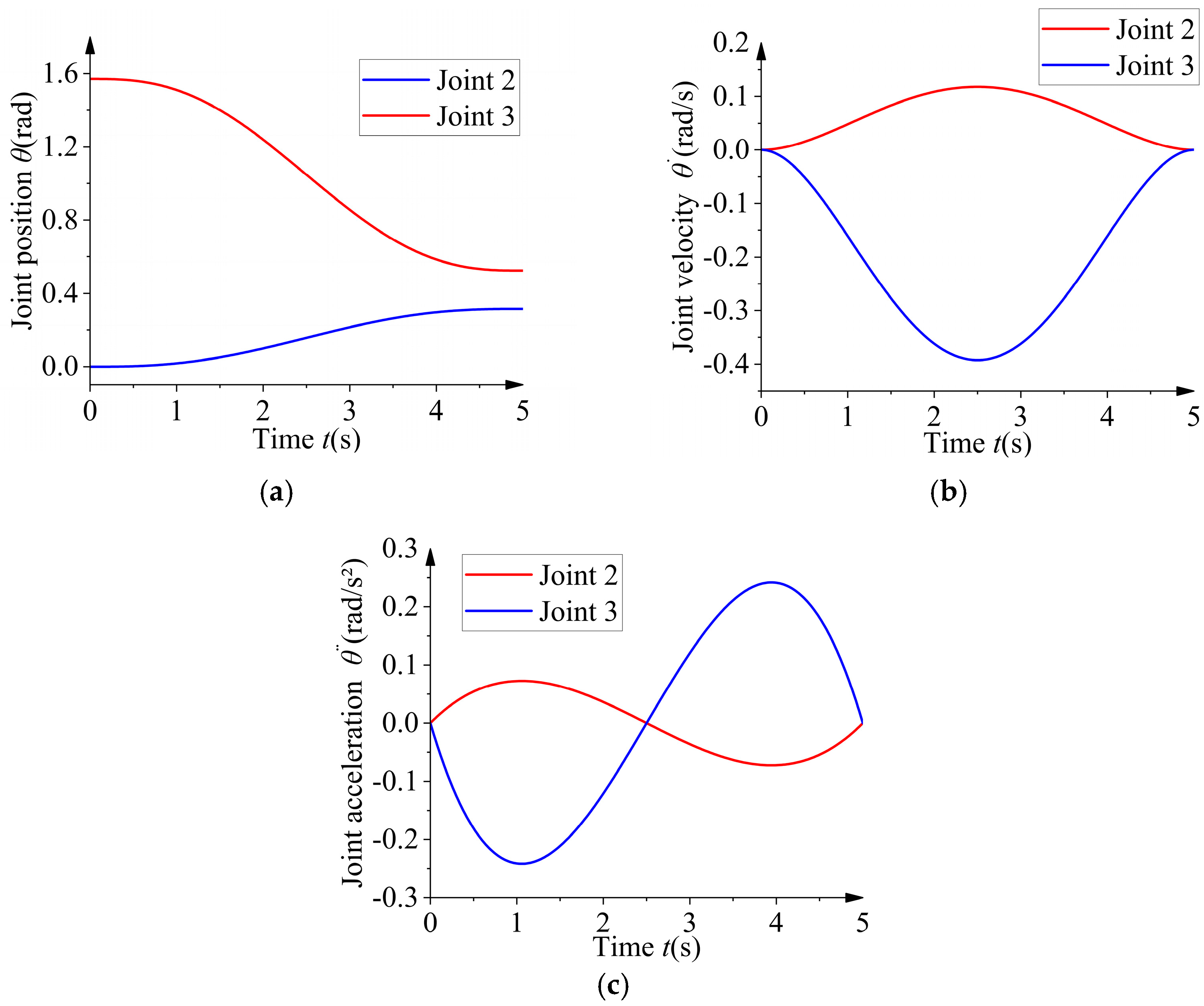
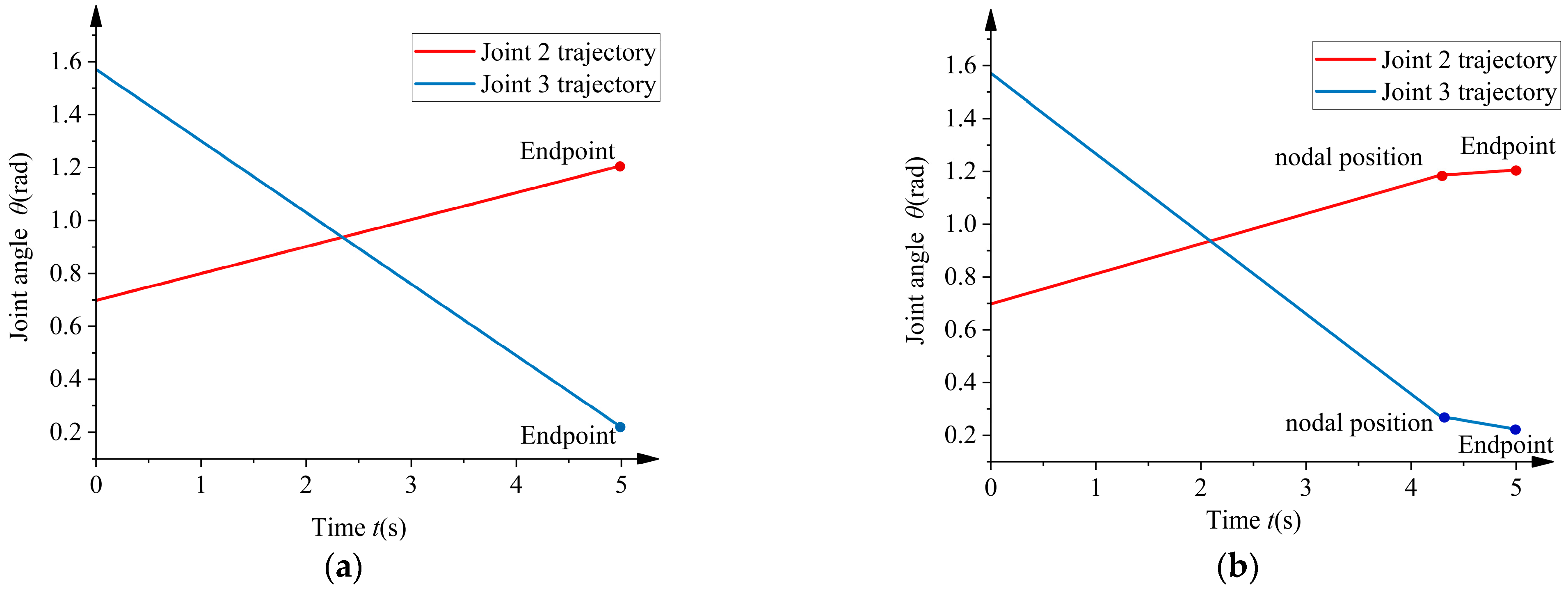
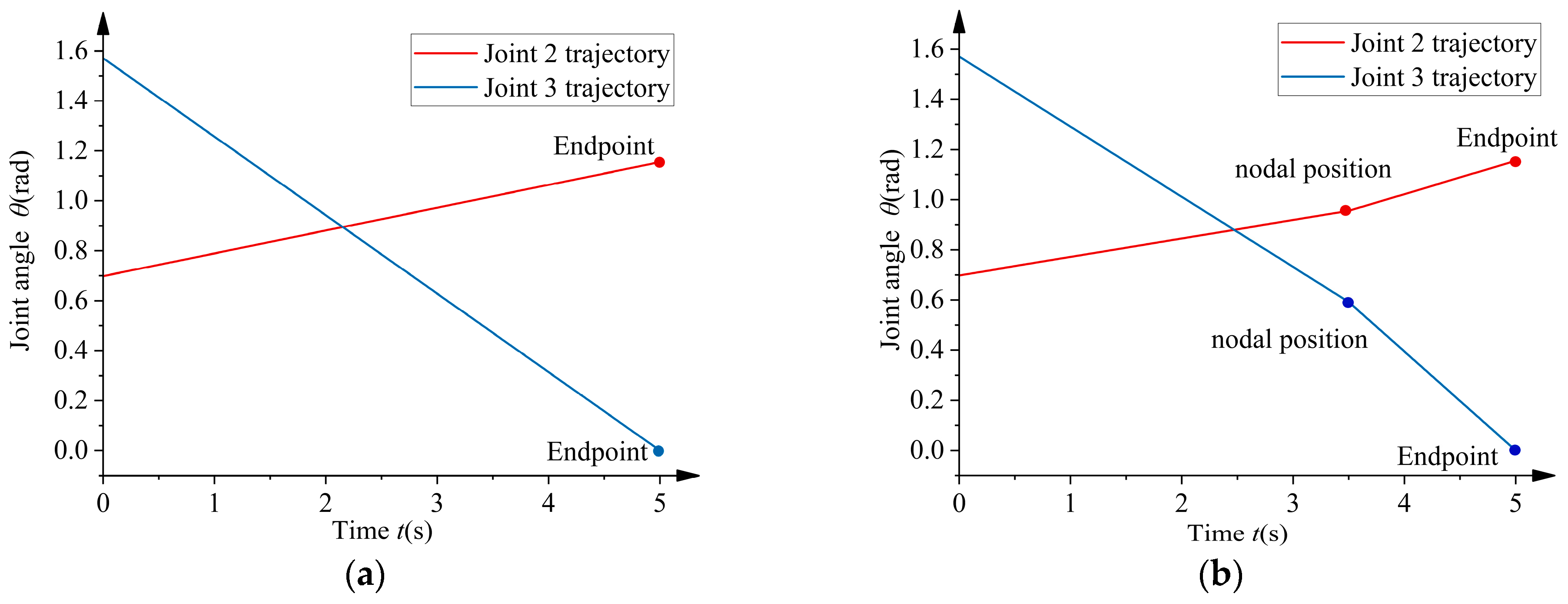
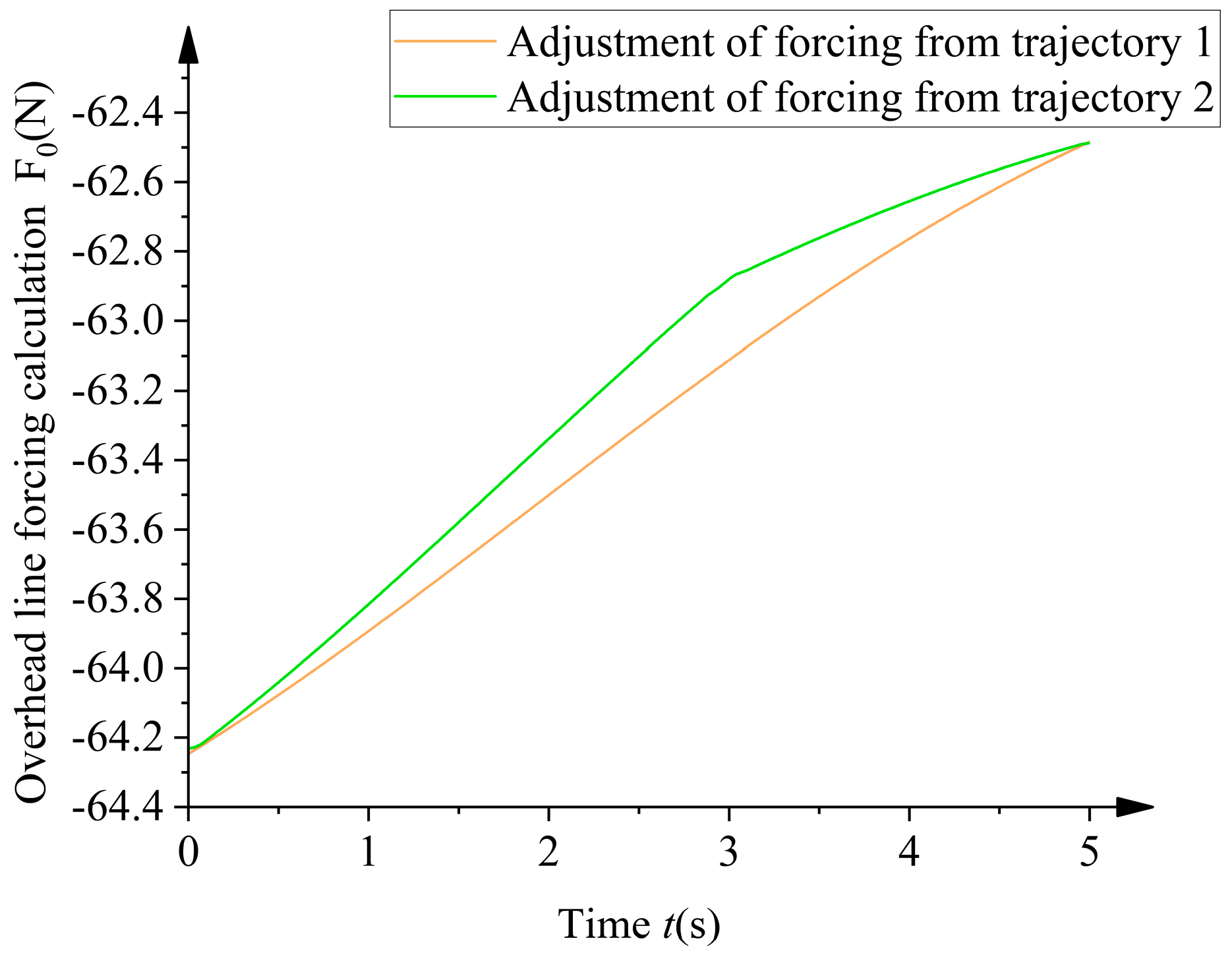
4. Active Compensation Trajectory Analysis
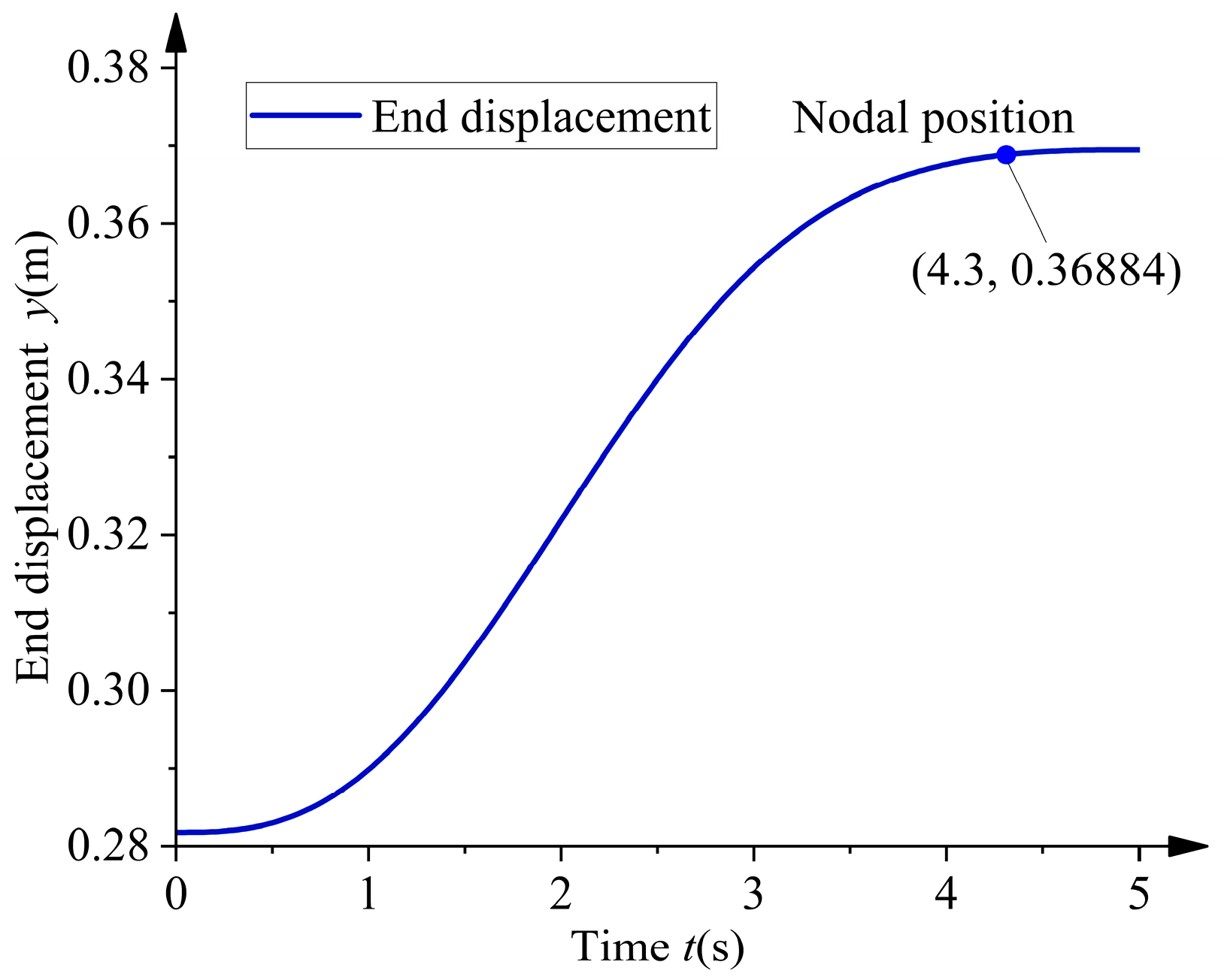
4.1. Under the Conditions of a 2 m Overhead Line
4.2. Under the Conditions of a 10 m Overhead Line
5. Experiments
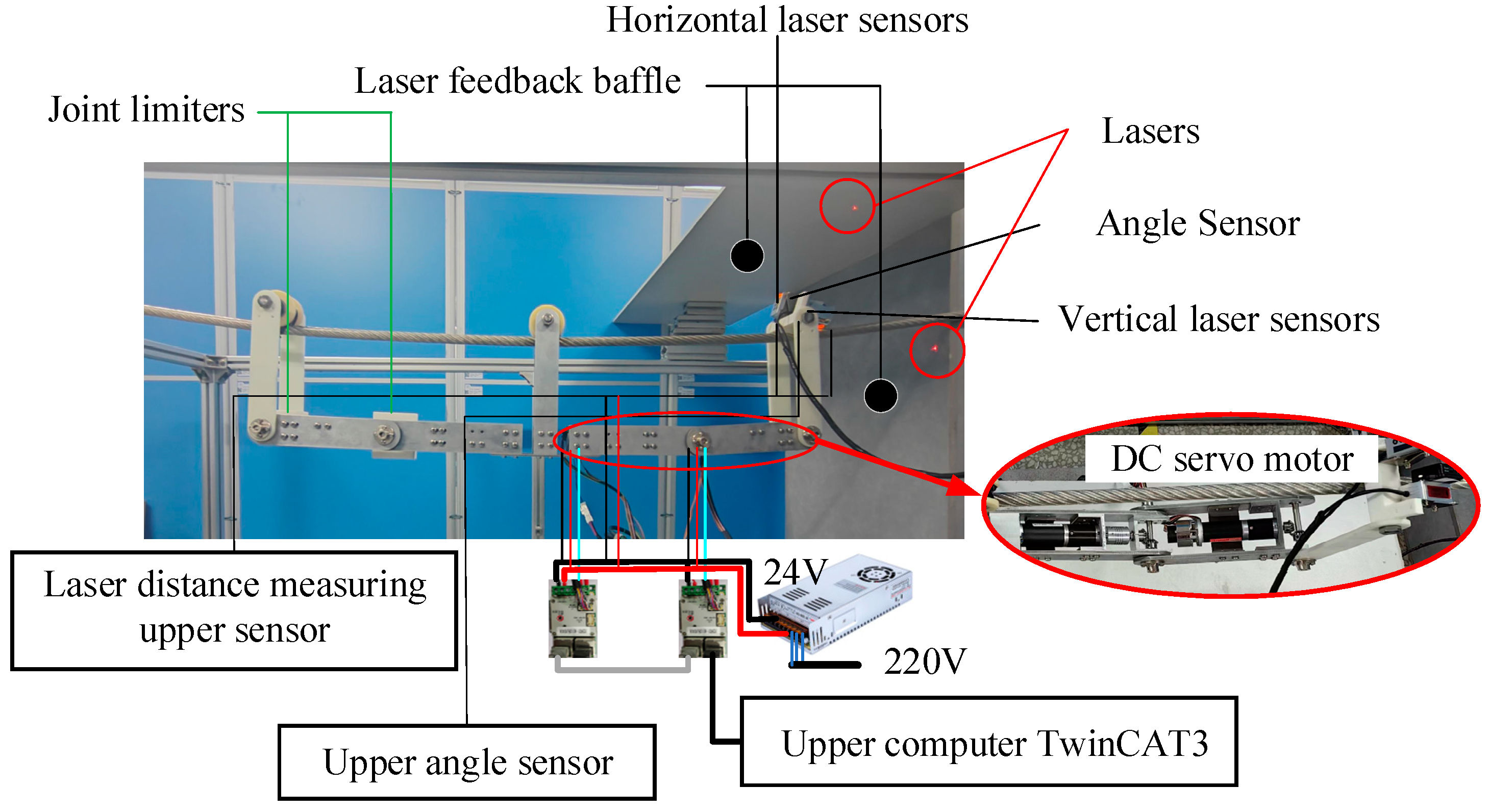
5.1. Experimental Preparations
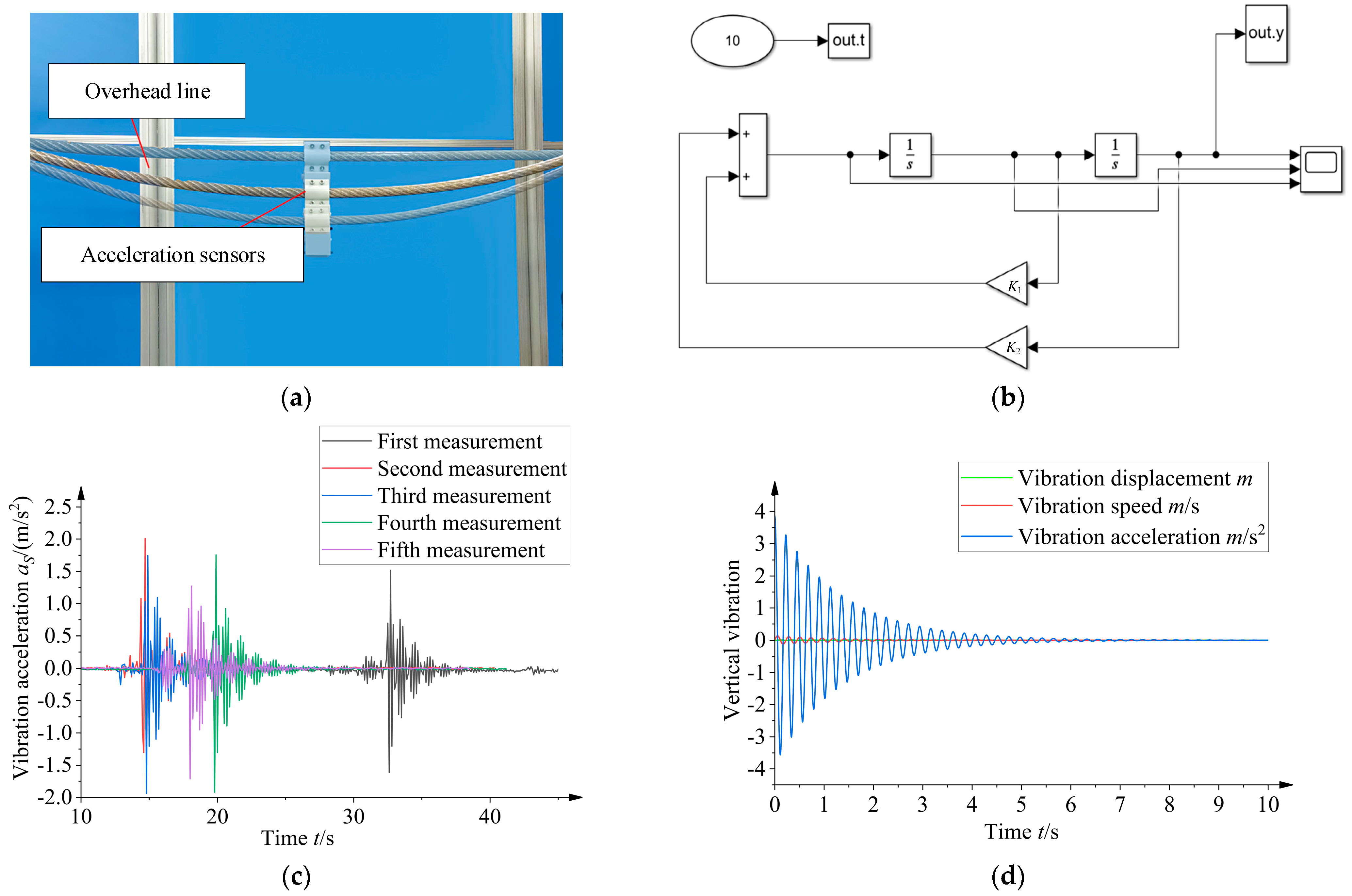
5.2. Overhead Line Characteristic Parameter Extraction Experiment
- (1)
- Build a two-meter overhead-line experiment platform.
- (2)
- In the middle of the overhead line, install a six-axis gyroscope angle sensor with its Z-axis perpendicular to the ground, as shown in Figure 23a. Measure the distance between the center of the overhead line and the ground, which was 104 mm.
- (3)
- Suspend a weight, with an equal weight to the robot, from the overhead line. After stabilization, the center of the overhead line drops under its gravity by 0.09 m. Therefore, the initial position of the system was set to 0.09 m and the initial velocity was 0 in the simulation model.
- (4)
- Remove the weight applied to the overhead line and allow the line to vibrate freely. Record the sensor data and output.
- (5)
- Repeat the above experimental steps several times. Export the experimental data and process them to obtain the vibration curve of the overhead line.
- (6)
- Establish a free vibration simulation system in the numerical simulation platform, as shown in Figure 23b.
- (7)
- Modify the gain module parameter K1 in the simulation system until the acceleration curve in the oscilloscope is consistent with the vibration acceleration curve measured by the experiment. The assumed spring coefficient and damping coefficient can be obtained. The calculation relationship is as follows:
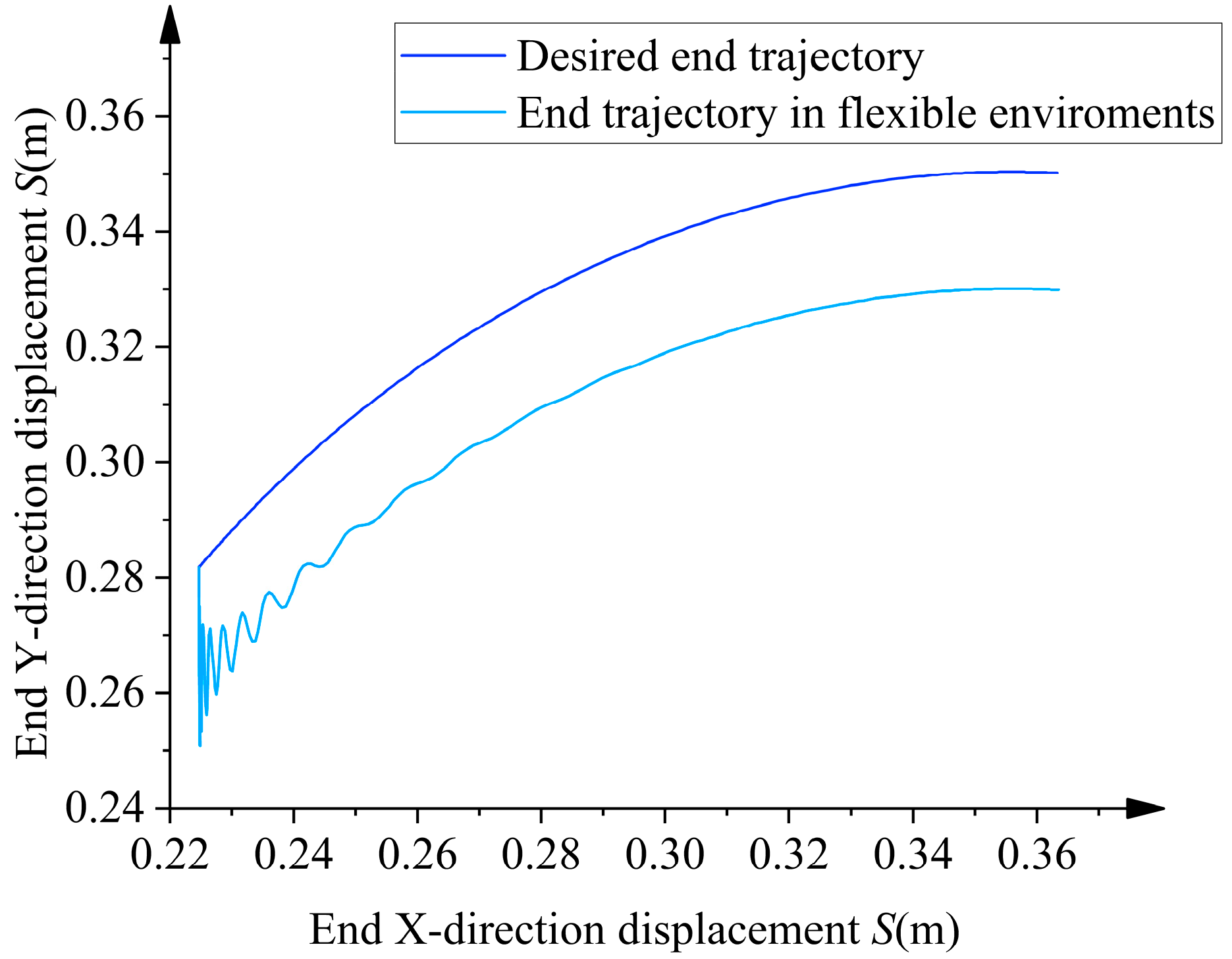
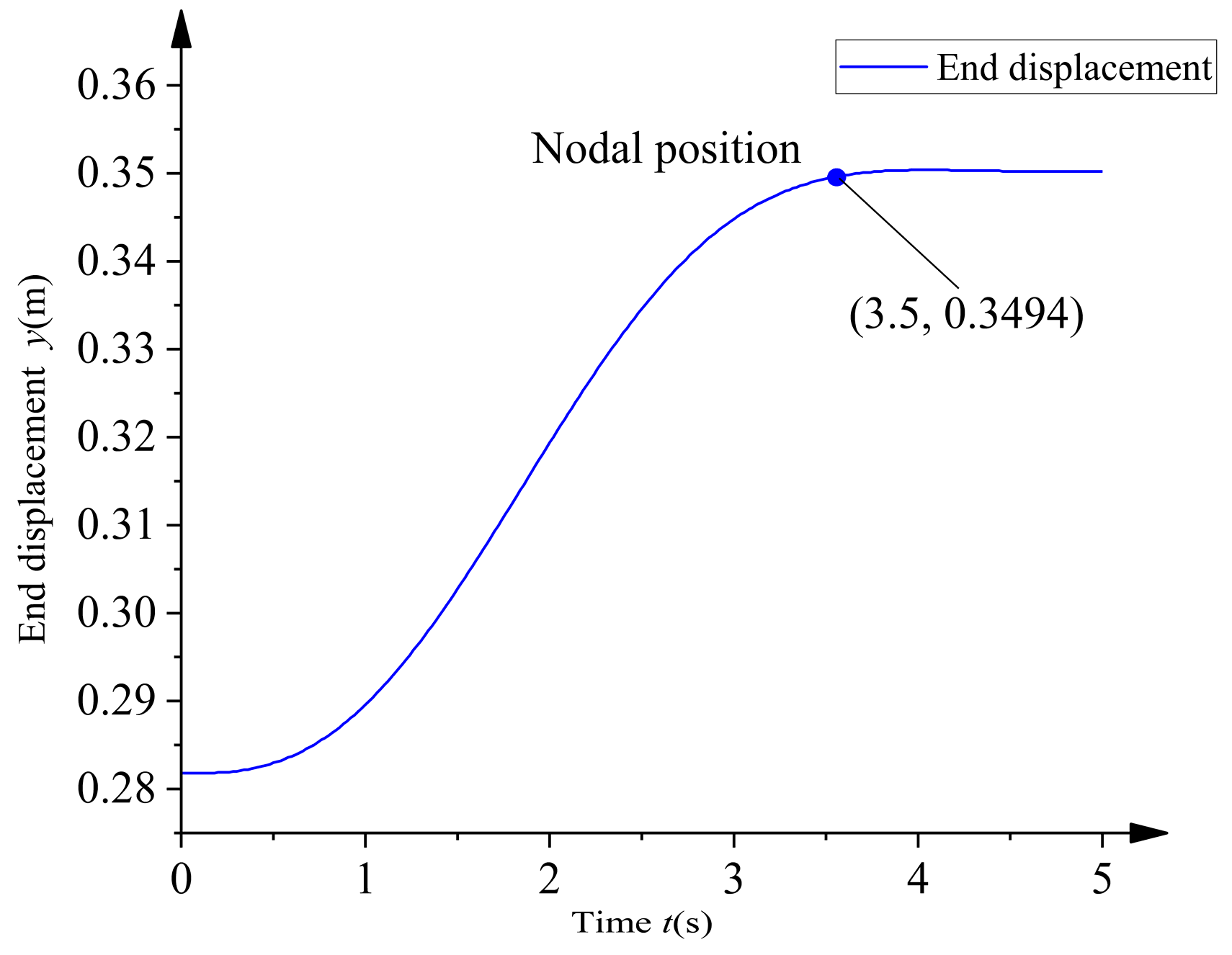
5.3. Experiment and Analysis of Actively Compensated Trajectory Motion
- (1)
- Power on the laser displacement sensor and the angle sensor, and connect them to their corresponding host computers. The sensor parameters are shown in Table 2.
- (2)
- Power on the motors. Using the host computer, adjust manipulator 2 to form a 40° angle with the horizontal direction. Adjust manipulator 3 to be perpendicular to manipulator 2.
- (3)
- Adjust the laser displacement sensor at the starting point position to be parallel to the laser feedback baffle, ensuring that the laser at the initial position vertically illuminates the baffle. Align the Z-axis of the angle sensor perpendicular to the ground, and zero out all three sensors.
- (4)
- Conduct multiple experiments on each trajectory adjustment, collect sensor data, and perform data processing.
6. Conclusions
- (1)
- Based on the Lagrange method and the substructure method, this study constructs a rigid–flexible coupled dynamic model of the mobile robot that considers the longitudinal deformation and vibration of the overhead line. The proposed model provides a more detailed description of the dynamic coupling between the robot and the flexible line. This study offers a new perspective for the academic community in this field of research.
- (2)
- This study applies Newton’s third law and forced vibration theory to analyze the relationship between the robotic arm’s motion trajectory and the overhead line’s vibration response. Based on the response of the rigid–flexible coupling dynamics model, two active compensation joint trajectories are proposed to ensure the robot’s motion accuracy.
- (3)
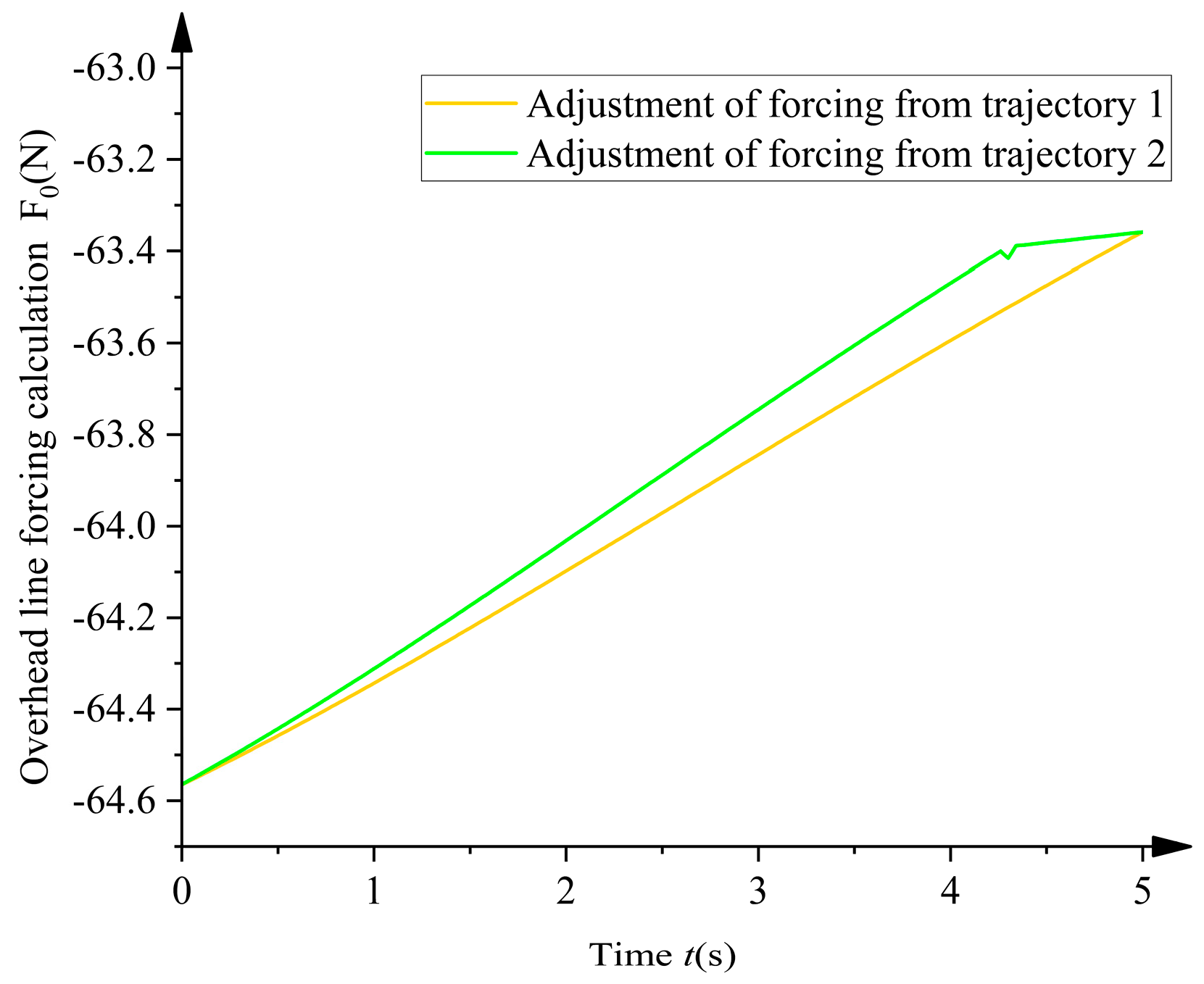
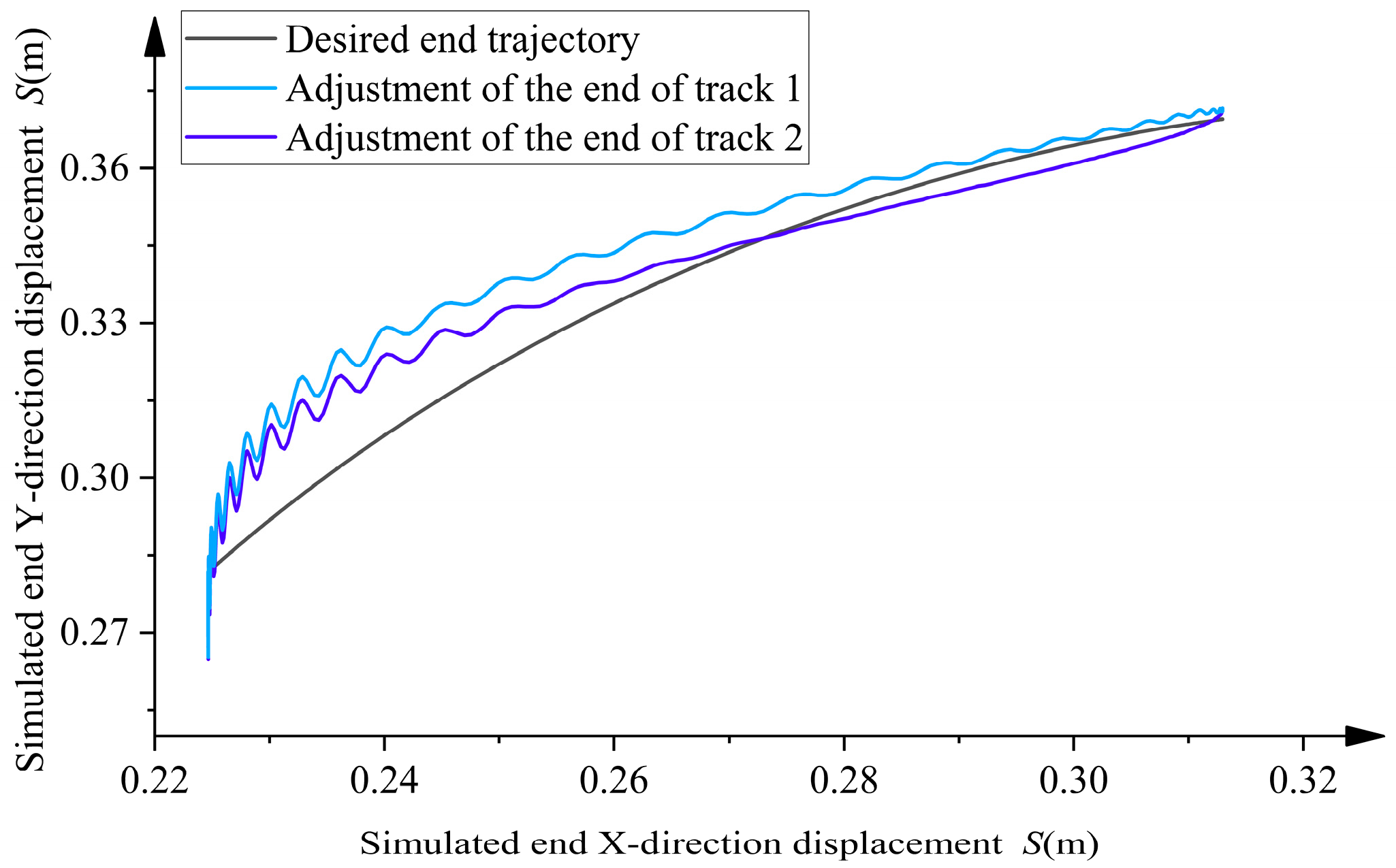
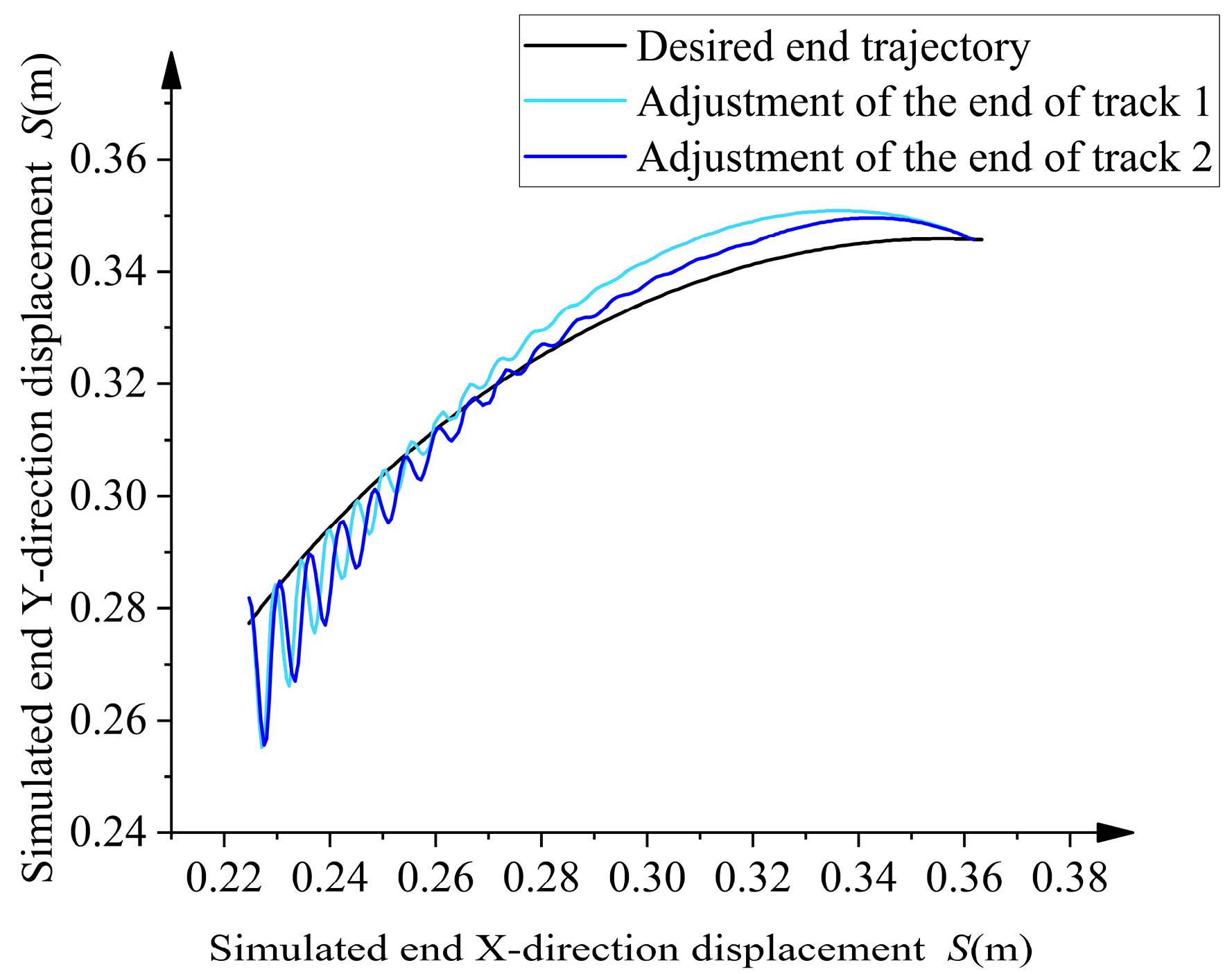
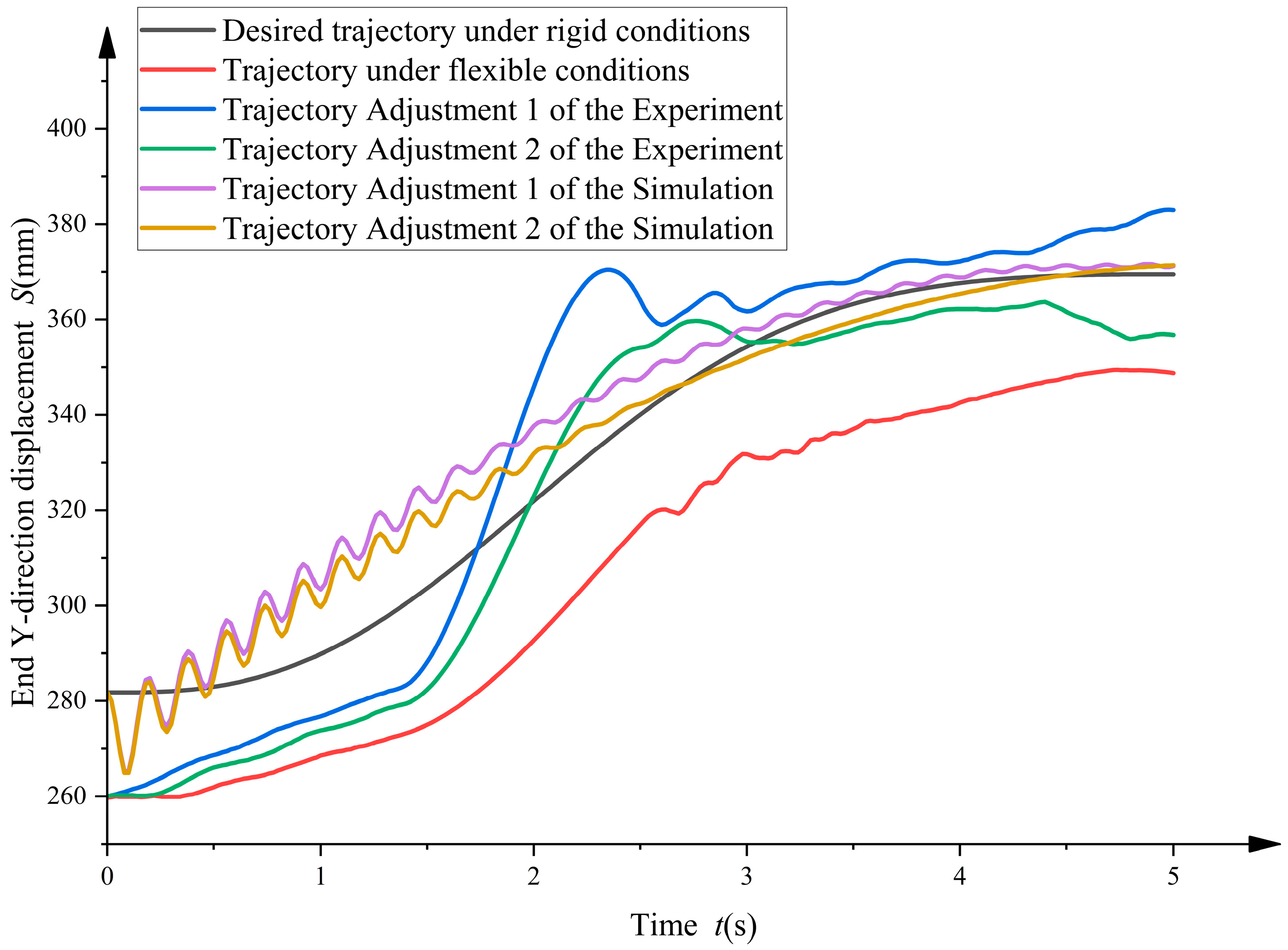
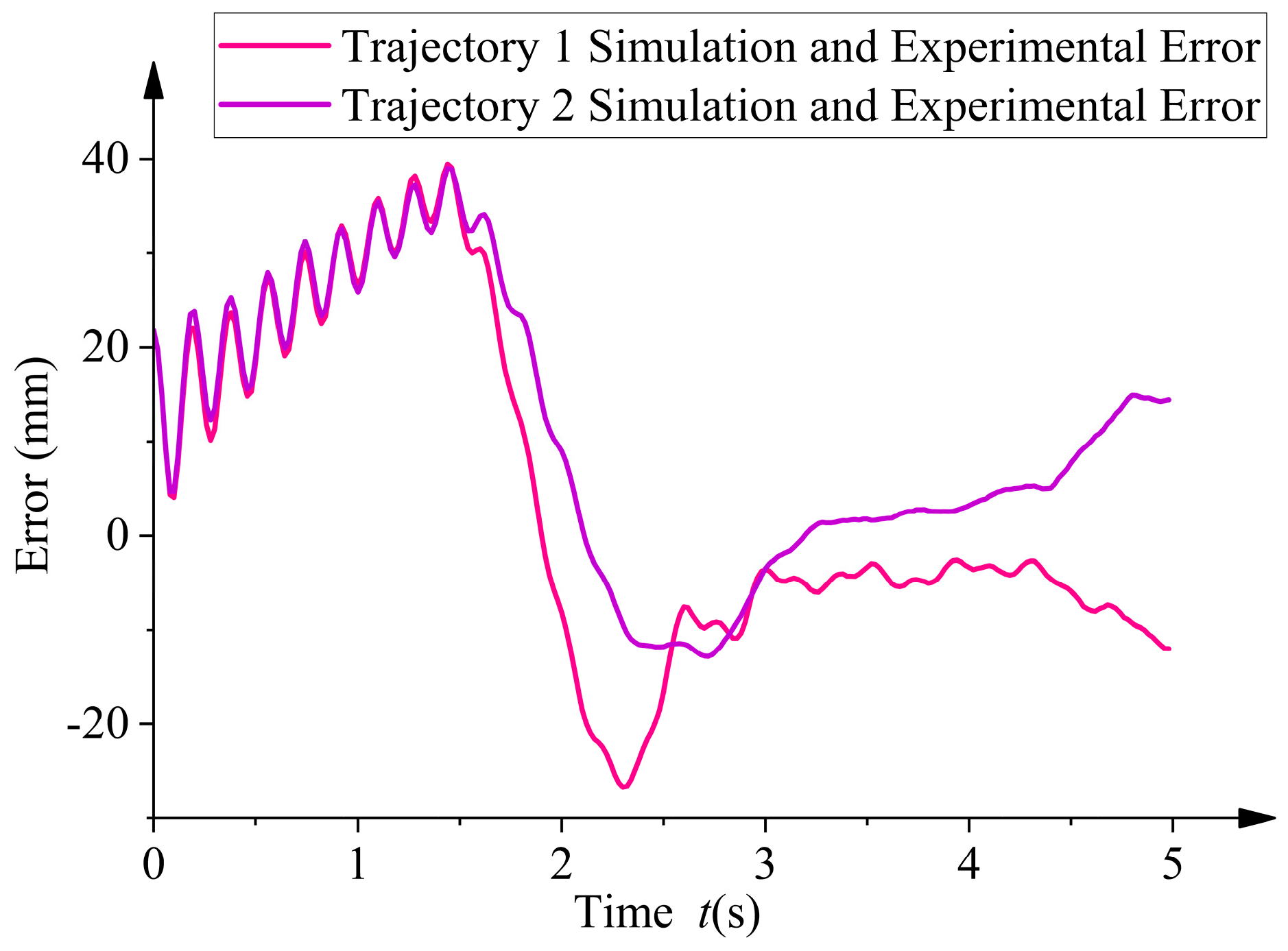
- By comparing simulation and experimental analyses, the results show that on a two-meter-span overhead line, the average error of trajectory adjustment 2 is reduced by 2.1 times compared to the original trajectory. Additionally, as shown in Figure 28, trajectory adjustment 2 is closer to the ideal trajectory than trajectory adjustment 1. This not only validates the effectiveness of the rigid–flexible coupling dynamics model but also demonstrates the practical feasibility of the model selection and optimization method.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kakou, P.; Bukhari, M.; Wang, J.; Barry, O. On the vibration suppression of power lines using mobile damping robots. Eng. Struct. 2021, 239, 112312. [Google Scholar] [CrossRef]
- Xiao, X.; Wu, G.; Du, E.; Li, S. Impacts of flexible obstructive working environment on dynamic performances of inspection robot for power transmission line. J. Cent. South Univ. Technol. 2008, 15, 869–876. [Google Scholar] [CrossRef]
- Zhang, M.; Zhao, G.; Li, J. Nonlinear Dynamic Analysis of High-Voltage Overhead Transmission Lines. Shock. Vib. 2018, 2018, 1247523. [Google Scholar] [CrossRef]
- Yang, L.; Wang, Y.; Wei, L.; Chen, Y. Structural Flexibility Effect on Spaceborne Solar Observation System’s Micro-Vibration Response. Aerospace 2024, 11, 65. [Google Scholar] [CrossRef]
- Wei, Y.; Zhang, J.; Fang, L.; Li, C. Walking Characteristics of Dual-Arm Inspection Robot with Flexible-Ca using ble. J. Robot. 2021, 2021, 8885919. [Google Scholar] [CrossRef]
- Fang, L.; Wei, Y.; Tao, G. Design of a Novel Dual-arm Inspection Robot with Flexible Cable. Robot 2013, 35, 319. [Google Scholar] [CrossRef]
- Gonçalves, R.S.; Carvalho, J.C.M. A mobile robot to be applied in high-voltage power lines. J. Braz. Soc. Mech. Sci. Eng. 2014, 37, 349–359. [Google Scholar] [CrossRef]
- Xiao, S.; Wang, H.; Zhang, J. Design and analysis of a novel inspection robot mechanism with assistant arms. In Proceedings of the IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems, Chengdu, China, 19–22 June 2016; pp. 19–22. [Google Scholar] [CrossRef]
- Shruthi, C.M.; Sudheer, A.P.; Joy, M.L. Dual arm electrical transmission line robot: Motion through straight and jumper cable. Automatika 2019, 60, 207–226. [Google Scholar] [CrossRef]
- Feng, C.; Qian, R. Mechanism Design and Crawling Process Force Analysis of Inspection Robot for Power Transmission Lines. In Proceedings of the IEEE International Conference on Unmanned Systems (ICUS), Beijing, China, 17–19 October 2019; pp. 221–225. [Google Scholar]
- Barry, O.; Zu, J.W.; Oguamanam, D.C.D. Forced Vibration of Overhead Transmission Line: Analytical and Experimental Investigation. J. Vib. Acoust. 2014, 136, 041012. [Google Scholar] [CrossRef]
- Li, X.; Fan, X.; Shang, D.; Peng, J. Dynamic performance analysis based on the mechatronic system of power transmission line inspection robot with dual-arm. Proc. Inst. Mech.Eng. Part C J. Mech. Eng. Sci. 2023, 237, 5391–5408. [Google Scholar] [CrossRef]
- Jiang, W.; Shi, Y.; Zou, D.; Zhang, H.; Li, H.J. Research on mechanism configuration and dynamic characteristics for multi-split transmission line mobile robot. Ind. Robot. Int. J. Robot. Res. Appl. 2021, 49, 200–211. [Google Scholar] [CrossRef]
- Zheng, X.; Wu, G.; Jiang, W.; Fan, F.; Zhu, J. Rigid–flexible coupling dynamics with contact estimator for robot/PTL system. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2020, 234, 635–649. [Google Scholar] [CrossRef]
- Yang, D.; Feng, Z.; Ren, X.; Lu, N. A novel power line inspection robot with dual-parallelogram architecture and its vibration suppression control. Adv. Robot. 2014, 28, 807–819. [Google Scholar] [CrossRef]
- Yang, D.; Feng, Z.; Zhang, X. A novel tribrachiation robot for power line inspection and its inverse kinematics analysis. In Proceedings of the IEEE/ASME (AIM) International Conference on Advanced Intelligent Mechatronics, Kaohsiung, Taiwan, 11–14 July 2012; pp. 502–507. [Google Scholar] [CrossRef]
- Wang, W.; Bai, Y.; Wu, G.; Li, S.; Chen, Q. The Mechanism of a Snake-Like Robot’s Clamping Obstacle Navigation on High Voltage Transmission Lines. Int. J. Adv. Robot. Syst. 2013, 10, 330. [Google Scholar] [CrossRef]
- Fan, W.; Zhang, S.; Zhu, W.; Zhu, H. An efficient dynamic formulation for the vibration analysis of a multi-span power transmission line excited by a moving deicing robot. Appl. Math. Model. 2022, 103, 619–635. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, C. Nonfragile Observer-Based Control With Passivity and H∞ Performance for a Class of Power-Line Inspection Robots With Input Time-Delay. IEEE Access 2024, 12, 102893–102903. [Google Scholar] [CrossRef]
- Zhao, Z.; Wen, S.; Li, F.; Zhang, C. Free vibration analysis of multi-span Timoshenko beams using the assumed mode method. Arch. Appl. Mech. 2018, 88, 1213–1228. [Google Scholar] [CrossRef]
- Zhang, L.; Fan, W.; Chen, Z.; Ren, H. Dynamics modeling and attitude-vibration hybrid control of a large flexible space structure. J. Vib. Control. 2024, 31, 555–568. [Google Scholar] [CrossRef]
- Wu, C.; Lu, Z.; Yu, S.; Zheng, H. A modeling scheme for flexible manipulators by sublinks and passive joints. Robot 2000, 22, 344–349. [Google Scholar]
- Hu, H.; Li, E.; Zhao, X.; Liang, Z.; Yu, W. Modeling and simulation of folding-boom aerial platform vehicle based on the flexible multi-body dynamics. In Proceedings of the International Conference on Intelligent Control and Information Processing (ICICIP), Dalian, China, 13–15 August 2010; pp. 798–802. [Google Scholar]
- Gao, Z.; Yun, C.; Bian, Y. Coupling Effectof Flexible Joint and Flexible Link on Dynamic Singularity of Flexible Manipulator. Chin. J. Mech. Eng. 2008, 21, 9–12. [Google Scholar] [CrossRef]
- Liu, Z.-y.; Hong, J.-z.; Cai, G.-p. A new dynamic model for a flexible hub-beam system. J. Shanghai Jiaotong Univ. (Sci.) 2009, 14, 245–251. [Google Scholar] [CrossRef]
- Zarafshan, P.; Moosavian, S.A.A. Manipulation control of a space robot with flexible solar panels. In Proceedings of the IEEE/ASME (AIM) International Conference on Advanced Intelligent Mechatronics, Montreal, QC, Canada, 6–9 July 2010; pp. 1099–1104. [Google Scholar]
- Heidari, H.R.; Korayem, M.H.; Haghpanahi, M.; Batlle, V.F. A new nonlinear finite element model for the dynamic modeling of flexible link manipulators undergoing large deflections. In Proceedings of the International Conference on Mechatronics (ICM), Istambul, Turkey, 13–15 April 2011; pp. 375–380. [Google Scholar]
- Kermanian, A.; Kamali E, A.; Taghvaeipour, A. Dynamic analysis of flexible parallel robots via enhanced co-rotational and rigid finite element formulations. Mech. Mach. Theory 2019, 139, 144–173. [Google Scholar] [CrossRef]
- Halim, D.; Luo, X.; Trivailo, P.M. Decentralized vibration control of a multi-link flexible robotic manipulator using smart piezoelectric transducers. Acta Astronaut. 2014, 104, 186–196. [Google Scholar] [CrossRef]
- Zhu, L.; Lu, B.; Cheng, L.; Zheng, S.; Hao, J. Rigid-Flexible Coupled Robot Simulation and Vibration Analysis. Chin. J. Mech. Eng. 2015, 13, 120–123. [Google Scholar] [CrossRef]
- Wang, Y.G.; Yu, H.D.; Xu, J.K. Design and Simulation on Inspection Robot for High-Voltage Transmission Lines. Appl. Mech. Mater. 2014, 615, 173–180. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, C.; Guo, K.; Sun, M.; Yao, Q. Dynamics modeling and characteristics analysis of scissor seat suspension. J. Vib. Control. 2015, 23, 2819–2829. [Google Scholar] [CrossRef]
- Sharifnia, M.; Akbarzadeh, A. Dynamics and vibration of a 3-PSP parallel robot with flexible moving platform. J. Vib. Control. 2014, 22, 1095–1116. [Google Scholar] [CrossRef]
- Srinil, N.; Rega, G.; Chucheepsakul, S. Three-dimensional non-linear coupling and dynamic tension in the large-amplitude free vibrations of arbitrarily sagged cables. J. Sound Vib. 2004, 269, 823–852. [Google Scholar] [CrossRef]
- Xia, D. Research on Dynamics and Reliability of Heavy Cable Crane Aerial Ropeway Systems in Hydropower Engineering. Ph.D. Thesis, Wuhan University, Wuhan, China, 2013. [Google Scholar]
- Avramov, K.V. Analysis of forced vibrations by nonlinear modes. Nonlinear Dyn. 2007, 53, 117–127. [Google Scholar] [CrossRef]
- Zhao, N.; Jia, S.; Zhu, Z.; Huang, X.; Xiao, W.; Wang, X. Direct convolution integration method for random vibration analysis of structures subjected to nonuniformly modulated nonstationary excitations. Mech. Syst. Signal Process. 2022, 178, 109294. [Google Scholar] [CrossRef]
- Ge, X.; Lei, Y.; Hou, X.; Lu, S.; Wang, J. Analysis of Mechanical Characteristics of Ice-Covered Conductor Galloping in Transmission Lines. Jiangxi Electr. Power 2019, 43, 33–38. [Google Scholar]
- Yang, J.; Zhang, Q.; Xu, C.; Cui, H. Analysis of Bending Deformation in Simply Supported Beams under Longitudinal and Transverse Loads. Jiangxi Sci. 2015, 33, 733–735. [Google Scholar]
- Chen, Y.; Guo, Y.; Zheng, T. Research on Automatic Shovel Trajectory and Trajectory Error Compensation for Loaders. Coal Mine Mach. 2024, 45, 33–36. [Google Scholar] [CrossRef]

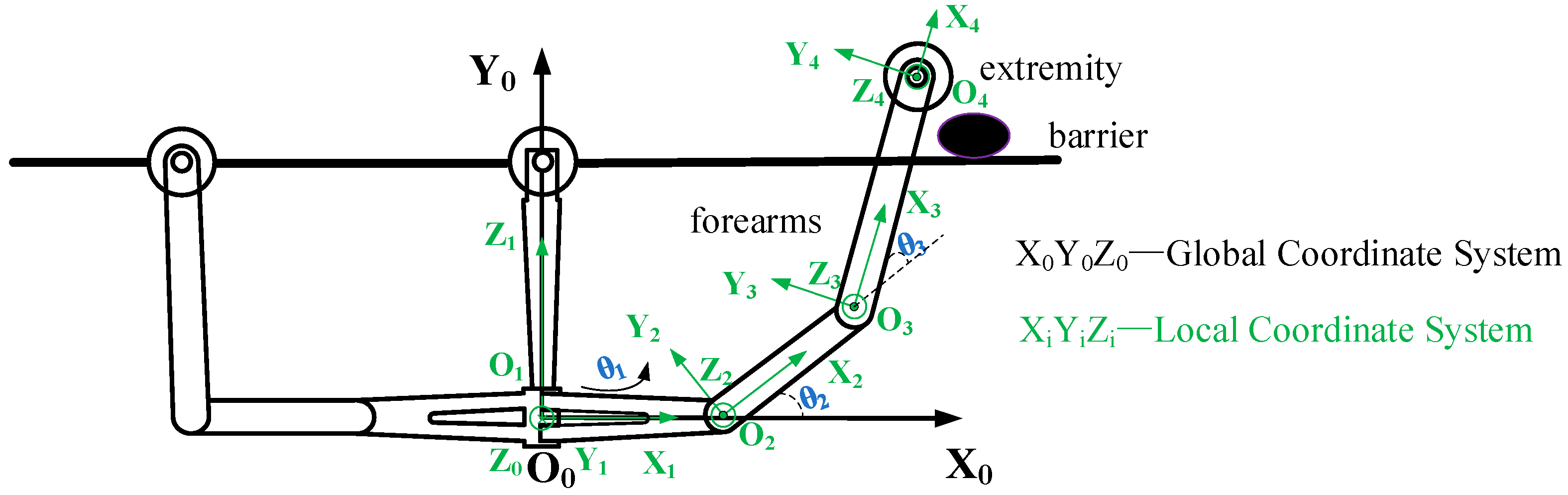

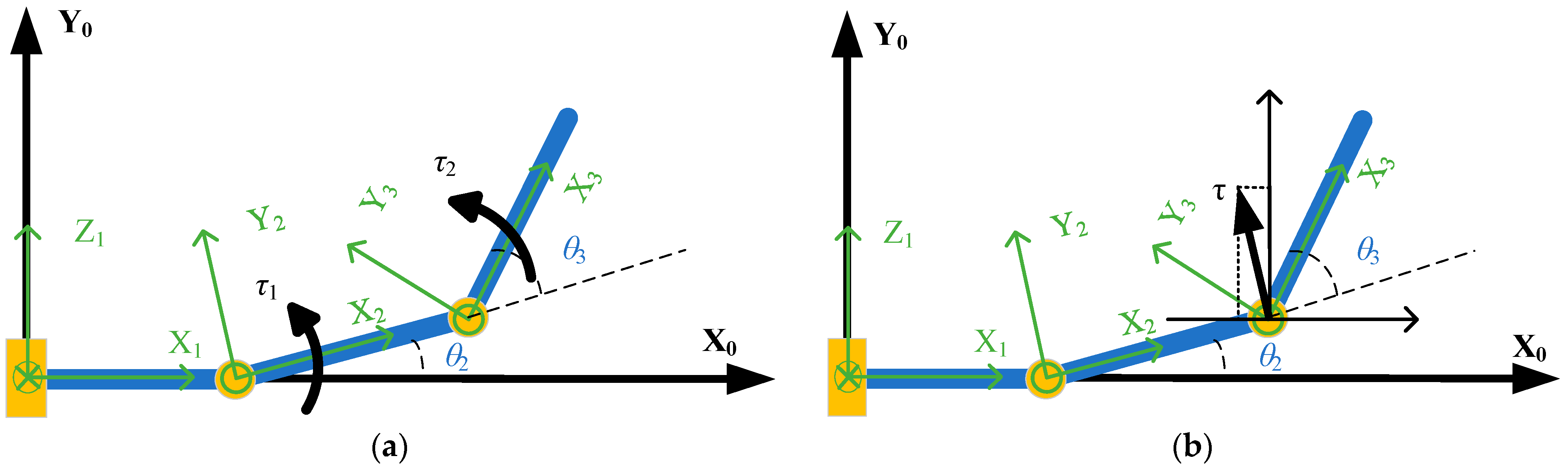
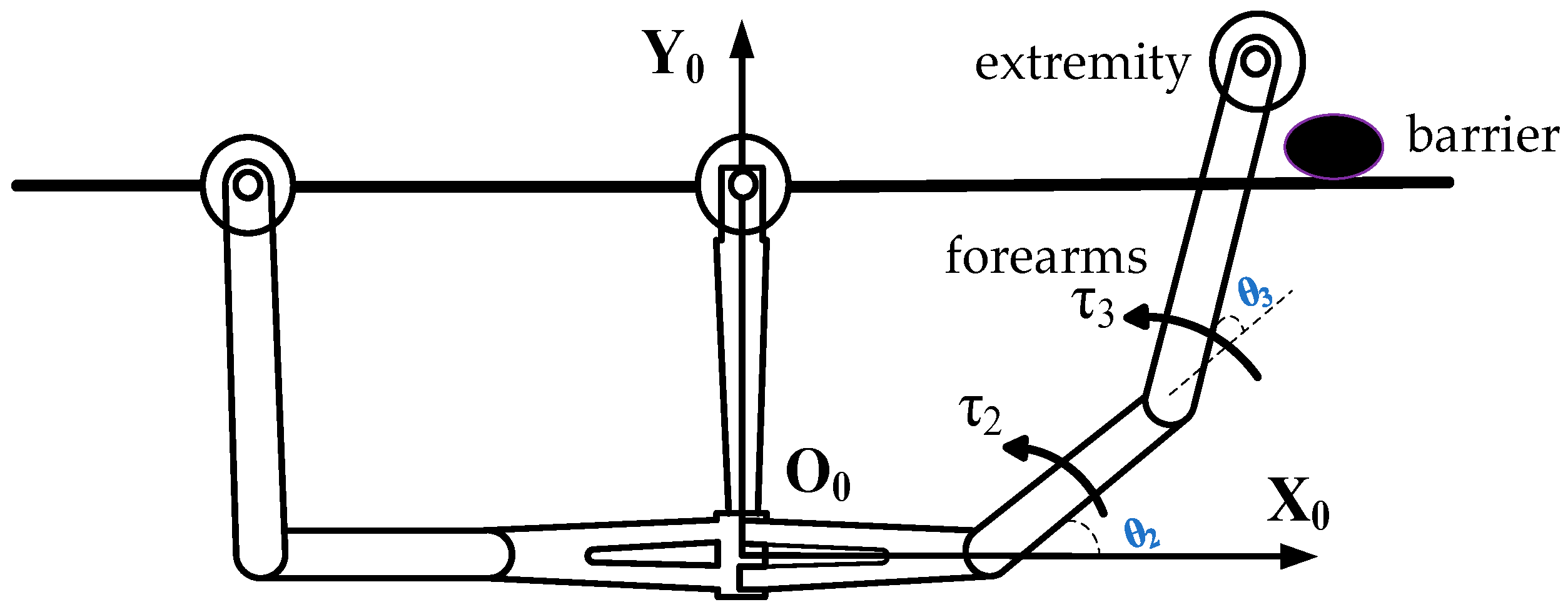






| Connecting Rod i | θi | αi−1 | ai−1 | di |
|---|---|---|---|---|
| 1 | θ1 | −90° | 0 | |
| 2 | θ2 | 90° | l1 | 0 |
| 3 | θ3 | 0 | l2 | 0 |
| 4 | 0 | l3 | 0 |
| Sensor Model | Range | Accuracy | Output Format | Main Function | Manufacturer, City, and Country |
|---|---|---|---|---|---|
| Laser Sensor BL-200NZ-485 | ±80 mm | 0.2 mm | RS485output | Measure the precise distance of objects | JORMU, Shenzhen, China. |
| Laser Sensor BL-400NZ-485 | ±200 mm | 0.8 mm | RS485output | Measure the precise distance of objects | JORMU, Shenzhen, China. |
| Angle Sensor WT901WIFI | X, Z: ±180°; Y: ±90° | XY: 0.2°; Z: 1° | Digital Signal | Detect deflection angle | WIT Intelligent, Huizhou, China. |
| Trajectory | Maximum Error (mm) | Average Error (mm) | Root Mean Square Error (mm) | Amount of Change in Trajectory Velocity (mm/s) |
|---|---|---|---|---|
| Original trajectory | 30.12 | 24.28 | 24.46 | 82.60 |
| Trajectory adjustment 1 of the experiment | 36.87 | 13.25 | 15.51 | 216.72 |
| Trajectory adjustment 2 of the experiment | 21.77 | 11.55 | 13.10 | 124.61 |
| Trajectory | Maximum Error (mm) | Average Error (mm) | Root Mean Square Error (mm) |
|---|---|---|---|
| Trajectory adjustment 1 | 39.46118 | 14.45028375 | 3.801352884 |
| Trajectory adjustment 2 | 39.00831 | 14.06134542 | 3.749846053 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, G.; Li, Y.; Wang, F.; Pan, W.; Cao, G. Rigid–Flexible Coupled Dynamics Modeling and Trajectory Compensation for Overhead Line Mobile Robots. Aerospace 2025, 12, 378. https://doi.org/10.3390/aerospace12050378
Tao G, Li Y, Wang F, Pan W, Cao G. Rigid–Flexible Coupled Dynamics Modeling and Trajectory Compensation for Overhead Line Mobile Robots. Aerospace. 2025; 12(5):378. https://doi.org/10.3390/aerospace12050378
Chicago/Turabian StyleTao, Guanghong, Yan Li, Fen Wang, Wenlong Pan, and Guoqiang Cao. 2025. "Rigid–Flexible Coupled Dynamics Modeling and Trajectory Compensation for Overhead Line Mobile Robots" Aerospace 12, no. 5: 378. https://doi.org/10.3390/aerospace12050378
APA StyleTao, G., Li, Y., Wang, F., Pan, W., & Cao, G. (2025). Rigid–Flexible Coupled Dynamics Modeling and Trajectory Compensation for Overhead Line Mobile Robots. Aerospace, 12(5), 378. https://doi.org/10.3390/aerospace12050378






