Transformation of Perturbations in Supersonic Gas Flow Subject to Oblique Shock Wave

Abstract

In a supersonic flow, disturbances of different parameters arise. These perturbations can have a significant impact on the interaction of the flow with the surface. When gas flow passes through a shock wave, perturbations are transformed depending on the initial parameters of the flow. Therefore, it is important to be able to correctly assess the intensity of these transformations. In this work, for the first time, a method has been proposed that allows us to estimate the dynamics of variation of disturbances of flow parameters when passing through an oblique shock wave. The influence of the shock wave inclination angle β, Mach number, intensity of disturbances of velocity, density, temperature, and pressure in front of the shock wave on perturbations of the flow parameters behind the shock wave was investigated. The Mach numbers ranged from 1.2 to 10 and the shock wave inclination angle varied from 15° to 90°. It was shown that the interaction of a supersonic gas flow with an oblique shock wave has a significant effect on the transformation of the perturbations of the flow parameters. The perturbations of temperature and pressure behind the shock wave increase significantly with the increasing angle β and Mach number in front of the shock wave. With the increasing Mach number, the velocity perturbations behind the shock wave first increase, then decrease, passing through a maximum, and afterwards the flow becomes more stable.

1. Introduction

Studies of the interaction of shock waves and the boundary layer are necessary in many aerospace and aviation applications to predict the flow around aerodynamic surfaces and create high-speed aircraft [1,2,3]. The shock-induced pressure jump affects the flow characteristics, flow structure, and transients in boundary layer transients.

The general characteristics of the interaction of shock waves, in particular, the various types of interaction and the occurrence and development of instability, are considered in the review [4].

Issues of controlling the interaction of shock waves are discussed. Free-stream fluctuations and mechanical vibrations can greatly influence the flow structure and heat transfer in the boundary layer [5].

Based on the theory of global linear stability, the interaction of an oblique shock wave with a laminar boundary layer was studied in [6,7]. The effect of the shock wave inclination angle, Reynolds and Mach numbers on the stability of the flow, and the length of the recirculation region was shown. It has been determined that instability is associated with fluctuations arising due to the presence of a shear layer.

The results of experimental studies of the interaction of an oblique shock wave with a cylindrical column of heavy gas are presented in [8]. The conditions for the formation of pairs of vortices rotating in opposite directions were determined. The effect of the Mach number and the angle of inclination of the shock wave on the development of flow instability was shown.

The works [9,10] present the results of modeling and analyzing the stability of the interaction of an oblique shock wave with a boundary layer at a speed of Mach 5.92. It was shown that an unfavorable pressure gradient of an oblique shock wave causes the separation of the boundary layer from the wall, which leads to the formation of a recirculation vortex. At sufficiently large angles of the oblique shock wave, the recirculation vortex is unstable for three-dimensional perturbations.

The results of the analysis of the linear stability of oblique shock waves in a stationary supersonic flow are presented in [11]. The linear stability of oblique shock waves in a stationary supersonic flow under three-dimensional perturbation in the oncoming flow was investigated. The conditions for the occurrence of instability for a shock front with a supersonic downward flow of isentropic gas were determined. Using direct numerical simulation, the characteristics of near-wall heat flow in a supersonic turbulent boundary layer interacting with an incident shock wave with an angle of 33.2° at a Mach number of 2.25 were analyzed in [12]. Analysis of velocity and temperature fluctuations showed that the contribution of large-scale structures in the outer region is enhanced by impact interaction and plays a leading role in the generation of perturbations after the interaction.

The flow of an ideal gas with a strong shock wave was analytically modeled in [13]. Unified self-similar solutions of converging (implosions) and diverging (explosions) shocks in planar, cylindrical, or spherical symmetry were proposed.

In [14], the shock wave change equations were obtained, which relate the shock wave dynamics to the partial derivatives describing the reaction fluid movement with the general equation of state in the flow tube with an arbitrary change in area. The general usefulness of these equations in the problems of reactive compressible flow was elucidated.

Analytical solutions of arbitrary non-ideal equations of state for a stationary normal shock wave and a centered rarefaction wave are presented in [15]. Generalized impact functions were outlined, revealing their well-functioning and locally convex nature, which facilitates a fast and accurate calculation of impact ratios.

The interaction of weak perturbations with an oblique shock wave, which has a theoretical solution, was studied in [16]. Numerical simulations using the shock capture method were carried out, and the results are compared with the results of theoretical analysis. It was shown that the numerical method allows one to reliably reproduce the interaction of weak external perturbations with an oblique shock wave.

Sansica et al. [17] presented the results of a numerical study of the interaction of an oblique shock wave with a laminar boundary layer on a flat plate at a free-stream Mach number of 1.5. It was shown that low-frequency oscillations occur in the absence of upstream perturbations and that they can be effectively controlled by broadband perturbations of the shear layer.

Numerical modeling [18] of the interaction of an oblique shock wave with a laminar boundary layer was performed for Mach numbers in the range from 2 to 6.85. It was shown that the introduction of low-amplitude perturbations in front of a separation vortex leads to the growth of organized longitudinal structures downstream of the vortex.

The results of the analysis of the dynamics of the mechanisms of linear convective instability during the interaction of a shock wave with a laminar boundary layer at a speed of Mach 1.7 are presented in [19]. The perturbing parameters that provide the greatest increase in perturbations in the circulation vortex induced by the impact were determined. The authors also discussed the characteristics of the mechanisms of convective instability during the interaction of a shock wave with the boundary layer.

The interaction of a normal shock wave with turbulence was analyzed in [20] using a direct numerical simulation. It was established that the scale of the shock wave deformation length is the integral scale of the turbulence length.

Werner et al. [21] numerically studied the interaction of a longitudinal vortex with an oblique shock wave in a laminar flow. The frequencies predicted by the global stability analysis were shown to be in reasonable agreement with the dominant frequencies observed in the non-stationary simulations.

An experimental study of the response of an oblique shock wave to periodic pressure perturbations downstream was performed in the work [22]. For Mach number 2.7, pressure perturbations downstream propagate upstream and cause shock wave oscillations. Based on experiments, a simple analytical model for analysis of an oblique shock wave was developed.

The works [23,24,25,26] present the results of the propagation of shock waves in a turbulent gas flow and in a gas flow with nanoparticles. In [27], an analytical analysis of an oblique shock wave in a turbulent adiabatic gas flow was performed. The research results show that the interaction of shock waves with a gas flow can lead to a significant change in the flow structure, loss of stability, and the formation of vortex structures. The need for further study of the mechanisms of instability of supersonic gas flows was pointed out.

Therefore, the objective of this work was to study the influence of an oblique shock wave on the transformation of perturbations in the parameters of a supersonic gas flow.

2. Mathematical Model

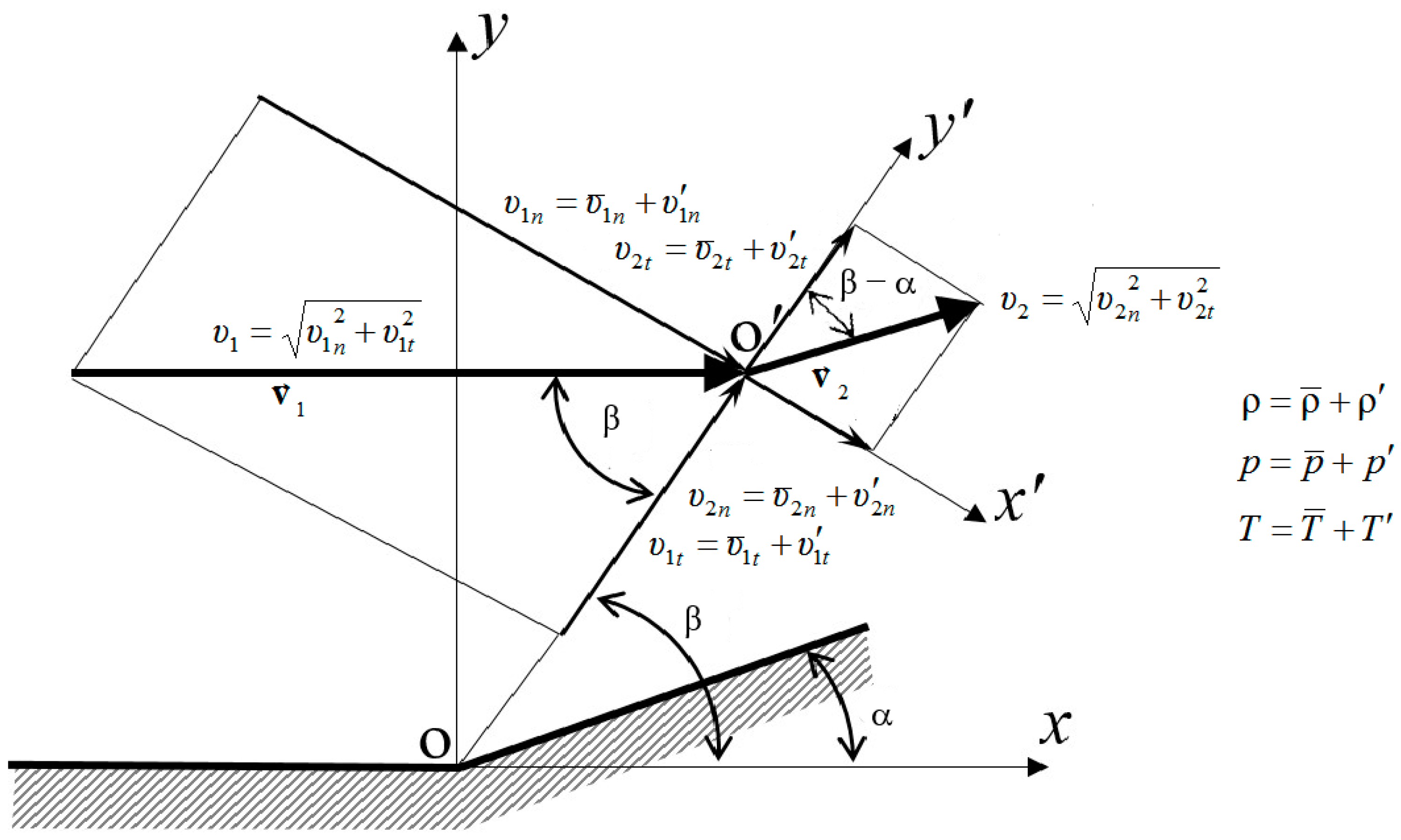
Let us consider a supersonic flow impinging on a wedge with a semi-angle α (Figure 1). A shock wave forms at the corner of the ramp at an angle β. For a mathematical description of the problem, it is a convenient move from the x-o-y coordinate system to the x’-o’-y’ coordinates.

The parameter ${\overline{v}}_1$ denotes the velocity vector in front of the shock wave, and ${\overline{v}}_2$ denotes the velocity vector behind the shock wave.

Then, the process of gas passage through a normal shock wave (Figure 1) can be described by the following system, which is one-dimensional (1D) with respect to the coordinates and two-dimensional (2D) with respect to velocity components. This system includes the flow continuity equation, two components of the momentum equation, and energy equation, as follows:

$${\displaystyle \frac{d\left(\rho {\upsilon }_n\right)}{dx\prime }}=0$$

(1)

$$\rho {\upsilon }_n{\displaystyle \frac{d{\upsilon }_n}{dx\prime }}=-{\displaystyle \frac{dp}{dx\prime }}$$

(2)

$$\rho {\upsilon }_n{\displaystyle \frac{d{\upsilon }_t}{dx\prime }}=0$$

(3)

$${\displaystyle \frac{d}{dx\prime }}\left(h+{\displaystyle \frac{{\upsilon }^2}{2}}\right)=0$$

(4)

In Equations (1)–(4), υ is the velocity defined as

$$\upsilon =\sqrt{{\upsilon }_n^2+{\upsilon }_t^2}$$

(5)

where ${\upsilon }_n$ and ${\upsilon }_t$ are the normal and tangential velocity components, respectively, ρ is the fluid density, p is the pressure, and h is the enthalpy

$$h=c_{p}T$$

(6)

The spatial derivatives of Equations (1)–(4) have a discontinuity at the shock wave. Therefore, linear analysis is carried out not on the basis of differential Equations (1)–(4), but on the basis of the algebraic system.

The algebraic system also includes the continuity equation, equations for two components of the momentum equation, and energy equation. Thus, combining Equations (1) and (2), (1) and (3), and then integrating, one can obtain

$${\rho }_1{\upsilon }_{1n}={\rho }_2{\upsilon }_{2n}$$

(7)

$$p_1+{\rho }_1{\upsilon }_{1n}^2=p_2+{\rho }_2{\upsilon }_{2n}^2$$

(8)

$${\rho }_1{\upsilon }_{1n}{\upsilon }_{1t}={\rho }_2{\upsilon }_{2n}{\upsilon }_{2t}$$

(9)

$$c_p{T}_1+{\displaystyle \frac{{\upsilon }_{1n}^2+{\upsilon }_{1t}^2}{2}}=c_p{T}_2+{\displaystyle \frac{{\upsilon }_{2n}^2+{\upsilon }_{2t}^2}{2}}$$

(10)

Here, the subscript “1” stands for the conditions before the shock wave, and the subscript “2” stands for the conditions behind the shock wave.

To close Equations (7)–(10), one can use the ideal gas equation of state

$$p=\rho \Re T$$

(11)

where $\Re$ is the individual (specific) gas constant.

It is convenient to represent the functions in Equations (7)–(11) as the sum of the unperturbed component (marked with an overbar) and the small perturbation value (marked with primes), as follows:

$${\upsilon }_n={\overline{\upsilon }}_n+{{\upsilon }^{\prime }}_n$$

(12)

$${\upsilon }_t={\overline{\upsilon }}_t+{{\upsilon }^{\prime }}_t$$

(13)

$$\rho =\overline{\rho }+{\rho }^{\prime }$$

(14)

$$p=\overline{p}+p^{\prime }$$

(15)

$$T=\overline{T}+T^{\prime }$$

(16)

Substitution of Equations (12)–(16) into Equations (7)–(11) gives

$$\left({\overline{\rho }}_1+{{\rho }^{\prime }}_1\right)\left({\overline{\upsilon }}_{1n}+{{\upsilon }^{\prime }}_{1n}\right)=\left({\overline{\rho }}_2+{{\rho }^{\prime }}_2\right)\left({\overline{\upsilon }}_{2n}+{{\upsilon }^{\prime }}_{2n}\right)$$

(17)

$$\left({\overline{p}}_1+{p^{\prime }}_1\right)+\left({\overline{\rho }}_1+{{\rho }^{\prime }}_1\right){\left({\overline{\upsilon }}_{1n}+{{\upsilon }^{\prime }}_{1n}\right)}^2=\left({\overline{p}}_2+{p^{\prime }}_2\right)+\left({\overline{\rho }}_{2n}+{{\rho }^{\prime }}_{2n}\right){\left({\overline{\upsilon }}_{2n}+{{\upsilon }^{\prime }}_{2n}\right)}^2$$

(18)

$${\overline{\upsilon }}_{1t}+{{\upsilon }^{\prime }}_{1t}={\overline{\upsilon }}_{2t}+{{\upsilon }^{\prime }}_{2t}$$

(19)

$$c_p\left({\overline{T}}_1+{T^{\prime }}_1\right)+{\displaystyle \frac{{\left({\overline{\upsilon }}_{1n}+{{\upsilon }^{\prime }}_{1n}+{\overline{\upsilon }}_{1t}+{{\upsilon }^{\prime }}_{1t}\right)}^2}{2}}=c_p\left({\overline{T}}_2+{T^{\prime }}_2\right)+{\displaystyle \frac{{\left({\overline{\upsilon }}_{2n}+{{\upsilon }^{\prime }}_{2n}+{\overline{\upsilon }}_{2t}+{{\upsilon }^{\prime }}_{2t}\right)}^2}{2}}$$

(20)

$${\overline{p}}_1+{p^{\prime }}_1=\Re \left({\overline{\rho }}_1+{{\rho }^{\prime }}_1\right)\left({\overline{T}}_1+{T^{\prime }}_1\right)$$

(21)

$${\overline{p}}_2+{p^{\prime }}_2=\Re \left({\overline{\rho }}_2+{{\rho }^{\prime }}_2\right)\left({\overline{T}}_2+{T^{\prime }}_2\right)$$

(22)

Taking into account that the unperturbed components satisfy the basic Equations (7)–(11) and performing linearization of the perturbing quantities, one can obtain the following equations

$$V_{1n}+R_1={\displaystyle \frac{V_{2n}}{W_n}}+R_2{W}_n$$

(23)

$$P_1+2V_{1n}+R_1=P_2+2V_{2n}+R_2{W}_n^2$$

(24)

$$V_{1t}=V_{2t}=V_t$$

(25)

$${\mathsf{\theta }}_1+\left(1+W_t\right)V_{1n}+V_t={\mathsf{\theta }}_2+\left(W_n+W_t\right)V_{2n}+W_n{V}_t$$

(26)

$$P_1=\Re \left({\displaystyle \frac{{\mathsf{\theta }}_1}{c_p}}+{\displaystyle \frac{R_1}{\Re }}{\displaystyle \frac{{\overline{p}}_1}{{\overline{\rho }}_1{{\overline{\upsilon }}_1}^2}}\right)={\displaystyle \frac{k-1}{k}}{\mathsf{\theta }}_1+{\displaystyle \frac{k{\overline{p}}_1/{\overline{\rho }}_1}{{k{\overline{\upsilon }}_1}^2}}{R}_1={\displaystyle \frac{k-1}{k}}{\mathsf{\theta }}_1+{\displaystyle \frac{1}{k{\mathrm{Ma}}_1^2}}{R}_1$$

(27)

$$P_2=\Re \left({\displaystyle \frac{{\mathsf{\theta }}_2}{c_p{W}_n}}+{\displaystyle \frac{R_2}{\Re }}{\displaystyle \frac{{\overline{p}}_1}{{{\overline{\rho }}_1{\overline{\upsilon }}_1}^2}}{\displaystyle \frac{{\overline{p}}_2}{{\overline{p}}_1}}\right)={\displaystyle \frac{k-1}{k{W}_n}}{\mathsf{\theta }}_2+{\displaystyle \frac{k{\overline{p}}_1/{\overline{\rho }}_1}{{k{\overline{\upsilon }}_1}^2}}{\displaystyle \frac{{\overline{p}}_2}{{\overline{p}}_1}}{R}_2={\displaystyle \frac{k-1}{k{W}_n}}{\mathsf{\theta }}_2+{\displaystyle \frac{\Pi }{k{\mathrm{Ma}}_1^2}}{R}_2$$

(28)

where

$$V_{1n}={\displaystyle \frac{{{\upsilon }^{\prime }}_{1n}}{{\overline{\upsilon }}_{1n}}},V_{2n}={\displaystyle \frac{{{\upsilon }^{\prime }}_{2n}}{{\overline{\upsilon }}_{1n}}},V_{1t}={\displaystyle \frac{{{\upsilon }^{\prime }}_{1t}}{{\overline{\upsilon }}_{1n}}},V_{2t}={\displaystyle \frac{{{\upsilon }^{\prime }}_{2t}}{{\overline{\upsilon }}_{1n}}},R_1={\displaystyle \frac{{{\rho }^{\prime }}_1}{{\overline{\rho }}_1}},R_2={\displaystyle \frac{{{\rho }^{\prime }}_2}{{\overline{\rho }}_1}},k=c_p/c_{\upsilon },$$

(29)

$${\mathsf{\theta }}_1={\displaystyle \frac{c_p{T^{\prime }}_1}{{\overline{\upsilon }}_{1n}^2}},{\mathsf{\theta }}_2={\displaystyle \frac{c_p{T^{\prime }}_2}{{\overline{\upsilon }}_{1n}^2}},P_1={\displaystyle \frac{{p^{\prime }}_1}{{\overline{\rho }}_1{\overline{\upsilon }}_{1n}^2}},P_2={\displaystyle \frac{{p^{\prime }}_2}{{\overline{\rho }}_1{\overline{\upsilon }}_{1n}^2}}$$

(30)

$$W_n\left({\mathrm{Ma}}_1^2\right)={\displaystyle \frac{{\overline{\upsilon }}_{2n}}{{\overline{\upsilon }}_{1n}}}={\displaystyle \frac{{\overline{\rho }}_1}{{\overline{\rho }}_2}}={\displaystyle \frac{1+\left(k-1\right){\mathrm{Ma}}_1^2{\sin }^2\left(\beta \right)/2}{\left(k+1\right){\mathrm{Ma}}_1^2{\sin }^2\left(\beta \right)/2}}$$

(31)

$$W_t={\displaystyle \frac{{\overline{\upsilon }}_{1t}}{{\overline{\upsilon }}_{1n}}}={\displaystyle \frac{{\overline{\upsilon }}_{2t}}{{\overline{\upsilon }}_{1n}}}=\cot \left(\beta \right)$$

(32)

$$\Pi \left({\mathrm{Ma}}_1^2\right)={\displaystyle \frac{{\overline{p}}_2}{{\overline{p}}_1}}={\displaystyle \frac{2k}{k+1}}{\mathrm{Ma}}_1^2{\sin }^2\left(\beta \right)-{\displaystyle \frac{k-1}{k+1}}$$

(33)

Here

$${\mathrm{Ma}}_1^2={\displaystyle \frac{{{\overline{\upsilon }}_1}^2}{k{\overline{p}}_1/{\overline{\rho }}_1}}$$

(34)

is the square of the Mach number in front of the shock wave.

When deriving Equations (23)–(28), it was taken into account that Equations (7)–(10) are valid for unperturbed quantities.

To reduce the number of equations, Equations (27) and (28) were substituted into Equation (24). This yields as a result

$${\displaystyle \frac{k-1}{k}}{\mathsf{\theta }}_1+\left(1+{\displaystyle \frac{1}{k{\mathrm{Ma}}_1^2}}\right)R_1+2V_{1n}={\displaystyle \frac{k-1}{k{W}_n}}{\mathsf{\theta }}_2+\left(W_n^2+{\displaystyle \frac{\Pi }{k{\mathrm{Ma}}_1^2}}\right)R_2+2V_{2n}$$

(35)

Thus, the system of Equations (23), (26), and (35) makes it possible to calculate how the perturbations of velocity, temperature, and density in front of the shock wave affect the corresponding perturbations behind it. Perturbations of pressure behind the shock wave can be calculated based on Equation (26). It is possible to build other options that enable calculating pressure perturbations directly. For example, if temperature perturbations based on Equations (27) and (28) are excluded according to the equations

$${\mathsf{\theta }}_1={\displaystyle \frac{k{\mathrm{Ma}}_1^2{P}_1-R_1}{\left(k-1\right){\mathrm{Ma}}_1^2}}$$

(36)

$${\mathsf{\theta }}_2={\displaystyle \frac{k{\mathrm{Ma}}_1^2{P}_2-R_2\Pi }{\left(k-1\right){\mathrm{Ma}}_1^2}}{W}_n$$

(37)

then Equation (26) can be transformed as

$$k{\mathrm{Ma}}_1^2{P}_1-R_1-k{\mathrm{Ma}}_1^2{P}_2{W}_n+W_n\Pi R_2+{\mathrm{Ma}}_1^2{V}_{1n}{W}_t\left(-1+k+W_n\left(1-k\right)\right)-V_{2n}{\mathrm{Ma}}_1^2\left(k-1\right)\left(W_n+W_t\right)+V_{1n}{\mathrm{Ma}}_1^2\left(k-1\right)\left(1+W_t\right)=0$$

(38)

Thus, we obtain Equations (14), (15), and (26), which allows to estimate how the perturbations of velocity, pressure, and density in front of the shock wave affect the corresponding perturbations behind it.

3. Calculation Results and Their Analysis

As a result of solving Equations (23), (26), and (35), an equation was obtained that characterizes the effect of velocity perturbations in front of the wave on the velocity perturbations behind it

$$V_{2n}={\displaystyle \frac{W_n\left(\left(k-1\right)M{a}_1^2{V}_{1n}+\Pi V_{1n}+R_1\left(\Pi +\left(-1+kM{a}_1^2\left(W_n-1\right)\right)W_n\right)+M{a}_1^2\left(V_{1n}\left(W_n-2\right)\left(k\left(W_n-W_t\right)+W_t\right)-\left(k-1\right)\left(W_n-1\right){\mathsf{\theta }}_1\right)\right)}{\Pi -M{a}_1^2{W}_n\left(W_n+W_t-k{W}_t\right)}}$$

(39)

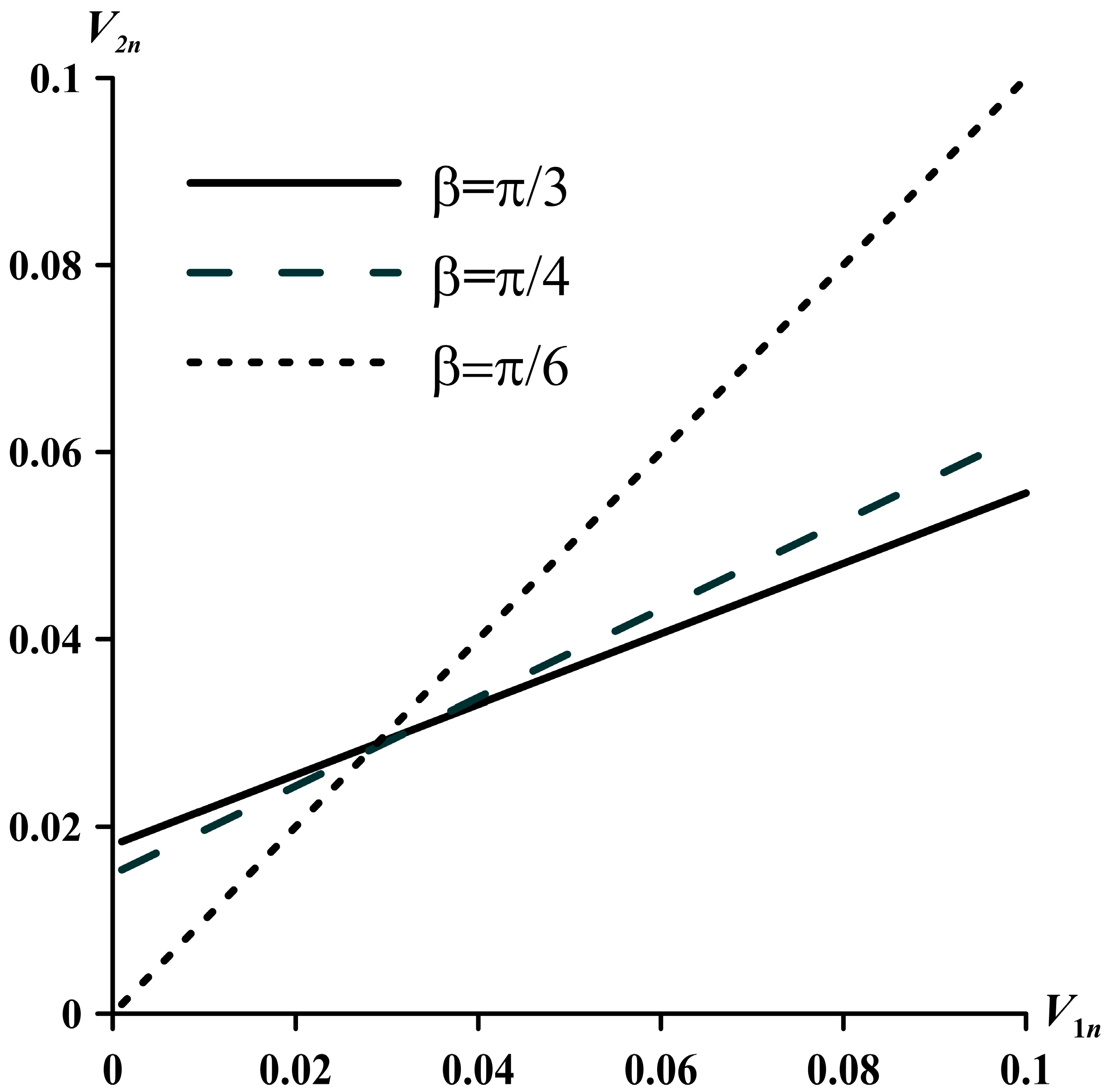
Figure 2 shows the effect of the perturbation of dimensionless velocity in front of the wave on the perturbation of velocity behind it for different values of the angle β.

With increasing angle, the influence of density and temperature disturbances on the velocity pulsations behind the wave increases at small values of velocity disturbances ahead of the wave. With increasing initial velocity disturbances ahead of the wave, this effect weakens. And at a certain point of velocity disturbances ahead of the wave, this effect becomes the same for all angles β. Therefore, an intersection point arises.

For a small angle β = π/6, the velocity perturbations behind and in front of the shock wave are the same. As the angle β increases, the perturbation of velocities behind the wave become smaller than those in front of it. The decrease in perturbations of velocity behind the shock wave at large angles β is associated with a decrease in the kinetic energy of the flow when passing through an oblique shock wave. At small angles, the decrease in the kinetic energy of the flow when passing through a shock wave is much weaker. Therefore, the level of perturbations of velocity behind the shock wave is the same as in front of the wave. 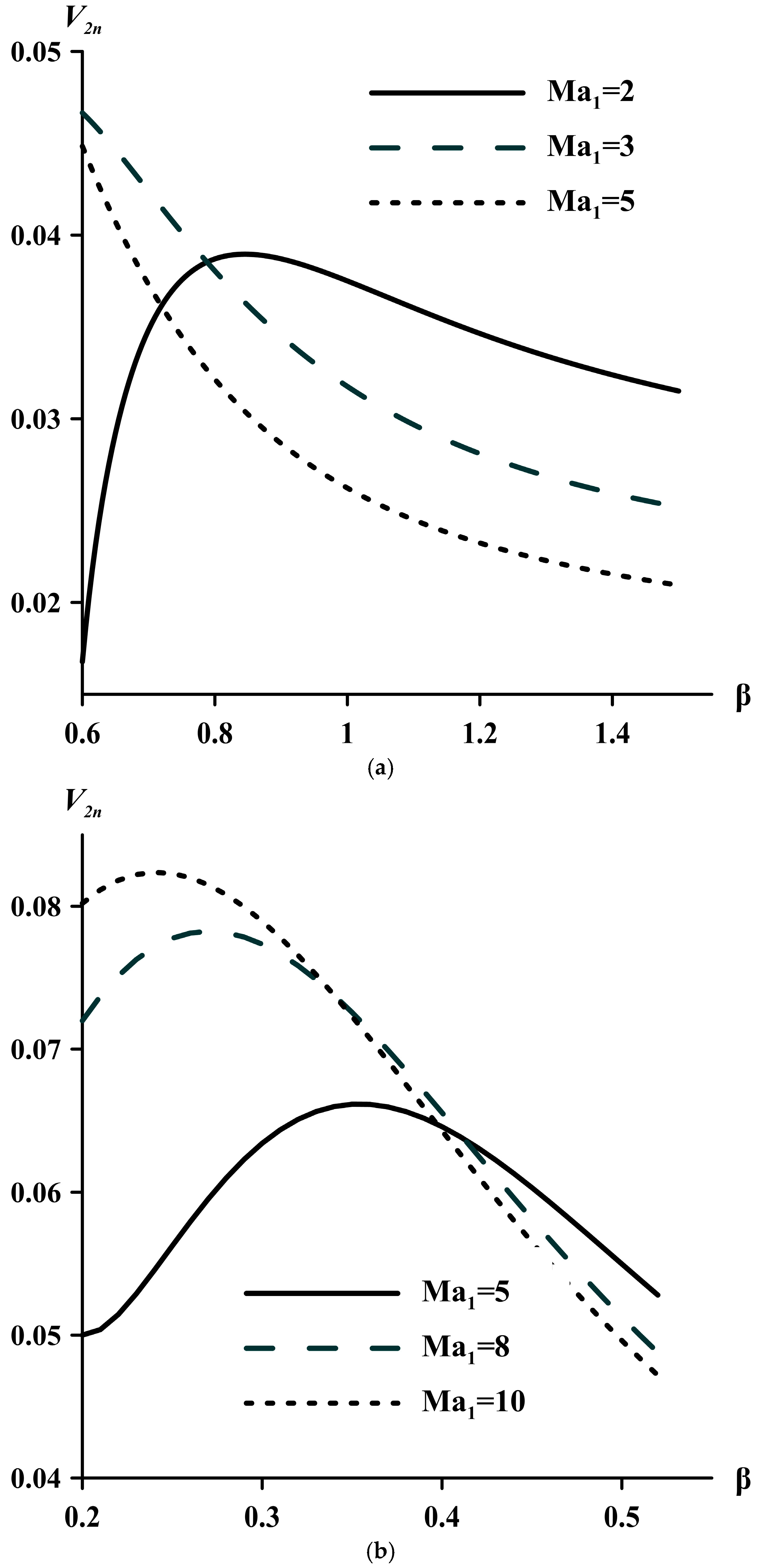This trend is reflected in Figure 3, which shows the effect of the angle β and the Mach number in front of the wave on the perturbations of dimensionless velocity perturbations behind it.

The dependence of the velocity pulsations behind the shock wave on the shock wave inclination angle β is of an extreme nature. With increasing Mach number, the maximum of the curves shifts to the region of smaller values of the angle β (Figure 3b). For large values of the Mach number (Ma > 5), the velocity disturbances behind the shock wave become greater than the velocity disturbances in front of the wave. This is due to the nature of the change in the kinetic energy of the flow behind the shock wave.

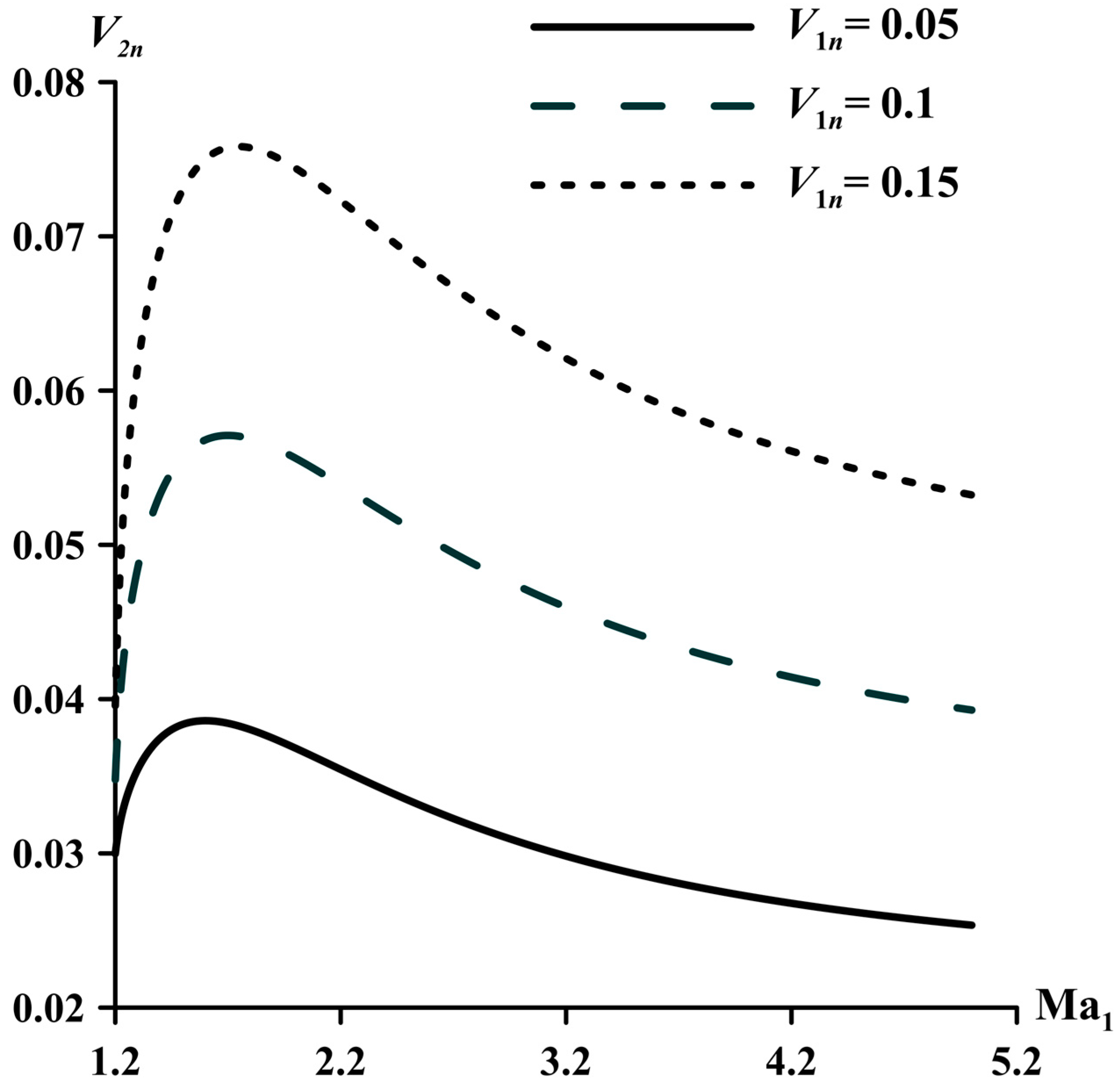
Figure 4 shows the influence of the Mach number in front of the wave on the perturbations of dimensionless velocity behind it for the angle β = π/3.

The perturbations of velocity behind the shock wave V_2n depending on the magnitude of the perturbations of velocity in front of the wave increase only in a narrow range of Mach number values from 1 to 1.8. For Ma₁ > 1.8, as Ma₁ increases, the perturbations of velocity behind the shock wave decrease, and the flow becomes more stable. The same character of the influence of the Mach number on the perturbations of velocity behind the shock wave is observed during a direct shock, which is consistent with the data of the work [28]. Thus, the well-known fact that compressibility stabilizes the flow is confirmed [28].

The influence of the perturbations of the flow parameters in front of the shock wave on the perturbations of density behind it is determined by Equation (40).

$$R_2={\displaystyle \frac{-R_1{W}_n+M{a}_1^2\left(R_1{W}_n\left(W_n+k\left(-1+W_n-W_t\right)+W_t\right)+V_{1n}\left(W_n-1\right)\left(1+W_n+k\right)\left(-1+W_n-2W_t\right)-\left(k-1\right)\left(W_n-1\right){\mathsf{\theta }}_1\right)}{W_n\left(-\Pi +M{a}_1^2{W}_n\left(W_n+W_t-k{W}_t\right)\right)}}$$

(40)

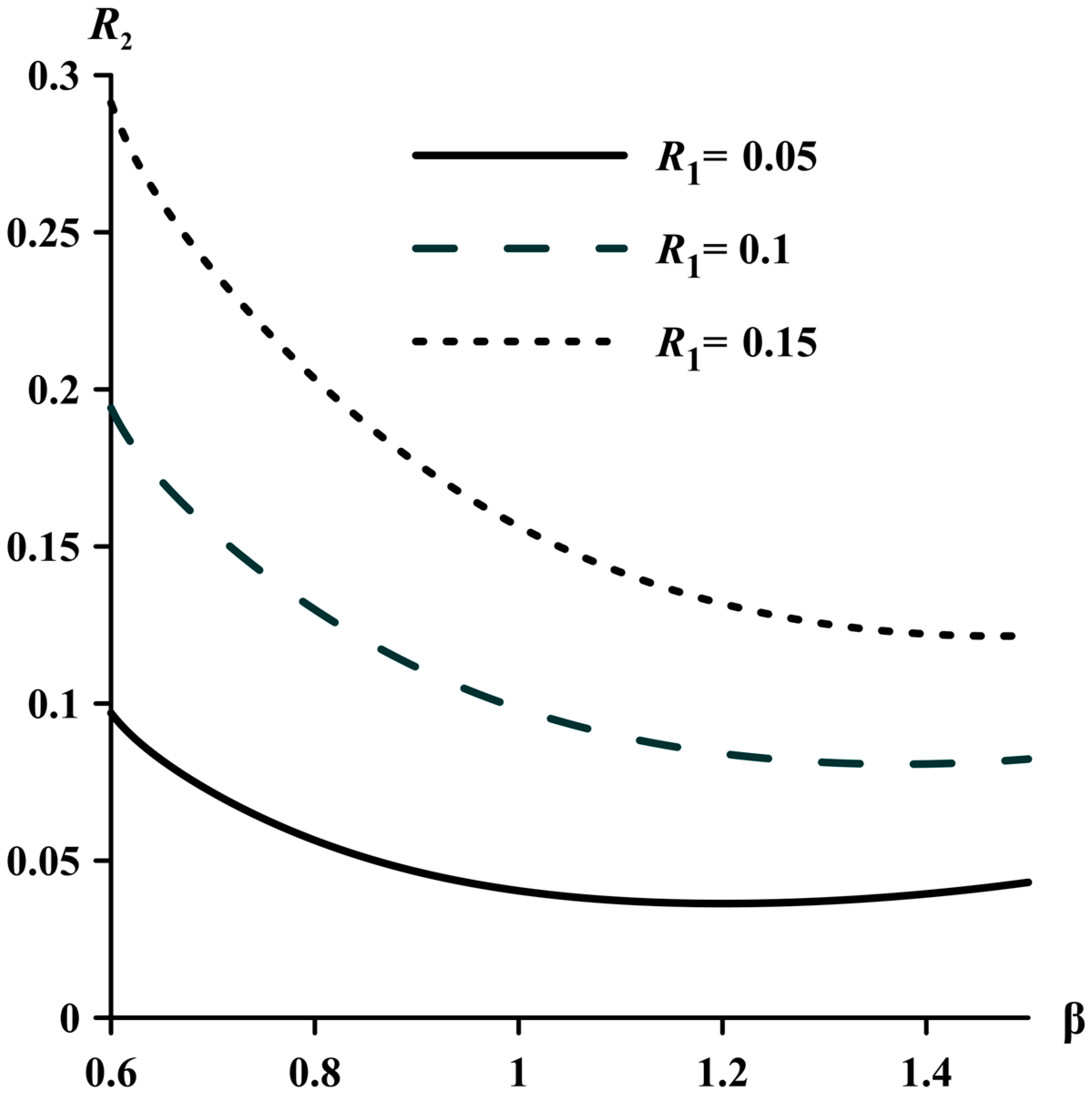
The effect of angle β on the nature of changes in perturbations of dimensionless density behind the shock wave is shown in Figure 5.

In the region of small values of the angle β, an increase in perturbations of density behind the shock wave is observed compared to perturbations of density in front of the wave. As the angle of perturbation increases, the density before and after the shock wave becomes almost identical. This nature of the change in perturbations of density during the passage of an oblique shock wave is due to the fact that at small values of the angle β, the increase in the density of flow behind the wave is insignificant. Against this background, the increase in the perturbations of density behind the shock wave becomes noticeable. At large values of the angle β, the increase in the density of flow behind the shock wave is large. Therefore, against the background of a strong increase in the density of flow behind the wave, the change in the perturbations of density of flow behind it is insignificant.

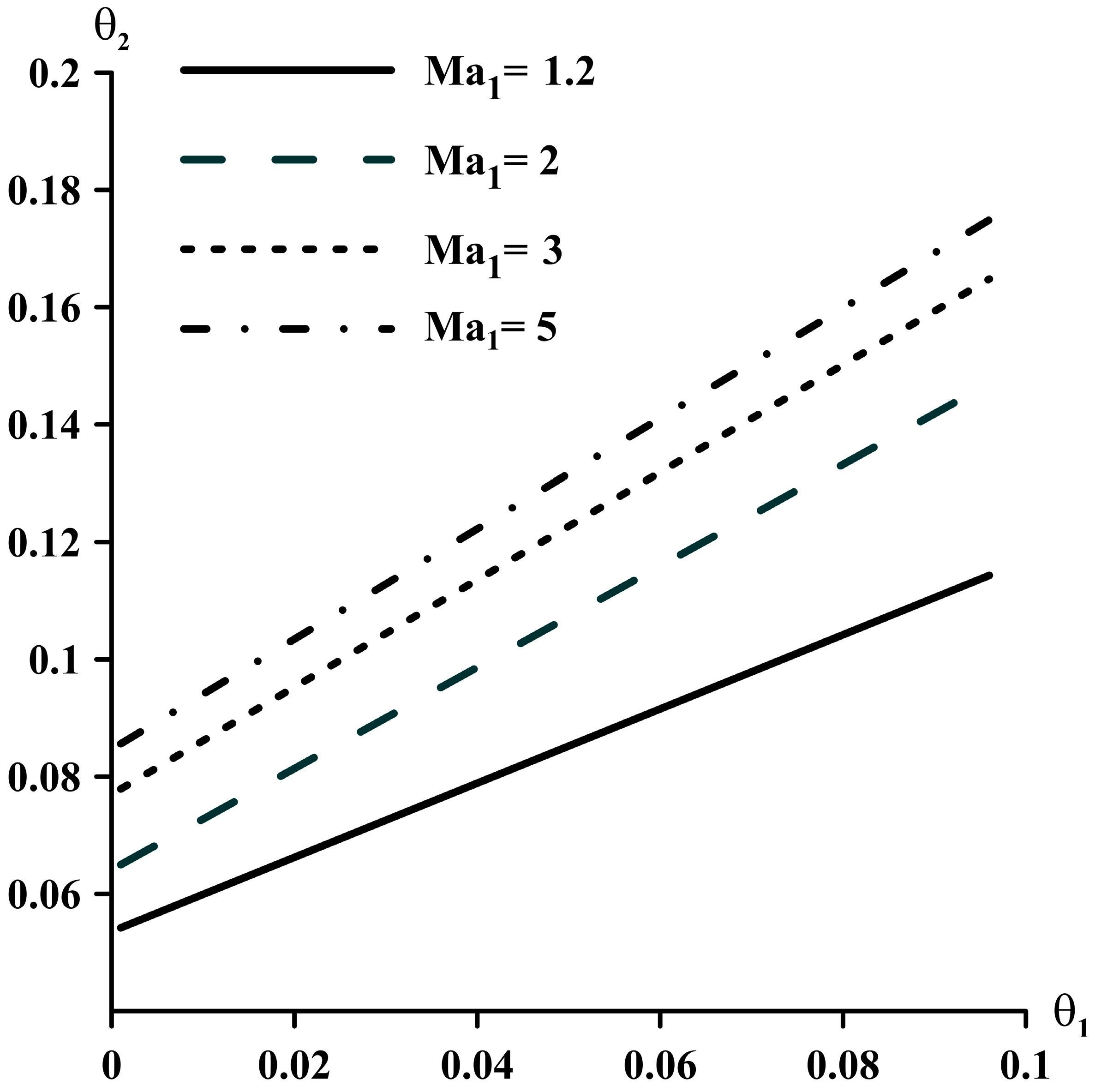
The effect of the perturbations of temperature in front of the wave on the perturbations of temperature behind it is described by Equation (41).

$${\mathsf{\theta }}_2={\displaystyle \frac{\Pi \left(-R_1{W}_n\left(W_n+W_t\right)-V_{1n}\left(W_n-1\right)\left(1+W_n+2W_t\right)+{\mathsf{\theta }}_1\right)+{W_n}^2\left(\left(W_n+W_t\right)\left(R_1-M{a}_1^2{\mathsf{\theta }}_1\right)+kM{a}_1^2\left(-\left(W_n-1\right)\left(V_{1n}\left(W_n-1\right)+R_1\left(W_n+W_t\right)\right)+\left(W_n+W_t-1\right){\mathsf{\theta }}_1\right)\right)}{\Pi -M{a}_1^2{W}_n\left(W_n+W_t-k{W}_t\right)}}$$

(41)

Figure 6 shows the influence of Mach numbers on the perturbations of dimensionless temperature behind the shock wave for the angle β = π/3.

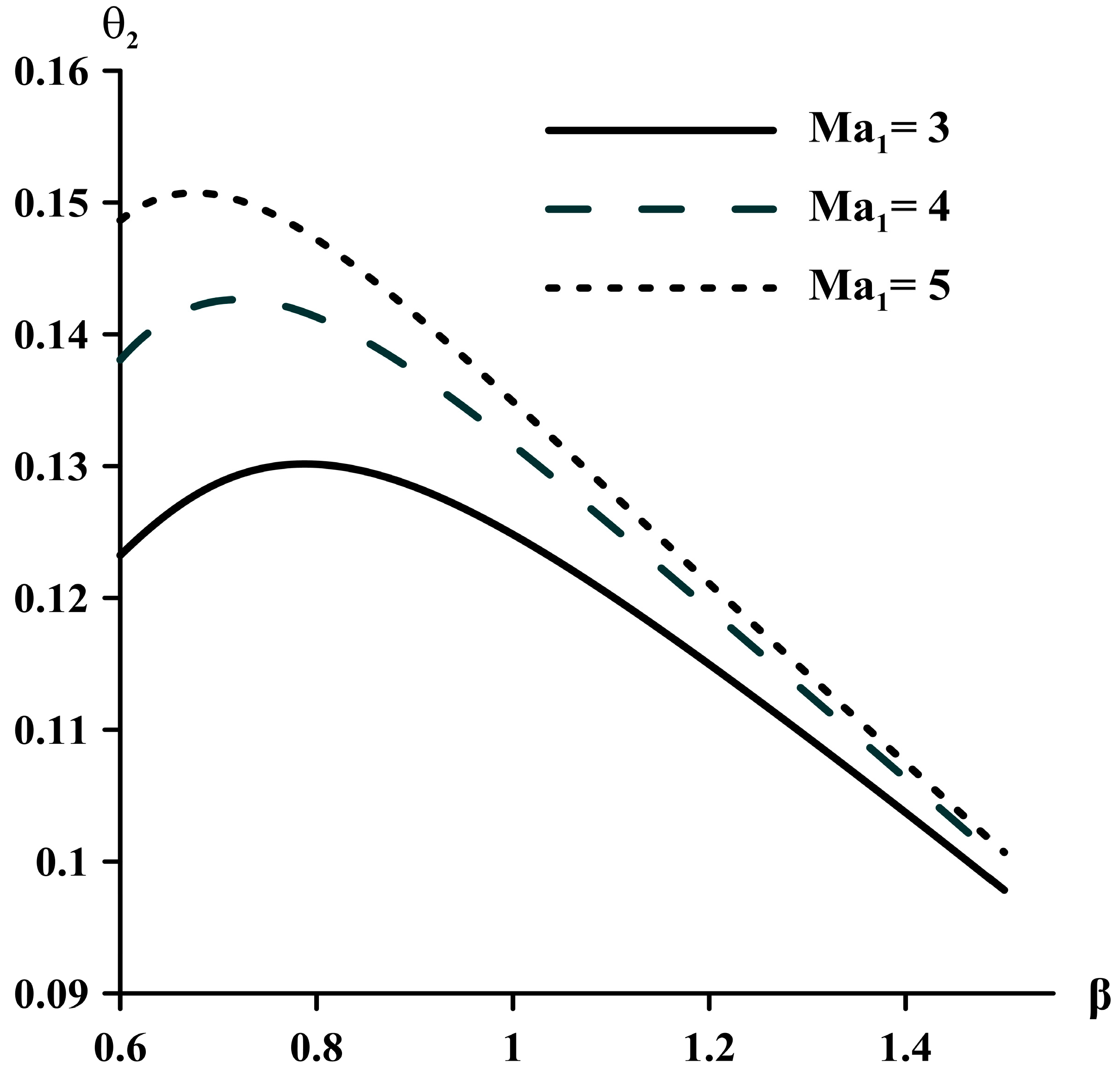
As the Mach number increases, the temperature of the flow behind the shock wave increases. And this also leads to an increase in temperature instability behind the shock wave. The combined influence of angle β and the Mach number on perturbations of dimensionless temperature ${\mathsf{\theta }}_2$ behind the shock wave is shown in Figure 7.

Temperature instability is extremely dependent on the angle β. As the Mach number increases, the maximum values of the perturbations of temperature behind the shock wave shift to smaller angles. At large angles β, the increase in the temperature of flow behind the shock is significant. Contrary to the trend of a strong increase in temperature, the relative values of temperature perturbations at large angles decrease.

As a result of solving Equations (23), (24), and (38), an equation was obtained that determines the influence of the pressure perturbations in front of the shock wave on the pressure perturbations behind it

$$P_2={\displaystyle \frac{-V_{1n}\left(W_n-1\right)\left(2\Pi +\left(k-1\right){\mathrm{Ma}}_1^2\left(W_n-1\right)W_n+R_1\left(\Pi +W_n-2\Pi W_n-\left(k-1\right){\mathrm{Ma}}_1^2\left(W_n-1\right)W_n\right)\left(W_n+W_t\right)\right)+P_1\left(\Pi +{\mathrm{Ma}}_1^2{W}_n\left(-W_n-W_t+k\left(-1+W_n+W_t\right)\right)\right)}{\Pi -{\mathrm{Ma}}_1^2{W}_n\left(W_n+W_t-k{W}_t\right)}}$$

(42)

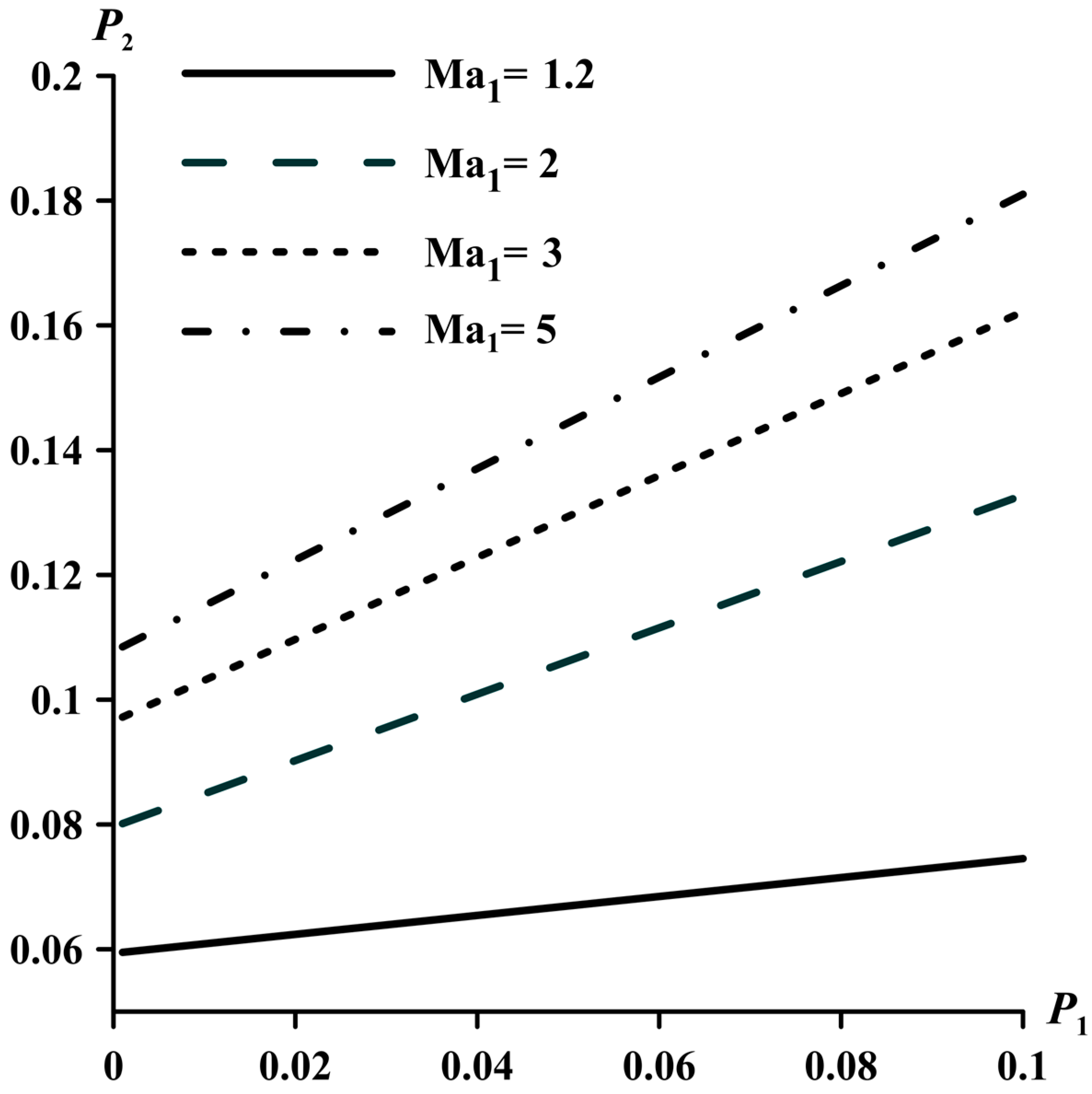
The effect of the perturbations of dimensionless pressure before the shock wave on the pressure perturbations behind it for different values of Mach numbers is shown in Figure 8.

As the Mach number and $P_1$ increases, the pressure perturbations behind the shock wave increase. For Ma₁ = 1.2, an increase in $P_1$ has little effect on the values $P_2$. Only small perturbations are amplified. For large values of Ma₁, the pressure perturbations behind the shock wave exceed the pressure perturbations in front of it. An increase in Mach numbers contributes to an increase in the instability of pressure behind the shock wave.

Fluctuations of velocity behind the shock wave V_2n (Figure 2), temperature θ₂ (Figure 6), and pressure P₂ (Figure 8) may not be equal to zero when the corresponding fluctuations before the shock wave are equal to zero, since they depend on fluctuations of other parameters before the shock wave, which are not equal to zero. Their values are indicated in the figure captions. For instance, in Figure 2, according to Equation (39), for V_1n = 0 it may turn out that V_2n > 0 due to the influence of density fluctuations R₁ = 0.05 and temperature θ₁ = 0.05. Similarly, in Figure 6 (Equation (41)), θ₂ depends not only on θ₁, but also on velocity fluctuations V_1n = 0.05 and density R₁ = 0.05. In Figure 8 (Equation (42)), P₂ depends on V_1n = 0.05 and R₁ = 0.05.

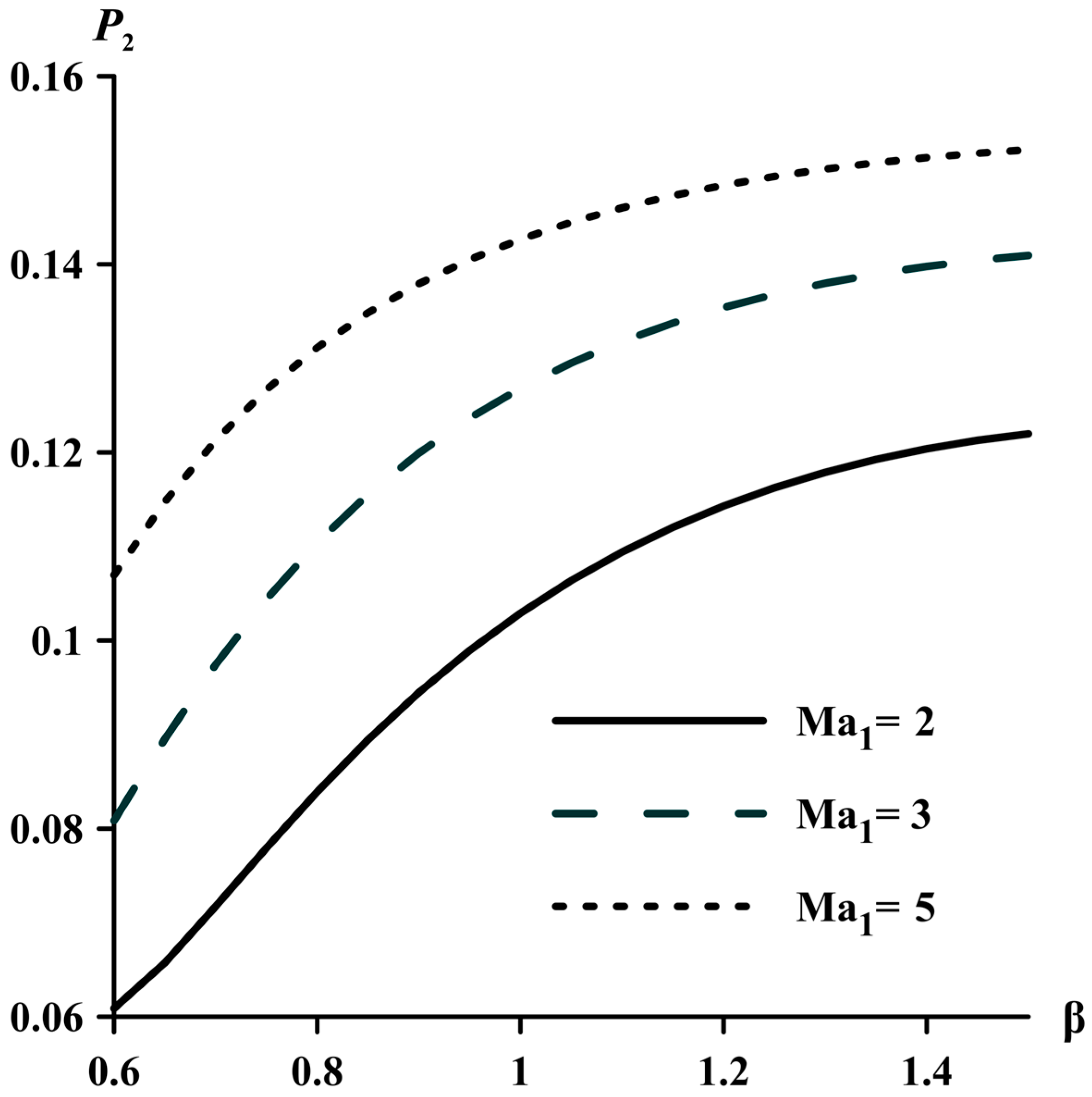
Figure 9 elucidates the combined influence of the angle β and Mach numbers on perturbations of dimensionless pressure behind the shock wave.

As the angle β and Mach number increase, the pressure perturbations behind the shock wave increase and remain larger than the pressure perturbations in front of the wave. As the angle β increases, the growth of $P_2$ slows down, which is associated with an increase in the pressure behind the shock wave. Contrary to the trend of a strong increase in flow pressure behind the shock wave, the relative values of perturbations of pressure at large angles decrease.

4. Conclusions

This work investigates the effect of an oblique shock wave on the transformation of perturbations in the parameters of a supersonic gas flow in the range of Mach number changes from 1.2 to 10 and shock wave inclination angles from 15° to 90°.

The effect of the shock wave inclination angle β, the Mach number, the intensity of the perturbations of the temperature, density, velocity, and pressure in front of the shock wave on the perturbations in the parameters of flow behind the shock wave is considered. The effect of the velocity perturbation in front of the wave on the velocity perturbation behind it is shown for different values of the angle β and the Mach number in front of the shock wave.

With increasing angle β, the velocity pulsations behind the shock wave first increase, reach a maximum, and then decrease. With the increasing Mach number, the maximum of the curves shifts to the region of smaller values of angle β.

The velocity perturbations behind the shock wave V_2n depending on the magnitude of velocity perturbations in front of the wave increase only in a narrow range of Mach numbers from 1 to 1.8. For Ma₁ > 1.8, as Ma₁ increases, the perturbations of velocity behind the shock wave decrease, and the flow becomes more stable. The same character of the influence of the Mach number on the velocity perturbations behind the shock wave is observed when the flow passes through a direct shock, which is consistent with the data of the work [28]. Thus, the well-known fact [28] that compressibility stabilizes the flow was confirmed.

The effect of the angle β on the density perturbations behind the shock wave was shown. In the region of small values of the angle β, an increase in the density perturbations behind the shock wave was observed compared to the density perturbations in front of the wave. As the angle of perturbation increases, the density perturbations before and after the shock wave become almost identical. This nature of variation in density perturbations during the passage of an oblique shock wave is due to the fact that at small values of the angle β, the increase in flow density behind the wave is insignificant. Contrary to this trend, the increase in the density perturbations behind the shock wave becomes noticeable. At large values of the angle β, the increase in the density of the flow behind the shock wave is large. Therefore, contrary to the trend, there is a strong increase in the density of flow behind the wave, and the variation of density perturbations behind it is insignificant.

The effect of the Mach number on the temperature perturbations behind the shock was analyzed. As the Mach number increases, the temperature of the flow behind the shock wave increases. And this also leads to an increase in temperature instability behind the shock wave. Temperature instability is extreme depending on the angle β. As the Mach number increases, the maximum values of the temperature perturbations behind the shock wave shift to smaller angles. At large angles β, the increase in the temperature of flow behind the shock is significant. Contrary to the trend of a strong increase in the temperature of flow, the relative values of the perturbations of temperature at large angles decrease.

The effect of the pressure perturbations in front of the wave on the pressure perturbations behind it was discussed. As the angle β and Mach number increase, the pressure perturbations behind the shock wave increase and remain larger than the pressure perturbations in front of the wave. As the angle β increases, the growth of $P_2$ slows down, which is associated with an increase in the pressure of flow behind the shock wave. Contrary to a strong increase in the pressure of flow behind the shock wave, the relative values of the pressure perturbations at large angles decrease.

In further studies, it is necessary to analyze the transformation of perturbations in the flow when passing through a shock wave for a nonideal gas, e.g., for a van der Waals gas. Also, an urgent task is to study the flow in a shock wave during the interaction of natural turbulence and external perturbations that are caused by certain technological processes.

The results of the work are useful for predicting the flow around supersonic aerodynamic surfaces. They demonstrate the importance of the effects of the amplification of flow disturbances and determine the way in which spatial structures arise in supersonic flows when interacting with an oblique shock wave. In the future, it is planned to conduct similar studies for turbulent flow for a non-ideal gas under the influence of chemical reactions.