Deep Learning-Based Navigation System for Automatic Landing Approach of Fixed-Wing UAVs in GNSS-Denied Environments
Abstract
1. Introduction
- -
- Implementing a comprehensive autonomous vision-based landing system that includes target detection, positioning, navigation, and control and applying it to the autonomous landing of a fixed-wing UAV equipped with a monocular camera.
- -
- Using deep learning frameworks to replace optical positioning methods can provide higher accuracy and robustness in complex environments.
- -
- Integrating the guidance law and controller enables the aircraft to be guided onto the glide slope and localizer, even if it deviates from the runway.
2. Related Works
3. System Overview
3.1. Research Overview
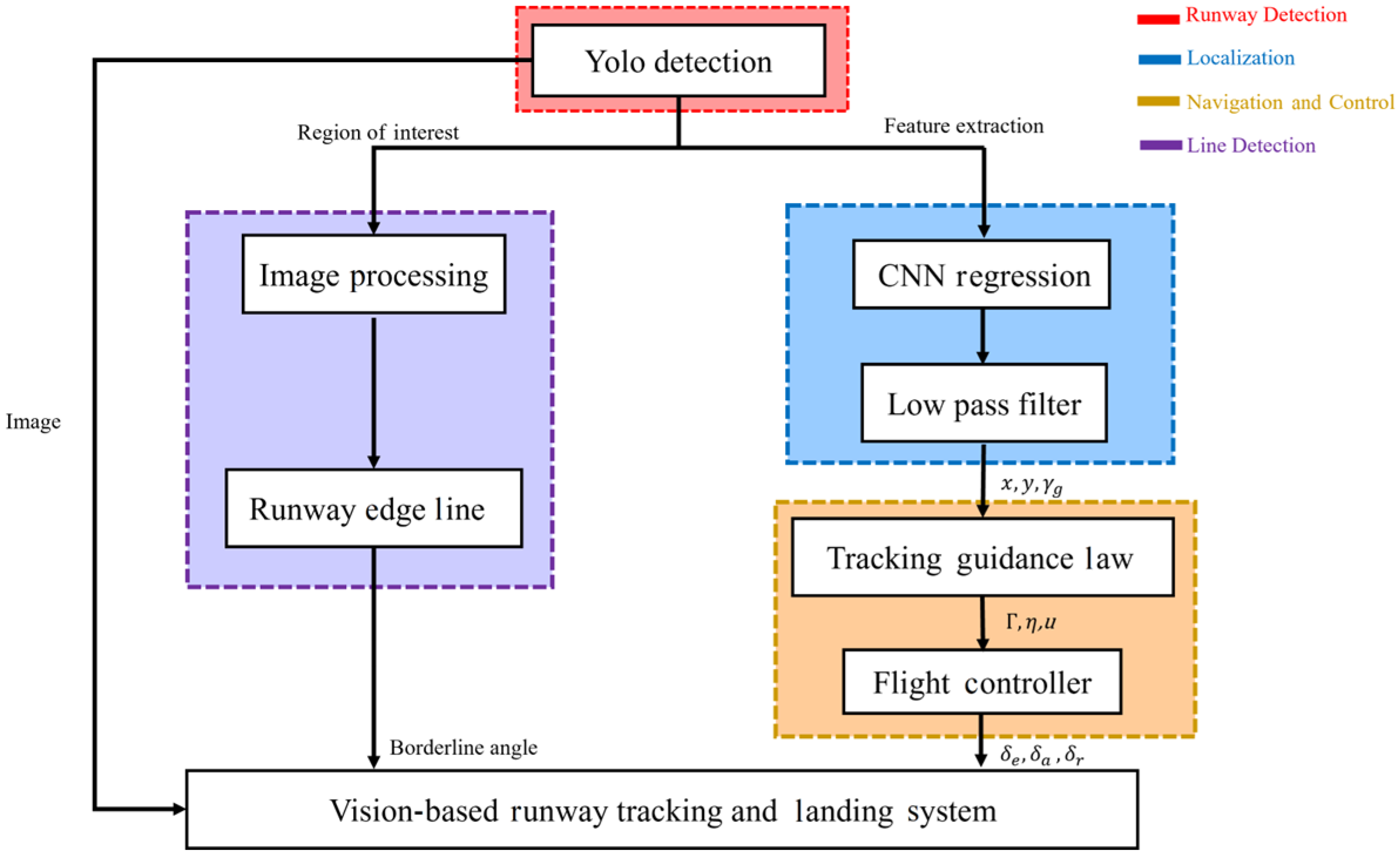
3.2. Architecture of Runway Detection and Tracking System
4. Runway Detection and Localization
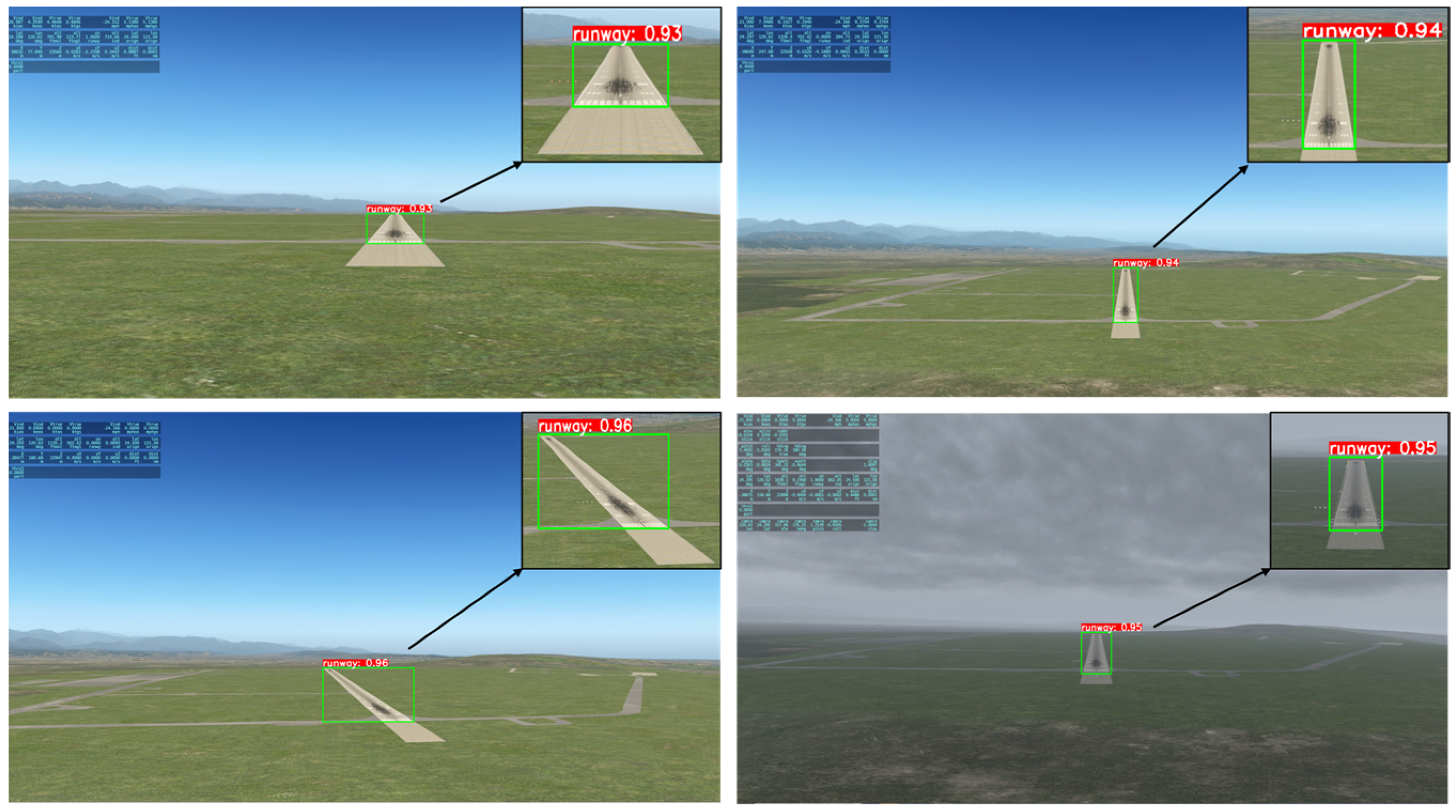
4.1. Real-Time Detection-YOLOv8
4.2. CNN Regression Model for Distance Estimation
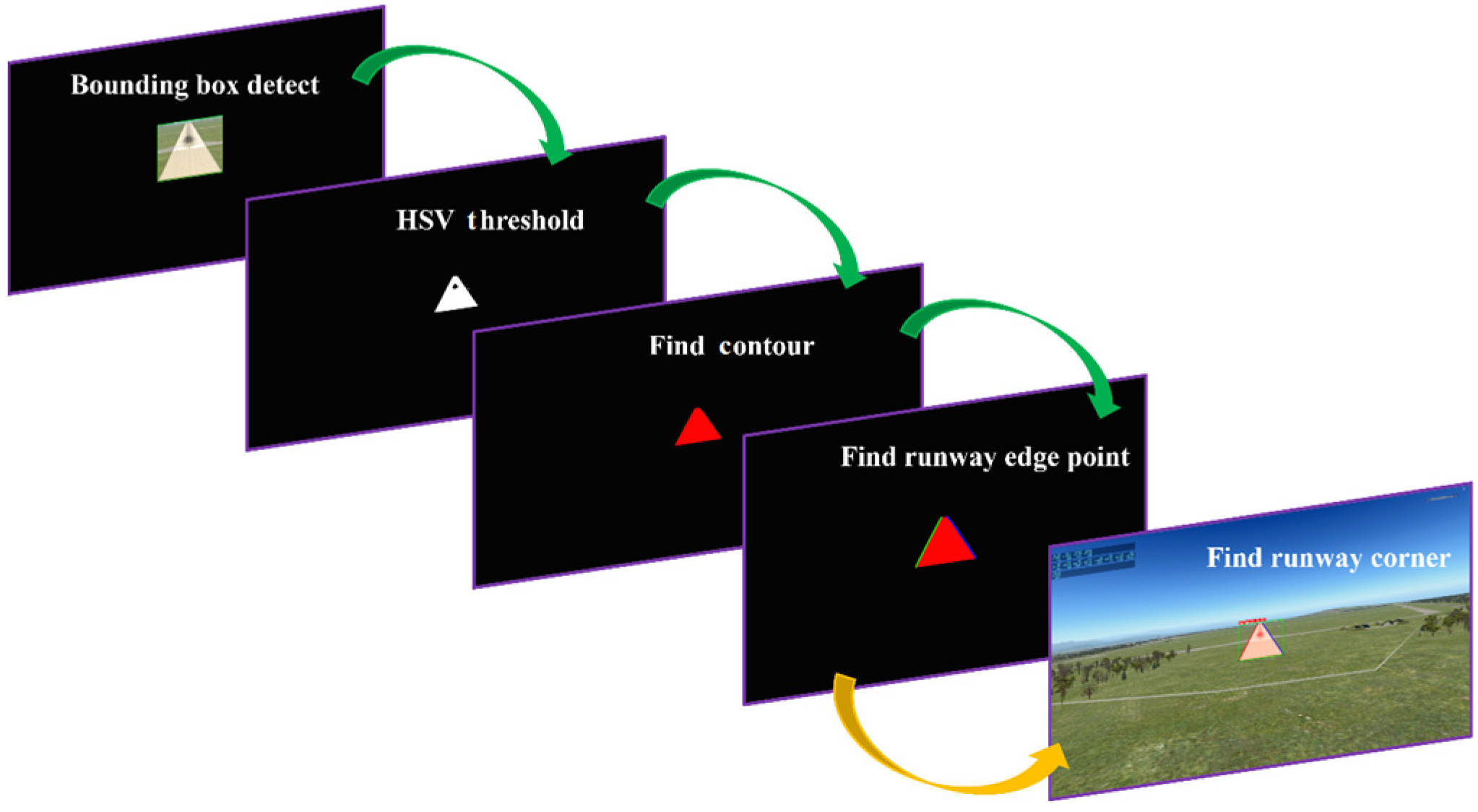
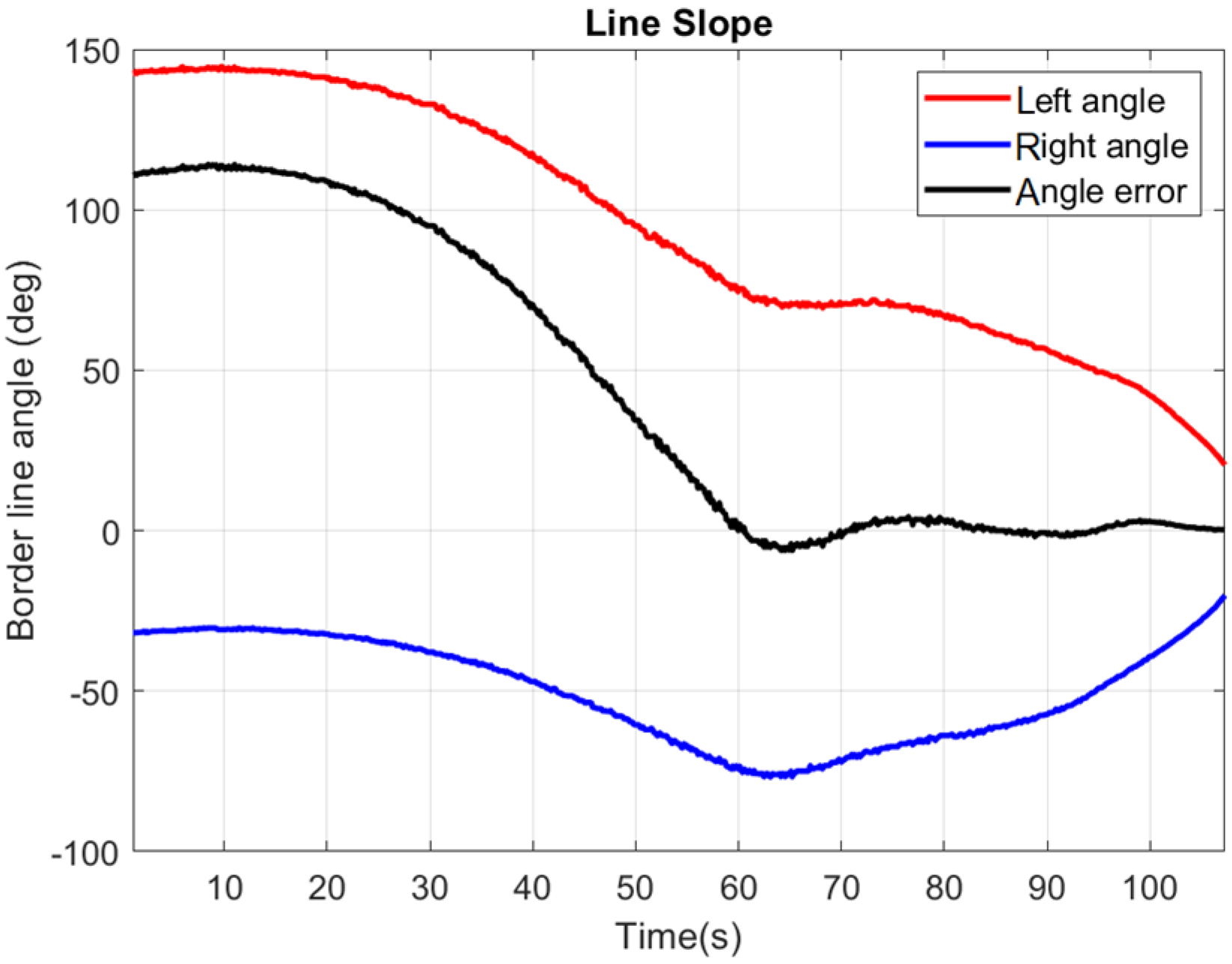
4.3. Image Processing for Runway Centerline Detection
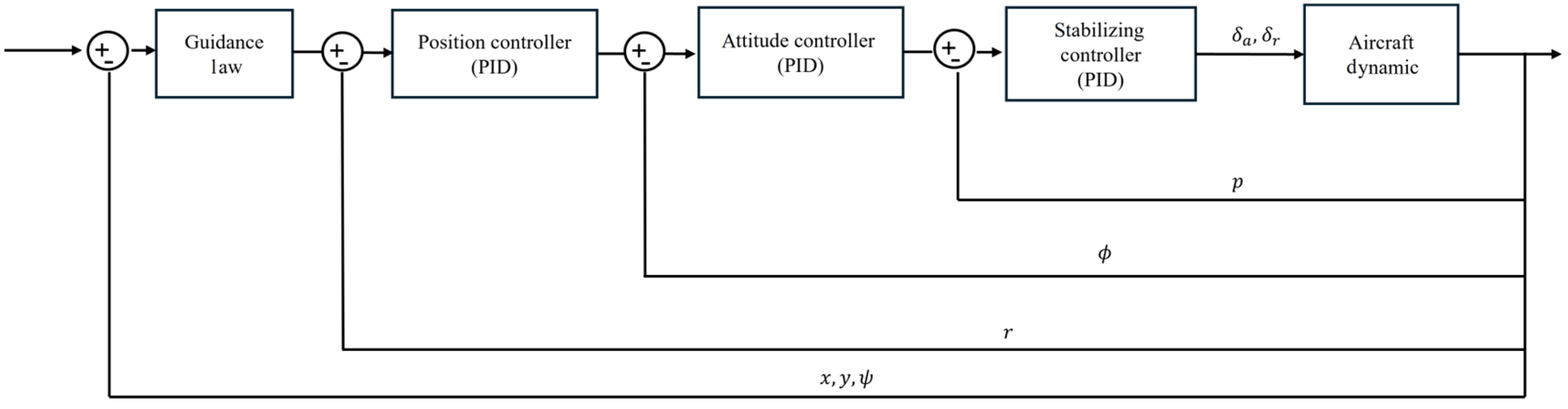
5. Runway Tracking and Automatic Landing Control
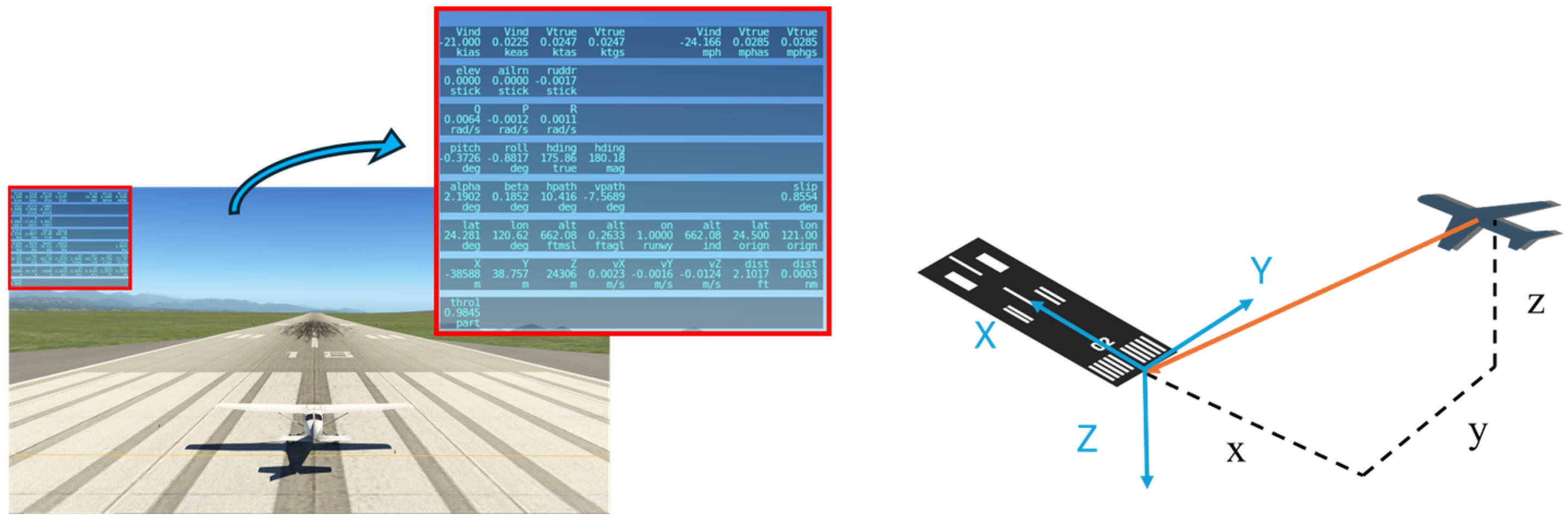
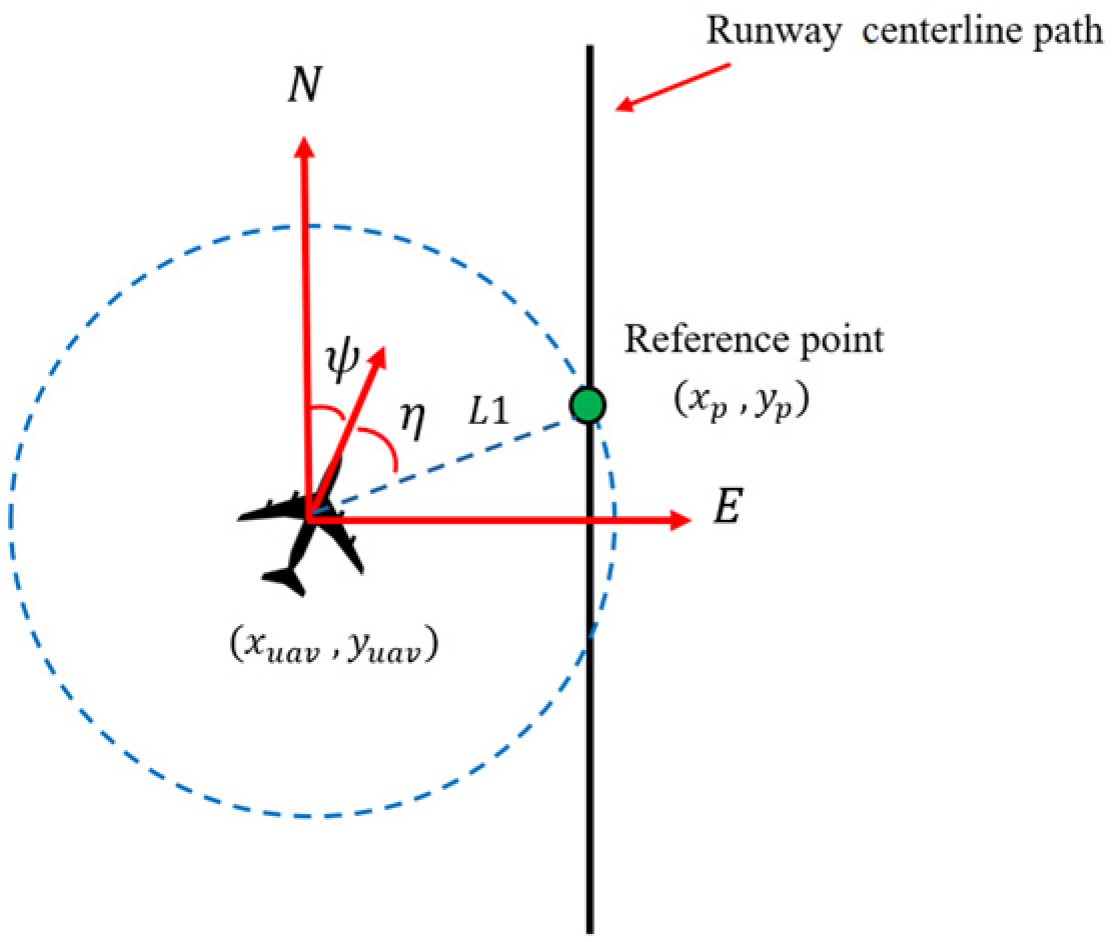
5.1. System Coordinate Definition
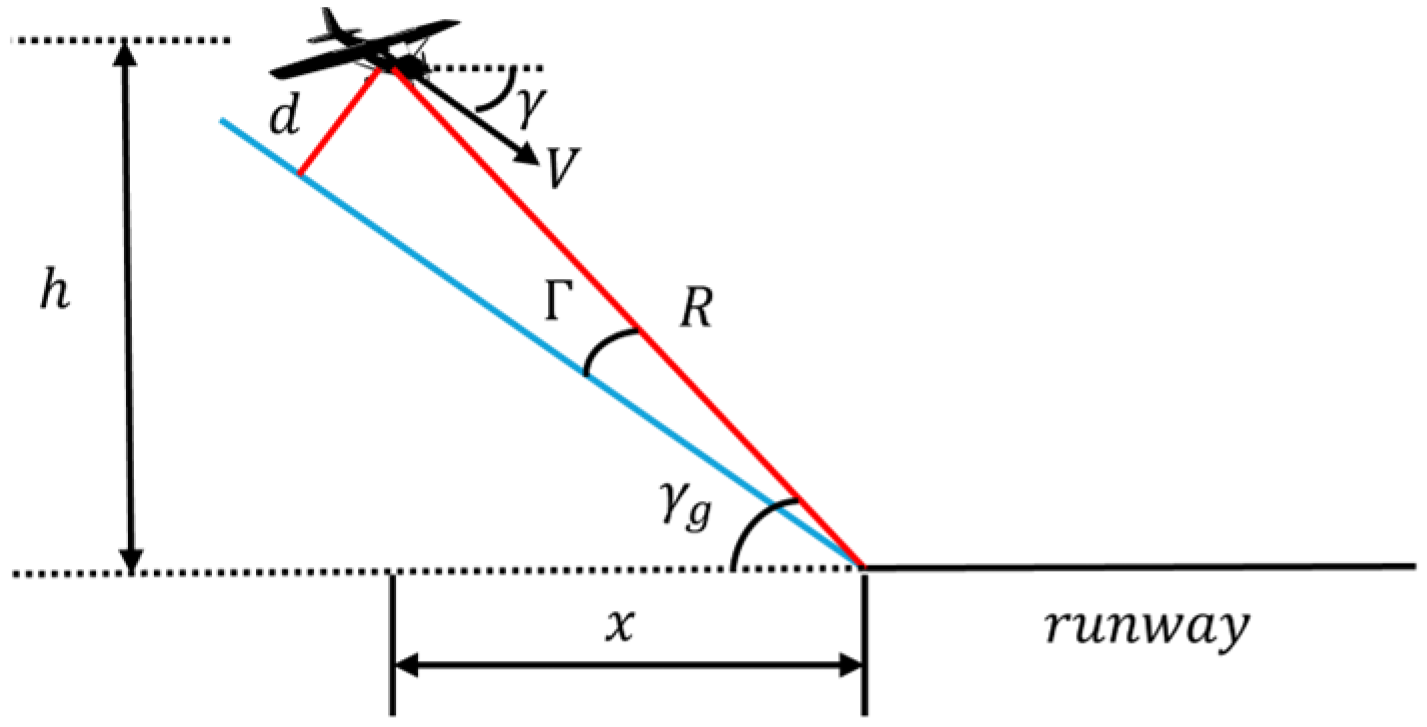
5.2. Glide Slope for Longitudinal Control
5.3. Runway Centerline Tracking for Lateral Control
6. Automatic Landing Simulations and Results
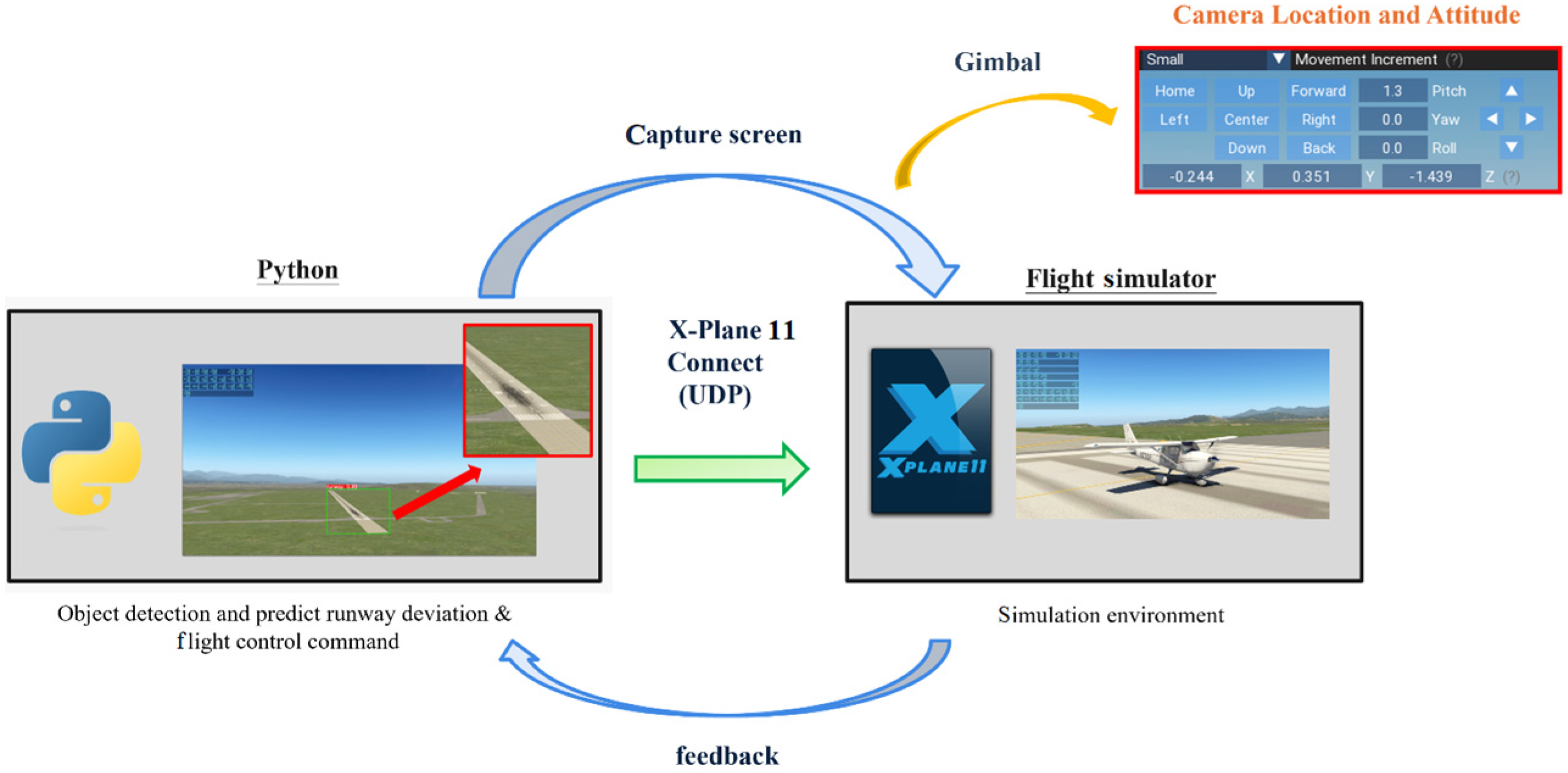
6.1. Simulation Environment Setup
6.2. Simulation Cases
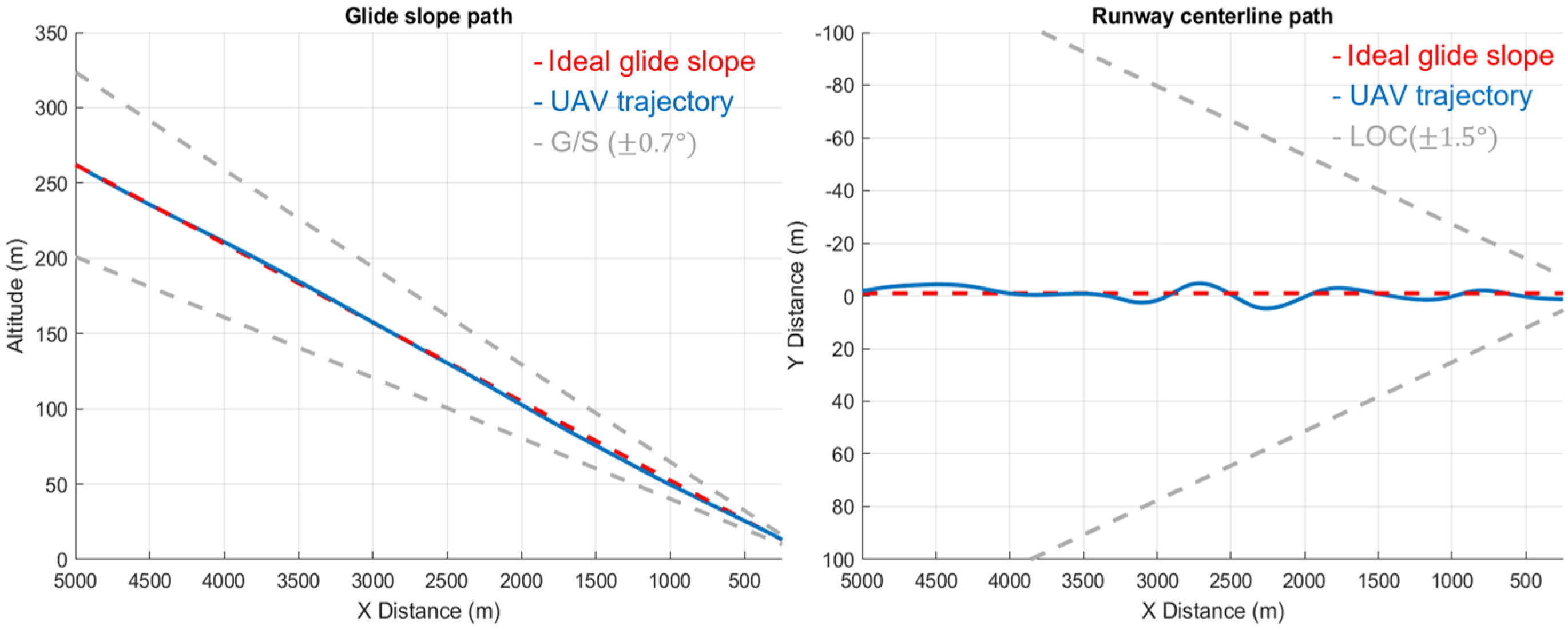
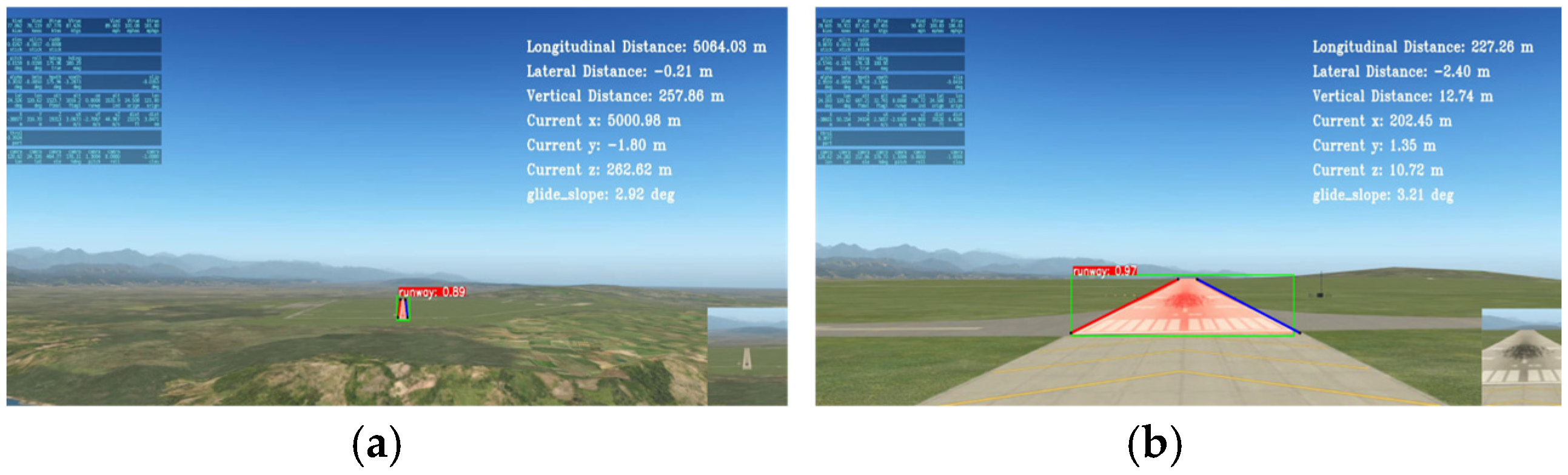
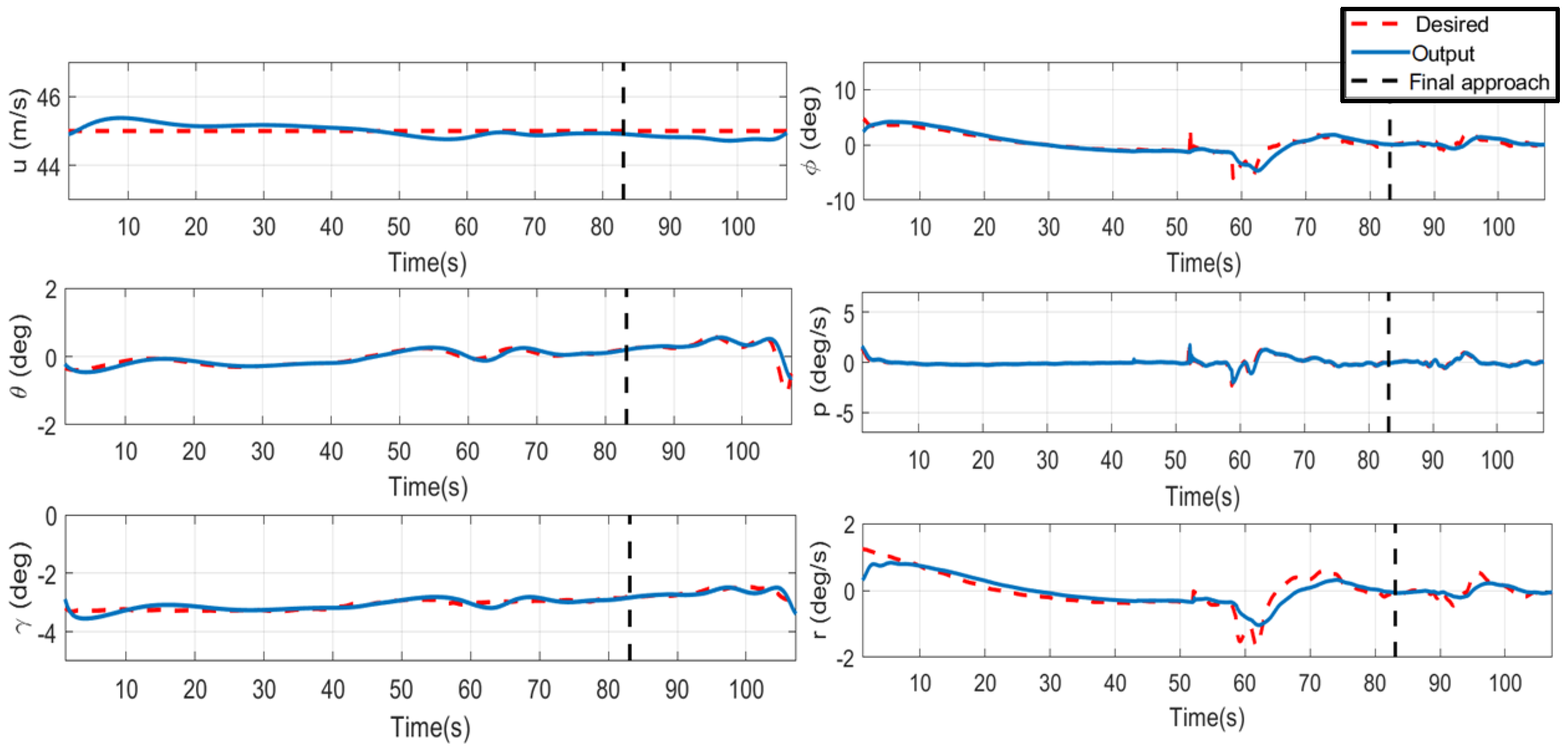
6.2.1. Case 1: 5 Km and 3° Glide Slope Landing
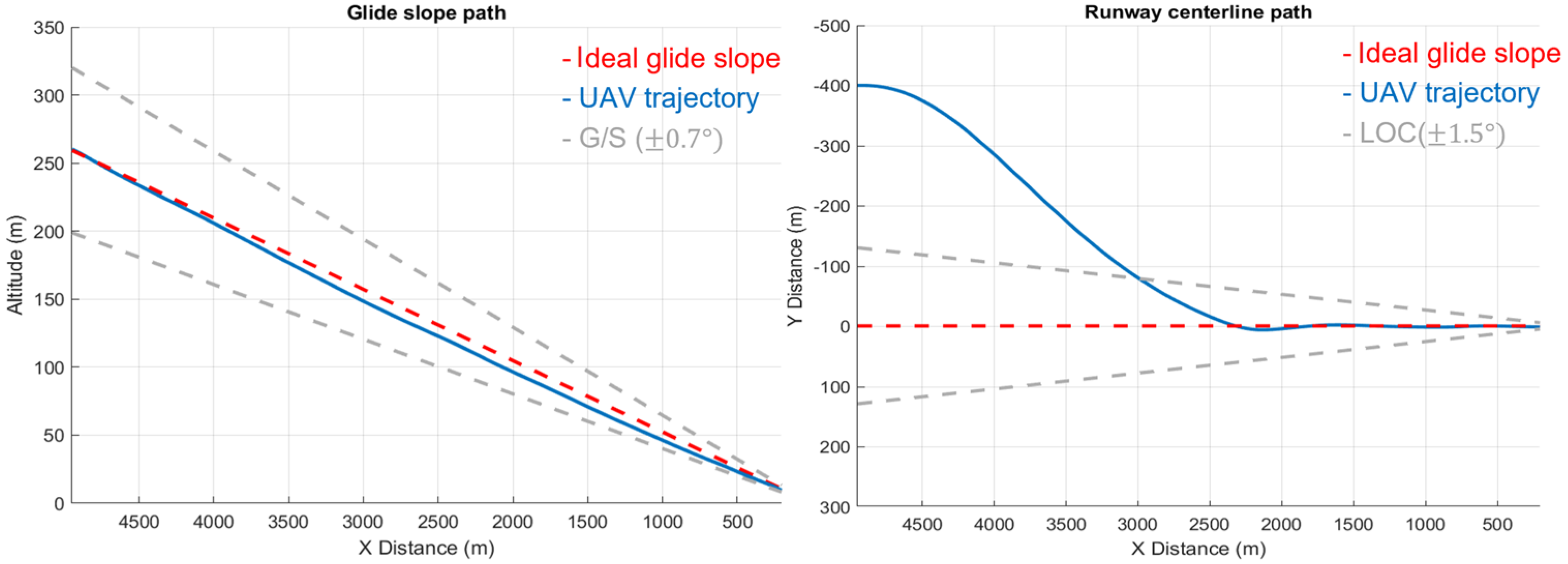
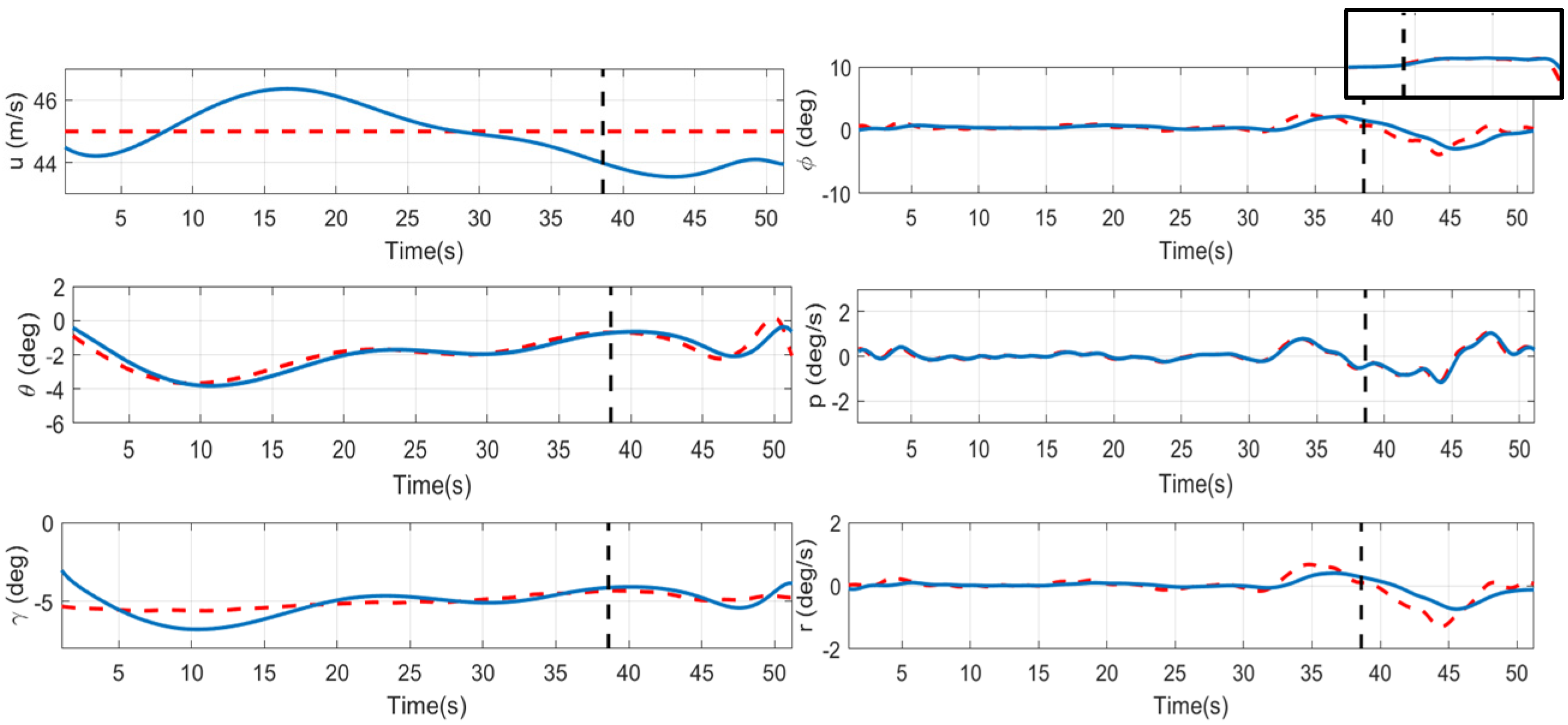
6.2.2. Case 2: Left Cross with 5° Path
6.2.3. Case 3: 2 Km and 5° Glide Slope Landing
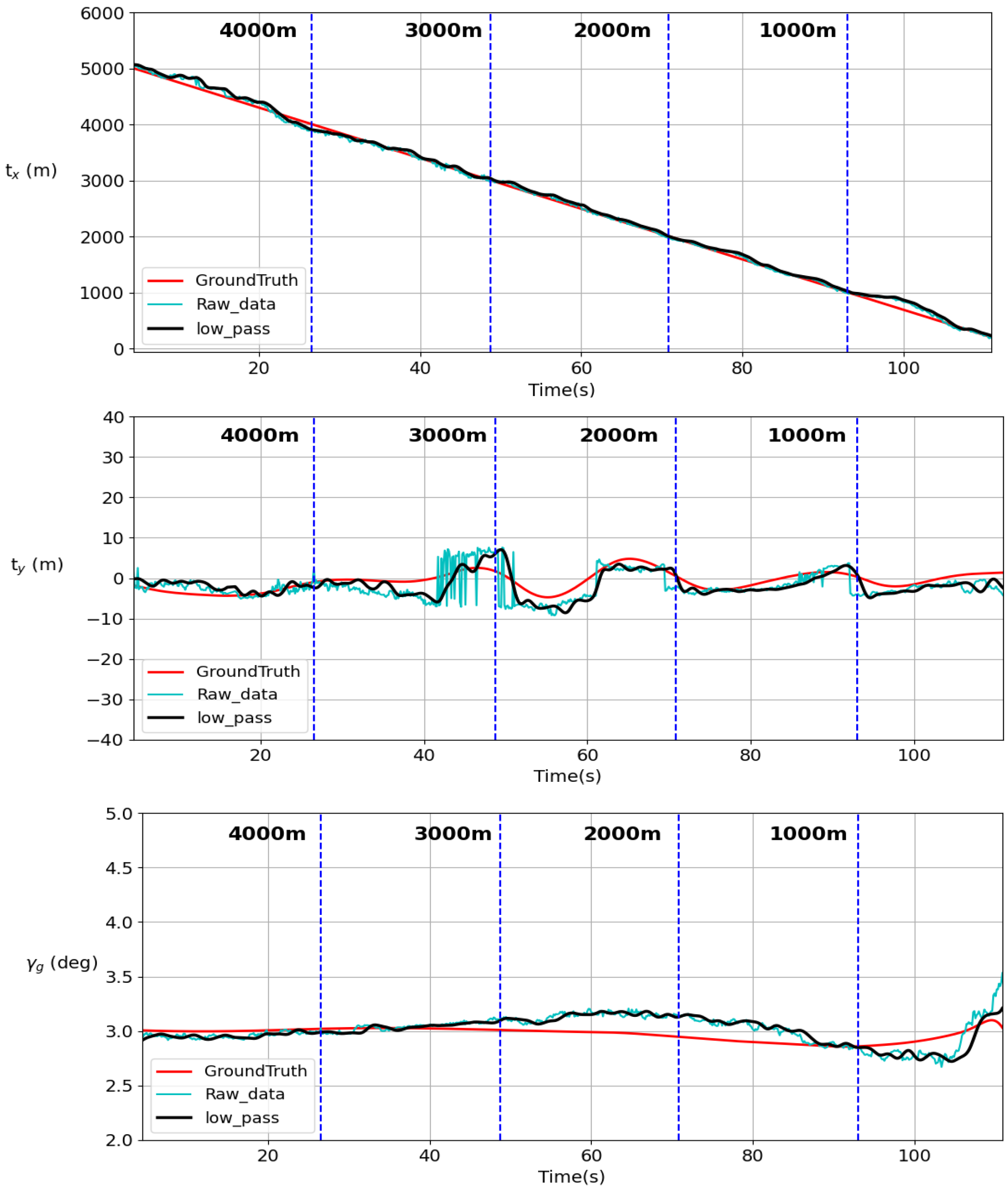
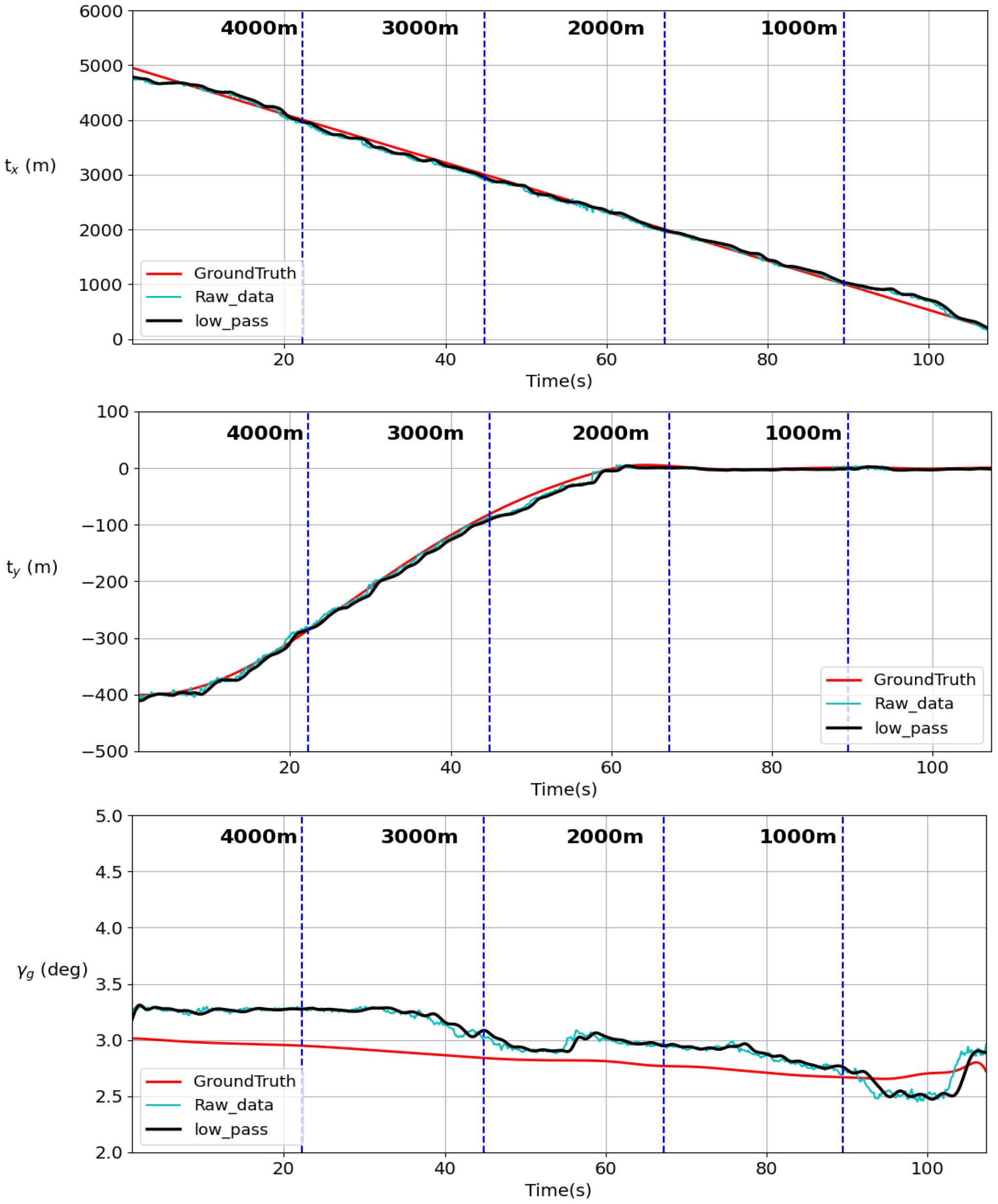
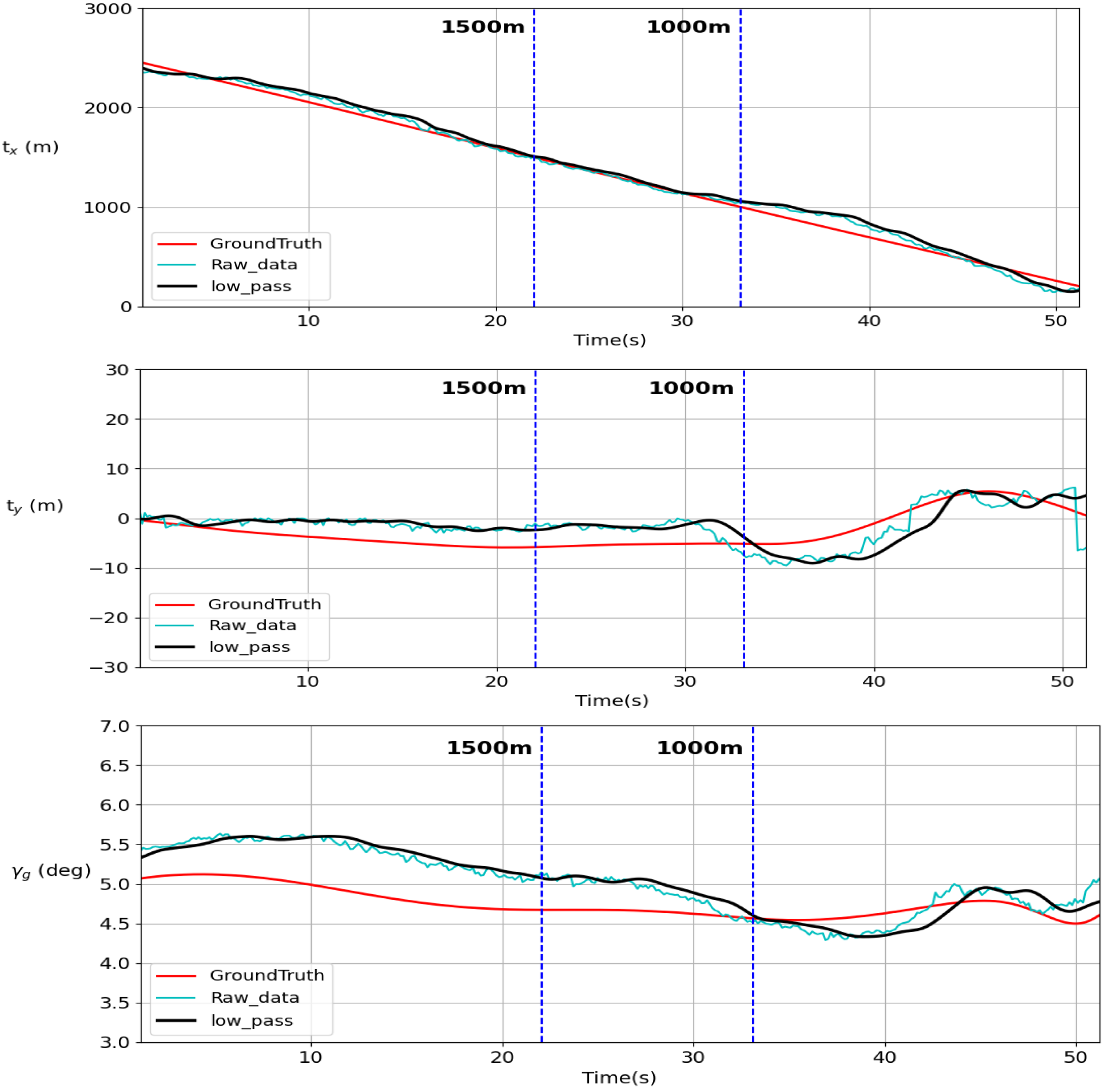
6.3. Simulation Result Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Balduzzi, G.; Ferrari Bravo, M.; Chernova, A.; Cruceru, C.; van Dijk, L.; de Lange, P.; Jerez, J.; Koehler, N.; Koerner, M.; Perret-Gentil, C. Neural Network Based Runway Landing Guidance for General Aviation Autoland; Department of Transportation, Federal Aviation Administration: Washington, DC, USA, 2021. [Google Scholar]
- Watanabe, Y.; Manecy, A.; Amiez, A.; Aoki, S.; Nagai, S. Fault-tolerant final approach navigation for a fixed-wing uav by using long-range stereo camera system. In Proceedings of the 2020 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 1–4 September 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1065–1074. [Google Scholar]
- Zhang, L.; Zhai, Z.; He, L.; Niu, W. Infrared-based autonomous navigation for civil aircraft precision approach and landing. IEEE Access 2019, 7, 28684–28695. [Google Scholar] [CrossRef]
- Kong, W.; Zhou, D.; Zhang, Y.; Zhang, D.; Wang, X.; Zhao, B.; Yan, C.; Shen, L.; Zhang, J. A ground-based optical system for autonomous landing of a fixed wing uav. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 4797–4804. [Google Scholar]
- Tripathi, A.K.; Patel, V.V.; Padhi, R. Vision based automatic landing with runway identification and tracking. In Proceedings of the 2018 15th International Conference on Control, Automation, Robotics and Vision (ICARCV), Singapore, 18–21 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1442–1447. [Google Scholar]
- Wang, Z.; Zhao, D.; Cao, Y. Visual navigation algorithm for night landing of fixed-wing unmanned aerial vehicle. Aerospace 2022, 9, 615. [Google Scholar] [CrossRef]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Terven, J.; Cordova-Esparza, D. A comprehensive review of yolo: From yolov1 to yolov8 and beyond. arXiv 2023, arXiv:2304.00501. [Google Scholar]
- Bolya, D.; Zhou, C.; Xiao, F.; Lee, Y.J. Yolact: Real-time instance segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 9157–9166. [Google Scholar]
- Wang, X.; Zhu, H.; Zhang, D.; Zhou, D.; Wang, X. Vision-based detection and tracking of a mobile ground target using a fixed-wing uav. Int. J. Adv. Robot. Syst. 2014, 11, 156. [Google Scholar] [CrossRef]
- Miyamoto, R.; Nakamura, Y.; Adachi, M.; Nakajima, T.; Ishida, H.; Kojima, K.; Aoki, R.; Oki, T.; Kobayashi, S. Vision-based road-following using results of semantic segmentation for autonomous navigation. In Proceedings of the 2019 IEEE 9th International Conference on Consumer Electronics (ICCE-Berlin), Berlin, Germany, 8–11 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 174–179. [Google Scholar]
- Ma, N.; Weng, X.; Cao, Y.; Wu, L. Monocular-vision-based precise runway detection applied to state estimation for carrier-based uav landing. Sensors 2022, 22, 8385. [Google Scholar] [CrossRef] [PubMed]
- Akbar, J.; Shahzad, M.; Malik, M.I.; Ul-Hasan, A.; Shafait, F. Runway detection and localization in aerial images using deep learning. In Proceedings of the 2019 Digital Image Computing: Techniques and Applications (DICTA), Perth, Australia, 2–4 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–8. [Google Scholar]
- Bhargavapuri, M.; Shastry, A.K.; Sinha, H.; Sahoo, S.R.; Kothari, M. Vision-based autonomous tracking and landing of a fully-actuated rotorcraft. Control Eng. Pract. 2019, 89, 113–129. [Google Scholar] [CrossRef]
- Chen, C.; Chen, S.; Hu, G.; Chen, B.; Chen, P.; Su, K. An auto-landing strategy based on pan-tilt based visual servoing for unmanned aerial vehicle in gnss-denied environments. Aerosp. Sci. Technol. 2021, 116, 106891. [Google Scholar] [CrossRef]
- Wolkow, S.; Schwithal, A.; Tonhäuser, C.; Angermann, M.; Hecker, P. Image-aided position estimation based on line correspondences during automatic landing approach. In Proceedings of the ION 2015 Pacific PNT Meeting, Honolulu, HI, USA, 20–23 April 2015; pp. 702–712. [Google Scholar]
- Wolkow, S.; Schwithal, A.; Angermann, M.; Dekiert, A.; Bestmann, U. Accuracy and availability of an optical positioning system for aircraft landing. In Proceedings of the 2019 International Technical Meeting of the Institute of Navigation, Reston, VA, USA, 28–31 January 2019; pp. 884–895. [Google Scholar]
- Lai, Y.-C.; Huang, Z.-Y. Detection of a moving uav based on deep learning-based distance estimation. Remote Sens. 2020, 12, 3035. [Google Scholar] [CrossRef]
- Ruchanurucks, M.; Rakprayoon, P.; Kongkaew, S. Automatic landing assist system using imu+ p n p for robust positioning of fixed-wing uavs. J. Intell. Robot. Syst. 2018, 90, 189–199. [Google Scholar] [CrossRef]
- Bicer, Y.; Moghadam, M.; Sahin, C.; Eroglu, B.; Üre, N.K. Vision-based uav guidance for autonomous landing with deep neural networks. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; p. 0140. [Google Scholar]
- Chaumette, F.; Hutchinson, S. Visual servo control. I. Basic approaches. IEEE Robot. Autom. Mag. 2006, 13, 82–90. [Google Scholar] [CrossRef]
- Machkour, Z.; Ortiz-Arroyo, D.; Durdevic, P. Classical and deep learning based visual servoing systems: A survey on state of the art. J. Intell. Robot. Syst. 2022, 104, 11. [Google Scholar] [CrossRef]
- Coutard, L.; Chaumette, F.; Pflimlin, J.-M. Automatic landing on aircraft carrier by visual servoing. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 2843–2848. [Google Scholar]
- Yang, L.; Liu, Z.; Wang, X.; Yu, X.; Wang, G.; Shen, L. Image-based visual servo tracking control of a ground moving target for a fixed-wing unmanned aerial vehicle. J. Intell. Robot. Syst. 2021, 102, 1–20. [Google Scholar] [CrossRef]
- You, D.I.; Jung, Y.D.; Cho, S.W.; Shin, H.M.; Lee, S.H.; Shim, D.H. A guidance and control law design for precision automatic take-off and landing of fixed-wing uavs. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Minneapolis, MN, USA, 13–16 August 2012; p. 4674. [Google Scholar]
- Park, S.; Deyst, J.; How, J. A new nonlinear guidance logic for trajectory tracking. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Providence, RI, USA, 16–19 August 2004; p. 4900. [Google Scholar]
- Lungu, R.; Lungu, M.; Grigorie, L.T. Alss with conventional and fuzzy controllers considering wind shear and gyro errors. J. Aerosp. Eng. 2013, 26, 794–813. [Google Scholar] [CrossRef]
- Shoouri, S.; Jalili, S.; Xu, J.; Gallagher, I.; Zhang, Y.; Wilhelm, J.; Jeannin, J.-B.; Ozay, N. Falsification of a vision-based automatic landing system. In Proceedings of the AIAA Scitech 2021 Forum, Virtual, 11–15 January 2021; p. 0998. [Google Scholar]
- Ultralytics YOLOv8. Available online: https://github.com/ultralytics/ultralytics (accessed on 27 February 2025).
- Wang, Q.; Feng, W.; Zhao, H.; Liu, B.; Lyu, S. Valnet: Vision-based autonomous landing with airport runway instance segmentation. Remote Sens. 2024, 16, 2161. [Google Scholar] [CrossRef]
- Shang, J.; Shi, Z. Vision-based runway recognition for uav autonomous landing. Int. J. Comput. Sci. Netw. Secur. 2007, 7, 112–117. [Google Scholar]







| Information on the Training Dataset | |
|---|---|
| Image resolution | 1920 × 1080 (pixels) |
| Field of View (FOV) | 60 (deg) |
| Longitudinal distance | 0~5500 (m) |
| Lateral distance | −900~900 (m) |
| Vertical distance | 0~900 (m) |
| Crossing angle | −10~10 (deg) |
| Glide slope angle | 2~10 (deg) |
| Distance (m) | 5000–3000 | 3000–1000 | 1000–200 | 5000–200 |
|---|---|---|---|---|
| Longitudinal (m) | 73.21 | 45.88 | 103.62 | 69.93 |
| Lateral (m) | 2.21 | 2.47 | 2.38 | 2.35 |
| Vertical (m) | 3.59 | 7.88 | 4.16 | 5.85 |
| Glide slope () | 0.044 | 0.148 | 0.135 | 0.114 |
| Distance (m) | 5000–3000 | 3000–1000 | 1000–200 | 5000–200 |
|---|---|---|---|---|
| Longitudinal (m) | 74.82 | 38.77 | 122.00 | 73.61 |
| Lateral (m) | 7.45 | 8.28 | 1.92 | 7.24 |
| Vertical (m) | 20.59 | 6.91 | 4.55 | 14.10 |
| Glide slope () | 0.311 | 0.165 | 0.143 | 0.234 |
| Distance (m) | 2500–1500 | 1500–1000 | 1000–200 | 2500–200 |
|---|---|---|---|---|
| Longitudinal (m) | 66.43 | 30.03 | 97.74 | 73.94 |
| Lateral (m) | 3.09 | 3.74 | 3.58 | 3.42 |
| Vertical (m) | 24.02 | 10.12 | 6.42 | 16.83 |
| Glide slope () | 0.522 | 0.332 | 0.179 | 0.390 |
| Simulation Case | Maximum Error (m) | RMSE (m) |
|---|---|---|
| Case 1 | 3.1945 | 1.6585 |
| Case 2 | 8.9085 | 6.3097 |
| Case 3 | 9.4858 | 6.2791 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.-X.; Lai, Y.-C. Deep Learning-Based Navigation System for Automatic Landing Approach of Fixed-Wing UAVs in GNSS-Denied Environments. Aerospace 2025, 12, 324. https://doi.org/10.3390/aerospace12040324
Lin Y-X, Lai Y-C. Deep Learning-Based Navigation System for Automatic Landing Approach of Fixed-Wing UAVs in GNSS-Denied Environments. Aerospace. 2025; 12(4):324. https://doi.org/10.3390/aerospace12040324
Chicago/Turabian StyleLin, Ying-Xi, and Ying-Chih Lai. 2025. "Deep Learning-Based Navigation System for Automatic Landing Approach of Fixed-Wing UAVs in GNSS-Denied Environments" Aerospace 12, no. 4: 324. https://doi.org/10.3390/aerospace12040324
APA StyleLin, Y.-X., & Lai, Y.-C. (2025). Deep Learning-Based Navigation System for Automatic Landing Approach of Fixed-Wing UAVs in GNSS-Denied Environments. Aerospace, 12(4), 324. https://doi.org/10.3390/aerospace12040324









