An Inverted Transformer Framework for Aviation Trajectory Prediction with Multi-Flight Mode Fusion
Abstract
1. Introduction
- Global Feature Aggregation: Each token encapsulates an entire variable’s history, enabling the self-attention mechanism to directly model long-term intra-variable dependencies and cross-variable interactions at the system level.
- Multi-Flight Knowledge Fusion: By processing data from multi-flights simultaneously, this enables model generalization to unseen flight phases through shared feature learning.
- Physical Consistency Preservation: The inverted structure naturally aligns with aviation domain constraints, and temporal causality is preserved within each token.
2. Related Work
2.1. Physical-Model-Based Trajectory Prediction
2.2. Trajectory Prediction Based on Machine Learning
2.2.1. Classification
2.2.2. Regression
2.3. Trajectory Prediction Models Based on Planning
2.4. Trajectory Prediction Based on Deep Learning
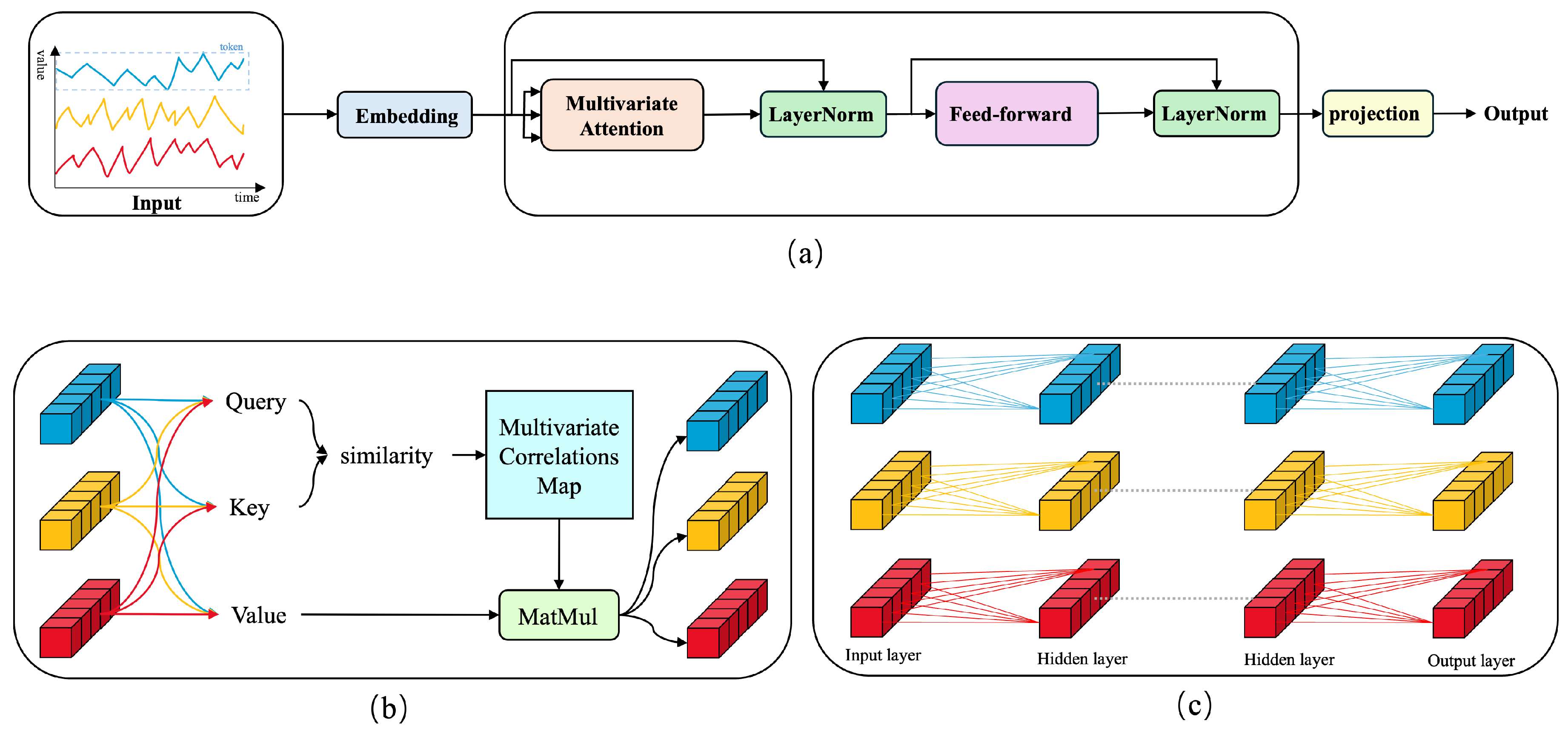
3. Network Architecture
- Heterogeneity of Simultaneous Measurements: Data points recorded at the same time step often represent distinct physical phenomena. Due to inconsistent recording practices across different variables, aggregating these points into a single token can obscure the inherent correlations between multiple variables. This aggregation can lead to a loss of critical information about the relationships between different physical processes, thereby hindering the model’s ability to capture multi-variate dependencies.
- Complexity of Temporal Representation: The presence of a large number of local receptive fields, combined with the representation of temporally inconsistent events at the same time point, makes it challenging for tokens formed at a single time step to convey meaningful information. This complexity arises because the same time step may capture diverse and nonsynchronous events, which, when combined, can introduce noise and ambiguity into the token representation, thereby reducing the model’s effectiveness in processing temporal patterns.
- Underutilization of Permutation-Invariant Attention: Although variations in sequences are significantly influenced by the order of the data, permutation-invariant attention mechanisms are not effectively utilized across the temporal dimension in traditional Transformer models. This limitation arises because the self-attention mechanism, while capable of capturing long-range dependencies, does not fully leverage the temporal structure of the data. As a result, the model may fail to effectively utilize the historical information and temporal context, leading to suboptimal performance in time series forecasting tasks.

3.1. Inverted Input Embedding
- Long-term intra-variable patterns;
- Global inter-variable correlations.
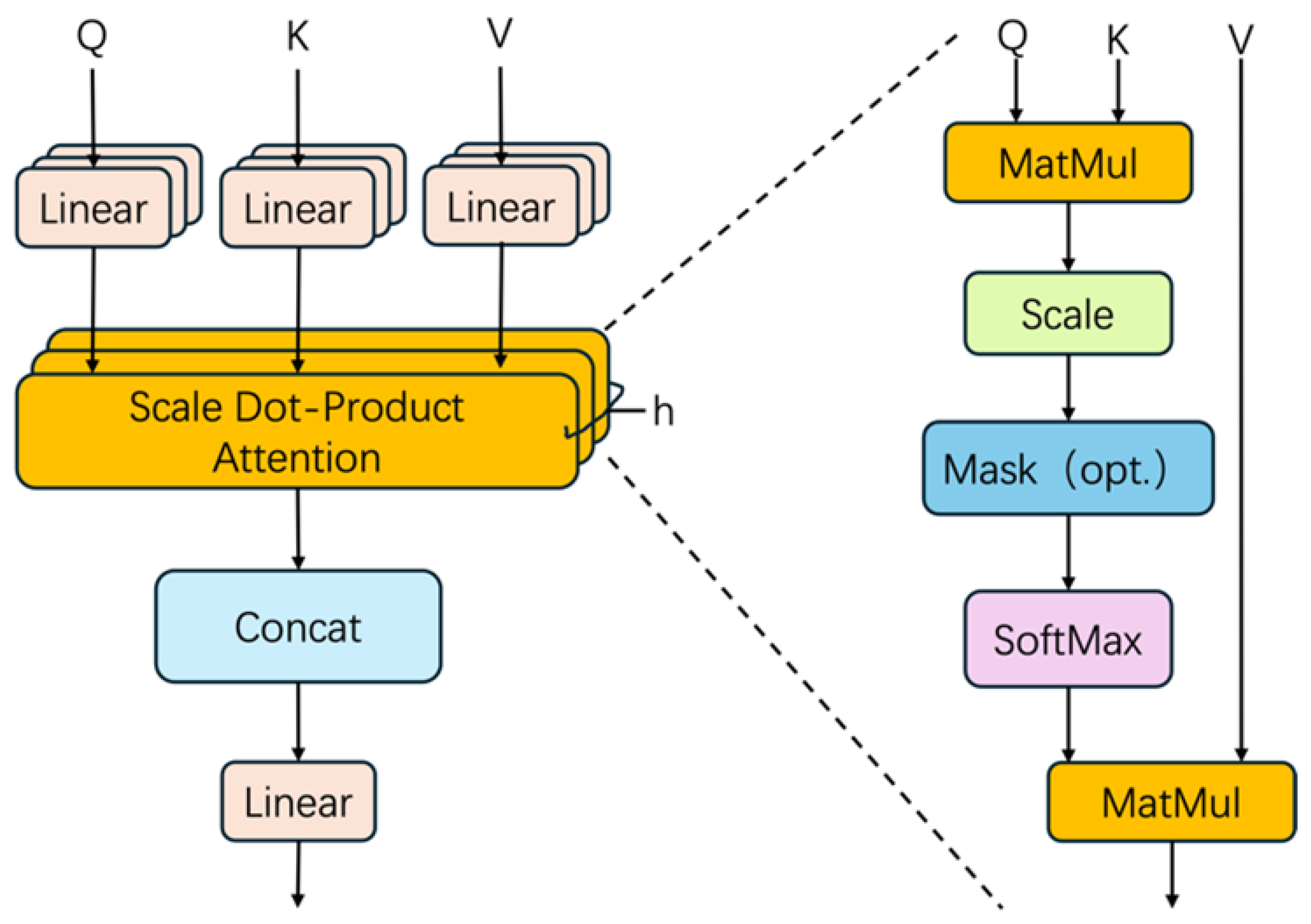
3.2. Self-Attention Mechanism
3.3. Layer Normalization
3.4. Feedforward Network
3.5. Projection
4. Experiments
4.1. Dataset
- Elimination of Redundant Features: The flight number and call sign were identified as noncontributory to the prediction objective and were consequently excluded as superfluous features.
- Temporal Feature Integration We amalgamated the data and temporal features to diminish the quantity of features, thereby streamlining operations.
- Uniform Sampling: The method of uniform sampling was employed to diminish the quantity of data points while concurrently maintaining their representativeness.
- Treatment of Missing Values: The missing data were imputed using the mean value method.
- Dataset Partitioning: The dataset was divided into training, validation, and test sets following a 70%, 20%, and 10% ratio, respectively.
4.2. Evaluation Metrics
5. Experiment Results
5.1. Experiment Performance
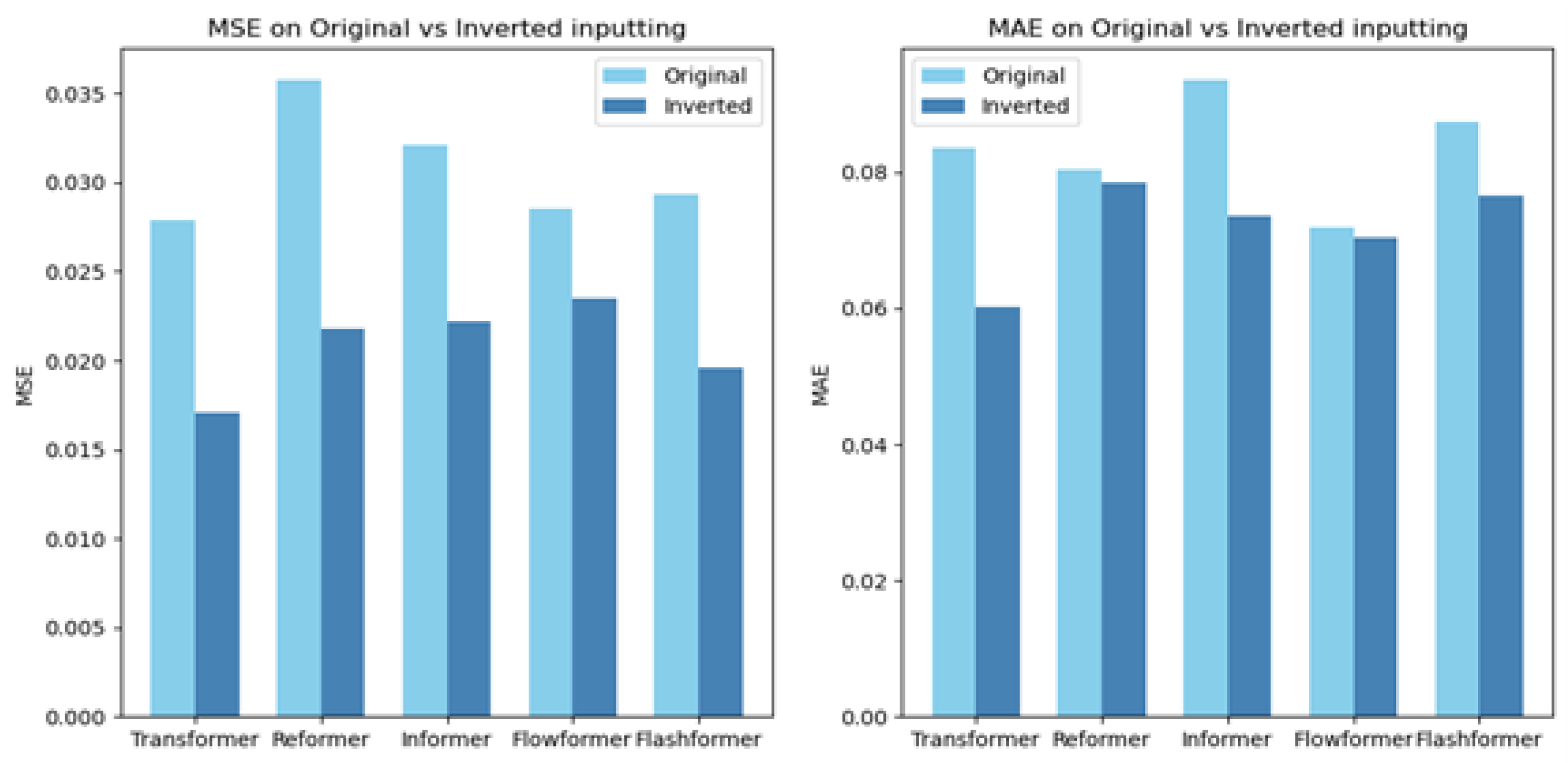
5.2. Inverted Transformer Performance
5.3. Result Visualization
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, S.; Zhou, S.; Miao, J.; Shang, H.; Cui, Y.; Lu, Y. Autonomous Trajectory Planning Method for Stratospheric Airship Regional Station-Keeping Based on Deep Reinforcement Learning. Aerospace 2024, 11, 753. [Google Scholar] [CrossRef]
- Dong, X.; Tian, Y.; Dai, L.; Li, J.; Wan, L. A New Accurate Aircraft Trajectory Prediction in Terminal Airspace Based on Spatio-Temporal Attention Mechanism. Aerospace 2024, 11, 718. [Google Scholar] [CrossRef]
- Xue, D.; Du, S.; Wang, B.; Shang, W.L.; Avogadro, N.; Ochieng, W.Y. Low-carbon benefits of aircraft adopting continuous descent operations. Appl. Energy 2025, 383, 125390. [Google Scholar] [CrossRef]
- Ammoun, S.; Nashashibi, F. Real time trajectory prediction for collision risk estimation between vehicles. In Proceedings of the 2009 IEEE 5Th International Conference on Intelligent Computer Communication and Processing, Cluj-Napoca, Romania, 27–29 August 2009; pp. 417–422. [Google Scholar]
- Schubert, R.; Richter, E.; Wanielik, G. Comparison and evaluation of advanced motion models for vehicle tracking. In Proceedings of the 2008 11th International Conference on Information Fusion, Cologne, Germany, 30 June–3 July 2008; pp. 1–6. [Google Scholar]
- Lytrivis, P.; Thomaidis, G.; Amditis, A. Cooperative path prediction in vehicular environments. In Proceedings of the 2008 11th International IEEE Conference on Intelligent Transportation Systems, Beijing, China, 12–15 October 2008; pp. 803–808. [Google Scholar]
- Barth, A.; Franke, U. Where will the oncoming vehicle be the next second? In Proceedings of the 2008 IEEE Intelligent Vehicles Symposium, Eindhoven, The Netherlands, 4–6 June 2008; pp. 1068–1073. [Google Scholar]
- Batz, T.; Watson, K.; Beyerer, J. Recognition of dangerous situations within a cooperative group of vehicles. In Proceedings of the 2009 IEEE Intelligent Vehicles Symposium, Xi’an, China, 3–5 June 2009; pp. 907–912. [Google Scholar]
- Kaempchen, N.; Weiss, K.; Schaefer, M.; Dietmayer, K.C. IMM object tracking for high dynamic driving maneuvers. In Proceedings of the IEEE Intelligent Vehicles Symposium, Parma, Italy, 14–17 June 2004; pp. 825–830. [Google Scholar]
- Jin, B.; Jiu, B.; Su, T.; Liu, H.; Liu, G. Switched Kalman filter-interacting multiple model algorithm based on optimal autoregressive model for manoeuvring target tracking. IET Radar Sonar Navig. 2015, 9, 199–209. [Google Scholar] [CrossRef]
- Okamoto, K.; Berntorp, K.; Di Cairano, S. Driver intention-based vehicle threat assessment using random forests and particle filtering. IFAC-PapersOnLine 2017, 50, 13860–13865. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.; Zuo, Z.; Li, Z.; Wang, L.; Luo, X. Trajectory planning and safety assessment of autonomous vehicles based on motion prediction and model predictive control. IEEE Trans. Veh. Technol. 2019, 68, 8546–8556. [Google Scholar] [CrossRef]
- Virjonen, P.; Nevalainen, P.; Pahikkala, T.; Heikkonen, J. Ship movement prediction using k-NN method. In Proceedings of the 2018 Baltic Geodetic Congress (BGC Geomatics), Olsztyn, Poland, 21–23 June 2018; pp. 304–309. [Google Scholar]
- Liu, J.; Shi, G.; Zhu, K. Vessel trajectory prediction model based on AIS sensor data and adaptive chaos differential evolution support vector regression (ACDE-SVR). Appl. Sci. 2019, 9, 2983. [Google Scholar] [CrossRef]
- Rong, H.; Teixeira, A.; Soares, C.G. Ship trajectory uncertainty prediction based on a Gaussian Process model. Ocean. Eng. 2019, 182, 499–511. [Google Scholar] [CrossRef]
- Silveira, P.; Teixeira, A.; Guedes-Soares, C. AIS based shipping routes using the Dijkstra algorithm. Transnav Int. J. Mar. Navig. Saf. Sea Transp. 2019, 13. [Google Scholar] [CrossRef]
- Martinsen, A.B.; Lekkas, A.M.; Gros, S. Optimal model-based trajectory planning with static polygonal constraints. IEEE Trans. Control. Syst. Technol. 2021, 30, 1159–1170. [Google Scholar] [CrossRef]
- Karbowska-Chilinska, J.; Koszelew, J.; Ostrowski, K.; Kuczynski, P.; Kulbiej, E.; Wolejsza, P. Beam search Algorithm for ship anti-collision trajectory planning. Sensors 2019, 19, 5338. [Google Scholar] [CrossRef] [PubMed]
- Lazarowska, A. Comparison of discrete artificial potential field algorithm and wave-front algorithm for autonomous ship trajectory planning. IEEE Access 2020, 8, 221013–221026. [Google Scholar] [CrossRef]
- Maw, A.A.; Tyan, M.; Nguyen, T.A.; Lee, J.W. iADA*-RL: Anytime graph-based path planning with deep reinforcement learning for an autonomous UAV. Appl. Sci. 2021, 11, 3948. [Google Scholar] [CrossRef]
- Wang, S.; Yan, X.; Ma, F.; Wu, P.; Liu, Y. A novel path following approach for autonomous ships based on fast marching method and deep reinforcement learning. Ocean. Eng. 2022, 257, 111495. [Google Scholar] [CrossRef]
- Akter, R.; Doan, V.S.; Lee, J.M.; Kim, D.S. CNN-SSDI: Convolution neural network inspired surveillance system for UAVs detection and identification. Comput. Netw. 2021, 201, 108519. [Google Scholar] [CrossRef]
- Jung, O.; Seong, J.; Jung, Y.; Bang, H. Recurrent neural network model to predict re-entry trajectories of uncontrolled space objects. Adv. Space Res. 2021, 68, 2515–2529. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Q.; Zhang, Y.; Zhu, Z. VGAE-AMF: A novel topology reconstruction algorithm for invulnerability of ocean wireless sensor networks based on graph neural network. J. Mar. Sci. Eng. 2023, 11, 843. [Google Scholar] [CrossRef]
- Lin, Z.; Zhang, X.; He, F. A GNN-LSTM-Based Fleet Formation Recognition Algorithm. In Proceedings of the International Conference on Guidance, Navigation and Control, Tianjin, China, 5–7 August 2022; pp. 7272–7281. [Google Scholar]
- Vaswani, A. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting. Adv. Neural Inf. Process. Syst. 2021, 34, 22419–22430. [Google Scholar]
- Wu, H.; Wu, J.; Xu, J.; Wang, J.; Long, M. Flowformer: Linearizing transformers with conservation flows. arXiv 2022, arXiv:2202.06258. [Google Scholar]
- Wu, H.; Hu, T.; Liu, Y.; Zhou, H.; Wang, J.; Long, M. Timesnet: Temporal 2d-variation modeling for general time series analysis. arXiv 2022, arXiv:2210.02186. [Google Scholar]
- Nie, Y.; Nguyen, N.H.; Sinthong, P.; Kalagnanam, J. A time series is worth 64 words: Long-term forecasting with transformers. arXiv 2022, arXiv:2211.14730. [Google Scholar]
- Kitaev, N.; Kaiser, L.; Levskaya, A. Reformer: The Efficient Transformer. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar]
- Dao, T.; Fu, D.; Ermon, S.; Rudra, A.; Ré, C. Flashattention: Fast and memory-efficient exact attention with io-awareness. Adv. Neural Inf. Process. Syst. 2022, 35, 16344–16359. [Google Scholar]
- Khan, W.A.; Ma, H.L.; Ouyang, X.; Mo, D.Y. Prediction of aircraft trajectory and the associated fuel consumption using covariance bidirectional extreme learning machines. Transp. Res. Part E Logist. Transp. Rev. 2021, 145, 102189. [Google Scholar] [CrossRef]

| Feature Name | Description |
|---|---|
| HBID | Flight number, the unique identification of the flight |
| WZSJ | The time of position, including date and time |
| JD | Longitude |
| WD | Latitude |
| GD | Altitude |
| SD | Airplane flying speed |
| Parameters | Sequence length | 10 | 30 | 50 | ||||||
| Encoder layer | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |
| Decoder layer | 2 | 3 | 4 | 2 | 3 | 4 | 2 | 3 | 4 | |
| Results | MAE | 0.01707 | 0.07209 | 0.09898 | 0.06055 | 0.10614 | 0.03966 | 0.05466 | 0.02167 | 0.19648 |
| RMSE | 0.13064 | 0.26841 | 0.31462 | 0.14588 | 0.32579 | 0.19915 | 0.23380 | 0.14721 | 0.44326 | |
| MAE | 0.06019 | 0.13311 | 0.10631 | 0.12304 | 0.15811 | 0.13908 | 0.13624 | 0.06150 | 0.05371 | |
| Model | Transformer | Reformer | Informer | Flowformer | Flashattention | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Metric | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE |
| Original | 0.0279 | 0.0835 | 0.0357 | 0.0803 | 0.0321 | 0.0935 | 0.0285 | 0.0719 | 0.0294 | 0.0873 |
| Inverted | 0.0171 | 0.0602 | 0.0218 | 0.0784 | 0.0222 | 0.0735 | 0.0235 | 0.0704 | 0.0196 | 0.0767 |
| Promotion | 63.3% | 38.8% | 63.7% | 2.4% | 45.0% | 21.2% | 21.4% | 2.2% | 49.9% | 13.9% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, G.; Ou, Y.; Li, W.; Zeng, X.; Zhang, Z.; Huang, D.; Kotenko, I. An Inverted Transformer Framework for Aviation Trajectory Prediction with Multi-Flight Mode Fusion. Aerospace 2025, 12, 319. https://doi.org/10.3390/aerospace12040319
Lu G, Ou Y, Li W, Zeng X, Zhang Z, Huang D, Kotenko I. An Inverted Transformer Framework for Aviation Trajectory Prediction with Multi-Flight Mode Fusion. Aerospace. 2025; 12(4):319. https://doi.org/10.3390/aerospace12040319
Chicago/Turabian StyleLu, Gaoyong, Yang Ou, Wei Li, Xinyu Zeng, Ziyang Zhang, Dongcheng Huang, and Igor Kotenko. 2025. "An Inverted Transformer Framework for Aviation Trajectory Prediction with Multi-Flight Mode Fusion" Aerospace 12, no. 4: 319. https://doi.org/10.3390/aerospace12040319
APA StyleLu, G., Ou, Y., Li, W., Zeng, X., Zhang, Z., Huang, D., & Kotenko, I. (2025). An Inverted Transformer Framework for Aviation Trajectory Prediction with Multi-Flight Mode Fusion. Aerospace, 12(4), 319. https://doi.org/10.3390/aerospace12040319








