Establishment of Lunar Soil Excavation Model and Experimental Simulation Study
Abstract
1. Introduction
2. Model Construction
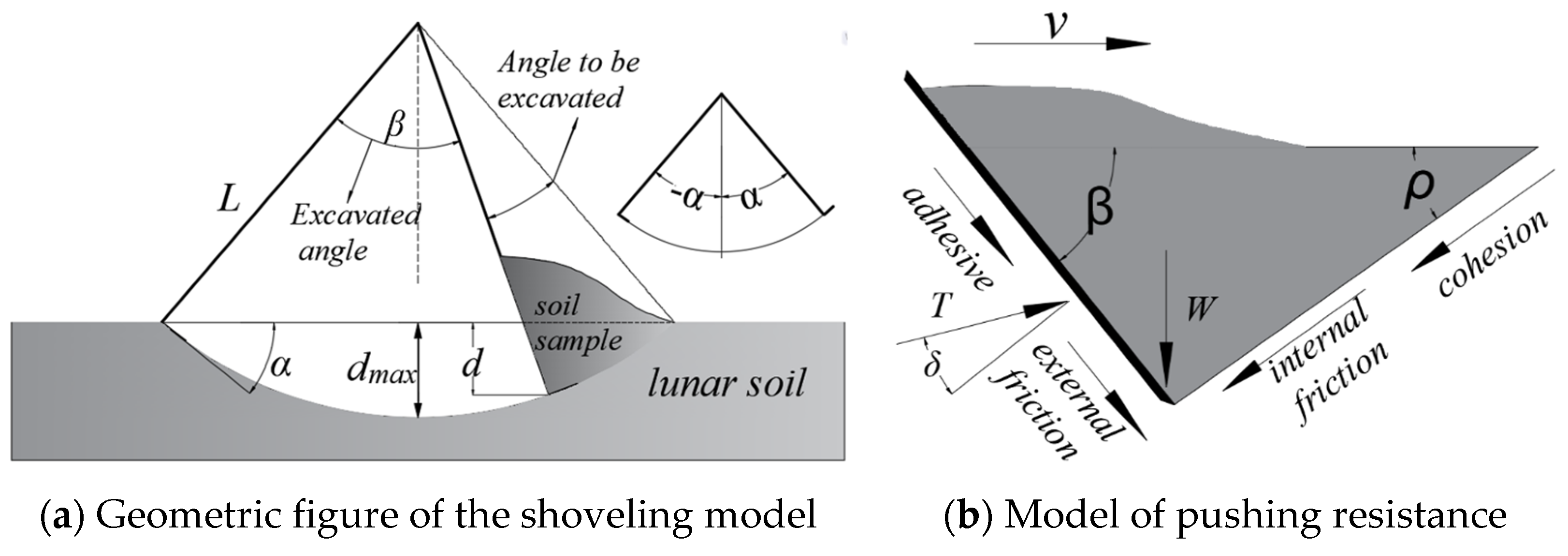
2.1. Analysis of Surface Sampling Process
2.2. Construction of the Digging Model
3. Test Simulation Analysis and Verification
3.1. Ground Test Content
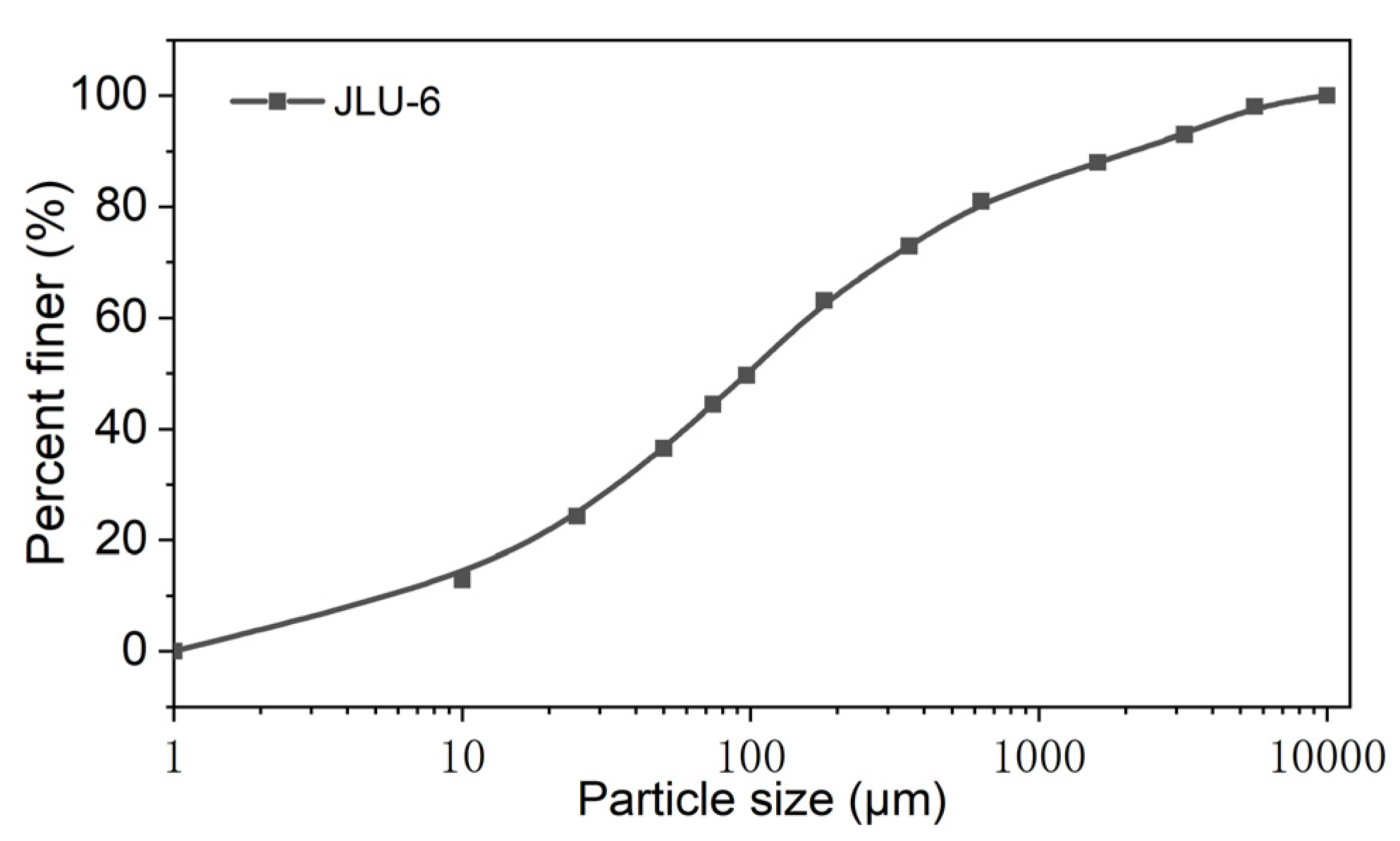
3.2. Establishment of Discrete Element Model
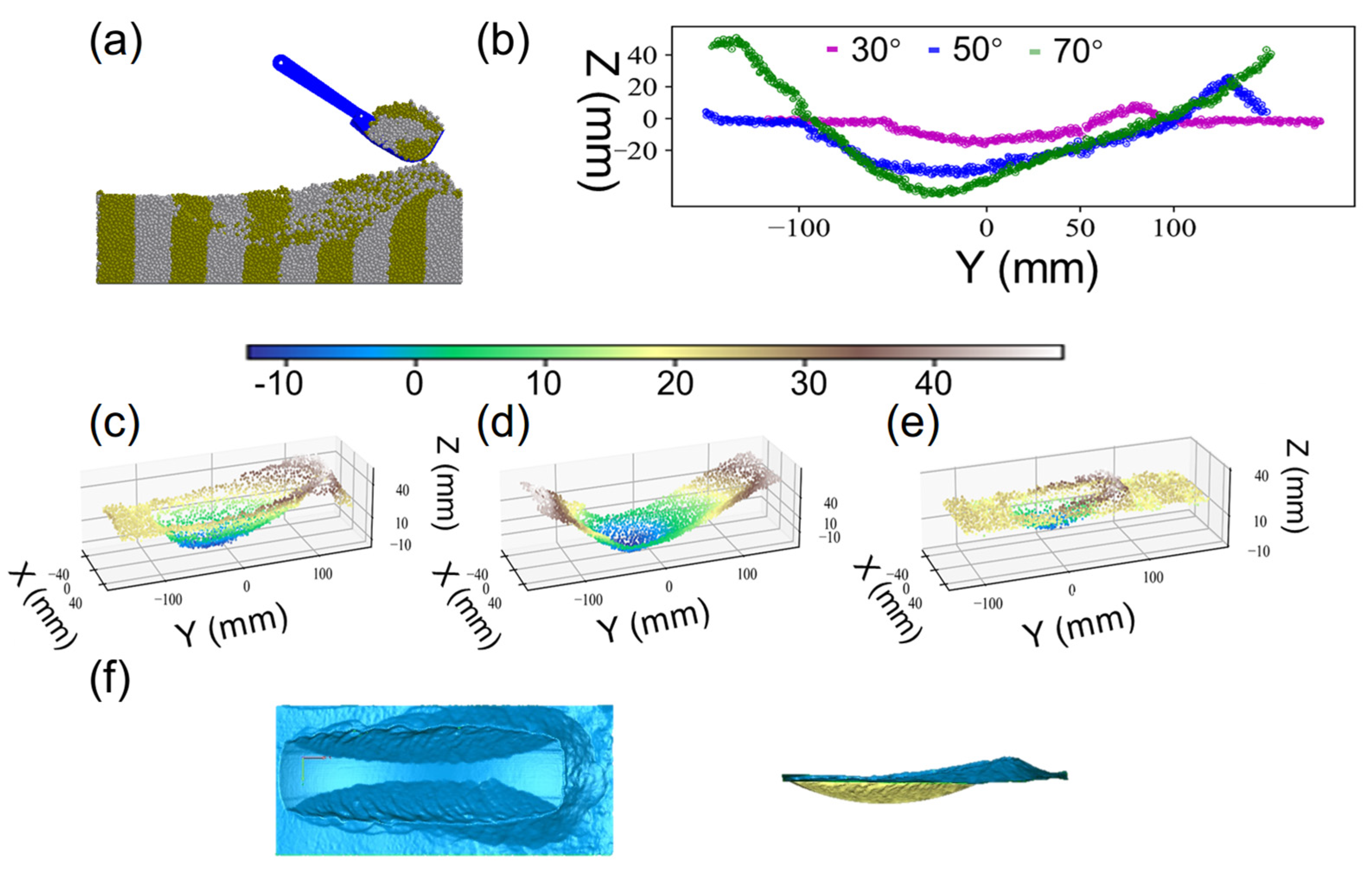
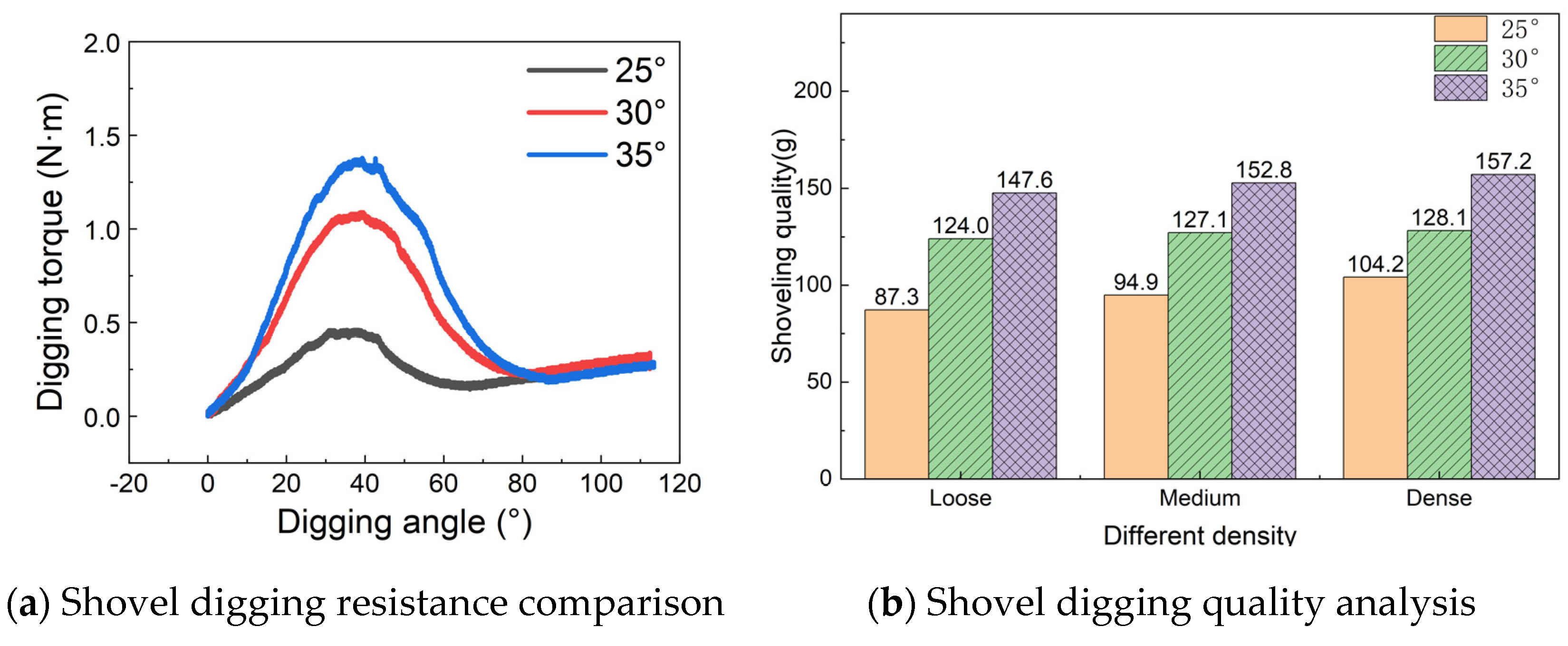
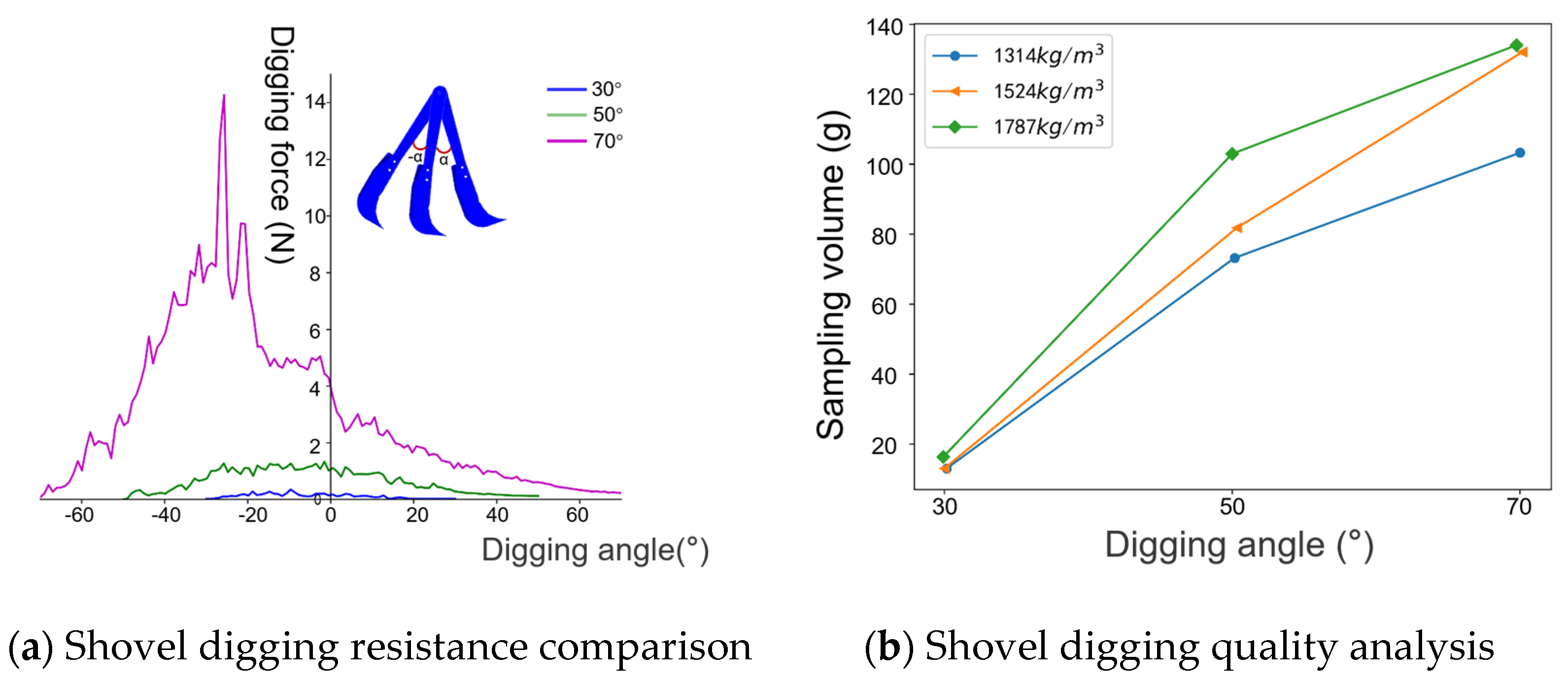
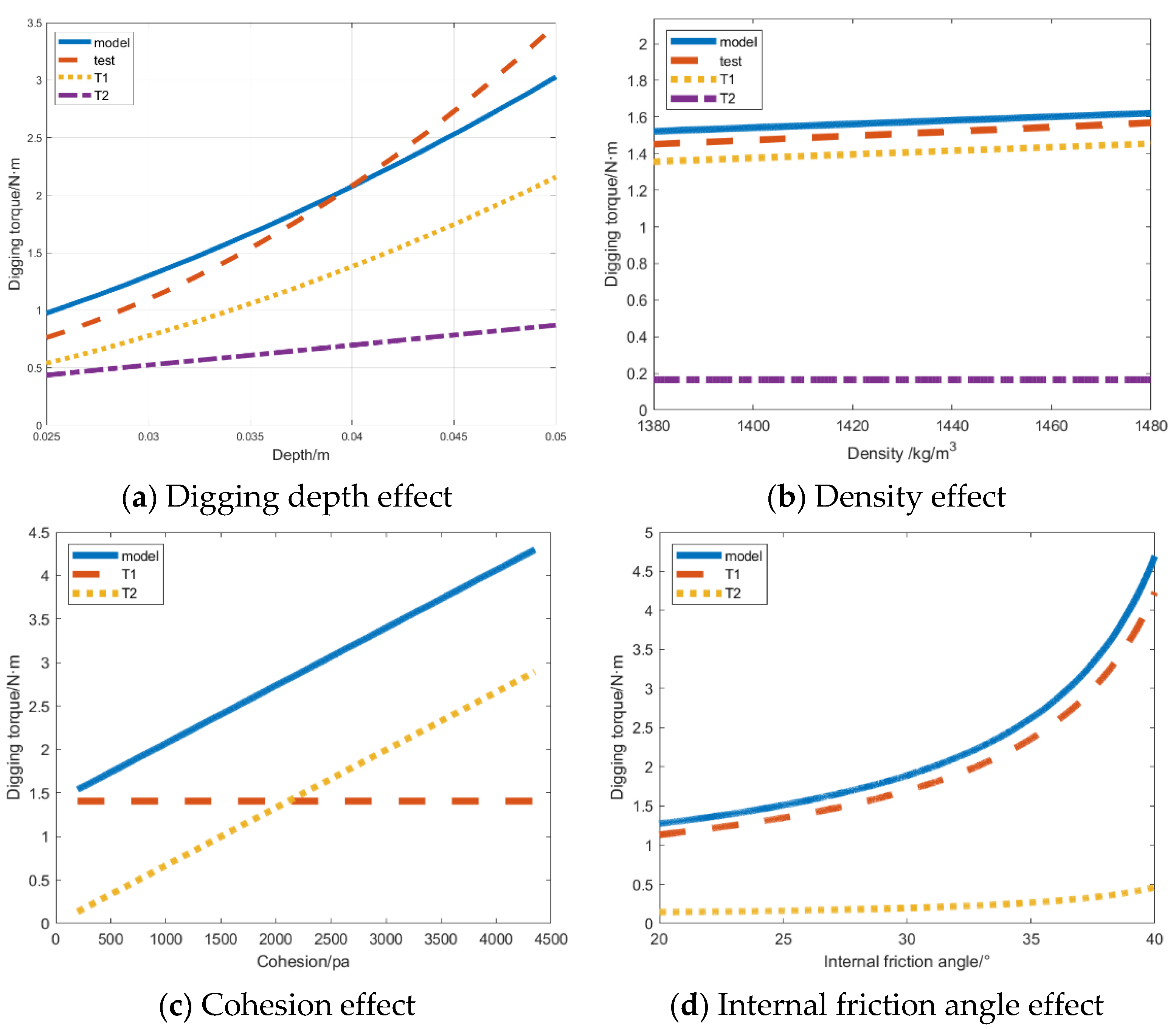
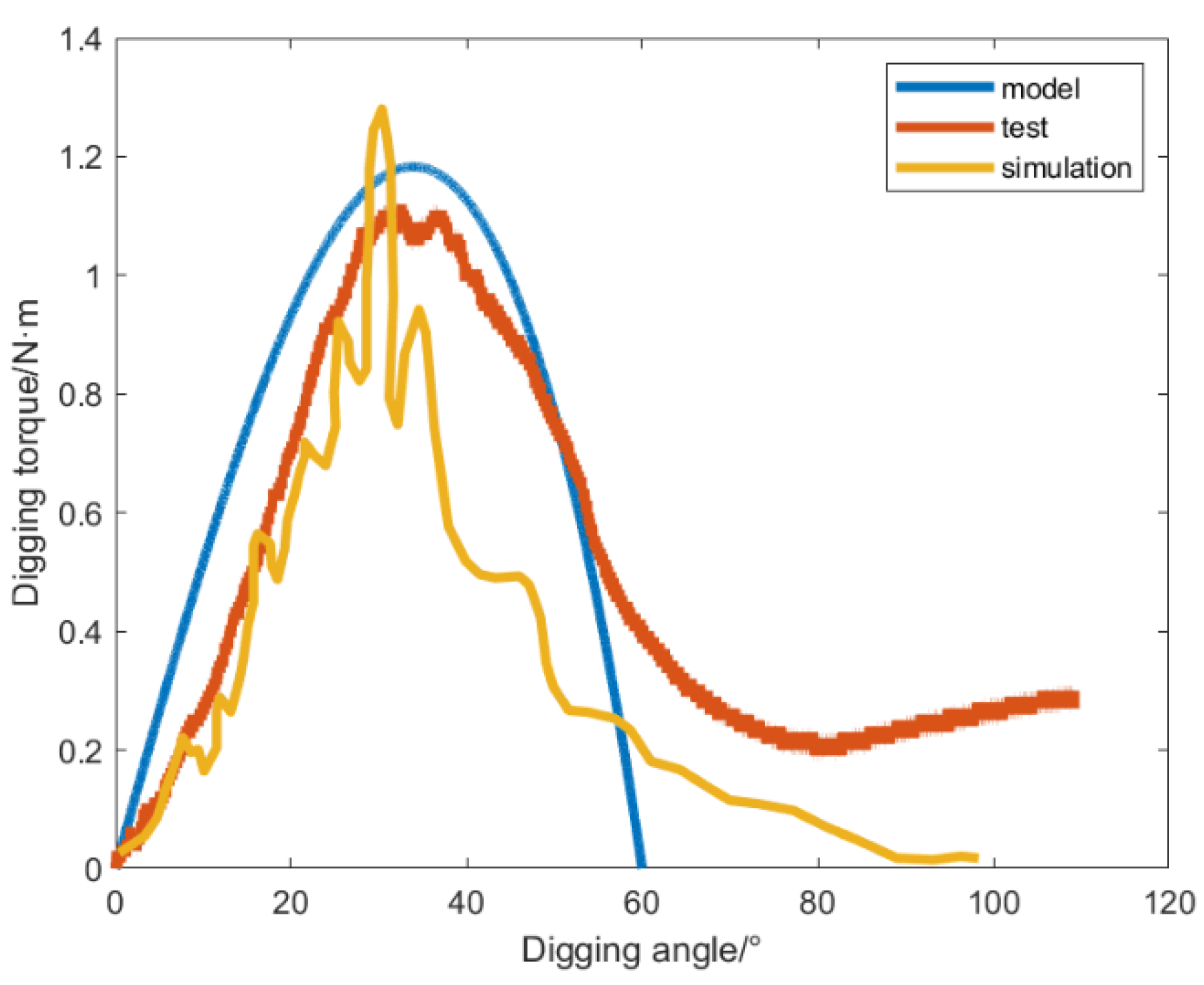
3.3. Analysis of Test and Simulation Results
3.4. Model Applicability and Digging Trend Prediction
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zheng, Y.-H.; Deng, X.-J.; Gu, Z.; Jin, S.-Y.; Li, Q. Lunar surface sampling point selection of Chang’E 5. Opt. Precis. Eng. 2021, 29, 2935–2943. [Google Scholar] [CrossRef]
- Wu, W.; Wang, Q.; Tang, Y. Design of Chang’e-4 Lunar Farside Soft-Landing Mission. J. Deep. Space Explor. 2017, 4, 111–117. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, J. A Chang’e-4 mission concept and vision of future Chinese lunar exploration activities. Acta Astronaut. 2016, 127, 678–683. [Google Scholar] [CrossRef]
- Zeng, X.; Liu, D.; Chen, Y.; Zhou, Q.; Ren, X.; Zhang, Z.; Yan, W.; Chen, W.; Wang, Q.; Deng, X.; et al. Landing site of the Chang’e-6 lunar farside sample return mission from the Apollo basin. Nat. Astron 2023, 7, 1188–1197. [Google Scholar] [CrossRef]
- Chuang, L. A Preliminary Study on Simulation of Lunar Surface Terrain. Spacecr. Environ. Eng. 2007, 24, 15–20. [Google Scholar]
- Rankine, W.J.M. On the Stability of Loose Earth. Philos. Trans. R. Soc. Lond. 1857, 147, 9–27. [Google Scholar]
- Li, Q.; Matsushima, T.; Xie, L.; Huo, Y. Reaction force calculation for planetary sampling devices based on the predicted zone of influence. Comput. Part. Mech. 2021, 8, 1–20. [Google Scholar] [CrossRef]
- Terzaghi, K. Erdbaumechanik Auf Bodenphysikalischer Grundlage; Franz Deuticke: Vienna, Austria, 1925. [Google Scholar]
- McKyes, E.; Ali, O.S. The cutting of soil by narrow blades. J. Terramech. 1977, 14, 43–58. [Google Scholar] [CrossRef]
- Gill, W.R.; Vanden Berg, G.E. Soil Dynamics in Tillage and Traction (Agricultural Handbook no. 316). Soil Sci. Soc. Am. J. 1968, 32, 340–429. [Google Scholar] [CrossRef]
- Sedara, A. A Review of Soil Dynamics in Traction Studies. J. Eng. Res. Rep. 2019, 4, 1–13. [Google Scholar] [CrossRef]
- Petrescu, R.V.; Aversa, R.; Akash, B.; Bucinell, R.; Apicella, A.; Petrescu, F.I.T. Lockheed Martin-A Short Review. J. Aircr. Spacecr. Technol. 2017, 1, 50–68. [Google Scholar] [CrossRef]
- Duke, M.; Muff, T.; King, R. Analysis of a small robot for Martian regolith excavation. In Proceedings of the AIAA Space 2001 Conference and Exposition, AIAA SPACE Forum, Albuquerque, NM, USA, 28–30 August 2001; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2001. [Google Scholar] [CrossRef]
- Marín Cabrera, L.O.; García de la Figal Costales, A.E.; Martínez Rodríguez, A. Predicción de Fuerza Traccional de herramienta de labranza estrecha mediante el Método de Elementos Finitos. Rev. Cienc. Técnicas Agropecu. 2022, 31. [Google Scholar]
- Mckyes, E. Agricultural Engineering Soil Mechanics; Elsevier: Amsterdam, The Netherlands, 1989. [Google Scholar]
- Zeng, X.; Burnoski, L.; Agui, J.; Wilkinson, A. Calculation of Excavation Force for ISRU on Lunar Surface. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Aerospace Sciences Meetings, Reno, Nevada, 8–11 January 2007; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2007. [Google Scholar] [CrossRef]
- Woods-Robinson, R.; Siegler, M.A.; Paige, D.A. A Model for the Thermophysical Properties of Lunar Regolith at Low Temperatures. J. Geophys. Res. Planets 2019, 124, 1989–2011. [Google Scholar] [CrossRef]
- Formisano, M.; De Sanctis, M.C.; De Angelis, S.; Carpenter, J.D.; Sefton-Nash, E. PROSPECTING the Moon: Numerical simulations of temperature and sublimation rate of a cylindric sample. Planet. Space Sci. 2019, 169, 8–14. [Google Scholar] [CrossRef]
- Formisano, M.; De Sanctis, M.C.; Boazman, S.; Frigeri, A.; Heather, D.; Magni, G.; Teodori, M.; De Angelis, S.; Ferrari, M. Thermal modeling of the lunar South Pole: Application to the PROSPECT landing site. Planet. Space Sci. 2024, 251, 105969. [Google Scholar] [CrossRef]
- Bernold, L.E.; Abourizk, S. Managing Performance in Construction; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Bernold Leonhard, E. Experimental Studies on Mechanics of Lunar Excavation. J. Aerosp. Eng. 1991, 4, 9–22. [Google Scholar] [CrossRef]
- Boles Walter, W.; Scott Wesley, D.; Connolly John, F. Excavation Forces in Reduced Gravity Environment. J. Aerosp. Eng. 1997, 10, 99–103. [Google Scholar] [CrossRef]
- Bucek, M.; Agui Juan, H.; Zeng, X.; Wilkinson, R.A. Experimental Measurements of Excavation Forces in Lunar Soil Test Beds. In Earth & Space 2008; American Society of Civil Engineers: Reston, VA, USA, 2012; pp. 1–10. [Google Scholar] [CrossRef]
- Agui Juan, H.; Wilkinson, R.A. Granular Flow and Dynamics of Lunar Simulants in Excavating Implements. In Earth and Space 2010; American Society of Civil Engineers: Reston, VA, USA, 2012; pp. 84–94. [Google Scholar] [CrossRef]
- Green, A.; Zacny, K.; Pestana, J.; Lieu, D.; Mueller, R. Investigating the Effects of Percussion on Excavation Forces. J. Aerosp. Eng. 2013, 26, 87–96. [Google Scholar] [CrossRef]
- Zou, M.; Li, J.Q.; Jia, Y.; Ren, L.Q.; Li, Y.W. Statics characteristics of lunar soil by DEM simulation. J. Jilin Univ. 2008, 38, 383–387. [Google Scholar]
- Swick, W.; Perumpral, J. A model for predicting soil-tool interaction. J. Terramech. 1988, 25, 43–56. [Google Scholar]
- Xi, B.; Jiang, M.; Cui, L.; Liu, J.; Lei, H. Experimental verification on analytical models of lunar excavation. J. Terramech. 2019, 83, 1–13. [Google Scholar] [CrossRef]
- Wilkinson, A.; DeGennaro, A. Digging and pushing lunar regolith: Classical soil mechanics and the forces needed for excavation and traction. J. Terramech. 2007, 44, 133–152. [Google Scholar] [CrossRef]
- Blouin, S.; Hemami, A.; Lipsett, M. Review of Resistive Force Models for Earthmoving Processes. J. Aerosp. Eng. 2001, 14, 102–111. [Google Scholar] [CrossRef]
- Ming, D.W. Lunar sourcebook. A user’s guide to the moon. Endeavour 1992, 16, 96. [Google Scholar] [CrossRef]
- Tong, X.; Zhu, X.; Ma, P.; Leng, Y. Study on the Strength Parameters of Loess in Granular Discrete Element Method. Chin. J. Undergr. Space Eng. 2019, 15, 435–442. [Google Scholar]
- Zhu, J.; Zou, M.; Liu, Y.; Gao, K.; Su, B.; Qi, Y. Measurement and calibration of DEM parameters of lunar soil simulant. Acta Astronaut. 2022, 191, 169–177. [Google Scholar] [CrossRef]


| Model Symbol | Content | Parameter | Units | Values |
|---|---|---|---|---|
| Sampling scoop | Tool width | w | m | 0.04 |
| Tool length | l | m | 0.145 | |
| Digging radius | L | m | 0.205 | |
| Soil–soil | Cohesion | c | pa | 200–1350 |
| Internal friction angle | Φ | deg | 20–35 | |
| Soil specific mass | γ | kg/m3 | 1–1.5 × 103 | |
| Soil–tools | External friction angle | δ | deg | 32 |
| Shear plane failure angle | ρ | deg | =45 + Φ/2 | |
| Test | Tool depth | d | m | 0–0.05 |
| Digging Angle | β | deg | 20–40 | |
| Gravity | Earth gravity | ge | m/s2 | 9.8 |
| Lunar gravity | gl | m/s2 | 1.633 |
| Max kg/m3 | Min kg/m3 | Trystate | Relative Compaction | Actual kg/m3 |
|---|---|---|---|---|
| 1550 | 1200 | Loose | 30% | 1290 |
| Medium | 50% | 1350 | ||
| Dense | 70% | 1430 |
| Trystate | Relative Compaction | Cohesion kpa | Internal Friction Angle ° |
|---|---|---|---|
| Loose | 30% | 0.25 | 26.20 |
| Medium | 50% | 0.50 | 27.4 |
| Dense | 70% | 1.15 | 25.9 |
| Depth/cm | Loose (kpa) | Medium (kpa) | Dense (kpa) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 2.5 | 0 | 0 | 0 |
| 5 | 0 | 35 | 175 |
| 7.5 | 35 | 316 | 491 |
| 10 | 351 | 842 | 1053 |
| 12.5 | 1018 | 1123 | 1650 |
| Symbol | Content | Values |
|---|---|---|
| Particle | Density (kg/m3) | 2500, 2900, 3400 |
| Diameter (mm) | 1.5 | |
| Shear modulus (GPa) | 1.35 × 107 | |
| Poisson ratio (−) | 0.39 | |
| Sampling Scoop | Density (kg/m3) | 5000 |
| Shear modulus (GPa) | 1 × 108 | |
| Poisson ratio (−) | 0.5 | |
| Particle–Particle | Coefficient of Static Friction | 0.75 |
| Coefficient of Rolling Friction | 0.6 | |
| Coefficient of Restitution | 0.84 | |
| Particle–Scoop | Coefficient of Static Friction | 0.5 |
| Coefficient of Rolling Friction | 0.5 | |
| Coefficient of Restitution | 0.5 | |
| Test | Digging angle (°) | 30, 50, 70 |
| Digging speed (°/s) | 10 | |
| Model Parameter | Surface energy (J/m2) | 0.1 |
| Angle (°) | Density (kg/m3) |
|---|---|
| 30 | 1314 |
| 1524 | |
| 1787 | |
| 50 | 1314 |
| 1524 | |
| 1787 | |
| 70 | 1314 |
| 1524 | |
| 1787 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, S.; Cao, H.; Deng, X.; Zheng, Y.; Xue, L.; Zou, M. Establishment of Lunar Soil Excavation Model and Experimental Simulation Study. Aerospace 2025, 12, 315. https://doi.org/10.3390/aerospace12040315
Jin S, Cao H, Deng X, Zheng Y, Xue L, Zou M. Establishment of Lunar Soil Excavation Model and Experimental Simulation Study. Aerospace. 2025; 12(4):315. https://doi.org/10.3390/aerospace12040315
Chicago/Turabian StyleJin, Shengyi, Hongtao Cao, Xiangjin Deng, Yanhong Zheng, Long Xue, and Meng Zou. 2025. "Establishment of Lunar Soil Excavation Model and Experimental Simulation Study" Aerospace 12, no. 4: 315. https://doi.org/10.3390/aerospace12040315
APA StyleJin, S., Cao, H., Deng, X., Zheng, Y., Xue, L., & Zou, M. (2025). Establishment of Lunar Soil Excavation Model and Experimental Simulation Study. Aerospace, 12(4), 315. https://doi.org/10.3390/aerospace12040315






