Noncooperative Spacecraft Pose Estimation Based on Point Cloud and Optical Image Feature Collaboration
Abstract
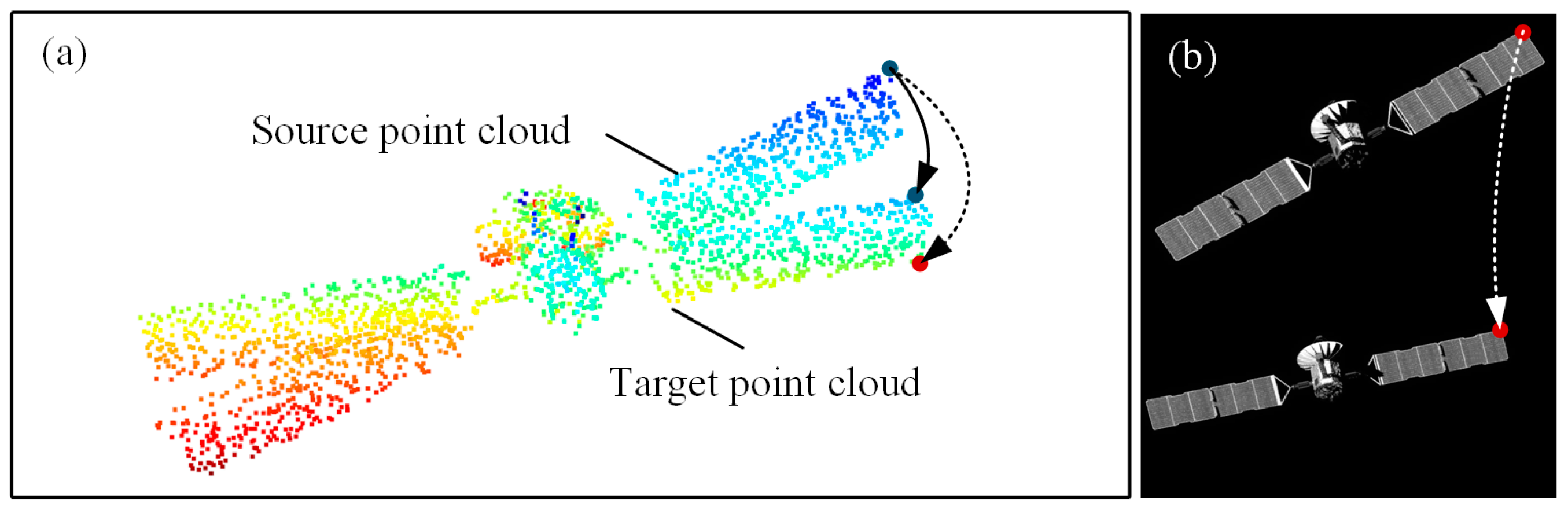
1. Introduction
- (1)
- This paper proposes a point cloud and optical image feature collaborative pose estimation network (POCPE-Net). The proposed network comprehensively considers both image features and point cloud features, providing a novel approach to pose estimation for spacecraft based on point cloud matching.
- (2)
- Based on the constructed point cloud and image dataset, comparative experiments and ablation studies were conducted between the proposed method and several existing methods. The results show that our method achieves superior accuracy on the validation set, with an MAE (R) of 0.84° and an MAE (t) of 0.022 m.
- (3)
- The method’s practicality was validated through a ground-based experiment using the measured data. The proposed approach achieves an MAE (R) of 0.97° and an MAE (t) of 0.015 m in real-world scenarios, demonstrating robust performance.
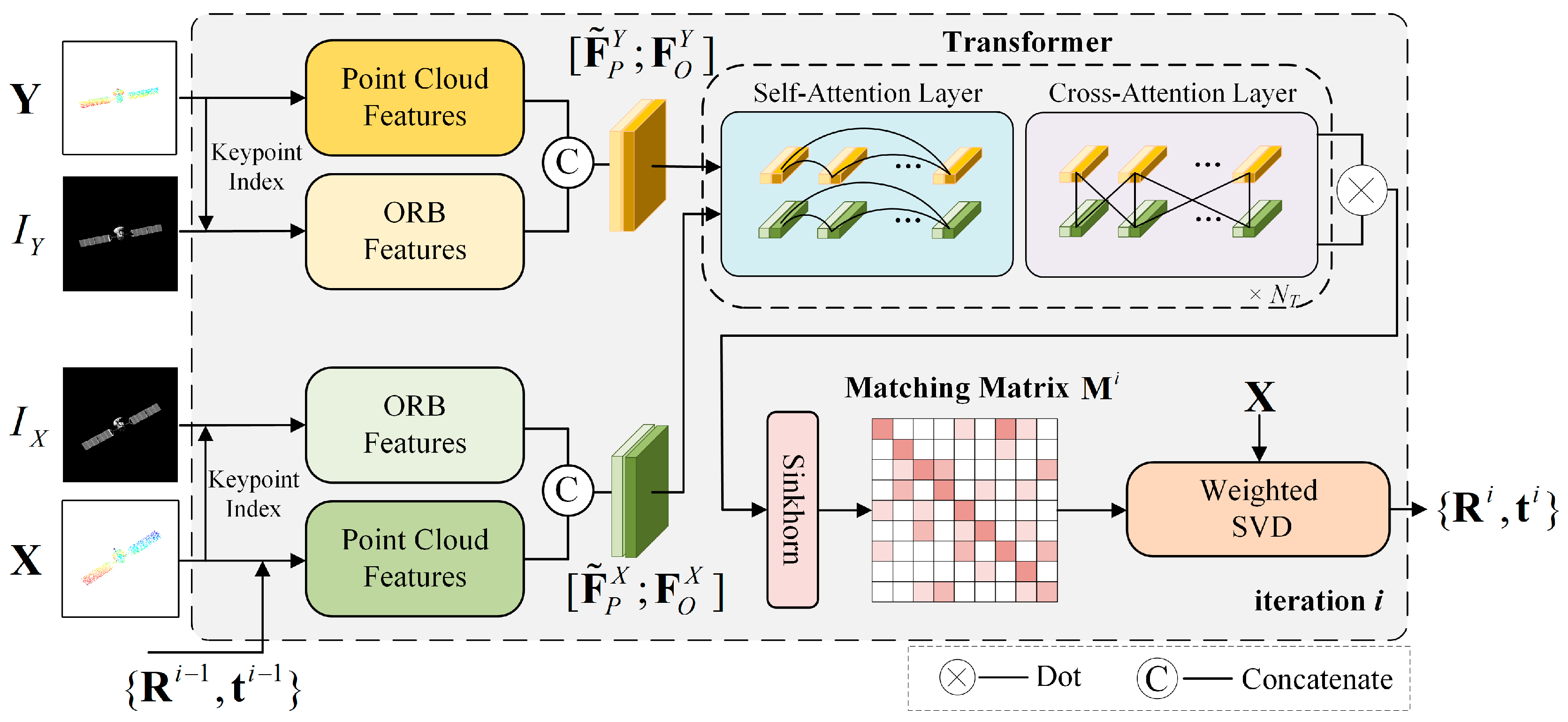
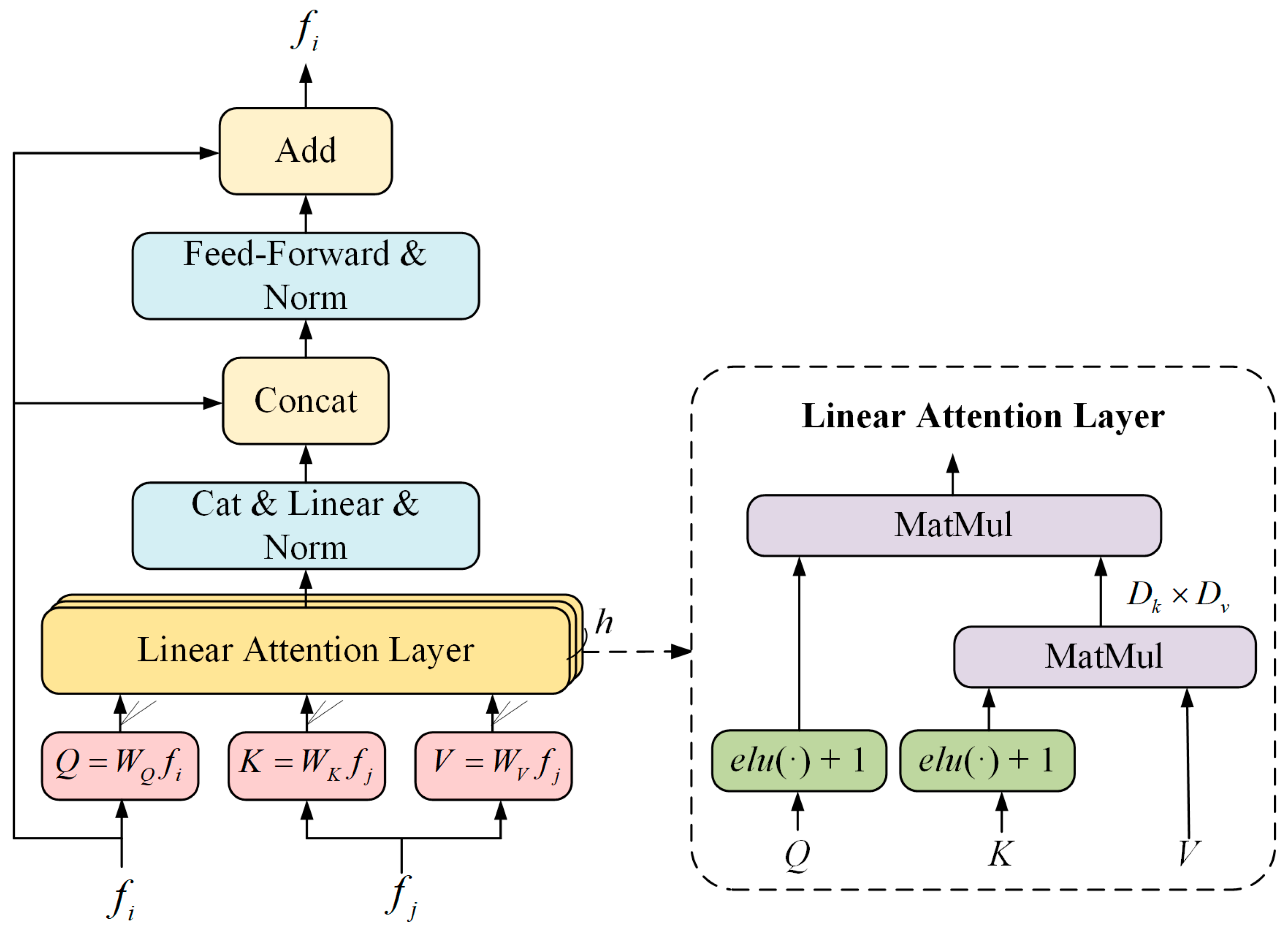
2. The Proposed Method
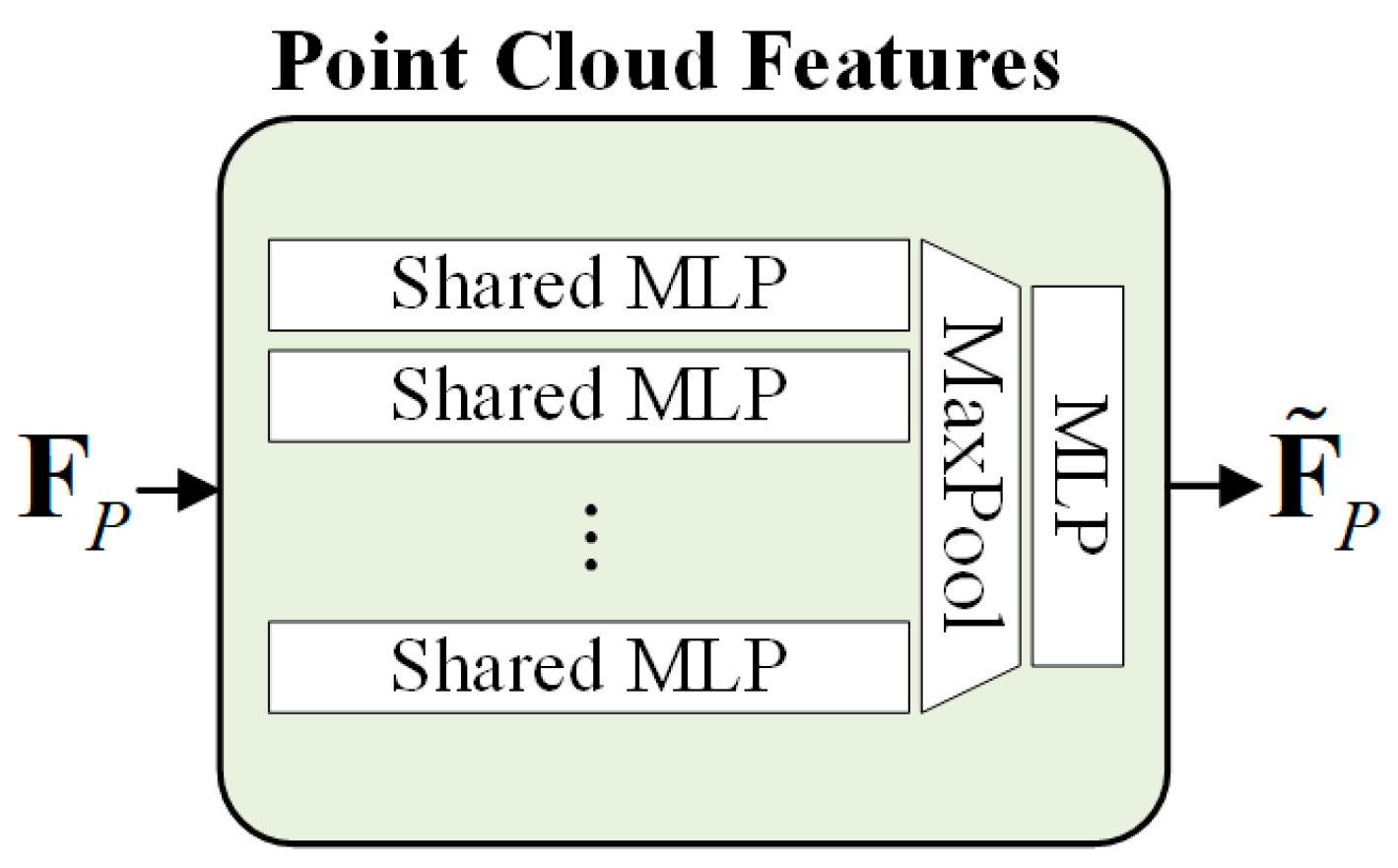
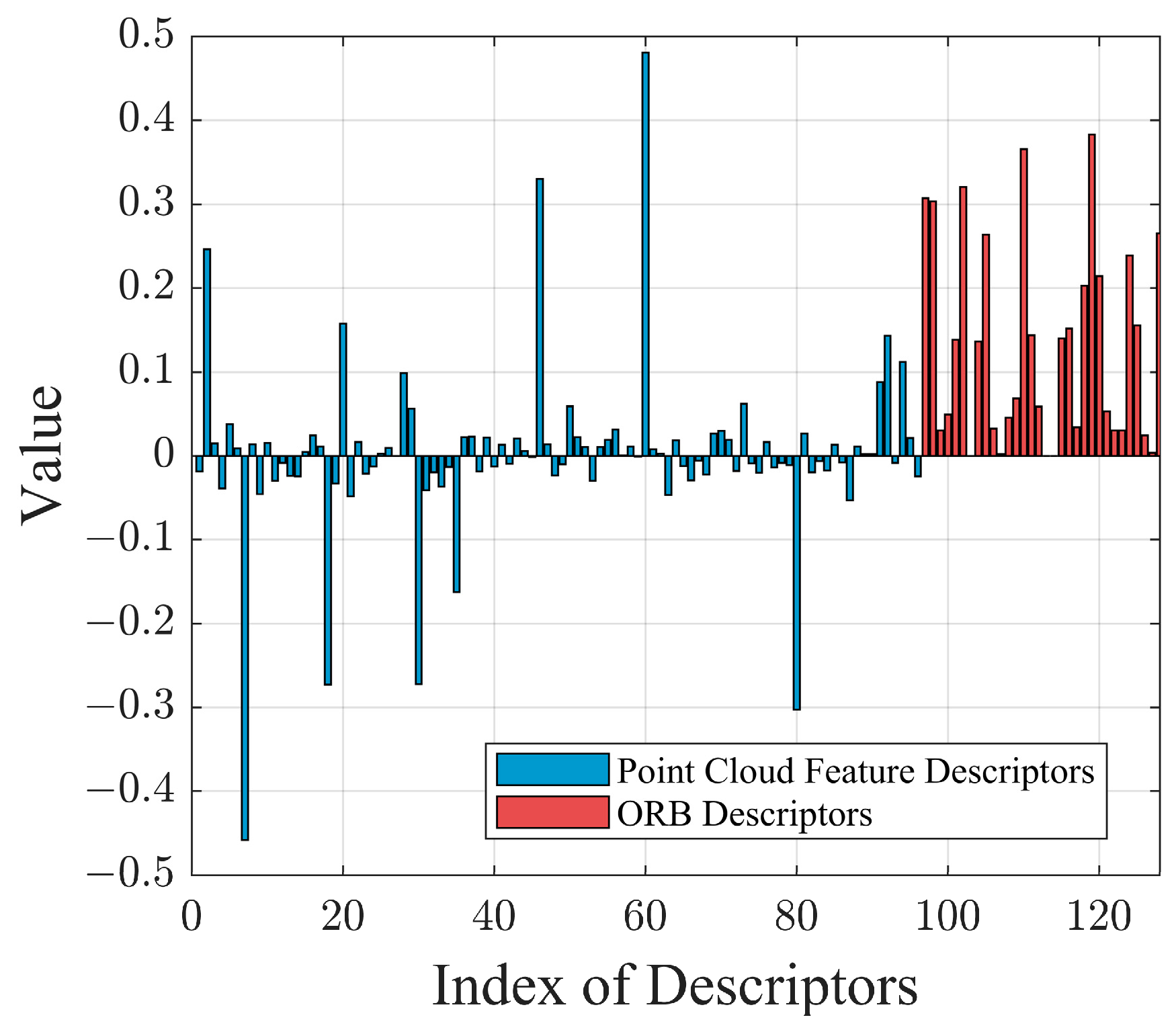
2.1. Feature Extraction
2.2. Transformer
2.3. Matching and Weighted SVD
3. Experiments
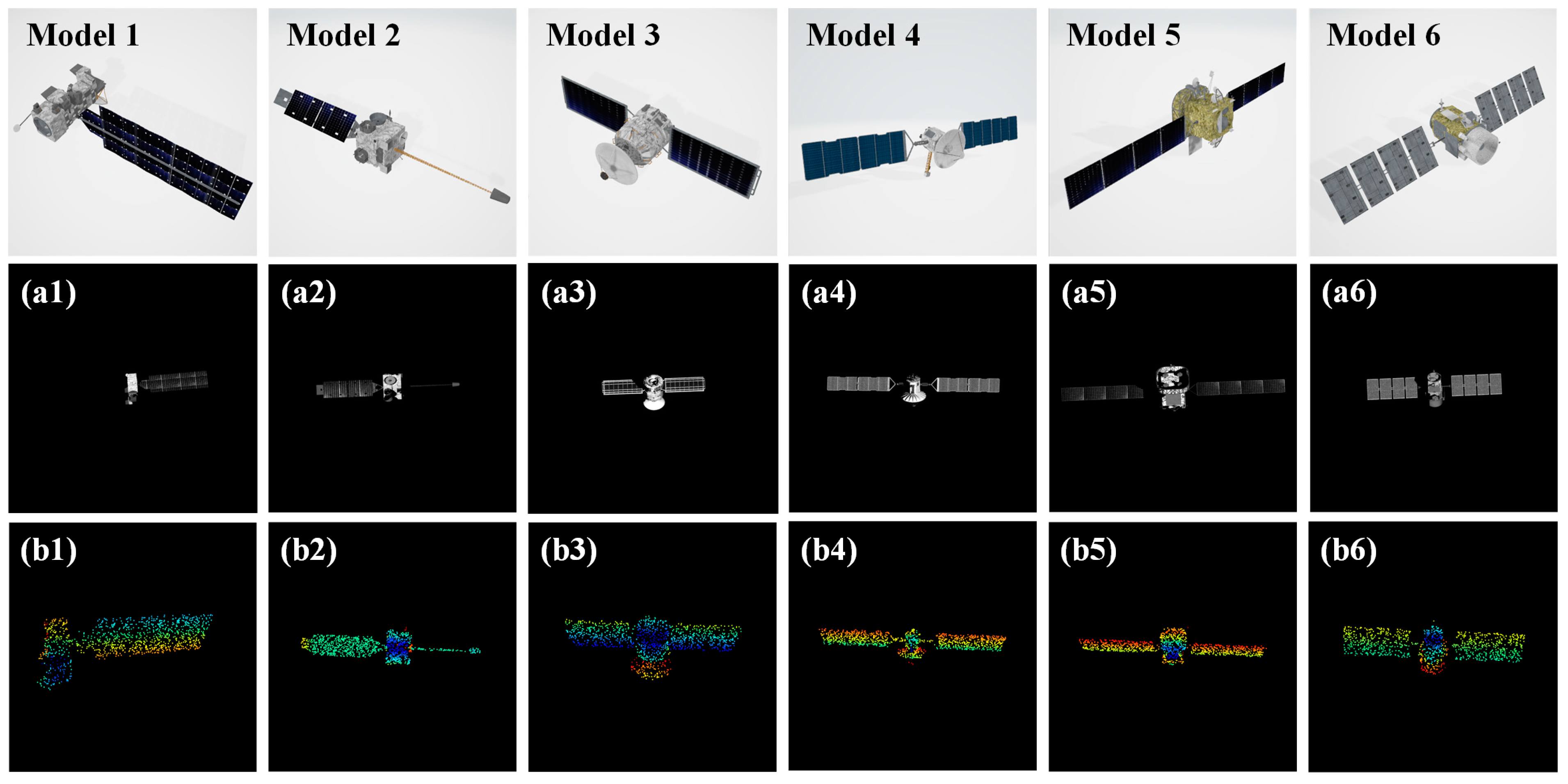
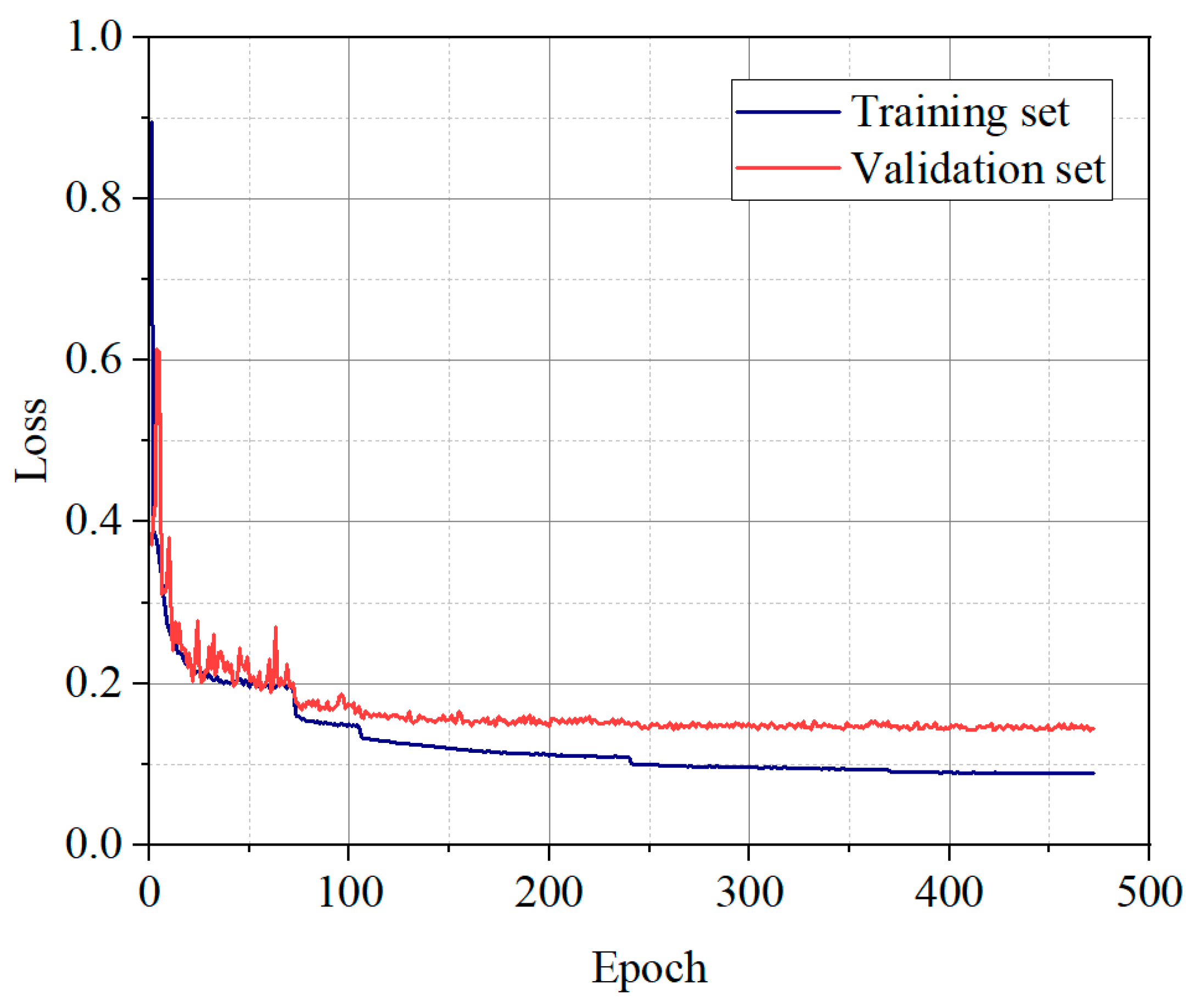
3.1. Dataset and Experimental Setup
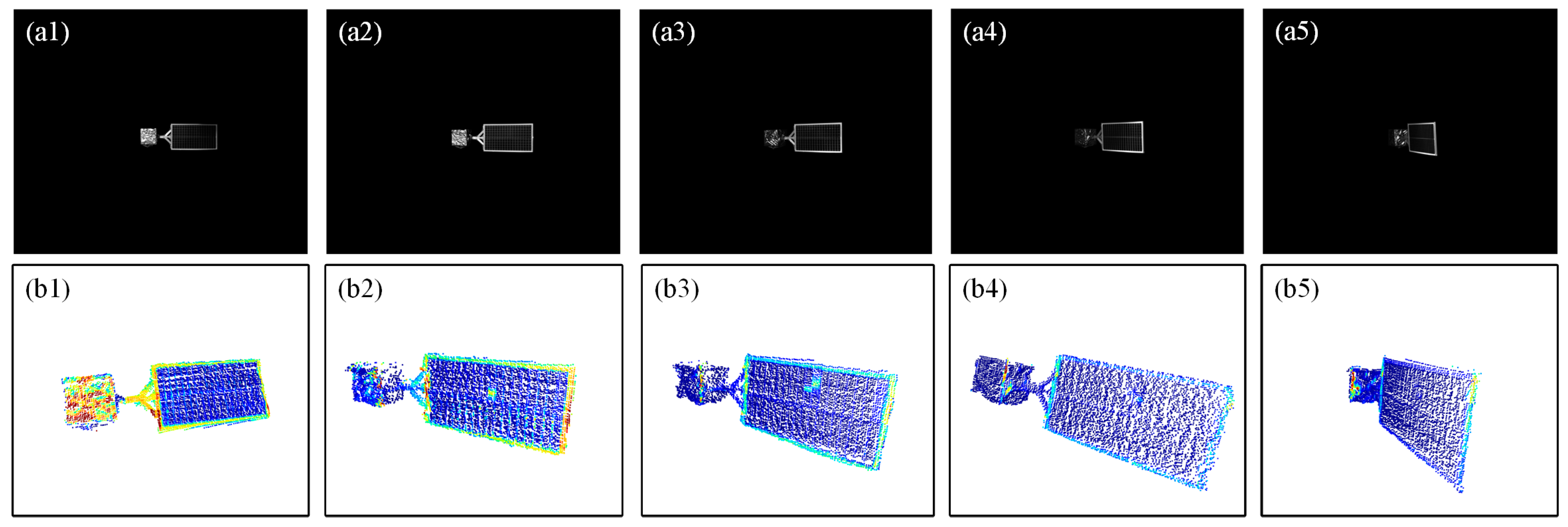
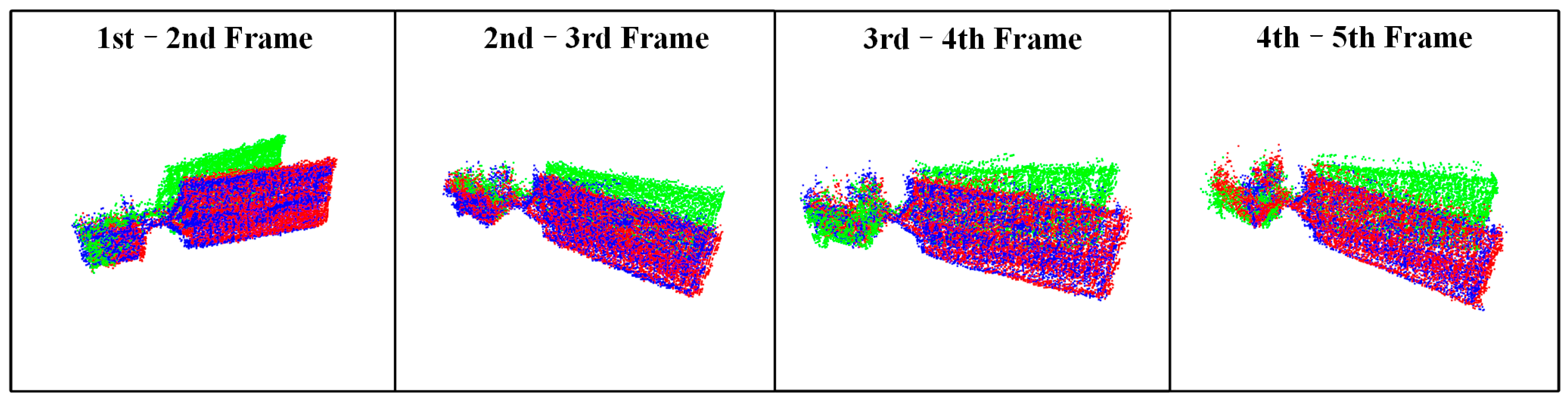
3.2. Experimental Results and Analysis
3.3. Ablation Studies
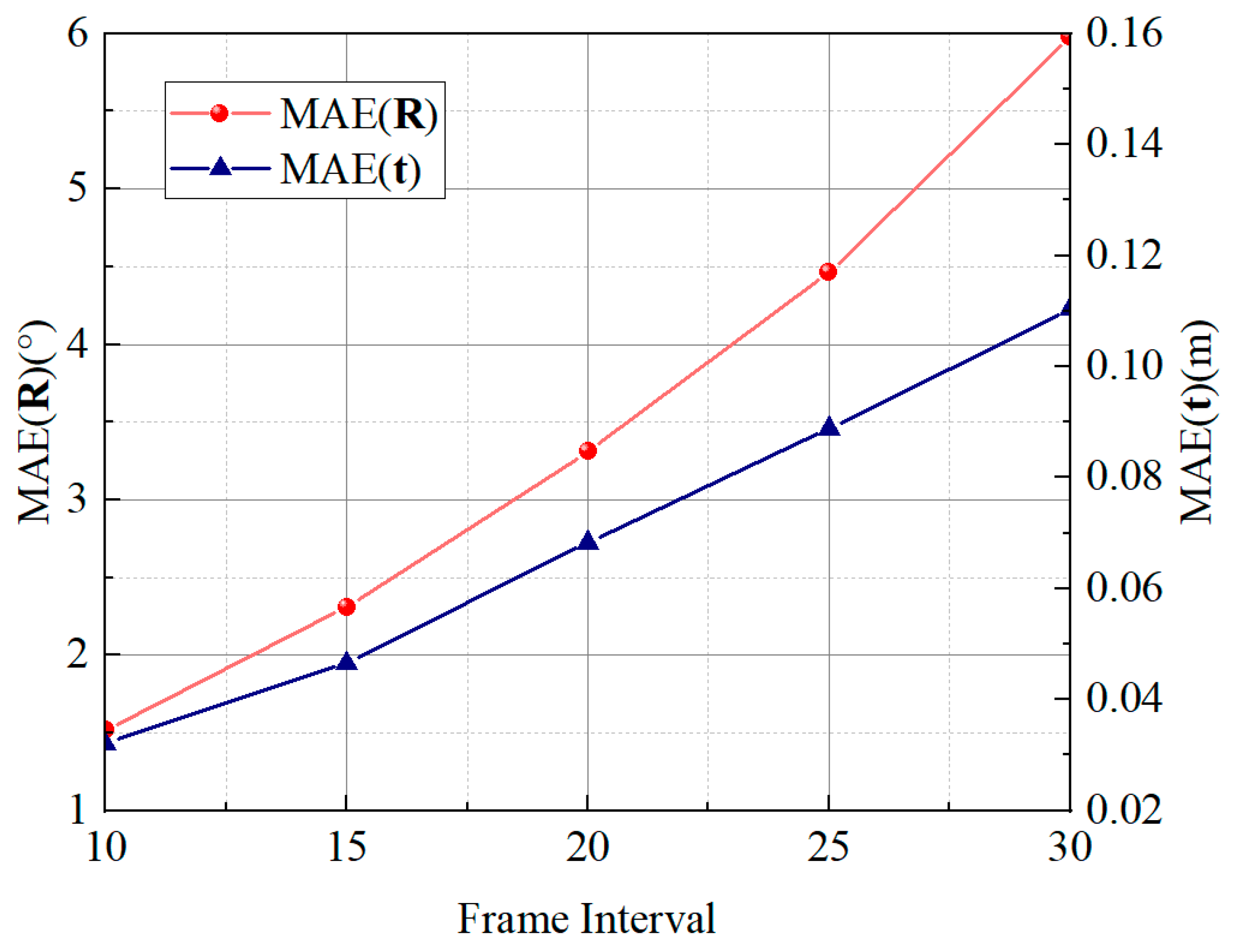
3.4. Validation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Amaya-Mejía, L.M.; Ghita, M.; Dentler, J.; Olivares-Mendez, M.; Martinez, C. Visual Servoing for Robotic On-Orbit Servicing: A Survey. In Proceedings of the 2024 International Conference on Space Robotics (iSpaRo), Luxembourg, 24–27 June 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 178–185. [Google Scholar]
- Ma, B.; Jiang, Z.; Liu, Y.; Xie, Z. Advances in space robots for on-orbit servicing: A comprehen-sive review. Adv. Intell. Syst. 2023, 5, 2200397. [Google Scholar] [CrossRef]
- Bigdeli, M.; Srivastava, R.; Scaraggi, M. Mechanics of Space Debris Removal: A Review. Aerospace 2025, 12, 277. [Google Scholar] [CrossRef]
- Bianchi, C.; Niccolai, L.; Mengali, G.; Ceriotti, M. Preliminary design of a space debris removal mission in LEO using a solar sail. Adv. Space Res. 2024, 73, 4254–4268. [Google Scholar]
- Nistér, D. An efficient solution to the five-point relative pose problem. IEEE Trans. Pat-Tern Anal. Mach. Intell. 2004, 26, 756–770. [Google Scholar]
- Zheng, Y.; Sugimoto, S.; Okutomi, M. A practical rank-constrained eight-point algorithm for fundamental matrix estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 1546–1553. [Google Scholar]
- Wang, Y.; Zhang, Z.; Huang, Y.; Su, Y. High Precision Pose Estimation for Uncooperative Targets Based on Monocular Vision and 1D Laser Fusion. J. Astronaut. Sci. 2024, 71, 43. [Google Scholar]
- Duba, P.K.; Mannam, N.P.B. Stereo vision based object detection for autonomous navigation in space environments. Acta Astronaut. 2024, 218, 326–329. [Google Scholar] [CrossRef]
- Mu, J.; Li, S.; Xin, M. Circular-feature-based pose estimation of noncooperative satellite using time-of-flight sensor. J. Guid. Control. Dyn. 2024, 47, 840–856. [Google Scholar] [CrossRef]
- Renaut, L.; Frei, H.; Nüchter, A. Deep learning on 3D point clouds for fast pose estimation during satellite rendezvous. Acta Astronaut. 2025, 232, 231–243. [Google Scholar]
- Augenstein, S.; Rock, S. Simultaneous Estimaton of Target Pose and 3-D Shape Using the FastSLAM Algorithm. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Chicago, IL, USA, 10–13 August 2009; p. 5782. [Google Scholar]
- Mur-Artal, R.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM: A versatile and accurate monocular SLAM system. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar]
- Jiang, L.; Tang, X.; Li, X.; He, X. Improved ORB-SLAM algorithm with deblurring image. In Proceedings of the 2024 4th International Conference on Electrical Engineering and Control Science (IC2ECS), Nanjing, China, 27–29 December 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 770–774. [Google Scholar]
- Besl, P.J.; McKay, N.D. Method for registra-tion of 3-D shapes. In Proceedings of the Sensor Fusion IV: Control Paradigms and Data Structures, Boston, MA, USA, 15 December 1991; SPIE: Bellingham, WA, USA, 1992; pp. 586–606. [Google Scholar]
- Wang, Q.; Lei, T.; Liu, X.; Cai, G.; Yang, Y.; Jiang, L.; Yu, Z. Pose estimation of non-cooperative target coated with MLI. IEEE Access 2019, 7, 153958–153968. [Google Scholar] [CrossRef]
- Chen, Z.; Li, L.; Wu, Y.; Hua, B.; Niu, K. A new pose estimation method for non-cooperative spacecraft based on point cloud. Int. J. Intell. Comput. Cybern. 2019, 12, 23–41. [Google Scholar] [CrossRef]
- Hu, J.; Li, S.; Xin, M. Real-time pose determination of ultra-close non-cooperative satellite based on time-of-flight camera. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 8239–8254. [Google Scholar]
- Zhang, H.; Zhang, Y.; Feng, Q.; Zhang, K. Research on Unknown Space Target Pose Estimation Method Based on Point Cloud. IEEE Access 2024, 12, 149381–149390. [Google Scholar] [CrossRef]
- Zhu, Y.; Jin, R.; Lou, T.S.; Zhao, L. PLD-VINS: RGBD visual-inertial SLAM with point and line features. Aerosp. Sci. Technol. 2021, 119, 107185. [Google Scholar] [CrossRef]
- He, Y.; Liang, B.; He, J.; Li, S. Non-cooperative spacecraft pose tracking based on point cloud feature. Acta Astronaut. 2017, 139, 213–221. [Google Scholar]
- Zhu, A.; Yang, J.; Cao, Z.; Wang, L.; Gu, Y. Pose estimation for non-cooperative targets using 3D feature correspondences grouped via local and global constraints. In Proceedings of the MIPPR 2019: Pattern Recognition and Computer Vision, Wuhan, China, 2–3 November 2019. [Google Scholar]
- Gao, X.; Liao, Y.; Zhou, H. Pose Estimation and Simulation of Non-Cooperative Spacecraft Based on Feature Points Detection. In Proceedings of the 2024 IEEE 25th China Conference on System Simulation Technology and its Application (CCSSTA), Tianjin, China, 21–23 July 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 12–16. [Google Scholar]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic graph CNN for learning on point clouds. ACM Trans. Graph. 2019, 38, 1–12. [Google Scholar] [CrossRef]
- Li, J.; Zhang, C.; Xu, Z.; Zhou, H.; Zhang, C. Iterative distance-aware similarity matrix convolution with mutual-supervised point elimination for efficient point cloud registration. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; pp. 378–394. [Google Scholar]
- Jin, S.; Li, Y.; Wang, Z.; Huang, W.; Li, M. Nested Transformer for Fast and Robust Point Cloud Registration. In Proceedings of the 2024 IEEE 6th Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 24–26 May 2024; IEEE: Piscataway, NJ, USA, 2024; Volume 6, pp. 788–794. [Google Scholar]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Yew, Z.J.; Lee, G.H. RPM-Net: Robust point matching using learned features. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11824–11833. [Google Scholar]
- Deng, H.; Birdal, T.; Ilic, S. PPFNet: Global context aware local features for robust 3D point matching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 195–205. [Google Scholar]
- Katharopoulos, A.; Pappas, V.N.; Fleuret, F. Transformers are RNNs: Fast autoregres-sive transformers with linear attention. In Proceedings of the International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 5156–5165. [Google Scholar]
- Pan, Y.; Yang, B.; Liang, F.; Dong, Z. Iterative global similarity points: A robust coarse-to-fine integration solution for pairwise 3D point cloud registration. In Proceedings of the 2018 International Conference on 3D Vision (3DV), Verona, Italy, 5–8 September 2018; pp. 180–189. [Google Scholar]
- Zhou, Q.-Y.; Park, J.; Koltun, V. Fast global registration. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; pp. 766–782. [Google Scholar]
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast point feature histograms (FPFH) for 3D registration. In Proceedings of the 2009 IEEE International Conference on Robotics And Automation, Kobe, Japan, 12–17 May 2009; pp. 3212–3217. [Google Scholar]
- Aoki, Y.; Goforth, H.; Srivatsan, R.A.; Lucey, S. PointNetLK: Robust efficient point cloud registration using pointnet. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 7163–7172. [Google Scholar]
- Liu, T.; Qin, Z.; Hong, Y.; Jiang, Z.-P. Distributed Optimization of Nonlinear Multiagent Systems: A Small-Gain Approach. IEEE Trans. Autom. Control. 2022, 67, 676–691. [Google Scholar] [CrossRef]
- Jin, Z.; Li, H.; Qin, Z.; Wang, Z. Gradient-Free Cooperative Source-Seeking of Quadrotor Under Disturbances and Communication Constraints. IEEE Trans. Ind. Electron. 2025, 72, 1969–1979. [Google Scholar]


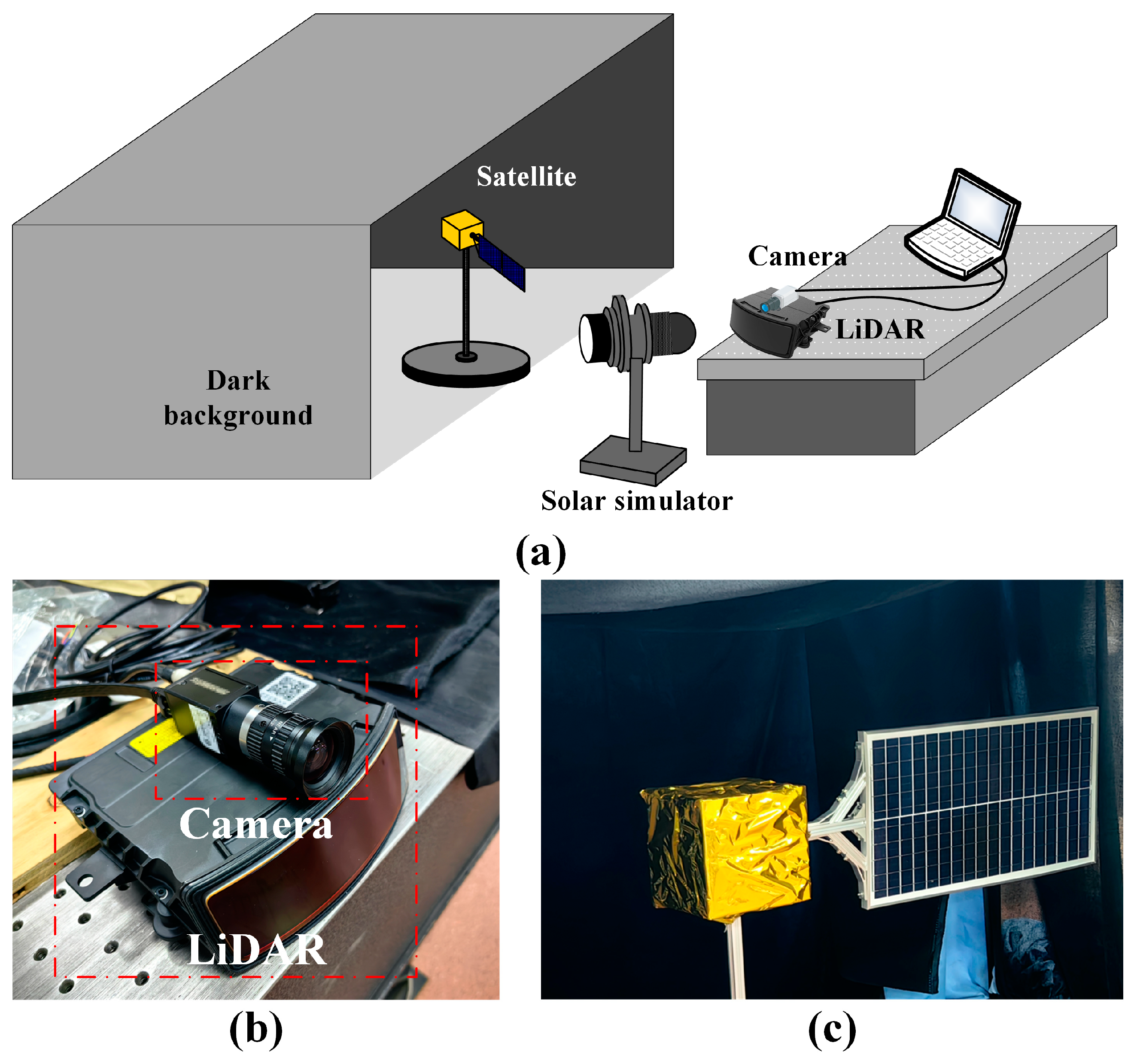

| Category | Sub-Category | Sensors | Key Algorithms |
|---|---|---|---|
| Image-based methods | Feature extraction and matching [5,6] | Monocular camera | Essential matrix solving |
| SLAM approaches [11,12,13] | Monocular/Stereo camera | Fast SLAM, ORB-SLAM | |
| Point cloud-based methods | ICP and ICP variants [14,15,16,17,18] | Monocular/Stereo/TOF camera, LiDAR | Euclidean distance |
| Geometry-based methods [19,20,21] | LiDAR/TOF camera | Euclidean distance, Normal vectors | |
| Learning-based methods [22,23,24,25] | LiDAR/TOF camera | 3D voxel CNN, Graph CNN, Transformer |
| Method | MAE (Anisotropic) | Error (Isotropic) | Time (ms) | ||
|---|---|---|---|---|---|
| R/° | t/m | R/° | t/m | ||
| ICP | 16.09 | 0.227 | 37.48 | 0.459 | 76 |
| FGR | 2.47 | 0.048 | 4.60 | 0.092 | 680 |
| SAC-IA | 2.08 | 0.040 | 4.04 | 0.078 | 257 |
| SAC-IA + ICP | 1.59 | 0.029 | 3.01 | 0.058 | 447 |
| PointNetLK | 12.22 | 0.479 | 23.06 | 0.928 | 66 |
| IDAM | 1.41 | 0.073 | 2.85 | 0.146 | 27 |
| RPM-Net | 0.91 | 0.024 | 1.83 | 0.050 | 106 |
| Ours | 0.84 | 0.022 | 1.72 | 0.045 | 68 |
| Method | MAE (Anisotropic) | Error (Isotropic) | ||
|---|---|---|---|---|
| R/° | t/m | R/° | t/m | |
| Baseline | 1.13 | 0.058 | 2.28 | 0.115 |
| Baseline + Trans | 0.86 | 0.023 | 1.77 | 0.047 |
| POCPE-Net (Baseline + Trans + ORB) | 0.84 | 0.022 | 1.72 | 0.045 |
| Method | MAE (Anisotropic) | Error (Isotropic) | ||
|---|---|---|---|---|
| R/° | t/m | R/° | t/m | |
| PointNetLK | 14.79 | 0.068 | 36.63 | 0.145 |
| IDAM(GNN) | 3.66 | 0.104 | 7.76 | 0.051 |
| RPM-Net | 1.64 | 0.020 | 3.39 | 0.039 |
| POCPE-Net (ours) | 0.97 | 0.015 | 1.77 | 0.028 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ning, Q.; Wang, H.; Yan, Z.; Wang, Z.; Lu, Y. Noncooperative Spacecraft Pose Estimation Based on Point Cloud and Optical Image Feature Collaboration. Aerospace 2025, 12, 314. https://doi.org/10.3390/aerospace12040314
Ning Q, Wang H, Yan Z, Wang Z, Lu Y. Noncooperative Spacecraft Pose Estimation Based on Point Cloud and Optical Image Feature Collaboration. Aerospace. 2025; 12(4):314. https://doi.org/10.3390/aerospace12040314
Chicago/Turabian StyleNing, Qianhao, Hongyuan Wang, Zhiqiang Yan, Zijian Wang, and Yinxi Lu. 2025. "Noncooperative Spacecraft Pose Estimation Based on Point Cloud and Optical Image Feature Collaboration" Aerospace 12, no. 4: 314. https://doi.org/10.3390/aerospace12040314
APA StyleNing, Q., Wang, H., Yan, Z., Wang, Z., & Lu, Y. (2025). Noncooperative Spacecraft Pose Estimation Based on Point Cloud and Optical Image Feature Collaboration. Aerospace, 12(4), 314. https://doi.org/10.3390/aerospace12040314


_Zhu.png)



