Design and Analysis of a Launcher Flight Control System Based on Incremental Nonlinear Dynamic Inversion †
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Related Work
1.3. Objectives and Outline
- Sensitivity to sensor noise and actuator delay. By relying on angular acceleration and control input measurements/estimates, INDI controllers are generally more sensitive to sensor noise and actuator delay than classical controllers. To assess the severity of this challenge, this paper shows a comprehensive nonlinear simulation campaign with wind disturbances and uncertainties, as well as different levels of sensor noise and actuator delay. These simulations serve as a basis to analyse the sensitivity to sensor noise and actuator delay in comparison to more classical approaches, and we showcase how to remediate or tackle these issues properly.
- Nonlinear stability analysis. The second challenge of INDI is that due to its nonlinear nature, attaining analytical proof of stability is not trivial [36]. For this second challenge, this paper proposes a simple yet insightful linearisation-based approach to evaluate stability degradation related to an inexact feedback linearisation and to deviations from the control tuning conditions. This method provides a new way to analyse and evaluate stability analysis of the nonlinear controller using linear control techniques; since INDI is designed from the theory of feedback linearisation, this approach is very intuitive in the sense that it provides a measure of degradation with respect to the feedback-linearised plant, and linear stability analysis can be performed.
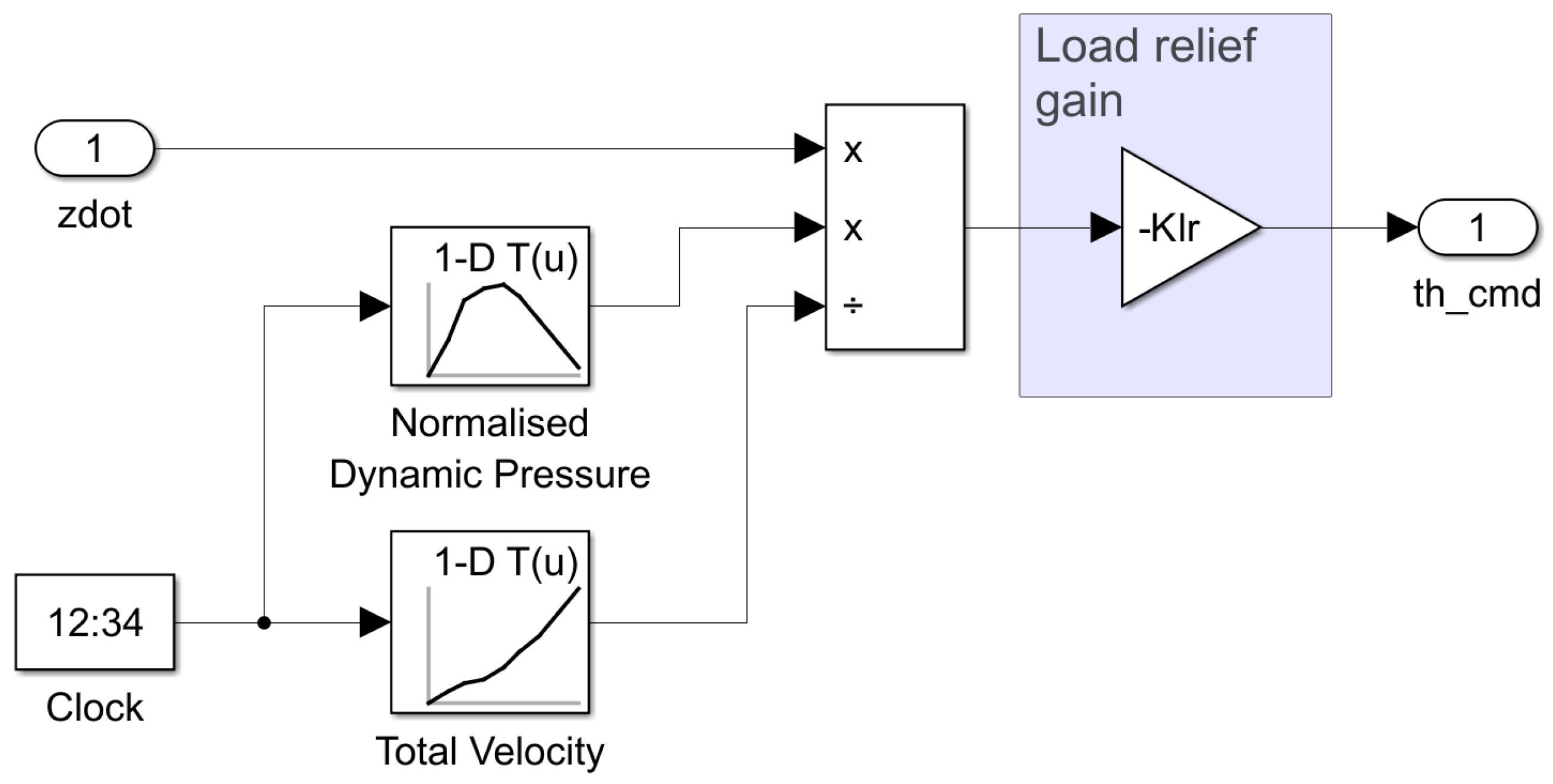
- Drift dynamics. We propose an extension to our launcher flight control system including an active load relief outer loop. Since the drift states can grow unbounded depending on the attitude control architecture, an outer loop providing the reference pitch angle for the inner-loop attitude and rate control can alleviate the drift and mitigate aerodynamic loads during ascent.
2. Basic Principles of (Incremental) Nonlinear Dynamic Inversion
2.1. Nonlinear Dynamic Inversion (NDI)
2.2. Incremental Nonlinear Dynamic Inversion (INDI)
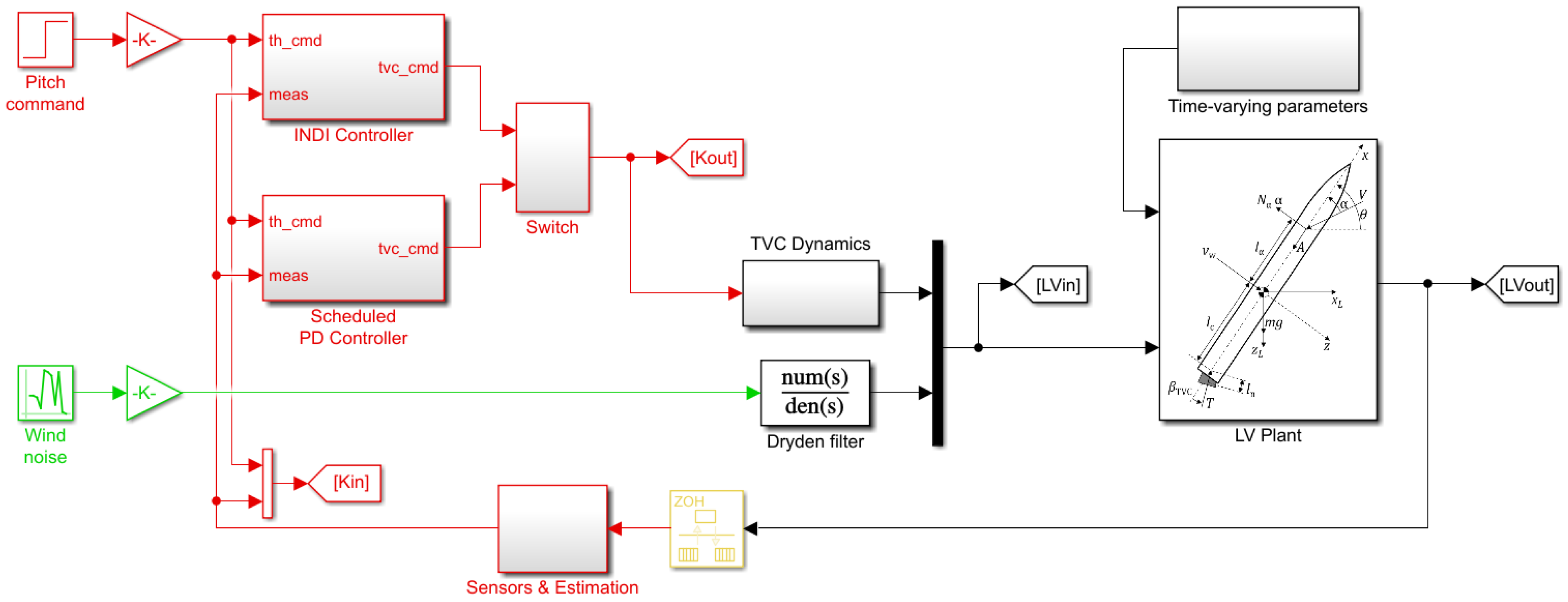
3. Launcher Flight Dynamics and Control Synthesis Models
3.1. Flight Dynamics
3.2. Actuator Dynamics
3.3. Nonlinear Model
3.4. Synthesis and Linear Models
4. Attitude Control Design Using Angular Acceleration Feedback
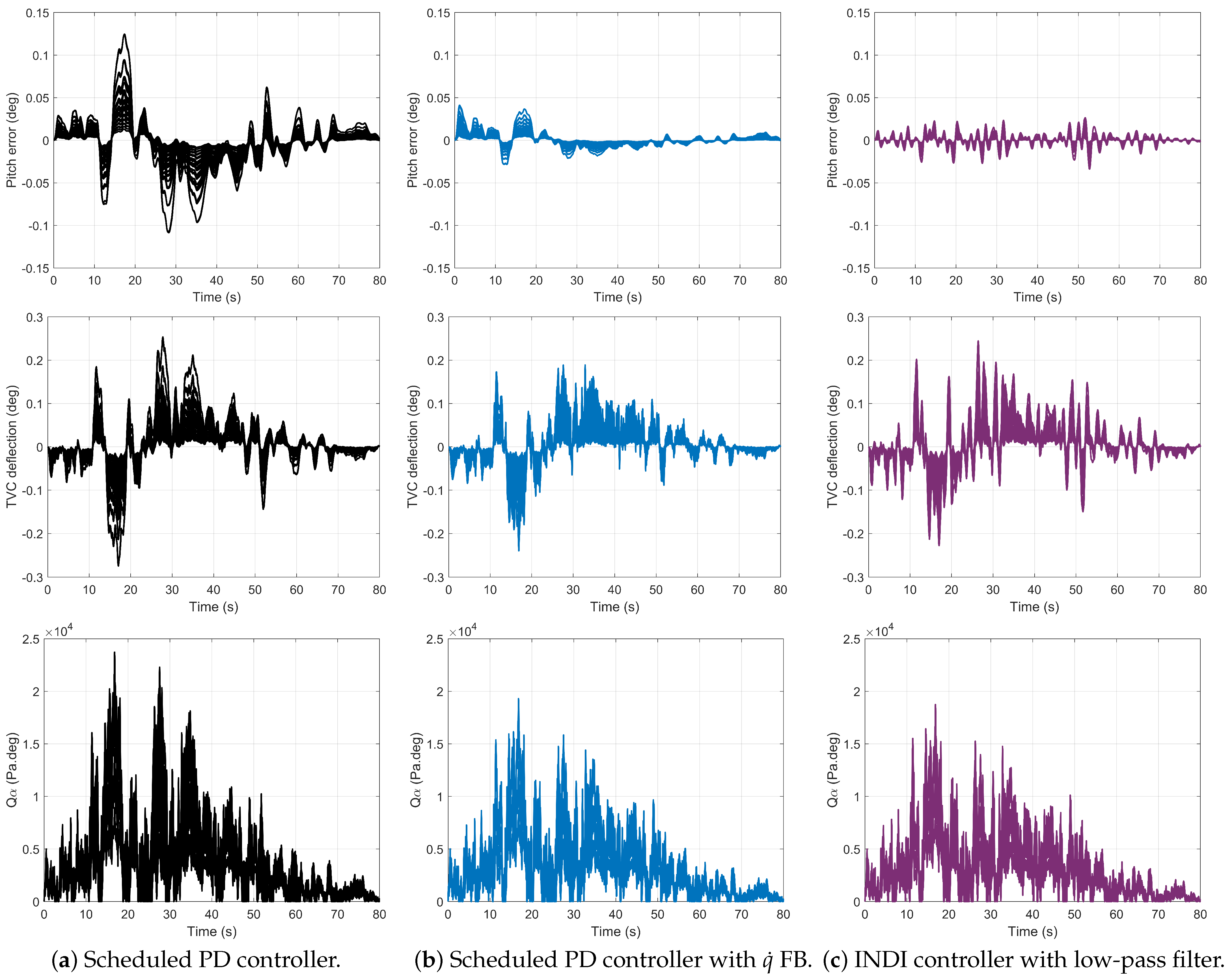
4.1. Scheduled PD Controller
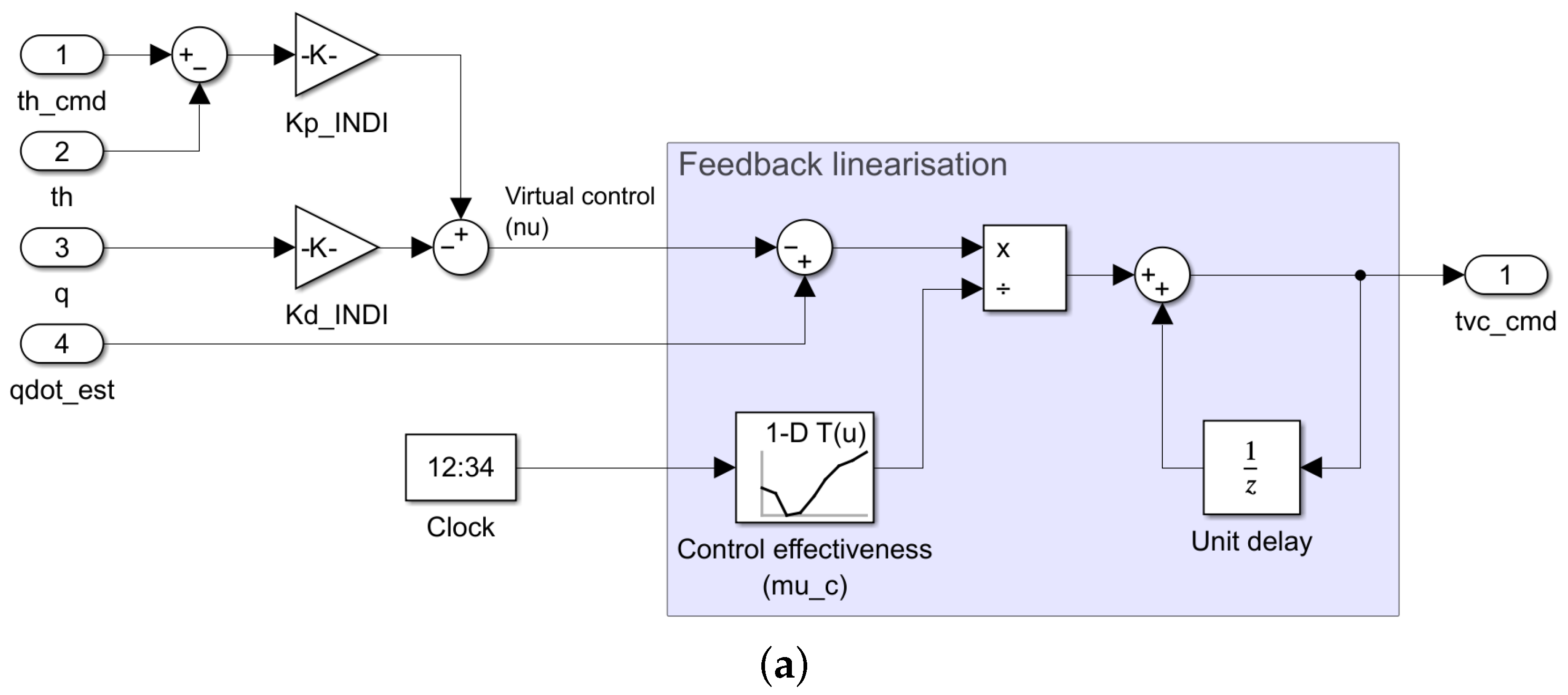
4.2. INDI Controller
4.3. Scheduled PD Controller with Feedback
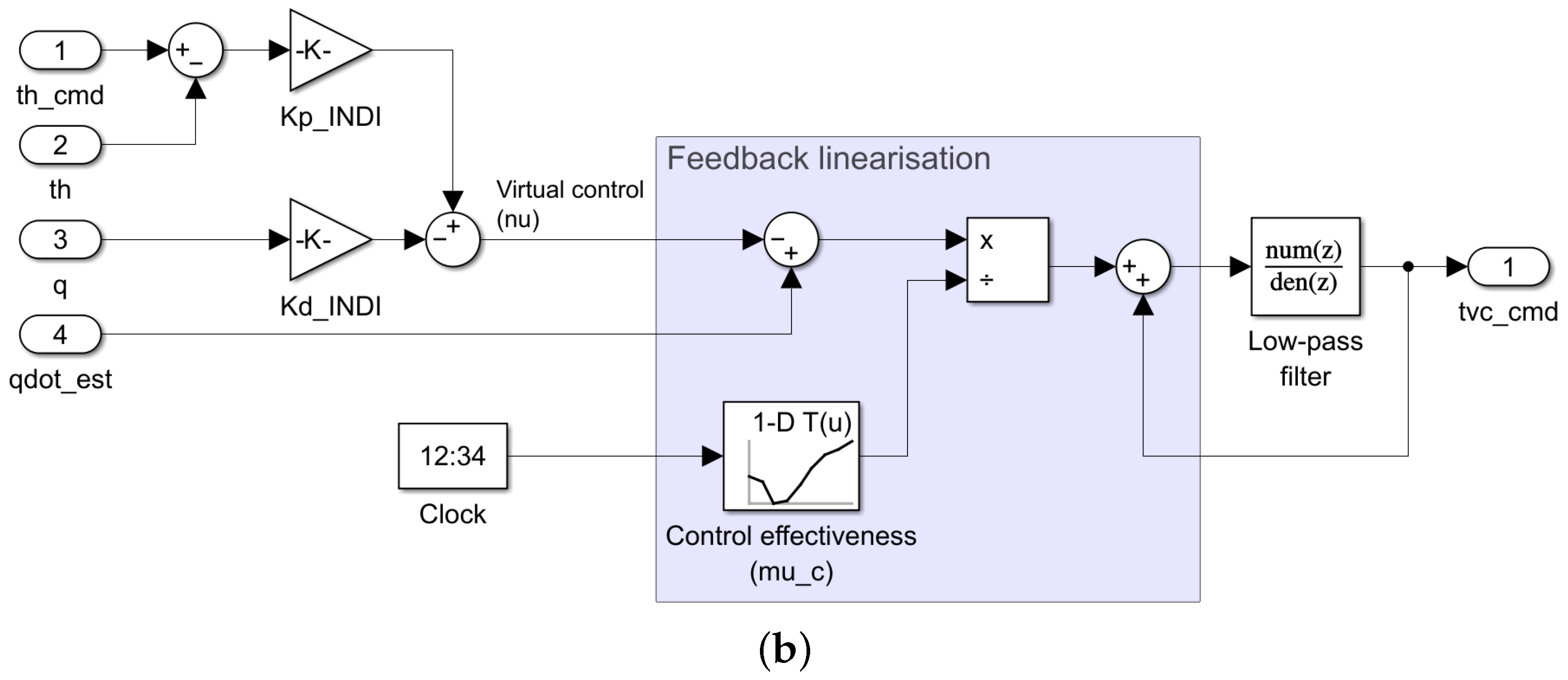
4.4. INDI Controller with Low-Pass Filter
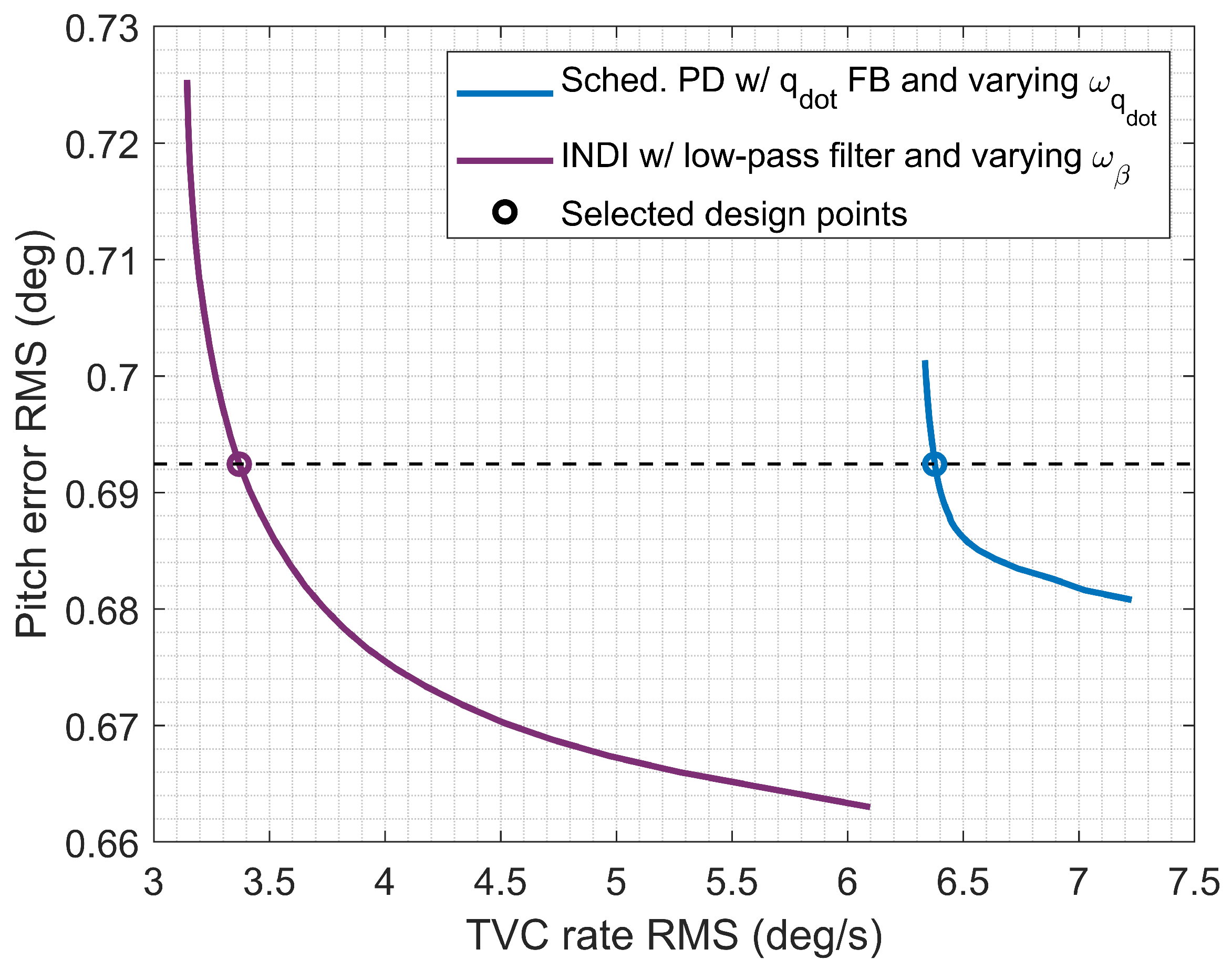
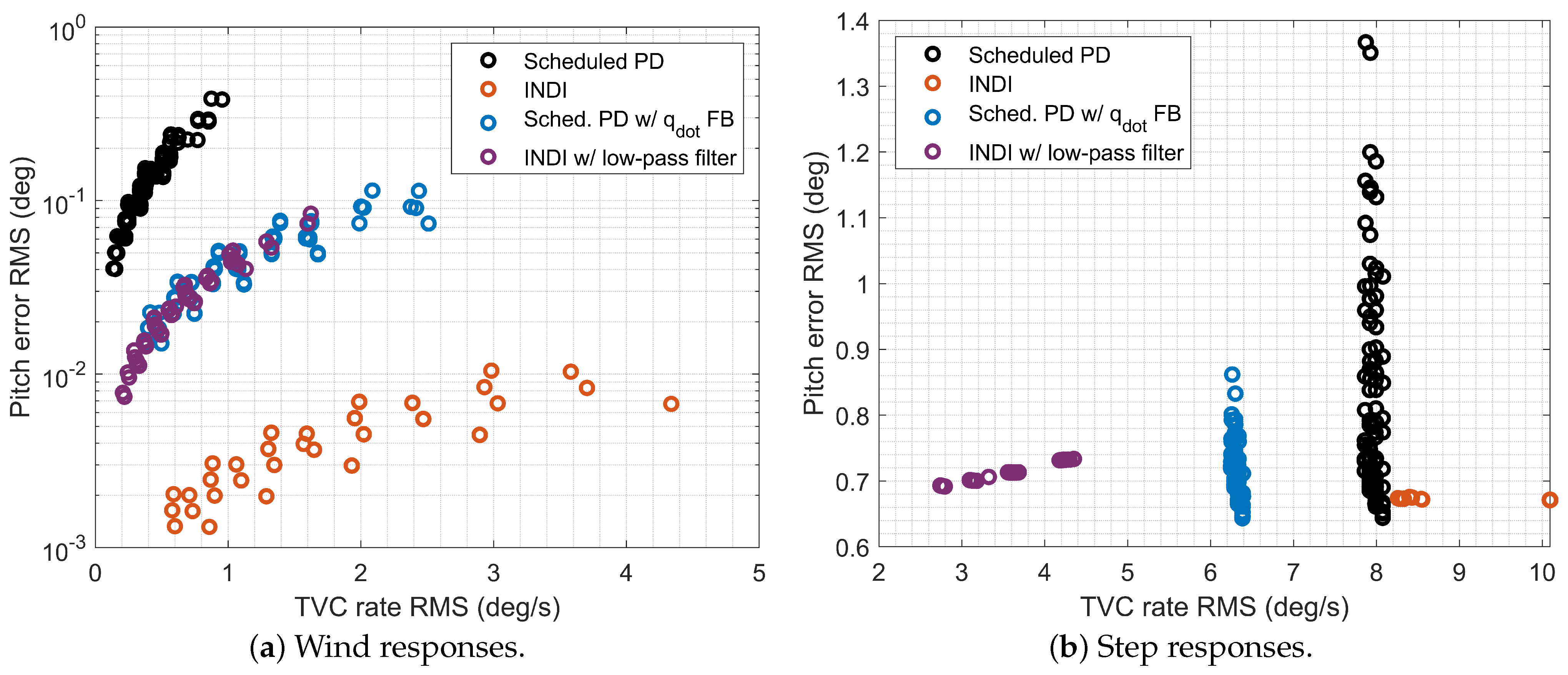
4.5. Control Design Summary
- Natural frequency rad/s;
- Damping ratio ;
- Steady-state error of 5%, i.e., , only applicable to Section 4.3.
5. Time-Domain Robust Performance Analysis
- Time delay of ms on the signal commanded to the TVC actuator, corresponding to a delay of control samples.
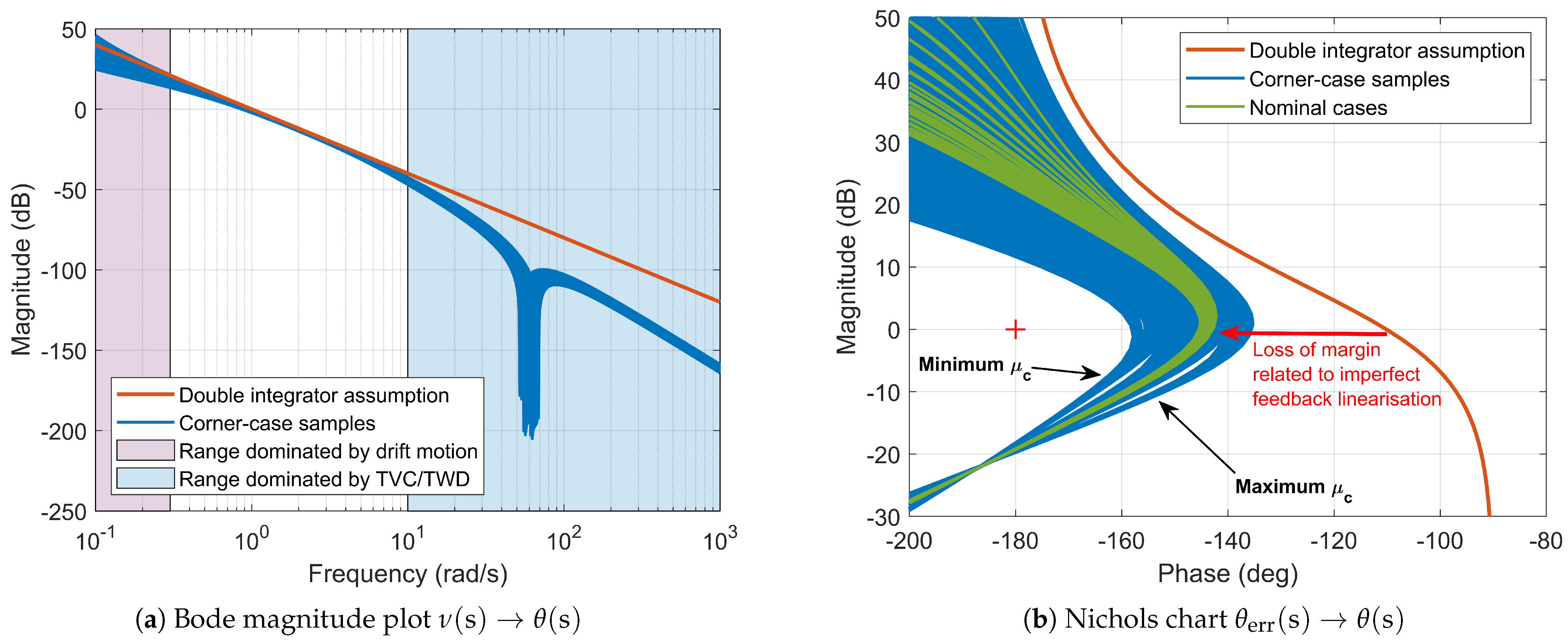
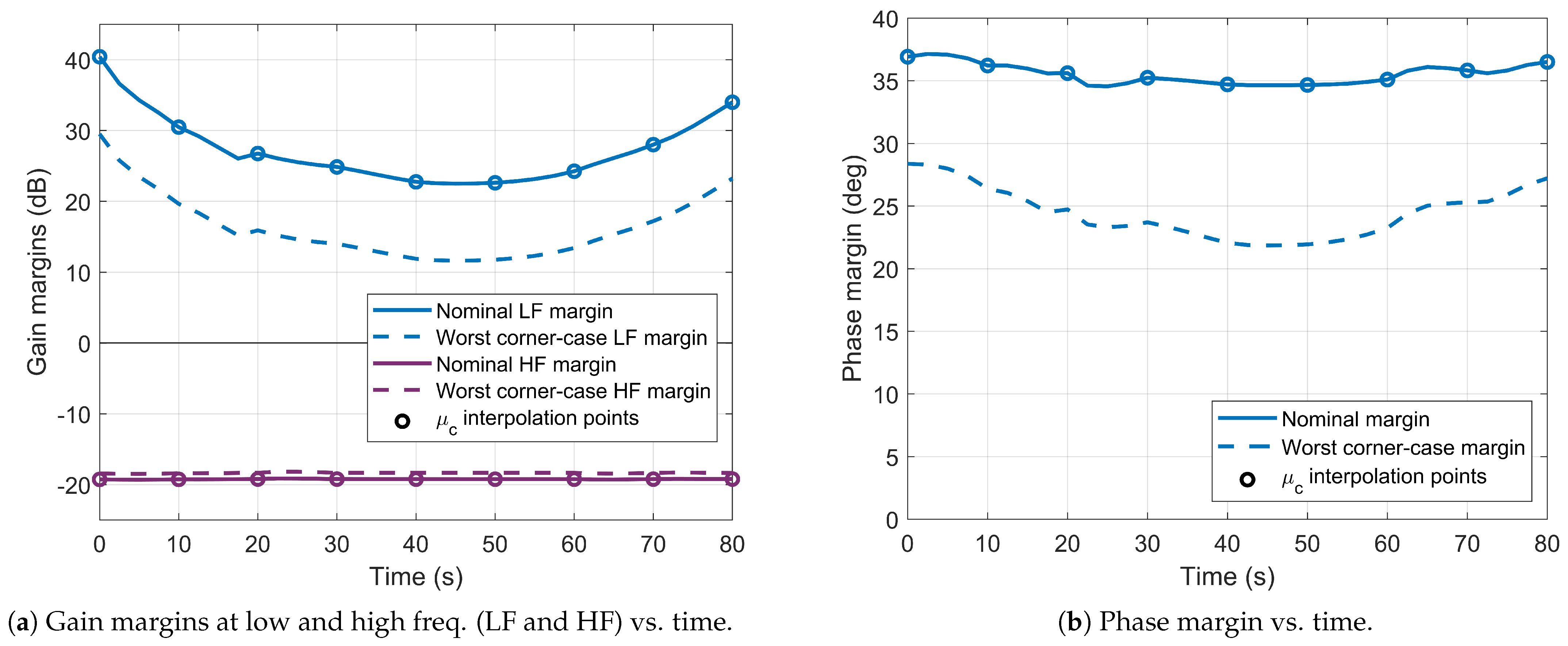
6. Frequency-Domain Robust Stability Analysis
- A dispersion of the linearised models, which is caused by deviations from the control tuning conditions due to the uncertain and time-varying nature of the model’s parameters;
- A mismatch between the linearised models and the double-integrator assumption, which grows in frequency ranges dominated by dynamical effects that are neglected in the feedback linearisation, i.e., drift motion at low frequencies (purple area) and TVC/TWD dynamics and filter at high frequencies (blue area).
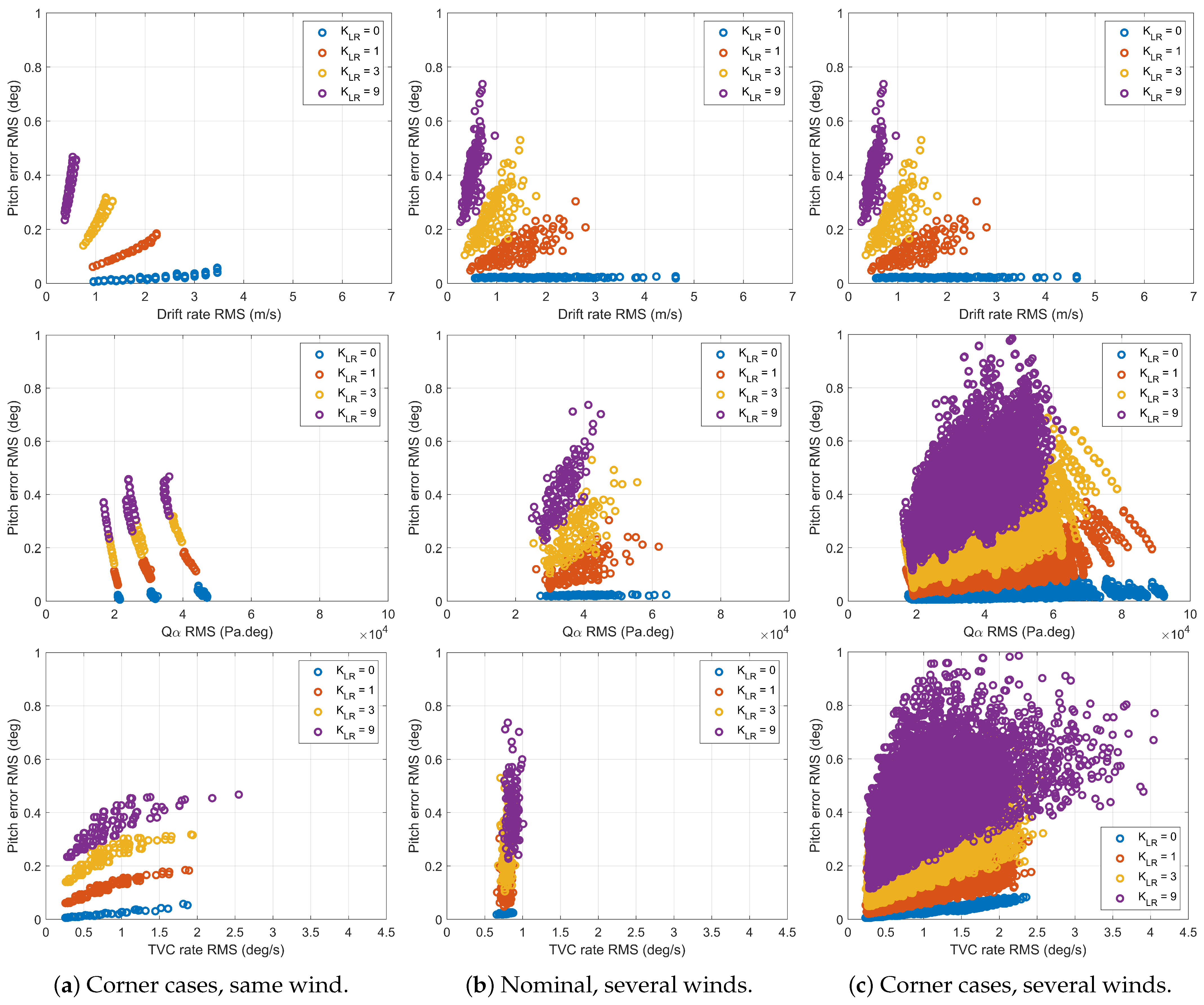
7. Extension to Launcher Control with Active Load Relief
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Marcos, A.; Navarro-Tapia, D.; Simplício, P.; Bennani, S. Robust Control for Launchers: VEGA study case. J. Soc. Instrum. Control Eng. 2020, 3, 192–202. [Google Scholar]
- Slotine, J.J.; Li, W. Applied Nonlinear Control; Prentice Hall Inc.: Hoboken, NJ, USA, 1990. [Google Scholar]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice Hall: Hoboken, NJ, USA, 2002. [Google Scholar]
- Enns, D.; Bugajski, D.; Hendrick, R.; Stein, G. Dynamic inversion: An evolving methodology for flight control design. Int. J. Control 1994, 59, 71–91. [Google Scholar]
- Reiner, J.; Balas, G.J.; Garrard, W.L. Flight Control Design Using Robust Dynamic Inversion and Time-scale Separation. Automatica 1996, 32, 1493–1504. [Google Scholar] [CrossRef]
- Smith, P.R. A Simplified Approach to Nonlinear Dynamic Inversion Based Flight Control. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Boston, MA, USA, 10–12 August 1998. [Google Scholar]
- Looye, G. Design of Robust Autopilot Control Laws with Nonlinear Dynamic Inversion. at–Automatisierungstechnik 2001, 49, 523–531. [Google Scholar]
- Lombaerts, T.J.; Huisman, H.O.; Chu, Q.P.; Mulder, J.A.; Joosten, D.A. Flight Control Reconfiguration based on Online Physical Model Identification and Nonlinear Dynamic Inversion. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008. [Google Scholar]
- Bennani, S.; Looye, G. Flight Control Law Design for a Civil Aircraft using Robust Dynamic Inversion. In Proceedings of the IEEE/SMC CESA’98, Hammamet, Tunisia, 8–12 April 1998. [Google Scholar]
- Smith, P.R.; Berry, A. Flight Test Experience of a Nonlinear Dynamic Inversion Control Law on the VAAC Harrier. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Toronto, ON, Canada, 2–5 August 2000. [Google Scholar]
- Bacon, B.J.; Ostroff, A.J. Reconfigurable Flight Control using Nonlinear Dynamic Inversion with a Special Accelerometer Implementation. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Providence, RI, USA, 16–19 August 2000. [Google Scholar]
- Bacon, B.J.; Ostroff, A.J.; Joshi, S.M. Nonlinear Dynamic Inversion Reconfigurable Controller Utilizing a Fault-Tolerant Accelerometer Approach; Technical Report; NASA Langley Research Center: Hampton, VA, USA, 2000. [Google Scholar]
- Bacon, B.J.; Ostroff, A.J.; Joshi, S.M. Reconfigurable NDI Controller using Inertial Sensor Failure Detection & Isolation. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 1373–1383. [Google Scholar]
- Chen, H.B.; Zhang, S.G. Robust Dynamic Inversion Flight Control Law Design. In Proceedings of the ISSCAA 2008, 2nd International Symposium on Systems and Control in Aerospace and Astronautics, Shenzhen, China, 10–12 December 2008. [Google Scholar]
- Sieberling, S.; Chu, Q.P.; Mulder, J.A. Robust Flight Control Using Incremental Nonlinear Dynamic Inversion and Angular Acceleration Prediction. J. Guid. Control Dyn. 2010, 33, 1732–1742. [Google Scholar] [CrossRef]
- Simplício, P.; Pavel, M.; van Kampen, E.; Chu, Q.P. An Acceleration Measurements-based Approach for Helicopter Nonlinear Flight Control using Incremental Nonlinear Dynamic Inversion. Control Eng. Pract. 2013, 21, 1065–1077. [Google Scholar] [CrossRef]
- Lu, P.; van Kampen, E.; Chu, Q.P. Robustness and Tuning of Incremental Backstepping Approach. In Proceedings of the AIAA Guidance, Navigation and Control Conference, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Lu, P.; van Kampen, E. Active Fault-Tolerant Control System using Incremental Backstepping Approach. In Proceedings of the AIAA Guidance, Navigation and Control Conference, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Smeur, E.J.; Chu, Q.P.; de Croon, G.C. Adaptive Incremental Nonlinear Dynamic Inversion for Attitude Control of Micro Air Vehicles. J. Guid. Control Dyn. 2016, 39, 450–461. [Google Scholar]
- Smeur, E.J.; de Croon, G.C.; Chu, Q.P. Gust Disturbance Alleviation with Incremental Nonlinear Dynamic Inversion. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016. [Google Scholar]
- Vlaar, C. Incremental Nonlinear Dynamic Inversion Flight Control. Master’s Thesis, Delft University of Technology, Faculty of Aerospace Engineering, Delft, The Netherlands, 2014. [Google Scholar]
- Grondman, F.; Looye, G.; Kuchar, R.O.; Chu, Q.P.; van Kampen, E. Design and Flight Testing of Incremental Nonlinear Dynamic Inversion-based Control Laws for a Passenger Aircraft. In Proceedings of the AIAA Guidance, Navigation and Control Conference, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Keijzer, T.; Looye, G.; Chu, Q.P.; van Kampen, E. Design and Flight Testing of Incremental Backstepping based Control Laws with Angular Accelerometer Feedback. In Proceedings of the AIAA SciTech Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Acquatella, B.P.; Falkena, W.; van Kampen, E.J.; Chu, Q.P. Robust Nonlinear Spacecraft Attitude Control Using Incremental Nonlinear Dynamic Inversion. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Minneapolis, MN, USA, 13–16 August 2012. [Google Scholar]
- Acquatella B., P.; Chu, Q.P. Agile Spacecraft Attitude Control: An Incremental Nonlinear Dynamic Inversion Approach. IFAC-PapersOnLine 2020, 53, 5709–5716. [Google Scholar]
- Acquatella B., P.; van Kampen, E.; Chu, Q.P. A Sampled-data Form of Incremental Nonlinear Dynamic Inversion for Spacecraft Attitude Control. In Proceedings of the AIAA SciTech Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar]
- Rickmers, P.; Bauer, W.; Stappert, S.; Sippel, M.; Redondo, Gutierrez, J.L.; Seelbinder, D.; Bernal, Polo, P.; Razgus, B.; Theil, S.; Acquatella, B.P.; et al. The Reusability Flight Experiment–ReFEx: From Design to Flight–Hardware. In Proceedings of the International Astronautical Congress (IAC), Dubai, United Arab Emirates, 25–29 October 2021. [Google Scholar]
- Rickmers, P.; Kottmar, S.; Wibbels, G.; Bauer, W. ReFEx: Reusability Flight Experiment–A Demonstration Experiment for Technologies for Aerodynamically Controlled RLV Stages. In Proceedings of the Aerospace Europe Conference 2023–10th EUCASS–9th CEAS, Lausanne, Switzerland, 9–13 July 2023. [Google Scholar]
- Redondo Gutierrez, J.L.; Seelbinder, D.; Theil, S.; Bernal Polo, P.; Gäßler, B.; Robens, J.; Acquatella, B.P. ReFEx: Reusability Flight Experiment–Architecture and Algorithmic Design of the GNC Subsystem. In Proceedings of the Aerospace Europe Conference 2023–10th EUCASS–9th CEAS, Lausanne, Switzerland, 9–13 July 2023. [Google Scholar]
- Gäßler, B.; Robens, J. Incremental Nonlinear Dynamic Inversion Flight Control for the DLR Reusability Flight Experiment ReFEx. In Proceedings of the AIAA SciTech Forum, Kissimmee, FL, USA, 6–10 January 2025. [Google Scholar]
- Mooij, E. Robust Control of a Conventional Aeroelastic Launch Vehicle. In Proceedings of the AIAA SciTech Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Mooij, E. Slosh Observer Design for Aeroelastic Launch Vehicles. In Proceedings of the AIAA SciTech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar] [CrossRef]
- Mooij, E.; Wang, X. Incremental Sliding Mode Control for Aeroelastic Launch Vehicles with Propellant Slosh. In Proceedings of the AIAA SciTech 2021 Forum, Virtual, 11–15, 19–21 January 2021. [Google Scholar] [CrossRef]
- Mooij, E. Dynamic Inversion Heat-Flux Tracking for Hypersonic Entry. In Proceedings of the AIAA SciTech Forum, National Harbor, MD, USA, 23–27 January 2023. [Google Scholar]
- Mooij, E.; Wang, X. Nonlinear Robust Control and Observation for Aeroelastic Launch Vehicles with Propellant Slosh in a Turbulent Atmosphere. In Proceedings of the AIAA SciTech Forum, National Harbor, MD, USA, 23–27 January 2023. [Google Scholar] [CrossRef]
- Wang, X.; van Kampen, E.; Chu, Q.P.; Lu, P. Stability Analysis for Incremental Nonlinear Dynamic Inversion Control. J. Guid. Control. Dyn. 2019, 42, 1116–1129. [Google Scholar] [CrossRef]
- Simplício, P.; Acquatella, P.; Bennani, S. Launcher Attitude Control based on Incremental Nonlinear Dynamic Inversion: A Feasibility Study towards Fast and Robust Design Approaches. In Proceedings of the 12th International ESA Conference on Guidance, Navigation and Control Systems, Sopot, Poland, 12–16 June 2023. [Google Scholar]
- Simplício, P.; Marcos, A.; Bennani, S. Reusable Launchers: Development of a Coupled Flight Mechanics, Guidance and Control Benchmark. J. Spacecr. Rocket. 2020, 57, 74–89. [Google Scholar] [CrossRef]
- Simplício, P.; Bennani, S.; Marcos, A.; Roux, C.; Lefort, X. Structured Singular-Value Analysis of the Vega Launcher in Atmospheric Flight. J. Guid. Control. Dyn. 2016, 39, 1342–1355. [Google Scholar] [CrossRef]
- Simplício, P.; Marcos, A.; Bennani, S. Launcher Flight Control Design using Robust Wind Disturbance Observation. Acta Astronaut. 2021, 186, 303–318. [Google Scholar] [CrossRef]
- Navarro-Tapia, D.; Marcos, A.; Bennani, S.; Roux, C. Structured H-infinity and Linear Parameter Varying control design for the VEGA Launch Vehicle. In Proceedings of the the 7th European Conference for Aeronautics and Space Sciences, Milan, Italy, 3–6 July 2017. [Google Scholar]
- Vandersteen, J.; Bennani, S.; Roux, C. Robust Rocket Navigation with Sensor Uncertainties: Vega Launcher Application. J. Spacecr. Rocket. 2018, 55, 153–166. [Google Scholar] [CrossRef]


| Type of Parameters | Variables | Uncertainty Level |
|---|---|---|
| Aerodynamics | , , , V | 20% |
| Mass/propulsion | m, J, , T | 10% |
| Control Design Method | Dependency on Model Parameters | Dependency on Measurements/Estimates |
|---|---|---|
| Scheduled PD | ||
| Scheduled PD with feedback | ||
| INDI with or without low-pass filter |
| Case | LF Gain Margin (dB) | Phase Margin (deg) | HF Gain Margin (dB) |
|---|---|---|---|
| Double-integrator assumption | ∞ | 69.84 | ∞ |
| Nominal | 22.62 | 34.66 | 19.21 |
| Nominal with deviation from interp. points | 22.50 | 34.55 | 19.13 |
| Worst-case | 11.76 | 21.94 | 18.32 |
| Worst-case with deviation from interp. points | 11.64 | 21.86 | 18.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simplício, P.; Acquatella, P.; Bennani, S. Design and Analysis of a Launcher Flight Control System Based on Incremental Nonlinear Dynamic Inversion. Aerospace 2025, 12, 296. https://doi.org/10.3390/aerospace12040296
Simplício P, Acquatella P, Bennani S. Design and Analysis of a Launcher Flight Control System Based on Incremental Nonlinear Dynamic Inversion. Aerospace. 2025; 12(4):296. https://doi.org/10.3390/aerospace12040296
Chicago/Turabian StyleSimplício, Pedro, Paul Acquatella, and Samir Bennani. 2025. "Design and Analysis of a Launcher Flight Control System Based on Incremental Nonlinear Dynamic Inversion" Aerospace 12, no. 4: 296. https://doi.org/10.3390/aerospace12040296
APA StyleSimplício, P., Acquatella, P., & Bennani, S. (2025). Design and Analysis of a Launcher Flight Control System Based on Incremental Nonlinear Dynamic Inversion. Aerospace, 12(4), 296. https://doi.org/10.3390/aerospace12040296








