An Analytical Study on the Thermal Post-Buckling Behaviors of Geometrically Imperfect FRC-Laminated Beams Using a Modified Zig-Zag Beam Model
Abstract
1. Introduction
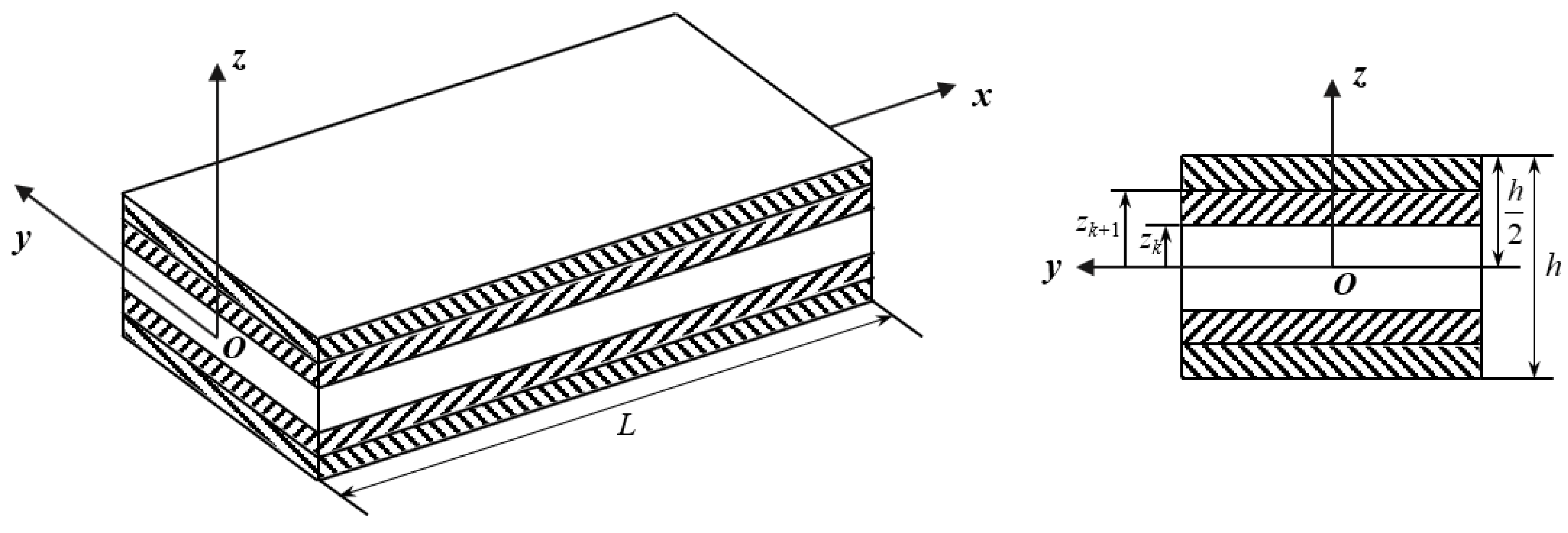
2. Modeling of FRC Laminated Beams
3. Approximate Analytical Solutions of Post-Buckling Response
3.1. Clamped–Clamped Support
3.2. Hinged–Hinged Support
4. Numerical Results and Discussion
4.1. Validation and Comparison
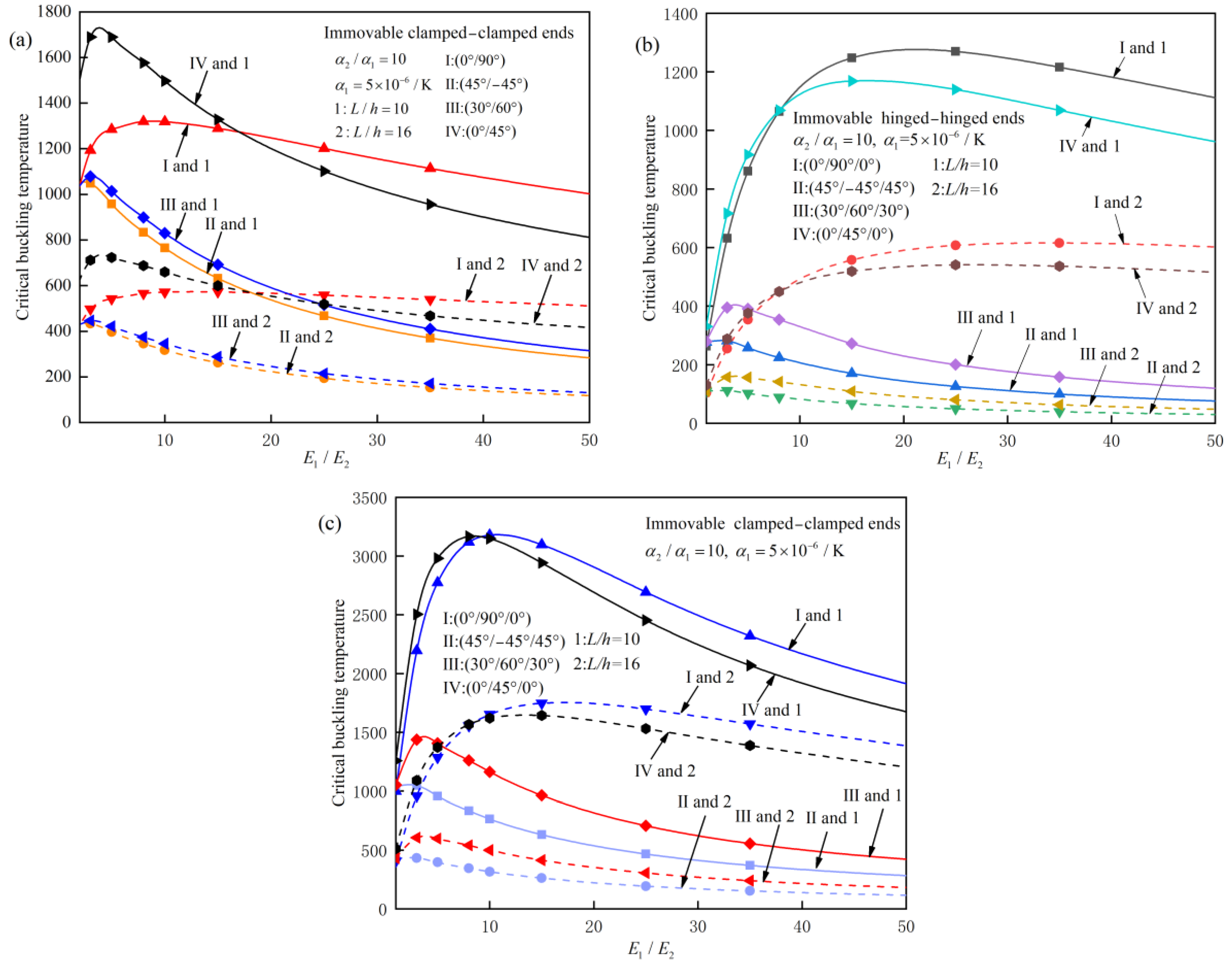
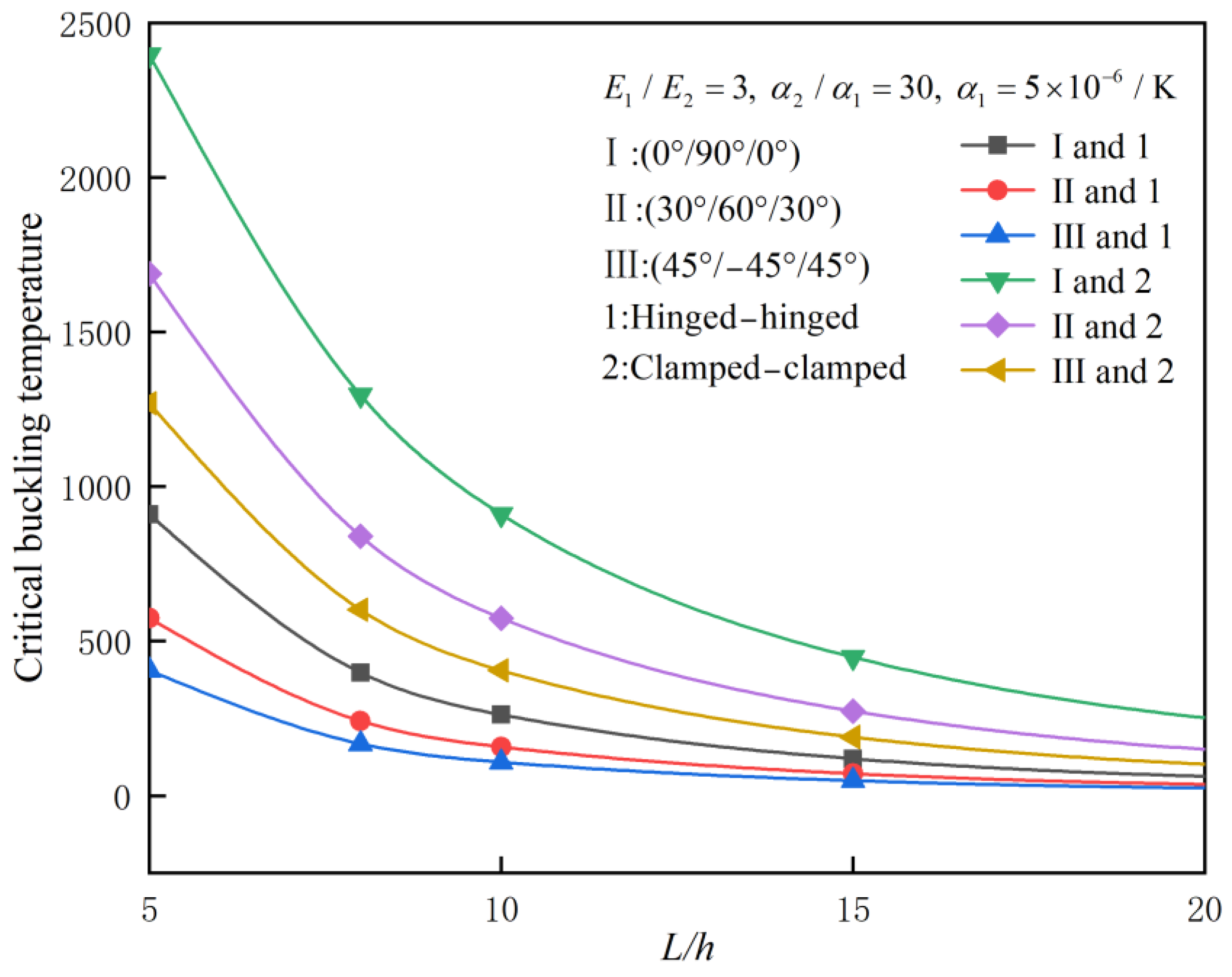
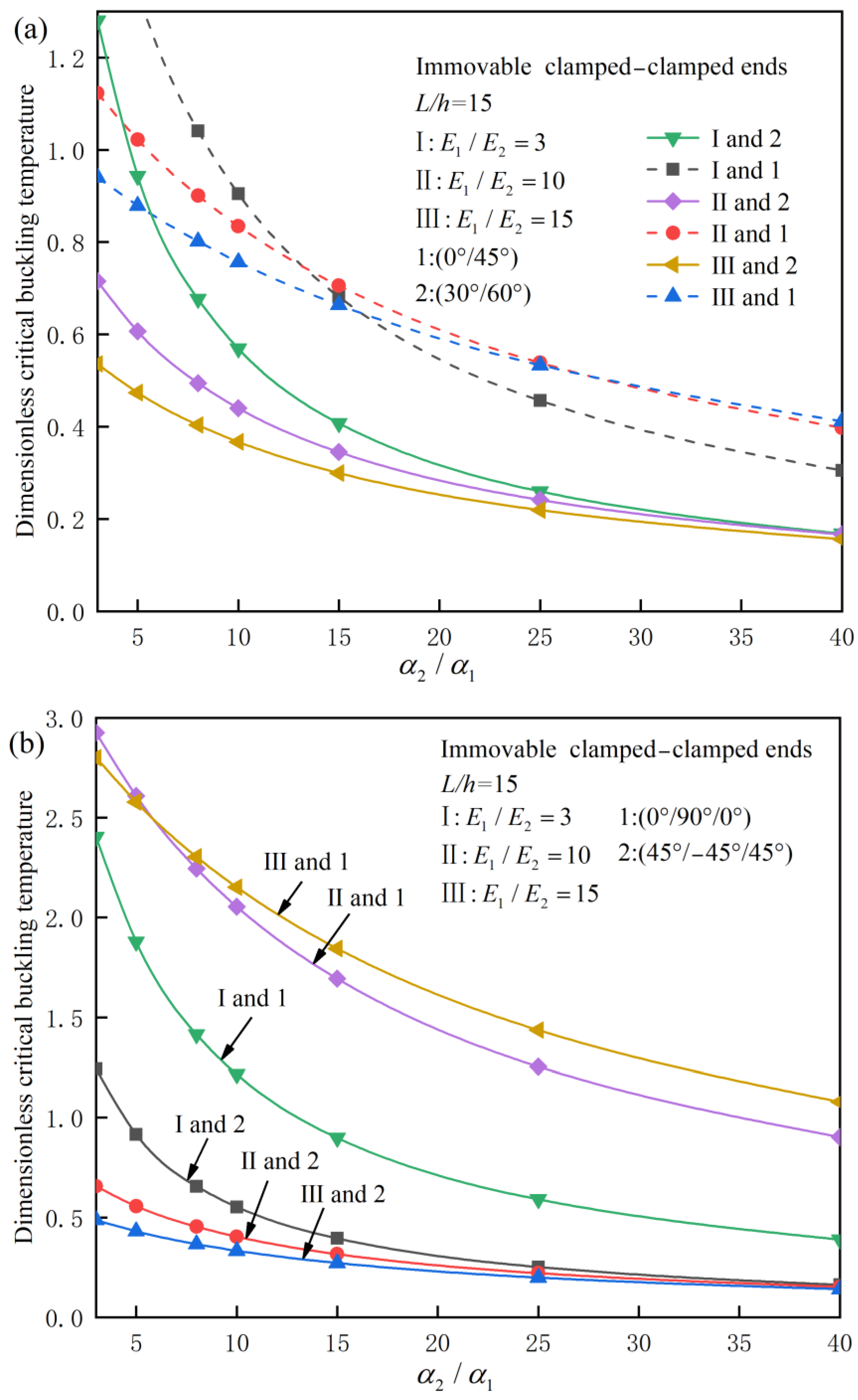
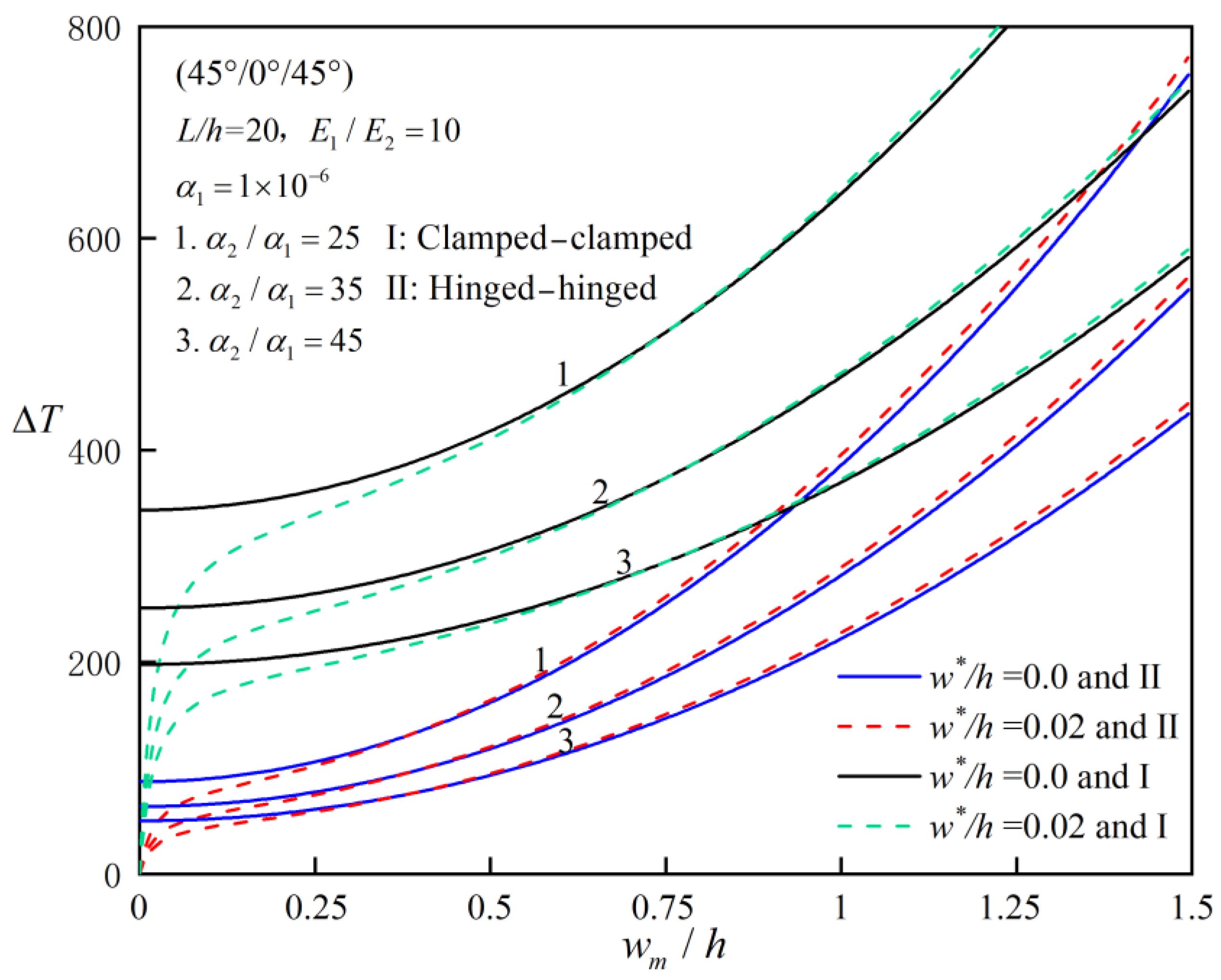
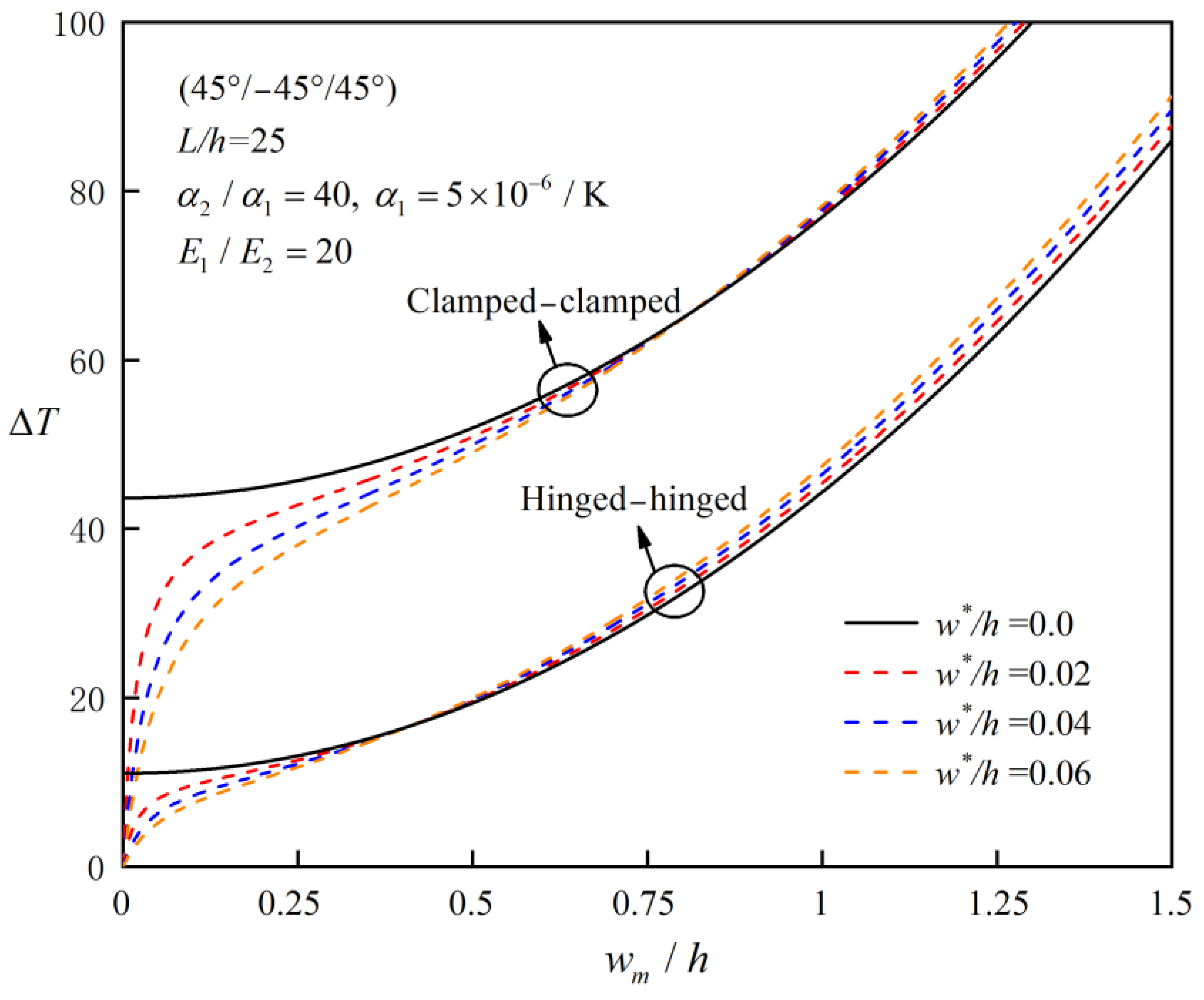
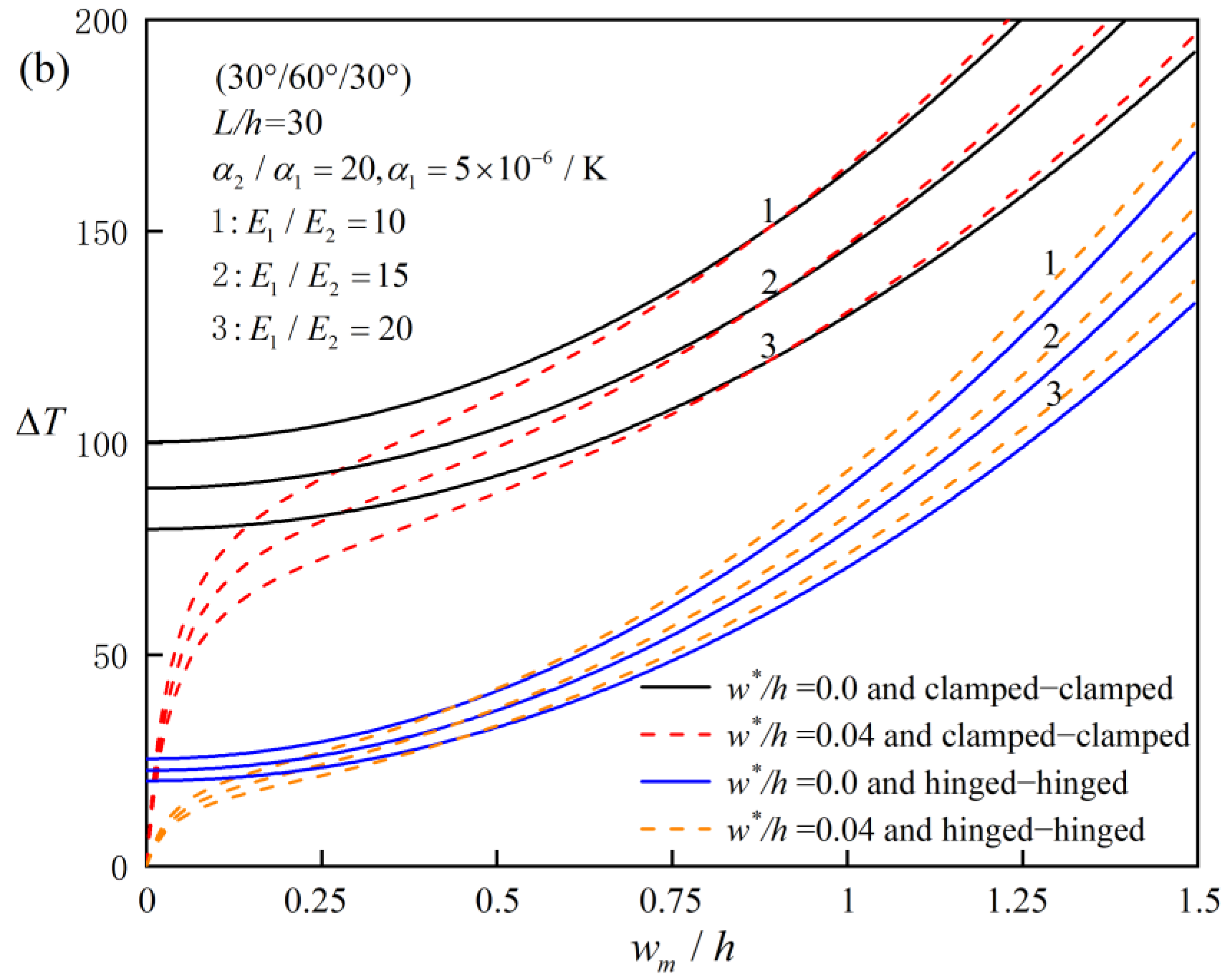
4.2. Parameter Analysis
5. Conclusions
- Comparison of Zig-Zag Model and Equivalent Single-Layer Theory: For symmetric or anti-symmetric laminated beams, the results of the zig-zag beam model and the equivalent single-layer theory are similar, with differences of less than 2%. However, for general asymmetric laminated beams, the zig-zag model provides more accurate predictions, especially when the slenderness ratio is small or the elastic modulus ratio is large. For example, for asymmetric (0°/90°) laminated beams with a slenderness ratio of 5, the zig-zag model predicts a critical buckling temperature of 0.511, while the equivalent single-layer theory overestimates this value by up to 10%.
- Effect of Slenderness Ratio: The critical buckling temperature increases with the slenderness ratio. For example, for a symmetric (0°/90°/0°) laminated beam with clamped–clamped ends, the critical buckling temperature increases from 0.682 for a slenderness ratio of 5 to 4.018 for a slenderness ratio of 50.
- Effect of Elastic Modulus Ratio: The critical buckling temperature generally increases with the elastic modulus ratio, but the effect is more pronounced for beams with a small slenderness ratio. For example, for a clamped–clamped (0°/90°) laminated beam with a slenderness ratio of 10, the critical buckling temperature increases by 15% when the elastic modulus ratio increases from 3 to 10.
- Effect of Thermal Expansion Coefficient Ratio: The critical buckling temperature decreases with the thermal expansion coefficient ratio. For example, for a clamped–clamped (45°/−45°/45°) laminated beam, the critical buckling temperature decreases by 20% when the thermal expansion coefficient ratio increases from 3 to 10.
- Initial Imperfection Sensitivity: The post-buckling behavior of FRC laminated beams is relatively insensitive to initial imperfections. However, in the deep post-buckling stage, the initial defect rate can enhance the bending stiffness of the beam by up to 10% due to stress redistribution caused by the geometric imperfection.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hudson, T.B.; Auwaijan, N.; Yuan, F.G. Guided wave-based system for real-time cure monitoring of composites using piezoelectric discs and phase-shifted fiber Bragg gratings. J. Compos. Mater. 2019, 53, 969–979. [Google Scholar] [CrossRef] [PubMed]
- Barile, C.; Casavola, C.; Cililis, F.D. Mechanical comparison of new composite materials for aerospace applications. Compos. Part B 2019, 162, 122–128. [Google Scholar] [CrossRef]
- Liu, X.; Sun, W.; Yan, X.; Du, D.; Liu, H.; Li, H. Nonlinear vibration analysis of carbon fiber-reinforced composites with frequency-dependence and strain-dependence: Experimental and theoretical studies. Thin-Walled Struct. 2023, 183, 110369. [Google Scholar] [CrossRef]
- Christian, W.J.R.; DiazDelaO, F.A.; Patterson, E.A. Strain-based damage assessment for accurate residual strength prediction of impacted composite laminates. Compos. Struct. 2018, 184, 1215–1223. [Google Scholar] [CrossRef]
- Jiang, H.; Ren, Y.; Zhang, S.; Liu, Z.; Yu, G.; Xiang, J. Damage and perforation resistance behaviors induced by projectile impact load on bonding-patch repaired and scarf-patch repaired composite laminates. Int. J. Damage Mech. 2019, 28, 502–537. [Google Scholar] [CrossRef]
- Eltaher, M.A.; Mohamed, N.; Mohamed, S.A.; Seddek, L. Periodic and nonperiodic modes of postbuckling and nonlinear vibration of beams attached to nonlinear foundations. Appl. Math. Model. 2019, 75, 414–445. [Google Scholar] [CrossRef]
- Yu, Y.; Shen, H.S.; Wang, H.; Hui, D. Postbuckling of sandwich plates with graphene-reinforced composite face sheets in thermal environments. Compos. Part B Eng. 2018, 135, 72–83. [Google Scholar] [CrossRef]
- Li, Z.M.; Qiao, P. Thermal postbuckling analysis of anisotropic laminated beams with different boundary conditions resting on two-parameter elastic foundations. Eur. J. Mech. A/Solids 2015, 54, 30–43. [Google Scholar] [CrossRef]
- Wu, H.L.; Yang, J.; Kitipornchai, S. Imperfection sensitivity of postbuckling behaviour of functionally graded carbon nanotube-reinforced composite beams. Thin-Walled Struct. 2016, 108, 225–233. [Google Scholar] [CrossRef]
- Shen, H.S.; Reddy, J.N.; Yu, Y. Postbuckling of doubly curved FG-GRC laminated panels subjected to lateral pressure in thermal environments. Mech. Adv. Mater. Struct. 2021, 28, 260–270. [Google Scholar] [CrossRef]
- Wu, H.L.; Zheng, Z.Q.; Guo, J.; Bao, Y.; Yang, J. Axisymmetric thermal postbuckling of functionally graded graphene nanocomposite annular plates with various geometric imperfections. Thin-Walled Struct. 2023, 185, 110594. [Google Scholar] [CrossRef]
- Nam, V.H.; Doan, C.V.M.; Phuong, N.T. A new analytical approach to the nonlinear buckling and postbuckling behavior of functionally graded graphene reinforced composite laminated cylindrical, parabolic, and half-sinusoid shallow imperfect panels. Polym. Compos. 2023, 44, 8928–8945. [Google Scholar] [CrossRef]
- Li, Z.M.; Yang, D.Q. Thermal postbuckling analysis of anisotropic laminated beams with tubular cross-section based on higher-order theory. Ocean Eng. 2016, 115, 93–106. [Google Scholar] [CrossRef]
- Yaghoobi, H.; Torabi, M. Post-buckling and nonlinear free vibration analysis of geometrically imperfect functionally graded beams resting on nonlinear elastic foundation. Appl. Math. Model. 2013, 37, 8324–8340. [Google Scholar] [CrossRef]
- Mohammadi, H.; Mahzoon, M.; Mohammadi, M.; Mohammadi, M. Postbuckling instability of nonlinear nanobeam with geometric imperfection embedded in elastic foundation. Nonlinear Dyn. 2014, 76, 2005–2016. [Google Scholar] [CrossRef]
- Fan, Y.; Wang, H. Nonlinear bending and postbuckling analysis of matrix cracked hybrid laminated plates containing carbon nanotube reinforced composite layers in thermal environments. Compos. Part B Eng. 2016, 86, 1–16. [Google Scholar] [CrossRef]
- Reddy, J.N. A simple higher-order theory for laminated composite plates. J. Appl. Mech. 1984, 51, 745–752. [Google Scholar] [CrossRef]
- Thai, C.H.; Ferreira, A.J.M.; Nguyen-Xuan, H. Isogeometric analysis of size-dependent isotropic and sandwich functionally graded microplates based on modified strain gradient elasticity theory. Compos. Struct. 2018, 192, 274–288. [Google Scholar] [CrossRef]
- Amabili, M.; Breslavsky, I.D.; Reddy, J.N. Nonlinear higher-order shell theory for incompressible biological hyperelastic materials. Comput. Methods Appl. Mech. Eng. 2019, 346, 841–861. [Google Scholar] [CrossRef]
- Kefal, A.; Hasim, K.A.; Yildiz, M. A novel isogeometric beam element based on mixed form of refined zigzag theory for thick sandwich and multilayered composite beams. Compos. Part B Eng. 2019, 167, 100–121. [Google Scholar] [CrossRef]
- Carrera, E.; Boscolo, M. Classical and mixed finite elements for static and dynamic analysis of piezoelectric plates. Int. J. Numer. Methods Eng. 2010, 70, 1135–1181. [Google Scholar] [CrossRef]
- Panteghini, A.; Bardella, L. Structural theory and finite element modelling of linear elastic sandwich beams subject to severe boundary conditions. Eur. J. Mech. A/Solids 2017, 61, 393–407. [Google Scholar] [CrossRef]
- Murakami, H. Laminated Composite Plate Theory with Improved In-Plane Responses. J. Appl. Mech. 1986, 53, 661. [Google Scholar] [CrossRef]
- Carrera, E. On the use of the Murakami’s zig-zag function in the modeling of layered plates and shells. Comput. Struct. 2004, 82, 541–554. [Google Scholar] [CrossRef]
- Xie, F.; Qu, Y.; Zhang, W.; Peng, Z.; Meng, G. Nonlinear aerothermoelastic analysis of composite laminated panels using a general higher-order shear deformation zig-zag theory. Int. J. Mech. Sci. 2019, 150, 226–237. [Google Scholar] [CrossRef]
- Su, J.; Kai, Z.; Qu, Y.; Hua, H. A variational formulation for vibration analysis of curved beams with arbitrary eccentric concentrated elements. Arch. Appl. Mech. 2018, 88, 1089–1104. [Google Scholar] [CrossRef]
- Chanda, A.G.; Kontoni, D.P.N.; Sahoo, R. Development of analytical and FEM solutions for static and dynamic analysis of smart piezoelectric laminated composite plates on elastic foundation. J. Eng. Math. 2023, 138, 12. [Google Scholar] [CrossRef]
- Yang, S.W.; Hao, Y.X.; Zhang, W.; Ma, W.S.; Wu, M.Q. Nonlinear Frequency and Bifurcation of Carbon Fiber-Reinforced Polymer Truncated Laminated Conical Shell. J. Vib. Eng. Technol. 2024, 12, 457–468. [Google Scholar] [CrossRef]
- Mohammadrezazadeh, S.; Jafari, A.A. Nonlinear vibration suppression of laminated composite conical shells on elastic foundations with magnetostrictive layers. Compos. Struct. 2021, 258, 113323. [Google Scholar] [CrossRef]
- Li, X.; Qin, Y.; Zhou, Z.H. Coupled Vibration Analysis of Rotating Composite Laminated Beams in Hygrothermal Environment Using the Green’s Function Method. Int. J. Struct. Stab. Dyn. 2023, 23, 2350016. [Google Scholar] [CrossRef]
- Yadav, A.; Amabili, M.; Panda, S.K.; Dey, T. Instability analysis of fluid-filled angle-ply laminated circular cylindrical shells subjected to harmonic axial loading. Eur. J. Mech. A/Solids 2023, 97, 104810. [Google Scholar] [CrossRef]
- Thai, C.H.; Nguyen-Xuan, H. A moving kriging interpolation meshfree method based on naturally stabilized nodal integration scheme for plate analysis. Int. J. Comput. Methods 2019, 16, 1850100. [Google Scholar] [CrossRef]
- Yang, S.C.; Yao, Y.; Li, Y.C.; Ma, L.; Zhang, Y.; Yang, Q. Geometrically Nonlinear Random Response of Stiffened Laminated Plates by Proper-Orthogonal-Decomposition-Based Reduced-Order Modeling. AIAA J. 2022, 60, 1861–1872. [Google Scholar] [CrossRef]
- Nazemizadeh, M.; Bakhtiari-Nejad, F.; Assadi, A. Size-dependent nonlinear dynamic modeling and vibration analysis of piezo-laminated nanomechanical resonators using perturbation method. Arch. Appl. Mech. 2020, 90, 1659–1672. [Google Scholar] [CrossRef]
- Carrera, E.; Valvano, S.; Filippi, M. Classical, higher-order, zig-zag and variable kinematic shell elements for the analysis of composite multilayered structures. Eur. J. Mech. A/Solids 2018, 72, 97–110. [Google Scholar] [CrossRef]
- Sahoo, R.; Singh, B.N. A new trigonometric zigzag theory for static analysis of laminated composite and sandwich plates. Aerosp. Sci. Technol. 2014, 35, 15–28. [Google Scholar] [CrossRef]
- Marguerre, K.; Woemle, H.T. Elastic Plates; Blaisdell Publishing Company: New York, NY, USA, 1969. [Google Scholar]
- Emam, S.; Eltaher, M.A. Buckling and postbuckling of composite beams in hygrothermal environments. Compos. Struct. 2016, 152, 665–675. [Google Scholar] [CrossRef]
- Shen, H.S.; Lin, F.; Xiang, Y. Nonlinear bending and thermal postbuckling of functionally graded graphene-reinforced composite laminated beams resting on elastic foundations. Eng. Struct. 2017, 140, 89–97. [Google Scholar] [CrossRef]
- Shen, H.S. Nonlinear analysis of functionally graded fiber reinforced composite laminated beams in hygrothermal environments, Part I: Theory and solutions. Compos. Struct. 2015, 125, 698–705. [Google Scholar] [CrossRef]
- Babaei, H.; Kiani, Y.; Eslami, M.R. Thermal buckling and post-buckling analysis of geometrically imperfect FGM clamped tubes on nonlinear elastic foundation. Appl. Math. Model. 2019, 71, 12–30. [Google Scholar] [CrossRef]
- She, G.L.; Yuan, F.G.; Ren, Y.R.; Xiao, W.S. On buckling and postbuckling behavior of nanotubes. Int. J. Eng. Sci. 2017, 121, 130–142. [Google Scholar] [CrossRef]
- Nguyen, N.D.; Nguyen, T.K.; Nguyen, T.N.; Thai, H.T. New Ritz-solution shape functions for analysis of thermo-mechanical buckling and vibration of laminated composite beams. Compos. Struct. 2018, 184, 452–460. [Google Scholar] [CrossRef]
- Aydogdu, M. Thermal buckling analysis of cross-ply laminated composite beams with general boundary conditions. Compos. Sci. Technol. 2007, 67, 1096–1104. [Google Scholar] [CrossRef]



| L/h | Reference | (0°/90°) |
|---|---|---|
| 5 | Present | 0.511 |
| Ngoc-Duong Nguyen [44] | 0.558 | |
| Aydogdu [43] | 0.557 | |
| Khdeir | 0.583 | |
| FOSDT | 0.505 | |
| 10 | Present | 0.850 |
| Ngoc-Duong Nguyen [44] | 0.887 | |
| Khdeir | 0.926 | |
| FOSDT | 0.841 | |
| 20 | Present | 1.029 |
| Ngoc-Duong Nguyen [44] | 1.045 | |
| Aydogdu [43] | 1.092 | |
| Khdeir | 1.090 | |
| FOSDT | 1.017 | |
| 30 | Present | 1.071 |
| Ngoc-Duong Nguyen [44] | 1.081 | |
| FOSDT | 1.063 | |
| 50 | Present | 1.094 |
| Ngoc-Duong Nguyen [44] | 1.100 | |
| Aydogdu [43] | 1.098 | |
| Khdeir | 1.148 | |
| FOSDT | 1.086 |
| L/h | Reference | BCs | |
|---|---|---|---|
| H-H | C-C | ||
| 5 | Present | 0.448 | 0.682 |
| Ngoc-Duong Nguyen [44] | 0.450 | 0.682 | |
| Khdeir | 0.468 | 0.710 | |
| FOSDT | 0.439 | 0.675 | |
| 10 | Present | 0.787 | 1.791 |
| Ngoc-Duong Nguyen [44] | 0.791 | 1.798 | |
| Aydogdu [43] | 0.79 | 1.797 | |
| Khdeir | 0.823 | 1.871 | |
| FOSDT | 0.772 | 1.791 | |
| 20 | Present | 0.976 | 3.149 |
| Ngoc-Duong Nguyen [44] | 0.979 | 3.163 | |
| Khdeir | 1.019 | 3.292 | |
| FOSDT | 0.962 | 3.133 | |
| 30 | Present | 1.021 | 3.674 |
| Ngoc-Duong Nguyen [44] | 1.025 | 3.680 | |
| FOSDT | 1.013 | 3.656 | |
| 50 | Present | 1.046 | 4.018 |
| Ngoc-Duong Nguyen [44] | 1.049 | 4.032 | |
| Aydogdu [43] | 1.049 | 4.030 | |
| Khdeir | 1.092 | 4.196 | |
| FOSDT | 1.037 | 4.006 |
| BCs | Reference | ||||||
|---|---|---|---|---|---|---|---|
| 3 | 10 | 20 | 50 | 100 | |||
| C-C | 3 | Present | 1.342 | 0.596 | 0.333 | 0.143 | 0.073 |
| Ngoc-Duong Nguyen | 1.368 | 0.608 | 0.339 | 0.146 | 0.075 | ||
| 10 | Present | 1.071 | 0.659 | 0.425 | 0.206 | 0.111 | |
| Ngoc-Duong Nguyen | 1.090 | 0.671 | 0.433 | 0.210 | 0.113 | ||
| 20 | Present | 0.850 | 0.623 | 0.451 | 0.247 | 0.141 | |
| Ngoc-Duong Nguyen | 0.887 | 0.650 | 0.471 | 0.257 | 0.147 | ||
| 40 | Present | 0.643 | 0.537 | 0.434 | 0.276 | 0.171 | |
| Ngoc-Duong Nguyen | 0.709 | 0.592 | 0.478 | 0.304 | 0.189 |
| BCs | Reference | ||||||
|---|---|---|---|---|---|---|---|
| 3 | 10 | 20 | 50 | 100 | |||
| H-H | 3 | Present | 0.624 | 0.316 | 0.185 | 0.083 | 0.043 |
| Ngoc-Duong Nguyen | 0.637 | 0.322 | 0.171 | 0.084 | 0.044 | ||
| Aydogudu | 0.637 | 0.323 | 0.189 | 0.293 | 0.153 | ||
| 10 | Present | 0.815 | 0.573 | 0.402 | 0.212 | 0.119 | |
| Ngoc-Duong Nguyen | 0.821 | 0.576 | 0.404 | 0.213 | 0.119 | ||
| 20 | Present | 0.787 | 0.638 | 0.502 | 0.306 | 0.185 | |
| Ngoc-Duong Nguyen | 0.791 | 0.641 | 0.504 | 0.307 | 0.186 | ||
| Khdeir | 0.823 | 0.708 | 0.590 | 0.393 | 0.253 | ||
| 40 | Present | 0.663 | 0.590 | 0.510 | 0.362 | 0.244 | |
| Ngoc-Duong Nguyen | 0.666 | 0.592 | 0.512 | 0.363 | 0.245 | ||
| C-C | 3 | Present | 2.170 | 1.098 | 0.643 | 0.287 | 0.149 |
| Ngoc-Duong Nguyen | 2.212 | 1.119 | 0.656 | 0.293 | 0.137 | ||
| 10 | Present | 2.263 | 1.589 | 1.115 | 0.588 | 0.329 | |
| Ngoc-Duong Nguyen | 2.278 | 1.599 | 1.122 | 0.592 | 0.331 | ||
| 20 | Present | 1.791 | 1.451 | 1.141 | 0.695 | 0.421 | |
| Ngoc-Duong Nguyen | 1.798 | 1.456 | 1.145 | 0.698 | 0.423 | ||
| Aydogudu | 1.804 | 1.462 | 1.148 | 0.699 | 0.423 | ||
| 40 | Present | 1.216 | 1.082 | 0.935 | 0.664 | 0.448 | |
| Ngoc-Duong Nguyen | 1.218 | 1.083 | 0.936 | 0.665 | 0.448 |
| BCs | w/h | Ply Angle | |||
|---|---|---|---|---|---|
| (30°/−30°) | (30°/30°) | (45°/0°/45°) | (45°/0°/−45°) | ||
| H-H | 0 | 233.816 | 233.816 | 177.947 | 177.947 |
| 0.2 | 262.185 | 262.185 | 243.095 | 243.095 | |
| 0.4 | 347.293 | 347.293 | 438.536 | 438.536 | |
| 0.6 | 489.138 | 489.138 | 764.271 | 764.271 | |
| 0.8 | 687.722 | 687.722 | 1220.301 | 1220.301 | |
| 1.0 | 943.044 | 943.044 | 1806.625 | 1806.625 | |
| 1.2 | 1255.104 | 1255.104 | 2523.243 | 2523.243 | |
| 1.4 | 1623.903 | 1623.903 | 3370.155 | 3370.155 | |
| C-C | 0 | 905.482 | 905.482 | 691.368 | 691.368 |
| 0.2 | 933.852 | 933.852 | 756.515 | 756.515 | |
| 0.4 | 1018.959 | 1018.959 | 951.957 | 951.957 | |
| 0.6 | 1160.804 | 1160.804 | 1277.692 | 1277.692 | |
| 0.8 | 1359.388 | 1359.388 | 1733.722 | 1733.722 | |
| 1.0 | 1614.710 | 1614.710 | 2320.046 | 2320.046 | |
| 1.2 | 1926.771 | 1926.771 | 3036.664 | 3036.664 | |
| 1.4 | 2295.569 | 2295.569 | 3883.576 | 3883.576 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Meng, Q. An Analytical Study on the Thermal Post-Buckling Behaviors of Geometrically Imperfect FRC-Laminated Beams Using a Modified Zig-Zag Beam Model. Aerospace 2025, 12, 138. https://doi.org/10.3390/aerospace12020138
Wang Z, Meng Q. An Analytical Study on the Thermal Post-Buckling Behaviors of Geometrically Imperfect FRC-Laminated Beams Using a Modified Zig-Zag Beam Model. Aerospace. 2025; 12(2):138. https://doi.org/10.3390/aerospace12020138
Chicago/Turabian StyleWang, Zhoumi, and Qingchun Meng. 2025. "An Analytical Study on the Thermal Post-Buckling Behaviors of Geometrically Imperfect FRC-Laminated Beams Using a Modified Zig-Zag Beam Model" Aerospace 12, no. 2: 138. https://doi.org/10.3390/aerospace12020138
APA StyleWang, Z., & Meng, Q. (2025). An Analytical Study on the Thermal Post-Buckling Behaviors of Geometrically Imperfect FRC-Laminated Beams Using a Modified Zig-Zag Beam Model. Aerospace, 12(2), 138. https://doi.org/10.3390/aerospace12020138





