A Comparative Analysis of Multi-Criteria Decision-Making Methods and Normalization Techniques in Holistic Sustainability Assessment for Engineering Applications
Abstract
1. Introduction
2. Definitions and Use Case
2.1. Definition of Sustainability
- (a)
- Mechanical performance is evaluated through static and dynamic analyses of the component, with key parameters, including total deformation and mode 1 eigenfrequency.
- (b)
- Costs are assessed based on raw material costs, manufacturing process costs, and recyclability costs of the component.
- (c)
- Environmental sustainability is represented by the carbon dioxide (CO2) emissions generated over the material’s life cycle.
- (d)
- Circularity is expressed through the recyclability potential of the component and its ability to be part of a closed-loop process, which depends on the quality of the recycled material.
- (e)
- Social impact is analyzed by considering the potential effects on various stakeholder groups throughout the product’s entire life cycle, including stages such as material extraction, manufacturing, and end-of-life.
2.2. Case Study
3. Methodology
3.1. MCDM Methods Considered
3.1.1. Weighted Sum Method (WSM)
3.1.2. Technique for Order Preference by Similarity to an Ideal Solution (TOPSIS)
3.1.3. Modified TOPSIS
3.1.4. VIKOR
3.1.5. COPRAS
- where Ri is the summation of the attributes that need to be minimized, and Pi is the summation of the attributes that need to be maximized:
3.2. Normalization Methods
4. Results
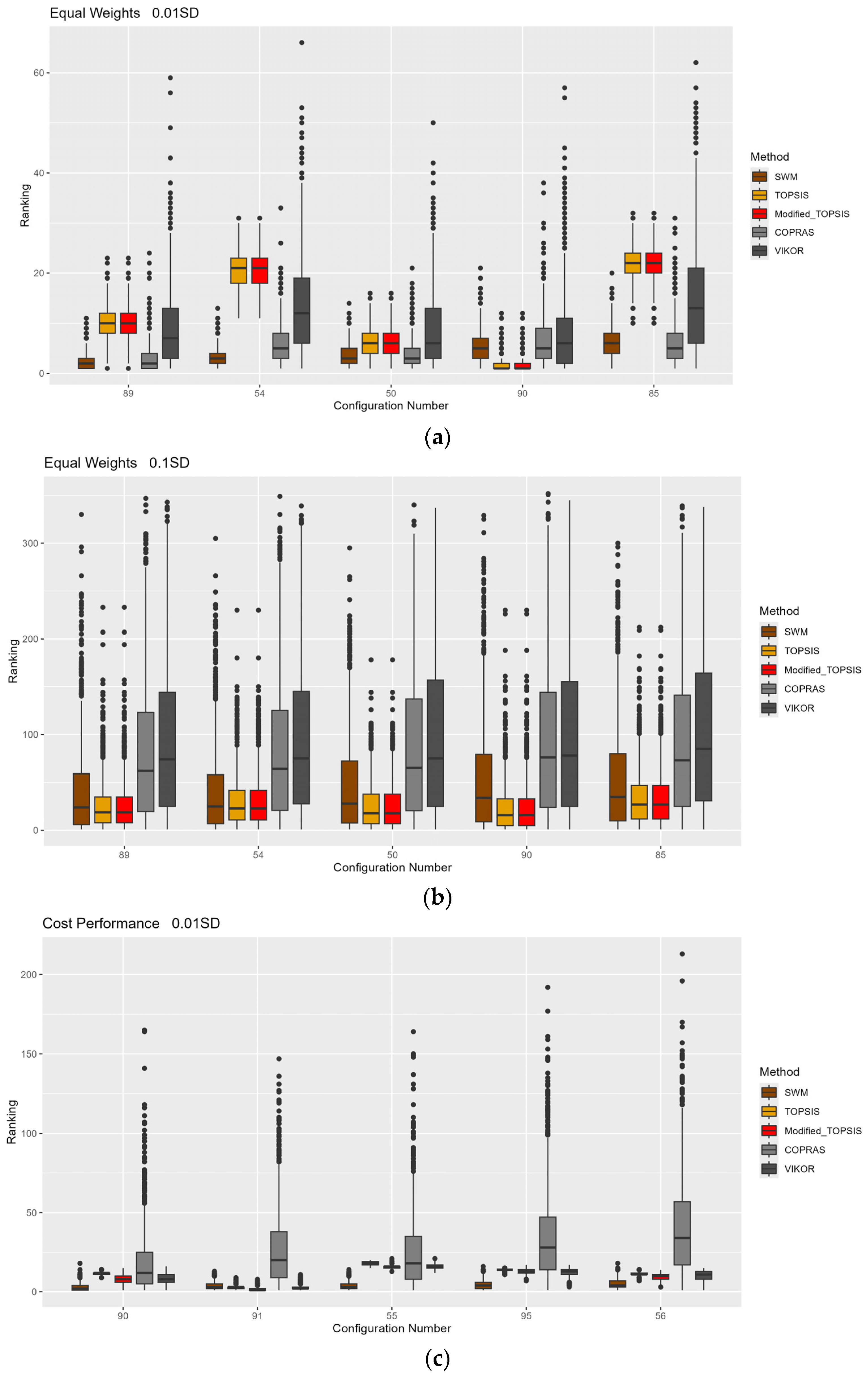
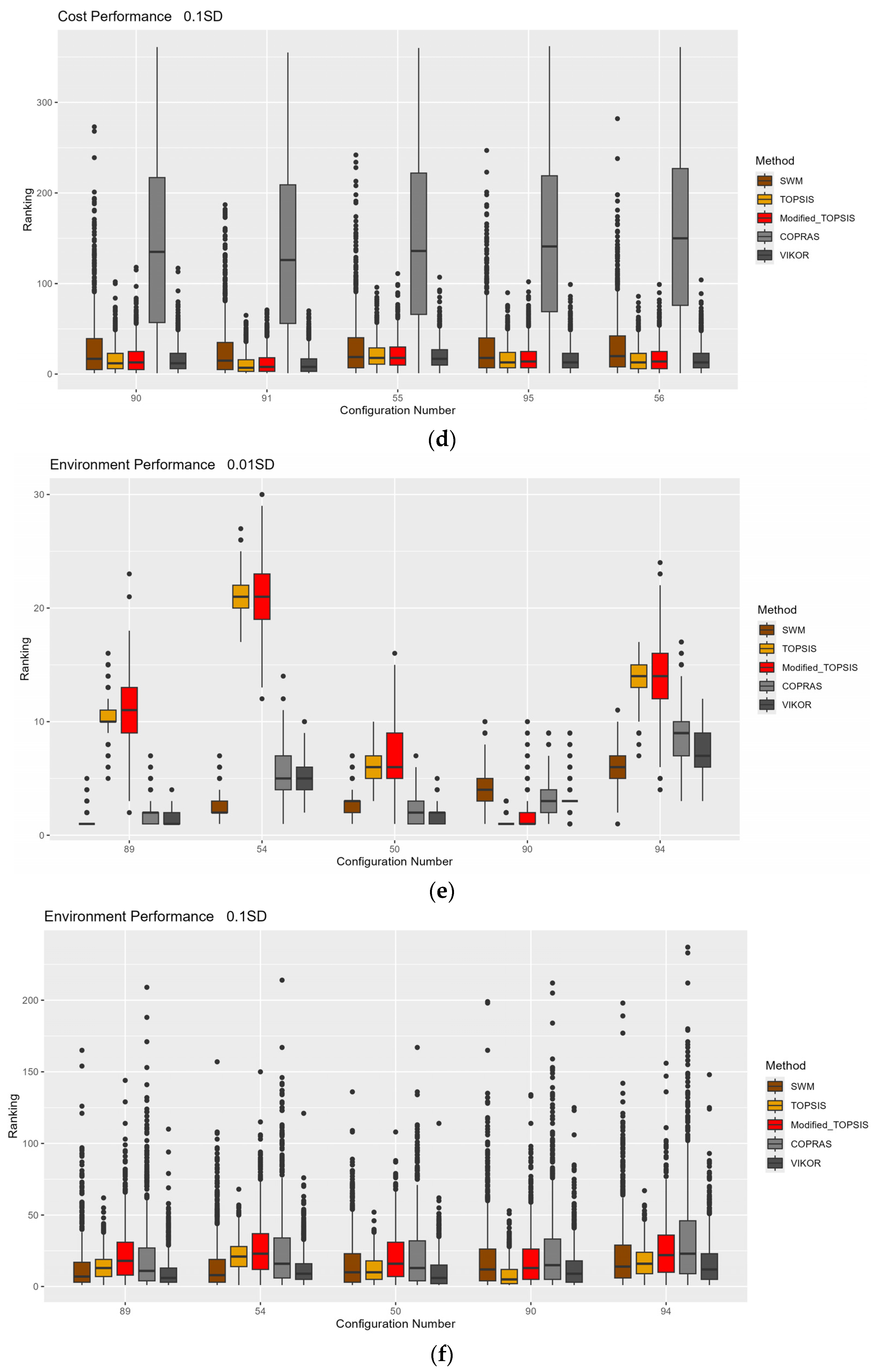
4.1. MCDM Impact Results
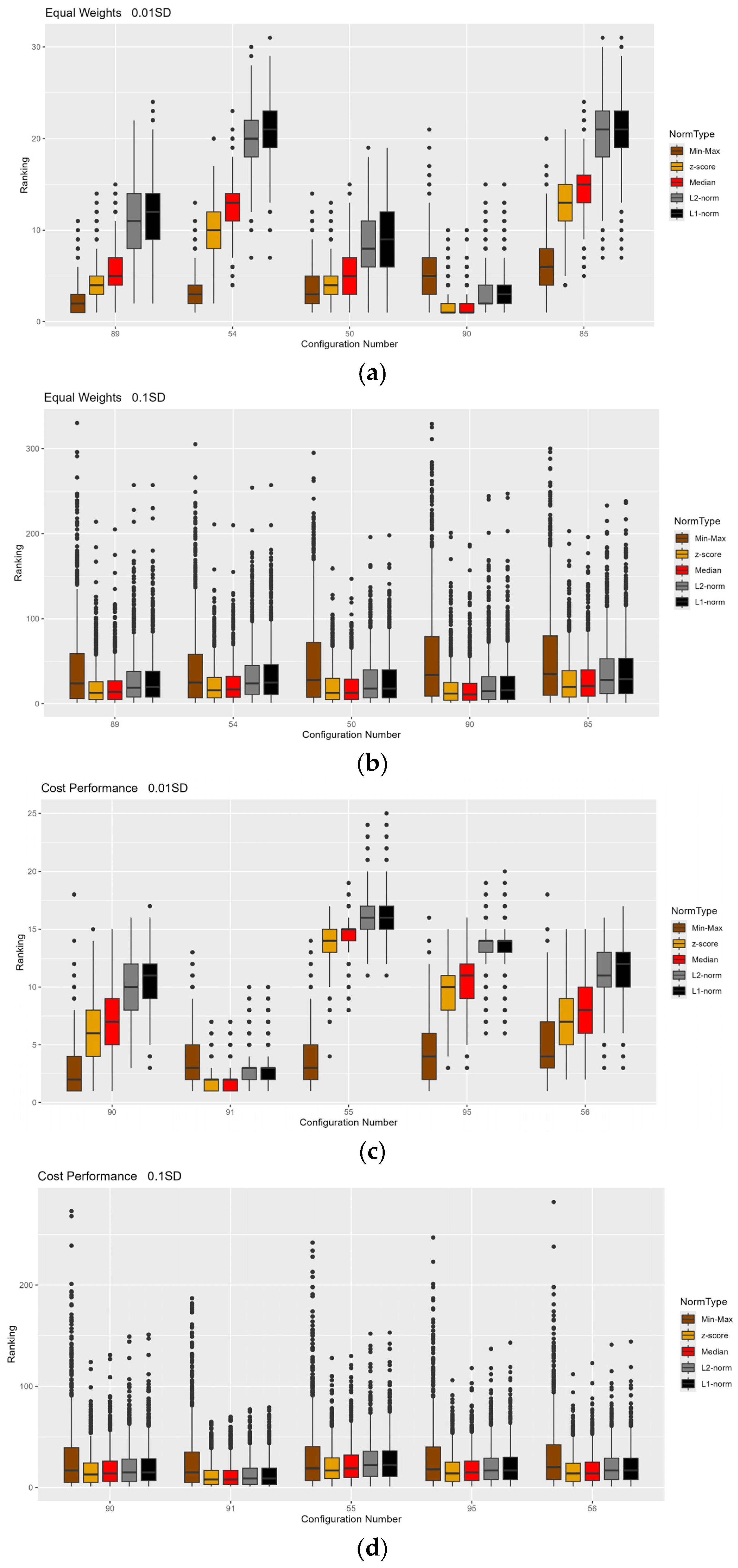
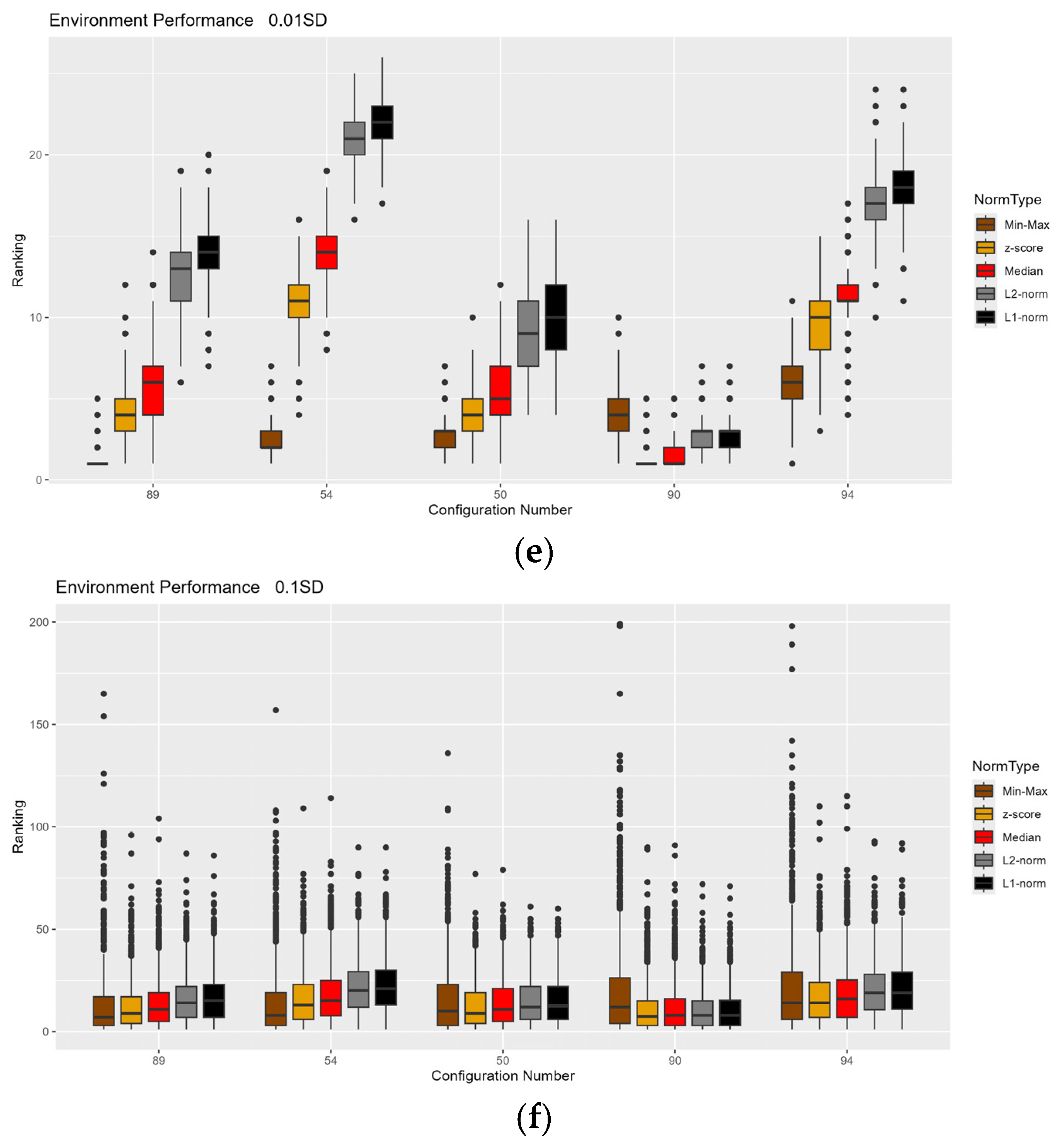
4.2. Normalization Impact Results
5. Conclusions and Future Perspectives
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| AHP | Analytic Hierarchy Process |
| CFRP | Carbon Fiber Reinforced Plastic |
| COPRAS | Complex Proportional Assessment |
| DANP | DEMATEL-based ANP |
| DEMATEL | Decision-Making Trial and Evaluation Laboratory |
| ELECTRE | Elimination and Choice Expressing Reality |
| ESM | Elimination Et Choice Translating Reality |
| GP | Goal Programming |
| GRA | Grey Relational Analysis |
| MARCOS | Measurement of Alternatives and Ranking According to Compromise Solution |
| MCDM | Multi-Criteria Decision Making |
| MOORA | Multi-Objective Optimization Ratio Analysis |
| PROMETHEE | Preference Ranking Optimization Method for Enrichment Evaluation |
| PSI | Population Stability Index |
| SI | Sustainability Index |
| SWARA | Stepwise Weight Assessment Ratio Analysis |
| TOPSIS | Technique for Order Preference by Similarity to Ideal Solution |
| VIKOR | VIseKriterijumskaOptimizacija I KompromisnoResenje |
| WASPAS | Weighted Aggregated Sum Product Assessment |
| SAW | Simple Additive Weighting |
| WPM | Weighted Product Method |
| WSM | Weighted Sum Model |
References
- Salas-Zapata, W.A.; Ortiz-Muñoz, S.M. Analysis of meanings of the concept of sustainability. Sustain. Dev. 2019, 27, 153–161. [Google Scholar] [CrossRef]
- European Partnership Under Horizon Europe Clean Aviation. Available online: https://research-and-innovation.ec.europa.eu/system/files/2020-07/ec_rtd_he-partnerships-clean-aviation.pdf (accessed on 20 November 2024).
- Markatos, D.N.; Pantelakis, S.G. Assessment of the Impact of Material Selection on Aviation Sustainability, from a Circular Economy Perspective. Aerospace 2022, 9, 52. [Google Scholar] [CrossRef]
- Filippatos, A.; Markatos, D.; Tzortzinis, G.; Abhyankar, K.; Malefaki, S.; Gude, M.; Pantelakis, S. Sustainability-Driven Design of Aircraft Composite Components. Aerospace 2024, 11, 86. [Google Scholar] [CrossRef]
- Ziemba, P. Application framework of multi-criteria methods in sustainability assessment. Energies 2022, 15, 9201. [Google Scholar] [CrossRef]
- Stojčić, M.; Zavadskas, E.K.; Pamučar, D.; Stević, Ž.; Mardani, A. Application of MCDM methods in sustainability engineering: A literature review 2008–2018. Symmetry 2019, 11, 350. [Google Scholar] [CrossRef]
- Zhang, H.; Peng, Y.; Tian, G.; Wang, D.; Xie, P. Green material selection for sustainability: A hybrid MCDM approach. PLoS ONE 2017, 12, e0177578. [Google Scholar] [CrossRef]
- Żak, J.; Hadas, Y.; Rossi, R. (Eds.) Advanced Concepts, Methodologies and Technologies for Transportation and Logistics; Springer: Berlin/Heidelberg, Germany, 2018; Volume 572. [Google Scholar] [CrossRef]
- Santos, R.; Matias, J.C.O.; Abreu, A. A Decision-Making Tool to Provide Sustainable Solutions to a Consumer. IFIP Adv. Inf. Commun. Technol. 2020, 577, 63–78. [Google Scholar] [CrossRef]
- Streimikiene, D.; Balezentis, T.; Krisciukaitien, I.; Balezentis, A. Prioritizing sustainable electricity production technologies: MCDM approach. Renew. Sustain. Energy Rev. 2012, 16, 3302–3311. [Google Scholar] [CrossRef]
- Kumar, A.; Sah, B.; Singh, A.R.; Deng, Y.; He, X.; Kumar, P.; Bansal, R.C. A review of multi criteria decision making (MCDM) towards sustainable renewable energy development. Renew. Sustain. Energy Rev. 2017, 69, 596–609. [Google Scholar] [CrossRef]
- Wang, W.; Tian, G.; Zhang, T.; Jabarullah, N.H.; Li, F.; Fathollahi-Fard, A.M.; Wang, D.; Li, Z. Scheme selection of design for disassembly (DFD) based on sustainability: A novel hybrid of interval 2-tuple linguistic intuitionistic fuzzy numbers and regret theory. J. Clean. Prod. 2021, 281, 124724. [Google Scholar] [CrossRef]
- Lindfors, A. Assessing sustainability with multi-criteria methods: A methodologically focused literature review. Environ. Sustain. Indic. 2021, 12, 100149. [Google Scholar] [CrossRef]
- Dožić, S. Multi-criteria decision making methods: Application in the aviation industry. J. Air Transp. Manag. 2019, 79, 101683. [Google Scholar] [CrossRef]
- Elhmoud, E.R.; Kutty, A.A. Sustainability Assessment in Aviation Industry: A Mini- Review on the Tools, Models and Methods of Assessment. 2020. Available online: http://qspace.qu.edu.qa/handle/10576/50466 (accessed on 8 December 2024).
- Kiracı, K.; Akan, E. Aircraft selection by applying AHP and TOPSIS in interval type-2 fuzzy sets. J. Air. Transp. Manag. 2020, 89, 101924. [Google Scholar] [CrossRef] [PubMed]
- Bağcı, B.; Kartal, M. A combined multi criteria model for aircraft selection problem in airlines. J. Air. Transp. Manag. 2024, 116, 102566. [Google Scholar] [CrossRef]
- Dožić, S.; Kalić, M. Comparison of Two MCDM Methodologies in Aircraft Type Selection Problem. Transp. Res. Procedia 2015, 10, 910–919. [Google Scholar] [CrossRef]
- Ardil, C. Commercial Aircraft Selection Decision Support Model Using Fuzzy Combinative Multiple Criteria Decision Making Analysis. J. Sustain. Manuf. Transp. 2023, 3, 38–55. [Google Scholar] [CrossRef]
- Markatos, D.N.; Pantelakis, S.G. Implementation of a Holistic MCDM-Based Approach to Assess and Compare Aircraft, under the Prism of Sustainable Aviation. Aerospace 2023, 10, 240. [Google Scholar] [CrossRef]
- Lu, M.T.; Hsu, C.C.; Liou, J.J.H.; Lo, H.W. A hybrid MCDM and sustainability-balanced scorecard model to establish sustainable performance evaluation for international airports. J. Air. Transp. Manag. 2018, 71, 9–19. [Google Scholar] [CrossRef]
- Janic, M.; Reggiani, A. An Application of the Multiple Criteria Decision Making (MCDM) Analysis to the Selection of a New Hub Airport. Eur. J. Transp. Infrastruct. Res. 2002, 2. [Google Scholar] [CrossRef]
- Chai, N.; Zhou, W. A novel hybrid MCDM approach for selecting sustainable alternative aviation fuels in supply chain management. Fuel 2022, 327, 125180. [Google Scholar] [CrossRef]
- Chen, L.; Ren, J. Multi-attribute sustainability evaluation of alternative aviation fuels based on fuzzy ANP and fuzzy grey relational analysis. J. Air. Transp. Manag. 2018, 68, 176–186. [Google Scholar] [CrossRef]
- Singh, J.; Rana, S.; Hamid, A.B.A.; Gupta, P. Who should hold the baton of aviation sustainability? Soc. Responsib. J. 2023, 19, 1161–1177. [Google Scholar] [CrossRef]
- Chatterjee, P.; Chakraborty, S. Flexible manufacturing system selection using preference ranking methods: A comparative study. Int. J. Ind. Eng. Comput. 2014, 5, 315–338. [Google Scholar] [CrossRef]
- Aytekin, A. Comparative Analysis of the Normalization Techniques in the Context of MCDM Problems. Decis. Mak. Appl. Manag. Eng. 2021, 4, 1–25. [Google Scholar] [CrossRef]
- Jafaryeganeh, H.; Ventura, M.; Soares, C.G. Effect of normalization techniques in multi-criteria decision making methods for the design of ship internal layout from a Pareto optimal set. Struct. Multidiscip. Optim. 2020, 62, 1849–1863. [Google Scholar] [CrossRef]
- Mhlanga, S.T.; Lall, M. Influence of Normalization Techniques on Multi-criteria Decision-making Methods. J. Phys. Conf. Ser. 2022, 2224, 012076. [Google Scholar] [CrossRef]
- Vafaei, N.; Ribeiro, R.A.; Camarinha-Matos, L.M. Assessing Normalization Techniques for Simple Additive Weighting Method. Procedia Comput. Sci. 2022, 199, 1229–1236. [Google Scholar] [CrossRef]
- Kacprzak, D. A new similarity measure for rankings obtained in MCDM problems using different normalization techniques. Oper. Res. Decis. 2024, 34, 47–64. [Google Scholar] [CrossRef]
- Kosareva, N.; Krylovas, A.; Zavadskas, E.K. Statistical analysis of MCDM data normalization methods using Monte Carlo approach. The case of ternary estimates matrix. Econ. Comput. Econ. Cybern. Stud. Res. 2018, 52, 159–175. [Google Scholar] [CrossRef]
- Do, D.T.; Tran, V.D.; Duong, V.D.; Nguyen, N.-T. Investigation of the Appropriate Data Normalization Method for Combination with Preference Selection Index Method in MCDM. Oper. Res. Eng. Sci. Theory Appl. 2023, 6. [Google Scholar] [CrossRef]
- Mukhametzyanov, I.Z. Normalization of Multidimensional Data for Multi-Criteria Decision Making Problems; Springer Nature: Dordrecht, The Netherlands, 2023; Volume 348. [Google Scholar] [CrossRef]
- Vafaei, N.; Ribeiro, R.A.; Camarinha-Matos, L.M. Comparison of Normalization Techniques on Data Sets with Outliers. Int. J. Decis. Support Syst. Technol. 2022, 14, 1–17. [Google Scholar] [CrossRef]
- Trung, D.D. Development of data normalization methods for multi-criteria decision making: Applying for MARCOS method. Manuf. Rev. 2022, 9, 22. [Google Scholar] [CrossRef]
- Mathew, M.; Sahu, S.; Upadhyay, A. Effect of Normalization Techniques in Robot Selection Using Weighted Aggregated Sum Product Assessment. Int. J. Innov. Res. Adv. Stud. 2017, 4, 59–63. [Google Scholar]
- Lakshmi, T.M.; Venkatesan, V.P. A Comparison of Various Normalization in Techniques for Order Performance By Similarity To Ideal Solution (topsis). Int. J. Comput. Algorithm 2014, 3, 255–259. Available online: http://www.hindex.org/2014/article.php?page=853 (accessed on 8 December 2024).
- Markatos, D.N.; Malefaki, S.; Pantelakis, S.G. Sensitivity Analysis of a Hybrid MCDM Model for Sustainability Assessment—An Example from the Aviation Industry. Aerospace 2023, 10, 385. [Google Scholar] [CrossRef]
- Ardil, C. Aircraft selection using multiple criteria decision making analysis method with different data normalization techniques. Int. J. Ind. Syst. Eng. 2019, 13, 744–756. Available online: https://www.academia.edu/52345173/Aircraft_Selection_Using_Multiple_Criteria_Decision_Making_Analysis_Method_with_Different_Data_Normalization_Techniques (accessed on 8 December 2024).
- Filippatos, A.; Markatos, D.; Tzortzinis, G.; Abhyankar, K.; Malefaki, S.; Gude, M.; Pantelakis, S. A proposal towards a step change from eco-driven to sustainability-driven design of aircraft components. In Proceedings of the ICAS 2024 Conference, Florence, Italy, 9–13 September 2024; Available online: https://www.researchgate.net/publication/385272877_A_PROPOSAL_TOWARDS_A_STEP_CHANGE_FROM_ECO-DRIVEN_TO_SUSTAINABILITY-DRIVEN_DESIGN_OF_AIRCRAFT_COMPONENTS (accessed on 20 November 2024).
- Clean Aviation. Eco-Design TA. Available online: https://www.clean-aviation.eu/ (accessed on 20 November 2024).
- Gupta, I.; Nandita, M.; Deepak, T. Triple bottom line: Evidence from aviation sector. Int. J. Bus. Ethics Gov. 2020, 3, 97–104. [Google Scholar] [CrossRef]
- Saaty, T.L. A scaling method for priorities in hierarchical structures. J. Math. Psychol. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Fishburn, P.C. Letter to the Editor—Additive Utilities with Incomplete Product Sets: Application to Priorities and Assignments. Oper. Res. 1967, 15, 537–542. [Google Scholar] [CrossRef]
- Saaty, T. The analytic hierarchy process: Planning, priority setting, resource allocation McGraw-Hill, New York, 1980, xiii. Eur. J. Oper. Res. 1980, 9, 97–98. Available online: https://search.worldcat.org/title/5352839 (accessed on 11 December 2024).
- Saaty, T.L. How to make a decision: The analytic hierarchy process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Hwang, C.-L.; Yoon, K. Multiple Attribute Decision Making. In Multiple Attribute Decision Making: Methods and Applications a State-of-the-Art Survey; Springer: Berlin/Heidelberg, Germany, 1981; Volume 186. [Google Scholar] [CrossRef]
- Ciardiello, F.; Genovese, A. A comparison between TOPSIS and SAW methods. Ann. Oper. Res. 2023, 325, 967–994. [Google Scholar] [CrossRef]
- Akay, H.; Koçyiğit, M.B. Investigation of Flood Hazard Susceptibility Using Various Distance Measures in Technique for Order Preference by Similarity to Ideal Solution. Appl. Sci. 2024, 14, 7023. [Google Scholar] [CrossRef]
- García-Cascales, M.S.; Lamata, M.T. On rank reversal and TOPSIS method. Math. Comput. Model. 2012, 56, 123–132. [Google Scholar] [CrossRef]
- Shyur, H.-J.; Shih, H.-S. Resolving Rank Reversal in TOPSIS: A Comprehensive Analysis of Distance Metrics and Normalization Methods. Informatica 2024, 35, 837–858. [Google Scholar] [CrossRef]
- Deng, H.; Yeh, C.H.; Willis, R.J. Inter-company comparison using modified TOPSIS with objective weights. Comput. Oper. Res. 2000, 27, 963–973. [Google Scholar] [CrossRef]
- Opricovic, S. Multicriteria Optimization of Civil Engineering Systems. Ph.D. Thesis, Faculty of Civil Engineering, Belgrade, Serbia, 1998; 302p. Available online: https://www.scirp.org/reference/referencespapers?referenceid=2827893 (accessed on 11 December 2024).
- Duckstein, L.; Opricovic, S. Multiobjective optimization in river basin development. Water Resour. Res. 1980, 16, 14–20. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.H. Multicriteria Planning of Post-Earthquake Sustainable Reconstruction. Comput.-Aided Civ. Infrastruct. Eng. 2002, 17, 211–220. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Kaklauskas, A.; Šarka, V. The new method of multicriteria complex proportional assessment of projects. Technol. Econ. Dev. Econ. 1994, 1, 131–139. [Google Scholar]
- Kraujalienė, L. Comparative analysis of multicriteria decision-making methods evaluating the efficiency of technology transfer. Bus. Manag. Econ. Eng. 2019, 17, 72–93. [Google Scholar] [CrossRef]
- Krishnan, A.R. Past efforts in determining suitable normalization methods for multi-criteria decision-making: A short survey. Front. Big Data 2022, 5, 990699. [Google Scholar] [CrossRef]
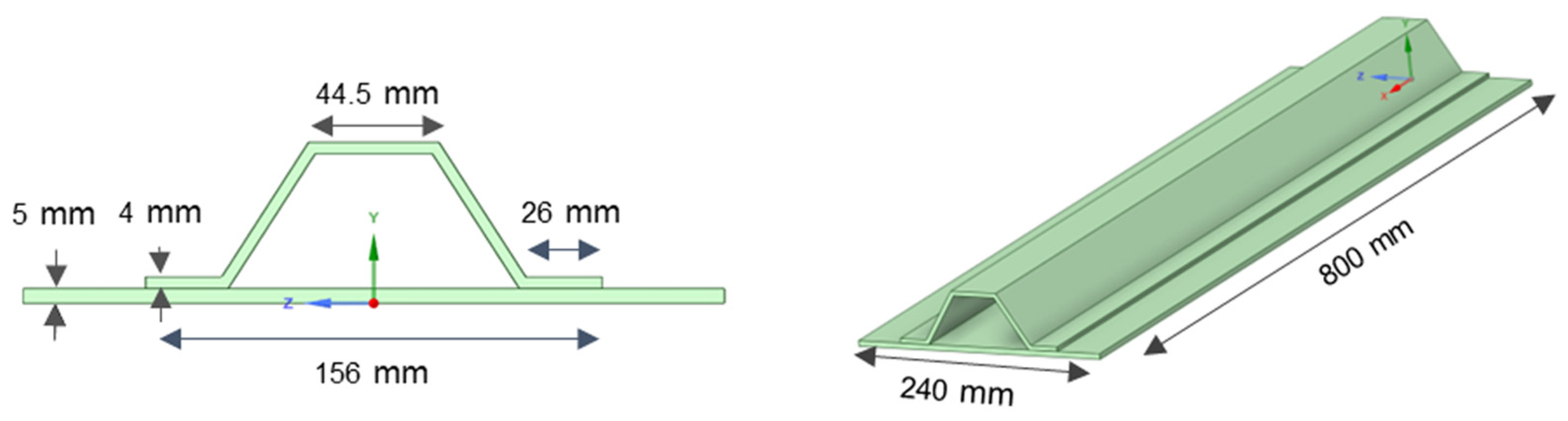
| Component Configurations | ||
|---|---|---|
| No | Skin | Stringer |
| 1 | Aluminium 2024 T3 | Aluminium 2024 T3 |
| 2 | CFRP (Carbon Fiber-Reinforced Plastic) | Aluminium 2024 T3 |
| 3 | Aluminium 2024 T3 | CFRP |
| 4 | CFRP | CFRP |
| 5 | 17-4PH Stainless Steel | CFRP |
| Method | For the Attribute That Needs to Be Maximized | For the Attribute That Need to Be Minimized |
|---|---|---|
| Min–Max | ||
| Z-Score | ||
| Robust Scaling | ||
| L1—Norm | ||
| L2—Norm |
| Ranking No. | Material Combination | SWM | TOPSIS | Modified TOPSIS | COPRAS | VIKOR |
|---|---|---|---|---|---|---|
| Equal Weighting | ||||||
| 1 | AL-AL | 89 | 90 | 90 | 89 | 90 |
| 2 | AL-AL | 54 | 51 | 51 | 50 | 50 |
| 3 | AL-AL | 50 | 91 | 91 | 85 | 91 |
| 4 | AL-AL | 90 | 52 | 52 | 90 | 89 |
| 5 | AL-AL | 85 | 50 | 50 | 54 | 51 |
| 6 | AL-AL | 94 | 55 | 55 | 46 | 55 |
| 7 | AL-AL | 55 | 95 | 95 | 51 | 52 |
| 8 | AL-AL | 123 | 56 | 56 | 123 | 92 |
| 9 | AL-AL | 51 | 92 | 92 | 94 | 54 |
| 10 | AL-AL | 128 | 89 | 89 | 55 | 85 |
| Prioritization to Performance and Costs Terms | ||||||
| Ranking No. | Material Combination | SWM | TOPSIS | Mod. TOPSIS | COPRAS | VIKOR |
| 1 | AL-AL | 90 | 92 | 91 | 89 | 92 |
| 2 | AL-AL | 91 | 93 | 92 | 50 | 93 |
| 3 | AL-AL | 55 | 91 | 93 | 85 | 91 |
| 4 | AL-AL | 95 | 97 | 52 | 54 | 52 |
| 5 | AL-AL | 56 | 98 | 96 | 90 | 97 |
| 6 | AL-AL | 94 | 53 | 53 | 46 | 53 |
| 7 | AL-AL | 96 | 52 | 97 | 51 | 96 |
| 8 | AL-AL | 51 | 96 | 57 | 123 | 90 |
| 9 | AL-AL | 89 | 57 | 90 | 94 | 57 |
| 10 | AL-AL | 92 | 58 | 56 | 55 | 98 |
| Prioritization to Performance and Environment Terms | ||||||
| Ranking No. | Material Combination | SWM | TOPSIS | Mod. TOPSIS | COPRAS | VIKOR |
| 1 | AL-AL | 89 | 90 | 90 | 89 | 89 |
| 2 | AL-AL | 54 | 51 | 91 | 50 | 50 |
| 3 | AL-AL | 50 | 91 | 51 | 90 | 90 |
| 4 | AL-AL | 90 | 52 | 52 | 85 | 54 |
| 5 | AL-AL | 94 | 50 | 50 | 51 | 85 |
| 6 | AL-AL | 85 | 55 | 55 | 54 | 51 |
| 7 | AL-AL | 55 | 95 | 95 | 91 | 94 |
| 8 | AL-AL | 123 | 56 | 56 | 55 | 55 |
| 9 | AL-AL | 51 | 92 | 92 | 94 | 86 |
| 10 | AL-AL | 128 | 89 | 89 | 86 | 91 |
| Aggregation Method | SWM | TOPSIS | Modified TOPSIS | COPRAS | VIKOR |
|---|---|---|---|---|---|
| Equal Weights | |||||
| SWM | 1 | 0.866 | 0.866 | 0.958 | 0.948 |
| TOPSIS | 0.866 | 1 | 1 | 0.943 | 0.869 |
| Modified TOPSIS | 0.866 | 1 | 1 | 0.943 | 0.869 |
| COPRAS | 0.958 | 0.943 | 0.943 | 1 | 0.976 |
| VIKOR | 0.948 | 0.869 | 0.869 | 0.976 | 1 |
| Prioritization to Performance and Environment Terms | |||||
| SWM | 1 | 0.856 | 0.890 | 0.898 | 0.941 |
| TOPSIS | 0.856 | 1 | 0.932 | 0.912 | 0.886 |
| Modified TOPSIS | 0.890 | 0.932 | 1 | 0.976 | 0.853 |
| COPRAS | 0.898 | 0.912 | 0.976 | 1 | 0.854 |
| VIKOR | 0.941 | 0.886 | 0.853 | 0.854 | 1 |
| Prioritization to Performance and Costs Terms | |||||
| SWM | 1 | 0.908 | 0.923 | 0.931 | 0.917 |
| TOPSIS | 0.908 | 1 | 0.999 | 0.826 | 0.987 |
| Modified TOPSIS | 0.923 | 0.999 | 1 | 0.843 | 0.988 |
| COPRAS | 0.931 | 0.826 | 0.843 | 1 | 0.809 |
| VIKOR | 0.917 | 0.987 | 0.988 | 0.809 | 1 |
| Ranking No. | Material | Min–Max | z-Score | Median | L2—Norm | L1—Norm |
|---|---|---|---|---|---|---|
| Equal Weighting | ||||||
| 1 | AL-AL | 89 | 90 | 90 | 91 | 91 |
| 2 | AL-AL | 54 | 91 | 91 | 90 | 90 |
| 3 | AL-AL | 50 | 50 | 51 | 92 | 92 |
| 4 | AL-AL | 90 | 89 | 50 | 51 | 51 |
| 5 | AL-AL | 85 | 51 | 89 | 52 | 52 |
| 6 | AL-AL | 94 | 55 | 55 | 50 | 93 |
| 7 | AL-AL | 55 | 95 | 92 | 56 | 56 |
| 8 | AL-AL | 123 | 56 | 95 | 93 | 50 |
| 9 | AL-AL | 51 | 94 | 56 | 95 | 96 |
| 10 | AL-AL | 128 | 92 | 52 | 96 | 95 |
| Prioritization to Performance and Costs Terms | ||||||
| 1 | AL-AL | 90 | 92 | 92 | 92 | 92 |
| 2 | AL-AL | 91 | 91 | 91 | 93 | 93 |
| 3 | AL-AL | 55 | 93 | 93 | 91 | 91 |
| 4 | AL-AL | 95 | 96 | 96 | 97 | 97 |
| 5 | AL-AL | 56 | 90 | 97 | 52 | 53 |
| 6 | AL-AL | 94 | 97 | 57 | 53 | 52 |
| 7 | AL-AL | 96 | 56 | 90 | 96 | 98 |
| 8 | AL-AL | 51 | 57 | 52 | 98 | 96 |
| 9 | AL-AL | 89 | 52 | 56 | 57 | 57 |
| 10 | AL-AL | 92 | 95 | 95 | 58 | 58 |
| Prioritization to Performance and Environment Terms | ||||||
| 1 | AL-AL | 89 | 90 | 90 | 91 | 91 |
| 2 | AL-AL | 54 | 91 | 91 | 92 | 92 |
| 3 | AL-AL | 50 | 51 | 51 | 90 | 90 |
| 4 | AL-AL | 90 | 50 | 50 | 51 | 51 |
| 5 | AL-AL | 94 | 89 | 89 | 52 | 52 |
| 6 | AL-AL | 85 | 55 | 92 | 93 | 93 |
| 7 | AL-AL | 55 | 95 | 55 | 56 | 56 |
| 8 | AL-AL | 123 | 56 | 95 | 50 | 96 |
| 9 | AL-AL | 51 | 92 | 56 | 96 | 95 |
| 10 | AL-AL | 128 | 94 | 52 | 95 | 50 |
| Normalization Method | Min–Max | z-Score | Median | L2—Norm | L1—Norm |
|---|---|---|---|---|---|
| Equal Weights | |||||
| Min–Max | 1 | 0.947 | 0.892 | 0.946 | 0.942 |
| z-Score | 0.947 | 1 | 0.990 | 0.996 | 0.996 |
| Median | 0.892 | 0.990 | 1 | 0.983 | 0.984 |
| L2—Norm | 0.946 | 0.996 | 0.983 | 1 | 1 |
| L1—Norm | 0.942 | 0.996 | 0.984 | 1 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malefaki, S.; Markatos, D.; Filippatos, A.; Pantelakis, S. A Comparative Analysis of Multi-Criteria Decision-Making Methods and Normalization Techniques in Holistic Sustainability Assessment for Engineering Applications. Aerospace 2025, 12, 100. https://doi.org/10.3390/aerospace12020100
Malefaki S, Markatos D, Filippatos A, Pantelakis S. A Comparative Analysis of Multi-Criteria Decision-Making Methods and Normalization Techniques in Holistic Sustainability Assessment for Engineering Applications. Aerospace. 2025; 12(2):100. https://doi.org/10.3390/aerospace12020100
Chicago/Turabian StyleMalefaki, Sonia, Dionysios Markatos, Angelos Filippatos, and Spiros Pantelakis. 2025. "A Comparative Analysis of Multi-Criteria Decision-Making Methods and Normalization Techniques in Holistic Sustainability Assessment for Engineering Applications" Aerospace 12, no. 2: 100. https://doi.org/10.3390/aerospace12020100
APA StyleMalefaki, S., Markatos, D., Filippatos, A., & Pantelakis, S. (2025). A Comparative Analysis of Multi-Criteria Decision-Making Methods and Normalization Techniques in Holistic Sustainability Assessment for Engineering Applications. Aerospace, 12(2), 100. https://doi.org/10.3390/aerospace12020100








