Investigation on Aerodynamic Characteristics of Propeller–Wing Combination Configuration Under Heavy Rainfall
Abstract
1. Introduction
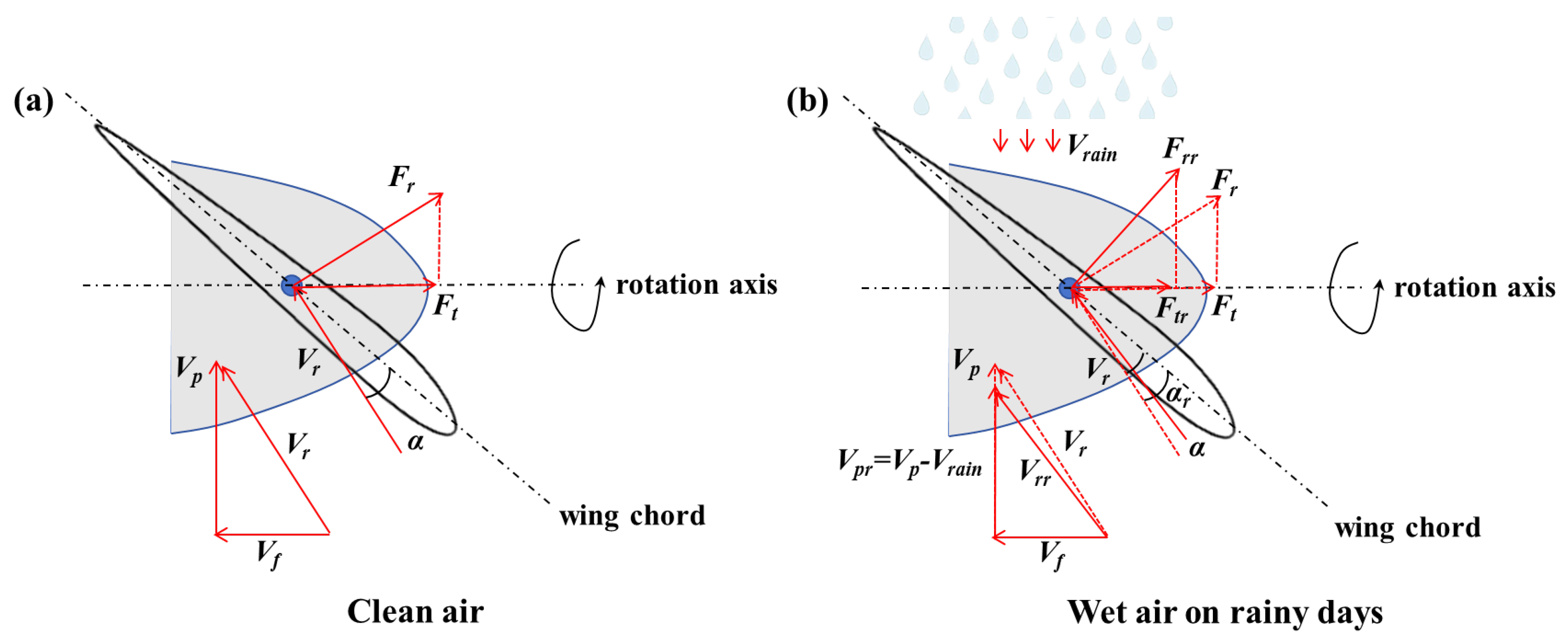
2. Preliminary Analysis of Aerodynamic Effects of Heavy Rainfall on Propeller–Wing Coupling Configuration
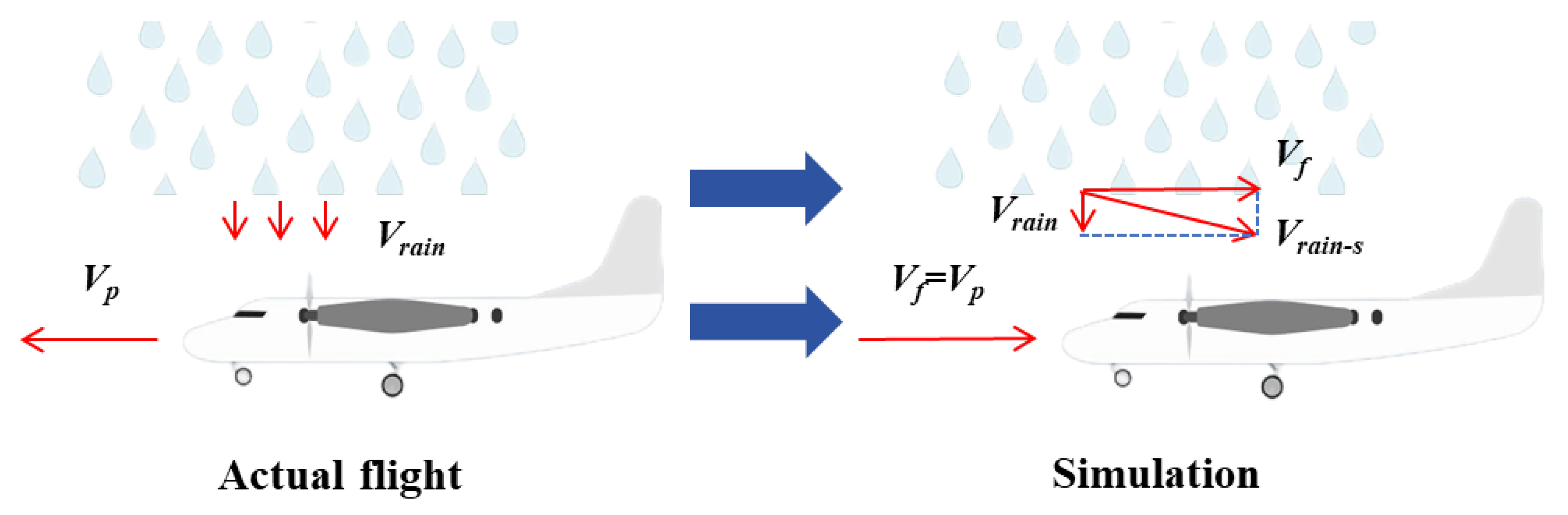
3. Construction of Service Environment for Turboprop Engines Under Heavy Rainfall Conditions
4. Aerodynamic Characteristic Analysis of Propeller Wing Combination Configuration Under Heavy Rainfall Conditions
4.1. Calculation Configuration and Simulation Methods
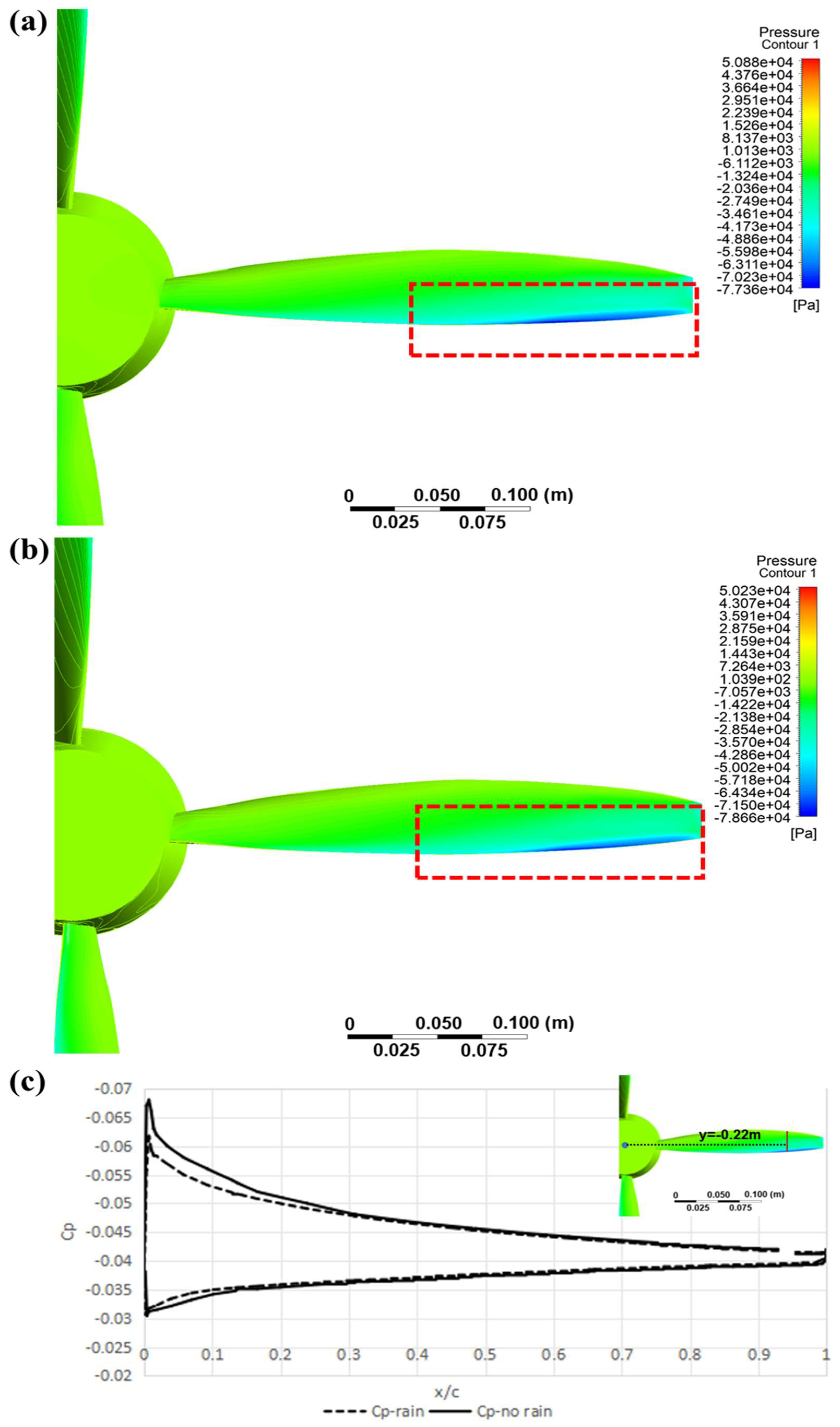
4.2. Analysis of Aerodynamic Changes in Blade–Wing Configuration Under Heavy Rainfall Conditions
4.3. Analysis of the Influence of Incoming Flow and Heavy Rainfall Parameters on the Aerodynamic Force of Propeller–Wing Combination
4.3.1. The Influence of Raindrop Falling Speed
4.3.2. The Influence of Raindrop Diameter
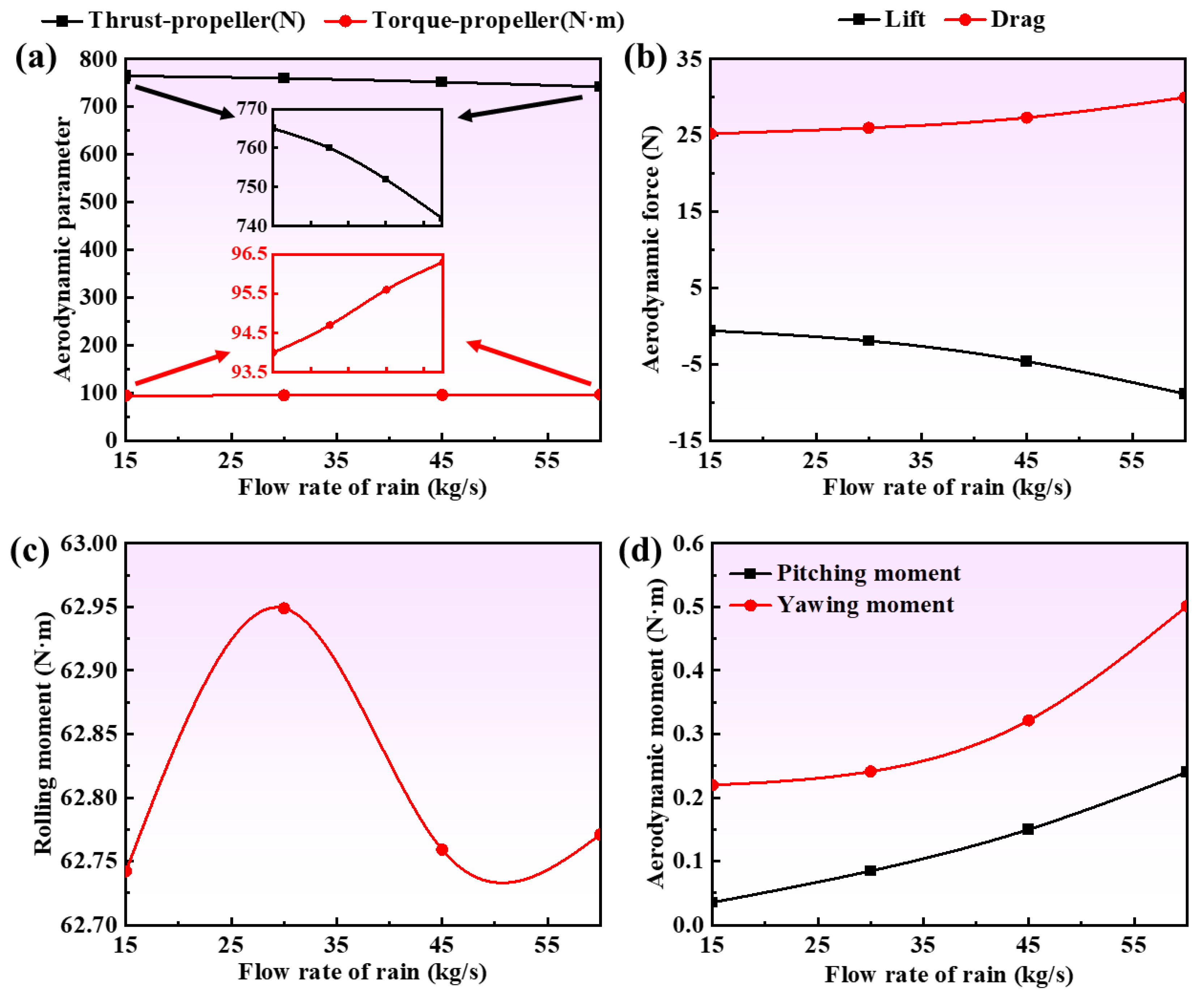
4.3.3. The Influence of Rainfall Amount
5. Conclusions
- (1)
- Raindrops hitting the blade reduce the local angle of attack, causing a decrease in its thrust force. Additionally, the kinetic energy of raindrops hitting the blade becomes drag, further affecting the net thrust force of the blade, resulting in a thrust force loss of up to 2.35%. Because the propeller rotates and collides with the gas–liquid mixture flow, more drag is generated during the blade rotation process, thus increasing the torque and power consumption. The maximum torque increment can reach 2.15%.
- (2)
- The impact of the mechanism of rainfall on the aft wing of the propeller is more complex. Firstly, it manifests as a decrease in lift and an increase in drag, with lift loss reaching 1.84% and drag increase reaching 12%. The main reason is that the coverage of the water film causes changes in the local shape of the cross-section, coupled with a decrease in the local angle of attack due to the speed of raindrops falling, resulting in a decrease in lift. The drag is composed of impact drag and pressure difference drag, caused by the easy separation of the rain film. The impact on the wing moment is relatively small, but it will enhance the yaw and rolling moment characteristics caused by the up-and-down washing of the propeller.
- (3)
- The greater the speed of raindrops falling, the larger the diameter of raindrops; the greater the amount of rainfall, the more it will cause a decrease in blade thrust, an increase in torque, and a further strengthening of the phenomenon of wing lift reduction, drag increase, and yaw and pitching moment increase. This reflects that under heavy rainfall conditions, the multiphase flow pattern of the airflow mixed with raindrops interferes with the mechanism of aerodynamic efficiency of the propeller blades, resulting in a deterioration of performance.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| DPM | Discrete Phase Model |
References
- Della Vecchia, P.; Nicolosi, F. Aerodynamic guidelines in the design and optimization of new regional turboprop aircraft. Aerosp. Sci. Technol. 2014, 38, 88–104. [Google Scholar] [CrossRef]
- Hu, Y.H.; Yan, J.Q.; Cao, E.T.; Yu, Y.M.; Tian, H.M.; Huang, H.Y. Approach and Landing Energy Prediction Based on a Long Short-Term Memory Model. Aerospace 2024, 11, 226. [Google Scholar] [CrossRef]
- Iwaniuk, A.; Wisniowski, W.; Zóltak, J. Multi-disciplinary optimisation approach for a light turboprop aircraft-engine integration and improvement. Aircr. Eng. Aerosp. Technol. 2016, 88, 348–355. [Google Scholar] [CrossRef]
- Jiang, Z.; Chen, Y.S.; An, Y.R.; Wang, Q.F. New actuator disk model for propeller-aircraft computation. Sci. China-Technol. Sci. 2016, 59, 1201–1207. [Google Scholar] [CrossRef]
- Simmons, B.M.; Gresham, J.L.; Woolsey, C.A. Aero-Propulsive Modeling for Propeller Aircraft Using Flight Data. J. Aircr. 2023, 60, 81–96. [Google Scholar] [CrossRef]
- Williams, A.; Marcotte, D. Wind measurements on a maneuvering twin-engine turboprop aircraft accounting for flow distortion. J. Atmos. Ocean. Technol. 2000, 17, 795–810. [Google Scholar] [CrossRef]
- Ashenden, R.; Marwitz, J.D. Turboprop aircraft performance response to various environmental conditions. J. Aircr. 1997, 34, 278–287. [Google Scholar] [CrossRef]
- Chauhan, S.S.; Martins, J. RANS-Based Aerodynamic Shape Optimization of a Wing Considering Propeller-Wing Interaction. J. Aircr. 2021, 58, 497–513. [Google Scholar] [CrossRef]
- Li, X.; Li, C.; Gao, J.; Li, S. Propeller slipstream effect on longitudinal aerodynamic characteristics of airplane. J. Exp. Fluid Mech. 2017, 31, 46. [Google Scholar]
- Mi, B.G.; Huang, H.Y. Intake grille design for an embedded ventilation-and-cooling system in an aircraft. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2022, 236, 2352–2365. [Google Scholar] [CrossRef]
- Phillips, E.H. FAA to ban turboprops in freezing rain, drizzle. Aviat. Week Space Technol. 1996, 144, 36–37. [Google Scholar]
- Zhao, S.; Li, J.; Jiang, Y.X.; Qian, R.Z.; Xu, R.F. Investigation of propeller slipstream effects on lateral and directional static stability of transport aircraft. Eng. Appl. Comp. Fluid Mech. 2022, 16, 551–569. [Google Scholar] [CrossRef]
- Thompson, B.E.; Jang, J.H. Aerodynamic efficiency of wings in rain. J. Aircr. 1996, 33, 1047–1053. [Google Scholar] [CrossRef]
- Wu, Z.; Cao, Y. Aerodynamic study of aerofoil and wing in simulated rain environment via a two-way coupled Eulerian-Lagrangian approach. Aeronaut. J. 2014, 118, 643–668. [Google Scholar] [CrossRef]
- Wu, Z.L.; Cao, Y.H.; Ismail, M. Numerical Simulation of Airfoil Aerodynamic Penalties and Mechanisms in Heavy Rain. Int. J. Aerosp. Eng. 2013, 2013, 13. [Google Scholar] [CrossRef]
- Ismail, M.; Cao, Y.H. Airfoils Aerodynamic Performance Analysis in Heavy Rain. Appl. Mech. Mater. 2012, 245, 297–302. [Google Scholar] [CrossRef]
- Ismail, M.; Umer, U. Aerodynamic Efficiency Study of GLC-305 Airfoil in Simulated Rain and Icing Conditions. In International Conference on Control Engineering and Mechanical Design (CEMD 2017); Li, C., Ed.; ASME Press: New York, NY, USA, 2018; p. 324. [Google Scholar]
- Wan, T.; Lin, J.-X.; Kuan, H.-C. Aerodynamic analysis of helicopter rotor blades in heavy rain condition. In Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition 2013, Grapevine, TX, USA, 7–10 January 2013; American Institute for Aeronautics and Astronautics (AIAA): Reston, VA, USA, 2013. [Google Scholar]
- Gahlot, A.S.; Eshcol, R.M.; Sankar, L.N.; Kreeger, R.E. Numerical Simulations of the Adverse Effects of Rain on Airfoil and Rotor Aerodynamic Characteristics. J. Am. Helicopter Soc. 2023, 68, 9. [Google Scholar] [CrossRef]
- Fatahian, H.; Salarian, H.; Nimvari, M.E.; Khaleghinia, J. Effect of Gurney flap on flow separation and aerodynamic performance of an airfoil under rain and icing conditions. Acta Mech. Sin. 2020, 36, 659–677. [Google Scholar] [CrossRef]
- Haines, P.; Luers, J. Aerodynamic penalties of heavy rain on landing airplanes. J. Aircr. 1983, 20, 111–119. [Google Scholar] [CrossRef]
- GB/T 28592-2012; Grade of Precipitation. China Meteorological Administration: Beijing, China, 2012.
- Foote, G.B.; Du Toit, P.S. Terminal Velocity of Raindrops Aloft. J. Appl. Meteorol. Climatol. 1969, 8, 249–253. [Google Scholar] [CrossRef]
- Trebble, W.J.G. Investigations of the aerodynamic performance and noise characteristics of a Dowty Rotol R212 propeller at full-scale in the 24 ft wind tunnel. Aeronaut. J. 1987, 91, 275–284. [Google Scholar] [CrossRef]
- Zhou, Q.; Joseph, P.F. Frequency-domain method for rotor self-noise prediction. AIAA J. 2006, 44, 1197–1206. [Google Scholar] [CrossRef]
- Benini, E.; Toffolo, A. Innovative procedure to minimize multi-row compressor blade dynamic loading using rotor-stator interaction optimization. Proc. Inst. Mech. Eng. Part A J. Power Energy 2007, 221, 59–66. [Google Scholar] [CrossRef]
- McNaughton, J.; Afgan, I.; Apsley, D.D.; Rolfo, S.; Stallard, T.; Stansby, P.K. A simple sliding-mesh interface procedure and its application to the CFD simulation of a tidal-stream turbine. Int. J. Numer. Methods Fluids 2014, 74, 250–269. [Google Scholar] [CrossRef]
- Nam, H.J.; Park, Y.M.; Kwon, O.J. Simulation of unsteady rotor-fuselage aerodynamic interaction using unstructured adaptive meshes. J. Am. Helicopter Soc. 2006, 51, 141–149. [Google Scholar] [CrossRef]
- Park, Y.M.; Kwon, O.J. Simulation of unsteady rotor flow field using unstructured adaptive sliding meshes. J. Am. Helicopter Soc. 2004, 49, 391–400. [Google Scholar] [CrossRef]
- Steijl, R.; Barakos, G. Sliding, mesh algorithm for CFD analysis of helicopter rotor-fuselage aerodynamics. Int. J. Numer. Methods Fluids 2008, 58, 527–549. [Google Scholar] [CrossRef]
- Xu, H.Y.; Xing, S.L.; Ye, Z.Y.; Ma, M.S. A simple and conservative unstructured sliding-mesh approach for rotor-fuselage aerodynamic interaction simulation. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2017, 231, 163–179. [Google Scholar] [CrossRef]
- Chitsomboon, T.; Thumthae, C. Adjustment of k-w SST Turbulence Model for an Improved Prediction of Stalls on Wind Turbine Blades. In Proceedings of the World Renewable Energy Congress, Linköping, Sweden, 8–13 May 2011. [Google Scholar] [CrossRef]
- Halder, P.; Rhee, S.H.; Samad, A. Numerical optimization of Wells turbine for wave energy extraction. Int. J. Nav. Archit. Ocean Eng. 2017, 9, 11–24. [Google Scholar] [CrossRef]
- Li, X.L.; Zhu, H.R.; Liu, C.L.; Ye, L.; Xu, Z.P.; Li, G.D.; Xu, W.J. Research on enhancing impingement structure heat transfer capability based on secondary impingement. Int. J. Therm. Sci. 2025, 211, 14. [Google Scholar] [CrossRef]
- Cai, P.; Nie, W.; Chen, D.W.; Yang, S.B.; Liu, Z.Q. Effect of air flowrate on pollutant dispersion pattern of coal dust particles at fully mechanized mining face based on numerical simulation. Fuel 2019, 239, 623–635. [Google Scholar] [CrossRef]
- Cheng, W.; Jia, B.; Dong, Z.C.; Wu, Z.Y.; Zhao, X.; Wan, X.P.; Liu, Z.; Huang, H.Y. Computational paradigm for Mg-Li alloy innovation: Decoding atomic doping mechanisms for targeted property enhancement. Results Eng. 2025, 27, 24. [Google Scholar] [CrossRef]
- Heald, J.; McEwan, I.; Tait, S. Sediment transport over a flat bed in a unidirectional flow: Simulations and validation. Philos. Trans. R. Soc. Lond. Ser. A-Math. Phys. Eng. Sci. 2004, 362, 1973–1986. [Google Scholar] [CrossRef] [PubMed]
- Peters, B. Measurements and application of a discrete particle model (DPM) to simulate combustion of a packed bed of individual fuel particles. Combust. Flame 2002, 131, 132–146. [Google Scholar] [CrossRef]
- Rashidi, S.; Esfahani, J.A.; Ellahi, R. Convective Heat Transfer and Particle Motion in an Obstructed Duct with Two Side by Side Obstacles by Means of DPM Model. Appl. Sci. 2017, 7, 431. [Google Scholar] [CrossRef]
- Chen, X.L.; Zhong, W.Q.; Sun, B.B.; Jin, B.S.; Zhou, X.G. Study on gas/solid flow in an obstructed pulmonary airway with transient flow based on CFD-DPM approach. Powder Technol. 2012, 217, 252–260. [Google Scholar] [CrossRef]






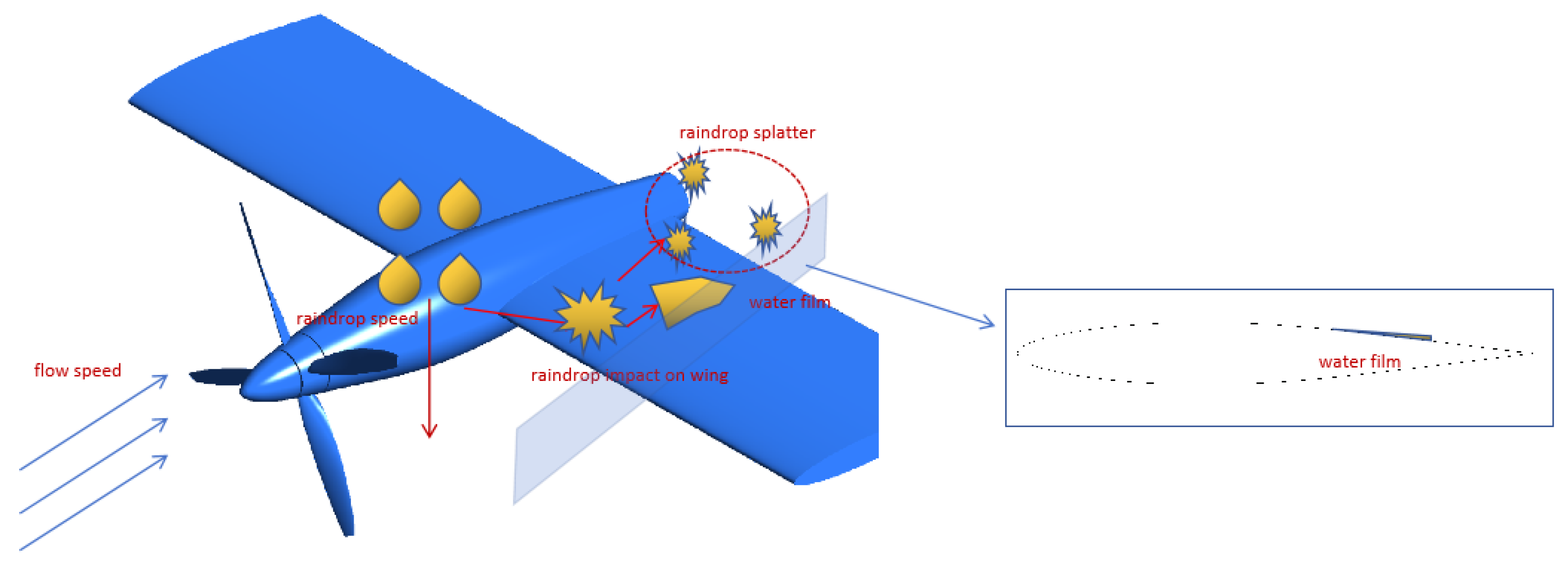
| Raindrop Diameter (mm) | Terminal Velocity (m/s) |
|---|---|
| 1 | 3.0–4.0 |
| 2 | 5.0–6.5 |
| 3 | 7.0–8.0 |
| 4 | 8.0–9.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xi, L.; Yan, J.; Zuo, Y.; Zhao, M.; Huang, H. Investigation on Aerodynamic Characteristics of Propeller–Wing Combination Configuration Under Heavy Rainfall. Aerospace 2025, 12, 975. https://doi.org/10.3390/aerospace12110975
Xi L, Yan J, Zuo Y, Zhao M, Huang H. Investigation on Aerodynamic Characteristics of Propeller–Wing Combination Configuration Under Heavy Rainfall. Aerospace. 2025; 12(11):975. https://doi.org/10.3390/aerospace12110975
Chicago/Turabian StyleXi, Liangliang, Jiaqi Yan, Yanan Zuo, Meiying Zhao, and Heyuan Huang. 2025. "Investigation on Aerodynamic Characteristics of Propeller–Wing Combination Configuration Under Heavy Rainfall" Aerospace 12, no. 11: 975. https://doi.org/10.3390/aerospace12110975
APA StyleXi, L., Yan, J., Zuo, Y., Zhao, M., & Huang, H. (2025). Investigation on Aerodynamic Characteristics of Propeller–Wing Combination Configuration Under Heavy Rainfall. Aerospace, 12(11), 975. https://doi.org/10.3390/aerospace12110975






