Dynamic Modeling and Active Stabilization of a Strake-Fin Hose–Drogue Aerial Refueling System

Abstract

Aerial refueling with hose–drogue systems provides operational flexibility but is highly susceptible to disturbances from tanker wakes, receiver bow waves, and atmospheric turbulence, which induce drogue oscillations and reduce docking success. To address these challenges, this study develops a dynamic model and introduces a strake-fin-based actively stabilized drogue. The hose is represented as a chain of rigid segments with aerodynamic drag estimated using Hoerner’s empirical correlations, while the drogue’s aerodynamic characteristics are obtained from CFD simulations. An efficient neighbor-cell search algorithm is implemented to map the hose–drogue configuration onto the CFD flow field, and atmospheric turbulence is modeled using the Dryden model. The drogue is equipped with two pairs of strake-type control fins, whose relative deflections are regulated by a linear quadratic regulator (LQR) to generate corrective aerodynamic forces. Simulation results under tanker wake, bow-wave, and severe turbulence conditions show that the proposed system effectively suppresses drogue oscillations, reducing displacement amplitudes by over 80% and maintaining positional deviations within 0.1 m. These results confirm the robustness of the modeling framework and demonstrate the potential of the strake-fin-based active stabilization strategy to ensure safe and reliable aerial refueling operations.

1. Introduction

Since the first operational use of the DH-4B aircraft for buddy refueling by the United States on 27 June 1923 [1], aerial refueling technology has undergone more than a century of continuous development. Aerial refueling is defined as the in-flight transfer of fuel from a tanker aircraft to one or more receiver aircrafts. This capability significantly enhances the operational effectiveness of military aviation through four primary mechanisms: (1) extending the operational radius by approximately 30% for fighter aircraft and doubling the range of transport aircraft per refueling cycle, thereby enabling global strike capability through successive refuelings; (2) mitigating the payload–range trade-off by allowing aircraft to carry maximum ordnance loads without compromising mission endurance; (3) enhancing strategic flexibility by reducing reliance on forward operating bases and improving survivability against enemy threats; and (4) sustaining prolonged airborne missions essential for intelligence, surveillance, and reconnaissance (ISR) operations.

In parallel, significant advances in unmanned aerial vehicle (UAV) technologies over the past decades have led to their extensive deployment in both military and civilian applications, including reconnaissance, logistics, and combat operations. Within this broader context, autonomous aerial refueling (AAR) has emerged as a critical research focus, representing a key extension of conventional aerial refueling systems. Current aerial refueling operations primarily adopt two configurations: the flying-boom method and the hose-and-drogue system. The latter offers notable operational advantages owing to its compact architecture, simplified deployment procedures, and unique capability for simultaneous multi-aircraft refueling. Studies conducted by the United States Air Force have demonstrated that coordinated control of multiple drogues provides enhanced compatibility with next-generation UAV swarm operations, thereby positioning the hose-and-drogue method as a prospective standard for both manned and unmanned platforms [2].

Despite these advantages, the practical implementation of hose–drogue AAR is challenged by complex aerodynamic interactions. In particular, the coupling of tanker wake vortices with atmospheric turbulence can induce pronounced oscillations in both the refueling hose and the receiver aircraft’s vertical stabilizer [3]. Pioneering studies by Bloy and colleagues employed simplified horseshoe-vortex models to investigate the effects of tanker wake on receiver stability, revealing oscillatory motions and reductions in longitudinal stability that depend strongly on vertical separation [4,5]. Subsequent extensions using vortex lattice methods achieved good agreement with wind-tunnel data, while more advanced planar vortex-sheet and rolled-up vortex models further improved the prediction of downwash distribution and induced rolling moments [6,7]. Moreover, the bow-wave effect generated by the approaching receiver aircraft produces an adverse pressure field near the drogue, displacing it upward and outward and thereby increasing the misalignment between the probe and drogue. In addition, wingtip vortices generated during flight create localized low-pressure regions that may deflect the drogue trajectory, further raising the risk of collision with the tanker’s fuselage or wing surfaces. These dynamic instabilities introduce nonlinear coupling effects between the drogue assembly and the receiver hose, while the compounded aerodynamic disturbances during both approach and docking phases substantially elevate operational risks. However, only a limited number of studies have focused on its modeling, such as the Rankine body model [8], its fitted variants [9] and some CFD-simulation analysis [10]. Zheng et al. [11] analyzed the hose–drogue under receiver bow-wave disturbances using a rigid ball–rod model with wake effects, providing useful insights for refueling safety.

Recent advances in hose–drogue modeling have established the multi-link discretization approach as a widely adopted method, in which the flexible hose is represented as a chain of interconnected rigid segments subjected to aerodynamic, gravitational, tensile, and torsional loads [12]. The aerodynamic loads along the hose are estimated using Hoerner’s inclined-cylinder correlations [13], which provide a widely adopted and computationally efficient approximation of aerodynamic drag on slender hoses under subsonic flow conditions. This method has been explicitly employed in previous hose–drogue dynamic studies—such as those by Ro et al. [14] and Vassberg et al. [15]—to evaluate the aerodynamic forces acting on flexible refueling hoses, confirming its suitability for system-level simulations. These works demonstrated that Hoerner’s empirical formulation can accurately capture the dominant drag characteristics while avoiding the high computational cost of full CFD–FSI coupling. Building on this foundation, Ro et al. [14] further developed parametric aerodynamic models for parachute-type drogues by combining wind-tunnel testing with CFD simulations, which revealed the dependence of drag coefficients on geometric parameters. At the system level, Vassberg et al. [15] performed six-degree-of-freedom analyses of KC-10 refueling operations using superimposed tanker–receiver flow fields to validate the aerodynamic behavior of the hose–drogue system, while NASA Dryden flight tests (2004–2005) further validated the dynamic interactions between the hose–drogue system and the receiver under operational conditions [16].

To mitigate instability induced by both high-frequency disturbances (e.g., tanker wake and atmospheric turbulence) and low-frequency effects (e.g., receiver bow wave), recent studies have explored various drogue-centric stabilization strategies. Passive methods, such as lattice-wing attachments [17], have shown moderate effectiveness, while active approaches—such as cruciform control surfaces [18] and electromechanical actuation [19]—achieved significant reductions in drogue motion in controlled environments. More recently, in addition to these approaches, Meng et al. [20] proposed a controllable drogue with adjustable strut angles and fuzzy logic control, effectively reducing swing amplitude under gust conditions, while Zhang et al. [21] presented a cooperative control scheme enabling wide-range maneuvering of morphing drogues using strut angle modulation. These methods demonstrate good stabilization capability in controlled environments; however, they are fundamentally constrained by the limited control authority of rudder- or strut-based mechanisms, which mainly act through canopy deformation rather than generating direct aerodynamic forces. As a result, roll control is weak or absent, and the achievable response bandwidth is limited by the structural dynamics of the canopy. Moreover, since these approaches depend heavily on accurate modeling of unsteady aerodynamic forces, their robustness degrades under large disturbances or uncertain flow conditions. Additionally, the coupling between deformation-induced forces often complicates control allocation, necessitating complex fuzzy or neural network–based algorithms to maintain performance.

In hose–drogue aerial refueling, such instabilities are primarily driven by three major disturbance sources: (i) tanker wake turbulence, which generates unsteady velocity fluctuations in the downstream region; (ii) receiver bow wave effects, which produce strong pressure gradients and displacement forces as the receiver approaches the drogue; and (iii) ambient atmospheric turbulence, which introduces broadband stochastic disturbances. These combined effects induce significant drogue oscillations and positional deviations, posing a major challenge for stable probe–drogue engagement.

Building upon these developments, the present study proposes a strake-fin-based actively stabilized hose–drogue system. The analysis focuses on the pre-contact phase of the aerial refueling operation, during which the hose is modeled as empty (non-fuel-filled), reflecting the typical configuration prior to probe engagement. A multibody dynamic model of the hose–drogue assembly is established, while the tanker wake and receiver-induced bow-wave effects are simulated using a flow-field search algorithm informed by computational fluid dynamics (CFD) results. Atmospheric turbulence is represented through the Dryden turbulence model. On this basis, a strake-fin stabilization strategy is developed and evaluated using CFD-derived aerodynamic coefficients. Strake fins are slender, fixed-chord aerodynamic surfaces capable of generating strong longitudinal vortices that enhance lateral and vertical stability. Compared with passive damping or canopy-modification strategies, they enable active and rapid control of drogue motion with minimal structural modification. This novel application of strake fins to drogue stabilization represents a key contribution of this work. A linear quadratic regulator (LQR) control algorithm is designed to exploit these control surfaces for active stabilization of the drogue. Finally, a dynamic simulation platform is constructed to evaluate control performance under combined atmospheric turbulence and bow-wave disturbances. The results confirm that the proposed approach effectively suppresses aerodynamic instabilities, thereby enhancing the safety and reliability of aerial refueling operations.

2. The Hose and Drogue Model

As a rope-like flexible structure, the aerial-refueling hose behaves similarly to an ideal cable under nominal operating conditions. Modeling methodologies for cable-like dynamics generally fall into two categories: (i) continuum formulations governed by partial differential equations (PDEs) and (ii) discretized finite-segment representations described by ordinary differential equations (ODEs) [12]. The former has been widely employed in high-fidelity theoretical analyses of flexible hose behavior, while the latter has been validated and extensively adopted in practical aerial refueling simulations (e.g., Ro et al. [14]; Vassberg et al. [15]; Paniagua et al. [17]) due to its favorable balance between computational efficiency and accuracy. This study adopts the latter, ODE-based discretization, to balance computational efficiency with practical applicability when capturing the aerodynamic–structural interactions intrinsic to aerial-refueling systems.

2.1. Model Description

As illustrated in Figure 1, the refueling hose is modeled as an open-chain multibody system, in which the hose is discretized into a sequence of massless rigid links connected by ideal spherical joints at nodes with lumped masses. The rigid links transmit loads and preserve kinematic continuity, while the spherical joints allow relative rotation but prohibit relative translation, maintaining geometric continuity of the hose. No torsional stiffness or friction is included at the joints, and no bending moment is directly transmitted through the connections.

For a hose with $n$ segments, nodes are indexed $0,\dots ,n$ (node 0 near the pod and node $n$ adjacent to the drogue), and segments are indexed $1,\dots ,n$ along the longitudinal axis. Each hose node is assigned three translational degrees of freedom ($x, y, z$), while rigid link constraints enforce constant segment lengths. The drogue is modeled as a rigid body with six degrees of freedom, including three translational and three rotational components, enabling full coupling between its position and attitude dynamics. Let $l_i$ denote the length of segment $i$. The lumped mass at node $i$ is

$$m_i=\left\{\begin{array}{cc}{\displaystyle \frac{(l_i+l_{i+1}){\rho }_{\mathrm{hose}}}{2}},& i=1,\dots ,n-1,\\ {\displaystyle \frac{l_i{\rho }_{\mathrm{hose}}}{2}}+m_{\mathrm{d}\mathrm{r}\mathrm{o}},& i=n,\end{array}\right.$$

(1)

where $m_{\mathrm{d}\mathrm{r}\mathrm{o}}$ is the drogue mass and ${\rho }_{\mathrm{hose}}$ represents the total mass per unit length of the hose. In the empty-hose condition, it corresponds to the structural mass of the hose shell alone. In the fuel-filled condition, the contribution of the internal fuel mass is added to the structural mass to obtain the total effective linear density.

Node 0 represents the fixed connection point between the hose and the tanker refueling pod. It is treated as a fixed boundary, and $m_0$ is assigned zero mass, acting purely as a kinematic constraint. The node position remains constant during simulation, transmitting loads between the hose and the pod without contributing to the system’s dynamic equations.

2.2. Coordinate System Definition

An inertial coordinate system ($O_r,X_r,Y_r,Z_r$) is defined with its origin at the tanker’s center of gravity. In this system, the $X_r$-axis is oriented opposite to the freestream velocity, the $Y_r$-axis points to the right and is perpendicular to the $X_r$-axis within the horizontal plane, and the $Z_r$-axis completes a right-handed coordinate system.

A local hose coordinate system ($O_i,X_i,Y_i,Z_i$), parallel to the inertial frame, is established at each node with its origin $O_i$ located at the node center. The spatial orientation of each hose segment is parameterized by Euler angles ${\mathsf{\theta }}_{i,1}$ (pitch) and ${\mathsf{\theta }}_{i,2}$ (yaw) with respect to this local frame, as illustrated in Figure 2. The $y_i$-axis of the ($O_i,X_i,Y_i,Z_i$) frame is aligned with the $i^{\mathrm{th}}$ segment vector $r_i$ through two successive rotations: (i) a rotation by ${\mathsf{\theta }}_{i,1}$ about the $z_i$-axis, followed by (ii) a rotation by ${\mathsf{\theta }}_{i,2}$ about the transformed axis $x_i^{\prime }$, where $x_i^{\prime }$ denotes the new $x$-axis orientation after the first rotation.

The drogue body coordinate system ($O_d,X_d,Y_d,Z_d$), fixed at the hose–drogue interface, is defined such that $X_d$ coincides with the drogue’s longitudinal axis pointing forward, $Y_d$ points laterally to starboard, and $Z_d$ points downward, ensuring a right-handed orthogonal system. A schematic overview of all coordinate system definitions is provided in Figure 3.

2.3. Kinematics of the Hose–Drogue System

The dynamic formulation adopted in this study follows well-established hose–drogue modeling approaches reported in the literature [12,14,15,22]. The multibody discretization framework, node force analysis, bending restoring force calculation, and constraint equations for hose segments are consistent with these prior works. In particular, the kinematic equations presented in Section 2.3.4 and the fundamental dynamic equations in Section 2.3.5 are derived directly from these classical formulations. On this basis, the present work introduces additional modeling features, including the incorporation of CFD-derived aerodynamic loads and strake-fin control effects, enabling fully coupled aero–structural–control simulations under realistic disturbances.

2.3.1. Node Force Analysis

The concentrated forces acting on each hose node include aerodynamic and gravitational forces from the neighboring hose segments, restoring forces generated by bending, and tensile forces transmitted through the adjacent segments. For the force analysis of an arbitrary node i in Figure 1, half of the aerodynamic and gravitational loads from the two adjacent segments are assigned to the node. In addition, the restoring force that acts to straighten the hose after bending is modeled as a concentrated force applied at the same node. Hence, the resultant external force at node $i$ can be expressed as

$$\begin{array}{c}\sum F_i=\left\{\begin{array}{cc}{\displaystyle \frac{D_i+D_{i+1}}{2}}+F_{ei}+m_{i}g,& i=1,\dots ,n-1,\\ {\displaystyle \frac{D_i}{2}}+D_{\mathrm{d}\mathrm{r}\mathrm{o}}+m_{i}g,& i=n,\end{array}\right.\end{array}$$

(2)

where $D_i$ is the aerodynamic force acting on the $i$-th hose segment, $F_{ei}$ is the restoring force at node $i$, $m_i$ is defined in Equation (1), $D_{\mathrm{dro}}$ is the aerodynamic force on the drogue, and $g$ is the gravitational acceleration.

Note that node 0, located at the tanker–hose interface, is treated as a fixed boundary and has no dynamic degrees of freedom. Consequently, no external force balance is written at this node, and it is not included in Equation (2). All forces are represented in the global inertial coordinate system. The aerodynamic forces ($D_i$) are initially computed in the local hose coordinate system ($O_i,X_i,Y_i,Z_i$) or the drogue body coordinate system ($O_d,X_d,Y_d,Z_d$) then projected into the inertial coordinate system ($O_r,X_r,Y_r,Z_r$) for nodal force assembly and dynamic integration.

2.3.2. Aerodynamic Force Model

The aerodynamic forces acting on the refueling hose are evaluated using Hoerner’s empirical correlations for inclined cylinders [13]. This approach provides an efficient and sufficiently accurate estimation of aerodynamic loads on slender flexible hoses under subsonic conditions and has been widely adopted in previous hose–drogue dynamic studies, including Ro and Kamman [14]. In line with these works, the present model considers only drag forces—comprising skin-friction and pressure drag—while neglecting lift and aerodynamic moments because of their small magnitude under typical refueling conditions. This simplification is consistent with studies such as Ro and Kamman [14], which applied Hoerner’s correlations to compute only the pressure- and skin-friction drag on the hose surface.

The aerodynamic loads are further evaluated under the quasi-steady assumption, whereby the instantaneous forces depend solely on the local velocity and orientation of each hose segment. This simplification is supported by the clear separation between the hose-drogue motion period ($\approx 1\text{–}3 \mathrm{s}$) and the much shorter aerodynamic response time of the subsonic flow ($\approx {10}^3 \mathrm{s}$), ensuring that unsteady effects have negligible influence on the global dynamics.

It should be noted that the aerodynamic model employed in this study is quasi-steady rather than strictly steady. In this formulation, the aerodynamic forces are updated at every time step according to the instantaneous local flow velocity and hose orientation. The steady-state Hoerner correlations [13] are applied at each step to evaluate the drag components, while unsteady aerodynamic lag and history effects are neglected. As a result, the aerodynamic loads vary dynamically with the hose motion but without temporal delay in their response. This treatment has been widely used and validated in previous hose–drogue dynamic analyses [23,24], which confirmed that quasi-steady modeling accurately captures the overall hose–drogue behavior under subsonic refueling conditions.

These assumptions strike a good balance between modeling fidelity and computational efficiency and are consistent with established aerodynamic formulations for hose–drogue systems.

(a)

Skin-friction drag

The skin-friction drag is induced by the shear stress of the tangential velocity component. Following Hoerner’s empirical correlations [13], the skin-friction drag on the $i$-th hose segment is written as

$$\begin{array}{c}{D}_{i,\mathrm{skin}}=C_f\cdot {\displaystyle \frac{1}{2}}\rho V_t^2\cdot \pi d_{\mathrm{hose}}\cdot l_i\end{array}$$

(3)

where ${\displaystyle \frac{1}{2}}\rho V_t^2$ is the dynamic pressure of the tangential flow, $\rho$ is the air density, $V_t$ is the tangential flow velocity relative to the hose, $d_{\mathrm{hose}}$ is the hose diameter, $l_i$ is the segment length, and $C_f$ is the skin-friction defined in Ref. [13].

(b)

Pressure drag

For viscous flows, when the velocity distribution of the incident airflow is parallel to the hose cross-section, the pressure behind the section becomes lower than that in front, resulting in pressure drag. Similar to the treatment of skin-friction drag, the empirical correlations proposed by Hoerner [13] are employed here. The pressure drag acting on the $i$-th hose segment is expressed as

$$\begin{array}{c}{D}_{i,\mathrm{pressure}}=C_d\cdot {\displaystyle \frac{1}{2}}\rho V_n^2\cdot d_{\mathrm{hose}}\cdot l_i\end{array}$$

(4)

where ${\displaystyle \frac{1}{2}}\rho V_n^2$ is the dynamic pressure corresponding to the normal flow velocity, $V_n$ denotes the flow velocity normal to the hose axis, $d_{\mathrm{hose}}$ is the hose diameter, $l_i$ is the segment length, and $C_d$ is the pressure-drag coefficient. The coefficient $C_d$ is defined in Ref. [13].

2.3.3. Restoring Force Calculation

In the kinematics of the hose–drogue system, the bending deformation of the refueling hose is considered, and the equivalent restoring force is denoted as $F_{ei}$ [22]. As illustrated in Figure 4, for all interior nodes except the first and last, the magnitude of the equivalent restoring force is related to the deflection angles ${\mathsf{\theta }}_L$ and ${\mathsf{\theta }}_R$ by

$$\begin{array}{c}{F}_{ei}={\displaystyle \frac{8EI}{|l_L+l_R{|}^2}}({\theta }_L+{\theta }_R)\end{array}$$

(5)

where $E$ is the Young’s modulus of the hose material, and $I$ is the second moment of area of the hose cross-section, defined in terms of the outer diameter $d_{ho}$ and inner diameter $d_{hi}$ as

$$\begin{array}{c}I={\displaystyle \frac{\pi }{64}}\left(d_{ho}^4-d_{hi}^4\right)\end{array}$$

(6)

The deflection angles ${\theta }_L$ and ${\theta }_R$ are calculated from the geometric relationships between the adjacent segments as

$$\begin{array}{c}\begin{array}{c}{\theta }_L={\mathrm{c}\mathrm{o}\mathrm{s}}^{-1}\left({\displaystyle \frac{L_L}{\left|L_L\right|}}\cdot {\displaystyle \frac{L_L+L_R}{|L_L+L_R|}}\right),{\theta }_R={\mathrm{c}\mathrm{o}\mathrm{s}}^{-1}\left({\displaystyle \frac{L_R}{\left|L_R\right|}}\cdot {\displaystyle \frac{L_L+L_R}{|L_L+L_R|}}\right)\end{array}\end{array}$$

(7)

where $L$ is the position vector between the $i$-th node and left or right node and the direction of the restoring force $F_{ei}$ is given by

$$\begin{array}{c}{r}_{ei}={\displaystyle \frac{L_R}{\left|L_R\right|}}-{\displaystyle \frac{L_L}{\left|L_L\right|}}\end{array}$$

(8)

Although more advanced finite-element or continuous beam models can provide higher accuracy, the present approach effectively captures the dominant low-frequency bending behavior while ensuring computational efficiency for dynamic simulation and control analysis.

It should be noted that the second moment of area $I$ is calculated based solely on the geometry of the hose shell, which primarily consists of rubber and braided steel layers. The corresponding bending stiffness $EI$ therefore reflects the structural rigidity of the hose wall rather than the influence of the internal fluid. In the present study, the hose is analyzed in the unfuelled condition, which is the relevant state for investigating the hose–drogue dynamics and aerodynamic stabilization prior to fuel transfer. Under such conditions, the presence or absence of fuel has negligible influence on the effective bending stiffness, as the fuel mainly affects the hose’s distributed mass but not its elastic rigidity.

This assumption is consistent with previous hose–drogue dynamic studies (e.g., Zhu and Meguid [25]; Ro and Kamman [14]), which also treated the hose bending stiffness as constant regardless of the internal fluid state. The additional fuel mass, when applicable, is included only in the lumped mass distribution (Section 2.1), influencing the inertial characteristics of the system but not its structural stiffness.

2.3.4. Kinematic Equations

As shown in Figure 2, consider the $i$-th hose segment for analysis. Let the position vectors of nodes $i-1$ and $i$ in the inertial coordinate system ($O_r,X_r,Y_r,Z_r$) be denoted as $P_{i-1}$ and $P_i$, respectively. Then

$$\begin{array}{c}{P}_i=P_{i-1}+r_i\end{array}$$

(9)

where $r_i$ is the vector of the $i$-th segment. Differentiating Equation (14) yields the velocity relation

$$\begin{array}{c}{v}_i=v_{i-1}+{\dot{r}}_i\end{array}$$

(10)

and further differentiation leads to the acceleration relation

$$\begin{array}{c}{a}_i=a_{i-1}+{\ddot{r}}_i\end{array}$$

(11)

Defining the partial derivatives

$$\begin{array}{c}{\displaystyle \frac{\partial r_i}{\partial {\theta }_{i,k}}}=r_{i,{\theta }_k} (k=1,2), {\displaystyle \frac{\partial r_i}{\partial l_i}}=r_{i,l_i}\end{array}$$

(12)

the velocity and acceleration of the segment can be expressed as

$$\begin{array}{c}{\dot{r}}_i={\displaystyle \sum _{k=1}^2} r_{i,{\theta }_{i,k}}{\dot{\theta }}_{i,k}+r_{i,l_i}{\dot{l}}_i\end{array}$$

(13)

$$\begin{array}{c}{\ddot{r}}_i={\displaystyle \sum _{k=1}^2} (r_{i,{\theta }_{i,k}}{\ddot{\theta }}_{i,k}+{\dot{r}}_{i,{\theta }_{i,k}}{\dot{\theta }}_{i,k})+r_{i,l_i}{\ddot{l}}_i+{\dot{r}}_{i,l_i}{\dot{l}}_i\end{array}$$

(14)

Multiplying by $r_{i,{\theta }_{i,j}}\left(j=1,2\right)$ gives the governing relation

$$\begin{array}{c}|r_{i,{\theta }_{i,j}}{|}^2{\ddot{\theta }}_{i,j}+\{{\displaystyle \sum _{k=1}^2} r_{i,{\theta }_{i,k}}{\dot{\theta }}_{i,k}+r_{i,l_i}{\dot{l}}_i+{\dot{r}}_{i,l_i}{\dot{l}}_i-a_i+a_{i-1}\}\cdot r_{i,{\theta }_j}=0,(j=1,2)\end{array}$$

(15)

Thus, given the nodal velocities, accelerations, and the time derivatives of segment lengths, the orientation angles and their time histories can be solved numerically using the Runge–Kutta method. A fixed time step of $1\times {10}^{-3} \mathrm{s}$ was adopted to ensure numerical stability and accuracy. The stability of the integration scheme was verified through time-step convergence studies, ensuring bounded energy behavior during the simulation.

2.3.5. Fundamental Dynamic Equations

For a rigid link, the displacement constraint is written as

$$\begin{array}{c}{r}_i^2=l_i^2\end{array}$$

(16)

Taking the second derivative of Equation (16) yields the acceleration constraint

$$\begin{array}{c}(a_i-a_{i-1})\cdot r_i+({\dot{r}}_i{)}^2=({\dot{l}}_i{)}^2+l_i{\ddot{l}}_i\end{array}$$

(17)

The tensile force in the $i$-th link is expressed as

$$\begin{array}{c}{T}_i=n_i{t}_i\end{array}$$

(18)

where $n_i$ is the unit vector along the link, and $t_i$ is the scalar tensile magnitude. $t_i$ is solved dynamically rather than prescribed as a constant, and it varies according to the instantaneous aerodynamic, gravitational, and inertial loads. Ref. [22], which investigated hose-whipping effects, provides quantitative hose tension data. Under non-whipping conditions, the tension magnitudes reported in [22] are comparable to those obtained in this study, confirming the physical reliability of the model. As the present study does not focus on the whipping behavior, detailed tension results are not presented throughout the paper. Substituting Equation (18) into Equation (17), the dynamic governing equation for the internal nodes becomes

$$\begin{array}{c}\begin{array}{c}{\displaystyle \frac{n_{i-1}\cdot n_i}{m_{i-1}}}{t}_{i-1}-\left({\displaystyle \frac{1}{m_{i-1}}}+{\displaystyle \frac{1}{m_i}}\right)t_i+{\displaystyle \frac{n_i\cdot n_{i+1}}{m_i}}{t}_{i+1}\end{array}\\ =\left({\displaystyle \frac{\sum F_i}{m_{i-1}}}-{\displaystyle \frac{\sum F_i}{m_i}}\right)\cdot n_i-{\displaystyle \frac{(v_i-v_{i-1}{)}^2}{l_i}},\left(i=2,\dots ,n-1\right)\end{array}$$

(19)

where $m_i$ is the lumped mass at node $i$, $F_i$ is the external force acting on node $i$, $v_i$ is the nodal velocity, and $l_i$ is the segment length.

2.4. Aircraft Flow-Field Simulation

As discussed in Section 2.3, the aerodynamic forces on the hose–drogue system depend on flow-field parameters such as velocity and density. In this study, the flow field is first obtained from CFD simulations, and the aerodynamic loads on the hose–drogue assembly are subsequently determined by mapping the interaction points to the corresponding CFD cells and extracting the relevant flow-field quantities.

2.4.1. Neighbor-Cell Search Algorithm [26]

A direct global search in a CFD mesh containing on the order of ${10}^7$ cells would be computationally prohibitive. To address this challenge, a neighbor-cell search algorithm is employed to efficiently locate the host cell corresponding to the instantaneous position of each hose or drogue element. The purpose of this algorithm is to establish a fast, stable, and deterministic mapping between the moving structure and the precomputed CFD flow field, thereby enabling real-time aerodynamic load evaluation during dynamic simulations.

This algorithm exploits the topological connectivity of the unstructured CFD mesh to construct a quasi-one-dimensional search path from an initial cell to the target cell, avoiding an expensive global search. To enhance clarity, the pseudocode of the algorithm is summarized below:

1. Select the initial search cell whose centroid is closest to the target point.

2. Compute the line segment connecting the centroid of the current cell to the target point.

3. Check the intersections of this line with all faces of the current cell.

4. If an intersection is found, identify the adjacent cell sharing that face and set it as the new current cell.

5. If no intersection is found, designate the current cell as the host cell.

6. Repeat Steps 2–5 until the target cell is reached.

This approach reduces the computational complexity from O(N) for a global search to O(K), where K is the number of locally connected cells typically $K\ll N$, providing a substantial improvement in efficiency for large unstructured CFD meshes.

The schematic illustration of the adjacent-cell search process is shown in Figure 5.

By combining this neighbor-cell search with local grid refinement in the region of interest, the algorithm ensures accurate and stable interpolation of the CFD flow field, allowing reliable computation of aerodynamic forces and moments on the hose–drogue system without re-meshing. This efficient CFD–structure coupling is essential for real-time dynamic simulation of aerial refueling operations.

2.4.2. CFD Simulations

In this study, CFD is employed to resolve the complex aerodynamic environment surrounding the hose–drogue assembly during aerial refueling. Compared with simplified analytical or empirical methods, the CFD approach captures the detailed flow structures induced by tanker wake and receiver bow wave, which are critical for accurately evaluating drogue stability. The flow field is computed under steady flight conditions, and it is assumed that the hose–drogue motion does not significantly alter the overall flow distribution. This allows aerodynamic information to be retrieved efficiently through a neighbor-cell search algorithm, providing a practical balance between fidelity and computational cost. A similar steady-flow-based aerodynamic field treatment was also adopted in [15] for investigating bow-wave effects, further supporting the applicability of this approach to aerial refueling problems.

The CFD simulations for both the tanker and the receiver were performed using un-structured grids with local refinement applied around the hose–drogue operating region and the receiver nose to accurately resolve strong flow-field gradients. The computational domain was sized to fully contain the entire motion envelope of the hose and drogue, ensuring that their displacements during dynamic simulations remained inside the refined flow region.

To incorporate the aerodynamic disturbances induced by the tanker wake and receiver bow wave, steady-state CFD flow fields of the tanker–receiver configuration without the hose–drogue system were first computed. These precomputed flow fields provide the ambient aerodynamic environment for subsequent dynamic simulations. During the simulation, local flow velocity and pressure data at each hose and drogue node were obtained through neighbor-cell search and interpolation within the CFD mesh, enabling the wake and bow wave effects to be accurately introduced without the need for fully coupled CFD calculations.

Additional local mesh refinement was applied in this region to maintain sufficient spatial resolution throughout the expected hose–drogue motion, allowing aerodynamic loads to be accurately retrieved without dynamic mesh deformation. The tanker and receiver meshes contained approximately 11.05 million and 4.44 million cells, respectively.

The Spalart–Allmaras one-equation turbulence model was adopted to simulate steady, viscous, and compressible flow under typical aerial-refueling conditions. The computations covered altitudes of 7500 ft and 25,000 ft, with true airspeeds ranging from 170 kt to 310 kt at 20 kt intervals, and a representative cruise case of Mach 0.5223 at 6000 m altitude.

The far-field boundary was prescribed using the pressure-far-field condition, while no-slip adiabatic wall conditions were applied to all solid surfaces. These settings ensured numerical stability and accurate representation of the aerodynamic environment sur-rounding the hose–drogue system.

2.5. Dryden Wind Turbulence Model [27]

In aerial refueling scenarios, accurate and efficient modeling of atmospheric turbulence is essential for evaluating the dynamic behavior of the hose–drogue system and its control response. Among the available turbulence representations, the Dryden model is widely adopted in aerospace engineering due to its well-defined spectral characteristics, analytical tractability, and ease of integration into dynamic simulation frameworks. It provides a balance between physical realism and computational efficiency, making it particularly suitable for flight control and refueling disturbance simulations.

In this study, wind-field disturbances are modeled using the Dryden turbulence model, which represents turbulence as a stationary, Gaussian, ergodic random process. The model characterizes turbulent velocity fluctuations along three orthogonal axes: longitudinal ($u$), lateral ($v$), and vertical ($w$).

These fluctuations are generated by passing white-noise signals through shaping filters whose transfer functions are derived from the Dryden power spectral density (PSD). The turbulence intensity and scale lengths are determined by the flight altitude and true airspeed, ensuring that the generated turbulence field reflects realistic atmospheric conditions.

The resulting time-correlated velocity components are then superimposed on the freestream flow experienced by the drogue and hose, introducing stochastic gust disturbances throughout the simulation. This enables the model to reproduce realistic turbulence effects without direct CFD simulation, thereby significantly reducing computational cost while maintaining dynamic fidelity.

2.5.1. Power Spectral Density Formulation

The model is formulated in the frequency domain using power spectral densities (PSDs). For the longitudinal component, the PSD is given by

$$\begin{array}{c}{\varphi }_u(\omega )={\displaystyle \frac{2{\sigma }_u^2{L}_u}{\pi V}}\cdot {\displaystyle \frac{1}{1+{\left(\frac{L_u\omega }{V}\right)}^2}}\end{array}$$

(20)

while for the lateral and vertical components, the PSDs are expressed as

$$\begin{array}{c}{\varphi }_v(\omega )={\displaystyle \frac{{\sigma }_v^2{L}_v}{\pi V}}\cdot {\displaystyle \frac{1+3{\left(\frac{L_v\omega }{V}\right)}^2}{[1+{\left(\frac{L_v\omega }{V}\right)}^2{]}^2}}\end{array}$$

(21)

$$\begin{array}{c}{\varphi }_w(\omega )={\displaystyle \frac{{\sigma }_w^2{L}_w}{\pi V}}\cdot {\displaystyle \frac{1+3{\left(\frac{L_w\omega }{V}\right)}^2}{[1+{\left(\frac{L_w\omega }{V}\right)}^2{]}^2}}\end{array}$$

(22)

where $V$ is the true airspeed of the aircraft ($\mathrm{m}/\mathrm{s}$), $\mathsf{\omega }$ is the circular frequency ($\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}$), ${\mathsf{\sigma }}_u$, ${\mathsf{\sigma }}_v$, and ${\mathsf{\sigma }}_w$ are the turbulence intensities ($\mathrm{m}/\mathrm{s}$), and $L_u$, $L_v$, and $L_w$ are the turbulence scale lengths ($\mathrm{m}$).

2.5.2. Time-Domain Representation

By applying the inverse Fourier transform, the Dryden model can be equivalently implemented in the time domain through linear shaping filters driven by independent white Gaussian noise inputs. For the longitudinal component, the transfer function of the shaping filter is given by

$$\begin{array}{c}{H}_u(s)={\sigma }_u\sqrt{{\displaystyle \frac{2L_u}{\pi V}}}\cdot {\displaystyle \frac{1}{1+\frac{L_u}{V}s}}\end{array}$$

(23)

and for the lateral component, the transfer function is expressed as

$$\begin{array}{c}{H}_v(s)={\sigma }_v\sqrt{{\displaystyle \frac{L_v}{\pi V}}}\cdot {\displaystyle \frac{1+\frac{\sqrt{3}{L}_v}{V}s}{{\left(1+\frac{L_v}{V}s\right)}^2}}\end{array}$$

(24)

The vertical component $H_w\left(s\right)$ takes an analogous form to $H_v\left(s\right)$, with $L_w$ and ${\mathsf{\sigma }}_w$ replacing $L_v$ and ${\mathsf{\sigma }}_v$. In numerical simulations, independent white noise processes, $n_u\left(t\right)$, $n_v\left(t\right)$, and $n_w\left(t\right)$ are passed through the corresponding filters to generate the correlated turbulence velocity components $u\left(t\right)$, $v\left(t\right)$, and $w\left(t\right)$, which are then superimposed onto the mean wind field.

2.5.3. Parameterization for Different Flight Conditions

The turbulence scale lengths ($L_u,L_v,L_w$) and intensity values (${\mathsf{\sigma }}_u,{\mathsf{\sigma }}_v,{\mathsf{\sigma }}_w$) are determined as functions of flight altitude and airspeed based on the empirical relations given in MIL-F-8785C [28]. Specifically, the turbulence intensities are scaled with the true airspeed ($V$), while the scale lengths are determined according to altitude-dependent standard atmospheric turbulence characteristics [29].

2.6. Model Accuracy Validation

To validate the accuracy of the proposed hose–drogue mathematical model, numerical simulations were conducted using the same tanker–hose–drogue parameters reported in Ref. [30]. The simulations were performed at flight altitudes of 7500 ft and 25,000 ft, with airspeeds ranging from 170 to 310 kt in increments of 20 kt.

For better visualization and clarity, Figure 6 presents only four representative flight speeds (170 kt, 210 kt, 250 kt, and 290 kt), while the complete set of results is provided in

Table 1. Comparison of drogue sinkage and its percentage of deviation.

Airspeed (kt)	Bank Angle (°)	Velocity (m/s)	Verticality (V1)	Verticality (V2)
Airspeed (kt)	Altitude(ft)
	7500		25,000
	VD	Δ (%)	VD	Δ (%)
170	20.83	−2.9%	28.67	−1.9%
190	18.04	−3.0%	26.47	1.0%
210	15.94	−1.8%	23.71	1.0%
230	14.33	0.6%	20.80	1.4%
250	13.02	3.6%	18.86	0.5%
270	11.32	1.7%	17.25	0.9%
290	10.14	2.3%	15.80	3.2%
310	9.22	3.7%	13.84	−1.4%

.

Figure 6 illustrates the steady-state hose–drogue configuration: (a) flight altitude of 7500 ft; (b) flight altitude of 25,000 ft. Figure 6 compares the simulated hose geometry and drogue position with those reported in Ref. [30], while Table 1 summarizes the drogue sinkage and the corresponding relative deviations. The results show close agreement between the computed data and the reference values, thereby confirming the robustness of the proposed mathematical model. The minor deviations are attributed to differences in the modeling of the tanker F-15 wake field: Ref. [30] employed the Helmholtz horseshoe-vortex model, whereas the present study adopted a CFD-based approach.

Furthermore, the simulation results were nondimensionalized using the drogue dimensionless vertical position (DDVP) defined in Ref. [30] and compared against flight-test data obtained by NASA. The DDVP is defined as

$$\mathrm{DDVP}={\displaystyle \frac{v_d}{l_d}}$$

(25)

where $v_d$ denotes the vertical distance between the hose–drogue connection point and the towed point, and $l_d$ represents the straight-line distance from the towed point to the hose–drogue coupling. The computed results exhibit trends consistent with the flight-test data reported in Ref. [16], as shown in Figure 7. This further confirms the validity of the numerical simulations and the reliability of the proposed mathematical model.

In addition to the quantitative comparison above, it is worth emphasizing that reproducing the static equilibrium configuration provides a solid foundation for the subsequent dynamic analyses. Similar validation methodologies have been widely adopted in previous hose–drogue investigations. For instance, García-Fogeda et al. [23] and Paniagua et al. [17] validated their numerical models against the static equilibrium configurations before performing dynamic and aeroelastic simulations. These studies demonstrate that accurately reproducing the static behavior of the system ensures that the underlying aerodynamic and structural characteristics are properly captured, thereby increasing confidence in the model’s capability to predict the subsequent dynamic response. Following this established practice, the present validation of the steady-state configuration confirms the reliability of the proposed model as a sound basis for the later dynamic analyses.

2.7. Simulation of the Bow Wave Effect

To evaluate the influence of the receiver-induced bow wave on the hose–drogue system, numerical simulations were conducted following the modeling approach described in Ref. [15]. In this approach, the bow wave generated by the receiver aircraft is represented as a steady perturbation velocity field superimposed on the freestream and the tanker wake. It should be noted that both the tanker and receiver flowfields were obtained from high-fidelity CFD calculations, as detailed in Section 2.4.2. The perturbation velocity fields (${V^{\prime }}_{KC-10}$) and (${V^{\prime }}_{F/A-18}$) were derived by subtracting the freestream velocity from these CFD solutions, enabling accurate representation of the aerodynamic environment around the drogue.

The combined flow field at the drogue location is expressed as:

$$\begin{array}{c}{V}_{flow}={V^{\prime }}_{KC-10}+{V^{\prime }}_{F/A-18}+V_{freestream}\end{array}$$

(26)

$${V^{\prime }}_{KC-10}=V_{KC-10}-V_{freestream}$$

(27)

$${V^{\prime }}_{F/A-18}=V_{F/A-18}-V_{freestream}$$

(28)

The simulation was performed for a representative pre-contact condition with the receiver positioned downstream of the drogue centerline. The initial equilibrium position of the drogue was obtained in the tanker wake alone, after which the receiver-induced bow wave was introduced to compute the new equilibrium configuration. The iterative procedure was repeated until convergence, corresponding to the static displacement of the drogue under the combined flow field of the tanker and receiver.

The parameters used in the numerical simulation are summarized in

Table 2. Parameters of the numerical simulation of the bow wave effect.

Parameter		Value
Hose	Total length/m	22.86
	Linear density (empty hose)/(kg · m−1) Inner diameter/m Outer diameter/m	2.38 0.058 0.067
	Elastic modulus/Pa	13,800,000
Drogue	Mass/kg	29.48
	Type/m2	0.23
Freestream	Altitude/m2	7620
	Mach Number	0.63

Note: The hose geometric and material parameters are taken from Vassberg et al. [15] to ensure consistency with the reference data used for model validation in Section 2.7. The corresponding elastic modulus of 2000 psi ($\approx 1.38\times {10}^7 \mathrm{P}\mathrm{a}$) is adopted to maintain direct comparability with the published simulation results.

.

Figure 8 illustrates the resulting drogue displacement trajectory during the simulation. The red circle represents the approximate shape of the steady drogue canopy region under the influence of the tanker wake alone, whereas the blue circle corresponds to the steady canopy shape when the receiver bow wave is also included. The orange line indicates the transient trajectory of the drogue center during the iterative convergence process. As expected, the introduction of the bow wave leads to an upward and outward displacement of the drogue relative to its initial position.

A qualitative comparison between the results obtained in this study and the reference solution presented in Ref. [15] shows good agreement in terms of displacement direction and relative magnitude. Although the reference does not provide explicit length scales, the displacement characteristics obtained here agree well with the reported trends in terms of both direction and relative magnitude, particularly when normalized by the drogue canopy diameter. This consistency further validates the implementation of the bow wave effect modeling method in the present work.

3. Active Stabilization Design of the Aerial Refueling Drogue

Although the hose–drogue aerial refueling system has been widely adopted for its structural simplicity and operational flexibility, the drogue remains highly susceptible to disturbances such as tanker wake turbulence, receiver bow-wave effects, and atmospheric gusts. Such disturbances often result in unstable drogue motion, increased probe–drogue misalignment, and reduced refueling success rates. To address these challenges, active stabilization of the drogue has been proposed as a promising solution. By integrating actuation mechanisms and control strategies into the drogue design, the system can enhance positional stability and improve docking reliability.

3.1. Structural Design of the Active Stabilization Drogue

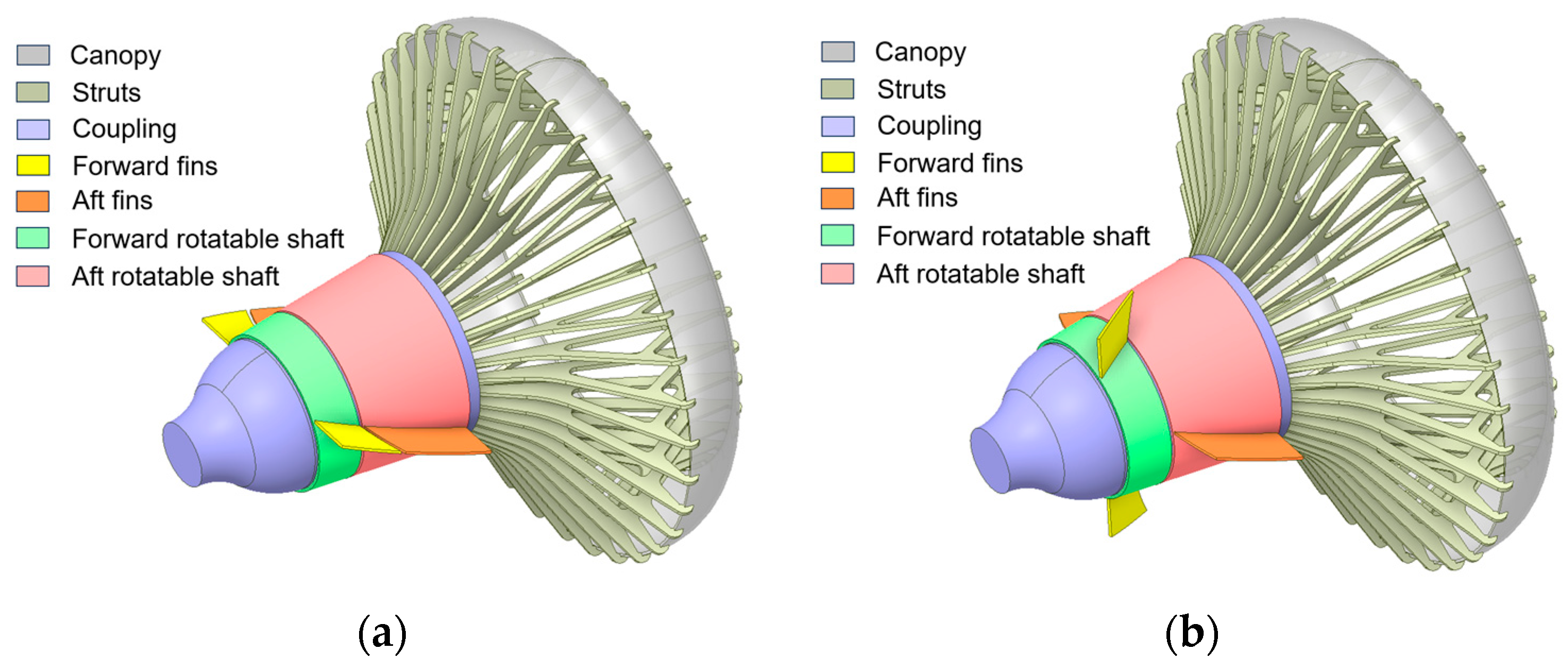
To enhance the aerodynamic stability of the drogue, two pairs of strake-type control fins are mounted on the outer surface of the conventional drogue shell, as shown in Figure 9. Each side consists of a single flat plate aligned along the shell and then axially split into a forward and an aft segment. These two segments are installed on independent coaxial rotating shafts, enabling differential deflection between the forward and aft fins and thereby generating controllable aerodynamic forces. The arrangement on the opposite side is a mirror image to maintain geometric and aerodynamic symmetry. It is assumed that the total mass of the drogue remains constant after the inclusion of the strake-fins, as their added weight is negligible compared with the overall drogue mass.

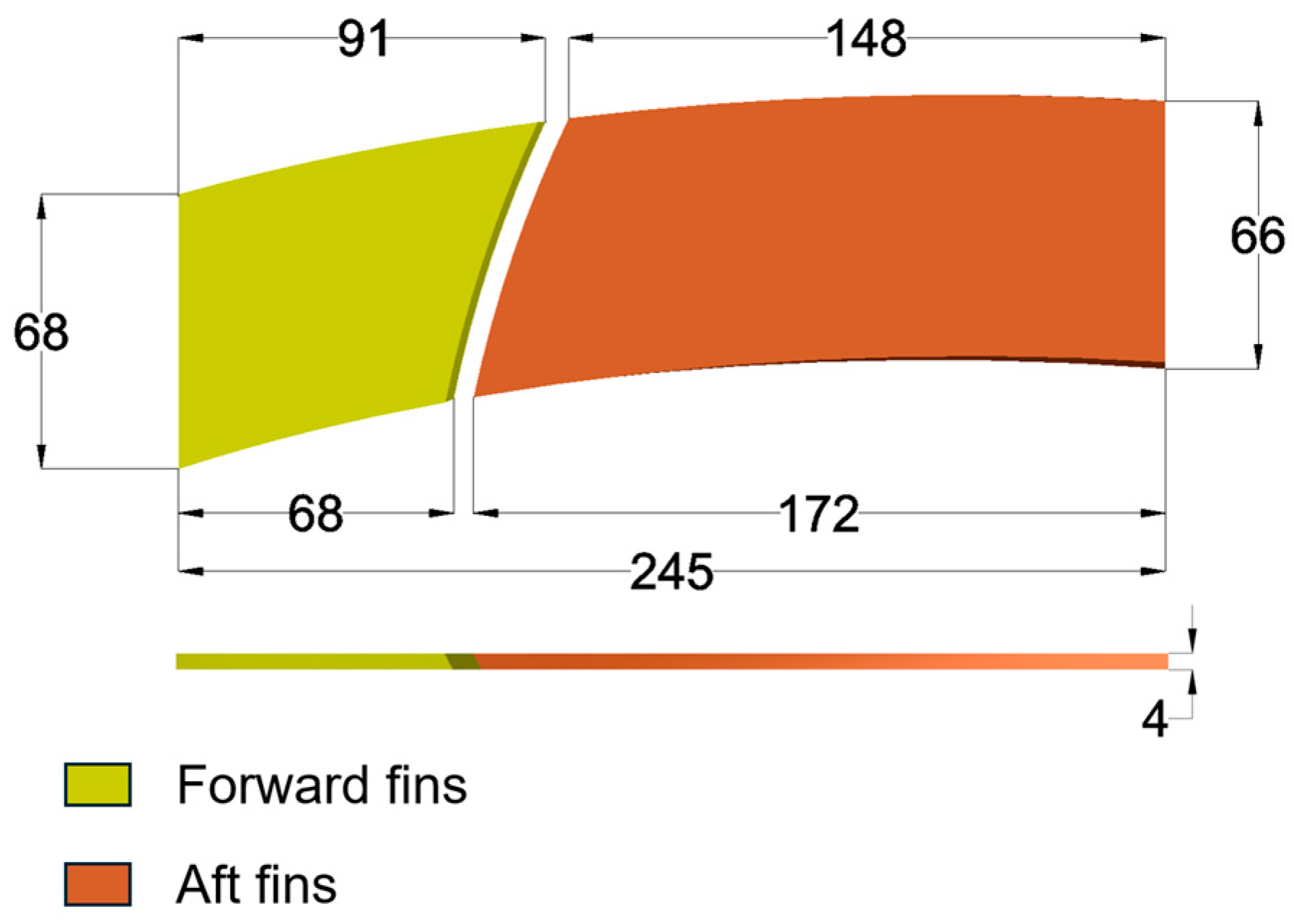
The term “strake-type” refers to slender, low-aspect-ratio aerodynamic surfaces aligned with the drogue shell. The fins adopt a rectangular–tapered planform, with their size determined by the available axial length of the drogue shell. To maximize control authority, the fins span nearly the full usable axial length of the drogue while remaining compatible with refueling pod retraction. The geometric configuration of the single-side strake-fin assembly is illustrated in Figure 10. Each single-side strake-fin assembly has a total axial length of 245 mm and a thickness of 4 mm. The forward fin has a root chord length of 68 mm and a span of 68 mm, while the aft fin has a root chord length of 172 mm and a span of 66 mm. These dimensions were obtained through CFD-based parametric studies to balance aerodynamic performance, flow quality, and structural integration.

The strake-type control fins generate lift, drag, and side forces, as well as the corresponding pitching and yawing moments acting on the drogue. By adjusting the deflection angles of the forward and aft fins, the magnitude and direction of these aerodynamic forces and moments can be effectively controlled, providing sufficient control authority to stabilize the drogue against various external disturbances. Importantly, the use of two axially distributed fin pairs rather than a single larger pair allows for greater control flexibility and finer aerodynamic modulation. By tuning the relative deflections of the forward and aft fins, the system can adjust not only the total magnitude of forces and moments but also their distribution along the drogue axis. This enhances the ability to regulate attitude precisely and improves the disturbance rejection capability under complex aerodynamic environments.

The functional principle is as follows:

1. Aft fins, located near the canopy rim, provide a longer effective moment arm and thus offer stronger control authority and faster dynamic response.

2. Forward fins, positioned near the mid-cone region, provide fine-tuning capability and enhance stability.

3. By adjusting the relative deflection angles of the forward and aft fins, the system can generate the required aerodynamic forces and moments to actively stabilize the drogue and suppress its oscillatory motion under disturbed flight conditions.

In addition to its active control capability, the strake-fin layout also enhances the drogue’s passive aerodynamic stability in quiescent flow by increasing restoring moments through its distributed fin arrangement.

3.2. Aerodynamic Data Analysis

CFD simulations were performed to establish an aerodynamic database for the drogue. An unstructured computational mesh containing approximately 2.1 million cells was employed. Local mesh refinement was applied around both the drogue surface and the strake-fin control surfaces to accurately resolve boundary-layer development, fin-induced vortical structures, and wake flow characteristics. Pressure far-field boundary conditions were imposed at the outer domain boundaries, and no-slip wall conditions were applied to all solid surfaces.

The resulting aerodynamic coefficients were organized into a multi-dimensional lookup table parameterized by angle of attack ($\mathsf{\alpha }$), sideslip angle ($\mathsf{\beta }$), and the relative deflection angle between the forward and aft fins ($\Delta \mathsf{\gamma }$). For each input triplet ($\mathsf{\alpha },\mathsf{\beta },\Delta \mathsf{\gamma }$), the lookup table returns the corresponding aerodynamic forces and moments of the drogue and fins for use in the dynamic simulation.

Because the drogue is specifically designed to operate within a defined flight speed range, its effective aerodynamic angles remain small under steady-state conditions. Therefore, the CFD sampling was limited to the range ($-6^{\circ }\le \mathsf{\alpha },\mathsf{\beta }\le 6^{\circ }$). Within this range, aerodynamic quantities during the simulation were obtained using trilinear interpolation between tabulated data points. For queries slightly outside the tabulated bounds, linear extrapolation was applied to ensure continuity while minimizing computational cost.

This small-angle assumption significantly reduces the computational effort required for database construction while remaining valid within the drogue’s operational envelope. The resulting database provides a high-fidelity and computationally efficient description of the drogue aerodynamics, enabling accurate force and moment prediction during dynamic simulations.

Figure 11 summarizes the dependence of lift on $\mathsf{\alpha }$, $\mathsf{\beta }$, and $\Delta \mathsf{\gamma }$. In Figure 11a, lift acting on the drogue body itself increases nearly linearly with $\mathsf{\alpha }$ in the range $0~6°$, whereas its sensitivity to $\mathsf{\beta }$ is weak, indicating that $\mathsf{\alpha }$ is the dominant factor. Figure 11b plots the lift coefficient generated by the strake-type fins as a function of $\Delta \mathsf{\gamma }$ for the four boundary cases. The curves exhibit a pronounced minimum near $\Delta \mathsf{\gamma }={180}^{\circ }$ and maxima near $\Delta \mathsf{\gamma }=0^{\circ }$ and $\Delta \mathsf{\gamma }={360}^{\circ }$, with approximate symmetry about $\Delta \mathsf{\gamma }={180}^{\circ }$. Increasing $\mathsf{\alpha }$ primarily shifts the entire curve upward, while varying $\mathsf{\beta }$ produces only minor changes.

Figure 12 summarizes the dependence of drag on $\alpha$, $\beta$, and $\Delta \mathsf{\gamma }$. As shown in Figure 12a, drag decreases gradually with increasing $\mathsf{\alpha }$ and $\mathsf{\beta }$; however, the overall reduction is less than 1%, indicating a relatively minor influence. Figure 12b plots the drag coefficient versus $\Delta \mathsf{\gamma }$ for the four boundary cases. The drag coefficient exhibits a periodic trend, first decreasing, then increasing, and finally decreasing again, with approximate symmetry about $\Delta \mathsf{\gamma }={180}^{\circ }$.

Figure 11b and Figure 12b illustrate the lift and drag coefficients of the strake-type fins as functions of the relative fin deflection angle ($\Delta \delta$), which is defined as the angular difference between the forward and aft strake fins. The coefficients are nondimensionalized using the drogue reference area ($S_d$) and the dynamic pressure ($q={\displaystyle \frac{1}{2}}\mathsf{\rho }{V}^2$). These figures explicitly show how the aerodynamic coefficients vary with the fin deflection angle, providing a clear representation of the lift and drag trends required for the control system design. Both ($C_L$) and ($C_D$) show near-symmetry about $\Delta \delta = 180°$, which reflects the geometric symmetry of the fin configuration. Increasing the angle of attack primarily shifts the entire $C_L$–$\Delta \delta$ and $C_D$–$\Delta \delta$ curves upward, while the sideslip angle introduces only minor deviations.

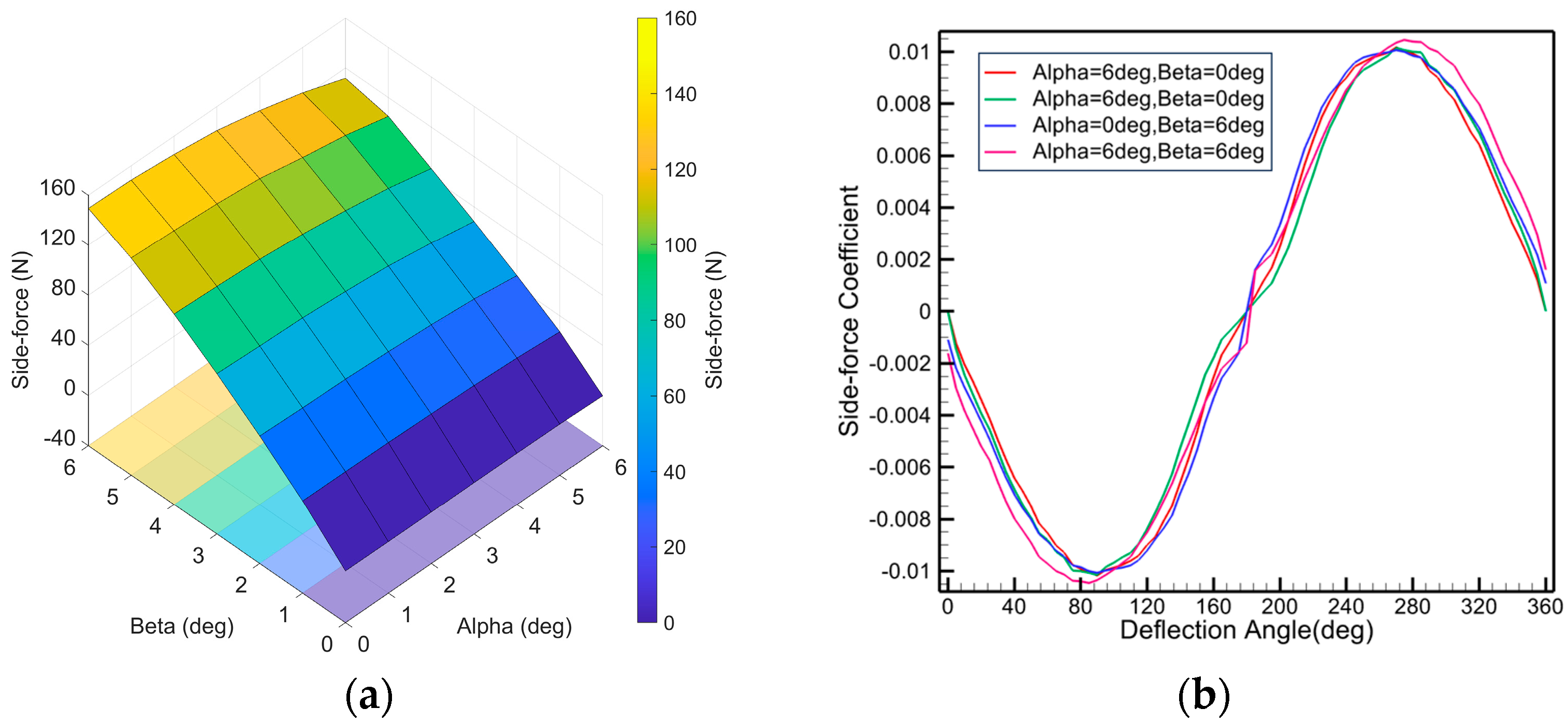
Figure 13 summarizes the dependence of side force on $\alpha$, $\beta$, and $\Delta \mathsf{\gamma }$. In Figure 13a, side force increases nearly linearly with $\mathsf{\beta }$ in the range $0~6°$, whereas its sensitivity to $\mathsf{\alpha }$ is weak, indicating that $\mathsf{\beta }$ is the dominant factor. Figure 13b shows that the lateral force coefficient varies approximately in a sinusoidal manner with the deflection angle from $0^{\circ }$ to ${360}^{\circ }$, reaching a negative peak near ${90}^{\circ }$, returning to zero around ${180}^{\circ }$, attaining a positive peak near ${270}^{\circ }$, and again approaching zero near ${360}^{\circ }$. This periodic trend highlights the geometric symmetry of the strake-fin configuration.

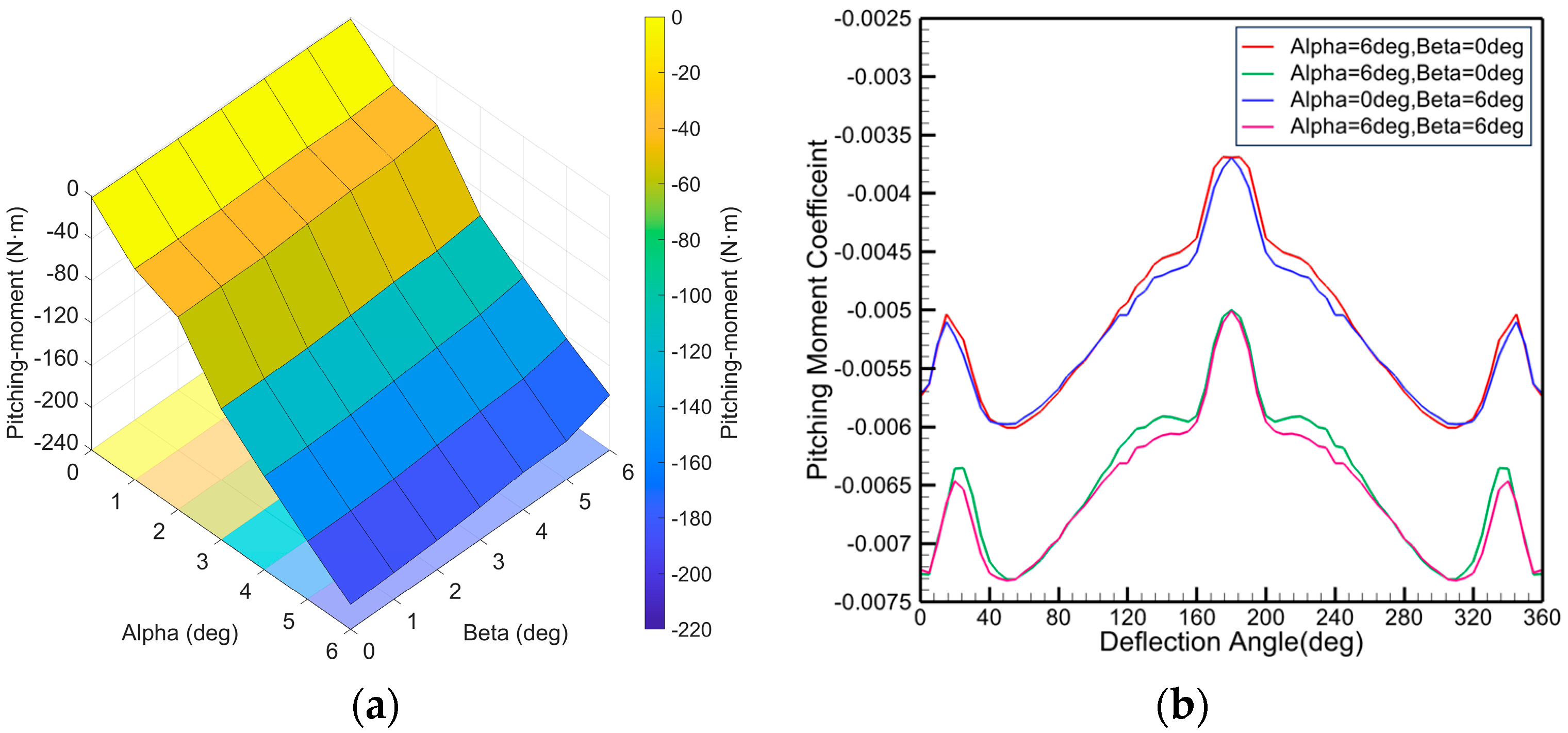
Figure 14 summarizes the dependence of pitching moment on $\alpha$, $\beta$, and $\Delta \mathsf{\gamma }$. In Figure 14a, pitching moment increases nearly linearly with $\mathsf{\alpha }$ in the range $0~6°$, whereas its sensitivity to $\mathsf{\beta }$ is weak, confirming that $\mathsf{\alpha }$ is the dominant factor. Figure 14b plots the pitching-moment coefficient versus $\Delta \mathsf{\gamma }$ for the four boundary cases. The curves exhibit a periodic distribution: a pronounced maximum occurs near $\Delta \mathsf{\gamma }={180}^{\circ }$, while local peaks appear near $\Delta \mathsf{\gamma }={25}^{\circ }$ and $\Delta \mathsf{\gamma }={335}^{\circ }$. The variation is approximately symmetric about $\Delta \mathsf{\gamma }={180}^{\circ }$. Increasing $\mathsf{\alpha }$ shifts the curves downward, thereby strengthening the nose-down moment, while the effect of $\mathsf{\beta }$ remains minor, producing only small amplitude changes.

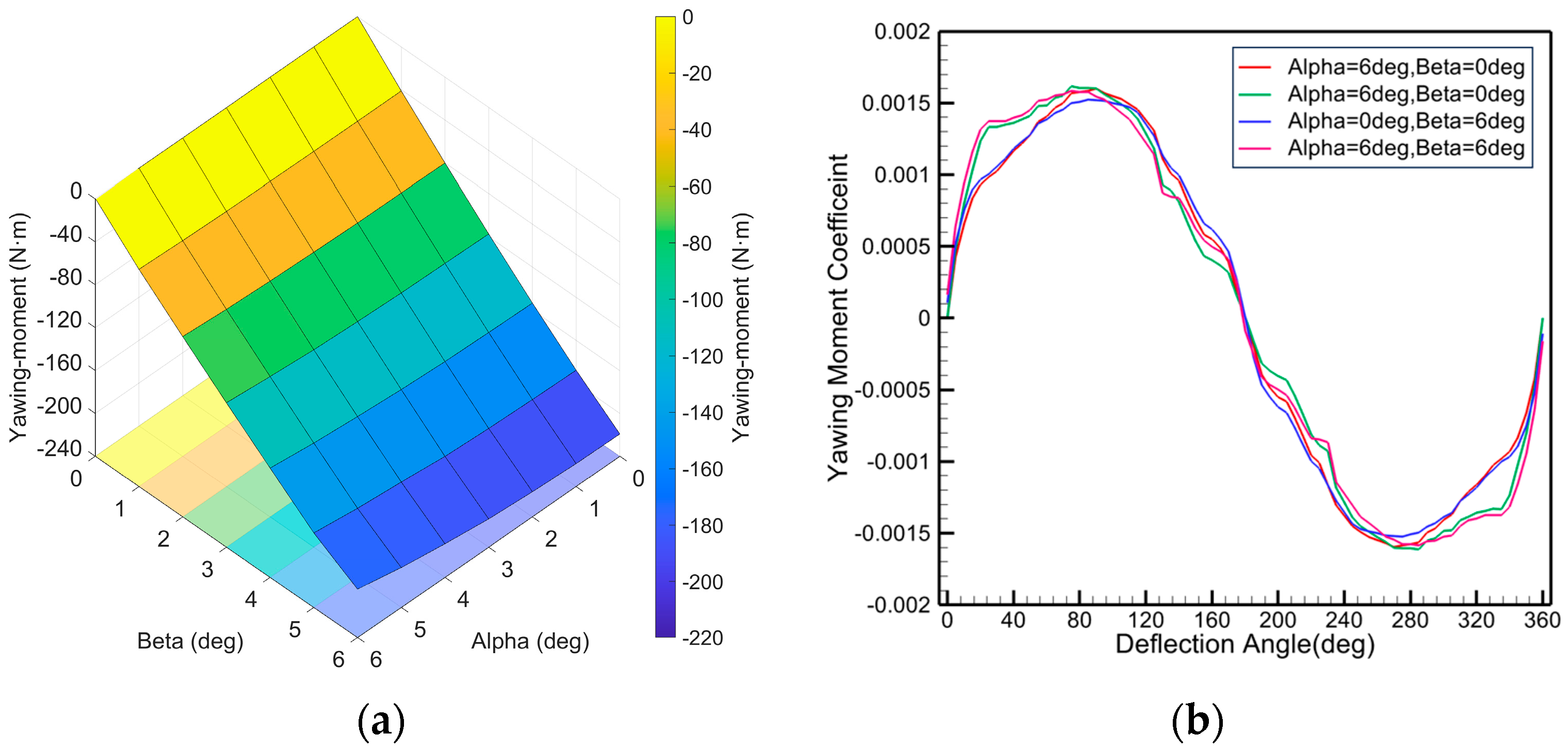
Figure 15 summarizes the dependence of yawing moment on $\alpha$, $\beta$, and $\Delta \mathsf{\gamma }$. In Figure 15a, yawing moment increases nearly linearly with $\mathsf{\beta }$ in the range $0~6°$, whereas its sensitivity to $\mathsf{\alpha }$ is weak, indicating that $\mathsf{\beta }$ is the dominant factor. Figure 15b shows that the yawing moment coefficient varies approximately in a sinusoidal manner with the deflection angle from $0^{\circ }$ to ${360}^{\circ }$, reaching a positive peak near ${90}^{\circ }$, returning to zero around ${180}^{\circ }$, attaining a negative peak near ${270}^{\circ }$, and again approaching zero near ${360}^{\circ }$.

3.3. Aerodynamic Modeling of the Stabilized Drogue

Based on the numerical simulation results, a simplified aerodynamic database for the drogue was constructed, from which an aerodynamic model of the stabilized drogue was derived. This model enables direct computation of the aerodynamic forces and moments acting on the drogue as functions of its attitude and the surrounding flow environment. During real-time simulation, the aerodynamic coefficients are obtained by interpolating this precomputed database according to the instantaneous flight conditions and fin deflection states. By prescribing the deflection angle of the fins, the corresponding aerodynamic control forces and moments can be efficiently evaluated without performing CFD calculations on the fly, and these loads are then applied to the drogue dynamic model.

The aerodynamic model is expressed in Equation (29), where $F_{dro}$ and $M_{dro}$ denote the aerodynamic forces and moments acting on the drogue, respectively; $q$ is the dynamic pressure; $L_w^r$ is the transformation matrix from the wind-axis system to the body-axis system; $C_0$ represents the physical parameters corresponding to the initial state of the drogue; $C_{\mathsf{\alpha }}$ and $C_{\mathsf{\beta }}$ are the aerodynamic derivatives of the drogue with respect to angle of attack $\mathsf{\alpha }$ and sideslip angle $\mathsf{\beta }$; and $C_{\mathsf{\theta }}$ is the coefficient corresponding to the aerodynamic contribution generated by fin deflection $\mathsf{\theta }$. Since the dependence of $C_{\mathsf{\theta }}$ on $\mathsf{\alpha }$, $\mathsf{\beta }$, and $\mathsf{\theta }$ exhibits weak linearity, three-dimensional table lookup interpolation is required to obtain accurate values.

$$\begin{array}{c}\left[\begin{array}{c}{F}_{dro}\\ M_{dro}\end{array}\right]=q{L}_w^r\left(C_0+\left[\begin{array}{cc}{C}_{\alpha }& C_{\beta }\end{array}\right]\left[\begin{array}{c}\alpha \\ \beta \end{array}\right]\right)+C_{\theta }\end{array}$$

(29)

The corresponding aerodynamic parameters of the stabilized drogue are provided in

Table 3. Baseline aerodynamic parameters of the stabilized drogue.

Parameter	Value
$C_{d0}$	0.3695
$C_{l0}$	0
$C_{c0}$	0
$C_{n0}$	0
$C_{m0}$	0

,

Table 4. Aerodynamic parameters of the stabilized drogue with respect to angle of attack.

Parameter	Value
$C_{d\alpha }$	0
$C_{l\alpha }$	0.00226
$C_{c\alpha }$	0
$C_{n\alpha }$	0
$C_{m\alpha }$	−0.00411

and

Table 5. Aerodynamic parameters of the stabilized drogue with respect to sideslip angle.

Parameter	Value
$C_{d\beta }$	0
$C_{l\beta }$	0
$C_{c\beta }$	−0.00226
$C_{n\beta }$	−0.00411
$C_{m\beta }$	0

.

3.4. Design of LQR Control System

An LQR-based control strategy is employed to actively regulate the aerodynamic forces acting on the stabilized drogue by adjusting the deflection angles of the forward and aft strake fins through servo actuators. The objective of the controller is to minimize the drogue’s position and attitude deviations caused by external disturbances—such as tanker wake, receiver bow wave, and atmospheric turbulence—thereby maintaining stable relative positioning between the drogue and the receiver probe.

The Linear Quadratic Regulator (LQR) is selected because it provides an optimal state-feedback control law that minimizes a quadratic cost function balancing system deviation and control effort. In real time, the drogue’s position, velocity, attitude, and angular rate are continuously fed back into the controller. Based on this state information, the LQR controller computes the optimal fin deflections required to counteract disturbance-induced motion. These commands are then transmitted to the fin actuators, which adjust the forward and aft fins’ deflection angles to generate corrective aerodynamic forces and moments. This closed-loop control mechanism ensures rapid disturbance rejection, suppresses drogue oscillations, and maintains the drogue within the required operational envelope for successful aerial refueling.

Compared with conventional PID control, which requires manual gain tuning and offers limited stability guarantees in coupled multivariable systems, the LQR formulation ensures global stability and smooth control allocation through the algebraic Riccati solution. Although Model Predictive Control (MPC) could handle constraints explicitly, its computational cost limits real-time applicability. The LQR approach therefore represents an effective balance between theoretical optimality, numerical efficiency, and practical implementation feasibility for active drogue stabilization.

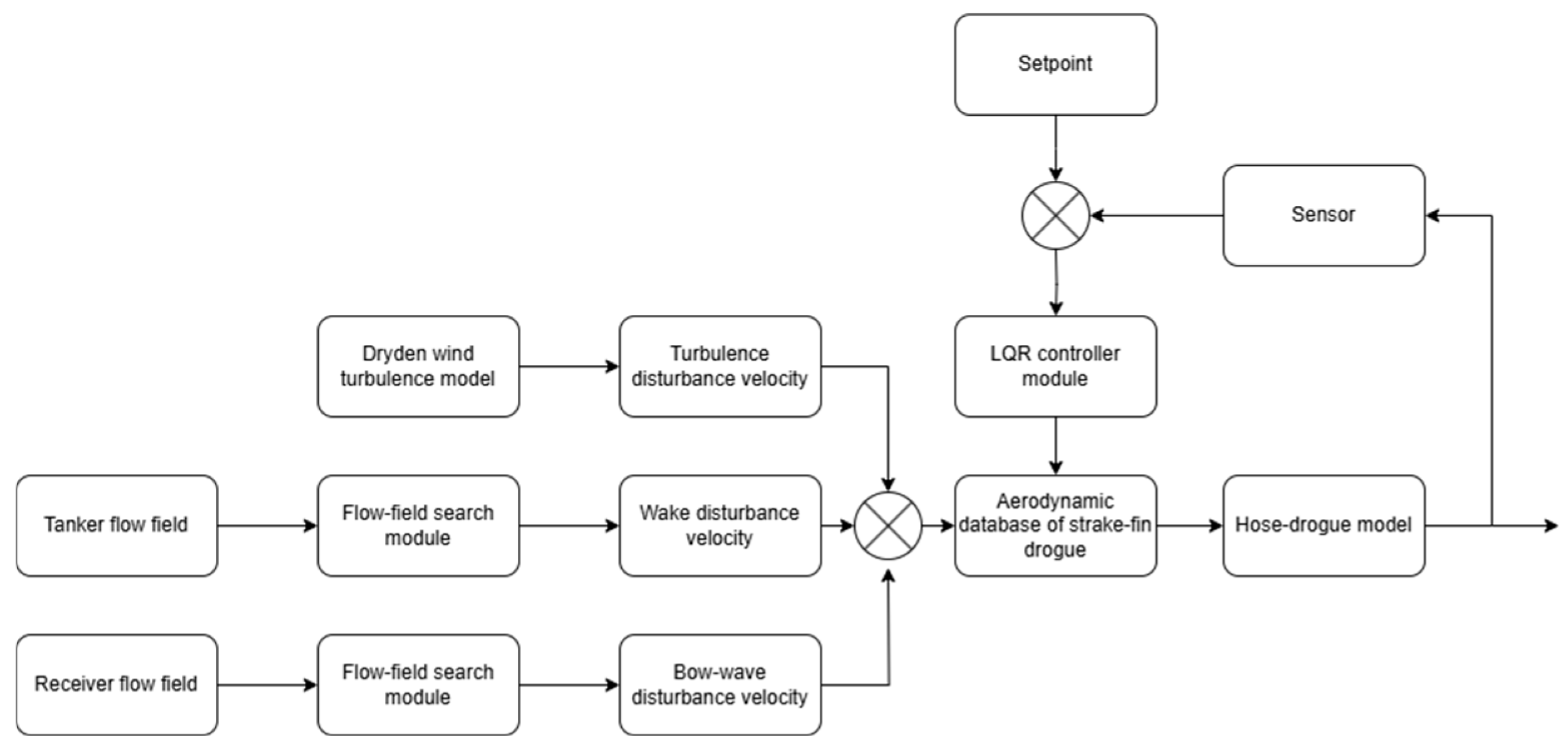
The simulation workflow of the LQR control system is illustrated in Figure 16. The model integrates aerodynamic and disturbance modules, including the tanker wake, receiver bow-wave, and atmospheric turbulence, with the LQR controller and drogue actuator dynamics.

The feedback signals required by the LQR controller include the drogue’s position, attitude, and angular rate. These quantities are assumed to be measured by an onboard Inertial Measurement Unit (IMU) and a Differential GPS (DGPS) system or a vision-based photogrammetric method. The IMU provides angular velocity and attitude information, while DGPS or optical tracking supplies the drogue’s relative position with respect to the tanker. For control design and simulation purposes, the sensor data are modeled as ideal (noise-free and delay-free) measurements, enabling assessment of the controller’s intrinsic performance.

The state vector in the LQR controller is defined as the deviation of the drogue’s motion variables from their equilibrium values,

$$X=\left[\begin{array}{c}y\\ z\\ v\\ w\\ \alpha \\ \beta \\ {\omega }_z\\ {\omega }_y\end{array}\right]-\left[\begin{array}{c}\overline{y}\\ \overline{z}\\ 0\\ 0\\ {\alpha }_0\\ {\beta }_0\\ 0\\ 0\end{array}\right]$$

(30)

Here, $y$ and $z$ represent lateral and vertical positions, $v$, $w$ denote velocity components, $\mathsf{\alpha }$, $\mathsf{\beta }$ are aerodynamic angles, and ${\mathsf{\omega }}_z$, ${\mathsf{\omega }}_y$ are angular rates. The overbarred quantities denote the desired target values corresponding to the commanded drogue position and attitude. The control input vector is defined as $u={\left[{\mathsf{\delta }}_f, {\mathsf{\delta }}_a\right]}^T$, where ${\mathsf{\delta }}_f$ and ${\mathsf{\delta }}_a$ are the forward and aft fin deflections.

The weighting matrices in the LQR controller are designed as follows:

$$Q=\left[\begin{array}{cccc}1.0\times {10}^{10}{I}_{2\times 2}& 0_{2\times 2}& 0_{2\times 2}& 0_{2\times 2}\\ 0_{2\times 2}& 1.0\times {10}^{-4}{I}_{2\times 2}& 0_{2\times 2}& 0_{2\times 2}\\ 0_{2\times 2}& 0_{2\times 2}& 1.0\times {10}^{-4}{I}_{2\times 2}& 0_{2\times 2}\\ 0_{2\times 2}& 0_{2\times 2}& 0_{2\times 2}& 1.0\times {10}^{-4}{I}_{2\times 2}\end{array}\right]$$

(31)

$$R=0.0612\times 10^7{I}_{2\times 2}$$

(32)

Here, the first block in Q corresponds to the drogue’s lateral and vertical position errors, which dominate the control objective. The remaining blocks represent the velocities, angles of attack and sideslip, and angular velocities, which receive significantly smaller weights. The relatively large ratio between Q and R ensures precise position tracking while limiting fin deflection amplitude and maintaining smooth actuator dynamics.

The LQR controller operates at an update rate of 100 Hz ($\Delta t=0.01 \mathrm{s}$). This update frequency enables real-time correction of drogue motion under aerodynamic disturbances.

The forward and aft strake fins are actuated by independent rotary motors that allow continuous 360° rotation about the drogue surface; thus, no mechanical angle saturation is applied. The LQR controller outputs the desired relative deflection angle ($\Delta \mathsf{\delta }$) between the two fin pairs, which can vary freely within 0–360°. To ensure smooth and realistic actuation, a symmetric rate limiter is introduced, constraining the maximum angular velocity to $\left({\mathsf{\omega }}_{max}=400 \mathrm{deg}/\mathrm{s}\right)$. This implementation maintains control smoothness and avoids unrealistic high-frequency responses while preserving full-range maneuverability of the strake fins.

The LQR controller operates in a pure feedback mode, where the control inputs are derived from real-time state deviations of the drogue. No feedforward term is introduced in the present framework; however, future extensions may include disturbance-prediction-based feedforward control to further improve the system’s transient performance.

3.5. Control Performance Evaluation of the Stabilized Drogue Under Atmospheric Turbulence and Bow-Wave Disturbances

Based on the preceding sections, a dynamic simulation platform for the hose–drogue system was developed. The platform integrates the hose–drogue model, LQR controller, disturbance modules, and an aerodynamic module, and was employed to evaluate the performance of the strake-fin-stabilized drogue in mitigating the effects of atmospheric turbulence and receiver bow-wave disturbances.

To investigate the effect of the receiver bow wave during the docking phase and to evaluate the performance of the strake-fin-stabilized drogue under realistic approach conditions, a dynamic simulation procedure was established. The simulation couples the tanker wake field, the receiver-induced bow-wave disturbance, and the hose–drogue dynamic model. The main computational steps are summarized as follows:

1. Flow field preparation: The steady flow fields of both the tanker and the receiver are computed using CFD methods.

2. Baseline configuration: Using the neighboring-cell search algorithm (Section 2.4), the tanker wake field is mapped onto the hose–drogue model to determine the initial equilibrium position of the system in the tanker wake.

3. Receiver approach modeling: At the start of the simulation ($T=T_0$), the receiver probe is located at position $A\left(x_{rp},y_{rp},z_{rp}\right)$. The drogue’s initial relative position is defined by $K(\Delta x_d,\Delta y_d,\Delta z_d$). As the receiver approaches, its position evolves according to a prescribed trajectory $S\left(i\right)$, driving a time-varying bow-wave disturbance field.

4. Force calculation: The local aerodynamic forces on each hose node and the drogue are obtained by mapping their instantaneous positions into the receiver flow field using the neighboring-cell algorithm.

5. Dynamic update: These disturbance forces are incorporated into the hose–drogue dynamic equations within the tanker wake, and the new node and drogue positions are solved at each time step.

6. Iteration: Steps 4 and 5 are repeated as the receiver moves closer according to $A + K + S\left(i\right)$, resulting in the continuous evolution of the drogue’s displacement under the combined influence of the tanker wake and receiver bow wave.

The simulation parameters used in this section are summarized in

Table 6. Parameters of the active-stabilization simulation.

Parameter		Value
Hose	Total length/m	20
	Linear density (empty hose)/(kg· m−1) Inner diameter/m Outer diameter/m	2.38 0.05 0.067
	Elastic modulus/Pa	13,800,000
Drogue	Mass/kg	29.5
	Type/m2	0.25
Freestream	Altitude/m2	6000
	Mach Number	0.5223

to ensure clarity and reproducibility. This configuration reflects a typical medium-speed flight regime used to evaluate the dynamic response and control performance of the proposed strake-fin drogue system. The simulations assumed that atmospheric conditions, as well as the drogue’s position and attitude, were measured with high accuracy to provide a reliable assessment of control effectiveness.

It is worth noting that the CFD flow fields are precomputed and stored as aerodynamic databases, and only neighbor-cell search and flow-field interpolation are performed during dynamic simulations. This approach minimizes computational overhead while preserving the key aerodynamic interactions. For a typical 7 s simulation with 40 hose nodes, the total CPU time is approximately 1 h on a 24-core workstation, which is orders of magnitude more efficient than fully coupled CFD–FSI methods.

To quantitatively assess drogue stabilization performance, the peak displacement amplitude in both the vertical and lateral directions was used as the primary evaluation metric. The suppression ratio was defined as the relative reduction in the maximum displacement amplitude after control activation.

To comprehensively evaluate the proposed stabilization system, the simulations were carried out under four disturbance scenarios, including tanker wake, receiver bow wave, atmospheric turbulence, and their combined effects.

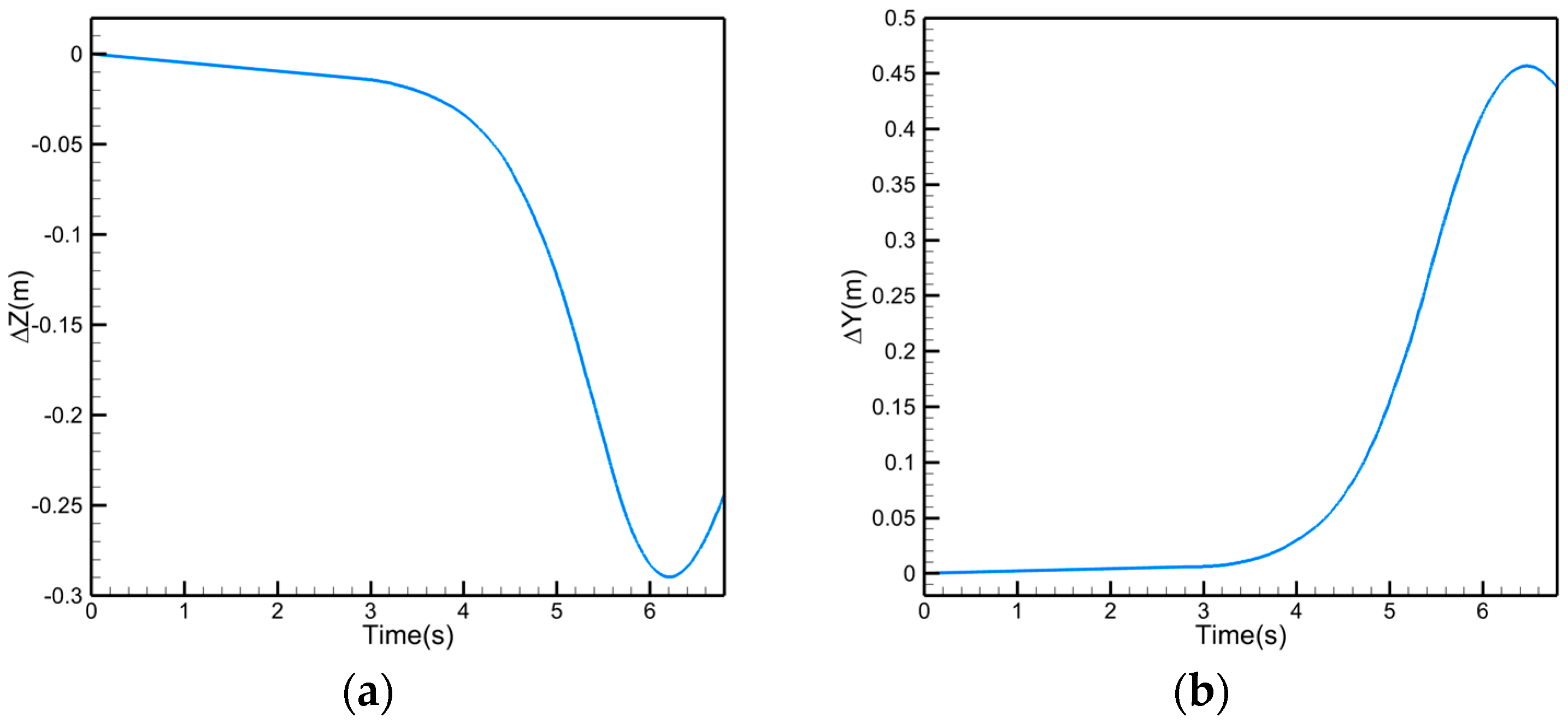
The simulation results are presented in the following figures to illustrate the stabilized drogue response under different disturbance environments. Figure 17 shows the vertical and lateral displacements of the drogue under the combined influence of tanker wake and receiver bow-wave disturbances. At $t=0 \mathrm{s}$, the receiver aircraft begins to approach the drogue from an initial distance of $10 \mathrm{m}$ at a velocity of $1.5 \mathrm{m}/\mathrm{s}$. As the probe moves closer, the airflow around the receiver nose pushes the drogue away, causing it to drift upward and outward (with the positive $z$-axis directed downward and the positive $y$-axis directed to the right). This shift is attributed to the pressure rise and flow acceleration around the receiver nose, which modifies the local velocity field near the drogue.

Unlike the steady superposed flow field applied in Section 2.7, this simulation resolves the time-accurate evolution of drogue displacement during the moving receiver’s approach. The results indicate that the bow wave effect induces a gradual but significant displacement, with the drogue drifting by approximately 0.3 m vertically and 0.45 m laterally at the end of the approach. This highlights the directional and cumulative nature of bow-wave disturbances, which can substantially degrade docking accuracy if not compensated for by active control mechanism.

Figure 18 illustrates the time histories of drogue displacement under severe atmospheric turbulence, both with and without active control. Without control, turbulence induces oscillation amplitudes exceeding $0.4$ m in the vertical direction and $0.5$ m laterally, which are sufficient to push the drogue outside the acceptable capture envelope. With the proposed LQR-based control strategy, the oscillation amplitudes are effectively suppressed to below $0.1$ m, demonstrating a significant enhancement in disturbance resistance. This result confirms that atmospheric turbulence plays a dominant role in destabilizing the drogue, and effective active stabilization is crucial to ensure successful docking under realistic operational conditions.

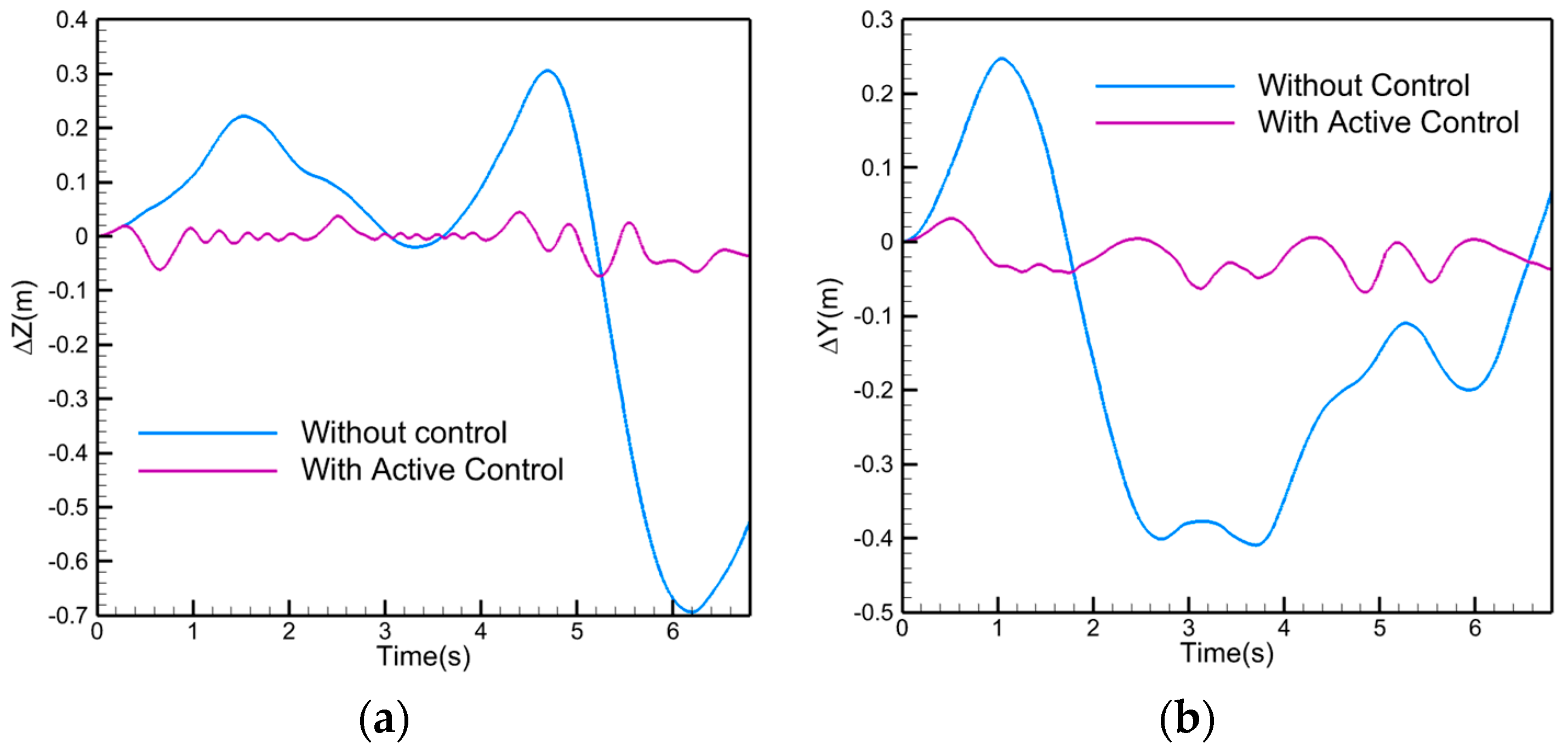
To evaluate the performance of the stabilization system under the most adverse operational conditions, Figure 19 illustrates the drogue response when subjected simultaneously to tanker wake, receiver bow wave, and severe atmospheric turbulence. Without active control, the drogue exhibits large-amplitude oscillations, with maximum deviations reaching approximately $0.7 \mathrm{m}$ in the vertical direction and $0.4 \mathrm{m}$ in the lateral direction, indicating a high level of instability during docking. When the LQR-based active control system is activated, the drogue exhibits only small-amplitude oscillations, with deviations from the reference position remaining within $0.1 \mathrm{m}$. This corresponds to an 80% reduction in peak displacement amplitude relative to the uncontrolled case, representing the decrease in the maximum observed deviations before and after control activation.

The stabilized drogue maintains its positional deviation within ±0.1 m under all combined disturbance conditions. This tolerance is consistent with the NASA Autonomous Aerial Refueling Demonstration (AARD) capture region criterion [31], which defines a cylindrical capture radius ($R_c$) around the drogue axis as the spatial envelope for successful docking. When the receiver probe remains within this radius, a 90% docking success rate can be achieved with minimal lateral and vertical velocities, whereas motion beyond the miss distance ($X_{\mathrm{MISS}}$) is classified as failed capture.

As shown in Figure 20, the present study adopts a capture radius of ($R_c=0.3 \mathrm{m}$) for the actively stabilized drogue, corresponding to the effective engagement envelope of the refueling system. The simulated positional deviations remain well within this limit, confirming compliance with established safety tolerances for probe–drogue docking.

The significance of this displacement suppression is twofold. First, reducing drogue oscillation amplitudes by more than $80\%$ ensures that the drogue remains inside the capture envelope during docking, directly improving engagement reliability. Second, the reduction in positional deviations minimizes the required corrective maneuvers by the receiver, improving operational safety margins and tolerance to external disturbances.

Therefore, the proposed active stabilization strategy not only suppresses drogue oscillations by more than 80%, but also ensures safe and reliable aerial refueling operations under complex disturbance environments.

4. Conclusions

This study presented a comprehensive dynamic modeling and control framework for an actively stabilized hose–drogue aerial refueling system. The hose was discretized into rigid segments, and its aerodynamic characteristics were estimated using Fluid-Dynamic Drag empirical correlations, while the drogue aerodynamics were obtained from high-fidelity CFD simulations. A neighboring-cell search algorithm was used to efficiently map hose–drogue elements onto the CFD flow field, enabling accurate aerodynamic load prediction while maintaining computational efficiency.

An innovative drogue configuration was designed by equipping two pairs of strake-type control fins in the forward and aft sections, each mounted on independent rotational shafts. By modulating the relative deflection angles of these fins through an LQR-based control strategy, the system effectively suppressed drogue oscillations, maintained positional stability, and preserved the desired attitude.

The proposed model was validated against both published numerical results and NASA flight-test data, successfully reproducing steady-state drogue positions, sinkage trends, and bow-wave effects reported in the literature. This agreement confirms the accuracy and credibility of the developed modeling framework in capturing the complex aerodynamic interactions of the hose–drogue system.

Under combined disturbances from tanker wake, receiver bow wave, and severe atmospheric turbulence, the uncontrolled drogue exhibited vertical and lateral displacements of approximately 0.7 m and 0.4 m, respectively. With the proposed active stabilization system, these deviations were reduced to within 0.1 m, corresponding to more than 80% reduction in oscillation amplitude. Furthermore, the stabilized drogue trajectories were evaluated against the NASA AARD capture criteria, confirming that the drogue remained well within the operational docking envelope, thereby satisfying the positional accuracy requirements for successful probe–drogue engagement. This enhanced stability reduces the probability of failed docking attempts, minimizes probe–drogue misalignment and impact risks, and ultimately improves the operational safety and success rate of aerial refueling missions. This robust behavior across diverse disturbance conditions highlights the stability, reliability, and practical applicability of the proposed aerodynamic modeling and control framework, providing a solid foundation for extending the approach to more complex aerial refueling scenarios.

Although the LQR controller demonstrated effective stabilization under nominal operating conditions, its sensitivity to parameter uncertainties has not yet been systematically evaluated. Variations in aerodynamic coefficients, hose mass distribution, or actuator characteristics may influence the control performance. This limitation will be addressed in future work through robustness and sensitivity analyses, with the goal of enhancing control adaptability across a broader operational envelope.

It should also be noted that this study focused on the pre-contact phase, during which the hose was modeled as empty (non-fuel-filled), reflecting the typical operational configuration prior to probe engagement. Extending the modeling and control framework to include post-contact and fuel-filled conditions will be an important future research direction.

Furthermore, although research on passive stabilization methods for hose–drogue refueling systems remains limited, the demonstrated performance of the proposed active stabilization strategy indicates a significant improvement in positional control and expected docking reliability compared with passive approaches. Future work will include direct performance comparisons between active and passive stabilization systems.

The current analysis assumes nominal operating conditions, fully functional actuation, and structural integrity. Potential failure modes, including fin malfunction, actuator faults, or hose rupture, are not considered but will be explored in subsequent studies to enhance the fault tolerance and operational safety of the system.

In summary, this work establishes a validated dynamic modeling and control framework that significantly enhances the disturbance resistance of hose–drogue refueling systems. The proposed strake-fin active stabilization approach provides a practical and efficient solution for improving positional accuracy, docking success rate, and overall mission robustness. Future research will focus on extending the methodology to dynamic position control during hose deployment and retrieval, integrating robust and fault-tolerant control strategies, and validating performance through hardware-in-the-loop or flight tests under realistic mission conditions.