SHM for Complex Composite Aerospace Structures: A Case Study on Engine Fan Blades
Abstract
1. Introduction
2. Case Study
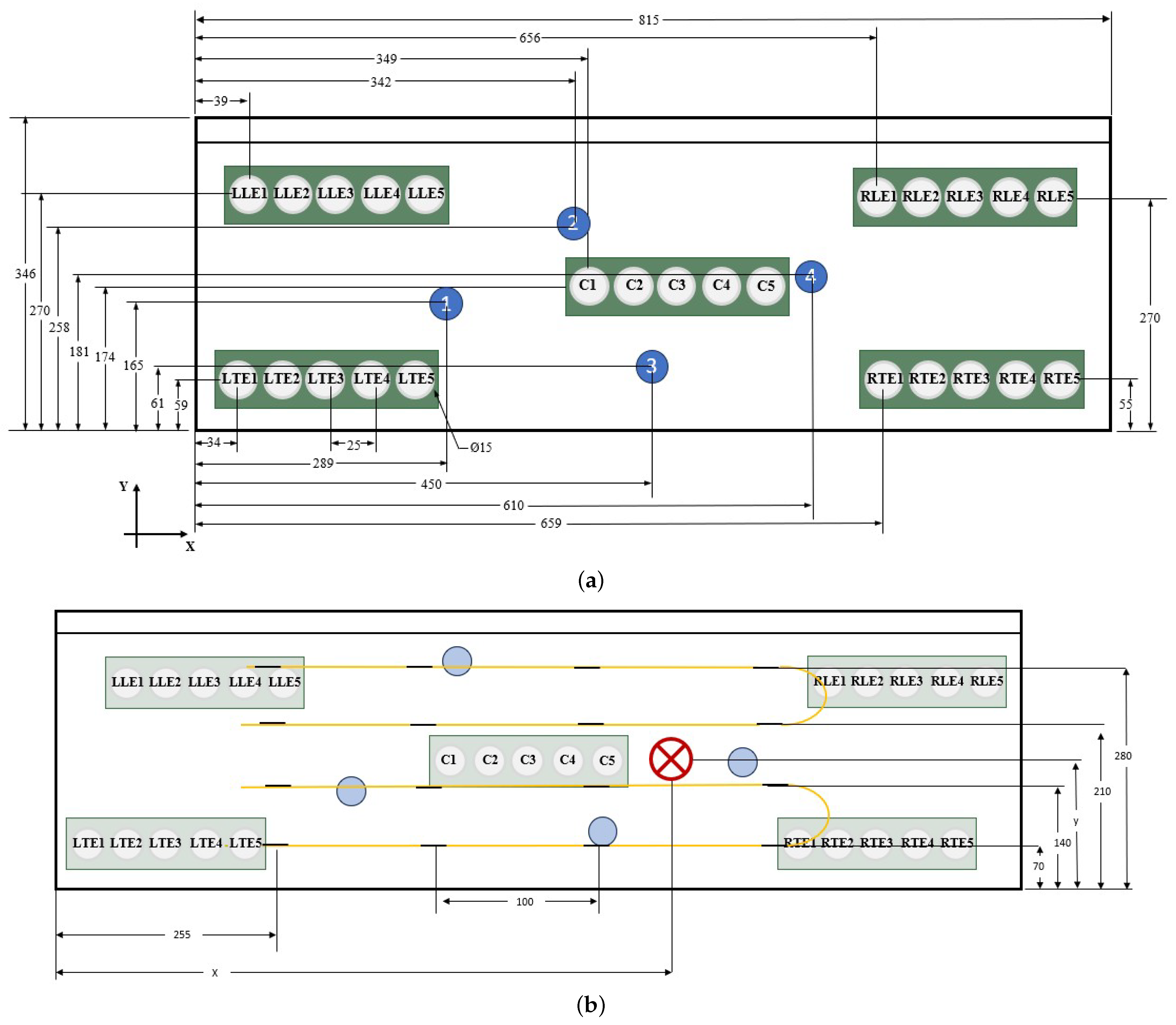
2.1. FOD Panel Definition
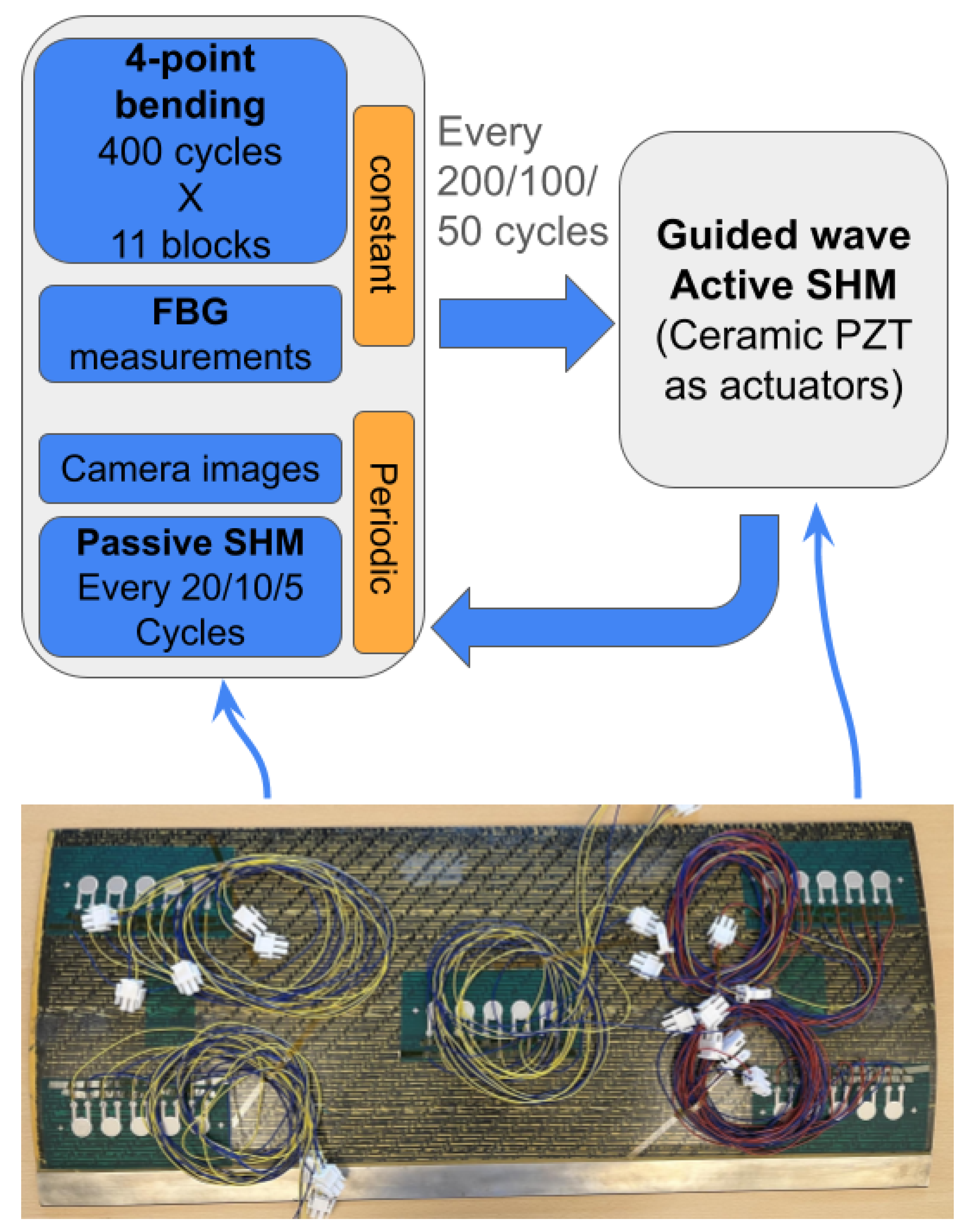
2.2. Experimental Campaign
3. Results
3.1. Failure Analysis by Visual Inspection
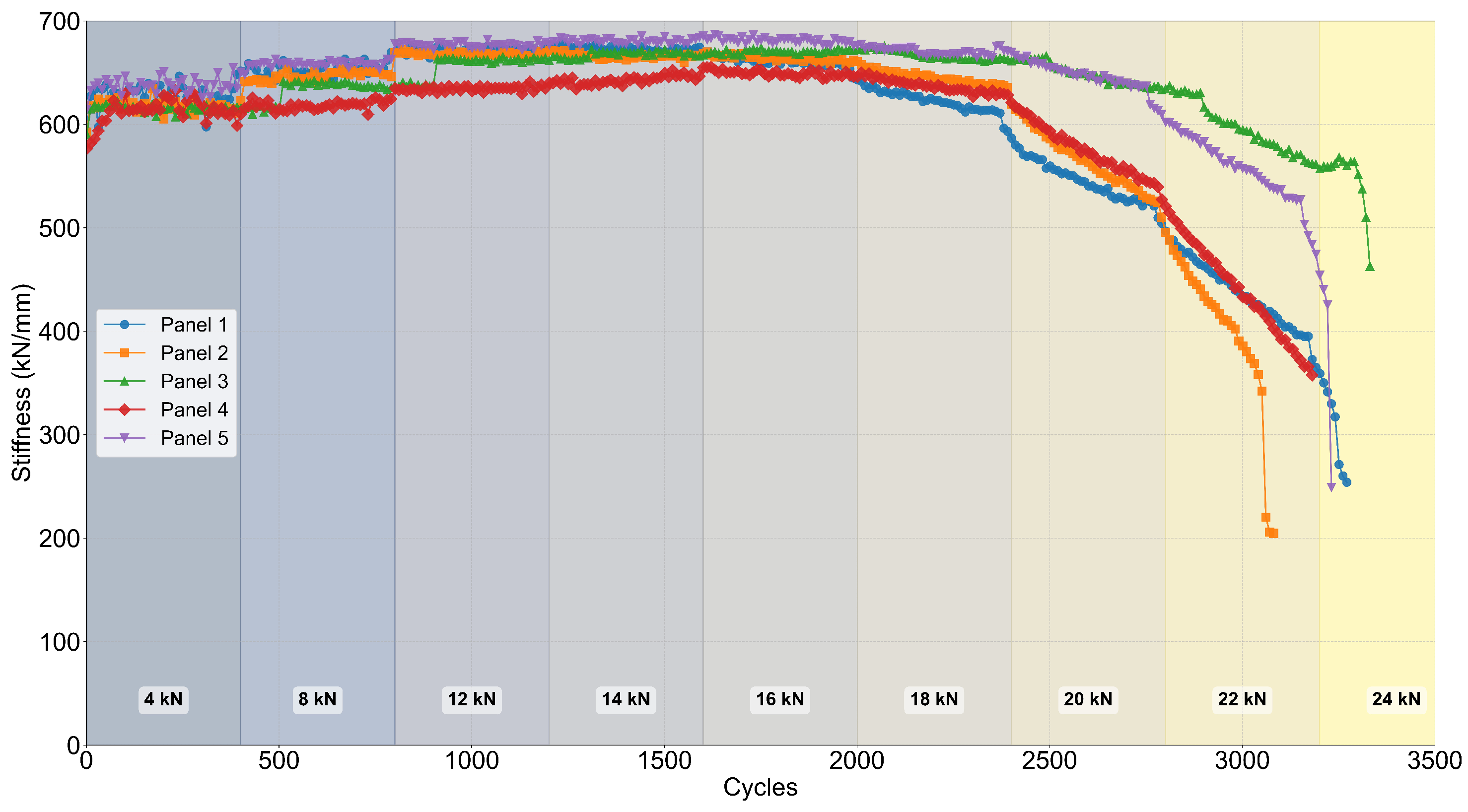
3.2. Hydraulic Test Machine Data
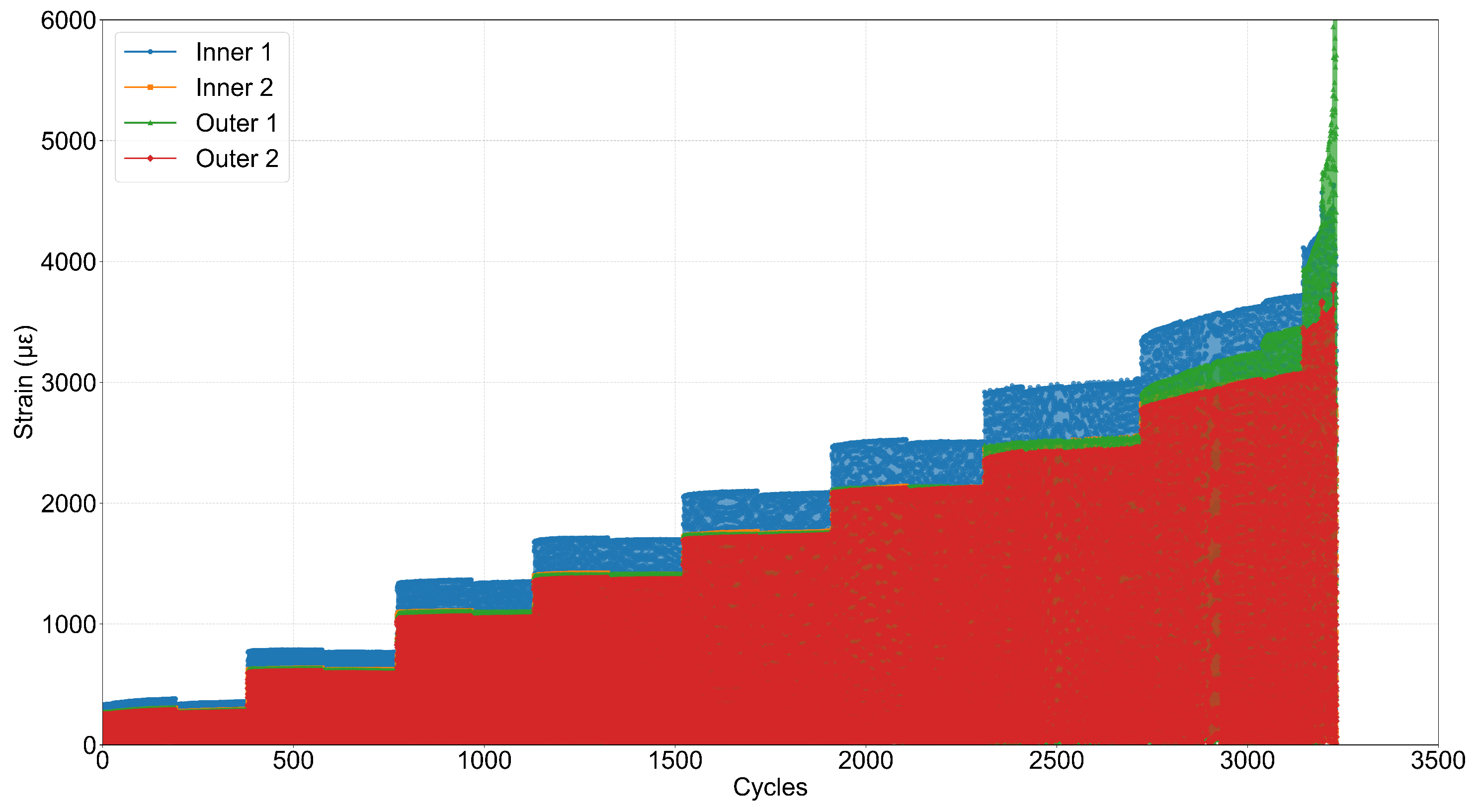
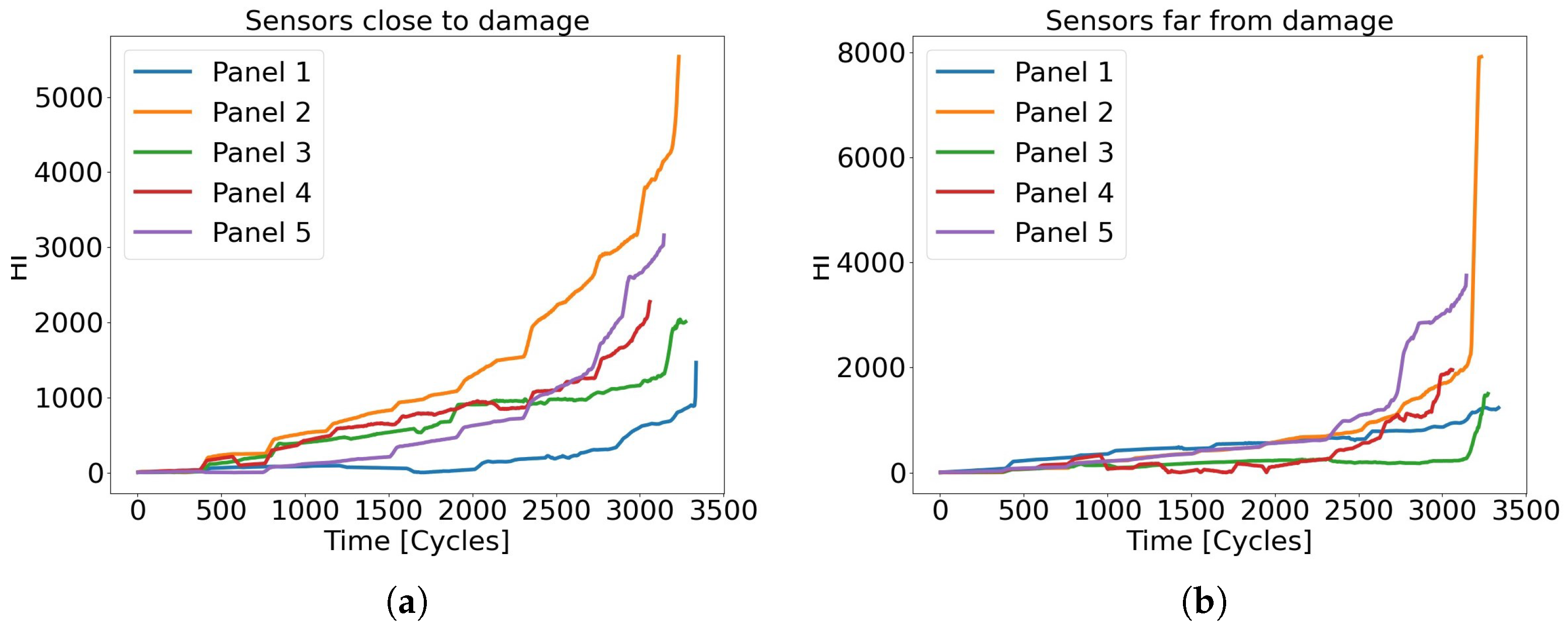
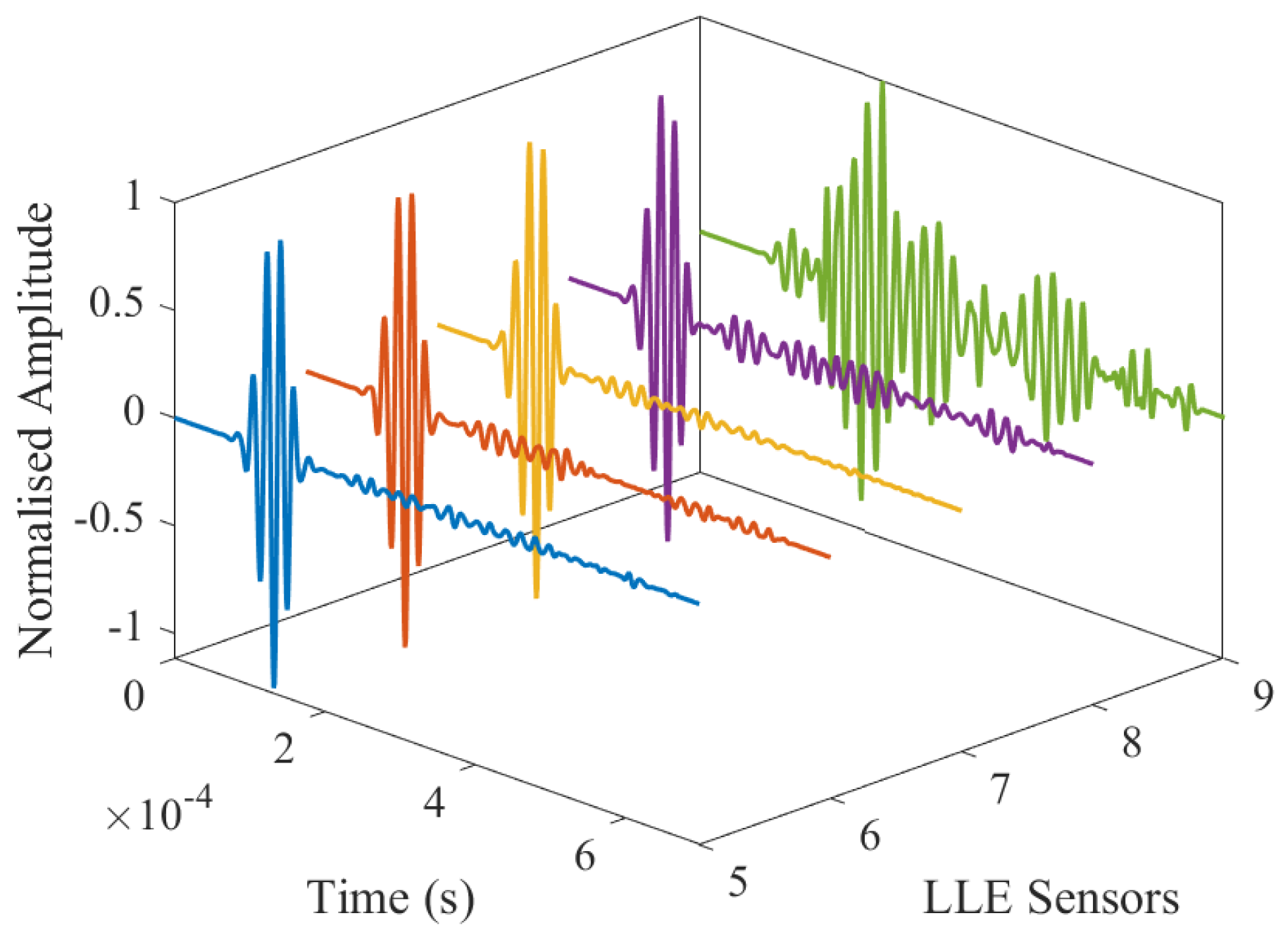
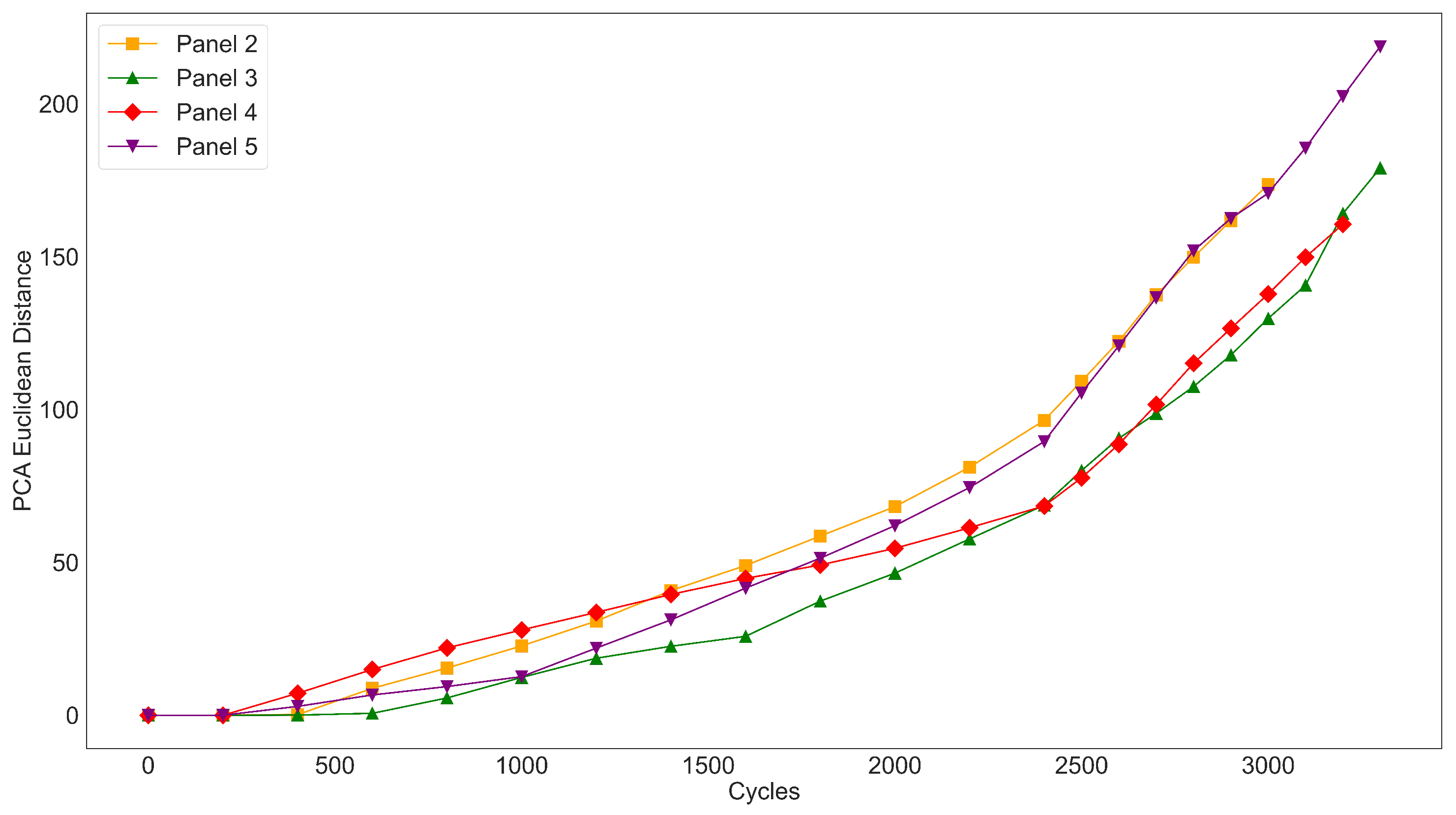
3.3. FBG Data
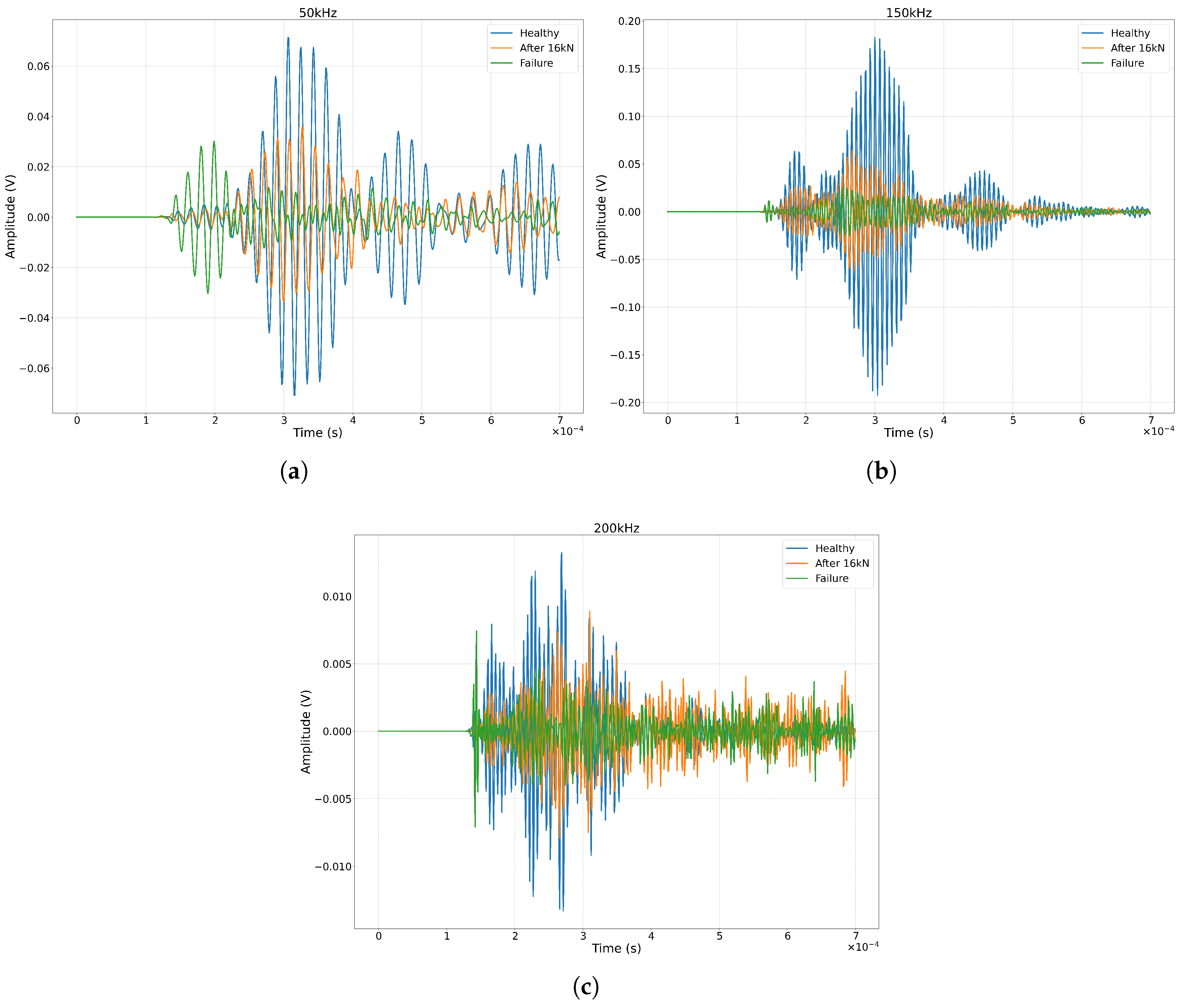
3.4. PZT Data
3.5. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kessler, S.S.; Spearing, S.M. Design of a piezoelectric-based structural health monitoring system for damage detection in composite materials. In Proceedings of the SPIE’s 9th Annual International Symposium on Smart Structures and Materials, San Diego, CA, USA, 17–21 May 2002; Volume 4701, pp. 86–96. [Google Scholar] [CrossRef]
- Cawley, P. Structural health monitoring: Closing the gap between research and industrial deployment. Struct. Health-Monit. Int. J. 2018, 17, 1225–1244. [Google Scholar] [CrossRef]
- Lima, R.A.A.; Perrone, R.; Carboni, M.; Bernasconi, A. Experimental analysis of mode I crack propagation in adhesively bonded joints by optical backscatter reflectometry and comparison with digital image correlation. Theor. Appl. Fract. Mech. 2021, 116, 103117. [Google Scholar] [CrossRef]
- Khodaei, Z.S.; Aliabadi, M.H. A Multi-Level Decision Fusion Strategy for Condition Based Maintenance of Composite Structures. Materials 2016, 9, 790. [Google Scholar] [CrossRef]
- Marques, R.; Unel, M.; Yildiz, M.; Suleman, A. Remaining useful life prediction of laminated composite materials using Thermoelastic Stress Analysis. Compos. Struct. 2019, 210, 381–390. [Google Scholar] [CrossRef]
- Abbas, S.; Li, F.C.; Qiu, J.X. A Review on SHM Techniques and Current Challenges for Characteristic Investigation of Damage in Composite Material Components of Aviation Industry. Mater. Perform. Charact. 2018, 7, 224–258. [Google Scholar] [CrossRef]
- Gholizadeh, S. A review of non-destructive testing methods of composite materials. Port. Conf. Fract. 2016, 1, 50–57. [Google Scholar] [CrossRef]
- Dorey, G. Impact and Crashworthiness of Composite Structures; Elsevier Science Publishing Co., Inc.: Amsterdam, The Netherlands, 1984; pp. 155–192. [Google Scholar]
- Azouaoui, K.; Azari, Z.; Pluvinage, G. Evaluation of impact fatigue damage in glass/epoxy composite laminate. Int. J. Fatigue 2010, 32, 443–452. [Google Scholar] [CrossRef]
- Sadighi, M.; Alderliesten, R. Impact fatigue, multiple and repeated low-velocity impacts on FRP composites: A review. Compos. Struct. 2022, 297, 115962. [Google Scholar] [CrossRef]
- Giurgiutiu, V. Structural Health Monitoring of Aerospace Composites; Academic Press: Waltham, MA, USA, 2015. [Google Scholar]
- Hunston, D.; McDonough, W.; Fanconi, B.; Mopsik, F.; Wang, F.; Phelan, F.; Chiang, M. Assessment of the State-of-the-Art for Process Monitoring Sensors for Polymer Composites; Technical Report NISTIR 4514; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1991. [Google Scholar]
- Lam, H.F.; Ko, J.M.; Wong, C.W. Detection of Damage Location Based on Sensitivity Analysis. In Proceedings of the 13th International Modal Analysis Conference, Nashville, TN, USA, 13–16 February 1995; Volume 2460, pp. 1499–1505. [Google Scholar]
- Kinet, D.; Mégret, P.; Goossen, K.W.; Qiu, L.; Heider, D.; Caucheteur, C. Fiber Bragg grating sensors toward structural health monitoring in composite materials: Challenges and solutions. Sensors 2014, 14, 7394–7419. [Google Scholar] [CrossRef]
- Qiu, Y.; Wang, Q.b.; Zhao, H.t.; Chen, J.a.; Wang, Y.y. Review on composite structural health monitoring based on fiber Bragg grating sensing principle. J. Shanghai Jiaotong Univ. 2013, 18, 129–139. [Google Scholar] [CrossRef]
- Saeedifar, M.; Zarouchas, D. Damage characterization of laminated composites using acoustic emission: A review. Compos. Part B Eng. 2020, 195, 108039. [Google Scholar] [CrossRef]
- Ono, K. Review on structural health evaluation with acoustic emission. Appl. Sci. 2018, 8, 958. [Google Scholar] [CrossRef]
- Saeedifar, M.; Mansvelder, J.; Mohammadi, R.; Zarouchas, D. Using passive and active acoustic methods for impact damage assessment of composite structures. Compos. Struct. 2019, 226, 111252. [Google Scholar] [CrossRef]
- Yue, N.; Khodaei, Z.S.; Aliabadi, M.H. Damage detection in large composite stiffened panels based on a novel SHM building block philosophy. Smart Mater. Struct. 2021, 30, 045004. [Google Scholar] [CrossRef]
- Salmanpour, M.S.; Khodaei, Z.S.; Aliabadi, M.H. Guided wave temperature correction methods in structural health monitoring. J. Intell. Mater. Syst. Struct. 2017, 28, 604–618. [Google Scholar] [CrossRef]
- Palaniappan, J.; Wang, H.; Ogin, S.L.; Thorne, A.; Reed, G.T.; Tjin, S.C. Use of conventional and chirped optical fibre Bragg gratings to detect matrix cracking damage in composite materials. Sens. Their Appl. XIII 2005, 15, 55–60. [Google Scholar] [CrossRef]
- Zhou, Z.D.; Liu, Q.; Ai, Q.S.; Xu, C. Intelligent monitoring and diagnosis for modern mechanical equipment based on the integration of embedded technology and FBGS technology. Measurement 2011, 44, 1499–1511. [Google Scholar] [CrossRef]
- Goossens, S.; De Pauw, B.; Geernaert, T.; Salmanpour, M.S.; Khodaei, Z.S.; Karachalios, E.; Saenz-Castillo, D.; Thienpont, H.; Berghmans, F. Aerospace-grade surface mounted optical fibre strain sensor for structural health monitoring on composite structures evaluated against in-flight conditions. Smart Mater. Struct. 2019, 28, 065008. [Google Scholar] [CrossRef]
- Todd, M.D.; Nichols, J.M.; Trickey, S.T.; Seaver, M.; Nichols, C.J.; Virgin, L.N. Bragg grating-based fibre optic sensors in structural health monitoring. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2007, 365, 317–343. [Google Scholar] [CrossRef]
- Broer, A.A.; Benedictus, R.; Zarouchas, D. The need for multi-sensor data fusion in structural health monitoring of composite aircraft structures. Aerospace 2022, 9, 183. [Google Scholar] [CrossRef]
- Mitra, M.; Gopalakrishnan, S. Guided wave based structural health monitoring: A review. Smart Mater. Struct. 2016, 25, 053001. [Google Scholar] [CrossRef]
- Ricci, F.; Monaco, E.; Boffa, N.; Maio, L.; Memmolo, V. Guided waves for structural health monitoring in composites: A review and implementation strategies. Prog. Aerosp. Sci. 2022, 129, 100790. [Google Scholar] [CrossRef]
- Lu, H.; Chandran, B.; Wu, W.; Ninic, J.; Gryllias, K.; Chronopoulos, D. Damage features for structural health monitoring based on ultrasonic Lamb waves: Evaluation criteria, survey of recent work and outlook. Measurement 2024, 232, 114666. [Google Scholar] [CrossRef]
- Cawley, P. Guided waves in long range nondestructive testing and structural health monitoring: Principles, history of applications and prospects. NDT Int. 2024, 142, 103026. [Google Scholar] [CrossRef]
- Andreades, C.; Malfense Fierro, G.P.; Meo, M. A nonlinear ultrasonic SHM method for impact damage localisation in composite panels using a sparse array of piezoelectric PZT transducers. Ultrasonics 2020, 108, 106181. [Google Scholar] [CrossRef] [PubMed]
- Balasubramaniam, K.; Sikdar, S.; Soman, R.; Malinowski, P. Multi step structural health monitoring approaches in debonding assessment in a sandwich honeycomb composite structure using ultrasonic guided waves. Measurement 2022, 194, 111057. [Google Scholar] [CrossRef]
- Kessler, S.S.; Spearing, S.M.; Soutis, C. Damage detection in composite materials using Lamb wave methods. Smart Mater. Struct. 2002, 11, 269. [Google Scholar] [CrossRef]
- Ihn, J.B.; Chang, F.K. Detection and monitoring of hidden fatigue crack growth using a built-in piezoelectric sensor/actuator network: II. Validation using riveted joints and repair patches. Smart Mater. Struct. 2004, 13, 621. [Google Scholar] [CrossRef]
- Saxena, A.; Goebel, K.F.; Larrosa, C.C.; Janapati, V.; Roy, S.; Chang, F.K. Accelerated Aging Experiments for Prognostics of Damage Growth in Composite Materials; Technical report; NASA Ames Research Center: Mountain View, CA, USA, 2011. [Google Scholar]
- Tabian, I.; Fu, H.L.; Khodaei, Z.S. A Convolutional Neural Network for Impact Detection and Characterization of Complex Composite Structures. Sensors 2019, 19, 4933. [Google Scholar] [CrossRef]
- Seno, A.H.; Khodaei, Z.S.; Aliabadi, M.H.F. Passive sensing method for impact localisation in composite plates under simulated environmental and operational conditions. Mech. Syst. Signal Process. 2019, 129, 20–36. [Google Scholar] [CrossRef]
- Banerjee, P.; Palanisamy, R.P.; Udpa, L.; Haq, M.; Deng, Y.M. Prognosis of fatigue induced stiffness degradation in GFRPs using multi-modal NDE data. Compos. Struct. 2019, 229, 111424. [Google Scholar] [CrossRef]
- Yue, N.; Broer, A.; Briand, W.; Rebillat, M.; Loutas, T.; Zarouchas, D. Assessing stiffness degradation of stiffened composite panels in post-buckling compression-compression fatigue using guided waves. Compos. Struct. 2022, 293, 115751. [Google Scholar] [CrossRef]
- Munian, R.K.; Mahapatra, D.R.; Gopalakrishnan, S. Ultrasonic guided wave scattering due to delamination in curved composite structures. Compos. Struct. 2020, 239, 111987. [Google Scholar] [CrossRef]
- Paunikar, S.; Gopalakrishnan, S. Wave propagation in adhesively bonded metallic and composite lap joints modelled through spectrally formulated elastically coupled double beam element. Int. J. Mech. Mater. Des. 2022, 18, 365–393. [Google Scholar] [CrossRef]
- Nerlikar, V.; Miorelli, R.; Recoquillay, A.; d’Almeida, O. A physics-embedded deep-learning framework for efficient multi-fidelity modeling applied to guided wave based structural health monitoring. Ultrasonics 2024, 141, 107325. [Google Scholar] [CrossRef] [PubMed]
- Feng, T.; Aliabadi, M.H.F. Influence of placing positions of PZT transducers in thick composites on ultrasonic guided waves. Procedia Struct. Integr. 2024, 52, 785–794. [Google Scholar] [CrossRef]
- Dziendzikowski, M.; Kurnyta, A.; Dragan, K.; Klysz, S.; Leski, A. In situ Barely Visible Impact Damage detection and localization for composite structures using surface mounted and embedded PZT transducers: A comparative study. Mech. Syst. Signal Process. 2016, 78, 91–106. [Google Scholar] [CrossRef]
- Di Sante, R. Fibre Optic Sensors for Structural Health Monitoring of Aircraft Composite Structures: Recent Advances and Applications. Sensors 2015, 15, 18666–18713. [Google Scholar] [CrossRef]
- Guemes, A.; Fernandez-Lopez, A.; Pozo, A.R.; Sierra-Pérez, J. Structural Health Monitoring for Advanced Composite Structures: A Review. J. Compos. Sci. 2020, 4, 13. [Google Scholar] [CrossRef]
- Frieden, J.; Cugnoni, J.; Botsis, J.; Gmür, T.; Coric, D. High-speed internal strain measurements in composite structures under dynamic load using embedded FBG sensors. Compos. Struct. 2010, 92, 1905–1912. [Google Scholar] [CrossRef]
- Falcetelli, F.; Martini, A.; Di Sante, R.; Troncossi, M. Strain Modal Testing with Fiber Bragg Gratings for Automotive Applications. Sensors 2022, 22, 946. [Google Scholar] [CrossRef]
- Yeager, M.; Todd, M.; Gregory, W.; Key, C. Assessment of embedded fiber Bragg gratings for structural health monitoring of composites. Struct. Health-Monit. Int. J. 2017, 16, 262–275. [Google Scholar] [CrossRef]
- Güemes, A.; Fernandez-Lopez, A.; Fernandez, P. Damage detection in composite structures from fibre optic distributed strain measurements. In Proceedings of the EWSHM-7th European Workshop on Structural Health Monitoring, Nantes, France, 8–11 July 2014. [Google Scholar]
- Balageas, D.; Bourasseau, S.; Dupont, M.; Bocherens, E.; Dewynter-Marty, V.; Ferdinand, P. Comparison between non-destructive evaluation techniques and integrated fiber optic health monitoring systems for composite sandwich structures. J. Intell. Mater. Syst. Struct. 2000, 11, 426–437. [Google Scholar] [CrossRef]
- Goossens, S.; Berghmans, F.; Muñoz, K.; Jiménez, M.; Karachalios, E.; Saenz-Castillo, D.; Geernaert, T. A global assessment of barely visible impact damage for CFRP sub-components with FBG-based sensors. Compos. Struct. 2021, 272, 114025. [Google Scholar] [CrossRef]
- Guemes, A.; Sierra-Pérez, J.; Rodellar, J.; Mujica, L. A robust procedure for Damage detection from strain measurements based on Principal Component Analysis. Struct. Health Monit. Res. Appl. 2013, 558, 128–138. [Google Scholar] [CrossRef]
- Güemes, A.; Fernández-López, A.; Díaz-Maroto, P.F.; Lozano, A.; Sierra-Perez, J. Structural Health Monitoring in Composite Structures by Fiber-Optic Sensors. Sensors 2018, 18, 1094. [Google Scholar] [CrossRef]
- Kahandawa, G.C.; Epaarachchi, J.; Wang, H.; Lau, K.T. Use of FBG Sensors for SHM in Aerospace Structures. Photonic Sens. 2012, 2, 203–214. [Google Scholar] [CrossRef]
- Datta, A.; Augustin, M.J.; Gupta, N.; Viswamurthy, S.R.; Gaddikeri, K.M.; Sundaram, R. Impact Localization and Severity Estimation on Composite Structure Using Fiber Bragg Grating Sensors by Least Square Support Vector Regression. IEEE Sens. J. 2019, 19, 4463–4470. [Google Scholar] [CrossRef]
- Sbarufatti, C.; Manes, A.; Giglio, M. Performance optimization of a diagnostic system based upon a simulated strain field for fatigue damage characterization. Mech. Syst. Signal Process. 2013, 40, 667–690. [Google Scholar] [CrossRef]
- Galanopoulos, G.; Eleftheroglou, N.; Milanoski, D.; Broer, A.; Zarouchas, D.; Loutas, T. A novel strain-based health indicator for the remaining useful life estimation of degrading composite structures. Compos. Struct. 2023, 306, 116579. [Google Scholar] [CrossRef]
- Galanopoulos, G.; Fytsilis, E.; Yue, N.; Broer, A.; Milanoski, D.; Zarouchas, D.; Loutas, T. A data driven methodology for upscaling remaining useful life predictions: From single- to multi-stiffened composite panels. Compos. Part C Open Access 2023, 11, 100366. [Google Scholar] [CrossRef]
- Rocha, H.; Semprimoschnig, C.; Nunes, J.P. Sensors for process and structural health monitoring of aerospace composites: A review. Eng. Struct. 2021, 237, 112231. [Google Scholar] [CrossRef]
- Elenchezhian, M.R.P.; Vadlamudi, V.; Raihan, R.; Reifsnider, K.; Reifsnider, E. Artificial intelligence in real-time diagnostics and prognostics of composite materials and its uncertainties-a review. Smart Mater. Struct. 2021, 30, 083001. [Google Scholar] [CrossRef]
- Paunikar, S.; Galanopoulos, G.; Rébillat, M. An Experimental Data Set for the SHM of a Substructure of an Engine Fan Blade from the MORPHO Project. 2025. Available online: https://zenodo.org/records/14627730 (accessed on 1 February 2025). [CrossRef]
- ASTM D7264/D7264M–07; Standard Test Method for Flexural Properties of Polymer Matrix Composite Materials. ASTM International: West Conshohocken, PA, USA, 2007.
- Wirth, I.; Rébillat, M.; Letellier, F.; Kohl, M.; Conen, J.; Becker, M.O.; Rusch, T. Integration of printed sensors for the functionalization of composite components. In Proceedings of the 10th ECCOMAS Thematic Conference on Smart Structures and Materials (SMART 2023), Patras, Greece, 3–5 July 2023; pp. 1817–1826. [Google Scholar]
- Wen, P.; Zhao, S.; Chen, S.; Li, Y. A generalized remaining useful life prediction method for complex systems based on composite health indicator. Reliab. Eng. Syst. Saf. 2021, 205, 107241. [Google Scholar] [CrossRef]
- Loukopoulos, P.; Zolkiewski, G.; Bennett, I.; Sampath, S.; Pilidis, P.; Duan, F.; Sattar, T.; Mba, D. Reciprocating compressor prognostics of an instantaneous failure mode utilising temperature only measurements. Appl. Acoust. 2019, 147, 77–86. [Google Scholar] [CrossRef]




| Load No. | Load | Expected MTS Displacement | Loading Rate |
|---|---|---|---|
| (kN) | (mm) | (mm/min) | |
| 1 | 4 | 6.62 | 15.0 |
| 2 | 8 | 13.22 | 29.0 |
| 3 | 12 | 21.10 | 44.5 |
| 4 | 14 | 25.78 | 53.0 |
| 5 | 16 | 31.00 | 63.0 |
| 6 | 18 | 35.54 | 72.5 |
| 7 | 20 | 39.95 | 83.0 |
| 8 | 22 | 43.70 | 94.0 |
| 9 | 24 | 48.33 | 105.5 |
| 10 | 26 | 56.00 | 117.5 |
| 11 | 28 | 70.12 | 130 |
| Spec No. | Impact Location [x,y] (in mm) | Impact Energy (in J) | Time of Impact (in Cycles) | Failure Timer (in Cycles) | Failure Load (in kN) |
|---|---|---|---|---|---|
| Panel 01 | [515,176] | 50 | 0 | 3300 | 24 |
| Panel 02 | [305,135] | 50 | 600 | 3065 | 22 |
| Panel 03 | No impact | - | - | 3226 | 24 |
| Panel 04 | [505,203] | 55 | 1400 | 3200 | 24 |
| Panel 05 | [514,180] | 55 | 0 | 3300 | 24 |
| Feature Name | Mathematical Formula | Description/Hyperparameters |
|---|---|---|
| Time-domain and Amplitude Features | ||
| mean | Arithmetic mean of the signal. | |
| std | Standard deviation of the signal. | |
| peak_amp | Maximum absolute amplitude. | |
| rms | Root mean square. | |
| zero_crossings | Times the signal value crosses zero. | |
| iqr | Interquartile range. | |
| mad | Mean absolute deviation from the mean. | |
| skewness | Asymmetry of probability distribution. | |
| kurtosis | Fisher’s (excess) kurtosis. | |
| p2p_amp | Peak-to-peak amplitude. | |
| energy | Sum of the squared signal values. | |
| crest_factor | Ratio of peak amplitude to the RMS. | |
| clearance_factor | Indicates the presence of impulses. | |
| impulse_factor | Ratio of peak value to mean absolute value. | |
| shape_factor | Ratio of RMS to mean absolute value. | |
| Peak Features (where k is the number of peaks found) | ||
| n_peaks | k | Total number of detected peaks. |
| Hyperparameter: min peak `height = 0’. | ||
| peak_mean | Mean amplitude of the detected peaks (). | |
| peak_std | Standard deviation of peak amplitudes. | |
| peak_dist_mean | Mean distance (in samples) between consecutive peaks (). | |
| peak_dist_std | Standard deviation of inter-peak distances. | |
| Envelope Features (where A is the signal envelope via Hilbert transform) | ||
| env_mean | Mean of the signal’s instantaneous amplitude. | |
| env_max | Maximum of the signal envelope. | |
| env_std | Standard deviation of the signal envelope. | |
| env_kurtosis | Kurtosis of the signal envelope values. | |
| env_skewness | Skewness of the signal envelope values. | |
| Frequency-domain Features (where is the Power Spectral Density) | ||
| dom_freq | Dominant frequency with the highest power. | |
| mean_freq | Spectral centroid; the “center of mass” of the spectrum. | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galanopoulos, G.; Paunikar, S.; Stamatelatos, G.; Loutas, T.; Mechbal, N.; Rébillat, M.; Zarouchas, D. SHM for Complex Composite Aerospace Structures: A Case Study on Engine Fan Blades. Aerospace 2025, 12, 963. https://doi.org/10.3390/aerospace12110963
Galanopoulos G, Paunikar S, Stamatelatos G, Loutas T, Mechbal N, Rébillat M, Zarouchas D. SHM for Complex Composite Aerospace Structures: A Case Study on Engine Fan Blades. Aerospace. 2025; 12(11):963. https://doi.org/10.3390/aerospace12110963
Chicago/Turabian StyleGalanopoulos, Georgios, Shweta Paunikar, Giannis Stamatelatos, Theodoros Loutas, Nazih Mechbal, Marc Rébillat, and Dimitrios Zarouchas. 2025. "SHM for Complex Composite Aerospace Structures: A Case Study on Engine Fan Blades" Aerospace 12, no. 11: 963. https://doi.org/10.3390/aerospace12110963
APA StyleGalanopoulos, G., Paunikar, S., Stamatelatos, G., Loutas, T., Mechbal, N., Rébillat, M., & Zarouchas, D. (2025). SHM for Complex Composite Aerospace Structures: A Case Study on Engine Fan Blades. Aerospace, 12(11), 963. https://doi.org/10.3390/aerospace12110963








