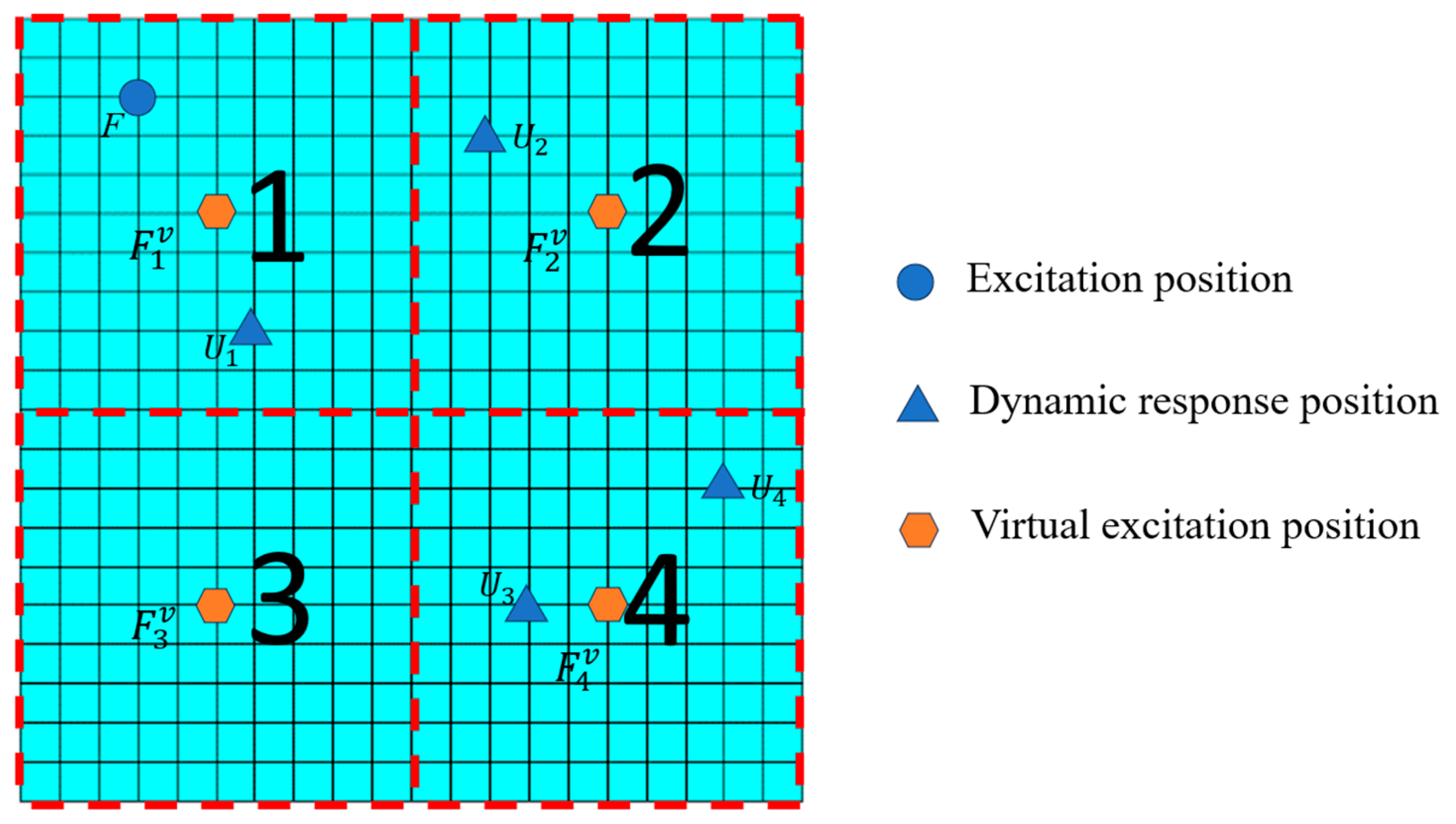
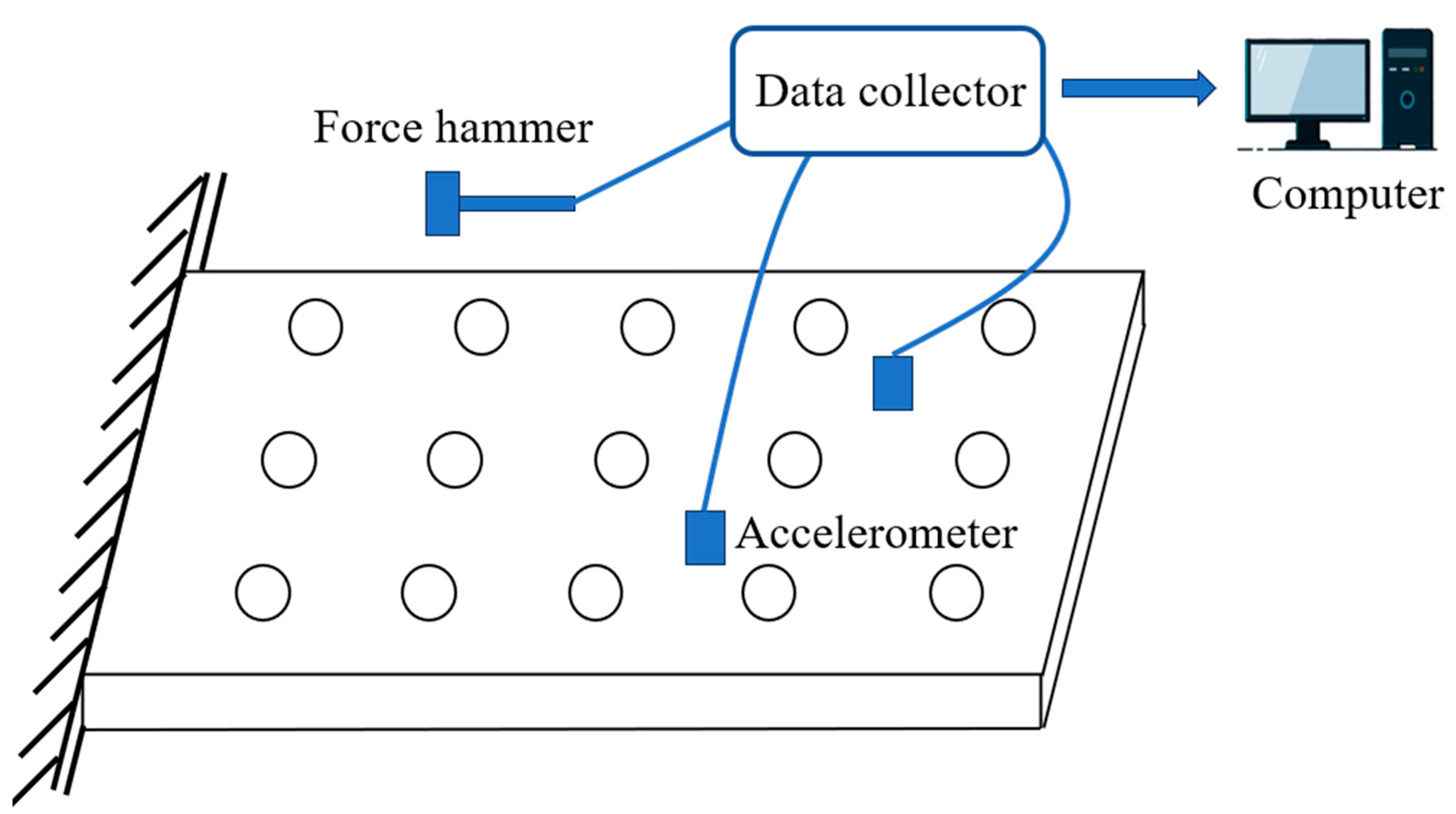
Figure 1.
Preliminary calibration diagram of thin plate.
Figure 1.
Preliminary calibration diagram of thin plate.
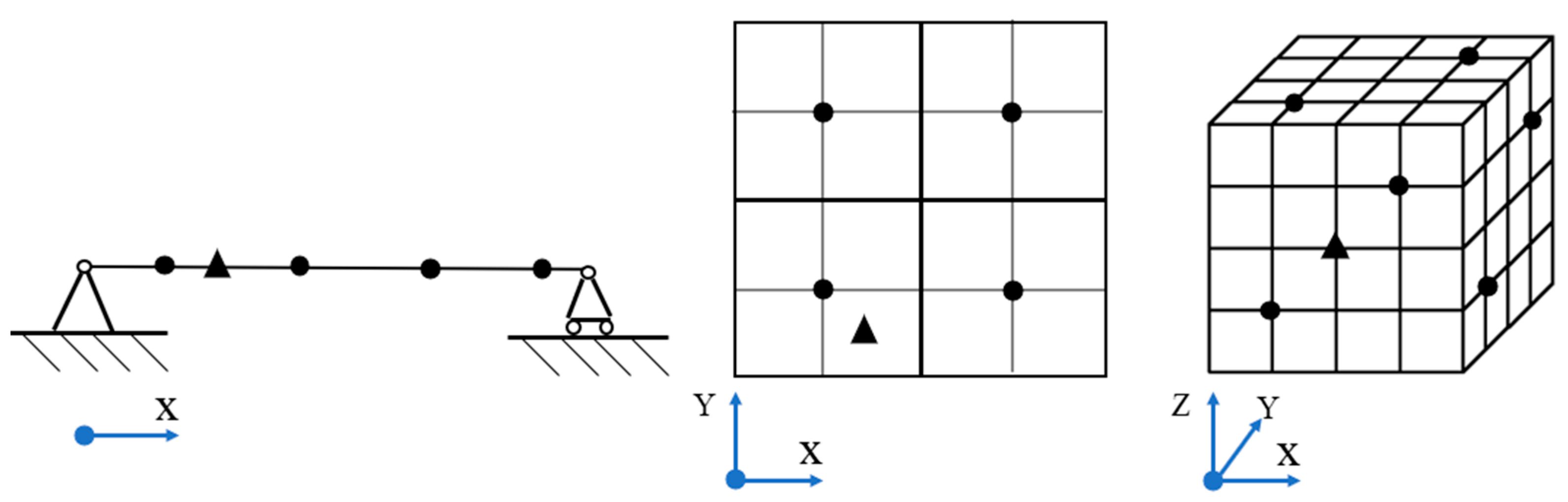
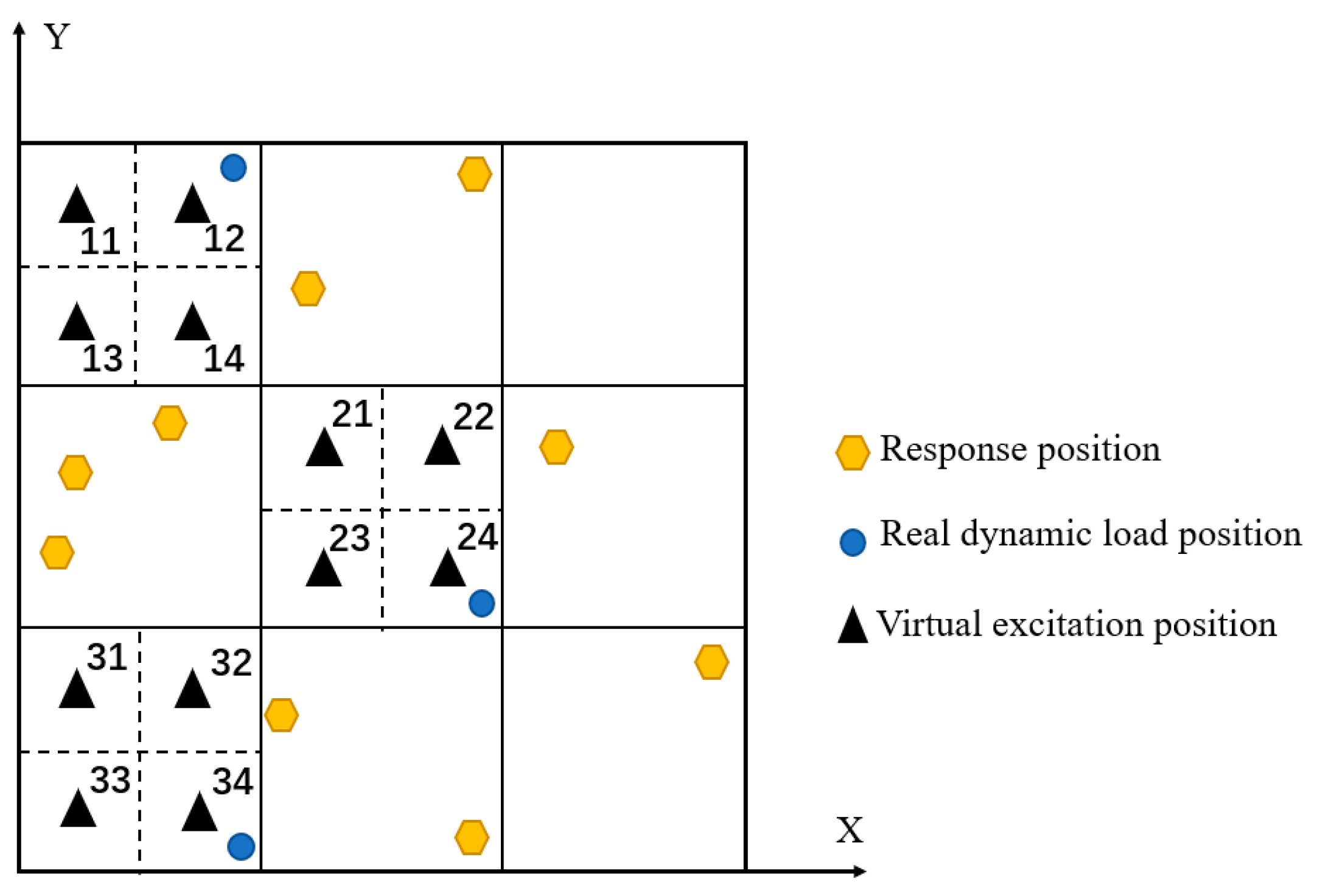
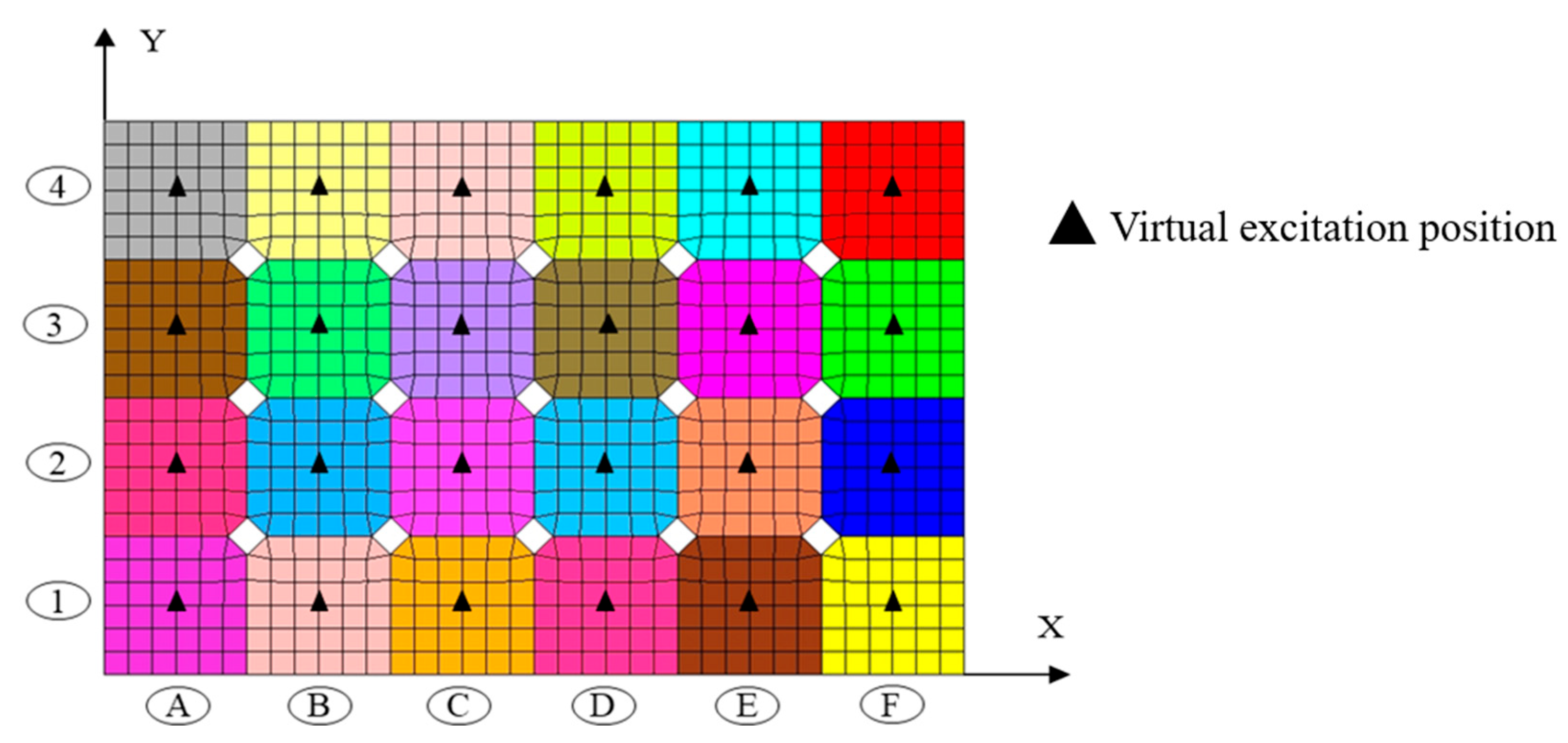
Figure 2.
Selection diagrams of virtual load points for different structures.
Figure 2.
Selection diagrams of virtual load points for different structures.
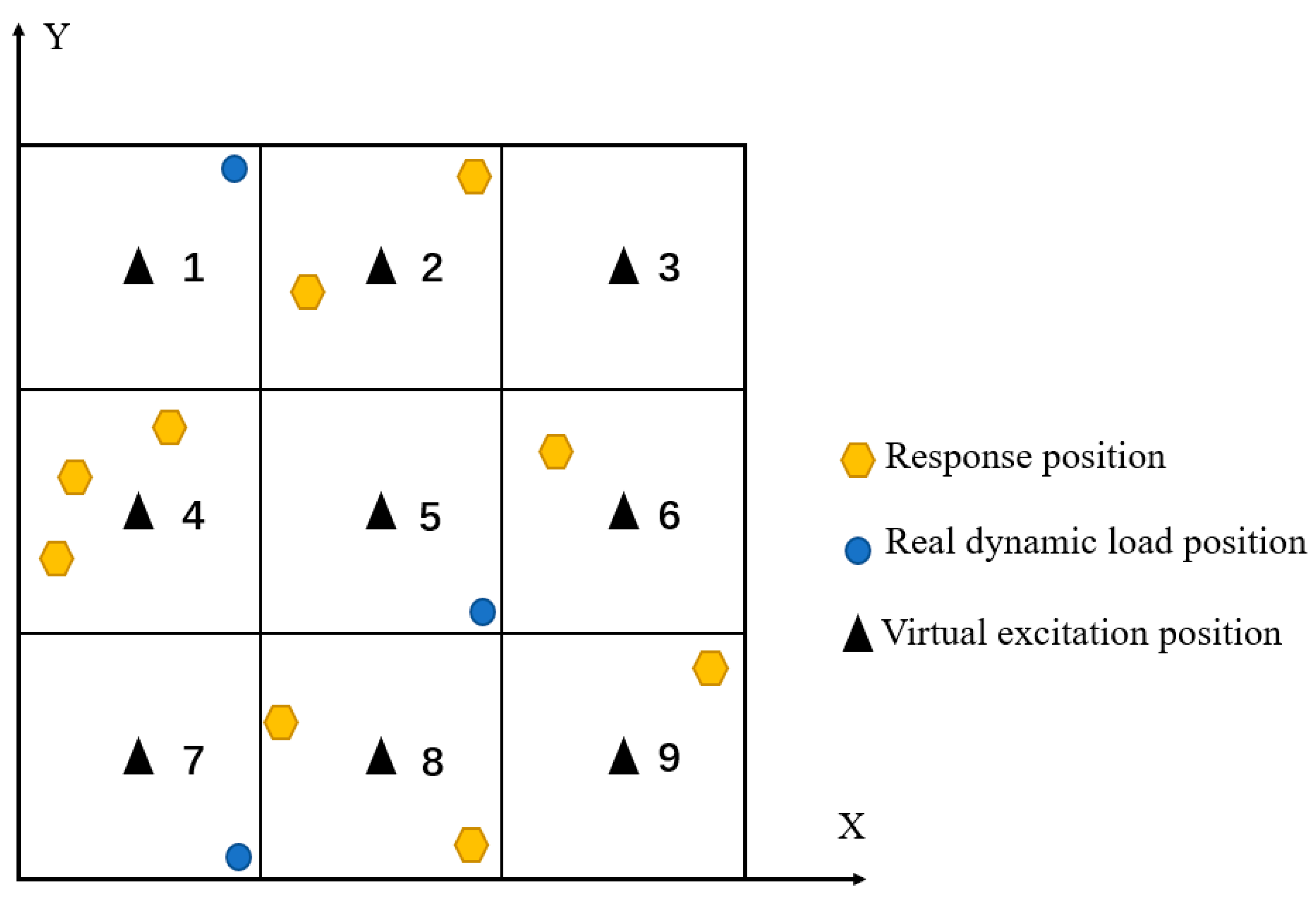
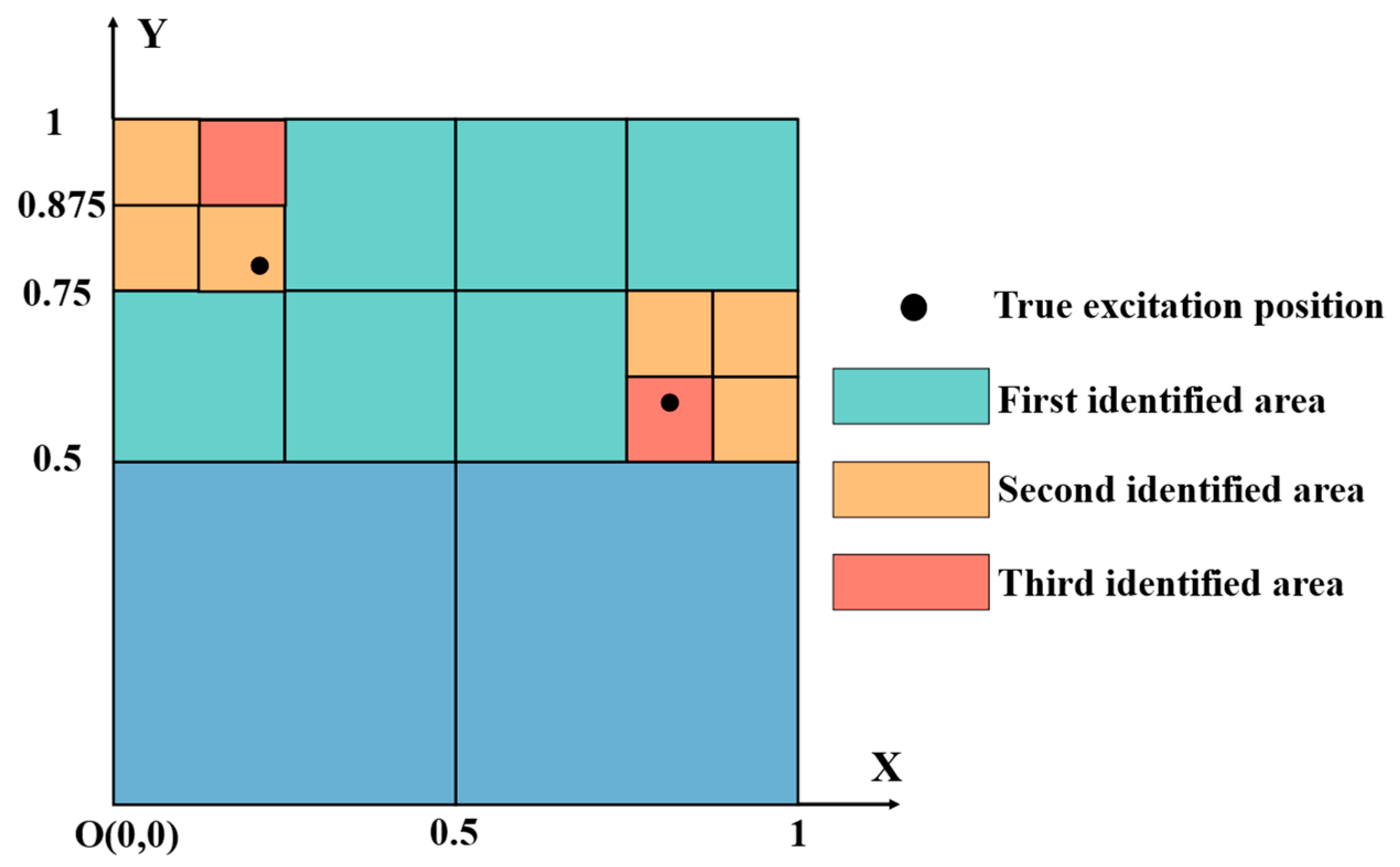
Figure 3.
Result of the first identification when the loads are too close.
Figure 3.
Result of the first identification when the loads are too close.
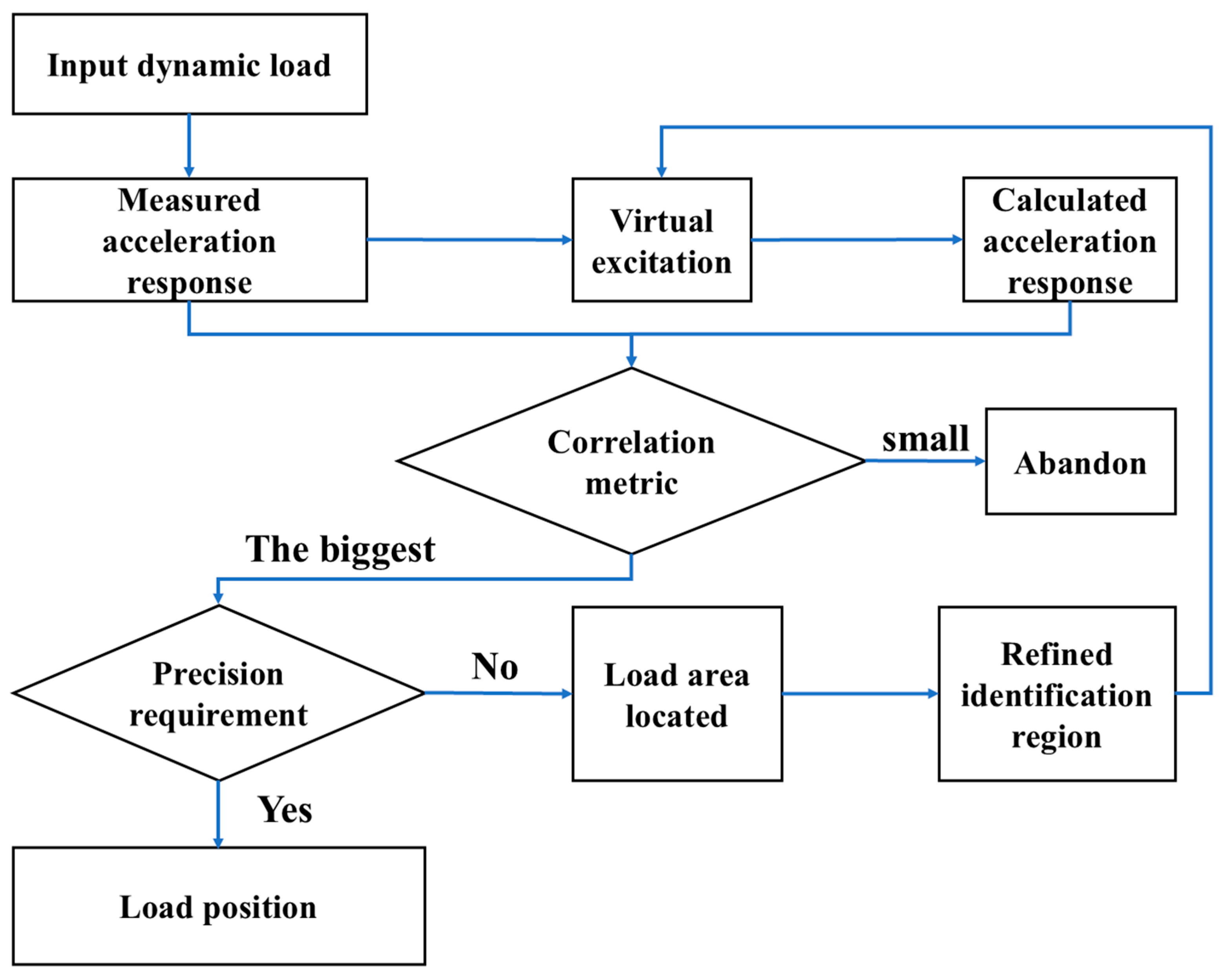
Figure 4.
Flowchart of multi-point identification of dynamic loads with multiple frequencies.
Figure 4.
Flowchart of multi-point identification of dynamic loads with multiple frequencies.
Figure 5.
Model for first identification.
Figure 5.
Model for first identification.
Figure 6.
Model for second identification.
Figure 6.
Model for second identification.
Figure 7.
Flow chart for stepwise identification.
Figure 7.
Flow chart for stepwise identification.
Figure 8.
Position of the acceleration sensors under two operational conditions.
Figure 8.
Position of the acceleration sensors under two operational conditions.
Figure 9.
Location of excitation and response points.
Figure 9.
Location of excitation and response points.
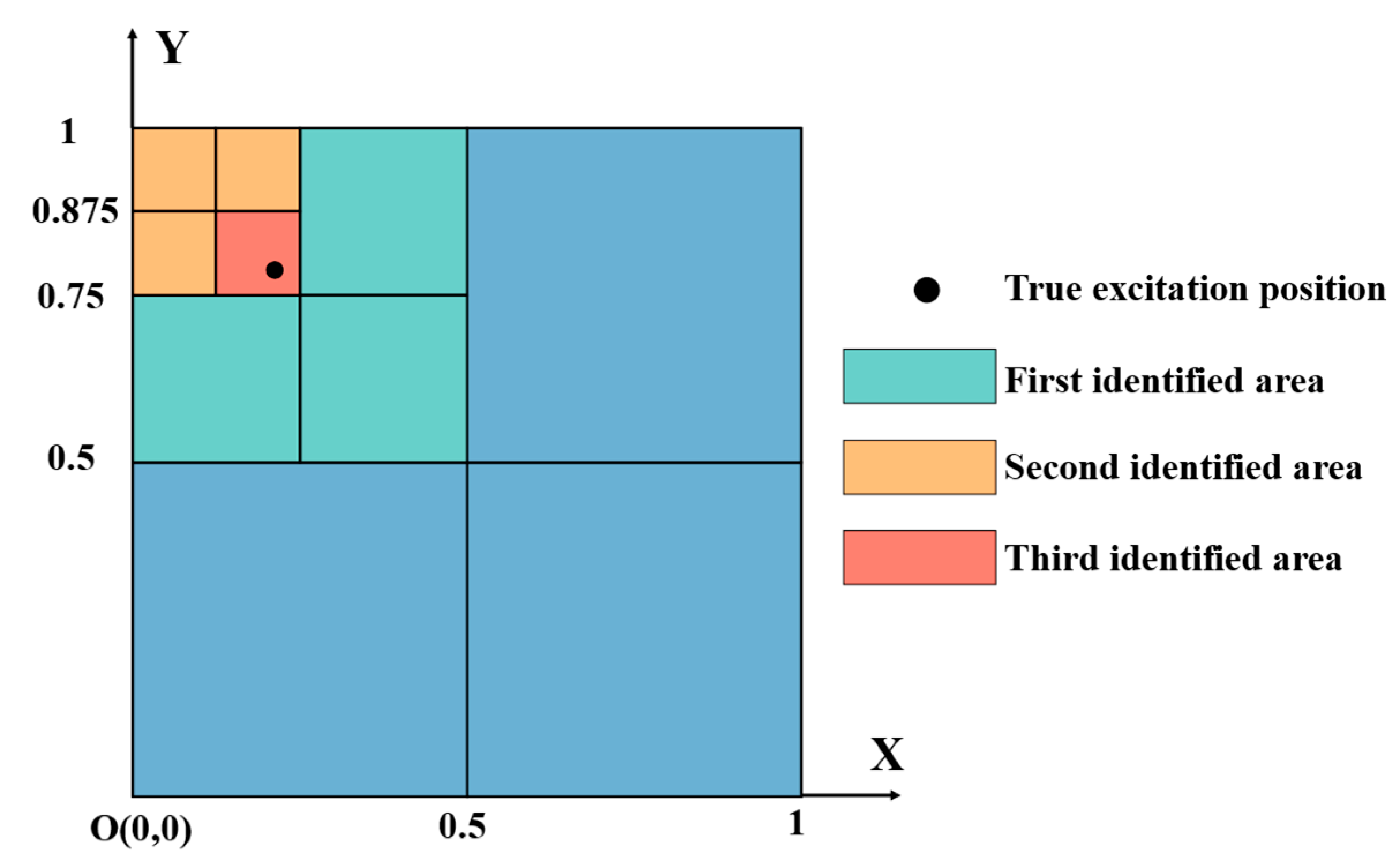
Figure 10.
Step-by-step identification diagram.
Figure 10.
Step-by-step identification diagram.
Figure 11.
Locations of excitation and response points on thin plate.
Figure 11.
Locations of excitation and response points on thin plate.
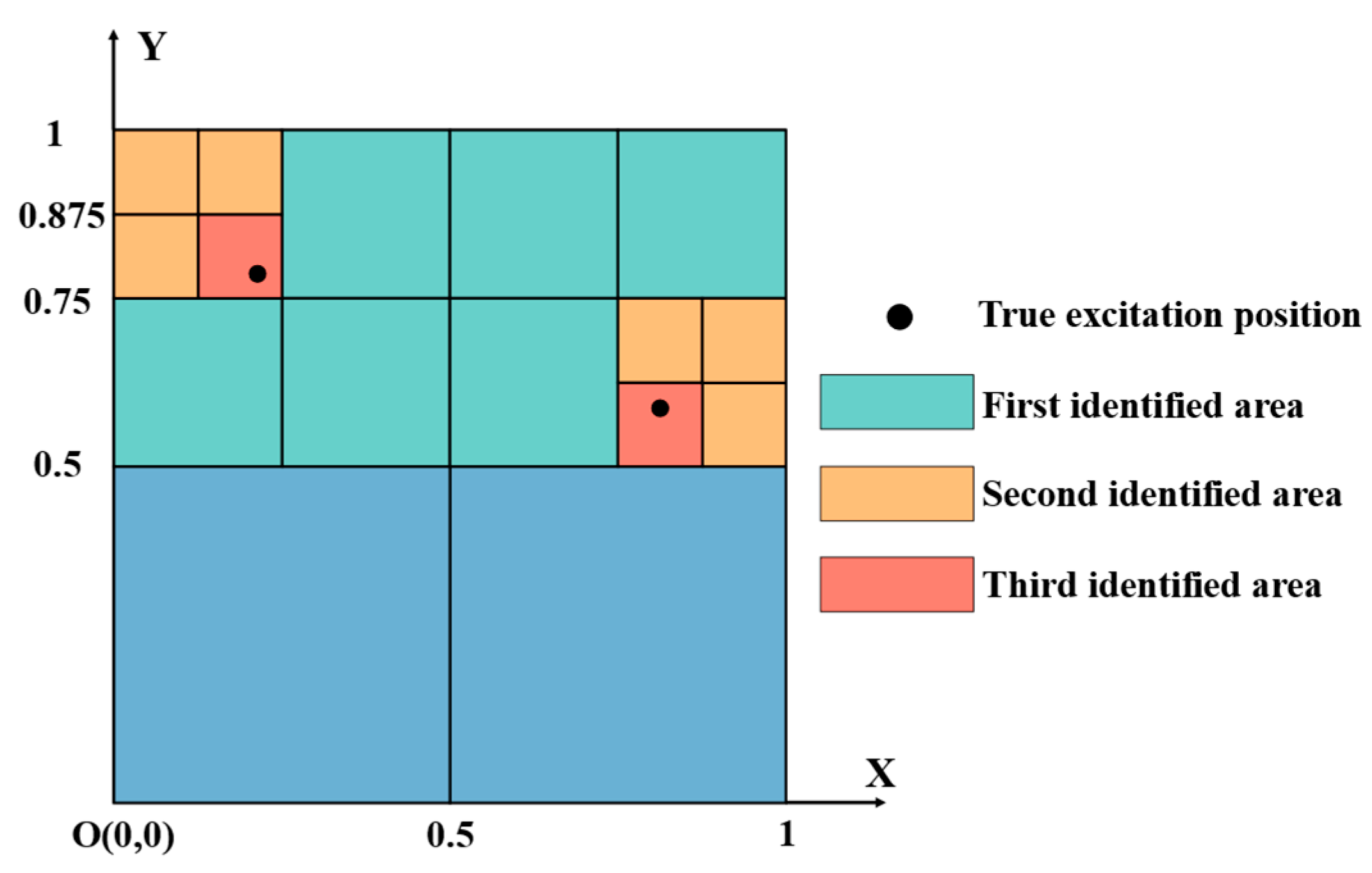
Figure 12.
Step-by-step identification diagram for multi-point dynamic load case.
Figure 12.
Step-by-step identification diagram for multi-point dynamic load case.
Figure 13.
Identification results of multi-point dynamic loads with 10% noise under operating condition 1.
Figure 13.
Identification results of multi-point dynamic loads with 10% noise under operating condition 1.
Figure 14.
Schematic diagram of sheet test.
Figure 14.
Schematic diagram of sheet test.
Figure 15.
Experimental schematic diagram of a thin plate with round holes.
Figure 15.
Experimental schematic diagram of a thin plate with round holes.
Figure 16.
Plane coordinates for test with thin plate.
Figure 16.
Plane coordinates for test with thin plate.
Figure 17.
Finite-element model of thin plate for first identification.
Figure 17.
Finite-element model of thin plate for first identification.
Figure 18.
Finite-element model of region E2 of thin plate for second identification.
Figure 18.
Finite-element model of region E2 of thin plate for second identification.
Table 1.
Structural parameters of thin plate.
Table 1.
Structural parameters of thin plate.
| Parameter | Length/m | Width/m | Thickness/m | Elastic
Modulus/GPa | Poisson’s Coefficient | Density/kg/m3 | Damping Ration |
|---|
| Parameter value | 1 | 1 | 0.01 | 70 | 0.3 | 2700 | 0.03 |
Table 2.
Locations of excitation position and response position.
Table 2.
Locations of excitation position and response position.
| | Excitation Position 1/m | Response Position 1/m | Response Position 2/m | Response Position 3/m | Response Position 4/m |
|---|
| x | 0.2 | 0.25 | 0.75 | 0.25 | 0.75 |
| y | 0.8 | 0.75 | 0.75 | 0.25 | 0.25 |
Table 3.
Virtual excitation locations.
Table 3.
Virtual excitation locations.
| | Step 1 | Step 2 | Step 3 |
|---|
| | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
| x | 0.25 | 0.75 | 0.25 | 0.75 | 0.125 | 0.375 | 0.125 | 0.375 | 0.0625 | 0.1875 | 0.0625 | 0.1875 |
| y | 0.75 | 0.75 | 0.25 | 0.25 | 0.875 | 0.875 | 0.625 | 0.625 | 0.9375 | 0.9375 | 0.8125 | 0.8125 |
Table 4.
Correlation metrics of noise-free single-point recognition under Operational condition 1.
Table 4.
Correlation metrics of noise-free single-point recognition under Operational condition 1.
| | Step 1 | Step 2 | Step 3 |
|---|
| Location number | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
| Correlation metric | 6.47 | 4.33 | 4.33 | 4.07 | 6.16 | 5.44 | 5.44 | 5.21 | 5.73 | 5.84 | 5.84 | 7.84 |
Table 5.
Correlation metrics of single-point recognition with 5% noise under Operational Condition 1.
Table 5.
Correlation metrics of single-point recognition with 5% noise under Operational Condition 1.
| | Step 1 | Step 2 | Step 3 |
|---|
| Location number | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
| Correlation metric | 3.0901 | 3.0645 | 3.0633 | 3.0419 | 3.0903 | 3.0883 | 3.0878 | 3.0858 | 3.0897 | 3.0901 | 3.0898 | 3.0905 |
Table 6.
Correlation metrics of single-point recognition with 10% noise under Operational Condition 1.
Table 6.
Correlation metrics of single-point recognition with 10% noise under Operational Condition 1.
| | Step 1 | Step 2 | Step 3 |
|---|
| Location number | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
| Correlation metric | 2.7539 | 2.7444 | 2.7420 | 2.7345 | 2.7536 | 2.7535 | 2.7526 | 2.7526 | 2.7533 | 2.7537 | 2.7532 | 2.7539 |
Table 7.
Locations of nine response positions.
Table 7.
Locations of nine response positions.
| Response Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|
| x/m | 0.25 | 0.5 | 0.75 | 0.25 | 0.5 | 0.75 | 0.25 | 0.5 | 0.75 |
| y/m | 0.75 | 0.75 | 0.75 | 0.5 | 0.5 | 0.5 | 0.25 | 0.25 | 0.25 |
Table 8.
Correlation metrics of single-point recognition with 5% noise under Operational Condition 2.
Table 8.
Correlation metrics of single-point recognition with 5% noise under Operational Condition 2.
| | Step 1 | Step 2 | Step 3 |
|---|
| Location number | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
| Correlation metric | 3.1025 | 3.0877 | 3.0796 | 3.0684 | 3.1027 | 3.1012 | 3.1012 | 3.0998 | 3.1024 | 3.1023 | 3.1028 | 3.1029 |
Table 9.
Correlation metrics of single-point recognition with 10% noise under Operational Condition 2.
Table 9.
Correlation metrics of single-point recognition with 10% noise under Operational Condition 2.
| | Step 1 | Step 2 | Step 3 |
|---|
| Location number | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
| Correlation metric | 2.7577 | 2.7518 | 2.7469 | 2.7430 | 2.7576 | 2.7572 | 2.7568 | 2.7566 | 2.7573 | 2.7574 | 2.7574 | 2.7577 |
Table 10.
Results of step-by-step identification.
Table 10.
Results of step-by-step identification.
| | Excitation Position/m |
|---|
| | x | y |
|---|
| True value | 0.2 | 0.8 |
| Identification result | 0.1875 | 0.8125 |
Table 11.
Comparison of computation for identification of single-point dynamic load between traditional and step-by-step methods.
Table 11.
Comparison of computation for identification of single-point dynamic load between traditional and step-by-step methods.
| | Number of Applied Loads | Number of Response Data | Number of Loads Applied in Traditional Method | Number of Responses Collected in Traditional Method |
|---|
| Step 1 | 4 | 16/36 | 441 | 1764/3969 |
| Step 2 | 8 | 32/72 |
| Step 3 | 12 | 48/108 |
Table 12.
Locations of excitation and response positions.
Table 12.
Locations of excitation and response positions.
| | Excitation Position 1 | Excitation Position 2 | Response Position 1 | Response Position 2 | Response Position 3 | Response Position 4 |
|---|
| x/m | 0.2 | 0.8 | 0.25 | 0.75 | 0.25 | 0.75 |
| y/m | 0.8 | 0.6 | 0.75 | 0.75 | 0.25 | 0.25 |
Table 13.
Locations of virtual excitation points.
Table 13.
Locations of virtual excitation points.
| | Excitation Position 1 | Excitation Position 2 | Excitation Position 3 | Excitation Position 4 |
|---|
| x/m | 0.25 | 0.75 | 0.25 | 0.75 |
| y/m | 0.75 | 0.75 | 0.25 | 0.25 |
Table 14.
Correlation metrics for the first noise-free identification under Operational Condition 1.
Table 14.
Correlation metrics for the first noise-free identification under Operational Condition 1.
| | First Identification |
|---|
| Location number | 1, 2 | 1, 3 | 1, 4 | 2, 3 | 2, 4 | 3, 4 |
| Correlation metric | 5.22 | 4.27 | 4.67 | 4.53 | 4.73 | 4.67 |
Table 15.
Locations of virtual excitation points in second recognition.
Table 15.
Locations of virtual excitation points in second recognition.
| | Number 1 in Step 1 | Number 2 in Step 1 |
|---|
| Location number | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
| x/m | 0.125 | 0.375 | 0.125 | 0.375 | 0.625 | 0.875 | 0.625 | 0.875 |
| y/m | 0.875 | 0.875 | 0.625 | 0.625 | 0.875 | 0.875 | 0.625 | 0.625 |
Table 16.
Correlation metrics for the second noise-free identification under Operational Condition 1.
Table 16.
Correlation metrics for the second noise-free identification under Operational Condition 1.
| | Second Identification |
|---|
| Location number | 1, 1 | 1, 2 | 1, 3 | 1, 4 | 2, 1 | 2, 2 | 2, 3 | 2, 4 |
| Correlation metric | 4.97 | 4.87 | 5.90 | 6.05 | 5.01 | 4.97 | 5.75 | 5.87 |
| Location number | 3, 1 | 3, 2 | 3, 3 | 3, 4 | 4, 1 | 4, 2 | 4, 3 | 4, 4 |
| Correlation metric | 4.90 | 4.80 | 5.35 | 5.38 | 5.07 | 5.05 | 5.30 | 5.35 |
Table 17.
Locations of virtual excitation points for third recognition.
Table 17.
Locations of virtual excitation points for third recognition.
| | Number 1 in Step 2 | Number 4 in Step 2 |
|---|
| Location number | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
| x/m | 0.0625 | 0.1875 | 0.0625 | 0.1875 | 0.8125 | 0.9375 | 0.8125 | 0.9375 |
| y/m | 0.9375 | 0.9375 | 0.8125 | 0.8125 | 0.6875 | 0.6875 | 0.5625 | 0.5625 |
Table 18.
Correlation metrics for the third noise-free identification under Operational Condition 1.
Table 18.
Correlation metrics for the third noise-free identification under Operational Condition 1.
| | The Third Identification |
|---|
| Location number | 1, 1 | 1, 2 | 1, 3 | 1, 4 | 2, 1 | 2, 2 | 2, 3 | 2, 4 |
| Correlation metric | 5.24 | 5.41 | 5.18 | 5.53 | 5.59 | 5.53 | 5.71 | 6.04 |
| Location number | 3, 1 | 3, 2 | 3, 3 | 3, 4 | 4, 1 | 4, 2 | 4, 3 | 4, 4 |
| Correlation metric | 5.70 | 5.71 | 5.73 | 5.53 | 5.70 | 5.13 | 6.23 | 5.27 |
Table 19.
Correlation metrics for the first identification under 5% noise in Operational Condition 1.
Table 19.
Correlation metrics for the first identification under 5% noise in Operational Condition 1.
| | First Identification |
|---|
| Location number | 1, 2 | 1, 3 | 1, 4 | 2, 3 | 2, 4 | 3, 4 |
| Correlation metric | 3.0861 | 3.0610 | 3.0778 | 3.0737 | 3.0803 | 3.0556 |
Table 20.
Correlation metrics for the second identification under 5% noise in Operational Condition 1.
Table 20.
Correlation metrics for the second identification under 5% noise in Operational Condition 1.
| | Second Identification |
|---|
| Location number | 1, 1 | 1, 2 | 1, 3 | 1, 4 | 2, 1 | 2, 2 | 2, 3 | 2, 4 |
| Correlation metric | 3.0839 | 3.0823 | 3.0890 | 3.0891 | 3.0844 | 3.0839 | 3.0887 | 3.0889 |
| Location number | 3, 1 | 3, 2 | 3, 3 | 3, 4 | 4, 1 | 4, 2 | 4, 3 | 4, 4 |
| Correlation metric | 3.0825 | 3.0807 | 3.0871 | 3.0870 | 3.0850 | 3.0846 | 3.0869 | 3.0871 |
Table 21.
Correlation metrics for the third identification under 5% noise in Operational Condition 1.
Table 21.
Correlation metrics for the third identification under 5% noise in Operational Condition 1.
| | The Third Identification |
|---|
| Location number | 1, 1 | 1, 2 | 1, 3 | 1, 4 | 2, 1 | 2, 2 | 2, 3 | 2, 4 |
| Correlation metric | 3.0872 | 3.0880 | 3.0868 | 3.0884 | 3.0886 | 3.0881 | 3.0889 | 3.0891 |
| Location number | 3, 1 | 3, 2 | 3, 3 | 3, 4 | 4, 1 | 4, 2 | 4, 3 | 4, 4 |
| Correlation metric | 3.0888 | 3.0884 | 3.0889 | 3.0891 | 3.0884 | 3.0852 | 3.0892 | 3.0863 |
Table 22.
Correlation metrics for the first identification under 10% noise in Operational Condition 1.
Table 22.
Correlation metrics for the first identification under 10% noise in Operational Condition 1.
| | First Identification |
|---|
| Location number | 1, 2 | 1, 3 | 1, 4 | 2, 3 | 2, 4 | 3, 4 |
| Correlation metric | 2.5312 | 2.5205 | 2.5271 | 2.5266 | 2.5290 | 2.5183 |
Table 23.
Correlation metrics for the second identification under 10% noise in Operational Condition 1.
Table 23.
Correlation metrics for the second identification under 10% noise in Operational Condition 1.
| | Second Identification |
|---|
| Location number | 1, 1 | 1, 2 | 1, 3 | 1, 4 | 2, 1 | 2, 2 | 2, 3 | 2, 4 |
| Correlation metric | 2.5304 | 2.5294 | 2.5326 | 2.5327 | 2.5307 | 2.5304 | 2.5323 | 2.5324 |
| Location number | 3, 1 | 3, 2 | 3, 3 | 3, 4 | 4, 1 | 4, 2 | 4, 3 | 4, 4 |
| Correlation metric | 2.5300 | 2.5291 | 2.5320 | 2.5317 | 2.5311 | 2.5310 | 2.5320 | 2.5320 |
Table 24.
Correlation metrics for the third identification under 10% noise in Operational Condition 1.
Table 24.
Correlation metrics for the third identification under 10% noise in Operational Condition 1.
| | The Third Identification |
|---|
| Location number | 1, 1 | 1, 2 | 1, 3 | 1, 4 | 2, 1 | 2, 2 | 2, 3 | 2, 4 |
| Correlation metric | 2.5326 | 2.5325 | 2.5321 | 2.5323 | 2.5319 | 2.5320 | 2.5321 | 2.5323 |
| Location number | 3, 1 | 3, 2 | 3, 3 | 3, 4 | 4, 1 | 4, 2 | 4, 3 | 4, 4 |
| Correlation metric | 2.5327 | 2.5324 | 2.5319 | 2.5323 | 2.5324 | 2.5321 | 2.5326 | 2.5310 |
Table 25.
Correlation metrics for the first identification under 5% noise in Operational Condition 2.
Table 25.
Correlation metrics for the first identification under 5% noise in Operational Condition 2.
| | First Identification |
|---|
| Location number | 1, 2 | 1, 3 | 1, 4 | 2, 3 | 2, 4 | 3, 4 |
| Correlation metric | 3.1078 | 3.0921 | 3.1029 | 3.0980 | 3.1025 | 3.0838 |
Table 26.
Correlation metrics for the second identification under 5% noise in Operational Condition 2.
Table 26.
Correlation metrics for the second identification under 5% noise in Operational Condition 2.
| | Second Identification |
|---|
| Location number | 1, 1 | 1, 2 | 1, 3 | 1, 4 | 2, 1 | 2, 2 | 2, 3 | 2, 4 |
| Correlation metric | 3.1057 | 3.1051 | 3.1095 | 3.1096 | 3.1056 | 3.1054 | 3.1093 | 3.1090 |
| Location number | 3, 1 | 3, 2 | 3, 3 | 3, 4 | 4, 1 | 4, 2 | 4, 3 | 4, 4 |
| Correlation metric | 3.1062 | 3.1056 | 3.1087 | 3.1088 | 3.1071 | 3.1069 | 3.1082 | 3.1083 |
Table 27.
Correlation metrics for the third identification under 5% noise in Operational Condition 2.
Table 27.
Correlation metrics for the third identification under 5% noise in Operational Condition 2.
| | The Third Identification |
|---|
| Location number | 1, 1 | 1, 2 | 1, 3 | 1, 4 | 2, 1 | 2, 2 | 2, 3 | 2, 4 |
| Correlation metric | 3.1075 | 3.1079 | 3.1072 | 3.1083 | 3.1085 | 3.1084 | 3.1088 | 3.1095 |
| Location number | 3, 1 | 3, 2 | 3, 3 | 3, 4 | 4, 1 | 4, 2 | 4, 3 | 4, 4 |
| Correlation metric | 3.1088 | 3.1090 | 3.1089 | 3.1096 | 3.1090 | 3.1074 | 3.1097 | 3.1084 |
Table 28.
Correlation metrics for the first identification under 10% noise in Operational Condition 2.
Table 28.
Correlation metrics for the first identification under 10% noise in Operational Condition 2.
| | First Identification |
|---|
| Location number | 1, 2 | 1, 3 | 1, 4 | 2, 3 | 2, 4 | 3, 4 |
| Correlation metric | 2.5391 | 2.5311 | 2.5362 | 2.5339 | 2.5366 | 2.5273 |
Table 29.
Correlation metrics for the second identification under 10% noise in Operational Condition 2.
Table 29.
Correlation metrics for the second identification under 10% noise in Operational Condition 2.
| | Second Identification |
|---|
| Location number | 1, 1 | 1, 2 | 1, 3 | 1, 4 | 2, 1 | 2, 2 | 2, 3 | 2, 4 |
| Correlation metric | 2.5385 | 2.5382 | 2.5398 | 2.5399 | 2.5385 | 2.5384 | 2.5397 | 2.5397 |
| Location number | 3, 1 | 3, 2 | 3, 3 | 3, 4 | 4, 1 | 4, 2 | 4, 3 | 4, 4 |
| Correlation metric | 2.5383 | 2.5378 | 2.5392 | 2.5392 | 2.5387 | 2.5385 | 2.5391 | 2.5391 |
Table 30.
Correlation metrics for the third identification under 10% noise in Operational Condition 2.
Table 30.
Correlation metrics for the third identification under 10% noise in Operational Condition 2.
| | The Third Identification |
|---|
| Location number | 1, 1 | 1, 2 | 1, 3 | 1, 4 | 2, 1 | 2, 2 | 2, 3 | 2, 4 |
| Correlation metric | 2.5393 | 2.5395 | 2.5389 | 2.5394 | 2.5397 | 2.5396 | 2.5395 | 2.5398 |
| Location number | 3, 1 | 3, 2 | 3, 3 | 3, 4 | 4, 1 | 4, 2 | 4, 3 | 4, 4 |
| Correlation metric | 2.5397 | 2.5397 | 2.5395 | 2.5397 | 2.5397 | 2.5389 | 2.5399 | 2.5392 |
Table 31.
Excitation positions.
Table 31.
Excitation positions.
| | | Step-By-Step Recognition Method | True Value | /% |
|---|
| x/m | 0.1875 | 0.2 | 1.25 |
| y/m | 0.8125 | 0.8 |
| x/m | 0.8125 | 0.8 | 2.5 |
| y/m | 0.5625 | 0.6 |
Table 32.
Excitation positions of multi-point dynamic loads with 10% noise under operating condition 1.
Table 32.
Excitation positions of multi-point dynamic loads with 10% noise under operating condition 1.
| | | Step-By-Step Recognition Method | True Value | /% |
|---|
| x/m | 0.1875 | 0.2 | 7.5 |
| y/m | 0.9375 | 0.8 |
| x/m | 0.8125 | 0.8 | 2.5 |
| y/m | 0.5625 | 0.6 |
Table 33.
Comparison of computation for identification of multi-point dynamic loads between traditional and step-by-step methods.
Table 33.
Comparison of computation for identification of multi-point dynamic loads between traditional and step-by-step methods.
| | Number of Applied Loads | Number of Response Data | Number of Loads Applied in Traditional Method | Number of Responses Collected in Traditional Method |
|---|
| Step 1 | 12 | 24/54 | | |
| Step 2 | 44 | 88/198 |
| Step 3 | 76 | 152/342 |
Table 34.
The first 4 orders of the natural frequency of sheet metal (in Hz).
Table 34.
The first 4 orders of the natural frequency of sheet metal (in Hz).
| Modes Order | 1 | 2 | 3 | 4 |
|---|
| Experimental data | 18.0 | 62.5 | 112.5 | 204 |
| Modal modification | 18.5 | 61.5 | 114.8 | 207.9 |
Table 35.
Correlation metrics for first identification for various regions.
Table 35.
Correlation metrics for first identification for various regions.
| | A | B | C | D | E | F |
|---|
| 1 | 0.9069 | 0.9260 | 0.9386 | 0.9454 | 0.9478 | 0.9479 |
| 2 | 0.9267 | 0.9361 | 0.9444 | 0.9492 | 0.9503 | 0.9495 |
| 3 | 0.9171 | 0.9290 | 0.9397 | 0.9467 | 0.9487 | 0.9482 |
| 4 | 0.8786 | 0.9071 | 0.9269 | 0.9383 | 0.9430 | 0.9442 |
Table 36.
Correlation metrics for second identification for various regions.
Table 36.
Correlation metrics for second identification for various regions.
| | A | B | C |
|---|
| 1 | 0.9532 | 0.9534 | 0.9533 |
| 2 | 0.9536 | 0.9537 | 0.9536 |
| 3 | 0.9534 | 0.9535 | 0.9534 |