Ice Film Growth Thickness on Simulated Lunar Rock Surfaces as a Function of Controlled Water Vapor Concentration
Abstract
1. Introduction
2. Water Molecule Generation and Adsorption Model on Particulate Surfaces
2.1. Water Molecule Generation and Adsorption Equations
2.2. Water Molecule Diffusion Equilibrium Equation
2.3. Numerical Calculation of Water Molecule Generation and Adsorption Equilibrium
2.3.1. Numerical Calculation of the Relationship Between Water Ice Sublimation Velocity
- (1)
- The relationship between sublimation speed and temperature
- (2)
- The relationship between sublimation speed and time
2.3.2. Numerical Calculation of Equilibrium Concentration in the System
3. Control Model of Water Molecule Flow Generation Rate and Its Detection Method
3.1. Simulation of Water Ice Sublimation Process and Concentration Control
3.1.1. Finite Element Model Construction and Parameter Setting
3.1.2. Analysis of Finite Element Simulation Results
- (1)
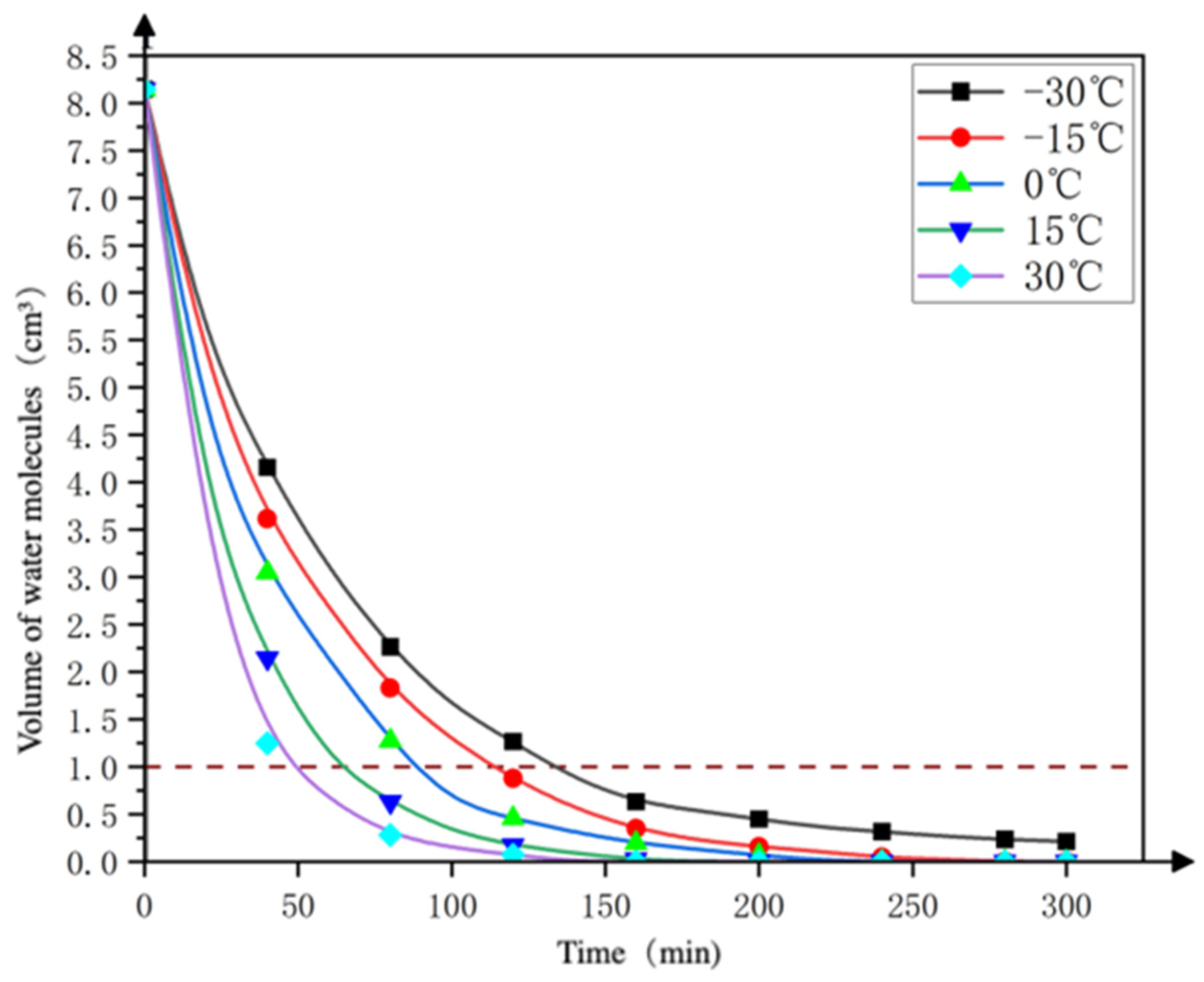
- Volume change of water ice
- (2).
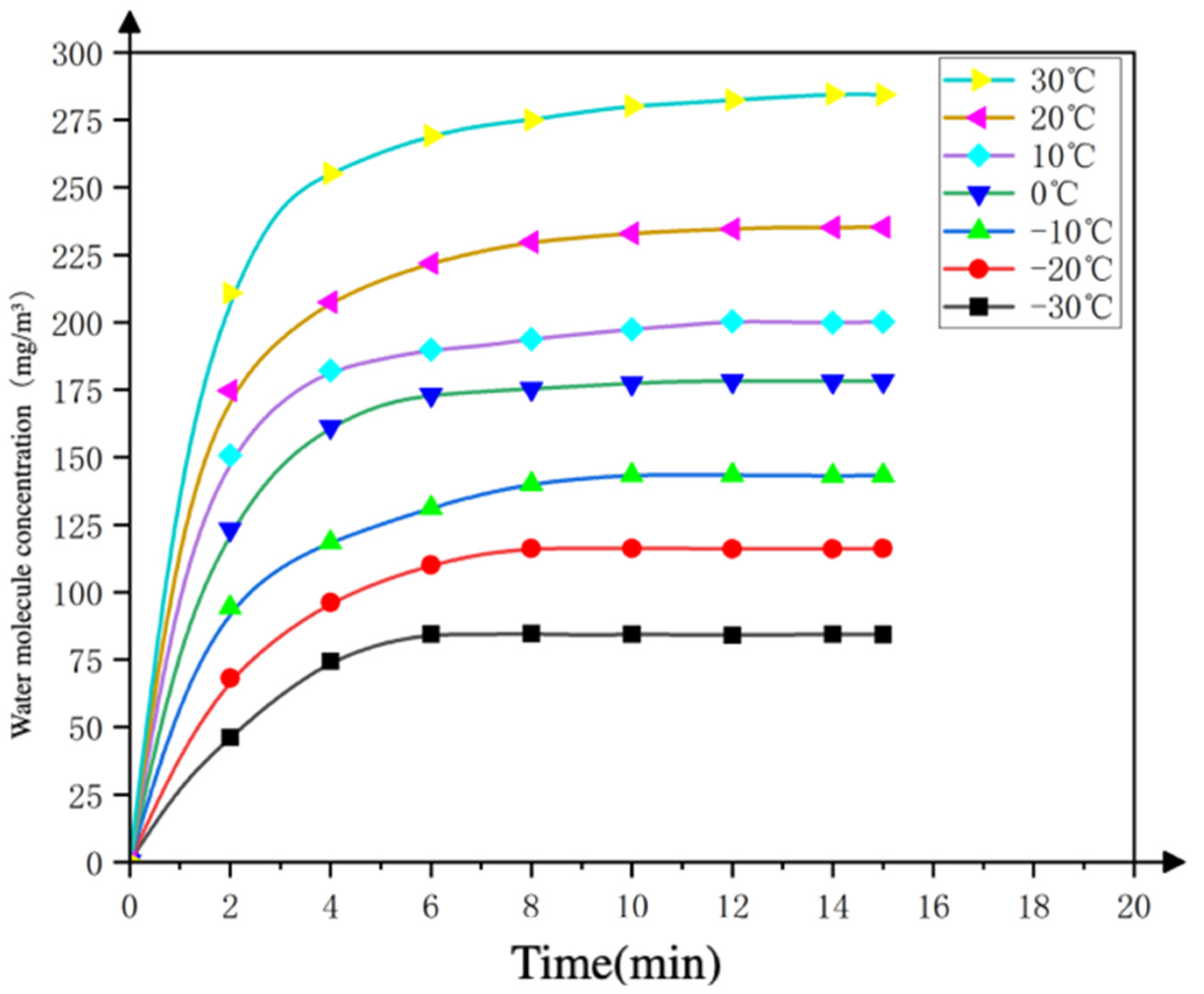
- Changes in the concentration of water molecules inside the device
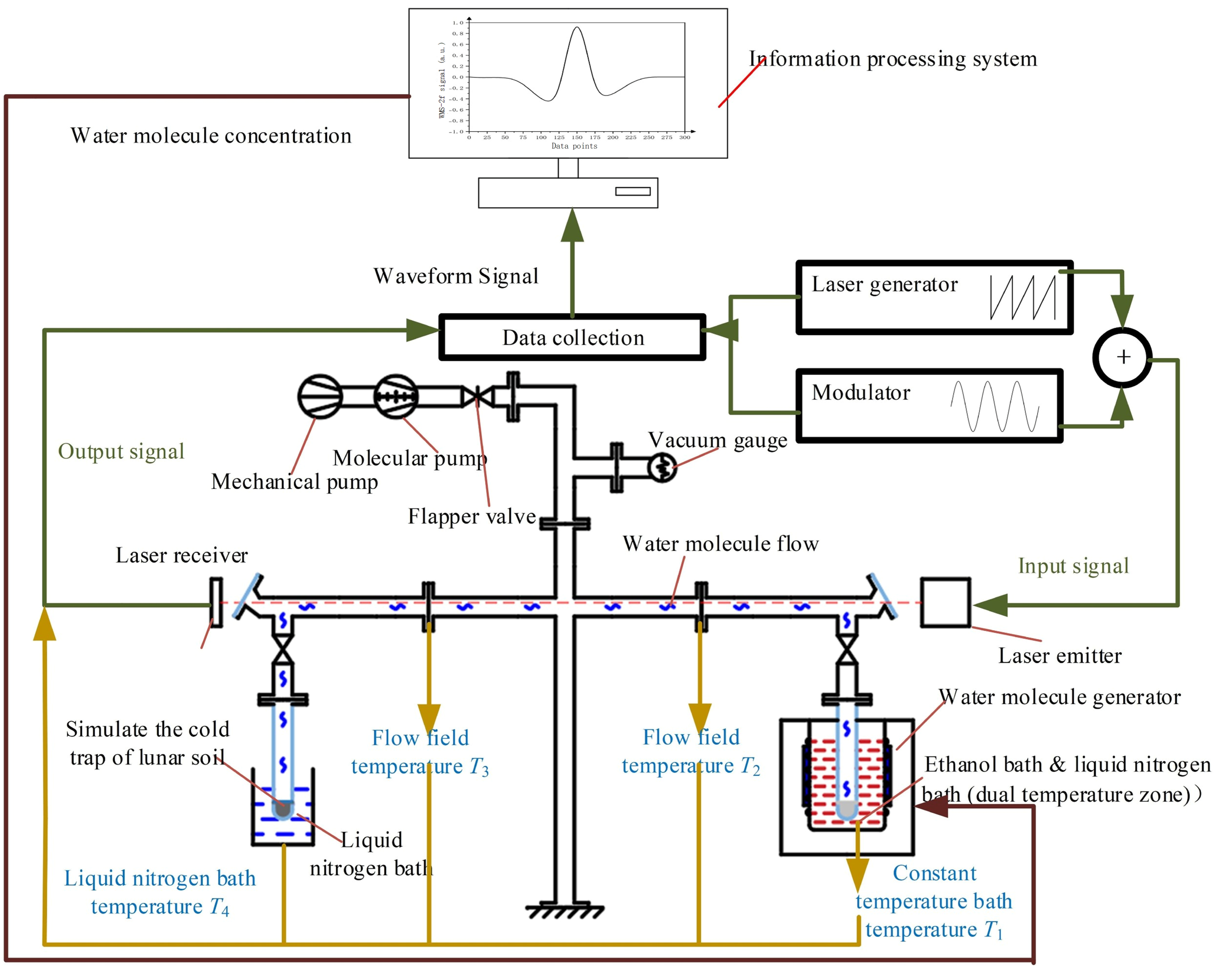
3.2. Construction of Water Molecule Flow Field Generation Control and Concentration Detection System
3.3. Analysis of the Test Results of Flow Field Generation Control and Concentration Detection
3.3.1. Accuracy Verification of Water Molecule Detection by TDLAS
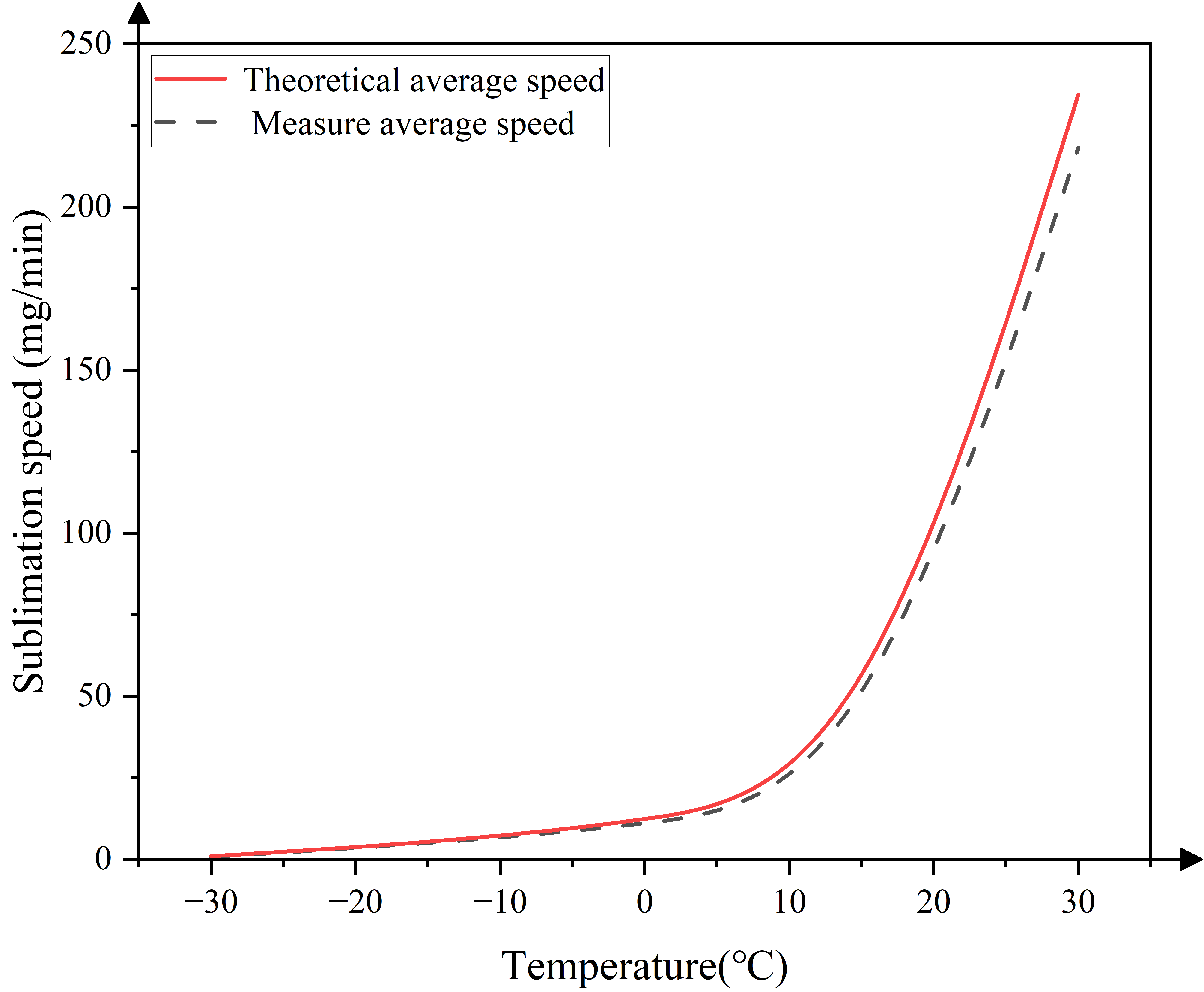
3.3.2. Comparative Analysis of Water Ice Sublimation Theory and Simulation
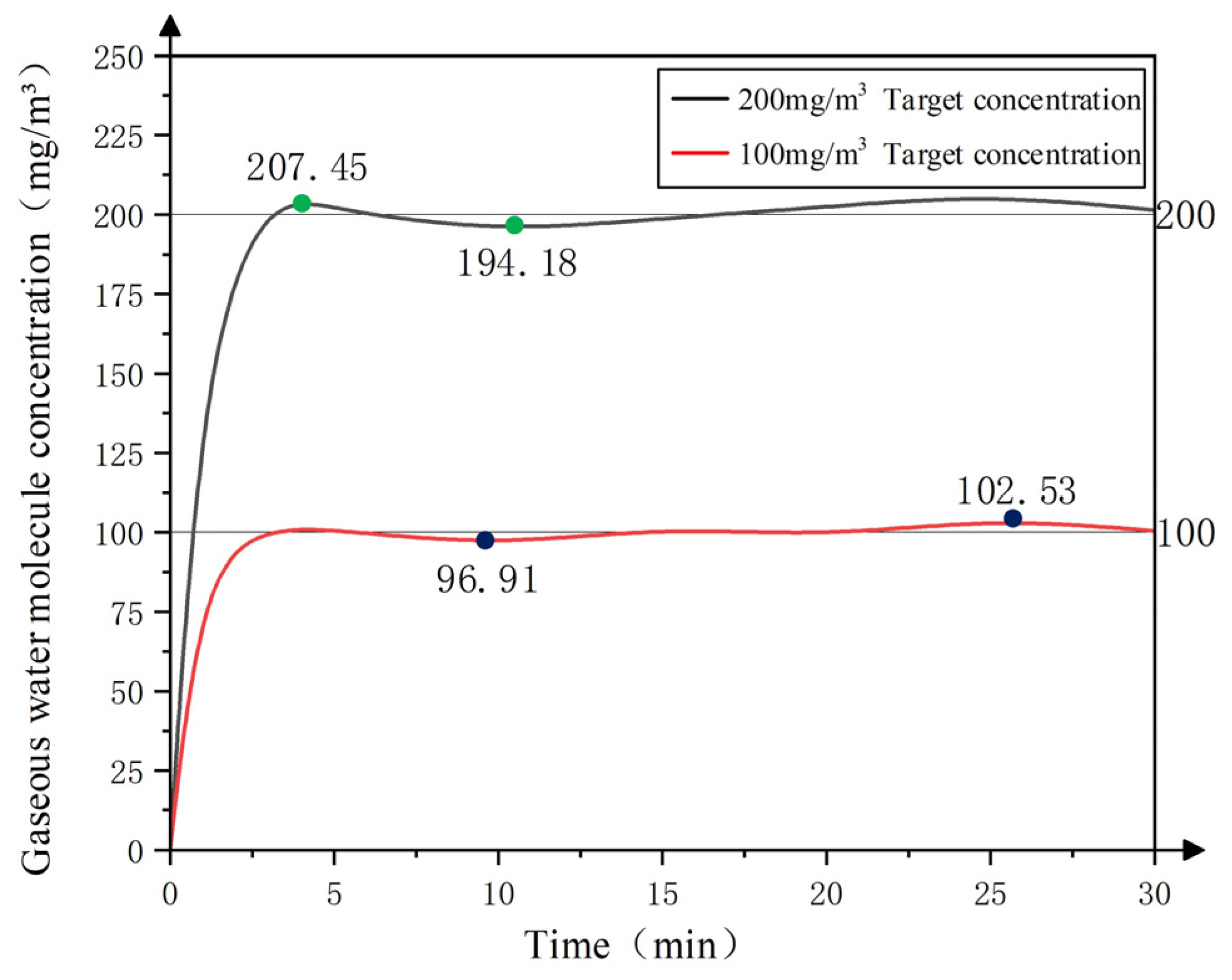
3.3.3. Performance Test of the Water Molecule Concentration Detection System
4. Test on the Thickness of Water Molecule Adsorption Deposition on the Surface of Simulated Lunar Rock
4.1. Design and Construction of Water Molecule Adsorption Deposition Inspection System
4.2. Test Results of Water Molecule Deposition Adsorption
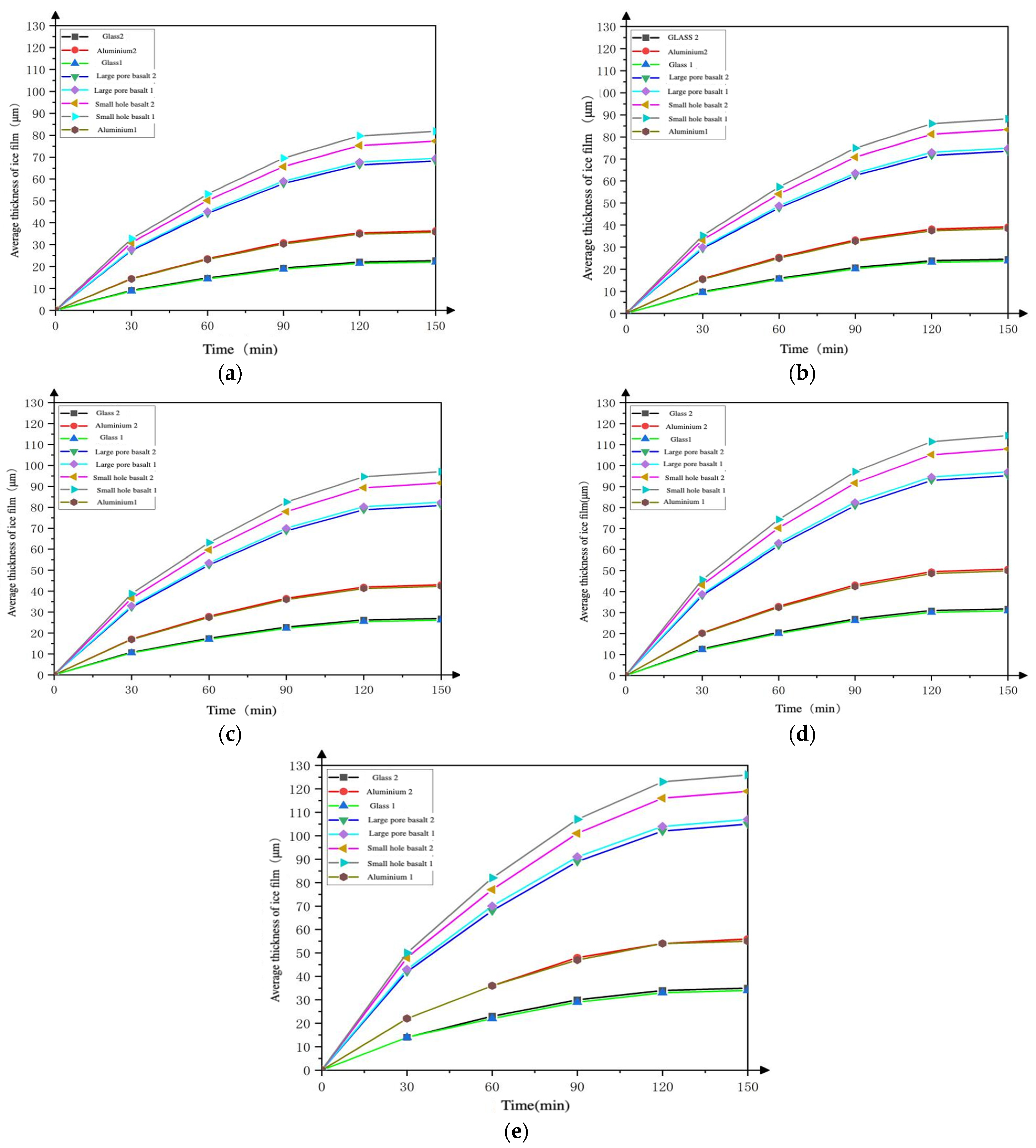
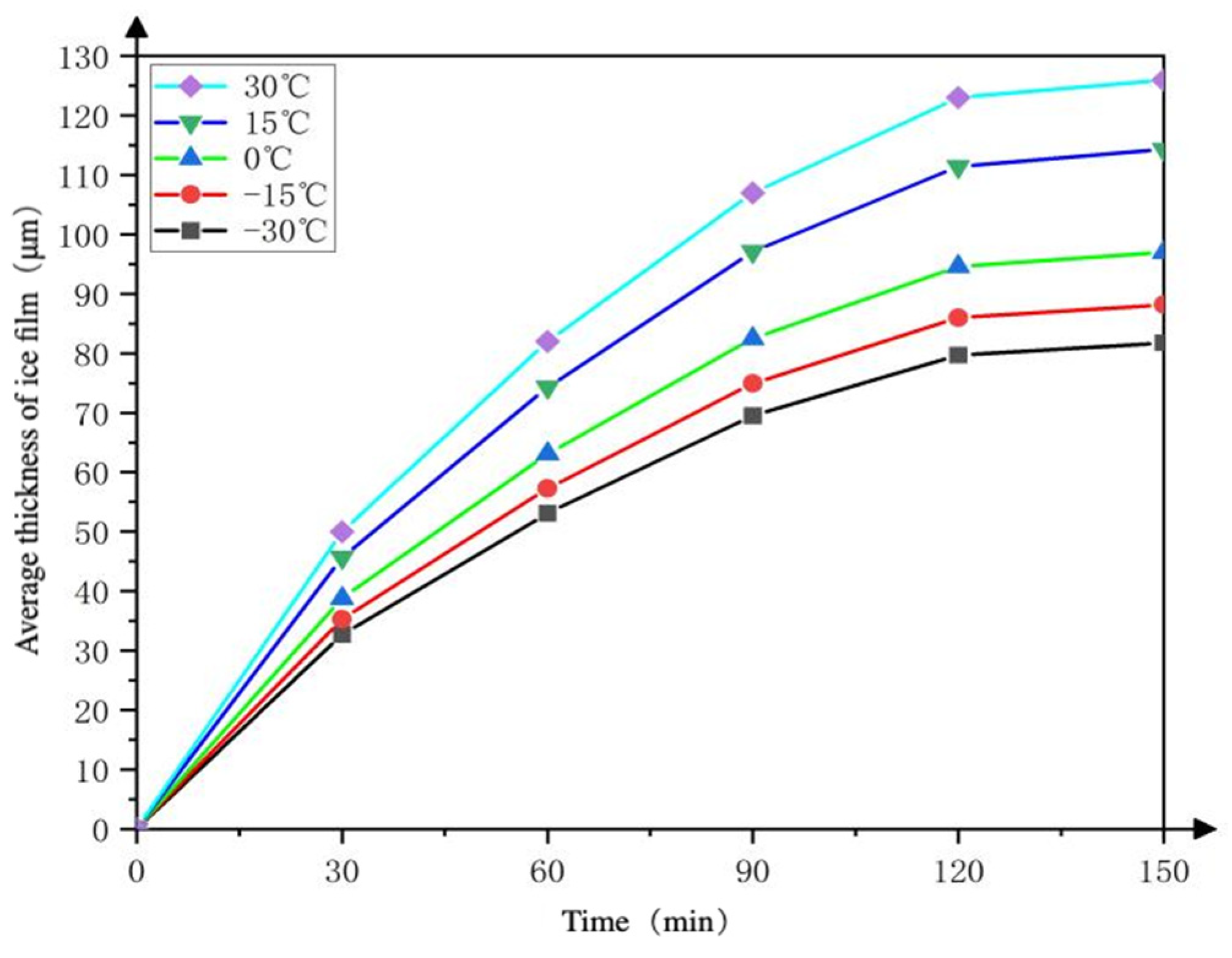
4.2.1. The Thickness of the Deposited Adsorption Ice Film
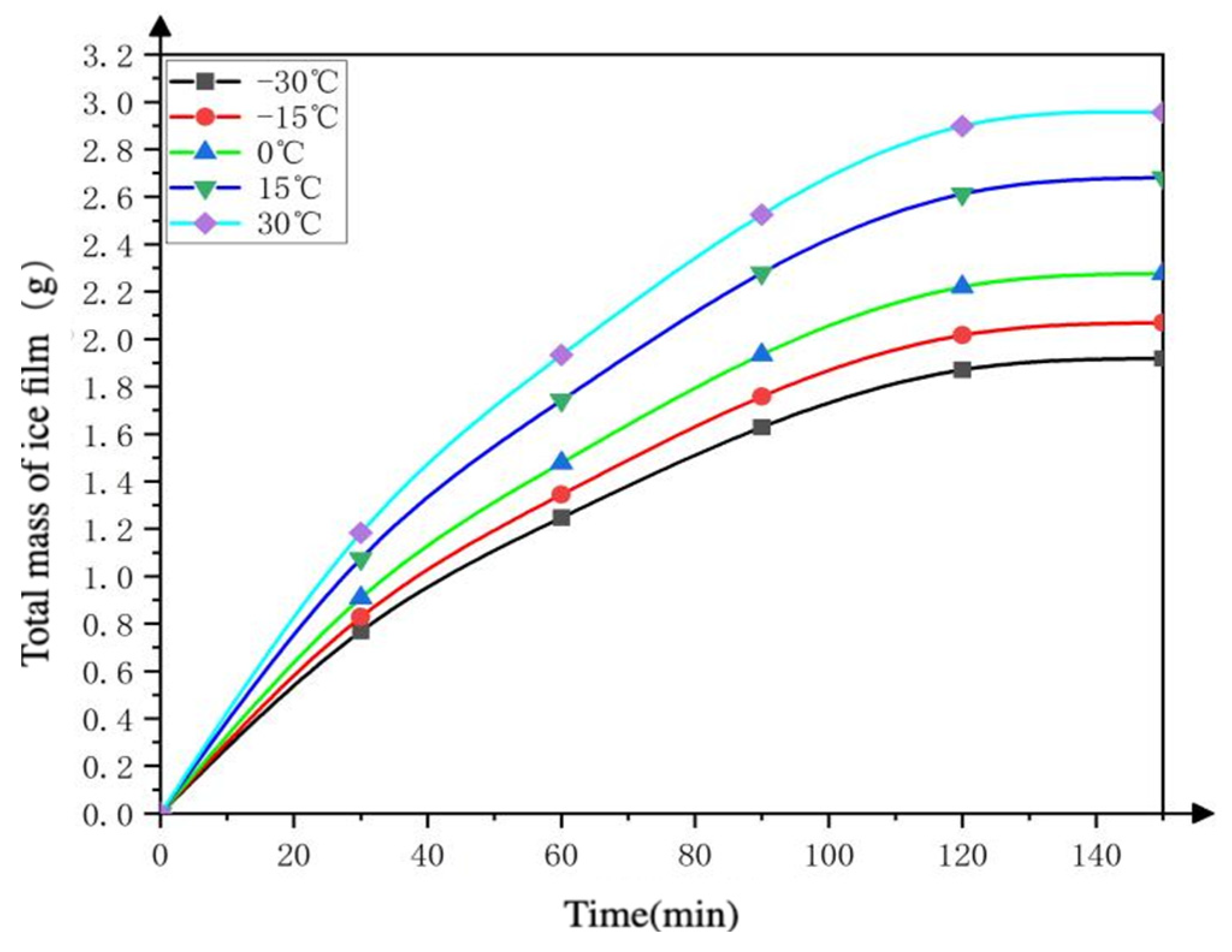
4.2.2. The Total Mass of the Deposited Adsorption Ice Film
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| TDLAS | Tunable Diode Laser Absorption Spectroscopy |
| A2 | The heat conduction area of Ninghua (m2) |
| J | Sublimation rate (kg/(m2·s)) |
| mice | The quality of the water ice (kg) |
| n | The amount of water molecular substances in the device (mol) |
| P0 | Known reference barometric pressure (kg/s) |
| Ps1 | Sublimate the actual air pressure on the surface (Pa) |
| Ps2 | The actual air pressure on the surface of Ninghua (Pa) |
| Pv(T1) | Equilibrium vapor pressure of ice at temperature T1 (Pa) |
| Pv(T2) | Saturated vapor pressure of ice at temperature T2 (Pa) |
| T0 | Known reference temperature (K) |
| T1 | Absolute temperature at sublimation (K) |
| The condensation rate of water molecules (kg/s) | |
| Vdev | The volume of the vapor deposition device (m3) |
References
- Nozette, S.; Rustan, P.; Pleasance, L.P.; Kordas, J.F.; Lewis, I.T.; Park, H.S.; Priest, R.E.; Horan, D.M.; Regeon, P.; Lichtenberg, C.L.; et al. The Clementine Mission to the Moon: Scientific Overview. Science 1994, 266, 1835–1839. [Google Scholar] [CrossRef]
- Nozette, S.; Lichtenberg, C.L.; Spudis, P.; Bonner, R.; Ort, W.; Malaret, E.; Robinson, M.; Shoemaker, E.M. The Clementine Bistatic Radar Experiment. Science 1996, 274, 1495–1498. [Google Scholar] [CrossRef]
- Sorensen, T.C.; Spudis, P.D. The Clementine Mission—A 10-Year Perspective. J. Earth Syst. Sci. 2005, 114, 645–668. [Google Scholar] [CrossRef]
- Binder, A.B. Lunar Prospector: Overview. Science 1998, 281, 1475–1476. [Google Scholar] [CrossRef] [PubMed]
- Feldman, W.C.; Maurice, S.; Binder, A.B.; Barraclough, B.L.; Elphic, R.C.; Lawrence, D.J. Fluxes of Fast and Epithermal Neutrons from Lunar Prospector: Evidence for Water Ice at the Lunar Poles. Science 1998, 281, 1496–1500. [Google Scholar] [CrossRef] [PubMed]
- Prettyman, T.H.; Hagerty, J.J.; Elphic, R.C.; Feldman, W.C.; Lawrence, D.J.; McKinney, G.W.; Vaniman, D.T. Elemental Composition of the Lunar Surface: Analysis of Gamma Ray Spectroscopy Data from Lunar Prospector. J. Geophys. Res. Planets 2006, 111, 2005JE002656. [Google Scholar] [CrossRef]
- Goswami, J.N.; Annadurai, M. Chandrayaan-1 Mission to the Moon. Acta Astronaut. 2008, 63, 1215–1220. [Google Scholar] [CrossRef]
- Putrevu, D.; Das, A.; Vachhani, J.G.; Trivedi, S.; Misra, T. Chandrayaan-2 Dual-Frequency SAR: Further Investigation into Lunar Water and Regolith. Adv. Space Res. 2016, 57, 627–646. [Google Scholar] [CrossRef]
- Barnes, J.J.; Tartèse, R.; Anand, M.; McCubbin, F.M.; Franchi, I.A.; Starkey, N.A.; Russell, S.S. The Origin of Water in the Primitive Moon as Revealed by the Lunar Highlands Samples. Earth Planet. Sci. Lett. 2014, 390, 244–252. [Google Scholar] [CrossRef]
- Hu, Z.-X. Review on Lunar Exploration of Water-Ice. Spacecr. Eng. 2010, 5, 111–116. [Google Scholar] [CrossRef]
- Zhang, D.-H.; Zhang, C.-H.; Liu, R.; Jiang, Y.-G. Lunar water ice detection based on Mini-RF radar data. Remote Sens. Land Resour. 2014, 26, 110–114. [Google Scholar] [CrossRef]
- Feldman, W.C.; Maurice, S.; Lawrence, D.J.; Little, R.C.; Lawson, S.L.; Gasnault, O.; Wiens, R.C.; Barraclough, B.L.; Elphic, R.C.; Prettyman, T.H.; et al. Evidence for Water Ice near the Lunar Poles. J. Geophys. Res. Planets 2001, 106, 23231–23251. [Google Scholar] [CrossRef]
- Schultz, P.H.; Hermalyn, B.; Colaprete, A.; Ennico, K.; Shirley, M.; Marshall, W.S. The LCROSS Cratering Experiment. Science 2010, 330, 468–472. [Google Scholar] [CrossRef]
- Zheng, Y.-C.; Zou, Y.-L.; Fu, X.-H. LRO and LCROSS Missions: Overview and Enlightenment for Future Lunar Exploration. Spacecr. Eng. 2011, 20, 117–129. [Google Scholar] [CrossRef]
- Li, C.; Hu, H.; Yang, M.-F.; Pei, Z.-Y.; Zhou, Q.; Ren, X.; Liu, B.; Liu, D.; Zeng, X.; Zhang, G.; et al. Characteristics of the Lunar Samples Returned by the Chang’E-5 Mission. Natl. Sci. Rev. 2022, 9, nwab188. [Google Scholar] [CrossRef]
- Lin, H.; Li, S.; Xu, R.; Liu, Y.; Wu, X.; Yang, W.; Wei, Y.; Lin, Y.; He, Z.; Hui, H.; et al. In Situ Detection of Water on the Moon by the Chang’E-5 Lander. Sci. Adv. 2022, 8, eabl9174. [Google Scholar] [CrossRef]
- Liu, J.; Liu, B.; Ren, X.; Li, C.; Shu, R.; Guo, L.; Yu, S.; Zhou, Q.; Liu, D.; Zeng, X.; et al. Evidence of Water on the Lunar Surface from Chang’E-5 in-Situ Spectra and Returned Samples. Nat. Commun. 2022, 13, 3119. [Google Scholar] [CrossRef]
- Vondrak, R.; Keller, J.; Chin, G.; Garvin, J. Lunar Reconnaissance Orbiter (LRO): Observations for Lunar Exploration and Science. Space Sci. Rev. 2010, 150, 7–22. [Google Scholar] [CrossRef]
- Chakraborty, T.; Syed, T.H.; Heggy, E.; Putrevu, D.; Dutta, U. On the Reachability and Genesis of Water Ice on the Moon. ISPRS J. Photogramm. Remote Sens. 2024, 211, 392–405. [Google Scholar] [CrossRef]
- Gundlach, B.; Skorov, Y.; Blum, J. Outgassing of Icy Bodies in the Solar System-I. The Sublimation of Hexagonal Water Ice through Dust Layers. Icarus 2011, 213, 710–719. [Google Scholar] [CrossRef]
- Andreas, E.L. New Estimates for the Sublimation Rate for Ice on the Moon. Icarus 2007, 186, 24–30. [Google Scholar] [CrossRef]
- Vasavada, A. Near-Surface Temperatures on Mercury and the Moon and the Stability of Polar Ice Deposits. Icarus 1999, 141, 179–193. [Google Scholar] [CrossRef]
- Paige, D.A.; Siegler, M.A.; Zhang, J.A.; Hayne, P.O.; Foote, E.J.; Bennett, K.A.; Vasavada, A.R.; Greenhagen, B.T.; Schofield, J.T.; McCleese, D.J.; et al. Diviner Lunar Radiometer Observations of Cold Traps in the Moon’s South Polar Region. Science 2010, 330, 479–482. [Google Scholar] [CrossRef] [PubMed]



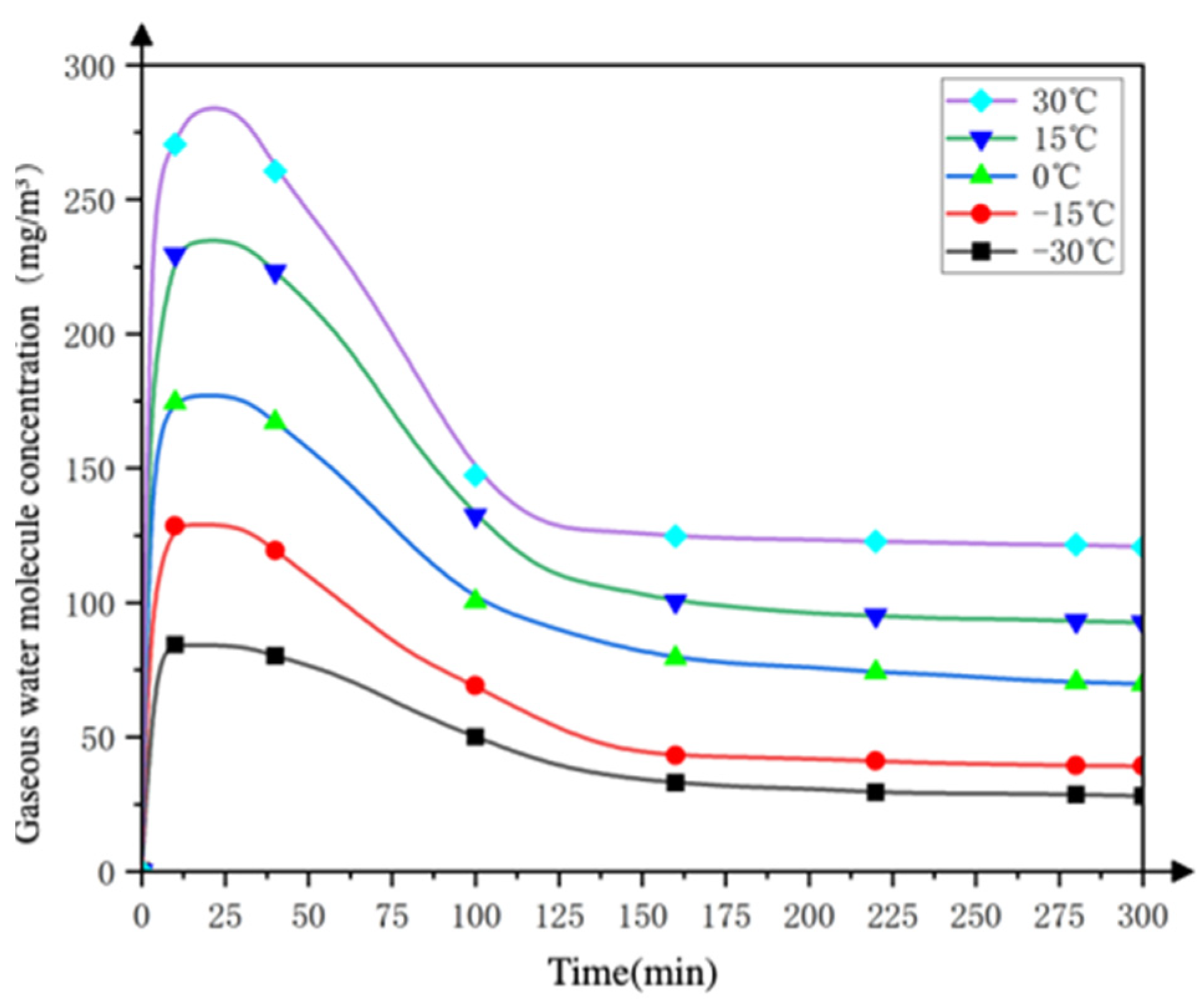







| Parameter Name | Numeric Value |
|---|---|
| Sublimated heat conduction area, A1 | 3.96 × 10−3 m2 |
| The heat conduction area of sublimation, A2 | 0.9765 m2 |
| The total volume of gas in the device, V | 2.646 × 10−3 m3 |
| Thermal conductivity of aluminum, kalu | 220 W/(m·K) |
| The thermal conductivity of borosilicate glass, kglass | 0.9 W/(m·K) |
| Simulate the thermal conductivity of lunar soil, klunar soil | 0.3 W/(m·K) |
| The initial air pressure inside the device, P0 | 10−2 Pa |
| Simulate the temperature of the lunar soil cold trap, T2 | −196 °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Wang, D.; Xu, W.; Tian, Y.; Bai, F.; Xiao, W.; Zhuang, M.; Lin, Y.; Guo, J.; Jiang, S. Ice Film Growth Thickness on Simulated Lunar Rock Surfaces as a Function of Controlled Water Vapor Concentration. Aerospace 2025, 12, 946. https://doi.org/10.3390/aerospace12110946
Zhang W, Wang D, Xu W, Tian Y, Bai F, Xiao W, Zhuang M, Lin Y, Guo J, Jiang S. Ice Film Growth Thickness on Simulated Lunar Rock Surfaces as a Function of Controlled Water Vapor Concentration. Aerospace. 2025; 12(11):946. https://doi.org/10.3390/aerospace12110946
Chicago/Turabian StyleZhang, Weiwei, Desen Wang, Wei Xu, Ye Tian, Fenghe Bai, Wentao Xiao, Minghui Zhuang, Yanbing Lin, Jingrun Guo, and Shengyuan Jiang. 2025. "Ice Film Growth Thickness on Simulated Lunar Rock Surfaces as a Function of Controlled Water Vapor Concentration" Aerospace 12, no. 11: 946. https://doi.org/10.3390/aerospace12110946
APA StyleZhang, W., Wang, D., Xu, W., Tian, Y., Bai, F., Xiao, W., Zhuang, M., Lin, Y., Guo, J., & Jiang, S. (2025). Ice Film Growth Thickness on Simulated Lunar Rock Surfaces as a Function of Controlled Water Vapor Concentration. Aerospace, 12(11), 946. https://doi.org/10.3390/aerospace12110946







