Study on Thermal Stratification and Heat Transfer Characteristics in a Fuel Tank of Hypersonic Vehicles
Abstract
1. Introduction
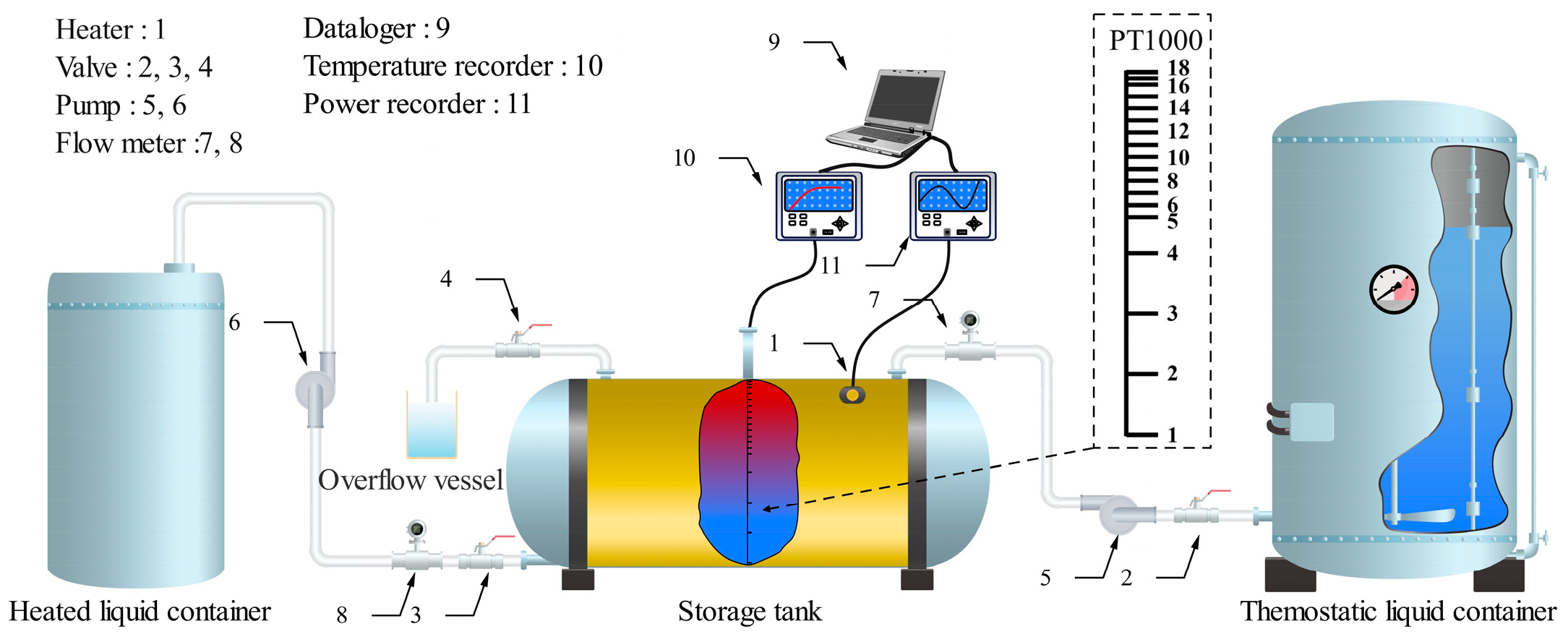
2. Experiment System
- To begin, activate the stirring apparatus in the thermostatic liquid container. Adjust the thermostat to ensure that the temperature of the inlet fluid remains constant and uniformly distributed.
- Open valves 2 and 4 while closing valve 3. Start pump 5 to transport the fluid from the thermostatic liquid container to the tank. Monitor flow meter 7 and regulate the pump flow rate to prevent any damage to the thermocouple caused by excessive flow. When a small amount of fluid overflows into the overflow vessel, close valve 2.
- Monitor the thermocouple readings. Once the temperature distribution is steady, switch on the heater and simultaneously activate the temperature and power recorder.
- After heating for 1600s, turn off the heater, temperature recorder, and power recorder. Open valve 3, activate pump 8, and transfer the heated fluid to the heated liquid container while observing flow meter 8. Once the fluid has been transferred, close valve 3 and stop pump 8.
3. Numerical Simulation
3.1. Numerical Method
3.2. Physical Parameters and Boundary Conditions
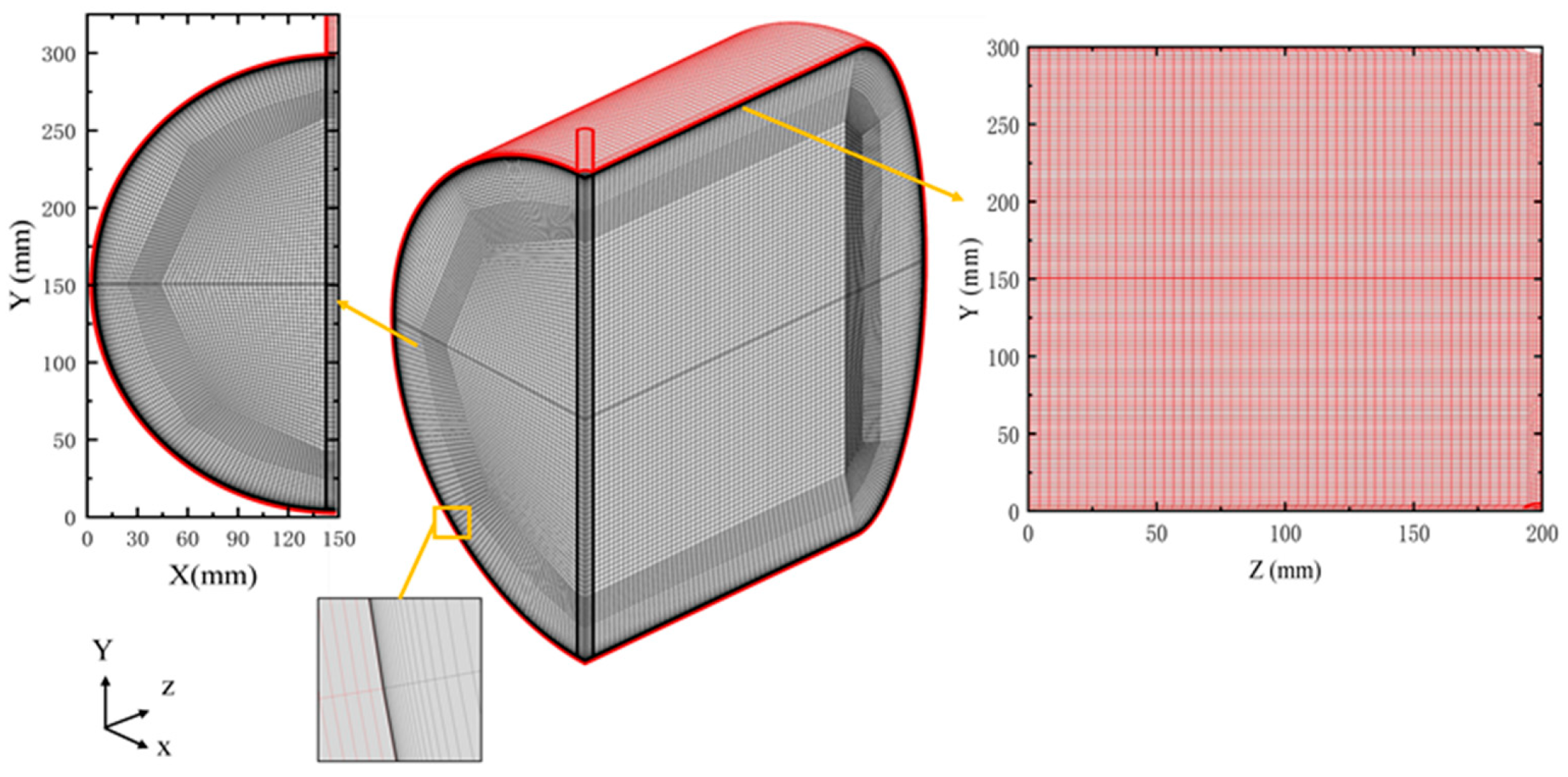
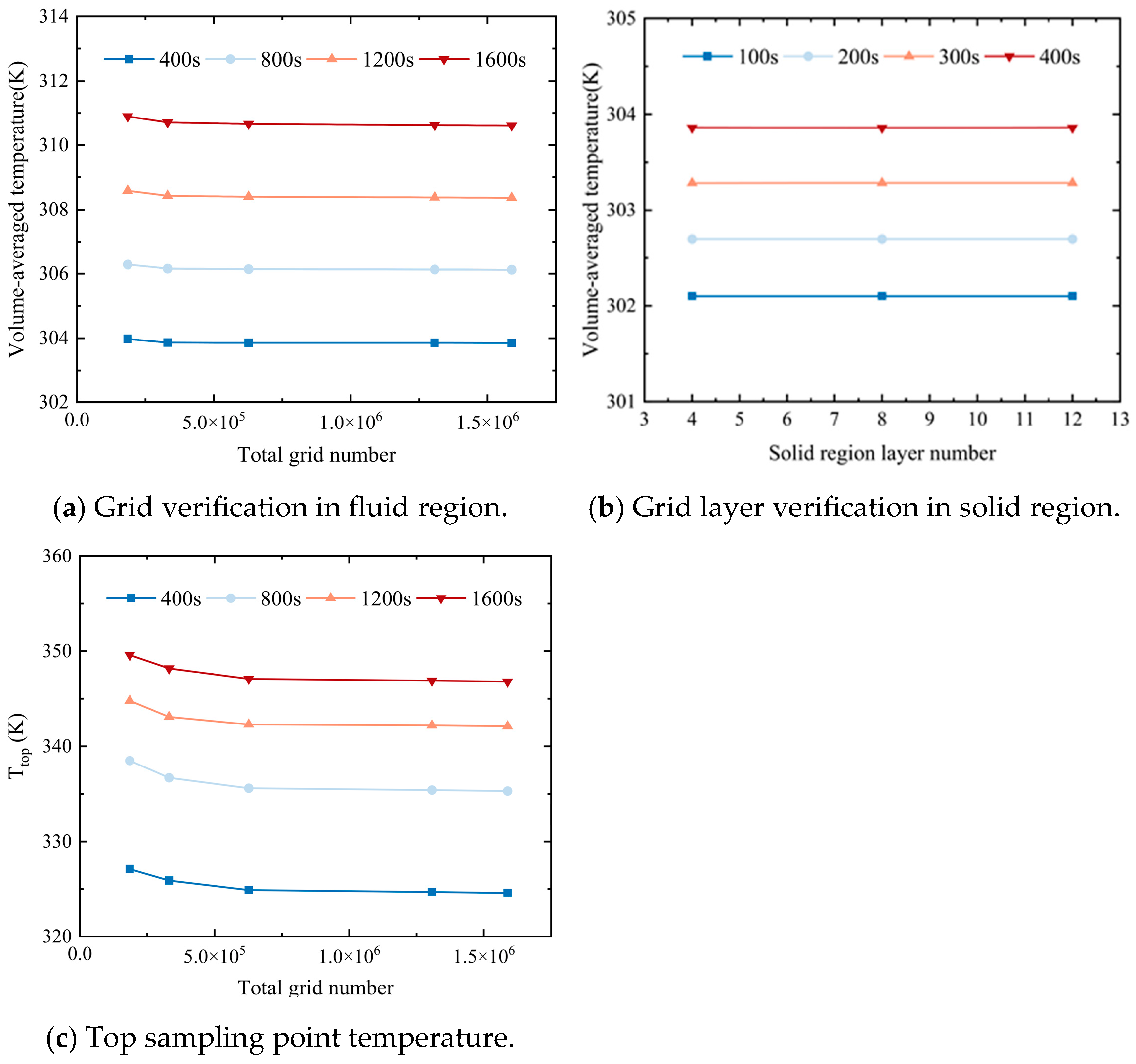
3.3. Grid Convergence
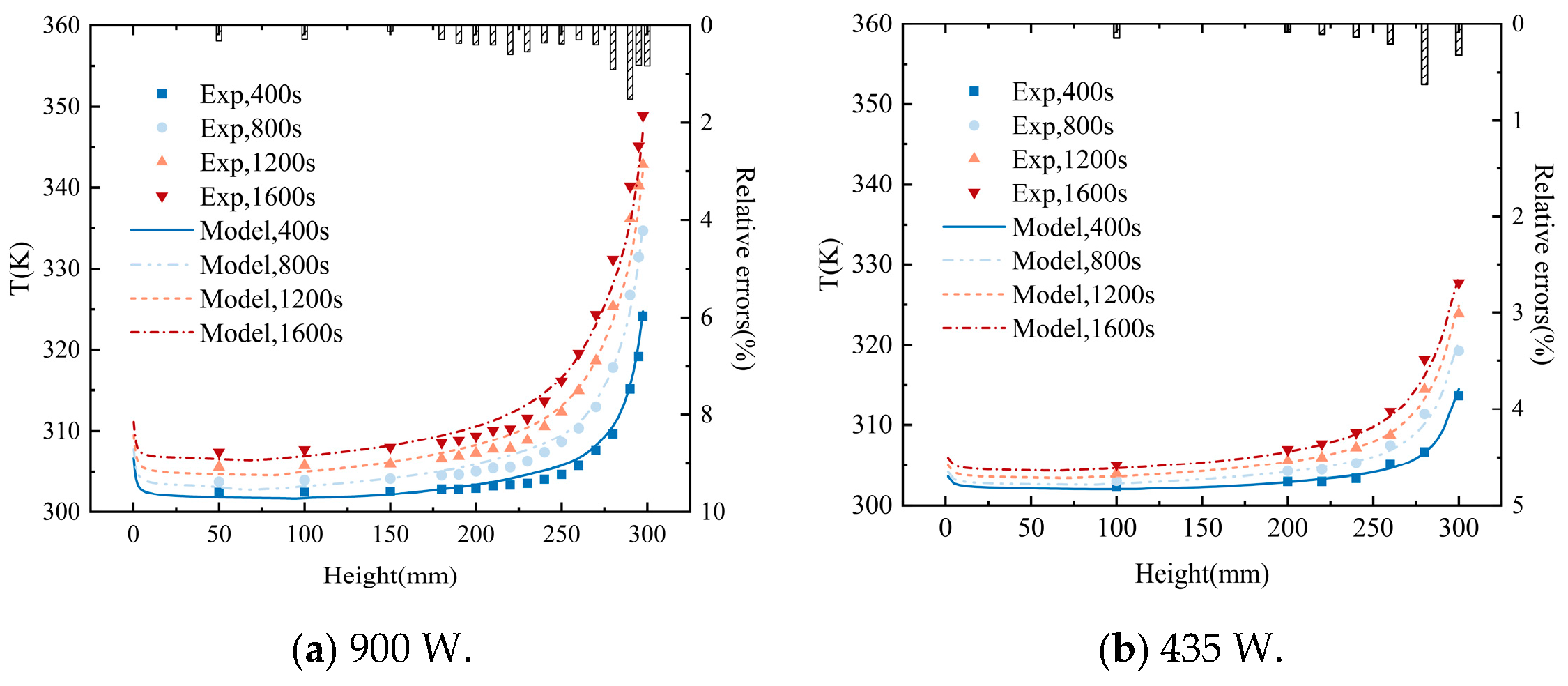
3.4. Validation of Numerical Methods
4. Theoretical Analysis Method
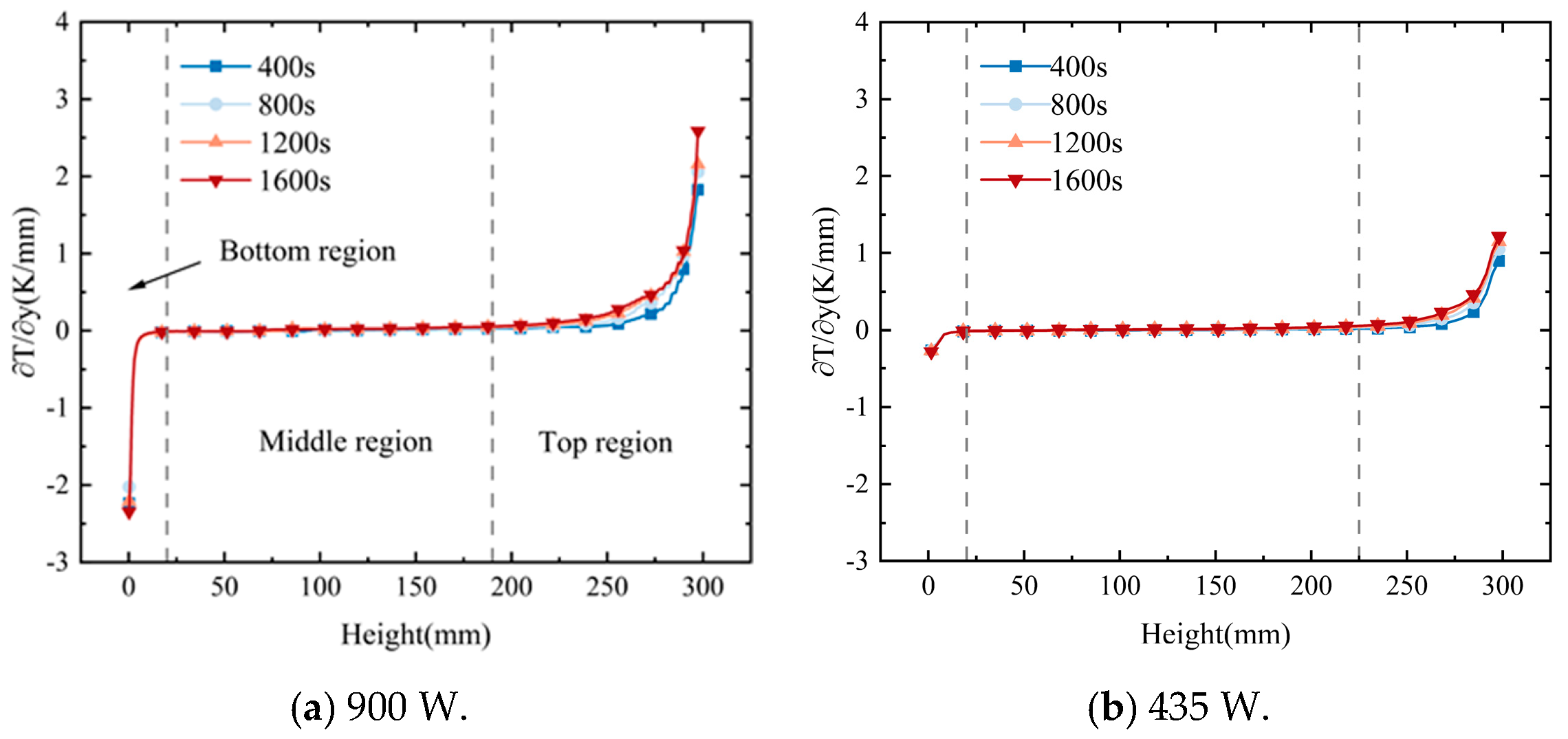
4.1. Quantification of Thermal Stratification
4.2. Field Synergy Principle
5. Results and Discussion
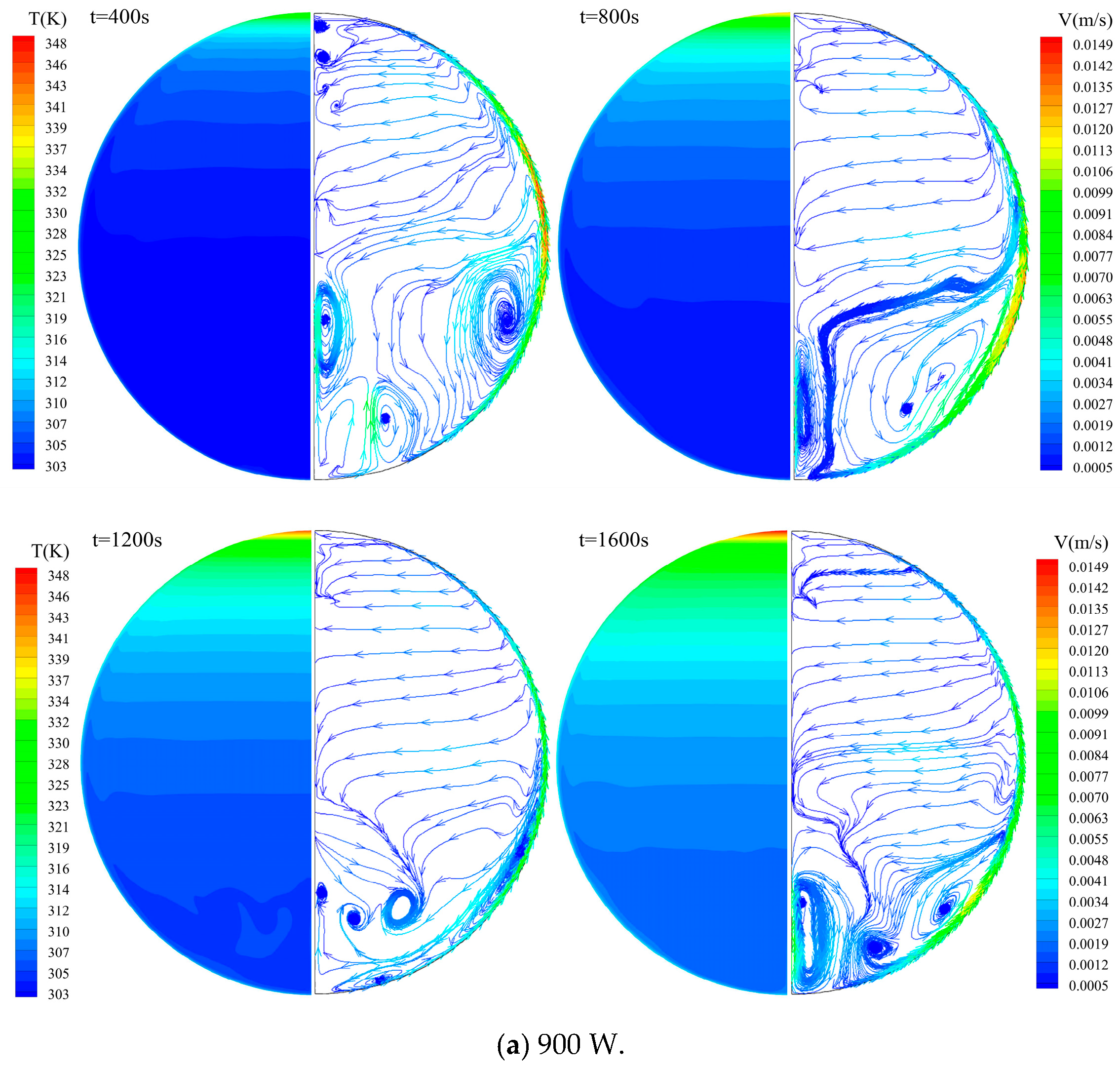
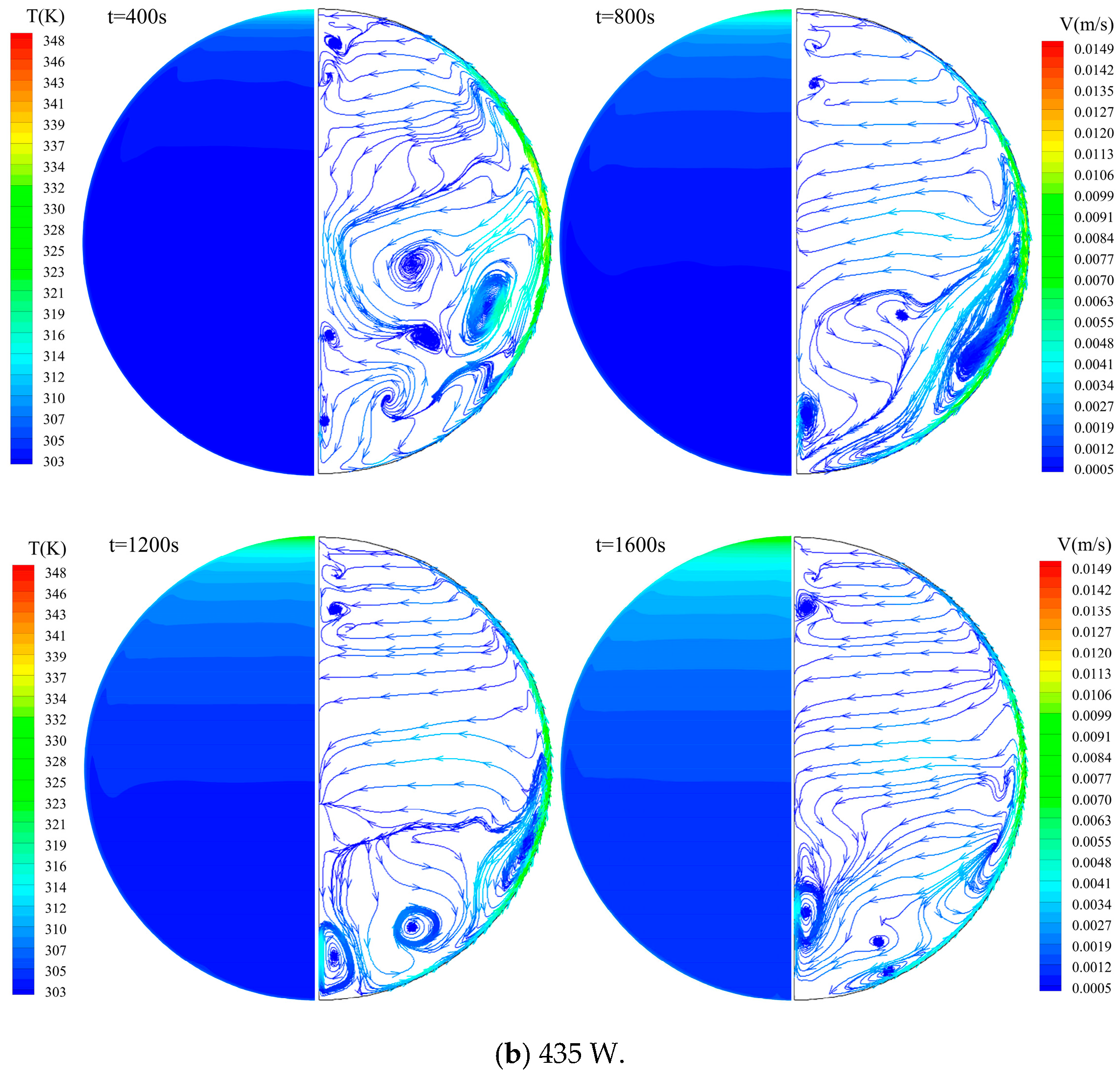
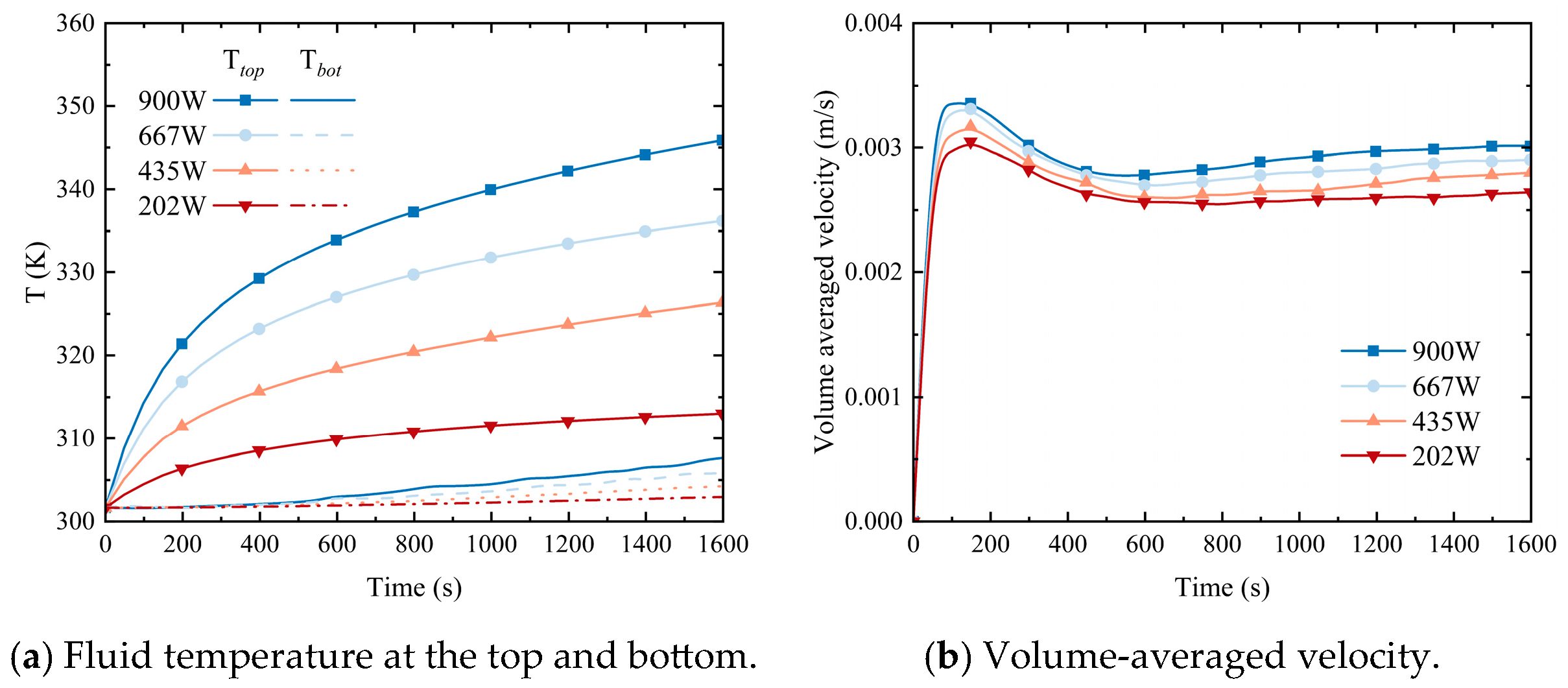
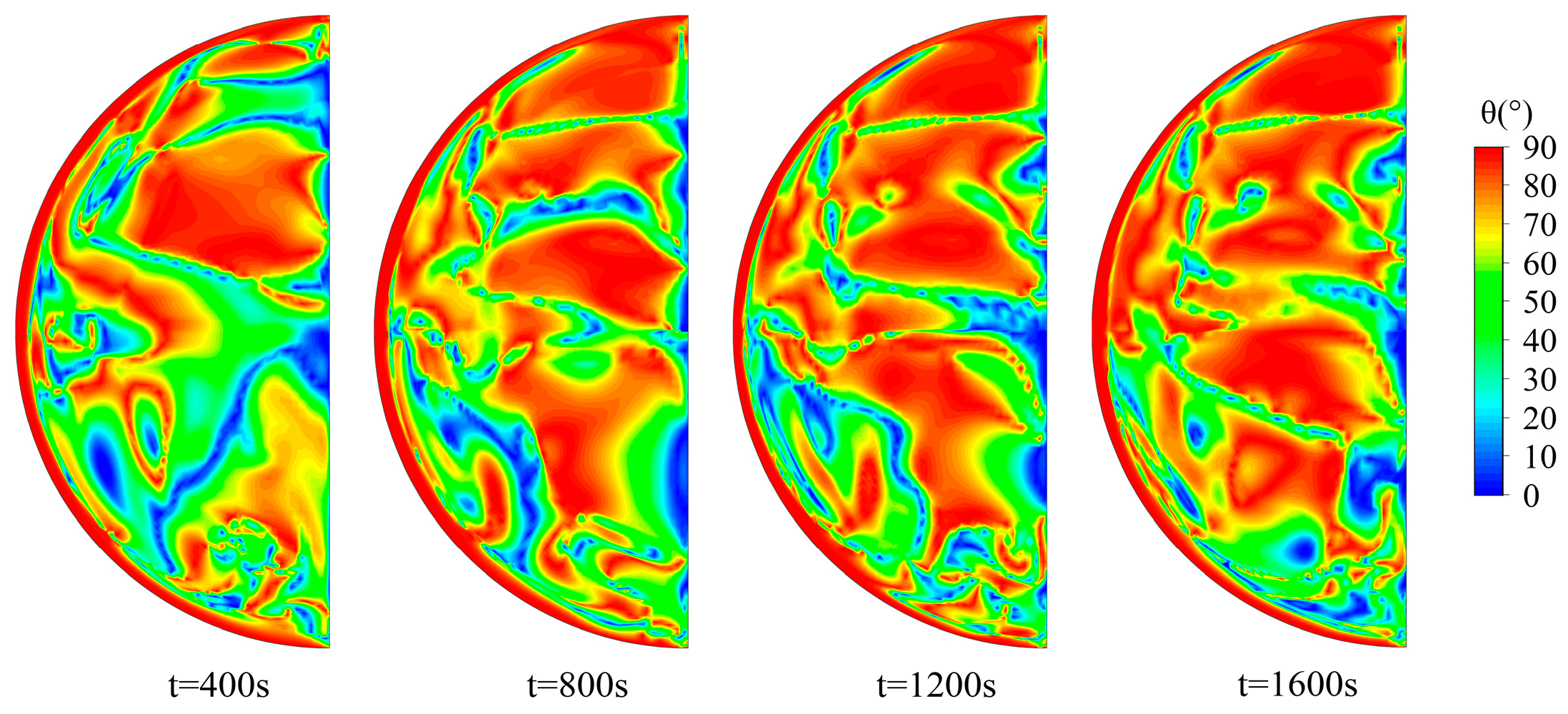
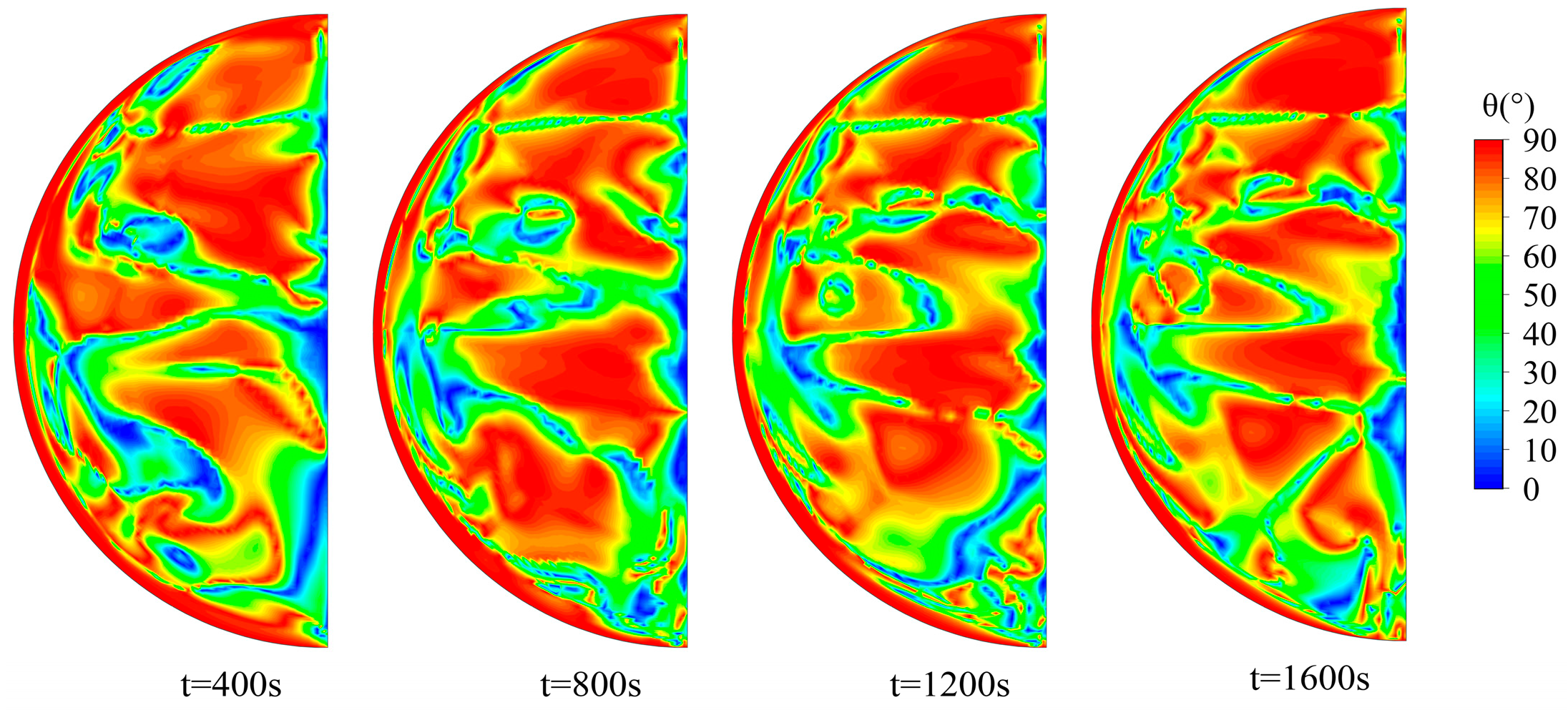
5.1. Temperature and Flow Field Distribution
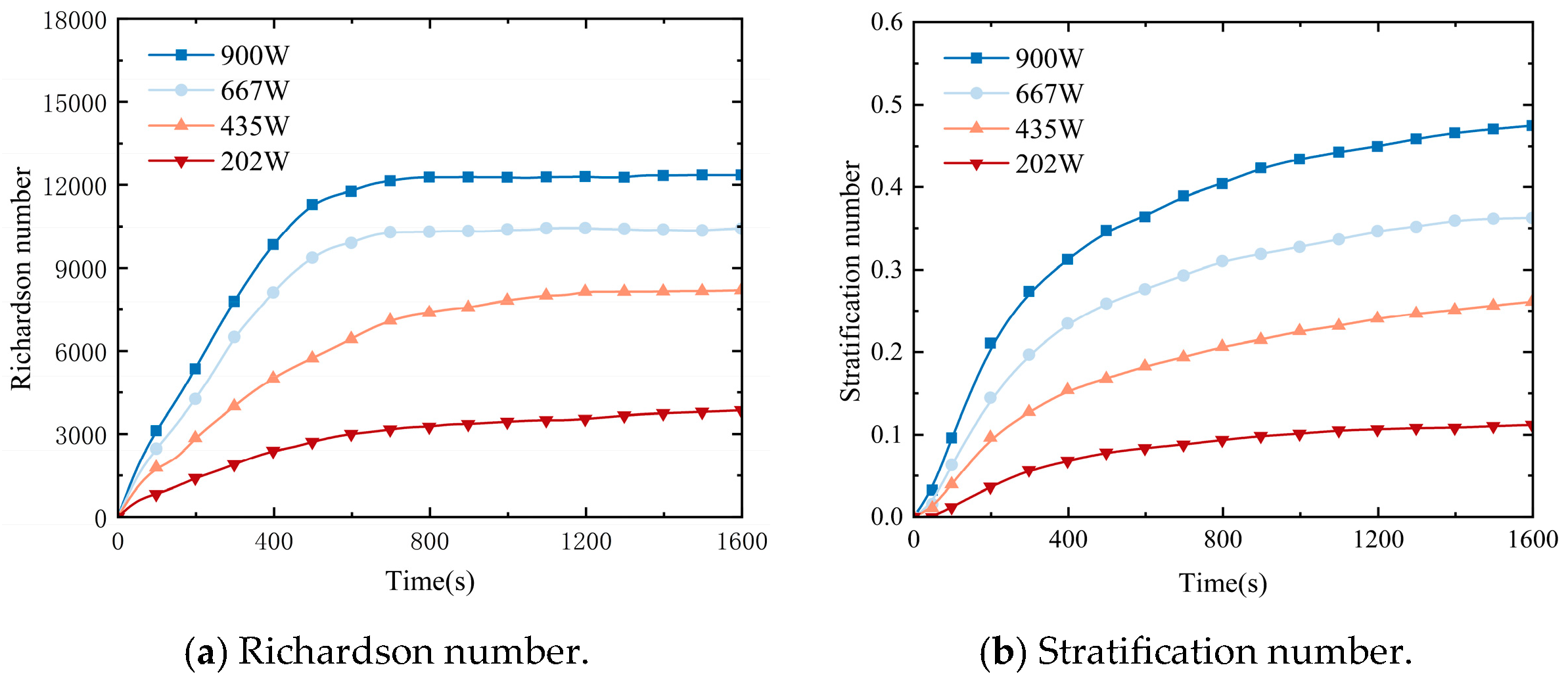
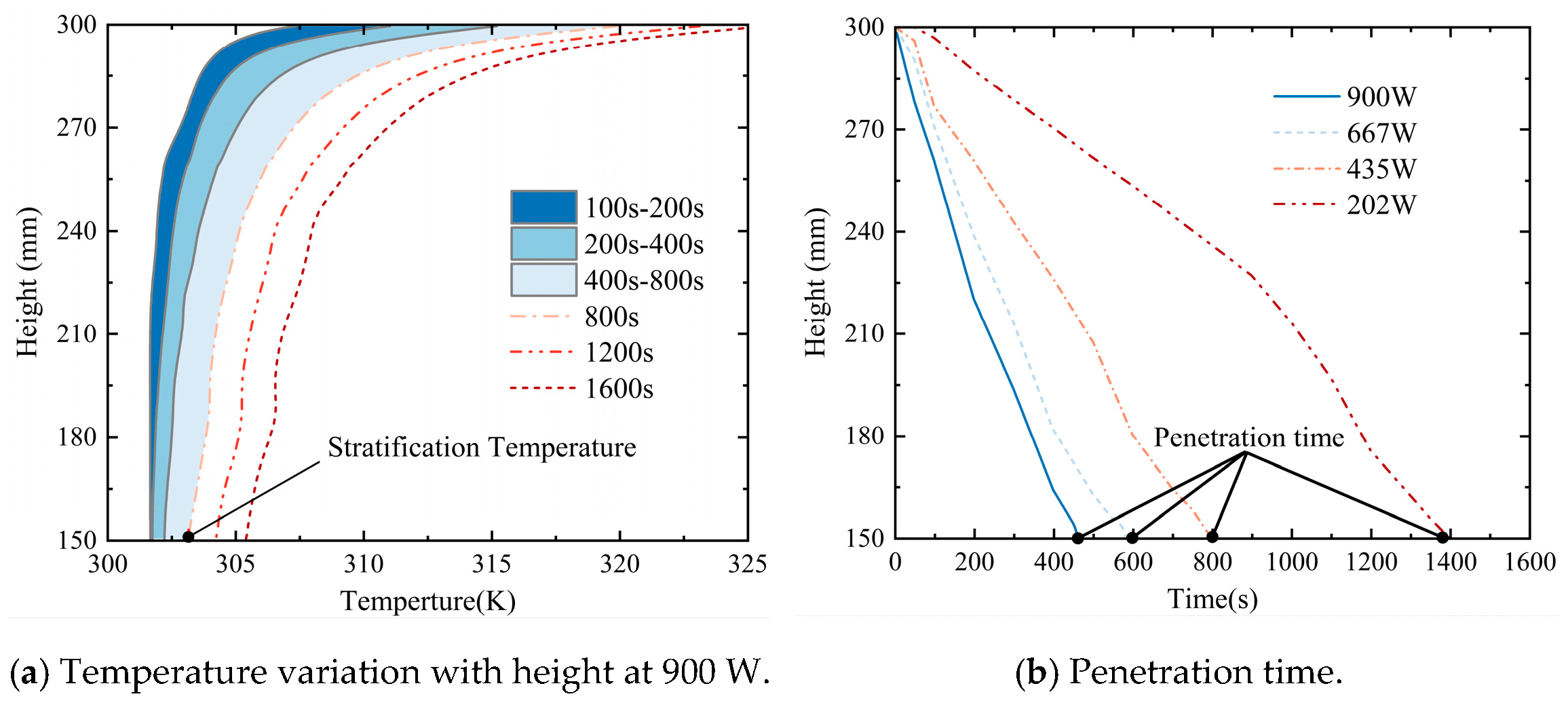
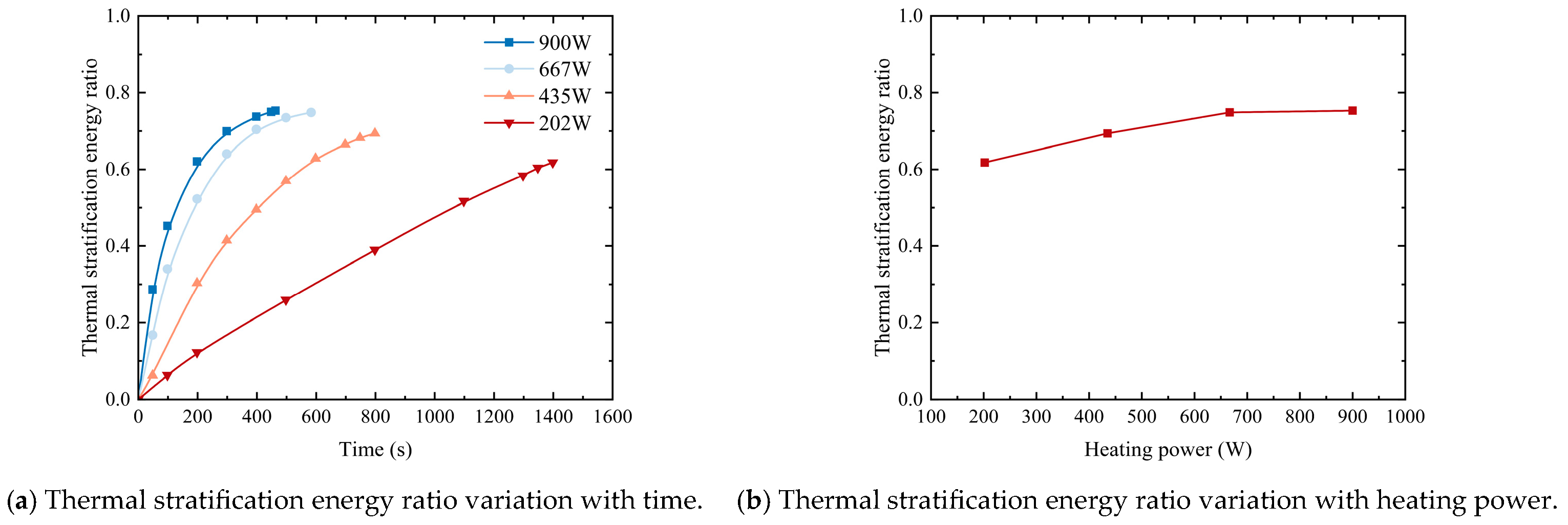
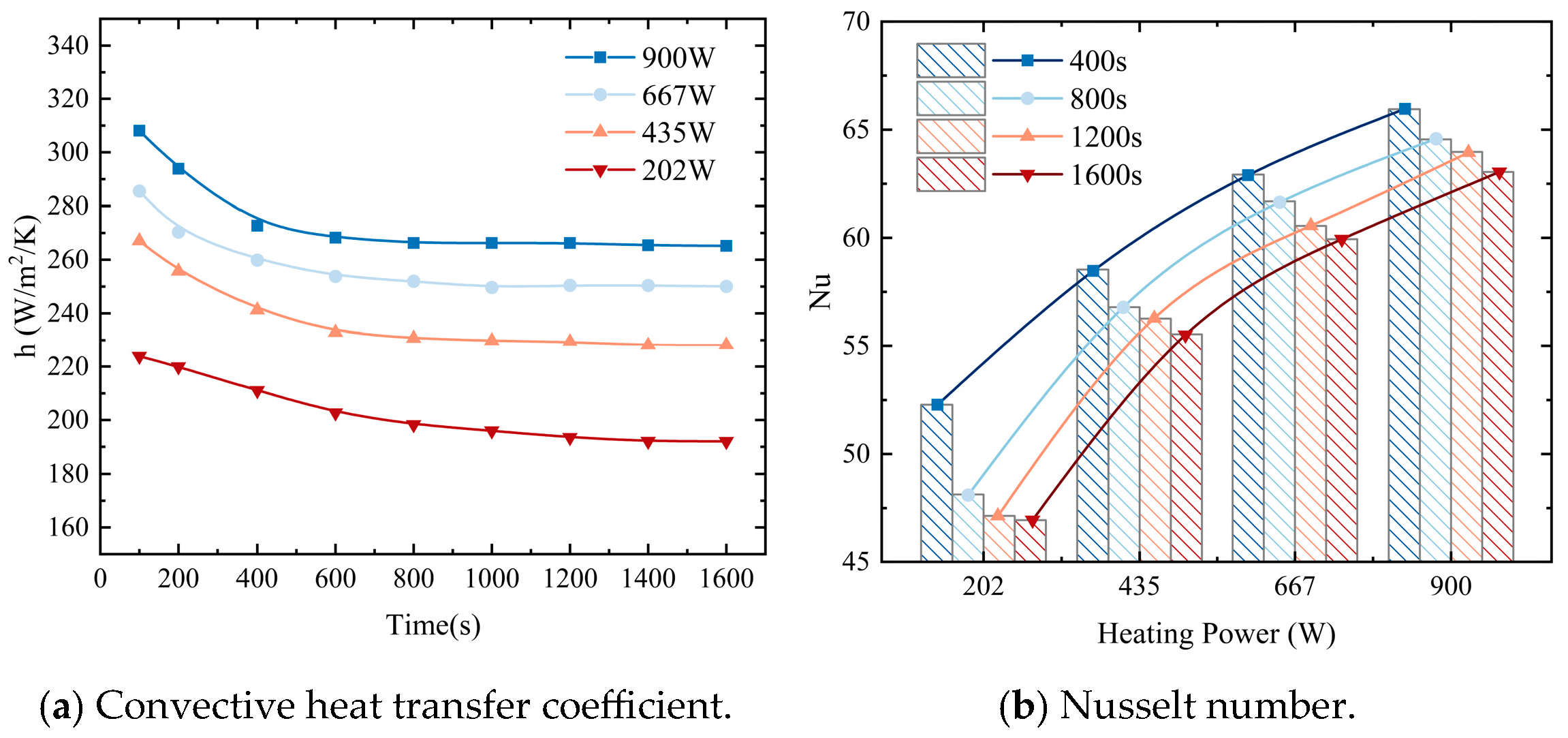
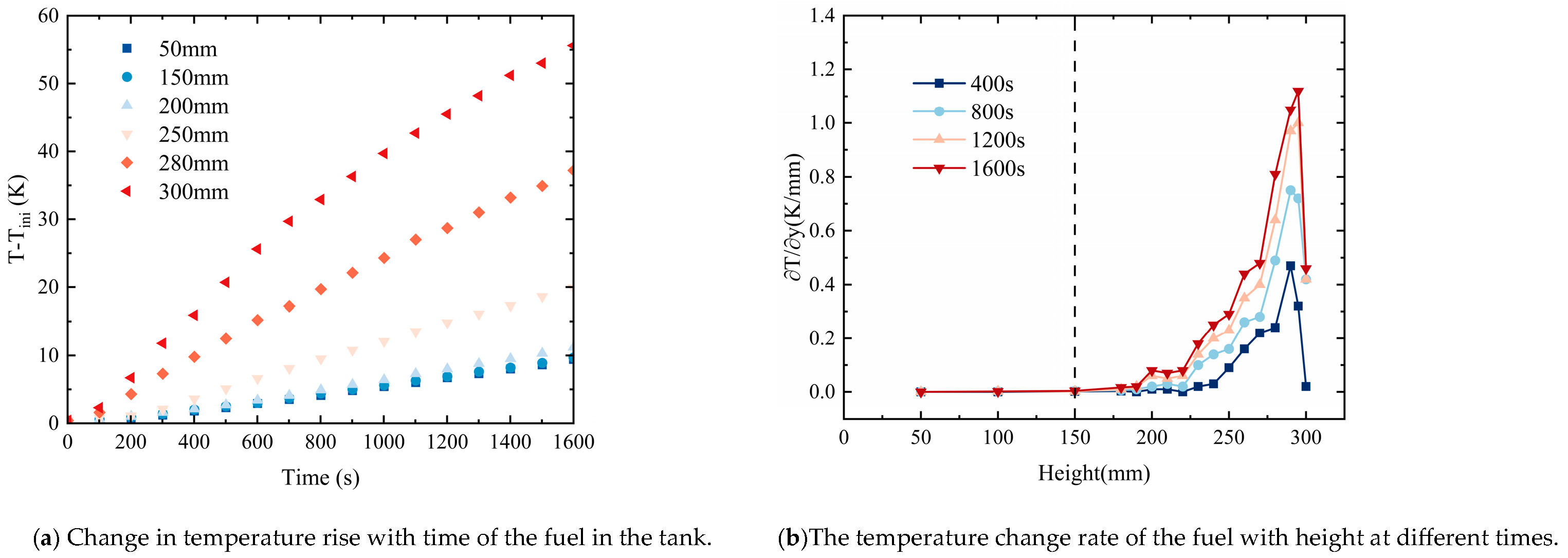
5.2. Quantitative Analysis of Thermal Stratification
5.3. Field Synergy Characteristics Analysis
5.4. Analysis of Thermal Stratification Characteristics of Fuel
6. Conclusions
- (1)
- For the circular fuel tank in this study, the heated fluid reaches the maximum upward-flow velocity at the middle height of the tank and then separates from the upper wall, resulting in a large-scale vortex. The higher the heating power, the more obvious the above phenomenon.
- (2)
- With the increase in heating time, the stability and strength of thermal stratification increase sharply at first and then tend to be stable gradually. A higher heating power markedly promotes the formation and stabilization of thermal stratification, resulting in a more uniform and stable temperature field. As the heating power increases from 202 W to 900 W, the stratification intensity increases by approximately 4.27 times, while the corresponding penetration time decreases by about 66.88%.
- (3)
- According to the field synergy principle, relatively stable heat conduction regions with high synergy angles (close to 90°) appear near the wall and at the top of the tank. The other regions are characterized by apparent unsteady and non-uniform alternating distributions of high and low synergy angles, where the high synergy angle region is more extensive. Therefore, the heat transfer of the fluid inside the tank is mainly dominated by conduction.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, S.; Li, X.; Zuo, J.; Qin, J.; Cheng, K.; Feng, Y.; Bao, W. Research Progress on Active Thermal Protection for Hypersonic Vehicles. Prog. Aerosp. Sci. 2020, 119, 100646. [Google Scholar] [CrossRef]
- Zhu, Y.; Peng, W.; Xu, R.; Jiang, P. Review on Active Thermal Protection and Its Heat Transfer for Airbreathing Hypersonic Vehicles. Chin. J. Aeronaut. 2018, 31, 1929–1953. [Google Scholar] [CrossRef]
- Birk, A.M.; Cunningham, M.H. Liquid Temperature Stratification and Its Effect on BLEVEs and Their Hazards. J. Hazard. Mater. 1996, 48, 219–237. [Google Scholar] [CrossRef]
- Zhang, W.; Cheng, J.; Song, Y.; Chen, Z.; Chen, W.; Gao, R. Experimental and Numerical Study of the Liquid Nitrogen Accumulator Based on Two-Phase Thermal Stratification. Int. J. Therm. Sci. 2023, 184, 107937. [Google Scholar] [CrossRef]
- Joseph, J.; Agrawal, G.; Agarwal, D.K.; Pisharady, J.C.; Sunil Kumar, S. Effect of Insulation Thickness on Pressure Evolution and Thermal Stratification in a Cryogenic Tank. Appl. Therm. Eng. 2017, 111, 1629–1639. [Google Scholar] [CrossRef]
- Liang, Z.; Liu, D.; Wang, X.; Zhang, J.; Wu, H.; Qing, X.; Wang, Y. FBG-Based Strain Monitoring and Temperature Compensation for Composite Tank. Aerosp. Sci. Technol. 2022, 127, 107724. [Google Scholar] [CrossRef]
- Vliet, G.C. Stratification with Bottom Heating. J. Spacecr. Rockets 1966, 3, 1142–1144. [Google Scholar] [CrossRef]
- Fan, S.C.; Chu, J.C.; Scott, L.E. Thermal Stratification in Closed Cryogenic Containers. In Advances in Cryogenic Engineering; Timmerhaus, K.D., Ed.; Springer: Boston, MA, USA, 1969; pp. 249–257. [Google Scholar]
- Daigle, M.J.; Smelyanskiy, V.N.; Boschee, J.; Foygel, M. Temperature Stratification in a Cryogenic Fuel Tank. J. Thermophys. Heat Transf. 2013, 27, 116–126. [Google Scholar] [CrossRef]
- Liu, Z.; Feng, Y.; Lei, G.; Li, Y. Fluid Thermal Stratification in a Non-Isothermal Liquid Hydrogen Tank under Sloshing Excitation. Int. J. Hydrogen Energy 2018, 43, 22622–22635. [Google Scholar] [CrossRef]
- Duan, Z.; Sun, H.; Cheng, C.; Tang, W.; Xue, H. A Moving-Boundary Based Dynamic Model for Predicting the Transient Free Convection and Thermal Stratification in Liquefied Gas Storage Tank. Int. J. Therm. Sci. 2021, 160, 106690. [Google Scholar] [CrossRef]
- Bouhal, T.; Fertahi, S.; Agrouaz, Y.; El Rhafiki, T.; Kousksou, T.; Jamil, A. Numerical Modeling and Optimization of Thermal Stratification in Solar Hot Water Storage Tanks for Domestic Applications: CFD Study. Sol. Energy 2017, 157, 441–455. [Google Scholar] [CrossRef]
- Rendall, J.; Abu-Heiba, A.; Gluesenkamp, K.; Nawaz, K.; Worek, W.; Elatar, A. Nondimensional Convection Numbers Modeling Thermally Stratified Storage Tanks: Richardson’s Number and Hot-Water Tanks. Renew. Sustain. Energy Rev. 2021, 150, 111471. [Google Scholar] [CrossRef]
- Ding, T.; Meng, Z.; Chen, K.; Fan, G.; Yan, C. Experimental Study on Thermal Stratification in Water Tank and Heat Transfer Characteristics of Condenser in Water-Cooled Passive Residual Heat Removal System of Molten Salt Reactor. Energy 2020, 205, 118052. [Google Scholar] [CrossRef]
- Abdelhak, O.; Mhiri, H.; Bournot, P. CFD Analysis of Thermal Stratification in Domestic Hot Water Storage Tank during Dynamic Mode. Build. Simul. 2015, 8, 421–429. [Google Scholar] [CrossRef]
- Kumar, K.; Singh, S. Investigating Thermal Stratification in a Vertical Hot Water Storage Tank under Multiple Transient Operations. Energy Rep. 2021, 7, 7186–7199. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, H.; Dou, B.; Huang, H.; Wu, W.; Wang, Z. Experimental and Numerical Research of Thermal Stratification with a Novel Inlet in a Dynamic Hot Water Storage Tank. Renew. Energy 2017, 111, 353–371. [Google Scholar] [CrossRef]
- Chandra, Y.P.; Matuska, T. Numerical Prediction of the Stratification Performance in Domestic Hot Water Storage Tanks. Renew. Energy 2020, 154, 1165–1179. [Google Scholar] [CrossRef]
- Gao, L.; Lu, H.; Sun, B.; Che, D.; Dong, L. Numerical and Experimental Investigation on Thermal Stratification Characteristics Affected by the Baffle Plate in Thermal Storage Tank. J. Energy Storage 2021, 34, 102117. [Google Scholar] [CrossRef]
- Kumar, G.S.; Nagarajan, D.; Chidambaram, L.A.; Kumaresan, V.; Ding, Y.; Velraj, R. Role of PCM Addition on Stratification Behaviour in a Thermal Storage Tank—An Experimental Study. Energy 2016, 115, 1168–1178. [Google Scholar] [CrossRef]
- Erdemir, D.; Altuntop, N. Improved Thermal Stratification with Obstacles Placed inside the Vertical Mantled Hot Water Tanks. Appl. Therm. Eng. 2016, 100, 20–29. [Google Scholar] [CrossRef]
- Erdemir, D.; Atesoglu, H.; Altuntop, N. Experimental Investigation on Enhancement of Thermal Performance with Obstacle Placing in the Horizontal Hot Water Tank Used in Solar Domestic Hot Water System. Renew. Energy 2019, 138, 187–197. [Google Scholar] [CrossRef]
- Fernández-Seara, J.; Uhı’a, F.J.; Sieres, J. Experimental Analysis of a Domestic Electric Hot Water Storage Tank. Part II: Dynamic Mode of Operation. Appl. Therm. Eng. 2007, 27, 137–144. [Google Scholar] [CrossRef]
- Guo, Z.Y.; Li, D.Y.; Wang, B.X. A Novel Concept for Convective Heat Transfer Enhancement. Int. J. Heat Mass Transf. 1998, 41, 2221–2225. [Google Scholar] [CrossRef]
- Zhang, L.; Li, J.; Li, Y.; Wu, J. Field Synergy Analysis for Helical Ducts with Rectangular Cross Section. Int. J. Heat Mass Transf. 2014, 75, 245–261. [Google Scholar] [CrossRef]
- Li, Y.; Liu, G.; Rao, Z.; Liao, S. Field Synergy Principle Analysis for Reducing Natural Convection Heat Loss of a Solar Cavity Receiver. Renew. Energy 2015, 75, 257–265. [Google Scholar] [CrossRef]
- Shen, J.; Zeng, L.; Liu, Z.; Liu, W. Performance Investigation of PEMFC with Rectangle Blockages in Gas Channel Based on Field Synergy Principle. Heat Mass Transf. 2019, 55, 811–822. [Google Scholar] [CrossRef]
- Wang, B.; Hong, Y.; Hou, X.; Xu, Z.; Wang, P.; Fang, X.; Ruan, X. Numerical Configuration Design and Investigation of Heat Transfer Enhancement in Pipes Filled with Gradient Porous Materials. Energy Convers. Manag. 2015, 105, 206–215. [Google Scholar] [CrossRef]
- Liu, Y.; Dong, Y.; Xie, L.; Zhang, C.; Xu, C. Heat Transfer Enhancement of Supercritical CO2 in Solar Tower Receiver by the Field Synergy Principle. Appl. Therm. Eng. 2022, 212, 118479. [Google Scholar] [CrossRef]
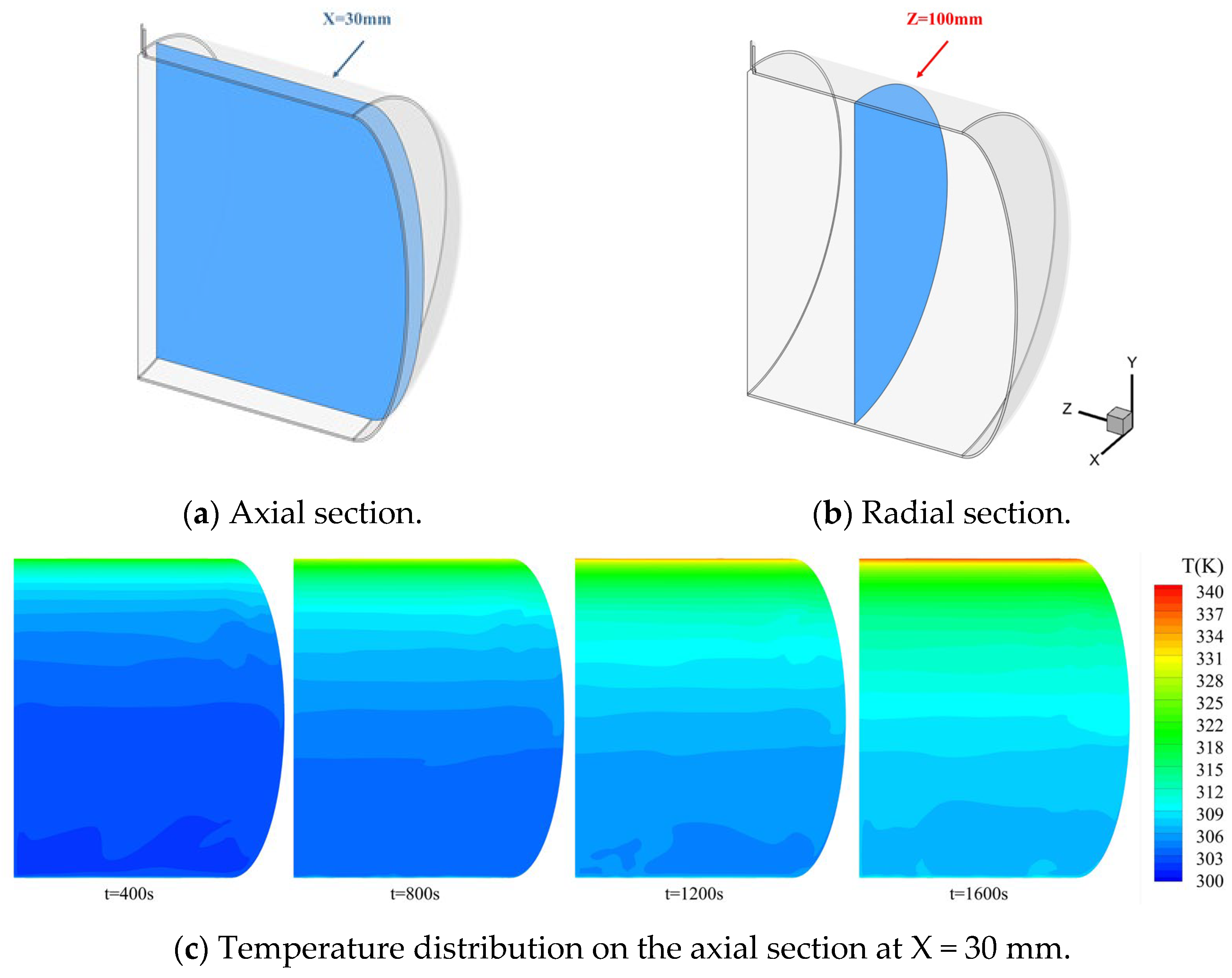
| No | X (mm) | Y (mm) | Z (mm) | No | X (mm) | Y (mm) | Z (mm) |
|---|---|---|---|---|---|---|---|
| 1 | 150 | 0 | 0 | 10 | 150 | 230 | 0 |
| 2 | 150 | 50 | 0 | 11 | 150 | 240 | 0 |
| 3 | 150 | 100 | 0 | 12 | 150 | 250 | 0 |
| 4 | 150 | 150 | 0 | 13 | 150 | 260 | 0 |
| 5 | 150 | 180 | 0 | 14 | 150 | 270 | 0 |
| 6 | 150 | 190 | 0 | 15 | 150 | 280 | 0 |
| 7 | 150 | 200 | 0 | 16 | 150 | 290 | 0 |
| 8 | 150 | 210 | 0 | 17 | 150 | 295 | 0 |
| 9 | 150 | 220 | 0 | 18 | 150 | 300 | 0 |
| Mesh 1 | Mesh 2 | Mesh 3 | Mesh 4 | Mesh 5 | |
|---|---|---|---|---|---|
| Grid type | Hexahedral | ||||
| Thickness of first row (mm) | 0.002 | 0.005 | 0.01 | 0.02 | 0.05 |
| Mesh gradient ratio | 1.2 | ||||
| Total grid number | 1,587,990 | 1,306,870 | 626,874 | 330,942 | 185,138 |
| Mesh S1 | Mesh S2 | Mesh S3 | |
|---|---|---|---|
| Grid type | Hexahedral | ||
| Solid region layer number | 4 | 8 | 12 |
| Thickness of each row (mm) | 0.5 | 0.25 | 0.1667 |
| Solid region grid number | 35,508 | 70,392 | 105,276 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, Y.; Li, H.; Fan, R.; Yan, Z.; Zhang, G.; Liu, H. Study on Thermal Stratification and Heat Transfer Characteristics in a Fuel Tank of Hypersonic Vehicles. Aerospace 2025, 12, 1020. https://doi.org/10.3390/aerospace12111020
Xin Y, Li H, Fan R, Yan Z, Zhang G, Liu H. Study on Thermal Stratification and Heat Transfer Characteristics in a Fuel Tank of Hypersonic Vehicles. Aerospace. 2025; 12(11):1020. https://doi.org/10.3390/aerospace12111020
Chicago/Turabian StyleXin, Yang, Haokun Li, Rui Fan, Zihang Yan, Guoxi Zhang, and Huaping Liu. 2025. "Study on Thermal Stratification and Heat Transfer Characteristics in a Fuel Tank of Hypersonic Vehicles" Aerospace 12, no. 11: 1020. https://doi.org/10.3390/aerospace12111020
APA StyleXin, Y., Li, H., Fan, R., Yan, Z., Zhang, G., & Liu, H. (2025). Study on Thermal Stratification and Heat Transfer Characteristics in a Fuel Tank of Hypersonic Vehicles. Aerospace, 12(11), 1020. https://doi.org/10.3390/aerospace12111020






