Aerodynamic Performance Enhancement of Ram Air Turbine Blades with Different Tip Configurations
Abstract
1. Introduction
2. Physical Model and Numerical Method
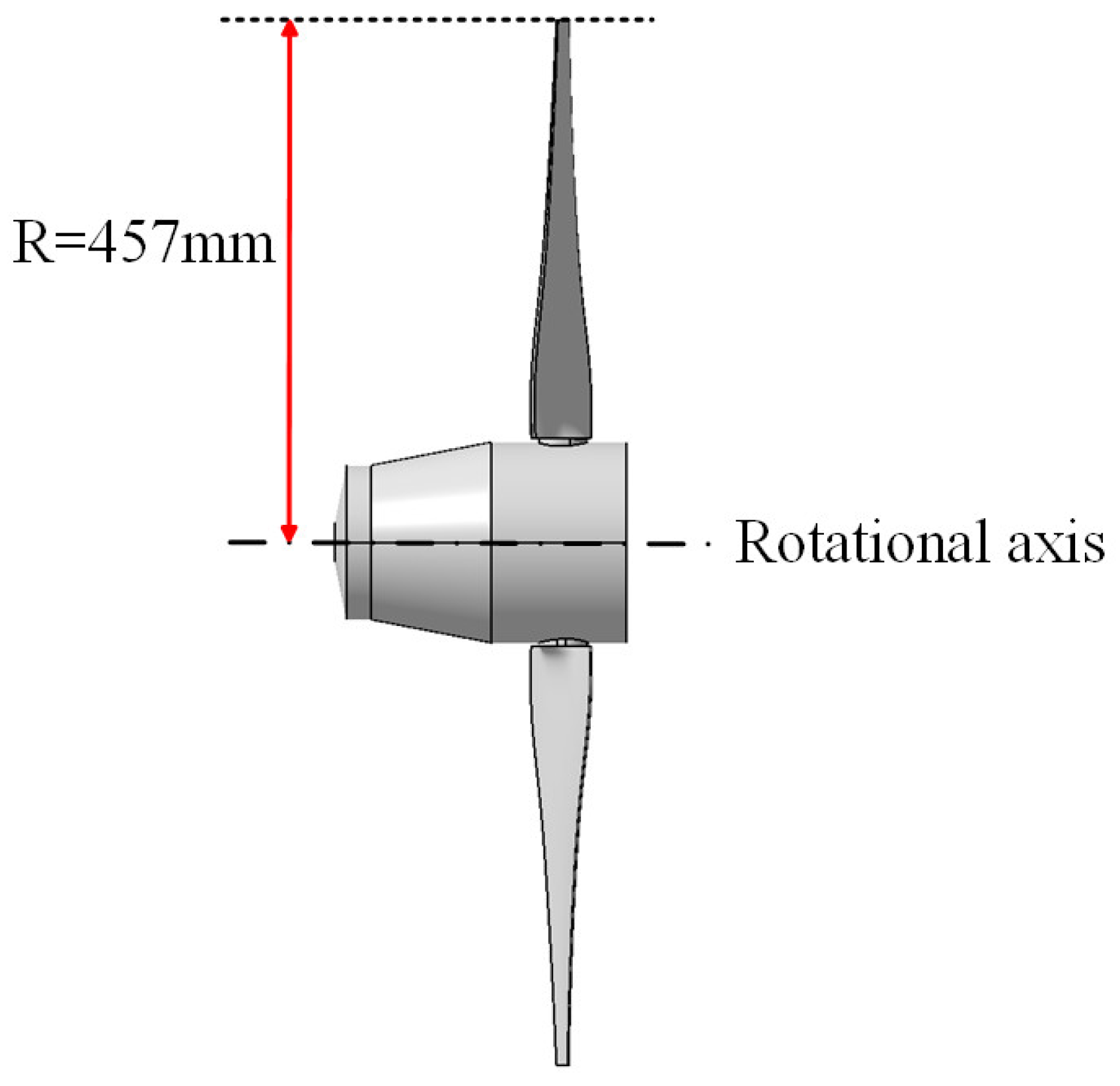
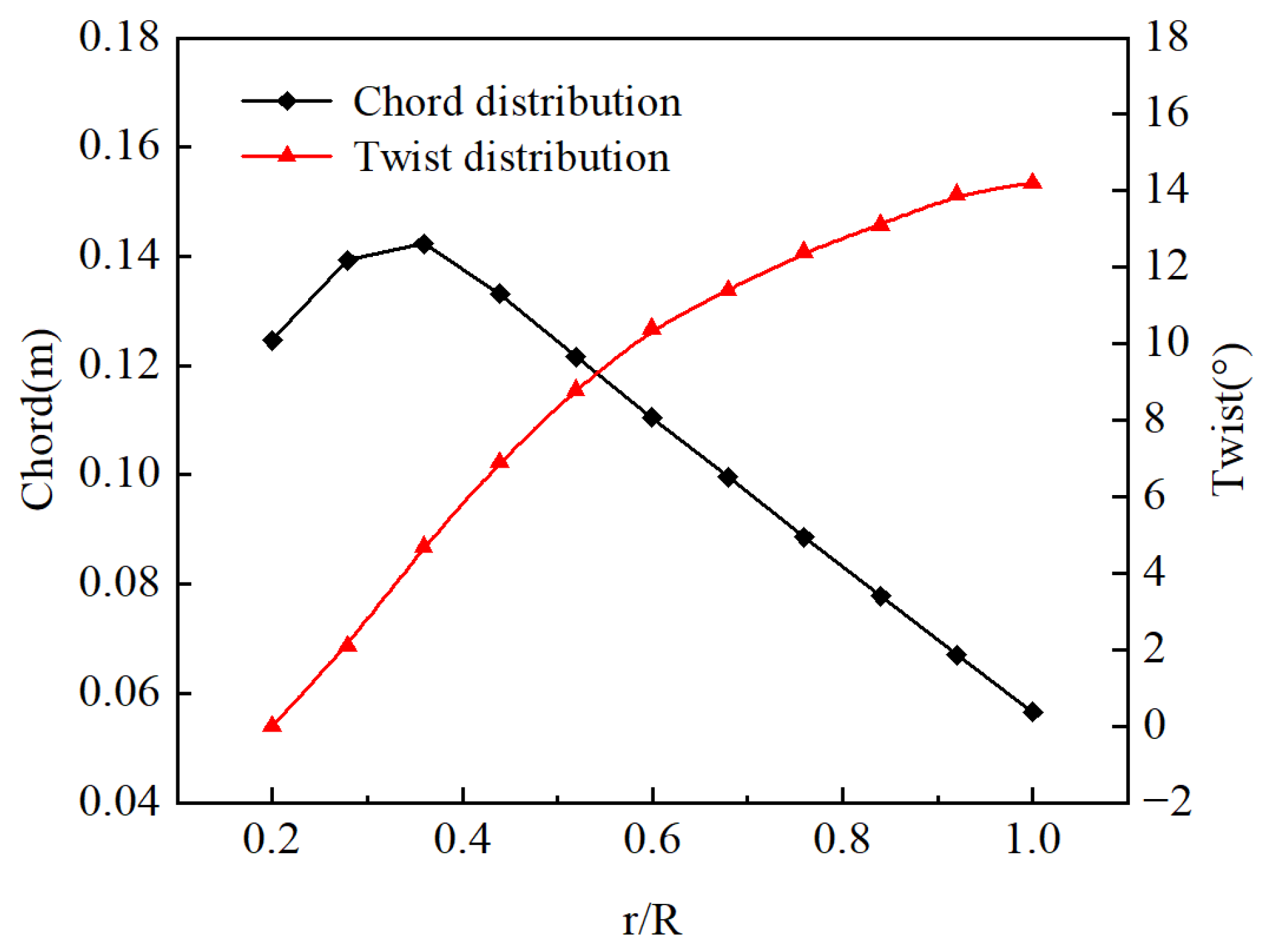
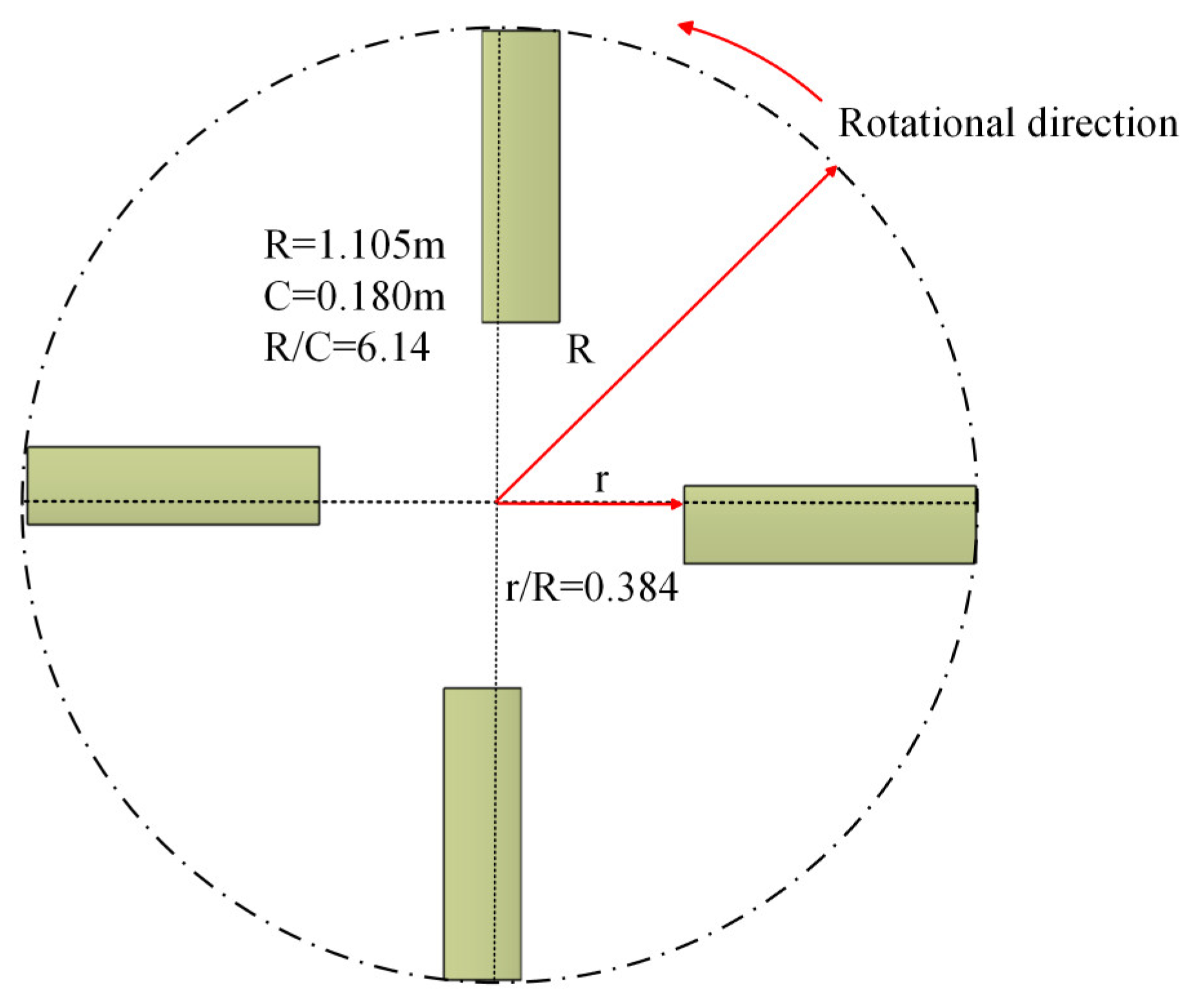
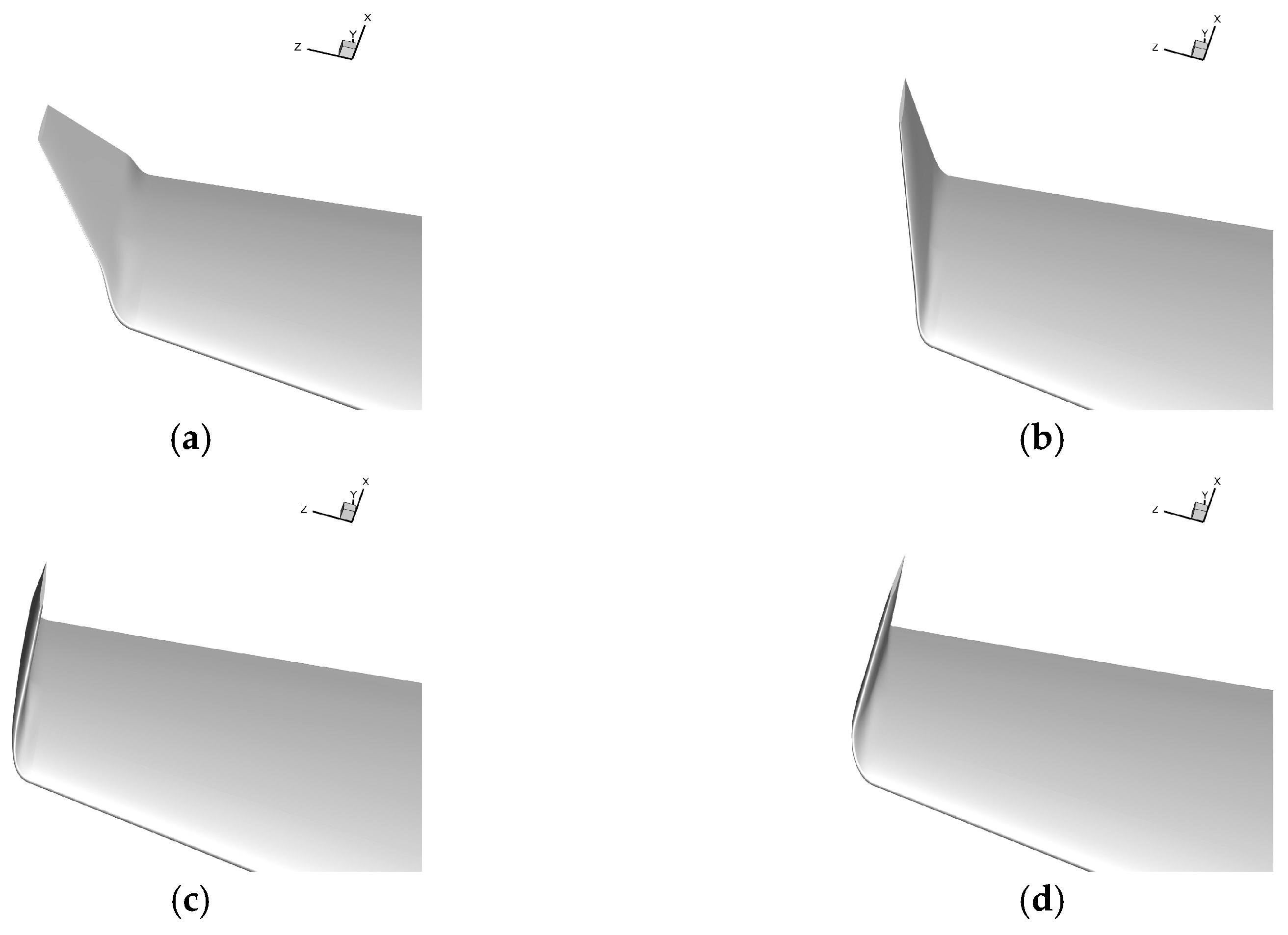
2.1. Physical Model Introduction
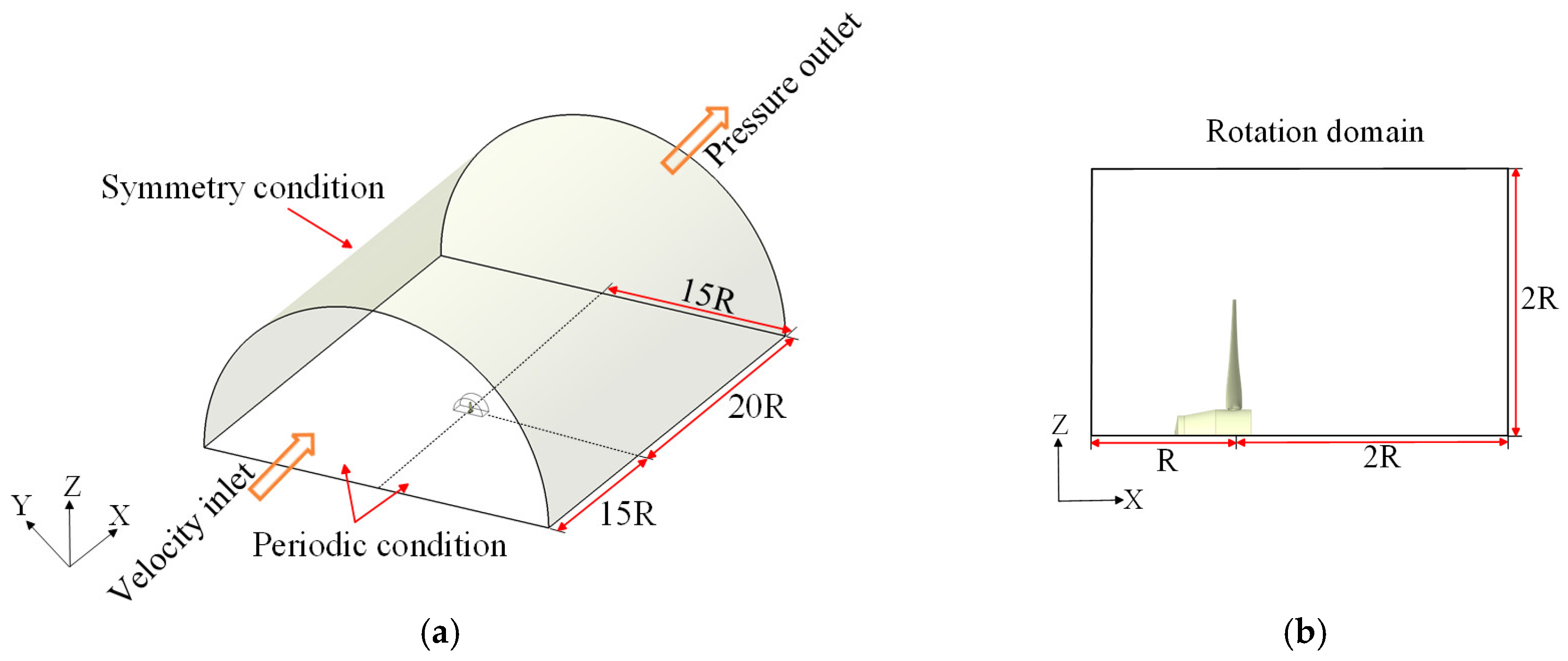
2.2. Modeling Strategy
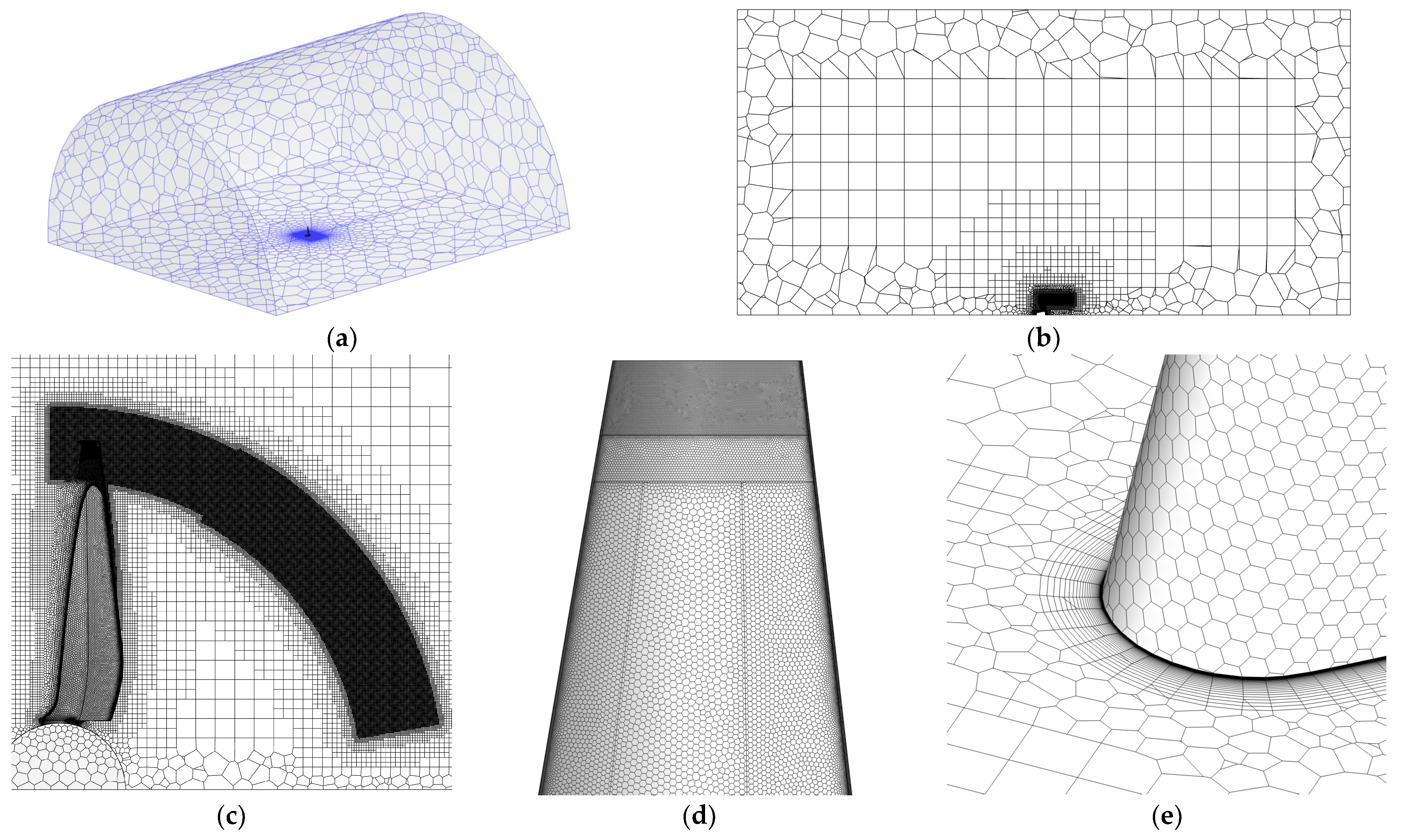
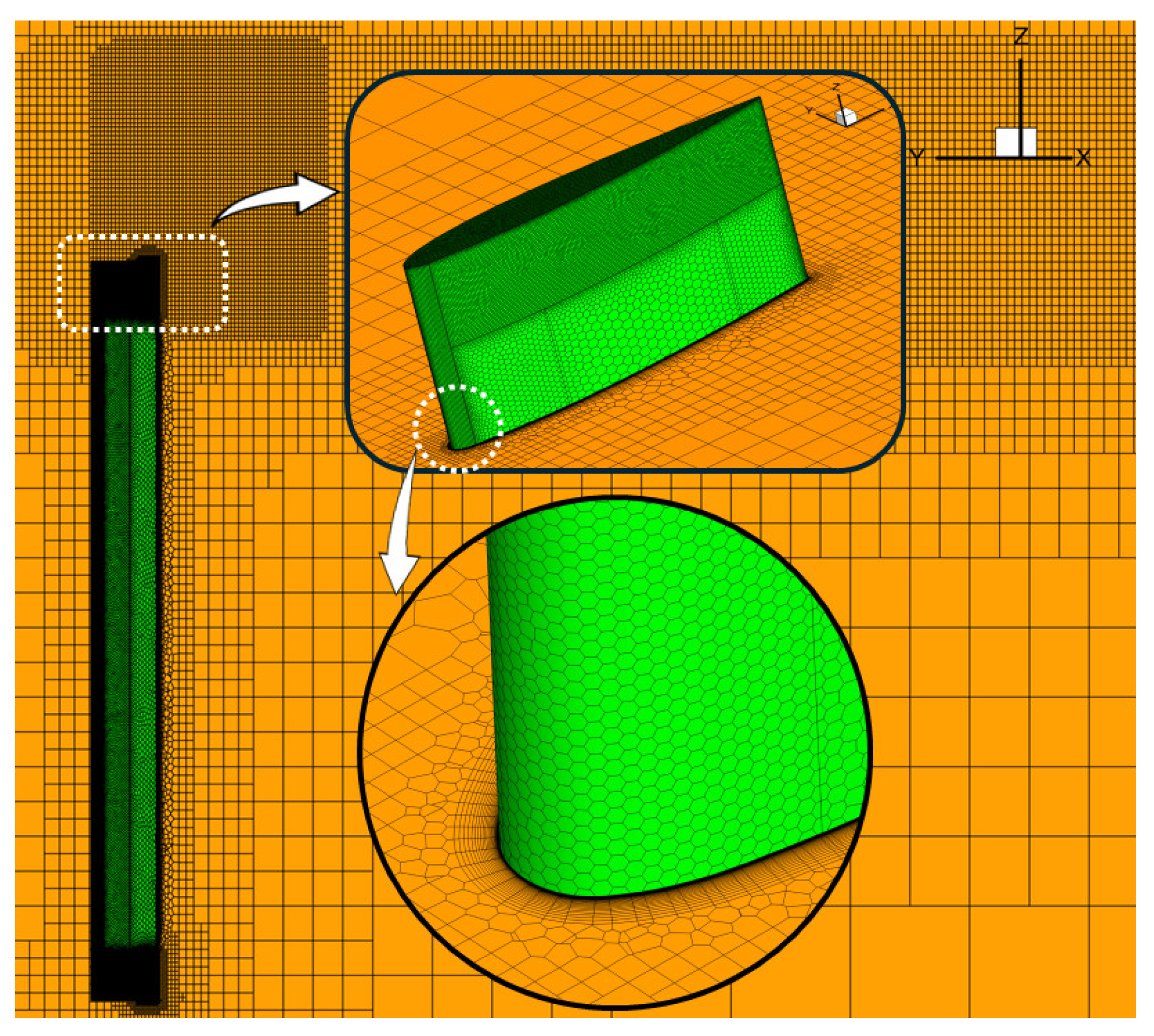
2.3. Grid Independence Analysis
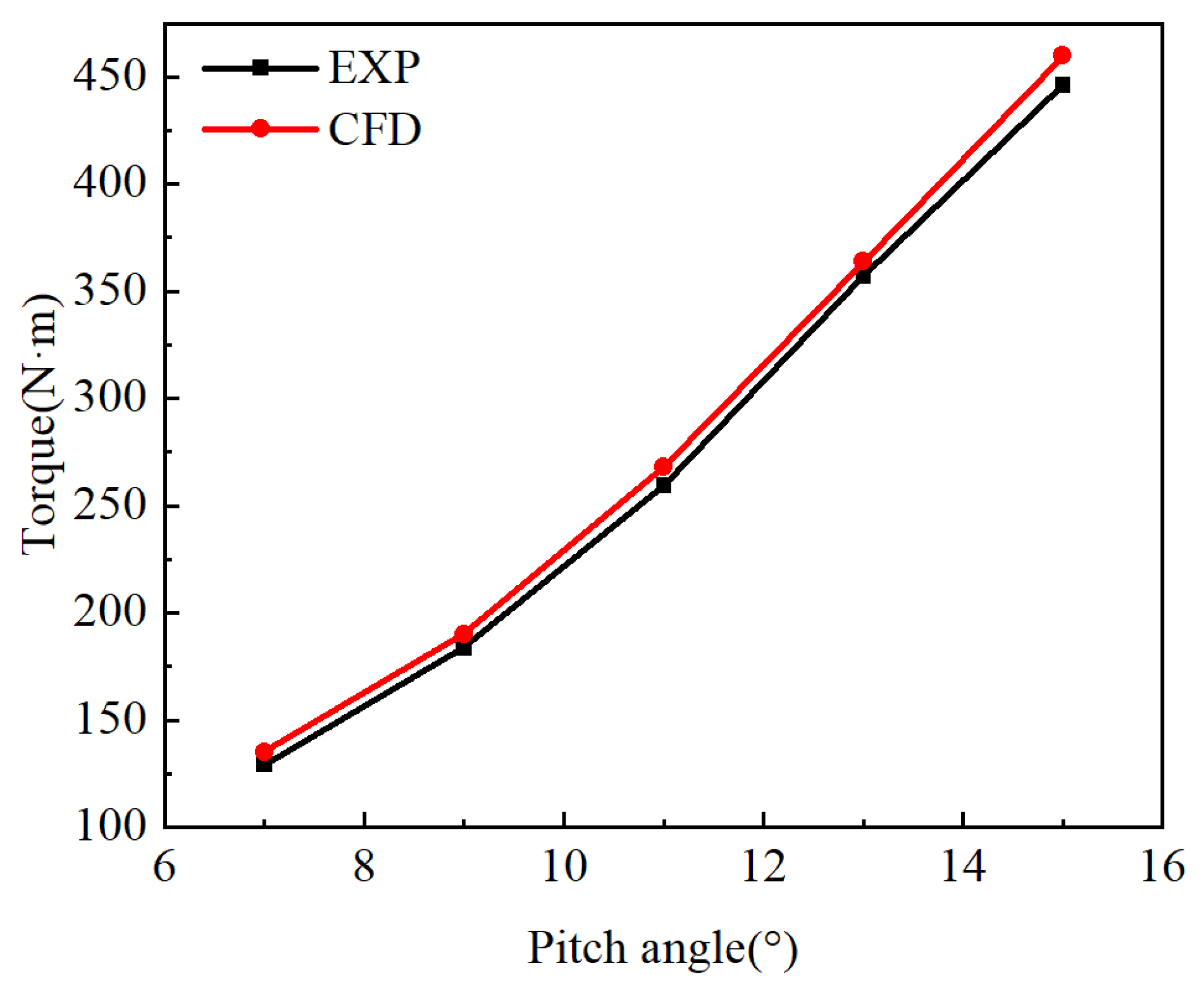
2.4. CFD Validation Using Experimental Data
3. Analysis of the Influence of Different Blade Tip Configurations on the Aerodynamic Performance of the RAT
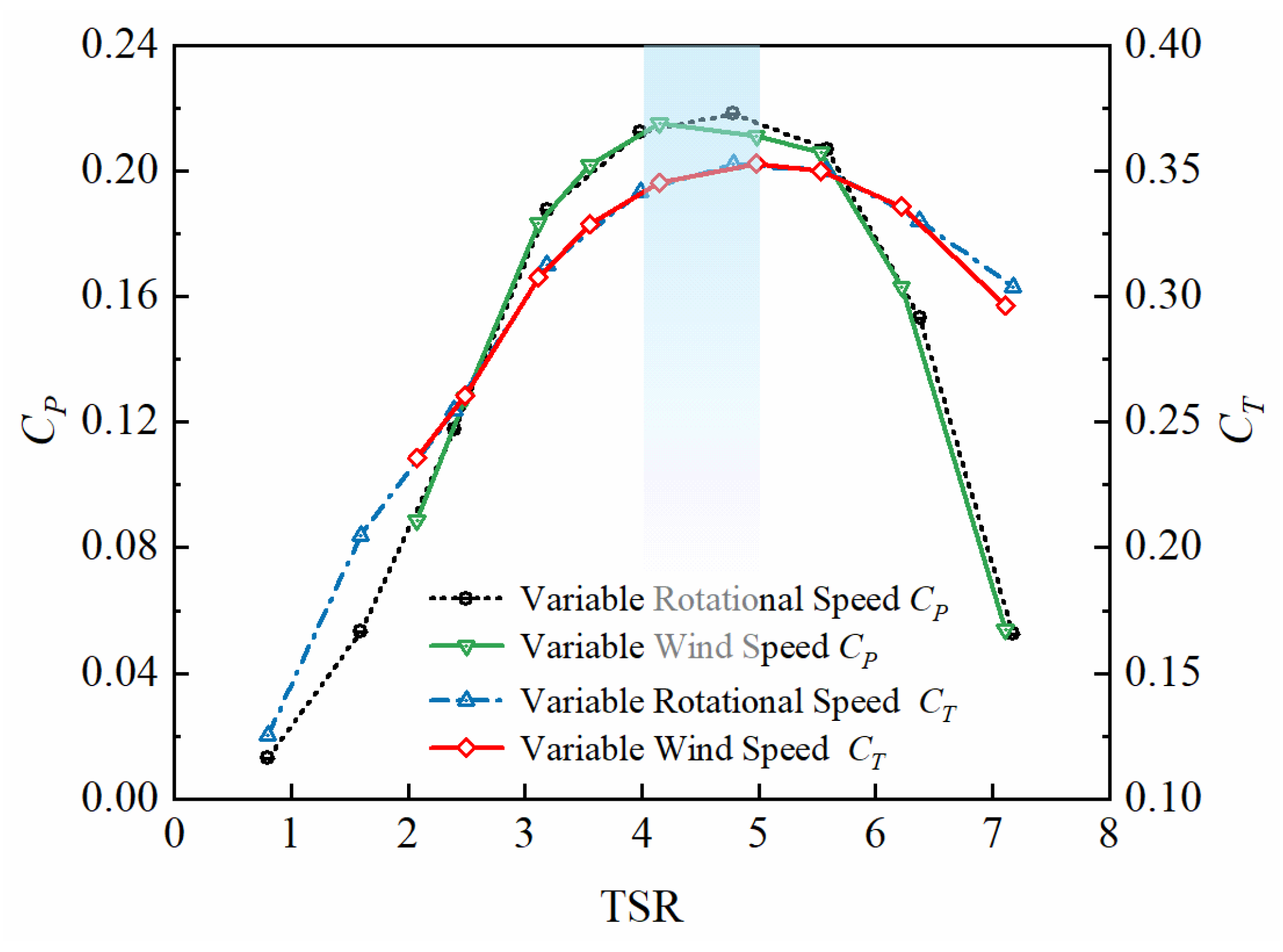
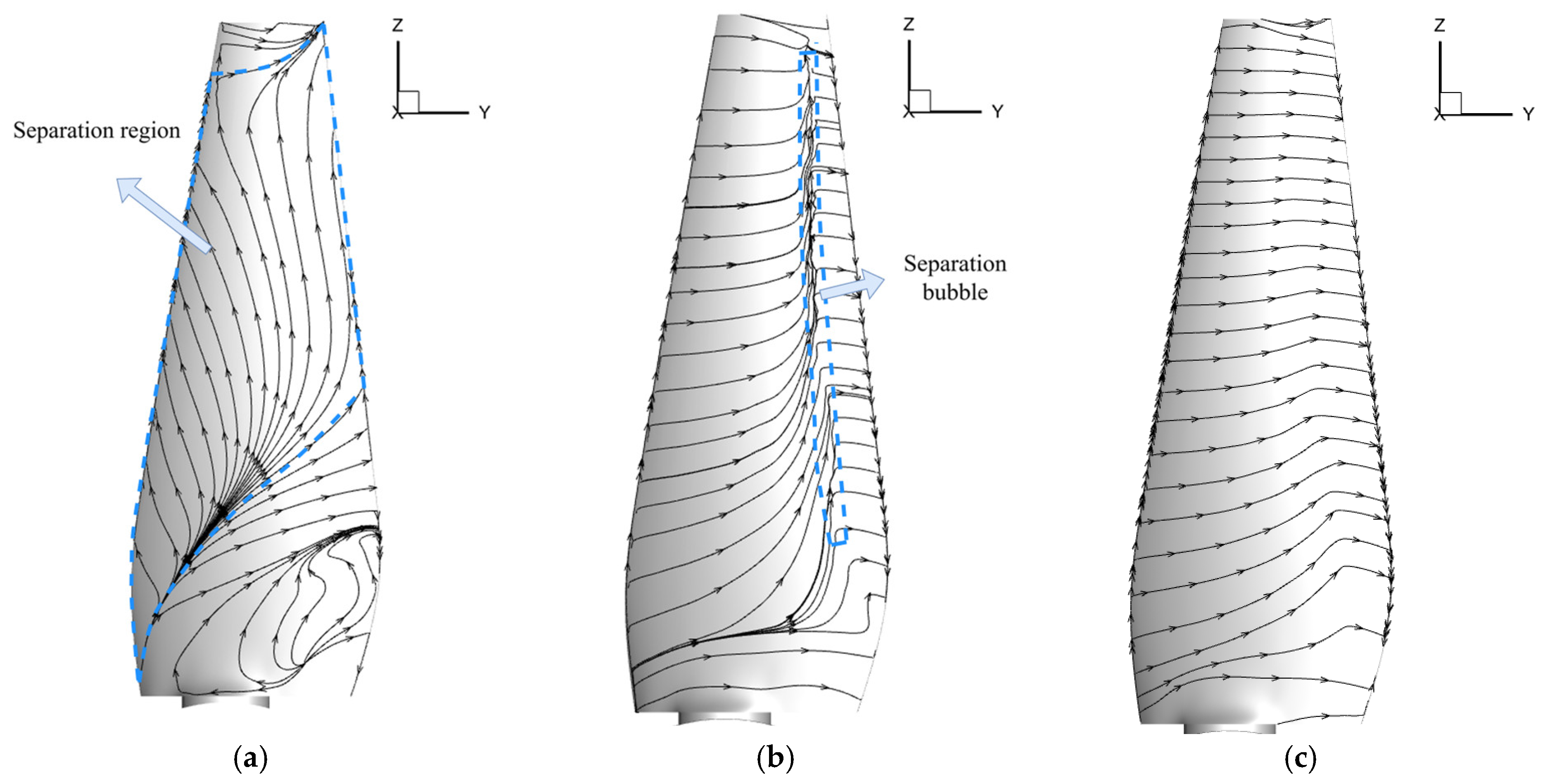
3.1. Aerodynamic Performance of the Baseline Configuration
3.2. Aerodynamic Performance of the Tip Plate Configuration
3.3. Aerodynamic Performance of the Blade Tip Contraction Configuration
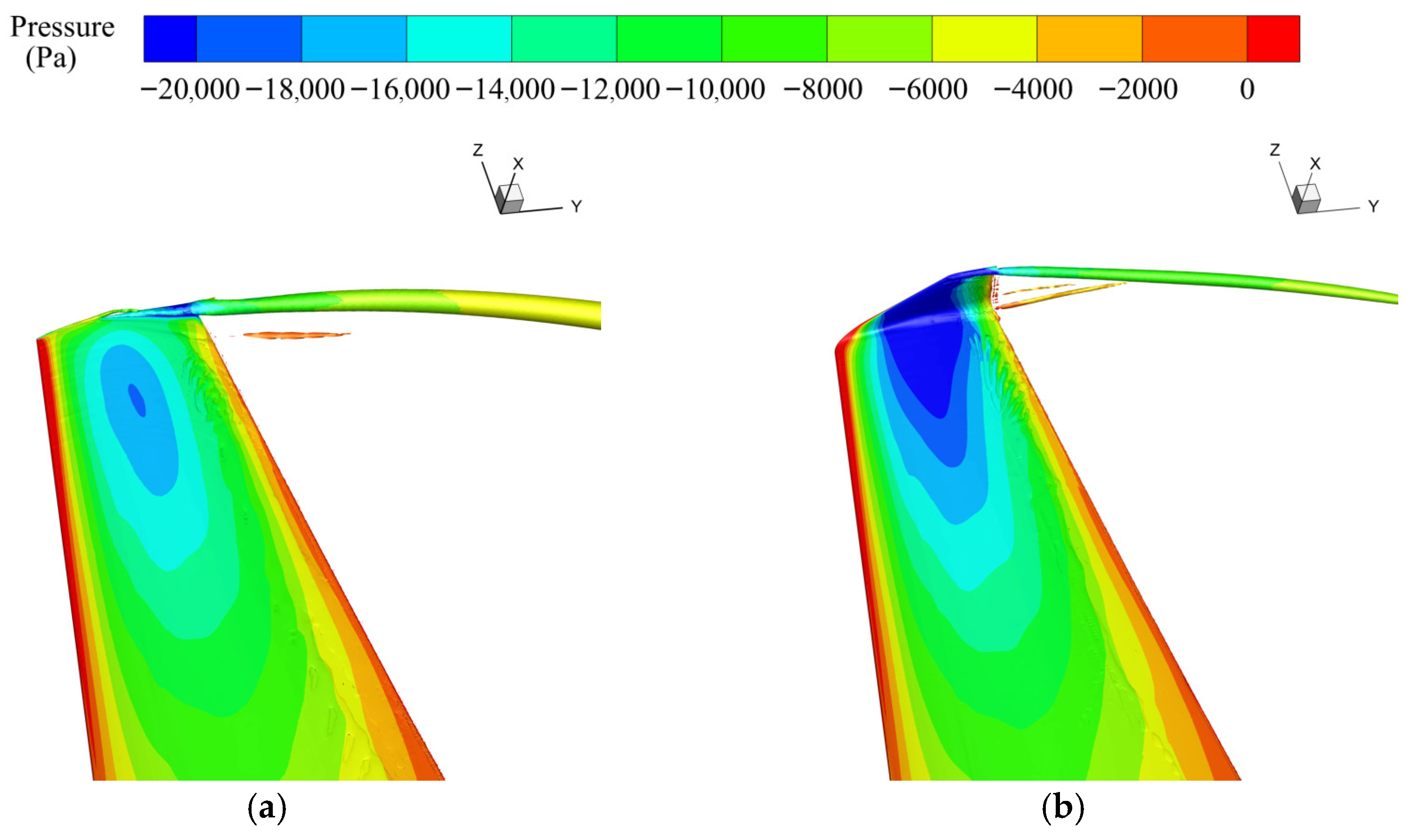
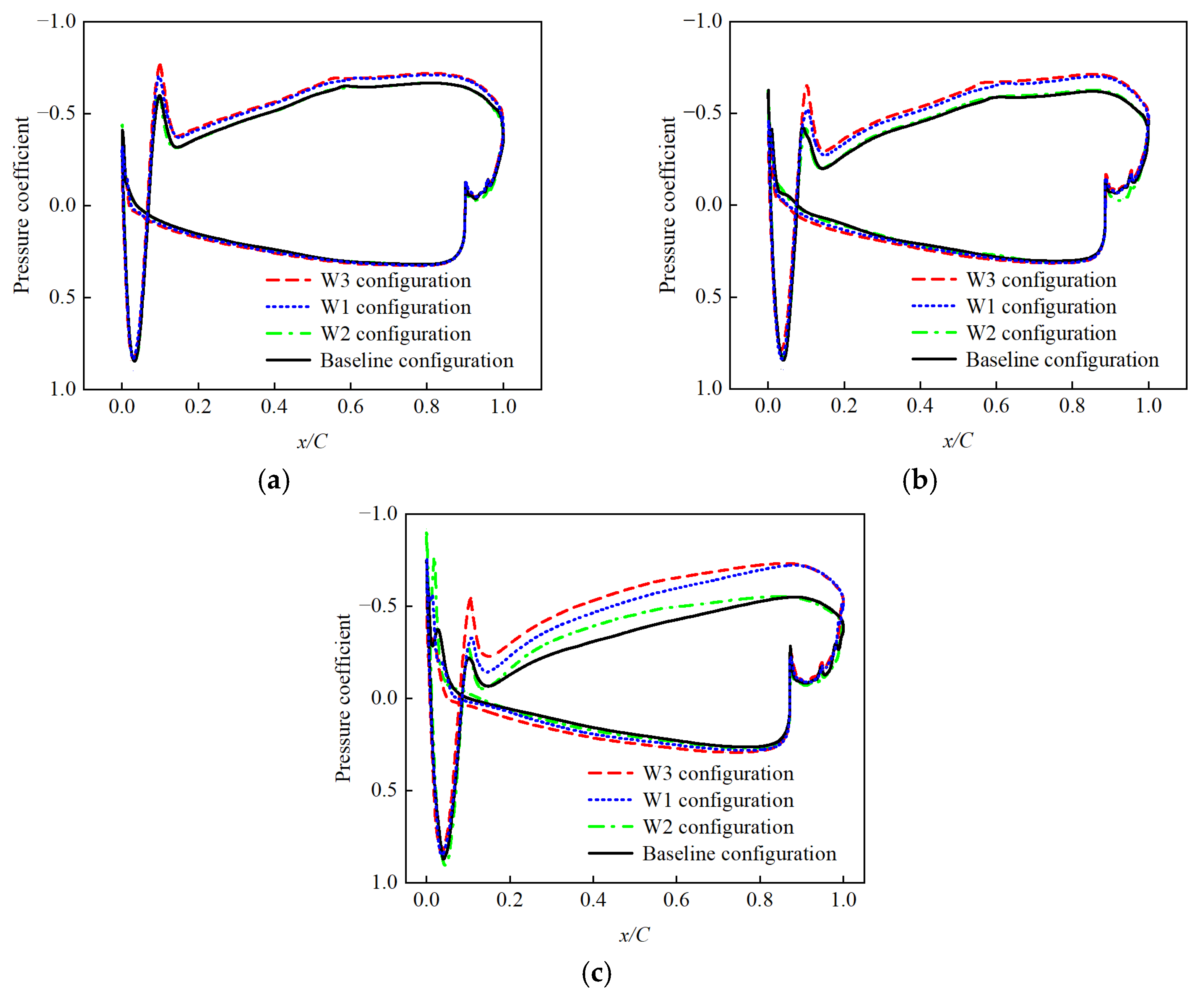
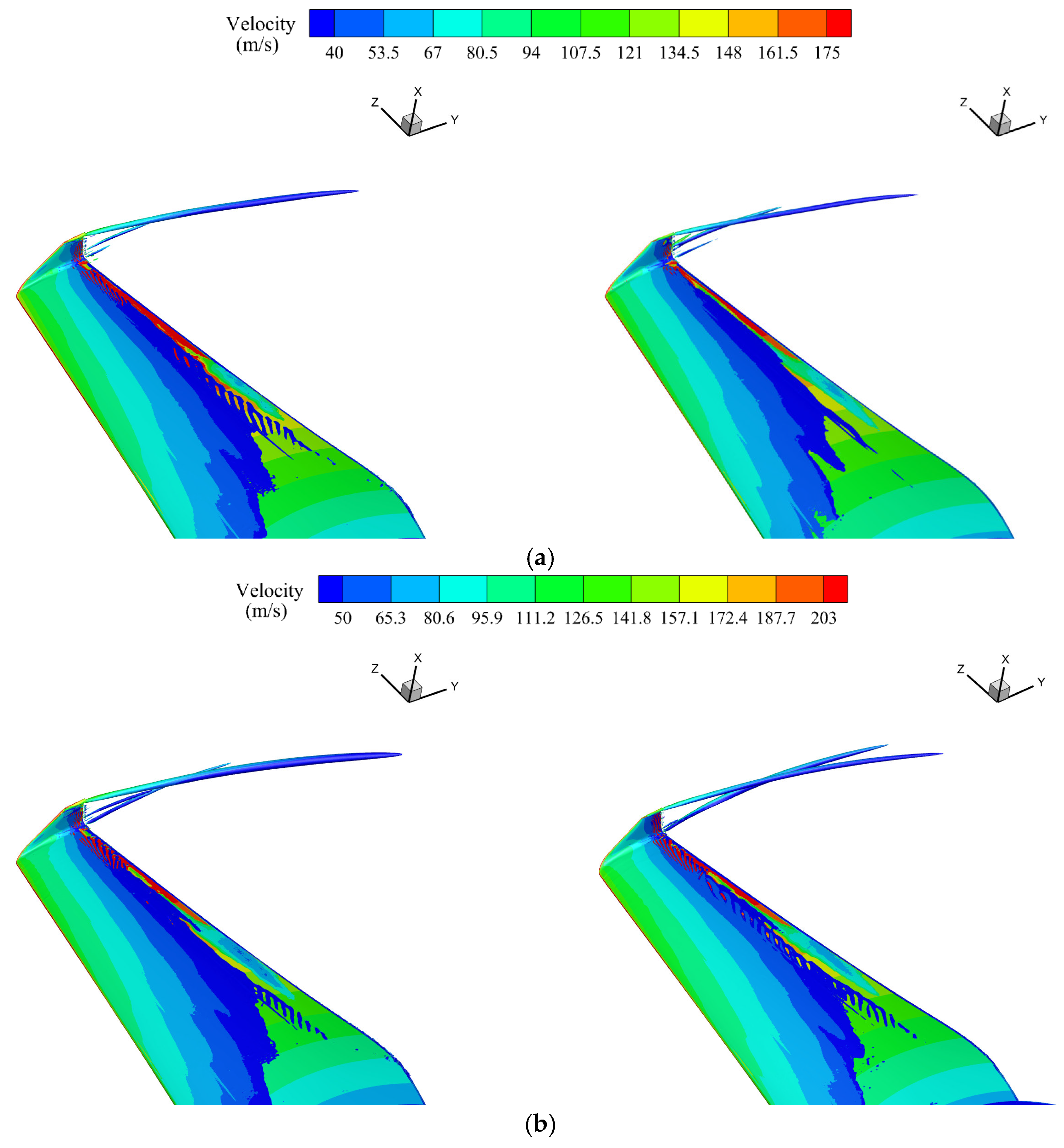
3.4. Aerodynamic Performance of the Winglet Configuration
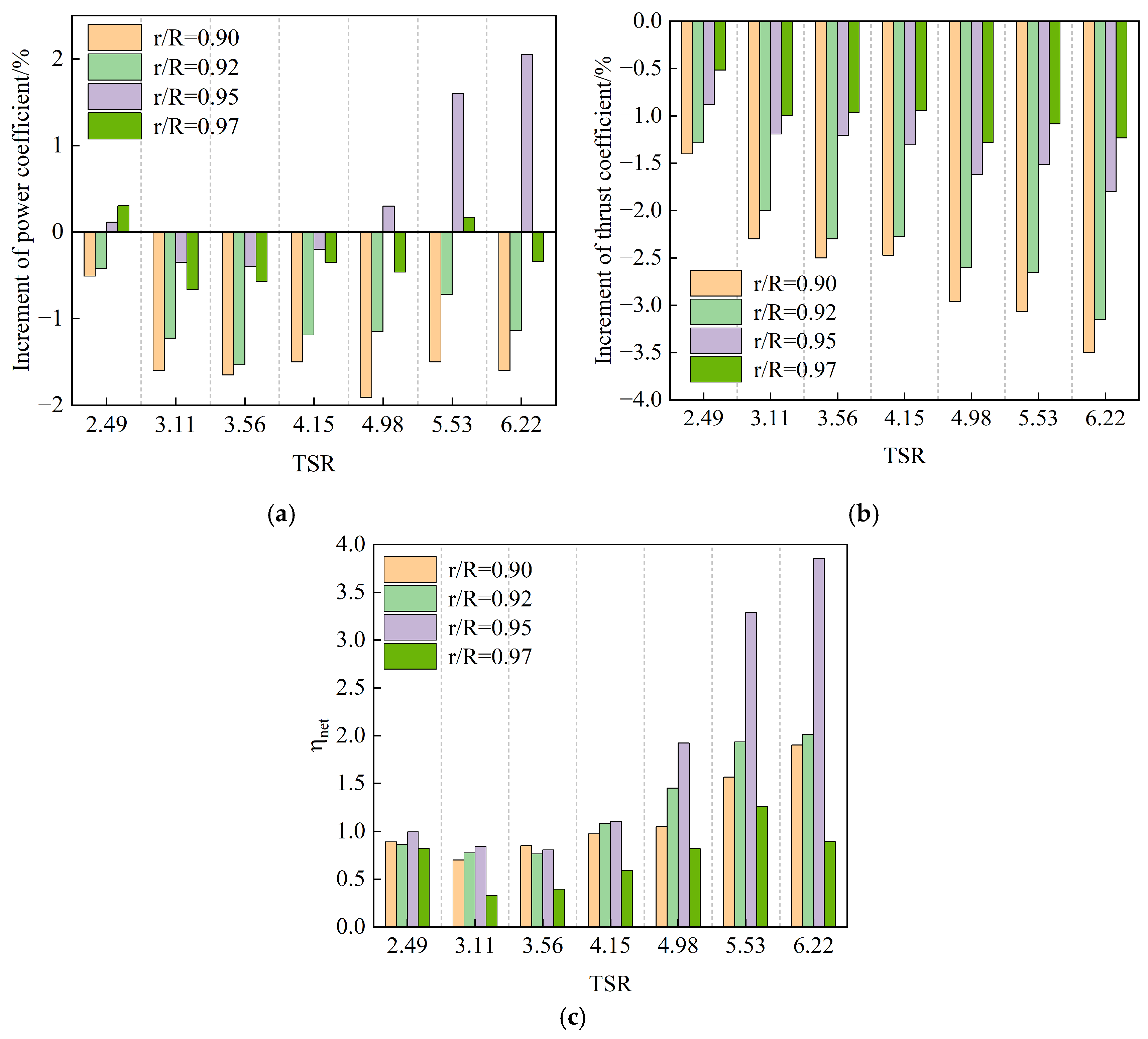
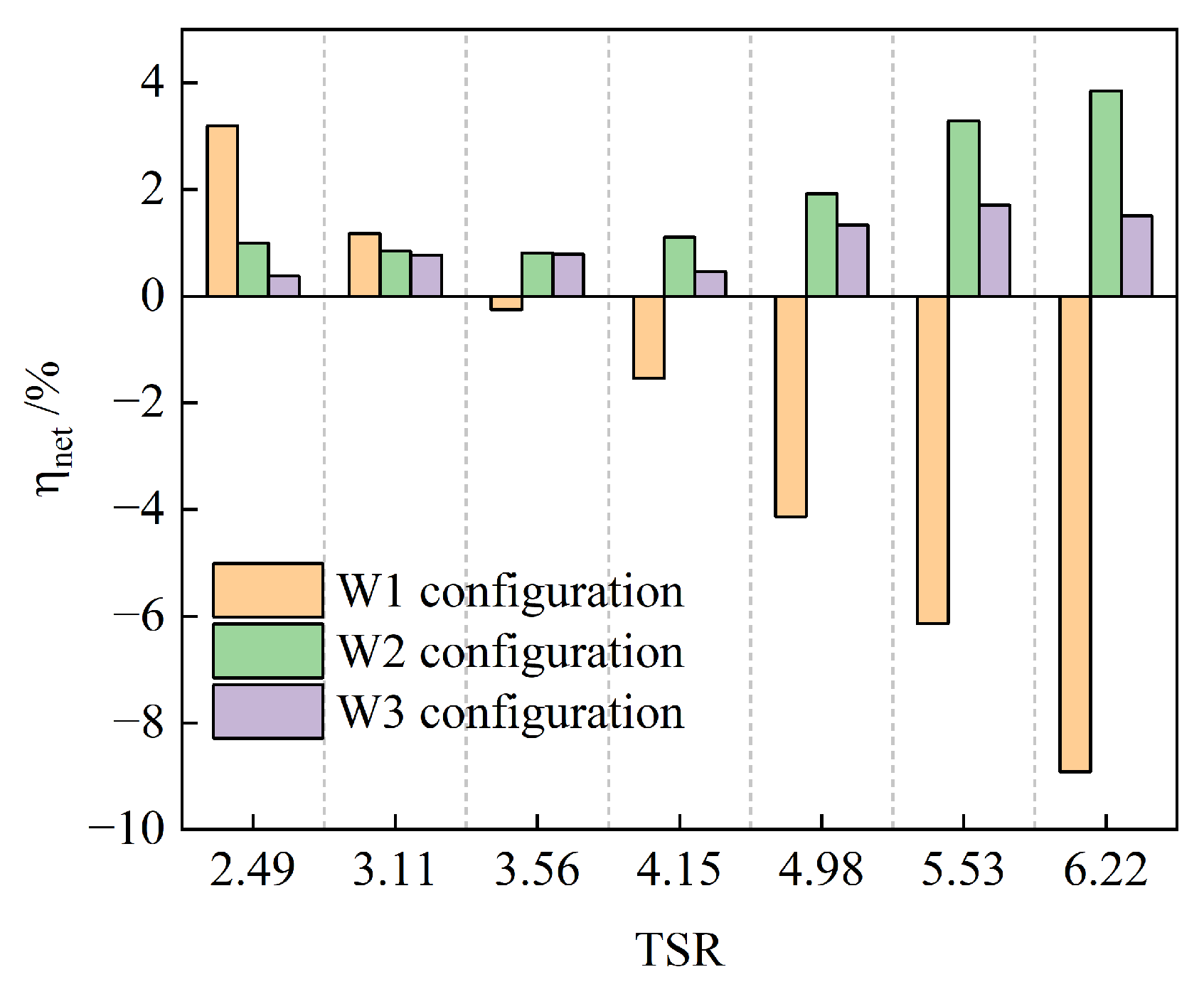
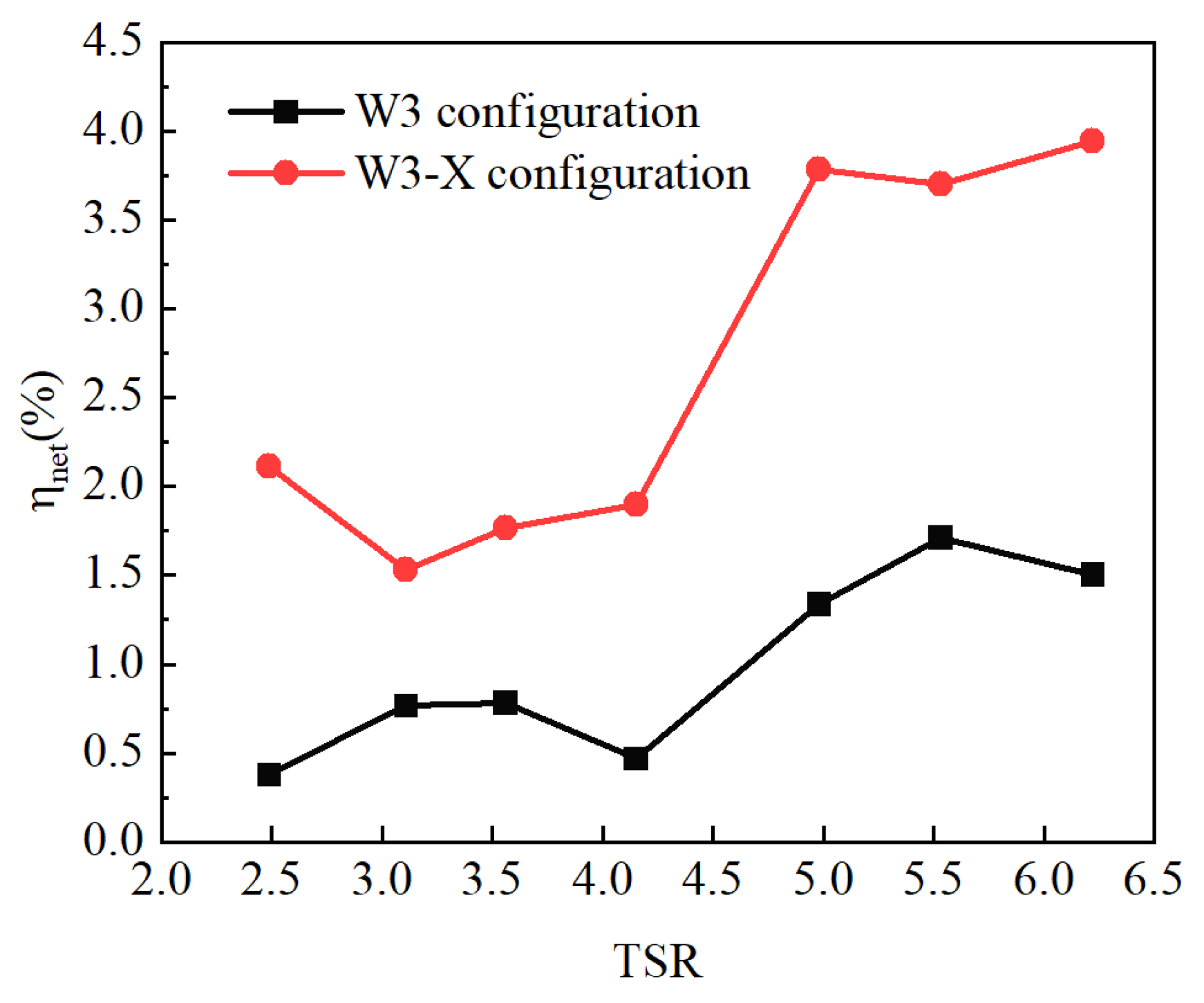
3.5. Comprehensive Performances of the Four Configurations
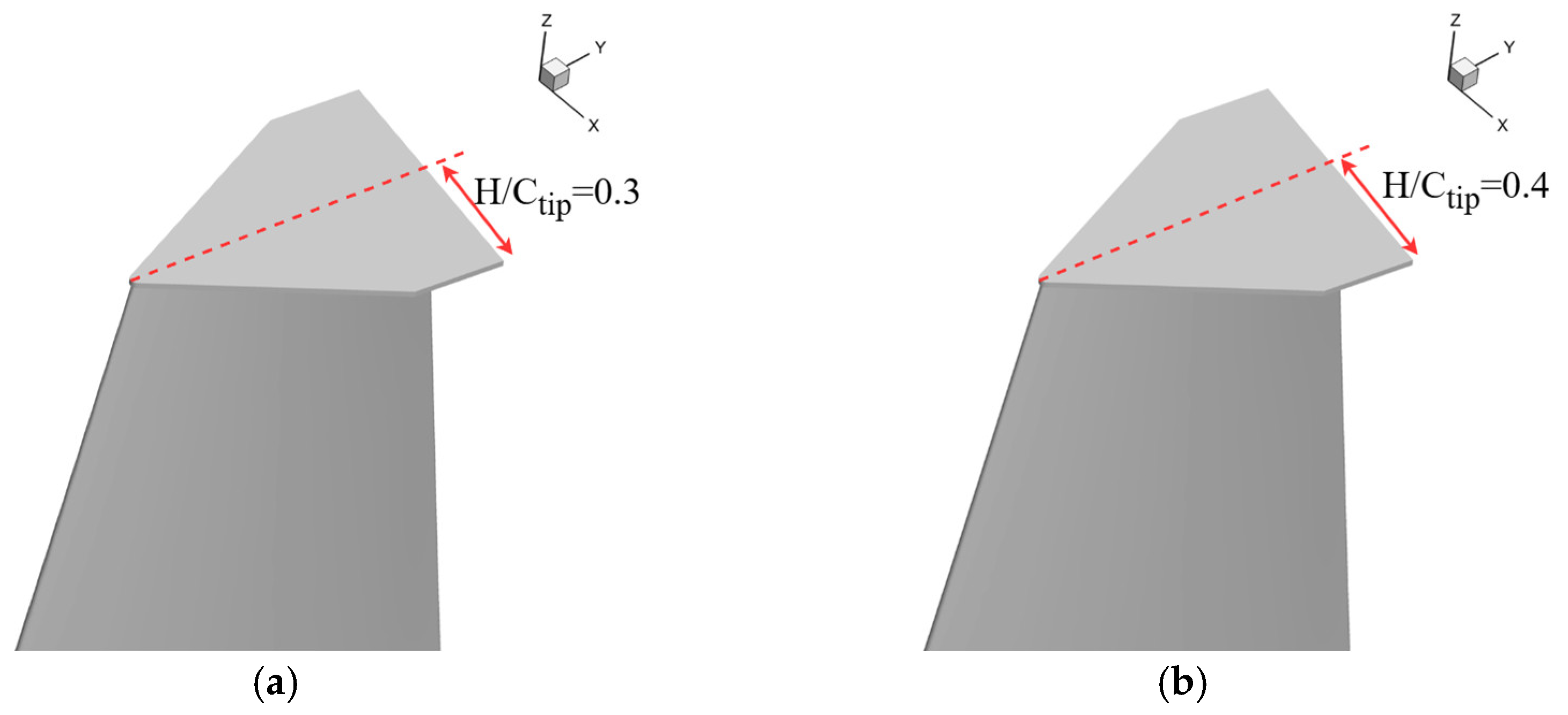
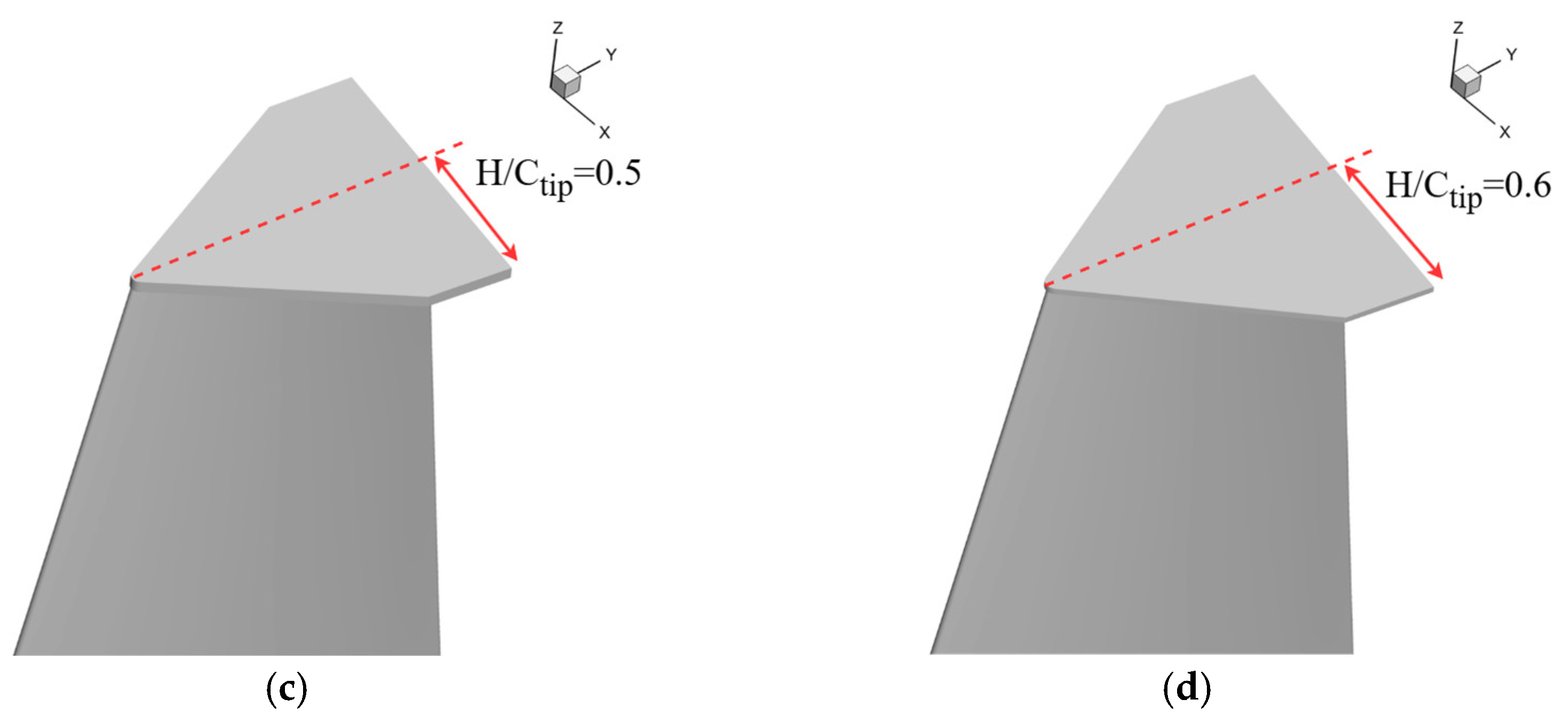
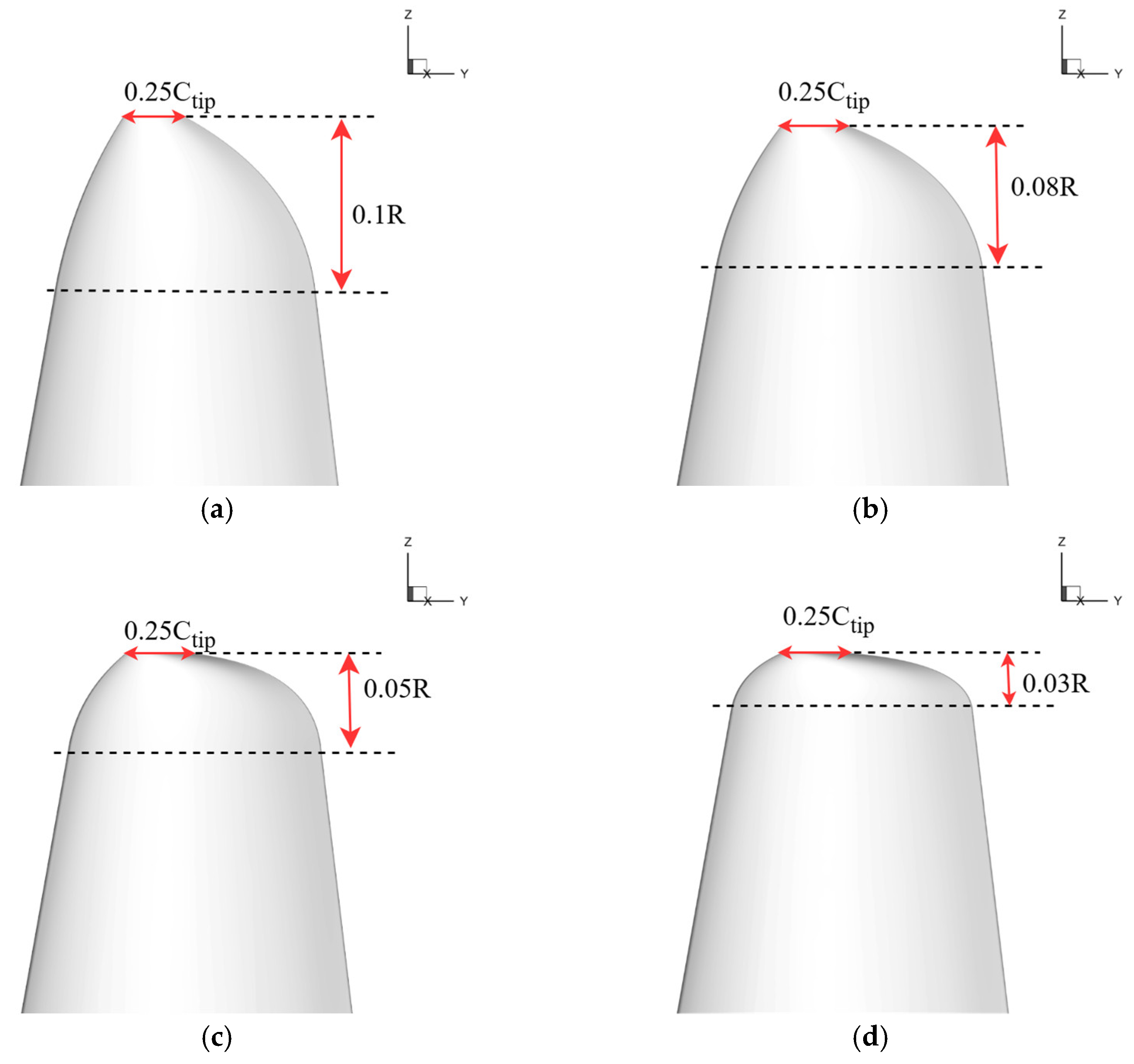
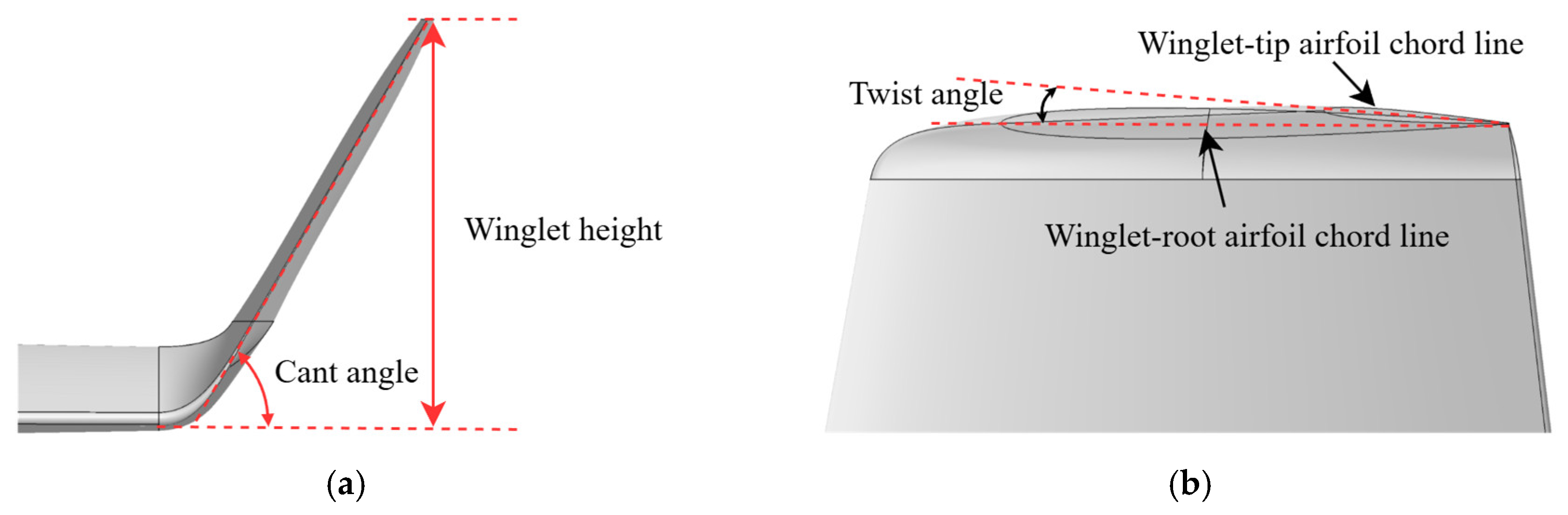
4. Parametric Optimization of the Winglet
4.1. Orthogonal Experimental Design (OED)
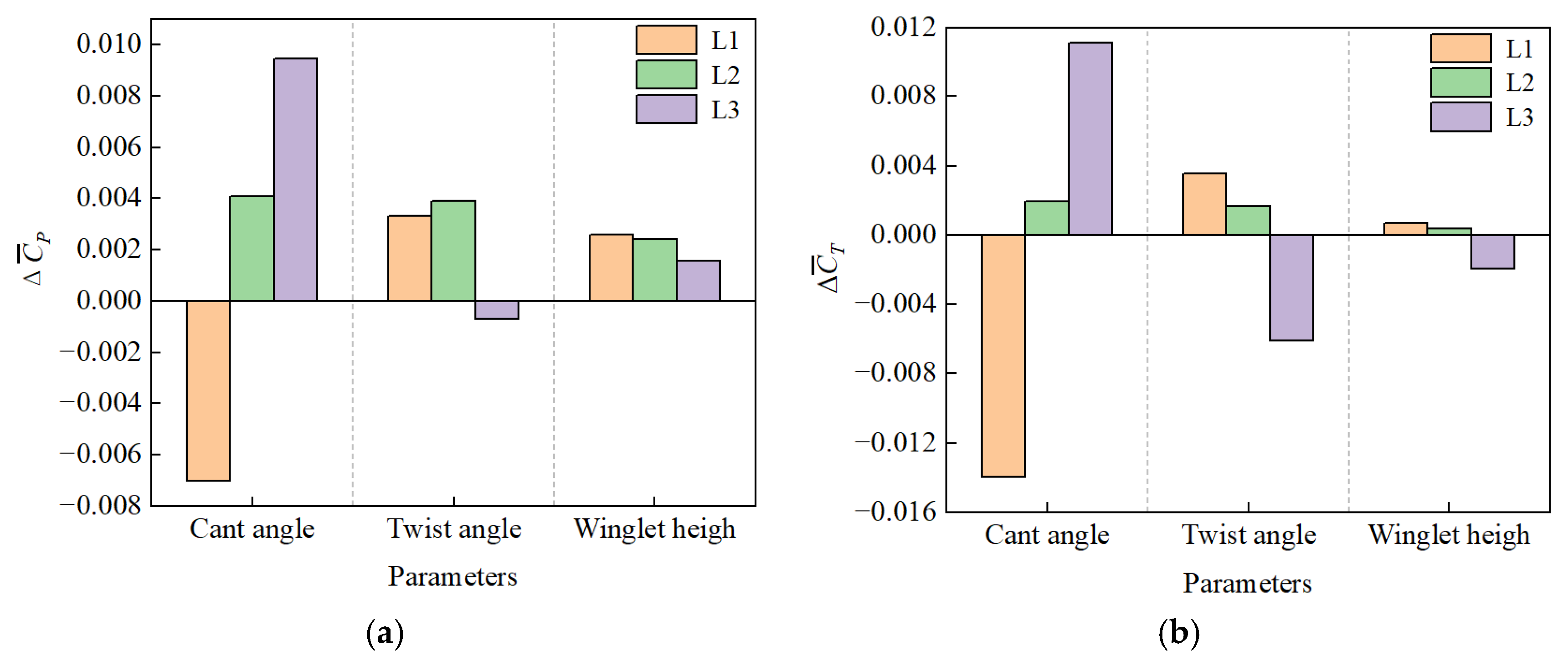
4.2. Analysis of OED Results
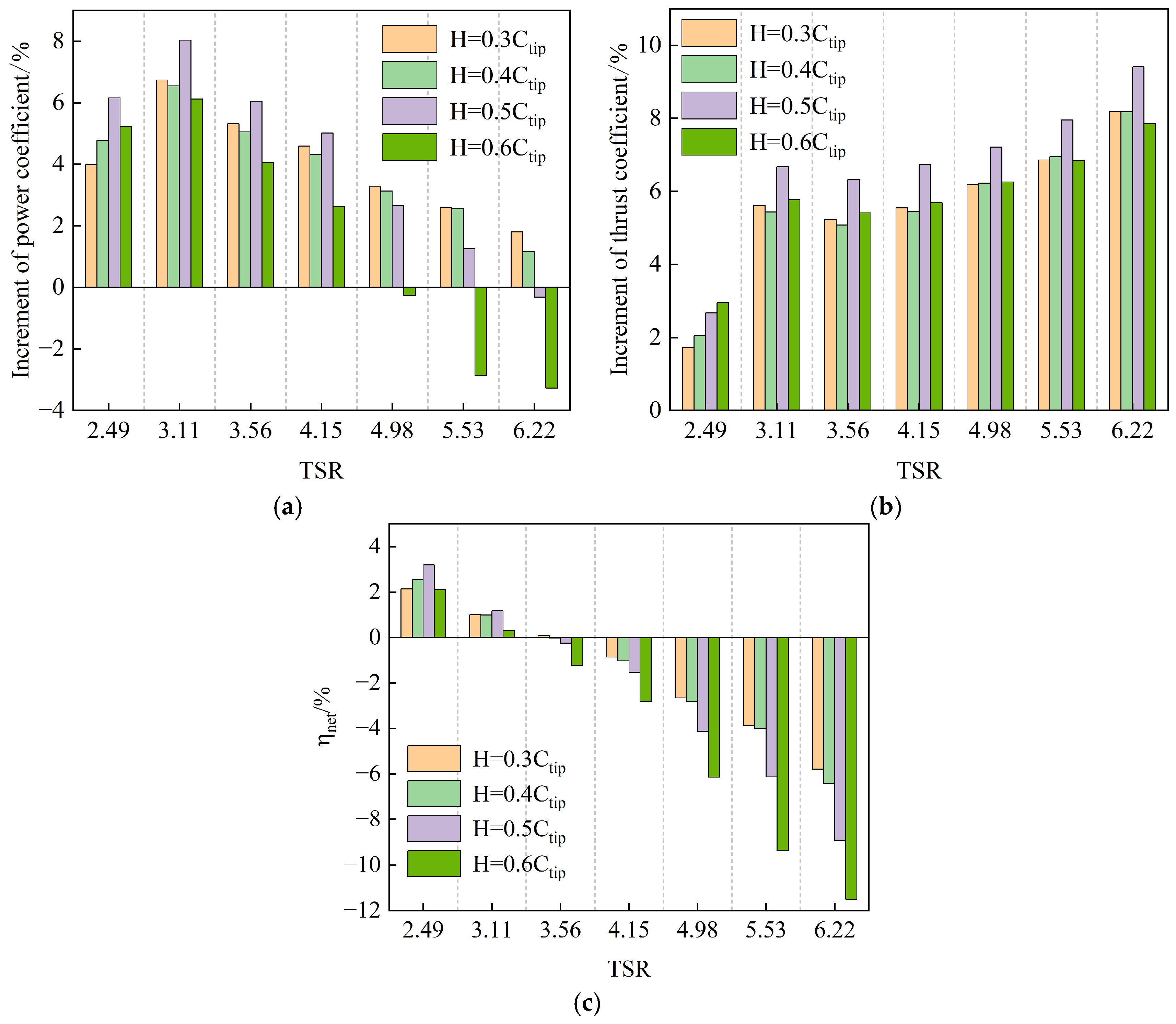
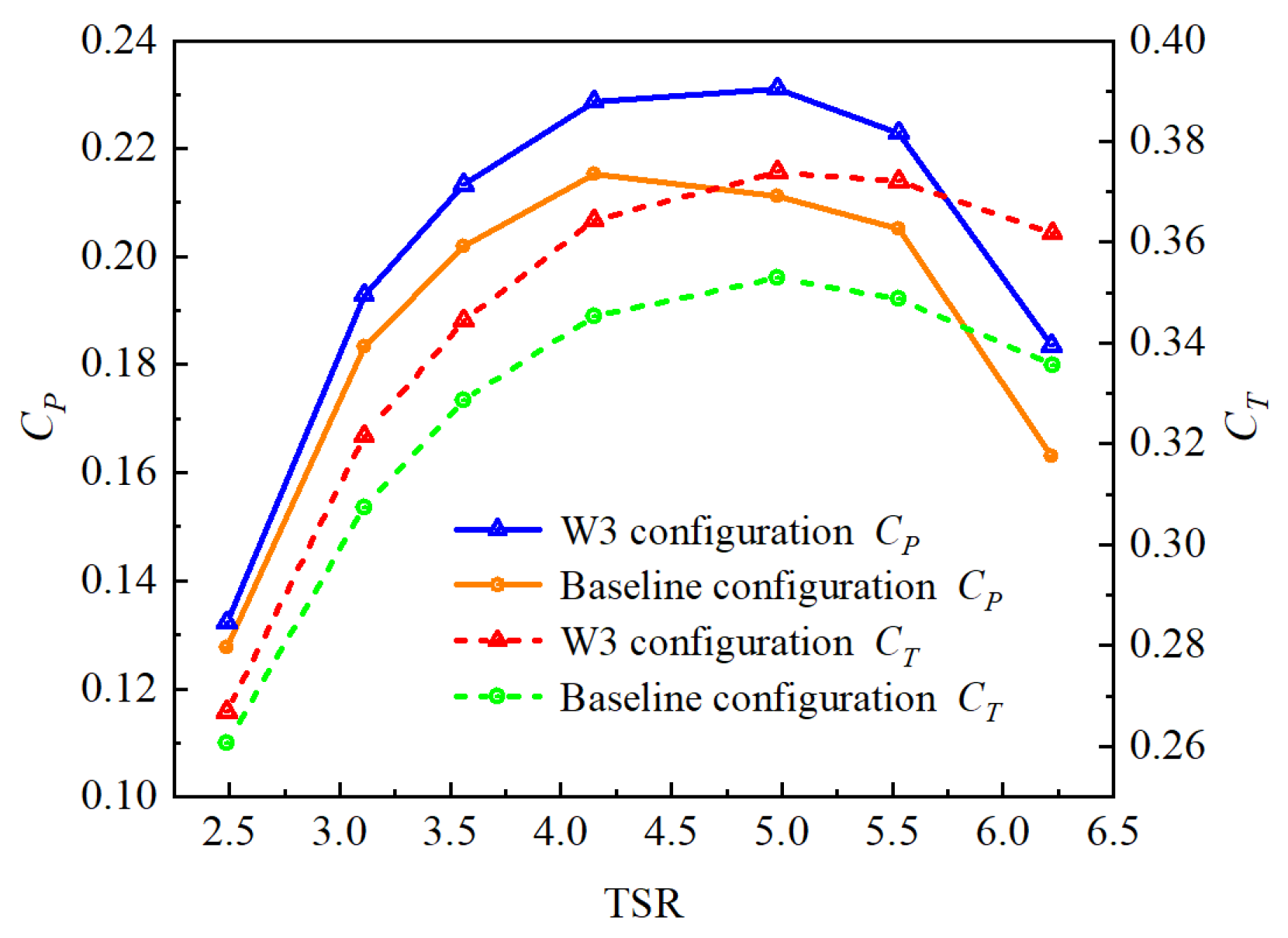
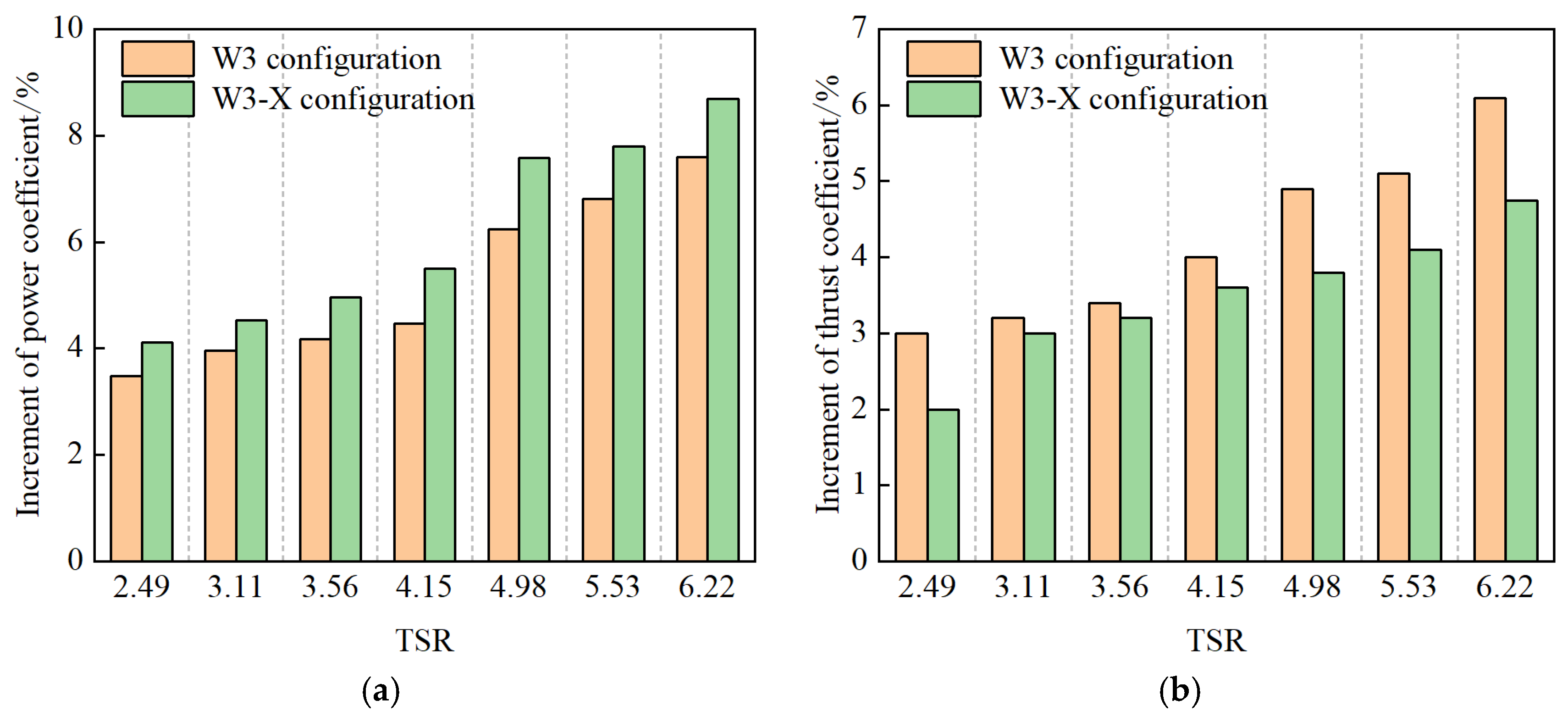
4.3. Aerodynamic Characterization of Winglet with Optimized Parameters
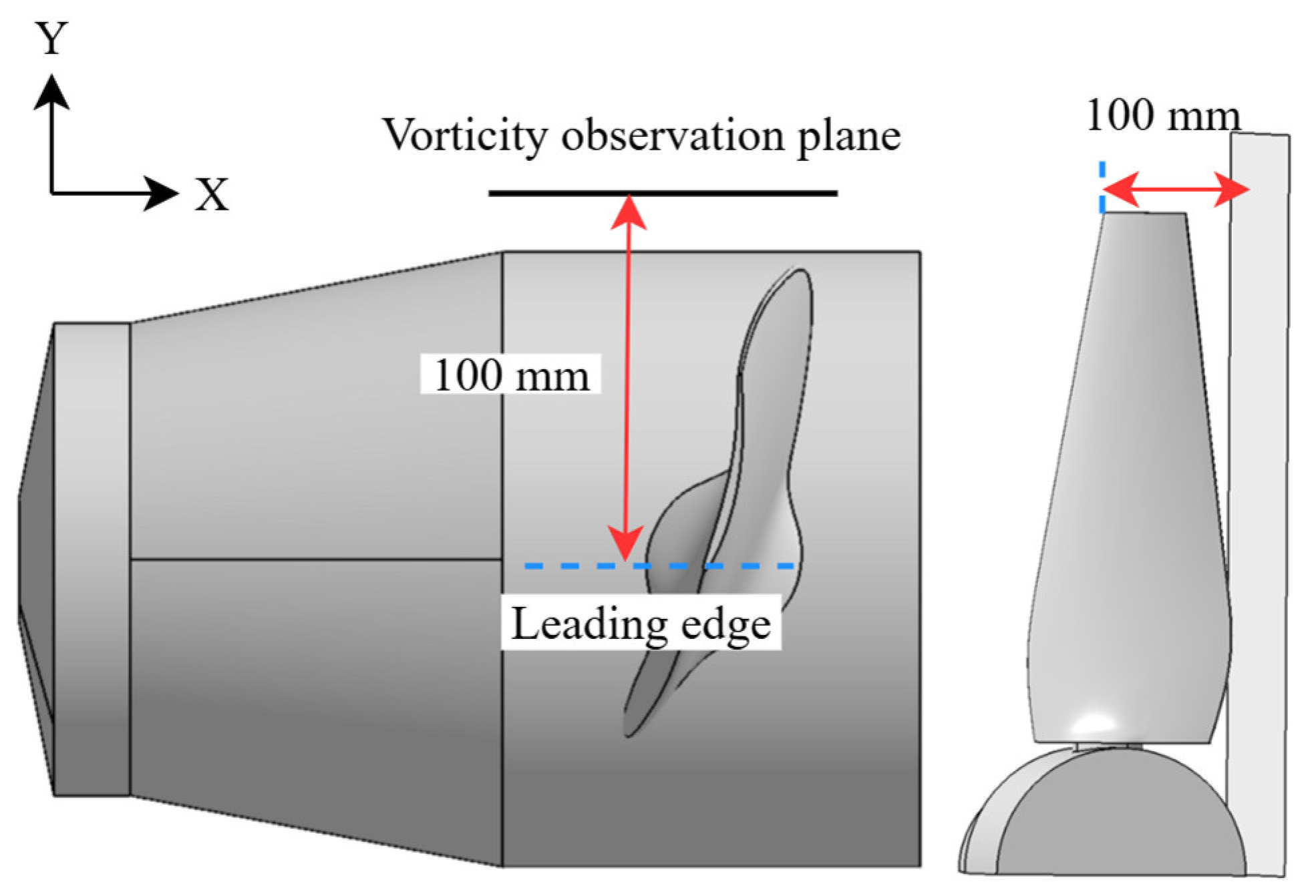
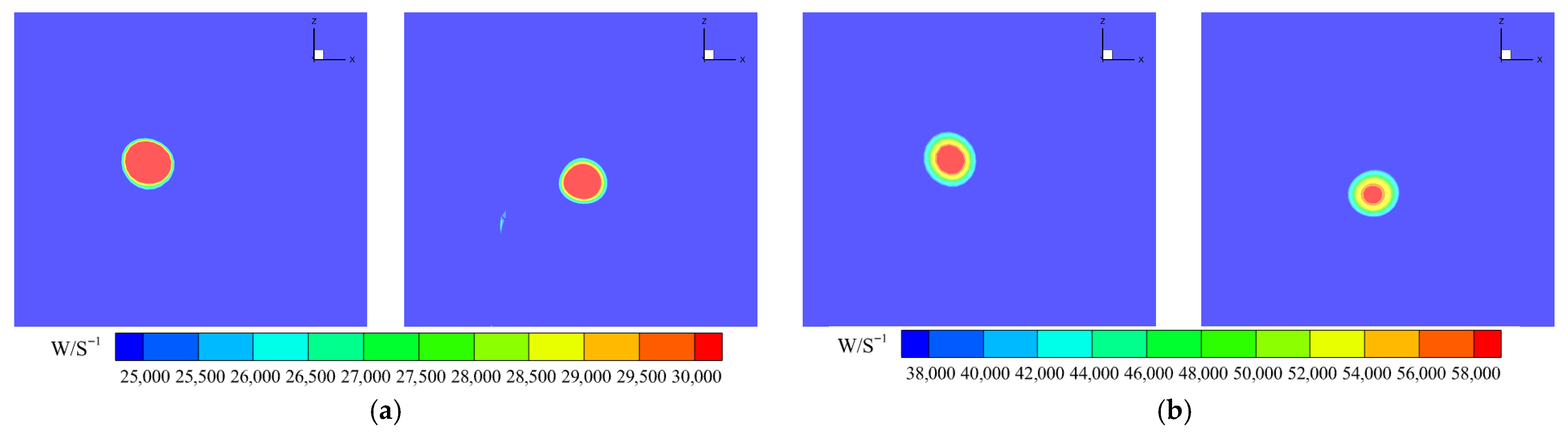
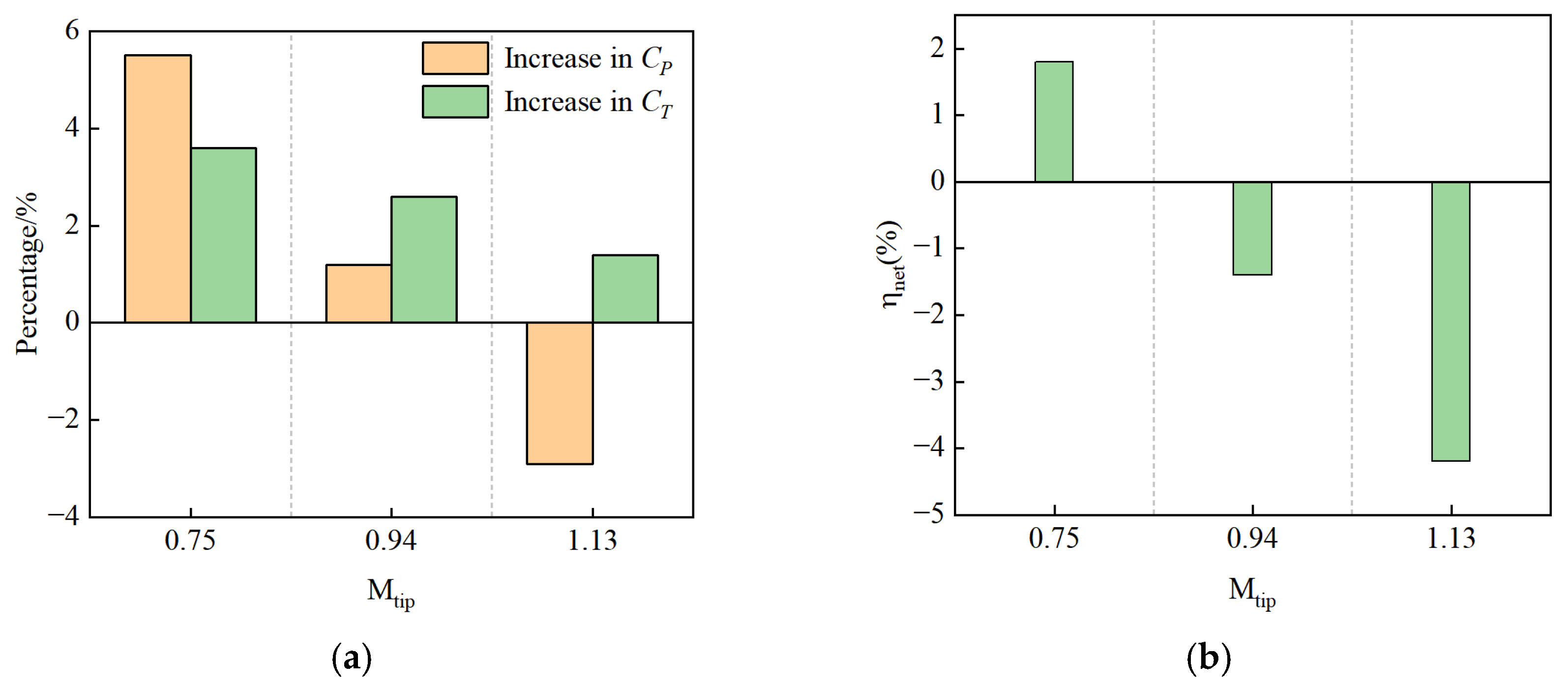
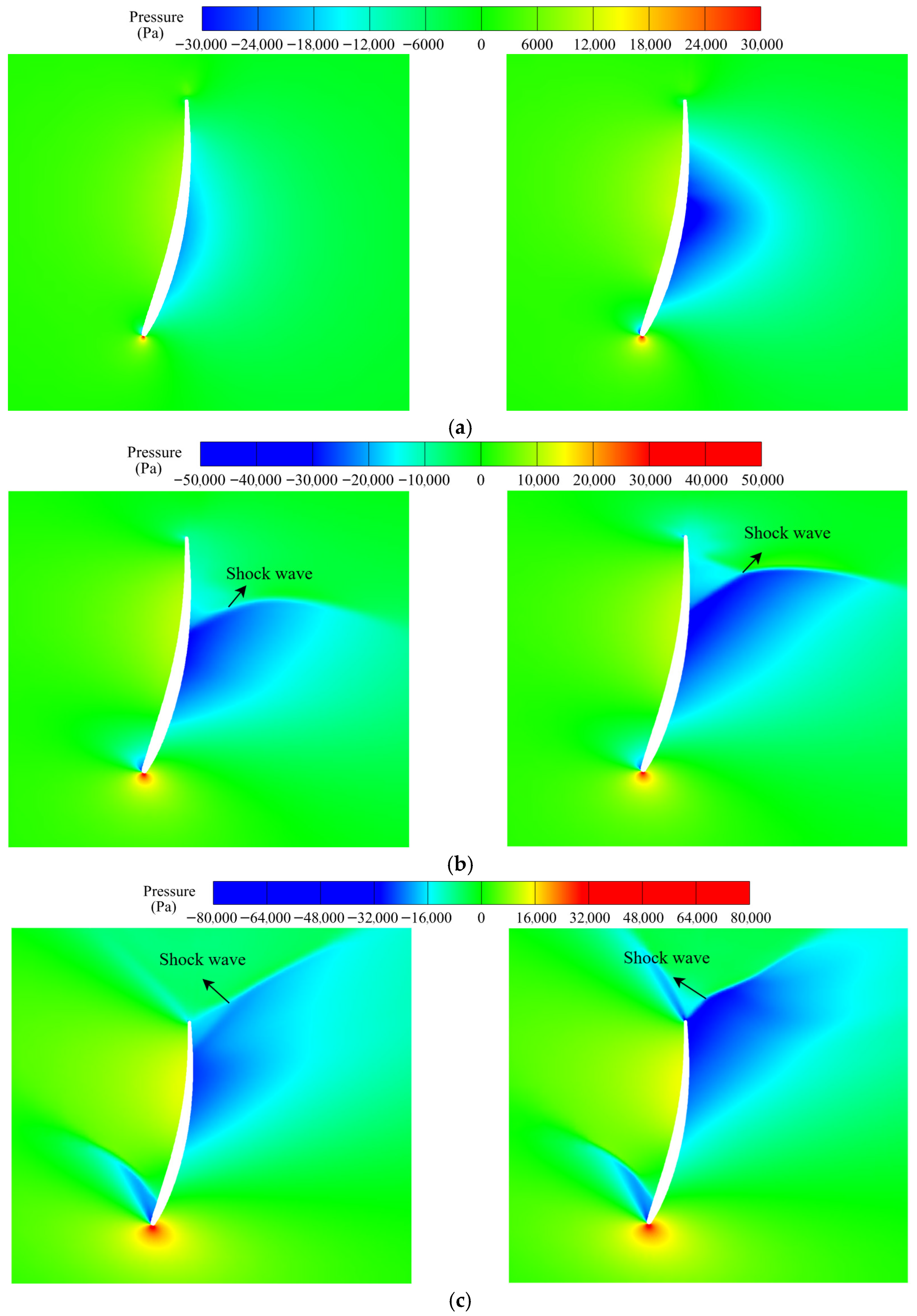
4.4. Influence of Blade Tip Mach Number on Winglet Aerodynamic Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Maré, J.-C.; Fu, J. Review on Signal-by-Wire and Power-by-Wire Actuation for More Electric Aircraft. Chin. J. Aeronaut. 2017, 30, 857–870. [Google Scholar] [CrossRef]
- Guo, X.; Jiang, J. Rotational Speed Stability of Ram Air Turbine Under Aerodynamic Loads. Int. J. Struct. Stab. Dyn. 2024, 2650058. [Google Scholar] [CrossRef]
- Zhang, X.; Ding, S.; Du, F.; Ji, F.; Guo, S. Numerical Simulation on Aerodynamic Performance of Ram Air Turbine Based on Mixed Flow Field. In Volume 7: Fluids Engineering, Proceedings of the ASME 2018 International Mechanical Engineering Congress and Exposition, Pittsburgh, PA, USA, 9 November 2018; American Society of Mechanical Engineers: Pittsburgh, PA, USA, 2018. [Google Scholar]
- Saad, M.; Moh, M.; Mohd, S.B.; Zulkafli, M.F. A Survey on the Use of Ram Air Turbine in Aircraft. In Proceedings of the AIP Conference Proceedings, Jogjakarta, Indonesia, 1–3 August 2017. [Google Scholar]
- Zhang, Q. The Design of More-Electric Engine Power Systems. Ph.D. Thesis, University of Strathclyde, Glasgow, UK, 16 February 2024. [Google Scholar]
- Xu, Z.; Qi, Y.; Guerrero, J.M.; Vasquez, J.C.; Wang, Y.; Zhao, H.; Li, W.; Wu, Y. Stability-Oriented Impedance Modeling, Analysis, and Shaping for Power Supply System in More-Electric Aircraft: A Review. IEEE Trans. Transp. Electrif. 2024, 10, 9351–9365. [Google Scholar] [CrossRef]
- Gębura, A.; Szelmanowski, A.; Jacyna-Gołda, I.; Gołda, P.; Kalbarczyk, M.; Tomaszewska, J. Concepts and Experiments on More Electric Aircraft Power Systems. Energies 2025, 18, 1653. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, L.; Zhou, M. Comparative Analysis of Ram Air Turbine System for Large Civil Aircraft. In Proceedings of the CSAA/IET International Conference on Aircraft Utility Systems (AUS 2022), Nanchang, China, 17–20 August 2022. [Google Scholar]
- Aguida, M.E.; Che, Y.; Yang, J. Technological Advancements and Future Prospects of Electrical Power Systems for Sustainable More Electric Aircraft. Propuls. Power Res. 2024, 13, 475–486. [Google Scholar] [CrossRef]
- Bolaños-Vera, M.A.; Ortiz-Pérez, A.S.; Durazo-Romero, E.S.; Pérez-Mota, J.E.; González-Uribe, L.A.; Pérez-Reyes, I. Numerical Analysis of Aerodynamic Performance of the Ram Air Turbine in an Aircraft. Heliyon 2024, 10, e32039. [Google Scholar] [CrossRef] [PubMed]
- Saad, M.M.M.; Mohd, S.; Zulkafli, M.F.; Samiran, N.A.; Didane, D.H. CFD Simulation Study on the Performance of a Modified Ram Air Turbine (RAT) for Power Generation in Aircrafts. Fluids 2021, 6, 391. [Google Scholar] [CrossRef]
- Gadda, K.S.; Avila Zaya, M.G.; Venkatesan, N.; Avital, E.J. Small Wind Ram Air Turbine Blade Geometric Modification for Performance. In Proceedings of the 14th UK Conference on Wind Engineering, Southampton, UK, 4–6 September 2024. [Google Scholar] [CrossRef]
- Zhang, D.; Yang, F.; Zhai, X.; Lu, Y. Research on Blade Tip Spoiler of Ram Air Turbine. In Proceedings of the 5th International Forum on Avionics Systems for Civil Aircraft, Shanghai, China, 19–21 April 2016. (In Chinese). [Google Scholar]
- Gharbia, Y.; Derakhshandeh, J.F.; Alam, M.M.; Amer, A.M. Developments in Wingtip Vorticity Mitigation Techniques: A Comprehensive Review. Aerospace 2023, 11, 36. [Google Scholar] [CrossRef]
- Cheng, H.; Ji, B.; Long, X.; Huai, W.; Farhat, M. A Review of Cavitation in Tip-Leakage Flow and Its Control. J. Hydrodyn. 2021, 33, 226–242. [Google Scholar] [CrossRef]
- Narayan, G.; John, B. Effect of Winglets Induced Tip Vortex Structure on the Performance of Subsonic Wings. Aerosp. Sci. Technol. 2016, 58, 328–340. [Google Scholar] [CrossRef]
- Gavrilović, N.N.; Rašuo, B.P.; Dulikravich, G.S.; Parezanović, V.B. Commercial Aircraft Performance Improvement Using Winglets. FME Trans. 2015, 43, 1–8. [Google Scholar] [CrossRef]
- Shelton, A.; Tomar, A.; Prasad, J.; Smith, M.J.; Komerath, N. Active Multiple Winglets for Improved Unmanned-Aerial-Vehicle Performance. J. Aircr. 2006, 43, 110–116. [Google Scholar] [CrossRef]
- Utomo, M.S.K.T.S.; Yohana, E.; Mahendra, C.; Utama, I.Y. Analysis of Blended Winglet Parameters on the Aerodynamic Characteristics of NXXX Aircraft Using Computational Fluid Dynamics (CFD). Results Eng. 2024, 24, 102901. [Google Scholar] [CrossRef]
- Farhan, A.; Hassanpour, A.; Burns, A.; Motlagh, Y.G. Numerical Study of Effect of Winglet Planform and Airfoil on a Horizontal Axis Wind Turbine Performance. Renew. Energy 2019, 131, 1255–1273. [Google Scholar] [CrossRef]
- Khaled, M.; Ibrahim, M.M.; Abdel Hamed, H.E.; AbdelGwad, A.F. Investigation of a Small Horizontal–Axis Wind Turbine Performance with and without Winglet. Energy 2019, 187, 115921. [Google Scholar] [CrossRef]
- Johansen, J.; Sørensen, N.N. Numerical Analysis of Winglets on Wind Turbine Blades Using CFD. In Proceedings of the European Wind Energy Congress, Milan, Italy, 7–10 May 2007. [Google Scholar]
- Zhang, Z.; Kuang, L.; Han, Z.; Zhou, D.; Zhao, Y.; Bao, Y.; Duan, L.; Tu, J.; Chen, Y.; Chen, M. Comparative Analysis of Bent and Basic Winglets on Performance Improvement of Horizontal Axis Wind Turbines. Energy 2023, 281, 128252. [Google Scholar] [CrossRef]
- Gertz, D.; Johnson, D.A.; Swytink-Binnema, N. An Evaluation Testbed for Wind Turbine Blade Tip Designs—Winglet Results. Wind Eng. 2012, 36, 389–410. [Google Scholar] [CrossRef]
- Madi, M.; Tuswan, T.; Arirohman, I.D.; Ismail, A. Comparative Analysis of Taper and Taperless Blade Design for Ocean Wind Turbines in Ciheras Coastline, West Java. Kapal 2021, 18, 8–17. [Google Scholar] [CrossRef]
- Johansen, J.; Sørensen, N.N. Numerical Investigation of Three Wind Turbine Blade Tips; Technical Report RISO-R-1353(EN); Risø National Laboratory, Wind Energy Department: Roskilde, Denmark, 2002; Available online: https://www.google.com/url?sa=t&source=web&rct=j&opi=89978449&url=https://orbit.dtu.dk/files/7712498/ris_r_1353.pdf&ved=2ahUKEwioiN3f16qQAxVcCTQIHTgCLpcQFnoECBcQAQ&usg=AOvVaw1o2yJUx_ED0twP3u7tOhY9 (accessed on 21 July 2025).
- Giguere, P.; Selig, M.S. Design of a Tapered and Twisted Blade for the NREL Combined Experiment Rotor; Technical Report NREL/SR-500-26173; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 1999.
- Kaya, M.; Elfarra, M. Effect of Taper Distribution on the Torque and Thrust Generated by a Wind Turbine Rotor Blade. In Proceedings of the 2019 10th International Renewable Energy Congress (IREC), Sousse, Tunisia, 26–28 March 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Madsen, M.H.A.; Zahle, F.; Horcas, S.G.; Barlas, T.K.; Sørensen, N.N. CFD-Based Curved Tip Shape Design for Wind Turbine Blades. Wind Energy Sci. 2022, 7, 1471–1501. [Google Scholar] [CrossRef]
- Song, K.; Huan, H.-T.; Wei, L.-C.; Liu, C.-X. Performance Analysis of a Modified Archimedes Spiral Wind Turbine Having Winglet on Blade. Energy 2025, 333, 137389. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, D.; Liu, X.; Xu, H.; Wang, Y.; Bi, R.; Qian, P. Unsteady Effects of a Winglet on the Performance of Horizontal-Axis Tidal Turbine. Renew. Energy 2024, 225, 120334. [Google Scholar] [CrossRef]
- Signor, D.B.; Acree, C.W.; Sebrell, W.A. Performance and Loads Data from an Outdoor Hover Test of a Lynx Tail Rotor; Technical Report NASA-TM-101057; National Aeronautics and Space Administration (NASA), Ames Research Center: Moffett Field, CA, USA, 1989.



| Grid | Blade Surface Mesh Number (×104) | Growth Rate | Mesh Number (×104) | Torque (N·m) | Thrust (N) |
|---|---|---|---|---|---|
| G01 | 32 | 1.20 | 773 | 50.72 | 643.16 |
| G02 | 53 | 1.15 | 1447 | 50.58 | 642.27 |
| G03 | 78 | 1.10 | 2135 | 50.51 | 641.78 |
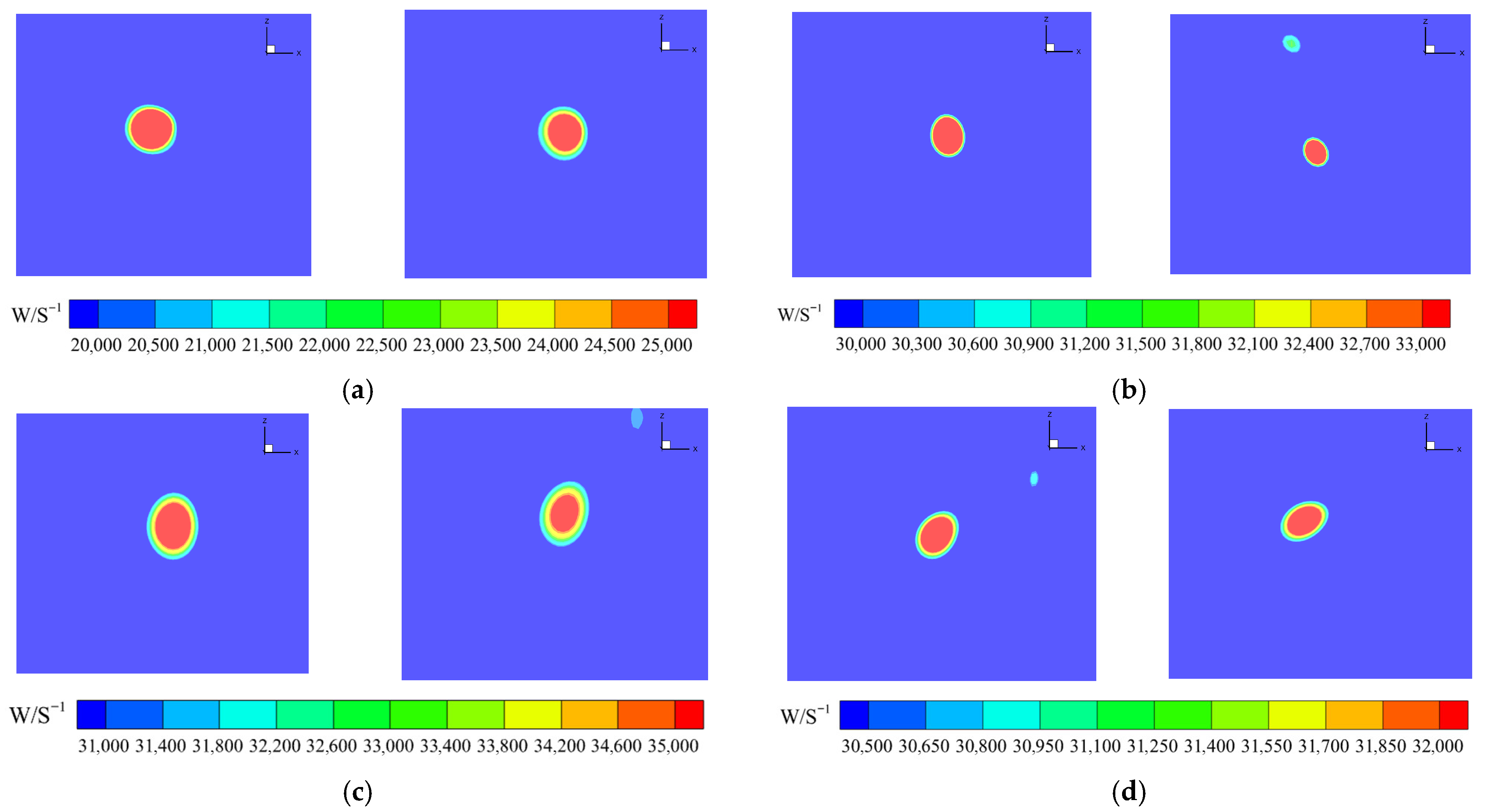
| TSR | Blade Tip Configuration | Maximum Vorticity (s−1) |
|---|---|---|
| 5.53 | Baseline configuration | 67,156 |
| 5.53 | W2 configuration | 61,008 |
| 6.22 | Baseline configuration | 52,804 |
| 6.22 | W2 configuration | 43,506 |
| Parameters | Levels | ||
|---|---|---|---|
| L1 | L2 | L3 | |
| Cant angle (°) | 30 | 60 | 90 |
| Twist angle (°) | 0 | 4 | 8 |
| Winglet height (mm) | 20 | 25 | 30 |
| OED No. | Cant Angle (°) | Twist Angle (°) | Winglet Height (mm) | CP | CT |
|---|---|---|---|---|---|
| 1 | 30 | 0 | 25 | 0.1966 | 0.3412 |
| 2 | 30 | 4 | 20 | 0.1986 | 0.3413 |
| 3 | 30 | 8 | 30 | 0.1895 | 0.3372 |
| 4 | 60 | 0 | 30 | 0.2081 | 0.3354 |
| 5 | 60 | 4 | 25 | 0.2060 | 0.3297 |
| 6 | 60 | 8 | 20 | 0.2039 | 0.3269 |
| 7 | 90 | 0 | 20 | 0.2110 | 0.3204 |
| 8 | 90 | 4 | 30 | 0.2128 | 0.3202 |
| 9 | 90 | 8 | 25 | 0.2103 | 0.3037 |
| Levels | Cant Angle (°) | Twist Angle (°) | Winglet Height (mm) | |
|---|---|---|---|---|
| L1 | −0.0070 | 0.0033 | 0.0026 | |
| L2 | 0.0041 | 0.0039 | 0.0024 | |
| L3 | 0.0095 | −0.0007 | 0.0016 | |
| / | 0.0165 | 0.0046 | 0.0010 | |
| L1 | −0.0140 | 0.0036 | 0.0007 | |
| L2 | 0.0019 | 0.0017 | 0.0003 | |
| L3 | 0.0111 | −0.0061 | −0.0020 | |
| / | 0.0251 | 0.0097 | 0.0027 |
| Case | Rotational Speed (r/min) | Freestream Velocity (m/s) | TSR | Mtip |
|---|---|---|---|---|
| 1 | 5200 | 60 | 4.15 | 0.75 |
| 2 | 6500 | 75 | 4.15 | 0.94 |
| 3 | 7800 | 90 | 4.15 | 1.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Zhong, W.; Ren, C.; Wang, J.; Liu, Y. Aerodynamic Performance Enhancement of Ram Air Turbine Blades with Different Tip Configurations. Aerospace 2025, 12, 937. https://doi.org/10.3390/aerospace12100937
Li H, Zhong W, Ren C, Wang J, Liu Y. Aerodynamic Performance Enhancement of Ram Air Turbine Blades with Different Tip Configurations. Aerospace. 2025; 12(10):937. https://doi.org/10.3390/aerospace12100937
Chicago/Turabian StyleLi, Haoyu, Wei Zhong, Chunyu Ren, Jian Wang, and Yilei Liu. 2025. "Aerodynamic Performance Enhancement of Ram Air Turbine Blades with Different Tip Configurations" Aerospace 12, no. 10: 937. https://doi.org/10.3390/aerospace12100937
APA StyleLi, H., Zhong, W., Ren, C., Wang, J., & Liu, Y. (2025). Aerodynamic Performance Enhancement of Ram Air Turbine Blades with Different Tip Configurations. Aerospace, 12(10), 937. https://doi.org/10.3390/aerospace12100937






