Particle-Laden Two-Phase Boundary Layer: A Review

Abstract

The presence of solid particles (or droplets) in a flow leads to a significant increase in heat fluxes, the occurrence of chemical reactions, and erosive surface wear of various aircraft moving in the dusty (or rainy) atmosphere of Earth or Mars. A review of computational, theoretical, and experimental work devoted to the study of the characteristics of the boundary layers (BL) of gas with solid particles was performed. The features of particle motion in laminar and turbulent boundary layers, as well as their inverse effect on gas flow, are considered. Available studies on the stability of the laminar boundary layer and the effect of particles on the laminar–turbulent transition are analyzed. At the end of the review, conclusions are drawn, and priorities for future research are discussed.

1. Introduction

The presence of solid particles or droplets in a flow can lead to a significant increase in heat fluxes as well as erosive wear of the surfaces of various aircraft moving in the dusty (or rainy) atmosphere of Earth or Mars or when two-phase coolants flow through the ducts of power plants [1,2,3,4,5,6,7,8,9,10]. This effect is caused by the combined action of several factors:

(i)

Changes in the structure of the two-phase flow approaching the body;

(ii)

Changes in the boundary layer (BL) developing on the body;

(iii)

Changes in turbulent wakes and vortexes;

(iv)

Particle collisions with the surface;

(v)

Changes in surface roughness, etc.

Let us immediately note that the study of factor (i) is an independent major problem, so the main emphasis in the work is an analysis of studies devoted to the study of the last four of the above-mentioned factors.

The first studies of two-phase (gas–solid particle) boundary layers began in the early 1960s with the development of two-fluid modeling approaches [11]. These works focused on investigating 1D unsteady dusty gas flow over a plate moving at a variable speed, as well as the steady boundary layer developing over a semi-infinite flat plate. For single-phase fluids, similar problems are often referred to as Rayleigh’s problem (for an infinite plate instantaneously set into motion at a constant velocity), Stokes’ problem (for a plate oscillating periodically in its own plane), or Blasius’ problem. For the case of an incompressible fluid and Stokesian particles, solutions to Rayleigh’s and Stokes’ problems were obtained in [12,13,14] using Laplace transforms.

The intensity of physical processes occurring in two-phase boundary layers (TPBL) depends on particle inertia and concentration. The inertia of particles moving within the boundary layer is directly determined by flow geometry and parameters and can vary over a wide range for the same particles [15]. The presence of different characteristic time (or length) scales—such as those of the carrier flow, intrinsic turbulent scales, etc.—significantly complicates the study of such flows and data generalization. The particle concentration profile in the boundary layer, where high velocity and temperature gradients exist, can exhibit complex behavior, often exceeding the initial concentration in the undisturbed flow by multiple times. The primary reasons for this include

(i)

particle deceleration in the near-wall region;

(ii)

particle–wall interactions;

(iii)

interparticle interactions;

(iv)

“ejection” and “sweep” events, etc.

The main research objectives in two-phase boundary layer studies [7] are as follows: (i) investigation particle motion within the boundary layer; (ii) determination of the reciprocal influence of particles on carrier gas characteristics.

The study of particle effects on boundary layer flow represents a highly non-trivial problem, as the dispersed phase can influence near-wall flow through two distinct mechanisms: (i) the dispersed phase may modify BL flow by altering the incoming free-stream flow characteristics and (ii) particles directly affect BL flow due to their inertial nature, specifically through dynamic slip and thermal slip (in non-isothermal flow conditions).

This work presents and analyzes results from computational, theoretical, and experimental studies focused on particle behavior in BLs and their impact on carrier phase parameters.

Despite the significant interest in the problem of particle-laden two-phase boundary layers, both laminar and turbulent, there is currently no proper systematization of the existing knowledge. In this review, an attempt is made to fully consider the problem, from the laminar region through the transitional (least studied) to the turbulent region. An attempt is also made to jointly consider two strongly interconnected physical processes: the behavior of particles in a gas flow and their reverse effect on its characteristics. The authors hope that the work will fill some existing gaps in the systematization of existing knowledge and give impetus to further study of boundary layer flows with particles.

This paper is organized as follows. Section 2 presents the dimensionless parameters and modern mathematical methods used to analyze particle motion in the carrier gas BL and their reciprocal influence on its characteristics. Section 3 provides an analysis of experimental and computational-theoretical studies of particle motion and its effect on laminar boundary layer flow. Section 4 reviews and evaluates research on the stability of TPBL and the transitional BL region. The concluding Section 5 analyzes experimental and computational-theoretical studies of particle motion and its influence on turbulent boundary layer flow. The review concludes with a summary of key findings and outlines promising directions for future research on TPBL with solid particles.

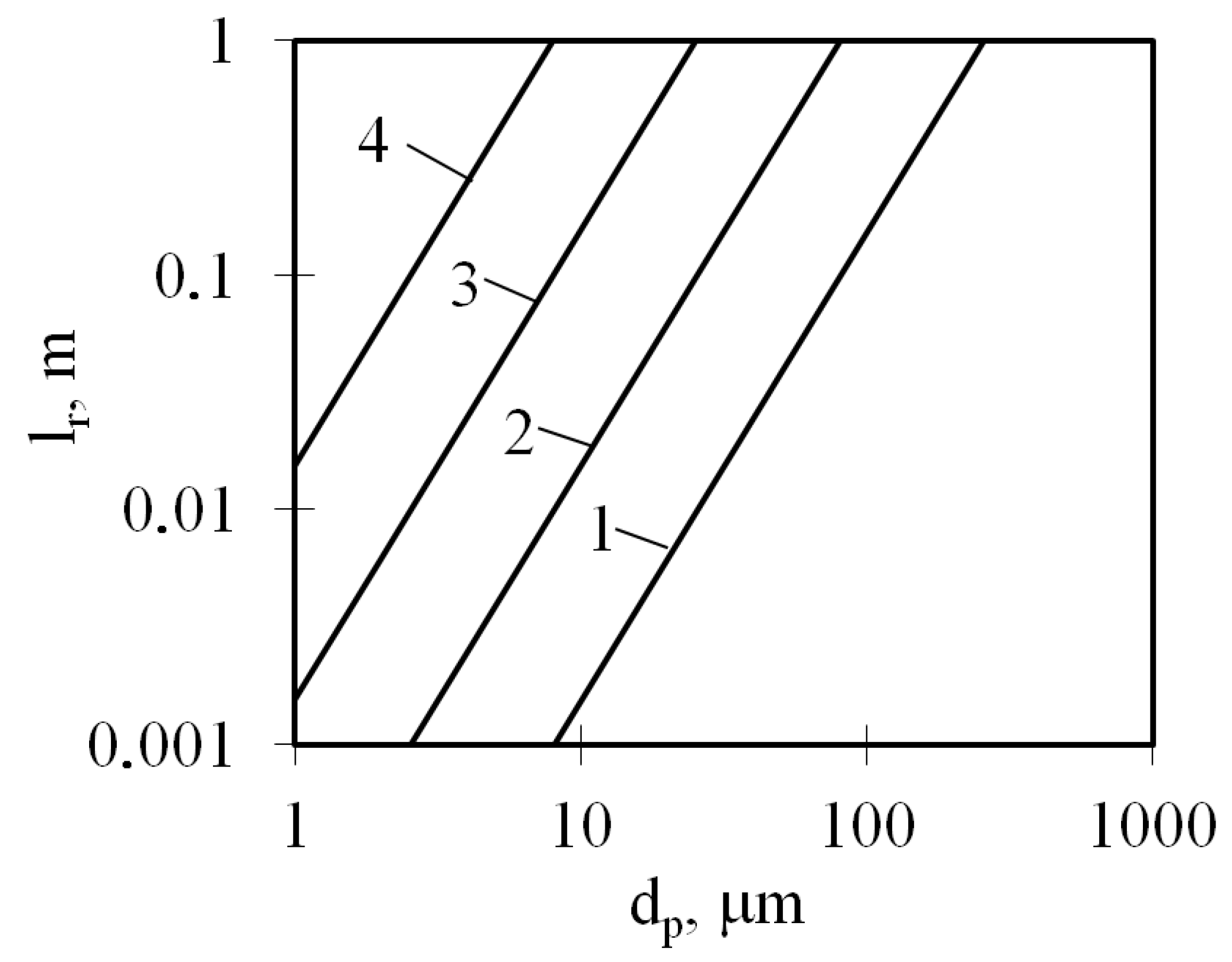
2. Dimensionless Parameters of Two-Phase Boundary Layers

This section describes the important parameters describing particle inertia in BL flows. The primary focus is on the local Stokes number in time-averaged flow (Section 2.1), along with other key dimensionless criteria (Section 2.2) used in both mathematical modeling and experimental investigations.

2.1. Dimensionless Characteristics of Two-Phase Boundary Layers

Particles exhibit inertial properties that cause their motion to differ from that of the carrier gas flow. The carrier gas velocity at the wall equals zero (Newton’s no-slip condition), i.e., $U_{xw}=0$, and a gradient velocity profile characteristic of the boundary layer is formed. Particles enter the BL with velocity $V_{x\infty }$. As a first approximation, we may assume their initial velocity equals the corresponding gas velocity, i.e., $V_{x\infty }\approx U_{x\infty }$ (Figure 1). Subsequently, a finite amount of time is required for phase velocity relaxation ($V_{xw}\to U_{xw}=0$). The region where particle deceleration occurs is called the boundary layer relaxation zone, or relaxation length l_r.

The important parameter describing particle inertia in boundary layer flow is the local Stokes number in the time-averaged flow Stk_f. This Stokes number describes the relaxation process of time-averaged gas and particle velocities near the surface and is defined as

$$St{k}_f={\displaystyle \frac{{\tau }_{p0}}{T_f}}={\displaystyle \frac{({\rho }_p d_p^2)/18\mu }{x/U_{x\infty }}},$$

(1)

where τ_p0 is the dynamic relaxation time of a Stokesian particle, T_f is the characteristic time of the carrier phase in time-averaged motion, ρ_p is the particle material density, d_p is the particle diameter, µ is the dynamic viscosity of the carrier medium, x is the downstream distance from the body’s stagnation point to the considered boundary layer section, and $U_{x\infty }$ is the characteristic velocity of the carrier phase in the free stream.

For non-Stokesian particles, the expression in (1) should use the corresponding particle dynamic relaxation time:

$${\tau }_p={\displaystyle \frac{{\tau }_{p0}}{C({\mathrm{Re}}_p)}}$$

(2)

where C (Re_p) is the correction function accounting for deviations from Stokes’ law, and Re_p is the particle Reynolds number.

In the range of Reynolds numbers < 1000, the following expression for the correction function has become widespread [10]: $C({\mathrm{Re}}_p)=1+0.15 {\mathrm{Re}}_p^{0.687}$.

For high-speed flows (subsonic, transitional transonic, and supersonic), correction functions accounting for Mach number effects must be incorporated when determining both the aerodynamic drag on particles and their relaxation time. The most reliable data from numerous experiments by various authors to determine the magnitude of the drag coefficient depending on the Mach number are given in [6,8,10].

Let us examine two limiting cases. If Stk_f →0, the particles are considered low-inertia, and their relaxation length $l_r\to 0$. In the opposite limiting case of large particles, Stk_f →∞ and $l_r\to \infty$. Let us perform simple estimates of the relaxation length for particles of different diameters. Using relation (1), we adopt the following assumptions:

(i)

Particles obey Stokes’ drag law (Stokesian particles);

(ii)

Particles have unit density ρ_p = 1000 kg/m³;

(iii)

Velocity relaxation completes ($x=l_r$) when the Stokes number reaches Stk_f = 0.2;

(iv)

The carrier gas has constant dynamic viscosity µ = 18·10⁻⁶ kg/(m·s).

Strictly note that the assumptions made that the particles are Stokesian and have unit density, the viscosity of the gas (air) is taken under normal conditions, and the boundary of the relaxation region is set by limiting the Stokes number lie on the surface (are obvious) and allow us to make estimates only in the very first approximation.

Simple estimates using expression (1) enable evaluation of the relaxation length for relatively low-inertia particles as a function of their diameter and free-stream velocity (Figure 2), i.e., $l_r=f(d_p, U_{x\infty })$. For instance, at a free-stream velocity of $U_{x\infty }=10$ m/s for d_p = 10 µm particles, the relaxation length is $l_r\cong 10$ mm; for d_p = 100 µm particles, it increases by two orders of magnitude to $l_r\cong 1$ m.

2.2. Other Dimensionless Parameters

In addition to the Stokes number Stk_f described above, several other dimensionless parameters are used to analyze particle motion within both horizontal and vertical boundary layers: drift parameter γ, various Stokes and Reynolds numbers, and Froude number.

The expressions for the aforementioned dimensionless parameters are given below (see, e.g., [16]). The drift parameter is defined as the ratio of the relative velocity W_x to the friction velocity U_∗.

$$\gamma ={\displaystyle \frac{W_x}{U_{*}}}.$$

(3)

The Stokes number based on the characteristic time scale τ of particle–turbulence interactions from a macroscopic perspective (the so-called “intermediate diffusion scale”) is expressed as

$$St{k}_{\tau }={\tau }_p/\tau .$$

(4)

The wall-based Stokes number (or friction-velocity Stokes number), defined using the friction velocity U_∗ and boundary layer thickness δ, is given by

$$St{k}_{\delta }={\displaystyle \frac{{\tau }_p}{{\tau }_{\delta }}}={\displaystyle \frac{{\tau }_p}{(\delta /U_{*})}}.$$

(5)

The momentum-thickness–based Stokes number, defined using the free-stream velocity U_x∞ and momentum thickness θ, is expressed as

$$St{k}_{\theta }={\displaystyle \frac{{\tau }_p}{{\tau }_{\theta }}}={\displaystyle \frac{{\tau }_p}{(\theta /U_{x\infty })}}.$$

(6)

The dimensionless Stokes number based on the normalized particle relaxation time ${\tau }^{+}$ is defined as

$$St{k}^{+}={\displaystyle \frac{{\tau }_p}{{\tau }^{+}}}={\displaystyle \frac{{\tau }_p}{(\nu /U_{*}^2)}}.$$

(7)

The Reynolds number based on centerline velocity U_xc and pipe diameter D is defined as

$${\mathrm{Re}}_D={\displaystyle \frac{U_{xc}D}{\nu }}.$$

(8)

The particle Reynolds number (Re), defined by the relative velocity $W_x$ and particle diameter d_p, is given by

$${\mathrm{Re}}_p={\displaystyle \frac{\left| W_x\right| d_p}{\nu }}.$$

(9)

The local Re, defined by the free-stream velocity $U_{x\infty }$ and streamwise coordinate x, is expressed as

$${\mathrm{Re}}_x={\displaystyle \frac{U_{x\infty } x}{\nu }}.$$

(10)

The wall Re (or friction Reynolds number), defined using the friction velocity $U_{*}$ and BL thickness δ, is expressed as

$${\mathrm{Re}}_{\tau }={\displaystyle \frac{U_{*}\delta }{\nu }}.$$

(11)

The BL Re, defined using the free-stream velocity $U_{x\infty }$ and boundary layer thickness δ, is given by

$${\mathrm{Re}}_{\delta }={\displaystyle \frac{U_{x\infty } \delta }{\nu }}.$$

(12)

The momentum-thickness Re, defined using the free-stream velocity $U_{x\infty }$ and momentum thickness θ, is expressed as

$${\mathrm{Re}}_{\theta }={\displaystyle \frac{U_{x\infty } \theta }{\nu }}.$$

(13)

The Froude number is expressed as

$$F{r}_{\delta }={\displaystyle \frac{U_{*}^2}{g\delta }},$$

where g is gravitational acceleration.

It should be noted that the numerous dimensionless criteria [6,7,10,16] listed above are generally recognized and widely used in both theoretical and experimental studies. The vast majority of them are used in the review further to describe and analyze the available results.

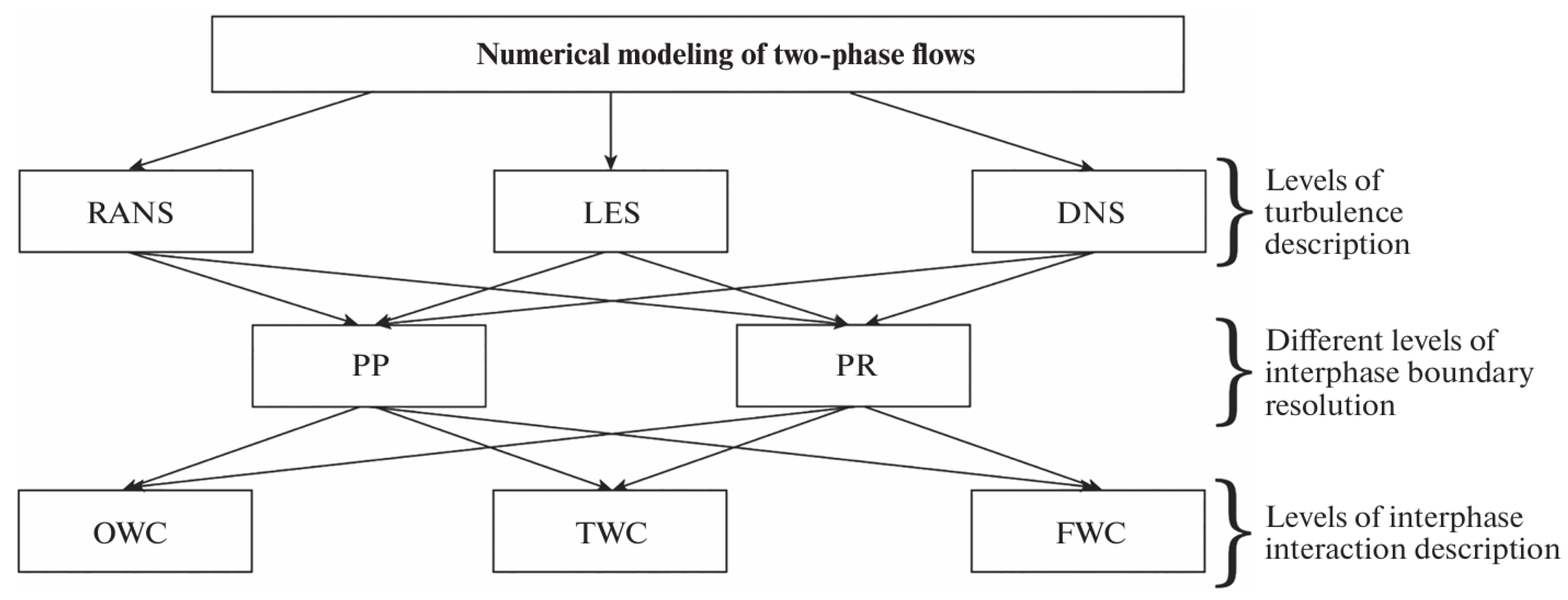
2.3. Numerical Simulation of Two-Phase Boundary Layers

Along with experimental studies, the last 20 to 30 years have seen a tremendous increase in works devoted to mathematical modeling. This also applies to two-phase boundary layers. Figure 3 presents the main modeling concepts for two-phase flows: (i) interface boundary resolution, (ii) interphase interactions, and (iii) carrier-phase turbulence.

First, mathematical models can employ different levels of interface boundary resolution (see Figure 3). Lagrangian methods (particle-point, PP methods) represent the oldest and most widely used approaches for particle motion description (e.g., [17,18,19]). These methods can simulate the motion of millions of particles, with their applicability requiring particle sizes to be small compared to the Kolmogorov spatial scale. In such cases, particles can be treated as point masses. The flow around individual particles is computed using interface-resolving methods (particle-resolved, PR methods) [20,21,22,23], where each particle’s behavior is determined by both external forces and the aerodynamic drag from the carrier gas, calculated during the simulation. These methods enable computation of interface deformation, which is crucial for flows containing droplets or bubbles [24]. Note that gas flow around each particle can only be resolved when the computational grid spacing is small relative to the particle size and the number of particles is limited. Separately, we note the method that has become extremely widespread for resolving time-varying interphase boundaries (drops, bubbles). This is the VOF method and its modifications (for example, the MCLS method is a computational method for mass conservation based on the Level-Set methodology).

Secondly, the particle concentration determines the required level of interphase interaction modeling [25,26] (see Figure 3):

(i)

Single-particle regime ($\mathrm{\Phi }\le 10^{-6}$), where their presence does not affect the carrier gas characteristics (“one-way coupling”, OWC);

(ii)

Dilute two-phase flow regime (dilute two-phase flows) (${10}^{-6}<\mathrm{\Phi }\le 10^{-3}$) with particle feedback effects (“two-way coupling”, TWC) [27,28,29,30];

(iii)

Dense two-phase flow regime (dense two-phase flows) ($\mathrm{\Phi }>10^{-3}$), where particle–particle collisions play an important role (“four-way coupling”, FWC) [31,32,33,34,35,36].

Thirdly, mathematical models can employ different approaches for modeling carrier-phase turbulence [15,36]; from RANS, where only averaged turbulence characteristics are computed, to LES and DNS, where only large eddies or eddies of all scales (down to Kolmogorov scale) are resolved (see Figure 3).

3. Two-Phase Laminar Boundary Layers

This section presents and analyzes the results of computational-theoretical and experimental studies of particle behavior and their reverse (back) influence on gas flow parameters in a laminar boundary layer.

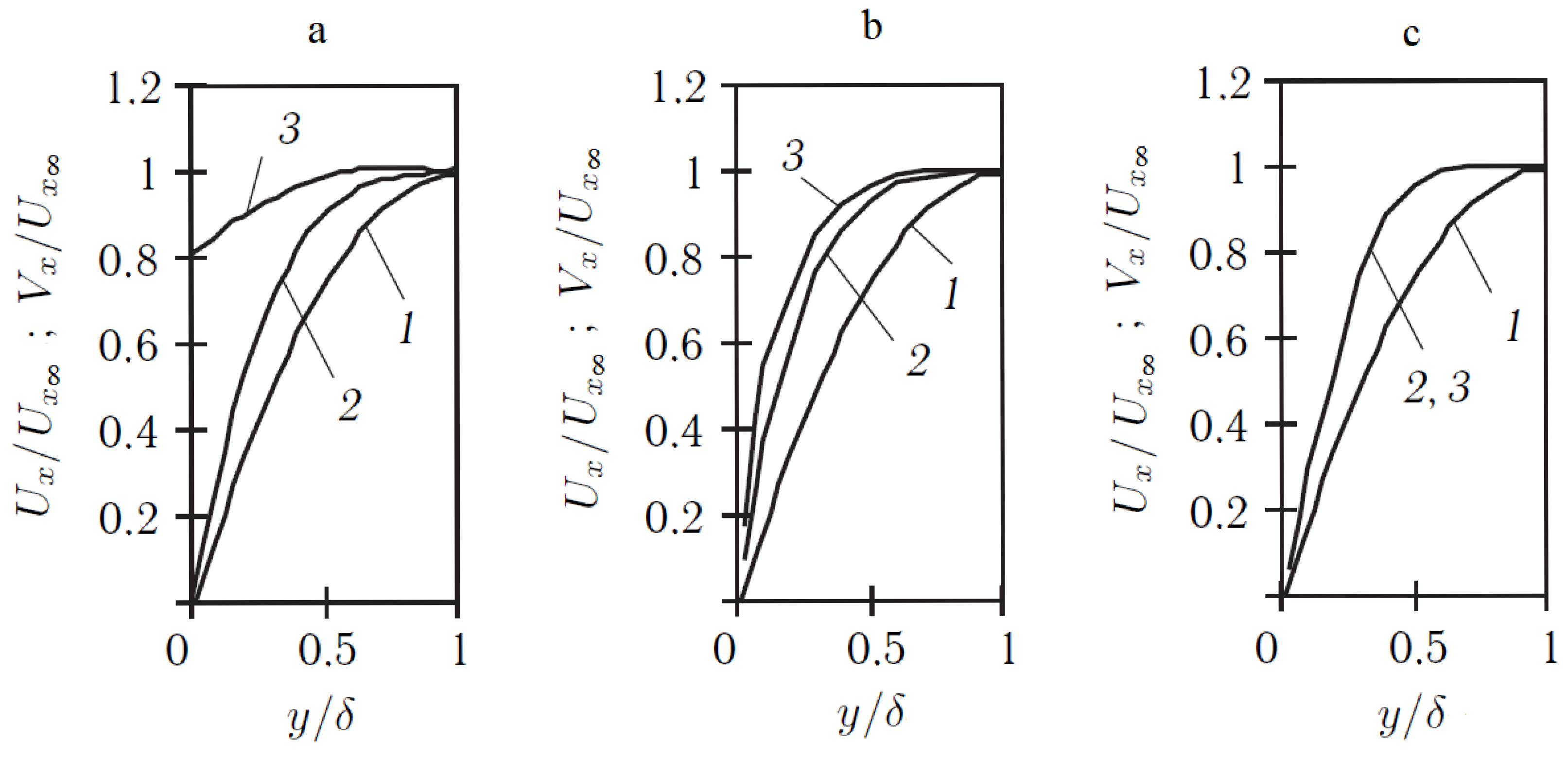
3.1. Particle Motion in Two-Phase Laminar Boundary Layers

Apparently, the first systematic studies of laminar boundary layers with particles were conducted by Soo S.L. [3,37]. The application of the momentum integral method to the equations of two-dimensional incompressible gas flow with particles yielded several important conclusions. It was shown that, as the two-phase flow moves along a flat plate, the particle velocity near the wall decreases, while the particle concentration increases. It was also noted that this tendency for particle concentration to rise indicates the possibility of particle deposition at some distance from the leading edge.

Later [38], conducted a detailed investigation of both particle motion characteristics in a laminar boundary layer and their reverse (back) influence on the carrier gas flow properties (see Section 3.2). The studied laminar boundary layer developed on a semi-infinite flat plate, with modeling performed within the framework of the interpenetrating continua model [39].

Particle inertia effects led to dynamic slip within the boundary layer, making the flow non-equilibrated. The study analyzed the development of particle velocity profiles––both longitudinal (Figure 4) and transverse (Figure 5) components––as well as concentration profiles. The velocity and concentration profiles are presented for various values of $\overline{x}$, defined (under the assumption $V_{x\infty }\approx U_{x\infty }$) as

$$\overline{x}={\displaystyle \frac{x}{l_r}}={\displaystyle \frac{x}{{\tau }_p V_{x\infty }}}\approx {\displaystyle \frac{x/U_{x\infty }}{({\rho }_p d_p^2)/18 \mu }}=St{k}_f^{-1}$$

(14)

Equation (14) shows that the dimensionless length $\overline{x}$ is the reciprocal of the local Stokes number in time-averaged flow.

Figure 4 shows that the longitudinal particle velocity exceeds the gas velocity throughout the entire BL, remaining non-zero at the plate surface when $\overline{x}<1$. This results from particle inertia. Study [38] notes that phase velocity relaxation essentially completes at $\overline{x}=5$ ($St{k}_f=0.2$), with the flow structure maintaining similar patterns across values of M particle mass concentration.

The calculations revealed (Figure 5) that, at small $\overline{x}$ (large $St{k}_f$), there exists a BL region where the transverse gas velocity component exceeds the corresponding particle velocity.

The obtained particle concentration distributions showed that, at $\overline{x}<1$ ($St{k}_f>1$), the dispersed phase density increases monotonically toward the plate, reaching a finite value at the wall $M_w=M_0/(1-\overline{x})$. At $\overline{x}\ge 1$ (Stk_f ≤ 1), the particle concentration tends toward infinity as the wall is approached. A later study [40] examined regions of unbounded particle concentration growth in flows, though these findings lack experimental confirmation.

Recall that, in [38], only the Stokes drag force was considered to govern particle motion in the laminar boundary layer. Attempts to account for the Saffman lift force arising from gas velocity field inhomogeneity were made in [41,42]. Regarding another transverse migration force––the Magnus force––research [42] demonstrated that, when Re_p < 10, where ${\mathrm{Re}}_p=U_{x0}{d}_p/\nu$, its transverse component becomes negligible compared to the Saffman force.

Experimental investigation of glass particle behavior (d_p=100 µm) in a laminar BL was conducted in [43]. The experiments used relatively inertial particles whose relaxation length is comparable to the extent of the laminar region in the boundary layer developing along the model surface. The measured particle velocity distributions indicate that the phase velocity relaxation process does not conclude by the final measurement cross-section. The Stokes numbers calculated using relation (1) for different cross-sections were $St{k}_f\approx 5$, $St{k}_f\approx 2$, and Stk_f ≈ 1. As shown in [38], phase velocity relaxation essentially completes at $\overline{x}=5$ (Stk_f = 0.2), with the flow structure maintaining similar patterns across different particle mass concentration values.

The experiments revealed that the intensity of particle velocity fluctuations at the outer boundary layer edge was ${\sigma }_{V_x}\approx 7.5\%$, exceeding the corresponding air velocity fluctuation intensity. The study employed relatively inertial particles with limited engagement in turbulent air vortex motion. The primary source of observed particle velocity fluctuations stemmed from the polydisperse nature of the particles used. The flow contained particles of varying sizes, consequently exhibiting different mean velocities. As the distance from the model surface decreased, particle velocity fluctuation intensity increased substantially. In the near-wall region, this enhancement primarily resulted from high carrier-phase mean velocity gradients. These air velocity gradients also induced non-uniformity in the particle mean velocity profile. Particle migration through regions with differing dispersed-phase mean velocities generated elevated velocity fluctuations near the wall. Similar enhancement of particle velocity fluctuations in non-uniform turbulent flows has been documented in studies [44,45,46].

3.2. Particles’ Back Influence on Two-Phase Laminar Boundary Layers

Let us continue the discussion of the results of the computational-theoretical work [38]. During the calculations, the mass concentration of particles varied over a wide range, leading to a significant influence of the dispersed phase on the gas flow parameters.

The results published in [42] allow us to conclude that neglecting the Saffman lift force acting on particles when calculating the laminar boundary layer for Re_p ≥ 1 can lead to significant errors.

In [47,48], important conclusions were made that the friction and heat transfer coefficients become larger, and the displacement thickness becomes smaller, compared to the case of single-phase flow. In [7,49], the distributions of velocities of clean air, air in the presence of particles, and the solid particles themselves in all regions of the BL, including the laminar region, were measured.

The boundary layer developed along the lateral surface of a cylinder installed inside a vertical pipe. The cylinder tip was hemispherical. The Reynolds number of the ascending air flow was ${\mathrm{Re}}_D=5.5\cdot {10}^4$. Aluminum oxide (Al₂O₃) particles with an average mass size of 50 µm were used as the dispersed phase in the experiments (Figure 6).

The presence of particles in the flow significantly affects the averaged velocity profile of the carrier phase in the “pseudo-laminar” boundary layer. The profile becomes fuller due to the acceleration of air by particles near the wall (Figure 6). This agrees with the conclusions of [38]. The difference between the velocities of single-phase and two-phase air flows reaches its maximum near the wall, where the difference in velocities of the gas and solid phases is greatest due to particle inertia. The particle Reynolds number in this region significantly exceeds the corresponding characteristic in the incoming flow and is Re_p = 15–25. By filling the averaged velocity profile, the particle gradient increases at the wall, leading to an increase in surface friction in the laminar region of the boundary layer.

Let us draw some conclusions. A laminar boundary layer with particles is a relatively simple and well-studied case. The calculations and experiments performed have clearly shown that the behavior of particles and their feedback on the carrier gas velocity profile is largely a process of momentum exchange. If the relaxation process of particle and gas velocities has not ended in the section under consideration, then we can expect an increase in surface friction (and heat transfer in the case of non-isothermal flow).

4. Stability of the Two-Phase Boundary Layer. Transitional Region

To date, a number of factors influencing the laminar–turbulent transition in the single-phase BL are known: the presence of a longitudinal pressure gradient, an increased degree of turbulence in the external turbulent flow [50,51,52], mechanical vibrations [53,54], roughness [55,56], surface heating [57,58], and many others.

4.1. Stability of Two-Phase Laminar Boundary Layers

It can be assumed that the stability of the laminar boundary layer will be determined by the interaction of particles with spatially and temporally periodic disturbances.

Generation of disturbances (turbulence) by extremely low-inertia particles [30,59,60,61]. In [1], it was concluded that the influence of particles on the stability of gas flow manifests in two ways. First, solid particles, due to their high physical density (${\rho }_p/\rho \cong O({10}^3)$), cause an increase in the “effective” density of the two-phase flow ρ_e, with increasing concentration, as

$${\rho }_e=\rho +\mathrm{\Phi } {\rho }_p=\rho (1+M)$$

(15)

An increase in the density of the carrier phase leads to a decrease in its effective kinematic viscosity ${\nu }_e=\mu /{\rho }_e$, which, in turn, increases the main flow characteristic—the Reynolds number. This is a destabilizing factor for laminar flow.

Second, this effect is caused by the presence of extremely low-inertia particles in the flow, whose relaxation time is much smaller than the Lagrangian integral turbulence scale (characterizing the lifetime of large energy-carrying vortices). In later works [30,59,60,61], the mechanism of turbulence generation due to the reduction in energy of small vortices, which involve extremely low-inertia particles in small-scale fluctuation motion and are responsible for turbulence energy suppression (dissipation), is investigated.

Dissipation of disturbances (turbulence) by relatively low-inertia particles. The first study of the stability of a gas carrying solid particles was conducted in [62]. The Navier–Stokes equation for the carrier gas was considered, taking into account the interphase interaction force (Stokes force). The analysis in this work largely followed the linearization method used in the study of single-phase flow stability [63], where small flow disturbances were assumed. As a result, a modified Orr–Sommerfeld equation was obtained, which differed from the corresponding equation for single-phase flow only in the use of a different (more complex) velocity profile. Analysis of the equation showed that, at small values of the parameter ${\alpha }^2{d}_p^2{\rho }_p/\rho$ ($\alpha$ is the wave number in the assumed velocity disturbance function for the fluid), the presence of particles leads to greater flow destabilization, whereas at large values of this parameter, the disturbance decay rate increases, and the flow stabilizes.

In [64], the stability of flow in an incompressible laminar boundary layer developing on a semi-infinite flat plate was considered. The study was conducted under the assumption that the main force factor determining particle behavior is the Stokes drag force. The solution of the modified Orr–Sommerfeld equations [62] was obtained in two different ways for the case of low mass content of particles. The results showed that the presence of particles suppresses unstable waves over a wide range of particle sizes. The most significant suppression occurs for particles of medium size, where their relaxation length is close to the Tollmien–Schlichting wavelength. For a stationary Tollmien–Schlichting wave in the case of monodisperse particles, a discontinuity in the eigenvalue due to resonant particle acceleration in the critical layer was identified.

In the pioneering work [65] and in [66,67,68,69,70], as well as in the authors’ earlier review [30], the mechanism of turbulence dissipation due to the reduction in energy of large vortices, which involve relatively low-inertia particles in large-scale fluctuation motion and are responsible for the magnitude of turbulence energy, is investigated.

Generation of disturbances (turbulence) by large particles. When large particles move in the laminar boundary layer at high Reynolds numbers (Re_p > 1000), turbulent wakes form behind them. Thus, it can be expected that the presence of such inertial particles in the flow will unambiguously lead to destabilization of laminar flow.

In [71,72], the mechanism of turbulence generation in turbulent wakes behind moving particles was studied. It was shown that the turbulence intensity of the carrier gas can increase significantly (up to several times) compared to its value in a single-phase flow.

It should be noted that large particles have high inertia and are not involved in the large-scale fluctuation motion of the carrier gas, and, therefore, do not absorb turbulent energy. Thus, additional dissipation of turbulent energy in flows with large particles is generally neglected.

4.2. Particles’ Influence on the Laminar–Turbulent Transition

The transition of laminar fluid (gas) flow to turbulent flow has attracted researchers’ attention for over 140 years. It is very important for predicting the location of the transitional region in the boundary layer.

Studies of the susceptibility of the supersonic boundary layer to the presence of solid particles in the flow are presented in [73,74]. These studies showed that, when interacting with the boundary layer, particles generate unstable wave packets (Tollmien–Schlichting waves). These waves amplify downstream and lead to the generation of turbulent spots.

Let us continue the discussion of the results of [7,49] started in Section 3.2. The experimental results obtained by these works allowed us to draw conclusions about the influence of particles on the laminar–turbulent transition.

In Section 3.2, it was noted that the presence of particles in the flow significantly affects the averaged velocity profile of the carrier phase in the laminar boundary layer (Figure 7).

This characteristic is defined as follows:

$$H={\displaystyle \frac{{\delta }^{*}}{\theta }}$$

(16)

where δ∗ and θ—are the displacement thickness and the momentum thickness, respectively.

Analyzing the obtained distributions of averaged velocity and shape parameter [7,49], concluded that, in the case of single-phase flow, the laminar–turbulent transition begins at x = 55–60 mm, which corresponds to the following range of Reynolds numbers: ${\mathrm{Re}}_{xcr1}=4.9\cdot {10}^4-5.3\cdot {10}^4$. In the case of two-phase flow, the laminar–turbulent transition begins earlier, namely at x = 40–50 mm (${\mathrm{Re}}_{xcr1}=3.6\cdot {10}^4-4.4\cdot {10}^4$) and x = 36–44 mm (${\mathrm{Re}}_{xcr1}=3.2\cdot {10}^4-3.9\cdot {10}^4$) for mass concentrations $M_0=0.18$ and $M_0=0.26$, respectively (Figure 7).

Let us draw some conclusions. To date, there is a small number of studies of the effect of particles on the laminar–turbulent transition in the boundary layer. This information is of great importance for engineering practice, since friction and heat transfer in different regions of the boundary layer change dramatically.

5. Two-Phase Turbulent Boundary Layers

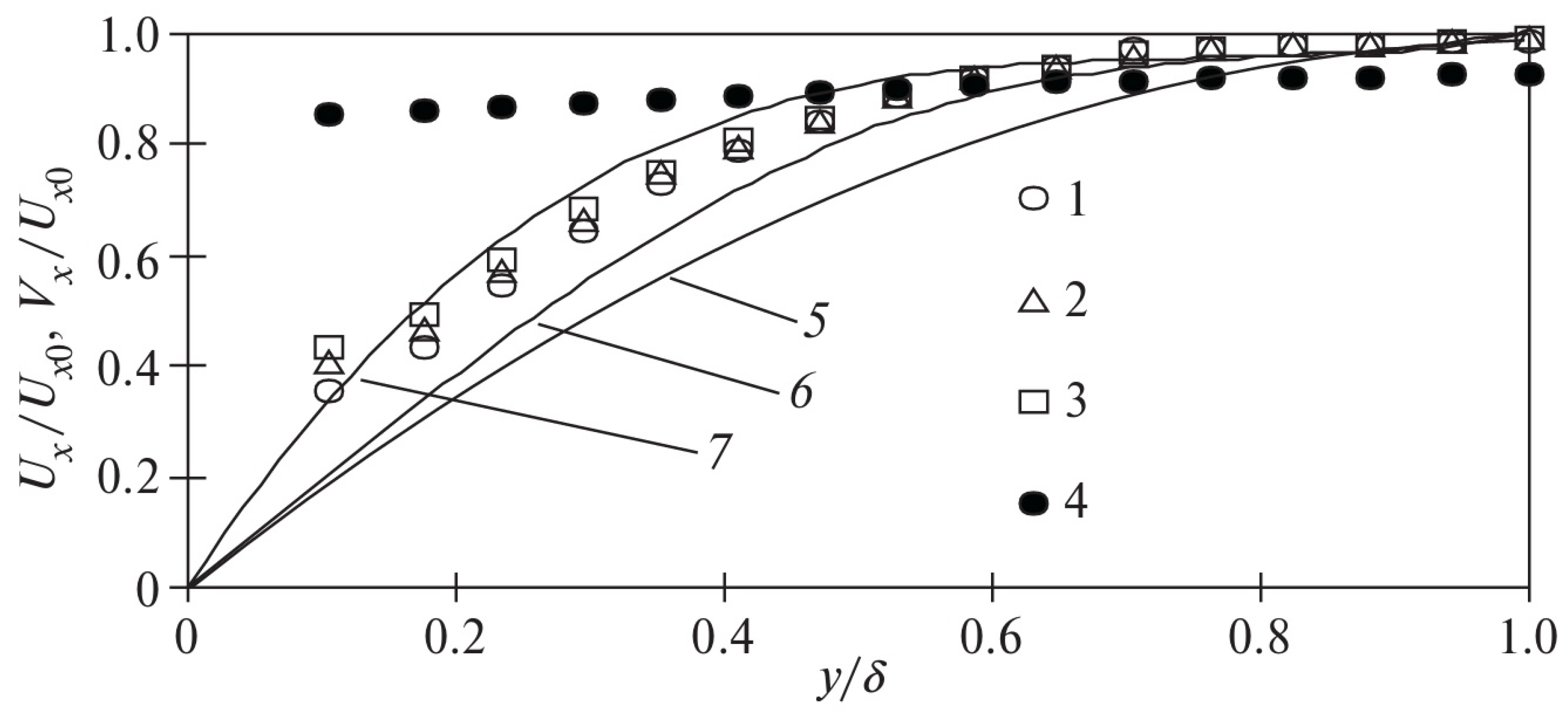
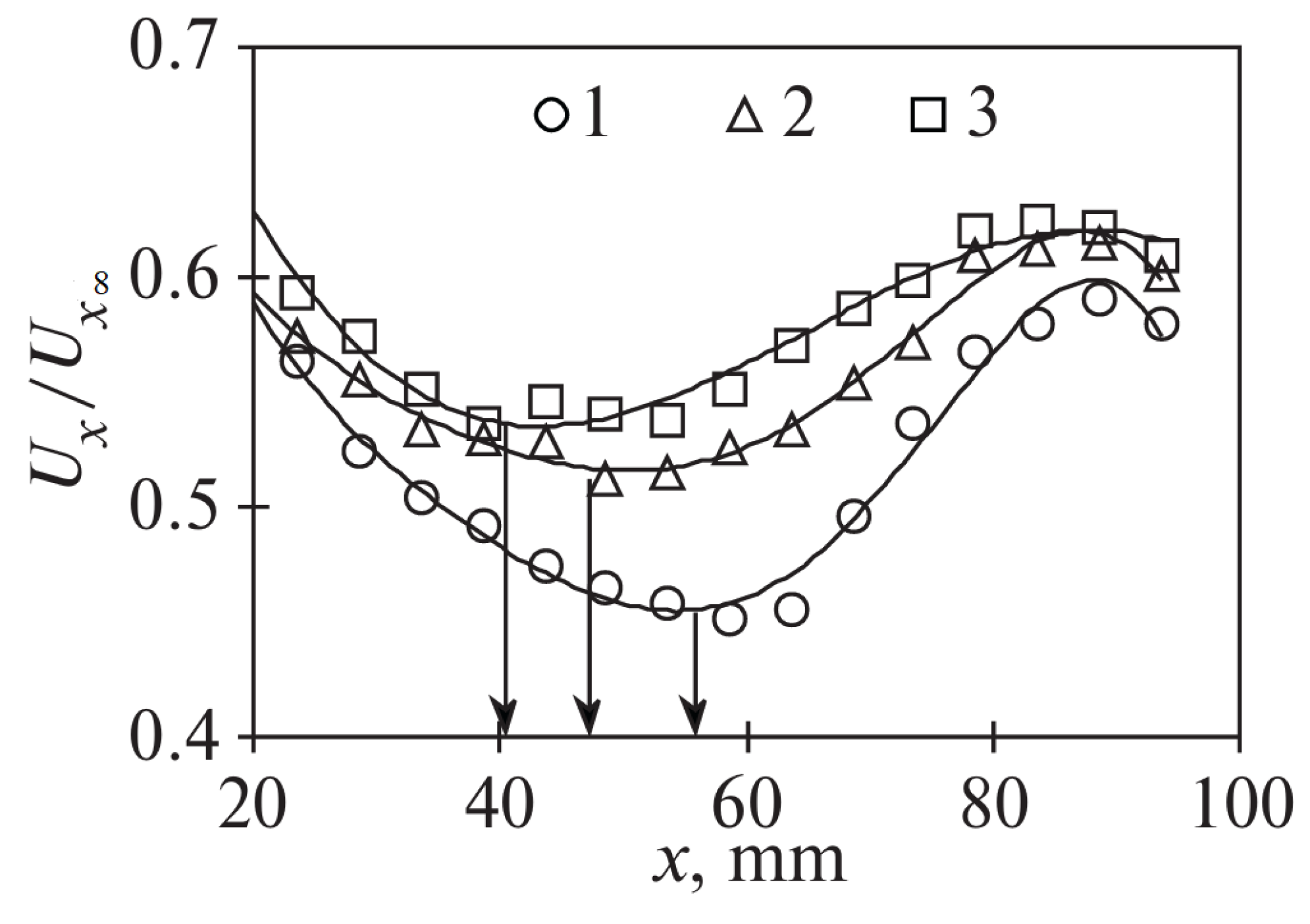
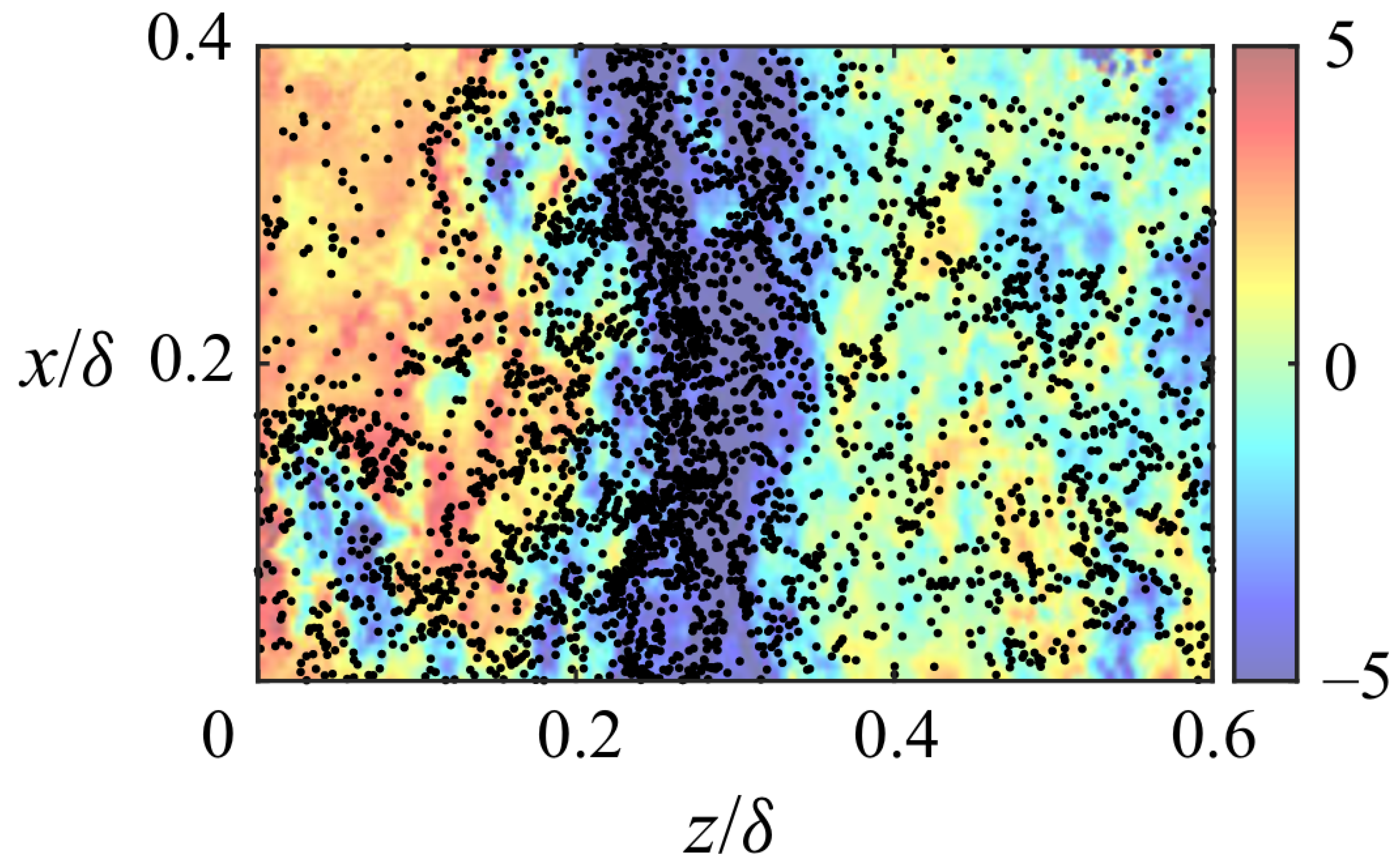
5.1. Particle Motion in Two-Phase Turbulent Boundary Layers

Particle motion in the turbulent boundary layer is largely determined by the possible presence of dynamic slip relative to the carrier gas. If the turbulent boundary layer lies in the relaxation region, the distribution of time-averaged particle velocities (as in the case of the laminar BL) differs from the gas corresponding distribution.

In [75], the now-classical relation for the normal fluctuation velocity of particles $\overline{v_y^{\prime 2}}$ was obtained:

$$\overline{v_y^{\prime 2}}(\infty )={\displaystyle \frac{{\tau }_L}{{\tau }_p+{\tau }_L}}\overline{v_y^{\prime 2}}$$

(17)

where the “∞” sign denotes local equilibrium, $\overline{v_y^{\prime 2}}$ is the normal fluctuation velocity of the gas, and ${\tau }_L$ is the integral time scale associated with the Lagrangian autocorrelation function of turbulent vortices of the carrier gas. In [76], a theory was developed, according to which a force acts on the particle in the direction of reducing the fluctuation velocity of the dispersed phase. The “turbophoresis” force has the form

$$F_t=-{\displaystyle \frac{d}{dy}}\overline{v_y^{\prime 2}}$$

(18)

An attempt to account for the non-equilibrium behavior (memory effect) of inertial particle stresses in the normal direction without considering the lift force was made in [77] using the following relationship:

$$\overline{v_y^{\prime 2}}=\left(1-{\tau }_{\beta }{\overline{V}}_y{\displaystyle \frac{d}{dy}}\right) \overline{v_y^{\prime 2}}(\infty )$$

(19)

where ${\tau }_{\beta }$ is the time to achieve local equilibrium for Reynolds stresses of particles, and ${\overline{V}}_y$ is the time-averaged normal velocity of particles. The relaxation time characterizes the degree of non-equilibrium depending on particle inertia and has the form

$${\tau }_{\beta }={\displaystyle \frac{\exp (-2/St{k}_{\tau })}{1-\exp (-2/St{k}_{\tau })}}\tau$$

(20)

where $St{k}_{\tau }={\tau }_p/\tau$ is the Stokes number, defined based on the characteristic time scale τ of particle interaction with turbulence from a macroscopic viewpoint (the so-called “intermediate diffusion scale” [77]). In [78], an attempt was made to account for the lift force on the process of particle deposition on the wall in turbulent boundary layers based on a previously developed approach [77].

In [79,80,81,82,83], the rotational motion of low-inertia particles (Stk_θ =1 and Stk_θ =5) in the turbulent boundary layer was studied. The mass concentration of the dispersed phase was M = 1. It was shown that particle motion is determined by three factors: (1) particle inertia; (2) particle clustering; and (3) the reverse (back) influence of particles on gas parameters.

In [81], instantaneous distributions of particles in various transverse sections of the boundary layer, superimposed on the fields of local longitudinal fluctuation velocity of the carrier phase, were obtained and analyzed. It was found in [82] that wall roughness leads to a decrease in the streamwise velocity of particles and an increase in their fluctuating velocities.

The calculations revealed that the fluctuation velocities of particles in the longitudinal direction throughout the boundary layer exceed the corresponding fluctuation velocities of the air. This confirms the data from [84], which was devoted to the study of particle behavior in a horizontal two-phase boundary layer on a plate.

Now for a few words about experimental studies. The characteristics of a turbulent two-phase boundary layer developing on a flat plate were investigated in [44,85,86]. It can be concluded that the presence of particles in the flow did not affect the distribution of the fluctuating velocity of the carrier phase in the boundary layer. The magnitude of velocity fluctuations for 50 μm glass particles is close to that of the air. The velocity fluctuations of larger 90 μm particles exceed those of the carrier phase. Simple estimates show that the smaller particles used in the experiments should be well entrained in the fluctuating motion by turbulent eddies.

Experimental studies of particle behavior in a turbulent boundary layer developing over a flat plate were conducted in [87,88]. It was found that the particle concentration profile was non-uniform and characterized by a maximum located within the boundary layer. Such particle distribution was explained by the action of a wall-directed lift force, as well as by particle–wall collisions.

One study [89] investigated the behavior of particles suspended in turbulent BLs at friction Re_τ to 19,000. These particles were visualized simultaneously with tracer particles, while PIV measurements enabled velocity measurements in the logarithmic region along the wall-normal plane. The experiments employed low mass concentrations, where particles did not affect the air flow. Larger particles exhibited qualitatively different behavior, likely due to nonlinear drag effects. All studied particles showed preferential sampling of specific flow regions: they favored areas with negative streamwise fluctuations, particularly “ejection” events. This pattern was observed across a wide Stokes number range, highlighting the multiscale nature of clustering phenomena. The study emphasizes that the identified features of high-Reynolds-number turbulent boundary layers significantly affect inertial particle transport, making these findings particularly relevant for environmental and geophysical flows.

Figure 8 [90] reveals a clear correlation between regions with a high particle concentration and large-scale regions of low-velocity (in terms of small fluctuation velocity values) flow. Thus, it has been established that the streamwise particle clusters are largely located within large-scale low-velocity flow regions.

The velocity and spatial distribution of inertial solid particles were studied in [91], using simultaneous PIV and particle tracking techniques, enabling analysis of particle dynamics and their spatial structures within the turbulent BL.

5.2. Particles’ Back Influence on Two-Phase Turbulent Boundary Layers

The analyses performed in [79,83] revealed a reduction in gas turbulent kinetic energy $k$ due to both decreased turbulence production term P and enhanced dissipation rate $\epsilon$.

As a clear illustration of the results obtained in these studies [79], Figure 9 presents instantaneous fields of streamwise vorticity ${\omega }_x$. The figure demonstrates that the presence of particles in a flow causes quasi-streamwise vortices to shift toward the wall. This phenomenon directly leads to the aforementioned effects of reduced BL thicknesses ($\delta$, ${\delta }^{*}$, $\theta$).

Another study [82] demonstrated that the reduction in particle near-wall capture is caused by three factors: (1) wall roughness increases particle–wall collision frequency and enhances transverse particle dispersion; (2) particles attenuate the counter-rotating vortex pairs and coherent structures responsible for particle entrainment and wallward transport; and (3) particles disrupt the shear layers generated above roughness elements that normally promote particle transport toward the wall.

Ref. [92] investigated the characteristics of a thermal turbulent BL over an isothermally heated wall with particles using the PP TWC DNS method. In [93], the features of turbulent combustion in a particle-laden BL over a flat plate were investigated using the PP TWC DNS method.

An attempt to investigate the effect of particles on the characteristics of a turbulent boundary layer developing over a flat plate was made in [94].

The longitudinal and normal components of gas velocity fluctuations were used in the following form:

$$R_{u_x}(x,y)={\displaystyle \frac{\overline{u_x^{\prime }(x_1,y_1) u_x^{\prime }(x_0,y_0)}}{{(\overline{u_x^{\prime 2}(x_1,y_1)})}^{1/2}{( \overline{u_x^{\prime 2}(x_0,y_0)})}^{1/2}}}$$

$$R_{u_y}(x,y)={\displaystyle \frac{\overline{u_y^{\prime }(x_1,y_1) u_y^{\prime }(x_0,y_0)}}{{(\overline{u_y^{\prime 2}(x_1,y_1)})}^{1/2}{( \overline{u_y^{\prime 2}(x_0,y_0)})}^{1/2}}}$$

(21)

where $u_x^{\prime }(x_1,y_1)$, $u_x^{\prime }(x_0,y_0)$, $u_y^{\prime }(x_1,y_1)$, and $u_y^{\prime }(x_0,y_0)$ are the longitudinal and normal gas velocity fluctuations at spatial points with coordinates $(x_1,y_1)$ and $(x_0,y_0)$, respectively.

In [95], the distributions of $R_{u_x}$ and $R_{u_y}$ directly characterize the properties of coherent turbulent structures. For the considered case of a turbulent BL, $R_{u_x}$ and $R_{u_y}$ characterize the streamwise length of coherent structures and the diameter of streamwise vortices, respectively [96,97]. It was found that the contours of $R_{u_x}$ and $R_{u_y}$ narrow significantly, indicating a reduction in both the extent of the coherent structure and the diameter of the streamwise vortex.

Let us draw some conclusions. To date, there are a significant number of works concerning the formation of non-uniform particle concentration profiles (clustering effect), the influence of particles on the magnitude of the kinetic energy of turbulence and individual components in the equation of its balance, the integral thicknesses of the boundary layer, various coherent structures, etc. However, systematization of the obtained data is greatly complicated, firstly, due to the variation in the inertia of particles in a large range, and, secondly, by the presence of a large number of dimensionless parameters characterizing such a complex type of flow as a turbulent boundary layer with particles.

6. Conclusions

The presence of solid particles or droplets in a flow can lead to a significant increase in heat fluxes as well as erosive wear of the streamlined surfaces of various aircraft moving in the dusty (or rainy) atmosphere of Earth or Mars. The presence of particles in a flow is an important factor (along with other well-known factors such as the longitudinal pressure gradient, surface roughness, increased turbulence of the external flow, and surface heating) influencing disturbances occurring in the single-phase boundary layer as well as the laminar–turbulent transition.

A review of work devoted to the mathematical and physical modeling of two-phase boundary layers of gas with solid particles was performed. The features of particle motion in laminar and turbulent boundary layers, as well as their inverse (back) effect on gas flow, were considered.

In recent years, a wide range of methods for mathematical modeling of two-phase flows in the boundary layer have been intensively developing, describing turbulence of the carrier phase (RANS, LES, DNS), interphase interactions (OWC, TWC, FWC), and interphase boundary (PP, PR) at different levels of complexity.

In our opinion, there are several relevant areas of future research:

(i)

Studying the effect of particles on various types of instabilities and laminar–turbulent transitions in the boundary layer with changes in the inertia and concentration of the dispersed phase in a wide range;

(ii)

The study of local areas of increased concentration (clustering effect) and the associated need to consider the inverse (back) effect of particles (TWC) and interparticle collisions (FWC);

(iii)

Developing methods for the numerical simulation of two-phase flows with interphase boundary resolution (PR) and comparing the results obtained with the results of calculations obtained using the point particle (PP) method.

It should be noted that a number of fundamental issues related to two-phase boundary layers of gas with solid particles remain outside the scope of this review due to space limitations: the recovery coefficients of particle velocities upon collision with a surface [98,99]; the phenomenon of particle thermophoresis in the boundary layer [100]; the influence of phase transitions leading, in particular, to particle melting [35,101]; the interaction of shock waves with particles (droplets) [102,103,104,105,106,107]; the effect of the angle of attack and mass entrainment from the surface; particle motion in concentrated vortices [108,109,110,111,112]; the presence of gas injection (suction) from the surface; and particle charging processes in the presence of external electric and magnetic fields.

This work only briefly touches on the issues mentioned above. For a more detailed examination, the following monographs and reviews can be recommended: [10,113,114,115,116,117].