A Review of Hybrid-Electric Propulsion in Aviation: Modeling Methods, Energy Management Strategies, and Future Prospects
Abstract
1. Introduction
2. Modeling: Hybrid Configuration and Method
2.1. Hybrid Configuration
2.1.1. Series Hybrid System Configuration
2.1.2. Parallel Hybrid System Configuration
2.1.3. Series-Parallel Hybrid System Configuration
| Program/ Model | Test/Expected Timeframe | Hybrid Configuration | Components | Component Performance | Ref. |
|---|---|---|---|---|---|
| DA36 E-Star2 | 2013 | Series hybrid | Wankel engine Generator | 70 kW | [37] |
| X-57 Maxwell | 2014 | Series hybrid | Motor Battery | 2 × 60 kW 12 × 9 kW | [38] |
| SONG | 2014 | Parallel hybrid | Engine Motor/Generator | 7.5 kW 12 kW | [39] |
| GL-10 | 2015 | Series hybrid | Generator Motor | 6 kW, 20 kW, 45 kW | [40] |
| LightningStrike | 2016 | Series hybrid | AE1107C turboshaft Generator Ducted fans | _ | [41] |
| LUH Germany | 2018 | Parallel hybrid | Engine Motor | 4 MW | [35] |
| ZA10 | 2018 | Series hybrid | Turboshaft Ducted fan Battery | 500 kW 500 kW 500 kW | [42] |
| Surefly | 2018 | Series hybrid | Piston engine Generator Motor | 150 kW - - | [43] |
| HEPS | 2019 | Series hybrid | Turbogenerator Battery | 600 kW | [26] |
| HEMEP | 2019 | Series hybrid | AE300 diesel engine Motor Battery | 110 kW 75 kW 12 kWh | [26] |
| PGS1 | 2021 | Series hybrid | High–power-density PM motor Li-ion battery | 2.5 MW 300 Wh/kg | [39] |
| Cambridge | ~2030 | Parallel hybrid | Battery | 750 Wh/kg | [44] |
| EVE | ~2030 | Parallel hybrid | Motor Battery | 1.8–2.6 MW 750 Wh/kg | [33] |
| UTRC | ~2030 | Parallel hybrid | Motor Battery | 2.1 MW | [5] |
| UTRC | ~2030 | Auxiliary power unit (fuel cell, cryogenic fuel) | Generator | 3–10 kW/kg | [5] |
| Boeing SUGAR | ~2030 | Parallel hybrid | Motor (1.3–5.3 MW) Battery | 3–5 kW/kg 750 Wh/kg | [31] |
| E-Thrust | ~2040 | Series hybrid | Turbofan Generator Ducted fans | 9 MW | [45] |
| Boeing SUGAR | ~2040 | Parallel hybrid (fuel cell, superconducting, cryogenic fuel, BLI) | Motor Battery | 8–10 kW/kg 1000 Wh/kg | [31] |
2.2. Modeling Method
2.2.1. System-Level Modeling
- (1)
- Power-flow models
- (2)
- Physics-based models
2.2.2. Component-Level Modeling
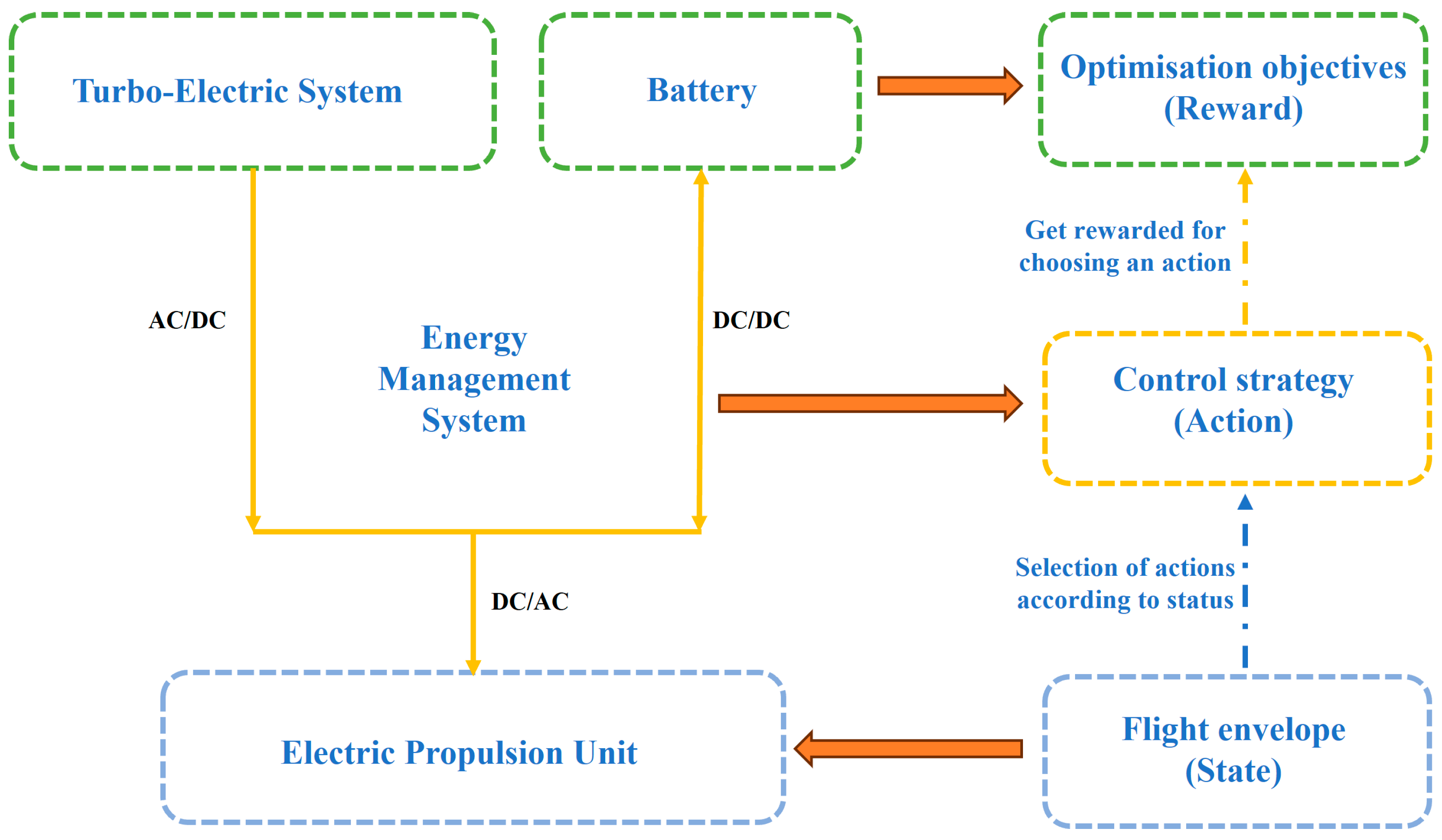
3. Energy Management Strategy: Control Algorithm
- Enforce primary flight-mechanics constraints (altitude, speed, attitude);
- Minimize secondary costs (fuel burn, emissions, thermal stress et al.);
- Suppress high-frequency power ripple that shortens component life;
- Satisfy device limits (battery C-rate, motor temperature, SOC et al.);
- Run in real time on embedded hardware with tight computational budgets.
3.1. Rule-Based Methods
3.1.1. Deterministic Rules
3.1.2. Fuzzy Rules
3.2. Optimization-Based Methods
3.2.1. Global Optimization
3.2.2. Real-Time Optimization
3.3. Learning-Based Methods
3.3.1. Fundamentals of Reinforcement Learning
- (1)
- Hierarchical Reinforcement Learning (Hierarchical RL): This approach decomposes complex problems into sub-problems, with a meta-controller issuing sub-goals for lower-level controllers. Jiang et al. [161] applied this method to energy management in microgrid systems, transforming sparse rewards into dense ones.
- (2)
- Safe Reinforcement Learning (Safe RL): Safe RL focuses on ensuring that the agent’s actions meet task requirements while adhering to safety constraints. Ma et al. [162] introduced a conservative penalty framework to balance reward and cost while maintaining safety, with additional safety checks proposed in [163].
- (3)
- Multi-Agent Reinforcement Learning (Multi-Agent RL): This approach adapts traditional RL algorithms to support multiple agents with independent evaluation and goal networks. Multi-agent RL has been successfully applied in energy management for hybrid electric vehicles, as demonstrated by [164]. Other algorithms, such as Q-Mix [165], MADDPG [166], and MAVEN [167], have been employed in swarm control and robotics.
- (4)
- Meta-Reinforcement Learning (Meta-RL): Meta-RL allows agents to adapt quickly to new tasks with minimal data. This technique has been applied in energy management systems (EMS) for transport vehicles, where power demand and operating conditions change frequently, enabling rapid adaptation to new scenarios [168].
3.3.2. Applications of Reinforcement Learning in EMS
- (1)
- Algorithmic perspective: Initially, this section reviews the evolution and applications of reinforcement learning (RL) algorithms in energy management strategies across diverse vehicles, illustrating how these algorithms have progressively advanced and improved in performance.
- (2)
- Domain-focused perspective: Subsequently, the discussion narrows to hybrid aerospace systems, thoroughly examining RL-based energy management strategies in two typical configurations: hydrogen fuel cell–lithium battery and turboshaft engine–generator–lithium battery hybrid systems.
4. Future Prospects: Key Energy Management Technologies
4.1. Real-Time Propulsive Power Prediction
4.2. Multi-Time-Scale Energy-Management and Control
4.3. Thermal Energy-Coupled Management
4.4. Certifiable EMS Baseline: Electro-Thermal–Health Coordination
4.5. Prospective Configurations and Modeling
5. Conclusions
- (1)
- On the configuration side, parallel and blended layouts offer complementary benefits. The selection should be guided by mission power profiles, allowable electrification depth, and integration constraints such as mass, volume, and thermal headroom. System-level power-flow models remain indispensable for rapid trade studies and controller prototyping, while physics-based, multi-domain models are essential for identifying operability limits, electro-thermal bottlenecks, and certification-relevant dynamics.
- (2)
- On the control side, rule-based schemes (deterministic and fuzzy) provide robust baselines for low-power avionics but tend to saturate in complex, time-varying missions. Optimization-based methods can supply benchmark optima (DP/PMP) and near-optimal real-time policies (ECMS/MPC) when accurate models and predictions are available. Learning-based controllers, particularly safe reinforcement learning, show strong potential for adaptability under uncertainty, provided they are trained with representative mission data, constrained to ensure safety, and validated against high-fidelity plant models and experiments.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| EMS | Energy Management System |
| ECMS | Equivalent Consumption Minimization Strategy |
| MPC | Model Predictive Control |
| DP | Dynamic Programming |
| PMP | Pontryagin’s Minimum Principle |
| RL | Reinforcement Learning |
| HIL | Hardware-in-the-Loop |
| SIL | Software-in-the-Loop |
| MIL | Model-in-the-Loop |
| BLI | Boundary-Layer Ingestion |
| HVDC | High-Voltage Direct Current |
| MRO | Maintenance, Repair and Overhaul |
| MEL | Minimum Equipment List |
| DAL | Design Assurance Level |
| UAV | Unmanned Aerial Vehicle |
| eVTOL | Electric Vertical Take-Off and Landing |
| UAM | Urban Air Mobility |
| GA | Genetic Algorithm |
| PSO | Particle Swarm Optimization |
| BA | Bee Algorithm |
| FLC | Fuzzy Logic Control |
| AFC | Adaptive Fuzzy Control |
| GT | Game-Theoretic |
| PI | Proportional–Integral |
| SMC | Sliding-Mode Control |
| FD | Frequency Decoupling |
| MDP | Markov Decision Process |
| CNN | Convolutional Neural Network |
| DQN | Deep Q-Network |
| DDPG | Deep Deterministic Policy Gradient |
| TD3 | Twin Delayed DDPG |
| PPO | Proximal Policy Optimization |
References
- Strategic Research and Innovation Agenda (SRIA)|Clean. Available online: https://www.clean-aviation.eu/news-events/strategic-research-and-innovation-agenda-sria (accessed on 25 August 2025).
- FlyZero: Academic Programme Research Findings and Recommendations; Aerospace Technology Institute: London, UK, 2022.
- NASA Aeronautics Strategic Implementation Plan 2023; NASA: Washington, DC, USA, 2023.
- Sahoo, S.; Zhao, X.; Kyprianidis, K. A Review of Concepts, Benefits, and Challenges for Future Electrical Propulsion-Based Aircraft. Aerospace 2020, 7, 44. [Google Scholar] [CrossRef]
- Commercial Aircraft Propulsion and Energy Systems Research: Reducing Global Carbon Emissions; National Academies Press: Washington, DC, USA, 2016; ISBN 978-0-309-44096-7.
- Culley, D.E.; Kratz, J.L.; Thomas, G.L. Turbine Electrified Energy Management (TEEM) For Enabling More Efficient Engine Designs. In Proceedings of the 2018 Joint Propulsion Conference, Cincinnati, OH, USA, 9–11 July 2018; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2018. [Google Scholar]
- Kratz, J.L.; Culley, D.E. Enhancement of a Conceptual Hybrid Electric Tilt-Wing Propulsion System through Application of the Turbine Electrified Energy Management Concept. In Proceedings of the AIAA Scitech 2021 Forum, Virtual Event, 11–15, 19–21 January 2021; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2021. [Google Scholar]
- Kratz, J.L.; Culley, D.E.; Lehan, J. Transient Optimization for the Betterment of Turbine Electrified Energy Management. In Proceedings of the AIAA SCITECH 2023 Forum, AIAA SciTech Forum, National Harbor, MD, USA, 23–27 January 2023; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2023. [Google Scholar]
- Kratz, J.L.; Culley, D.E.; Thomas, G.L. A Control Strategy for Turbine Electrified Energy Management. In Proceedings of the 2019 AIAA/IEEE Electric Aircraft Technologies Symposium (EATS), Indianapolis, IN, USA, 22–24 August 2019; pp. 1–19. [Google Scholar]
- Kratz, J.L.; Culley, D.E.; Thomas, G.L. Evaluation of Electrical System Requirements for Implementing Turbine Electrified Energy Management. In Proceedings of the 2019 AIAA/IEEE Electric Aircraft Technologies Symposium (EATS), Indianapolis, IN, USA, 22–24 August 2019; pp. 1–19. [Google Scholar]
- Hu, L.; Yan, X.; Yuan, Y. Development and Challenges of Autonomous Electric Vertical Take-off and Landing Aircraft. Heliyon 2025, 11, e41055. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Y.; Zheng, Y. Overall eVTOL Aircraft Design for Urban Air Mobility. Green Energy Intell. Transp. 2024, 3, 100150. [Google Scholar] [CrossRef]
- Yang, X.-G.; Liu, T.; Ge, S.; Rountree, E.; Wang, C.-Y. Challenges and Key Requirements of Batteries for Electric Vertical Takeoff and Landing Aircraft. Joule 2021, 5, 1644–1659. [Google Scholar] [CrossRef]
- Ayyaswamy, A.; Vishnugopi, B.S.; Mukherjee, P.P. Revealing Hidden Predicaments to Lithium-Ion Battery Dynamics for Electric Vertical Take-off and Landing Aircraft. Joule 2023, 7, 2016–2034. [Google Scholar] [CrossRef]
- Dixit, M.; Bisht, A.; Essehli, R.; Amin, R.; Kweon, C.-B.M.; Belharouak, I. Lithium-Ion Battery Power Performance Assessment for the Climb Step of an Electric Vertical Takeoff and Landing (eVTOL) Application. ACS Energy Lett. 2024, 9, 934–940. [Google Scholar] [CrossRef]
- Fay, T.-A.; Semmler, F.-B.; Cigarini, F.; Göhlich, D. Feasibility Study of Current and Emerging Battery Chemistries for Electric Vertical Take-Off and Landing Aircraft (eVTOL) Applications. World Electr. Veh. J. 2025, 16, 137. [Google Scholar] [CrossRef]
- Kim, S.; Choi, Y.; Chang, D. Techno–Economic Analysis of Fuel Cell Powered Urban Air Mobility System. Int. J. Hydrogen Energy 2024, 50, 988–1004. [Google Scholar] [CrossRef]
- Rendón, M.A.; Sánchez, R.C.D.; Gallo, M.J.; Anzai, A.H. Aircraft Hybrid-Electric Propulsion: Development Trends, Challenges and Opportunities. J. Control Autom. Electr. Syst. 2021, 32, 1244–1268. [Google Scholar] [CrossRef]
- Tian, W.; Zhang, X.; Zhou, P.; Guo, R. Review of Energy Management Technologies for Unmanned Aerial Vehicles Powered by Hydrogen Fuel Cell. Energy 2025, 323, 135751. [Google Scholar] [CrossRef]
- Cyrille, N.A.; Jean Calvin, N.; Ghislain, M.M.; Olivier Thierry, S.M. Critical Review on Integrated Real-Time Energy Management Strategy and Digital Twin Applied to Hybrid Electric UAVs. Electr. Eng. 2025, 107, 3979–4001. [Google Scholar] [CrossRef]
- Gao, Q.; Lei, T.; Yao, W.; Zhang, X.; Zhang, X. A Health-Aware Energy Management Strategy for Fuel Cell Hybrid Electric UAVs Based on Safe Reinforcement Learning. Energy 2023, 283, 129092. [Google Scholar] [CrossRef]
- Shen, H.; Zhang, Y.; Mao, J.; Yan, Z.; Wu, L. Energy Management of Hybrid UAV Based on Reinforcement Learning. Electronics 2021, 10, 1929. [Google Scholar] [CrossRef]
- GE Claims World First with High-Voltage High-Altitude Power Demo|Aviation Week Network. Available online: https://aviationweek.com/shownews/farnborough-airshow/ge-claims-world-first-high-voltage-high-altitude-power-demo (accessed on 27 August 2025).
- Rolls-Royce Advances Hybrid-Electric Flight with New Technology to Lead the Way in Advanced Air Mobility. Available online: https://www.rolls-royce.com/media/press-releases/2022/22-06-2022-rr-advances-hybrid-electric-flight-with-new-technology.aspx (accessed on 27 August 2025).
- Honeywell’s 1-Megawatt Generator Achieves New Milestone. Available online: https://aerospace.honeywell.com/us/en/about-us/press-release/2022/05/honeywell-megawatt-generator-achieves-milestone (accessed on 27 August 2025).
- Brelje, B.J.; Martins, J.R.R.A. Electric, Hybrid, and Turboelectric Fixed-Wing Aircraft: A Review of Concepts, Models, and Design Approaches. Prog. Aerosp. Sci. 2019, 104, 1–19. [Google Scholar] [CrossRef]
- Barabanova, K. ZeroAvia Flight Testing Hydrogen-Electric Powerplant; ZeroAvia: Hollister, CA, USA, 2023. [Google Scholar]
- Joby Completes Landmark 523-Mile Hydrogen-Electric Flight|Joby. Available online: https://www.jobyaviation.com/news/joby-demonstrates-potential-regional-journeys-landmark-hydrogen-electric-flight/ (accessed on 27 August 2025).
- Qin, F. China’s First Ton-Class Liquid Hydrogen VTOL Drone Takes Flight. Available online: https://www.chinadaily.com.cn/a/202501/14/WS67861db7a310f1265a1dac2f.html (accessed on 27 August 2025).
- NASA Technical Reports Server (NTRS) NASA Technical Reports Server (NTRS) 20110011321: Subsonic Ultra Green Aircraft Research; NASA: Washington, DC, USA, 2011.
- NASA Technical Reports Server (NTRS) NASA Technical Reports Server (NTRS) 20150017039: Subsonic Ultra Green Aircraft Research: Phase 2. Hybrid Electric Design Exploration; NASA: Washington, DC, USA, 2015; Volume 2.
- Thomas, G.L.; Culley, D.E.; Kratz, J.L.; Fisher, K.L. Dynamic Analysis of the hFan, a Parallel Hybrid Electric Turbofan Engine. In Proceedings of the 2018 Joint Propulsion Conference, Cincinnati, OH, USA, 9–11 July 2018; AIAA Propulsion and Energy Forum. American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2018. [Google Scholar]
- Perullo, C.; Trawick, D.; Armstrong, M.; Tai, J.C.; Mavris, D.N. Cycle Selection and Sizing of a Single-Aisle Transport with the Electrically Variable Engine(TM) (EVE) for Fleet Level Fuel Optimization. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017; AIAA SciTech Forum. American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2017. [Google Scholar]
- Lents, C.E.; Hardin, L.W.; Rheaume, J.; Kohlman, L. Parallel Hybrid Gas-Electric Geared Turbofan Engine Conceptual Design and Benefits Analysis. In Proceedings of the 52nd AIAA/SAE/ASEE Joint Propulsion Conference; Salt Lake City, UT, USA, 25–27 July 2016, AIAA Propulsion and Energy Forum; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2016. [Google Scholar]
- Hoelzen, J.; Liu, Y.; Bensmann, B.; Winnefeld, C.; Elham, A.; Friedrichs, J.; Hanke-Rauschenbach, R. Conceptual Design of Operation Strategies for Hybrid Electric Aircraft. Energies 2018, 11, 217. [Google Scholar] [CrossRef]
- Connolly, J.; Stalcup, E. Dynamic Modeling, Controls, and Testing for Electrified Aircraft; NASA: Washington, DC, USA, 2017.
- Paur, J. Siemens Builds the Chevrolet Volt of Airplanes. Available online: https://www.wired.com/2011/06/electric-airplane-uses-hybrid-power-similar-to-chevy-volt/ (accessed on 27 August 2025).
- Schnulo, S.L.; Chin, J.; Falck, R.D.; Gray, J.S.; Papathakis, K.V.; Clarke, S.C.; Reid, N.; Borer, N.K. Development of a Multi-Segment Mission Planning Tool for SCEPTOR X-57. In Proceedings of the 2018 Multidisciplinary Analysis and Optimization Conference, Atlanta, GA, USA, 25 June 2018; AIAA AVIATION Forum. American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2018. [Google Scholar]
- Jansen, R.; Duffy, K.P.; Brown, G. Partially Turboelectric Aircraft Drive Key Performance Parameters. In Proceedings of the 53rd AIAA/SAE/ASEE Joint Propulsion Conference, Atlanta, GA, USA, 10–12 July 2017; AIAA Propulsion and Energy Forum. American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2017. [Google Scholar]
- McSwain, R.G.; Glaab, L.J.; Theodore, C.R.; Rhew, R.D.; North, D.D. Greased Lightning (GL-10) Performance Flight Research: Flight Data Report; NASA: Washington, DC, USA, 2017.
- Aurora Flight Sciences to Develop High-Speed DARPA VTOL X-Plane. Available online: https://www.militaryaerospace.com/uncrewed/article/16708951/aurora-flight-sciences-to-develop-high-speed-darpa-vtol-x-plane (accessed on 27 August 2025).
- Zunum Aero and Safran Helicopter Engines Join Forces to Deliver Electric Commercial Aircraft with Unparalleled Efficiency. Available online: https://www.safran-group.com/pressroom/zunum-aero-and-safran-helicopter-engines-join-forces-deliver-electric-commercial-aircraft-2018-10-04 (accessed on 27 August 2025).
- Saeed, A.S.; Younes, A.B.; Cai, C.; Cai, G. A Survey of Hybrid Unmanned Aerial Vehicles. Prog. Aerosp. Sci. 2018, 98, 91–105. [Google Scholar] [CrossRef]
- Friedrich, C.; Robertson, P.A. Hybrid-Electric Propulsion for Aircraft. J. Aircr. 2015, 52, 176–189. [Google Scholar] [CrossRef]
- Juvé, L.; Joubert, E.; Ferran, B.; Fouquet, N. Aircraft Electric Propulsion versus Reliability and Safety, the eFAN Experience. In Proceedings of the 53rd AIAA/SAE/ASEE Joint Propulsion Conference; Atlanta, GA, USA, 10–12 July 2017, American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2017. [Google Scholar]
- An Electrical Modeling and Thermal Analysis Toolbox for Electrified Aircraft Propulsion Simulation. Available online: https://arc.aiaa.org/doi/10.2514/6.2020-3676 (accessed on 28 August 2025).
- Modeling, Simulation and Control of Turboelectric Propulsion Systems for More Electric Aircrafts Using Modelica. Available online: https://arc.aiaa.org/doi/10.2514/6.2022-3873 (accessed on 28 August 2025).
- Choi, J.; Park, H.-J.; Han, J. Development of Hydrogen Fuel Cell–Battery Hybrid Multicopter System Thermal Management and Power Management System Based on AMESim. Energies 2025, 18, 447. [Google Scholar] [CrossRef]
- Lytle, J.K. The Numerical Propulsion System Simulation: A Multidisciplinary Design System for Aerospace Vehicles; NASA: Washington, DC, USA, 1999.
- NASA Technical Reports Server (NTRS) NASA Technical Reports Server (NTRS) 20000120213: Numerical Propulsion System Simulation (NPSS) 1999 Industry Review; NASA: Washington, DC, USA, 2000.
- Chapman, J.W. Propulsion System Simulation Using the Toolbox for the Modeling and Analysis of Thermodynamic System T-MATS; NASA: Washington, DC, USA, 2014.
- None, N. Generic Analysis Methods for Gas Turbine Engine Performance. Ph.D. Thesis, TU Delft, Delft, The Netherlands, 2015. [Google Scholar] [CrossRef]
- Kalkan, O. A Commercial Turbofan Engine Modeling and Exergy Analysis. KONJES 2024, 12, 109–122. [Google Scholar] [CrossRef]
- Joksimovic, A.; Duplaa, S.; Bousquet, Y.; Tantot, N. Performance Prediction Methodology and Analysis of a Variable Pitch Fan Turbofan Engine. Aeronaut. Aerosp. Open Access J. 2018, 2, 394–402. [Google Scholar] [CrossRef]
- Amphlett, J.C.; Baumert, R.M.; Mann, R.F.; Peppley, B.A.; Roberge, P.R.; Harris, T.J. Performance Modeling of the Ballard Mark IV Solid Polymer Electrolyte Fuel Cell: I. Mechanistic Model Development. J. Electrochem. Soc. 1995, 142, 1. [Google Scholar] [CrossRef]
- Truc, N.T.; Ito, S.; Fushinobu, K. Numerical and Experimental Investigation on the Reactant Gas Crossover in a PEM Fuel Cell. Int. J. Heat Mass Transf. 2018, 127, 447–456. [Google Scholar] [CrossRef]
- Saygili, Y.; Eroglu, I.; Kincal, S. Model Based Temperature Controller Development for Water Cooled PEM Fuel Cell Systems. Int. J. Hydrogen Energy 2015, 40, 615–622. [Google Scholar] [CrossRef]
- Han, I.-S.; Chung, C.-B. A Hybrid Model Combining a Support Vector Machine with an Empirical Equation for Predicting Polarization Curves of PEM Fuel Cells. Int. J. Hydrogen Energy 2017, 42, 7023–7028. [Google Scholar] [CrossRef]
- Li, Q.; Chen, W.; Liu, Z.; Guo, A.; Huang, J. Nonlinear Multivariable Modeling of Locomotive Proton Exchange Membrane Fuel Cell System. Int. J. Hydrogen Energy 2014, 39, 13777–13786. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Yang, D.; Chen, Z. Adaptive Energy Management Strategy for Fuel Cell/Battery Hybrid Vehicles Using Pontryagin’s Minimal Principle. J. Power Sources 2019, 440, 227105. [Google Scholar] [CrossRef]
- Yang, D.; Wang, L.; Yu, K.; Liang, J. A Reinforcement Learning-Based Energy Management Strategy for Fuel Cell Hybrid Vehicle Considering Real-Time Velocity Prediction. Energy Convers. Manag. 2022, 274, 116453. [Google Scholar] [CrossRef]
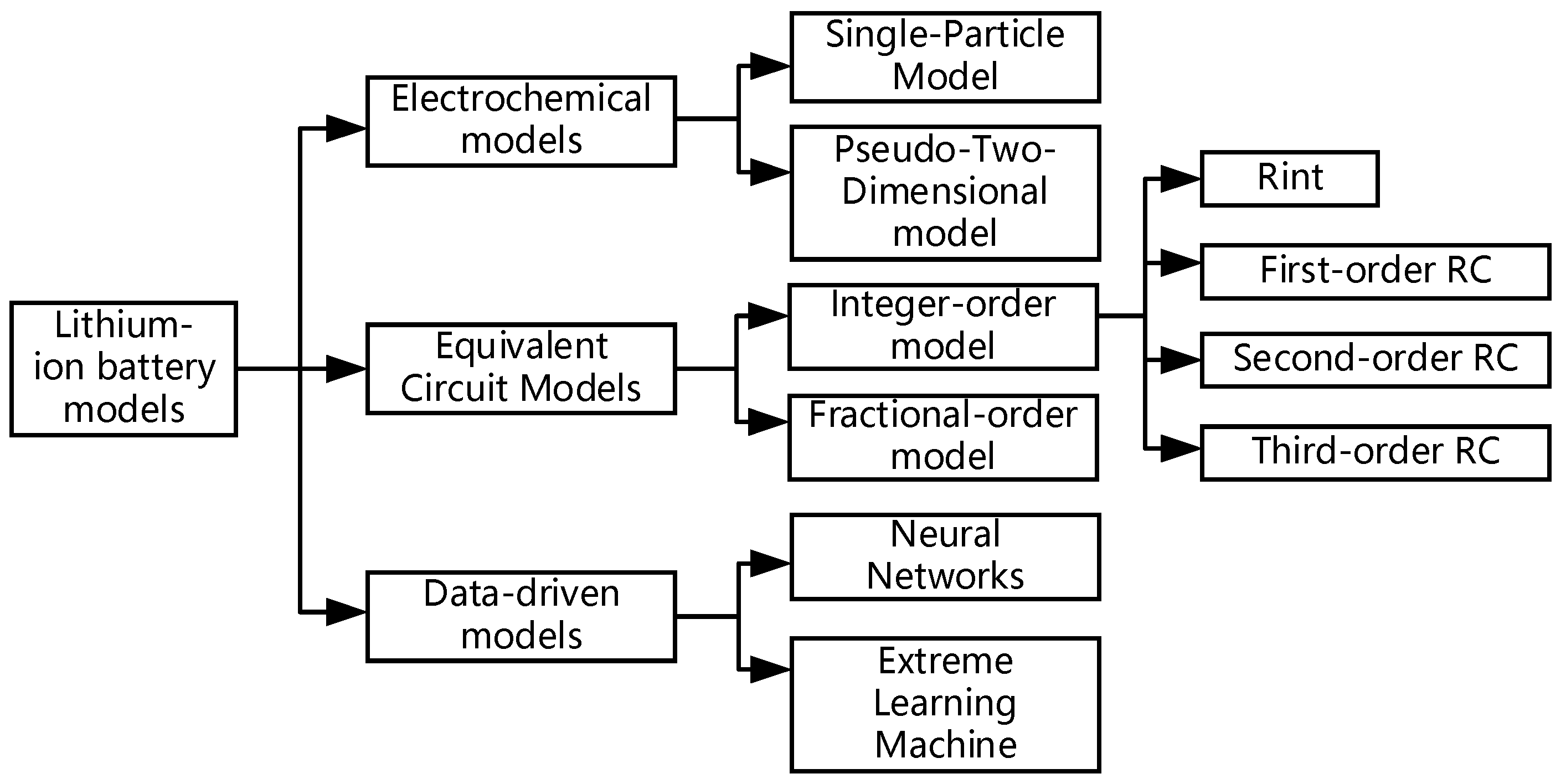
- Wang, Y.; Tian, J.; Sun, Z.; Wang, L.; Xu, R.; Li, M.; Chen, Z. A Comprehensive Review of Battery Modeling and State Estimation Approaches for Advanced Battery Management Systems. Renew. Sustain. Energy Rev. 2020, 131, 110015. [Google Scholar] [CrossRef]
- Grandjean, T.R.B.; Li, L.; Odio, M.X.; Widanage, W.D. Global Sensitivity Analysis of the Single Particle Lithium-Ion Battery Model with Electrolyte. In Proceedings of the 2019 IEEE Vehicle Power and Propulsion Conference (VPPC), Hanoi, Vietnam, 14–17 October 2019; pp. 1–7. [Google Scholar]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell. J. Electrochem. Soc. 1993, 140, 1526. [Google Scholar] [CrossRef]
- Han, X.; Ouyang, M.; Lu, L.; Li, J. Simplification of Physics-Based Electrochemical Model for Lithium Ion Battery on Electric Vehicle. Part II: Pseudo-Two-Dimensional Model Simplification and State of Charge Estimation. J. Power Sources 2015, 278, 814–825. [Google Scholar] [CrossRef]
- Ding, Q.; Wang, Y.; Chen, Z. Parameter Identification of Reduced-Order Electrochemical Model Simplified by Spectral Methods and State Estimation Based on Square-Root Cubature Kalman Filter. J. Energy Storage 2022, 46, 103828. [Google Scholar] [CrossRef]
- Yann Liaw, B.; Nagasubramanian, G.; Jungst, R.G.; Doughty, D.H. Modeling of Lithium Ion Cells—A Simple Equivalent-Circuit Model Approach. Solid State Ion. 2004, 175, 835–839. [Google Scholar] [CrossRef]
- Freeborn, T.J.; Maundy, B.; Elwakil, A.S. Fractional-Order Models of Supercapacitors, Batteries and Fuel Cells: A Survey. Mater. Renew. Sustain. Energy 2015, 4, 9. [Google Scholar] [CrossRef]
- Yang, Q.; Xu, J.; Cao, B.; Li, X. A Simplified Fractional Order Impedance Model and Parameter Identification Method for Lithium-Ion Batteries. PLoS ONE 2017, 12, e0172424. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.-K.; He, Y.-J.; Shen, J.-N.; Ma, Z.-F.; Zhong, G.-B. A Unified Modeling Framework for Lithium-Ion Batteries: An Artificial Neural Network Based Thermal Coupled Equivalent Circuit Model Approach. Energy 2017, 138, 118–132. [Google Scholar] [CrossRef]
- Yang, D.; Wang, Y.; Pan, R.; Chen, R.; Chen, Z. State-of-Health Estimation for the Lithium-Ion Battery Based on Support Vector Regression. Appl. Energy 2018, 227, 273–283. [Google Scholar] [CrossRef]
- Li, S.; He, H.; Li, J. Big Data Driven Lithium-Ion Battery Modeling Method Based on SDAE-ELM Algorithm and Data Pre-Processing Technology. Appl. Energy 2019, 242, 1259–1273. [Google Scholar] [CrossRef]
- Khalesidoost, S.; Faiz, J.; Mazaheri-Tehrani, E. An Overview of Thermal Modelling Techniques for Permanent Magnet Machines. IET Sci. Meas. Technol. 2022, 16, 219–241. [Google Scholar] [CrossRef]
- Hanappier, N.; Charkaluk, E.; Triantafyllidis, N. A Coupled Electromagnetic–Thermomechanical Approach for the Modeling of Electric Motors. J. Mech. Phys. Solids 2021, 149, 104315. [Google Scholar] [CrossRef]
- Liu, H.; Luta, J.A.; Pekarek, S.D.; Weibel, J.A. Electromagnetic-Thermal Co-Optimization to Minimize Case-to-Winding Temperature Rise in Permanent Magnet Machines. Appl. Therm. Eng. 2024, 238, 122132. [Google Scholar] [CrossRef]
- Ba, X.; Gong, Z.; Guo, Y.; Zhang, C.; Zhu, J. Development of Equivalent Circuit Models of Permanent Magnet Synchronous Motors Considering Core Loss. Energies 2022, 15, 1995. [Google Scholar] [CrossRef]
- Cheng, M.; Zhao, X.; Dhimish, M.; Qiu, W.; Niu, S. A Review of Data-Driven Surrogate Models for Design Optimization of Electric Motors. IEEE Trans. Transp. Electrif. 2024, 10, 8413–8431. [Google Scholar] [CrossRef]
- Fateh, L.; Ahmed, O.; Amar, O.; Abdelhak, D.; Lakhdar, B. Modeling and Control of a Permanent Magnet Synchronous Generator Dedicated to Standalone Wind Energy Conversion System. Front. Energy 2016, 10, 155–163. [Google Scholar] [CrossRef]
- Hashemi, F.; Ghadimi, N.; Salehi, M.; Ghadimi, R. Modelling and Simulation of Microturbine as Distributed Generation and Present a New Method for Islanding Detection. Energy Procedia 2012, 14, 87–93. [Google Scholar] [CrossRef]
- Son, D.-H.; Kim, S.-A. Simplified V/f Control Algorithm for Reduction of Current Fluctuations in Variable-Speed Operation of Induction Motors. Energies 2024, 17, 1699. [Google Scholar] [CrossRef]
- Majout, B.; El Alami, H.; Salime, H.; Zine Laabidine, N.; El Mourabit, Y.; Motahhir, S.; Bouderbala, M.; Karim, M.; Bossoufi, B. A Review on Popular Control Applications in Wind Energy Conversion System Based on Permanent Magnet Generator PMSG. Energies 2022, 15, 6238. [Google Scholar] [CrossRef]
- Rim, C.T.; Hu, D.Y.; Cho, G.H. The Graphical D-Q Transformation of General Power Switching Converters. In Proceedings of the Conference Record of the 1988 IEEE Industry Applications Society Annual Meeting, Pittsburgh, PA, USA, 2–7 October 1988; Volume 1, pp. 940–945. [Google Scholar]
- Bouafia, A.; Gaubert, J.-P.; Krim, F. Design and Implementation of Predictive Current Control of Three-Phase PWM Rectifier Using Space-Vector Modulation (SVM). Energy Convers. Manag. 2010, 51, 2473–2481. [Google Scholar] [CrossRef]
- Sanders, S.R.; Noworolski, J.M.; Liu, X.Z.; Verghese, G.C. Generalized Averaging Method for Power Conversion Circuits. IEEE Trans. Power Electron. 1991, 6, 251–259. [Google Scholar] [CrossRef]
- Lehman, B.; Bass, R.M. Switching Frequency Dependent Averaged Models for PWM DC-DC Converters. IEEE Trans. Power Electron. 1996, 11, 89–98. [Google Scholar] [CrossRef]
- Van Dijk, E.; Spruijt, J.N.; O’Sullivan, D.M.; Klaassens, J.B. PWM-Switch Modeling of DC-DC Converters. IEEE Trans. Power Electron. 1995, 10, 659–665. [Google Scholar] [CrossRef]
- Kazmierkowski, M.P.; Malesani, L. Current Control Techniques for Three-Phase Voltage-Source PWM Converters: A Survey. IEEE Trans. Ind. Electron. 1998, 45, 691–703. [Google Scholar] [CrossRef]
- Sun, J. Impedance-Based Stability Criterion for Grid-Connected Inverters. IEEE Trans. Power Electron. 2011, 26, 3075–3078. [Google Scholar] [CrossRef]
- Xin, H.; Li, Z.; Dong, W.; Zhang, L.; Wang, Z.; Zhao, J. Generalized-Impedance and Stability Criterion for Grid-Connected Converters. arXiv 2017, arXiv:1706.05625. [Google Scholar]
- Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodríguez, P. Control of Power Converters in AC Microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Lü, X.; Wu, Y.; Lian, J.; Zhang, Y.; Chen, C.; Wang, P.; Meng, L. Energy Management of Hybrid Electric Vehicles: A Review of Energy Optimization of Fuel Cell Hybrid Power System Based on Genetic Algorithm. Energy Convers. Manag. 2020, 205, 112474. [Google Scholar] [CrossRef]
- Ting, C.-C.; Tsai, D.-Y.; Hsiao, C.-C. Developing a Mechanical Roadway System for Waste Energy Capture of Vehicles and Electric Generation. Appl. Energy 2012, 92, 1–8. [Google Scholar] [CrossRef]
- Boukoberine, M.N.; Zhou, Z.; Benbouzid, M. A Critical Review on Unmanned Aerial Vehicles Power Supply and Energy Management: Solutions, Strategies, and Prospects. Appl. Energy 2019, 255, 113823. [Google Scholar] [CrossRef]
- Zeng, Y.; Xu, J.; Zhang, R. Energy Minimization for Wireless Communication With Rotary-Wing UAV. IEEE Trans. Wirel. Commun. 2019, 18, 2329–2345. [Google Scholar] [CrossRef]
- Wei, Z.; Ma, Y.; Xiang, C.; Liu, D. Power Prediction-Based Model Predictive Control for Energy Management in Land and Air Vehicle with Turboshaft Engine. Complexity 2021, 2021, 2953241. [Google Scholar] [CrossRef]
- Zhang, P.; Yan, F.; Du, C. A Comprehensive Analysis of Energy Management Strategies for Hybrid Electric Vehicles Based on Bibliometrics. Renew. Sustain. Energy Rev. 2015, 48, 88–104. [Google Scholar] [CrossRef]
- Xie, Y.; Savvarisal, A.; Tsourdos, A.; Zhang, D.; Gu, J. Review of Hybrid Electric Powered Aircraft, Its Conceptual Design and Energy Management Methodologies. Chin. J. Aeronaut. 2021, 34, 432–450. [Google Scholar] [CrossRef]
- Njoya Motapon, S.; Dessaint, L.-A.; Al-Haddad, K. A Comparative Study of Energy Management Schemes for a Fuel-Cell Hybrid Emergency Power System of More-Electric Aircraft. IEEE Trans. Ind. Electron. 2014, 61, 1320–1334. [Google Scholar] [CrossRef]
- Lei, T.; Yang, Z.; Lin, Z.; Zhang, X. State of Art on Energy Management Strategy for Hybrid-Powered Unmanned Aerial Vehicle. Chin. J. Aeronaut. 2019, 32, 1488–1503. [Google Scholar] [CrossRef]
- Xu, L.; Ouyang, M.; Li, J.; Yang, F.; Lu, L.; Hua, J. Application of Pontryagin’s Minimal Principle to the Energy Management Strategy of Plugin Fuel Cell Electric Vehicles. Int. J. Hydrogen Energy 2013, 38, 10104–10115. [Google Scholar] [CrossRef]
- Ruan, J.; Walker, P.D.; Zhang, N.; Wu, J. An Investigation of Hybrid Energy Storage System in Multi-Speed Electric Vehicle. Energy 2017, 140, 291–306. [Google Scholar] [CrossRef]
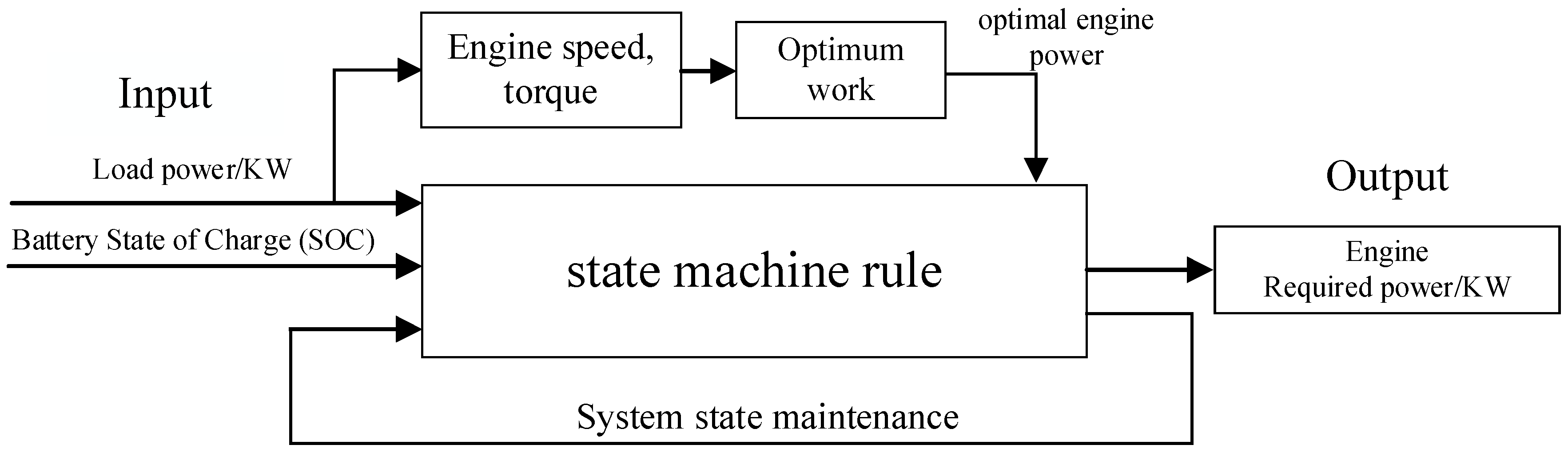
- Li, Q.; Yang, H.; Han, Y.; Li, M.; Chen, W. A State Machine Strategy Based on Droop Control for an Energy Management System of PEMFC-Battery-Supercapacitor Hybrid Tramway. Int. J. Hydrogen Energy 2016, 41, 16148–16159. [Google Scholar] [CrossRef]
- Tao, S.; Chen, W.; Gan, R.; Li, L.; Zhang, G.; Han, Y.; Li, Q. Energy Management Strategy Based on Dynamic Programming with Durability Extension for Fuel Cell Hybrid Tramway. Railw. Eng. Sci. 2021, 29, 299–313. [Google Scholar] [CrossRef]
- Li, Q.; Su, B.; Pu, Y.; Han, Y.; Wang, T.; Yin, L.; Chen, W. A State Machine Control Based on Equivalent Consumption Minimization for Fuel Cell/Supercapacitor Hybrid Tramway. IEEE Trans. Transp. Electrif. 2019, 5, 552–564. [Google Scholar] [CrossRef]
- Yun, H.; Liu, S.; Zhao, Y.; Xie, J.; Liu, C.; Hou, Z.; Wang, K. Energy Management for Fuel Cell Hybrid Vehicles Based on a Stiffness Coefficient Model. Int. J. Hydrogen Energy 2015, 40, 633–641. [Google Scholar] [CrossRef]
- Sulaiman, N.; Hannan, M.A.; Mohamed, A.; Majlan, E.H.; Wan Daud, W.R. A Review on Energy Management System for Fuel Cell Hybrid Electric Vehicle: Issues and Challenges. Renew. Sustain. Energy Rev. 2015, 52, 802–814. [Google Scholar] [CrossRef]
- Buticchi, G.; Costa, L.F.; Barater, D.; Liserre, M.; Amarillo, E.D. A Quadruple Active Bridge Converter for the Storage Integration on the More Electric Aircraft. IEEE Trans. Power Electron. 2018, 33, 8174–8186. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, L.; Dai, Y. Fuzzy State Machine Energy Management Strategy for Hybrid Electric UAVs with PV/Fuel Cell/Battery Power System. Int. J. Aerosp. Eng. 2018, 2018, 2852941. [Google Scholar] [CrossRef]
- Zargham Nejhad, A.; Asaei, B. A Fuzzy—Genetic Algorithm Approach for Finding a New HEV Control Strategy Idea. In Proceedings of the 2010 1st Power Electronic & Drive Systems & Technologies Conference (PEDSTC), Tehran, Iran, 17–18 February 2010; pp. 224–229. [Google Scholar]
- Zhang, X.; Liu, L.; Dai, Y.; Lu, T. Experimental Investigation on the Online Fuzzy Energy Management of Hybrid Fuel Cell/Battery Power System for UAVs. Int. J. Hydrogen Energy 2018, 43, 10094–10103. [Google Scholar] [CrossRef]
- Dazhi, W.; Jie, Y.; Qing, Y.; Dongsheng, W.; Hui, J. Estimation and Control of Hybrid Electric Vehicle Using Artificial Neural Networks. In Proceedings of the 2007 2nd IEEE Conference on Industrial Electronics and Applications, Harbin, China, 23–25 May 2007; pp. 35–40. [Google Scholar]
- Poursamad, A.; Montazeri, M. Design of Genetic-Fuzzy Control Strategy for Parallel Hybrid Electric Vehicles. Control Eng. Pract. 2008, 16, 861–873. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, C.-H.; Cui, N.-X. Fuzzy Energy Management Strategy for a Hybrid Electric Vehicle Based on Driving Cycle Recognition. Int. J. Automot. Technol. 2012, 13, 1159–1167. [Google Scholar] [CrossRef]
- Shi, G.; Jing, Y.; Xu, A.; Ma, J. Study and Simulation of Based-Fuzzy-Logic Parallel Hybrid Electric Vehicles Control Strategy. In Proceedings of the Sixth International Conference on Intelligent Systems Design and Applications, Ji’an, China, 16 October 2006; IEEE Computer Society: Washington, DC, USA; Volume 1, pp. 280–284. [Google Scholar]
- Mohebbi, M.; Charkhgard, M.; Farrokhi, M. Optimal Neuro-Fuzzy Control of Parallel Hybrid Electric Vehicles. In Proceedings of the 2005 IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 7 September 2005; pp. 26–30. [Google Scholar]
- Chen, Z.; Guo, N.; Zhang, Q.; Shen, J.; Xiao, R. An Optimized Rule Based Energy Management Strategy for a Fuel Cell/Battery Vehicle. In Proceedings of the 2017 IEEE Vehicle Power and Propulsion Conference (VPPC), Belfort, France, 11–14 December 2017; pp. 1–6. [Google Scholar]
- Hou, S.; Gao, J.; Zhang, Y.; Chen, M.; Shi, J.; Chen, H. A Comparison Study of Battery Size Optimization and an Energy Management Strategy for FCHEVs Based on Dynamic Programming and Convex Programming. Int. J. Hydrogen Energy 2020, 45, 21858–21872. [Google Scholar] [CrossRef]
- Wakuta, K. The Bellman’s Principle of Optimality in the Discounted Dynamic Programming. J. Math. Anal. Appl. 1987, 125, 213–217. [Google Scholar] [CrossRef]
- Larsson, V.; Johannesson, L.; Egardt, B. Analytic Solutions to the Dynamic Programming Subproblem in Hybrid Vehicle Energy Management. IEEE Trans. Veh. Technol. 2015, 64, 1458–1467. [Google Scholar] [CrossRef]
- Lin, C.-C.; Peng, H.; Grizzle, J.W. A Stochastic Control Strategy for Hybrid Electric Vehicles. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2004; Volume 5, pp. 4710–4715. [Google Scholar]
- Ansarey, M.; Shariat Panahi, M.; Ziarati, H.; Mahjoob, M. Optimal Energy Management in a Dual-Storage Fuel-Cell Hybrid Vehicle Using Multi-Dimensional Dynamic Programming. J. Power Sources 2014, 250, 359–371. [Google Scholar] [CrossRef]
- Fares, D.; Chedid, R.; Panik, F.; Karaki, S.; Jabr, R. Dynamic Programming Technique for Optimizing Fuel Cell Hybrid Vehicles. Int. J. Hydrogen Energy 2015, 40, 7777–7790. [Google Scholar] [CrossRef]
- Delprat, S.; Hofman, T.; Paganelli, S. Hybrid Vehicle Energy Management: Singular Optimal Control. IEEE Trans. Veh. Technol. 2017, 66, 9654–9666. [Google Scholar] [CrossRef]
- Kowalski, A.; Agati, G.; Grzegorzewska, M.; Kosson, R.; Kusznierewicz, B.; Chmiel, T.; Bartoszek, A.; Tuccio, L.; Grifoni, D.; Vågen, I.M.; et al. Valorization of Waste Cabbage Leaves by Postharvest Photochemical Treatments Monitored with a Non-Destructive Fluorescence-Based Sensor. J. Photochem. Photobiol. B Biol. 2021, 222, 112263. [Google Scholar] [CrossRef] [PubMed]
- Dobrokhodov, V.; Jones, K.D.; Walton, C.; Kaminer, I.I. Energy-Optimal Trajectory Planning of Hybrid Ultra-Long Endurance UAV in Time-Varying Energy Fields. In AIAA Scitech 2020 Forum; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2020. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Donateo, T.; De Pascalis, C.L.; Ficarella, A. Many-Objective Optimization of Mission and Hybrid Electric Power System of an Unmanned Aircraft. In Proceedings of the Applications of Evolutionary Computation, Trieste, Italy, 23–25 April 2025; Sim, K., Kaufmann, P., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 231–246. [Google Scholar]
- Bahari, M.; Rostami, M.; Entezari, A.; Ghahremani, S.; Etminan, M. Performance Evaluation and Multi-Objective Optimization of a Novel UAV Propulsion System Based on PEM Fuel Cell. Fuel 2022, 311, 122554. [Google Scholar] [CrossRef]
- Xie, Y.; Savvaris, A.; Tsourdos, A. Sizing of Hybrid Electric Propulsion System for Retrofitting a Mid-Scale Aircraft Using Non-Dominated Sorting Genetic Algorithm. Aerosp. Sci. Technol. 2018, 82–83, 323–333. [Google Scholar] [CrossRef]
- Vukadinović, A.; Radosavljević, J.; Đorđević, A.; Protić, M.; Petrović, N. Multi-Objective Optimization of Energy Performance for a Detached Residential Building with a Sunspace Using the NSGA-II Genetic Algorithm. Sol. Energy 2021, 224, 1426–1444. [Google Scholar] [CrossRef]
- Chen, S.-Y.; Wu, C.-H.; Hung, Y.-H.; Chung, C.-T. Optimal Strategies of Energy Management Integrated with Transmission Control for a Hybrid Electric Vehicle Using Dynamic Particle Swarm Optimization. Energy 2018, 160, 154–170. [Google Scholar] [CrossRef]
- Juang, C.-F. A Hybrid of Genetic Algorithm and Particle Swarm Optimization for Recurrent Network Design. IEEE Trans. Syst. Man Cybern. Part B 2004, 34, 997–1006. [Google Scholar] [CrossRef]
- Paganelli, G.; Guerra, T.M.; Delprat, S.; Santin, J.-J.; Delhom, M.; Combes, E. Simulation and Assessment of Power Control Strategies for a Parallel Hybrid Car. Proc. Inst. Mech. Eng. Part. D J. Automob. Eng. 2000, 214, 705–717. [Google Scholar] [CrossRef]
- Sciarretta, A.; Serrao, L.; Dewangan, P.C.; Tona, P.; Bergshoeff, E.N.D.; Bordons, C.; Charmpa, L.; Elbert, P.; Eriksson, L.; Hofman, T.; et al. A Control Benchmark on the Energy Management of a Plug-in Hybrid Electric Vehicle. Control Eng. Pract. 2014, 29, 287–298. [Google Scholar] [CrossRef]
- García, P.; Torreglosa, J.P.; Fernández, L.M.; Jurado, F. Viability Study of a FC-Battery-SC Tramway Controlled by Equivalent Consumption Minimization Strategy. Int. J. Hydrogen Energy 2012, 37, 9368–9382. [Google Scholar] [CrossRef]
- Motapon, S.N.; Dessaint, L.-A.; Al-Haddad, K. A Robust \hboxH_2-Consumption-Minimization-Based Energy Management Strategy for a Fuel Cell Hybrid Emergency Power System of More Electric Aircraft. IEEE Trans. Ind. Electron. 2014, 61, 6148–6156. [Google Scholar] [CrossRef]
- Zeng, T.; Zhang, C.; Zhang, Y.; Deng, C.; Hao, D.; Zhu, Z.; Ran, H.; Cao, D. Optimization-Oriented Adaptive Equivalent Consumption Minimization Strategy Based on Short-Term Demand Power Prediction for Fuel Cell Hybrid Vehicle. Energy 2021, 227, 120305. [Google Scholar] [CrossRef]
- Li, H.; Ravey, A.; N’Diaye, A.; Djerdir, A. A Novel Equivalent Consumption Minimization Strategy for Hybrid Electric Vehicle Powered by Fuel Cell, Battery and Supercapacitor. J. Power Sources 2018, 395, 262–270. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Sadollah, A.; Bahreininejad, A.; Eskandar, H.; Hamdi, M. Mine Blast Algorithm: A New Population Based Algorithm for Solving Constrained Engineering Optimization Problems. Appl. Soft Comput. 2013, 13, 2592–2612. [Google Scholar] [CrossRef]
- Rezk, H.; Nassef, A.M.; Abdelkareem, M.A.; Alami, A.H.; Fathy, A. Comparison among Various Energy Management Strategies for Reducing Hydrogen Consumption in a Hybrid Fuel Cell/Supercapacitor/Battery System. Int. J. Hydrogen Energy 2021, 46, 6110–6126. [Google Scholar] [CrossRef]
- Kocer, B.B.; Tjahjowidodo, T.; Lee Seet, G.G. UAV Push Recovery Operation by Symmetrical Control and Estimation in Receding Horizon. In Proceedings of the 2018 15th International Conference on Control, Automation, Robotics and Vision (ICARCV), Singapore, 18–21 November 2018; pp. 978–983. [Google Scholar]
- Wang, Y.; Zhang, T.; Cai, Z.; Zhao, J.; Wu, K. Multi-UAV Coordination Control by Chaotic Grey Wolf Optimization Based Distributed MPC with Event-Triggered Strategy. Chin. J. Aeronaut. 2020, 33, 2877–2897. [Google Scholar] [CrossRef]
- Baca, T.; Hert, D.; Loianno, G.; Saska, M.; Kumar, V. Model Predictive Trajectory Tracking and Collision Avoidance for Reliable Outdoor Deployment of Unmanned Aerial Vehicles. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 6753–6760. [Google Scholar]
- Wang, Y.; Wang, L.; Li, M.; Chen, Z. A Review of Key Issues for Control and Management in Battery and Ultra-Capacitor Hybrid Energy Storage Systems. eTransportation 2020, 4, 100064. [Google Scholar] [CrossRef]
- Greenwell, W.; Vahidi, A. Predictive Control of Voltage and Current in a Fuel Cell–Ultracapacitor Hybrid. IEEE Trans. Ind. Electron. 2010, 57, 1954–1963. [Google Scholar] [CrossRef]
- Chen, Q.; Gao, L.; Dougal, R.A.; Quan, S. Multiple Model Predictive Control for a Hybrid Proton Exchange Membrane Fuel Cell System. J. Power Sources 2009, 191, 473–482. [Google Scholar] [CrossRef]
- Tan, J.; Wang, L. Enabling Reliability-Differentiated Service in Residential Distribution Networks With PHEVs: A Hierarchical Game Approach. IEEE Trans. Smart Grid 2016, 7, 684–694. [Google Scholar] [CrossRef]
- Amjadi, Z.; Williamson, S.S. Power-Electronics-Based Solutions for Plug-in Hybrid Electric Vehicle Energy Storage and Management Systems. IEEE Trans. Ind. Electron. 2010, 57, 608–616. [Google Scholar] [CrossRef]
- Thounthong, P.; Rael, S.; Davat, B. Control Strategy of Fuel Cell and Supercapacitors Association for a Distributed Generation System. IEEE Trans. Ind. Electron. 2007, 54, 3225–3233. [Google Scholar] [CrossRef]
- Wu, L.; Ho, D.W.C.; Li, C.W. Sliding Mode Control of Switched Hybrid Systems with Stochastic Perturbation. Syst. Control Lett. 2011, 60, 531–539. [Google Scholar] [CrossRef]
- Tan, H.; Zhang, H.; Peng, J.; Jiang, Z.; Wu, Y. Energy Management of Hybrid Electric Bus Based on Deep Reinforcement Learning in Continuous State and Action Space. Energy Convers. Manag. 2019, 195, 548–560. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-Level Control through Deep Reinforcement Learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Granacher, J.; Nguyen, T.-V.; Castro-Amoedo, R.; Maréchal, F. Overcoming Decision Paralysis—A Digital Twin for Decision Making in Energy System Design. Appl. Energy 2022, 306, 117954. [Google Scholar] [CrossRef]
- Yi, C.; Qi, M. Research on Virtual Path Planning Based on Improved DQN. In Proceedings of the 2020 IEEE International Conference on Real-time Computing and Robotics (RCAR), Asahikawa, Japan, 28–29 September 2020; pp. 387–392. [Google Scholar]
- Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M. Deterministic Policy Gradient Algorithms. In Proceedings of the 31st International Conference on International Conference on Machine Learning, Beijing, China, 21 June 2014; JMLR.org: New York, NY, USA; Volume 32, pp. I-387–I-395. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous Control with Deep Reinforcement Learning. arXiv 2019, arXiv:1509.02971. [Google Scholar]
- Fujimoto, S.; van Hoof, H.; Meger, D. Addressing Function Approximation Error in Actor-Critic Methods. arXiv 2018, arXiv:1802.09477. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar] [CrossRef]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor. arXiv 2018, arXiv:1801.01290. [Google Scholar]
- Jiang, N.; Jin, S.; Zhang, C. Hierarchical Automatic Curriculum Learning: Converting a Sparse Reward Navigation Task into Dense Reward. Neurocomputing 2019, 360, 265–278. [Google Scholar] [CrossRef]
- Ma, Y.J.; Shen, A.; Bastani, O.; Jayaraman, D. Conservative and Adaptive Penalty for Model-Based Safe Reinforcement Learning. arXiv 2021, arXiv:2112.07701. [Google Scholar] [CrossRef]
- Thananjeyan, B.; Balakrishna, A.; Nair, S.; Luo, M.; Srinivasan, K.; Hwang, M.; Gonzalez, J.E.; Ibarz, J.; Finn, C.; Goldberg, K. Recovery RL: Safe Reinforcement Learning With Learned Recovery Zones. IEEE Robot. Autom. Lett. 2021, 6, 4915–4922. [Google Scholar] [CrossRef]
- Shi, W.; Huangfu, Y.; Xu, L.; Pang, S. Online Energy Management Strategy Considering Fuel Cell Fault for Multi-Stack Fuel Cell Hybrid Vehicle Based on Multi-Agent Reinforcement Learning. Appl. Energy 2022, 328, 120234. [Google Scholar] [CrossRef]
- Rashid, T.; Samvelyan, M.; de Witt, C.S.; Farquhar, G.; Foerster, J.; Whiteson, S. QMIX: Monotonic Value Function Factorisation for Deep Multi-Agent Reinforcement Learning. arXiv 2018, arXiv:1803.11485. [Google Scholar] [CrossRef]
- Lowe, R.; Wu, Y.; Tamar, A.; Harb, J.; Abbeel, P.; Mordatch, I. Multi-Agent Actor-Critic for Mixed Cooperative-Competitive Environments. arXiv 2020, arXiv:1706.02275. [Google Scholar]
- Mahajan, A.; Rashid, T.; Samvelyan, M.; Whiteson, S. MAVEN: Multi-Agent Variational Exploration. arXiv 2020, arXiv:1910.07483. [Google Scholar] [CrossRef]
- Zhang, J.; Tao, J.; Xu, H. A Meta-EMS for Lithium-Battery/Supercapacitor Hybrid Electric Vehicles. In Proceedings of the 2023 IEEE 18th Conference on Industrial Electronics and Applications (ICIEA), Ningbo, China, 18–22 August 2023; pp. 251–256. [Google Scholar]
- Lian, R.; Peng, J.; Wu, Y.; Tan, H.; Zhang, H. Rule-Interposing Deep Reinforcement Learning Based Energy Management Strategy for Power-Split Hybrid Electric Vehicle. Energy 2020, 197, 117297. [Google Scholar] [CrossRef]
- Zhou, Q.; Li, J.; Shuai, B.; Williams, H.; He, Y.; Li, Z.; Xu, H.; Yan, F. Multi-Step Reinforcement Learning for Model-Free Predictive Energy Management of an Electrified off-Highway Vehicle. Appl. Energy 2019, 255, 113755. [Google Scholar] [CrossRef]
- Han, X.; He, H.; Wu, J.; Peng, J.; Li, Y. Energy Management Based on Reinforcement Learning with Double Deep Q-Learning for a Hybrid Electric Tracked Vehicle. Appl. Energy 2019, 254, 113708. [Google Scholar] [CrossRef]
- Li, Q.; Meng, X.; Gao, F.; Zhang, G.; Chen, W. Approximate Cost-Optimal Energy Management of Hydrogen Electric Multiple Unit Trains Using Double Q-Learning Algorithm. IEEE Trans. Ind. Electron. 2022, 69, 9099–9110. [Google Scholar] [CrossRef]
- Tang, X.; Chen, J.; Pu, H.; Liu, T.; Khajepour, A. Double Deep Reinforcement Learning-Based Energy Management for a Parallel Hybrid Electric Vehicle With Engine Start–Stop Strategy. IEEE Trans. Transp. Electrif. 2022, 8, 1376–1388. [Google Scholar] [CrossRef]
- Liu, B.; Xu, B.; He, T.; Yu, W.; Guo, F. Hybrid Deep Reinforcement Learning Considering Discrete-Continuous Action Spaces for Real-Time Energy Management in More Electric Aircraft. Energies 2022, 15, 6323. [Google Scholar] [CrossRef]
- Gao, Q.; Lei, T.; Deng, F.; Min, Z.; Yao, W.; Zhang, X. A Deep Reinforcement Learning Based Energy Management Strategy for Fuel-Cell Electric UAV. In Proceedings of the 2022 International Conference on Power Energy Systems and Applications (ICoPESA), Singapore, 25–27 February 2022; pp. 524–530. [Google Scholar]
- Zhang, H.; Peng, J.; Dong, H.; Tan, H.; Ding, F. Hierarchical Reinforcement Learning Based Energy Management Strategy of Plug-in Hybrid Electric Vehicle for Ecological Car-Following Process. Appl. Energy 2023, 333, 120599. [Google Scholar] [CrossRef]
- Hu, B.; Li, J. An Adaptive Hierarchical Energy Management Strategy for Hybrid Electric Vehicles Combining Heuristic Domain Knowledge and Data-Driven Deep Reinforcement Learning. IEEE Trans. Transp. Electrif. 2022, 8, 3275–3288. [Google Scholar] [CrossRef]
- Yang, N.; Han, L.; Liu, R.; Wei, Z.; Liu, H.; Xiang, C. Multiobjective Intelligent Energy Management for Hybrid Electric Vehicles Based on Multiagent Reinforcement Learning. IEEE Trans. Transp. Electrif. 2023, 9, 4294–4305. [Google Scholar] [CrossRef]
- Liu, Z.E.; Zhou, Q.; Li, Y.; Shuai, S.; Xu, H. Safe Deep Reinforcement Learning-Based Constrained Optimal Control Scheme for HEV Energy Management. IEEE Trans. Transp. Electrif. 2023, 9, 4278–4293. [Google Scholar] [CrossRef]
- Kaya, K.; Hames, Y. A Study on Fuel Cell Electric Unmanned Aerial Vehicle. In Proceedings of the 2019 4th International Conference on Power Electronics and their Applications (ICPEA), Elazig, Turkey, 25–27 September 2019; pp. 1–6. [Google Scholar]
- Lee, B.; Kwon, S.; Park, P.; Kim, K. Active Power Management System for an Unmanned Aerial Vehicle Powered by Solar Cells, a Fuel Cell, and Batteries. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 3167–3177. [Google Scholar] [CrossRef]
- Bradley, T.; Moffitt, B.; Parekh, D.; Fuller, T.; Mavris, D. Energy Management for Fuel Cell Powered Hybrid-Electric Aircraft. In Proceedings of the 7th International Energy Conversion Engineering Conference, Denver, CO, USA, 2–5 August 2009; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2009. [Google Scholar]
- Ma, R.; Song, J.; Xie, R.; Zhang, H.; Chai, X.; Sun, H.; Wang, C. A Novel Energy Management Strategy Based on Minimum Internal Loss for a Fuel Cell Unmanned Aircraft Vehicle Hybrid Power System. IEEE Trans. Ind. Appl. 2023, 59, 7175–7187. [Google Scholar] [CrossRef]
- Lei, T.; Wang, Y.; Jin, X.; Min, Z.; Zhang, X.; Zhang, X. An Optimal Fuzzy Logic-Based Energy Management Strategy for a Fuel Cell/Battery Hybrid Power Unmanned Aerial Vehicle. Aerospace 2022, 9, 115. [Google Scholar] [CrossRef]
- Ma, R.; Song, J.; Zhang, Y.; Zhang, H.; Yuan, M. Lifetime-Optimized Energy Management Strategy for Fuel Cell Unmanned Aircraft Vehicle Hybrid Power System. IEEE Trans. Ind. Electron. 2023, 70, 9046–9056. [Google Scholar] [CrossRef]
- Doff-Sotta, M.; Cannon, M.; Bacic, M. Optimal Energy Management for Hybrid Electric Aircraft. IFAC-PapersOnLine 2020, 53, 6043–6049. [Google Scholar] [CrossRef]
- Doff-Sotta, M.; Cannon, M.; Bacic, M. Predictive Energy Management for Hybrid Electric Aircraft Propulsion Systems. IEEE Trans. Control Syst. Technol. 2023, 31, 602–614. [Google Scholar] [CrossRef]
- Li, S.; Zhao, P.; Gu, C.; Bu, S.; Pei, X.; Zeng, X.; Li, J.; Cheng, S. Hybrid Power System Topology and Energy Management Scheme Design for Hydrogen-Powered Aircraft. IEEE Trans. Smart Grid 2024, 15, 1201–1212. [Google Scholar] [CrossRef]
- Bai, M.; Yang, W.; Song, D.; Kosuda, M.; Szabo, S.; Lipovsky, P.; Kasaei, A. Research on Energy Management of Hybrid Unmanned Aerial Vehicles to Improve Energy-Saving and Emission Reduction Performance. Int. J. Environ. Res. Public Health 2020, 17, 2917. [Google Scholar] [CrossRef]
- Kim, Y.; Kang, S. Development of Optimal Energy Management Strategy for Proton Exchange Membrane Fuel Cell-Battery Hybrid System for Drone Propulsion. Appl. Therm. Eng. 2025, 258, 124646. [Google Scholar] [CrossRef]
- Zhang, J.; Roumeliotis, I.; Zolotas, A. Model-Based Fully Coupled Propulsion-Aerodynamics Optimization for Hybrid Electric Aircraft Energy Management Strategy. Energy 2022, 245, 123239. [Google Scholar] [CrossRef]
- He, L.; Chen, F.; Tian, P.; Gou, H. An Improved Energy Management Strategy for Hybrid Electric Powered Aircraft Based on Deep Reinforcement Learning. Aerosp. Sci. Technol. 2024, 149, 109137. [Google Scholar] [CrossRef]
- Misley, A.; D’Arpino, M.; Ramesh, P.; Canova, M. A Real-Time Energy Management Strategy for Hybrid Electric Aircraft Propulsion Systems. In Proceedings of the 2021 AIAA/IEEE Electric Aircraft Technologies Symposium (EATS), Denver, CO, USA, 11–13 August 2021; pp. 1–11. [Google Scholar]
- Yu, F.; Tang, W.; Chen, J.; Wang, J.; Sun, X.; Chen, X. Deep Reinforcement Learning Based Energy Management Strategy for Vertical Take-Off and Landing Aircraft with Turbo-Electric Hybrid Propulsion System. Aerospace 2025, 12, 355. [Google Scholar] [CrossRef]
- Zhai, Y.; Wang, X.; Zhang, H. A Fuzzy-Adaptive ECMS Based Energy Management Strategy for Series Hybrid Electric Aircraft; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2024. [Google Scholar]
- Yang, C.; Liang, B.; Wang, W.; Wang, H.; Yang, L.; Chen, Y.; Wang, M. An Efficient Energy Management Strategy Based on Heuristic Dynamic Programming Specialized for Hybrid Electric Unmanned Delivery Aerial Vehicles. J. Clean. Prod. 2024, 453, 142222. [Google Scholar] [CrossRef]
- Wen, Q.; Liang, D.; Xue, Y.; Liang, Z.; Zhang, L.; Liang, Y. Research on Energy Management Strategies for Integrated Energy System in Electric Propulsion Aircraft. IEEE Trans. Power Electron. 2025, 40, 13754–13766. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, W.; Yang, C.; Liang, B.; Liu, W. An Efficient Energy Management Strategy of a Hybrid Electric Unmanned Aerial Vehicle Considering Turboshaft Engine Speed Regulation: A Deep Reinforcement Learning Approach. Appl. Energy 2025, 390, 125837. [Google Scholar] [CrossRef]
- Kumar, P.; Al-Nadawi, Y.K.; Ilak, M. Fast Real-Time Power Splitting for Hybrid Electric Propulsion Using Neural Network Based Approximate Model Predictive Control. In AIAA SCITECH 2024 Forum; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2024. [Google Scholar]
- Wang, W.; Koeln, J.P. Hierarchical Multi-Timescale Energy Management for Hybrid-Electric Aircraft; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2021. [Google Scholar]
- Yuan, J.; Zhang, G.; Yu, S.S.; Chen, Z.; Li, Z.; Zhang, Y. A Multi-Timescale Smart Grid Energy Management System Based on Adaptive Dynamic Programming and Multi-NN Fusion Prediction Method. Knowl.-Based Syst. 2022, 241, 108284. [Google Scholar] [CrossRef]
- Coutinho, M.; Bento, D.; Souza, A.; Cruz, R.; Afonso, F.; Lau, F.; Suleman, A.; Barbosa, F.R.; Gandolfi, R.; Affonso, W.; et al. A Review on the Recent Developments in Thermal Management Systems for Hybrid-Electric Aircraft. Appl. Therm. Eng. 2023, 227, 120427. [Google Scholar] [CrossRef]
- Asli, M.; König, P.; Sharma, D.; Pontika, E.; Huete, J.; Konda, K.R.; Mathiazhagan, A.; Xie, T.; Höschler, K.; Laskaridis, P. Thermal Management Challenges in Hybrid-Electric Propulsion Aircraft. Prog. Aerosp. Sci. 2024, 144, 100967. [Google Scholar] [CrossRef]





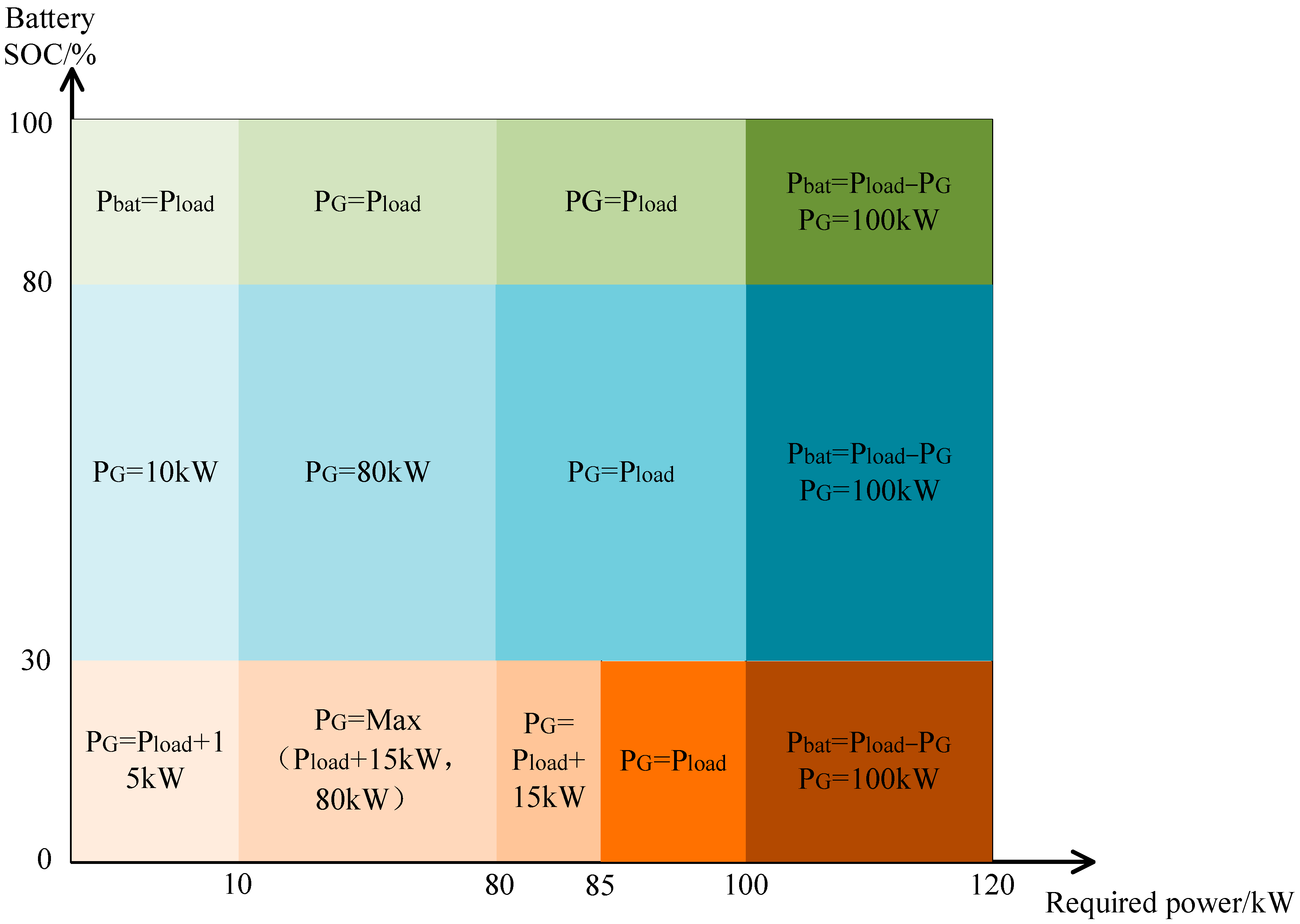
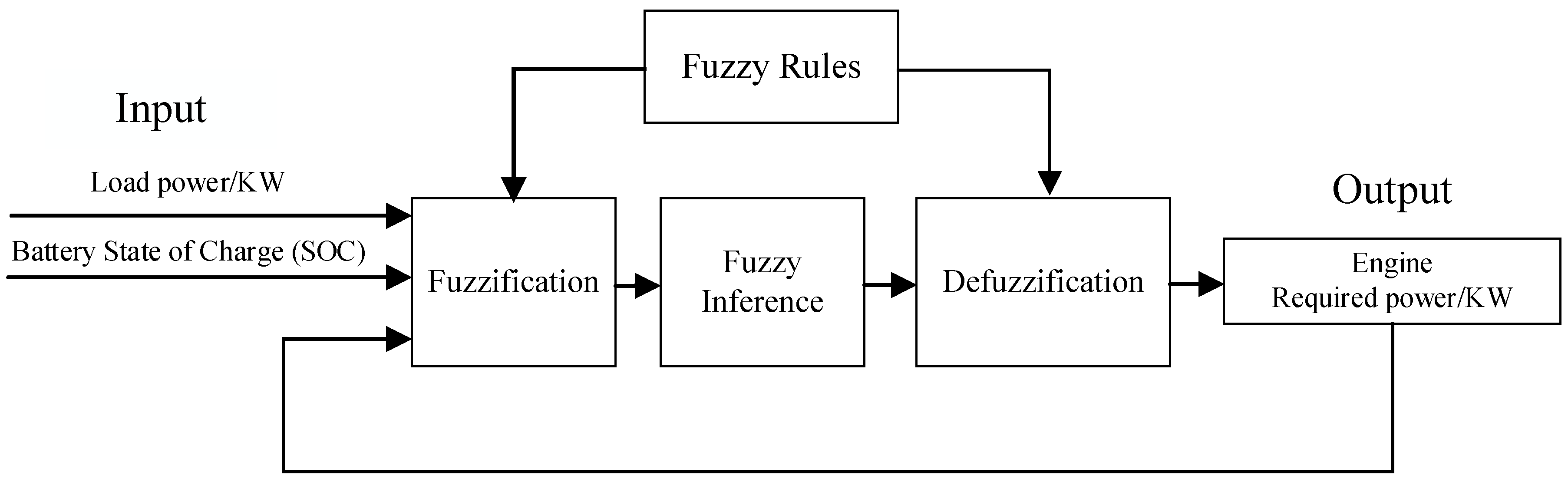
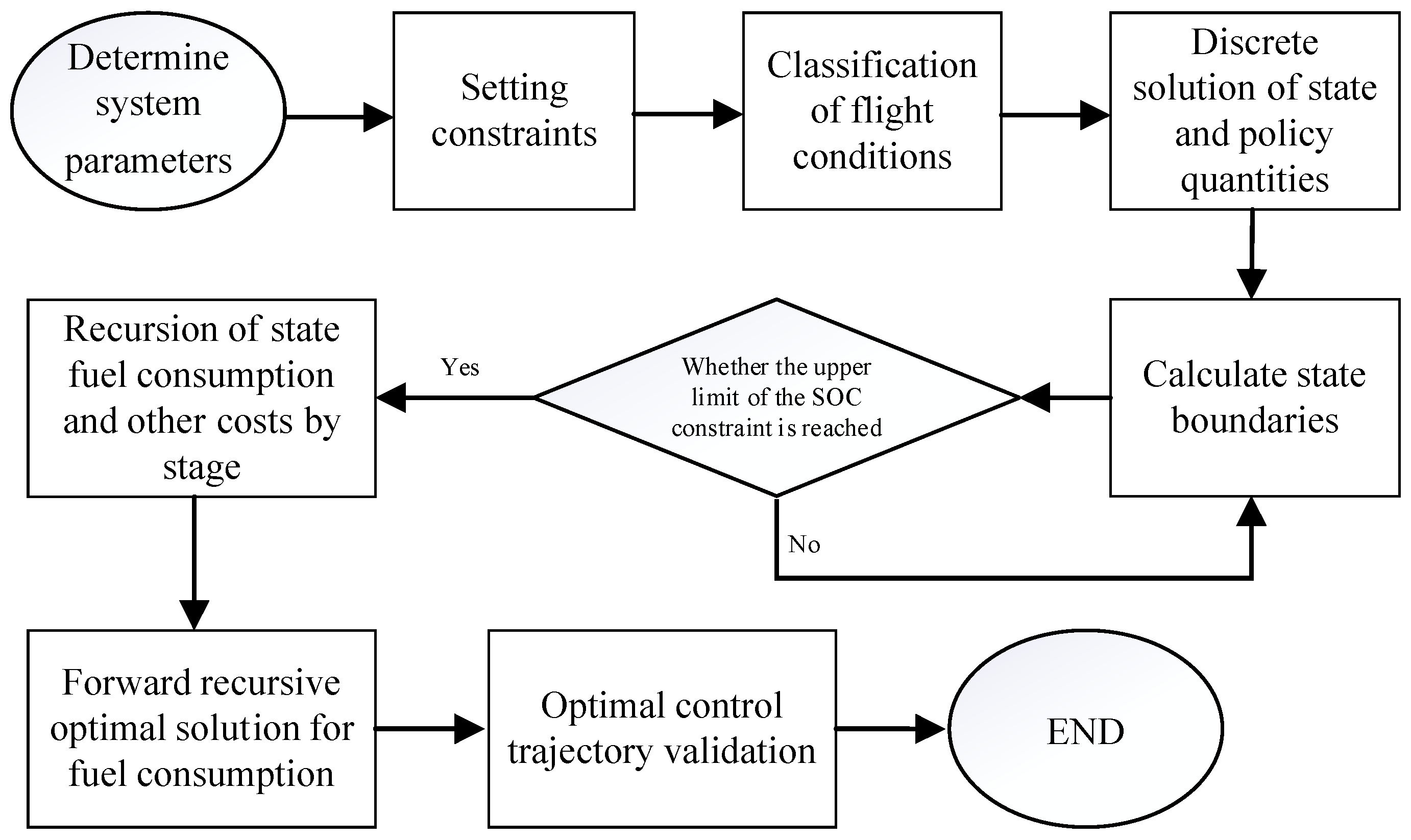





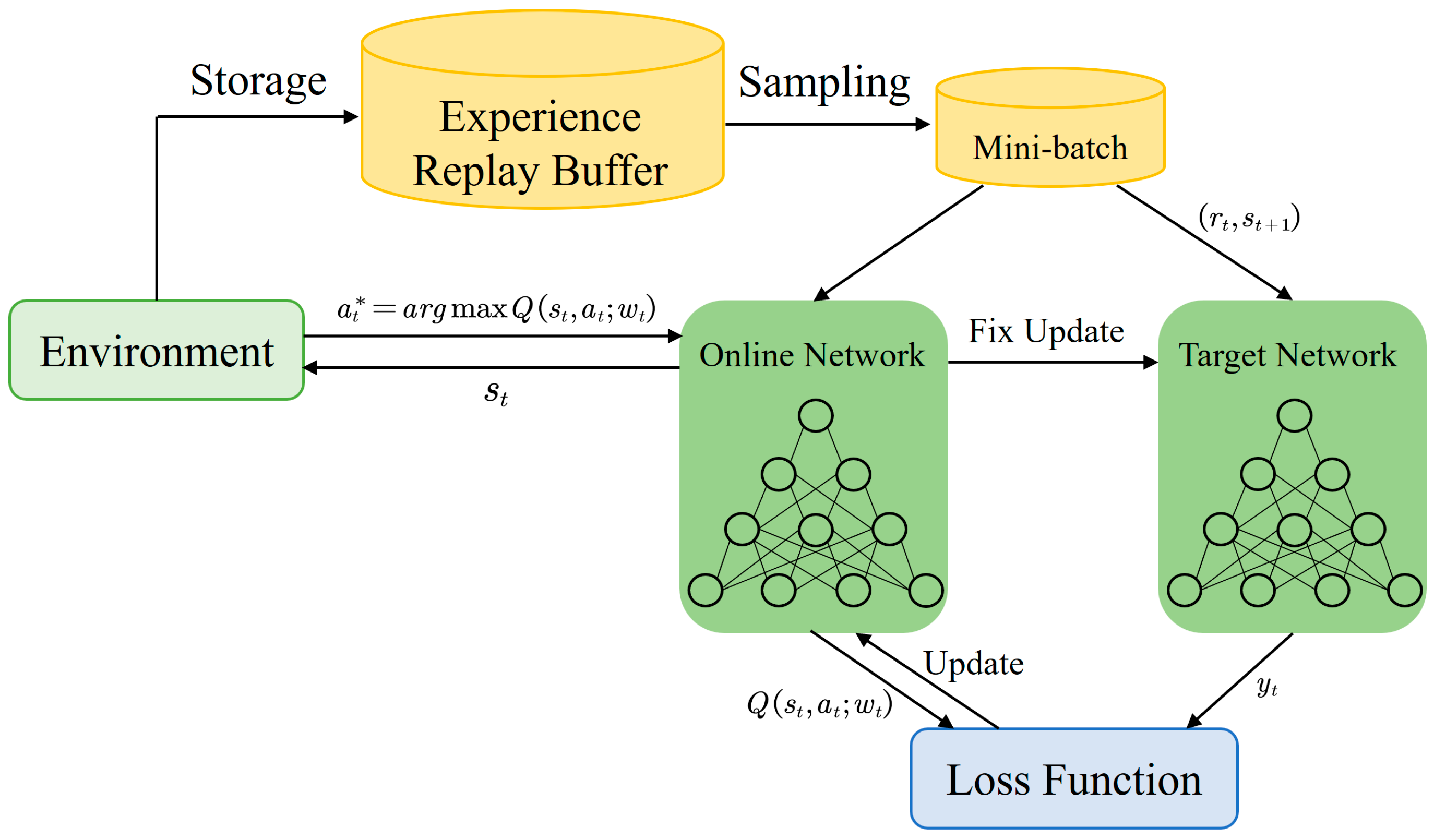


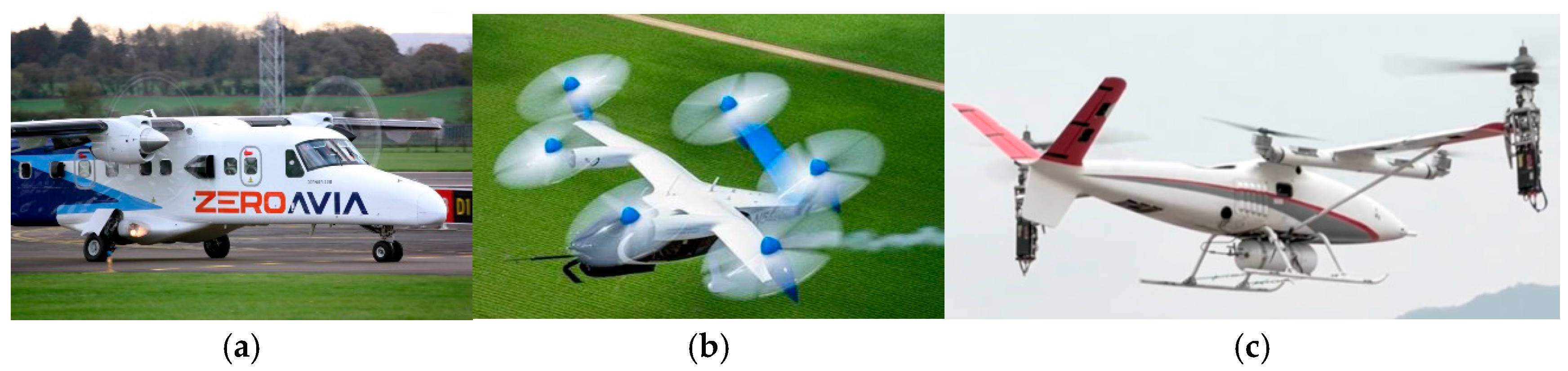
| Configuration | Required Power Sources | Energy Conversion Efficiency | Maintenance-Free Operating Time | Specific Power (kW/kg) | Size/Volume | Advantages | Disadvantages |
|---|---|---|---|---|---|---|---|
| Conventional Fuel-based | Aero-engine (turbofan/turbojet) | High (~35–40%) | Long, high reliability | Relatively high (limited by thermal efficiency) | Compact | High maturity, long range, easy refueling | High carbon emissions, fuel dependence, environmental pressure |
| Series Hybrid | (ICE/aero-engine + generator)/Fuel cell + battery + motor | Moderate (~25–35%), affected by multi-stage conversion | Moderate, limited by battery degradation | Moderate (restricted by battery specific energy) | Distributed configuration | Flexible motor placement, easier optimization and control | Long energy chain, efficiency losses, limited battery lifetime |
| Parallel Hybrid | Engine + motor (independent or combined output) | Relatively high (~30–40%), optimal source selection by mission phase | Moderate to long | Relatively high (engine and motor synergy improves power density) | Relatively compact | Flexible switching between power sources during takeoff/cruise, improved fuel economy | Higher control complexity, mechanical coupling challenges |
| Series-Parallel Hybrid | Engine + motor + battery + generator | Potentially higher (~35–45%), enabled by adaptive operation | Moderate to long | Relatively High (multi-source power aggregation) | Largest, most complex | Strong adaptability across mission phases, balance between endurance and emissions | Complex architecture, high cost, demanding control strategies |
| Model Type | Modeling Focus | Digital Platform | Advantages | Limitations | Primary Uses |
|---|---|---|---|---|---|
| Power-flow model | System power connectivity and allocation; bus voltages and load relationships | Simulink (NASA’s EMTAT library) | Fast simulation; modular structure; easy integration with non-electrical subsystems | Limited dynamic fidelity (mainly steady/quasi-steady analysis) | Controller prototyping; overall performance assessment |
| Physics-based model | Internal device mechanisms; coupled losses; true dynamic responses | Simulink (Simscape library), Dymola (Modelica), AMESim | High theoretical accuracy; suitable for detailed analyses | High complexity and computational cost; strong parameter dependence | Optimal/control co-design; real-time energy management development; high-fidelity performance simulation |
| Modeling Approach | Typical Fidelity & Scope | Automotive Suitability | Aerospace Suitability | Aviation-Specific Blockers/Required Adaptations |
|---|---|---|---|---|
| 0D/1D lumped electro-thermal (cells, bus, engine-gen) | Fast, low-CPU; limited spatial gradients | ✓ | △ | Requires conservative margins for DO-160 environments; needs traceability for thermal derating and aging across long missions |
| Grey-box (physics + identified params) | Balanced fidelity; identifiable | ✓ | ✓ | Parameter identification must cover hot-high, icing, turbulence; evidence for extrapolation beyond test points |
| Surrogate/meta-models (RSM, GP, NN) | Very fast once trained; opaque | ✓ | △ | Must demonstrate bounded error and explainability; runtime monitors or envelopes to ensure policy stays in training domain |
| High-fidelity electro-thermal–mechanical co-models (multi-domain) | Accurate; CPU-intensive | △ | ✓ | Acceptable for offline design/certification evidence; for onboard use, needs reduced-order models with verified error bounds |
| CFD/FEA-in-the-loop | Highest fidelity; non-real time | × | △ | Not for onboard EMS; only for design substantiation and offline envelope generation |
| Aging/SOH coupled battery-generator models | Degradation and lifecycle captured | △ | ✓ | Required for dispatch reliability; must tie to maintenance intervals/MEL and health-monitoring evidence |
| Uncertainty-aware/envelope models | Worst-case + robustness | △ | ✓ | Needed for DAL-level safety targets; used to generate certifiable constraints for controllers |
| Categories | Method | Techniques | Advantages | Disadvantages |
|---|---|---|---|---|
| Rule-Based Control Strategies | Deterministic Rule-based |
|
|
|
| Fuzzy Logic-based |
|
|
| |
| Optimization-Based Control Strategies | Global Optimization |
|
|
|
| Real-time Optimization |
|
|
| |
| Learning-Based Control Strategy | Learning-based |
|
|
|
| EMS Method | Real-Time and Determinism | Constraint Handling | Explainability | Automotive | Aerospace | Why Impractical/How to Adapt for Aviation |
|---|---|---|---|---|---|---|
| Rule-based/heuristics | Hard real-time | Explicit by design | High | ✓ | ✓ | Baseline for early TRL/HIL; scales poorly to multi-physics unless structured with envelopes |
| ECMS (Equivalent Cons. Min.) | Real-time capable | Soft via penalties; can add hard bounds | Medium | ✓ | ✓ | Works if penalties are certified with margins; needs envelope guards for thermal/SOC hard limits |
| DP (global offline) + policy tables | Offline global optimal; lookup online | Constraints baked in | High | ✓ | △ | Online DP is ×; offline DP OK for table generation; requires interpolation guards and coverage analysis |
| MPC (QP/NLP) | Deterministic if QP | Hard constraints natural | Medium | ✓ | ✓ | Preferred for certifiable runtime if convex; for NLP needs proof of timing bounds or fallback to QP |
| Model-free RL (DQN/TD3/PPO) | Non-deterministic by default | Implicit | Low | ✓ | × | Impractical without safety shields, action filters, and timing guarantees; black-box nature blocks certification |
| Safe-RL (constrained RL, shields, Lyapunov/CBF layers) | Near real-time if small nets | Hard/soft via safety layer | Medium | △ | △/✓ | Conditionally viable with a certifiable supervisory shell + monitors; policy size and timing must be bounded |
| Hybrid supervisory: MPC/ECMS outer + RL inner (advisory) | Deterministic outer loop | Hard via outer; RL proposals filtered | Medium-High | △ | ✓ | Recommended path: outer layer enforces safety/traceability; RL only proposes within a certifiable envelope |
| Online learning/adaptation | May violate timing | Risk to constraints | Low | △ | × | Disallowed unless adaptation is bounded, logged, and reverted on anomalies; typically performed on ground, not in flight |
| Type | Components | Strategies | Remark | Ref. |
|---|---|---|---|---|
| FC hybrid configuration | FC/BS/SC | SM, FL, PI, ECMS | Simulation only | [98] |
| FC hybrid configuration | FC/BS | Online fuzzy energy management | Simulation only | [110] |
| FC hybrid configuration | FC/SC | PI, PID-PWM | Experiment & simulation | [150] |
| FC hybrid configuration | FC/S | PMP | Experiment & simulation | [125] |
| FC hybrid configuration | FC/BS/SC | MBA, SSA | Simulation only | [141] |
| FC hybrid configuration | FC/BS/SC | Customization strategies based on electronic control units | Simulation only | [180] |
| FC hybrid configuration | FC/BS/S | Rule based | Experiment & simulation | [181] |
| FC hybrid configuration d | FC/SC | MPC, Rule based | Experiment & simulation | [146] |
| FC hybrid configuration | FC/BS | DP, Sequential Quadratic Programming | Simulation only | [182] |
| FC hybrid configuration | FC/BS | PMP | Experiment & simulation | [183] |
| FC hybrid configuration | FC/BS | FL, PSO-FL | Experiment & simulation | [184] |
| FC hybrid configuration | FC/BS | MPC, LOMPC | Experiment & simulation | [185] |
| Engine hybrid configuration | T/BS | MPC | Simulation only | [186] |
| Engine hybrid configuration | T/BS | MPC | Simulation only | [187] |
| FC hybrid configuration | FC/BS | DP | Simulation only | [188] |
| Engine hybrid configuration | E/BS | Q-Learning, Power Tracking | Simulation only | [189] |
| FC hybrid configuration | FC/BS | Rule based | Simulation only | [190] |
| Engine hybrid configuration | E/BS | Double Q-Learning | Simulation only | [22] |
| Engine hybrid configuration | T/BS | NSGA-II | Simulation only | [191] |
| Engine hybrid configuration | T/BS | TD3 | Simulation only | [192] |
| Engine hybrid configuration | T/BS | PMP | Experiment & simulation | [193] |
| Engine hybrid configuration | T/BS | DDPG | Simulation only | [194] |
| Engine hybrid configuration | T/BS | Fuzzy-A-ECMS | Simulation only | [195] |
| Engine hybrid configuration | T/BS | Heuristic DP | Experiment & simulation | [196] |
| Other hybrid configuration | E/FC/BS/SC | diffusion-based distributed optimization, decentralized droop control | Experiment & simulation | [197] |
| Engine hybrid configuration | T/BS | PPO | Experiment & simulation | [198] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, F.; Chen, J.; Gao, P.; Kong, Y.; Sun, X.; Wang, J.; Chen, X. A Review of Hybrid-Electric Propulsion in Aviation: Modeling Methods, Energy Management Strategies, and Future Prospects. Aerospace 2025, 12, 895. https://doi.org/10.3390/aerospace12100895
Yu F, Chen J, Gao P, Kong Y, Sun X, Wang J, Chen X. A Review of Hybrid-Electric Propulsion in Aviation: Modeling Methods, Energy Management Strategies, and Future Prospects. Aerospace. 2025; 12(10):895. https://doi.org/10.3390/aerospace12100895
Chicago/Turabian StyleYu, Feifan, Jiajie Chen, Panao Gao, Yu Kong, Xiaokang Sun, Jiqiang Wang, and Xinmin Chen. 2025. "A Review of Hybrid-Electric Propulsion in Aviation: Modeling Methods, Energy Management Strategies, and Future Prospects" Aerospace 12, no. 10: 895. https://doi.org/10.3390/aerospace12100895
APA StyleYu, F., Chen, J., Gao, P., Kong, Y., Sun, X., Wang, J., & Chen, X. (2025). A Review of Hybrid-Electric Propulsion in Aviation: Modeling Methods, Energy Management Strategies, and Future Prospects. Aerospace, 12(10), 895. https://doi.org/10.3390/aerospace12100895