Effects of Unplanned Incoming Flights on Airport Relief Processes After a Major Natural Disaster

Abstract

The severity of natural disasters is increasing every year, having an impact on many people’s lives. During the response phase of disasters, airports are important hubs where relief aid arrives while people need to be evacuated to safety. However, the airport often forms a bottleneck in these relief operations because of the sudden need for increased capacity. Limited research is carried out on the operational side of airport disaster management. Experts identify the main problems as first the asymmetry of information between the airport and the incoming flights, and second the lack of resources. The goal of this research is to gain understanding of the effects of incomplete knowledge of incoming flights with different resource allocation strategies on the performance of the cargo handling operations in an airport after a natural disaster event. An agent-based model is created, where realistic offloading strategies with different degrees of information uncertainty are implemented. Model calibration and verification are performed with experts in the field. The model performance is measured by the average turnaround time, which can be split into offloading time, boarding time and the cumulative waiting times. The results show that the effects of one unplanned aircraft are negligible. However, the waiting times and other inefficiencies rapidly increase with the more unplanned aircraft arriving.

1. Introduction

The number of natural disasters increases with every passing year. Between 1994 and 2013, it was recorded that a total of 6873 natural disasters occurred worldwide [1]. At the same time, due to climate change, the severity of these natural disasters is increasing every year [2]. Many of those natural disasters already have a negative impact on many people’s lives. Per year around 218 million people are affected by these disasters, and on average 68,000 die [1]. Airports often play the role of important hubs during the response phase of a humanitarian crisis. However, during the response phase, often a bottleneck arises in the ground handling operations of the airport as there is a sudden increase in incoming cargo while not all resources of the airport are available because of the disaster [3,4]. At the same time, many people need to be evacuated out of the area, adding complexity to the operations. Lives can be saved if these ground handling operations are executed more efficiently.

Despite the high stakes involved, airport disaster management remains under-researched, particularly in its operational and business dimensions [5]. Existing studies tend to focus retrospectively on incidents occurring within airports, rather than considering airports as critical nodes in broader disaster response networks. A related field, disaster resilience, is defined as “the capacity of a system, community or society potentially exposed to hazards to adapt, by resisting or changing in order to reach and maintain an acceptable level of functioning and structure” [6]. While both disaster management and resilience aim to enhance emergency response capabilities, there is a notable lack of systematic research on how resource allocation strategies affect aircraft handling performance—especially under conditions of uncertainty, such as limited information about incoming support flights during island-wide crises.

One of the few exceptions is the van Liere study [7], which simulates the cargo handling and passenger evacuation operations during the response phase at the Saint Martin Princess Juliana International Airport (PJIA) after the hurricanes in 2017 using the agent-based modelling paradigm. One of the main modelling challenges with conducting such research is the lack of recorded data, which is often multimodal, noisy, fragmented, and contradictory.

Agent-based Modelling and Simulation (ABMS) enables the formal representation of complex sociotechnical systems through autonomous, interacting agents, allowing researchers in disaster management to explore system behaviours via computational scenarios. Agents in the agent-based modelling paradigm possess beliefs, goals, and plans and act based on perceived information, making ABMS well-suited for modelling micro-level behaviours that impact macro-level outcomes [8]. This approach facilitates the investigation of how local agent interactions influence overall system performance, particularly in relation to coordination [9] and anticipation of disruptions [10]. Given the sociotechnical complexity of airports, ABMS has been widely applied to airport operations [8,11,12,13,14,15], supporting its suitability for this study. The proposed model focuses on three key challenges: limited information on incoming flights, constrained resources, and insufficient planning.

As little research has been conducted on this topic, expert knowledge is essential for the model development. According to experts, in similar disaster relief there are generally three main reasons for delays: the arrival of unannounced flights, the airport not being equipped for handling large cargo aircraft, and the preparation of airport management for such a disaster [16]. These issues were also considered in van Liere’s case study of Saint Martin Island.

As the case study of Saint Martin addresses many general problems that occur during and after natural disasters, in particular related to lack of resources and information, this case will also be used in this research. Furthermore, for this study we were able to collect information both from documents and experts, who were involved in the disaster relief operations at Saint Martin. The previously developed model [7], which we used as the basis for our study, simulates the cargo handling and passenger evacuation. It was used to gain a better understanding of the general bottlenecks that occur during airport cargo handling after a natural disaster event. Van Liere’s study does not provide a detailed analysis of civilian operations during the disaster relief. This paper will also focus on the offloading of civilian aircraft, as the airport focused largely on civilian operations, and the military and civilian operations were separated from each other.

The amount of knowledge possessed by airport employees of the incoming flights can create a situation of asymmetry of information. If the flight schedule is fully known, the airport operations coordinator can make decisions for resource allocations, integrating aircraft times of arrival, aircraft types, and cargo types. If the schedule is partially known or completely unknown, the predictions made by the operation coordinator, and based on them the corresponding resource allocation decisions, may not be efficient.

The research objective of this work was to gain understanding of the effects of incomplete knowledge of incoming flights, with different resource allocation strategies, on the performance of the cargo handling operations in an airport after a natural disaster event.

Addressing this problem will provide more understanding of what offloading coordinator decisions are the most appropriate under different conditions. To address the research objective, first the agent-based model was developed to realistically represent an airport after a natural disaster event. The main agents in this model were the offloading coordinators, whose goals, performance metrics, and resource allocation strategies to offload aircraft were modelled in detail. Using this model, the influence of the amount of information on incoming flights on the performance of the system was analysed by performing agent-based simulations.

More specifically, the following methodological steps were taken: first, to process the necessary background data for the research and understanding of the case study, in addition to understanding the existing model of van Liere and its limits. This is addressed in Section 2. The second step is the development of the agent-based model, based on the existing model. The changes to the existing model and the agent-based model for this research are explained in Section 3. In Section 4 the agent-based model is analysed and calibrated. The third step is to create and implement realistic scenarios with resource allocation strategies for offloading. These are more extensively explained in Section 5. In Section 6 the results of the experiments are given and discussed. Lastly, Section 8 provides the conclusion of this research.

2. Background Information and Case Study

The context of airport disasters, and in particular the case of Saint Martin in 2017, is detailed in this section.

2.1. Airports and Disasters

A humanitarian disaster is “an event or series of events that represents a critical threat to the health, safety, security, or well-being of a community or other large group of people, usually over a wider area.” [17]. This paper focuses on sudden onset natural disasters, which are “triggered by a hazardous event that emerges quickly or unexpectedly.” [18]. Examples of such a disaster are the tsunami in Tonga in the beginning of 2022 and the hurricanes in Saint Martin in 2017.

Disaster management is often described in a cycle of four phases: mitigation, preparedness, response, and recovery [19]. This paper will focus on the response phase, which starts during or right after the disaster event. Reduction or elimination of the negative effects is the goal of this phase. It is in this phase when the airport forms a bottleneck, as extensive relief aid needs to go to the impacted areas, but the means are not always present [20,21]. Logistics is a large part of these humanitarian operations, and it has become a popular research field for the past ten years. The Humanitarian Supply Chain however, is mostly looked at from an overall point of view, and not only the airport is considered [22,23].

To gain understanding of the general problems related to the airport during the response phase, an interview was held with an expert on airport disaster logistics. Delays were identified as one of the essential problems, and the main causes the expert identified for delays can be summarised as [16]:

• Scheduled flights are often not a problem, but the extra unscheduled flights cause a bottleneck, especially when the content of the cargo is unknown.
• Island holiday destinations are mostly not equipped for handling large cargo aircraft, as normally most cargo comes in by ship or belly cargo.
• Not all countries and airports have plans in case there is a disaster and part of the airport is destroyed. Moreover, if there is one, it is often not executed as it is specified.

2.2. Case Study: Saint Martin 2017

On 6 September 2017 a category 5 hurricane on the Saffir-Simpson scale called Irma passed Saint Martin. This is the highest category on this scale. The hurricane reached wind speeds of 260 km/h [24]. There were 4 fatalities and 23 injuries, and over 70% of the buildings on the islands were destroyed. This affected a lot of people, and the total damage cost was estimated to be around 1.5 billion US dollars [25]. On 8 September and 18 September, two other hurricanes passed the Caribbean, called Jose and Maria, respectively; they did not go over Saint Martin but caused tropical storms [26,27].

On the first day after Hurricane Irma, all efforts were put into making the airport operational again. There was a lot of destruction, causing waiting times at the airport. The main issues were similar to the general problems identified by experts [16]:

• There was no electricity, mobile connection, internet or civil air traffic control. Hence, there was no knowledge of incoming civilian aircraft, and all communication was carried out face-to-face.
• Most buildings were destroyed, as well as equipment and aircraft. Meaning there was a lack of resources, equipment and personnel.
• As the airport management did not show up, there was a lack of overall coordination.

There was no electricity, and in the beginning of such operations gas is scarce [16,28]. All communication was carried out face-to-face, and everybody had to walk to exchange information and coordinate.

Furthermore, at that time in Saint Martin, the military could use only one of the two highloaders, as the safety barrier was in the way when going under the aircraft. For one of the highloaders the safety barrier was taken off [7].

As the case study fits the general identified problems that occur during and after disasters, it makes it a suitable case study to investigate.

3. PJIA Agent-Based Model

In this section, we describe our model for Princess Juliana International Airport (PJIA).

3.1. General Overview of the Model

In the existing model [7], used as the basis for our model, three different operations were considered: civilian offloading, military offloading, and evacuation operations.

The latter two operations were simplified in our model, as we largely focused on civilian offloading.

The influence of military offloading on the civilian offloading operations is mainly through the use of equipment and the use of parking spots. Therefore, the military aircraft are still modelled, but their offloading is represented as a time penalty.

Evacuation operations always occur after offloading is finished. The impact of the evacuation on the civilian offloading operations is the time when the tasks after evacuation can start, as well as the time when the parking spot is used. For this reason, the evacuation operation is only modelled as a time penalty.

According to the experts, the main goal of the Offloading Coordinator (OC) is to lower the turnaround time (TAT). Subsequently, the resource allocation strategies used at PJIA and in general were established in consultation with the experts as follows [16,28,29,30]:

• Aircraft are offloaded in chronological order of arrival.
• The maximum set of resources is deployed to offload an aircraft. This means that for each available cargo door, one civilian handling agent with the necessary Ground Support Equipment (GSE) is allocated, and that each civilian handling agent can use up to two drivers with a tug and dollies.
• If it is known that another aircraft is coming in, this will be taken into account in order to allocate the resources (we refer to this strategy as resource allocation with anticipation).
• Even though the general rule is offloading in chronological order, priority also plays a role. This can be a humanitarian priority, such as an aircraft with medical equipment. It can also be a business priority, such as a regular client, as contractors are still a business.

In the model, these offloading strategies were implemented.

In accordance with the existing literature and experts, we assume that information about the arriving military flights is always known in advance. Besides time, this information also includes the type and amount of cargo. Based on this information, some GSEs, such as a highloader and tugs with dollies with the corresponding personnel, are reserved in advance. Similarly, when the Offloading Coordinator agent uses the resource allocation strategy with anticipation, it also takes the needs of the declared flights for the GSEs and personnel in advance and reserves these resources for the future accordingly. The undeclared flights are always handled using only the currently available resources. It means that if some resources are currently reserved for some declared (e.g., military or priority flights), the undeclared flights would need to wait until the necessary resources are available. Another difference in handling declared and undeclared flights is that the offloading coordinator agent always expects the declared flights, and when they arrive, the agent goes directly to them to obtain information about their cargo. At the time of arrival of some undeclared flights, the Offloading Coordinator agent might be busy with handling other aircraft, and the undeclared aircraft might need to wait until they are observed by the agent.

3.2. PJIA Model: Environment Specifications

The layout of the modelled airport environment can be found in Figure 1. Aircraft come in from taxiway 5i. They taxi over the taxi lines to a parking spot. The military parking spots are in the top part of the tarmac; the civilian parking spots are at the bottom part. The aircraft exits through the leftmost taxiway, taxiway 5e. The OC, civilian handling agents and drivers can be found in the Menzies Aviation building at 8. At 9 all the GSEs can be found. The military offloading coordinator is standing on the tarmac in between 9 and 10. In front of the terminal building, 10 and 11 are cargo drop-off areas for civilian and military cargo, respectively. The MOVCON can most of the time be found at 11. The military ATC agent can mostly be found at 7, the Ground Tower. The airport apron covers an area of 84,500 square metres, providing sufficient capacity for the simultaneous parking of up to ten wide-body aircraft.

One step time in the model is equal to five seconds. The environment also includes objects; there are cargo objects and GSE equipment objects.

Figure 1. Princess Juliana International Airport layout [7].

Figure 1. Princess Juliana International Airport layout [7].

3.2.1. Cargo Objects

There are three types of cargo objects. After offloading, the cargo from civilian or military aircraft is put in the civilian or military drop-off area, respectively.

• One LD3 ULD has an approximate weight of 1600 kg. They can be found in medium to large civilian aircraft.
• One 463L Master Pallet has an approximate weight of 4500 kg. They can be found in large military aircraft.
• One ICU has an approximate weight of 500 kg. This represents cargo in the form of boxes, packages and loose items. They can be found in all aircraft.

3.2.2. Ground Support Equipment Objects

All GSE vehicles move with the maximum allowed speed on a tarmac: 30 km/h. The GSE is located at the ground support equipment parking. There are four GSE types in the model:

• Pax steps are used on large civilian aircraft to get passengers on the aircraft, as well as for the aircraft crew to come down or the OC to go up.
• Tugs with dollies are the carts that bring the cargo from the aircraft to the terminal building.
• Belt loaders are used to get ICU from large aircraft onto the dollies.
• Highloaders are used to get LD3 ULD and 463L Master Pallet onto the dollies. However, only one of the two high loaders can be used on military aircraft.

In general, a GSE has two states: it is either parked or in use. The change in state is caused by a driver or a civilian handling agent using the GSE. In case the GSE is used for military purposes, the GSE also has a ‘reserved’ state. This state is induced by the OC agent.

3.3. PJIA Model: Agent Specifications

In this section, the properties, states, and interdependencies of all agents are explained. Figure 2 gives an overview of the model.

3.3.1. Aircraft

Each aircraft crew and their aircraft were modelled as one agent. There are two types of aircraft agents: the Civilian Aircraft agent and the Military Aircraft agent (see the details in Table 1). The arrival time of the agents is determined by the flight schedule, as explained in Section 5.1. An overview of the turnaround timeline for a civilian aircraft is given in Figure 3. The TAT is defined from the moment the aircraft arrives until it exits the taxilane. In Table 2, a brief explanation for all the time parameters is given. All time parameters used in our model are measured in minutes.

Call ATC Property

This is only carried out by military aircraft. Fifteen minutes before its arrival, the aircraft calls the ATC and gives the following information: its agent ID, arrival time, types of cargo, and amount of cargo per type.

Figure 2. Overview of the agents and their interactions in the PJIA Model.

Figure 2. Overview of the agents and their interactions in the PJIA Model.

Taxiing Property

The aircraft moves over the taxilines from its starting point to its destination point, using a predefined sequence of nodes.

ARRIVAL: Arrival always starts at taxiway 5i, and its destination point is a free parking spot closest to the OC building.

EXIT: Exit starts from the parking spot to the destination point at taxiway 5e.

As mentioned in Section 3.2, the military and civilian parking spots are different. As an overflow measure in the model, it is possible for civilian aircraft to park in a military parking spot in case no civilian parking spots are left. Vice versa for the military aircraft.

Parked Property

The OC agent comes by and checks the aircraft content. The information the OC needs is the type of aircraft (large/small), the types of cargo, and the amount of each cargo type. The OC agent leaves; the aircraft’s status is changed to ‘checked’. If the aircraft carry cargo, they wait for offloading.

Table 1. Aircraft Types and Specifications. Mil, Civ refer to Military and Civilian Aircraft. L, S, C, C* respectively refer to Large, Small, Cargo, also available without cargo.

Category	Aircraft Type	On-Board Cargo			#Seats
		LD3 [kg]	463L [kg]	ICU [kg]
Mil: L, C	C-130H		13,500		22
	C-130H-30		13,500		70
	A400M		1800		150
Mil: L	C-130H				80
Mil: S, C	MPA-D8			3000	30
Civ: L, C	DC-8	18,000		5000	30
		20,000		6000
	B737	15,000		5000	40
		20,000		8000
	B747	20,000		5000	50
		25,000		8000
Civ: S, C*	DHC-TO			2000	19
				2500
	Unspecified			500	6
				1000

Table 1. Aircraft Types and Specifications. Mil, Civ refer to Military and Civilian Aircraft. L, S, C, C* respectively refer to Large, Small, Cargo, also available without cargo.

Category	Aircraft Type	On-Board Cargo			#Seats
		LD3 [kg]	463L [kg]	ICU [kg]
Mil: L, C	C-130H		13,500		22
	C-130H-30		13,500		70
	A400M		1800		150
Mil: L	C-130H				80
Mil: S, C	MPA-D8			3000	30
Civ: L, C	DC-8	18,000		5000	30
		20,000		6000
	B737	15,000		5000	40
		20,000		8000
	B747	20,000		5000	50
		25,000		8000
Civ: S, C*	DHC-TO			2000	19
				2500
	Unspecified			500	6
				1000

Offloading Property

If a large civilian aircraft carries cargo, then it will interact with the civilian handling agents. For a small civilian aircraft, the interaction is directly with the Driver agent. At each step, the civilian handling agent or driver agent is aware of the remaining cargo in the aircraft that they need to offload. They are only aware of another cargo type in the aircraft after they finish, as they can observe whether the aircraft is empty or not. If it is empty, they communicate to the aircraft that the offloading is finished.

For military aircraft a time penalty per kilogram of cargo is implemented. The timer starts at the moment when all the GSEs and personnel are present at the aircraft.

Boarding Property

When pax can be evacuated with the aircraft, a time penalty is implemented per pax.

Figure 3. Timeline of the turnaround process of a Civilian Aircraft.

Figure 3. Timeline of the turnaround process of a Civilian Aircraft.

In this model, the time between offloading and boarding is set to 12 min, which is equal to the average $T_{BB}$ from van Liere’s model.

Table 2. Explanation of the time parameters in the aircraft turnaround timeline.

Time	Explanation
$T_{BP}$	Before Parked Time
$T_{BPS}$	Before Paxsteps Ready Time
$T_{BC}$	Before Cargo Content is Checked Time
$T_{BO}$	Before Offloading Time
$T_{Offl}$	Offloading Time
$T_{BB}$	Before Boarding Time
$T_{Board}$	Boarding Time
$T_{BPSR}$	Before Paxsteps Removed Time
$T_E$	Exit Time

Table 2. Explanation of the time parameters in the aircraft turnaround timeline.

Time	Explanation
$T_{BP}$	Before Parked Time
$T_{BPS}$	Before Paxsteps Ready Time
$T_{BC}$	Before Cargo Content is Checked Time
$T_{BO}$	Before Offloading Time
$T_{Offl}$	Offloading Time
$T_{BB}$	Before Boarding Time
$T_{Board}$	Boarding Time
$T_{BPSR}$	Before Paxsteps Removed Time
$T_E$	Exit Time

3.3.2. Offloading Coordinator Agent

At each step, when the OC agent is waiting at its building, the OC performs the following actions:

• For the civilian aircraft currently being processed, send a driver to supply or retrieve pax steps.
• For the civilian aircraft currently being processed, send personnel and GSE for civilian offloading.
• Send/reserve personnel and GSE for military offloading.
• Check a newly arrived aircraft, obtain information about its cargo, and put it on the list of the aircraft to be processed.

Resource Allocation Strategies

In Section 3.1, the realistic offloading or resource allocation strategies, as established by experts, are described. The simplest strategies include chronological offloading and maximum available resources. Knowledge of the schedule is not used in these strategies. Thus, to make the model more realistic and predictive, a cognitive function was implemented in the OC agent. This cognitive function enabled the OC agent to use the information about the flight schedule and available resources to make predictions about the needs of future aircraft and allocate the available resources according to these predictions. As there was no electricity, and thus no computers, all calculations in the model should be reasonable for a human to perform manually and quickly. The resource allocation strategies were implemented in the model as follows:

1:

Maximal available: One civilian handling agent with GSE and one or two driver(s) with a tug with dollies per aircraft, per cargo door. The number that is allocated depends on the number that is available at that time step. Even if there are two cargo doors, only one civilian handling agent with GSE can be allocated.

2:

Maximal set available + anticipation: Is largely the same as the previous strategy, only now the OC agent is also able to estimate the duration of the tasks and can use that information to estimate when personnel and GSE will be free, as well as to take the needs for the next aircraft into account.

In

Table 3. Resource sets for each cargo type, aircraft type and strategy (1 is ‘maximum available’ and 2 is ‘maximal set available + anticipation’).

Cargo Type	AC Type	Strategy	Civilian Handling Agent	Highloader	Belt Loader	Driver + Tug and Dollies
ULD	Civ Large	1	1	1	-	1
	Civ Large	2	1	1	-	1 or 2
ICU	Civ Large	1	1	-	1	1
	Civ Large	2	1	-	1	1 or 2
	Civ Small	1 & 2	-	-	-	1
463L	Mil Large	1 & 2	1	1	-	-

, the resources that can be allocated to an aircraft depending on the cargo type, aircraft type and strategy are shown.

Pax Steps Property

RETRIEVE: It is assumed that the OC agent has the knowledge of when an aircraft is finished with boarding passengers or when no boarding is needed. It will send a free driver to retrieve the PAX steps.

SUPPLY: It is assumed that the OC agent can observe the whole tarmac from its office window but is only aware of the civilian aircraft. When the OC agent observes a large civilian aircraft arriving and one driver and one paxstep are free, the OC agent will send the driver with paxsteps.

Arrange Offloading Property

Resource allocation for offloading is performed chronologically with respect to the arrival time. The OC agent tries to match the offloading needs for each aircraft with the available personnel and GSE. When a large aircraft has an LD3 ULD on board, it needs at least one civilian handling agent with a highloader and one driver with a tug and dollies. When a large aircraft has an ICU, it needs at least one civilian handling agent with a belt loader and one driver with a tug and dollies. When it concerns a small aircraft, then only one driver with a tug and dollies is sent to offload the ICU. More explanation about the used function can be found in Section 5.2. The OC agent assigns the civilian handling agent and/or drivers with their corresponding tasks. After assigning the tasks to its personnel, the OC agent resumes its waiting state.

Military Reservations Property

After the MOVCON interacts with the OC agent and requests a highloader reservation, the OC checks the availability, as only one of the highloaders can be used on military aircraft. When available, the OC agent changes the status of the highloader to ‘reserved’ and will not use it. When the military offloading coordinator interacts with the OC agent, the OC will also do the highloader reservation. The OC agent gets the information about the time necessary for the aircraft offloading and boarding from the military offloading coordinator. If all requested GSEs are available, the turnaround process begins.

Checking Aircraft Property

When the OC agent observes an arriving civilian aircraft, it goes to the aircraft to check the cargo content. In the case of a large aircraft, it first sends a driver with pax steps ahead. After the OC interacts with the aircraft agent, the OC knows the cargo types and amount, if any. Afterwards, if another aircraft has arrived, the OC will check that aircraft; otherwise, it will return to its office. It can check a maximum of three aircraft with cargo content in one go.

3.3.3. Civilian Handling Agents

The civilian handling agents have two main tasks: offloading large civilian aircraft and offloading large military aircraft. If the civilian handling agent is not busy with offloading, it waits at the office building. The civilian handling agents can also be reserved for handling certain aircraft in the future. The walking speed of the civilian handling agent is 5 km/h, and the driving speed for driving belt loaders and highloaders, is 30 km/h.

Civilian Offloading Property

First, the civilian handling agent walks to its corresponding GSE, which is a highloader or a belt loader. Then it drives the GSE to its target aircraft together with its assigned driver, who drives the tug and dollies. The duration of the offloading, from one vehicle to another or to the drop-off point, is determined by a time penalty. This time penalty takes the type of vehicle and the amount of cargo into account. When the aircraft is empty, the agent will communicate this to the driver agent. Then the civilian handling agent will drive the GSE back to its parking spot. After parking the GSE, the civilian handling agent will walk back to the office.

Military Offloading Property

First, the civilian handling agent walks to its corresponding GSE, which is the reserved highloader. Then it drives the highloader to the target aircraft. There it waits for the duration of the time penalty for the complete offloading of a military aircraft. The time penalty is based on the amount of cargo (kg) and the offloading rate (kg/s). Afterwards the civilian handling agent will drive the GSE back to its parking spot. After parking the GSE, the civilian handling agent will walk back to the office.

3.3.4. Driver Agents

Driver agents can have several tasks, namely, taking pax steps to and from aircraft and offloading large and small aircraft. In between these tasks the driver waits at the office building until instructions are given. The walking speed of the driver is 5 km/h, and the driving speed is 30 km/h.

Pax Steps Property

First, the driver walks to the pax steps, assuming the driver knows the location. Then the driver drives the pax steps to a destination point. This destination point is communicated by the OC agent. Next, the driver agent walks back to the office.

Offloading Large Aircraft Property

The driver agent walks to the tug and dollies; it then drives the tug and dollies to the target aircraft. The driver agent waits while the civilian handling agent loads cargo on the dollies. When the dollies are filled, the driver drives to the terminal building to drop the cargo. When the last batch of cargo is offloaded, the civilian handling agent will communicate this information to the driver agent. As long as this is not communicated, the driver agent drives back to the aircraft and the process is repeated. When the driver agent is finished, it drives to the parking spot of the tug and dollies and walks back to the office.

Offloading Small Aircraft Property

The driver agent walks to the tug and dollies; it then drives the tug and dollies to the target aircraft. The driver agent communicates with the aircraft agent and therefore always knows how much cargo is left in the aircraft. The driver loads the cargo on the dollies. When the dollies are filled, the driver drives to the terminal building to drop the cargo. In case there is more cargo remaining in the aircraft, the driver drives back to the aircraft and repeats the process. When finished, the driver drives to the parking spot of the tug and dollies and walks back to the office.

3.3.5. ATC

In this model, the ATC agent has only one task: to give the information about incoming military flights to the MOVCON. As the ATC agent is a military agent, the agent walks with the speed of 6 km/h.

Find MOVCON Property

After a military aircraft calls in, see ‘Call ATC Property’ in Section 3.3.1, the ATC walks to the MOVCON and repeats the given information. The information includes the aircraft agent ID, arrival time, types of cargo, and amount of cargo of each type. After the interaction the ATC walks back to its tower.

It is assumed that a second ATC agent stays in the tower to receive incoming calls. However, that agent is not modelled.

3.3.6. MOVCON

Movement Control is a military unit; in the case study, the MOVCON oversees the airport. In this model, the MOVCON is the connection between the ATC, the military offloading coordinator and the OC agent. The MOVCON is a military agent and therefore walks with the speed of 6 km/h. The waiting spot of the MOVCON is the military cargo drop-off area.

If the MOVCON gets information from the ATC about an incoming aircraft with 463L Master Pallets onboard, the MOVCON agent needs to make a reservation so it could use the civilian GSE and civilian handling agent at the time of arrival of the aircraft.

Highloader Reservation Property

The MOVCON walks to the OC office building. If the OC is not present or available, the MOVCON waits. When the OC is present and available, the MOVCON interacts with the OC agent. The MOVCON gives the arrival time of the aircraft and asks for a highloader reservation. After the interaction, the MOVCON walks back to its waiting spot.

3.3.7. Military Offloading Coordinator

The military offloading coordinator’s waiting spot is near the military parking spots, in between the OC’s office and the terminal building. The military offloading coordinator is a military agent and walks with the speed of 6 km/h.

Handle Aircraft Property

When a military aircraft is parked, the military offloading coordinator walks to the OC office building. If the OC is not present or available, the MOVCON waits. When the OC is present and available, the military offloading coordinator interacts with the OC. The military offloading coordinator requests to reserve a tug with dollies. In the case of a large military aircraft, the military offloading coordinator also requests the civilian handling agent and the highloader that have been reserved by the MOVCON. A military handling agent drives the requested tug and dollies, as well as a forklift truck. However, the military handling agent and forklift trucks were not modelled. Instead, the military offloading coordinator makes a reservation in its military handling agent list and forklift truck list. These lists have the same length as the number of military handling agents and forklift trucks; each entry is either a 0 (is available), an integer (the amount of time steps that it is not available) or a string (‘reserved’). It is assumed that the military offloading coordinator knows when the reserved GSE are available. At that step, the military offloading coordinator changes a ‘reserved’ entry in its military handling agents list and its forklift truck list to the corresponding timer entry. After the interaction the military offloading coordinator walks back to its waiting spot.

Table 4. Number of the different Ground Support Equipment (GSE) and Agents.

GSE	Personnel	Personnel
Objects	Executing Agents	Coordinating Agents
Beltloaders: 4	Driver personnel: 5	MAMD: 1
Tugs-Dollies: 8	Civilian handling personnel: 4	MOC: 1
High-loaders: 2	Military handling personnel: 4	EC: 1
Pax-stairs: 8	Marines personnel: 6	MOVCON: 1
Forklifts: 2	Pax: indefinite
	ATCO: 1
	Aircraft: according to schedules

presents detailed information on the types and quantities of Ground Support Equipment and the different types of Agents.

4. Model Calibration

The agent-based model has been implemented in Python 3.9 using the Mesa framework (version 1.0), a dedicated library for developing and analysing agent-based simulations. In total, six parameters needed to be calibrated, which were also used in van Liere’s model.

The calibration was completed in two steps explained in Section 4.1 and Section 4.2. First, the PJIA model was calibrated before implementing the new resource allocation strategy in order to compare and analyse the PJIA model with respect to van Liere’s model. The second step is the calibration after the implementation of the new resource allocation strategy, to guarantee a realistic model output with respect to the expert knowledge.

We report the calibration results as cumulative builds C0–C6 (i.e., labelled configurations rather than free coefficients) in two calibration steps.

Terminology (C0–C6). C0 is the uncalibrated baseline using van Liere’s parameters; C1–C3 implement the first calibration step by applying three successive parameter adjustments under the baseline resource strategy (463L aircraft→GSE offload rate; military boarding rate; civilian boarding rate). After switching to the ‘maximum available’ allocation strategy, C4–C6 adjust ICU and ULD offload rates to achieve realistic TAT, in accordance with expert opinion.

• C0: uncalibrated baseline.
• C1: 463L (AC→GSE) offload rate ↑ to 10 kg/s
• C2: Military boarding rate ↓ to 22.5 s/pax
• C3: Civilian boarding rate ↓ to 47 s/pax
• C4: ICU offload rate ↓ to 4.5 kg/s
• C5: ULD (AC→GSE) offload rate ↓ to 5.7 kg/s
• C6: ULD (GSE→TB) offload rate ↓ to 40 kg/s

The main performance indicator of the model is TAT; therefore, it is important that this indicator provides realistic values. In Section 3.3.1 the timeline for the aircraft TAT is shown. TAT can be split into three main parts: the offloading time, the boarding time, and the cumulative waiting time. The parameters, which directly influence TAT and thus need to be calibrated, are the offloading and boarding rates. Therefore, only the calibration results for TAT, offloading time, and boarding time are shown here. In order to compare the proposed model with van Liere’s model, only the outcomes for large aircraft with cargo and pax are given.

4.1. Step 1: Calibrating the Baseline Model

In

Table 5. The results for the first calibration step in minutes for large aircraft with cargo and evacuation, compared with values of experts and van Liere’s model [7].

	Civilian			Military
	TAT	Offloading	Boarding	TAT	Offloading	Boarding
Experts	120–150	60	30	60–90	30	30
van Liere model	125.2	57.5	30.6	79.8	32.5	30.2
PJIA model C0	129.7	53.9	37.3	97.0	37.0	40.0
PJIA model C3	119.1	52.5	29.2	79.0	29.0	30.0

, a comparison of the calibration outcomes for the PJIA and van Liere’s models is shown. Here, the same resource allocation strategy is used in the PJIA model as in van Liere’s model. In the first row of the table, the expectations of experts concerning TAT and offloading and boarding time are provided [16,28,30].

As can be seen in Table 5 for the PJIA model build C0, the average offloading time of the civilian aircraft is lower than the experts’ value, which is as expected, since not all processes were modelled in the PJIA. The civilian boarding time, as well as the military boarding time, are 37.3 and 40.0 min, respectively, which is more than 20% higher than the corresponding values provided by the experts. To match the expert values, we recalibrated the passenger boarding rates, taking into account the actual numbers of passengers on the corresponding flights (38 civilian and 80 military). The military offloading time in the PJIA model was biased by a single combat offload time estimate in van Liere’s model. Since a combat offload is an exception and, therefore, is not representative of the usual military offloading process, we recalibrated the corresponding 463L (AC→GSE) offload rate used to calculate the military offload time. Table 6 presents all calibrated model parameters.

Van Liere’s model and the PJIA model have exactly the same number of military aircraft, with exactly the same arrival time. In both models, there are seven large civilian aircraft. Their arrival times were randomised in van Liere’s model, meaning they are also randomised in each of the 120 schedules. In van Liere’s model there were on average 30 small aircraft with cargo and 15 small aircraft without the schedules of the baseline model have on average 30.3 and 15.8, respectively.

The calibrated parameters of the baseline model had the desired effect, although the civilian TAT and offloading time were still lower than the expert values. We continued with the second calibration step, in which the baseline PJIA model was extended with a new resource allocation strategy.

Table 6. Parameters changed by calibration. C0 shows the baseline (van Liere), and C1–C6 are cumulative builds where each row indicates the first build where that single change is applied; C6 is the final calibrated configuration.

	van Liere Model (C0)	PJIA Model (C6)	Parameter Change
Offloading Rates
463L (AC to GSE) [kg/s]	7.5	10	C1
ICU (general) [kg/s]	5	4.5	C4
ULD (AC to GSE) [kg/s]	7.1	5.7	C5
ULD (GSE to TB) [kg/s]	45	40	C6
Boarding Rates
Boarding military [s/pax]	30	22.5	C2
Boarding civilian [s/pax]	60	47	C3

Table 6. Parameters changed by calibration. C0 shows the baseline (van Liere), and C1–C6 are cumulative builds where each row indicates the first build where that single change is applied; C6 is the final calibrated configuration.

	van Liere Model (C0)	PJIA Model (C6)	Parameter Change
Offloading Rates
463L (AC to GSE) [kg/s]	7.5	10	C1
ICU (general) [kg/s]	5	4.5	C4
ULD (AC to GSE) [kg/s]	7.1	5.7	C5
ULD (GSE to TB) [kg/s]	45	40	C6
Boarding Rates
Boarding military [s/pax]	30	22.5	C2
Boarding civilian [s/pax]	60	47	C3

4.2. Step 2: Calibrating PJIA Model Extended with a New Resource Allocation Strategy

In this section, the PJIA model with a new resource allocation strategy is calibrated to fit the expert knowledge. The calibrated baseline PJIA model (build C3) was extended with the ‘maximum available’ resource allocation strategy, described in Section 3.1. Because this strategy shortened offloading by >4 min and reduced TAT, we lowered ICU and ULD offload rates (C4–C6) to ensure that the model outputs approach the expert values (refer to

Table 7. Second step calibration results in minutes for large civilian aircraft, to compare the base model with expert values.

	Civilian			Military
	TAT	Offloading	Boarding	TAT	Offloading	Boarding
Experts	120–150	60	30	60–90	30	30
PJIA model C3	115.7	48.1	29.2	79.0	29.0	30.0
PJIA model C6	126.6	58.8	29.0	79.0	29.0	30.0

for the resulting C3 vs. C6 comparison).

5. Experiments

This section presents the experiments to answer the main research question concerning the effects of unannounced incoming flights on the performance of the system using different resource allocation strategies. In Section 5.1 the experiments will be explained. Afterwards, in Section 5.2, the implementation of these experiments in the model is elaborated.

5.1. Experiments: Strategies and Scenarios

After a natural disaster event, most scheduled flights fly if possible. However, additional flights may arrive, and their arrival is not always announced. According to experts, this often causes a disruption in the planning [16]. An overview of all experiments in this research is summarised in

Table 8. Simulation experiments.

		Scenarios
		A: Unknown Flight Schedule	B: Known Flight Schedule	C: Incomplete Flight Schedule
Strategies	1: Max available	Case 1A	Case 1B	Case 1C u1
				Case 1C u7
	2: Max available + anticipation	Case 2A	Case 2B	Case 2C u1
				Case 2C u7

.

Incoming Flight Scenarios

In the case study the airport was not operational, so most flights were not scheduled. However, the military received the information on incoming flights in the morning of each day; the civilian flights all arrived unannounced. According to experts, in general the civilian schedule is known, but there are always unannounced aircraft causing delays [16]. To achieve a better understanding of the influence of incomplete knowledge of incoming flights, three different incoming civilian flight scenarios are created:

A:

Unknown Flight Schedule: The flight schedule is not known by the OC agent.

B:

Known Flight Schedule: The OC agent has full knowledge of the incoming civilian flight schedule. This scenario is used to compare the case with complete information with the cases with incomplete information about the flight schedule.

C:

Incomplete Flight Schedule: The OC agent has access to the incoming civilian flight schedule, but unannounced aircraft will come in. In the implementation of this scenario some large aircraft in scenario B arrive unannounced. This scenario is used to analyse how unannounced flights can disrupt the overall system.

In Table 8 it can be seen that for scenario C there are two test cases, u1 and u7. This stands for one unannounced large civilian aircraft and seven unannounced large civilian aircraft, respectively. There are only seven large civilian aircraft in the schedule in the system in total.

To be able to compare all the experiments, the same schedules should be used. The military flight schedule is fixed for all cases. Civilian aircraft arrive at random intervals. When there are fewer than four civilian aircraft on the tarmac, a new aircraft is introduced. The size and contents of each aircraft are also randomised. As the exact schedule of the case study is not known, one schedule is not sufficient to perform the research. Therefore, the baseline model has been run 120 times. All the cases were analysed using the same set of 120 schedules. All simulated scenarios were conducted based on a one-day operational schedule.

For the simulation of civilian aircraft operations, the inter-arrival times, the number of small aircraft, and the cargo types and corresponding loads (subject to the maximum allowable values presented in Table 1) were all modelled using uniform distributions. This choice reflects an assumption of equal probability across the defined ranges, in the absence of detailed empirical data for these variables, and simulates a wide range of possible configurations. The uniform distribution ensures that all values within the specified minimum and maximum bounds are equally likely to occur, thereby introducing variability while maintaining control over the simulation parameters.

5.2. Implementation of the Resource Allocation Strategies

In this section, the implementation of the resource allocation strategy ‘max available with anticipation’ of the OC agent is explained.

For small aircraft there is only one option for resource allocation—‘max available’. For large aircraft, an algorithm is implemented to find the best resource allocation plan, in terms of total TAT, for aircraft A being serviced, taking the next aircraft, B, into account.

In Algorithm 1, the function RA_function() could be realised either by RA_available() or RA_ahead() functions. RA_available() is used to determine the maximum Option Set for the current time step (max availability strategy), while the function RA_ahead() is used to determine the minimum or maximum Option Set and establish when these Option Sets are possible (planning with anticipation). These functions are defined in Table 9. Both these functions output the Option Set containing the following:

• AMA: Amount Assigned
• est_ULD: Estimated ULD offloading finish time step
• est_ICU: Estimated ICU offloading finish time step
• start_step: (Estimated) step when offloading will start

The Best Option algorithm requires the list of estimated resources as input. This list contains each resource and the estimated timestep when the task is finished. In this list a distinction is made between available and unavailable resources. For the unavailable resources, the OC agent knows the estimated timestep when that resource becomes available. Here, the estimations for each task are the average time durations when the resources are used in a certain task, taken from case 1A. For the offloading times, the OC agent has a different estimation for each cargo type, the amount of cargo and the number of drivers. The use of two drivers can reduce the offloading time between 11 and 13% for ULD cargo and 32 and 35% for ICU cargo. The range is dependent on the amount of cargo. An overview of these times is given in Table 10. Furthermore, the aircraft IDs of the first two aircraft to be offloaded are provided as input to the algorithm. The IDs are a part of the internal knowledge the OC agent has about the aircraft. Finally, the algorithm outputs the best option, which is then used to determine the next state of the OC agent. If the best option has a start_step equal to the current timestep, the OC’s new state is ‘interacting_personnel’, else the OC sets its state to ‘waiting’.

Table 9. Definition of the RA_functions: RA_available() and RA_ahead().

RA_available()
Purpose	Determine maximum Option Set based on the available resources
Input	free_rss: available resources list
	X_ID: ID of aircraft X
Output	Options Set = {AMA, est_ULD, est_ICU, start_step}
RA_ahead()
Purpose	Determine minimum and/or maximum Option Set for one or both cargo types
Output	Options Set = {AMA, est_ULD, est_ICU, start_step}
Input	est_rss: resource estimation list
	X_ID: ID of aircraft X
	‘ULD’, ‘ICU’, ‘All’: cargo type
	‘Max’, ‘Min’, ‘Best’: Option Set
Output	Options Set = {AMA, est_ULD, est_ICU, start_step}

Table 9. Definition of the RA_functions: RA_available() and RA_ahead().

RA_available()
Purpose	Determine maximum Option Set based on the available resources
Input	free_rss: available resources list
	X_ID: ID of aircraft X
Output	Options Set = {AMA, est_ULD, est_ICU, start_step}
RA_ahead()
Purpose	Determine minimum and/or maximum Option Set for one or both cargo types
Output	Options Set = {AMA, est_ULD, est_ICU, start_step}
Input	est_rss: resource estimation list
	X_ID: ID of aircraft X
	‘ULD’, ‘ICU’, ‘All’: cargo type
	‘Max’, ‘Min’, ‘Best’: Option Set
Output	Options Set = {AMA, est_ULD, est_ICU, start_step}

Table 10. Average offloading times in minutes per cargo type, amount of cargo, and the number of drivers.

	Cargo Amount (kg)	15,000	18,000	20,000
ULD	1 driver	52	61	70
	2 drivers	46	54	61
	Cargo Amount (kg)	5000	6000	8000
ICU	1 driver	35	37	54
	2 drivers	21	25	33

Table 10. Average offloading times in minutes per cargo type, amount of cargo, and the number of drivers.

	Cargo Amount (kg)	15,000	18,000	20,000
ULD	1 driver	52	61	70
	2 drivers	46	54	61
	Cargo Amount (kg)	5000	6000	8000
ICU	1 driver	35	37	54
	2 drivers	21	25	33

There are two sets of possible RA_function() combinations for aircraft A and B. These combinations are given in

Table 11. All resource allocation function combinations of Option Set A and Option Set B.

	Set i	Option Set A	Option Set B
Time_min_A >current step	1:	RA_ahead(A_ID, est_rss, ULD, min)	RA_ahead(A_ID, est_rss, ICU, Best)
	2:	RA_ahead(A_ID, est_rss, ULD, max)	RA_ahead(A_ID, est_rss, ICU, Best)
	3:	RA_ahead(A_ID, est_rss, ICU, min)	RA_ahead(A_ID, est_rss, ULD, Best)
	4:	RA_ahead(A_ID, est_rss, ICU, min)	RA_ahead(A_ID, est_rss, ULD, Best)
Time_min_A <= current step	1:	RA_ahead(A_ID, est_rss, All, min)	RA_ahead(B_ID, est_rss, All, Best)
	2:	RA_ahead(A_ID, est_rss, All, max)	RA_ahead(B_ID, est_rss, All, Best)
	3:	RA_available(A_ID, free_rss)	RA_ahead(B_ID, est_rss, All, Best)

. When the minimum set of resources for aircraft A cannot be reached at the current time step, it means that there are enough resources for only one cargo type to be offloaded. In that case, the option set for aircraft B is equal to the option set for aircraft A, but with the other cargo type. For example, the first option set that will be generated is used for Option Set A, aircraft A with only ULD cargo. For Option Set B, it is aircraft A with ICU cargo. In case the minimum set of resources for aircraft A can be reached at that time step, the minimum, the maximum, and the maximum available Option Sets are evaluated.

Algorithm 1: Generate Best Option

6. Results

In this section, the results of the experiments are presented. The main results are discussed in Section 6.1. In Section 6.2, the results of the experiments with different Arrival Time Interval Factors (ITIF) are provided.

6.1. Comparison of Strategies and Scenarios

The average TAT and offloading time per scenario are presented in

Table 12. The average TAT and Offloading Times, including standard deviation, for large civilian aircraft per test case.

			Scenarios
			A	B	C u1	C u7
Strategies	1	TAT	130.4 ± 5.6	110.8 ± 4.8	111.8 ± 4.7	121.4 ± 5.2
		Offl	60.0 ± 3.9	59.4 ± 3.8	59 ± 3.7	59 ± 3.9
	2	TAT	128.7 ± 5.9	110.3 ± 4.8	111.2 ± 4.7	120.5 ± 5.4
		Offl	58.2 ± 3.7	58.2 ± 3.6	57.8 ± 3.7	57.9 ± 3.7

. The average offloading times do not vary significantly per test case, but the average TAT changes per scenario. The average boarding time is the same for all cases, namely 29.1 min with a standard deviation of 1.1 min.

The Cliff’s Delta statistic was used to determine the effect size for the experiments comparing two datasets. If the effect size is large, it is likely that a randomly chosen datapoint of set 1 is smaller than a randomly chosen datapoint of set 2. The magnitude thresholds used in this research (negligible, small, medium, large) are defined as in [31].

The two resource allocation strategies were compared for each scenario using the Cliff’s Delta statistic. This analysis showed that the differences are all negligible. When comparing the scenarios for each strategy, see

Table 13. Cliff’s Delta effect size results per scenario (N = negligible).

Compare	TAT	${\mathbf{T}}_{\mathit{BPS}}$	${\mathbf{T}}_{\mathit{BC}}$	${\mathbf{T}}_{\mathit{BO}}$	${\mathbf{T}}_{\mathit{Offl}}$	${\mathbf{T}}_{\mathit{Board}}$	${\mathbf{T}}_{\mathit{BPSR}}$
1A vs. 1B	Large	Large	Large	Large	N	N	Medium
1B vs. 1C u1	N	N	N	N	N	N	N
1C u1 vs. 1C u7	Medium	Large	Large	Large	N	N	N
1C u7 vs. 1A	Small	Medium	Small	Small	N	N	Medium
2A vs. 2B	Large	Large	Large	Large	N	N	Medium
2B vs. 2C u1	N	N	N	N	N	N	N
2C u1 vs. 2C u7	Small	Large	Large	Large	N	N	N
2C u7 vs. 2A	Small	Medium	Small	Small	N	N	Medium

, small to large differences can be detected. One unannounced aircraft does not influence the performance of the system in either of the strategies, whereas seven unannounced aircraft do make a difference. This difference in TAT is mainly due to the change in waiting times, as the differences in offloading and boarding times are all negligible. This is also shown in Figure 4, which shows the distribution of the TAT for strategy 1 per scenario in order of decreasing available knowledge. From this figure it is clear that, as expected, the boarding times, computed as a time penalty, do not change. Furthermore, the offloading times barely vary per test case. Only the total waiting times increase with decreasing available information.

Figure 5 presents the different waiting times. $T_{BPSR}$ does not vary significantly, unless the flight schedule is fully unknown. The $T_{BO}$ increases slightly with less available information. When the schedule is known, the cargo content does not need to be checked; hence, the $T_{BC}$ increases with increasing unannounced flights. Interestingly, scenario A still has higher $T_{BC}$ even though there are only seven large civilian aircraft for each run. Next to that, the $T_{BPS}$ also increases with decreasing knowledge.

From these results, one can see that the offloading times do not change, regardless of the strategy or scenario. Additionally, the overall difference between strategies is negligible. This might be because the resources are always sufficient to serve the demand. The interarrival time interval, impacting the demand for resources, will be changed to investigate this phenomenon further.

Figure 4. Distribution of the Turnaround Time for the large civilian aircraft for all test cases of strategy 1 in order of decreasing knowledge.

Figure 4. Distribution of the Turnaround Time for the large civilian aircraft for all test cases of strategy 1 in order of decreasing knowledge.

Figure 5. Distribution of the Waiting Times of the large civilian aircraft for all test cases of strategy 1 in order of decreasing knowledge.

Figure 5. Distribution of the Waiting Times of the large civilian aircraft for all test cases of strategy 1 in order of decreasing knowledge.

6.2. Effects of Changes in the Interarrival Time Interval

To be able to compare the experiments with a change in the interarrival time interval, all schedules were run with an Interarrival Time Interval Factor (ITIF), which modifies the arrival times.

In

Table 14. Overview of average TAT and Offloading times per ITIF for all cases.

ITIF	TAT		Offloading		TAT		Offloading
	Case 1A				Case 2A
1.2	125.3	±5.2	59.2	±3.8	123.6	±5.6	57.1	±3.7
1	130.4	±5.6	60.0	±3.9	128.7	±5.9	58.2	±3.7
0.8	140.4	±8.2	62.4	±5.6	139.7	±7.3	61.1	±4.6
0.6	162.1	±11.2	65.0	±5.1	161.6	±13.3	64.8	±6.3
	Case 1B				Case 2B
1.2	109.4	±4.7	58.3	±3.7	108.7	±4.7	57.0	±3.6
1	110.8	±4.8	59.4	±3.8	110.3	±4.8	58.2	±3.6
0.8	113.2	±5.4	60.6	±4.0	113.5	±5.4	59.5	±4.0
0.6	120.1	±6.8	62.9	±4.6	121.0	±6.5	62.8	±4.6
	Case 1C u1				Case 2C u1
1.2	110.3	±4.6	58.1	±3.8	109.6	±4.9	57.0	±3.8
1	111.8	±4.7	59.0	±3.7	111.2	±4.7	57.8	±3.7
0.8	114.2	±5.1	60.1	±4.1	114.0	±5.3	59.1	±4.0
0.6	121.3	±6.9	62.9	±4.6	121.8	±6.4	62.4	±4.3
	Case 1C u7				Case 2C u7
1.2	119.2	±4.7	58.5	±3.6	118.1	±4.8	57.1	±3.8
1	121.4	±5.2	59.0	±3.9	120.5	±5.4	57.9	±3.7
0.8	125.5	±6.0	60.6	±3.9	124.8	±6.3	59.3	±4.1
0.6	134.4	±8.2	62.6	±4.7	134.5	±8.6	62.0	±4.9

an overview is given of all the average TAT and Offloading times for all cases with four different ITIFs: 1.2, 1.0, 0.8, and 0.6. An increment and decrement of 0.2 is chosen to systematically observe an effect on the system’s performance. Note that factor 1.0 is the original interarrival time interval.

It can be seen in Table 14 that, as expected, both the TAT and offloading time increase with decreasing ITIF. The difference between strategy 1 and strategy 2 is still negligible, which is confirmed by the Cliff’s-delta test. Even though the offloading times increase with smaller ITIF, this increase is not as substantial as the increase of the TATs. This suggests that it is again mainly the waiting times that influence the increase in TATs. Table 14 also shows that the standard deviation increases with decreasing interval.

In

Table 15. Cliff’s deltas for the TAT and offloading time for ITIF 0.6 and ITIF 1.2, when comparing strategies.

	Delta TATs		Delta ${\mathit{T}}_{\mathit{Offl}}$
	ITIF 0.6	ITIF 1.2	ITIF 0.6	ITIF 1.2
1A vs. 2A	0.004	0.056	0.12	0.018
1B vs. 2B	−0.026	0.042	0.09	0.007
1C u1 vs. 2C u1	−0.016	0.045	0.08	0.027
1C u7 vs. 2C u7	0.01	0.047	0.093	0.04

, the deltas for the TAT and $T_{Offl}$, calculated using the Cliff’s Delta statistic for ITIF 0.6 and ITIF 1.2, are shown. Even though the values in the table are all considered negligible, as they are below 0.147, there is a clear increase seen in the deltas of the offloading time.

7. Discussion

7.1. Discussion About the ‘Maximum Available’ Strategy

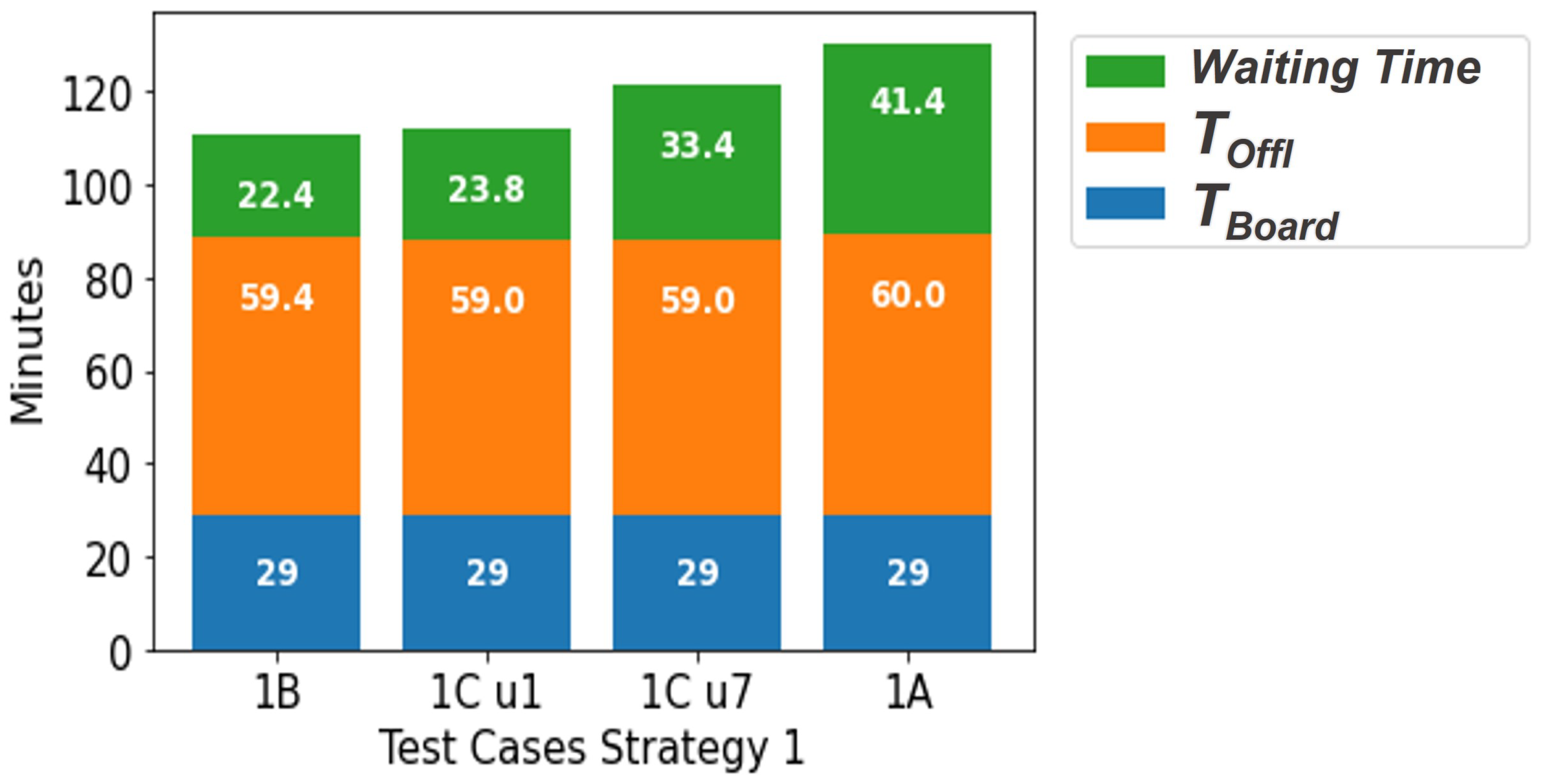
For each strategy, in all test cases the offloading time stays largely the same. In the ‘maximum available’ strategy, a factor that could influence a change in the offloading time is that the OC agent does not need to check the cargo content. Hence, offloading can start earlier. Comparing the two most extreme cases, scenario A and B, the average time difference for the start of offloading is 18 min. This can also be seen in Figure 6, which represents a timeline with three incoming flights. When the offloading of aircraft A is finished, the resources are available for aircraft B. On one hand, in scenario B, the first aircraft has just departed when the second aircraft arrives. The resources are available immediately. On the other hand, in scenario A, the first aircraft has not departed while the second aircraft arrives. The offloading of aircraft A has been finished, i.e., the resources are available to offload the second aircraft. However, the second aircraft still needs pax steps, and its content needs to be checked. For the first task, a driver is needed. This takes a longer time, as the first aircraft also needs a driver to remove its pax steps. This also contributes to the $T_{BPS}$ increase. For the second and third aircraft, it can be seen that even though the TAT is shorter, the offloading time differs. This suggests that the offloading can start earlier and therefore also finishes earlier. Nevertheless, this will not make a difference for aircraft B, as it can start offloading earlier as well.

7.2. Discussion About the Resource Allocation Strategy with Anticipation

In the resource allocation strategy with anticipation, the OC agent can make a resource allocation decision for aircraft A while taking the need for resources for aircraft B into account. This means that even though there are enough resources to start offloading aircraft A, the OC can decide to wait. The OC can also decide to give aircraft A the minimum amount of resources, despite more resources being available. The OC bases its decision on the earliest finish time for both aircraft A and B, and not the lowest offloading time.

The decrease in waiting times for increasing certainty in information can be explained by the availability of the OC agent. When the OC agent has knowledge of an incoming flight, it also has knowledge of that flight’s cargo content. This means that the OC does not need to go to the aircraft to check the cargo content. This, on one hand, decreases the waiting time $T_{BC}$. On the other hand, the OC is not leaving its office and is available to react to new tasks, thus decreasing the waiting times of other tasks. As other tasks are finished earlier, the resources are free at an earlier point in time. This, in its turn, also makes it possible to start a new task sooner.

In our study we evaluated three scenarios with unannounced flights: one large aircraft, all large aircraft, and all aircraft. The results showed that one unannounced aircraft did not have a visible effect on the TAT. The explanation for this is that the OC agent only needed to leave its office once, so the effects on other waiting aircraft because of the absence of the OC agent are not so strong. Seven unannounced aircraft, on the contrary, do have a clear effect on the average TATs and the average waiting times.

7.3. Discussion About the Interarrival Time Interval Factors

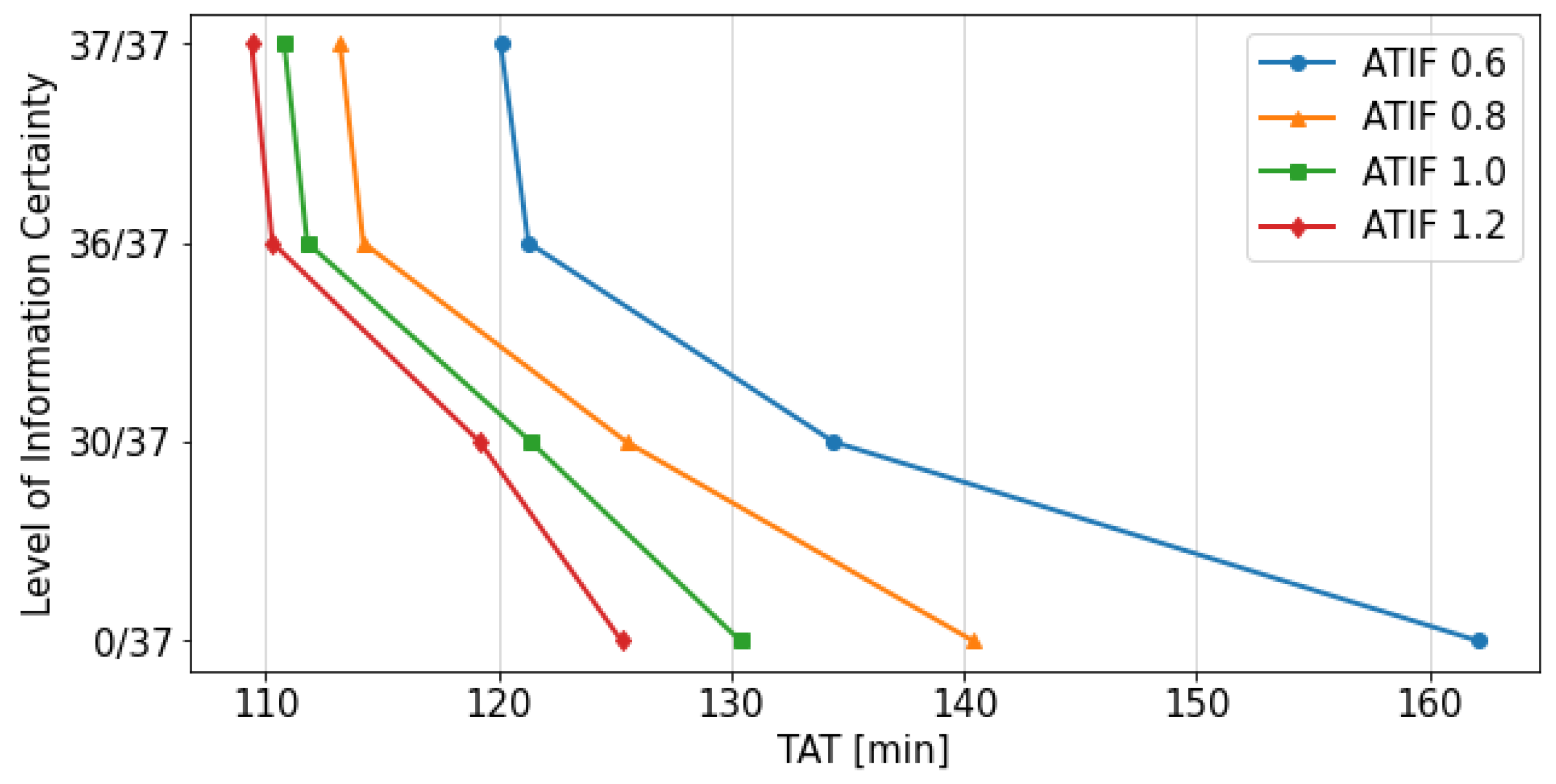
The results of the experiments with different ITIFs suggest that the waiting times were more affected than the offloading times. Analysing the results of the different ITIFs, the TAT increases with decreasing interarrival interval time (refer to Figure 7).

The difference in results between the strategies is negligible for all ITIFs. However, the increase in the deltas in Table 15 indicates that further increasing the ITIF results in a noticeable difference in offloading time between the two strategies. This can be explained by the airport being too congested. Waiting for more resources to become available in order to have faster offloading will always take longer than settling for the available and probably, minimum amount of resources. This is most likely also the reason why the offloading times increase when the airport is more congested.

7.4. Validation

Validation of agent-based simulation models in humanitarian logistics and emergency management presents many challenges. The validity of a simulation model is determined by the degree of model accuracy over its domain of applicability that is often defined by a set of relevant scenarios or experimental conditions. Model validation is a continuous process, which spans throughout the whole period of model development. In the early phases it is important to validate model assumptions, either objectively, using well-established theory and/or real data, or otherwise, subjectively, e.g., based on expert opinion. Some authors (e.g., [32]) emphasise the importance of defining valid humanitarian logistics scenarios to increase trust of practitioners in simulation models and, to this end, proposed methodologies. Calibration of simulation models for emergency management is also an important validation step. In this paper, the parameters of the agent-based model were calibrated using a mix of historical data and expert judgement, similarly to other papers in the area of crisis and disaster management (e.g., [33]). Sargent et al. [34] distinguish between the subjective and objective validation approaches. The subjective approach includes different forms of exploration of model behavior (e.g., by analysing input-output relations, exploring the model behaviour under extreme values of input variables, local and global sensitivity analysis). This form of validation was performed in this paper. Expert validation of the outcomes of a simulation model could also be considered a subjective form of validation. However, more advanced approaches of consensus building and integration of opinions of different experts could increase the confidence in the expert judgement. Furthermore, serious games, in which expert and non-expert participants are making decisions in the context of operational scenarios, are a valuable approach to validate a simulation model for disaster management applications [35]. The objective approach involves comparison to other models using statistical tests and procedures. Where applicable and possible, historical data from past disasters could be used to compare with simulated results.

7.5. Resilience

This study investigates the resilience of Saint Martin at two levels. The first level is the resilience of the island after the hurricane disaster. Many buildings and infrastructures were damaged, and the recovery process has been effective due, among other things, to ports and airports. Goods, food, and other resources have been carried by ships and planes and delivered to the island. Consequently, efficient airport operations contributed to the island community’s resilience. The second level is the airport level. Ongoing cargo and passenger handling operations can be significantly disturbed by unannounced incoming flights. These flights need to receive instructions regarding the use of runways, taxiways, parking spots, etc. The airport performance, which corresponds to the turnaround time in this study, can be impacted by unannounced incoming aircraft. The offloading coordinator needs to manage these aircraft and adapt plans to the new information.

Resilience can be seen as the capacity to anticipate undesirable situations and to be ready to efficiently respond to unknown events [36]. These unknown events can create disturbances in the system’s organization. This corresponds to the airport’s cargo handling operations as analyzed in the study: the OC can make a prediction regarding the resources needed by an incoming flight to unload its cargo and handle the passengers that need to be evacuated. The OC needs to adapt the resource allocation schedule in real time to any new unplanned flights. Our results showed that the offloading operations were only slightly impacted by one unannounced aircraft: the average offloading times remain constant. However, when more disruptions occur (7 or 37 unplanned flights), the system’s performance decreases. This corresponds to an increase in the turnaround time. The system extends its handling capacity until the decompensation occurs. At that stage, the system has exhausted its adaptive capacity, and the performance gracefully degrades. There is no collapse of the system in the investigated scenarios (i.e., the situation where aircraft cannot be unloaded); however, a significantly higher ITIF could make the airport performance collapse. This would be the case in the following conflicting situation: when incoming aircraft need to use the runway to land but there are no parking spots available, and at the same time aircraft on the ground need to use the runway to take off.

7.6. Study Limitations and Future Work

Due to the highly context-specific nature of hurricane impacts on airport operations, no standardized real-world datasets or baseline models are available for direct comparison. As such, the agent-based model is used as an exploratory tool to assess plausible operational dynamics under degraded conditions.

Future extensions of the model could incorporate a priority mechanism to differentiate between civilian and military cargo handling. This would allow for more realistic representation of airport operations during disaster scenarios, particularly when military aircraft are involved in critical relief efforts. Implementing such features would require access to detailed data on military protocols and procedures, which were beyond the scope of the current study.

Although this research aimed to be as close to reality as possible, assumptions needed to be made. One promising avenue for addressing computational challenges and enabling more extensive scenario testing is the use of surrogate modelling techniques within ABMS, as explored in [37]. For one, the evacuation operations are modeled as a time penalty. The evacuation operations are likely to cause more delays. Secondly, it is assumed that when the OC agent has knowledge of the incoming flight, that knowledge is always correct. Unfortunately, in a real situation that is not always the case. The same applies to the communication between all agents. In reality miscommunications happen, especially in such a complex system. Furthermore, in the future, the number of unannounced flights could be varied to examine which number of unannounced flights gives significant results. In addition, different case studies could be tested, as well as the effects of miscommunication on TAT of the aircraft. significant To study the influence estimation and anticipation have on the performance of the system, the ITIF could be increased even more. Additionally, other anticipation strategies, e.g., optimizing for offloading time, could be examined as well.

8. Conclusions

In this research an agent-based model was developed to gain understanding of the effects of incomplete knowledge of incoming flights with different resource allocation strategies, on the performance of the cargo handling operations in an airport after a natural disaster event. In the model realistic offloading strategies with different degrees of information uncertainty were implemented. Model calibration and verification was performed with experts in the field. The model performance was measured by the average turnaround time, which was split in offloading time, boarding time and the cumulative waiting times.

The evaluation of the performance of the TAT was performed by simulating different scenarios while implementing the identified strategies. The simulation results showed that the effect of one unannounced aircraft on the total average TAT is negligible. If all seven large aircraft arrive unannounced, the TATs increased significantly.

Furthermore, in all experiments the difference in offloading time and boarding time was negligible, whereas the waiting times were influenced the most. With decreasing knowledge of incoming flights, the waiting times increase. This was largely because the OC agent needed to walk to each unannounced aircraft to check its content. When the OC agent is not at its office, it cannot react to new tasks.

Additionally, it can be concluded that the difference between the two resource allocation strategies was negligible for this particular case study. When changing the interarrival time interval between the aircraft, these effects were still insignificant. However, the differences between the outcomes of different scenarios do increase when increasing the interarrival time interval. This suggests that when this interarrival time interval is widened more, an effect might be noticeable between the two resource allocation strategies. Nevertheless, the results suggest that, for this case study, the maximum available resource allocation strategy would have been sufficient.