Force–Position Coordinated Compliance Control in the Adhesion/Detachment Process of Space Climbing Robot

Abstract

Adhesion-based space climbing robots, with their flexibility and multi-functional capabilities, are seen as a promising candidate for in-orbit maintenance. However, challenges such as uncertain adhesion establishment, unexpected detachment, and body motion unsteadiness in microgravity environments persist. To address these issues, this paper proposes a coordinated force–position compliance control method that integrates novel adhesion establishment and rotational detachment strategies, integrated into the gait schedule for a space climbing robot. By monitoring the foot-end reaction forces in real time, the proposed method establishes adhesion without risking damaging the spacecraft exterior, and smooth detachment is achieved by rotating the foot joint instead of direct pulling. These strategies are dedicated to reducing unnecessary control actions and, accordingly, the required adhesion forces in all feet, reducing the possibility of unexpected detachment. Climbing experiments have been conducted in a suspension-based gravity compensation system to examine the merits of the proposed method. The experimental results demonstrate that the proposed rotational detaching method decreases the required pulling force by 65.5% compared to direct pulling, thus greatly reducing the disturbance introduced to the robot body and other supporting legs. When stepping on an obstacle, the compliant control method is shown to reduce unnecessarily aggressive control actions and result in a reduction in relevant normal and shear adhesion forces in the supporting legs by 44.8% and 35.1%, respectively, compared to a PID controller.

1. Introduction

Space robots have effectively aided astronauts in extravehicular tasks, including solar panel repairs, component upgrades, and cargo retrieval, highlighting their potential for future space assembly and spacecraft life extension efforts [1,2]. Although most space robots are robotic arms mounted on spacecraft exteriors (e.g., Canadarm2 [3], Chinese Space Station Arm [4]), mobile space robots offer promising solutions for future large-scale infrastructure maintenance due to their lightweight design and extensive range. Mobile space robots can be categorized by their mobility mechanisms, which include free-flying (e.g., repair robots from the Phoenix Program [5]) and climbing (anchor-based or adhesion-based). While free-flying robots offer operational flexibility, they are constrained by fuel consumption, control challenges, collision risks, and susceptibility to disturbances [6]. Anchor-based climbing robots rely on pre-installed anchor points to ascend spacecraft exteriors [7,8]. This method is considered safe but involves complex mechanical interfaces, high-weight penalties, and limits to flexibility and operational scope. In contrast, adhesion-based climbing robots do not require anchor points, offer greater mission flexibility, and employ multi-limbed grasping, making them highly promising for microgravity environments [9,10].

As for adhesion-based climbing robots, the foot-end adhesive material and control schemes are crucial for ensuring safety [11,12,13]. Among various adhesion techniques, dry adhesion stands out due to its ability to operate in microgravity environments, where alternative techniques such as wet adhesion [14], vacuum suction [15], or electromagnetic forces [16] are infeasible due to their reliance on a wet environment, atmospheric pressure, and conductive surfaces, respectively. Instead, dry adhesion utilizes thousands of microfibers to generate adhesive forces via van der Waals interactions [17]. A notable demonstration of its feasibility was seen in 2015, when five geckos aboard Russia’s “Foton-M4” satellite successfully crawled on inner surfaces in microgravity using dry adhesion [18]. This milestone underscored the potential of such materials for space climbing robots.

However, using dry adhesion materials in space climbing robots imposes unique challenges due to the constraints of microgravity and the properties of the adhesion materials [19,20]. Specifically, the controller should address three challenges: (1) The normal pressure at the foot-end should reach a certain threshold before the establishment of adhesive force is confirmed. (2) The controller should avoid unnecessarily aggressive control actions, which impose high loads on foot-end adhesion and increase the risk of unexpected detachment. (3) The detachment of adhered foot-ends should introduce minimal disturbance to the robot dynamics.

Several studies have attempted to address some aspects of the aforementioned challenges. AnyClimb-II [21] focused on the linkage design of an adhesion-based climbing robot with a compliant motion but did not fully address the challenge of confirming the establishment of adhesion. Ribeiro et al. [22] proposed optimized foot-end swing trajectories to reduce the required adhesive forces, and in subsequent studies [23] they introduced a reaction-aware motion planning method that uses the robot’s redundant degrees of freedom to distribute the given momentum changes, thereby reducing momentum shifts during microgravity locomotion. However, their study focused primarily on the motion planning of the robot, instead of the controller of the robot legs. In addition, the authors are not aware of any study addressing the issue of revoking the foot-end adhesion in microgravity conditions.

To address the challenges of achieving adhesion establishment and reducing force disturbance during detachment, this paper proposes a coordinated force–position compliance control method aimed at managing both the adhesion and detachment processes of space climbing robots, which incorporates two key strategies: compliant adhesion establishment and a rotation detachment strategy. By equipping the robot’s joints with torque sensors, the system perceives the contact force to obtain real-time normal pressure values, which serve as feedback for controlling the robot’s joint motions, enabling both compliant control and secure adhesion establishment for each leg. During detachment, a rotational motion, instead of direct pulling, is adopted to reduce the required control effort in the foot-ends for the detaching action. Based on these strategies, in addition to the conventional support and swing phases of climbing robots, attachment and detachment phases are introduced. These additional phase are dedicated to smooth transitions during attaching and detaching actions, which help prevent oscillations caused by step responses in pose within a non-structured microgravity environment.

The paper is structured as follows: Section 2 describes the task scenario alone with the robot’s kinematic and dynamic models. Section 3 details the method design, which lays the foundation for the control theory simulations in Section 4. Section 5 constructs a microgravity experimental system to validate the effectiveness and stability of the proposed method in enabling the robot to climb on spacecraft surfaces in a simulated microgravity environment. Finally, Section 6 presents the conclusions of the study.

2. Robot Modeling

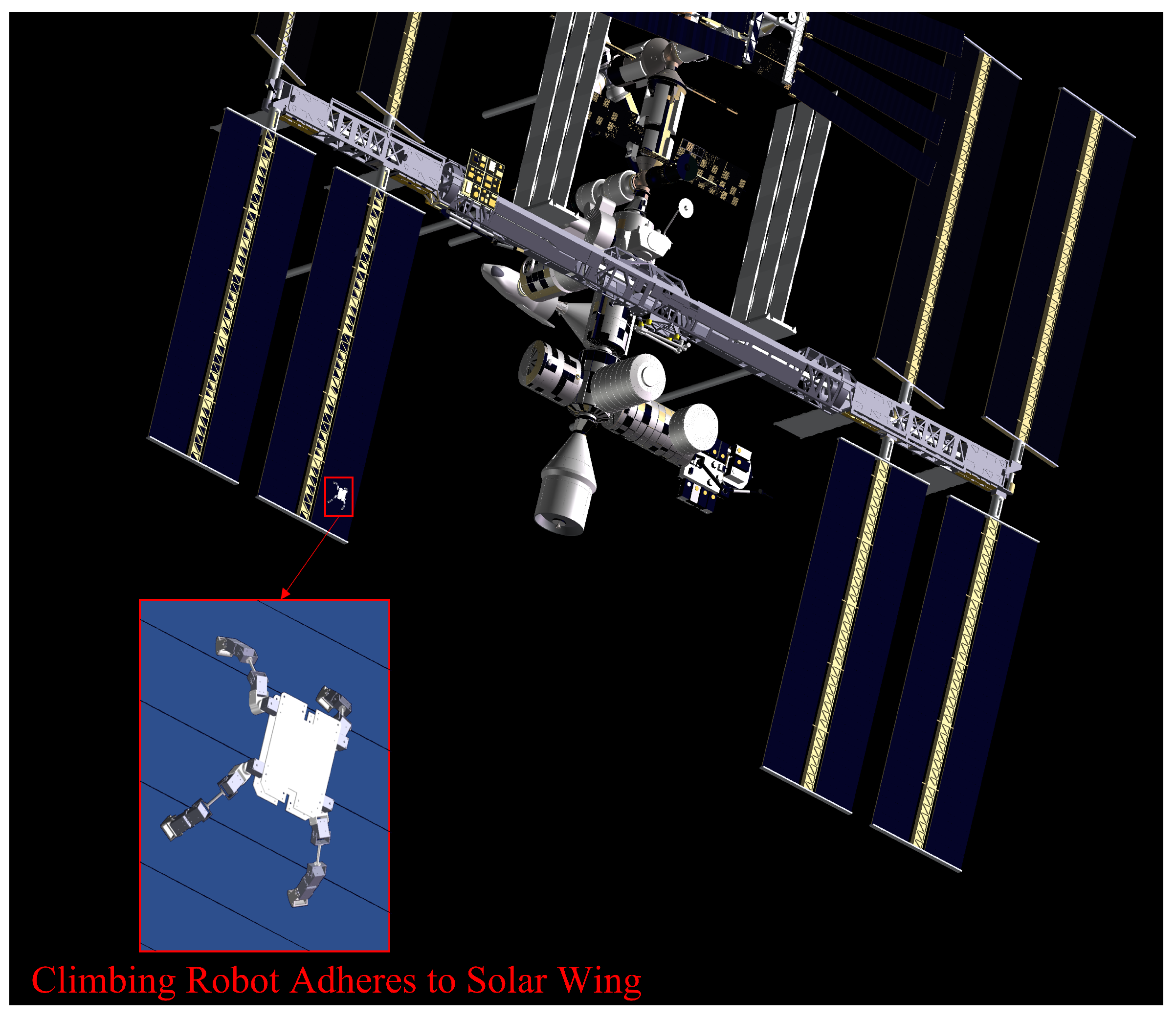
2.1. Task Scenario Description

For space climbing robots tasked with performing extravehicular inspection and maintenance on the surface of a space station, the robot must be capable of stable attachment and climbing on the spacecraft’s exterior surface. A significant challenge is overcoming the limitations of traditional position feedback controllers, which often fail to ensure a sufficient normal force for foot attachment and detachment. This can result in insufficient adhesion, incomplete detachment, or even destabilization of the robot’s overall posture during movement.

The spacecraft’s outer surfaces are typically covered with solar panels and thermal control multi-layer insulation, which are prone to damage from space debris, making inspection and repair tasks necessary. Solar panels are generally composed of hard, smooth glass, as shown in Figure 1, which represents the primary working environments.

Compared to small-scale space climbing robots, the space station weighs 420 tons, possessing far greater inertia. The space station uses its attitude control system to maintain a stable posture. As a result, the movement of the robot across the surface of the space station has a negligible impact on the station itself. In this paper, we assume the robot operates on a stable platform, disregarding any influence on the spacecraft’s angular momentum.

2.2. Kinematic Modeling

The overall structure of the space climbing robot is depicted in Figure 2a, and its key technical features are outlined as follows.

• Each leg of the robot is configured with a yaw–pitch–pitch–pitch joint arrangement. The first three degrees of freedom of the leg allow the controller to control the adhesive foot in Cartesian space, ensuring free movement within the workspace and enabling floating-base torso posture adjustment.
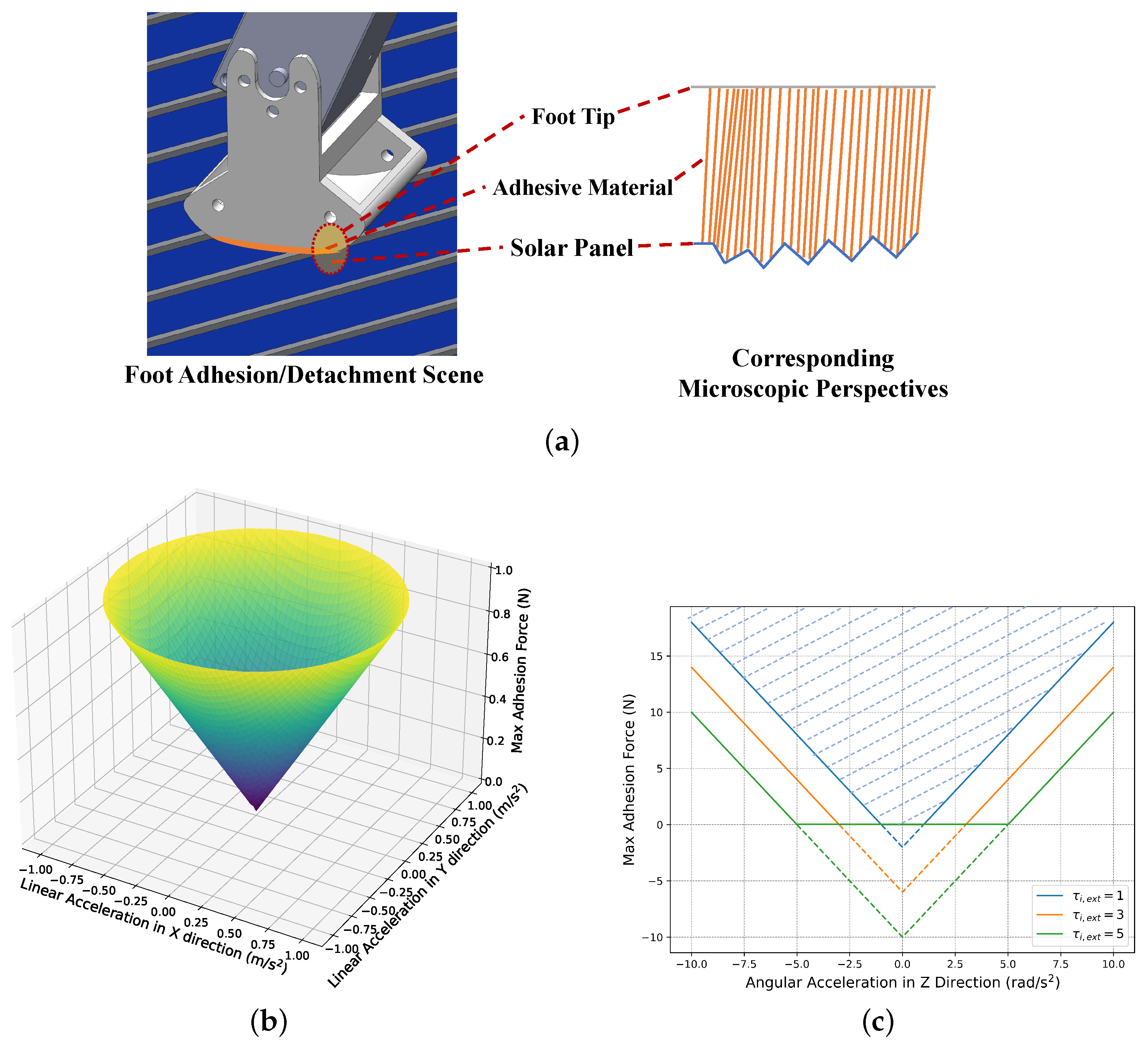
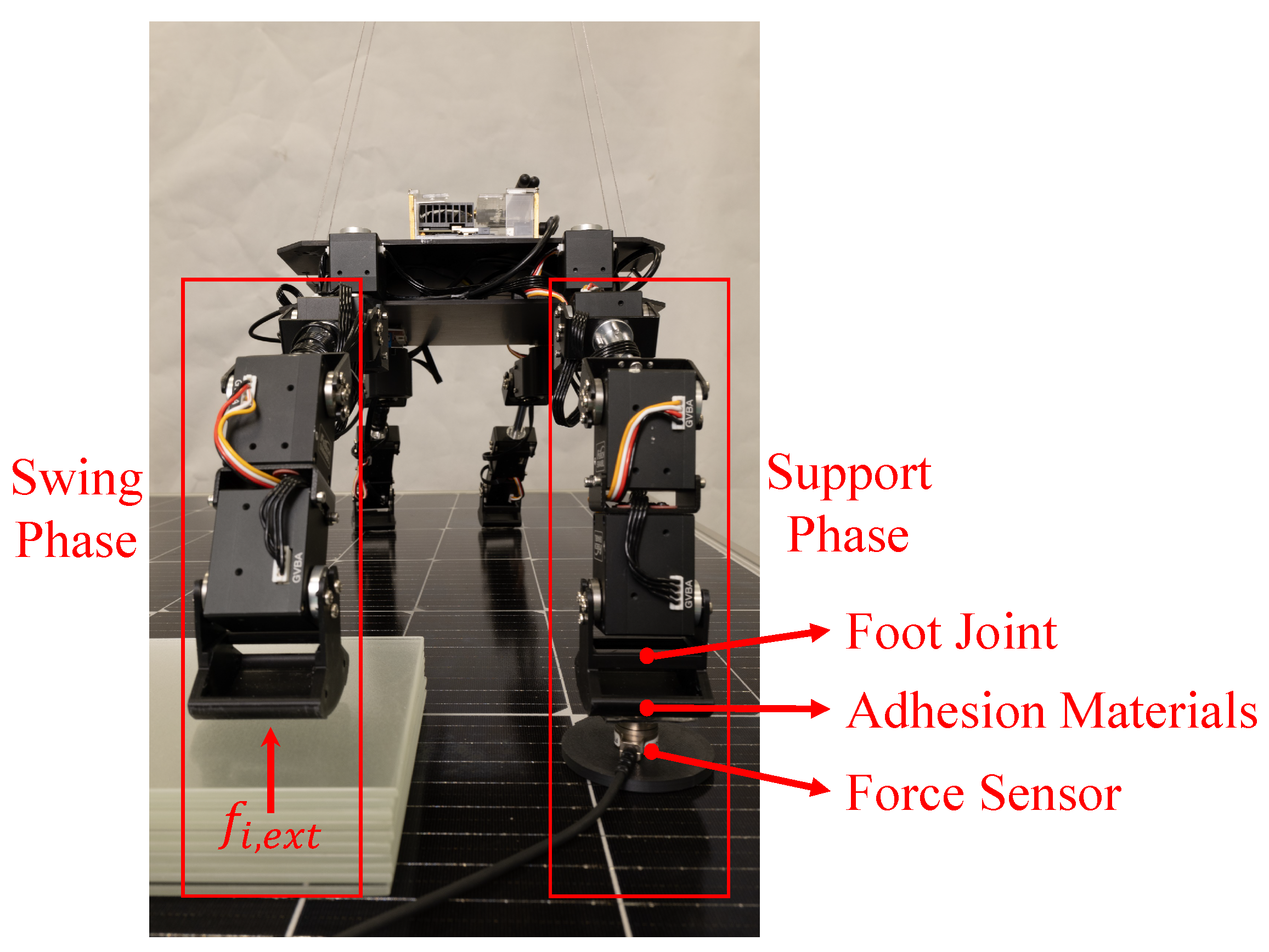
• Unlike traditional spherical point-contact foot models, the robot’s foot is equipped with adhesive material featuring bio-inspired micro-nano structures that create surface contact with the environment. The inclusion of redundant degrees of freedom allows the motors to rotate the foot, controlling its inclination angle. This ensures that during the adhesion process, the adhesive material applies force precisely along the normal direction of the contact surface, while also allowing controlled rotational detachment.

To clarify the leg configuration in the following sections, the robot’s four legs are numbered clockwise as i, where $\mathit{i}\in \{1,2,3,4\}$, and the joints from the body to the end-effector are labeled j, where $\mathit{j}\in \{1,2,3,4\}$, as shown in Figure 2b. The pair $(i,j)$ represents the j-th joint of the i-th leg. The robot’s body-fixed coordinate frame $\left\{\mathbf{B}\right\}$ is defined as $Bxyz$, where the origin B is at the robot’s center of mass, the x-axis points in the direction of the robot’s forward movement, and the z-axis is perpendicular to the robot’s body plane. The y-axis follows the right-hand rule. The space station coordinate frame $\left\{\mathbf{O}\right\}$ is defined as $Oxyz$, fixed to the space station structure.

The Denavit–Hartenberg (DH) method [24] is used to model the robot’s kinematics, enabling the transformation of joint angles and end-effector positions under the controller for both forward and inverse kinematic calculations. The forward kinematics for the i-th leg are analyzed using modified DH parameters, as summarized in

Table 1. Modified Denavit–Hartenberg parameters for the four links of leg i.

Link	${\mathit{\alpha }}_{\mathit{i},\mathit{j}}$	${\mathit{a}}_{\mathit{i},\mathit{j}}$	${\mathit{d}}_{\mathit{i},\mathit{j}}$	${\mathit{\theta }}_{\mathit{i},\mathit{j}}$
j = 1	$-\pi /2$	$l_1$	0	${\theta }_{i,1}$
j = 2	0	$l_2$	0	${\theta }_{i,2}$
j = 3	0	$l_3$	0	${\theta }_{i,3}$
j = 4	0	$l_4$	0	${\theta }_{i,4}$

$$\begin{array}{cc}\hfill {}_j{}^{j-1}{T}_i& =Rot(x_{i,j-1},{\alpha }_{i,j-1})·Trans(x_{i,j-1},a_{i,j-1})·Rot(z_{i,j},{\theta }_{i,j})·Trans(z_{i,j},d_{i,j})\hfill \\ \hfill & =\left[\begin{array}{cccc}cos{\theta }_{i,j}& -sin{\theta }_{i,j}& 0& a_{i,j-1}\\ sin{\theta }_{i,j}cos{\alpha }_{i,j-1}& cos{\theta }_{i,j}cos{\alpha }_{i,j-1}& -sin{\alpha }_{i,j-1}& -d_{i,j}sin{\alpha }_{i,j-1}\\ sin{\theta }_{i,j}sin{\alpha }_{i,j-1}& cos{\theta }_{i,j}sin{\alpha }_{i,j-1}& cos{\alpha }_{i,j-1}& d_{i,j}cos{\alpha }_{i,j-1}\\ 0& 0& 0& 1\end{array}\right]\hfill \end{array}$$

(1)

${\theta }_{i,j}$, $d_{i,j}$, $a_{i,j}$, and ${\alpha }_{i,j}$ represent the joint angle, link offset, link length, and link twist angle of the i-th leg, respectively. The transformation matrix ${}_j{}^{j-1}{T}_i$ represents the homogeneous transformation of the j-th joint’s coordinates relative to the $j-1$-th joint’s coordinates. The transformation of the end-effector’s position with respect to joint (i,1)’s coordinate frame is given by the following:

$${}_e{}^1{T}_i={}_2{}^1{T}_i{}_3{}^2{T}_i{}_4{}^3{T}_i{}_e{}^4{T}_i=\left[\begin{array}{cccc}{n}_x& o_x& a_x& p_x\\ n_y& o_y& a_y& p_y\\ n_z& o_z& a_z& p_z\\ 0& 0& 0& 1\end{array}\right]$$

(2)

2.3. Dynamic Analysis

Without gravity, the dynamic model simplifies to an inertia-dominated system using the Newton–Euler equations. For floating-base underactuated robots with n joints, we aim to describe the relationship between the foot-end contact wrench with the robot’s centroidal momentum [25]. The robot’s linear and angular momenta are defined as $P\in {\mathbb{R}}^3$ and $L\in {\mathbb{R}}^3$, respectively. The interaction between the robot’s foot and the environment surface is simplified into contact forces $f_{i,ext}\in {\mathbb{R}}^3$ and torques ${\tau }_{i,ext}\in {\mathbb{R}}^3$ applied at specific contact points for each foot-end, as shown in Figure 2a. The relationship between the robot’s centroidal momentum rates and external forces and torques is as follows [26]:

$$m_t{\ddot{r}}_c=\sum _{i=1}^4{f}_{i,ext}$$

(3)

$$\dot{L}=\sum _{i=1}^4[(r_i-r_c)\times f_{i,ext}+{\tau }_{i,ext}]$$

(4)

$$L=Av$$

(5)

where $m_t$ is the total mass of the robot, $r_i\in {\mathbb{R}}^3$ is the position of the i-th leg’s contact point, and $r_c\in {\mathbb{R}}^3$ is the position of robot’s center of mass. $A\in {\mathbb{R}}^{3\times (n+6)}$ is the centroidal angular momentum matrix. $v\in {\mathbb{R}}^{n+6}$ is the robot’s posture velocity for the floating base and joints.

As the linear and angular momenta of the center of mass are influenced by the resultant forces and torques from all feet, significant variation in these quantities may prevent the foot from providing sufficient adhesive force and torque to maintain contact. If, at any given moment, the required adhesion force and torque exceed the capacity of the adhesive material, the robot will begin to lose contact with the surface. To mitigate this, a quasi-static walking gait should be adopted, ensuring that at least three feet stay attached, maximizing adhesion limits. The movement of the robot’s foot-ends is subject to several constraints:

$$|f_{i,ext}| \le f_{max}\forall i\in \{1,2,3,4\}$$

(6)

$$|{\tau }_{i,ext}| \le {\tau }_{max}\forall i\in \{1,2,3,4\}$$

(7)

where $f_{max}\in {\mathbb{R}}^3$ is the maximum adhesive force of the foot-end, and ${\tau }_{max}\in {\mathbb{R}}^3$ is the maximum adhesive torque of the foot-ends.

The risk of the robot detaching from the surface is closely related to the rate of change of its linear and angular momenta. The constraint on the linear acceleration of the center of mass relative to the maximum adhesive force demands that the acceleration in the direction of motion remains within a cone, with its apex at the origin and height defined by the maximum adhesive force, as shown in Figure 3b. The cone’s slope is determined by the robot’s total mass $m_t$. A greater mass results in a steeper slope. Figure 3c illustrates the constraint between the angular acceleration and adhesive force, where different colored curves represent various maximum adhesive torques. Given a maximum adhesive force, the angular acceleration must remain within the shaded region enclosed by the adhesive force curves.

3. Control Method Design

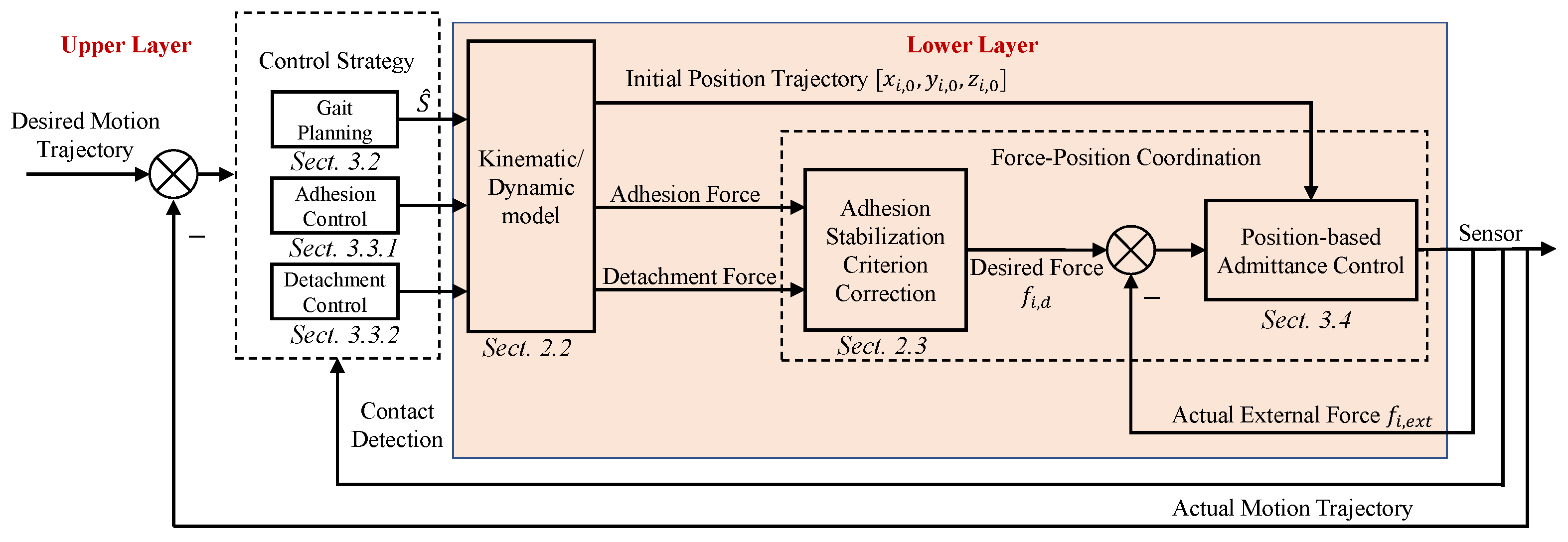
3.1. Hierarchical Modular Control Architecture

The control framework of the space climbing robot adopts a modular hierarchical design, as depicted in Figure 4.

The control architecture consists of two levels: the upper layer and the lower layer. The upper layer includes the input module, control strategy module, and sensing module. Inputs include the desired motion trajectory and the initial gait sequence. The control strategy uses sensor-detected forces for contact detection and gait-phase switching. The controller applies different control strategies based on the current phase. The sensing module utilizes force sensors, joint encoders, and an inertial measurement unit (IMU) for feedback. The lower layer contains the kinematics/dynamics module, adhesion stability correction, and force–position coordination control module. The kinematics/dynamics and adhesion stability correction modules were introduced in Section 2, while the force–position coordination control module integrates multi-sensor data for control. This closed-loop system combines outer-loop force control with inner-loop position control to achieve controlled motion.

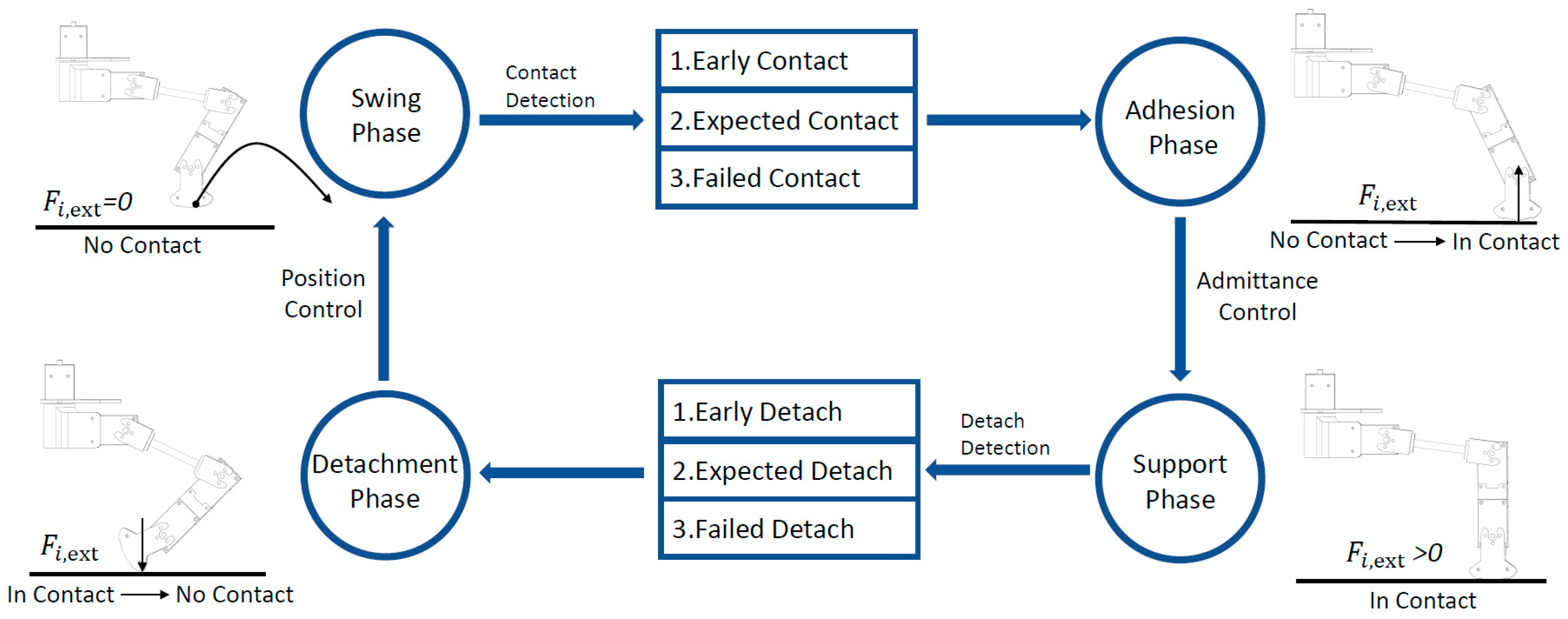
3.2. Four-Phase Gait Planning

Stable motion for the space climbing robot imposes stringent requirements on gait planning. As analyzed in Section 2.3, to maximize adhesion force limits the robot must maintain at least three feet in contact, allowing only one leg in the swing phase at a time, following the 1–3–2–4 sequence. In microgravity, once a leg completes its swing phase, there is a risk of the foot failing to adhere, causing detachment. Additionally, after the support phase ends, detachment forces can induce body posture oscillations. Therefore, the robot’s gait planning needs to be optimized in two ways: first, by ensuring stable adhesion at the end of the swing phase; and second, by ensuring stable detachment at the end of the support phase.

The single-leg gait design of the robot is illustrated in Figure 5, where the stride cycle ${\widehat{S}}_{stride}$ consists of the support phase ${\widehat{S}}_{st}$, swing phase ${\widehat{S}}_{sw}$, adhesion phase ${\widehat{S}}_{ad}$, and detachment phase ${\widehat{S}}_{de}$, such that ${\widehat{S}}_{stride}={\widehat{S}}_{st}+{\widehat{S}}_{sw}+{\widehat{S}}_{ad}+{\widehat{S}}_{de}$. By integrating the adhesion and detachment phases into the gait cycle and using force sensors for ground-contact detection, the robot can detect the contact status in real time and switch between phases precisely, allowing it to adapt to more complex environments.

3.3. Force-Based Outer-Loop Controller Design

3.3.1. Perception-Based Adhesion Control

The magnitude of the preloading contact force is an indicator of whether the robot is adhering to the surface. By applying the Jacobian matrix of the current joint space state, the joint motor torques are mapped to end-effector contact forces, allowing the robot to detect the contact state.

$$f_{i,ext}={}_O{}^{B}R{J}_i^{-T}{\tau }_{i,joint}$$

(8)

For the i-th leg, ${\tau }_{i,joint}$ represents the generalized torque vector, $J_i$ is the end-effector Jacobian matrix, and ${}_O{}^{B}R$ is the rotation matrix between the environment coordinate frame and the robot body coordinate frame. First, the robot’s baseline torque data are collected when there is no contact throughout the entire gait cycle. During normal operation, variations in the contact force relative to the baseline data during specific phases are analyzed. By monitoring the peak of the contact-force variation, the timing of contact with the environment can be determined. If the actual peak occurs in an earlier or non-existent contact phase, premature or failed contact is identified.

For adhesion control on stepped terrain, the robot relies on sensor feedback. In a zero-gravity environment, the robot’s pitch angle relative to the environment coordinate frame remains unaffected by gravity and does not require center-of-mass adjustments. However, during the foot-end adhesion phase, the foot contact point must be perpendicular to the surface’s normal direction. This ensures foot contact with the surface, thereby maximizing adhesion. The robot’s real-time posture changes are detected using an IMU. By gathering pitch angle data, the robot’s posture is continuously monitored, and the foot-end joint is adjusted by compensating for the pitch angle ${\theta }_{i,pitch}$ to maintain alignment with the surface normal.

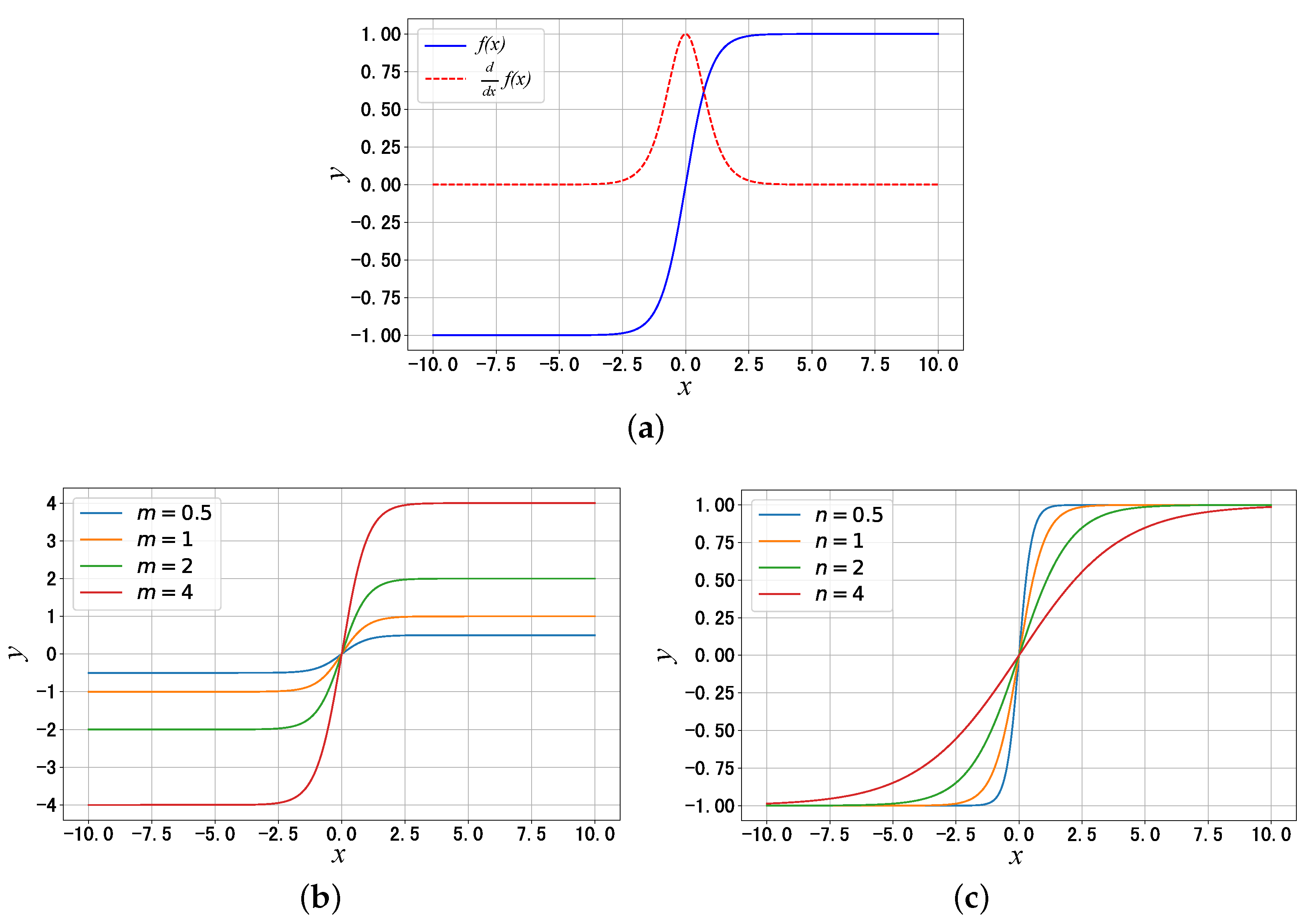
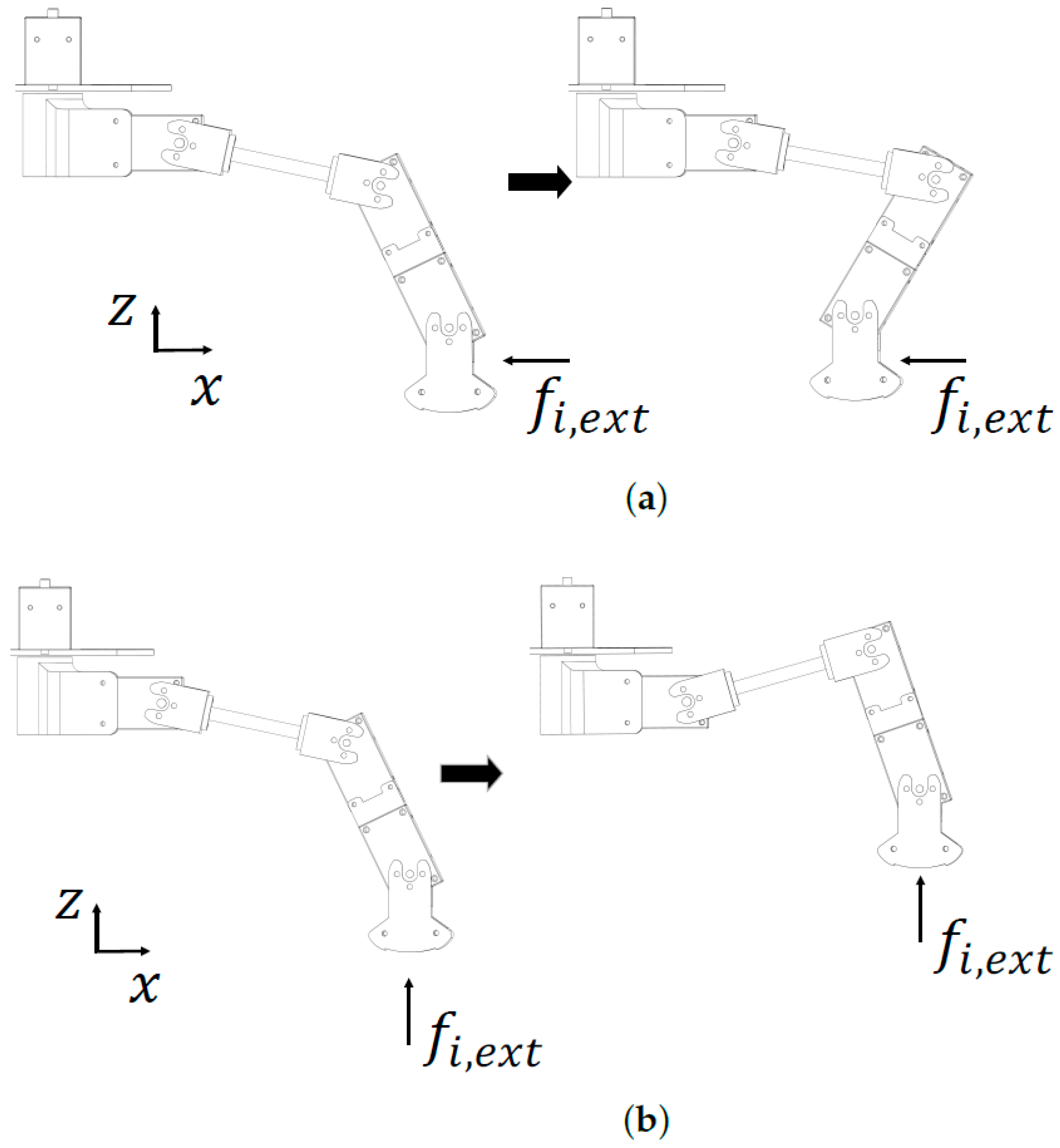
3.3.2. Rotational Detachment Control

At the beginning of the support phase, the robot maintains its motion by applying adhesive forces and torques. During this stage, the joint motors at the robot’s legs experience slow angular changes. As the support phase progresses, preparing for the upcoming swing phase, the joint motors make rapid angular adjustments, rotating from their alignment with the surface normal to a specific angle, eventually achieving detachment during the detachment phase. A tanh-like activation function is proposed to describe the time-varying behavior of the joint angles at the foot. The tanh function, shown in Equation (9), is parameterized by m and n, which control the amplitude and scaling of the function, respectively. These parameters adjust the range of the function’s output and input scaling. When the input variable x is near zero, the derivative of the tanh-like function becomes large, resulting in significant variation. As x increases, the derivative decreases, and the function approaches saturation, as illustrated in Figure 6.

$$f\left(x\right)=m·tanh\left(x\right)=m·{\displaystyle \frac{1-e^{-2(x/n)}}{1+e^{-2(x/n)}}}$$

(9)

Since the joint angle transitions are continuous, a ‘neutral point’ exists in the joint space, determined by the joint angles during the gait phases. Before reaching this neutral point, the leg remains in the support phase. Once the neutral point is reached, the foot structure starts rotating, transitioning from the support phase to the detachment phase, as depicted in Figure 7.

To analyze the motion of the i-th leg of a quadruped robot, the foot joint angle ${\theta }_{i,4}$ is defined as a function of the (i,2) and (i,3) joint angles ${\theta }_{i,2}$ and ${\theta }_{i,3}$. The specific expression is given by

$${\theta }_{i,4}=\left\{\begin{array}{cc}\lambda -({\theta }_{i,2}+{\theta }_{i,3})\hfill & {\theta }_{i,2}+{\theta }_{i,3}\le \lambda \hfill \\ m·{\displaystyle \frac{1-e^{-2[({\theta }_{i,2}+{\theta }_{i,3}-\lambda )/n]}}{1+e^{-2[({\theta }_{i,2}+{\theta }_{i,3}-\lambda )/n]}}}\hfill & {\theta }_{i,2}+{\theta }_{i,3}>\lambda \hfill \end{array}\right.$$

(10)

where $\lambda$ represents the sum of the $(i,2)$ and $(i,3)$ joint angles at the neutral point, which is set to $\lambda ={90}^{°}$, with amplitude factor $m={20}^{°}$ and scaling factor n = 2.

As shown in Figure 8, the robot’s gait cycle ${\widehat{S}}_{stride}$ lasts 10 s. Taking the first leg $i=1$ as an example, after the foot detaches at the end of the previous cycle, the next gait cycle starts with a 2.5-second transition from the detachment phase to the swing phase, enabling the forward movement of a single leg. This process continues until the foot-end contacts the surface, achieving adhesion. During this phase ${\theta }_{i,2}+{\theta }_{i,3}<\lambda$ and the foot is aligned with the surface normal. The value of ${\theta }_{i,2}+{\theta }_{i,3}$ gradually increases until it reaches $\lambda$, at which point the leg transitions from the support phase to the detachment phase, completing the rotational detachment of the foot from the environment.

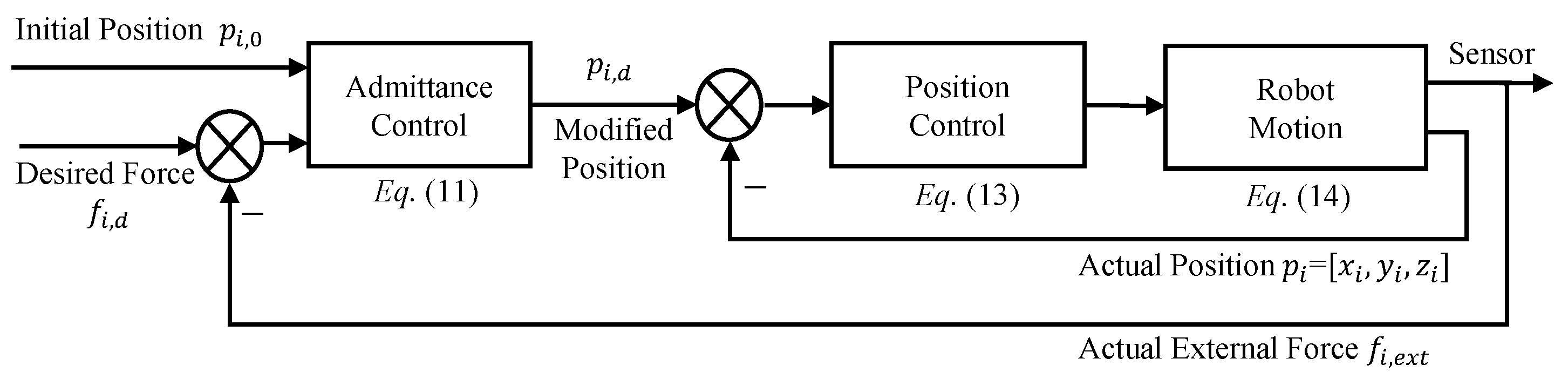
3.4. Position-Based Inner-Loop Admittance Controller Design

Rigid contact between the robot and the environment can lead to vibrations and oscillations, where excessive contact forces may potentially damage the surface structures of the space station or solar panels. For adhesion-based climbing robots, rigid collisions increase the risk of unexpected detachment during motion. External disturbances, such as changes in terrain and inertial forces generated by acceleration or deceleration, cause the controller to command aggressive control actions to achieve its originally desired position. To address this issue, admittance control is implemented as it can dynamically modify control objectives based on external forces, providing virtual compliance in the Cartesian space [27]. How external force modifies the desired position is presented in Equation (11) and illustrated in Figure 9.

$$f_{i,d}-f_{i,ext}=M_i({\ddot{p}}_{i,d}-{\ddot{p}}_{i,0})+D_i({\dot{p}}_{i,d}-{\dot{p}}_{i,0})+K_i(p_{i,d}-p_{i,0})$$

(11)

The compliant controller parameters for the i-th leg are denoted as $M_i$, $D_i$, and $K_i$, respectively. These parameters are an analogy of a spring–mass–damper system in terms of how the control objective changes. The acceleration, velocity, and position of the i-th leg’s end-effector in the direction of motion under the initial conditions are represented by ${\ddot{p}}_{i,0}$, ${\dot{p}}_{i,0}$, and $p_{i,0}$ while the desired values under external forces are denoted as ${\ddot{p}}_{i,d}$, ${\dot{p}}_{i,d}$, and $p_{i,d}$, respectively. $f_{i,d}$ is the desired interaction force that the robot is expected to apply during the interaction. One can solve Equation (11) to obtain the updated desired position $p_{i,d}$, which is then fed to the robot’s joint controllers, such as a PID controller.

Figure 10 illustrates the block diagram for the position-based admittance controller. The position controller receives the corrected desired trajectory from the admittance controller, and the position error is represented by Equation (12).

$$e_i=p_{i,d}-p_i$$

(12)

$$f_{i,con}=k_p{e}_i+k_i\int e_{i}dt+k_d{\displaystyle \frac{d{e}_i}{dt}}$$

(13)

$$m_i{\ddot{p}}_i=f_{i,ext}+f_{i,con}$$

(14)

By adjusting the system’s admittance parameters, the robot can exhibit the desired dynamic behavior during interactions with the environment [28]. The expected control force generated by the position controller is defined as $f_{i,con}$, as given in Equation (13). The system’s motion equation can be written as Equation (14), where $m_i$ denotes the mass of the i-th leg, and ${\ddot{p}}_i$, ${\dot{p}}_i$, and $p_i$ are the current acceleration, velocity, and position of the i-th leg’s end-effector.

4. Simulation Experiments

4.1. Experimental Setup

In order to evaluate the robot’s response to external forces under the admittance controller, a simulation experiment is performed on a single leg. Given that $M_i$, $D_i$, $K_i$ are all diagonal positive definite matrices, we can decouple the forces applied at the end effector along the x, y, and z axes to investigate the specific impact of forces in each direction on the model. This force application method simulates potential instantaneous external disturbances the robot may encounter in real-world operations, effectively assessing the model’s dynamic characteristics and adaptability.

4.2. Control Simulation

The settings of the “mass”, “damping”, and “stiffness” parameters in the admittance controller significantly affect the system’s dynamic response. With baseline values of $M_{i,z}$, $D_{i,z}$, and $K_{i,z}$ all set to 1, the effects of various admittance parameters on the end-effector’s desired position under the same external force $f_{i,z}$ are analyzed, as shown in Figure 11. Increasing the admittance mass parameter leads to a longer response time at the foot-end. Higher damping decreases the expected displacement at the foot-end while increasing stiffness accelerates the system response but introduces displacement oscillations. To handle the climbing motion on rigid solar panel surfaces during on-orbit maintenance tasks, the admittance parameters are set to 1, 10, and 20 for mass, damping, and stiffness, respectively, to minimize the foot-end displacement lag while reducing the robot’s vibration.

Taking one leg’s force in the $xz$-plane as an example, as shown in Figure 12, the joint torque responses under external forces in different directions are analyzed. The mass, damping, and stiffness parameters for the x and z directions are set to $M_{i,x}=M_{i,z}=1$, $D_{i,x}=D_{i,z}=1$, $K_{i,x}=K_{i,z}=1$.

Figure 13 displays the decoupled external force variation curves and the corresponding joint motor torque responses. From this figure, it is evident that a pure position control system strictly tracks the set position. When an external force is applied, the controller generates significant joint torques to counteract the force and maintain the set position. In contrast, the admittance control system provides a smoother dynamic response to force variations, reducing the impact of sudden forces on joint torque. For instance, under an external force in the x-direction, the peak torque ${\tau }_{i,2}$ decreased from 0.156 N·m to 0.117 N·m, a reduction of 25.32%, ${\tau }_{i,3}$ decreased from 0.108 N·m to 0.077 N·m, a reduction of 28.83%, ${\tau }_{i,4}$ decreased from 0.030 N·m to 0.021 N·m, a reduction of 30.41%. This capability allows the robot to maintain foot-end adhesion with reduced mechanical stress and impact, enhancing overall stability.

4.3. Summary

First, we conducted simulations to assess the robot’s compliant motion response under decoupled external forces and qualitatively analyze the admittance parameters applicable to the space climbing robots. Subsequently, we compared position-based admittance control with ideal pure position control. The simulation results showed that the admittance controller reduced the joint torque fluctuations by at least 25%, lowering joint mechanical stress and impact response, and providing the basis for subsequent physical experiments.

5. Climbing Robot Experiments

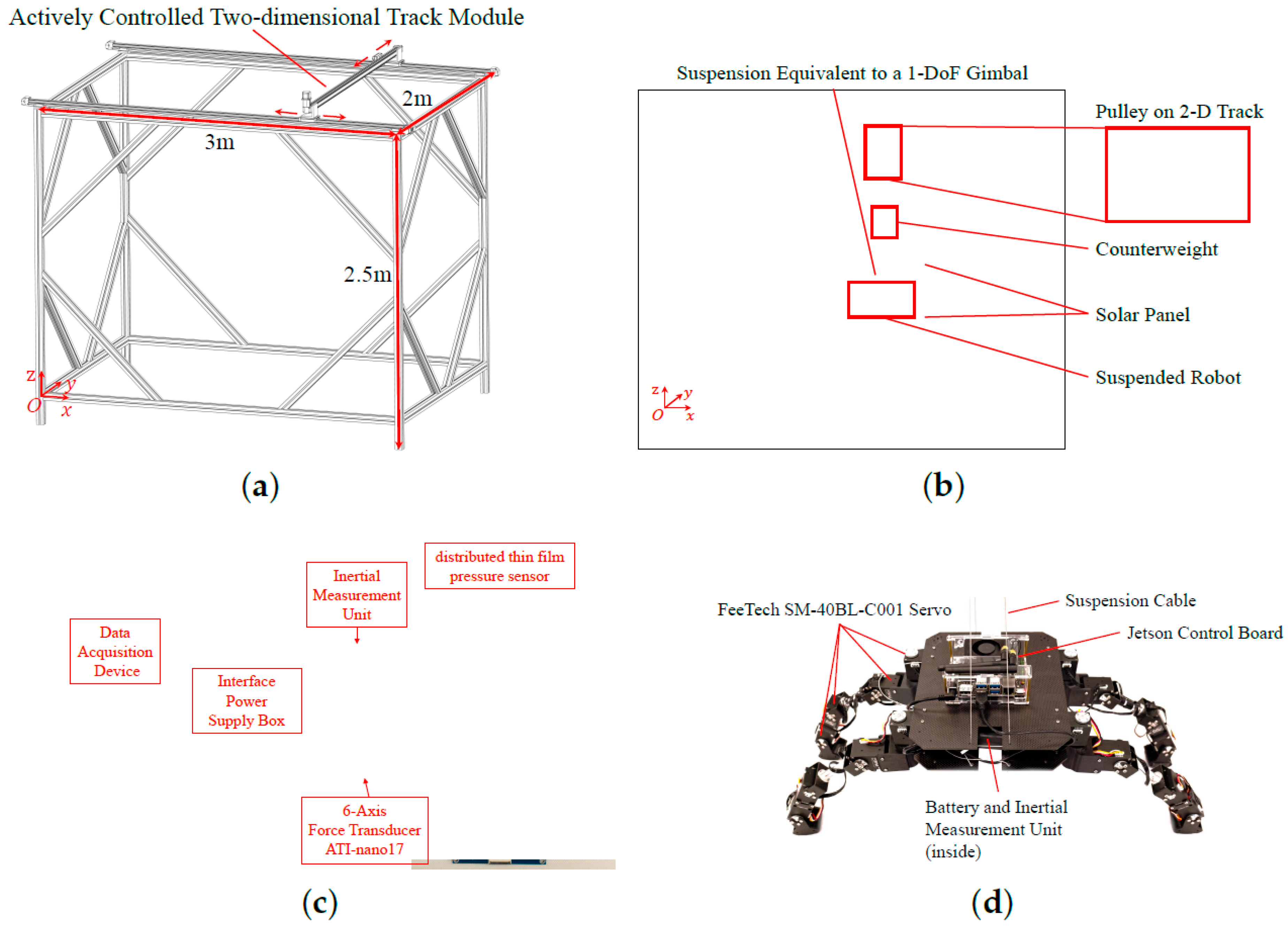
5.1. Experimental Setup

In order to evaluate the effectiveness of the presented control strategies in low-gravity conditions, a suspension-based gravity compensation system is designed and used in the experiments described in this section. The gravity compensation system suspends the robot’s body to offload its gravity [29]. The setup of the experiment stage is shown in Figure 14, which presents the supporting frame of the testing stage and the active-control two-dimensional track module that makes sure the suspension cable is always vertical during robots’ movements. Such a gravity compensation system has several limitations in terms of its performance and application. First, the suspension of the robot body does not offload the gravity of the legs. Second, the movement of the legs shifts the location of center of gravity (CG), leading to a rolling or pitching moment created by the suspension cable. Third, there is a vertical offset between suspension pivots and CG height, and thus the robot body’s rolling or pitching motions will shift the CG horizontally and again, causing misalignment between the suspension cable and CG. Despite these limitations, such a gravity compensation system is believed to provide a reasonable experiment setup in simulating a low-gravity condition if the robot body pitch and roll motion are mild and the leg motions are limited in terms of their speeds and ranges. In the experiment presented in this paper, the robot is commanded to move slowly; the robot leg is limited in terms of its range of motion; the thickness of the robot body is low in the vertical direction, and thus mild pitch and roll motion do not shift the CG significantly. In addition, the purpose of the experiments in this study is primarily to compare the behavior of different robot controllers under a given robot motion. Thus, the authors believe this gravity compensation system is sufficient to compare the controller difference in low-gravity conditions.

During the experiment, to evaluate individual performance such as adhesion and detachment for space climbing robots, solar panels with varying heights are arranged as the test environment. To test comprehensive performances, such as gait planning, vertically aligned solar panels are used. During the experiment, sensors capture the robot’s motion data. Specifically, joint torque sensors and joint encoders within the joint motors calculate the contact forces and foot-end positions during movement, with a sampling frequency of 1000 Hz. A six-dimension force sensor is used to measure normal/shear force during the adhesion/detachment process for the experiment, with a sampling frequency of 62.5 Hz. The accelerometer and gyroscope measure the robot’s posture, with a gyroscope precision of 0.01°/s and a sampling frequency of 200 Hz. A thin-film force sensor is employed to measure the contact force of the robot foot-end in the robot’s initial state, which helps evaluate the gravity offloading performance of the gravity compensation system.

5.2. Experiment for Examining Controller Function

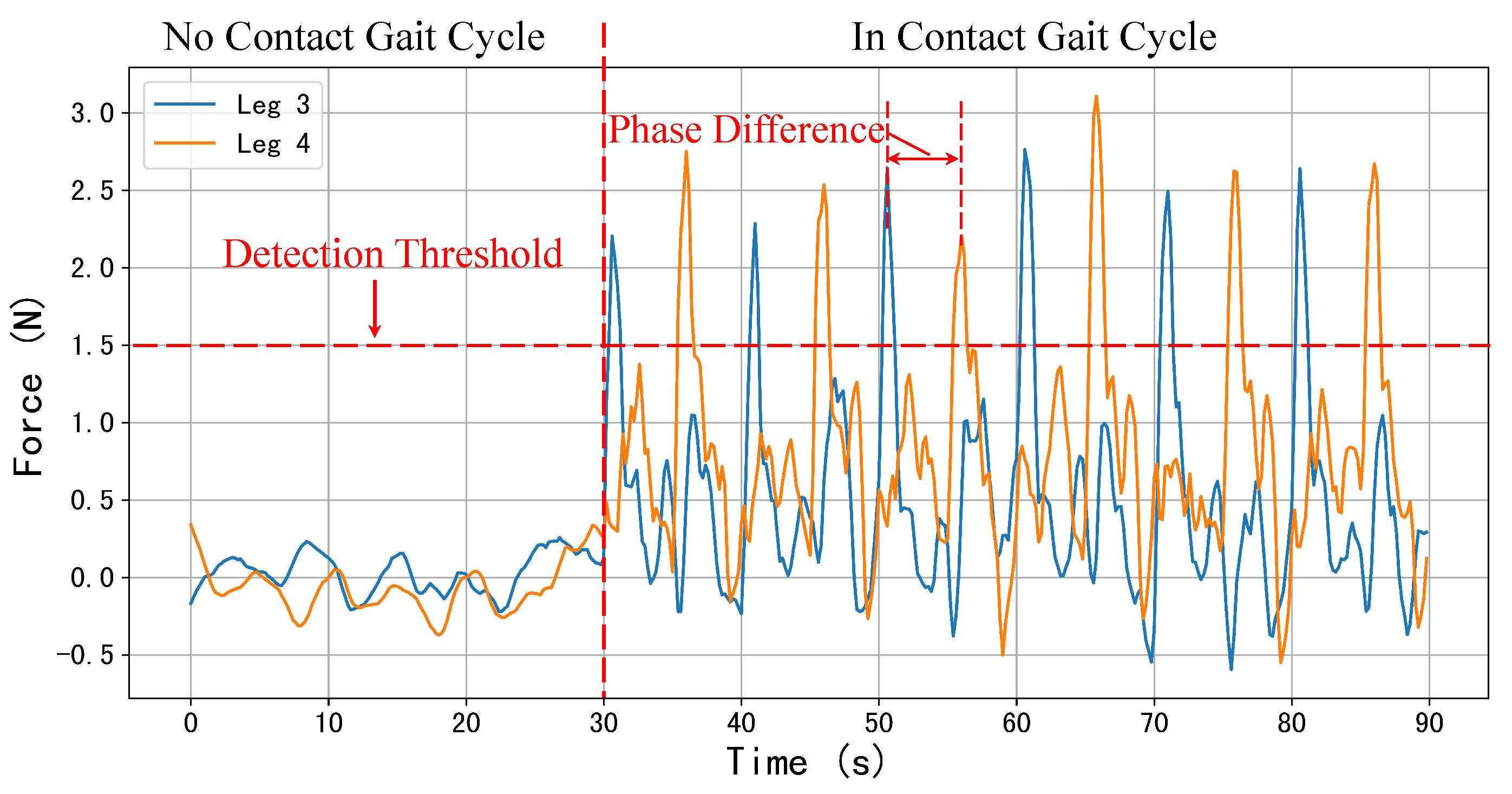
5.2.1. Contact Detection Test at the Foot

The variation in forces before and after contact determines whether the foot-end makes pre-press contact, serving as a criterion for subsequent control. To achieve this, the method introduced in Section 3.3 is used to map the joint torques to the foot-end contact force. The robot uses a 1–3–2–4 leg swinging sequence for movement. Legs 3 and 4, which have a gait phase difference of half a cycle, are used as examples to record changes in foot-end contact forces (Figure 15). Here, 0–30 s corresponds to the no-contact phase, while 30–90 s represents the in-contact phase. The pre-press contact detection threshold is set at 1.5 N.

In the no-contact phase, the contact forces of legs 3 and 4 fluctuate within $\left[\begin{array}{c}-0.3 \mathrm{N},0.3 \mathrm{N}\end{array}\right]$, with negative values indicating tensile forces. Considering sensor noise, the average foot-end force during the no-contact phase can be regarded as 0 N. At this time, there is no clear correlation between the peak force timings of the two legs. Upon contact, leg 3 first reaches a peak force of 2.2 N, exceeding the detection threshold of 1.5 N, indicating contact is established. Leg 4 reaches a peak of 2.7 N later, also establishing contact with the solar panel. The phase difference between the contact timings of legs 3 and 4 is approximately 5 s in the contact gait cycle.

5.2.2. Terrain Detection and Adaptation

By integrating a pre-press contact detection mechanism at the foot-end, the adhesion control performance of the climbing robot in microgravity is evaluated. As shown in Figure 16, after completing its swing phase, the robot determines whether to initiate the adhesion control based on the detected contact condition. If no contact is detected, this suggests an unexpected height discrepancy, as shown in Figure 16a. In this case, the robot further adjusts its control strategy based on force feedback, driving the foot-end to continue pressing down until adhesion is achieved. If contact is detected, it indicates the situation is as expected, and the robot proceeds with the next planned step.

During the adhesion process, different foot-end postures result in varying contact areas, leading to differences in adhesion force magnitudes. To maximize the adhesion force at the foot-end, this study incorporates both force sensors and IMU into the control framework, allowing the robot to adapt to different terrains. The test results (Figure 17) show that compared to adhesion without IMU attitude feedback, the proposed control method uses IMU feedback to keep the foot structure’s normal direction aligned with the contact surface throughout the adhesion phase, allowing the robot to adapt to different spans of solar panels.

5.2.3. Single-Leg Rotational Detachment Control Test

To verify the effectiveness of joint motor rotation control during the detachment process of foot-end adhesive materials, a comparative experiment is designed. Detachment forces are tested under two conditions: with and without rotational detachment for a single leg across three identical consecutive gait cycles. A six-dimension force sensor is utilized to measure both shear and normal forces during the detachment process (Figure 18), providing a comprehensive understanding of force distribution.

Under rotational detachment conditions, the rotational motion of the joint motor effectively disperses the local peeling stress of the adhesive material, reducing peak adhesion force and shifting the peak time earlier. As shown in Figure 19, the peak detachment normal force under rotational detachment is 3.93 N, averaging 65.5% lower than the non-rotational detachment peak normal force of 11.40 N, with the peak time occurring about half a cycle earlier. For shear forces, the peak force under non-rotational detachment was measured at 8.09 N, while rotational detachment reduced it to 6.88 N. The shear force during non-rotational detachment primarily arises from the foot-end being constrained to maintain alignment with the surface normal direction, leading to abrupt changes in force. Furthermore, the change in foot-end joint angle is modeled using a tanh function, which provides a smooth transition of angular motion. Compared to the non-rotational method, this approach mitigates large step changes in force and prevents oscillations.

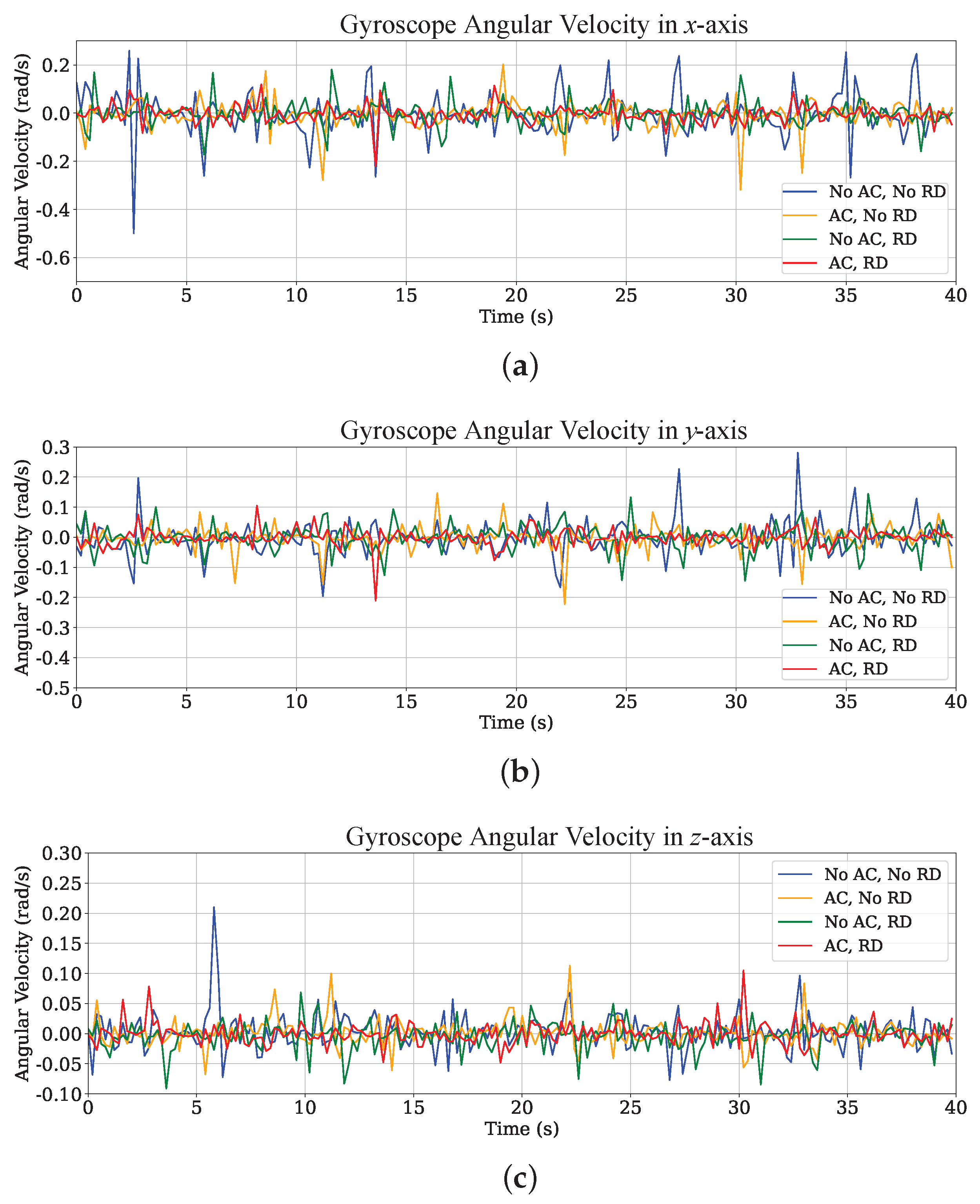
5.2.4. Impact of Compliance Controller on Supporting Leg Loadings

To test the effect of foot-end contact during the swing phase in a microgravity environment on the adhesion force of other supporting legs, a test scenario (Figure 20) is set up. The robot is suspended to offload gravity. The swinging leg makes early contact with a fixed-height obstacle, generating contact force, and the force at the foot-end of the supporting leg is measured using a six-dimension force sensor.

In this experiment, both normal and shear forces are analyzed under two conditions: without and with admittance control. Without admittance control, the normal and shear forces measured are 5.92 N and 5.18 N, respectively. With admittance control, these forces are reduced to 3.27 N and 3.36 N, respectively. The test results (Figure 21) reveal that the incorporation of an admittance controller effectively reduces both normal and shear forces by 44.8% and 35.1%, lowering the risk of excessive force buildup at the supporting leg. The phase cycle remains unchanged, demonstrating that an admittance controller based on position control reduces the need for foot-end adhesion force, enabling stable multi-leg motion of the space climbing robot.

5.3. Comprehensive Climbing Tests on the Vertical Surface

To assess the stability during climbing, a solar panel aligned in the vertical direction is selected as the test environment (Figure 14), testing the effects of admittance control (AC) and rotational detachment (RD) on the robot’s overall movement. The test results, as shown in Figure 22, indicate that after adopting the compliant control method proposed in this paper, the robot’s foot-end successfully achieves adhesion and detachment on the solar panel, ensuring the stability of the entire robot’s movement. The robot climbs 60 cm along the plumb direction within 55 s, resulting in a climbing speed of 1.1 cm/s.

To further evaluate the stability impact, body angular velocity fluctuations are selected as a quantitative evaluation criterion for body stability. The baseline control strategy, without admittance control and rotating detachment, is tested for body oscillations due to adhesion/detachment, with IMU measurements of angular velocity changes, as shown in Figure 23.

The peak, valley, and standard deviation of angular velocities under different methods are statistically analyzed, as shown in

Table 2. Angular velocity change during climbing in x-axis.

Method	Peak Value (rad/s)	Min Value (rad/s)	Standard Deviation
Baseline	0.259	−0.499	0.089
AC	0.202	−0.318	0.056
RD	0.181	−0.173	0.052
AC & RD	0.120	−0.221	0.037

,

Table 3. Angular velocity change during climbing in y-axis.

Method	Peak Value (rad/s)	Min Value (rad/s)	Standard Deviation
Baseline	0.281	−0.196	0.055
AC	0.146	−0.223	0.040
RD	0.145	−0.145	0.044
AC & RD	0.104	−0.210	0.029

and

Table 4. Angular velocity change during climbing in z-axis.

Method	Peak Value (rad/s)	Min Value (rad/s)	Standard Deviation
Baseline	0.210	−0.077	0.030
AC	0.113	−0.068	0.022
RD	0.068	−0.091	0.023
AC & RD	0.105	−0.048	0.018

. The admittance control and rotational detachment strategies reduce the angular velocity fluctuation peaks along the $xyz$-axes by 58.2%, 47.3%, and 40.0%, respectively, effectively reducing the robot’s motion oscillations, improving its motion stability and validating the effectiveness of the proposed method.

5.4. Discussion

Research on space climbing robots using bio-inspired dry adhesion materials has covered various aspects, including adhesion material selection, motion trajectory planning, gait planning, and stability control. This paper addresses the issue of single-leg motion during adhesion/detachment affecting overall robot stability. By equipping joints with torque sensors to detect foot-end pre-press contact and introducing adhesion and detachment phases, we integrate a tanh function and admittance control to achieve smooth and stable robot control. Experiments demonstrate that this method effectively prevents oscillations caused by step responses in a microgravity unstructured environment. Compared to conventional methods, the proposed approach reduces the robot’s angular velocity fluctuations across all three axes by at least 40%.

6. Conclusions

This paper addresses the challenges faced by spaceborne robots utilizing dry adhesion materials for climbing in microgravity environments. These challenges include uncertain adhesion establishment, unexpected detachment, and instability exhibited in the robot’s motion during the adhesion and detachment phases. To overcome these issues, we propose a set of control methods that employ coordinated force–position compliance control for each leg. An adhesion perception approach and a novel rotational detaching motion have been introduced to minimize the required control effort during attaching and detaching actions, thus reducing the possibility of unexpected detachment. Single-leg simulations and robot experiments have been conducted to evaluate the merit of the proposed methods. The experimental results suggest that the rotational detaching motion significantly eliminated the force overshoot at the instance of detachment, effectively reducing the normal force by 65.5%, thus greatly improving the robot’s stability and reducing the required control effort on other feet. The merits of using compliant control were similar, reducing the possibility of unexpected detachment by significantly reducing the unnecessarily aggressive control actions and resultant adhesion normal and shear forces by 44.8% and 35.1%, respectively. Climbing tests in a simulated microgravity environment suggest that the proposed methods reduce robot body waggle by at least 40%. Future research could focus on further optimizing adhesion detection methods and refining admittance control parameters to enhance the robot’s adaptability and reliability in more complex space environments.